Mechanoelectrical Effects in Natural Fiber-Reinforced Polymers as Structural Health Monitoring
Abstract
1. Introduction
2. Materials and Methods
2.1. Manufacturing of Flax Fiber-Reinforced Polymer Samples
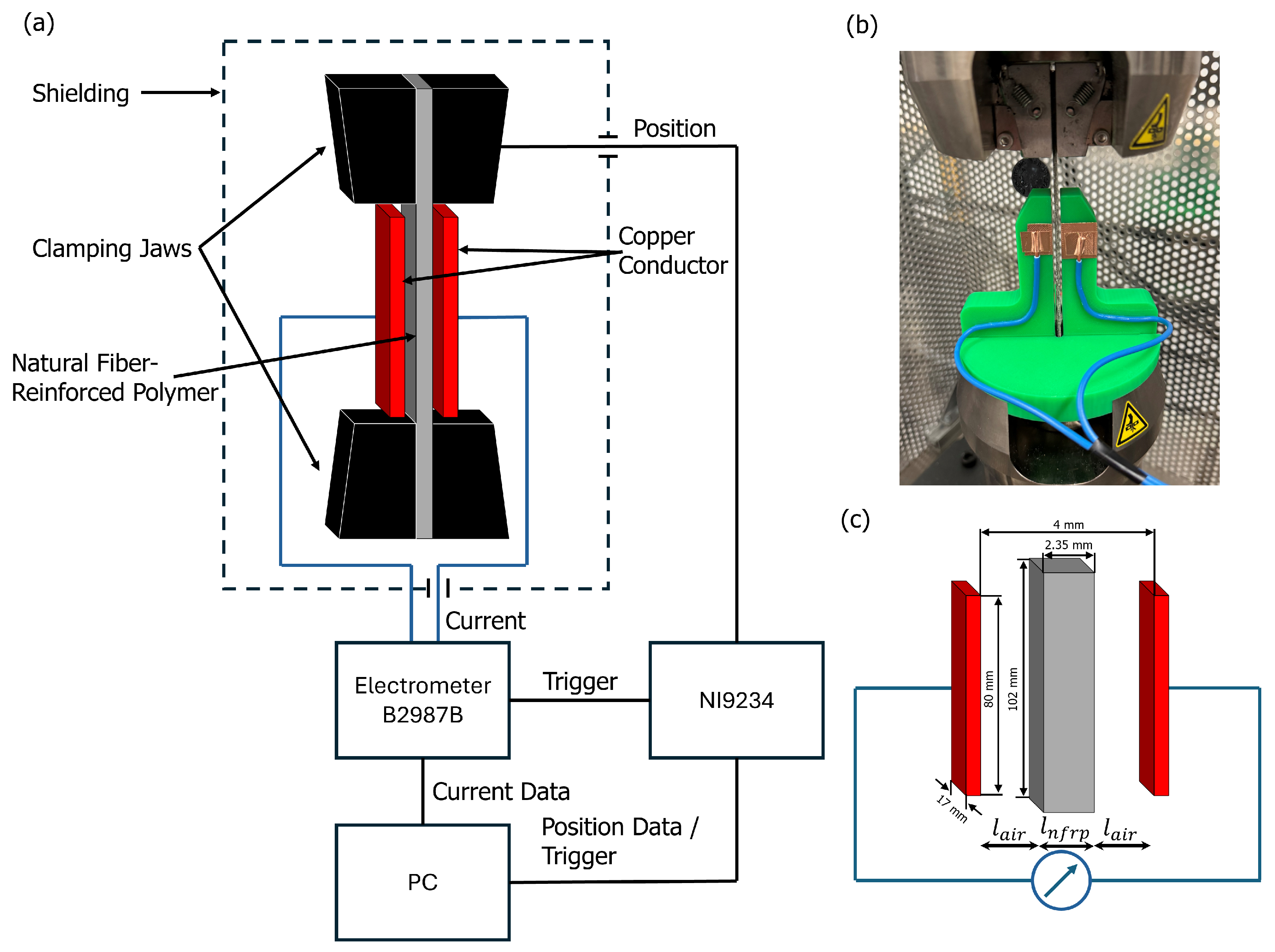
2.2. Dynamic Investigation of the Composite Material
2.3. Electrical Measurement Setup
2.4. Derivation of Composite Material Polarization
2.5. Procedure Before the Experiment
2.6. Data Processing
3. Results and Discussion
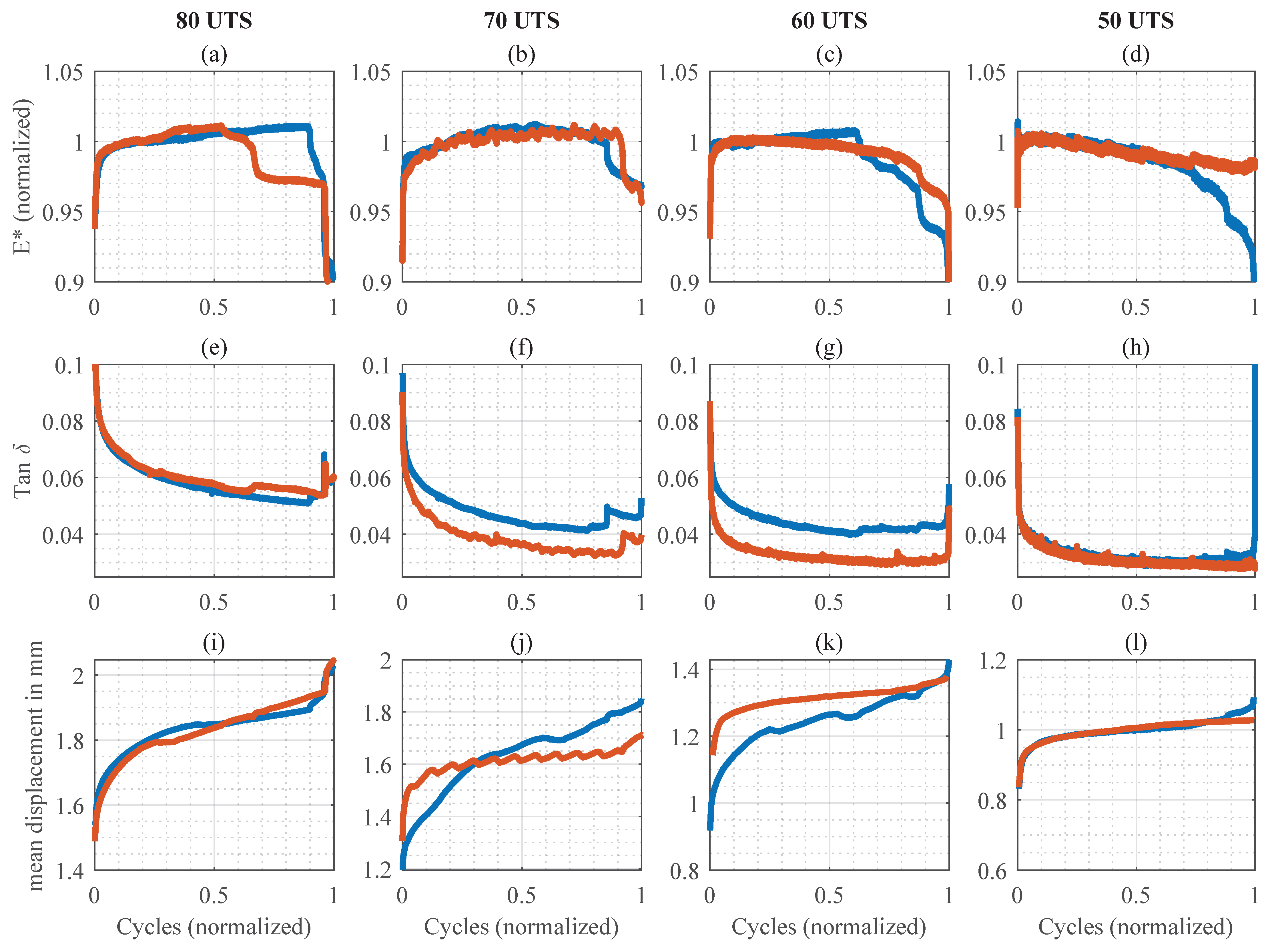
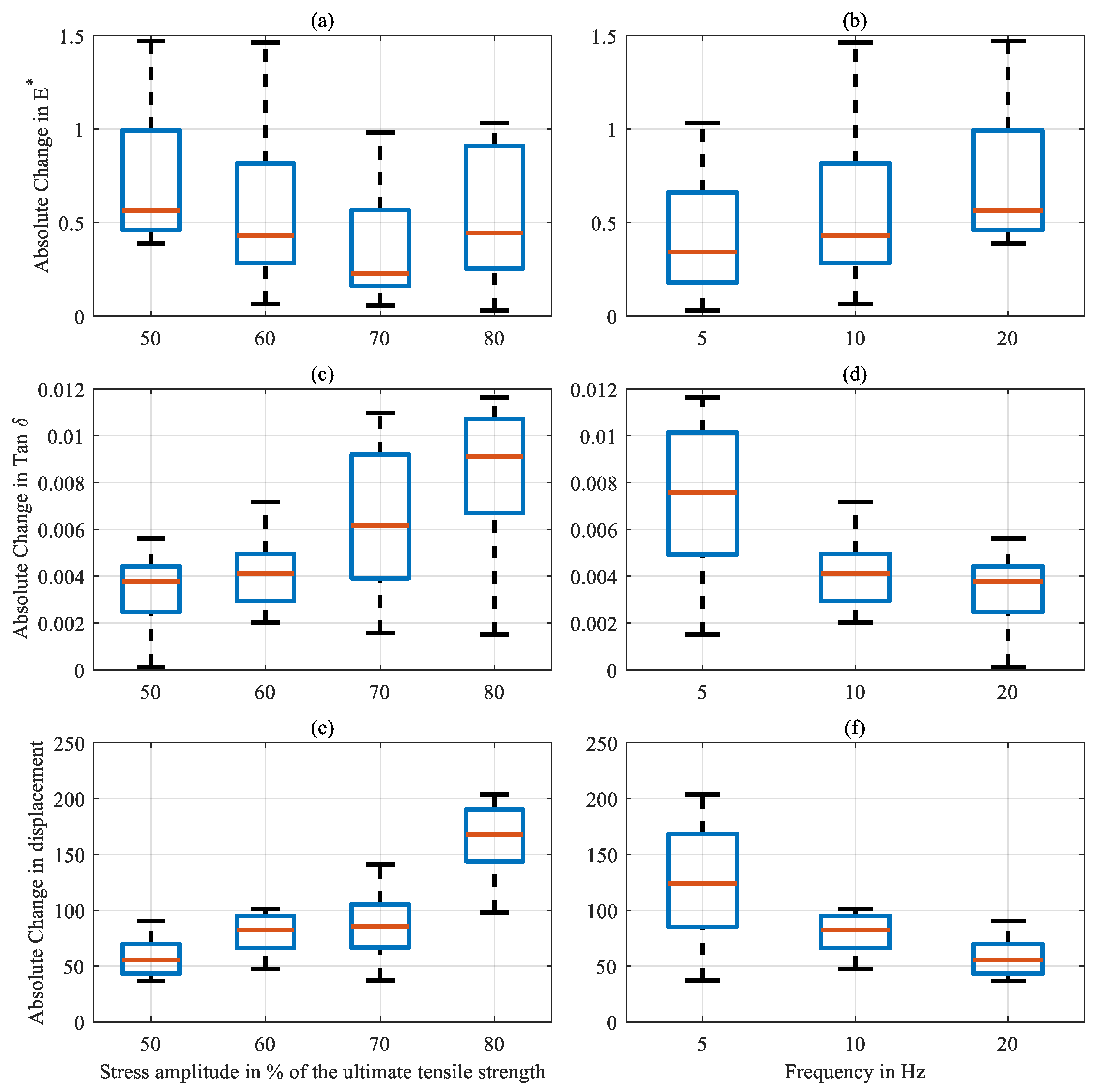
3.1. Mechanical Analysis
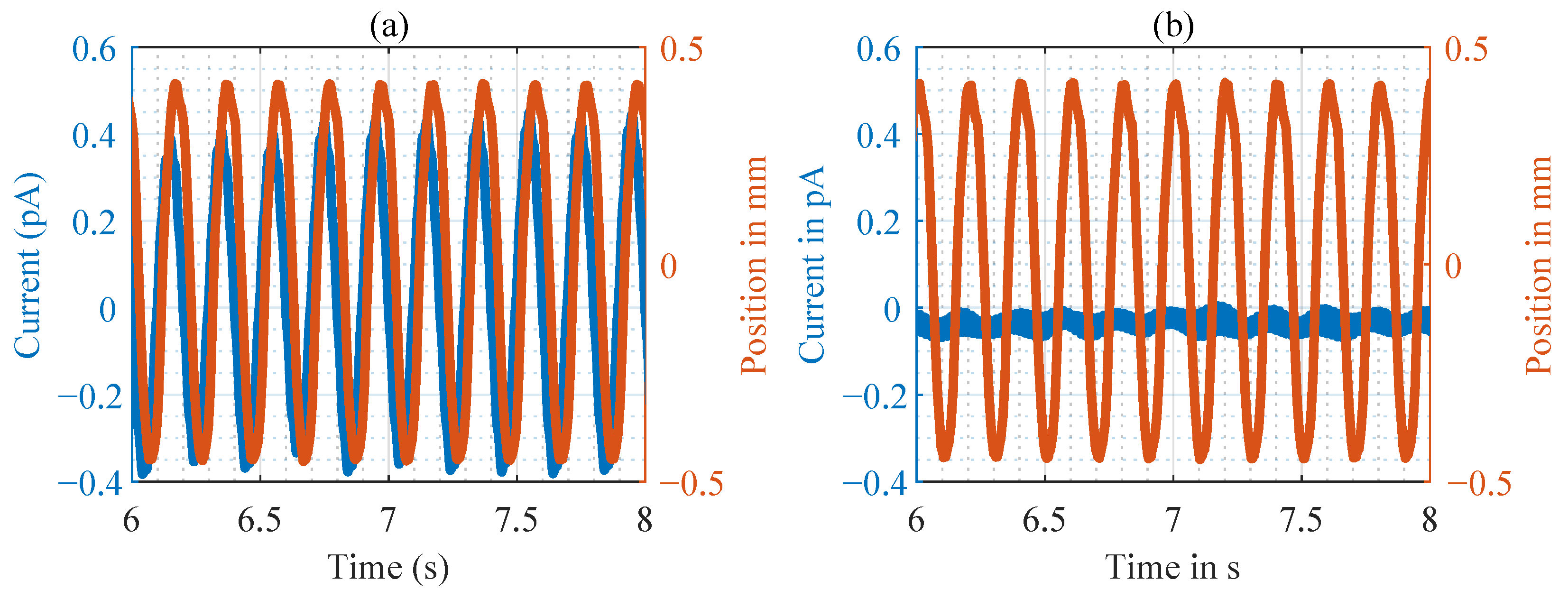
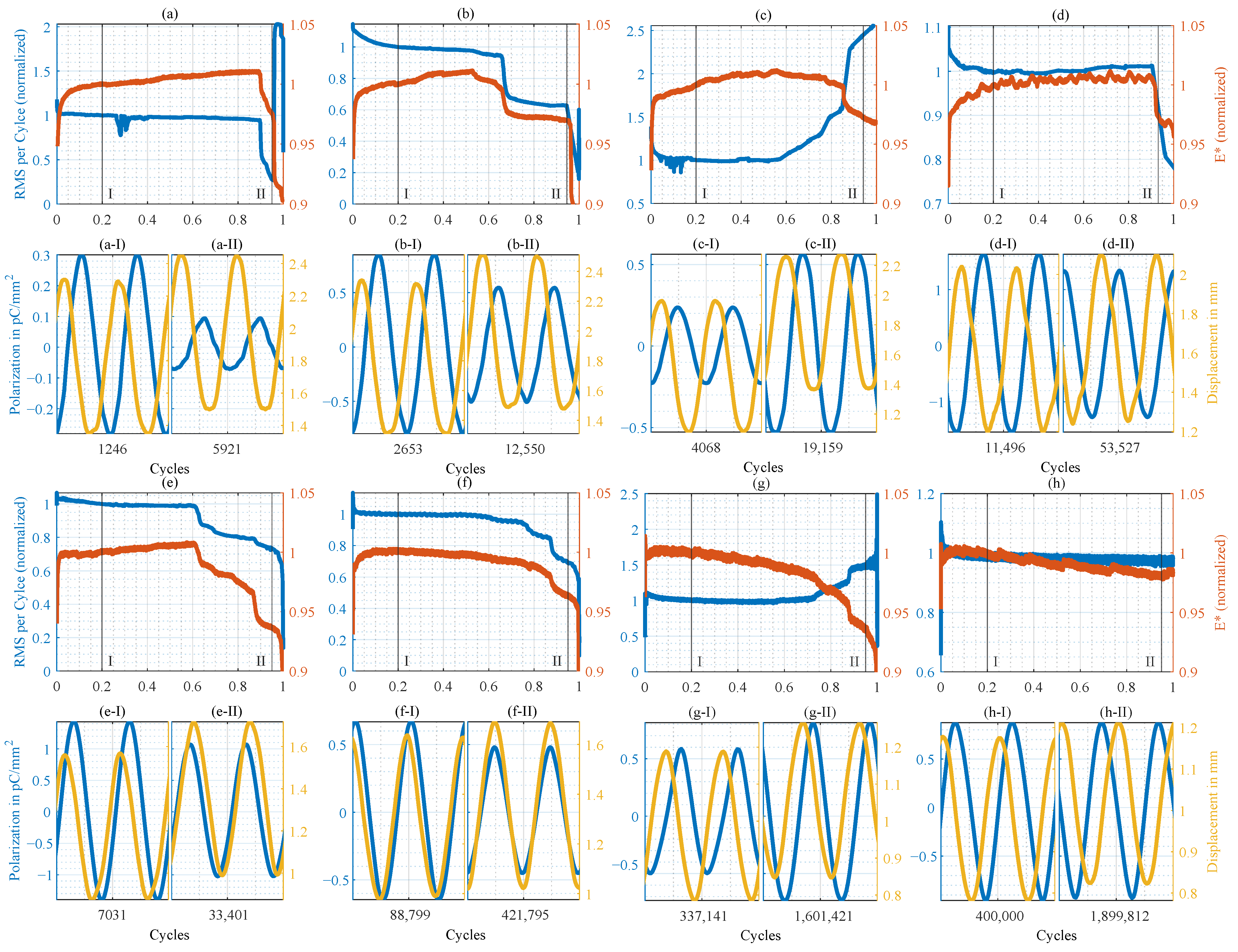
3.2. Mechanoelectrial Analysis
3.3. Cause of the Electrical Effect
3.4. Future Challenges
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Measurement of the Permittivity of Natural Fiber-Reinforced Polymers at Low Frequencies
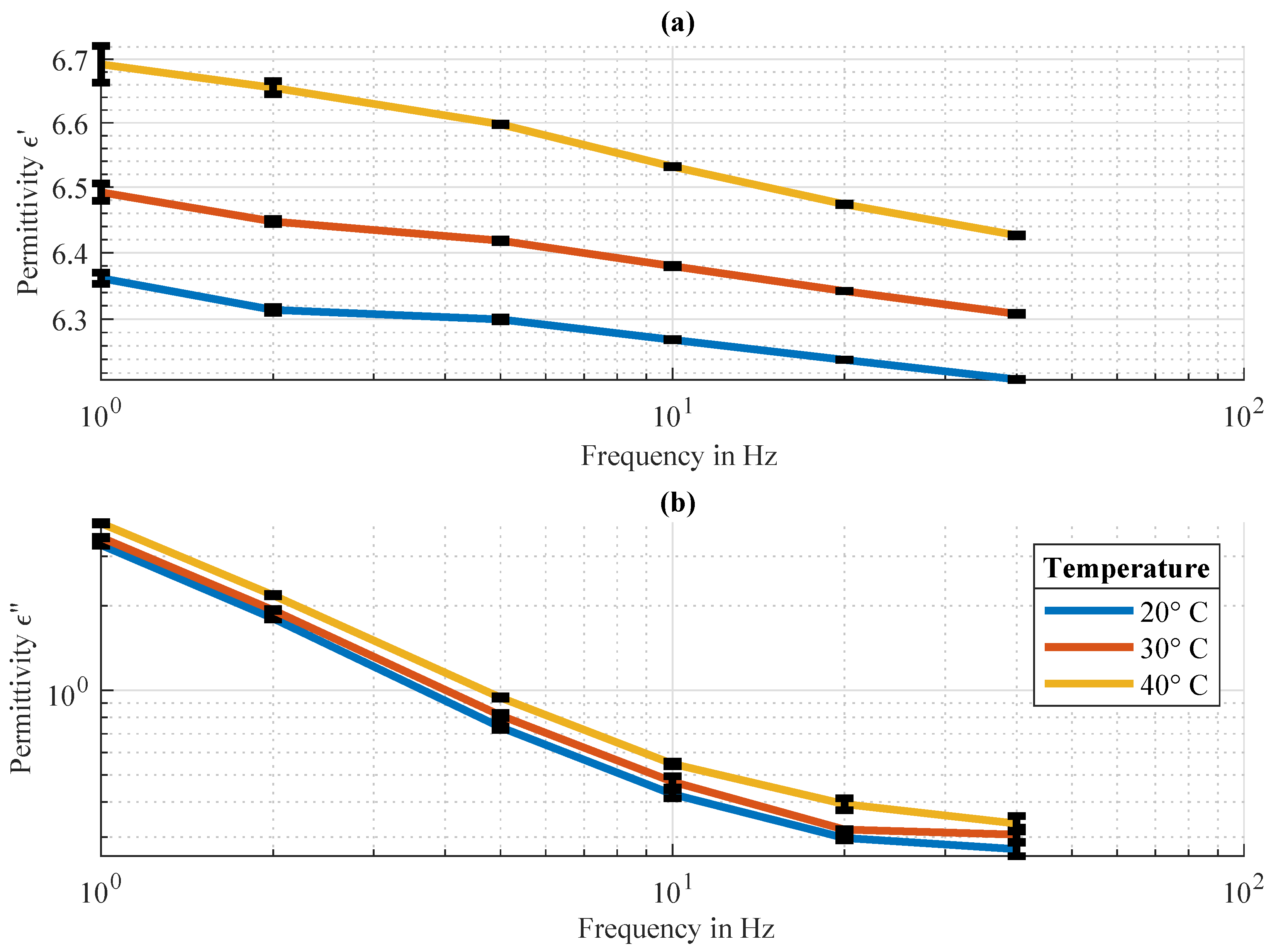
| UTS in % | Excitation Frequency (Hz) | Temperature ( °C) | ||
|---|---|---|---|---|
| 80 | 5 | 40 | 6.6 | 0.94 |
| 70 | 5 | 40 | 6.6 | 0.94 |
| 60 | 10 | 40 | 6.53 | 0.55 |
| 50 | 20 | 40 | 6.47 | 0.39 |
Appendix B. Simulation of Mechanoelectrical Effects with Variable Stiffness
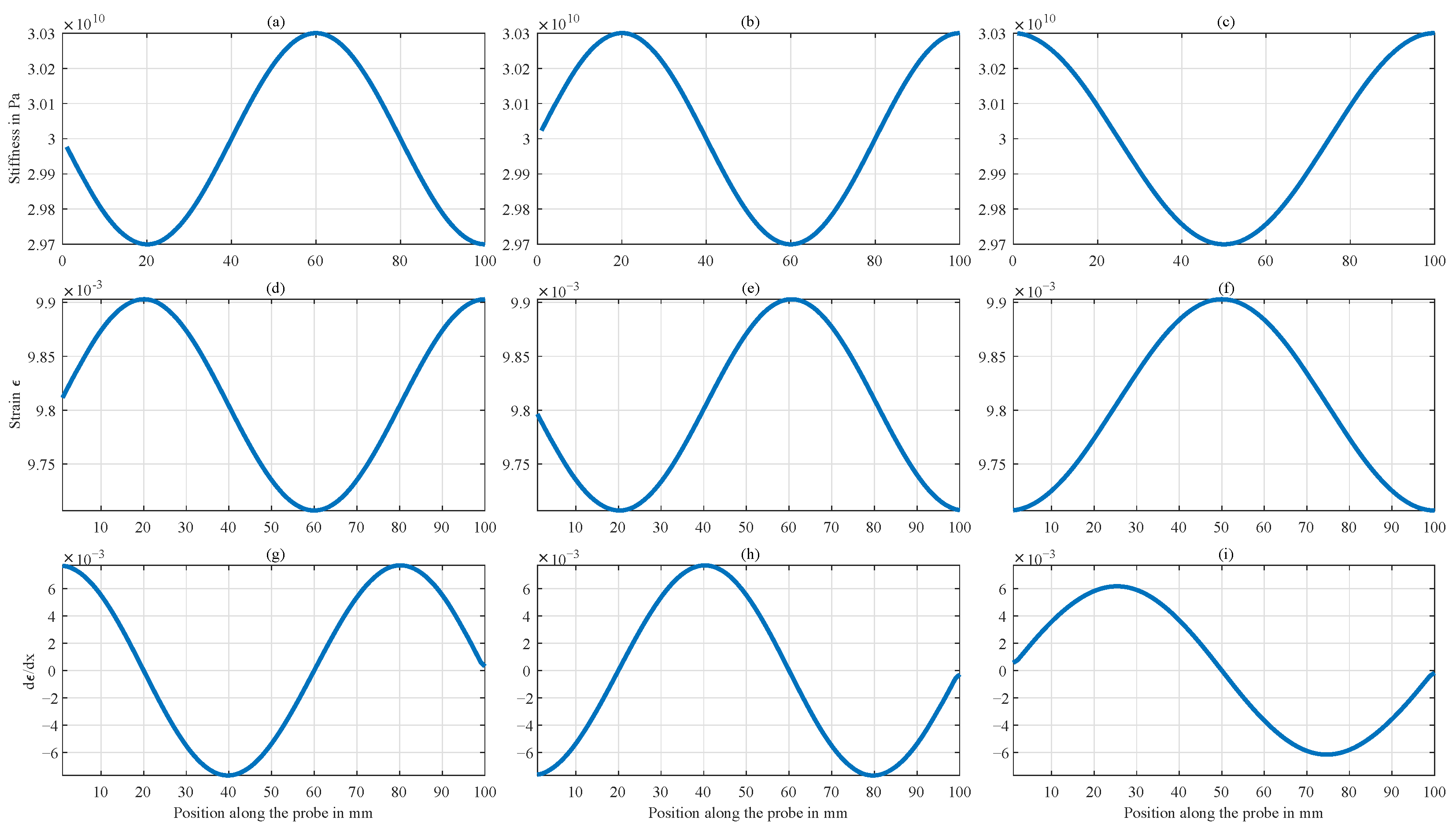
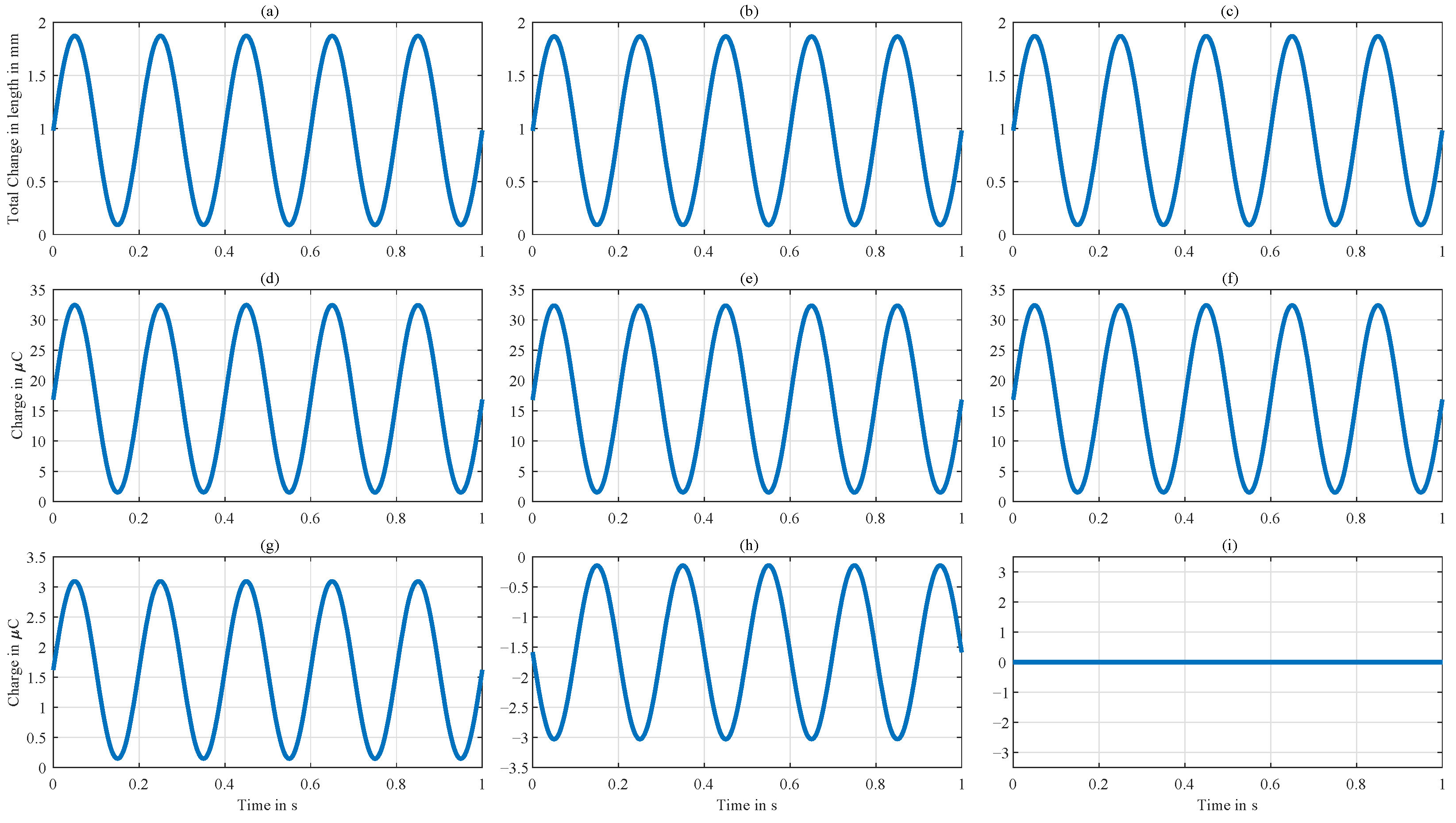
Appendix C. Values Used for Normalization
| Specimen | E* in MPa | RMS Polarization | Cycles |
|---|---|---|---|
| P04 P1 | 20,644.69 | 0.2073 | 6.233 |
| P04 P2 | 21,061.19 | 0.5786 | 13.268 |
| P06 P1 | 20,927.75 | 0.1669 | 20.344 |
| P07 P5 | 21,819.09 | 1.1318 | 57.482 |
| P09 P4 | 23,372.05 | 0.9952 | 35.159 |
| P09 P5 | 23,903.58 | 0.4608 | 443.995 |
| P10 P6 | 22,948.86 | 0.3654 | 1685.707 |
| P11 P3 | 23,072.00 | 0.6357 | 2000.000 |
References
- de Beus, N.; Carus, M.; Barth, M. Carbon Footprint and Sustainability of Different Natural Fibres for Biocomposites and Insulation Material: Study Providing Data for the Automotive and Insulation Industry. Available online: https://renewable-carbon.eu/publications/product/carbon-footprint-and-sustainability-of-different-natural-fibres-for-biocomposites-and-insulation-material-%E2%88%92-full-version-update-2019/ (accessed on 1 June 2025).
- Summerscales, J.; Dissanayake, N.P.; Virk, A.S.; Hall, W. A review of bast fibres and their composites. Part 1—Fibres as reinforcements. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1329–1335. [Google Scholar] [CrossRef]
- Wambua, P.; Ivens, J.; Verpoest, I. Natural fibres: Can they replace glass in fibre reinforced plastics? Compos. Sci. Technol. 2003, 63, 1259–1264. [Google Scholar] [CrossRef]
- Joshi, S.; Drzal, L.; Mohanty, A.; Arora, S. Are natural fiber composites environmentally superior to glass fiber reinforced composites? Compos. Part A Appl. Sci. Manuf. 2004, 35, 371–376. [Google Scholar] [CrossRef]
- Andersons, J.; Sparnins, E.; Joffe, R.; Wallstrom, L. Strength distribution of elementary flax fibres. Compos. Sci. Technol. 2005, 65, 693–702. [Google Scholar] [CrossRef]
- Ren, B.; Mizue, T.; Goda, K.; Noda, J. Effects of fluctuation of fibre orientation on tensile properties of flax sliver-reinforced green composites. Compos. Struct. 2012, 94, 3457–3464. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef]
- Maier, C.; Koch, K.P.; Fischer, G. Measuring Deformation in Natural Fiber-Reinforced Polymer Using Mechanoelectrical Effect. IEEE Sens. Lett. 2024, 8, 2502504. [Google Scholar] [CrossRef]
- Hassani, S.; Mousavi, M.; Gandomi, A.H. Structural Health Monitoring in Composite Structures: A Comprehensive Review. Sensors 2021, 22, 153. [Google Scholar] [CrossRef]
- Baron, P.; Lenz, P.; Wittmann, A.; Fischer, G. Integrity-Sensing Based on Surface Roughness of Copper Conductors for Future Use in Natural Fiber Composites. IEEE Sens. Lett. 2021, 5, 1–4. [Google Scholar] [CrossRef]
- Baron, P. Entwicklung Eines Mechano-Elektrischen Sensorelements zur Strukturellen Bauteilüberwachung von Naturfaserverbundwerkstoffen Mittels Hochfrequenter Wechselströme; FAU Forschungen Reihe B: Erlangen, Germany; FAU University Press: Erlangen, Germany, 2024; Volume 46. [Google Scholar]
- Wen, J.; Xia, Z.; Choy, F. Damage detection of carbon fiber reinforced polymer composites via electrical resistance measurement. Compos. Part B Eng. 2011, 42, 77–86. [Google Scholar] [CrossRef]
- Brown, S.C.; Robert, C.; Koutsos, V.; Ray, D. Methods of modifying through-thickness electrical conductivity of CFRP for use in structural health monitoring, and its effect on mechanical properties—A review. Compos. Part A Appl. Sci. Manuf. 2020, 133, 105885. [Google Scholar] [CrossRef]
- Burkov, M.; Eremin, A. Hybrid CFRP/SWCNT Composites with Enhanced Electrical Conductivity and Mechanical Properties. J. Mater. Eng. Perform. 2018, 27, 5984–5991. [Google Scholar] [CrossRef]
- Du, J.; Zeng, J.; Wang, H.; Ding, H.; Wang, H.; Bi, Y. Using acoustic emission technique for structural health monitoring of laminate composite: A novel CNN-LSTM framework. Eng. Fract. Mech. 2024, 309, 110447. [Google Scholar] [CrossRef]
- Ghadarah, N.; Ayre, D. A Review on Acoustic Emission Testing for Structural Health Monitoring of Polymer-Based Composites. Sensors 2023, 23, 6945. [Google Scholar] [CrossRef]
- Masmoudi, S.; El Mahi, A.; Turki, S. Fatigue behaviour and structural health monitoring by acoustic emission of E-glass/epoxy laminates with piezoelectric implant. Appl. Acoust. 2016, 108, 50–58. [Google Scholar] [CrossRef]
- Ghezzo, F.; Huang, Y.; Nemat-Nasser, S. Onset of Resin Micro-Cracks in Unidirectional Glass Fiber Laminates with Integrated SHM Sensors: Experimental Results. Struct. Health Monit. 2009, 8, 477–491. [Google Scholar] [CrossRef]
- Tuloup, C.; Harizi, W.; Aboura, Z.; Meyer, Y. Integration of piezoelectric transducers (PZT and PVDF) within polymer-matrix composites for structural health monitoring applications: New success and challenges. Int. J. Smart Nano Mater. 2020, 11, 343–369. [Google Scholar] [CrossRef]
- Niezrecki, C.; Baqersad, J.; Sabato, A. Digital Image Correlation Techniques for NDE and SHM. Mech. Eng. Publ. 2018, 111, 1–46. [Google Scholar] [CrossRef]
- Yu, B.; Blanc, R.; Soutis, C.; Withers, P.J. Evolution of damage during the fatigue of 3D woven glass-fibre reinforced composites subjected to tension–tension loading observed by time-lapse X-ray tomography. Compos. Part A Appl. Sci. Manuf. 2016, 82, 279–290. [Google Scholar] [CrossRef]
- Hung, Y.Y.; Yang, L.X.; Huang, Y.H. (Eds.) Non-Destructive Evaluation (NDE) of Composites: Digital Shearography; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Ye, X.W.; Dong, C.Z.; Liu, T. A Review of Machine Vision-Based Structural Health Monitoring: Methodologies and Applications. J. Sens. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Payawal, J.M.G.; Kim, D.K. Image-Based Structural Health Monitoring: A Systematic Review. Appl. Sci. 2023, 13, 968. [Google Scholar] [CrossRef]
- Shah, D.U. Developing plant fibre composites for structural applications by optimising composite parameters: A critical review. J. Mater. Sci. 2013, 48, 6083–6107. [Google Scholar] [CrossRef]
- Lotfi, A.; Li, H.; Dao, D.V.; Prusty, G. Natural fiber–reinforced composites: A review on material, manufacturing, and machinability. J. Thermoplast. Compos. Mater. 2021, 34, 238–284. [Google Scholar] [CrossRef]
- Bcomp Ltd. ampliTexTM; Bcomp Ltd.: Fribourg, Switzerland, 2021. [Google Scholar]
- Rask, M.; Madsen, B. Twisting of fibres in yarns for natural fibre composites. In Proceedings of the 18th International Conference on Composite Materials, ICCM18, Jeju, Republic of Korea, 21–26 August 2011. [Google Scholar]
- Baley, C.; Gomina, M.; Breard, J.; Bourmaud, A.; Drapier, S.; Ferreira, M.; Le Duigou, A.; Liotier, P.J.; Ouagne, P.; Soulat, D.; et al. Specific features of flax fibres used to manufacture composite materials. Int. J. Mater. Form. 2019, 12, 1023–1052. [Google Scholar] [CrossRef]
- Entropy Resins. 305—Compression Moulding Epoxy; Entropy Resins: Bay City, MI, USA, 2024. [Google Scholar]
- Entropy Resins. CPF Fast; Entropy Resins: Bay City, MI, USA, 2024. [Google Scholar]
- Kern & Sohn. Kern Digitalscale EMB 1000-2; Kern & Sohn: Balingen, Germany, 2024. [Google Scholar]
- Muthuvel, B.; Bhattacharyya, D.; Bickerton, S. Development of innovative flow visualisation methods to investigate the stages of Wet Compression Moulding (WCM) process. IOP Conf. Ser. Mater. Sci. Eng. 2020, 912, 052013. [Google Scholar] [CrossRef]
- DIN EN ISO 527-4; Plastics-Determination of Tensile Properties, Part 4: Test Conditions for Isotropic and Orthotropic Fibre-Reinforced Plastic Composites. ISO: Geneva, Switzerland, 2023.
- BS ISO 13003; Fibre-Reinforced Plastics. Determination of Fatigue Properties Under Cyclic Loading Conditions. ISO: Geneva, Switzerland, 2004.
- ASTM D 3039; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D 3479; Standard Test Method for Tension-Tension Fatigue of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2019.
- Roe, P.J.; Ansell, M.P. Jute-reinforced polyester composites. J. Mater. Sci. 1985, 20, 4015–4020. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Yu, T.; Li, Q.; Li, Z. Anisotropic behaviors of moisture absorption and hygroscopic swelling of unidirectional flax fiber reinforced composites. Compos. Struct. 2022, 297, 115941. [Google Scholar] [CrossRef]
- Liang, S.; Gning, P.B.; Guillaumat, L. A comparative study of fatigue behaviour of flax/epoxy and glass/epoxy composites. Compos. Sci. Technol. 2012, 72, 535–543. [Google Scholar] [CrossRef]
- Jeannin, T.; Gabrion, X.; Ramasso, E.; Placet, V. About the fatigue endurance of unidirectional flax-epoxy composite laminates. Compos. Part B Eng. 2019, 165, 690–701. [Google Scholar] [CrossRef]
- El Sawi, I.; Fawaz, Z.; Zitoune, R.; Bougherara, H. An investigation of the damage mechanisms and fatigue life diagrams of flax fiber-reinforced polymer laminates. J. Mater. Sci. 2014, 49, 2338–2346. [Google Scholar] [CrossRef]
- Katunin, A.; Wachla, D.; Santos, P.; Reis, P.N. Fatigue life assessment of hybrid bio-composites based on self-heating temperature. Compos. Struct. 2023, 304, 116456. [Google Scholar] [CrossRef]
- Jouenne, J.B.; Barbier, D.; Hounkpati, V.; Cauret, L.; Vivet, A. Influence of flax fibers on the curing kinetics of bio-based epoxy resin. J. Mater. Sci. 2024, 59, 12418–12432. [Google Scholar] [CrossRef]
- Vyazovkin, S. Isoconversional Kinetics of Polymers: The Decade Past. Macromol. Rapid Commun. 2017, 38, 1600615. [Google Scholar] [CrossRef]
- Mahboob, Z.; Bougherara, H. Fatigue of flax-epoxy and other plant fibre composites: Critical review and analysis. Compos. Part A Appl. Sci. Manuf. 2018, 109, 440–462. [Google Scholar] [CrossRef]
- Jeannin, T.; Berges, M.; Gabrion, X.; Léger, R.; Person, V.; Corn, S.; Piezel, B.; Ienny, P.; Fontaine, S.; Placet, V. Influence of hydrothermal ageing on the fatigue behaviour of a unidirectional flax-epoxy laminate. Compos. Part B Eng. 2019, 174, 107056. [Google Scholar] [CrossRef]
- Liang, S.; Gning, P.B.; Guillaumat, L. Properties evolution of flax/epoxy composites under fatigue loading. Int. J. Fatigue 2014, 63, 36–45. [Google Scholar] [CrossRef]
- Carvalho, G.B.; Canevarolo, S.; de Sousa, J.A. Correlation of fatigue behavior and dynamic mechanical properties of hybrid composites of polypropylene/short glass fibers/hollow glass beads. J. Thermoplast. Compos. Mater. 2023, 36, 2233–2259. [Google Scholar] [CrossRef]
- El Archi, Y.; Lahellec, N.; Lejeunes, S.; Jouan, A.; Tranquart, B. Multiscale simulation and experimental analysis of damping in CFRP structures containing rubber. Compos. Struct. 2022, 289, 115456. [Google Scholar] [CrossRef]
- Saba, N.; Jawaid, M.; Alothman, O.Y.; Paridah, M.T. A review on dynamic mechanical properties of natural fibre reinforced polymer composites. Constr. Build. Mater. 2016, 106, 149–159. [Google Scholar] [CrossRef]
- Surya Nagendra, P.; Prasad, V.; Ramji, K. A Study on Dynamic Mechanical Analysis of Natural Nano Banana Particle Filled Polymer Matrix Composites. Mater. Today Proc. 2017, 4, 9081–9086. [Google Scholar] [CrossRef]
- Idicula, M.; Malhotra, S.K.; Joseph, K.; Thomas, S. Dynamic mechanical analysis of randomly oriented intimately mixed short banana/sisal hybrid fibre reinforced polyester composites. Compos. Sci. Technol. 2005, 65, 1077–1087. [Google Scholar] [CrossRef]
- Kaiser, K.L.; Palmer, K.I. Cable transient voltages due to microphonics. J. Electrost. 2007, 65, 723–727. [Google Scholar] [CrossRef]
- Tian, D.; Jeong, D.Y.; Fu, Z.; Chu, B. Flexoelectric Effect of Ferroelectric Materials and Its Applications. Actuators 2023, 12, 114. [Google Scholar] [CrossRef]
- Wang, H.; Adamski, N.; Mu, S.; van de Walle, C.G. Piezoelectric effect and polarization switching in Al1-xScxN. J. Appl. Phys. 2021, 130, 104101. [Google Scholar] [CrossRef]
- Zhang, H.X.; Wang, P.F.; Yao, C.G.; Chen, S.P.; Cai, K.D.; Shi, F.N. Recent advances of ferro-/piezoelectric polarization effect for dendrite-free metal anodes. Rare Met. 2023, 42, 2516–2544. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics, 1st ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Kersani, M.; Lomov, S.V.; van Vuure, A.W.; Bouabdallah, A.; Verpoest, I. Damage in flax/epoxy quasi-unidirectional woven laminates under quasi-static tension. J. Compos. Mater. 2015, 49, 403–413. [Google Scholar] [CrossRef]
- Saadati, Y.; Lebrun, G.; Chatelain, J.F.; Beauchamp, Y. Experimental investigation of failure mechanisms and evaluation of physical/mechanical properties of unidirectional flax–epoxy composites. J. Compos. Mater. 2020, 54, 2781–2801. [Google Scholar] [CrossRef]
- Karray, M.; Triki, A.; Poilâne, C.; Picart, P.; Gargouri, M. Dielectric relaxation phenomena in flax fibers composite. Fibers Polym. 2016, 17, 88–96. [Google Scholar] [CrossRef]
- Triki, A.; Karray, M.; Poilâne, C.; Picart, P.; Gargouri, M. Dielectric analysis of the interfacial polarization of alkali treated woven flax fibers reinforced epoxy composites. J. Electrost. 2015, 76, 67–72. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Zheng, Z. Effect of physiochemical structure on energy absorption properties of plant fibers reinforced composites: Dielectric, thermal insulation, and sound absorption properties. Compos. Commun. 2018, 10, 163–167. [Google Scholar] [CrossRef]
- Baron, P.; Lenz, P.; Koch, K.P.; Wittmann, A.; Fischer, G. Dielectric properties of unidirectional and biaxial flax/epoxy composites at frequencies up to 1 GHz. Mater. Today Commun. 2023, 36, 106656. [Google Scholar] [CrossRef]
- Ueki, Y.; Lilholt, H.; Madsen, B. Stiffening effect of fatigue and creep loading in unidirectional flax fibre/epoxy composites. IOP Conf. Ser. Mater. Sci. Eng. 2018, 388, 012018. [Google Scholar] [CrossRef]
- Kek, T.; Potočnik, P.; Misson, M.; Bergant, Z.; Sorgente, M.; Govekar, E.; Šturm, R. Characterization of Biocomposites and Glass Fiber Epoxy Composites Based on Acoustic Emission Signals, Deep Feature Extraction, and Machine Learning. Sensors 2022, 22, 6886. [Google Scholar] [CrossRef] [PubMed]
- Haggui, M.; El Mahi, A.; Jendli, Z.; Akrout, A.; Haddar, M. Static and fatigue characterization of flax fiber reinforced thermoplastic composites by acoustic emission. Appl. Acoust. 2019, 147, 100–110. [Google Scholar] [CrossRef]
- Ueki, Y.; Lilholt, H.; Madsen, B. Fatigue behaviour of uni-directional flax fibre/epoxy composites. In Proceedings of the 20th International Conference on Composite Materials, Copenhagen, Denmark, 19–24 July 2015. [Google Scholar]
- Asgarinia, S.; Viriyasuthee, C.; Phillips, S.; Dubé, M.; Baets, J.; van Vuure, A.; Verpoest, I.; Lessard, L. Tension–tension fatigue behaviour of woven flax/epoxy composites. J. Reinf. Plast. Compos. 2015, 34, 857–867. [Google Scholar] [CrossRef]
- Shah, D.U. Damage in biocomposites: Stiffness evolution of aligned plant fibre composites during monotonic and cyclic fatigue loading. Compos. Part A Appl. Sci. Manuf. 2016, 83, 160–168. [Google Scholar] [CrossRef]
- Wielage, B.; Lampke, T.; Utschick, H.; Soergel, F. Processing of natural-fibre reinforced polymers and the resulting dynamic–mechanical properties. J. Mater. Process. Technol. 2003, 139, 140–146. [Google Scholar] [CrossRef]
- Shen, Y.; Tan, J.; Fernandes, L.; Qu, Z.; Li, Y. Dynamic Mechanical Analysis on Delaminated Flax Fiber Reinforced Composites. Materials 2019, 12, 2559. [Google Scholar] [CrossRef]
- Bai, P.; Zhu, G.; Jing, Q.; Yang, J.; Chen, J.; Su, Y.; Ma, J.; Zhang, G.; Wang, Z.L. Membrane–Based Self–Powered Triboelectric Sensors for Pressure Change Detection and Its Uses in Security Surveillance and Healthcare Monitoring. Adv. Funct. Mater. 2014, 24, 5807–5813. [Google Scholar] [CrossRef]
- Zhang, H.; Quan, L.; Chen, J.; Xu, C.; Zhang, C.; Dong, S.; Lü, C.; Luo, J. A general optimization approach for contact-separation triboelectric nanogenerator. Nano Energy 2019, 56, 700–707. [Google Scholar] [CrossRef]
- Perls, T.A. Electrical Noise from Instrument Cables Subjected to Shock and Vibration. J. Appl. Phys. 1952, 23, 674–680. [Google Scholar] [CrossRef]
- Le Duigou, A.; Kervoelen, A.; Le Grand, A.; Nardin, M.; Baley, C. Interfacial properties of flax fibre–epoxy resin systems: Existence of a complex interphase. Compos. Sci. Technol. 2014, 100, 152–157. [Google Scholar] [CrossRef]
- Maier, C.; Beckmann, A.; Wittmann, A.; Koch, K.P.; Fischer, G. Investigation of the Discrepancy Between Optically and Gravimetrically Calculated Fiber Volume Fraction in Flax-Fiber-Reinforced Polymer. J. Compos. Sci. 2025, 9, 103. [Google Scholar] [CrossRef]
- Kim, W.G.; Kim, D.W.; Tcho, I.W.; Kim, J.K.; Kim, M.S.; Choi, Y.K. Triboelectric Nanogenerator: Structure, Mechanism, and Applications. ACS Nano 2021, 15, 258–287. [Google Scholar] [CrossRef] [PubMed]
- Zou, H.; Zhang, Y.; Guo, L.; Wang, P.; He, X.; Dai, G.; Zheng, H.; Chen, C.; Wang, A.C.; Xu, C.; et al. Quantifying the triboelectric series. Nat. Commun. 2019, 10, 1427. [Google Scholar] [CrossRef] [PubMed]
- Sundar, V.; Newnham, R.E. Converse method measurements of electrostriction coefficients in low-K dielectrics. Mater. Res. Bull. 1996, 31, 545–554. [Google Scholar] [CrossRef]
- Yu, J.; Janolin, P.E. Defining “giant” electrostriction. J. Appl. Phys. 2022, 131, 170701. [Google Scholar] [CrossRef]
- Tagantsev, A.K.; Yudin, P.V. Flexoelectricity in Solids; World Scientific: Singapore, 2016. [Google Scholar] [CrossRef]
- Lu, J.; Liang, X.; Hu, S. Flexoelectricity in Solid Dielectrics: From Theory to Applications. Comput. Mater. Contin. 2015, 45, 145–162. [Google Scholar] [CrossRef]
- Trellu, H.; Le Scornec, J.; Leray, N.; Moreau, C.; Villares, A.; Cathala, B.; Guiffard, B. Flexoelectric and piezoelectric effects in micro- and nanocellulose films. Carbohydr. Polym. 2023, 321, 121305. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Buckley, A.; Welche, P.R.L.; Scott, J.F. Strain-gradient-induced polarization in SrTiO3 single crystals. Phys. Rev. Lett. 2007, 99, 167601. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, W.; Zhang, S. Flexoelectric nano-generator: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Lefeuvre, A.; Bourmaud, A.; Morvan, C.; Baley, C. Elementary flax fibre tensile properties: Correlation between stress–strain behaviour and fibre composition. Ind. Crops Prod. 2014, 52, 762–769. [Google Scholar] [CrossRef]
- Baley, C.; Gomina, M.; Breard, J.; Bourmaud, A.; Davies, P. Variability of mechanical properties of flax fibres for composite reinforcement. A review. Ind. Crops Prod. 2020, 145, 111984. [Google Scholar] [CrossRef]
- Aslan, M.; Chinga-Carrasco, G.; Sørensen, B.F.; Madsen, B. Strength variability of single flax fibres. J. Mater. Sci. 2011, 46, 6344–6354. [Google Scholar] [CrossRef]
- Barneto, A.G.; Vila, C.; Ariza, J.; Vidal, T. Thermogravimetric measurement of amorphous cellulose content in flax fibre and flax pulp. Cellulose 2011, 18, 17–31. [Google Scholar] [CrossRef]
- Poddar, S.; Foreman, K.; Adenwalla, S.; Ducharme, S. Finite-size scaling of flexoelectricity in Langmuir-Blodgett polymer thin films. Appl. Phys. Lett. 2016, 108, 012908. [Google Scholar] [CrossRef]
- Guiffard, B.; Saadeh, M.; Frère, P.; Seveno, R.; El-Gibari, M.; Sghaier, T.; Merupo, V.I.; Kassiba, A. Potentialities of flexoelectric effect in soft polymer films for electromechanical applications. J. Phys. Conf. Ser. 2019, 1322, 012041. [Google Scholar] [CrossRef]
- Li, J.F. Lead-Free Piezoelectric Materials; Wiley-VCH: Weinheim, Germany, 2021. [Google Scholar]
- Trolier-McKinstry, S. Crystal Chemistry of Piezoelectric Materials. In Piezoelectric and Acoustic Materials for Transducer Applications; Safari, A., Akdoğan, E.K., Eds.; Springer: Boston, MA, USA, 2008; pp. 39–56. [Google Scholar] [CrossRef]
- Fukada, E. Piezoelectricity as a fundamental property of wood. Wood Sci. Technol. 1968, 2, 299–307. [Google Scholar] [CrossRef]
- Werling, K.A.; Hutchison, G.R.; Lambrecht, D.S. Piezoelectric Effects of Applied Electric Fields on Hydrogen-Bond Interactions: First-Principles Electronic Structure Investigation of Weak Electrostatic Interactions. J. Phys. Chem. Lett. 2013, 4, 1365–1370. [Google Scholar] [CrossRef]
- Werling, K.A.; Griffin, M.; Hutchison, G.R.; Lambrecht, D.S. Piezoelectric hydrogen bonding: Computational screening for a design rationale. J. Phys. Chem. A 2014, 118, 7404–7410. [Google Scholar] [CrossRef]
- García, Y.; Ruiz-Blanco, Y.B.; Marrero-Ponce, Y.; Sotomayor-Torres, C.M. Orthotropic Piezoelectricity in 2D Nanocellulose. Sci. Rep. 2016, 6, 34616. [Google Scholar] [CrossRef]
- Nakai, T.; Hamatake, M.; Nakao, T. Relationship between piezoelectric behavior and the stress – strain curve of wood under combined compression and vibration stresses. J. Wood Sci. 2004, 50, 97–99. [Google Scholar] [CrossRef]
- Gindl, W.; Emsenhuber, G.; Plackner, J.; Konnerth, J.; Keckes, J. Converse piezoelectric effect in cellulose I revealed by wide-angle X-ray diffraction. Biomacromolecules 2010, 11, 1281–1285. [Google Scholar] [CrossRef] [PubMed]
- Chae, I.; Jeong, C.K.; Ounaies, Z.; Kim, S.H. Review on Electromechanical Coupling Properties of Biomaterials. ACS Appl. Bio Mater. 2018, 1, 936–953. [Google Scholar] [CrossRef] [PubMed]
- Abdel-karim, A.M.; Salama, A.H.; Hassan, M.L. Electrical conductivity and dielectric properties of nanofibrillated cellulose thin films from bagasse. J. Phys. Org. Chem. 2018, 31. [Google Scholar] [CrossRef]
- Knuffel, W.; Pizzi, A. The Piezoelectric Effect in Structural Timber. Holzforschung 1986, 40, 157–162. [Google Scholar] [CrossRef]
- Arnau, A.; Soares, D. Fundamentals of Piezoelectricity. In Piezoelectric Transducers and Applications; Vives, A.A., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–38. [Google Scholar] [CrossRef]
- DIN EN IEC 62631-2-1; Dielectric and Resistive Properties of Solid Insulating Materials—Part 2-1: Relative Permittivity and Dissipation Factor—Technical Frequencies (0,1 Hz to 10 MHz)—AC Methods. IEC: Geneva, Switzerland, 2018.
- Chen, Y.C.; Lin, H.C.; Lee, Y.D. The Effects of Filler Content and Size on the Properties of PTFE/SiO 2 Composites. J. Polym. Res. 2003, 10, 247–258. [Google Scholar] [CrossRef]
- Subodh, G.; Joseph, M.; Mohanan, P.; Sebastian, M.T. Low Dielectric Loss Polytetrafluoroethylene/TeO 2 Polymer Ceramic Composites. J. Am. Ceram. Soc. 2007, 90, 3507–3511. [Google Scholar] [CrossRef]
- Ben Amor, I.; Rekik, H.; Kaddami, H.; Raihane, M.; Arous, M.; Kallel, A. Effect of Palm Tree Fiber Orientation on Electrical Properties of Palm Tree Fiber-reinforced Polyester Composites. J. Compos. Mater. 2010, 44, 1553–1568. [Google Scholar] [CrossRef]
- Tataroglu, A.; Durmuş, H.; Vahid, A.F.; Avar, B.; Altındal, Ş. High-temperature sensitivity complex dielectric/electric modulus, loss tangent, and AC conductivity in Au/(S:DLC)/p-Si (MIS) structures. J. Mater. Sci. Mater. Electron. 2024, 35. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maier, C.; Huber, P.; Wittmann, A.; Koch, K.P.; Fischer, G. Mechanoelectrical Effects in Natural Fiber-Reinforced Polymers as Structural Health Monitoring. J. Compos. Sci. 2025, 9, 430. https://doi.org/10.3390/jcs9080430
Maier C, Huber P, Wittmann A, Koch KP, Fischer G. Mechanoelectrical Effects in Natural Fiber-Reinforced Polymers as Structural Health Monitoring. Journal of Composites Science. 2025; 9(8):430. https://doi.org/10.3390/jcs9080430
Chicago/Turabian StyleMaier, Christoph, Philipp Huber, Armin Wittmann, Klaus Peter Koch, and Georg Fischer. 2025. "Mechanoelectrical Effects in Natural Fiber-Reinforced Polymers as Structural Health Monitoring" Journal of Composites Science 9, no. 8: 430. https://doi.org/10.3390/jcs9080430
APA StyleMaier, C., Huber, P., Wittmann, A., Koch, K. P., & Fischer, G. (2025). Mechanoelectrical Effects in Natural Fiber-Reinforced Polymers as Structural Health Monitoring. Journal of Composites Science, 9(8), 430. https://doi.org/10.3390/jcs9080430







