An Exact 3D Shell Model for Free Vibration Analysis of Magneto-Electro-Elastic Composite Structures

Abstract

The present paper proposes a three-dimensional (3D) spherical shell model for the magneto-electro-elastic (MEE) free vibration analysis of simply supported multilayered smart shells. A mixed curvilinear orthogonal reference system is used to write the unified 3D governing equations for cylinders, cylindrical panels and spherical shells. The closed-form solution of the problem is performed considering Navier harmonic forms in the in-plane directions and the exponential matrix method in the thickness direction. A layerwise approach is possible, considering the interlaminar continuity conditions for displacements, electric and magnetic potentials, transverse shear/normal stresses, transverse normal magnetic induction and transverse normal electric displacement. Some preliminary cases are proposed to validate the present 3D MEE free vibration model for several curvatures, materials, thickness values and vibration modes. Then, new benchmarks are proposed in order to discuss possible effects in multilayered MEE curved smart structures. In the new benchmarks, first, three circular frequencies for several half-wave number couples and for different thickness ratios are proposed. Thickness vibration modes are shown in terms of displacements, stresses, electric displacement and magnetic induction along the thickness direction. These new benchmarks are useful to understand the free vibration behavior of MEE curved smart structures, and they can be used as reference for researchers interested in the development of of 2D/3D MEE models.

1. Introduction

In the aerospace sector, the health monitoring of structures is becoming a crucial activity in order to increase safety and design maintenance procedures. The interest in the behavior of smart structures is very attractive for academics and companies, in particular, owing to their vibration suppression characteristics. As this peculiarity is fundamental to increasing the life of aerospace products (spacecraft, airplanes and satellites) and to organizing better maintenance cycles and procedures, the deep comprehension of smart-structure free vibration behavior is mandatory. In addition, smart material structures involving magneto-electro-elastic (MEE) coupling can be successfully used to detect and monitor possible damages thanks to the possibility of sending electric and/or magnetic inputs. Free vibration behavior can be analyzed for both laminated and functionally graded magneto-electro-elastic (MEE) curved and flat smart structures [1,2,3,4,5,6,7,8,9,10]. For this reason, the study of smart material structures is an interesting topic for researchers from all over the world.

In past years, many numerical and analytical models for the free vibration analysis of MEE plates were developed by researchers all over the world. Pan and Heyliger [11] proposed an analytical solution for the free vibration study of anisotropic MEE multilayered rectangular plates under simply supported boundary conditions. In [12], the free vibration behavior of a multifunctional laminated nanoplate was proposed when piezoelectric and magnetostrictive face layers with a graphene-reinforced core layer were included. A higher-order sinusoidal shear deformation theory was presented. Ramirez et al. [13] developed an approximate solution for the free vibration problem of two-dimensional MEE flat laminates. In [14], Chen et al. investigated the free vibration problem of simply supported rectangular plates with general inhomogeneous material properties along the thickness direction: two independent state equations were used. Razavi and Shooshtari [15] proposed the nonlinear free vibration of symmetric MEE laminated rectangular plates with simply supported boundary conditions. Milazzo [16] developed 2D refined equivalent single-layer models for multilayered and functionally graded smart MEE plates subjected to quasi-static electromagnetic fields. In [17], the free vibration analysis of carbon nanotube-reinforced MEE rectangular and skew plates was analyzed using the finite element method. In Farajpour [18], a nonlocal continuum model was developed for nonlinear free vibrations of size-dependent MEE nanoplates subjected to external electric and magnetic potentials.

Numerical and analytical models for free vibrations of curved MEE multilayered smart structures are more complicated and less widespread in the literature. Buchanan [19] proposed a three-dimensional finite element formulation for cylinders infinitely long in the rectilinear direction. An analytical formulation for nonlinear and linear free vibration analysis of symmetrically laminated MEE doubly curved thin shells was proposed in [20] in a case in which they were resting on an elastic foundation. In [21], a finite element formulation was presented for the investigation of the linear thermal buckling and vibration behavior of clamped–clamped layered and multiphase MEE cylinders. In [22], an analytical solution for layered MEE cylindrical shells adhesively bonded by a viscoelastic interlayer was developed to predict its time-dependent mechanical, electric and magnetic behavior. A study on geometrically nonlinear free vibration behavior was performed by Vinyas and Harursampath [23] via the finite element method for a carbon nanotube-reinforced MEE doubly curved shell. Annigeri et al. [24,25] presented a semi-analytical finite element model for the study of an MEE cylindrical shell considering different constraint conditions. Free vibrations of simply supported MEE doubly curved thin shells resting on Pasternak foundations based on Donnell theory were investigated in [26]. In [27], a dynamic study of MEE cylindrical shells under moving loads was proposed. Wang et al. [28] showed the free vibration behavior of MEE cylindrical panels based on the three-dimensional theory; both general solutions for transversely isotropic MEE materials and displacement functions were introduced. In the work by Ghadiri and Safarpour [29], size-dependent effects were investigated in the free vibration analysis of an embedded MEE nanoshell subjected to thermo-electro magnetic loads. In [30], a free vibration analysis of embedded MEE cylindrical shells with step-wise thicknesses was performed within the framework of symplectic mechanics to understand energy harvesting in these structures. The isogeometric analysis approach was used by Tu et al. [31] to model and analyze free and forced vibrations of doubly curved MEE composite shallow shells resting on a visco-Pasternak foundation in a hygro-temperature environment.

The present 3D shell model for the MEE free vibration analysis of simply supported multilayered smart structures allows for analysis of different curved geometries such as cylinders, cylindrical panels and spherical shells, thanks to the use of a mixed curvilinear orthogonal reference system and a proper evaluation of radii of curvature. This formulation implements the layerwise approach to take into account the correct evaluation of displacements, electric and magnetic potentials, stresses, electric displacements and magnetic inductions for the case of transversely anisotropic structures. In addition, the use of the exponential matrix method gives a simple and elegant formulation with low computational costs. The present work is a magneto-electro-elastic extension of past authors’ works about electro-elastic [32] and magneto-elastic [33] analysis of curved structures. The present 3D MEE model fills the gap with respect to 3D models for curved smart structures; furthermore, it gives a reference solution for researchers interested in the development of 2D/3D numerical/analytical formulations for MEE smart curved structures.

2. Three-Dimensional Magneto-Electro-Elastic Model for Shells

The formulation and solution methodology for the 3D magneto-electro-elastic shell model are presented in this section. The Section 2.1 is devoted to the presentation of the set of 3D second-order differential equations for the magneto-electro-elastic problem of spherical shells. The Section 2.2 shows geometrical and constitutive equations. In the Section 2.3, the solution methodology, involving Navier harmonic forms and the exponential matrix method, is proposed.

2.1. Set of 3D Differential Equations for the Magneto-Electro-Elastic Problem

The set of 3D differential equations for the magneto-electro-elastic problem is composed of five equations: three 3D equations of motion [34], a 3D divergence equation for electric displacement [32] and a 3D divergence equation for magnetic induction [33]. Equation (1a) was derived from [34], considering the particular case where the in-plane radii of curvature are constant. Equations (1b)–(1c) come from the procedure exposed by Povstenko for the thermoelastic analysis in the mixed curvilinear reference system [35]. Equation (1) are written in the mixed curvilinear orthogonal reference system $(\alpha ,\beta ,z)$. In compact form, the set is expressed as follows:

$$\begin{array}{cc}\hfill & H_{\beta }\left(z\right){\displaystyle \frac{\partial }{\partial \alpha }}\left\{\begin{array}{c}{\sigma }_{\alpha \alpha }^k\\ {\sigma }_{\alpha \beta }^k\\ {\sigma }_{\alpha z}^k\end{array}\right\}+H_{\alpha }\left(z\right){\displaystyle \frac{\partial }{\partial \beta }}\left\{\begin{array}{c}{\sigma }_{\alpha \beta }^k\\ {\sigma }_{\beta \beta }^k\\ {\sigma }_{\beta z}^k\end{array}\right\}+H_{\alpha }\left(z\right)H_{\beta }\left(z\right){\displaystyle \frac{\partial }{\partial z}}\left\{\begin{array}{c}{\sigma }_{\alpha z}^k\\ {\sigma }_{\beta z}^k\\ {\sigma }_{zz}^k\end{array}\right\}+{\displaystyle \frac{H_{\beta }\left(z\right)}{R_{\alpha }}}(\left\{\begin{array}{c}{\sigma }_{\alpha z}^k\\ {\sigma }_{\beta z}^k\\ {\sigma }_{zz}^k\end{array}\right\}-\left\{\begin{array}{c}-{\sigma }_{\alpha z}^k\\ 0\\ {\sigma }_{\alpha \alpha }^k\end{array}\right\})+\hfill \\ & +{\displaystyle \frac{H_{\alpha }\left(z\right)}{R_{\beta }}}(\left\{\begin{array}{c}{\sigma }_{\alpha z}^k\\ {\sigma }_{\beta z}^k\\ {\sigma }_{zz}^k\end{array}\right\}-\left\{\begin{array}{c}0\\ -{\sigma }_{\beta z}^k\\ {\sigma }_{\beta \beta }^k\end{array}\right\})=\left\{\begin{array}{c}{\rho }^k{H}_{\alpha }\left(z\right)H_{\beta }\left(z\right){\ddot{u}}^k\\ {\rho }^k{H}_{\alpha }\left(z\right)H_{\beta }\left(z\right){\ddot{v}}^k\\ {\rho }^k{H}_{\alpha }\left(z\right)H_{\beta }\left(z\right){\ddot{w}}^k\end{array}\right\},\hfill \end{array}$$

(1a)

$$\mathbf{\nabla }·\left\{\begin{array}{c}{\displaystyle \frac{1}{H_{\alpha }\left(z\right)}}{\mathcal{D}}_{\alpha }^k\\ {\displaystyle \frac{1}{H_{\beta }\left(z\right)}}{\mathcal{D}}_{\beta }^k\\ {\mathcal{D}}_z^k\end{array}\right\}=0,$$

(1b)

$$\mathbf{\nabla }·\left\{\begin{array}{c}{\displaystyle \frac{1}{H_{\alpha }\left(z\right)}}{\mathcal{B}}_{\alpha }^k\\ {\displaystyle \frac{1}{H_{\beta }\left(z\right)}}{\mathcal{B}}_{\beta }^k\\ {\mathcal{B}}_z^k\end{array}\right\}=0,$$

(1c)

where the ${\sigma }_{\alpha \alpha }^k$, ${\sigma }_{\alpha \beta }^k$, ${\sigma }_{\alpha z}^k$, ${\sigma }_{\beta \beta }^k$, ${\sigma }_{\beta z}^k$ and ${\sigma }_{zz}^k$ terms are the stress components; ${\mathcal{D}}_{\alpha }^k$, ${\mathcal{D}}_{\beta }^k$ and ${\mathcal{D}}_z^k$ are the electric displacement components; ${\mathcal{B}}_{\alpha }^k$, ${\mathcal{B}}_{\beta }^k$ and ${\mathcal{B}}_z^k$ are the magnetic induction components; $R_{\alpha }$ and $R_{\beta }$ are the radii of curvature in the two in-plane directions ($\alpha$ and $\beta$, respectively); ${\rho }^k$ is the mass density of the material lamina; ${\ddot{u}}^k$, ${\ddot{v}}^k$ and ${\ddot{w}}^k$ are the second time derivatives of displacements; $\mathbf{\nabla }·$ is the divergence operator; and ${\displaystyle \frac{\partial }{\partial \alpha }}$, ${\displaystyle \frac{\partial }{\partial \beta }}$ and ${\displaystyle \frac{\partial }{\partial z}}$ indicate partial derivatives with respect to $\alpha$, $\beta$ and z, respectively. In Equation (1), $H_{\alpha }\left(z\right)$ and $H_{\beta }\left(z\right)$ are the curvature parameters in the $\alpha$ and $\beta$ directions, respectively. They are explicitly defined as follows:

$$H_{\alpha }\left(z\right)=1+{\displaystyle \frac{z}{R_{\alpha }}},H_{\beta }\left(z\right)=1+{\displaystyle \frac{z}{R_{\beta }}},H_z\left(z\right)=1,with-{\displaystyle \frac{h}{2}}<z<{\displaystyle \frac{h}{2}}.$$

(2)

$R_{\alpha }$ and $R_{\beta }$ are defined in the middle reference surface (${\Omega }_0$), and different curved geometries (cylinders, cylindrical panels and spherical shells) can be analyzed with the same set of equations, thanks to proper considerations for radii of curvature ($R_{\alpha }$ and $R_{\beta }$) and curvature parameters ($H_{\alpha }\left(z\right)$ and $H_{\beta }\left(z\right)$). Figure 1 shows the mixed curvilinear orthogonal reference system; the reference surface (${\Omega }_0$); all the possible analyzable structures; and the considerations for $R_{\alpha }$, $R_{\beta }$, $H_{\alpha }$ and $H_{\beta }$ for cylinders, cylindrical shells and spherical shells.

2.2. Geometrical and Constitutive Relations for the 3D Magneto-Electro-Elastic Shell Problem

Geometrical relations for the 3D magneto-electro-elastic problem for spherical shells must be introduced in the set of 3D governing equations (Equation (1)) to link strains with displacements, the electric field with electric potential and the magnetic field with magnetic potential. Geometrical relations can be written for each k layers as follows:

$${\mathit{\epsilon }}^k=\left({\mathbf{\Delta }}_M\left(z\right)\right){\mathit{u}}^k,$$

(3a)

$${\mathcal{E}}^k=-(\mathbf{\Delta }\left(z\right)){\varphi }^k$$

(3b)

$${\mathcal{H}}^k=-(\mathbf{\Delta }\left(z\right)){\psi }^k$$

(3c)

where ${\epsilon }^k={\left\{{\epsilon }_{\alpha \alpha }^k{\epsilon }_{\beta \beta }^k{\epsilon }_{zz}^k{\gamma }_{\beta z}^k{\gamma }_{\alpha z}^k{\gamma }_{\alpha \beta }^k\right\}}^T$ is the $6\times 1$ strain vector, ${\mathit{u}}^k={\left\{u^k{v}^k{w}^k\right\}}^T$ is the $3\times 1$ displacement vector, ${\mathcal{E}}^k={\left\{{\mathcal{E}}_{\alpha }^k{\mathcal{E}}_{\beta }^k{\mathcal{E}}_z^k\right\}}^T$ is the $3\times 1$ electric field vector, ${\varphi }^k$ is the scalar electric potential, ${\mathcal{H}}^k={\left\{{\mathcal{H}}_{\alpha }^k{\mathcal{H}}_{\beta }^k{\mathcal{H}}_z^k\right\}}^T$ is the $3\times 1$ magnetic field vector and ${\psi }^k$ is the scalar magnetic potential. T is the transpose of a vector or a matrix. Geometrical matrices ${\mathbf{\Delta }}_M\left(z\right)$ and $\mathbf{\Delta }\left(z\right)$ can be explicitly written as

$${\mathbf{\Delta }}_M\left(z\right)=\left[\begin{array}{ccc}{\displaystyle \frac{1}{H_{\alpha }}}{\displaystyle \frac{\partial }{\partial \alpha }}& 0& {\displaystyle \frac{1}{H_{\alpha }{R}_{\alpha }}}\\ 0& {\displaystyle \frac{1}{H_{\beta }}}{\displaystyle \frac{\partial }{\partial \beta }}& {\displaystyle \frac{1}{H_{\beta }{R}_{\beta }}}\\ 0& 0& {\displaystyle \frac{\partial }{\partial z}}\\ 0& {\displaystyle \frac{\partial }{\partial z}}-{\displaystyle \frac{1}{H_{\beta }{R}_{\beta }}}& {\displaystyle \frac{1}{H_{\beta }}}{\displaystyle \frac{\partial }{\partial \beta }}\\ {\displaystyle \frac{\partial }{\partial z}}-{\displaystyle \frac{1}{H_{\alpha }{R}_{\alpha }}}& 0& {\displaystyle \frac{1}{H_{\alpha }}}{\displaystyle \frac{\partial }{\partial \alpha }}\\ {\displaystyle \frac{1}{H_{\beta }}}{\displaystyle \frac{\partial }{\partial \beta }}& {\displaystyle \frac{1}{H_{\alpha }}}{\displaystyle \frac{\partial }{\partial \alpha }}& 0\end{array}\right],$$

(4)

$$\mathbf{\Delta }\left(z\right)=\left\{\begin{array}{c}{\displaystyle \frac{1}{H_{\alpha }}}{\displaystyle \frac{\partial }{\partial \alpha }}\\ {\displaystyle \frac{1}{H_{\beta }}}{\displaystyle \frac{\partial }{\partial \beta }}\\ {\displaystyle \frac{\partial }{\partial z}}\end{array}\right\},$$

(5)

and include curvature terms, radii of curvature and partial derivatives. They are written for spherical shells, and they degenerate to those for cylinders and cylindrical shells, thanks to simple considerations about radii of curvature ($R_{\alpha }$ and $R_{\beta }$) and parameters $H_{\alpha }$ and $H_{\beta }$ (see Figure 1). Constitutive relations are used to couple the three involved fields, i.e., magnetic, electric and elastic fields. They can be written in matrix form for each k layers as follows:

$${\mathit{\sigma }}^k={\mathit{C}}^k{\mathbf{\epsilon }}^k-{\mathit{e}}^{kT}{\mathcal{E}}^k-{\mathit{q}}^{kT}{\mathcal{H}}^k,$$

(6a)

$${\mathcal{D}}^k={\mathit{e}}^k{\mathit{\epsilon }}^k+{\mathit{ϵ}}^k{\mathcal{E}}^k+{\mathit{d}}^k{\mathcal{H}}^k,$$

(6b)

$${\mathcal{B}}^k={\mathit{q}}^k{\mathit{\epsilon }}^k+{\mathit{d}}^k{\mathcal{E}}^k+{\mathit{\mu }}^k{\mathcal{H}}^k.$$

(6c)

where ${\mathit{\sigma }}^k$ is the $6\times 1$ stress vector, ${\mathit{C}}^k$ is the $6\times 6$ elastic coefficient matrix for orthotropic materials, ${\mathit{e}}^k$ is the $3\times 6$ piezoelectric coefficient matrix, ${\mathit{q}}^k$ is the $3\times 6$ piezomagnetic coefficient matrix, ${\mathcal{D}}^k$ is the $3\times 1$ electric displacement vector, ${\mathit{ϵ}}^k$ is the $3\times 3$ electric permittivity matrix, ${\mathit{d}}^k$ is the $3\times 3$ electro-magnetic coupling coefficient matrix, ${\mathcal{B}}^k$ is the $3\times 1$ magnetic induction vector and ${\mathit{\mu }}^k$ is the $3\times 3$ magnetic permittivity matrix. The explicit forms of these matrices and vectors are expressed as follows:

$${\mathit{\sigma }}^k=\left\{\begin{array}{c}{\sigma }_{\alpha \alpha }^k\\ {\sigma }_{\beta \beta }^k\\ {\sigma }_{zz}^k\\ {\sigma }_{\beta z}^k\\ {\sigma }_{\alpha z}^k\\ {\sigma }_{\alpha \beta }^k\end{array}\right\},$$

(7)

$${\mathit{C}}^k=\left[\begin{array}{cccccc}{C}_{11}^k& C_{12}^k& C_{13}^k& 0& 0& 0\\ C_{12}^k& C_{22}^k& C_{23}^k& 0& 0& 0\\ C_{13}^k& C_{23}^k& C_{33}^k& 0& 0& 0\\ 0& 0& 0& C_{44}^k& 0& 0\\ 0& 0& 0& 0& C_{55}^k& 0\\ 0& 0& 0& 0& 0& C_{66}^k\end{array}\right],$$

(8)

$${\mathit{e}}^k=\left[\begin{array}{cccccc}0& 0& 0& 0& e_{15}^k& 0\\ 0& 0& 0& e_{24}^k& 0& 0\\ e_{31}^k& e_{32}^k& e_{33}^k& 0& 0& 0\end{array}\right],$$

(9)

$${\mathit{q}}^k=\left[\begin{array}{cccccc}0& 0& 0& 0& q_{15}^k& 0\\ 0& 0& 0& q_{24}^k& 0& 0\\ q_{31}^k& q_{32}^k& q_{33}^k& 0& 0& 0\end{array}\right],$$

(10)

$${\mathcal{D}}^k=\left\{\begin{array}{c}{\mathcal{D}}_{\alpha }^k\\ {\mathcal{D}}_{\beta }^k\\ {\mathcal{D}}_z^k\end{array}\right\},$$

(11)

$${\mathit{ϵ}}^k=\left[\begin{array}{ccc}{ϵ}_{11}^k& 0& 0\\ 0& {ϵ}_{22}^k& 0\\ 0& 0& {ϵ}_{33}^k\end{array}\right],$$

(12)

$${\mathit{d}}^k=\left[\begin{array}{ccc}{d}_{11}^k& 0& 0\\ 0& d_{22}^k& 0\\ 0& 0& d_{33}^k\end{array}\right],$$

(13)

$${\mathcal{B}}^k=\left\{\begin{array}{c}{\mathcal{B}}_{\alpha }^k\\ {\mathcal{B}}_{\beta }^k\\ {\mathcal{B}}_z^k\end{array}\right\},$$

(14)

$${\mathit{\mu }}^k=\left[\begin{array}{ccc}{\mu }_{11}^k& 0& 0\\ 0& {\mu }_{22}^k& 0\\ 0& 0& {\mu }_{33}^k\end{array}\right].$$

(15)

Constitutive Equations (6)–(15) are written only for a $0^{\circ }$ or ${90}^{\circ }$ orthotropic lamination angle in order to obtain closed-form solutions.

2.3. Solution Methodology

In the following, the solution of 3D governing equations for the magneto-electro-elastic problem for spherical shells is proposed.

In order to obtain second-order differential equations in terms of displacements, electric potential and magnetic potential, Equation (3) must be included in Equation (6); then, the resulting set of equations must be introduced in Equation (1). In this way, displacements, electric potential and magnetic potential are the primary variables of the problem.

In the in-plane directions ($\alpha$ and $\beta$), harmonic forms are imposed as follows:

$$u^k(\alpha ,\beta ,z,t)=U^k\left(z\right)\cos \left(\overline{\alpha }\alpha \right)\sin \left(\overline{\beta }\beta \right)e^{i\omega t},$$

(16a)

$$v^k(\alpha ,\beta ,z,t)=V^k\left(z\right)\sin \left(\overline{\alpha }\alpha \right)\cos \left(\overline{\beta }\beta \right)e^{i\omega t},$$

(16b)

$$w^k(\alpha ,\beta ,z,t)=W^k\left(z\right)\sin \left(\overline{\alpha }\alpha \right)\sin \left(\overline{\beta }\beta \right)e^{i\omega t},$$

(16c)

$${\varphi }^k(\alpha ,\beta ,z,t)={\mathrm{\Phi }}^k\left(z\right)\sin \left(\overline{\alpha }\alpha \right)\sin \left(\overline{\beta }\beta \right)e^{i\omega t},$$

(16d)

$${\psi }^k(\alpha ,\beta ,z,t)={\mathrm{\Psi }}^k\left(z\right)\sin \left(\overline{\alpha }\alpha \right)\sin \left(\overline{\beta }\beta \right)e^{i\omega t},$$

(16e)

where $U{\left(z\right)}^k$, $V{\left(z\right)}^k$, $W{\left(z\right)}^k$, $\mathrm{\Phi }{\left(z\right)}^k$ and $\mathrm{\Psi }{\left(z\right)}^k$ are the amplitudes of the primary variables; $\omega =2\pi f$ is the circular frequency (f is the frequency); t is the time; i is the imaginary unit; and $\overline{\alpha }$ and $\overline{\beta }$ are defined as follows:

$$\overline{\alpha }={\displaystyle \frac{m\pi }{a}},\overline{\beta }={\displaystyle \frac{n\pi }{b}},$$

(17)

where m and n are the half-wave numbers and a and b are the length and width of the structure. Harmonic forms fulfill the simply supported boundary conditions at the edges; they can be explicitly written as follows:

$$\begin{array}{cc}\hfill & v^k=0,w^k=0,{\varphi }^k=0,{\psi }^k=0,{\sigma }_{\alpha \alpha }^k=0\mathrm{for}\alpha =0,a,\hfill \\ \hfill & u^k=0,w^k=0,{\varphi }^k=0,{\psi }^k=0,{\sigma }_{\beta \beta }^k=0\mathrm{for}\beta =0,b.\hfill \end{array}$$

(18)

The simply supported boundary conditions are the only ones that can be set up to have a closed-form solution because they naturally fulfill the Navier harmonic forms at the edges.

Introducing Equations (16), the modified version of Equation (1) can be written as follows:

$$\begin{array}{cc}\hfill & \left(-{\displaystyle \frac{H_{\beta }{C}_{55}^k}{H_{\alpha }{R}_{\alpha }^2}}-{\displaystyle \frac{C_{55}^k}{R_{\alpha }{R}_{\beta }}}-{\overline{\alpha }}^2{\displaystyle \frac{C_{11}^k{H}_{\beta }}{H_{\alpha }}}-{\overline{\beta }}^2{\displaystyle \frac{C_{66}^k{H}_{\alpha }}{H_{\beta }}}+{\rho }^k{H}_{\alpha }{H}_{\beta }{\omega }^2\right)U^k+\hfill \\ & +\left(-\overline{\alpha }\overline{\beta }{C}_{12}^k-\overline{\alpha }\overline{\beta }{C}_{66}^k\right)V^k+\left(\overline{\alpha }{\displaystyle \frac{C_{11}^k{H}_{\beta }}{H_{\alpha }{R}_{\alpha }}}+\overline{\alpha }{\displaystyle \frac{C_{12}^k}{R_{\beta }}}+\overline{\alpha }{\displaystyle \frac{C_{55}^k{H}_{\beta }}{H_{\alpha }{R}_{\alpha }}}+\overline{\alpha }{\displaystyle \frac{C_{55}^k}{R_{\beta }}}\right)W^k+\hfill \\ & +\left({\displaystyle \frac{C_{55}^k{H}_{\beta }}{R_{\alpha }}}+{\displaystyle \frac{C_{55}^k{H}_{\alpha }}{R_{\beta }}}\right)U_{,z}^k+\left(\overline{\alpha }{C}_{13}^k{H}_{\beta }+\overline{\alpha }{C}_{55}^k{H}_{\beta }\right)W_{,z}^k+C_{55}^k{H}_{\alpha }{H}_{\beta }{U}_{,zz}^k+\hfill \\ & +\left(+2\overline{\alpha }{\displaystyle \frac{e_{15}^k{H}_{\beta }}{H_{\alpha }{R}_{\alpha }}}+\overline{\alpha }{\displaystyle \frac{e_{15}^k}{R_{\beta }}}\right){\mathrm{\Phi }}^k+\left(\overline{\alpha }{e}_{31}^k{H}_{\beta }+\overline{\alpha }{e}_{15}^k{H}_{\beta }\right){\mathrm{\Phi }}_{,z}^k+\hfill \\ & +\left(+2\overline{\alpha }{\displaystyle \frac{q_{15}^k{H}_{\beta }}{H_{\alpha }{R}_{\alpha }}}+\overline{\alpha }{\displaystyle \frac{q_{15}^k}{R_{\beta }}}\right){\mathrm{\Psi }}^k+\left(\overline{\alpha }{q}_{31}^k{H}_{\beta }+\overline{\alpha }{q}_{15}^k{H}_{\beta }\right){\mathrm{\Psi }}_{,z}^k=0,\hfill \end{array}$$

(19a)

$$\begin{array}{cc}\hfill & \left(-{\displaystyle \frac{H_{\alpha }{C}_{44}^k}{H_{\beta }{R}_{\beta }^2}}-{\displaystyle \frac{C_{44}^k}{R_{\alpha }{R}_{\beta }}}-{\overline{\alpha }}^2{\displaystyle \frac{C_{66}^k{H}_{\beta }}{H_{\alpha }}}-{\overline{\beta }}^2{\displaystyle \frac{C_{22}^k{H}_{\alpha }}{H_{\beta }}}+{\rho }^k{H}_{\alpha }{H}_{\beta }{\omega }^2\right)V^k+\hfill \\ & +\left(-\overline{\alpha }\overline{\beta }{C}_{12}^k-\overline{\alpha }\overline{\beta }{C}_{66}^k\right)U^k+\left(\overline{\beta }{\displaystyle \frac{C_{44}^k{H}_{\alpha }}{H_{\beta }{R}_{\beta }}}+\overline{\beta }{\displaystyle \frac{C_{44}^k}{R_{\alpha }}}+\overline{\beta }{\displaystyle \frac{C_{22}^k{H}_{\alpha }}{H_{\beta }{R}_{\beta }}}+\overline{\beta }{\displaystyle \frac{C_{12}^k}{R_{\alpha }}}\right)W^k+\hfill \\ & +\left({\displaystyle \frac{C_{44}^k{H}_{\alpha }}{R_{\beta }}}+{\displaystyle \frac{C_{44}^k{H}_{\beta }}{R_{\alpha }}}\right)V_{,z}^k+\left(\overline{\beta }{C}_{44}^k{H}_{\alpha }+\overline{\beta }{C}_{23}^k{H}_{\alpha }\right)W_z^k+C_{44}^k{H}_{\alpha }{H}_{\beta }{V}_{,zz}^k+\hfill \\ & +\left(+2\overline{\beta }{\displaystyle \frac{e_{24}^k{H}_{\alpha }}{H_{\beta }{R}_{\beta }}}+\overline{\beta }{\displaystyle \frac{e_{24}^k}{R_{\alpha }}}\right){\mathrm{\Phi }}^k+\left(\overline{\beta }{e}_{32}^k{H}_{\alpha }+\overline{\beta }{e}_{24}^k{H}_{\alpha }\right){\mathrm{\Phi }}_{,z}^k+\hfill \\ & +\left(+2\overline{\beta }{\displaystyle \frac{q_{24}^k{H}_{\alpha }}{H_{\beta }{R}_{\beta }}}+\overline{\beta }{\displaystyle \frac{q_{24}^k}{R_{\alpha }}}\right){\mathrm{\Psi }}^k+\left(\overline{\beta }{q}_{32}^k{H}_{\alpha }+\overline{\beta }{q}_{24}^k{H}_{\alpha }\right){\mathrm{\Psi }}_{,z}^k=0,\hfill \end{array}$$

(19b)

$$\begin{array}{cc}\hfill & \left({\displaystyle \frac{C_{13}^k}{R_{\alpha }{R}_{\beta }}}+{\displaystyle \frac{C_{23}^k}{R_{\alpha }{R}_{\beta }}}-{\displaystyle \frac{C_{11}^k{H}_{\beta }}{H_{\alpha }{R}_{\alpha }^2}}-{\displaystyle \frac{2C_{12}^k}{R_{\alpha }{R}_{\beta }}}-{\displaystyle \frac{C_{22}^k{H}_{\alpha }}{H_{\beta }{R}_{\beta }^2}}-{\overline{\alpha }}^2{\displaystyle \frac{C_{55}^k{H}_{\beta }}{H_{\alpha }}}-{\overline{\beta }}^2{\displaystyle \frac{C_{44}^k{H}_{\alpha }}{H_{\beta }}}+{\rho }^k{H}_{\alpha }{H}_{\beta }{\omega }^2\right)W^k+\hfill \\ & +\left(\overline{\alpha }{\displaystyle \frac{C_{55}^k{H}_{\beta }}{H_{\alpha }{R}_{\alpha }}}-\overline{\alpha }{\displaystyle \frac{C_{13}^k}{R_{\beta }}}+\overline{\alpha }{\displaystyle \frac{C_{11}^k{H}_{\beta }}{H_{\alpha }{R}_{\alpha }}}+\overline{\alpha }{\displaystyle \frac{C_{12}^k}{R_{\beta }}}\right)U^k+\hfill \\ & +\left(\overline{\beta }{\displaystyle \frac{C_{44}^k{H}_{\alpha }}{H_{\beta }{R}_{\beta }}}-\overline{\beta }{\displaystyle \frac{C_{23}^k}{R_{\alpha }}}+\overline{\beta }{\displaystyle \frac{C_{22}^k{H}_{\alpha }}{H_{\beta }{R}_{\beta }}}+\overline{\beta }{\displaystyle \frac{C_{12}^k}{R_{\alpha }}}\right)V^k+\hfill \\ & +\left(-\overline{\alpha }{C}_{55}^k{H}_{\beta }-\overline{\alpha }{C}_{13}^k{H}_{\beta }\right)U_{,z}^k+\left(-\overline{\beta }{C}_{44}^k{H}_{\alpha }-\overline{\beta }{C}_{23}^k{H}_{\alpha }\right)V_{,z}^k+\left({\displaystyle \frac{C_{33}^k{H}_{\beta }}{R_{\alpha }}}+{\displaystyle \frac{C_{33}^k{H}_{\alpha }}{R_{\beta }}}\right)W_{,z}^k+\hfill \\ & +C_{33}^k{H}_{\alpha }{H}_{\beta }{W}_{,zz}^k+\left(-{\overline{\alpha }}^2{\displaystyle \frac{e_{15}^k{H}_{\beta }}{H_{\alpha }}}-{\overline{\beta }}^2{\displaystyle \frac{e_{24}^k{H}_{\alpha }}{H_{\beta }}}\right){\mathrm{\Phi }}^k+\left(-{\overline{\alpha }}^2{\displaystyle \frac{q_{15}^k{H}_{\beta }}{H_{\alpha }}}-{\overline{\beta }}^2{\displaystyle \frac{q_{24}^k{H}_{\alpha }}{H_{\beta }}}\right){\mathrm{\Psi }}^k+\hfill \\ & +\left(-{\displaystyle \frac{e_{31}^k{H}_{\beta }}{R_{\alpha }}}-{\displaystyle \frac{e_{32}^k{H}_{\alpha }}{R_{\beta }}}+{\displaystyle \frac{e_{33}^k{H}_{\beta }}{R_{\alpha }}}+{\displaystyle \frac{e_{33}^k{H}_{\alpha }}{R_{\beta }}}\right){\mathrm{\Phi }}_{,z}^k+e_{33}^k{H}_{\alpha }{H}_{\beta }{\mathrm{\Phi }}_{,zz}^k+\hfill \\ & +\left(-{\displaystyle \frac{q_{31}^k{H}_{\beta }}{R_{\alpha }}}-{\displaystyle \frac{q_{32}^k{H}_{\alpha }}{R_{\beta }}}+{\displaystyle \frac{q_{33}^k{H}_{\beta }}{R_{\alpha }}}+{\displaystyle \frac{q_{33}^k{H}_{\alpha }}{R_{\beta }}}\right){\mathrm{\Psi }}_{,z}^k+q_{33}^k{H}_{\alpha }{H}_{\beta }{\mathrm{\Psi }}_{,zz}^k=0,\hfill \end{array}$$

(19c)

$$\begin{array}{cc}\hfill & \overline{\alpha }{\displaystyle \frac{e_{15}^k}{H_{\alpha }^2{R}_{\alpha }}}{U}^k+\overline{\beta }{\displaystyle \frac{e_{24}^k}{H_{\beta }^2{R}_{\beta }}}{V}^k+\left(-{\overline{\alpha }}^2{\displaystyle \frac{e_{15}^k}{H_{\alpha }^2}}-{\overline{\beta }}^2{\displaystyle \frac{e_{24}^k}{H_{\beta }^2}}\right)W^k+\left(-\overline{\alpha }{\displaystyle \frac{e_{15}^k}{H_{\alpha }}}-\overline{\alpha }{\displaystyle \frac{e_{31}^k}{H_{\alpha }}}\right)U_{,z}^k+\hfill \\ & +\left(-\overline{\beta }{\displaystyle \frac{e_{24}^k}{H_{\beta }}}-\overline{\beta }{\displaystyle \frac{e_{32}^k}{H_{\beta }}}\right)V_{,z}^k+\left({\displaystyle \frac{e_{31}^k}{H_{\alpha }{R}_{\alpha }}}+{\displaystyle \frac{e_{32}^k}{H_{\beta }{R}_{\beta }}}\right)W_{,z}^k+e_{33}^k{W}_{zz}^k+\hfill \\ & +\left({\overline{\alpha }}^2{\displaystyle \frac{{ϵ}_{11}^k}{H_{\alpha }^2}}+{\overline{\beta }}^2{\displaystyle \frac{{ϵ}_{22}^k}{H_{\beta }^2}}\right){\mathrm{\Phi }}^k-{ϵ}_{33}^k{\mathrm{\Phi }}_{,zz}^k+\left({\overline{\alpha }}^2{\displaystyle \frac{d_{11}^k}{H_{\alpha }^2}}+{\overline{\beta }}^2{\displaystyle \frac{d_{22}^k}{H_{\beta }^2}}\right){\mathrm{\Psi }}^k-d_{33}^k{\mathrm{\Psi }}_{,zz}^k=0,\hfill \end{array}$$

(19d)

$$\begin{array}{cc}\hfill & \overline{\alpha }{\displaystyle \frac{q_{15}^k}{H_{\alpha }^2{R}_{\alpha }}}{U}^k+\overline{\beta }{\displaystyle \frac{q_{24}^k}{H_{\beta }^2{R}_{\beta }}}{V}^k+\left(-{\overline{\alpha }}^2{\displaystyle \frac{q_{15}^k}{H_{\alpha }^2}}-{\overline{\beta }}^2{\displaystyle \frac{q_{24}^k}{H_{\beta }^2}}\right)W^k+\left(-\overline{\alpha }{\displaystyle \frac{q_{15}^k}{H_{\alpha }}}-\overline{\alpha }{\displaystyle \frac{q_{31}^k}{H_{\alpha }}}\right)U_{,z}^k+\hfill \\ & +\left(-\overline{\beta }{\displaystyle \frac{q_{24}^k}{H_{\beta }}}-\overline{\beta }{\displaystyle \frac{q_{32}^k}{H_{\beta }}}\right)V_{,z}^k+\left({\displaystyle \frac{q_{31}^k}{H_{\alpha }{R}_{\alpha }}}+{\displaystyle \frac{q_{32}^k}{H_{\beta }{R}_{\beta }}}\right)W_{,z}^k+q_{33}^k{W}_{zz}^k+\hfill \\ & +\left({\overline{\alpha }}^2{\displaystyle \frac{d_{11}^k}{H_{\alpha }^2}}+{\overline{\beta }}^2{\displaystyle \frac{d_{22}^k}{H_{\beta }^2}}\right){\mathrm{\Phi }}^k-d_{33}^k{\mathrm{\Phi }}_{,zz}^k+\left({\overline{\alpha }}^2{\displaystyle \frac{{\mu }_{11}^k}{H_{\alpha }^2}}+{\overline{\beta }}^2{\displaystyle \frac{{\mu }_{22}^k}{H_{\beta }^2}}\right){\mathrm{\Psi }}^k-{\mu }_{33}^k{\mathrm{\Psi }}_{,zz}^k=0.\hfill \end{array}$$

(19e)

At this point, the unknowns of the 3D magneto-electro-elastic problem are the amplitudes of the primary variables ($U^k\left(z\right)$, $V^k\left(z\right)$, $W^k\left(z\right)$, ${\mathrm{\Phi }}^k\left(z\right)$ and ${\mathrm{\Psi }}^k\left(z\right)$) with related first and second derivatives in the z direction.

The use of the exponential matrix method in the thickness direction requires a mandatory characteristic: first-order differential equations with constant coefficients. Constant coefficients can be obtained thanks to the introduction of a total number (M) of mathematical layers by opportunely dividing each physical layer. This procedure is done because curvature terms $H_{\alpha }$ and $H_{\beta }$ are functions of z. Mathematical layers must have a proper thickness in order to consider curvature terms as constant. For this reason, equations are now written for a generic mathematical layer (j). It is possible to have first-order differential equations by redoubling the number of variables in Equations (19). The redoubling of equations and variables is an important peculiarity of the model, as it permits derivatives in the z direction for displacements, as well as electric potential and magnetic potential as primary variables. In this way, variables such as stresses, electric displacement components and magnetic induction components can be exactly computed using constitutive Equation (6).

The resulting set of first-order differential equations can be compacted in a matrix form as follows:

$$\begin{array}{c}\begin{array}{c}\left[\begin{array}{cccccccccc}{A}_{10}^j& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& A_{20}^j& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& P_1^j& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& P_1^j& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& P_1^j& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& A_{10}^j& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& A_{20}^j& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& P_1^j& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& P_1^j& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& P_1^j\end{array}\right]\hfill \end{array}{\left\{\begin{array}{c}{U}^j\\ V^j\\ W^j\\ {\mathrm{\Phi }}^j\\ {\mathrm{\Psi }}^j\\ U_{,z}^j\\ V_{,z}^j\\ W_{,z}^j\\ {\mathrm{\Phi }}_{,z}^j\\ {\mathrm{\Psi }}_{,z}^j\end{array}\right\}}_{,z}=\hfill \\ \left[\begin{array}{cccccccccc}0& 0& 0& 0& 0& A_{10}^j& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& A_{20}^j& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& P_1^j& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& P_1^j& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& P_1^j\\ -A_1^j& -A_2^j& -A_3^j& -A_4^j& -A_5^j& -A_6^j& 0& -A_7^j& -A_8^j& -A_9^j\\ -A_{11}^j& -A_{12}^j& -A_{13}^j& -A_{14}^j& -A_{15}^j& 0& -A_{16}^j& -A_{17}^j& -A_{18}^j& -A_{19}^j\\ -P_2^j& -P_3^j& -P_4^j& -P_5^j& -P_6^j& -P_7^j& -P_8^j& -P_9^j& -P_{10}^j& -P_{11}^j\\ -P_{12}^j& -P_{13}^j& -P_{14}^j& -P_{15}^j& -P_{16}^j& -P_{17}^j& -P_{18}^j& -P_{19}^j& -P_{20}^j& -P_{21}^j\\ -P_{22}^j& -P_{23}^j& -P_{24}^j& -P_{25}^j& -P_{26}^j& -P_{27}^j& -P_{28}^j& -P_{29}^j& -P_{30}^j& -P_{31}^j\end{array}\right]\left\{\begin{array}{c}{U}^j\\ V^j\\ W^j\\ {\mathrm{\Phi }}^j\\ {\mathrm{\Psi }}^j\\ U_{,z}^j\\ V_{,z}^j\\ W_{,z}^j\\ {\mathrm{\Phi }}_{,z}^j\\ {\mathrm{\Psi }}_{,z}^j\end{array}\right\}\Rightarrow {\mathit{D}}^j{\mathit{X}}_{,\mathit{z}}^{\mathit{j}}={\mathit{A}}^j{\mathit{X}}^j.\hfill \end{array}$$

(20)

The resolution of the problem, considering the exponential matrix method, can be explicitly written as follows:

$${\mathit{X}}^j\left(h_j\right)={\mathit{A}}^{**j}{\mathit{X}}^j\left(0\right)=\left[\sum _{n=0}^N{\displaystyle \frac{{\left({\mathit{A}}^{*j}\right)}^n}{n!}}{h}_j^n\right]{\mathit{X}}^j\left(0\right).$$

(21)

where ${\mathit{A}}^{*j}={\mathit{D}}^{j^{-1}}{\mathit{A}}^j$ and ${\mathit{A}}^{**j}$ is the exponential matrix computed considering the Taylor approach. ${\left({\mathit{A}}^{*j}\right)}^0=\mathit{I}$ is the $10\times 10$ identity matrix. Equation (21) links the bottom ($\tilde{z}=0$) of layer j with the top ($\tilde{z}=h_j$) of the same layer (j).

In order to implement the layerwise approach, interlaminar continuity conditions at interfaces between two contiguous layers have to be imposed on displacements, electric potential, magnetic potential, transverse normal stress, transverse shear stresses, transverse normal electric displacement and transverse normal magnetic induction. These conditions can be written as follows:

$$u_b^j=u_t^{j-1},v_b^j=v_t^{j-1},w_b^j=w_t^{j-1},{\varphi }_b^j={\varphi }_t^{j-1},{\psi }_b^j={\psi }_t^{j-1},$$

(22a)

$${\sigma }_{x{z}_b}^j={\sigma }_{x{z}_t}^{j-1},{\sigma }_{y{z}_b}^j={\sigma }_{y{z}_t}^{j-1},{\sigma }_{z{z}_b}^j={\sigma }_{z{z}_t}^{j-1},{\mathcal{D}}_{z_b}^j={\mathcal{D}}_{z_t}^{j-1},{\mathcal{B}}_{z_b}^j={\mathcal{B}}_{z_t}^{j-1}.$$

(22b)

where t indicates the $top$ of the $j-1$ layer and b indicates the $bottom$ of the j layer. Interlaminar continuity conditions in matrix form are expressed as follows:

$${\left\{\begin{array}{c}U\\ V\\ W\\ \mathrm{\Phi }\\ \mathrm{\Psi }\\ U_{,z}\\ V_{,z}\\ W_{,z}\\ {\mathrm{\Phi }}_{,z}\\ {\mathrm{\Psi }}_{,z}\end{array}\right\}}_b^j={\left[\begin{array}{cccccccccc}1& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0& 0& 0\\ T_1& 0& T_2& T_3& T_4& T_5& 0& 0& 0& 0\\ 0& T_6& T_7& T_8& T_9& 0& T_{10}& 0& 0& 0\\ T_{11}& T_{12}& T_{13}& 0& 0& 0& 0& T_{14}& T_{15}& T_{16}\\ T_{17}& T_{18}& T_{19}& 0& 0& 0& 0& T_{20}& T_{21}& T_{22}\\ T_{23}& T_{24}& T_{25}& 0& 0& 0& 0& T_{26}& T_{27}& T_{28}\end{array}\right]}^{j,j-1}{\left\{\begin{array}{c}U\\ V\\ W\\ \mathrm{\Phi }\\ \mathrm{\Psi }\\ U_{,z}\\ V_{,z}\\ W_{,z}\\ {\mathrm{\Phi }}_{,z}\\ {\mathrm{\Psi }}_{,z}\end{array}\right\}}_t^{j-1}\Rightarrow {\mathit{X}}_b^j={\mathit{T}}^{j,j-1}{\mathit{X}}_t^{j-1}$$

(23)

where ${\mathit{T}}^{j,j-1}$ is the transfer matrix. The full solution along the thickness direction (z) can be obtained thanks to the repeated substitution of Equation (23) into Equation (21) for $M-1$ times, where M is the total number of mathematical layers. This repeated substitution can be written in a compact form as follows:

$${\mathit{X}}^M\left(h_M\right)={\mathit{A}}^{**M}{\mathit{T}}^{M,M-1}\dots {\mathit{T}}^{2,1}{\mathit{A}}^{**1}{\mathit{X}}^1\left(0\right)={\mathit{H}}_{\mathit{m}}{\mathit{X}}^1\left(0\right),$$

(24)

where matrix ${\mathit{H}}_m$ is the multilayered matrix. This matrix includes all geometrical and material peculiarities from the first mathematical layer to the last one. In this way, the bottom ($\tilde{z}=0$) of the first (1) layer is linked with the top ($\tilde{z}=h_M$) of the last (M) layer by means of matrix ${\mathit{H}}_{\mathit{m}}$.

Load boundary conditions must be imposed for both open-circuit and closed-circuit cases. For the open-circuit case, they can be written as follows:

$${\sigma }_{z{z}_t}^M=0,{\sigma }_{\alpha z_t}^M=0,{\sigma }_{\beta z_t}^M=0,{\mathcal{D}}_{z_t}^M=0,{\mathcal{B}}_{z_t}^M=0.$$

(25a)

$${\sigma }_{z{z}_b}^1=0,{\sigma }_{\alpha z_b}^1=0,{\sigma }_{\beta z_b}^1=0,{\mathcal{D}}_{z_b}^1=0,{\mathcal{B}}_{z_b}^1=0.,$$

(25b)

For the closed-circuit case, they are expressed as follows:

$${\sigma }_{z{z}_t}^M=0,{\sigma }_{\alpha z_t}^M=0,{\sigma }_{\beta z_t}^M=0,{\varphi }_t^M=0,{\psi }_t^M=0,$$

(26a)

$${\sigma }_{z{z}_b}^1=0,{\sigma }_{\alpha z_b}^1=0,{\sigma }_{\beta z_b}^1=0,{\varphi }_b^1=0,{\psi }_b^1=0.$$

(26b)

where t is the top of the last (M) layer and b is the bottom of the first (1) layer.

The two load boundary conditions expressed in Equations (25) and (26) can be generally written in matrix form as follows:

$${\mathit{B}}_t^M{\mathit{X}}^M\left(h_M\right)=0,$$

(27)

$${\mathit{B}}_b^1{\mathit{X}}^1\left(0\right)=0,$$

(28)

The final resolution equation is obtained by combining Equation (27) (after the substitution of Equation (24)) and Equation (28):

$$\left[\begin{array}{c}{\mathit{B}}_t^M\\ {\mathit{B}}_b^1\end{array}\right]\left\{\begin{array}{c}{\mathit{X}}^M\left(h_M\right)\\ {\mathit{X}}^1\left(0\right)\end{array}\right\}=\left\{\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right\}\Rightarrow \left[\begin{array}{c}{\mathit{B}}_t^M{\mathit{H}}_{\mathit{m}}\\ {\mathit{B}}_b^1\end{array}\right]{\mathit{X}}^1\left(0\right)=\left\{\begin{array}{c}\mathbf{0}\\ \mathbf{0}\end{array}\right\}\Rightarrow \mathit{E}{\mathit{X}}^1\left(0\right)=\mathbf{0}.$$

(29)

Eigenvalues and eigenvectors can be computed by solving the homogeneous matrix Equation (29). Matrix $\mathit{E}$ is ${\omega }^2$-dependent. Computing the determinant of matrix $\mathit{E}$, ${\omega }^2$ is calculated. In order to obtain the ${\omega }^2$ value that makes the matrix $\mathit{E}$ space null, the smallest value have to be chosen. By substituting the ${\omega }^2$ term in matrix $\mathit{E}$, it becomes purely numerical. By computing the determinant of the purely numeric matrix $\mathit{E}$, eigenvalues and eigenvectors are those that make null the space of matrix $\mathit{E}$. Eigenvalues give the circular frequencies, and eigenvectors give vibration modes through the thickness direction. The solution gives the ${\mathit{X}}^1\left(0\right)$ vector at the bottom of the first layer in order to reconstruct the graphical trends along the thickness direction via the repeated substitution of Equation (23) into Equation (21) for M−1 interfaces.

The presented magneto-electro-elastic 3D shell formulation was implemented using academic in-house code in a Matlab (R2024b) environment called 3DES—Three-Dimensional Exact Solutions.

3. Results

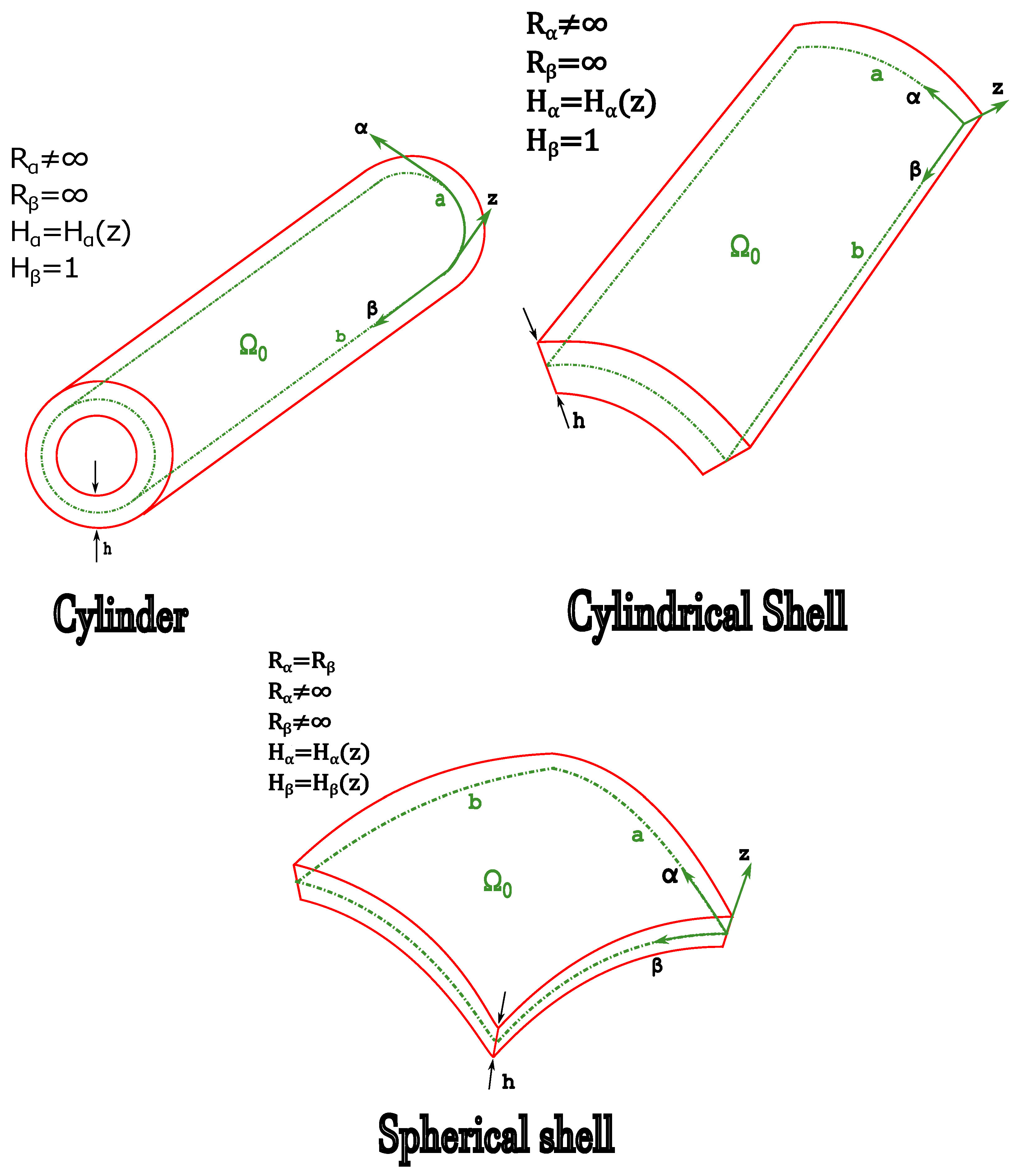
In this section, results obtained using the so called 3D-u-$\varphi$-$\psi$ model are proposed. This acronym aims to shortly collect the main peculiarities of the model: a three-dimensional (3D) formulation where primary variables are displacement components (u), electric potential ($\varphi$) and magnetic potential ($\psi$) (and their first derivatives in z). In the first subsection, the 3D-u-$\varphi$-$\psi$ model is validated using other 3D analytical theories available in the literature. Validation is performed to understand if all possible involved effects in MEE curved structures are correctly depicted (magneto-electro-elastic coupling, material-layer effects, thickness-layer effects and curvature effects). In [36], a convergence analysis for free elastic vibrations suggests $M=300$ mathematical layers and $N=3$ as an exponential matrix expansion in order to obtain correct results for each thickness ratio. The small number of 3D magneto-electro-elastic shell models available in the literature is compensated for by the use of a 3D electro-elastic shell model (3D-u-$\varphi$) and a 3D magneto-elastic shell model (3D-u-$\psi$) to separately validate the electro-elastic coupling and the magneto-elastic coupling in the 3D-u-$\varphi$-$\psi$ model. Validation cases are presented considering different $(m,n)$ half-wave couples couples and $R_{\alpha }/h$ thickness ratios. Therefore, new benchmark cases involving a multilayered cylinder, a multilayered cylindrical panel and a multilayered spherical shell are proposed considering different $(m,n)$ couples, thickness ratios (from thick to thin shells) and load boundary conditions (open- and closed-circuit configurations). When the couple ($m,n$) is imposed, the 3D model provides a huge number of frequencies and thickness vibration modes (theoretically, from I to infinite). In the Results, the first three frequencies (from I to III) are presented for each imposed ($m,n$) couple.

3.1. Validation Cases

In the first validation case, a multilayered, simply supported spherical shell panel is analyzed. The multilayered configuration is PZT-4/$0^{\circ }$/${90}^{\circ }$/$0^{\circ }$/PZT-4. The thickness of each PZT-4 external face is $h_{PZT-4}=0.125h$; the thickness of each composite layer is $h_{Composite}=0.25h$. h is the total thickness of the spherical shell. Geometrical data are collected in

Table 1. Geometrical data on shells for validation cases.

	Case 1	Case 2
a [m]	${\displaystyle \frac{\pi }{3}}{R}_{\alpha }$	${\displaystyle \frac{\pi }{3}}{R}_{\alpha }$
b [m]	${\displaystyle \frac{\pi }{3}}{R}_{\beta }$	1
h [m]	variable	variable
$R_{\alpha }$[m]	10	10
$R_{\beta }$[m]	10	∞

under the first column; material data are presented in

Table 2. Elastic, electric and magnetic characteristics of materials involved in validation cases and new benchmarks.

	PZT-4 [32]	Composite [32]	CoFe2O4 [33]	Adaptive Wood [37]
$E_1$ [GPa]	81.3	172.37	154.32	154.32
$E_2$ [GPa]	81.3	6.895	154.32	154.32
$E_3$ [GPa]	64.5	6.895	142.83	142.83
${\nu }_{12}$	0.329	0.25	0.36564	0.36564
${\nu }_{13}$	0.432	0.25	0.40133	0.40133
${\nu }_{23}$	0.432	0.25	0.40133	0.40133
$G_{12}$ [GPa]	30.6	3.447	56.5	56.5
$G_{13}$ [GPa]	25.6	3.447	45.3	45.3
$G_{23}$ [GPa]	25.6	1.379	45.3	45.3
$e_{15}$ [C/m2]	12.72	0	0	11.6
$e_{24}$ [C/m2]	12.72	0	0	11.6
$e_{31}$ [C/m2]	−5.20	0	0	−4.4
$e_{32}$ [C/m2]	−5.20	0	0	−4.4
$e_{33}$ [C/m2]	15.08	0	0	18.6
${ϵ}_1$ [nF/m]	0.008854	0.008854	0.08	0.08
${ϵ}_2$ [nF/m]	0.008854	0.008854	0.08	0.08
${ϵ}_3$ [nF/m]	0.008854	0.008854	0.093	0.093
$q_{15}$ [T]	0	0	550	560
$q_{24}$ [T]	0	0	550	560
$q_{31}$ [T]	0	0	580.3	580
$q_{32}$ [T]	0	0	580.3	580
$q_{33}$ [T]	0	0	699.7	700
${\mu }_1$ [nH/m]	$4\pi ·{10}^2$	$4\pi ·{10}^2$	$-590·{10}^3$	$590·{10}^3$
${\mu }_2$ [nH/m]	$4\pi ·{10}^2$	$4\pi ·{10}^2$	$-590·{10}^3$	$590·{10}^3$
${\mu }_3$ [nH/m]	$4\pi ·{10}^2$	$4\pi ·{10}^2$	$157·{10}^3$	$157·{10}^3$
$d_1$ [Ns/VC]	0	0	0	$3·{10}^{-12}$
$d_2$ [Ns/VC]	0	0	0	$3·{10}^{-12}$
$d_3$ [Ns/VC]	0	0	0	$3·{10}^{-12}$
$\rho$ [kg/m3]	7600	1500	5300	5300

under the first two columns. The solution used as a reference is the 3D-u-$\varphi$ model in [32], where only the electro-elastic coupling is evaluated. Both closed-circuit (${\varphi }_t^M$ = ${\varphi }_b^1=0$ and ${\psi }_t^M$ = ${\psi }_b^1=0$) and open-circuit (${\mathcal{D}}_{z_t}^M$ = ${\mathcal{D}}_{z_b}^1=0$ and ${\mathcal{B}}_{z_t}^M$ = ${\mathcal{B}}_{z_b}^1=0$) configurations are considered for different $(m,n)$ couples and thickness ratios (from thin to thick structures). Results presented in

Table 3. Case 1: simply supported multilayered electro-elastic spherical shell in closed-circuit configuration.

${\mathit{R}}_{\mathit{\alpha }}/\mathit{h}$		10	20	50	100
$\overline{\omega }=\omega /100$
(1,1)-I	3D-u-$\varphi$ [32]	3.7882	3.4339	3.2971	3.2756
	3D-u-$\varphi$-$\psi$	3.7882	3.4339	3.2971	3.2756
(1,1)-II	3D-u-$\varphi$ [32]	13.388	13.547	13.591	13.597
	3D-u-$\varphi$-$\psi$	13.388	13.547	13.591	13.597
(1,1)-III	3D-u-$\varphi$ [32]	19.879	20.107	20.162	20.170
	3D-u-$\varphi$-$\psi$	19.879	20.107	20.162	20.170
$\overline{\omega }=\omega /100$
(1,2)-I	3D-u-$\varphi$ [32]	5.9061	4.6934	4.0384	3.9198
	3D-u-$\varphi$-$\psi$	5.9061	4.6934	4.0384	3.9198
(1,2)-II	3D-u-$\varphi$ [32]	18.982	19.268	19.349	19.361
	3D-u-$\varphi$-$\psi$	18.982	19.268	19.349	19.361
(1,2)-III	3D-u-$\varphi$ [32]	28.513	29.523	29.794	29.832
	3D-u-$\varphi$-$\psi$	28.513	29.523	29.794	29.832
$\overline{\omega }=\omega /100$
(2,2)-I	3D-u-$\varphi$ [32]	7.6476	5.5963	3.9621	3.5802
	3D-u-$\varphi$-$\psi$	7.6476	5.5963	3.9621	3.5802
(2,2)-II	3D-u-$\varphi$ [32]	25.881	26.821	27.097	27.137
	3D-u-$\varphi$-$\psi$	25.882	26.821	27.097	27.137
(2,2)-III	3D-u-$\varphi$ [32]	36.982	38.175	38.400	38.429
	3D-u-$\varphi$-$\psi$	36.982	38.175	38.400	38.429

(for the closed circuit configuration) and

Table 4. Case 1: simply supported multilayered electro-elastic spherical shell in open-circuit configuration.

${\mathit{R}}_{\mathit{\alpha }}/\mathit{h}$		10	20	50	100
$\overline{\omega }=\omega /100$
(1,1)-I	3D-u-$\varphi$ [32]	3.7864	3.4325	3.2958	3.2744
	3D-u-$\varphi$-$\psi$	3.7864	3.4325	3.2958	3.2744
(1,1)-II	3D-u-$\varphi$ [32]	13.388	13.548	13.592	13.598
	3D-u-$\varphi$-$\psi$	13.388	13.548	13.592	13.598
(1,1)-III	3D-u-$\varphi$ [32]	19.885	20.114	20.169	20.177
	3D-u-$\varphi$-$\psi$	19.885	20.114	20.169	20.177
$\overline{\omega }=\omega /100$
(1,2)-I	3D-u-$\varphi$ [32]	5.9053	4.6926	4.0378	3.9193
	3D-u-$\varphi$-$\psi$	5.9053	4.6926	4.0378	3.9193
(1,2)-II	3D-u-$\varphi$ [32]	18.982	19.268	19.349	19.361
	3D-u-$\varphi$-$\psi$	18.982	19.268	19.349	19.361
(1,2)-III	3D-u-$\varphi$ [32]	28.519	29.529	29.799	29.838
	3D-u-$\varphi$-$\psi$	28.519	29.529	29.799	29.838
$\overline{\omega }=\omega /100$
(2,2)-I	3D-u-$\varphi$ [32]	7.6477	5.5958	3.9616	3.5798
	3D-u-$\varphi$-$\psi$	7.6477	5.5958	3.9616	3.5798
(2,2)-II	3D-u-$\varphi$ [32]	25.882	26.822	27.097	27.137
	3D-u-$\varphi$-$\psi$	25.882	26.822	27.097	27.137
(2,2)-III	3D-u-$\varphi$ [32]	36.991	38.182	38.404	38.434
	3D-u-$\varphi$-$\psi$	36.991	38.182	38.404	38.434

(for the open circuit configuration) in terms of the first three circular frequencies ($\overline{\omega }$) attest to the perfect accordance for each considered $R_{\alpha }/h$. Results are perfectly coincident in both configurations. Thanks to this assessment, electro-elastic coupling in closed- and open-circuit configurations was verified, together with the thickness-layer effect, the material-layer effect and the curvature effect.

The second validation case is devoted to a single-layered cylindrical panel made of a CoFe₂O₄ magnetostrictive material. Geometrical data can be seen in Table 1 (second column). Material data are in the third column of Table 2. In the present validation case, magnetic permittivity coefficients ${\mu }_1$ and ${\mu }_2$ have a negative sign in order to be consistent with the reference solution. The reference solution is the 3D-u-$\psi$ model proposed in [33], where only the magneto-elastic coupling is evaluated. Comparison results regarding the open-circuit configuration (${\mathcal{D}}_{z_t}^M$ = ${\mathcal{D}}_{z_b}^1=0$ and ${\mathcal{B}}_{z_t}^M$ = ${\mathcal{B}}_{z_b}^1=0$) are presented in

Table 5. Case 2: simply supported multilayered magneto-elastic cylindrical panel in open-circuit configuration.

	${\mathit{R}}_{\mathit{\alpha }}/\mathit{h}$	4	10	20	50	100
$\omega$
(1,0)-I	3D-u-$\psi$ [33]	0.00911	0.00395	0.00200	0.00080	0.00040
	3D-u-$\varphi$-$\psi$	0.00911	0.00395	0.00200	0.00080	0.00040
(1,0)-II	3D-u-$\psi$ [33]	0.03103	0.03099	0.03098	0.03098	0.03097
	3D-u-$\varphi$-$\psi$	0.03103	0.03099	0.03098	0.03098	0.03097
(1,0)-III	3D-u-$\psi$ [33]	0.05630	0.05776	0.05794	0.05799	0.05800
	3D-u-$\varphi$-$\psi$	0.05630	0.05776	0.05794	0.05799	0.05800
$\omega$
(2,0)-I	3D-u-$\psi$ [33]	0.03304	0.01700	0.00896	0.00364	0.00183
	3D-u-$\varphi$-$\psi$	0.03304	0.01700	0.00896	0.00364	0.00183
(2,0)-II	3D-u-$\psi$ [33]	0.06193	0.06197	0.06196	0.06195	0.06195
	3D-u-$\varphi$-$\psi$	0.06193	0.06197	0.06196	0.06195	0.06195
(2,0)-III	3D-u-$\psi$ [33]	0.10392	0.11052	0.11131	0.11152	0.11155
	3D-u-$\varphi$-$\psi$	0.10392	0.11052	0.11131	0.11152	0.11155
$\omega$
(3,0)-I	3D-u-$\psi$ [33]	0.06066	0.03622	0.02016	0.00836	0.00420
	3D-u-$\varphi$-$\psi$	0.06066	0.03622	0.02016	0.00836	0.00420
(3,0)-II	3D-u-$\psi$ [33]	0.09256	0.09295	0.09293	0.09293	0.09292
	3D-u-$\varphi$-$\psi$	0.09256	0.09295	0.09293	0.09293	0.09292
(3,0)-III	3D-u-$\psi$ [33]	0.14401	0.16312	0.16538	0.16596	0.16605
	3D-u-$\varphi$-$\psi$	0.14401	0.16312	0.16538	0.16596	0.16605

considering the first three circular frequencies for several $(m,n)$ couples and $R_{\alpha }/h$ thickness ratios (from thick to thin shells). Results collected in Table 5, in terms of circular frequencies, show an accordance for each proposed thickness ratio (thick, moderately thick and thin shells). This assessment is presented in order to separately validate the magneto-elastic coupling in terms of thickness-layer effects, material-layer effects and curvature effects.

3.2. Benchmarks

Thanks to the subsection previously discussed, the 3D-u-$\varphi$-$\psi$ model is considered validated when $M=300$ fictitious layers and $N=3$ for the exponential matrix expansion order are employed. In fact, with these values, all the involved effects in curved MEE smart structures are correctly depicted. New benchmark cases are now proposed and discussed in order to evaluate the full coupling between elastic, magnetic and electric fields. The three proposed benchmarks have the same lamination scheme, i.e.,B Adaptive Wood/$0^{\circ }$/${90}^{\circ }$/$0^{\circ }$/Adaptive Wood. A single adaptive wood external face is $0.05h$ thick, and a single composite lamina is $0.3h$ thick, where h is the total thickness of the structure. Material properties for composite material and adaptive wood are presented in the second and fourth columns of Table 2. For each benchmark, the closed-circuit configuration states ${\varphi }_t^M$ = ${\varphi }_b^1=0$ and ${\psi }_t^M$ = ${\psi }_b^1=0$, and the open-circuit configuration states ${\mathcal{D}}_{z_t}^M$ = ${\mathcal{D}}_{z_b}^1=0$ and ${\mathcal{B}}_{z_t}^M$ = ${\mathcal{B}}_{z_b}^1=0$. Adaptive wood laminae have the same magnetic properties as the CoFe₂O₄ material but with permittivity magnetic coefficients ${\mu }_1$ and ${\mu }_2$ with positive signs, as justified by Pan in [38]. All the other material coefficients are obtained from Tornabene’s book [37].

Benchmark number one (B1) is devoted to a multilayered, simply supported cylinder. Geometrical data on the cylinder are presented in the first column of

Table 6. Geometrical data on shells for new benchmarks.

	B1	B2	B3
a [m]	$2\pi R_{\alpha }$	${\displaystyle \frac{\pi }{3}}{R}_{\alpha }$	${\displaystyle \frac{\pi }{3}}{R}_{\alpha }$
b [m]	10	10	${\displaystyle \frac{\pi }{3}}{R}_{\beta }$
h [m]	variable	variable	variable
$R_{\alpha }$ [m]	10	10	10
$R_{\beta }$ [m]	∞	∞	10

.

Table 7. Benchmark 1: simply supported, multilayered electro-magneto-elastic cylinder in closed-circuit configuration. First three circular frequencies via the 3D-u-$\varphi$-$\psi$ model for each imposed half-wave number couple.

$\overline{\mathit{\omega }}=\mathit{\omega }/100$
${\mathit{R}}_{\mathit{\alpha }}/\mathbf{h}$	4	10	20	50	100
(0,1)-I	6.7531	6.7752	6.7777	6.7784	6.7784
(0,1)-II	8.6009	8.5080	8.4537	8.4303	8.4265
(0,1)-III	14.073	21.879	22.132	22.205	22.216
(0,2)-I	10.149	9.6534	9.0774	8.6008	8.4966
(0,2)-II	13.158	13.496	13.542	13.555	13.556
(0,2)-III	19.022	33.025	43.570	44.148	44.234
(2,1)-I	4.8958	4.6414	4.4990	4.4378	4.4278
(2,1)-II	12.138	12.572	12.660	12.687	12.691
(2,1)-III	15.820	22.260	22.512	22.583	22.593
(2,2)-I	8.7928	8.3013	7.6348	7.0667	6.9400
(2,2)-II	15.950	16.395	16.521	16.568	16.575
(2,2)-III	20.162	33.944	43.726	44.303	44.389
(4,1)-I	4.0332	3.4993	3.1150	2.9179	2.8835
(4,1)-II	16.366	17.703	17.961	18.041	18.053
(4,1)-III	18.487	24.110	24.388	24.460	24.470
(4,2)-I	7.7696	7.1194	6.2119	5.3658	5.1642
(4,2)-II	20.177	21.614	21.999	22.164	22.191
(4,2)-III	22.127	36.349	44.243	44.815	44.898
(6,1)-I	4.2221	3.4544	2.7096	2.1808	2.0701
(6,1)-II	18.648	20.430	20.760	20.858	20.872
(6,1)-III	19.846	29.230	29.782	29.916	29.935
(6,2)-I	7.5204	6.7275	5.5741	4.3365	4.0049
(6,2)-II	21.955	27.299	28.083	28.408	28.461
(6,2)-III	25.230	39.301	45.310	45.874	45.954
(8,1)-I	4.9480	4.0395	2.9860	1.9374	1.6440
(8,1)-II	19.664	21.722	22.066	22.164	22.178
(8,1)-III	20.837	34.724	37.195	37.456	37.492
(8,2)-I	7.7636	6.8686	5.5223	3.8278	3.2930
(8,2)-II	22.289	32.436	33.746	34.263	34.346
(8,2)-III	28.258	41.789	47.425	47.998	48.076
(10,1)-I	5.9251	4.9157	3.6676	2.0785	1.4856
(10,1)-II	20.463	22.811	23.170	23.272	23.287
(10,1)-III	21.723	35.661	45.105	45.558	45.618
(10,2)-I	8.3165	7.3398	5.8649	3.7104	2.8928
(10,2)-II	22.506	36.130	37.926	38.600	38.705
(10,2)-III	29.988	43.563	51.375	52.065	52.157

and

Table 8. Benchmark 1: simply supported, multilayered electro-magneto-elastic cylinder in open-circuit configuration. First three circular frequencies via the 3D-u-$\varphi$-$\psi$ model for each imposed half-wave number couple.

$\overline{\mathit{\omega }}=\mathit{\omega }/100$
${\mathit{R}}_{\mathit{\alpha }}/\mathbf{h}$	4	10	20	50	100
(0,1)-I	6.7531	6.7752	6.7777	6.7784	6.7784
(0,1)-II	8.6015	8.5082	8.4539	8.4305	8.4267
(0,1)-III	14.073	21.881	22.134	22.207	22.218
(0,2)-I	10.150	9.6541	9.0777	8.6010	8.4968
(0,2)-II	13.158	13.496	13.542	13.555	13.556
(0,2)-III	19.022	33.025	43.573	44.152	44.238
(2,1)-I	4.8940	4.6401	4.4978	4.4367	4.4267
(2,1)-II	12.141	12.575	12.664	12.691	12.695
(2,1)-III	15.823	22.261	22.513	22.585	22.595
(2,2)-I	8.7931	8.3013	7.6345	7.0665	6.9398
(2,2)-II	15.951	16.396	16.522	16.569	16.576
(2,2)-III	20.162	33.945	43.729	44.307	44.392
(4,1)-I	4.0309	3.4977	3.1139	2.9171	2.8827
(4,1)-II	16.370	17.707	17.966	18.046	18.057
(4,1)-III	18.493	24.113	24.391	24.463	24.474
(4,2)-I	7.7694	7.1189	6.2114	5.3654	5.1639
(4,2)-II	20.178	21.616	22.001	22.166	22.193
(4,2)-III	22.127	36.350	44.245	44.818	44.902
(6,1)-I	4.2200	3.4529	2.7086	2.1803	2.0697
(6,1)-II	18.650	20.433	20.763	20.860	20.874
(6,1)-III	19.853	29.234	29.789	29.924	29.943
(6,2)-I	7.5200	6.7269	5.5734	4.3361	4.0045
(6,2)-II	21.955	27.302	28.086	28.411	28.464
(6,2)-III	25.232	39.303	45.312	45.878	45.958
(8,1)-I	4.9462	4.0382	2.9851	1.9370	1.6437
(8,1)-II	19.666	21.724	22.067	22.166	22.180
(8,1)-III	20.842	34.725	37.203	37.465	37.501
(8,2)-I	7.7632	6.8679	5.5216	3.8274	3.2927
(8,2)-II	22.289	32.439	33.748	34.266	34.349
(8,2)-III	28.259	41.791	47.428	48.002	48.081
(10,1)-I	5.9237	4.9147	3.6669	2.0781	1.4854
(10,1)-II	20.466	22.812	23.170	23.273	23.288
(10,1)-III	21.724	35.662	45.112	45.567	45.627
(10,2)-I	8.3165	7.3392	5.8642	3.7099	2.8925
(10,2)-II	22.506	36.132	37.929	38.602	38.707
(10,2)-III	29.988	43.566	51.379	52.071	52.163

show the first three circular frequencies for several $R_{\alpha }/h$ thickness ratios and $(m,n)$ couples in closed-circuit and open-circuit configurations, respectively. For each imposed (m,n) couple, the first three vibration modes are discussed. For the closed-circuit configuration, it is possible to notice a slight decrease for the first circular frequency as the thickness ratio increases. This feature is due to the decreasing stiffness of the cylinder. On the contrary, for the second and third circular frequencies, the $\overline{\omega }$ value increases for thin structures. This particular behavior is possible thanks to the curvature effect. This described trend of $\overline{\omega }$ values is valid for all $(m,n)$ couples, except for $(0,1)$. The same considerations mentioned above are also valid for the open-circuit configuration. In Figure 2 and Figure 3, the first three vibration modes in terms of normalized $u^{*}$, $v^{*}$, $w^{*}$, ${\varphi }^{*}$, ${\psi }^{*}$, ${\sigma }_{zz}^{*}$, ${\mathcal{D}}_z^{*}$ and ${\mathcal{B}}_z^{*}$ values are presented along the z thickness direction for the closed-circuit configuration and the open-circuit configuration. In Figure 2, the first two vibration modes are flexural, as $w^{*}$ is symmetrical along the thickness direction, while the third vibration mode is membranal due to the antisymmetrical trend along the thickness direction of $w^{*}$. In addition, the antisymmetrical trend of ${\varphi }^{*}$ and ${\psi }^{*}$ must be noted for each vibration mode. This behavior is typical for such smart structures involving adaptive wood, as piezoelectric and piezomagnetic coefficients $e_{31},e_{32}$ and $q_{31},q_{32}$ have opposite signs. These antisymmetric trends along the thickness direction are also reflected onto the normalized variables (${\mathcal{D}}_z$ and ${\mathcal{B}}_z$). Concerning Figure 3, the first two vibration modes are flexural, and the third one is membranal as well, considering the same trends along the thickness direction for $w^{*}$. Electric and magnetic variables also present the same antisymmetric trend along the thickness direction, as described for the closed-circuit configuration. Normalization is performed considering the maximum value of each variable. The zigzag effect along the thickness direction is evident for both closed-circuit (Figure 2) and open-circuit (Figure 3) configurations. Slopes of variables change in correspondence with each physical interface. A layerwise approach is correctly implemented in the model, as trends along the thickness direction are continuous. For the open-circuit configuration, ${\varphi }_t^M$ = ${\varphi }_b^1=0$ and ${\psi }_t^M$ = ${\psi }_b^1=0$ are correctly imposed; for the closed-circuit configuration, ${\mathcal{D}}_{z_t}^M$ = ${\mathcal{D}}_{z_b}^1=0$ and ${\mathcal{B}}_{z_t}^M$ = ${\mathcal{B}}_{z_b}^1=0$ are opportunely imposed on external surfaces. In Figure 2 and Figure 3, the magneto-electro-elastic coupling, material-layer effects and curvature effects are clearly shown. The differences, in terms of $\overline{\omega }$, are very small between open-circuit and closed-circuit configurations.

In benchmark number two (B2), a multilayered cylindrical panel with simply supported boundary conditions is shown. Geometrical data can be seen in Table 6.

Table 9. Benchmark 2: simply supported, multilayered electro-magneto-elastic cylindrical shell panel in closed-circuit configuration. First three circular frequencies via the 3D-u-$\varphi$-$\psi$ model for each imposed half-wave number couple.

$\overline{\mathit{\omega }}=\mathit{\omega }/100$
${\mathit{R}}_{\mathit{\alpha }}/\mathbf{h}$	4	10	20	50	100
(0,1)-I	6.7531	6.7752	6.7777	6.7784	6.7784
(0,1)-II	8.6009	8.5080	8.4537	8.4303	8.4265
(0,1)-III	14.073	21.879	22.132	22.205	22.216
(0,2)-I	10.149	9.6534	9.0774	8.6008	8.4966
(0,2)-II	13.158	13.496	13.542	13.555	13.556
(0,2)-III	19.022	33.025	43.570	44.148	44.234
(2,1)-I	7.0259	5.9239	4.5542	2.4975	1.5493
(2,1)-II	21.237	23.939	24.318	24.427	24.443
(2,1)-III	22.599	36.672	53.133	53.867	53.961
(2,2)-I	9.0722	8.0181	6.4631	3.8943	2.7334
(2,2)-II	22.759	38.346	40.440	41.176	41.288
(2,2)-III	30.954	44.883	57.184	58.183	58.314
(4,1)-I	14.399	12.829	11.029	7.3454	4.3258
(4,1)-II	25.494	32.230	32.950	33.209	33.249
(4,1)-III	29.610	45.122	67.659	104.60	105.23
(4,2)-I	15.435	13.912	12.088	8.1165	4.8485
(4,2)-II	25.887	45.097	47.834	48.684	48.811
(4,2)-III	35.911	51.730	73.304	105.97	106.72
(6,1)-I	22.092	20.247	18.032	13.586	8.9003
(6,1)-II	31.291	41.446	43.250	43.951	44.066
(6,1)-III	36.951	55.938	76.012	152.37	156.80
(6,2)-I	22.803	20.940	18.767	14.172	9.3032
(6,2)-II	31.578	52.092	55.632	56.716	56.900
(6,2)-III	41.896	58.554	80.793	155.16	157.71
(8,1)-I	29.882	27.852	25.298	20.246	14.445
(8,1)-II	38.984	50.238	53.908	55.490	55.755
(8,1)-III	44.209	60.589	86.208	157.92	208.06
(8,2)-I	30.441	28.351	25.846	20.729	14.796
(8,2)-II	39.290	58.305	64.499	66.100	66.407
(8,2)-III	48.223	63.629	90.132	160.60	208.69
(10,1)-I	34.910	35.574	32.733	27.091	20.555
(10,1)-II	51.615	58.495	64.346	67.336	67.847
(10,1)-III	57.479	64.418	97.490	164.77	258.72
(10,2)-I	55.522	35.965	33.160	27.503	20.869
(10,2)-II	60.851	63.232	73.767	76.337	76.853
(10,2)-III	119.35	70.404	100.69	167.27	259.18

and

Table 10. Benchmark 2: simply supported, multilayered electro-magneto-elastic cylindrical shell panel in open-circuit configuration. First three circular frequencies via the 3D-u-$\varphi$-$\psi$ model for each imposed half-wave number couple.

$\overline{\mathit{\omega }}=\mathit{\omega }/100$
${\mathit{R}}_{\mathit{\alpha }}/\mathbf{h}$	4	10	20	50	100
(0,1)-I	6.7531	6.7752	6.7777	6.7784	6.7784
(0,1)-II	8.6015	8.5082	8.4539	8.4305	8.4267
(0,1)-III	14.073	21.881	22.134	22.207	22.218
(0,2)-I	10.150	9.6541	9.0777	8.6010	8.4968
(0,2)-II	13.158	13.496	13.542	13.555	13.556
(0,2)-III	19.022	33.025	43.573	44.152	44.238
(2,1)-I	7.0251	5.9231	4.5536	2.4971	1.5491
(2,1)-II	21.239	23.940	24.318	24.428	24.444
(2,1)-III	22.599	36.673	53.140	53.876	53.970
(2,2)-I	9.0728	8.0177	6.4625	3.8939	2.7332
(2,2)-II	22.759	38.348	40.442	41.177	41.290
(2,2)-III	30.954	44.885	57.188	58.189	58.320
(4,1)-I	14.410	12.830	11.030	7.3452	4.3257
(4,1)-II	25.500	32.231	32.951	33.209	33.250
(4,1)-III	29.613	45.124	67.659	104.60	105.24
(4,2)-I	15.447	13.914	12.089	8.1164	4.8483
(4,2)-II	25.895	45.100	47.835	48.685	48.812
(4,2)-III	35.914	51.736	73.305	105.98	106.73
(6,1)-I	22.134	20.254	18.034	13.586	8.9003
(6,1)-II	31.348	41.447	43.250	43.951	44.067
(6,1)-III	36.954	55.940	76.012	152.37	156.81
(6,2)-I	22.847	20.946	18.769	14.172	9.3031
(6,2)-II	31.637	52.093	55.634	56.716	56.901
(6,2)-III	41.899	58.558	80.795	155.16	157.72
(8,1)-I	29.980	27.868	25.303	20.247	14.446
(8,1)-II	39.164	50.238	53.908	55.490	55.755
(8,1)-III	44.214	60.599	86.209	157.92	208.07
(8,2)-I	30.541	28.367	25.851	20.730	14.796
(8,2)-II	39.477	58.307	64.501	66.100	66.407
(8,2)-III	48.241	63.640	90.135	160.60	208.70
(10,1)-I	37.037	35.606	32.742	27.092	20.556
(10,1)-II	51.608	58.495	64.347	67.336	67.847
(10,1)-III	57.476	64.443	97.491	164.77	258.73
(10,2)-I	55.538	35.998	33.169	27.504	20.869
(10,2)-II	60.870	63.249	73.769	76.337	76.853
(10,2)-III	71.215	70.415	100.69	167.27	259.19

show the first three circular frequencies ($\overline{\omega }$) for closed- and open-circuit configurations, respectively. Thick and thin (from $R_{\alpha }/h=4$ to $R_{\alpha }/h=100$) structures are presented. In both open- and closed-circuit configurations, the first circular frequency tends to decrease as the cylindrical shell panel becomes thinner (this is true from $(0,2)$ to $(10,2)$ half-wave couples). On the contrary, for a $(0,1)$ half-wave couple, the first $\overline{\omega }$ increases for thinner structures, but the other two frequencies decrease due to the curvature effect. In addition, $\overline{\omega }$ values for $(0,1)$ and $(0,2)$ are quite similar when the thickness ratio changes. For these two half-wave couples, the vibration modes occur at the same frequencies in both closed- and open-circuit configurations. Results for half-wave couples (0, 1) and (0, 2) are the same for cylinders (benchmark 1) and cylindrical panels (benchmark 2) because $m=0$ in the $\alpha$ direction means that it is not important if the a dimension be equal to $2\pi R_{\alpha }$ or equal to ${\displaystyle \frac{\pi }{3}}{R}_{\alpha }$. In Figure 4 (closed-circuit configuration) and Figure 5 (open-circuit configuration), the same eight normalized variables seen in B1 are proposed in the z thickness direction. In Figure 4, the first vibration mode for $R_{\alpha }/h=10$ is flexural, the second and the third are membranal due to the fact that $w^{*}$ has a symmetrical first vibration mode and antisymmetrical trends for the second and third vibration modes along the thickness direction. The particular trends presented in Figure 4 are also influenced by the thickness-layer effect. In addition, the antisymmetrical nature of the normalized electric potential and the normalized magnetic potential is confirmed. In Figure 5, the first vibration mode is purely flexural as $w^{*}$ is constant, while the second and third vibration modes are purely membranous. The antisymmetrical nature of ${\varphi }^{*}$ and ${\psi }^{*}$ is confirmed. The differences between open- and closed-circuit configurations are quite small in terms of $\overline{\omega }$, but they are much more evident in terms of vibration modes through the thickness direction. In both configurations, the change in slope in each different physical layer clearly states the correct depiction of zigzag effects. Interlaminar continuity conditions are correctly imposed, as no discontinuities occur in either interface. Both closed- and open-circuit configurations are properly modeled because, on the external surfaces, the zero value is correctly imposed for electric and magnetic potentials (closed-circuit configuration) and for transverse normal electric displacement and transverse normal magnetic induction (open-circuit configuration). Magneto-electro-elastic effects, curvature effects, material-layer effects and thickness-layer effects are clearly visualized in Figure 4 and Figure 5.

Benchmark number three (B3) proposes a simply supported, multilayered spherical shell. Geometrical data are collected in the third column of Table 6.

Table 11. Benchmark 3: simply supported, multilayered electro-magneto-elastic spherical shell panel in closed-circuit configuration. First three circular frequencies via the 3D-u-$\varphi$-$\psi$ model for each imposed half-wave number couple.

$\overline{\mathit{\omega }}=\mathit{\omega }/100$
${\mathit{R}}_{\mathit{\alpha }}/\mathbf{h}$	4	10	20	50	100
(1,1)-I	4.9572	4.4839	4.0677	3.8110	3.7623
(1,1)-II	17.043	19.514	19.888	19.993	20.008
(1,1)-III	20.610	30.011	30.689	30.848	30.870
(1,2)-I	7.5540	6.8532	5.8896	4.9453	4.7115
(1,2)-II	22.076	26.453	27.293	27.621	27.673
(1,2)-III	23.759	39.143	44.514	45.088	45.166
(2,1)-I	7.8060	7.0518	6.1108	4.9390	4.5763
(2,1)-II	20.236	23.484	23.929	24.047	24.063
(2,1)-III	23.304	36.522	53.397	54.152	54.249
(2,2)-I	9.2978	8.3574	7.0250	5.0406	4.3059
(2,2)-II	22.997	36.851	39.056	39.754	39.858
(2,2)-III	28.927	44.581	57.109	58.137	58.271
(3,1)-I	11.286	10.280	9.0338	6.8168	5.7238
(3,1)-II	23.298	27.379	27.921	28.082	28.103
(3,1)-III	25.694	40.308	64.319	79.360	79.643
(3,2)-I	12.241	11.091	9.5916	6.6963	5.0997
(3,2)-II	24.270	40.467	43.076	43.829	43.937
(3,2)-III	31.786	47.840	69.826	81.305	81.654
(4,1)-I	14.961	13.709	12.201	9.1769	7.0808
(4,1)-II	25.778	31.795	32.561	32.825	32.862
(4,1)-III	29.231	45.011	67.534	104.71	105.35
(4,2)-I	15.635	14.281	12.625	9.1065	6.5079
(4,2)-II	26.201	43.767	46.541	47.356	47.474
(4,2)-III	34.911	51.524	72.761	105.98	106.72
(5,1)-I	18.743	17.265	15.499	11.894	8.7636
(5,1)-II	28.418	36.426	37.614	38.058	38.125
(5,1)-III	32.922	50.297	71.437	129.86	131.13
(5,2)-I	19.249	17.704	15.867	11.918	8.3651
(5,2)-II	28.728	47.378	50.333	51.241	51.381
(5,2)-III	38.225	55.816	76.271	130.76	132.17

presents the first three circular frequencies for different $(m,n)$ couples and different thickness ratios. The first circular frequency for each $(m,n)$ couple decreases as the spherical shell becomes thinner. On the other hand, the second and third circular frequencies increase as the geometry becomes thinner. The same behavior is shown for the open-circuit configuration in

Table 12. Benchmark 3: simply supported, multilayered electro-magneto-elastic spherical shell panel in open-circuit configuration. First three circular frequencies via the 3D-u-$\varphi$-$\psi$ model for each imposed half-wave number couple.

$\overline{\mathit{\omega }}=\mathit{\omega }/100$
${\mathit{R}}_{\mathit{\alpha }}/\mathbf{h}$	4	10	20	50	100
(1,1)-I	4.9523	4.4807	4.0654	3.8090	3.7604
(1,1)-II	17.048	19.516	19.889	19.994	20.010
(1,1)-III	20.612	30.019	30.703	30.864	30.886
(1,2)-I	7.5515	6.8511	5.8880	4.9443	4.7106
(1,2)-II	22.076	26.453	27.293	27.621	27.674
(1,2)-III	23.761	39.144	44.524	45.100	45.180
(2,1)-I	7.8035	7.0498	6.1092	4.9378	4.5752
(2,1)-II	20.241	23.486	23.930	24.048	24.065
(2,1)-III	23.304	36.523	53.404	54.162	54.260
(2,2)-I	9.2970	8.3559	7.0237	5.0397	4.3053
(2,2)-II	22.996	36.854	39.057	39.755	39.859
(2,2)-III	28.937	44.583	57.115	58.147	58.282
(3,1)-I	11.288	10.279	9.0329	6.8160	5.7231
(3,1)-II	23.298	27.380	27.922	28.083	28.104
(3,1)-III	25.700	40.309	64.319	79.369	79.652
(3,2)-I	12.245	11.090	9.5908	6.6956	5.0991
(3,2)-II	24.271	40.471	43.077	43.831	43.939
(3,2)-III	31.798	47.841	69.827	81.313	81.663
(4,1)-I	14.970	13.710	12.201	9.1764	7.0804
(4,1)-II	25.784	31.797	32.562	32.825	32.863
(4,1)-III	29.237	45.012	67.534	104.72	105.36
(4,2)-I	15.646	14.282	12.624	9.1060	6.5075
(4,2)-II	26.209	43.772	46.542	47.357	47.476
(4,2)-III	34.922	51.527	72.762	105.98	106.73
(5,1)-I	18.764	17.268	15.500	11.894	8.7633
(5,1)-II	28.442	36.427	37.615	38.058	38.126
(5,1)-III	32.926	50.298	71.437	129.87	131.14
(5,2)-I	19.272	17.707	15.868	11.918	8.3648
(5,2)-II	28.755	47.382	50.334	51.242	51.383
(5,2)-III	38.234	55.820	76.272	130.77	132.18

. In Figure 6 and Figure 7, all the effects involved in a magneto-electro-elastic smart structure can be seen in both closed- and open-circuit configurations: magneto-electro-elastic coupling, material-layer effects, thickness-layer effects and curvature effects. In Figure 6, thanks to the considerations regarding the trend along the thickness direction of the normalized variable ($w^{*}$), it is possible to state that the first vibration mode is a flexural mode, while the second and third ones are membrane modes. The same consideration is also valid for vibration modes depicted in Figure 7. For both open-circuit and closed-circuit configurations, normalized trends of electric and magnetic potential are antisymmetrical with respect to each other. In addition, a zigzag effect is clearly depicted as the slope changes in each physical layer. A layerwise approach is correctly implemented in the model, as no discontinuities occur in correspondence with each physical interface. Configuration conditions on the external surfaces are correctly imposed in both closed-circuit (see top and bottom values in Figure 6 for $\varphi$ and $\psi$ variables) and open-circuit (see top and bottom values in Figure 7 for ${\mathcal{D}}_z$ and ${\mathcal{B}}_z$ variables) configurations.

4. Conclusions

In this paper, a three-dimensional shell model has been proposed for the magneto-electro-elastic free vibration analysis of simply supported, multilayered smart cylinders; cylindrical panels; and spherical shells. The mixed curvilinear orthogonal reference system allows the three-dimensional governing equations for magneto-electro-elastic spherical shells to be written. The correct evaluation of radii of curvature ($R_{\alpha }$ and $R_{\beta }$) on the reference surface allows for the analysis of several geometries (cylinders, cylindrical panels and spherical shells) using the same 3D governing equations. The resolution methodology involves the use of the Navier harmonic forms in the in-plane directions and the exponential matrix method in the thickness direction. Moreover, a layerwise approach was implemented, considering interlaminar continuity conditions for the three displacement components, the electric potential, the magnetic potential, transverse shear/normal stresses, the transverse normal magnetic induction and transverse normal electric displacement. Validation cases were proposed, comparing results with those of other three-dimensional models. Due to the lack of three-dimensional multilayered magneto-electro-elastic shell models in the literature, validation cases were performed separately considering the electro-elastic effect and the magneto-elastic effect. The present 3D model shows perfect accordance in terms of circular frequencies with results proposed in the literature for considered each thickness ratio and half-wave couple. New benchmark cases propose a fully coupled electro-magneto-elastic analysis for several geometries and different thickness ratios. Results are proposed in tabular form (in terms of circular frequencies) and in graphical form along the thickness direction (in terms of vibration modes). Based on the benchmark cases, the following effects are clearly involved in magneto-electro-elastic curved smart structures: magneto-electro-elastic coupling, thickness-layer effects, material-layer effects and curvature effects. These results can be useful for scientists involved in the development of numerical/analytical 2D/3D models for the magneto-electro-elastic free vibration analysis of curved structures.