Numerical and Experimental Study on the Deformation of Adaptive Elastomer Fibre-Reinforced Composites with Embedded Shape Memory Alloy Wire Actuators
Abstract
1. Introduction
2. Materials and Experimental Results
2.1. Shape Memory Alloy
2.2. Polymer
2.3. Composite
2.4. Specimen with Embedded SMA Actuators


3. Material Modelling
3.1. Shape Memory Alloy
3.2. Polymer
3.3. Composite
4. Numerical Modelling of Deformation Experiments
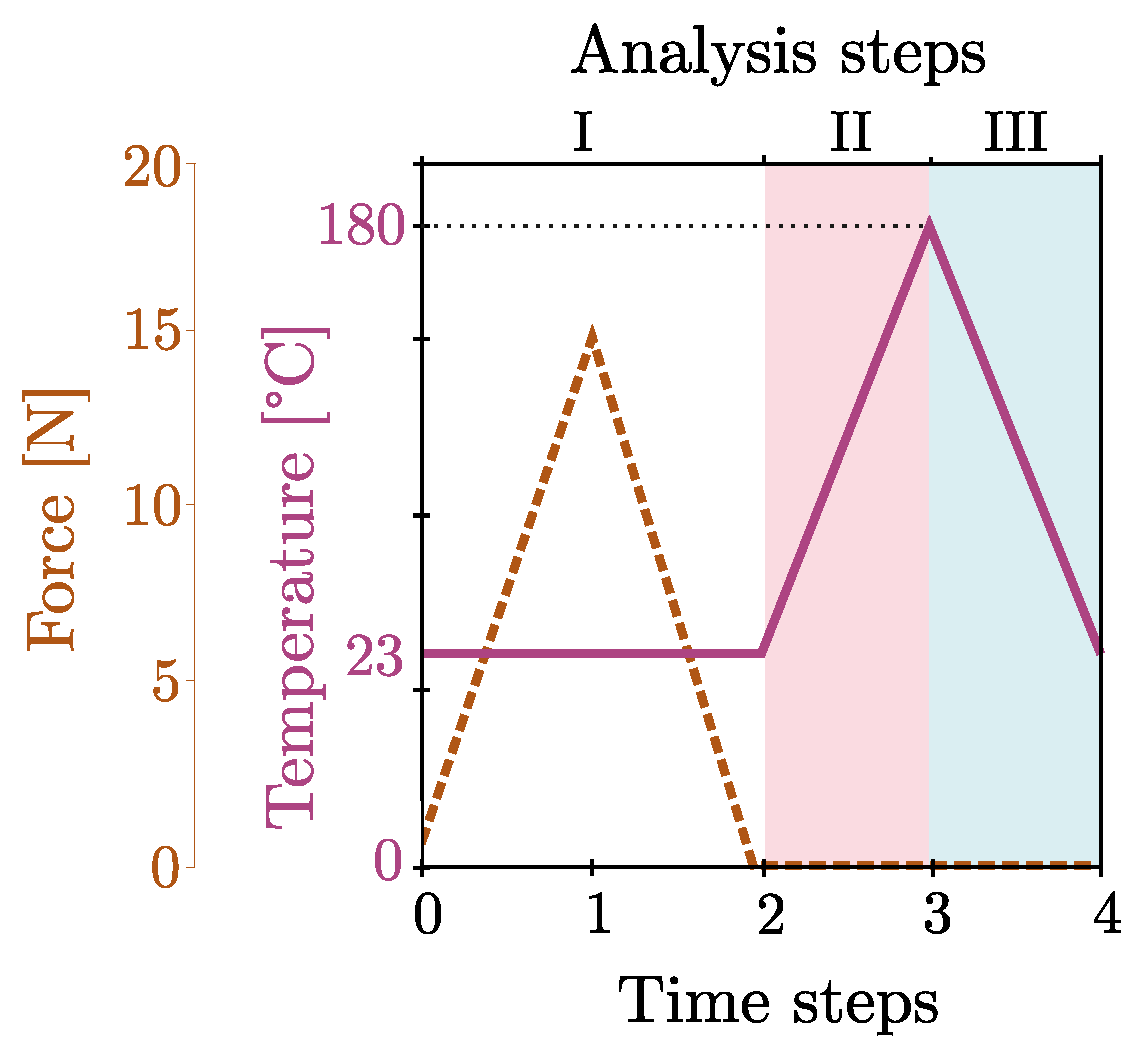
4.1. Multi-Step Analysis
4.2. Finite Element Model
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPU | central processing unit |
| DIN | German Institute for Standardisation |
| DSC | differential scanning calorimetry |
| FEA | finite element analysis |
| GB | gigabyte |
| GF | glass fibre |
| PDMS | dimethylpolysiloxane |
| PTFE | polytetrafluoroethylene |
| RAM | random access memory |
| SE | superelasticity |
| SMA | shape memory alloy |
| SME | shape memory effect |
References
- Intelligence, M. Robotics Market Size & Share Analysis—Growth Trends & Forecasts (2024–2029). Available online: https://www.mordorintelligence.com/industry-reports/soft-robotics-market (accessed on 13 March 2024).
- Majidi, C. Soft-Matter Engineering for Soft Robotics. Adv. Mater. Technol. 2019, 4, 1800477. [Google Scholar] [CrossRef]
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef]
- Case, J.C.; White, E.L.; Kramer, R.K. Soft Material Characterization for Robotic Applications. Soft Robot. 2015, 2, 80–87. [Google Scholar] [CrossRef]
- Rodrigue, H.; Wang, W.; Han, M.W.; Kim, T.J.; Ahn, S.H. An overview of shape memory alloy-coupled actuators and robots. Soft Robot. 2017, 4, 3–15. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. (1980–2015) 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Sobczyk, M.; Wiesenhütter, S.; Noennig, J.R.; Wallmersperger, T. Smart materials in architecture for actuator and sensor applications: A review. J. Intell. Mater. Syst. Struct. 2022, 33, 379–399. [Google Scholar] [CrossRef]
- Sakon, T. (Ed.) Shape Memory Alloys 2017; MDPI AG: Geneva, Switzerland, 2018. [Google Scholar] [CrossRef]
- Costanza, G.; Tata, M.E.; Libertini, R. Effect of Temperature on the Mechanical Behaviour of Ni-Ti Shape Memory Sheets. In TMS 2016: 145th Annual Meeting & Exhibition: Supplemental Proceedings; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 433–439. [Google Scholar] [CrossRef]
- Akbari, S.; Sakhaei, A.H.; Panjwani, S.; Kowsari, K.; Serjouei, A.; Ge, Q. Multimaterial 3D Printed Soft Actuators Powered by Shape Memory Alloy Wires. Sensors Actuators A Phys. 2019, 290, 177–189. [Google Scholar] [CrossRef]
- Alshebly, Y.S.; Nafea, M.; Mohamed Ali, M.S.; Almurib, H.A. Review on recent advances in 4D printing of shape memory polymers. Eur. Polym. J. 2021, 159, 110708. [Google Scholar] [CrossRef]
- Zeng, C.; Liu, L.; Lin, C.; Xin, X.; Liu, Y.; Leng, J. 4D printed continuous fiber reinforced shape memory polymer composites with enhanced mechanical properties and shape memory effects. Compos. Part A Appl. Sci. Manuf. 2024, 180, 108085. [Google Scholar] [CrossRef]
- Waidi, Y.O. Recent Advances in 4D-Printed Shape Memory Actuators. Macromol. Rapid Commun. 2025, 46, 2401141. [Google Scholar] [CrossRef]
- Kluge, A.; Henneberg, J.; Nocke, A.; Cherif, C. Methods for adhesion/friction reduction of novel wire-shaped actuators, based on shape memory alloys, for use in adaptive fiber-reinforced plastic composites. J. Ind. Text. 2015, 44, 757–768. [Google Scholar] [CrossRef]
- Bettini, P.; Riva, M.; Sala, G.; Di Landro, L.; Airoldi, A.; Cucco, J. Carbon Fiber Reinforced Smart Laminates with Embedded SMA Actuators—Part I: Embedding Techniques and Interface Analysis. J. Mater. Eng. Perform. 2009, 18, 664–671. [Google Scholar] [CrossRef]
- Mahmood Baitab, D.; Laila Abang Haji Abdul Majid, D.; Junita Abdullah, E.; Faisal Abdul Hamid, M. A review of techniques for embedding shape memory alloy (SMA) wires in smart composites. Int. J. Eng. Technol. 2018, 7, 129–136. [Google Scholar] [CrossRef]
- Gapeeva, A.; Vogtmann, J.; Zeller-Plumhoff, B.; Beckmann, F.; Gurka, M.; Carstensen, J.; Adelung, R. Electrochemical Surface Structuring for Strong SMA Wire–Polymer Interface Adhesion. ACS Appl. Mater. Interfaces 2021, 13, 21924–21935. [Google Scholar] [CrossRef]
- Cherif, C.; Hickmann, R.; Nocke, A.; Schäfer, M.; Röbenack, K.; Wießner, S.; Gerlach, G. Development and testing of controlled adaptive fiber-reinforced elastomer composites. Text. Res. J. 2018, 88, 345–353. [Google Scholar] [CrossRef]
- Ren, Z.; Zarepoor, M.; Huang, X.; Sabelhaus, A.P.; Majidi, C. Shape Memory Alloy (SMA) Actuator With Embedded Liquid Metal Curvature Sensor for Closed-Loop Control. Front. Robot. AI 2021, 8, 599650. [Google Scholar] [CrossRef]
- Acevedo-Velazquez, A.I.; Wang, Z.; Winkler, A.; Modler, N.; Röbenack, K. Manufacture and Deformation Angle Control of a Two-Direction Soft Actuator Integrated with SMAs. Materials 2024, 17, 758. [Google Scholar] [CrossRef]
- Yu, Y.; Fu, T. Design and Experimental Study of Cavity Structure of Pneumatic Soft Actuator. Actuators 2023, 12, 314. [Google Scholar] [CrossRef]
- Annadata, A.R.; Acevedo-Velazquez, A.I.; Woodworth, L.A.; Gereke, T.; Kaliske, M.; Röbenack, K.; Cherif, C. Investigation and Validation of a Shape Memory Alloy Material Model Using Interactive Fibre Rubber Composites. Materials 2024, 17, 1163. [Google Scholar] [CrossRef]
- Rodinò, S.; Maletta, C. Multiphysics modeling and optimization of an innovative shape memory alloy-polymer active composite. Polymer 2024, 307, 127316. [Google Scholar] [CrossRef]
- Tuyboyov, O.V.; Lee, G.S.; Lee, G.Y. Multi-mode Soft Composite Bending Actuators Based on Glass fiber Textiles Interwoven with Shape Memory Alloy Wires: Development and use in the Preparation of Soft Grippers. Int. J. Precis. Eng. Manuf.-Green Technol. 2023, 10, 1263–1280. [Google Scholar] [CrossRef]
- Lee, J.; Chung, Y.S.; Rodrigue, H. Long Shape Memory Alloy Tendon-based Soft Robotic Actuators and Implementation as a Soft Gripper. Sci. Rep. 2019, 9, 11251. [Google Scholar] [CrossRef] [PubMed]
- Lalegani Dezaki, M.; Bodaghi, M.; Serjouei, A.; Afazov, S.; Zolfagharian, A. Adaptive reversible composite-based shape memory alloy soft actuators. Sensors Actuators A Phys. 2022, 345, 113779. [Google Scholar] [CrossRef]
- Pietsch, M.; Henkel, K.; Körbitz, R.; Hüttner, R.; Uhlig, K.; Bruk, S.; Fischer, M.; Hampe, J.; Richter, A.; Brinkmann, F. A deflectable video camera system for laparoscopic surgery based on shape memory alloy actuators. Sci. Rep. 2025, 15, 11354. [Google Scholar] [CrossRef]
- Wollmann, J.; Muschalski, L.; Wang, Z.; Zichner, M.; Winkler, A.; Modler, N. Application of genetic algorithm for the synthesis of path-generating compliant mechanisms. Smart Mater. Struct. 2023, 33, 015023. [Google Scholar] [CrossRef]
- Coyle, S.; Majidi, C.; LeDuc, P.; Hsia, K.J. Bio-inspired soft robotics: Material selection, actuation, and design. Extrem. Mech. Lett. 2018, 22, 51–59. [Google Scholar] [CrossRef]
- Beter, J.; Schrittesser, B.; Lechner, B.; Mansouri, M.R.; Marano, C.; Fuchs, P.F.; Pinter, G. Viscoelastic Behavior of Glass-Fiber-Reinforced Silicone Composites Exposed to Cyclic Loading. Polymers 2020, 12, 1862. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhong, D.; Rudykh, S.; Zhou, H.; Qu, S.; Yang, W. A Review of Physically Based and Thermodynamically Based Constitutive Models for Soft Materials. J. Appl. Mech. 2020, 87, 110801. [Google Scholar] [CrossRef]
- Whitney, J.M. Basic Mechanics of Fiber Reinforced Composite Materials. Text. Res. J. 1967, 37, 1056–1062. [Google Scholar] [CrossRef]
- Brinson, L. One-Dimensional Constitutive Behavior of Shape Memory Alloys: Thermomechanical Derivation with Non-Constant Material Functions and Redefined Martensite Internal Variable. J. Intell. Mater. Syst. Struct. 1993, 4, 229–242. [Google Scholar] [CrossRef]
- Lagoudas, D.; Hartl, D.; Chemisky, Y.; Machado, L.; Popov, P. Constitutive model for the numerical analysis of phase transformation in polycrystalline shape memory alloys. Int. J. Plast. 2012, 32–33, 155–183. [Google Scholar] [CrossRef]
- Auricchio, F.; Sacco, E. A one-dimensional model for superelastic shape-memory alloys with different elastic properties between austenite and martensite. Int. J. Non-Linear Mech. 1997, 32, 1101–1114. [Google Scholar] [CrossRef]
- He, B.; Dong, X.; Nie, R.; Wang, Y.; Ao, S.; Wang, G. Comprehensive shape memory alloys constitutive models for engineering application. Mater. Des. 2023, 225, 111563. [Google Scholar] [CrossRef]
- Woodworth, L.A.; Wang, X.; Lin, G.; Kaliske, M. A multi-featured shape memory alloy constitutive model incorporating tension–compression asymmetric interpolation. Mech. Mater. 2022, 172, 104392. [Google Scholar] [CrossRef]
- Turner, T.L. A New Thermoelastic Model for Analysis of Shape Memory Alloy Hybrid Composites. J. Intell. Mater. Syst. Struct. 2000, 11, 382–394. [Google Scholar] [CrossRef]
- Pan, J.; Yu, J.; Li, G.; Wu, H.; Pei, X. A lightweight bending actuator based on shape memory alloy and application to gripper. Mech. Adv. Mater. Struct. 2023, 30, 4372–4382. [Google Scholar] [CrossRef]
- Böhm, H.; Winkler, A.; Senf, B.; Voigt, I.; Drossel, W.G.; Gude, M. Experimental and numerical analysis of bending performance for a glass-epoxy composite with integrated sheet-shaped shape memory alloy actuator elements. Mech. Adv. Mater. Struct. 2025, 32, 391–402. [Google Scholar] [CrossRef]
- Airoldi, A.; Rigamonti, D.; Sala, G.; Bettini, P.; Villa, E.; Nespoli, A. Development of an actuated corrugated laminate for morphing structures. Aeronaut. J. 2021, 125, 180–204. [Google Scholar] [CrossRef]
- Böhm, H.; Schmidt, A.; Kopelmann, K.; Hornig, A.; Cherif, C.; Gude, M. Thermomechanical characterisation of a shape memory alloy for numerical modeling of its actuation response. Mater. Res. Express 2024, 11, 125701. [Google Scholar] [CrossRef]
- Moučka, R.; Sedlačík, M.; Osička, J.; Pata, V. Mechanical properties of bulk Sylgard 184 and its extension with silicone oil. Sci. Rep. 2021, 11, 19090. [Google Scholar] [CrossRef]
- Lohse, F.; Kopelmann, K.; Grellmann, H.; Ashir, M.; Gereke, T.; Häntzsche, E.; Sennewald, C.; Cherif, C. Experimental and numerical analysis of the deformation behavior of adaptive fiber-rubber composites with integrated shape memory alloys. Materials 2022, 15, 582. [Google Scholar] [CrossRef]
- Lohse, F.; Annadata, A.R.; Häntzsche, E.; Gereke, T.; Trümper, W.; Cherif, C. Hinged Adaptive Fiber-Rubber Composites Driven by Shape Memory Alloys - Development and Simulation. Materials 2022, 15, 3830. [Google Scholar] [CrossRef]
- Endesfelder, A.; Annadata, A.R.; Acevedo-Velazquez, A.I.; Koenigsdorff, M.; Gerlach, G.; Röbenack, K.; Cherif, C.; Zimmermann, M. Deflection and Performance Analysis of Shape Memory Alloy-Driven Fiber–Elastomer Composites with Anisotropic Structure. Materials 2024, 17, 4855. [Google Scholar] [CrossRef]
- Lohse, F.M. Numerische Auslegung und Entwicklung von adaptiven Strukturen auf Basis von Formgedächtnislegierungen am Beispiel textilverstärkter Elastomerkomposite. Ph.D. Thesis, TUD Dresden University of Technology, Dresden, Germany, 2022. [Google Scholar]
- Souza, A.C.; Mamiya, E.N.; Zouain, N. Three-dimensional model for solids undergoing stress-induced phase transformations. Eur. J. Mech.-A/Solids 1998, 17, 789–806. [Google Scholar] [CrossRef]
- Auricchio, F.; Petrini, L. Improvements and algorithmical considerations on a recent three-dimensional model describing stress-induced solid phase transformations. Int. J. Numer. Methods Eng. 2002, 55, 1255–1284. [Google Scholar] [CrossRef]
- Auricchio, F.; Petrini, L. A three dimensional model describing stress temperature induced solid phase transformations: Solution algorithm and boundary value problems. Int. J. Numer. Methods Eng. 2004, 61, 807–836. [Google Scholar] [CrossRef]
- Auricchio, F.; Petrini, L. A three dimensional model describing stress temperature induced solid phase transformations: Thermomechanical coupling and hybrid composite applications. Int. J. Numer. Methods Eng. 2004, 61, 716–737. [Google Scholar] [CrossRef]
- Grassi, E.N.D.; Chagnon, G.; de Oliveira, H.M.R.; Favier, D. Anisotropy and Clausius-Clapeyron relation for forward and reverse stress-induced martensitic transformations in polycrystalline NiTi thin walled tubes. Mech. Mater. 2020, 146, 103392. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some Forms of the Strain Energy Function for Rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- ANSYS® Enterprise Mechanical, 2023 R1, Help System, Mechanical APDL Material Reference, 4.15 Shape Memory Alloy (SMA). ANSYS, Inc.: Canonsburg, PA, USA, 2023.
- Woodworth, L.A.; Kaliske, M. A temperature dependent constitutive model for functional fatigue in shape memory alloys. Mech. Mater. 2022, 165, 104126. [Google Scholar] [CrossRef]











| Temperature | Symbol | Unit | Value |
|---|---|---|---|
| Martensite Finish | °C | 30 | |
| Martensite Start | °C | 50 | |
| Austenite Start | °C | 67 | |
| Austenite Finish | °C | 77 |
| Property | Parameter | Unit | 23 °C | 60 °C | 90 °C | 130 °C |
|---|---|---|---|---|---|---|
| Elastic modulus | E | N/mm2 | 35,000 | 35,000 | 70,000 | 70,000 |
| Poisson’s ratio | - | 0.3 | 0.3 | 0.3 | 0.3 | |
| Elastic modulus (Martensite) | N/mm2 | 21,650 | 21,650 | 21,650 | 21,650 | |
| Hardening parameter | h | MPa | 600 | 600 | 800 | 1000 |
| Reference temperature | °C | 23 | 60 | 60 | 60 | |
| Temperature scaling | MPa/K | 7.2 | 7.2 | 7.2 | 7.2 | |
| Elastic stress limit | R | MPa | 60 | 120 | 120 | 120 |
| Max. transformation strain | % | 4.0 | 4.0 | 4.0 | 4.0 | |
| Lode parameter | m | - | 0 | 0 | 0 | 0 |
| Parameter | Unit | Value |
|---|---|---|
| C10 | N/mm2 | 0.2204960 |
| C20 | N/mm2 | −0.0339723 |
| C30 | N/mm2 | 0.0422553 |
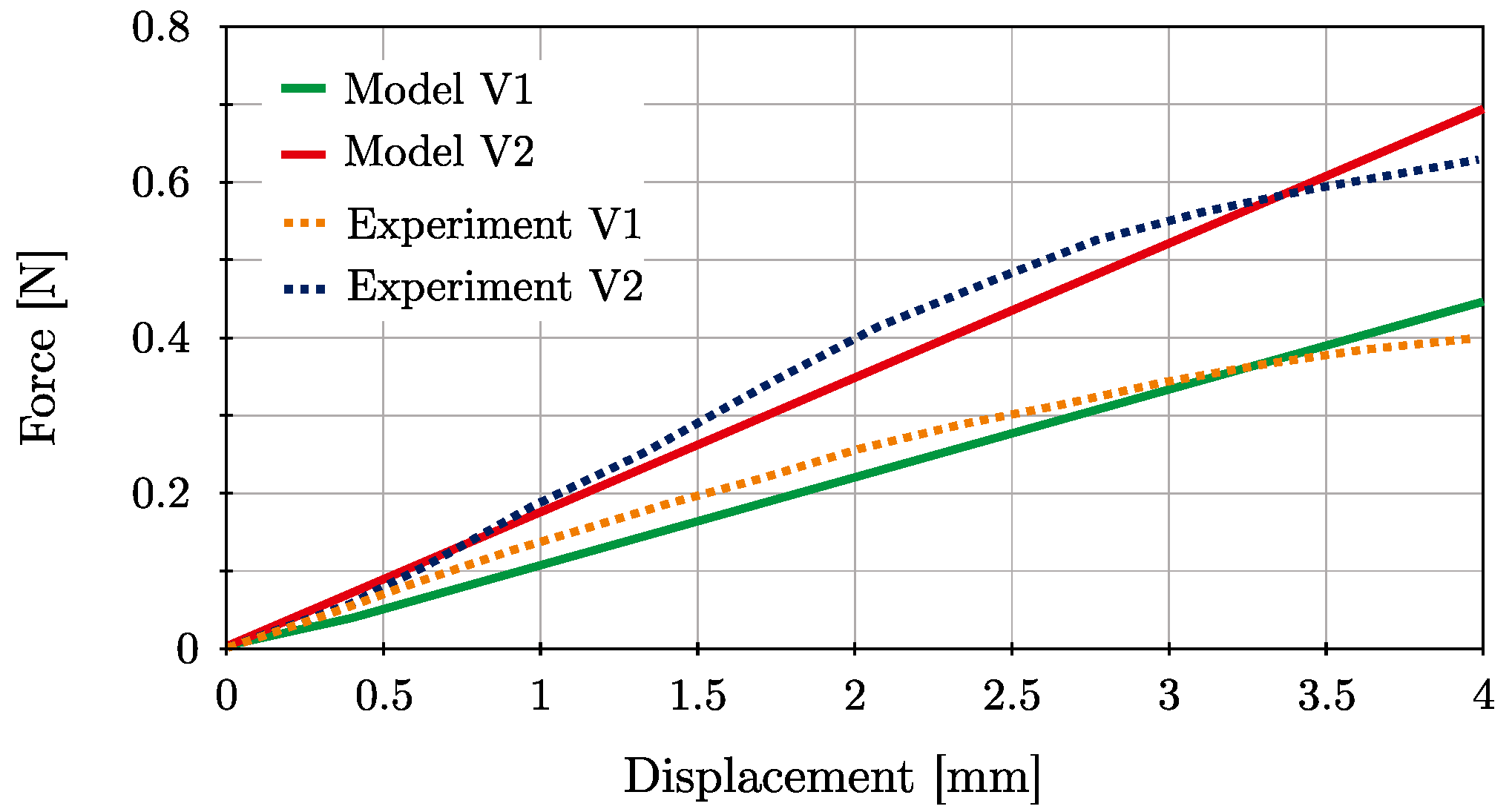
| Configuration | Parameter | Unit | Value |
|---|---|---|---|
| V1 | E | N/mm2 | 450 |
| V2 | E | N/mm2 | 700 |
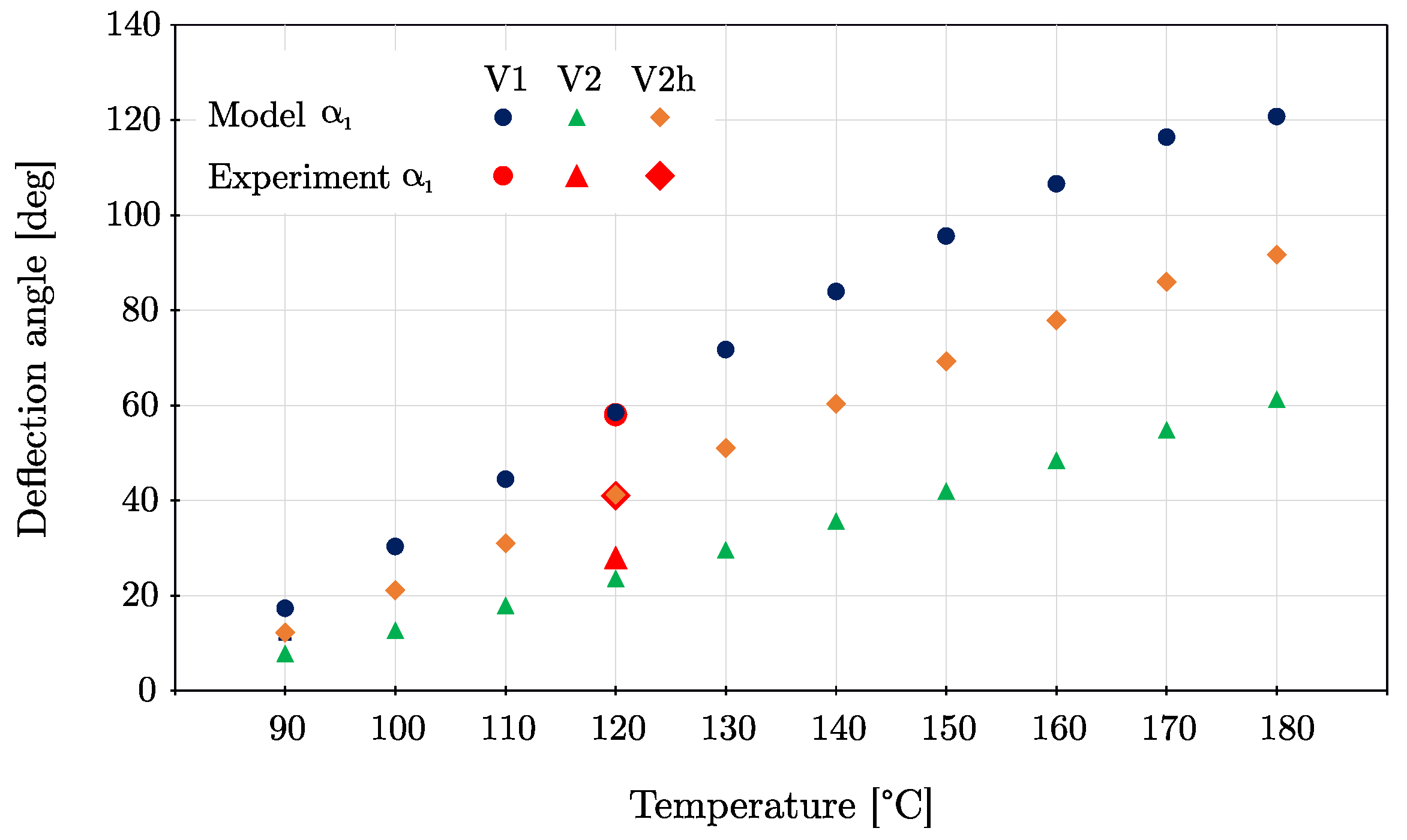
| V1 | V2 | V2h | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T | |||||||||
| °C | mm | deg | mm | deg | mm | deg | |||
| 90 | 13.7 | 1.7 | 17.3 | 6.2 | 0.4 | 7.8 | 9.7 | 1.0 | 12.2 |
| 100 | 23.7 | 4.7 | 30.3 | 10.1 | 1.0 | 12.7 | 16.6 | 2,5 | 21.1 |
| 110 | 34.0 | 9.8 | 44.5 | 14.2 | 1.8 | 17.9 | 24.2 | 5.2 | 31.0 |
| 120 | 43.2 | 16.2 | 58.5 | 18.6 | 3.0 | 23.6 | 31.5 | 9.0 | 41.2 |
| 130 | 50.6 | 23.4 | 71.7 | 23.2 | 4.6 | 29.6 | 39.8 | 13.3 | 51.1 |
| 140 | 56.4 | 30.9 | 83.9 | 27.8 | 6.5 | 35.7 | 43.8 | 18.2 | 60.4 |
| 150 | 60.8 | 38.5 | 95.6 | 32.4 | 8.8 | 42.0 | 48.6 | 23.2 | 69.3 |
| 160 | 64.0 | 46.0 | 106.6 | 36.8 | 11.5 | 48.5 | 52.7 | 28.5 | 77.9 |
| 170 | 65.9 | 52.8 | 116.4 | 41.1 | 14.5 | 54.9 | 56.0 | 33.8 | 86.0 |
| 180 | 66.6 | 55.9 | 120.7 | 45.0 | 17.8 | 61.3 | 58.1 | 37.5 | 91.7 |
| 90 °C | 120 °C | 150 °C | 180 °C | |
|---|---|---|---|---|
| V1 | 170 s | 597 s | 861 s | 1090 s |
| V2 | 172 s | 373 s | 485 s | 727 s |
| V2h | 340 s | 732 s | 859 s | 1689 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Böhm, H.; Hornig, A.; Cherif, C.; Gude, M. Numerical and Experimental Study on the Deformation of Adaptive Elastomer Fibre-Reinforced Composites with Embedded Shape Memory Alloy Wire Actuators. J. Compos. Sci. 2025, 9, 371. https://doi.org/10.3390/jcs9070371
Böhm H, Hornig A, Cherif C, Gude M. Numerical and Experimental Study on the Deformation of Adaptive Elastomer Fibre-Reinforced Composites with Embedded Shape Memory Alloy Wire Actuators. Journal of Composites Science. 2025; 9(7):371. https://doi.org/10.3390/jcs9070371
Chicago/Turabian StyleBöhm, Holger, Andreas Hornig, Chokri Cherif, and Maik Gude. 2025. "Numerical and Experimental Study on the Deformation of Adaptive Elastomer Fibre-Reinforced Composites with Embedded Shape Memory Alloy Wire Actuators" Journal of Composites Science 9, no. 7: 371. https://doi.org/10.3390/jcs9070371
APA StyleBöhm, H., Hornig, A., Cherif, C., & Gude, M. (2025). Numerical and Experimental Study on the Deformation of Adaptive Elastomer Fibre-Reinforced Composites with Embedded Shape Memory Alloy Wire Actuators. Journal of Composites Science, 9(7), 371. https://doi.org/10.3390/jcs9070371









