Abstract
Nanomedicine is rapidly evolving, with tailored nanoparticles enabling precise cellular-level interventions. Despite significant advances, challenges, such as rapid clearance and off-target effects, hinder the clinical translation of many nanosystems. Among the available nanoplatforms, gold nanoparticles (AuNPs) stand out due to their unique surface chemistry, low toxicity, and excellent biocompatibility. In this work, we present a multi-level computational investigation of ultra-small AuNPs coated with non-conventional amphiphilic polymer chains via atomistic and coarse-grained molecular dynamics. Through high-level-resolution atomistic simulations, we investigate how variations in grafting density impact the collective behaviors of these amphiphilic polymer chains within the coating by quantifying relevant conformational, structural, and energetic descriptors, such as the radius of gyration, terminal group presentation, polymer coating thickness, brush height, and solvation energy. Our results reveal a conformational shift of polymer chains from coiled to stretched as grafting density increases, with a direct effect on the polymer conformational regime, terminal group presentation, and coating thickness. In parallel, we further benchmark low-level coarse-grained models using the atomistic data as a reference, demonstrating their ability to correctly reproduce the atomistic trends. This computational investigation reveals how key descriptors vary with grafting density and provides the tools for conducting similar studies on broader time and length scales, thereby advancing the rational design of nanosystems for nanomedicine.
1. Introduction
Nanomedicine is the application of nanotechnology that allows for medical intervention at a single-cell scale, with the purpose of treating and/or diagnosing diseases [1]. Nanomedicine’s transformative potential has been proven in its real-world applications for cancer treatment, facilitating enhanced multimodal tumor imaging [2,3] and enabling the integration of photothermal, chemotherapy, photodynamic, and immunotherapy for improved therapeutic outcomes [4,5].
Although nanomedicine has evolved rapidly over the last decade, it is still facing several challenges, such as extending the circulation time of drugs, minimizing premature clearance, and off-targeting effects [6]. Overcoming these obstacles is crucial for reducing drug dosage and achieving precise targeting to specific tumor cells. Consequently, the development of nanomaterials for cancer diagnosis and treatment has become a primary focus in nanomedical research [7].
Nanoparticles (NPs) are at the forefront of the design and development of these nanomedical platforms, with gold nanoparticles (AuNPs) still remaining among the preferred inorganic NPs due to their easy preparation, controllable size and shape, low toxicity, and high biocompatibility [8]. These NPs offer promising applications in photodynamic and photothermal therapies, catalyzing lipid membrane photo-oxidation [9] and localized heating of tumor sites with minimal invasiveness while also acting as imaging agents across varying imaging modalities [10,11].
However, once NPs are recognized as a foreign material, the immune system actively works to eliminate them by limiting their circulation. Ideally, they should remain in the bloodstream long enough to accumulate at the target site before being cleared. To avoid that, NPs must be given stealth properties, allowing them to remain invisible to the immune system. Another important aspect to be considered in NPs’ design is avoiding tight binding of serum proteins on their surface (i.e., protein corona formation [12]) once they get in contact with the biological milieu [13].
Recently, considerable effort has been made to mitigate these practical issues, with polymer coating of inorganic NPs emerging as a leading strategy. In this respect, the gold standard remains polyethylene glycol (PEG) coating, which offers a combo of biocompatibility, flexibility, and low toxicity [14]. More recently, PEG-based architectures featuring hydrophobic alkyl (ALK) segments covalently bonded to the hydrophilic PEG blocks (ALK-PEG) have been introduced, offering distinct advantages over conventional PEG coatings [15,16]. Amphiphilic polymer coating provides more stable anchoring to the hydrophobic AuNP surface, and its amphipathic nature also allows for precise fine tuning of the hydrophobic/hydrophilic balance within the coating, a key factor for drug loading and release [17,18,19] and the modulation of bio–nano interactions [20]. Moreover, experimental studies have demonstrated the synthesis and biomedical applications of these amphiphilic ALK-PEG ligands with a PEG segment as short as four monomeric units. In particular, the self-assembled monolayers of these short ALK-PEG ligands on gold surfaces create amphiphilic coatings that selectively bind biomolecules and reduce non-specific protein adsorption, making them valuable for biosensing, blood deheparinization, and stealth nanocarrier design [21,22].
However, understanding how variations in critical design parameters of these AuNPs in solution, such as the polymer grafting density [23], impact their conformational and structural properties and, consequently, their interactions with the biological milieu are remarkably complex and require sophisticated computational methods. Multi-level simulation studies, which integrate methods at varying levels of resolution, enables both atomic-level precision and the capture of broader spatial and temporal dynamic processes, supporting in-depth and robust investigation to advance the design and tailoring of nanomedical devices.
Atomistic (AA) and coarse-grained (CG) simulations stand out as a perfect blend of computational approaches to tackle these challenges. On the one hand, AA simulations provide atomic-level details about the nanosystems under study but are limited in system size and simulation time [24,25]. On the other hand, CG simulations enable the study of larger nanosystems over longer time scales, although at the cost of chemical accuracy in the models [26,27,28,29].
In this work, we present a multi-level computational investigation of ultra-small gold nanoparticles coated with amphiphilic alkyl-PEG ligands, providing molecular-level information into their coating behavior. Specifically, we employ AA simulations to explore how grafting density can be tuned to tailor the properties of the amphiphilic polymer coating, assessing the structural and dynamic characteristics of the ligand shell. Expanding on previous work by Franco-Ulloa et al. [30,31], we then use the AA simulations as a reliable reference dataset to benchmark low-resolution CG models based on the MARTINI force field. By combining these multi-level approaches, we not only refine our understanding of nanoparticle functionalization with amphiphilic coatings at the atomistic level but also establish a cost-effective framework for modeling similar nanomaterials with a proper balance between computational cost and accuracy at the coarse-grained level.
We begin by examining how variations in grafting density modulate the stretching of amphiphilic ALK-PEG chains and the terminal group presentation around the AuNP core. Next, we turn our attention to explaining how transitioning from a low to high grafting density regime influences the conformational behavior of amphiphilic ALK-PEG chains within the polymer coating. Finally, we focus our investigation on understanding the extent to which the polymeric shielding of AuNPs—considered in terms of coating thickness—can be modulated by adjusting the grafting density.
2. Computational Methods
2.1. Simulated Models
Two ALK-PEG-coated gold nanoparticle (AuNP) systems with distinct grafting density regimes were studied herein. Each system consists of a spherical Au core approximately 2 nm in diameter, functionalized with ALK-PEG chains attached via the sulfur atom of a thiol group in the AA models. In the CG models, functionalization was implemented to mimic the same attachment pattern as those in its atomistic counterparts. Two grafting density regimes were considered: low (1 ligand/nm2) and high (5 ligands/nm2). For each regime, simulations were conducted at both atomistic and coarse-grained resolutions, resulting in a total of four distinct models. To ensure statistical reliability, three independent replicas were simulated for each system.
To balance computational cost with the demands of all-atom (AA) simulations, our study focuses on a single polymer chain length—we selected the short ALK-PEG ligand as a simple yet biomedically relevant model for mimicking experimental coating compositions while remaining manageable for AA simulations—at the abovementioned representative grafting density commonly achievable in experimental systems [32,33]. This approach enabled us to capture key behaviors while maintaining feasibility for atomistic simulations of polymer-coated nanoparticles.
The grafting density (in ligands/nm2) was estimated from the initial configuration by approximating the gold nanoparticle as a sphere with a diameter of approximately 2 nm and calculating its surface area using the standard formula . To achieve grafting densities of approximately 1 and 5 ligands/nm2, the appropriate number of polymer chains was added accordingly. This grafting density remains constant throughout all AA and CG simulations, as the gold core in both cases preserves its spherical structure and the polymer chains remain anchored via stable covalent bonds.
Figure 1 displays the ALK-PEG-coated AuNPs studied at low and high grafting densities represented at AA (Figure 1a,c) and CG (Figure 1b,d) levels of resolution together with the CG mapping scheme (Figure 1e) and MARTINI building blocks (Figure 1f) adopted in this work.
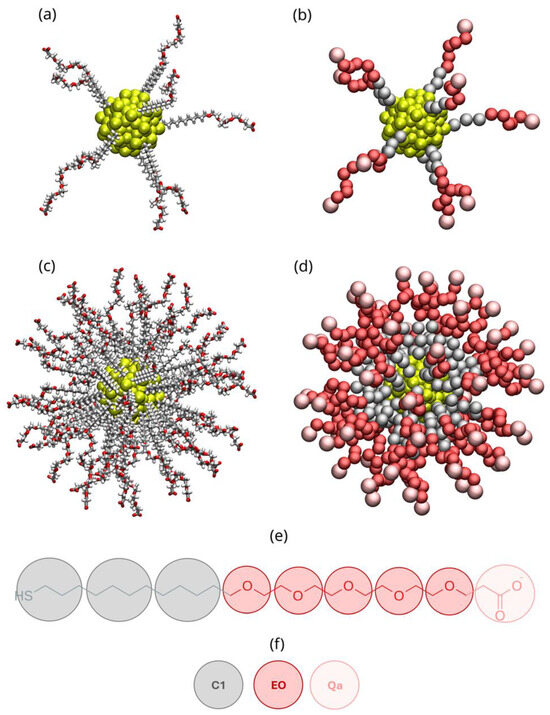
Figure 1.
Initial configurations of ALK−PEG−coated gold nanoparticles. Panels (a,b) display the atomistic and coarse-grained models, respectively, at low grafting density (1 ligand/nm2, top), while panels (c,d) show the corresponding models at high grafting density (5 ligands/nm2, bottom). Panel (e) illustrates the MARTINI mapping scheme used to coarse-grain the atomistic ALK-PEG chain. Panel (f) depicts the MARTINI bead types: C5 (yellow), C1 (silver), EO (red), and Qa (pink). Color scheme for the atomistic model: gold (yellow), carbon (silver), oxygen (red), hydrogen (white).
The amphiphilic ALK-PEG chain consists of a hydrophobic C11-alkyl segment grafted onto the AuNP surface via a thiol group. This alkyl segment functions as a linker, covalently bonding the hydrophobic AuNP core to an intermediate hydrophilic segment composed of five PEG monomeric units, capped at its distal end with a deprotonated (negatively charged) carboxylate group. The chemical formula of the ALK-PEG is HS(CH2)11(CH2OCH2)5CH2COO−.
2.2. Atomistic Simulation Protocol
The AA MD simulations of ALK-PEG-coated AuNPs were carried out using the GROMACS (2021.3 version) package [34,35,36,37,38]. The partial atomic charges for the ALK-PEG chains were derived using the Restrained Electrostatic Potential method (RESP) via the R.E.D. Server [39,40,41]. Initial molecular geometries were optimized at the HF/6-31* level of theory as required for the RESP charge derivation protocol for compatibility with AMBER FF. The electrostatic potential (ESP) was then computed on the optimized geometry, and the RESP method was utilized to obtain the RESP-fitted charges. The General AMBER FF (GAFF) [42,43] parameters were utilized for the assignment of Lennard Jones parameters for each atom type in ALK-PEG using the parmchk2 tool implemented in AMBERTools18 [44]. The AuNP core was generated and coated with the ALK-PEG chains at two different grafting densities (1 ligand/nm2 and 5 ligands/nm2) using the NANOMODELER webserver [31]. The INTERFACE force field [45] parameters were assigned to the Au atoms. PACKMOL [46] was used to solvate the atomistic system models in cubic-shaped simulation boxes with dimensions of 9.6 × 9.6 × 9.6 nm3, filled with SPC/E water molecules [47] at the experimental density of 1 g/cm3. A minimum distance of at least 1 nm between the solute and the box edges was maintained to avoid boundary artifacts. The proper number of Na+ counter-ions was added to ensure the electroneutrality of the system. After energy minimization, the systems were heated up to 303 K and equilibrated for 50 ns, then an NPT MD simulation was run up to 5 µs. The Parrinello–Rahman barostat [48,49] was used to control temperature and pressure. The temperature was set at 303 K and the pressure at 1 atm. Newton’s equations of motion were integrated using the Velocity–Verlet algorithm with a timestep of 2 fs. Long-range electrostatic interactions were handled with the Particle Mesh Ewald (PME) method [50] with a cutoff distance of 12 Å, while short-range repulsive and attractive interactions were treated with the Lennard–Jones (12-6) potential, using Lorentz–Berthelot combining rules. An energy switching function was implemented for the LJ potential, which ramps smoothly between an inner cutoff of 10 Å and an outer cutoff of 12 Å.
2.3. Coarse-Grained Simulation Protocol
The CG MD simulations were carried out using the GROMACS (2021.3 version) package and using the interaction matrix of MARTINI v2.2refPol force field [51,52,53]. The ALK-PEG chains’ topologies were generated with the POLYPLY suite [54] and the interaction matrix for its bead types taken from previous parametrization by Rossi et. al [55,56], further validated as coating ligands for AuNPs by Franco-Ulloa et. al [30]. The CG AuNP core with a 2 nm diameter was constructed from FCC lattices, and the ALK-PEG ligands were grafted on the gold core surface at the same grafting densities adopted for its AA counterpart (1 ligand/nm2 and 5 ligands/nm2) using the NANOMODELER webserver [30]. The AuNP’s beads were modeled as hydrophobic C5 MARTINI interaction sites connected by an elastic network with a force constant of 32,500 kJ mol−1 nm−2. The C5 MARTINI bead mass was assigned to match the bulk density of gold (19.3 g nm−3). PACKMOL [46] was used to solvate the ALK-PEG-coated AuNPs in cubic-shaped simulation boxes with dimensions of 14.9 × 14.9 × 14.9 nm3 using the refined polarizable MARTINI water model optimized for PME electrostatics [48]. The water beads were added at the experimental density of 1 g/cm3, and a minimum distance of at least 1 nm was maintained between the ALK-PEG-coated AuNP and the box edges to prevent boundary artifacts. The proper number of Na+ counter-ions was added to ensure electroneutrality of the systems. After a minimization phase, an equilibration phase was conducted for 50 ns in an NPT ensemble, with the temperature set at 303 K and the pressure set at 1 atm, using the V-rescale thermostat and the isotropic Berendsen ( and ) [57] barostat. Once the systems reached the target temperature and pressure, a production phase 5 µs long was conducted with an integration timestep of 20 fs and coupled to the isotropic Parrinello–Rahman barostat ( and ) [48,49] to keep constant the pressure at 1 atm and the temperature at 303 K.
3. Simulation Analysis
3.1. End-to-End Distance
The end-to-end distance was calculated as the distance between the first and last beads of the ALK-PEG chains in the CG models. For the sake of comparison, the end-to-end distance in the AA ALK-PEG chains was estimated between the centers of mass of the atom groups that correspond to the mapped first and last CG beads.
3.2. Radius of Gyration
The radius of gyration Rg was computed to estimate the effective size of polymer chains, revealing their degree of coiling within the amphiphilic coating. Rg depends on the mass of each atom (in AA models) or bead (in CG models) and their distance from the center of mass of the polymer chains, and it can be expressed by Equation (1):
where is the position vector of the particle, is the center of the mass, and is the mass of the particle.
3.3. Polymer Coating Thickness
To estimate the average coating thickness, we integrated the non-normalized radial number density profile of all particles making up the polymer coating, using the NP core’s geometric center as the reference. Here, the coating thickness is defined as the difference between the position of the NP surface and the maximum distance from it at which 95% of the coating particles are likely to be found [58].
The number density profiles of the ALK-PEG coating particles were calculated at specific distances r from the reference position—defined here as the geometric center of the AuNP core—using a spherical crown thickness of 0.1 Å. This can be read as in Equation (2):
where is the total number of particles in the coating, is the Euclidean distance from the i-th particle to the AuNP’s geometric center, and is the Dirac delta function. The number density profiles and their integration were performed using a Tcl/Tk in-house script in VMD (Visual Molecular Dynamics) [59], setting a spherical crown thickness of 0.1 Å. The coating thickness for each system was estimated as the average distance from the AuNP surface to the radial distance containing a total of 95% of the coating particles. Figures S1 and S2 show the integral curves of the number density profiles of PEG ligands used for coating thickness predictions.
3.4. Brush Height
We estimated the brush height for each simulation replica as the average minimum distance between the terminal groups of grafted ALK-PEG chains and the surface of the AuNP. This minimum distance was estimated for each chain in every frame of the MD trajectory and averaged to obtain the brush height. A global average and the standard deviation were then calculated over all frames to quantify the overall polymer extension from the AuNP surface.
3.5. Statistical Analysis
For the sake of reproducibility, three simulation replicas were run for each AA and CG nanosystem model. For each independent simulation run, the mean and standard deviation values were computed using Equation (3):
The standard deviation over the three independent runs was calculated using the error propagation methods, as given in Equation (4):
where is the number of replicas and is the sum of squares of individual standard deviations of the simulation replicas.
Several structural quantities were computed for both the AA and CG models of the ALK-PEG-coated AuNPs and compared among them. These analyses were carried out using in-house codes via Tcl/Tk scripting in VMD.
All reported quantities were estimated from three independent 5 µs long production simulations, conducted using different initial velocity seeds for both AA and CG systems. From each replica, the final 1 µs segment of the trajectory was used for analysis. This segment was sampled with a stride of 2000 ps to extract 500 configurations per replica. From these, one 1 µs long simulation block was assembled per replica, and the resulting three uncorrelated blocks—one from each independent run—were used to compute the ensemble-averaged values presented in the study.
4. Results and Discussion
In the sections that follow, two different ALK-PEG-coated AuNPs were studied: one with an ALK-PEG chain grafting density of 1 ligand/nm2 and another with a density of 5 ligands/nm2. Both systems feature coatings composed of ALK-PEG chains (please see Section 2 and Section 3 for further details). We begin by investigating how varying grafting densities on the AuNP surface influences the stretching of amphiphilic ALK-PEG chains, polymer conformational brushes, and the presentation of their terminal groups in the coating. Next, we evaluate the impact of grafting density on a key experimental structural descriptor of amphiphilic chains within the coating—the radius of gyration (Rg). By comparing CG and AA data, we critically evaluate the predictive capability of the CG models implemented for this conformational descriptor. Finally, we unveil how the polymeric shielding of the AuNP core, discussed in terms of coating thickness and brush height, and the solvation stability, discussed in terms of nanosystem–solvent non-bonded interactions, are affected by the choice of grafting density. Throughout the results and discussion, we outline the advantages and limitations of CG models in capturing the atomistic behavior of such complex systems in solution.
4.1. Polymer Chain Stretching, Conformational Brushes, and Terminal Group Presentation
Understanding how different surface polymer crowding conditions—modulated by varying the ALK-PEG chain grafting density, a tunable experimental parameter—influence the conformational properties of polymer chains is fundamental for tailoring surface coatings. In this section, we analyze the end-to-end distance of ALK-PEG chains across different grafting densities and compare the results from AA simulations with predictions from their CG counterparts.
In Table 1, we report the average end-to-end distance of ALK-PEG chains coating the 2 nm AuNP with grafting densities of 1 or 5 ligands/nm2, as predicted from three replicas of AA and CG simulations (please see Section 3 for details).

Table 1.
Average end-to-end distances of ALK-PEG chains coating a 2 nm AuNP with grafting density of 1 or 5 ligands/nm2 as predicted by AA and CG simulations. Reported values of end-to-end distance for each replica are averages (±standard deviations) as defined in Equation (3). The overall end-to-end averages (±standard deviations) across all replicas are given as defined in Equation (4).
Table 1.
Average end-to-end distances of ALK-PEG chains coating a 2 nm AuNP with grafting density of 1 or 5 ligands/nm2 as predicted by AA and CG simulations. Reported values of end-to-end distance for each replica are averages (±standard deviations) as defined in Equation (3). The overall end-to-end averages (±standard deviations) across all replicas are given as defined in Equation (4).
| Simulation Resolution | 1 Ligand/nm2 (nm) | 5 Ligands/nm2 (nm) |
|---|---|---|
| AA simulation (Replica #1) | 1.25 (±0.39) | 1.98 (±0.41) |
| AA simulation (Replica #2) | 1.25 (±0.46) | 2.00 (±0.47) |
| AA simulation (Replica #3) | 1.28 (±0.47) | 1.95 (±0.42) |
| AA simulations avg (±std) | 1.26 (±0.26) | 1.98 (±0.25) |
| CG simulation (Replica #1) | 1.85 (±0.39) | 2.11 (±0.27) |
| CG simulation (Replica #2) | 1.85 (±0.37) | 2.11 (±0.27) |
| CG simulation (Replica #3) | 1.82 (±0.39) | 2.11 (±0.27) |
| CG simulations avg (±std) | 1.84 (±0.22) | 2.11 (±0.16) |
Table 1 shows that increasing the grafting density from 1 to 5 ligands/nm2 induces the stretching of ALK-PEG chains within the amphiphilic coating, regardless of the resolution level adopted. This effect indicates that higher grafting densities facilitate the transition from a mushroom-like to a brush-like polymer conformation, likely driven by steric repulsion among densely packed polymer chains.
At low grafting density, the ALK-PEG chains experience minimal crowding, allowing them to adopt a more collapsed conformation near the AuNP surface. While at high grafting density the CG models exhibit excellent agreement with their AA counterparts, with an end-to-end distance deviation of less than 0.20 nm between the means, at low grafting density, CG simulations tend to overestimate the end-to-end distance by approximately 0.60 nm compared to the AA predictions.
To further support the identification of high grafting density yielding to polymer conformational brushes and the low grafting density systems as adopting mushroom-like conformations, we refer to the log–log radial number density profiles shown in Figure S3 (Supplementary Materials). In the top curves of Figure S3 (high grafting density regime), both AA (red stars) and CG (green stars) profiles follow the expected r−4/3 scaling over a wide range of distance from the AuNP surface, confirming the brush-like behavior. For the lower grafting density regime (bottom curves in Figure S3), the density profiles drop more steeply and deviate significantly from the Daoud–Cotton scaling. This behavior is consistent with the mushroom regime, where the polymer chains are more isolated and freer to collapse on the AuNP surface. Due to the lack of chain crowding, both density profiles decay almost linearly, and no power-law scaling is respected.
Figure 2 shows the 2D histogram of distances between the terminal COO− groups of ALK-PEG chains to the AuNP geometric center for the AA and CG models at low and high grafting density regimes.
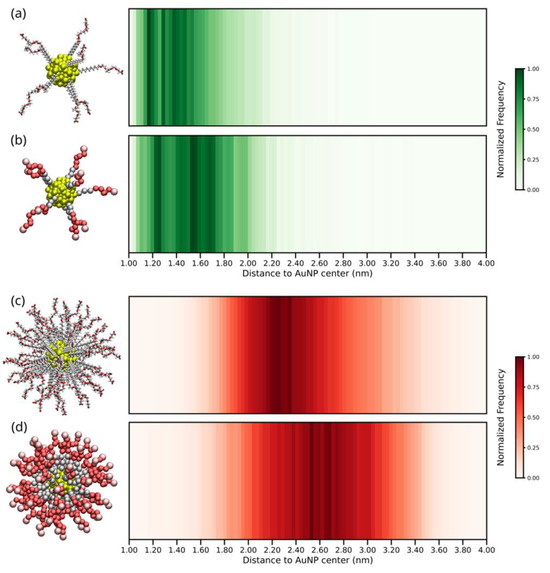
Figure 2.
2D histogram distribution of the distance between terminal COO− groups of ALK-PEG chains and the geometric center of the AuNP core: low grafting density (a) atomistic and (b) coarse-grained models; high grafting density (c) atomistic and (d) coarse-grained models. The x-axis shows the distance (in nm), while the color intensity in the bar on the left-hand side represents the normalized frequency of the COO− group distance occurrence relative to the AuNP core’s geometric center over the simulation time.
Analysis of Figure 2 reveals a trend consistent with the end-to-end distance analysis—the higher the grafting density of ALK-PEG coating on the AuNP surface, the farther the COO− terminal groups expose themselves towards the bulk-water. Interestingly, despite the difference in resolution, similar regions of the histogram are populated across both models, confirming the qualitative predictive capability of CG simulations. However, while CG models show considerable overlap with AA predictions in their histogram distributions, they also populate a broader range of terminal COO− group distances.
Regardless of the resolution level adopted, the end-to-end and terminal COO− group distance analysis consistently reflects the expected transition from low to high grafting density regimes. The longer end-to-end and terminal COO− group distances at higher grafting density are likely due to both the increased number of interactions among the chains and the steric effects imposed by adjacent chains. These factors prevent ALK-PEG chains from collapsing onto the AuNP surface, instead forcing them into an extended configuration towards the bulk-water.
4.2. Radius of Gyration as a Descriptor of Conformational Transitions
Rg is a useful metric for characterizing the spatial extent and flexibility of polymer chains in solution. Here, we examine how different grafting densities affect Rg and evaluate the degree to which CG models reproduce the AA trends. This analysis serves as a critical step in assessing the structural accuracy of CG representations beyond simple chain elongation, as seen in the previous section.
In Table 2, we report the average Rg of ALK-PEG chains coating a 2 nm AuNP with grafting density of 1 or 5 ligands/nm2, respectively, obtained from three AA and CG simulation replicas.

Table 2.
Average Rg of ALK-PEG chains coating a 2 nm AuNP with grafting density of 1 or 5 ligands/nm2 from AA and CG simulations. Reported values of Rg for each replica are averages (±standard deviations), as defined in Equation (3). The overall Rg averages (±standard deviations) across all replicas are given as defined in Equation (4).
Table 2.
Average Rg of ALK-PEG chains coating a 2 nm AuNP with grafting density of 1 or 5 ligands/nm2 from AA and CG simulations. Reported values of Rg for each replica are averages (±standard deviations), as defined in Equation (3). The overall Rg averages (±standard deviations) across all replicas are given as defined in Equation (4).
| Simulation Resolution | 1 Ligand/nm2 (nm) | 5 Ligands/nm2 (nm) |
|---|---|---|
| AA simulation (Replica #1) | 0.58 (±0.09) | 0.67 (±0.10) |
| AA simulation (Replica #2) | 0.57 (±0.09) | 0.68 (±0.11) |
| AA simulation (Replica #3) | 0.60 (±0.08) | 0.66 (±0.10) |
| AA simulations avg (±std) | 0.58 (±0.05) | 0.67 (±0.06) |
| CG simulation (Replica #1) | 0.69 (±0.07) | 0.73 (±0.06) |
| CG simulation (Replica #2) | 0.69 (±0.06) | 0.73 (±0.06) |
| CG simulation (Replica #3) | 0.69 (±0.07) | 0.73 (±0.06) |
| CG simulations avg (±std) | 0.69 (±0.04) | 0.73 (±0.03) |
Similarly to the end-to-end distance analysis, the Rg is always larger for the ALK-PEG chains coating the AuNP with higher grafting density. This is likely due to tighter packing and enhanced interchain interactions promoting more extended ALK-PEG conformations, as previously discussed in Section 4.1.
The CG models slightly overestimate Rg at both grafting densities compared to their AA counterparts. However, the Rg values obtained from AA and CG models show excellent agreement across both grafting densities, with differences between the averages around 0.10 nm, regardless of the resolution level adopted in the simulations.
Furthermore, the AA and CG simulations show a high degree of consistency in the averages among the simulation replicas, confirming the reproducibility of the results. Because Rg represents an important structural parameter for validating the CG models, such a satisfactory level of agreement suggests that our CG models are robust enough for studying the behavior of ALK-PEG-coated AuNPs within the investigated grafting density range.
4.3. Modulation of Coating Thickness and Solvation Stability Through Grafting Density
Coating thickness is a key experimental parameter for understanding the collective behavior of grafted polymers on inorganic supports [60], and it is closely related to the brush height of grafted polymer ligands within the coating layer. Both structural quantities influence the solvation stability of nanosystems in aqueous environments, as interactions between different components of these systems vary with grafting density.
In this section, we predict the coating thickness and brush height using CG models and benchmark the results against reference AA data. In addition, we quantify the solvation energy between the nanosystems and the surrounding solution. This final validation allows us to evaluate the overall reliability of the CG models for simulating such nanosystems.
In Table 3, we report the average monolayer coating thickness by ALK-PEG chains grafted on the 2 nm AuNP at grafting density values of 1 or 5 ligands/nm2 obtained from three AA and CG simulation replicas.

Table 3.
Average monolayer coating thickness and brush height of ALK-PEG-coated 2 nm AuNPs at grafting densities of 1 or 5 ligands/nm2, as predicted by AA and CG simulations. Reported values of coating thickness are averages (±standard deviations) across all simulation replicas, as defined in Equation (3).
Table 3.
Average monolayer coating thickness and brush height of ALK-PEG-coated 2 nm AuNPs at grafting densities of 1 or 5 ligands/nm2, as predicted by AA and CG simulations. Reported values of coating thickness are averages (±standard deviations) across all simulation replicas, as defined in Equation (3).
| Simulation Resolution | 1 Ligand/nm2 (nm) | 5 Ligands/nm2 (nm) | ||
|---|---|---|---|---|
| Coating Thickness | Brush Height | Coating Thickness | Brush Height | |
| AA simulation (Replica #1) | 0.77 | 0.63 ± 0.35 | 1.67 | 1.65 ± 0.40 |
| AA simulation (Replica #2) | 0.70 | 0.68 ± 0.34 | 1.83 | 1.73 ± 0.47 |
| AA simulation (Replica #3) | 0.63 | 0.60 ± 0.23 | 1.63 | 1.64 ± 0.38 |
| AA simulations avg (±std) | 0.70 (0.06) | 0.64 (±0.18) | 1.71 (0.09) | 1.67 (±0.24) |
| CG simulation (Replica #1) | 0.85 | 0.89 (±0.31) | 1.85 | 2.07 (±0.38) |
| CG simulation (Replica #2) | 0.83 | 0.87 (±0.29) | 1.88 | 2.07 (±0.37) |
| CG simulation (Replica #3) | 0.80 | 0.86 (±0.29) | 1.85 | 2.07 (±0.37) |
| CG simulations avg (±std) | 0.83 (0.02) | 0.87 (±0.17) | 1.86 (0.01) | 2.07 (±0.22) |
As expected, transitioning from a low to high density regime results in a pronounced increase—more than two-fold—in the coating thickness surrounding the AuNP core. In the high-density regime, the concerted effect of reduced surface accessibility of the AuNP core to both water molecules and ALK-PEG chains, along with the increased amount of polymer content and enhanced chain–chain interactions, lead to a denser and thicker polymer coating.
The CG simulations effectively capture the pronounced, approximately two-fold increase in coating thickness observed in the transition from low to high grafting density, closely matching the trend predicted at the AA level of resolution. However, in terms of absolute values, the CG models predict thicker polymer coatings compared to their AA counterparts.
These trends in coating thickness are further supported by the analysis of brush height, defined as the average height of ALK-PEG chains from the AuNP surface (Section 3.4). In both AA and CG simulations, brush height increases with ligand density, reflecting the expected stretching of the polymer layer in more densely grafted systems. The values closely follow those of the coating thickness, with AA simulations showing an increase from 0.64 to 1.67 nm and CG simulations from 0.87 to 2.07 nm. This agreement reinforces the reliability of the calculations and highlights the consistent structural behavior captured across different levels of resolution.
Increasing the density of grafted ligands on the AuNP surface not only regulates the coating thickness but also plays a role in modulating the solvation stability of these nanosystems in solution. To assess the effect of varying grafting density regimes on the solvation interaction energy of the nanosystems, we computed the non-bonded interaction energy between the nanosystem and the surrounding solvent for all four systems, both at the AA and CG levels of resolution (Table S1a). Due to the inherent approximations in CG models, direct comparison of absolute solvation interaction energies between AA and CG representations is not meaningful. Instead, we focus on the relative change in solvation interaction energy as the grafting density increases. Specifically, increasing the grafting density of ALK-PEG chains from 1 to 5 ligands/nm² results in a 4.7-fold decrease in solvation interaction energy at the AA level. Notably, a comparable trend is observed in the CG simulations, with an approximate 4.5-fold decrease, indicating consistent behavior across resolutions despite methodological differences.
Next, to evaluate the potential steric stabilization effect of the high grafting regime, we evaluate the non-bonded interaction energies between the AuNP core and the solvent (Table S1b), thereby isolating the influence of the polymer shell. Across both AA and CG models, we see a sharp decrease in core–solvent Lennard–Jones interactions as grafting density increases. At low ligand density, the core remains largely exposed, resulting in considerable attractive LJ interactions with the solvent. In contrast, at high grafting density, these interactions become negligible, reflecting the formation of a dense, protective polymer corona that sterically stops solvent molecules from approaching the core. This trend provides direct energetic evidence of steric stabilization, as the polymer corona increasingly screens the core from solvent contact at higher coverage.
Overall, our findings validate the predictive power of CG models in quantitatively capturing coating thickness and brush height trends across the studied range of grafting densities. While the CG models tend to overestimate the absolute values compared to their AA counterparts, the overall increase in both coating thickness and brush height is accurately reproduced, especially given the inherent limitations and the qualitative nature of CG approaches when modeling such complex systems. Furthermore, as grafting density increases, both AA and CG simulations consistently reflect a significant reduction in solvation energy, highlighting their role in enhancing the overall stability of these nanosystems in solution. Additionally, the sharp decline in core–solvent interactions at higher ligand densities confirms the steric stabilization effect, as the dense polymer corona effectively shields the nanoparticle core from solvent contact.
5. Conclusions
In this work, we investigate, at AA resolution, how variations in grafting density—spanning low and high regimes—affect the structural organization and conformational behavior of amphiphilic ALK-PEG chains coating an ultra-small 2 nm AuNP. Furthermore, we critically evaluate the predictive power of the implemented CG models built on and benchmarked against the AA simulations, taken as a reference.
CG models correctly capture and reproduce AA trends for key structural, conformational, and energetic descriptors, such as end-to-end distances, terminal COO− group distributions, polymer conformational regimes, solvation interaction energy, and Rg, across the investigated grafting densities. While they exhibit a slight overestimation of absolute AA values, statistical analysis confirms that these deviations are within an acceptable range, with no statistically significant difference observed, except in some punctual cases.
These good agreements between AA and CG outcomes provide a robust framework for understanding the grafting density dependence of structural and conformational transitions of amphiphilic ALK-PEG chains within the polymer coating.
As the grafting density increases, both methods predict a significant shift in ALK-PEG chains from mushroom-like to extended brush-like conformations within the coating layer, as seen in the end-to-end distances and Rg and confirmed by the polymer conformational regime analysis. This transition is followed by a more pronounced exposure of terminal COO− groups towards the bulk-water and a more than two-fold increase in the thickness of the amphiphilic ALK-PEG coating, effectively enhancing the shielding of the AuNP core.
These grafting-density-driven transitions put grafting density as a key experimental parameter for modulating polymer conformation and structure, polymer coating thickness, terminal group exposure and distribution, and the nanosystem’s stability in solution. Benchmarking CG models against AA simulations further provides the means to explore time and length scales beyond those accessible with AA simulations, broadening their applicability for studying AuNP-based nanosystems.
Given the important role of polymer coatings in determining AuNP interactions within biological environments, precise control over grafting density opens new opportunities for tailoring surface properties. This is of utmost importance for the rational design of functional nanomaterials, especially in nanomedicine, where tailored surface characteristics will dictate biocompatibility, targeting efficiency, cellular uptake, and, ultimately, the therapeutic outcome. In this context, an in-depth investigation of scaling behavior—particularly the transition between mushroom and brush regimes, as well as the possible existence of a concentrated brush regime across a wider range of grafting densities than explored in this study— and electrokinetic properties (e.g., zeta potential [61]) will be essential to fully understand and optimize these coatings.
As a final remark, we envision that this work will enable efficient bottom–up studies of analogous AuNP systems, readily extendable for studies of controlled bio–nano interactions and drug delivery applications.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/jcs9060294/s1, Figure S1: Cumulative number of ALK-PEG coating particles as a function of radial distance from the center of the Au nanoparticle core from atomistic simulations. Figure S2: Cumulative number of ALK-PEG coating particles as a function of radial distance from the center of the Au nanoparticle core from coarse-grained simulations. Figure S3: Number density profiles as a function of distance from the AuNP surface. Figure S4: TCL/Tk script utilized to calculate the average radius of gyration (Rg) of ALK-PEG residues across multiple frames of a molecular dynamics trajectory using the VMD command line. Figure S5: TCL/Tk script utilized to calculate the average end-to-end distance of ALK-PEG residues across multiple frames of a molecular dynamics trajectory using the VMD command line. Table S1: Non-bonded interaction energies between the Au nanoparticle and the solution and between the nanosystem and the solution.
Author Contributions
Conceptualization, P.S. and C.D.V.; methodology, P.S.; formal analysis, P.S., E.D. and M.D.; investigation, P.S, E.D., G.F. and M.D.; resources, C.D.V.; data curation, P.S. and M.D.; writing—original draft preparation, P.S.; writing—review and editing, P.S, E.D., G.F. and C.D.V.; supervision, P.S and C.D.V.; project administration, C.D.V.; funding acquisition, C.D.V. All authors have read and agreed to the published version of the manuscript.
Funding
This project has received funding from the European Union’s Horizon—NextGenerationEU through the Italian Ministry of University and Research under PNRR—M4C2-l1.3 Project PE_00000019 “HEAL ITALIA” to Cristiana Di Valentin CUP H43C22000830006 of the University of Milano Bicocca.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author(s).
Acknowledgments
We thank Roberto Fiammengo and Emanuele Papini for their useful discussions and Lorenzo Ferraro for his technical support.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in the manuscript:
| NP | Nanoparticle |
| AuNP | Gold nanoparticle |
| ALK | Alkyl |
| PEG | Polyethylene Glycol |
| ALK-PEG | Alkyl Polyethylene glycol |
| AA | Atomistic |
| CG | Coarse-grained |
| Rg | Radius of gyration |
References
- Webster, T.J. Nanomedicine: What’s in a Definition? Int. J. Nanomed. 2006, 1, 115–116. [Google Scholar] [CrossRef] [PubMed]
- Bouché, M.; Hsu, J.C.; Dong, Y.C.; Kim, J.; Taing, K.; Cormode, D.P. Recent Advances in Molecular Imaging with Gold Nanoparticles. Bioconjug. Chem. 2020, 31, 303–314. [Google Scholar] [CrossRef] [PubMed]
- Alle, M.; Sharma, G.; Lee, S.-H.; Kim, J.-C. Next-Generation Engineered Nanogold for Multimodal Cancer Therapy and Imaging: A Clinical Perspectives. J. Nanobiotechnol. 2022, 20, 222. [Google Scholar] [CrossRef] [PubMed]
- Turkmen Koc, S.N.; Rezaei Benam, S.; Aral, I.P.; Shahbazi, R.; Ulubayram, K. Gold Nanoparticles-Mediated Photothermal and Photodynamic Therapies for Cancer. Int. J. Pharm. 2024, 655, 124057. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Yung, L.-Y.L.; Tan, P.H.; Bay, B.H. Harnessing the Immunogenic Potential of Gold Nanoparticle-Based Platforms as a Therapeutic Strategy in Breast Cancer Immunotherapy: A Mini Review. Front. Immunol. 2022, 13, 865554. [Google Scholar] [CrossRef]
- Wu, L.-P.; Wang, D.; Li, Z. Grand Challenges in Nanomedicine. Mater. Sci. Eng. C 2020, 106, 110302. [Google Scholar] [CrossRef]
- Kurul, F.; Turkmen, H.; Cetin, A.E.; Topkaya, S.N. Nanomedicine: How Nanomaterials Are Transforming Drug Delivery, Bio-Imaging, and Diagnosis. Next Nanotechnol. 2025, 7, 100129. [Google Scholar] [CrossRef]
- Arvizo, R.; Bhattacharya, R.; Mukherjee, P. Gold Nanoparticles: Opportunities and Challenges in Nanomedicine. Expert. Opin. Drug Deliv. 2010, 7, 753–763. [Google Scholar] [CrossRef]
- De Souza, R.M.; Siani, P.; Schmidt, T.F.; Itri, R.; Dias, L.G. Methylene Blue Location in (Hydroperoxized) Cardiolipin Monolayer: Implication in Membrane Photodegradation. J. Phys. Chem. B 2017, 121, 8512–8522. [Google Scholar] [CrossRef]
- Siani, P.; de Souza, R.M.; Dias, L.G.; Itri, R.; Khandelia, H. An Overview of Molecular Dynamics Simulations of Oxidized Lipid Systems, with a Comparison of ELBA and MARTINI Force Fields for Coarse Grained Lipid Simulations. Biochim. Biophys. Acta BBA-Biomembr. 2016, 1858, 2498–2511. [Google Scholar] [CrossRef]
- Riley, R.S.; Day, E.S. Gold Nanoparticle-mediated Photothermal Therapy: Applications and Opportunities for Multimodal Cancer Treatment. WIREs Nanomed. Nanobiotechnol. 2017, 9, e1449. [Google Scholar] [CrossRef] [PubMed]
- Siani, P.; Di Valentin, C. Effect of Dopamine-Functionalization, Charge and PH on Protein Corona Formation around TiO2 Nanoparticles. Nanoscale 2022, 14, 5121–5137. [Google Scholar] [CrossRef] [PubMed]
- Piella, J.; Bastús, N.G.; Puntes, V. Size-Dependent Protein–Nanoparticle Interactions in Citrate-Stabilized Gold Nanoparticles: The Emergence of the Protein Corona. Bioconjug. Chem. 2017, 28, 88–97. [Google Scholar] [CrossRef]
- Zhang, X.-D.; Wu, D.; Shen, X.; Liu, P.-X.; Yang, N.; Zhao, B.; Zhang, H.; Sun, Y.-M.; Zhang, L.-A.; Fan, F.-Y. Size-Dependent in Vivo Toxicity of PEG-Coated Gold Nanoparticles. Int. J. Nanomed. 2011, 6, 2071. [Google Scholar] [CrossRef]
- Tarnawski, R.; Ulbricht, M. Amphiphilic Gold Nanoparticles: Synthesis, Characterization and Adsorption to PEGylated Polymer Surfaces. Colloids Surf. A Physicochem. Eng. Asp. 2011, 374, 13–21. [Google Scholar] [CrossRef]
- Lin, C.-A.J.; Sperling, R.A.; Li, J.K.; Yang, T.Y.; Li, P.-Y.; Zanell, M.; Chang, W.H.; Parak, W.J. Design of an Amphiphilic Polymer for Nanoparticle Coating and Functionalization. In Bio-Nano Interfaces; Jenny Stanford Publishing: New York, NY, USA, 2024; pp. 361–379. [Google Scholar]
- Motta, S.; Siani, P.; Levy, A.; Di Valentin, C. Exploring the Drug Loading Mechanism of Photoactive Inorganic Nanocarriers through Molecular Dynamics Simulations. Nanoscale 2021, 13, 13000–13013. [Google Scholar] [CrossRef]
- Motta, S.; Siani, P.; Donadoni, E.; Frigerio, G.; Bonati, L.; Di Valentin, C. Metadynamics Simulations for the Investigation of Drug Loading on Functionalized Inorganic Nanoparticles. Nanoscale 2023, 15, 7909–7919. [Google Scholar] [CrossRef]
- Frigerio, G.; Motta, S.; Siani, P.; Donadoni, E.; Di Valentin, C. Unveiling the Drug Delivery Mechanism of Graphene Oxide Dots at the Atomic Scale. J. Control. Release 2025, 379, 344–362. [Google Scholar] [CrossRef]
- Donadoni, E.; Siani, P.; Frigerio, G.; Milani, C.; Cui, Q.; Di Valentin, C. The Effect of Polymer Coating on Nanoparticles’ Interaction with Lipid Membranes Studied by Coarse-Grained Molecular Dynamics Simulations. Nanoscale 2024, 16, 9108–9122. [Google Scholar] [CrossRef]
- Gonçalves, I.C.; Martins, M.C.L.; Barbosa, M.A.; Naeemi, E.; Ratner, B.D. Selective Protein Adsorption Modulates Platelet Adhesion and Activation to Oligo(Ethylene Glycol)-Terminated Self-Assembled Monolayers with C18 Ligands. J. Biomed. Mater. Res. A 2009, 89, 642–653. [Google Scholar] [CrossRef]
- Martins, M.C.L.; Ochoa-Mendes, V.; Ferreira, G.; Barbosa, J.N.; Curtin, S.A.; Ratner, B.D.; Barbosa, M.A. Interactions of Leukocytes and Platelets with Poly(Lysine/Leucine) Immobilized on Tetraethylene Glycol-Terminated Self-Assembled Monolayers. Acta Biomater. 2011, 7, 1949–1955. [Google Scholar] [CrossRef] [PubMed]
- Donadoni, E.; Siani, P.; Gambari, S.; Campi, D.; Frigerio, G.; Di Valentin, C. Optimizing Polyethylene Glycol Coating for Stealth Nanodiamonds. ACS Appl. Mater. Interfaces 2025, 17, 19304–19316. [Google Scholar] [CrossRef] [PubMed]
- Dahal, U.; Dormidontova, E.E. Chain Conformation and Hydration of Polyethylene Oxide Grafted to Gold Nanoparticles: Curvature and Chain Length Effect. Macromolecules 2020, 53, 8160–8170. [Google Scholar] [CrossRef]
- Brancolini, G.; Toroz, D.; Corni, S. Can Small Hydrophobic Gold Nanoparticles Inhibit β2-Microglobulin Fibrillation? Nanoscale 2014, 6, 7903–7911. [Google Scholar] [CrossRef]
- Colangelo, E.; Chen, Q.; Davidson, A.M.; Paramelle, D.; Sullivan, M.B.; Volk, M.; Lévy, R. Computational and Experimental Investigation of the Structure of Peptide Monolayers on Gold Nanoparticles. Langmuir 2017, 33, 438–449. [Google Scholar] [CrossRef]
- Gabellini, C.; Şologan, M.; Pellizzoni, E.; Marson, D.; Daka, M.; Franchi, P.; Bignardi, L.; Franchi, S.; Posel, Z.; Baraldi, A.; et al. Spotting Local Environments in Self-Assembled Monolayer-Protected Gold Nanoparticles. ACS Nano 2022, 16, 20902–20914. [Google Scholar] [CrossRef]
- Şologan, M.; Marson, D.; Polizzi, S.; Pengo, P.; Boccardo, S.; Pricl, S.; Posocco, P.; Pasquato, L. Patchy and Janus Nanoparticles by Self-Organization of Mixtures of Fluorinated and Hydrogenated Alkanethiolates on the Surface of a Gold Core. ACS Nano 2016, 10, 9316–9325. [Google Scholar] [CrossRef]
- Siani, P.; Khandelia, H.; Orsi, M.; Dias, L.G. Parameterization of a Coarse-Grained Model of Cholesterol with Point-Dipole Electrostatics. J. Comput. Aided Mol. Des. 2018, 32, 1259–1271. [Google Scholar] [CrossRef]
- Franco-Ulloa, S.; Riccardi, L.; Rimembrana, F.; Grottin, E.; Pini, M.; De Vivo, M. NanoModeler CG: A Tool for Modeling and Engineering Functional Nanoparticles at a Coarse-Grained Resolution. J. Chem. Theory Comput. 2023, 19, 1582–1591. [Google Scholar] [CrossRef]
- Franco-Ulloa, S.; Riccardi, L.; Rimembrana, F.; Pini, M.; De Vivo, M. Nano Modeler: A Webserver for Molecular Simulations and Engineering of Nanoparticles. J. Chem. Theory Comput. 2019, 15, 2022–2032. [Google Scholar] [CrossRef]
- Corbierre, M.K.; Cameron, N.S.; Lennox, R.B. Polymer-Stabilized Gold Nanoparticles with High Grafting Densities. Langmuir 2004, 20, 2867–2873. [Google Scholar] [CrossRef]
- Lu, J.; Xue, Y.; Shi, R.; Kang, J.; Zhao, C.-Y.; Zhang, N.-N.; Wang, C.-Y.; Lu, Z.-Y.; Liu, K. A Non-Sacrificial Method for the Quantification of Poly(Ethylene Glycol) Grafting Density on Gold Nanoparticles for Applications in Nanomedicine. Chem. Sci. 2019, 10, 2067–2074. [Google Scholar] [CrossRef] [PubMed]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A Message-Passing Parallel Molecular Dynamics Implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Páll, S.; Abraham, M.J.; Kutzner, C.; Hess, B.; Lindahl, E. Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS. In Solving Software Challenges for Exascale; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2015; Volume 8759, pp. 3–27. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Vanquelef, E.; Simon, S.; Marquant, G.; Garcia, E.; Klimerak, G.; Delepine, J.C.; Cieplak, P.; Dupradeau, F.-Y.R.E.D. Server: A Web Service for Deriving RESP and ESP Charges and Building Force Field Libraries for New Molecules and Molecular Fragments. Nucleic Acids Res. 2011, 39 (Suppl. 2), W511–W517. [Google Scholar] [CrossRef]
- Dupradeau, F.-Y.; Pigache, A.; Zaffran, T.; Savineau, C.; Lelong, R.; Grivel, N.; Lelong, D.; Rosanski, W.; Cieplak, P. The R.E.D. Tools: Advances in RESP and ESP Charge Derivation and Force Field Library Building. Phys. Chem. Chem. Phys. 2010, 12, 7821. [Google Scholar] [CrossRef]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic Atom Type and Bond Type Perception in Molecular Mechanical Calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Cerutti, D.S.; Cisneros, G.A.; Cruzeiro, V.W.D.; Forouzesh, N.; Giese, T.J.; Götz, A.W.; Gohlke, H.; et al. AmberTools. J. Chem. Inf. Model. 2023, 63, 6183–6191. [Google Scholar] [CrossRef] [PubMed]
- Heinz, H.; Lin, T.-J.; Kishore Mishra, R.; Emami, F.S. Thermodynamically Consistent Force Fields for the Assembly of Inorganic, Organic, and Biological Nanostructures: The INTERFACE Force Field. Langmuir 2013, 29, 1754–1765. [Google Scholar] [CrossRef] [PubMed]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Nosé, S.; Klein, M.L. Constant Pressure Molecular Dynamics for Molecular Systems. Mol. Phys. 1983, 50, 1055–1076. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Michalowsky, J.; Schäfer, L.V.; Holm, C.; Smiatek, J. A Refined Polarizable Water Model for the Coarse-Grained MARTINI Force Field with Long-Range Electrostatic Interactions. J. Chem. Phys. 2017, 146, 054501. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
- Michalowsky, J.; Zeman, J.; Holm, C.; Smiatek, J. A Polarizable MARTINI Model for Monovalent Ions in Aqueous Solution. J. Chem. Phys. 2018, 149, 163319. [Google Scholar] [CrossRef] [PubMed]
- Grünewald, F.; Alessandri, R.; Kroon, P.C.; Monticelli, L.; Souza, P.C.T.; Marrink, S.J. Polyply; a Python Suite for Facilitating Simulations of Macromolecules and Nanomaterials. Nat. Commun. 2022, 13, 68. [Google Scholar] [CrossRef] [PubMed]
- Rossi, G.; Fuchs, P.F.J.; Barnoud, J.; Monticelli, L. A Coarse-Grained MARTINI Model of Polyethylene Glycol and of Polyoxyethylene Alkyl Ether Surfactants. J. Phys. Chem. B 2012, 116, 14353–14362. [Google Scholar] [CrossRef] [PubMed]
- Grunewald, F.; Rossi, G.; de Vries, A.H.; Marrink, S.J.; Monticelli, L. Transferable MARTINI Model of Poly(Ethylene Oxide). J. Phys. Chem. B 2018, 122, 7436–7449. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Siani, P.; Bianchetti, E.; Di Valentin, C. Building up Accurate Atomistic Models of Biofunctionalized Magnetite Nanoparticles from First-Principles Calculations. NPJ Comput. Mater. 2025, 11, 20. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Krpetić, Ž.; Davidson, A.M.; Volk, M.; Lévy, R.; Brust, M.; Cooper, D.L. High-Resolution Sizing of Monolayer-Protected Gold Clusters by Differential Centrifugal Sedimentation. ACS Nano 2013, 7, 8881–8890. [Google Scholar] [CrossRef]
- Siani, P.; Frigerio, G.; Donadoni, E.; Di Valentin, C. Modeling Zeta Potential for Nanoparticles in Solution: Water Flexibility Matters. J. Phys. Chem. C 2023, 127, 9236–9247. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).