Predicting and Unraveling Flexural Behavior in Fiber-Reinforced UHPC Through Based Machine Learning Models
Abstract
1. Introduction
1.1. Background
1.2. Bibliographical Overview
1.3. Scope and Significance of the Research
2. Materials and Methods
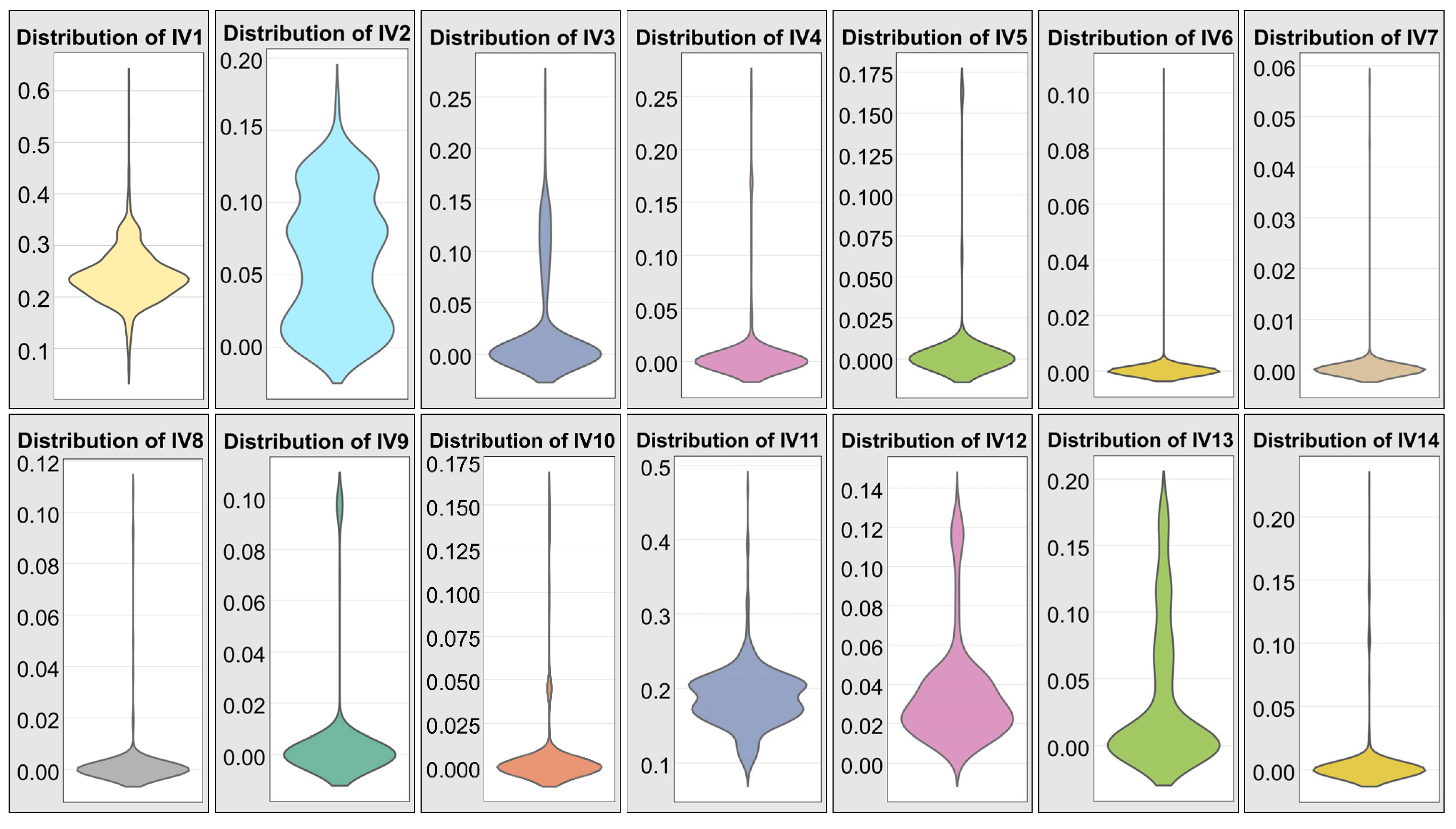
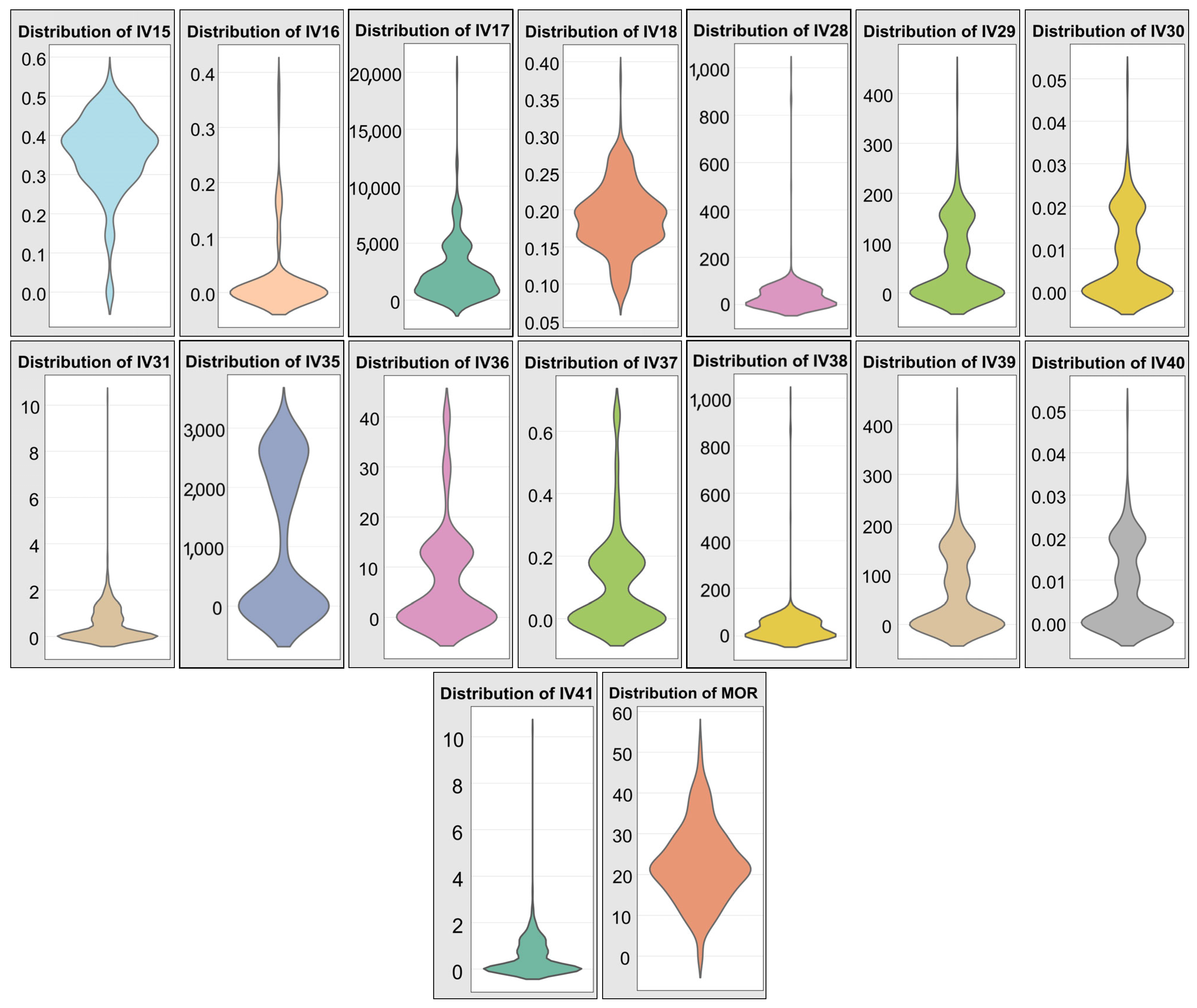
2.1. Data Compilation
2.1.1. Literature-Based Dataset for Models Development
- Group 1: IV1–IV14 (UHPC paste-making constituents):
- These variables represent the volumetric content (m3/m3) of different binder components in the UHPC mix:
- ∘
- IV1: Cement.
- ∘
- IV2: Silica Fume (SF).
- ∘
- IV3: Fly Ash (FA).
- ∘
- IV4: Ground Granulated Blast-Furnace Slag (GGBFS).
- ∘
- IV5: Ground Recycled Glass.
- ∘
- IV6: Rice Husk Ash (RHA).
- ∘
- IV7: Fluid Catalytic Cracking Catalyst Residue (FC3R) from petroleum refining.
- ∘
- IV8: Metakaolin.
- ∘
- IV9: Calcium Carbonate.
- ∘
- IV10: Other SCMs not listed in IV2–IV8 (m3/m3).
- ∘
- IV11: Water content.
- ∘
- IV12: Superplasticizer dosage.
- ∘
- IV13: Quartz powder.
- ∘
- IV14: Other non-reactive additions (excluding IV9 and IV13).
- Group 2: IV15–IV17 (A—ggregates):
- ∘
- IV15: Fine aggregate (sand) content (m3/m3).
- ∘
- IV16: Coarse aggregate content (m3/m3).
- ∘
- IV17: Maximum aggregate size (μm).
- Group 3: IV18–IV19 (Mix Proportioning and Mechanical Properties):
- ∘
- IV18: Water-to-binder ratio.
- ∘
- IV19: Compressive strength of UHPC (MPa).
- Group 4: IV20–IV21 (Global Fiber Properties):
- ∘
- IV20: Total fiber volume fraction (m3/m3).
- ∘
- IV21: Global fiber factor for the UHPC mix.
- Group 5: IV22–IV31 (Fiber Type 1 Characteristics):
- ∘
- IV22: Binary variable indicating if Fiber 1 is straight steel (1 = yes, 0 = no).
- ∘
- IV23: Hooked-end steel fiber (1 = yes, 0 = no).
- ∘
- IV24: Polymeric fiber (1 = yes, 0 = no).
- ∘
- IV25: Tensile strength of Fiber 1 (MPa).
- ∘
- IV26: Length of Fiber 1 (mm).
- ∘
- IV27: Equivalent diameter of Fiber 1 (mm).
- ∘
- IV28: Aspect ratio (length-to-diameter) of Fiber 1.
- ∘
- IV29: Mass of Fiber 1 in the mix (kg/m3).
- ∘
- IV30: Volume fraction of Fiber 1 (m3/m3).
- ∘
- IV31: Fiber factor for Fiber 1.
- Group 6: IV32–IV41 (Fiber Type 2 Characteristics):
- ∘
- IV32: Binary variable indicating if Fiber 2 is straight steel (1 = yes, 0 = no).
- ∘
- IV33: Hooked-end steel fiber (1 = yes, 0 = no).
- ∘
- IV34: Polymeric fiber (1 = yes, 0 = no).
- ∘
- IV35: Tensile strength of Fiber 2 (MPa).
- ∘
- IV36: Length of Fiber 2 (mm).
- ∘
- IV37: Equivalent diameter of Fiber 2 (mm).
- ∘
- IV38: Aspect ratio of Fiber 2.
- ∘
- IV39: Mass of Fiber 2 in the mix (kg/m3).
- ∘
- IV40: Volume fraction of Fiber 2 (m3/m3).
- ∘
- IV41: Fiber factor for Fiber 2.
2.1.2. Experimental Dataset for External Model Validation
2.2. Machine Learning
2.2.1. Linear Regression Models
2.2.2. K-Nearest Neighbors (KNN) Models
- i.
- The algorithm computes the distance between a query point and all points in the training dataset using a metric such as the Euclidean distance;
- ii.
- Identifies the k closest neighbors;
- iii.
- Predicts the output as the average of the target values of these neighbors.
2.2.3. Support Vector Regression Model
- ➢
- is the predicted value for input a.
- ➢
- is the weight vector.
- ➢
- ϕ(a) is a feature function that maps the input a to a higher-dimensional space.
- ➢
- c is a bias term.
2.2.4. Random Forest
2.2.5. Extreme Random Trees
- ➢
- is the final prediction of the model after t-iterations.
- ➢
- is the prediction from the previous iteration.
- ➢
2.2.6. Extreme Gradient Boosting
- ➢
- is the predicted output for the sample.
- ➢
- represents the output of the decision tree (weak learner) based on input features .
- ➢
- T is the total number of trees in the ensemble.
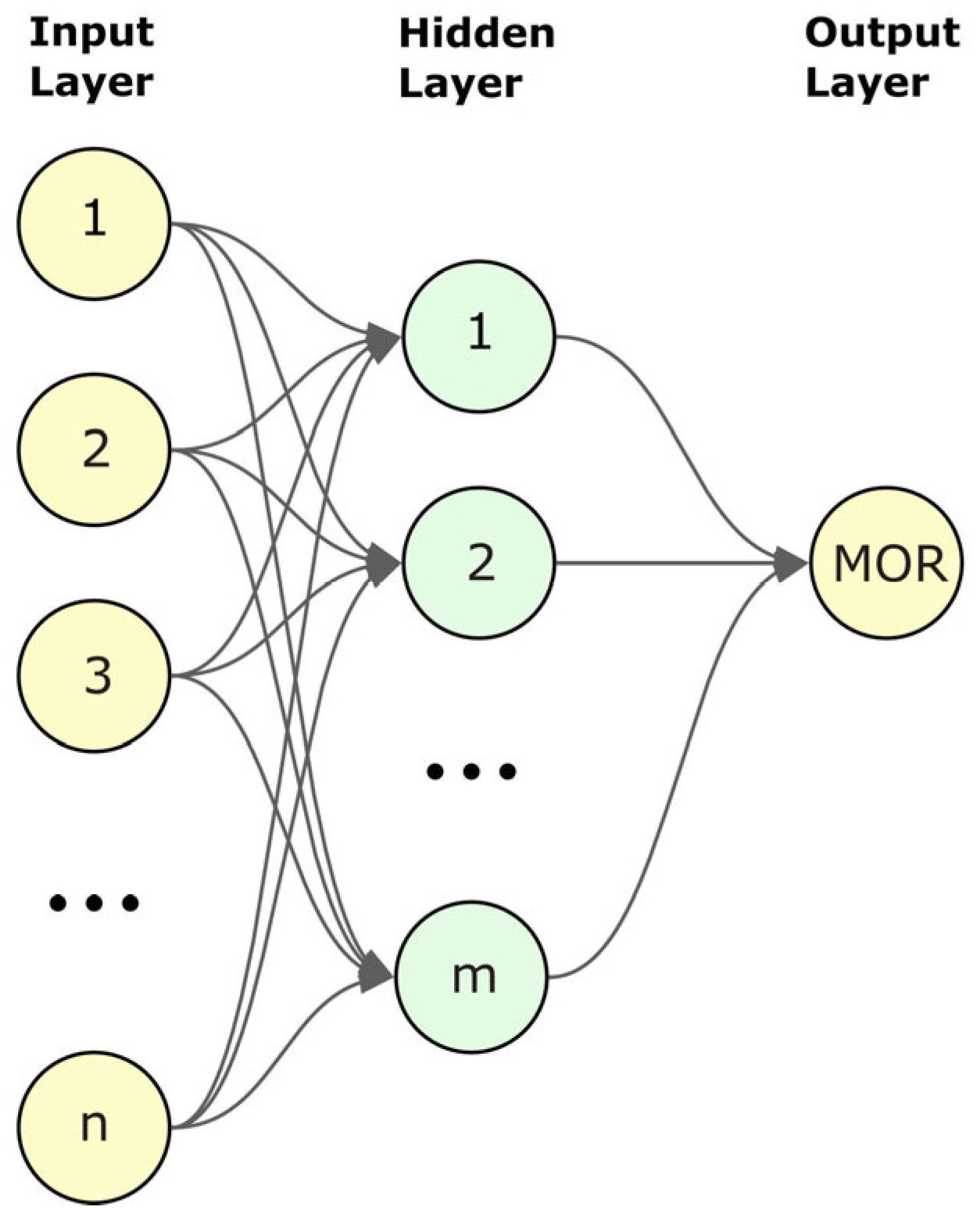
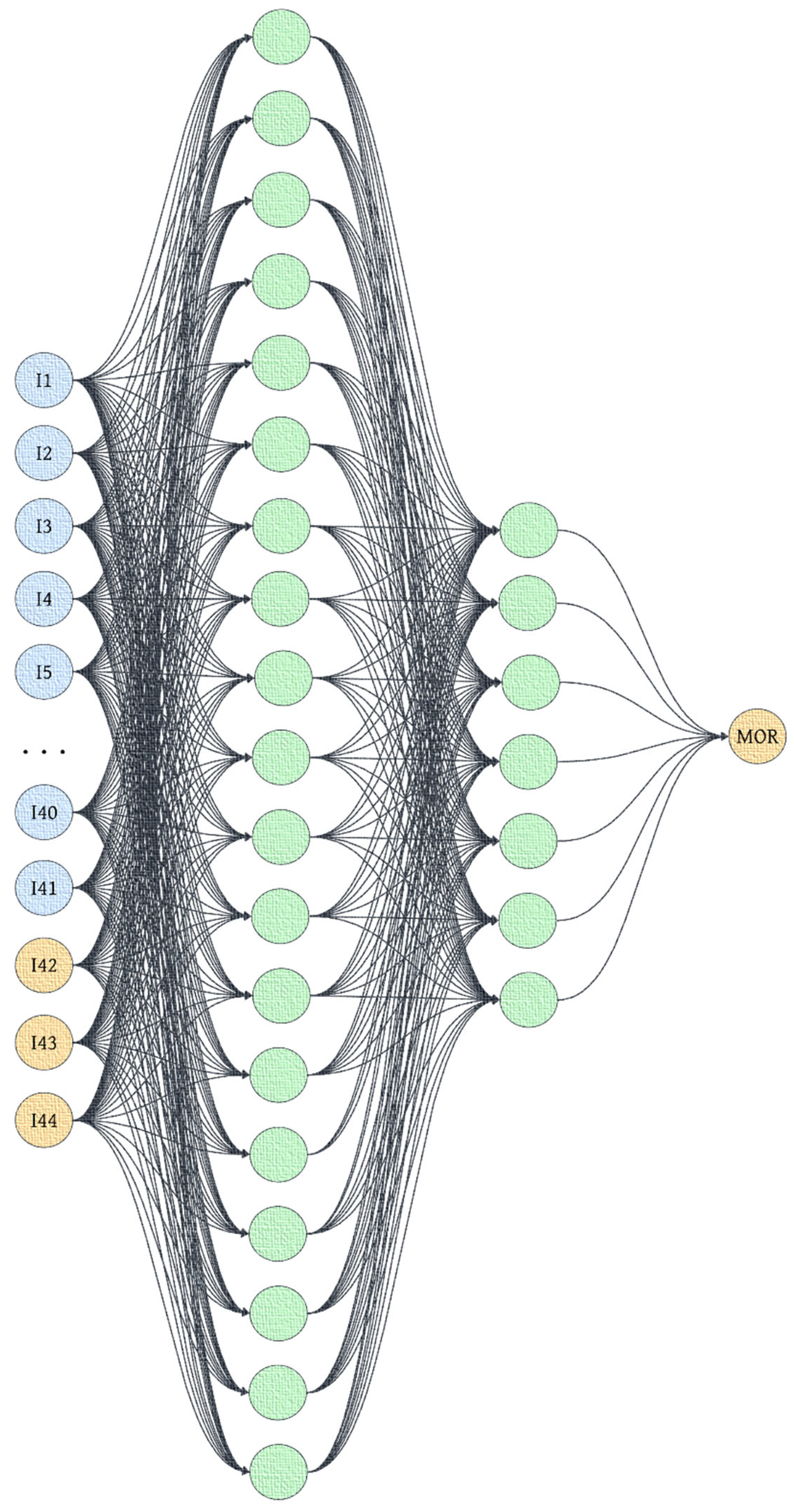
2.2.7. Artificial Neural Networks
- ➢
- is the output of neuron j in the current layer.
- ➢
- represents the weights between neuron i in the previous layer and neuron j in the current layer.
- ➢
- is the input from neuron i.
- ➢
- is the bias term for neuron j.
- ➢
- f is the activation function (such as ReLU, Sigmoid, or Tanh), which introduces nonlinearity into the model.
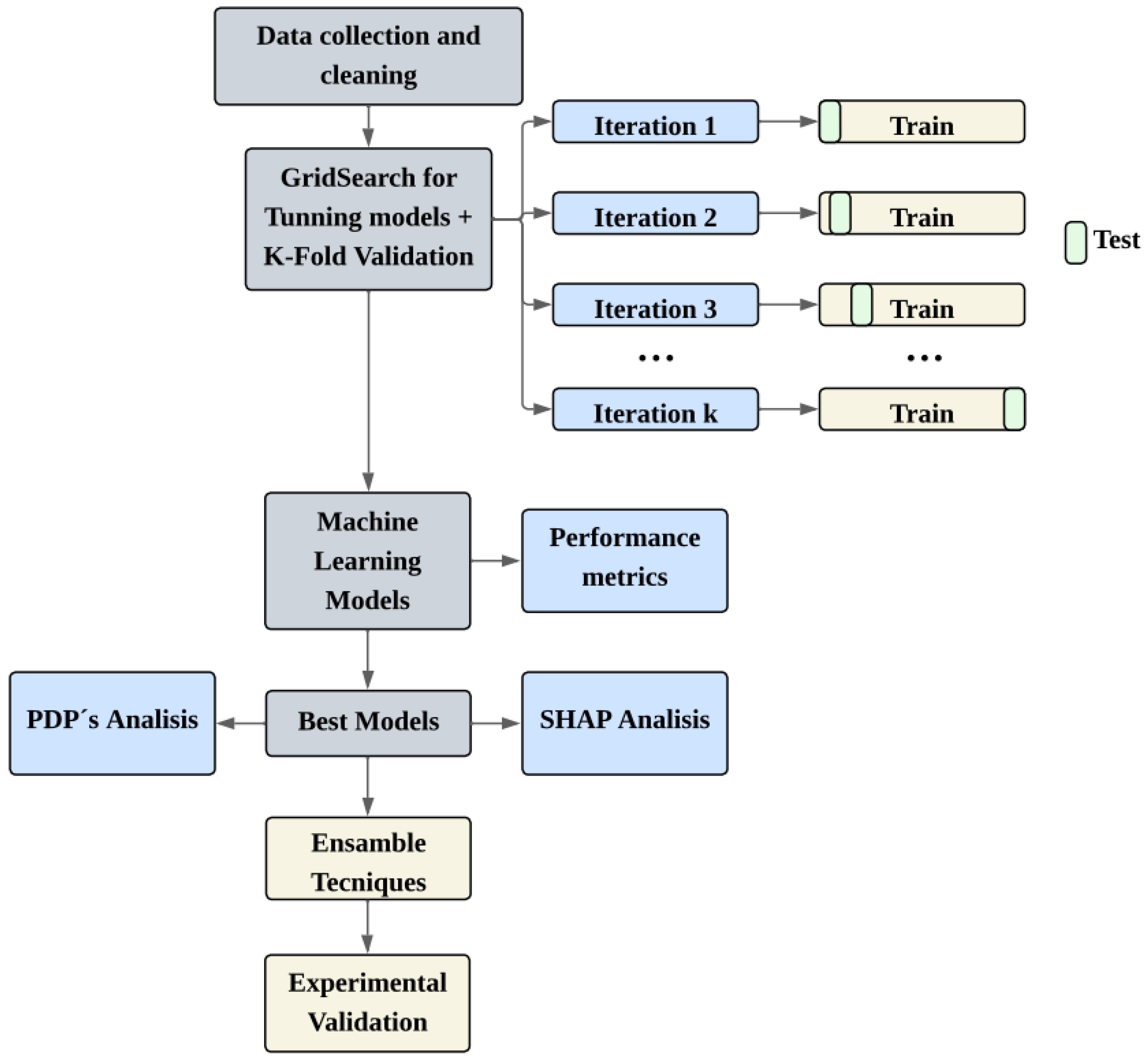
2.3. Model Tunning and Evaluation
2.3.1. Computational Resources and Execution Time
2.3.2. Model Tunning
2.3.3. K-Fold Validation
2.3.4. Prediction Performance Metric
2.4. SHAP (Shapley Additive ExPlanations)
- ➢
- is the prediction made by the model.
- ➢
- is the baseline prediction (the average prediction of the model without any features).
- ➢
- is the Shapley value for feature i, representing its contribution to the prediction.
- ➢
- is the value of feature i for the given instance.
- ➢
- is the Shapley value for feature i.
- ➢
- K is a subset of features without feature i.
- ➢
- M is the set of all features.
- ➢
- N is the total number of features.
- ➢
- Represents the predicted value of the model when the feature set K is used.
2.5. Partial Dependence Plots
- ➢
- denotes the values of the feature(s) of interest.
- ➢
- represents the complementary features (i.e., the remaining predictors not in S).
- ➢
- is the prediction function of the model.
- ➢
- is the marginal probability distribution of the complementary features.
2.6. Ensemble Learning Techniques
2.6.1. Bagging
2.6.2. Stacking
- ➢
- is the final predicted output.
- ➢
- represents the prediction from the ith base model.
- ➢
- are the learned weights of each base model’s prediction, learned by the meta-model.
- ➢
- is the bias term learned by the meta-model.
2.6.3. Boosting
- is the final predicted output for the ith sample.
- is the prediction from the tth model.
- is the weight assigned to each model’s prediction, based on its accuracy.
2.6.4. Hybrid Neural Network
- ➢
- is the final prediction of the Hybrid Neural Network.
- ➢
- are the outputs from the base models (RF, XRF, XGB), each with an R2 value greater than 0.8.
- ➢
- are the original input features, such as fiber content, water-to-binder ratio, cement content, etc.
3. Results
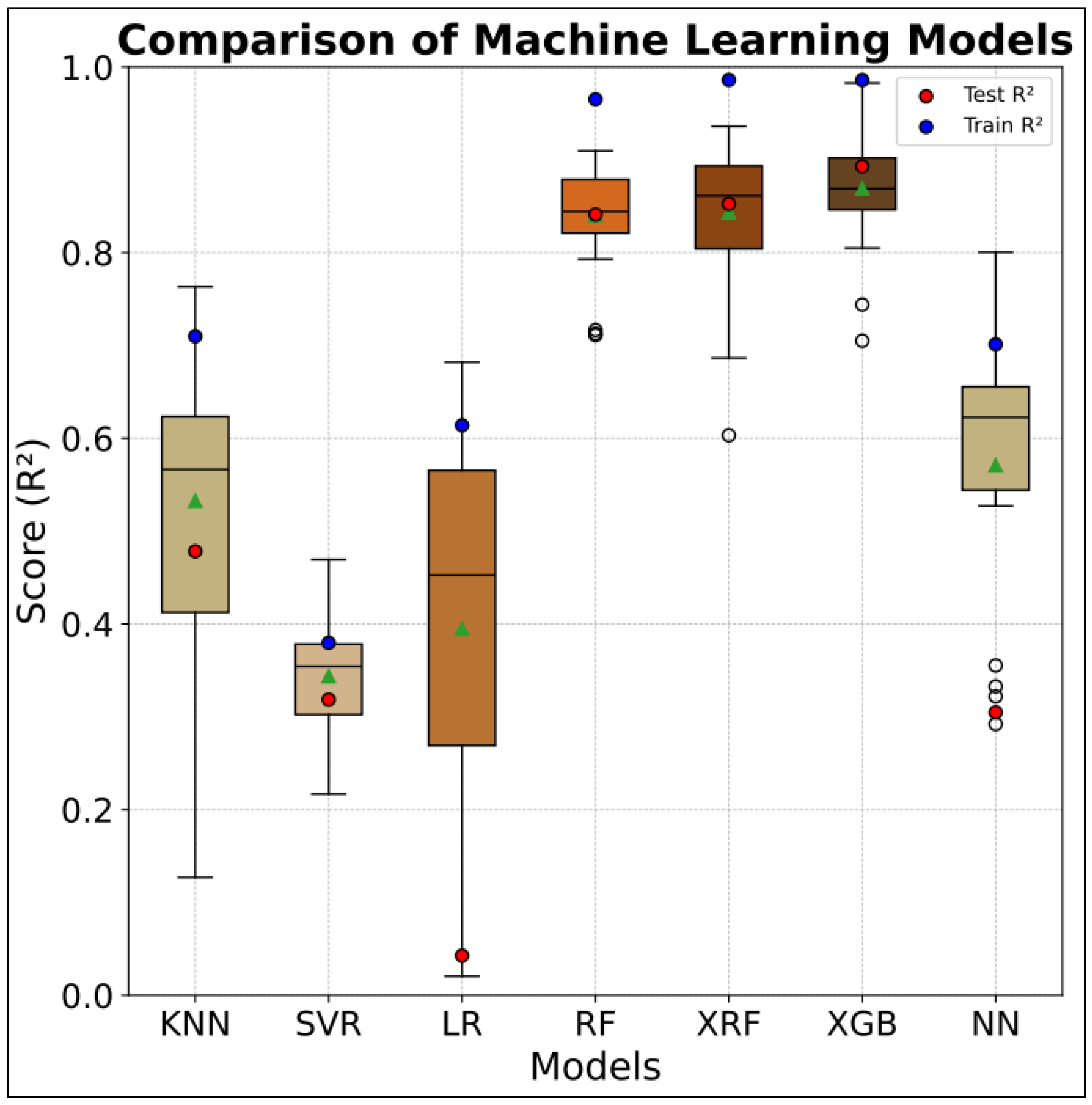
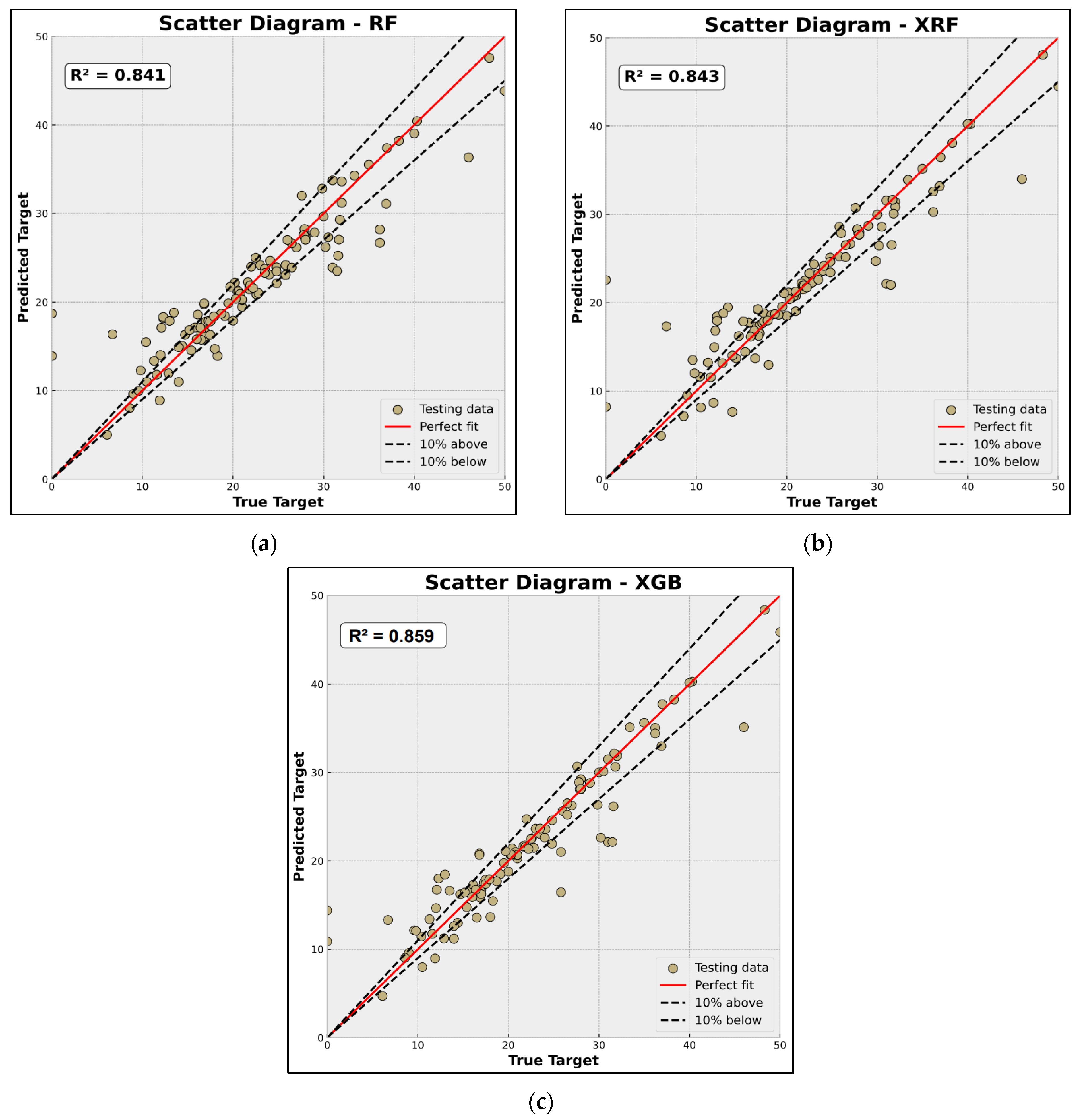
3.1. Performance of the Individual Machine Learning Models
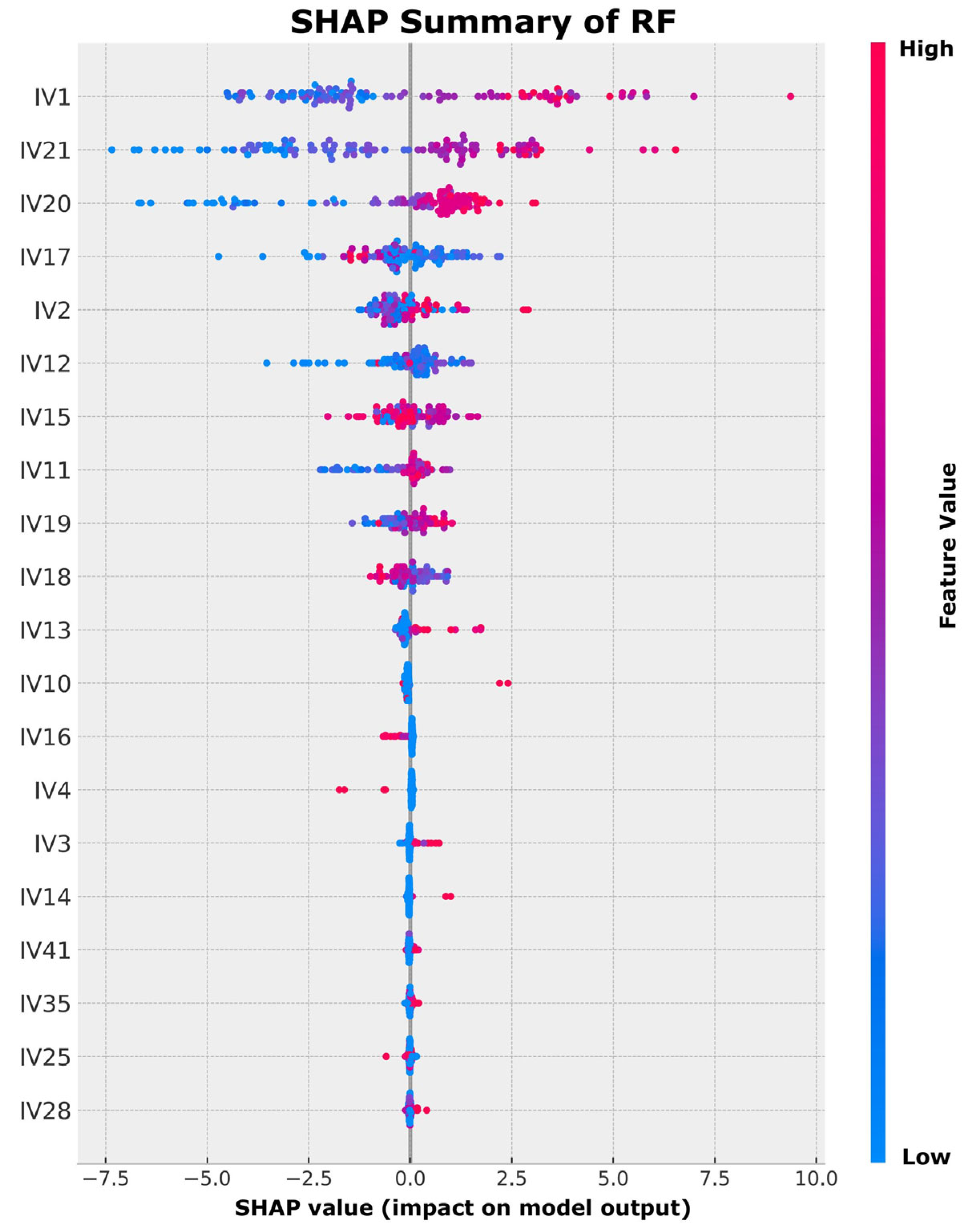
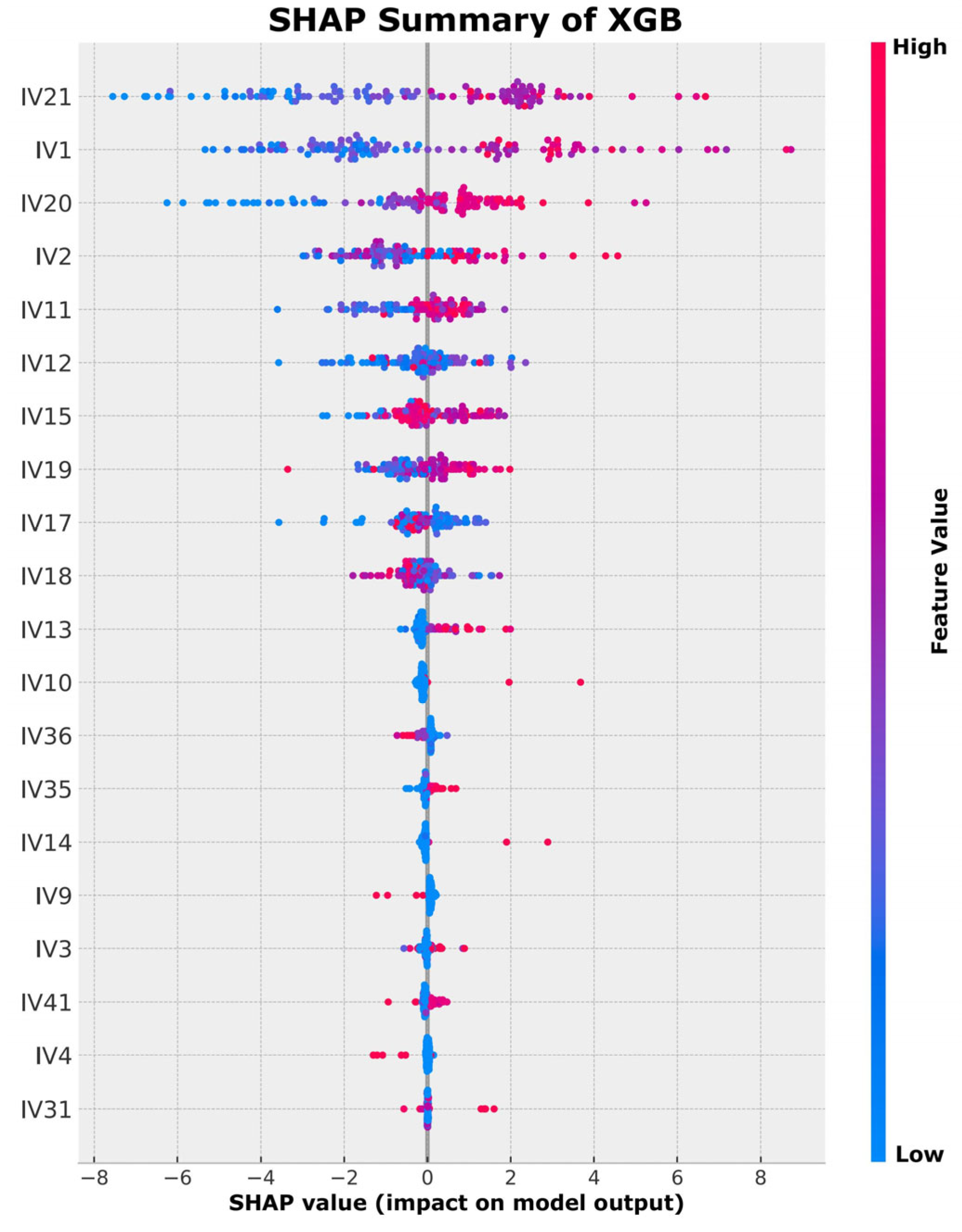
3.2. Feature Importance Analysis Using SHAP
3.2.1. Interpretability of Individual Models via Shapley Additive Explanations
3.2.2. Scientific Pattern of SHAP-Identified Factors
3.3. Partial-Dependence Analysis
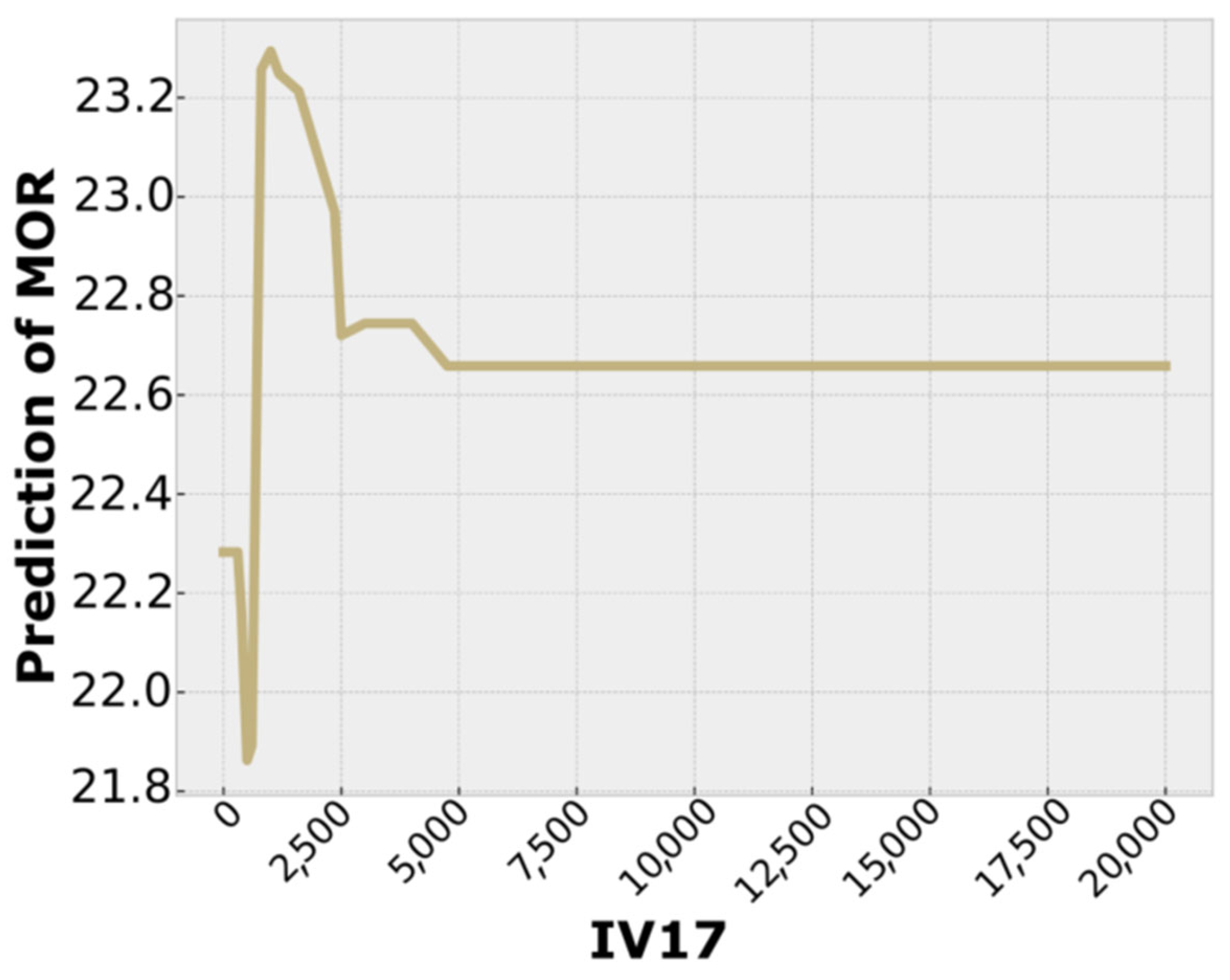
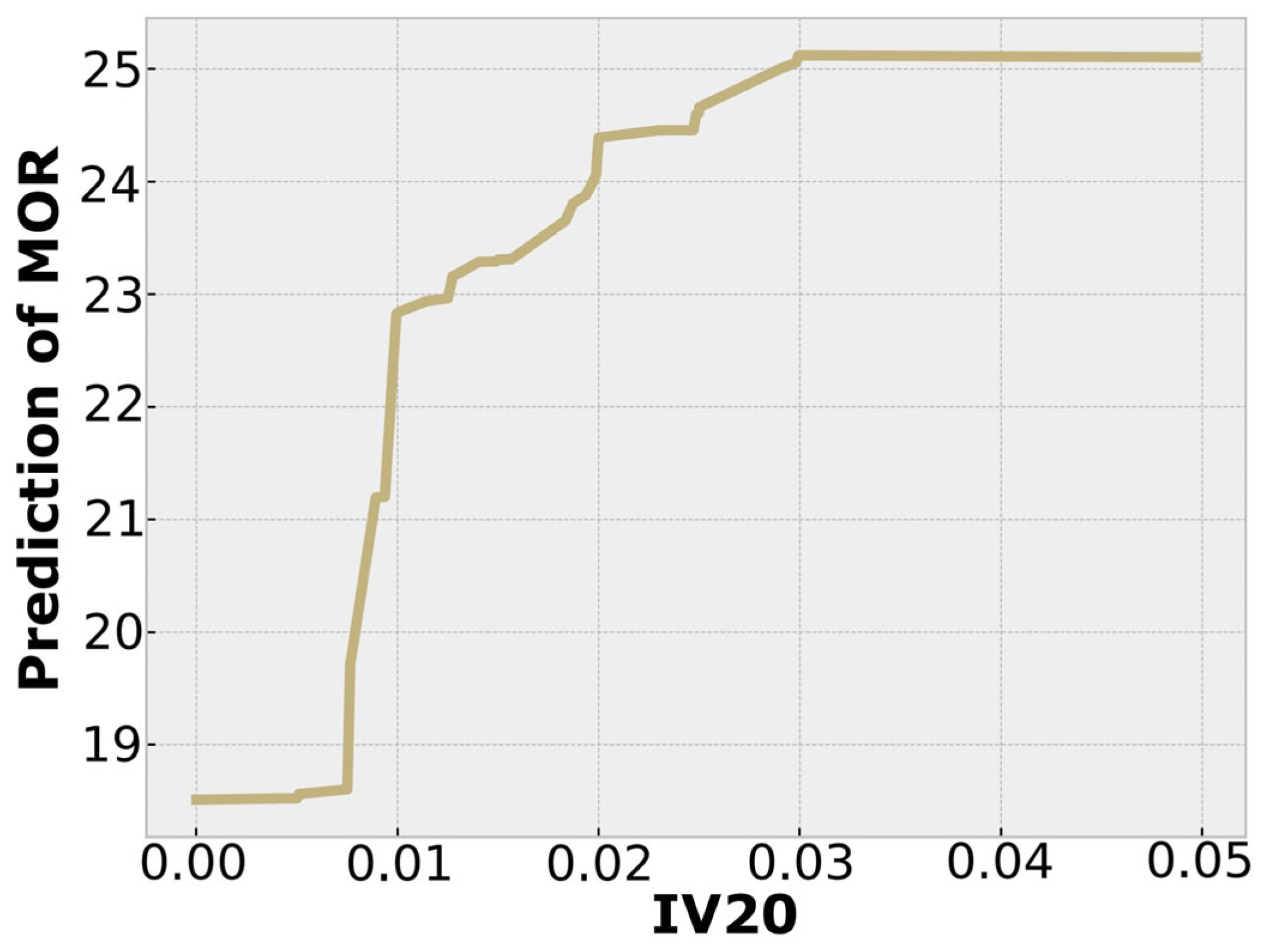
3.3.1. One-Way Partial-Dependence Analysis
3.3.2. Two-Way Partial-Dependence Analysis
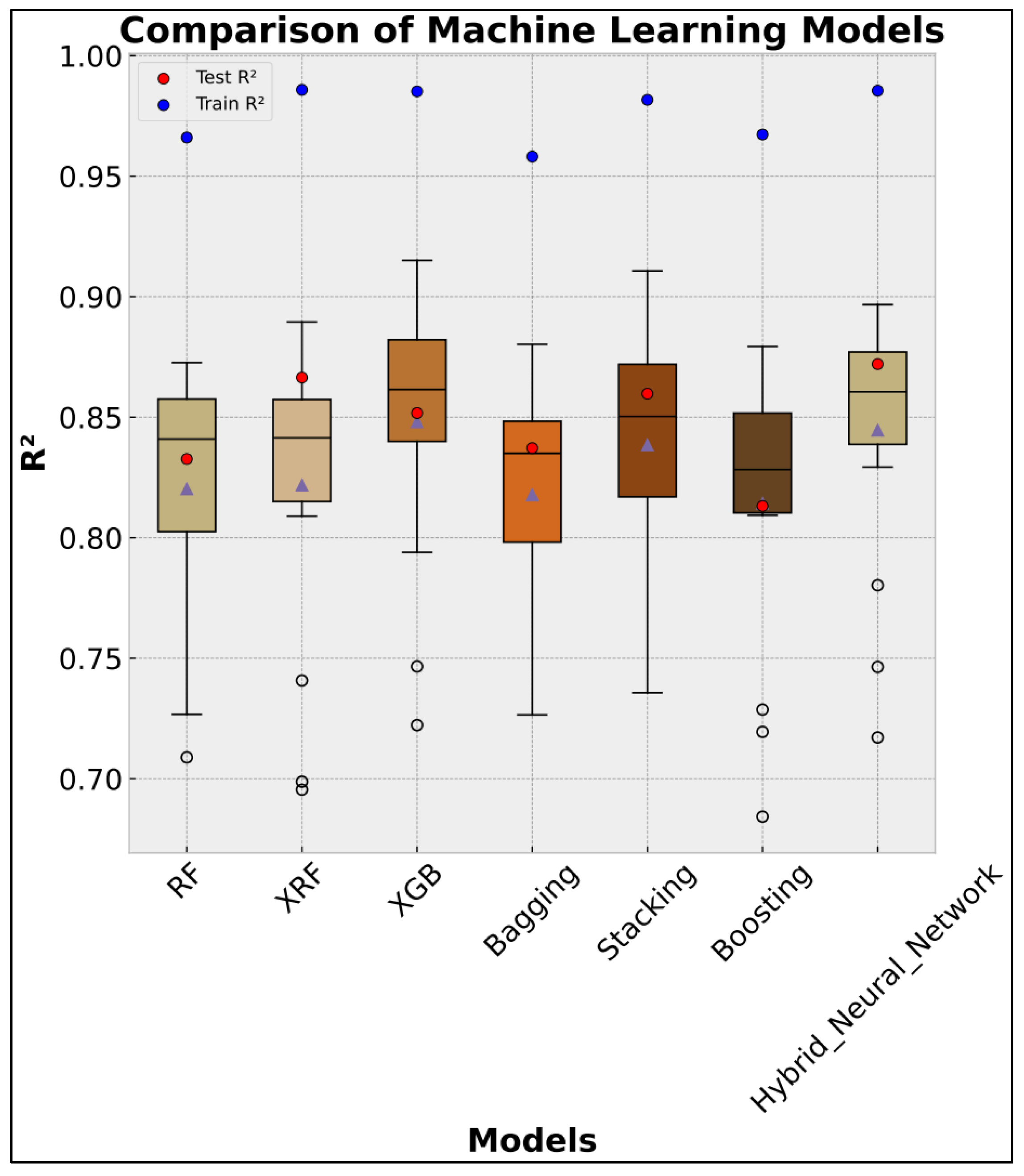
3.4. Ensemble Learning Results
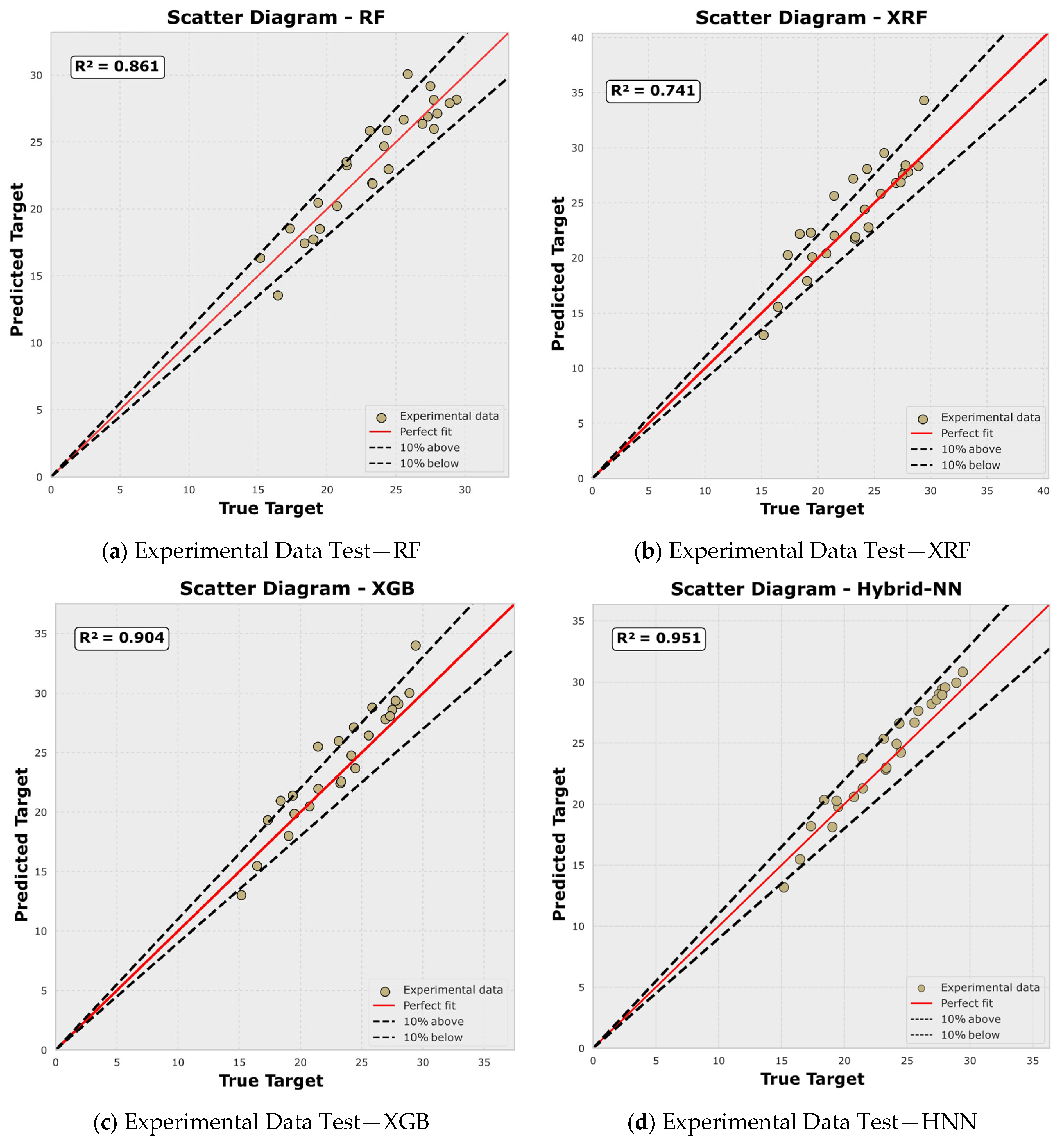
3.5. Experimental Validation of the Developed Models
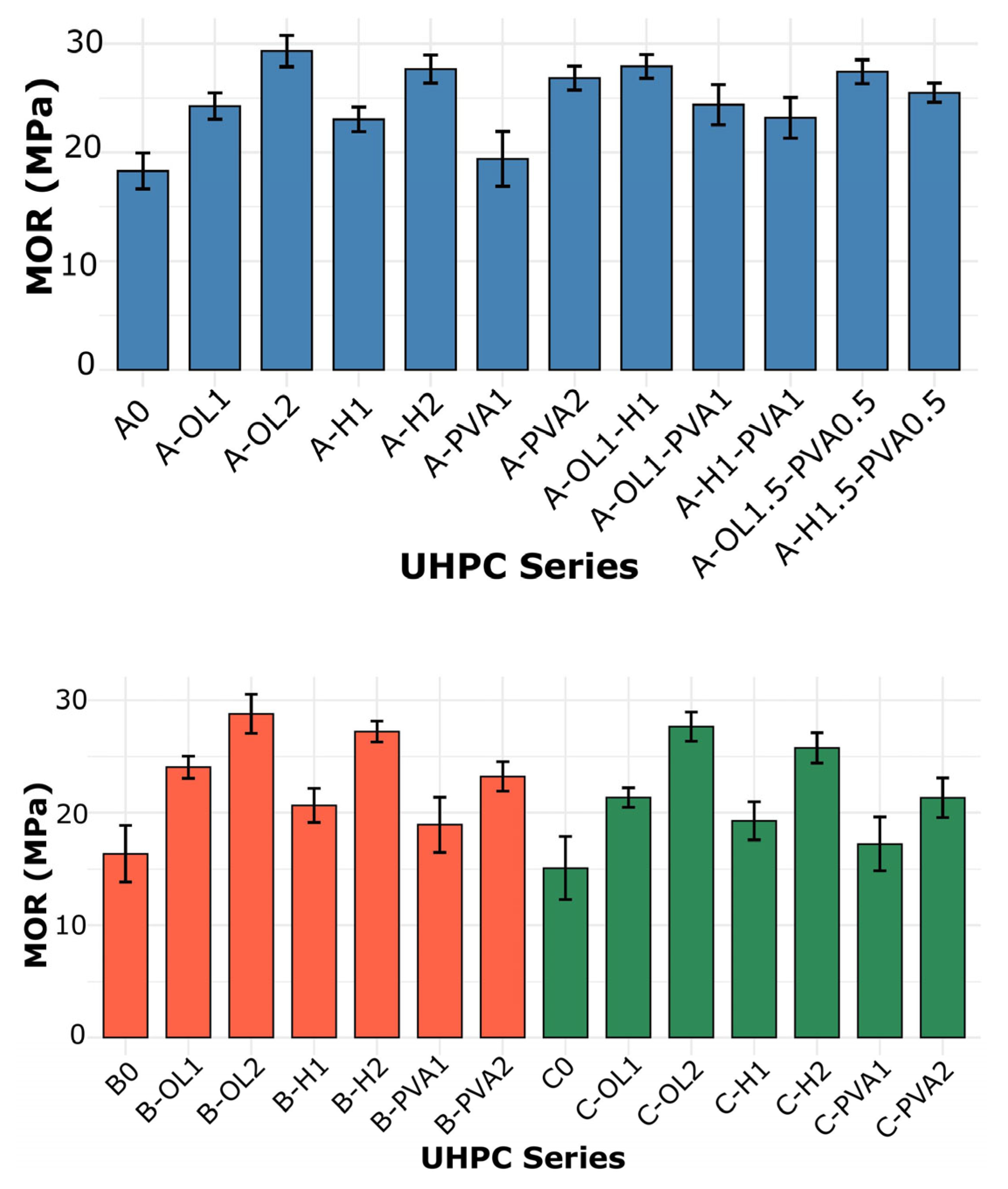
3.5.1. Experimental Findings
3.5.2. Machine Learning Evaluation by Means of the Experimental Findings
4. Conclusions
- (1)
- Among the evaluated models, Random Forest (RF), Extremely Randomized Forest (XRF), and XGBoost (XGB) demonstrated superior predictive capabilities, each achieving R2 scores above 0.80 on the testing subset, significantly outperforming traditional models such as Linear Regression, K-Nearest Neighbors, Support Vector Regression, and conventional Artificial Neural Networks.
- (2)
- SHAP-based interpretability highlighted cement content, fiber factor, total fiber volume fraction, silica fume dosage, water-to-binder ratio, and maximum aggregate size as the dominant parameters influencing flexural strength. These insights were scientifically consistent with the current understanding of UHPC material behavior.
- (3)
- The application of ensemble methods further enhanced predictive performance. While Bagging, Stacking, and Boosting showed notable improvements, the Hybrid Neural Network model achieved the highest predictive accuracy with an R2 of 0.872, outperforming all other approaches on the testing dataset.
- (4)
- An independent experimental campaign involving 26 novel UHPC mixtures confirmed the robustness of the developed models. The Hybrid Neural Network again provided the best performance, achieving an R2 of 0.951 against the experimental results, thereby demonstrating exceptional generalization capability and reliability.
- (5)
- The experimental findings, aligned with SHAP interpretations, confirmed that the incorporation of supplementary cementitious materials such as fly ash, recycled glass powder, and calcium carbonate marginally impacted flexural strength, supporting the potential for sustainable UHPC mix designs without compromising mechanical performance.
- (6)
- A detailed one-way Partial Dependence Plot (PDP) analysis was conducted on six key variables—cement content, silica fume content, superplasticizer dosage, maximum aggregate size, fiber volume fraction, and fiber factor. Each variable exhibited a characteristic nonlinear effect: cement and silica fume improved strength up to optimal dosages (~0.27 m3/m3 and ~0.093 m3/m3, respectively), beyond which negative effects such as porosity and agglomeration could emerge. Superplasticizer content showed benefits up to ~0.04 m3/m3 but declined thereafter possibly due to porosity and hydration interference. Coarse aggregate size negatively impacted MOR, which could be ascribed to poor fiber dispersion and orientation, reducing effectiveness. Fiber volume and fiber factor enhanced flexural strength up to ~3% and ~2, respectively, before plateauing or declining what can be explained by due to poor dispersion and fiber clustering.
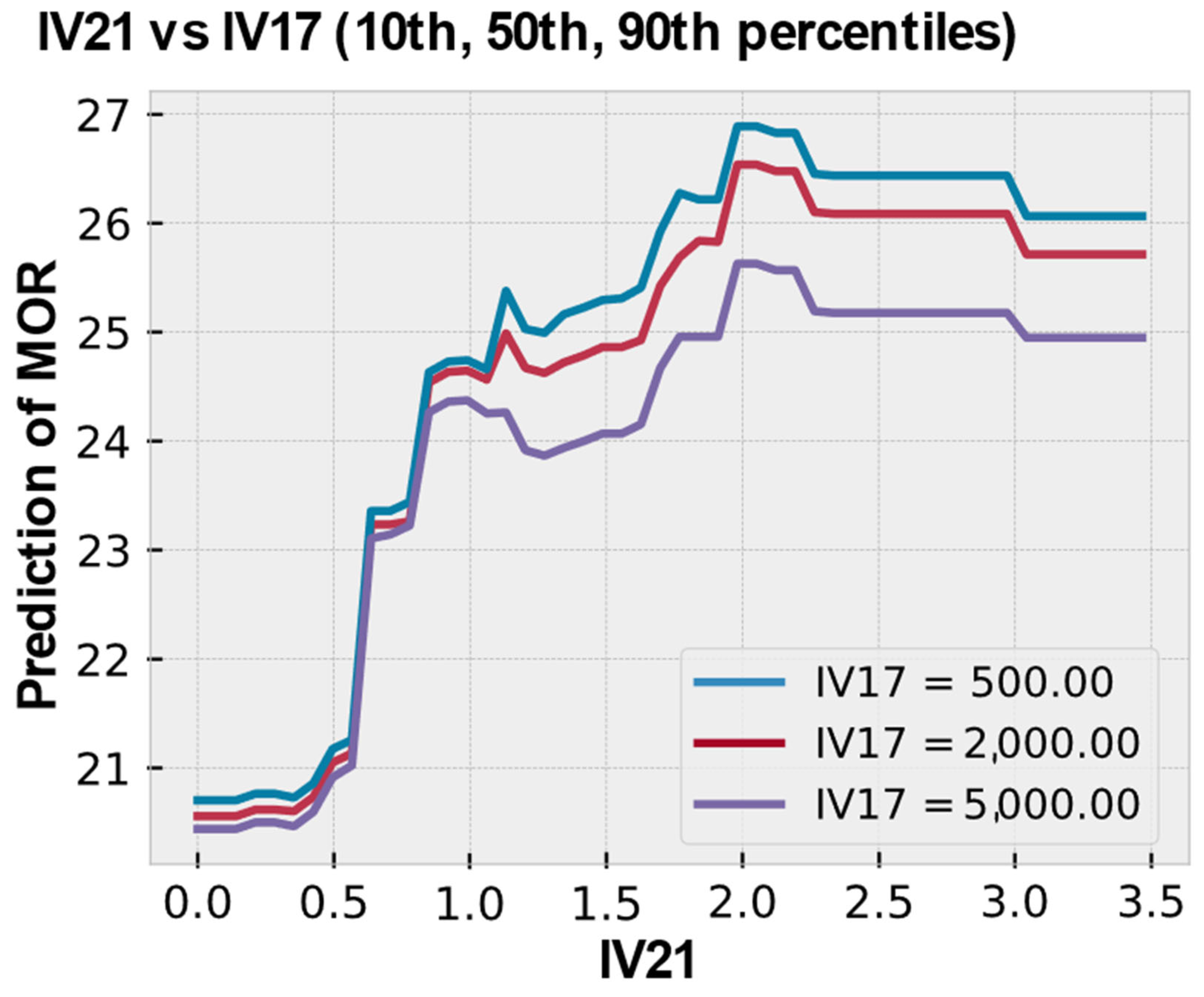
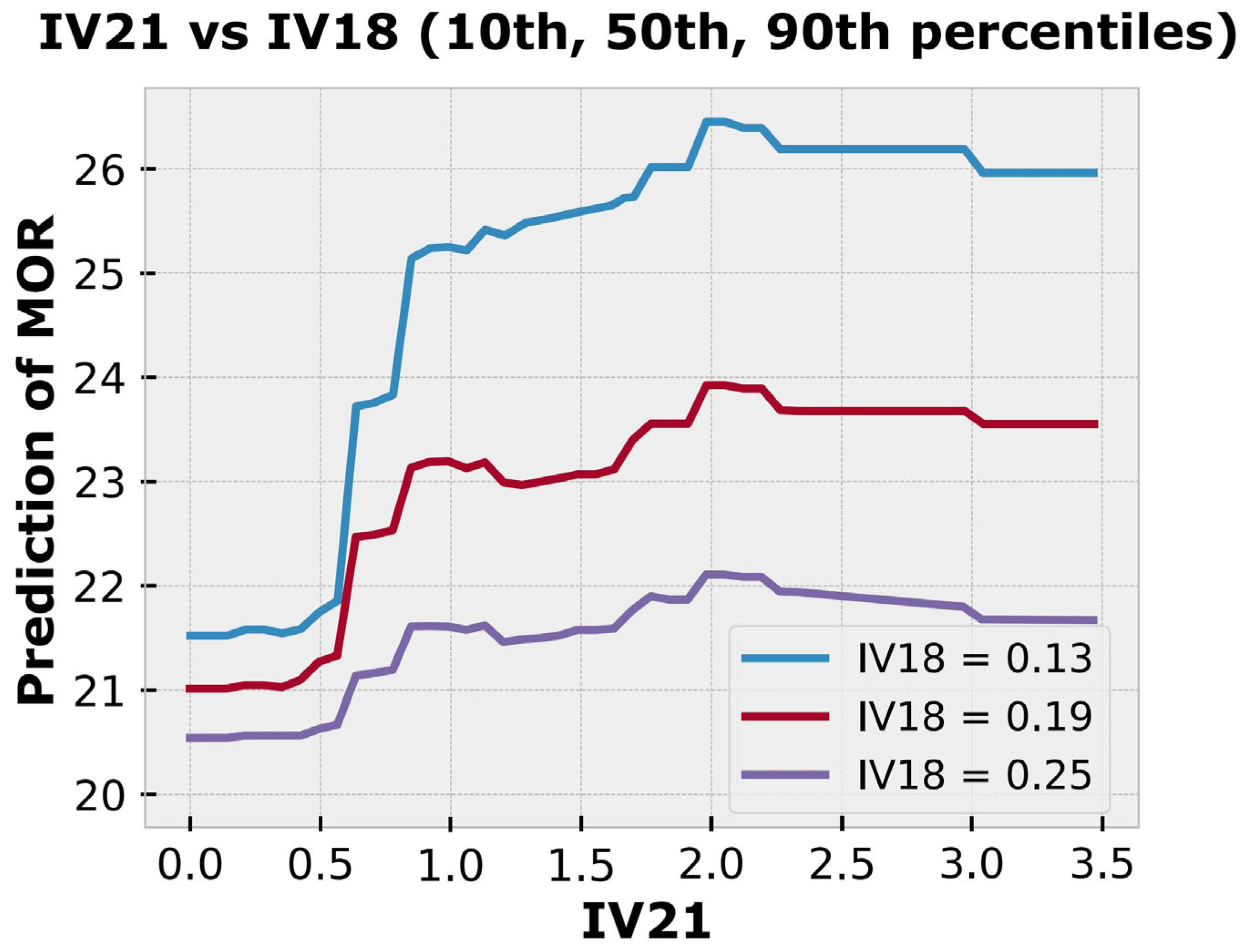
- (7)
- In two-way partial-dependence interaction analyses (PDPs), the interaction of global fiber factor (IV21) with relevant matrix properties—maximum aggregate size, water-to-binder ratio, and matrix compressive strength—was investigated to modulate MOR. These bivariate PDPs showed diminishing marginal returns at a fiber factor of ~1.8–2.0. Other conclusions of the analysis include the following:
- a.
- Smaller aggregate sizes enhance MOR due to improved fiber alignment and higher effective aspect ratios.
- b.
- Lower water-to-binder ratios amplify IV21’s effect by improving fiber-matrix bond strength and matrix density.
- c.
- Higher compressive strengths increase MOR by enabling better stress transfer and fiber anchorage.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Azmee, N.M.; Shafiq, N. Ultra-High Performance Concrete: From Fundamental to Applications. Case Stud. Constr. Mater. 2018, 9, e00197. [Google Scholar] [CrossRef]
- Abbas, S.; Nehdi, M.L.; Saleem, M.A. Ultra-High Performance Concrete: Mechanical Performance, Durability, Sustainability and Implementation Challenges. Int. J. Concr. Struct. Mater. 2016, 10, 271–295. [Google Scholar] [CrossRef]
- Bajaber, M.A.; Hakeem, I.Y. UHPC Evolution, Development, and Utilization in Construction: A Review. J. Mater. Res. Technol. 2021, 10, 1058–1074. [Google Scholar] [CrossRef]
- Tang, M.-C. High Performance Concrete—Past, Present and Future. In Proceedings of the international symposium on UHPC, Kassel, Germany, 13–15 September 2004; ISBN 3899580869. [Google Scholar]
- Scheydt, J.C.; Müller, H.S. Microstructure of Ultra High Performance Concrete (UPHC) and Its Impact on Durability. In Proceedings of the Hipermat 2012—3rd International Symposium on UHPC and Nanotechnology for Construction Materials, Kassel, Germany, 7–9 March 2012; Kassel University: Kassel, Germany, 2012; pp. 349–356. [Google Scholar]
- Schmidt, M.; Fehling, E. Ultra-High-Performance Concrete: Research, Development and Application in Europe. ACI Symp. Publ. 2005, 228, 51–78. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W.; Wu, L. Effects of Steel Fiber Content and Shape on Mechanical Properties of Ultra High Performance Concrete. Constr. Build. Mater. 2016, 103, 8–14. [Google Scholar] [CrossRef]
- Meng, W.; Khayat, K.H. Effect of Hybrid Fibers on Fresh Properties, Mechanical Properties, and Autogenous Shrinkage of Cost-Effective UHPC. J. Mater. Civ. Eng. 2018, 30, 04018030. [Google Scholar] [CrossRef]
- Nasiri, H.; Pourbaba, M.; Lotfollahi Yaghin, M.A. Numerical Study on the Flexural and Shear Behavior of Steel Fiber and High-strength Steel Combination in Ultra-high-performance Fiber-reinforced Concrete Beams under Cyclic Loading. Struct. Concr. 2024, 26, 3663–3677. [Google Scholar] [CrossRef]
- Abellán-García, J.; Carvajal-Muñoz, J.S.; Ramírez-Munévar, C. Application of Ultra-High-Performance Concrete as Bridge Pavement Overlays: Literature Review and Case Studies. Constr. Build. Mater. 2024, 410, 134221. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhang, Y.; Guo, M.; Zhang, L.; Ning, H.; Liu, S. Mechanical and Fracture Properties of Ultra-High Performance Concrete (UHPC) Containing Waste Glass Sand as Partial Replacement Material. J. Clean. Prod. 2020, 277, 123501. [Google Scholar] [CrossRef]
- Nasrin, S.; Ibrahim, A. Flexural Response of Ultra-High-Performance Concrete (UHPC) Hybrid Bridge Deck Connections Made with Local Materials. Constr. Build. Mater. 2021, 270, 121451. [Google Scholar] [CrossRef]
- Tayeh, B.A. Ultra-High-Performance Concrete (UHPC)—Applications Worldwide: A State-of-the-Art Review. J. Eng. Res. Tecnol. 2023, 10, 12–27. [Google Scholar] [CrossRef]
- Zhang, K. The Characteristics of Ultra-High Performance Concrete and Its Application in Structures. Highlights Sci. Eng. Technol. 2024, 106, 513–518. [Google Scholar] [CrossRef]
- Perry, V.H. Ultra-High-Performance-Concrete Advancements and Industrialization—The Need for Standard Testing. Adv. Civ. Eng. Mater. 2015, 4, 1–16. [Google Scholar] [CrossRef]
- Schmidt, C.; Schmidt, M. ‘Whitetopping’ of Asphalt and Concrete Pavements with Thin Layers of Ultra-High-Performance Concrete—Construction and Economic Efficiency. In Proceedings of the Hipermat 2012—3rd International Symposium on UHPC and Nanotechnology for Construction Materials, Kassel, Germany, 7–9 March 2012; Fröhlich, M., Schmidt, E., Fehling, C., Glotzbach, S., Piotrowski, S., Eds.; Kassel University: Kassel, Germany, 2012; pp. 921–927. [Google Scholar]
- Teng, L.; Khayat, K.H. Effect of Overlay Thickness, Fiber Volume, and Shrinkage Mitigation on Flexural Behavior of Thin Bonded Ultra-High-Performance Concrete Overlay Slab. Cem. Concr. Compos. 2022, 134, 104752. [Google Scholar] [CrossRef]
- Hiew, S.Y.; Bin Teoh, K.; Raman, S.N.; Kong, D.; Hafezolghorani, M. A Generalised Predictive Model for the Mechanical Properties of Mono/Hybrid Fibre-Reinforced Ultra-High-Performance Concrete. Constr. Build. Mater. 2024, 426, 136154. [Google Scholar] [CrossRef]
- Du, J.; Meng, W.; Khayat, K.H.; Bao, Y.; Guo, P.; Lyu, Z.; Abu-obeidah, A.; Nassif, H.; Wang, H. New Development of Ultra-High-Performance Concrete (UHPC). Compos. Part B Eng. 2021, 224, 109220. [Google Scholar] [CrossRef]
- Alabduljabbar, H.; Khan, M.; Awan, H.H.; Eldin, S.M.; Alyousef, R.; Mohamed, A.M. Predicting Ultra-High-Performance Concrete Compressive Strength Using Gene Expression Programming Method. Case Stud. Constr. Mater. 2023, 18, e02074. [Google Scholar] [CrossRef]
- Marani, A.; Jamali, A.; Nehdi, M.L. Predicting Ultra-High-Performance Concrete Compressive Strength Using Tabular Generative Adversarial Networks. Materials 2020, 13, 4757. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, Y. Prediction of Compressive Strength of Ultra-High Performance Concrete (UHPC) Containing Supplementary Cementitious Materials. In Proceedings of the 2017 International Conference on Smart Grid and Electrical Automation (ICSGEA), Changsha, China, 27–28 May 2017; pp. 522–525. [Google Scholar] [CrossRef]
- Ergen, F.; Katlav, M. Machine and Deep Learning-Based Prediction of Flexural Moment Capacity of Ultra-High Performance Concrete Beams with/out Steel Fiber. Asian J. Civ. Eng. 2024, 25, 4541–4562. [Google Scholar] [CrossRef]
- Soni, A.; Nateriya, R. Exploring Ultimate Flexural Strengths of Ultra-High-Performance Concrete (UHPC) Samples through Experimental Analysis in Comparison with Ordinary Concrete Structures. Natl. Acad. Sci. Lett. 2024. [Google Scholar] [CrossRef]
- Lima, C.; Coelho, A.; Von Zuben, F. Ensembles of Support Vector Machines for Regression Problems. In Proceedings of the International Joint Conference on Neural Network, Honolulu, HI, USA, 1 February 2002; Volume 3, pp. 2381–2386. [Google Scholar]
- Qian, Y.; Su, M.; Hakamy, A.; Deifalla, A.F.; El-said, A. Application of Machine Learning Algorithms to Evaluate the in Fl Uence of Various Parameters on the Fl Exural Strength of Ultra-High-Performance Concrete. Front. Mater. 2023, 9, 1114510. [Google Scholar] [CrossRef]
- Das, P.; Kashem, A. Hybrid Machine Learning Approach to Prediction of the Compressive and Flexural Strengths of UHPC and Parametric Analysis with Shapley Additive Explanations. Case Stud. Constr. Mater. 2024, 20, e02723. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H.J.H. Mix Design and Properties Assessment of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC). Cem. Concr. Res. 2014, 56, 29–39. [Google Scholar] [CrossRef]
- Šerelis, E.; Vaitkevičius, V.; Kerševičius, V. Mechanical Properties and Microstructural Investigation of Ultra-High Performance Glass Powder Concrete. J. Sustain. Archit. Civ. Eng. 2016, 1, 5–11. [Google Scholar] [CrossRef]
- Huang, H.; Gao, X.; Wang, H.; Ye, H. Influence of Rice Husk Ash on Strength and Permeability of Ultra-High Performance Concrete. Constr. Build. Mater. 2017, 149, 621–628. [Google Scholar] [CrossRef]
- Yu, R.; Tang, P.; Spiesz, P.; Brouwers, H.J.H. A Study of Multiple Effects of Nano-Silica and Hybrid Fibres on the Properties of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC) Incorporating Waste Bottom Ash (WBA). Constr. Build. Mater. J. 2014, 60, 98–110. [Google Scholar] [CrossRef]
- Li, Z. Proportioning and Properties of Ultra-High-Performance Concrete Mixtures for Application in Shear Keys of Precast Concrete Bridges; Clemson University: Clemson, SC, USA, 2015. [Google Scholar]
- Chen, T.; Gao, X.; Ren, M. Effects of Autoclave Curing and Fly Ash on Mechanical Properties of Ultra-High Performance Concrete. Constr. Build. Mater. 2018, 158, 864–872. [Google Scholar] [CrossRef]
- Ibrahim, M.A.; Farhat, M.; Issa, M.A.; Hasse, J.A. Effect of Material Constituents on Mechanical & Fracture Mechanics Properties of Ultra-High-Performance Concrete. ACI Struct. J. 2017, 114, 453–465. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W. Comparative Study on Flexural Properties of Ultra-High Performance Concrete with Supplementary Cementitious Materials under Different Curing Regimes. Constr. Build. Mater. 2017, 136, 307–313. [Google Scholar] [CrossRef]
- Hassan, A.M.T.; Jones, S.W.; Mahmud, G.H. Experimental Test Methods to Determine the Uniaxial Tensile and Compressive Behaviour of Ultra High Performance Fibre Reinforced Concrete (UHPFRC). Constr. Build. Mater. 2012, 37, 874–882. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H.J.H. Development of Ultra-High Performance Fibre Reinforced Concrete (UHPFRC): Towards an Efficient Utilization of Binders and Fibres. Constr. Build. Mater. 2015, 79, 273–282. [Google Scholar] [CrossRef]
- Vatannia, S.; Kearsley, E.; Mostert, D. The Mechanical Properties of Uhpc Reinforced By Different Types of Fiber. In Proceedings of the FIB Symposium 2016 Performance-Based Approaches for Concrete Structures, Cape Town, South Africa, 21–23 November 2016. [Google Scholar]
- Filho, R.D.T.; Koenders, E.A.B.; Formagini, S.; Fairbairn, E.M.R. Performance Assessment of Ultra High Performance Fiber Reinforced Cementitious Composites in View of Sustainability. Mater. Des. 2012, 36, 880–888. [Google Scholar] [CrossRef]
- Abdulkareem, O.M.; Ben Fraj, A.; Bouasker, M.; Khelidj, A. Mixture Design and Early Age Investigations of More Sustainable UHPC. Constr. Build. Mater. 2018, 163, 235–246. [Google Scholar] [CrossRef]
- Wang, R.; Gao, X. Relationship between Flowability, Entrapped Air Content and Strength of UHPC Mixtures Containing Different Dosage of Steel Fiber. Appl. Sci. 2016, 6, 216. [Google Scholar] [CrossRef]
- Askar, L.K.; Tayeh, B.A.; Bakar, B.H. Effect of Different Curing Conditions on the Mechanical Properties of UHPFC. Iran. J. Energy Environ. 2013, 4, 299–303. [Google Scholar] [CrossRef]
- Šerelis, E.; Vaitkevičius, V.; Kerševičius, V. Research of UHPC Properties Prepared with Industrial Mixer. IOP Conf. Ser. Mater. Sci. Eng. 2017, 246, 012048. [Google Scholar] [CrossRef]
- Meng, W.; Khayat, K. Effects of Saturated Lightweight Sand Content on Key Characteristics of Ultra-High-Performance Concrete. Cem. Concr. Res. 2017, 101, 46–54. [Google Scholar] [CrossRef]
- Costa, H. Design of UHPFRC with Enhanced Ductility and Flowability Design of Uhpfrc with Enhanced Ductility and Flowability. In Proceedings of the 8th Rilem International Symposium on Fiber Reinforced Concrete, Guimares, Portugal, 19–21 September 2012. [Google Scholar]
- Yoo, D.-Y.; Banthia, N.; Yoon, Y.-S. Impact Resistance of Ultra-High-Performance Fiber-Reinforced Concrete with Different Steel Fibers. In Proceedings of the 9th RILEM International Symposium on Fiber Reinforced Concrete—BEFIB 2016, Vancouver, BC, Canada, 19 September 2016; pp. 398–405. [Google Scholar]
- Ghafari, E.; Costa, H.; Nuno, E.; Santos, B. RSM-Based Model to Predict the Performance of Self-Compacting UHPC Reinforced with Hybrid Steel Micro-Fibers. Constr. Build. Mater. 2014, 66, 375–383. [Google Scholar] [CrossRef]
- Liu, J.; Ou, Z.; Mo, J.; Chen, Y.; Guo, T.; Deng, W. Effectiveness of Saturated Coral Aggregate and Shrinkage Reducing Admixture on the Autogenous Shrinkage of Ultrahigh Performance Concrete. Adv. Mater. Sci. Eng. 2017, 2017, 2703264. [Google Scholar] [CrossRef]
- Schmidt, M.; Fehling, E.; Geisenhanslükem, C. (Eds.) Proceedings of the International Symposium on Ultra High Performance Concrete; University of Kassel: Kassel, Germany, 2004. [Google Scholar]
- Habel, K.; Charron, J.-P.; Braike, S.; Hooton, R.D.; Gauvreau, P.; Massicotte, B. Ultra-High Performance Fibre Reinforced Concrete Mix Design in Central Canada. Can. J. Civ. Eng. 2008, 35, 217–224. [Google Scholar] [CrossRef]
- Prem, P.R. Influence of Curing Regime and Steel Fibres on the Mechanical Properties of UHPC. Mag. Concr. Res. 2015, 67, 988–1002. [Google Scholar] [CrossRef]
- Kim, D.J.; Park, S.H.; Ryu, G.S.; Koh, K.T. Comparative Flexural Behavior of Hybrid Ultra High Performance Fiber Reinforced Concrete with Different Macro Fibers. Constr. Build. Mater. 2014, 25, 4144–4155. [Google Scholar] [CrossRef]
- Konvalinka, P. Mixture Design and Testing of Ultra High Performance Fiber Reinforced Concrete. Malays. J. Civ. Eng. 2013, 25, 74–87. [Google Scholar]
- Ren, G.M.; Wu, H.; Fang, Q.; Liu, J.Z. Effects of Steel Fiber Content and Type on Static Mechanical Properties of UHPCC. Constr. Build. Mater. 2018, 163, 826–839. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Slowik, V.; Kabele, P. Strain-Hardening Cement-Based Composites: SHCC4; RILEM Bookseries; Springer: Berlin/Heidelberg, Germany, 2018; Volume 15, pp. 3–4. [Google Scholar] [CrossRef]
- Fehling, E.; Schmidt, C.; Stüwald, S. (Eds.) Proceedings of the Second International Symposium on Ultra High Performance Concrete; University of Kassel: Kassel, Germany, 2008. [Google Scholar]
- Proceedings of Hipermat 2012 3rd International Symposium on UHPC and Nanotechnology for High Performance Construction Materials. 2012. Available online: https://books.google.com.hk/books/about/Ultra_high_Performance_Concrete_and_Nano.html?id=eAKkMwEACAAJ&redir_esc=y (accessed on 10 May 2025).
- Camacho Torregrosa, E. Dosage Optimization and Bolted Connections for UHPFRC Ties. Ph.D. Thesis, Polytechnic University of Valencia, Valencia, Spain, 2013. [Google Scholar]
- Kou, S.C.; Xing, F. The Effect of Recycled Glass Powder and Reject Fly Ash on the Mechanical Properties of Fibre-Reinforced Ultrahigh Performance Concrete. Hindawi Publ. Corp. Adv. Mater. Sci. Eng. 2012, 2012, 263243. [Google Scholar] [CrossRef]
- Amanjean, E.N.; Vidal, T. Low Cost Ultra-High Performance Fiber Reinforced Concrete (UHPFRC) with Flash Metakaolin. Key Eng. Mater. 2015, 629–630, 55–63. [Google Scholar] [CrossRef]
- Vaitkevicius, V.; Šerelis, E.; Hilbig, H. The Effect of Glass Powder on the Microstructure of Ultra High Performance Concrete. Constr. Build. Mater. 2014, 68, 102–109. [Google Scholar] [CrossRef]
- ASTM C1609/C1609M-19; Standard Test Method for Flexural Performance of Fiber-Reinforced Concrete (Using Beam with Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 2019.
- Huang, P.; Dai, K.; Yu, X. Machine Learning Approach for Investigating Compressive Strength of Self-Compacting Concrete Containing Supplementary Cementitious Materials and Recycled Aggregate. J. Build. Eng. 2023, 79, 107904. [Google Scholar] [CrossRef]
- Kang, M.C.; Yoo, D.Y.; Gupta, R. Machine Learning-Based Prediction for Compressive and Flexural Strengths of Steel Fiber-Reinforced Concrete. Constr. Build. Mater. 2021, 266, 121117. [Google Scholar] [CrossRef]
- Khan, M.I.; Abbas, Y.M. Intelligent Data-Driven Compressive Strength Prediction and Optimization of Reactive Powder Concrete Using Multiple Ensemble-Based Machine Learning Approach. Constr. Build. Mater. 2023, 404, 133148. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? In Proceedings of the Machine Learning and Data Mining in Pattern Recognition: 8th International Conference, MLDM 2012, Berlin, Germany, 13–20 July 2012; 7376 LNAI. pp. 154–168. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Ni, X.; Duan, K. Machine Learning-Based Models for Shear Strength Prediction of UHPFRC Beams. Mathematics 2022, 10, 2918. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, C.; Gao, C.; Malin, B.A.; Chen, Y. Predicting Missing Values in Medical Data Via XGBoost Regression. J. Healthc. Inform. Res. 2020, 4, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, N.; Londhe, S.; Kulkarni, S. Modeling Compressive Strength of Recycled Aggregate Concrete by Artificial Neural Network, Model Tree and Non-Linear Regression. Int. J. Sustain. Built Environ. 2014, 3, 187–198. [Google Scholar] [CrossRef]
- Sahoo, K.; Sarkar, P.; Robin Davis, P. Artificial Neural Networks for Prediction of Compressive Strength of Recycled Aggregate Concrete. In Proceedings of the International Conference on Environment, Agricultural and Civil Engineering (ICEACE-2016), London, UK, 24–25 March 2016. [Google Scholar] [CrossRef]
- Kushari, S.; Chakraborty, A.; Mukhopadhyay, T.; Maity, S.R.; Dey, S. ANN-Based Random First-Ply Failure Analyses of Laminated Composite Plates. In Recent Advances in Computational Mechanics and Simulations; Saha, S.K., Mukherjee, M., Eds.; Springer: Singapore, 2021; pp. 131–142. ISBN 9789811581380. [Google Scholar]
- Gotlib, V.A.; Sato, T.; Beltzer, A.I. Neural Computing of Effective Properties of Random Composite Materials. Comput. Struct. 2001, 79, 1–6. [Google Scholar] [CrossRef]
- Kaminski, M. Probabilistic Entropy and Relative Entropy for the Effective Characteristics of the Fiber-Reinforced Composites with Stochastic Interface Defects. Comput. Methods Appl. Mech. Eng. 2024, 432, 117308. [Google Scholar] [CrossRef]
- Kumar Tipu, R.; Batra, V.; Suman; Pandya, K.S.; Panchal, V.R. Shear Capacity Prediction for FRCM-Strengthened RC Beams Using Hybrid ReLU-Activated BPNN Model. Structures 2023, 58, 105432. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 1–10. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Friedman, J. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Le Hoang, A.; Fehling, E. Influence of Steel Fiber Content and Aspect Ratio on the Uniaxial Tensile and Compressive Behavior of Ultra High Performance Concrete. Constr. Build. Mater. 2017, 153, 790–806. [Google Scholar] [CrossRef]
- Abellán-García, J.; Ortega-Guzmán, J.J.; Chaparro-Ruiz, D.A.; García-Castaño, E. A Comparative Study of LASSO and ANN Regressions for the Prediction of the Direct Tensile Behavior of UHPFRC. Adv. Civ. Eng. Mater. 2022, 11, 235–262. [Google Scholar] [CrossRef]
- Ryu, G.S.; Kim, S.H.; Ahn, G.H.; Koh, K.T. Evaluation of the Direct Tensile Behavioral Characteristics of UHPC Using Twisted Steel Fibers. Adv. Mater. Res. 2012, 602–604, 96–101. [Google Scholar] [CrossRef]
- Abellan-Garcia, J. Tensile Behavior of Recycled-Glass-UHPC under Direct Tensile Loading. Case Stud. Constr. Mater. 2022, 17, e01308. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, D.J.; Ryu, G.S.; Koh, K.T. Tensile Behavior of Ultra High Performance Hybrid Fiber Reinforced Concrete. Cem. Concr. Compos. 2012, 34, 172–184. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Sohn, H.K.; Borges, P.H.R.; Fediuk, R.; Kim, S. Enhancing the Tensile Performance of Ultra-High-Performance Concrete through Strategic Use of Novel Half-Hooked Steel Fibers. J. Mater. Res. Technol. 2020, 9, 2914–2925. [Google Scholar] [CrossRef]
- Abellán-García, J.; Guzmán-Guzmán, J.S. Random Forest-Based Optimization of UHPFRC under Ductility Requirements for Seismic Retrofitting Applications. Constr. Build. Mater. 2021, 285, 122869. [Google Scholar] [CrossRef]
- Abellán-García, J. Comparison of Artificial Intelligence and Multivariate Regression in Modeling the Flexural Behavior of UHPFRC. Dyna 2020, 87, 239–248. [Google Scholar] [CrossRef]
- Shi, C.; Wu, Z.; Xiao, J.; Wang, D.; Huang, Z.; Fang, Z. A Review on Ultra High Performance Concrete: Part I. Raw Materials and Mixture Design. Constr. Build. Mater. 2015, 101, 741–751. [Google Scholar] [CrossRef]
- Shi, C.; Wu, Z.; Xiao, J.; Wang, D.; Huang, Z.; Fang, Z. A Review on Ultra High Performance Concrete: Part II. Hydration, Microstructure and Properties. Constr. Build. Mater. 2015, 96, 368–377. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Shi, C.; Yuan, Q.; Zhang, Z. Durability of Ultra-High Performance Concrete—A Review. Constr. Build. Mater. 2020, 255, 119296. [Google Scholar] [CrossRef]
- Amin, M.; Zeyad, A.M.; Tayeh, B.A.; Saad Agwa, I. Effect of Ferrosilicon and Silica Fume on Mechanical, Durability, and Microstructure Characteristics of Ultra High-Performance Concrete. Constr. Build. Mater. 2022, 320, 126233. [Google Scholar] [CrossRef]
- Al-azzawi, A.A.; Ali, A.S.; Risan, H.K. Behavior of Ultra High Performance Concrete Structures. ARPN J. Eng. Appl. Sci. 2011, 6, 95–109. [Google Scholar]
- Park, S.; Wu, S.; Liu, Z.; Pyo, S. The Role of Supplementary Cementitious Materials (Scms) in Ultra High Performance Concrete (Uhpc): A Review. Materials 2021, 14, 1472. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Zhang, Z.; Shi, C.; Wu, Z.; Zhang, C. Steel Fiber–Matrix Interfacial Bond in Ultra-High Performance Concrete: A Review. Engineering 2022, 22, 215–232. [Google Scholar] [CrossRef]
- Li, S.; Cheng, S.; Mo, L.; Deng, M. Effects of Steel Slag Powder and Expansive Agent on the Properties of Ultra-High Performance Concrete (UHPC): Based on a Case Study. Materials 2020, 13, 683. [Google Scholar] [CrossRef]
- Abellán, J.; Fernández, J.; Torres, N.; Núñez, A. Statistical Optimization of Ultra-High-Performance Glass Concrete. ACI Mater J. 2020, 117, 243–254. [Google Scholar] [CrossRef]
- Wang, W.; Wu, C.; Liu, Z.; Si, H. Compressive Behavior of Ultra-High Performance Fiber-Reinforced Concrete (UHPFRC) Confined with FRP. Compos. Struct. 2018, 204, 419–437. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Park, J.J.; Kim, S.W. Fiber Pullout Behavior of HPFRCC: Effects of Matrix Strength and Fiber Type. Compos. Struct. 2017, 174, 263–276. [Google Scholar] [CrossRef]
- Abdallah, S.; Fan, M.; Zhou, X. Pull-Out Behaviour of Hooked End Steel Fibres Embedded in Ultra-High Performance Mortar with Various W/B Ratios. Int. J. Concr. Struct. Mater. 2017, 11, 301–313. [Google Scholar] [CrossRef]
- Viet Thein An, V.; Ludwig, H.-M. Proportioning Optimization of UHPC Containing Rice Husk Ash and Ground Granulated Blast-Furnace Slag. In Proceedings of the Hipermat 2012—3rd International Symposium on UHPC and Nanotechnology for Construction Materials, Kassel, Germany, 7–9 March 2012; Schmidt, M., Fehling, E., Glotzbach, C., Fröhlich, S., Piotrowski, S., Eds.; Kassel University: Kassel, Germany, 2012; pp. 197–205. [Google Scholar]
- Abellán-García, J. Study of Nonlinear Relationships between Dosage Mixture Design and the Compressive Strength of UHPC. Case Stud. Constr. Mater. 2022, 17, e01228. [Google Scholar] [CrossRef]
- Tram, N.-T.; Nguyen, D.-H. Influence of Matrix Strength on the Pullout Behavior of High Strength Steel Fibers. In CIGOS 2021, Emerging Technologies and Applications for Green Infrastructure; Ha-Minh, C., Tang, A.M., Bui, T.Q., Huynh, D.V.K., Eds.; Springer: Singapore, 2022; pp. 697–704. ISBN 978-981-16-7160-9. [Google Scholar]
- Abbass, W.; Khan, M.I.; Mourad, S. Evaluation of Mechanical Properties of Steel Fiber Reinforced Concrete with Different Strengths of Concrete. Constr. Build. Mater. 2018, 168, 556–569. [Google Scholar] [CrossRef]
- He, Z.H.; Du, S.G.; Chen, D. Microstructure of Ultra High Performance Concrete Containing Lithium Slag. J. Hazard. Mater. 2018, 353, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Han, F.; Cui, G.; Zhang, Q.; Lv, J.; Zhang, L.; Yang, Z. Combined Effect of Coarse Aggregate and Fiber on Tensile Behavior of Ultra-High Performance Concrete. Constr. Build. Mater. 2016, 121, 310–318. [Google Scholar] [CrossRef]
- Abellán-García, J.; Fernández-Gómez, J.; Torres-Castellanos, N.; Núñez-López, A. Tensile Behavior of Normal Strength Steel Fiber Green UHPFRC. ACI Mater. J. 2021, 118, 127–138. [Google Scholar] [CrossRef]
- Abellan-Garcia, J.; Fernández, J.; Khan, M.I.; Abbas, Y.M.; Carrillo, J. Uniaxial Tensile Ductility Behavior of Ultrahigh-Performance Concrete Based on the Mixture Design—Partial Dependence Approach. Cem. Concr. Compos. 2023, 140, 105060. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, H.; Wang, W.D.; Li, Y. Research on Mix Proportion Design Method of Cement Concrete for Road Mixed with Antifreeze Admixtures Sealed in Capsules. Key Eng. Mater. 2020, 861, 429–437. [Google Scholar] [CrossRef]
- Li, S.; Jensen, O.M.; Wang, Z.; Yu, Q. Influence of Micromechanical Property on the Rate-Dependent Flexural Strength of Ultra-High Performance Concrete Containing Coarse Aggregates (UHPC-CA). Compos. Part B Eng. 2021, 227, 109394. [Google Scholar] [CrossRef]
- Witkowski, P.; Kuczma, M.; Demby, M.; Rudnicki, T. Influence of Compressive Strength and Curing Time of Fiber Reinforced Concrete on Its Residual Flexural Tensile Strength. Adv. Sci. Technol. Res. J. 2025, 19, 329–341. [Google Scholar] [CrossRef]
- Wu, Z.; Khayat, K.H.; Shi, C. Changes in Rheology and Mechanical Properties of Ultra-High Performance Concrete with Silica Fume Content. Cem. Concr. Res. 2019, 123, 105786. [Google Scholar] [CrossRef]
- Subban, N.; Muthusamy, N.; Natarajan, B. Optimizing High Strength Concrete: A Comprehensive Study on the Synergistic Effects of Natural Fibres and Silica Fume on Workability, Mechanical and Flexural Behavior. Rev. Mater. 2024, 29, e20240525. [Google Scholar] [CrossRef]
- Wu, Z.; Khayat, K.H.; Shi, C. How Do Fiber Shape and Matrix Composition Affect Fiber Pullout Behavior and Flexural Properties of UHPC? Cem. Concr. Compos. 2018, 90, 193–201. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Liu, X.Y.; Wei, D.F. Influence of Silica Fume Content on Performance of High-Performance Concrete. In Proceedings of the 3rd International Symposium on Architecture Research Frontiers and Ecological Environment (ARFEE 2020), Zhangjiajie, China, 18–20 December 2020; Agnès, H., Ed.; EDP Sciences—Web of Conferences: Les Ulis, France, 2021; Volume 03039, pp. 1–4. [Google Scholar]
- Zhang, J.P.; Liu, L.M.; Zhu, Z.D.; Zhang, F.T.; Cao, J.Z. Flexural Fracture Toughness and First-Crack Strength Tests of Steel Fiber-Silica Fume Concrete and Its Engineering Applications. Strength Mater. 2018, 50, 166–175. [Google Scholar] [CrossRef]
- Jansen, D.; Neubauer, J.; Goetz-Neunhoeffer, F.; Haerzschel, R.; Hergeth, W.-D. Change in Reaction Kinetics of a Portland Cement Caused by a Superplasticizer—Calculation of Heat Flow Curves from XRD Data. Cem. Concr. Res. 2012, 42, 327–332. [Google Scholar] [CrossRef]
- Shen, C.; Wang, H.; Tang, D.; Lyu, Z.; Zhang, H.; Yu, L.; Yang, C. Investigating the Influence of Coarse Aggregate Characteristics and Fiber Dispersion on the Flexural Performance of Ultra-High Performance Concrete (UHPC). J. Build. Eng. 2024, 97, 110738. [Google Scholar] [CrossRef]
- Han, J.; Zhao, M.; Chen, J.; Lan, X. Effects of Steel Fiber Length and Coarse Aggregate Maximum Size on Mechanical Properties of Steel Fiber Reinforced Concrete. Constr. Build. Mater. 2019, 209, 577–591. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Soleimani-Dashtaki, S.; Oh, T.; Chun, B.; Banthia, N.; Lee, S.-J.; Yoon, Y.-S. Strain-Hardening Effect on the Flexural Behavior of Ultra-High-Performance Fiber-Reinforced Concrete Beams with Steel Rebars. Dev. Built Environ. 2024, 17, 100343. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; Khayat, K.H. Investigation of Mechanical Properties and Shrinkage of Ultra-High Performance Concrete: Influence of Steel Fiber Content and Shape. Compos. Part B Eng. 2019, 174, 107021. [Google Scholar] [CrossRef]
- Nguyen, C.T.; Pham, H.H.; Nguyen, V.T.; Pham, S.D.; Cu, V.H. Evaluating the Effect of Steel Fibers on Some Mechanical Properties of Ultra-High Performance Concrete. In Proceedings of the ICSCEA 2019 International Conference on Sustainable Civil Engineering and Architecture; Reddy, J.N., Wang, C.M., Luong, V.H., Le, A.T., Eds.; Springer: Singapore, 2020; pp. 493–501. [Google Scholar]
- Teng, L.; Meng, W.; Khayat, K.H. Rheology Control of Ultra-High-Performance Concrete Made with Different Fiber Contents. Cem. Concr. Res. 2020, 138, 106222. [Google Scholar] [CrossRef]
- El-Tair, A.M. The Impact of Different Steel Fibers Percentages on the Mechanical Properties of Ultra-High-Strength Concrete toward a Sustainable Composition. Innov. Infrastruct. Solut. 2024, 9, 199. [Google Scholar] [CrossRef]
- Li, P.P.; Cao, Y.Y.Y.; Sluijsmans, M.J.C.; Brouwers, H.J.H.; Yu, Q. Synergistic Effect of Steel Fibres and Coarse Aggregates on Impact Properties of Ultra-High Performance Fibre Reinforced Concrete. Cem. Concr. Compos. 2021, 115, 103866. [Google Scholar] [CrossRef]
- Feng, S.; Xiao, H.; Ma, M.; Zhang, S. Experimental Study on Bonding Behaviour of Interface between UHPC and Concrete Substrate. Constr. Build. Mater. 2021, 311, 125360. [Google Scholar] [CrossRef]
- Jeong, G.Y.; Jang, S.J.; Kim, Y.C.; Yun, H. Do Effects of Steel Fiber Strength and Aspect Ratio on Mechanical Properties of High-Strength Concrete TT—Effects of Steel Fiber Strength and Aspect Ratio on Mechanical Properties of High-Strength Concrete. J. Korea Concr. Inst. 2018, 30, 197–205. [Google Scholar] [CrossRef]
- Luo, X.; Zhang, S.; Li, A.; Zhang, D. Fiber Content Optimization of UHPC and R-UHPC Oriented to Tensile Behavior and Cost Reduction. Constr. Build. Mater. 2023, 395, 132314. [Google Scholar] [CrossRef]
- Shao, Y.; Billington, S.L. Impact of UHPC Tensile Behavior on Steel Reinforced UHPC Flexural Behavior. J. Struct. Eng. 2022, 148, 4021244. [Google Scholar] [CrossRef]
- Kim, H.; Kang, D.; Oh, S.J.; Joo, C. Nondestructive Evaluation on Dispersion of Steel Fibers in UHPC Using THz Electromagnetic Waves. Constr. Build. Mater. 2018, 172, 293–299. [Google Scholar] [CrossRef]











| Notation | Material | Type/Shape | Tensile Strength | Length (mm) | Diameter (mm) | lf/df |
|---|---|---|---|---|---|---|
| OL | Steel | Straight | 2650 (MPa) | 13 | 0.20 | 65 |
| H | Steel | Hooked | 1800 (MPa) | 35 | 0.50 | 70 |
| PVA | PVA | Straight | 1600 (MPa) | 6 | 0.02 | 300 |
| Notation | IV1 | IV2 | IV3 | IV5 | IV9 | IV11 | IV12 | IV15 | IV17 | IV18 | IV19 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 0.254 | 0.115 | 0 | 0 | 0.061 | 0.2 | 0.036 | 0.325 | 600 | 0.16 | 157 |
| B | 0.254 | 0.045 | 0.084 | 0.061 | 0.061 | 0.216 | 0.021 | 0.319 | 600 | 0.15 | 153 |
| C | 0.231 | 0.068 | 0 | 0.085 | 0.033 | 0.226 | 0.024 | 0.334 | 600 | 0.19 | 124 |
| UHPC’s Series Notation | Matrix | Fiber 1 Type | Fiber 1 Volume Fraction | Fiber 2 Type | Fiber 2 Volume Fraction |
|---|---|---|---|---|---|
| A0 | A | - | - | - | - |
| A-OL1 | A | OL | 1% | - | - |
| A-OL2 | A | OL | 2% | - | - |
| A-H1 | A | H | 1% | - | - |
| A-H2 | A | H | 2% | - | - |
| A-PVA1 | A | PVA | 1% | - | - |
| A-PVA2 | A | PVA | 2% | - | - |
| A-OL1-H1 | A | OL | 1% | H | 1% |
| A-OL1-PVA | A | OL | 1% | PVA | 1% |
| A-H1-PVA1 | A | H | 1% | PVA | 1% |
| A-OL1.5-PVA0.5 | A | OL | 1.5% | PVA | 0.5% |
| A-H1.5-PVA0.5 | A | H | 1.5% | PVA | 0.5% |
| B0 | B | - | - | - | - |
| B-OL1 | B | OL | 1% | - | - |
| B-OL2 | B | OL | 2% | - | - |
| B-H1 | B | H | 1% | - | - |
| B-H2 | B | H | 2% | - | - |
| B-PVA1 | B | PVA | 1% | - | - |
| B-PVA2 | B | PVA | 2% | - | - |
| C0 | C | - | - | - | - |
| C-OL1 | C | OL | 1% | - | - |
| C-OL2 | C | OL | 2% | - | - |
| C-H1 | C | H | 1% | - | - |
| C-H2 | C | H | 2% | - | - |
| C-PVA1 | C | PVA | 1% | - | - |
| C.PVA2 | C | PVA | 2% | - | - |
| UHPC’s Series Notation | IV20 | IV21 |
|---|---|---|
| A-OL1 | 0.01 | 0.65 |
| A-OL2 | 0.02 | 1.3 |
| A-H1 | 0.01 | 0.7 |
| A-H2 | 0.02 | 1.4 |
| A-PVA1 | 0.01 | 3 |
| A-PVA2 | 0.02 | 6 |
| A-OL1-H1 | 0.02 | 1.35 |
| A-OL1-PVA | 0.02 | 3.65 |
| A-H1-PVA1 | 0.02 | 3.7 |
| A-OL1.5-PVA0.5 | 0.02 | 2.15 |
| A-H1.5-PVA0.5 | 0.02 | 2.55 |
| B-OL1 | 0.01 | 0.65 |
| B-OL2 | 0.02 | 1.3 |
| B-H1 | 0.01 | 0.7 |
| B-H2 | 0.02 | 1.4 |
| B-PVA1 | 0.01 | 3 |
| B-PVA2 | 0.02 | 6 |
| C-OL1 | 0.01 | 0.65 |
| C-OL2 | 0.02 | 1.3 |
| C-H1 | 0.01 | 0.7 |
| C-H2 | 0.02 | 1.4 |
| C-PVA1 | 0.01 | 3 |
| C.PVA2 | 0.02 | 6 |
| UHPC’s Series Notation | IV22 | IV23 | IV24 | IV25 | IV26 | IV27 | IV28 | IV29 | IV30 | IV31 |
|---|---|---|---|---|---|---|---|---|---|---|
| A-OL1 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 78.5 | 0.01 | 0.65 |
| A-OL2 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 157 | 0.02 | 1.3 |
| A-H1 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 78.5 | 0.01 | 0.7 |
| A-H2 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 157 | 0.02 | 1.4 |
| A-PVA1 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 11.5 | 0.01 | 3 |
| A-PVA2 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 23 | 0.02 | 6 |
| A-OL1-H1 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 78.5 | 0.01 | 0.65 |
| A-OL1-PVA1 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 78.5 | 0.01 | 0.65 |
| A-H1-PVA1 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 78.5 | 0.01 | 0.7 |
| A-OL1.5-PVA0.5 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 78.5 | 0.015 | 0.975 |
| A-H1.5-PVA0.5 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 78.5 | 0.015 | 1.05 |
| B-OL1 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 78.5 | 0.01 | 0.65 |
| B-OL2 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 157 | 0.02 | 1.3 |
| B-H1 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 78.5 | 0.01 | 0.7 |
| B-H2 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 157 | 0.02 | 1.4 |
| B-PVA1 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 11.5 | 0.01 | 3 |
| B-PVA2 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 23 | 0.02 | 6 |
| C-OL1 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 78.5 | 0.01 | 0.65 |
| C-OL2 | 1 | 0 | 0 | 2650 | 13 | 0.2 | 65 | 157 | 0.02 | 1.3 |
| C-H1 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 78.5 | 0.01 | 0.7 |
| C-H2 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 157 | 0.02 | 1.4 |
| C-PVA1 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 11.5 | 0.01 | 3 |
| C.PVA2 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 23 | 0.02 | 6 |
| UHPC’s Series Notation | IV32 | IV33 | IV34 | IV35 | IV36 | IV37 | IV38 | IV39 | IV40 | IV41 |
|---|---|---|---|---|---|---|---|---|---|---|
| A-OL1-H1 | 0 | 1 | 0 | 1800 | 35 | 0.5 | 70 | 78.5 | 0.01 | 0.7 |
| A-OL1-PVA1 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 11.5 | 0.01 | 3 |
| A-H1-PVA1 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 11.5 | 0.01 | 3 |
| A-OL1.5-PVA0.5 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 11.5 | 0.005 | 1.5 |
| A-H1.5-PVA0.5 | 0 | 0 | 1 | 1600 | 6 | 0.02 | 300 | 11.5 | 0.005 | 1.5 |
| Model | Selected Hyperparameters |
|---|---|
| Linear Regression (LR) |
|
| KNN |
|
| RF |
|
| XRF |
|
| XGBoost |
|
| ANN |
|
| Model | R2 | MAE | RMSE | MSE | MAPE |
|---|---|---|---|---|---|
| RF | 0.841 | 2.3014 | 3.6531 | 13.3481 | 19.4000 |
| XRF | 0.843 | 2.0124 | 3.5402 | 12.5290 | 19.1101 |
| XGB | 0.859 | 1.9468 | 3.2823 | 10.7695 | 16.9485 |
| Hybrid | 0.872 | 1.8597 | 3.1315 | 9.8083 | 16.6920 |
| Model | R2 | MAE | RMSE | MSE | MAPE |
|---|---|---|---|---|---|
| RF | 0.861 | 1.6627 | 2.0372 | 4.1511 | 6.2277 |
| XRF | 0.741 | 2.2224 | 3.7521 | 14.0733 | 7.8542 |
| XGB | 0.904 | 1.5267 | 1.7958 | 3.2250 | 5.4667 |
| Hybrid | 0.951 | 1.3892 | 1.6528 | 2.7328 | 3.7331 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escalante-Tovar, J.D.; Abellán-García, J.; Fernández-Gómez, J. Predicting and Unraveling Flexural Behavior in Fiber-Reinforced UHPC Through Based Machine Learning Models. J. Compos. Sci. 2025, 9, 333. https://doi.org/10.3390/jcs9070333
Escalante-Tovar JD, Abellán-García J, Fernández-Gómez J. Predicting and Unraveling Flexural Behavior in Fiber-Reinforced UHPC Through Based Machine Learning Models. Journal of Composites Science. 2025; 9(7):333. https://doi.org/10.3390/jcs9070333
Chicago/Turabian StyleEscalante-Tovar, Jesus D., Joaquin Abellán-García, and Jaime Fernández-Gómez. 2025. "Predicting and Unraveling Flexural Behavior in Fiber-Reinforced UHPC Through Based Machine Learning Models" Journal of Composites Science 9, no. 7: 333. https://doi.org/10.3390/jcs9070333
APA StyleEscalante-Tovar, J. D., Abellán-García, J., & Fernández-Gómez, J. (2025). Predicting and Unraveling Flexural Behavior in Fiber-Reinforced UHPC Through Based Machine Learning Models. Journal of Composites Science, 9(7), 333. https://doi.org/10.3390/jcs9070333









