Influence of Various Crack Widths in RC Bridge Decks on the Initiation of Chloride-Induced Corrosion
Abstract
1. Introduction
2. Framework and Research Methodology Modelling
2.1. Overview of the Modelling Approach
- Integration of Climate Projections: Climate data from the CCCR and IPCC RCP scenarios were incorporated to simulate future environmental conditions. These projections were used to adjust the chloride diffusion coefficient on the basis of the maximum temperature and RH.
- Monte Carlo simulation for probabilistic modelling: MCS was used to assess the variability in the time to corrosion initiation by randomly sampling key input parameters (assessing the PCI under stochastic environmental and structural conditions). For each scenario, 100,000 simulations were performed to account for the variability in key parameters, including the chloride surface concentration (Cs), the concrete cover thickness (x), and the chloride threshold levels (Cth).
- Correction of the Chloride Diffusion Coefficient: The chloride diffusion coefficient (D) was adjusted to reflect the effects of temperature, maturation time, and relative humidity via an adaptation of Saetta et al.’s [41] approach.
- Modelling of Chloride Ingress: Chloride ingress was modelled via Fick’s second law of diffusion for uncracked concrete. For cracked concrete, the diffusion coefficient (Dcc) was partitioned into contributions from uncracked and cracked regions, as described by Djerbi et al. [18] and Takewaka et al. [33]. The influence of crack width (0.1 mm to 0.35 mm) on corrosion initiation time was evaluated via polynomial relationships derived from regression analyses.
- Analysis of Environmental Parameters: A comparative analysis was performed to independently assess the influences of temperature and relative humidity on the PCI.
- Evaluation of Supplementary Cementing Materials: The model incorporated the mitigating role of SCMs in reducing chloride diffusion and extending corrosion-free service life.
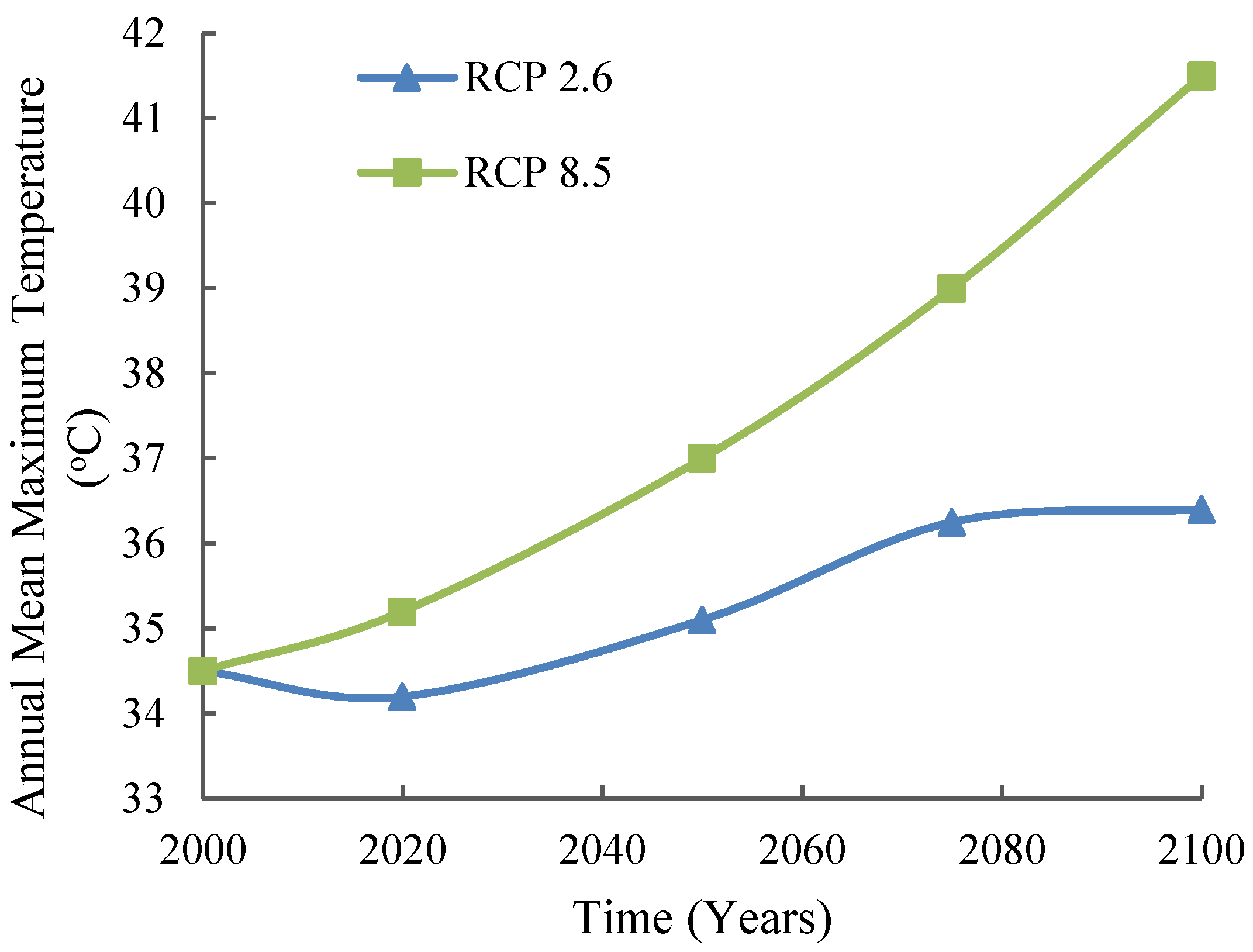
2.2. Projection of the Maximum Temperature for Toronto Under Different Climate Scenarios
- RCP2.6 (Low-Emission Scenario): This scenario reflects aggressive mitigation strategies to limit the rise in global temperature. Under RCP2.6, Toronto’s maximum annual temperature will reach 36.4 °C by 2100.
- RCP8.5 (High-Emission Scenario): This scenario represents a future with continued high energy consumption and limited climate action. Under RCP8.5, Toronto’s maximum annual temperature could rise to 41.7 °C by 2100.
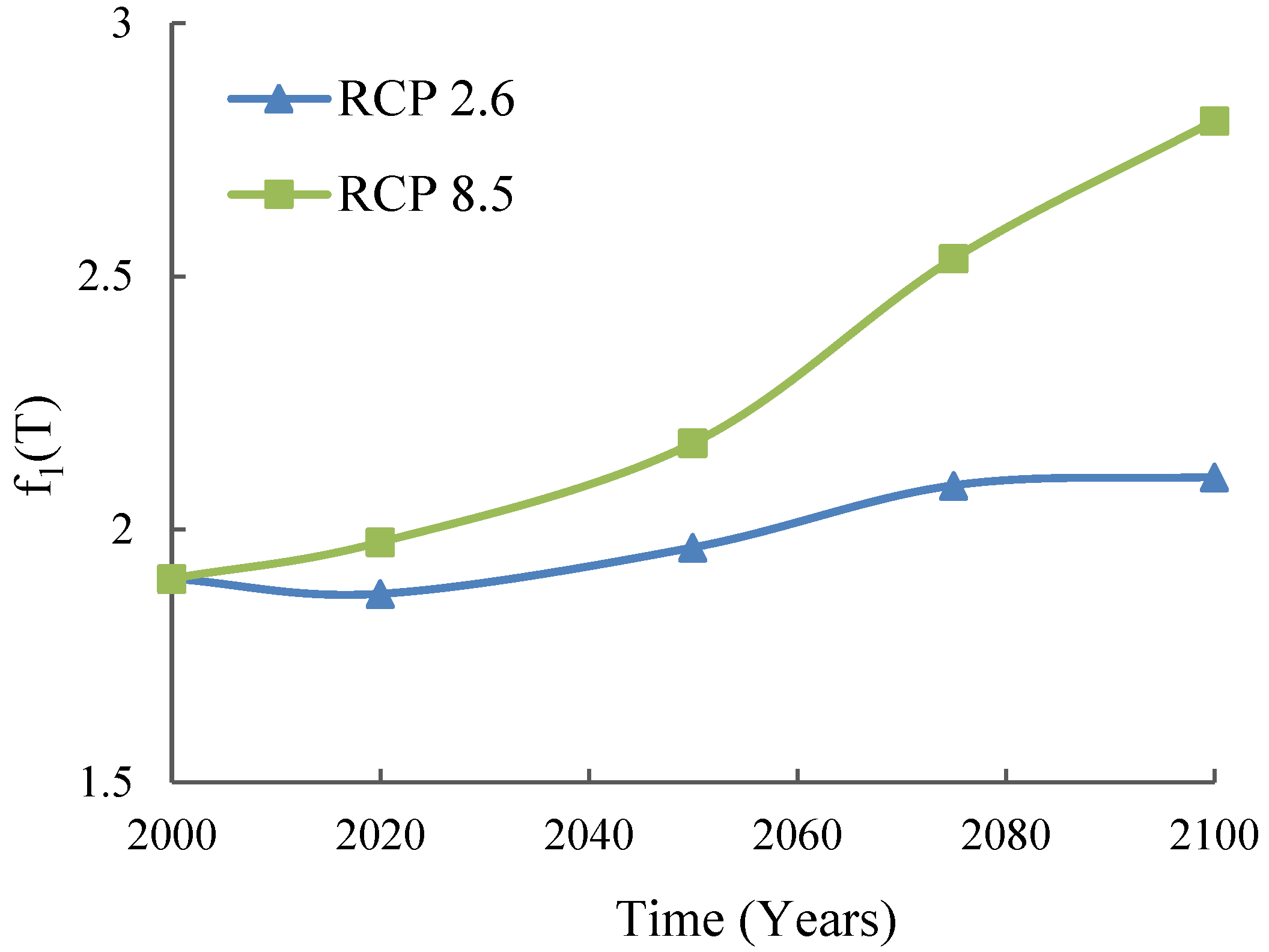
2.3. Performance Function for Chloride-Induced Corrosion Initiation
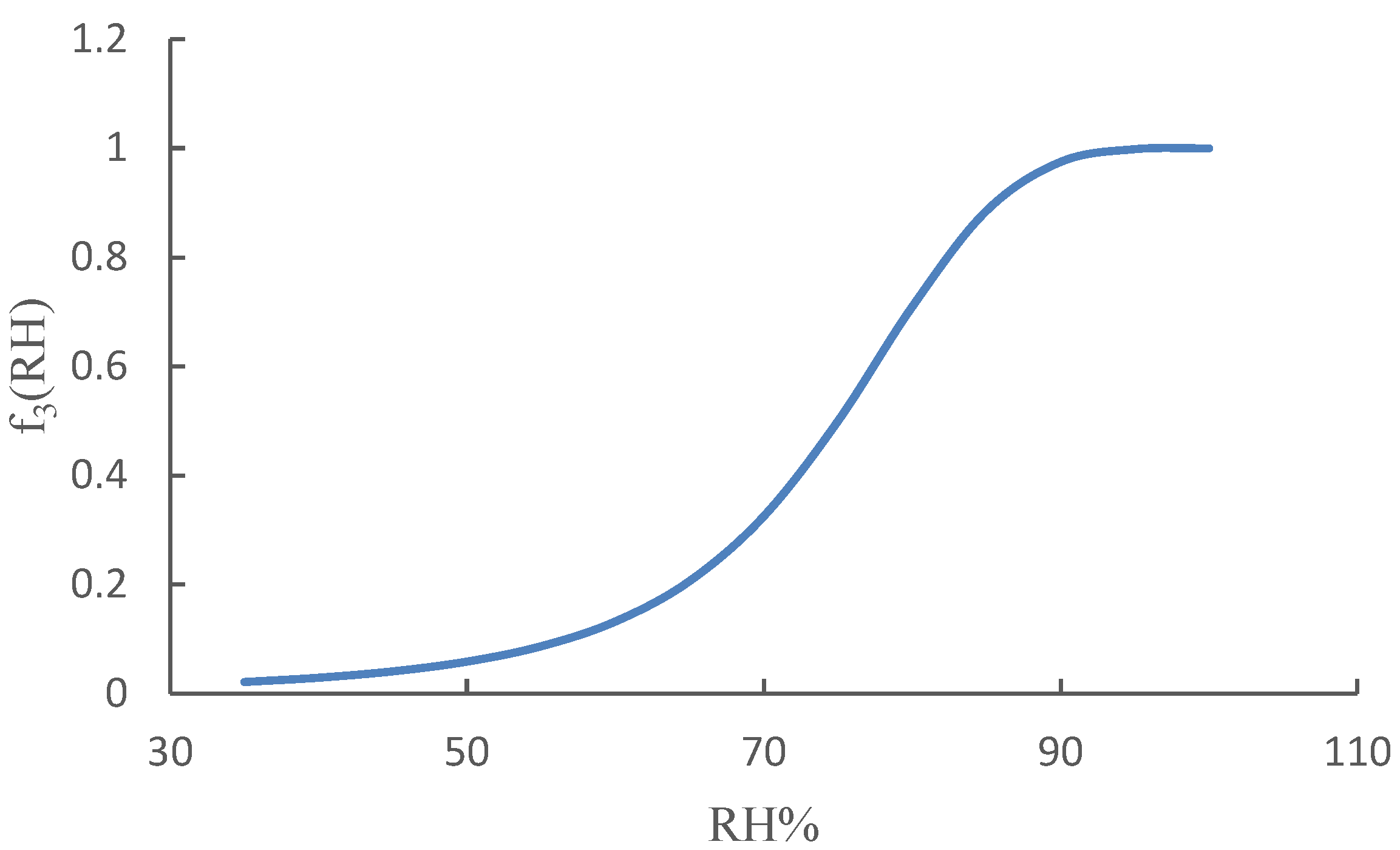
2.4. Corrected Chloride Diffusion Coefficient (Dc)
2.5. Probabilistic Approach for Climate-Related Corrosion Initiation Assessment
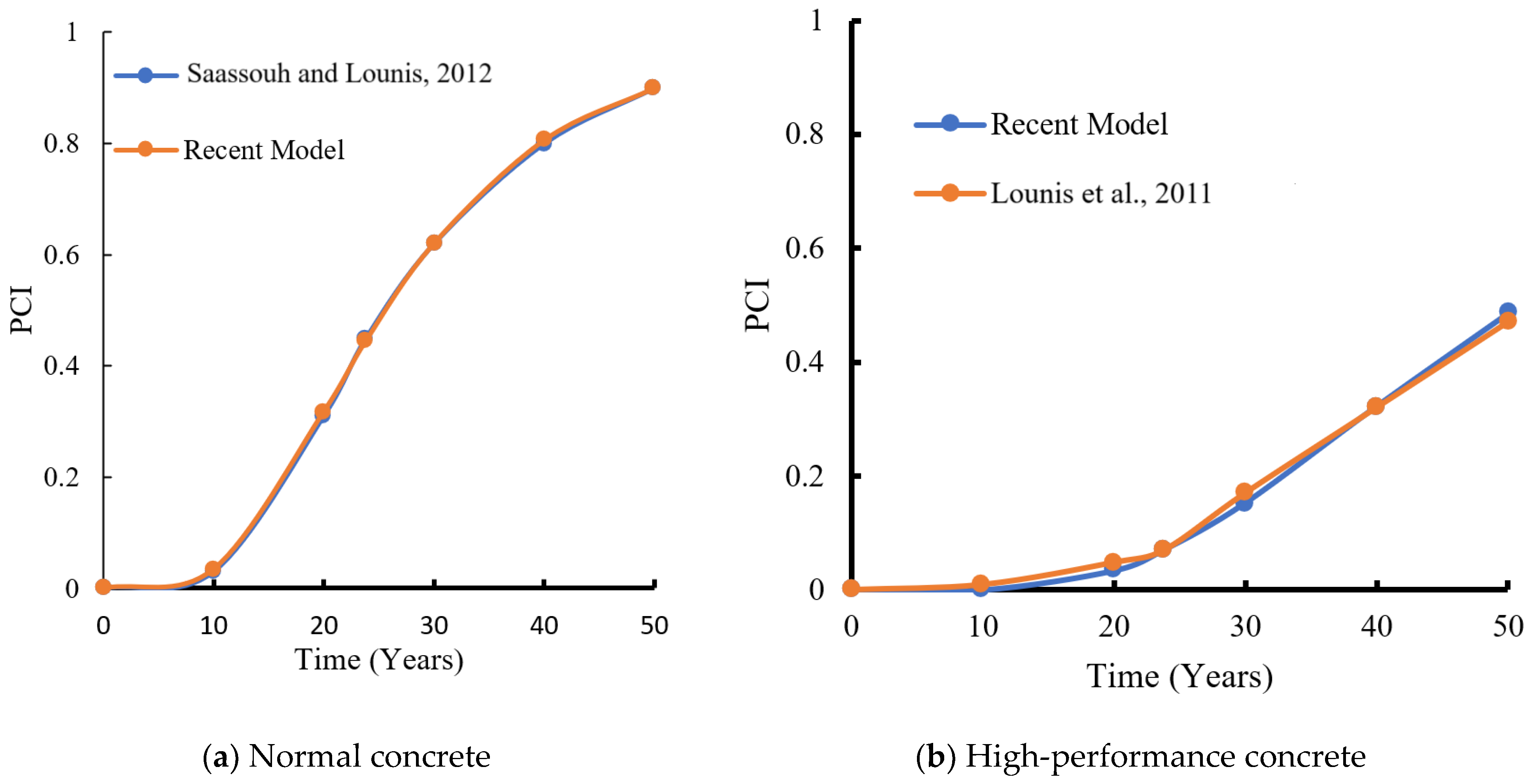
2.6. Validation of the Chloride-Induced Corrosion Initiation Model
3. Results and Discussion
3.1. Impact of the Maximum Temperature and Relative Humidity on the PCI
3.2. Chloride-Induced Corrosion Initiation in Uncracked and Cracked Concrete
3.2.1. Corrosion Initiation Model and Assumptions
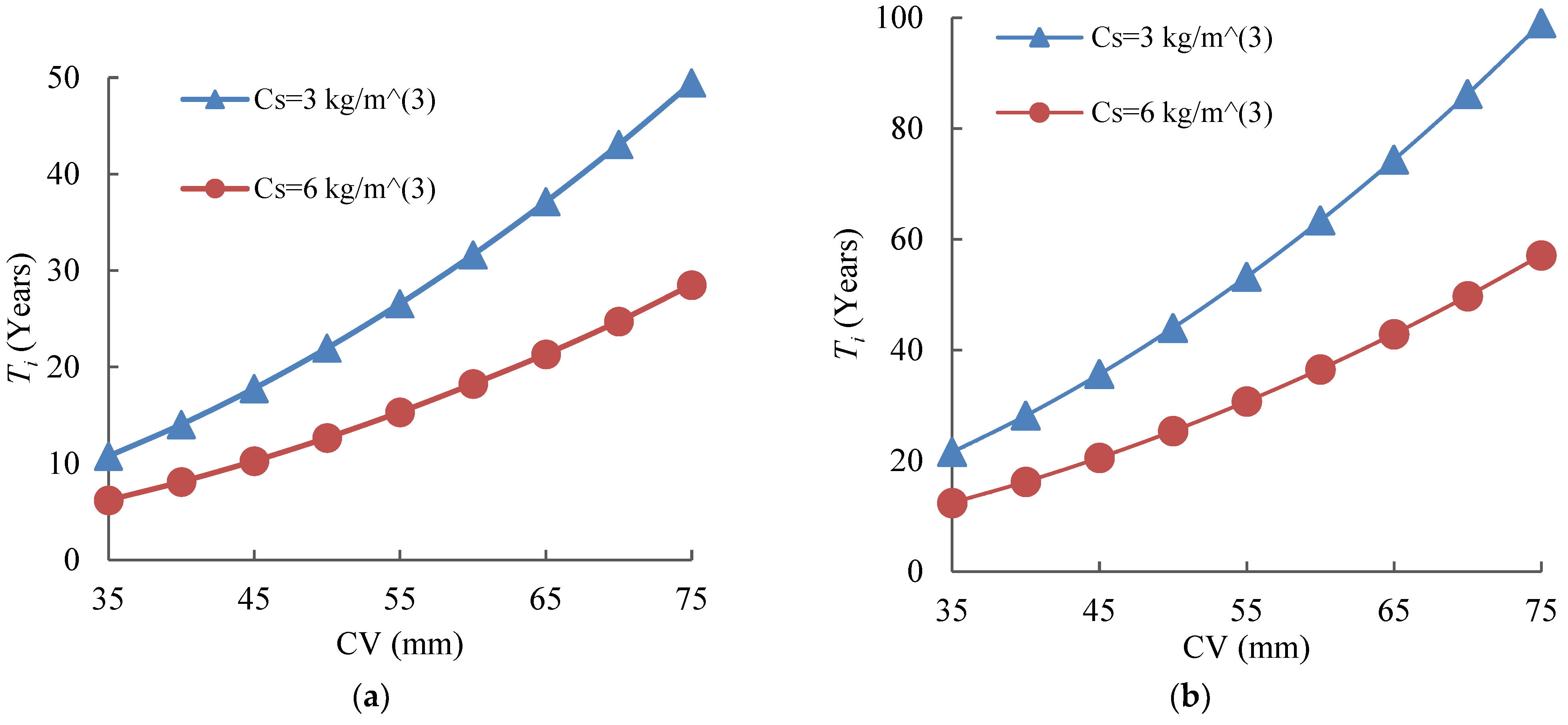
3.2.2. Time to Corrosion Initiation for Uncracked Concrete
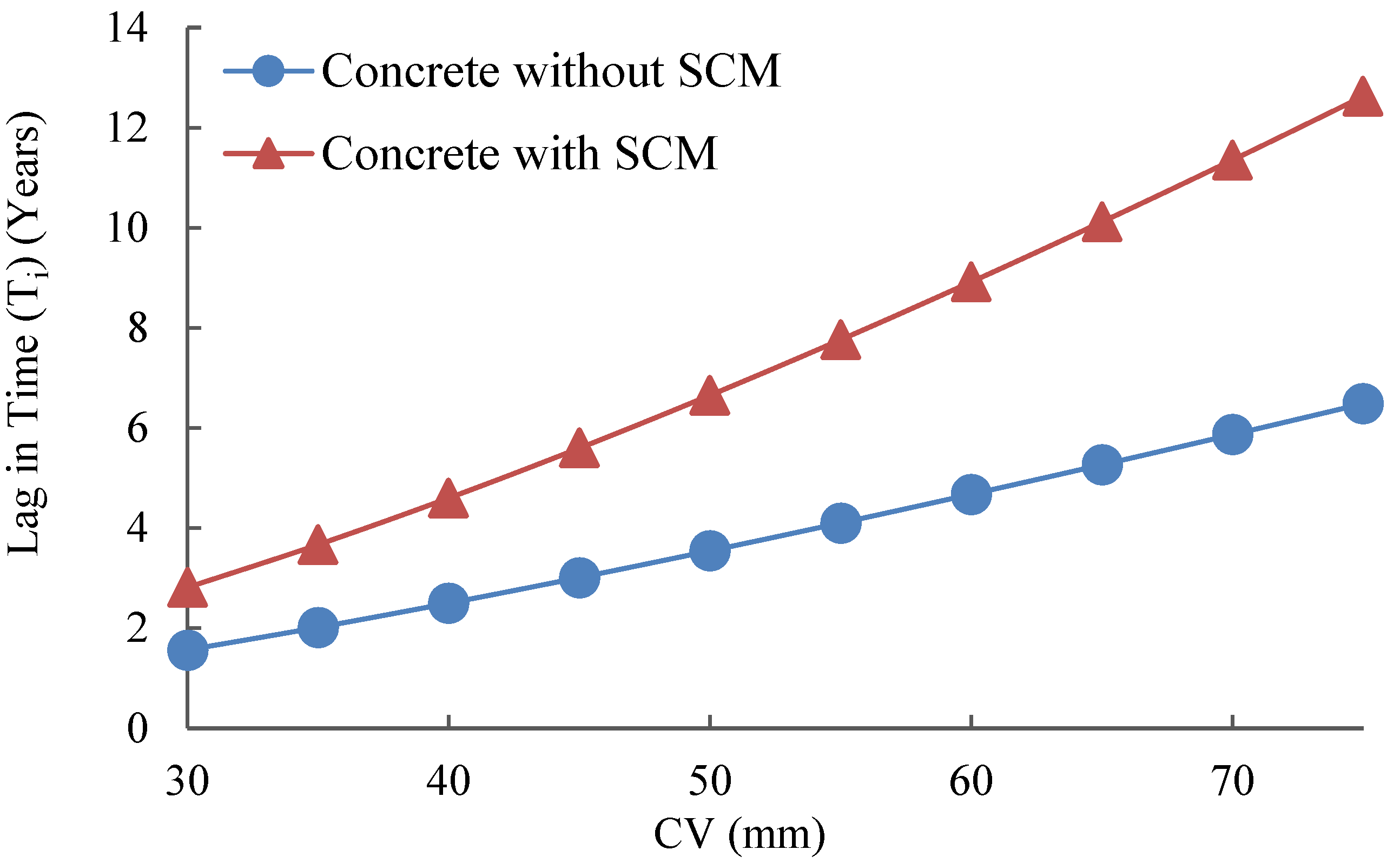
3.2.3. Lag Time Due to Chloride Concentration Differences
3.2.4. Cracked vs. Uncracked Concrete Performance
- Compared with the uncracked concrete, the cracked concrete has substantially lower Ti values across all the cases. For example, in SCM-modified concrete, cracking reduces the quadratic coefficient from 0.0047 to 0.0037 and introduces a significant negative linear term, reflecting the sharp decline in corrosion resistance due to cracking.
- For concrete without SCMs, the Ti values are the lowest, particularly under cracked conditions, emphasizing the compounding negative effects of cracking and the absence of SCMs on long-term durability.
3.2.5. Lag Time: Cracked vs. Uncracked
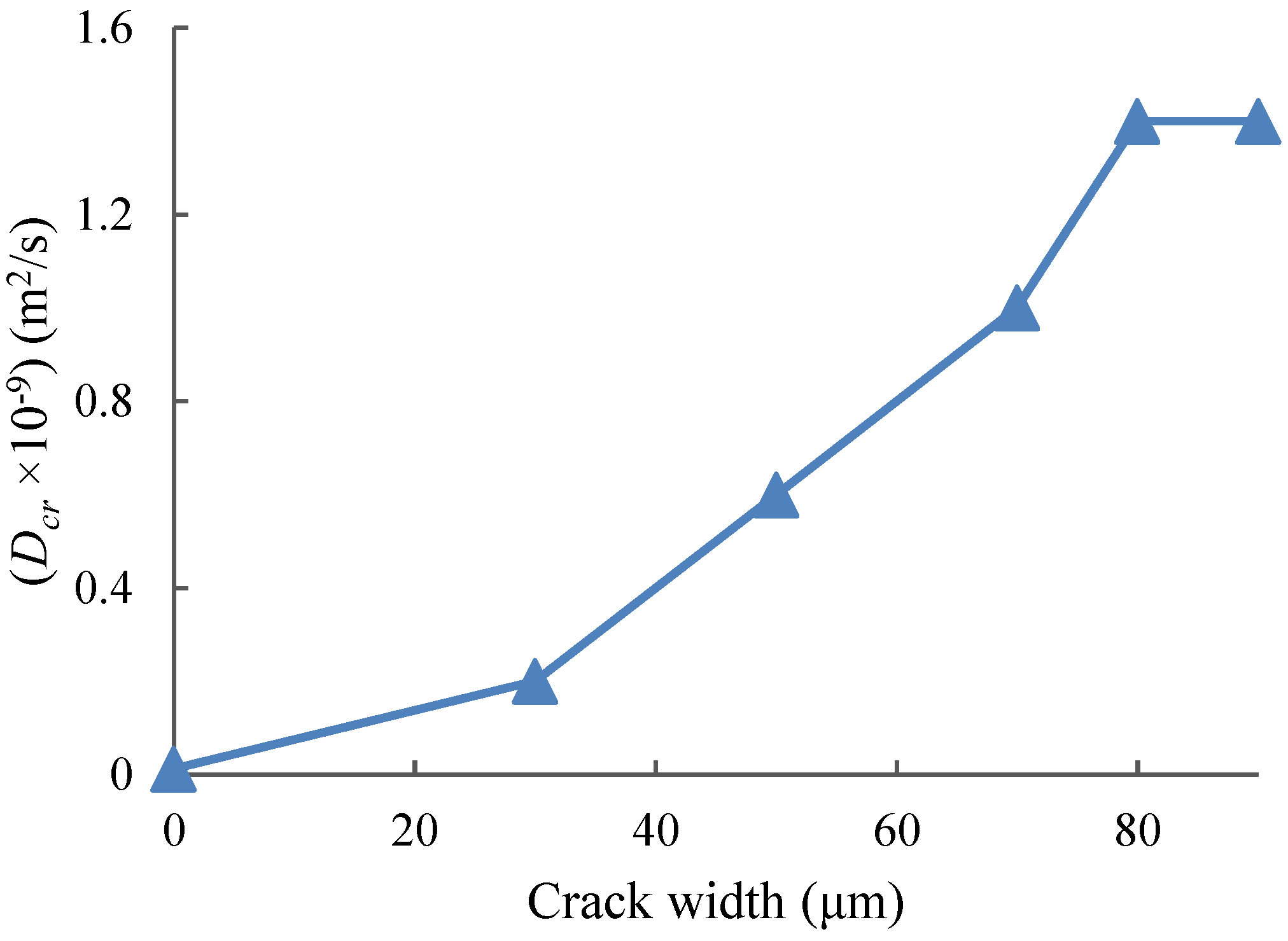
3.3. Effect of Crack Width on Chloride Diffusion and Corrosion Initiation
3.3.1. Influence of the Crack Width on the Diffusion Coefficient
3.3.2. Time to Corrosion Initiation Based on Crack Width
3.3.3. Practical Implications for Cover Design and SCM Use
4. Conclusions
- The crack width significantly accelerates corrosion initiation. For a 0.25 mm crack (maximum allowed by CHBDC for exposure to deicing salts), the corrosion initiation time is reduced by 34–41%, with a greater reduction in unmodified normal concrete (NC) than in SCM-enhanced concrete.
- High-performance concrete (HPC) with SCMs offers superior durability, nearly doubling the corrosion initiation time compared with that of NC under identical exposure. HPC also demonstrates reduced sensitivity to humidity due to its dense microstructure.
- Temperature has a dominant influence on the PCI. Under the RCP8.5 scenario, projected increases in maximum temperatures (40–45 °C) sharply reduce service life in both NC and HPC. In contrast, relative humidity (60–75%) had a minimal effect on the HPC but significantly worsened the PCI in NC.
- Both the crack width and cover depth affect the PCI in a nonlinear manner. The corrosion initiation time follows a second-degree polynomial relationship with respect to both parameters, enabling accurate service life estimation. Increased cover improves durability but shows diminishing returns beyond 70 mm.
- Polynomial equations developed for various parameters (e.g., crack width, chloride concentration, and SCM use) provide a scalable tool for predicting corrosion initiation, offering actionable insights for engineers and code developers.
5. Study Limitations
6. Practical Implications
- Durability-Based Design Updates: The study highlights the need to revise current crack width limits and concrete cover requirements in bridge design codes, such as the CHBDC, to account for accelerated chloride ingress under elevated temperatures and humidity projections.
- Material Selection Strategies: The superior performance of HPC observed under cracked conditions and variable climates suggests that incorporating SCMs such as silica fume or fly ash should be encouraged in future infrastructure projects to enhance durability and service life.
- Crack Control as a Priority: The strong influence of crack width on corrosion initiation underscores the importance of stringent crack control measures during construction and inspection. Design specifications should prioritize minimizing crack formation, particularly in regions exposed to deicing salts and climate change effects.
- Climate-Resilient Infrastructure Planning: By integrating probabilistic modelling with climate projections (RCP2.6 and RCP8.5), this study provides a scalable framework for evaluating the long-term performance of RC bridge decks. These tools can assist infrastructure owners and policymakers in prioritizing rehabilitation strategies and allocating maintenance resources more effectively.
- Future Asset Management Systems: The probabilistic models developed can be incorporated into bridge management systems to better predict future maintenance needs, optimize intervention timing, and reduce life-cycle costs associated with corrosion-induced deterioration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Uhlig, H. Corrosion, and Corrosion Control; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1963; Volume 67. [Google Scholar] [CrossRef]
- Hansson, C.M. An introduction to corrosion of engineering materials. In Corrosion of Steel in Concrete; Poursaee, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Revie, R.W.; Uhlig, H.H. Corrosion, and Corrosion Control: An Introduction to Corrosion Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 9780470277270. [Google Scholar] [CrossRef]
- Mehta, P.K.; Monteiro, P.J.M. Concrete Microstructure, Properties and Materials; McGraw Hill Professional: New York, NY, USA, 2006; pp. 177–178. [Google Scholar]
- Qu, F.; Zhang, J.; Liu, G.; Zhao, S. Experimental Study on Chloride Ion Diffusion in Concrete Affected by Exposure Conditions. Materials 2022, 15, 2917. [Google Scholar] [CrossRef]
- Bier, T.; Kropp, J.; Hilsdorf, H. Formation of silica gel during carbonation of cementitious systems containing slag cement. In Proceedings of the 3rd International Conference Fly Ash, Silica Fume, Slag and Natural Pozzolans in Concrete, Trondheim, Norway, 18–23 June 1989; American Concrete Institute: Farmington Hills, MI, USA, 1989. [Google Scholar]
- Balestra, C.E.T.; Reichert, T.A.; Pansera, W.A.; Savaris, G. Evaluation of chloride ion penetration through concrete surface electrical resistivity of field naturally degraded structures present in marine environment. Constr. Build. Mater. 2020, 230, 116979. [Google Scholar] [CrossRef]
- Tuutti, K. Corrosion of Steel in Concrete. Ph.D. Thesis, Division of Building Materials, Swedish Cement and Concrete Research Institute, Stockholm, Sweden, 1982; p. 469. [Google Scholar]
- López, W.; González, J. Influence of the degree of pore saturation on the resistivity of concrete and the corrosion rate of steel reinforcement. Cem. Concr. Res. 1993, 23, 368–376. [Google Scholar] [CrossRef]
- Al-Sulaimani, G.J.; Kaleemullah, M.; Basunbul, I.A. Rasheeduzzafar. Influence of Corrosion and Cracking on Bond Behavior and Strength of Reinforced Concrete Members. ACI Struct. J. 1990, 87, 220–231. [Google Scholar] [CrossRef]
- Andrade, C.; Alonso, C. Durability design based on models for corrosion rates. In The Modelling of Microstructure and Its Potential for Studying Transport Properties and Durability; Springer: Dordrecht, The Netherlands, 1996; pp. 473–492. [Google Scholar]
- Amleh, L.; Mirza, S. Corrosion Influence on Bond between Steel and Concrete. ACI Struct. J. 1999, 96, 415–423. [Google Scholar] [CrossRef]
- Cabrera, J.G.; Ghoddoussi, P. The Effect of Reinforcement Corrosion on the Strength of the Steel/Concrete Bond. In Proceedings of the International Conference Bond in Concrete from Research to Practice: Proceedings Topics, Riga, Latvia, 15–17 October 1992; CEB: Mumbai, India, 2001; pp. 11–24. [Google Scholar]
- Amleh, L.; Ghosh, A. Modeling the effect of corrosion on bond strength at the steel-concrete interface with finite-element analysis. Can. J. Civ. Eng. 2006, 33, 673–682. [Google Scholar] [CrossRef]
- Lothenbach, B.; Scrivener, K.; Hooton, R.D. Supplementary cementitious materials. Cem. Concr. Res. 2011, 41, 1244–1256. [Google Scholar] [CrossRef]
- Thomas, M.D.A.; Hooton, R.D.; Scott, A.; Zibara, H. The effect of supplementary cementitious materials on chloride binding in hardened cement paste. Cem. Concr. Res. 2012, 42, 1–7. [Google Scholar] [CrossRef]
- Cheng, S.; Shen, L.; Chen, W.; Zhu, H.; You, P.; Chen, L. Mechanical Properties and Chloride Penetration Resistance of Concrete Combined with Ground Granulate Blast Furnace Slag and Macro Synthetic Fiber. Materials 2024, 17, 4735. [Google Scholar] [CrossRef]
- Djerbi, A.; Bonnet, S.; Khelidj, A.; Baroghel-bouny, V. Influence of traversing crack on chloride diffusion into concrete. Cem. Concr. Res. 2008, 38, 877–883. [Google Scholar] [CrossRef]
- Andrade, C.; Castillo, A. Evolution of reinforcement corrosion due to climatic variations. Mater. Corros. 2003, 54, 379–386. [Google Scholar] [CrossRef]
- Yuan, Y.; Jiang, J. Prediction of temperature response in concrete in a natural climate environment. Constr. Build. Mater. 2011, 25, 3159–3167. [Google Scholar] [CrossRef]
- Lindvall, A. Duracrete- Probabilistic Performance-Based Durability Design of the Concrete Structure, 1st ed.; Chalmers University of Technology: Gothenburg, Sweden, 1999. [Google Scholar]
- Bastidas-Arteaga, E.; Chateauneuf, A.; Sanchez-Silva, M.; Bressolette, P.; Schoefs, F. Influence of weather and global warming in chloride ingress into concrete: A stochastic approach. Struct. Saf. 2010, 32, 238–249. [Google Scholar] [CrossRef]
- Yuan, Q.; Shi, C.; De Schutter, G.; Audenaert, K. Effect of temperature on the transport of chloride ions in concrete. In Concrete Repair, Rehabilitation, and Retrofitting II; Taylor & Francis Group: London, UK, 2008; pp. 159–160. [Google Scholar]
- Maeda, S.; Takewaka, K.; Yamaguchi, T. Quantification of Chloride Diffusion Process into Concrete Under Marine Environment. Proc. Jpn. Soc. Civ. Engineers 2004, 63, 109–120. [Google Scholar]
- Zhang, J.; Gao, Y.; Han, Y. Interior humidity of concrete under dry-wet cycles. J. Mater. Civ. Eng. 2012, 24, 289–298. [Google Scholar] [CrossRef]
- Akduman, S.; Öztürk, H. Effect of Reinforcement Corrosion on Structural Behavior in Reinforced Concrete Structures According to Initiation and Propagation Periods. Buildings 2024, 14, 4026. [Google Scholar] [CrossRef]
- Liu, X.; Li, H.; Qi, M.; Yang, Y.; Zhu, Z.; Yu, Z. Experimental Study on the Influence of Transverse Crack on Chloride Ingress in Concrete Slab Track of High-Speed Railway. Materials 2023, 16, 3524. [Google Scholar] [CrossRef]
- Wang, X.-Y.; Zhang, L.-N. Simulation of Chloride Diffusion in Cracked Concrete with Different Crack Patterns. Adv. Mater. Sci. Eng. 2016, 2016, 1075452. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, G.; Tong, Y.; Gu, C. A Numerical Study on Chloride Diffusion in Cracked Concrete. Crystals 2021, 11, 742. [Google Scholar] [CrossRef]
- Félix, E.F.; Falcão, I.d.S.; dos Santos, L.G.; Carrazedo, R.; Possan, E. A Monte Carlo-Based Approach to Assess the Reinforcement Depassivation Probability of RC Structures: Simulation and Analysis. Buildings 2023, 13, 993. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, X.; Zhao, H.; Hu, D.; Gu, X.; Li, R. A probabilistic stress-strain relationship model for steel bars including the non-uniform corrosion effects in chloride environments. Case Stud. Constr. Mater. 2025, 22, e04262. [Google Scholar] [CrossRef]
- Shao, W.; He, X.; Shi, D.; Zhu, W. Prediction of Crack Width in RC Piles Exposed to Local Corrosion in Chloride Environment. Materials 2023, 16, 6403. [Google Scholar] [CrossRef]
- Takewaka, K.; Yamaguchi, T.; Maeda, S. Simulation model for deterioration of concrete structures due to chloride attack. J. Adv. Concr. Technol. 2005, 1, 139–146. [Google Scholar] [CrossRef]
- Amleh, L.; Hassan, M.; Hussein, L. Influence of Climate Change on the Probability of Chloride-Induced Corrosion Initiation for RC Bridge Decks Made of Geopolymer Concrete. Sustainability 2024, 16, 8200. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Bush, E.; Lemmen, D.S. (Eds.) Canada Changing Climate Report 2019; CCCR: Ottawa, ON, Canada, 2019. [Google Scholar]
- Pan, Z.; Li, T.; Ruan, X. Effect of Seasonal Characteristics of Temperature and Relative Humidity on Chloride Diffusion Process in Concrete: A Preliminary Theoretical Study. Sustainability 2019, 11, 6330. [Google Scholar] [CrossRef]
- Wang, X.; Stewart, M.G.; Nguyen, M.N. Impact of Climate Change on Corrosion and Damage to Concrete Infrastructure in Australia. Clim. Change 2011, 110, 941–957. [Google Scholar] [CrossRef]
- Fode, T.A.; Chande Jande, Y.A.; Kivevele, T. Effects of different supplementary cementitious materials on durability and mechanical properties of cement composite—Comprehensive review. Heliyon 2023, 9, e17924. [Google Scholar] [CrossRef] [PubMed]
- Raghav, M.; Park, T.; Yang, H.-M.; Lee, S.-Y.; Karthick, S.; Lee, H.-S. Review of the Effects of Supplementary Cementitious Materials and Chemical Additives on the Physical, Mechanical and Durability Properties of Hydraulic Concrete. Materials 2021, 14, 7270. [Google Scholar] [CrossRef] [PubMed]
- Saetta, A.V.; Scotta, R.V.; Vitaliani, R.V. Analysis of chloride diffusion into partially saturated concrete. ACI Mater. J. 1993, 90, 441–451. [Google Scholar]
- Page, C.L.; Short, N.R.; El Tarras, A. Diffusion of chloride ions in hardened cement pastes. Cem. Concr. Res. 1981, 11, 395–406. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Najjar, L.J. Drying of concrete as a nonlinear diffusion problem. Cem. Concr. Res. 1971, 1, 461–473. [Google Scholar] [CrossRef]
- Lounis, Z.; Saassouh, B.; Zhang, J. Probability-Based Modeling of Chloride-Induced Corrosion in Concrete Structures Including Parameters Correlation. In Applications of Statistics and Probability in Civil Engineering; National Research Council Canada: Ottawa, ON, Canada, 2011; pp. 1206–1212. [Google Scholar]
- Alinaghimaddah, S.; Shayanfar, M.A.; Bagha, M.G. Effect of distance from the sea on reinforced concrete chloride corrosion probability. AUT J. Civ. Eng. 2020, 4, 199–208. [Google Scholar] [CrossRef]
- Hassan, M.; Amleh, L.; Othman, H. Effect of Different Cement Content and Water Cement Ratio on Carbonation Depth and Probability of Carbonation Induced Corrosion for Concrete. Cem. Wapno Beton 2022, 27, 126–143. [Google Scholar] [CrossRef]
- Hassan, M.; Amleh, L. Influence of Climate Change on Probability of Carbonation-Induced Corrosion Initiation. Period. Polytech. Civ. Eng. 2024, 68, 57–67. [Google Scholar] [CrossRef]
- Saassouh, B.; Lounis, Z. Probabilistic modeling of chloride-induced corrosion in concrete structures using first- and second-order reliability methods. Cem. Concr. Compos. 2012, 34, 1082–1093. [Google Scholar] [CrossRef]
- Hassan, M.; Amleh, L.; Hussein, L. Projection of the Carbonation Depths and its Probability of Corrosion Initiation for the Uncracked and Cracked Concrete. Int. Rev. Civ. Eng. (IRECE) 2024, 15, 381–398. [Google Scholar] [CrossRef]
- Kroese, D.P.; Brereton, T.; Taimre, T.; Botev, Z.I. Why the Monte Carlo method is so important today. Wiley Interdiscip. Rev. Comput. Stat. 2014, 6, 386–392. [Google Scholar] [CrossRef]
- Choi, S.K.; Grandhi, R.V.; Canfield, R.A. Reliability-Based Structural Design; Springer: New York, NY, USA, 2007. [Google Scholar]
- Sobol, I.M. A Primer for the Monte Carlo Method; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Kalos, M.H.; Whitlock, P.A. Monte Carlo Methods, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2008. [Google Scholar]
- Costa, A.; Appleton, J. Chloride penetration into concrete in the marine environment Part I: Main parameters affecting chloride penetration. Mater. Struct. 1999, 32, 252–259. [Google Scholar] [CrossRef]
- CSA S6:19; Canadian Highway Bridge Design Code. CSA Group: Toronto, ON, Canada, 2019.
- Weyers, R.; Prowell, B.; Sprinkel, M.; Vorster, M. Concrete Bridge Protection, Repair, and Rehabilitation Relative to Reinforcement Corrosion: A Methods Application Manual; SHRP-S-360; National Research Council: Ottawa, ON, Canada, 1993. [Google Scholar]
- Berke, N.; Hicks, M. Predicting chloride profiles in concrete. Corrosion 1994, 50, 234–239. [Google Scholar] [CrossRef]
- Amey, S.; Johnson, D.; Miltenberger, M.; Farzam, K. Predicting the service life of concrete marine structures: An environmental methodology. ACI Struct. J. 1998, 95, 205–214. [Google Scholar] [CrossRef]
- Bentz, E. Probabilistic modeling of service life for structures subjected to chlorides. ACI Mater. J. 2003, 100, 391–397. [Google Scholar] [CrossRef]
- Lounis, Z.; Daigle, L. Reliability-based decision support tool for life cycle design and management of highway bridge decks. In Proceedings of the Annual Conference of the Transportation Association of Canada (TAC), Toronto, ON, Canada, 21–24 September 2008; pp. 1–19. [Google Scholar]
- Rodriguez, O.G.; Hooton, D.R. Influence of cracks on chloride ingress into concrete. ACI Mater. J. 2003, 100, 120–126. [Google Scholar]
- Lounis, Z.; Mirza, M.S. Reliability-based Service Life Prediction of Deteriorating Concrete Structures. In Concrete Under Severe Conditions; Banthia, N., Ed.; National Research Council: Ottawa, ON, Canada, 2001; pp. 965–972. [Google Scholar]
- Ghoddousi, P.; Salehi, A.M.; Shirzadi Javid, A.A.; Etebari Ghasbeh, M.A.; Sajjadi, S. Evaluation of Concrete Bulk Resistivity as the Key Performance Index for Chloride Transport in Concrete and Rate of Hydration. Int. J. Civ. Eng. 2022, 21, 507–522. [Google Scholar] [CrossRef]



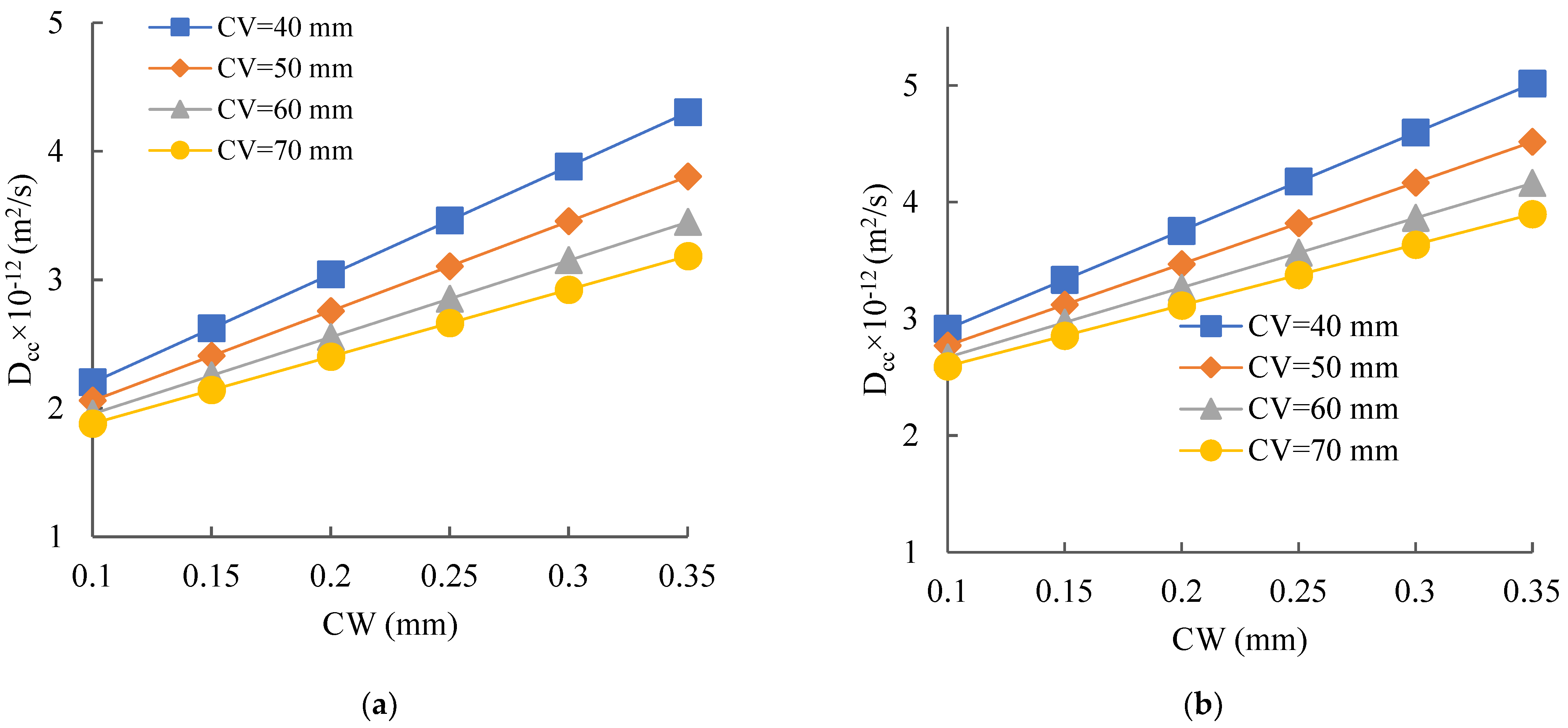

| Random Variables | Mean Value (μ) | Coefficient of Variation (COV) | Distribution |
|---|---|---|---|
| Chloride Concentration (Cs) (kg/m3) | 6 | 30% | Log-normal |
| Concrete Cover (x) (mm) | 70 | 20% | |
| Chloride threshold (Cth) (kg/m3) | 0.7 | 20% | |
| D (m2/s) for NC | 1.27 × 10−12 | 25% | |
| D (m2/s) for HPC | 6.342 × 10−13 | 25% |
| Concrete Type | Cs = 3 kg/m3 | Cs = 6 kg/m3 |
|---|---|---|
| NC | Ti = 0.0088 (CV)2 – 7 × 10−6(CV) + 0.0002 | Ti = 0.0051 (CV)2 − 0.0015 × (CV) + 0.0629 |
| HPC | Ti = 0.0176 (CV)2 – 8 × 10−6(CV) + 0.0002 | Ti = 0.0102 (CV)2 − 2 × 10−6(CV) + 7 × 10−5 |
| Concrete Type | Cracked Concrete (w = 0.25 mm) | Uncracked Concrete |
|---|---|---|
| SCM | Ti = 0.0037 (CV)2 − 0.1118 (CV) + 1.4843 | Ti = 0.0047 (CV)2 − 5 × 10−7 (CV) + 4 × 10−5 |
| without SCM | Ti = 0.0027 (CV)2 − 0.0677 (CV) + 0.8386 | Ti = 0.0031 × (CV)2 + 2 × 10−6 × (CV) – 7 × 10−5 |
| Concrete Cover (mm) | Types of Concrete Used for the RC Bridge Deck | |
|---|---|---|
| Concrete with SCM | Concrete Without SCM | |
| 40 | Dcc = −8 × 10−25·(CW)2 + 8 × 10−12·(CW) + 1 × 10−12 | Dcc = −4 × 10−25 (CW)2 + 8 × 10−12 (CW) + 2 × 10−12 |
| 50 | Dcc = 4 × 10−25 (CW)2 + 7 × 10−12 (CW) + 1 × 10−12 | Dcc = 7 × 10−12 × (CW) +2 × 10−12 |
| 60 | Dcc = 6 × 10−12 (CW) + 1x10−12 | Dcc = 4 × 10−25 (CW)2 + 6 × 10−12 (CW) +2 × 10−12 |
| 70 | Dcc = 4 × 10−25 (CW)2 + 5 × 10−12 (CW) + 1 × 10−12 | Dcc = −4 × 10−25 (CW)2 + 5 × 10−12 (CW) +2 × 10−12 |
| Concrete Cover (mm) | Without SCM | With SCM |
|---|---|---|
| 40 | Ti = 12.638(CW)2 − 11.531(CW) + 4.5521 | Ti = 23.875(CW)2 − 19.705(CW) + 6.3891 |
| 60 | Ti = 21.821(CW)2 − 22.149(CW) + 10.665 | Ti = 45.579(CW)2 − 40.709(CW) +15.424 |
| 70 | Ti = 26.179(CW)2 − 27.910(CW) + 14.675 | Ti = 56.836(CW)2 − 52.681(CW) + 21.430 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, M.; Amleh, L. Influence of Various Crack Widths in RC Bridge Decks on the Initiation of Chloride-Induced Corrosion. J. Compos. Sci. 2025, 9, 242. https://doi.org/10.3390/jcs9050242
Hassan M, Amleh L. Influence of Various Crack Widths in RC Bridge Decks on the Initiation of Chloride-Induced Corrosion. Journal of Composites Science. 2025; 9(5):242. https://doi.org/10.3390/jcs9050242
Chicago/Turabian StyleHassan, Mostafa, and Lamya Amleh. 2025. "Influence of Various Crack Widths in RC Bridge Decks on the Initiation of Chloride-Induced Corrosion" Journal of Composites Science 9, no. 5: 242. https://doi.org/10.3390/jcs9050242
APA StyleHassan, M., & Amleh, L. (2025). Influence of Various Crack Widths in RC Bridge Decks on the Initiation of Chloride-Induced Corrosion. Journal of Composites Science, 9(5), 242. https://doi.org/10.3390/jcs9050242






