Finite Element Analysis of Strain-Mediated Direct Magnetoelectric Coupling in Multiferroic Nanocomposites for Material Jetting Fabrication of Tunable Devices
Abstract
1. Introduction
2. Magnetoelectric Numerical Model
| BaTiO3 Form | Piezoelectric Coupling Coefficient (pC/N) | Dielectric Constant K | Reference | ||
|---|---|---|---|---|---|
| d33 | d31 | d15 | |||
| Single crystal | 85.6 | −34.5 | 392 | 130 | Zgonik et al. [57] |
| Conventional ceramic | 190 | −34.5 | 270 | 1700 | Jaffe et al. [58] |
| Microwave-sintered ceramic | 260 | - | - | 3300 | Shen et al. [59] |
| Spark plasma-sintered ceramic, 100 nm domain | 416 | - | - | - | Shen et al. [59] |
| Epitaxial film (10 nm) by PLD | <2 | - | - | - | Kelley et al. [60] |
| Spin coat film (300 nm) sintered at 900 °C | - | - | - | ~600 | Bajac et al. [61] |
| Spray pyrolysis thin film | - | - | - | 20–25 | Golego et al. [62] |
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Run, A.; Terrell, D.R.; Scholing, J.H. An in situ grown eutectic magnetoelectric composite material: Part 2 physical properties. J. Mater. Sci. 1974, 9, 1710–1714. [Google Scholar] [CrossRef]
- Nan, T.; Zhou, Z.; Liu, M.; Yang, X.; Gao, Y.; Assaf, B.A.; Lin, H.; Velu, S.; Wang, X.; Luo, H.; et al. Quantification of strain and charge co-mediated magnetoelectric coupling on ultra-thin Permalloy/PMN-PT interface. Sci. Rep. 2014, 4, 3688. [Google Scholar] [CrossRef] [PubMed]
- Leung, C.M.; Li, J.; Viehland, D.; Zhuang, X. A review on applications of magnetoelectric composites: From heterostructural uncooled magnetic sensors, energy harvesters to highly efficient power converters. J. Phys. D Appl. Phys. 2018, 51, 263002. [Google Scholar] [CrossRef]
- Marauska, S.; Jahns, R.; Greve, H.; Quandt, E.; Knöchel, R.; Wagner, B. MEMS magnetic field sensor based on magnetoelectric composites. J. Micromechanics Microengineering 2012, 22, 065024. [Google Scholar] [CrossRef]
- Bibes, M.; Barthélémy, A. Towards a magnetoelectric memory. Nat. Mater. 2008, 7, 425–426. [Google Scholar] [CrossRef]
- Amiri, M.H.; Dehsari, H.S.; Asadi, K. Magnetoelectric coupling coefficient in multiferroic capacitors: Fact vs. Artifacts. J. Appl. Phys. 2022, 132, 164102. [Google Scholar] [CrossRef]
- Liu, Y.X.; Wan, J.G.; Liu, J.-M.; Nan, C.W. Effect of magnetic bias field on magnetoelectric coupling in magnetoelectric composites. J. Appl. Phys. 2003, 94, 5118–5122. [Google Scholar] [CrossRef]
- Gupta, R.; Kotnala, R.K. A review on current status and mechanisms of room-temperature magnetoelectric coupling in multiferroics for device applications. J. Mater. Sci. 2022, 57, 12710–12737. [Google Scholar] [CrossRef]
- Corral-Flores, V.; Bueno-Baques, D.; Carrillo-Flores, D.; Matutes-Aquino, J.A. Enhanced magnetoelectric effect in core-shell particulate composites. J. Appl. Phys. 2006, 99, 08J503. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E. On the magneto-electrical effects in antiferromagnets. Sov. Phys. JETP 1960, 10, 628–629. [Google Scholar]
- Van Suchtelen, J. Product properties: A new application of composite materials. Phillips Res. Rep. 1972, 27, 28–37. [Google Scholar]
- Newnham, R.; Skinner, D.; Cross, L. Connectivity and piezoelectric-pyroelectric composites. Mater. Res. Bull. 1978, 13, 525–536. [Google Scholar] [CrossRef]
- Nan, C.-W.; Bichurin, M.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Getman, I. Magnetoelectric composite materials: Theoretical approach to determine their properties. Ferroelectrics 1994, 162, 45–50. [Google Scholar] [CrossRef]
- Mori, K.; Wuttig, M. Magnetoelectric coupling in Terfenol-D/polyvinylidenedifluoride composites. Appl. Phys. Lett. 2002, 81, 100–101. [Google Scholar] [CrossRef]
- Zhang, J.X.; Li, Y.L.; Schlom, D.G.; Chen, L.Q.; Zavaliche, F.; Ramesh, R.; Jia, Q.X. Phase-field model for epitaxial ferroelectric and magnetic nanocomposite thin films. Appl. Phys. Lett. 2007, 90, 052909. [Google Scholar] [CrossRef]
- Liu, G.; Nan, C.-W.; Cai, N.; Lin, Y. Calculations of giant magnetoelectric effect in multiferroic composites of rare-earth-iron alloys and PZT by finite element method. Int. J. Solids Struct. 2004, 41, 4423–4434. [Google Scholar] [CrossRef]
- Yang, Q.; Tao, L.; Jiang, Z.; Zhou, Y.; Tsymbal, E.Y.; Alexandrov, V. Magnetoelectric Effect at the Ni/HfO2 Interface Induced by Ferroelectric Polarization. Phys. Rev. Appl. 2019, 12, 024044. [Google Scholar] [CrossRef]
- Zhu, W.; Yang, C.; Huang, B.; Guo, Y.; Xie, L.; Zhang, Y.; Wang, J. Predicting and optimizing coupling effect in magnetoelectric multi-phase composites based on machine learning algorithm. Compos. Struct. 2021, 271, 114175. [Google Scholar] [CrossRef]
- Talleb, H.; Ren, Z. Finite element modeling of magnetoelectric laminate composites in considering nonlinear and load effects for energy harvesting. J. Alloys Compd. 2014, 615, 65–74. [Google Scholar] [CrossRef]
- Nan, C.W.; Li, M.; Huang, J.H. Calculations of giant magnetoelectric effects in ferroic composites of rare-earth–iron alloys and ferroelectric polymers. Phys. Rev. B 2001, 63, 144415. [Google Scholar] [CrossRef]
- Nan, C.-W.; Cai, N.; Shi, Z.; Zhai, J.; Liu, G.; Lin, Y. Large magnetoelectric response in multiferroic polymer-based composites. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 71, 014102. [Google Scholar] [CrossRef]
- Cai, N.; Zhai, J.; Nan, C.-W.; Lin, Y.; Shi, Z. Dielectric, ferroelectric, magnetic, and magnetoelectric properties of multiferroic laminated composites. Phys. Rev. B 2003, 68, 224103. [Google Scholar] [CrossRef]
- Liang, X.; Chen, H.; Sun, N.X. Magnetoelectric materials and devices. APL Mater. 2021, 9, 041114. [Google Scholar] [CrossRef]
- Patil, D.R.; Kumar, A.; Ryu, J. Recent progress in devices based on magnetoelectric composite thin films. Sensors 2021, 21, 8012. [Google Scholar] [CrossRef]
- Henrichs, L.F.; Mu, X.; Scherer, T.; Gerhards, U.; Schuppler, S.; Nagel, P.; Merz, M.; Kübel, C.; Fawey, M.H.; Hansen, T.C.; et al. First-time synthesis of a magnetoelectric core–shell composite via conventional solid-state reaction. Nanoscale 2020, 12, 15677–15686. [Google Scholar] [CrossRef]
- Wan, J.G.; Wang, X.W.; Wu, Y.J.; Zeng, M.; Wang, Y.; Jiang, H.; Zhou, W.Q.; Wang, G.H.; Liu, J.M. Magnetoelectric CoFe2O4–Pb (Zr, Ti) O3 composite thin films derived by a sol-gel process. Appl. Phys. Lett. 2005, 86, 122501. [Google Scholar] [CrossRef]
- Hohenberger, S.; Lazenka, V.; Selle, S.; Patzig, C.; Temst, K.; Lorenz, M. Magnetoelectric coupling in epitaxial multiferroic BiFeO3–BaTiO3 composite thin films. Phys. Status Solidi B 2020, 257, 1900613. [Google Scholar] [CrossRef]
- Jahns, R.; Piorra, A.; Lage, E.; Kirchhof, C.; Meyners, D.; Gugat, J.L.; Krantz, M.; Gerken, M.; Knöchel, R.; Quandt, E. Giant magnetoelectric effect in thin-film composites. J. Am. Ceram. Soc. 2013, 96, 1673–1681. [Google Scholar] [CrossRef]
- Nam, C.; Na, Y.; Park, S.C.; Kim, H.; Jeong, C.K.; Hwang, G.-T.; Park, K.-I. Energy harvesting of fully-flexible magnetoelectric composites using a piezoelectric P (VDF-TrFE) and magnetostrictive CoFe 2 O 4 nanofiber. J. Mater. Chem. A 2023, 11, 559–568. [Google Scholar] [CrossRef]
- Jiang, Q.; Shen, Z.; Zhou, J.; Shi, Z.; Nan, C.-W. Magnetoelectric composites of nickel ferrite and lead zirconnate titanate prepared by spark plasma sintering. J. Eur. Ceram. Soc. 2007, 27, 279–284. [Google Scholar] [CrossRef]
- Divakaran, N.; Das, J.P.; Mohanty, S.; Ramadoss, A.; Nayak, S.K. Comprehensive review on various additive manufacturing techniques and its implementation in electronic devices. J. Manuf. Syst. 2022, 62, 477–502. [Google Scholar] [CrossRef]
- Betal, S.; Saha, A.K.; Ortega, E.; Dutta, M.; Ramasubramanian, A.K.; Bhalla, A.S.; Guo, R. Core-shell magnetoelectric nanorobot–A remotely controlled probe for targeted cell manipulation. Sci. Rep. 2018, 8, 1755. [Google Scholar] [CrossRef] [PubMed]
- Murali, N.; Mukherjee, D.; Das, S.B.; Dhillon, A.K.; Siddhanta, S.; Mallick, D.; Betal, S. Magnetoelectric Core–Shell Nanoparticle–Based Wearable Hybrid Energy Harvesters for Biomedical Applications. Adv. Eng. Mater. 2023, 25, 2301061. [Google Scholar] [CrossRef]
- Pradhan, D.K.; Kumari, S.; Rack, P.D.; Kumar, A. Applications of strain-coupled Magnetoelectric composites. Encycl. Smart Mater. 2021, 2021. [Google Scholar]
- Avakian, A.; Gellmann, R.; Ricoeur, A. Nonlinear modeling and finite element simulation of magnetoelectric coupling and residual stress in multiferroic composites. Acta Mech. 2015, 226, 2789–2806. [Google Scholar] [CrossRef]
- Labusch, M.; Etier, M.; Lupascu, D.C.; Schröder, J.; Keip, M.-A. Product properties of a two-phase magneto-electric composite: Synthesis and numerical modeling. Comput. Mech. 2014, 54, 71–83. [Google Scholar] [CrossRef]
- Liu, Y.X.; Wan, J.G.; Liu, J.-M.; Nan, C.W. Numerical modeling of magnetoelectric effect in a composite structure. J. Appl. Phys. 2003, 94, 5111–5117. [Google Scholar] [CrossRef]
- Do, T.A.; Talleb, H.; Gensbittel, A.; Ren, Z. Homogenization of magnetoelectric 0–3 type composites by 3-D multiphysics finite-element modeling. IEEE Trans. Magn. 2019, 55, 7401004. [Google Scholar] [CrossRef]
- Fernández, C.L.; Pereira, N.; Lanceros-Mendez, S.; Martins, P. Evaluation and optimization of the magnetoelectric response of CoFe2O4/poly (vinylidene fluoride) composite spheres by computer simulation. Compos. Sci. Technol. 2017, 146, 119–130. [Google Scholar] [CrossRef]
- Fernández, C.L.; Pereira, N.; Martins, P.; Lanceros-Méndez, S. Theoretical design of high-performance polymer-based magnetoelectric of fibrilar structures. Compos. Sci. Technol. 2018, 155, 126–136. [Google Scholar] [CrossRef]
- Martins, P.; Fernandez, C.; Silva, D.; Lanceros-Méndez, S. Theoretical optimization of magnetoelectric multilayer laminates. Compos. Sci. Technol. 2021, 204, 108642. [Google Scholar] [CrossRef]
- Sudersan, S.; Maniprakash, S.; Arockiarajan, A. Nonlinear magnetoelectric effect in unsymmetric laminated composites. Smart Mater. Struct. 2018, 27, 125005. [Google Scholar] [CrossRef]
- Yu, N.; Wu, X.; Liu, X.; Li, R.; Zhang, H.; Gao, L. Hybrid mesh for magnetotelluric forward modeling based on the finite element method. Sci. Rep. 2023, 13, 532. [Google Scholar] [CrossRef]
- Kish, L.L.; Thaler, A.; Lee, M.; Zakrzewski, A.V.; Reig-I-Plessis, D.; Wolin, B.A.; Wang, X.; Littrell, K.C.; Budakian, R.; Zhou, H.D.; et al. Domain wall patterning and giant response functions in ferrimagnetic spinels. Adv. Sci. 2021, 8, 2101402. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, X. A nonlinear constitutive model for magnetostrictive materials. Acta Mech. Sin. 2005, 21, 278–285. [Google Scholar] [CrossRef]
- Beedasy, V.; Smith, P.J. Printed electronics as prepared by inkjet printing. Materials 2020, 13, 704. [Google Scholar] [CrossRef]
- Kumar, S.; Meena, S.K.; Jain, R. Structural and elastic studies of cobalt ferrites nanoparticles. Int. J. Adv. Eng. Technol. 2021, 12, 32–37. [Google Scholar]
- Mohaideen, K.K.; Joy, P. Influence of initial particle size on the magnetostriction of sintered cobalt ferrite derived from nanocrystalline powders. J. Magn. Magn. Mater. 2013, 346, 96–102. [Google Scholar] [CrossRef]
- Stein, C.R.; Bezerra, M.T.S.; Holanda, G.H.A.; André-Filho, J.; Morais, P.C. Structural and magnetic properties of cobalt ferrite nanoparticles synthesized by co-precipitation at increasing temperatures. AIP Adv. 2018, 8, 056303. [Google Scholar] [CrossRef]
- Zheng, P.; Zhang, J.; Tan, Y.; Wang, C. Grain-size effects on dielectric and piezoelectric properties of poled BaTiO3 ceramics. Acta Mater. 2012, 60, 5022–5030. [Google Scholar] [CrossRef]
- McNeal, M.P.; Jang, S.-J.; Newnham, R.E. The effect of grain and particle size on the microwave properties of barium titanate (BaTiO3). J. Appl. Phys. 1998, 83, 3288–3297. [Google Scholar] [CrossRef]
- Jayachandran, K.P.; Guedes, J.M.; Rodrigues, H.C. Homogenization method for microscopic characterization of the composite magnetoelectric multiferroics. Sci. Rep. 2020, 10, 1276. [Google Scholar] [CrossRef] [PubMed]
- Bichurin, M.; Sokolov, O.; Ivanov, S.; Ivasheva, E.; Leontiev, V.; Lobekin, V.; Semenov, G. Modeling the Magnetoelectric Composites in a Wide Frequency Range. Materials 2023, 16, 5813. [Google Scholar] [CrossRef]
- Wu, P.; Ma, X.; Zhang, J.; Chen, L. Phase-field model of multiferroic composites: Domain structures of ferroelectric particles embedded in a ferromagnetic matrix. Philos. Mag. 2010, 90, 125–140. [Google Scholar] [CrossRef]
- Reher, M.; Spaldin, N.A.; Weber, S.F. First-principles study of structural, electronic, and magnetic properties at the (0001) Cr2O3−(111) Pt interface. Phys. Rev. Res. 2024, 6, 033263. [Google Scholar] [CrossRef]
- Zgonik, M.; Bernasconi, P.; Duelli, M.; Schlesser, R.; Günter, P.; Garrett, M.H.; Rytz, D.; Zhu, Y.; Wu, X. Dielectric, elastic, piezoelectric, electro-optic, and elasto-optic tensors of BaTiO3 crystals. Phys. Rev. B 1994, 50, 5941. [Google Scholar] [CrossRef]
- Jaffe, B.E.; Cook, W.R.; Jaffe, H.J. The piezoelectric effect in ceramics. In Piezoelectric ceramics; Academic Press: Boston, MA, USA, 1971; pp. 7–21. [Google Scholar]
- Shen, Z.-Y.; Li, J.-F. Enhancement of piezoelectric constant d33 in BaTiO3 ceramics due to nano-domain structure. J. Ceram. Soc. Jpn. 2010, 118, 940–943. [Google Scholar] [CrossRef]
- Kelley, K.P.; Yilmaz, D.E.; Collins, L.; Sharma, Y.; Lee, H.N.; Akbarian, D.; Van Duin, A.C.T.; Ganesh, P.; Vasudevan, R.K. Thickness and strain dependence of piezoelectric coefficient in BaTiO3 thin films. Phys. Rev. Mater. 2020, 4, 024407. [Google Scholar] [CrossRef]
- Bajac, B.; Vukmirovic, J.; Tripković, Đ.; Djurdjic, E.; Stanojev, J.; Cvejic, Z.; Skoric, B.; Srdić, V.V. Structural characterization and dielectric properties of BaTiO3 thin films obtained by spin coating. Process. Appl. Ceram. 2014, 8, 219–224. [Google Scholar] [CrossRef]
- Golego, N.; Studenikin, S.A.; Cocivera, M. Properties of dielectric BaTiO3 thin films prepared by spray pyrolysis. Chem. Mater. 1998, 10, 2000–2005. [Google Scholar] [CrossRef]
- Kukhar, V.G.; A Pertsev, N.; Kholkin, A.L. Thermodynamic theory of strain-mediated direct magnetoelectric effect in multiferroicfilm–substrate hybrids. Nanotechnology 2010, 21, 265701. [Google Scholar] [CrossRef] [PubMed]
- Begué, A.; Ciria, M. Strain-mediated giant magnetoelectric coupling in a crystalline multiferroic heterostructure. ACS Appl. Mater. Interfaces 2021, 13, 6778–6784. [Google Scholar] [CrossRef] [PubMed]
- Nizamov, T.R.; Amirov, A.A.; Kuznetsova, T.O.; Dorofievich, I.V.; Bordyuzhin, I.G.; Zhukov, D.G.; Ivanova, A.V.; Gabashvili, A.N.; Tabachkova, N.Y.; Tepanov, A.A.; et al. Synthesis and Functional Characterization of CoxFe3− xO4-BaTiO3 Magnetoelectric Nanocomposites for Biomedical Applications. Nanomaterials 2023, 13, 811. [Google Scholar] [CrossRef]
- Wang, L.; Lu, Q.; Lv, X.; Su, Y. Magnetoelectric coupling property of 0-3 type CoFe2O4-BaTiO3 nanocomposites. Ceram. Int. 2023, 49, 16363–16369. [Google Scholar] [CrossRef]
- Gao, B.; Xu, S.; Xu, Q. CO2-Induced Spin-Lattice Coupling for Strong Magnetoelectric Materials. Adv. Sci. 2024, 11, 2303692. [Google Scholar] [CrossRef]
- Amrillah, T.; Bitla, Y.; Shin, K.; Yang, T.; Hsieh, Y.-H.; Chiou, Y.-Y.; Liu, H.-J.; Do, T.H.; Su, D.; Chen, Y.-C.; et al. Flexible multiferroic bulk heterojunction with giant magnetoelectric coupling via van der Waals epitaxy. Acs. Nano. 2017, 11, 6122–6130. [Google Scholar] [CrossRef]
- Sun, G.; Lan, M.; Zhang, Y.; Zhong, S.; Li, H.; Chen, C.; Ren, K.; Ding, Y.; Deng, X.; Gao, R.; et al. Enhanced magnetoelectric coupling performance in CoFe2O4@ BaTiO3 multiferroic liquid by tuning the CoFe2O4 morphology. Mater. Today Commun. 2023, 37, 107423. [Google Scholar] [CrossRef]
- Betal, S.; Bhalla, A.S.; Guo, R. Interface studies in heterostructured core-shell magnetoelectric nanocomposites. Ferroelectrics 2018, 534, 89–94. [Google Scholar] [CrossRef]
- Kaviraj, P.; Pramanik, R.; Arockiarajan, A. Influence of individual phases and temperature on properties of CoFe2O4-BaTiO3 magnetoelectric core-shell nanocomposites. Ceram. Int. 2019, 45, 12344–12352. [Google Scholar] [CrossRef]
- Kaviraj, P.; Pramanik, R.; Arockiarajan, A. Magnetoelectric composites: Applications, coupling mechanisms, and future directions. Nanomaterials 2020, 10, 2072. [Google Scholar] [CrossRef] [PubMed]
- Ortega, N.; Kumar, A.; Scott, J.F.; Katiyar, R.S. Multifunctional magnetoelectric materials for device applications. J. Phys. Condens. Matter 2015, 27, 504002. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Peng, B.; Hu, Z.; Zhou, Z.; Liu, M. Recent development and status of magnetoelectric materials and devices. Phys. Lett. A 2018, 382, 3018–3025. [Google Scholar] [CrossRef]
- Chu, Z.; PourhosseiniAsl, M.; Dong, S. Review of multi-layered magnetoelectric composite materials and devices applications. J. Phys. D Appl. Phys. 2018, 51, 243001. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Lin, Y.; Nan, C.-W. Multiferroic magnetoelectric composite nanostructures. NPG Asia Mater. 2010, 2, 61–68. [Google Scholar] [CrossRef]
- Wang, Y.; Su, Y.; Li, J.; Weng, G.J. A theory of magnetoelectric coupling with interface effects and aspect-ratio dependence in piezoelectric-piezomagnetic composites. J. Appl. Phys. 2015, 117, 164106. [Google Scholar] [CrossRef]
- Pesquera, D.; Khestanova, E.; Ghidini, M.; Zhang, S.; Rooney, A.P.; Maccherozzi, F.; Riego, P.; Farokhipoor, S.; Kim, J.; Moya, X.; et al. Large magnetoelectric coupling in multiferroic oxide heterostructures assembled via epitaxial lift-off. Nat. Commun. 2020, 11, 3190. [Google Scholar] [CrossRef]
- Hu, J.-M.; Nan, C.-W. Opportunities and challenges for magnetoelectric devices. APL Mater. 2019, 7, 080905. [Google Scholar] [CrossRef]
- Ding, Z.; Li, P.; Qin, Z.; Huang, W.; Zhao, P.; Zhou, D.; Meng, X.; Sato, Y.S.; Dong, H. Strain-mediated defect engineering toward rapid atomic migration in Fe–Al diffusion couples. Nano Lett. 2024, 24, 12171–12178. [Google Scholar] [CrossRef]
- Pak, S.; Lee, J.; Lee, Y.W.; Jang, A.R.; Ahn, S.; Ma, K.Y.; Kim, J.M. Strain-mediated interlayer coupling effects on the excitonic behaviors in an epitaxially grown MoS2/WS2 van der Waals heterobilayer. Nano Lett. 2017, 17, 5634–5640. [Google Scholar] [CrossRef]
- Rey, M.; Walter, J.; Harrer, J.; Perez, C.M.; Chiera, S.; Nair, S.; Ickler, M.; Fuchs, A.; Michaud, M.; Uttinger, M.J.; et al. Versatile strategy for homogeneous drying patterns of dispersed particles. Nat. Commun. 2022, 13, 2840. [Google Scholar] [CrossRef] [PubMed]
- Dadkhah, M.; Tulliani, J.-M.; Saboori, A.; Iuliano, L. Additive manufacturing of ceramics: Advances, challenges, and outlook. J. Eur. Ceram. Soc. 2023, 43, 6635–6664. [Google Scholar] [CrossRef]
- Travitzky, N.; Bonet, A.; Dermeik, B.; Fey, T.; Filbert-Demut, I.; Schlier, L.; Schlordt, T.; Greil, P. Additive manufacturing of ceramic-based materials. Adv. Eng. Mater. 2014, 16, 729–754. [Google Scholar] [CrossRef]
- Verding, P.; Mary Joy, R.; Reenaers, D.; Kumar, R.S.N.; Rouzbahani, R.; Jeunen, E.; Thomas, S.; Desta, D.; Boyen, H.G.; Pobedinskas, P.; et al. The influence of UV–ozone, O2 plasma, and CF4 plasma treatment on the droplet-based deposition of diamond nanoparticles. ACS Appl. Mater. Interfaces 2023, 16, 1719–1726. [Google Scholar] [CrossRef]

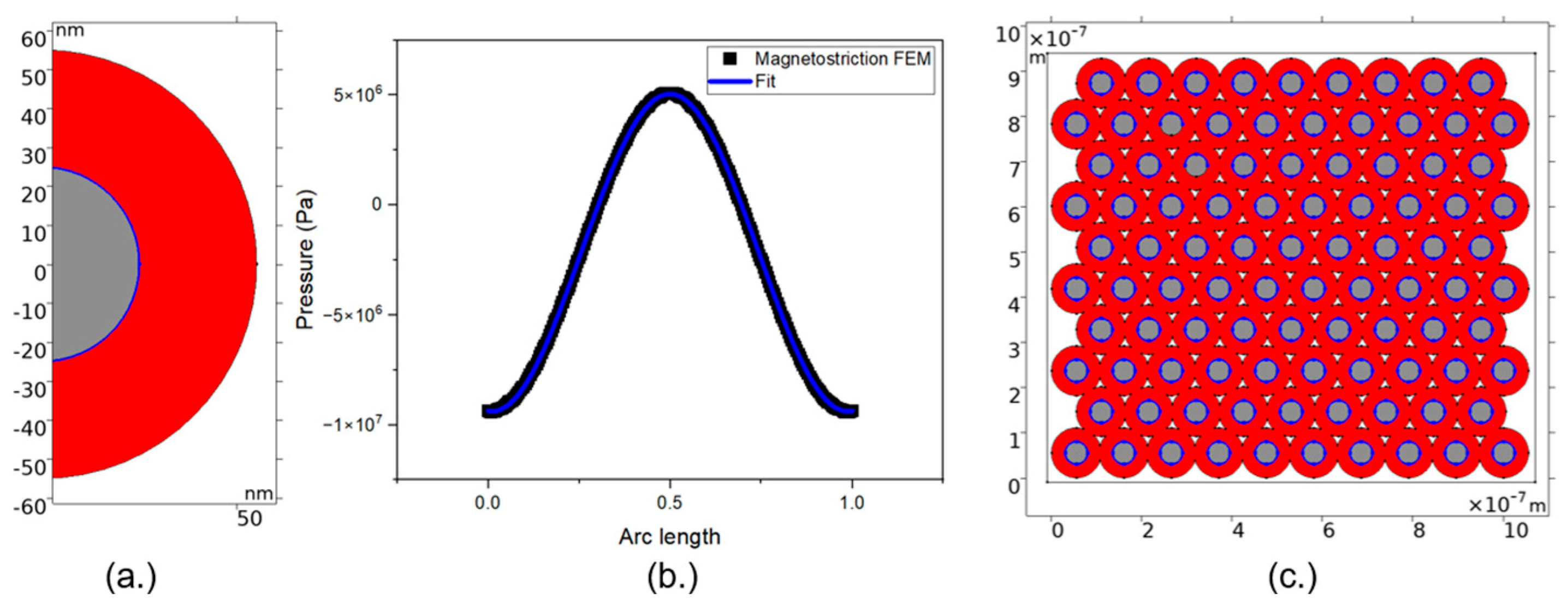

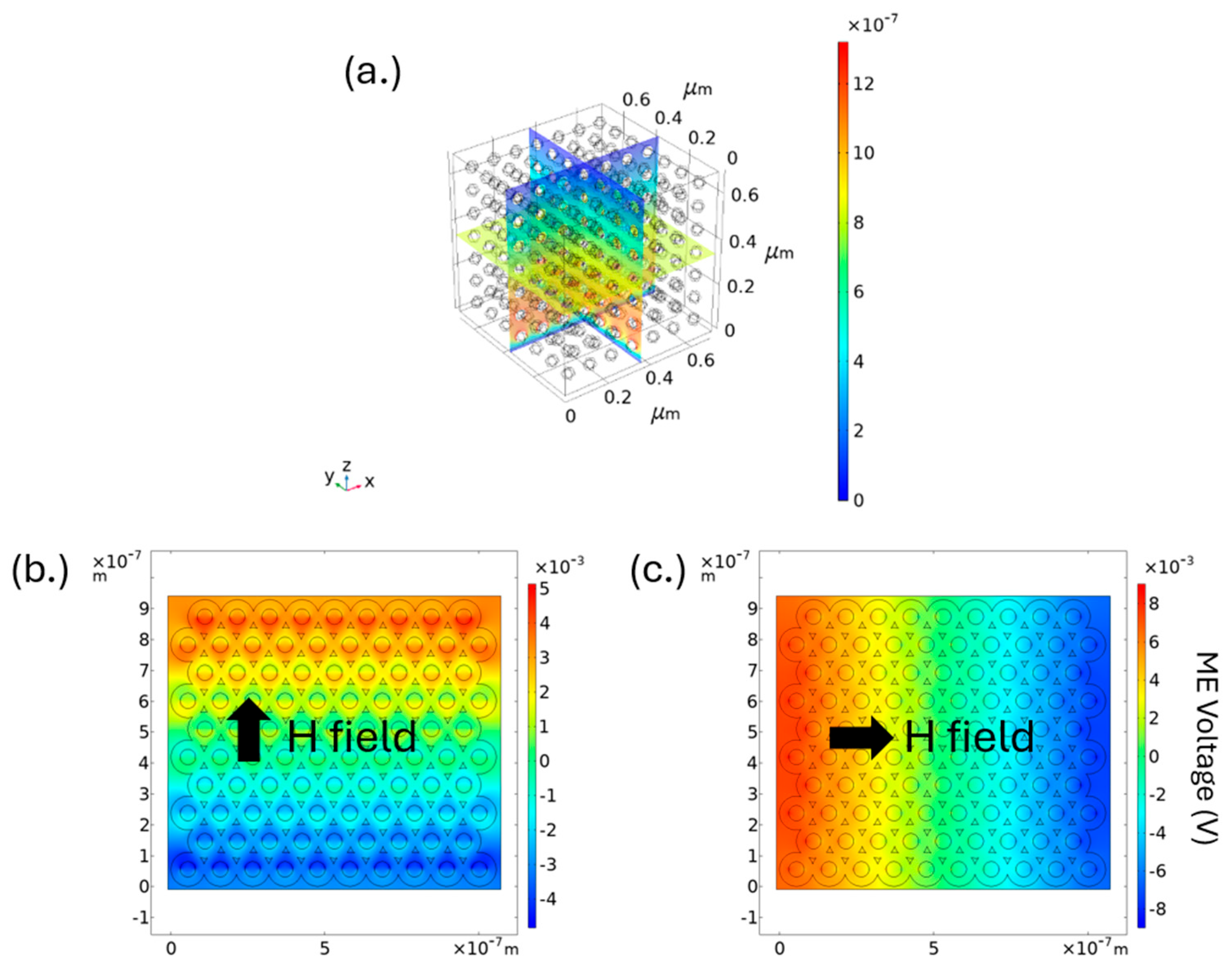


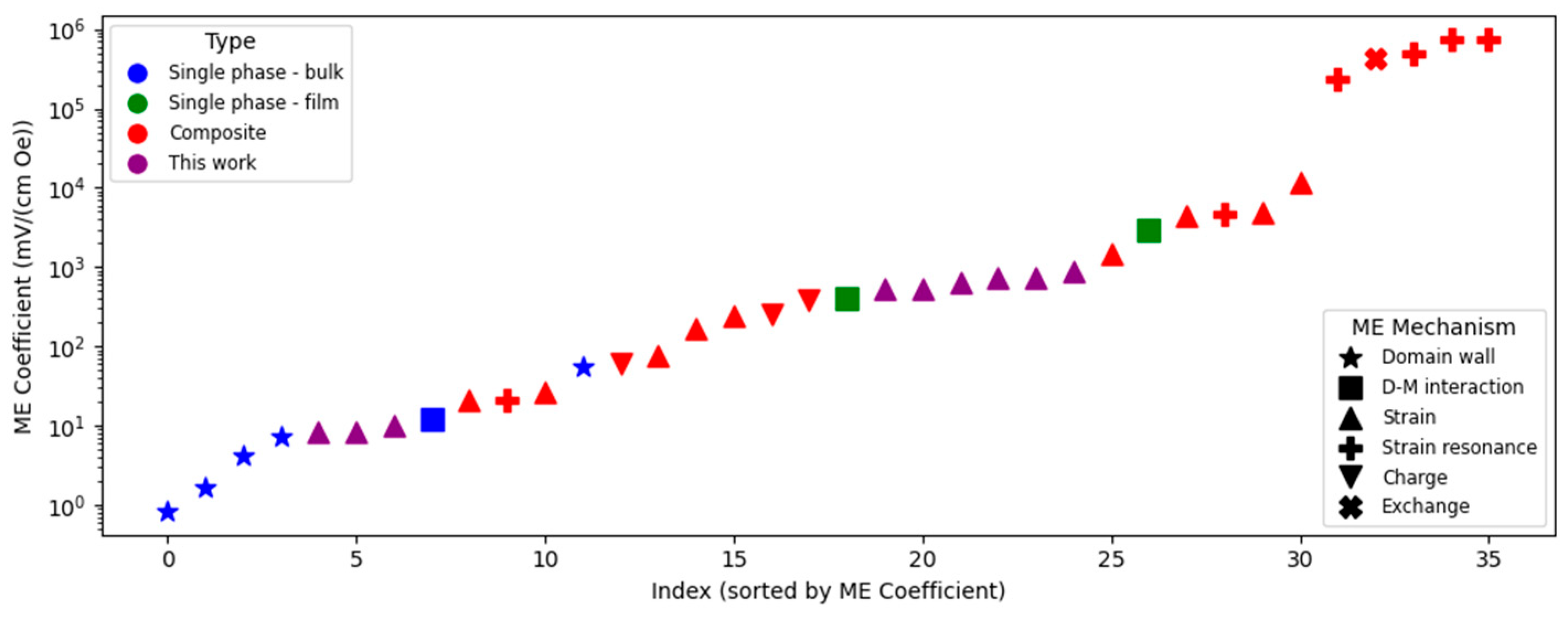
| Composite Connectivity | CFO NP Size (nm) | |||
|---|---|---|---|---|
| Ceramic | Single Crystal | Thin Film | ||
| 0-3 | 40 | 899.7 | 652.5 | 9.9 |
| 60 | 744.7 | 540.1 | 8.2 | |
| 4 | 696.9 | 501 | 7.6 | |
| 2-2 | 40 | 336.9 | 98.3 | 3 |
| 60 | 267 | 60.6 | 2.3 | |
| 4 | 247.9 | 56.3 | 2.2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flynn, W.P.; Garnsey, S.; Bhalla, A.S.; Guo, R. Finite Element Analysis of Strain-Mediated Direct Magnetoelectric Coupling in Multiferroic Nanocomposites for Material Jetting Fabrication of Tunable Devices. J. Compos. Sci. 2025, 9, 228. https://doi.org/10.3390/jcs9050228
Flynn WP, Garnsey S, Bhalla AS, Guo R. Finite Element Analysis of Strain-Mediated Direct Magnetoelectric Coupling in Multiferroic Nanocomposites for Material Jetting Fabrication of Tunable Devices. Journal of Composites Science. 2025; 9(5):228. https://doi.org/10.3390/jcs9050228
Chicago/Turabian StyleFlynn, William Paul, Sean Garnsey, Amar S. Bhalla, and Ruyan Guo. 2025. "Finite Element Analysis of Strain-Mediated Direct Magnetoelectric Coupling in Multiferroic Nanocomposites for Material Jetting Fabrication of Tunable Devices" Journal of Composites Science 9, no. 5: 228. https://doi.org/10.3390/jcs9050228
APA StyleFlynn, W. P., Garnsey, S., Bhalla, A. S., & Guo, R. (2025). Finite Element Analysis of Strain-Mediated Direct Magnetoelectric Coupling in Multiferroic Nanocomposites for Material Jetting Fabrication of Tunable Devices. Journal of Composites Science, 9(5), 228. https://doi.org/10.3390/jcs9050228






