Abstract
The growing demand for passenger comfort and environmental protection, as well as reducing fuel consumption and exhaust emissions, drives the search for new, high-performance materials. Composite leaf springs, applied as part of elastic suspension systems and with the advantages of being strong and lightweight, with a high load-carrying capacity, are a possible method with which to achieve those goals. In this study, an epoxy thermoset was blended with 10–50 wt.% polysulfide rubber and reinforced with 10 wt.% alumina powder. The characteristics of the copolymer composite blend were studied by performing ASTM mechanical tests, including tensile strength, impact strength, hardness, and damping ratio tests. The experimental outcomes showed that increasing the proportion of polysulfide rubber caused a reduction in the maximum tensile strength, modulus at fracture, natural as well as damped frequency, and hardness, whereas a significant improvement was observed in impact strength, logarithmic decrement, and the damping ratio. Reinforcement with alumina powder caused a meaningful increase in the maximum tensile strength and natural frequency, with a good improvement in deformation strength. Impact strength and the damping ratio were maximized when alumina powder was increasingly added. This increase was contrary to what occurred for the hardness, which decreased upon reinforcement. Statistical methods, altering the design of the experiments, and linear regression were used to optimize the composite mixture for manufacturing leaf springs. Finally, the model was validated using analysis of variance and probability plots (normal distribution). The regression equations of tensile and impact strength, hardness, and damping ratio test results proved composite suitability for the application of leaf springs under representative loading and operating conditions. Finite element analysis of the composite material was performed using SolidWorks Simulation 22 Mechanical software. ANSYS 2022 R1 was used to study the mechanical properties of the leaf spring model fabricated from the proposed composite material. The finite element analysis results showed a significant reduction in the weight of leaf springs, with very good mechanical properties, including the tensile and impact strength, hardness, and damping ratio, when using the proposed copolymer-reinforced composite material.
1. Introduction
The design fundamentals of vehicles in traffic concern construction strength and passengers’ comfort while driving. In the leaf spring suspension system of light-duty trucks, payload capacity, drive comfort, and vibration amplitude depend on the properties of the material. Composite materials are the best option because of their high strength/weight ratio, as well as their appropriate mechanical properties that simultaneously result in a vehicle’s weight reducing and the improvement of fuel consumption, with a comfortable ride. Considering this, the main goal of the present research is to determine a new composite material for leaf springs, reducing weight and elasticity while maintaining strength, hardness, damping ability, and toughness at sufficient levels [1].
In practice, an elastic suspension system consisting of composite materials, as a linkage between wheels and the vehicle body, needs to absorb vibration from roads to enhance passenger comfort. This is why this composite was chosen. Elastic suspension systems of light- and heavy-duty trucks usually consist of semi-elliptic leaf springs, specifically for rear axles. Leaf springs have many elliptical laminated elements called leaves, which are different in length. An initial curvature, or camber, is usually given to the leaf elements, starting from the master leaf, so that they flatten under loading during the utilization of trucks (Figure 1).
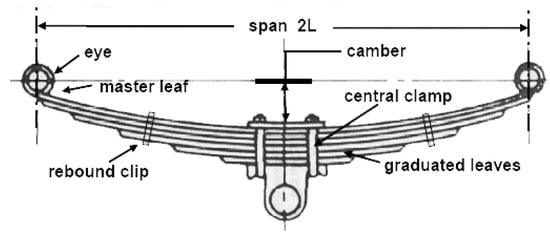
Figure 1.
Leaf spring sketch.
The analysis of leaf springs is based on the theory of beams with uniform strength. The longest master leaf is bound by the other graduated leaves using straps [2,3].
In practice, a vast amount of strain energy could be stored using leaf springs, depending on their application and loading, to enhance any rebound by releasing energy [4].
Leaf springs are connected to the axle and frame of a vehicle, and their front eyes are connected to the frame of a vehicle using a pin joint. To allow translational motion along the longitudinal axis of a vehicle, the rear eye end is suspended and connected with the frame by a flexible “U” link [5].
Many studies have examined the start of the existing base before defining leaf spring designs consisting of composite materials with the appropriate strength and stiffness, as well as reducing the weight and cost of manufacturing.
In the literature [6], authors have researched the structural design of experimental composite leaf springs, according to MATLAB calculation flows. Experimental and finite element method (FEM) analyses were realized for different spring dimensions at three points during the bending test. Simulation and experimental results confirmed that the bending stiffness of the experimental leaf spring was adequate for vehicle applications.
A group of researchers, as an example, designed and manufactured a composite-based mono-leaf spring made from a polymer material, with the goal of replacing the mono-leaf metal leaf springs of light-duty trucks. Abaqus (6.12-1 Dassault Systemes Simulia Corp., RI, US) software was used for testing experimental polymer materials with reinforcement in the form of fibers. After the comparison of simulated mechanical properties, the choice of a better mixture of materials was confirmed. According to experimental test results of the prototype composite spring, an 80% reduction in weight was achieved, as was an improvement in mechanical properties [7].
On the other hand, in the automotive and aircraft industries, with the goal of achieving lower fuel consumption and higher frame strength, the possibilities regarding changes in standard chromium steel material SAE 5160 with polymer composite material reinforced with carbon fibers have been researched. In this case, finite element analysis (FEA) is used, and the results of modeling are applicable for the comparison of the mechanical characteristics of both materials in the domains of flexural fatigue life and damages. Good results were also achieved with composite materials [8].
Some researchers are concerned about the applicability of springs consisting of hybrid composites with integrated carbon and flax fibers in the form of reinforcements (primary and secondary). The main advantage concerns the fact that the composite leaf spring has a 93% higher natural frequency compared to a leaf spring consisting of steel material. In this manner, the coefficient of safety increased, as did the damping coefficient of leaf springs [9].
Studies exist regarding the dynamic behavior of so-called CFRP (carbon-fiber-reinforced plastic) leaf springs. An analysis of the experimental model was used for the investigation. The steel spring was used as a reference for comparing the impact and shaker test excitation at different temperatures. The results showed an increase in damping at lower temperatures, and this was greater for composite materials than for steel springs [10].
There is also research regarding the application of glass-fiber-reinforced polyester composite (GFRP) leaf springs with aluminum oxide and silicon carbide as fillers. More experimental and numerical results are available from studies on the bending of leaf springs. The results show an improvement in bending characteristics and strength when a specific amount of filler is applied [11,12].
Generally, as an introduction to this research, extensive work has been conducted on the application of composite materials in the production of leaf springs. Even though the fiber-reinforced polymeric matrix enhanced strength and flexibility, the blending of polysulfide (PS) rubber composites with a rigid polymer (epoxy) was proved to enhance strength and flexibility. There was additional improvement when they were reinforced with high-compressive-strength alumina powders (ALs).
The novelty of this research lies in the limited or rare investigations into the blending of epoxy with PS and its reinforcement with AL specifically to improve strength, toughness, and flexibility, making it a promising candidate for leaf spring manufacturing.
2. Materials and Methods
For the purpose of this experiment, the designed spring composite materials consist of the copolymer matrix and the reinforcement. The matrix is a blend of two materials: epoxy and PS. The first matrix material is Swancor 901, an epoxy vinyl resin polymer from Swancor Ind. Co., Ltd. Company (from Nantou, Taiwan), and the second material is Polyseal PS (from Delhi, India), a two-component joint sealant with 10–50 wt.%. The reinforcing material is AL with 99.5% purity from Accuratus Corp. (Phillipsburg, NJ, USA). The mechanical properties of the experimental material are shown in Table 1.

Table 1.
Mechanical properties of epoxy, PS, and alumina.
Experimental Procedure
During the experiment, to prepare the composite, a weighted amount of PS was mixed with weighted epoxy resin by using an ultrasonic device for 30 min to achieve the good blending of components. The amount of 10% AL was heated to 100 °C and added to the blend and then mixed for 1 h using the ultrasonic device to ensure the homogeneous dispersion of all components. The hardener of epoxy and PS, according to the mixing percentage, was added to the blend (1). The reinforced blend was then poured into a mold-released, wax-coated system, and the upper plate was covered with heavy weights to reduce bubbles and ensure a smooth surface. After the curing process was completed for three days, the composite was kept in a 60 °C oven for 1 h to extract air bubbles. The obtained cast was cut according to ASTM method samples. Table 2 shows the composite material percentages used during experimental research.

Table 2.
The partial percentages of the composite material.
Experimental tests were carried out to study the mechanical properties of composite materials (142 samples). These tests include the assessment of tensile strength to evaluate how much load the composite material can bear before yielding. The tensile strength of the material is important to ensure that the leaf spring can withstand vehicle force without failing.
Tensile and compression tests of plastic material were carried out according to the ASTM D638 standard by using a Tinius Olsen H50K-T UTM tensile tester (144 samples of composite material) (Figure 2a,b) [13,14].

Figure 2.
(a,b) Tensile blend and composite samples. (c,d) Impact blend and composite samples. (e,f) Damping blend and composite samples, before and after testing.
Impact strength is critical for leaf springs in automobiles, which must endure dynamic impacts without failing. Impact strength imitates a composite’s capability to absorb energy during unexpected loading.
The standard test method according to ASTM D-256 was performed by using an (XJU-22 D IZOD) impact testing machine (manufacturer: Jinan Liangong Testing Technology Co., Ltd. Shandong Province, China). In this manner, the impact strength of the composite samples was studied (Figure 2c,d).
A material’s resistance to deformation is measured, and wear resistance can be improved when the material has high hardness.
A hardness test according to the ASTM D 2240 standard was performed by averaging the three readings using a digital Shore hardness tester (AFFRI Inc. Induno Olona, Italy).
To explore the real-world leaf spring behavior when damping is present, damped frequency is taken as the physical vibration frequency. Damped frequency has values lower than natural frequency. The frequency at which a spring vibrates when disturbed is where natural frequency resonance may occur, when the operating frequency is considered alongside the natural frequency, causing harmful vibrations. On the other hand, the damping ratio determines how fast vibrations vanish. An appropriate damping ratio guaranties that the spring does not oscillate unreasonably to ensure ride comfort and the stability of vehicles and passengers.
The hammering force in the impulse damping test was used to strike the composite material samples and examine their behavior under dynamic conditions, simulated during experimental research. A piezoelectric charge accelerometer (B&K type KISTLER 4371 with a charge sensitivity of 9.8 pC/g ± 2% at 159.2 Hz) was used to measure the induced motion according to the ASTM E 756-05 standard for material damping properties (Figure 2e,f). A conditioning signal amplifier and NEXUS control software type 7749 recorded the signal and transformed it into a digital data code by using an Instek GDS-810C 100 MHz Digital Storage Oscilloscope, manufactured by B&K, to analyze the obtained signal. The natural frequency was recorded by using SIGVIEW, a signal analysis software package v2.6 program from FFT function readings. Figure 2 below shows tensile blends, damping blends, impact blends, and composite samples before and after performing experimental testing.
3. Results
3.1. Experimental Test Results
3.1.1. Tensile Strength Test Results
The tensile strength test results in Table 3 were used to evaluate the composite material’s flexibility and strength (which were at their maximum for the N5 sample), while the modulus at fracture (which was at its maximum for the N1 sample) was calculated due to its importance in leaf spring design [15]. It can be seen that the addition of PS caused a reduction in the maximum stress and elastic modulus at fracture while the maximum strain percentage was increased. The addition of alumina powder caused a significant increase in the maximum stress and modulus at fracture due to the presence of hard particles of AL imparting strength to the polymeric blend.

Table 3.
Maximum stress and strain of the composite materials.
3.1.2. Impact Test Results
The impact test results in Figure 3 show that increasing the PS percentage with the addition of AL caused a continuous increase in impact strength because PS flexibility absorbed impact energy and AL reinforcement improved the stiffness of the material mixture, which, in turn, enhanced the impact strength [16].
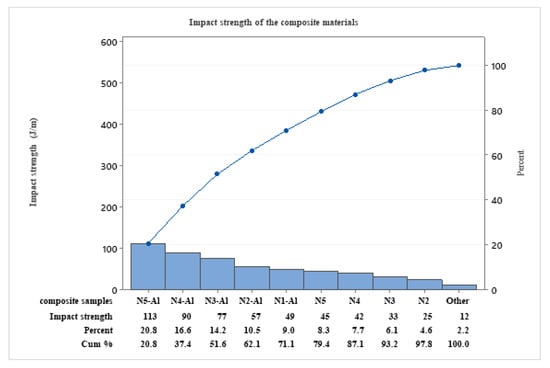
Figure 3.
Impact strength of the epoxy vs. PS, and of the composite materials.
3.1.3. Hardness Test Results
In analyzing hardness as one of test results, Figure 4 shows that all of the composites have higher hardness than the mixtures because of the dense network and hardness of AL particles within the epoxy matrix.
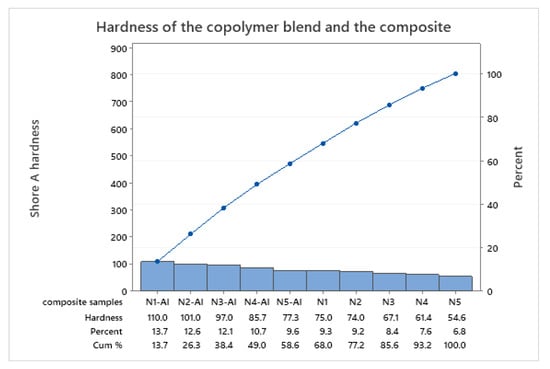
Figure 4.
Hardness of the epoxy vs. PS, and of the composite materials.
AL reinforcement of the blend enhances the ability to dissipate vibrational energy by absorbing energy, which, in turn, increases the composite damping characteristics.
3.1.4. Natural Frequency Test Results
Figure 5 shows that the natural frequency of the N1-AL mixture is the highest because of the addition of PS, and AL increased the density and weight inside the composite material. In parallel with this, N5 has the lowest natural frequency due to the absence of AL and the increasing ductility effect of a high percentage of PS.
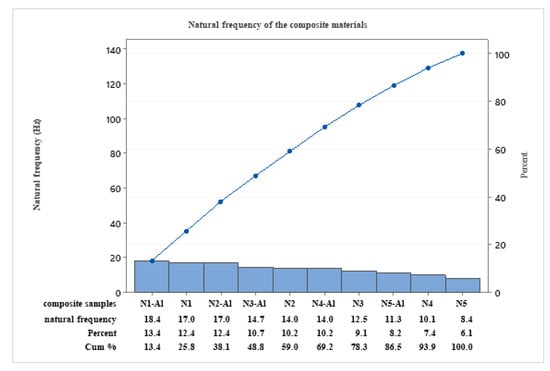
Figure 5.
Natural frequency of the epoxy vs. PS, and of the composite materials.
3.1.5. Damped Frequency Test Results
Figure 6 shows that the damped frequencies of N1-AL and N1 are the highest because of low percentages of PS, while N5 has the lowest value due to the effect of PS, with ductile properties, on the copolymer’s composite stiffness.
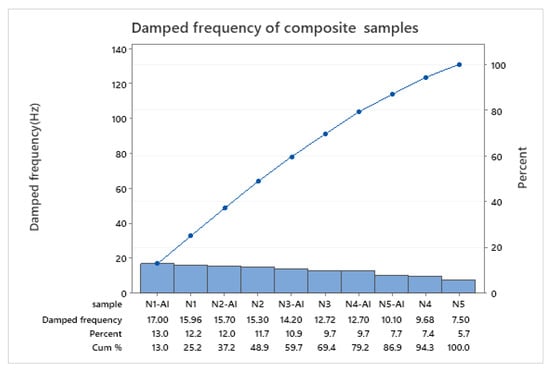
Figure 6.
Damped frequency of epoxy vs. PS, and of composite materials.
3.1.6. Logarithmic Test Results
In contrast with damped frequency, logarithmic decrement has the highest value in the N5 copolymer because of a high percentage of rubbery PS, while N1 has the lowest value. PS’s flexibility and ductile properties increase the composite energy absorption and, in turn, increase logarithmic decrement (see Figure 7).
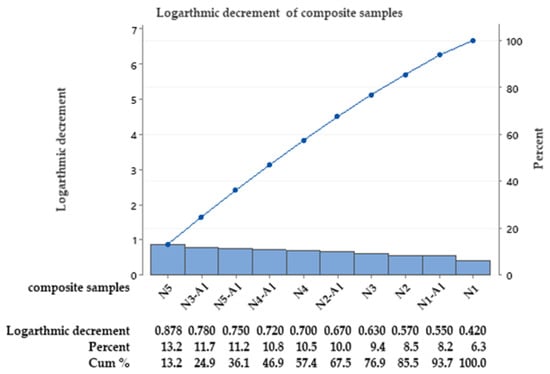
Figure 7.
Logarithmic decrement of the epoxy vs. PS, and of the composite materials.
3.1.7. Damping Ration Test Results
Figure 8 shows that N5-AL having the highest value for the damping ratio is because of a high percentage of ductile PS, with AL’s effect of dissipating energy through internal friction or hysteresis. Conversely, AL reduces the damping ratio if the composite is harder, leading to less energy dissipating [17].
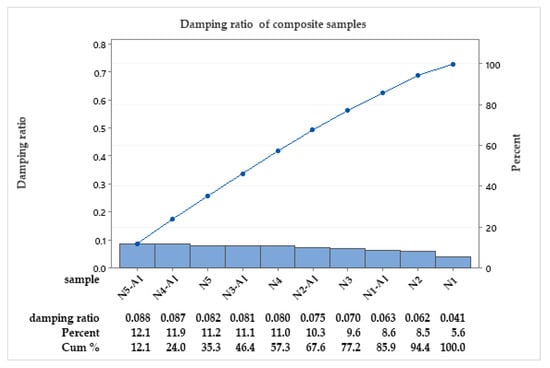
Figure 8.
Damping ratio of epoxy vs. PS, and of composite materials.
3.2. Optimization of the Experimental Results
The statistical methodology design of experiments (DOE) is used to analyze, plan, conduct, and understand experimental results, which include many variable factors [18]. Factors affecting the process of mixing two polymers (epoxy and PS) and reinforcing the resulting blend with AL were optimized by using a general linear regression model (GLM). The DOE framework commonly employs a GLM when the response is linearly related to many input factors, since multiple linear models are used [19]. The data are analyzed, and the relationship between the input factors and the resulting responses is analyzed using the first-order equation below:
where the following apply:
Y = β0 + β1×1 + β2×2 + βe×e + εf
- Y —response variable;
- β0 —intercept;
- β1, β2, βe —coefficients of the factors x1, x2, xe;
- εf —error term.
Using a GLM, the coefficient β values are evaluated, their statistical significance is estimated, and the response of variables for many combinations of factor levels is predicted [20].
Similarly, when an interaction term is added to a first-order model with two variables in Equation (1) above, the model is as follows:
where the following apply:
- ;
- .
Estimating the parameter when the least squares normal equation and matrix approach are derived, the fitted regression model is as follows:
Experimental results were used to build a fitted regression model of a GLM, and analysis of variance (ANOVA) and probability plots were used to study each component’s effect on the composite mechanical properties [21].
ANOVA tables show that the p-value of the tested model is valid for the damped and natural frequencies, damping ratio, impact strength, and hardness, with a stronger value in PS with some variation in the AL source. The p-value of the logarithmic decrement showed a smaller value in PS, while it was not significant for epoxy and AL sources. Meanwhile, AdjMS (mean squares-adjusted) and AdjSS (sums of squares-adjusted) show that the fitted model is a good fit for model data. The AdjMS values of epoxy are the highest values for the natural and damped frequencies, hardness, and impact strength, meaning that it has the highest outcome with strong evidence of valid model data. Meanwhile, the AdjMS values of PS are the highest for the logarithmic decrement and damping ratio, indicating that PS has a larger output in these responses, as shown in Table 4.

Table 4.
ANOVA of the experimental test results.
The probability plots of mechanical test results are in Figure 9. As can be noticed from these figures, all the points of the analyzed data values are located in a straight line or near it, and this indicates the normal distribution of the obtained data with a standard distribution with a fit illustration model.
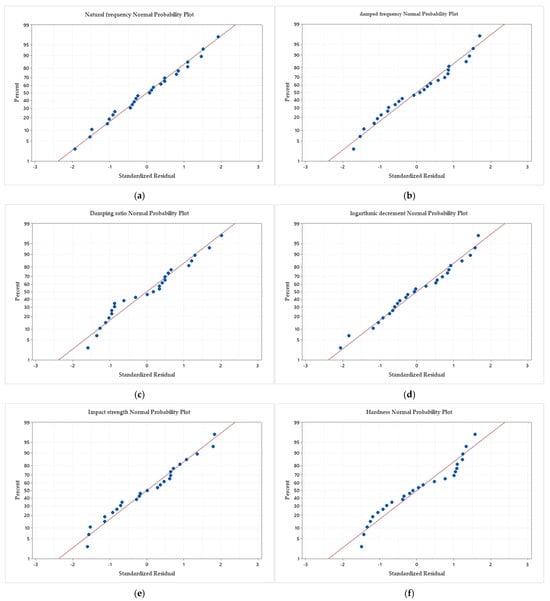
Figure 9.
Probability plot of the GLM data: (a) natural frequency; (b) damped frequency; (c) damping ratio; (d) logarithmic decrement; (e) impact strength; and (f) hardness.
Using the obtained data of the experimental test results to build a GLM showed the following equations, which describe each response in accordance with the affecting factors. The regression equation of a GLM for the natural frequency is as follows:
Natural frequency = 13.744 + (0.984 epoxy_1) + (1.476 epoxy_2) + (0.984 epoxy_3) + (1.476 epoxy_4) − (0.984 epoxy_5) + (3.39 PS_1) + (2.53 PS_2) − (0.41 PS_3) − (2.164 PS_4) − (4.184 PS_5) + (0.076 AL_1) + (0.176 AL_2) − (0.164 AL_3) − (0.084 AL_4) − (0.004 AL_5)
The regression equation analysis of the natural frequency showed that increasing the epoxy percentage caused an increase in the natural frequency, and increasing the PS percentage led to a decrease in the natural frequency, with a maximum value of (3.396).
The further increase in PS causes a decrease in the natural frequency of (−4.184). There were (0.076) and (0.176) increments in the natural frequency in N1-AL_1 and N2-AL_2, while the reinforcement caused a reduction in the natural frequency of (−0.164), (−0.084), and (−0.004). The regression equation of a GLM for the damped frequency is as follows:
Damped frequency = 12.915 − (0.683 epoxy_1) + (1.025 epoxy_2) − (0.683 epoxy_3) − (1.025 epoxy4) − (0.683 epoxy_5) + (3.461 PS_1) + (2.545 PS_2) + (0.397 PS_3) − (2.027 PS_4) − (4.37PS_5) + (0.13 AL_1) + (0.129 AL_2) − (0.08 AL_3) − (0.179 AL_4) − (0.001 AL_5)
The regression equation of the damped frequency showed an increase of 1.025 in N2, while all of the other composites showed a decrease in the damped frequency. The addition of PS caused an increase of 3.461, 2.545, and 0.397 in the damped frequency, with a (−2.027) decrease in the N4 sample. The addition of AL to the N1 and N2 samples showed an increase in the damped frequency of 0.133 and 0.129, while the other samples have a reduction effect on the damped frequency. The regression equation of a GLM for the damping ratio is as follows:
Damping ratio = 0.071720 − (0.00472 epoxy_1) + (0.007 epoxy_2) − (0.004 epoxy_3) + (0.007 epoxy_4) − (0.0047 epoxy_5) − (0.021 PS_1) − (0.004 PS_2) + (0.0026 PS_3) + (0.011 PS_4) + (0.012PS_5) − (0.001 AL_1) + (0.001 AL_2) − (0.0009 AL_3) − (0.0018 AL_4) − (0.0007 AL_5)
Analyzing the regression equation of the damping ratio showed that decreasing the epoxy percent led to a decrease in the damping ratio, while PS had the opposite effect. The addition of AL to N2 showed an increase in the damping ratio in spite of the decrease in the damping ratio of the other composite. The regression equation of a GLM for the logarithmic decrement is as follows:
Logarithmic decrement = 0.6614 − (0.0218 epoxy_1) + (0.032 epoxy_2) − (0.0218 epoxy_3) + (0.032 epoxy_4) − (0.021 epoxy_5) − (0.189 PS_1) − (0.05 PS_2) + (0.028 PS_3) + (0.046 PS_4) + (0.165 PS_5) − (0.017 AL_1) + (0.008 AL_2) − (0.0274 AL_3) + (0.034 AL_4) + (0.002 AL_5)
Studying the regression equation of the logarithmic decrement showed a fluctuating effect of epoxy on the logarithmic decrement, with a positive trend in the N2 sample. PS addition in N1 and N2 showed a decrease of (−0.1894) and (−0.0514), while other samples showed an increase of 0.0286, 0.0466, and 0.1654 in N3, N4, and N5, respectively. The maximum increment in the logarithmic decrement is in the N4-AL sample, of 0.0342. The regression equation of a GLM for impact strength is as follows:
Impact strength = 44.12 − (13.12 epoxy_1) + (19.68 epoxy_2) − (13.12 epoxy_3) + (19.68 epoxy_4) − (13.12 epoxy_5) − (18.52 PS_1) + (1.68 PS_2) + (1.68 PS_3) + (5.88 PS_4) + (9.28 PS_5) − (2.52 AL_1) − (1.32 AL_2) + (1.48 AL_3) + (1.08 AL_4) + (1.28 AL_5)
The equation shows that the impact strength increased when increasing PS, while the epoxy effect fluctuated. AL has an increasing effect on impact strength [22]. The regression equation of a GLM for hardness is as follows:
Hardness = 77.684 − (11.54 epoxy_1) + (17.32 epoxy_2) + (11.54 epoxy_3) + (17.32 epoxy_4) − (11.54 epoxy_5) + (11.32 PS_1) + (7.88 PS_2) + (1.38 PS_3) − (6.56 PS_4) − (14.00 PS_5) − (1.02 AL_1) + (0.32 AL_2) + (0.52 AL_3) + (1.44 AL_4) + (0.20 AL_5)
The regression equation of hardness showed that epoxy has an increasing effect, while increasing PS led to a decrease in hardness. The addition of AL causes an increase in hardness.
To use these composite materials in the manufacturing of leaf springs, a proper percentage of composite components should be chosen. A high percentage of epoxy is beneficial in enhancing the natural frequency, damped frequency, and hardness, while the addition of PS enhanced the damping ratio, impact strength, maximum strain, and logarithmic decrement. AL has a beneficial effect on increasing the tensile strength, modulus at fracture, and dynamic properties. Balanced composite properties were found in N2-AL. These composite properties will be simulated using the mechanical software ANSYS 2022 R1.
4. Finite Element Analysis of the Composite Material
Whilst investigating the composite materials’ characteristics in the base of their responses to the applied loads of experimental tests, noticeable properties have been noted for the N2-AL composite. An FEM model was used to identify N2-AL properties as input parameters for simulation. ANSYS 2022 R1 software, in particular, was used to perform the composite leaf spring simulation. The specifications of the composite multi-leaf spring of a Toyota Hilux vehicle are in Table 5.

Table 5.
The FEM leaf spring model specifications.
The two ends of the main leaf were constrained as fixed geometry when the applied load of 4000 N was applied at the bottom end of the box. All leaf springs were connected in parallel and coincidentally according to their motion. The constraints and loads were applied, meshing the model shown in Figure 10.
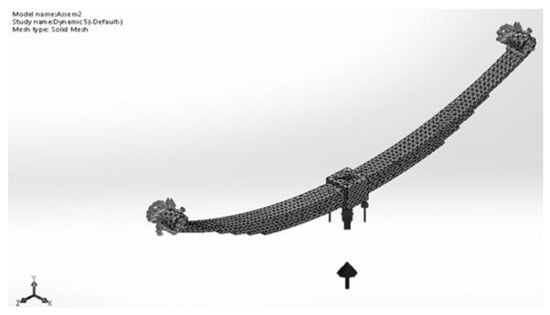
Figure 10.
FEM 3D model mesh constraints and applied loads of the composite leaf spring.
The meshing was performed with a fine curvature based on four Jacobian points, with a maximum element size of 15.3179 mm and a minimum element size of 5.10591 mm. There were 3728 total nodes, 9504 total elements, and a maximum aspect ratio of 5.7982. Linear dynamic analysis was chosen to study the modal behavior of the composite leaf spring with the specifications listed in Table 6.

Table 6.
FEM leaf spring model mechanical properties.
5. Finite Element Analysis Results
Figure 11 shows the von Mises stress of the leaf spring with a maximum value equal to (1.765 × 107 Pa), which is less than the maximum stress of the N2-AL composite sample, which is equal to (131 × 106 Pa). This refers to exhibiting less stress and enduring harder applied loads upon working due to the presence of PS, which imparts ductility to the composite, and the ceramic alumina with hard particles that enhance tensile strength.

Figure 11.
FEM von Mises stress of the composite leaf spring model.
The maximum value of the resultant displacement is equal to 34.0643 mm at the main leaf ends, as shown in Figure 12. Due to the sudden change in leaf geometry and the type of loadings [23], the end connection with rotating parts of a vehicle led to concentrated stress at the main leaf ends.
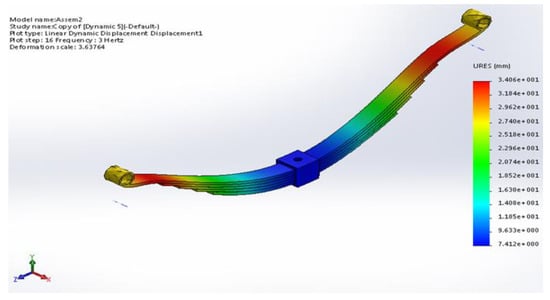
Figure 12.
FEM resultant displacement of the composite leaf spring model.
The resultant strain of the composite model is the highest at the main leaf ends, as shown in (Figure 13). The composite leaf spring geometry variation in thickness, curvature, and width affects the distribution of strain, leading to higher strains at the leaf spring ends in addition to the deformation in each leaf, which might add to each other, causing a cumulative effect.
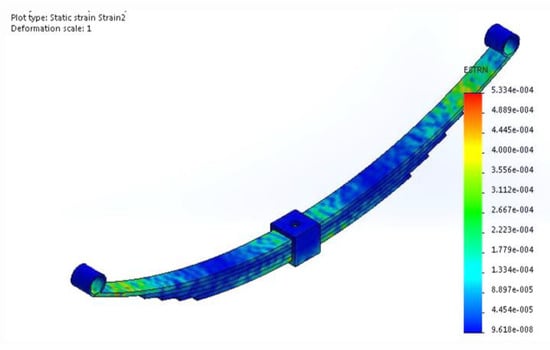
Figure 13.
FEM strain of the composite leaf spring model.
Strain energy density, as a measure of stored energy per unit volume due to deformation, is shown in Figure 14. Its maximum value is equal to 268.616 Nm/m3 at the position near to the leaf spring ends since the deformation is important. Having no degree of freedom in movement at the end of the spring led to the exertion of more load on the spring’s flexible leaves.
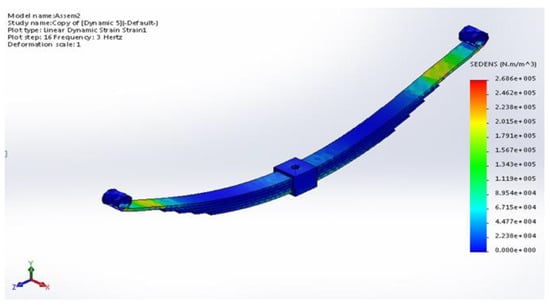
Figure 14.
FEM strain energy density of the composite leaf spring model.
Modal analysis is a method used to find a structure’s dynamic behavior, including mode shapes, the natural frequency, and the damping ratio [24]. Figure 15 shows the first six mode shapes. In these modes, the maximum deformations were at the center of the leaves, while the ends experienced no deformation due to the applied constraints. The first mode shape of the lowest natural frequency shows the uniform bends of the entire leaf spring in one direction, leading to comfort in riding with some primary dynamics, while the second mode shape at moderate frequencies shows a single node bend along its length, with secondary vibration. The third mode shape at frequencies higher than the second mode deforms in a complex wave shape because it is bent with two nodes that localize the stresses, causing vibrational effects with noise. The fourth mode shape shows three nodes bending with a complicated wave pattern. Springs at this mode shape may experience resonant frequencies at extreme conditions. This mode shape is not practical for operational dynamics, and it is not preferred. Another two shapes show deformation in complex waves at three nodes, which are not practical for operating conditions.
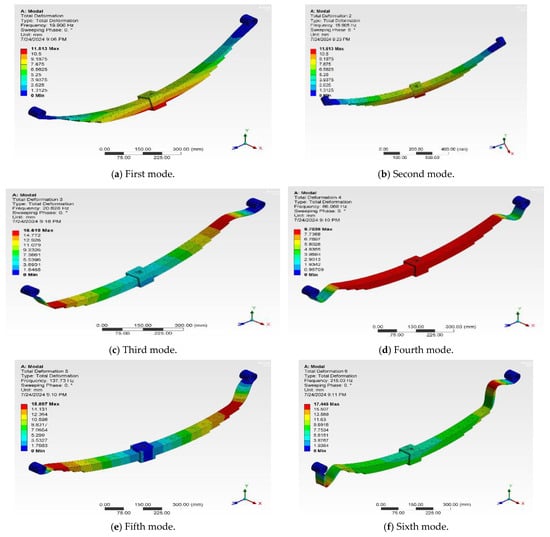
Figure 15.
FEM composite leaf spring model mode shapes.
The constraints and boundary condition of the leaf spring led to movement in accordance with the degree of freedom that can be reached.
Table 7 shows the resonant frequency of the first five mode shapes with the time period of each mode. Resonant frequencies were calculated in order to avoid them for more reliable performance of the leaf springs.

Table 7.
The resonant frequency of the first five modes.
6. Weight Reduction in the Composite Material
One of the most effective variables in terms of selecting leaf spring material is weight reduction, which leads to reduced fuel consumption, saving the environment and saving money. Composite material weight can be calculated by calculating the density of the composite using the rule of mixtures as below, multiplied by volume [25]:
The copolymer and the composite density in Table 8 show that the addition of PS and AL increased the copolymer and the composite density because these two materials have a larger density than epoxy, and the crosslinking of the composite materials increases its density [26,27].

Table 8.
The copolymer blend and the composite density.
Table 9 shows the FEM comparison of the mass, volume, and weight of each component of the composite leaf spring and traditional steel spring, showing the advantages of using composite materials when considering their light weight. The total weight of each component of the steel leaf spring is 18.05 kg. The total weight of each component of the experimental composite (N2-AL) leaf spring is 3.33 kg.

Table 9.
FEM comparison of composite and steel leaf spring component characteristics.
The weight reduction, which is a manufacturing demand in the transportation industry, when the composite material was used was 81%.
The effective mass participation factor (EMPF) is the percentage of the mass of the system participating in a specific mode. The EMPF is a measure of how much energy is contained in each mode, considering the effective mass of the system, not the true mass [28].
The EMPF of the FEM composite leaf spring model is shown in Table 10, showing that, in mode 1, the significant movement in the X direction is with 86.3% of the system mass participating. The movement in the other two axes can be considered null. Mode 2 saw movement in the Z direction with 24.3% of the system mass participating, and the two other axes are considered null. About 73.5% of the system mass participated in mode 3 with movement in the Y direction, and movement in the other axes can be neglected. Mode 4 shows 0.019% of the system mass participating in movement in the Y direction, which is the smallest mass participation of the first five modes. About 20.19% of the system mass participates in the movement in the Y direction in mode 5. Mode 1 is a mode with large mass participation, so it is a significant contributor to the system response [29].

Table 10.
EMPF of the FEM composite leaf spring.
7. Conclusions
Because of their high strength, low density, and high stiffness, advanced composite materials are the most popular materials. The use of composite materials of epoxy PS reinforced with AL in manufacturing leaf springs proves to be a promising approach for enhancing strength, durability, and weight reduction, while maintaining optimal performance under dynamic loading conditions.
The comparative mechanical property results of the composite materials are favorable when compared to those of traditional steel, especially in terms of tensile strength: N1-AL has a maximum stress equal to 145 MPa due to the hard nature of AL and epoxy stiffness.
The maximum impact strength of the N5-AL composite is equal to 113 J/m because of PS ductility with AL strength, while the minimum value equal to 12 J/m of N1 showed the significance of blending epoxy and composites.
Hardness and damping characteristics show the development of harder, stronger, lighter, and more durable materials due to the hard particles of AL and the flexibility of PS.
Using composite materials with high mechanical properties has a notable impact on industrial fields, such as the aerospace, automotive, and marine industries, since composite materials might reduce fuel consumption and emissions.
A significant reduction in weight in comparison to steel led to lower costs with comfortable riding.
The FEM model results show that the von Mises stress, resultant strain, and displacement are fairly good in comparison with those of traditional materials in terms of withstanding the applied loads, considering the applied working conditions of the designed composite materials.
The mode shapes of the composite leaf spring were studied, and the natural frequencies were listed to approve the validity of the used materials compared to steel.
A further investigation of the working conditions of the leaf spring, with carbon fiber as a secondary reinforcement material to epoxy polysulfide copolymer, is essential for expanding the application of the composite materials in manufacturing leaf springs.
An important contribution of this work is the database, whose statistical processing can be used to perform optimizations and spring material selection whilst saving time and resources. In addition to the Taguchi method, other methods can be applied, such as TOPSIS and others [30].
Author Contributions
Conceptualization, E.E.K. and S.M.; methodology, E.E.K. and A.M.A.; software, E.E.K.; validation, A.M.A. and B.S.; formal analysis, A.M.A., M.R. and S.S.; resources, B.S., E.E.K. and S.M.; writing—original draft preparation, B.S. and S.M.; writing—review and editing, M.R. and S.M.; supervision, B.S., S.M. and SS.; funding acquisition, M.R. and S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Acknowledgments
E.E.K. and A.M.M. like to acknowledge the University of Diyala, College of Engineering—Engineering Materials department for technical support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sivasankar, A.; Ramanathan, B. Design and Numerical Investigation of Static and Dynamic Loading Characters of Heterogeneous Model Leaf Spring. Int. J. Mech. Eng. Res. 2015, 5, 143–162. [Google Scholar]
- Triveni, Z.; Babu, B.A. Finite Element Analysis on Leaf Spring Made of Composite Material. Int. J. Adv. Sci. Res. Eng. 2016, 5, 542–552. [Google Scholar]
- Nešić, N.; Simonović, J.; Blagojević, M.; Milojević, S.; Jović, S. Vehicle Suspension System with Integrated Inerter—Extended Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1271, 012030. [Google Scholar] [CrossRef]
- Noronha, B.; Yesudasan, S.; Chacko, S. Static and Dynamic Analysis of Automotive Leaf Spring: A Comparative Study of Various Materials Using ANSYS. J. Fail. Anal. Preven 2020, 20, 804–818. [Google Scholar] [CrossRef]
- Edan Kader, E.; Adwan, R.; Yousuf Zedan, L. Fabrication of hybrid composite materials leaf spring. J. Mech. Eng. Res. Dev. 2021, 44, 132–140. [Google Scholar]
- Ma, L.; He, J.; Gu, Y.; Zhang, Z.; Yu, Z.; Zhou, A.; Tam, L.-H.; Wu, C. Structure Design of GFRP Composite Leaf Spring: An Experimental and Finite Element Analysis. Polymers 2021, 13, 1193. [Google Scholar] [CrossRef]
- Oztoprak, N.; Gunes, M.; Tanoglu, M.; Aktas, E.; Egilmez, O.; Senocak, C.; Kulac, G. Developing polymer composite-based leaf spring systems for automotive industry. Sci. Eng. Compos. Mater. 2018, 25, 1167–1176. [Google Scholar] [CrossRef]
- Loganathan, T.G.; Kumar, K.V.; Madhu, S. Flexural and fatigue of a composite leaf spring using finite element analysis. Mater. Today Proc. 2020, 22, 1014–1019. [Google Scholar] [CrossRef]
- Varma, N.; Ahuje, R.; Vijayakumar, T.; Kannan, C. Design and analysis of composite mono leaf spring for passenger cars. Mater. Today Proc. 2021, 46, 7090–7098. [Google Scholar] [CrossRef]
- Krall, S.; Zemann, R. Investigation of the Dynamic Behaviour of CFRP Leaf Springs. Procedia Eng. 2015, 100, 646–655. [Google Scholar] [CrossRef][Green Version]
- Howida, M.; Aly, M.F.; Shokry, A. Numerical and Experimental Characterization of Composite Leaf Spring Subjected to Bending. J. Mech. Eng. Res. Dev. 2020, 43, 371–383. [Google Scholar]
- Adwan, R.; Edan Kader, E.; Yousuf Zedan, L. Experimental analysis of composite materials leaf spring used in automotive. Diyala J. Eng. Sci. 2021, 14, 26–36. [Google Scholar] [CrossRef]
- Kader, E.E.; Abed, A.M.; Asaad, L.M. Structural properties of Epoxy–polysulfide copolymer reinforced with silicon carbide powder. J. Mech. Eng. Res. Develop. 2021, 44, 289–295. [Google Scholar]
- Radojković, M.; Stojanović, B.; Milojević, S.; Marić, D.; Savić, S.; Skulić, A.; Krstić, B. Square Openings as Sources of Stress Concentration in Parts of Machines and Devices. Teh. Vjesn. 2023, 30, 474–480. [Google Scholar] [CrossRef]
- Milojević, S.; Savić, S.; Mitrović, S.; Marić, D.; Krstić, B.; Stojanović, B.; Popović, V. Solving the Problem of Friction and Wear in Auxiliary Devices of Internal Combustion Engines on the Example of Reciprocating Air Compressor for Vehicles. Teh. Vjesn. 2023, 30, 122–130. [Google Scholar] [CrossRef]
- Suhas, J.D.Q.; Hanumanthraya, R.; Vaishak, N.L.; Davanageri, M.B. Investigation on different Compositions of E-Glass/Epoxy Composite and its application in Leaf Spring. IOSR-JMCE 2014, 11, 74–80. [Google Scholar] [CrossRef]
- Zhou, J.; Hu, C.; Wang, Z.; Ren, Z.; Wang, X.; Mao, K. Study on dynamic characteristics of leaf spring system in vibration screen. J. Low Freq. Noise Vib. Act. Control. 2021, 40, 1818–1832. [Google Scholar] [CrossRef]
- Milojević, S.; Glišović, J.; Savić, S.; Bošković, G.; Bukvić, M.; Stojanović, B. Particulate Matter Emission and Air Pollution Reduction by Applying Variable Systems in Tribologically Optimized Diesel Engines for Vehicles in Road Traffic. Atmosphere 2024, 15, 184. [Google Scholar] [CrossRef]
- Edan, E.; Al-Ezzi, A.S. Optimization and analysis of SiC reinforced copolymer blend composite structural springs. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023. [Google Scholar] [CrossRef]
- Milojević, S.; Stojanović, B. Determination of tribological properties of aluminum cylinder by application of Taguchi method and ANN-based model. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 571. [Google Scholar] [CrossRef]
- Krishnaiah, K.; Shahabudeen, P. Applied Design of Experiments and Taguchi Method; PHI Learning Pvt. Ltd.: New Delhi, India, 2012; pp. 22–27. [Google Scholar]
- Mittal, M. Application of Taguchi Method for Optimization of Process Parameters in Improving the Productivity of Corrugation Operation. Int. J. Res. 2015, 2, 537–545. [Google Scholar]
- Milojevic, S.; Pesic, R. Theoretical and experimental analysis of a CNG cylinder rack connection to a bus roof. Int. J. Automot. Technol. 2012, 13, 497–503. [Google Scholar] [CrossRef]
- Borhade, A.P.; Jayant, T.P. Dynamic Analysis of Steel Leaf Spring. Int. Res. J. Eng. Tech. 2014, 3, 306–310. [Google Scholar]
- Elsheltat, S.; Alshara, A.; Elshara, W. Modeling and Finite Element Analysis of Leaf Spring Using Pro-Engineer and ANSYS Softwares. In Proceedings of the First Conference for Engineering Sciences and Technology (CEST-2018), Garaboulli, Libya, 25–27 September 2018. [Google Scholar]
- Kurniawan, P.; Andoko, A.; Sunu, P.W. Leaf spring type simulation with finite element method approach. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1034, 012015. [Google Scholar] [CrossRef]
- Karim, A.A.; Kader, E.E.; Hamod, A.A.; Abdulrahman, A.J. Mechanical properties of a hybrid composite material (epoxy-polysulfide rubber) reinforced with fibres. IOP Conf. Ser. Mater. Sci. Eng. 2018, 433, 012050. [Google Scholar] [CrossRef]
- Khaleel, H.H.; Assaad, A.S.; Noor, H.D.; Nawfel, M.B. Modeling and analysis of leaf spring using finite elements method. Int. J. Mech. Eng. Technol. 2018, 9, 48–56. [Google Scholar]
- Mantilla, D.; Nelson, A.; Oscar, A. Optimal design of leaf springs for vehicle suspensions under cyclic conditions. Ingeniare. Rev. Chil. Ing. 2022, 30, 23–36. [Google Scholar] [CrossRef]
- Gajević, S.; Marković, A.; Milojević, S.; Ašonja, A.; Ivanović, L.; Stojanović, B. Multi-Objective Optimization of Tribological Characteristics for Aluminum Composite Using Taguchi Grey and TOPSIS Approaches. Lubricants 2024, 12, 171. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).






