Underwater Explosion Analysis on Composite Marine Structures: A Comparison Between CEL and UEL Methods
Abstract
1. Introduction
2. Modelling Approach
2.1. Coupled Eulerian–Lagrangian (CEL) Strategy
2.2. Uncoupled Eulerian–Lagrangian (UEL) Strategy
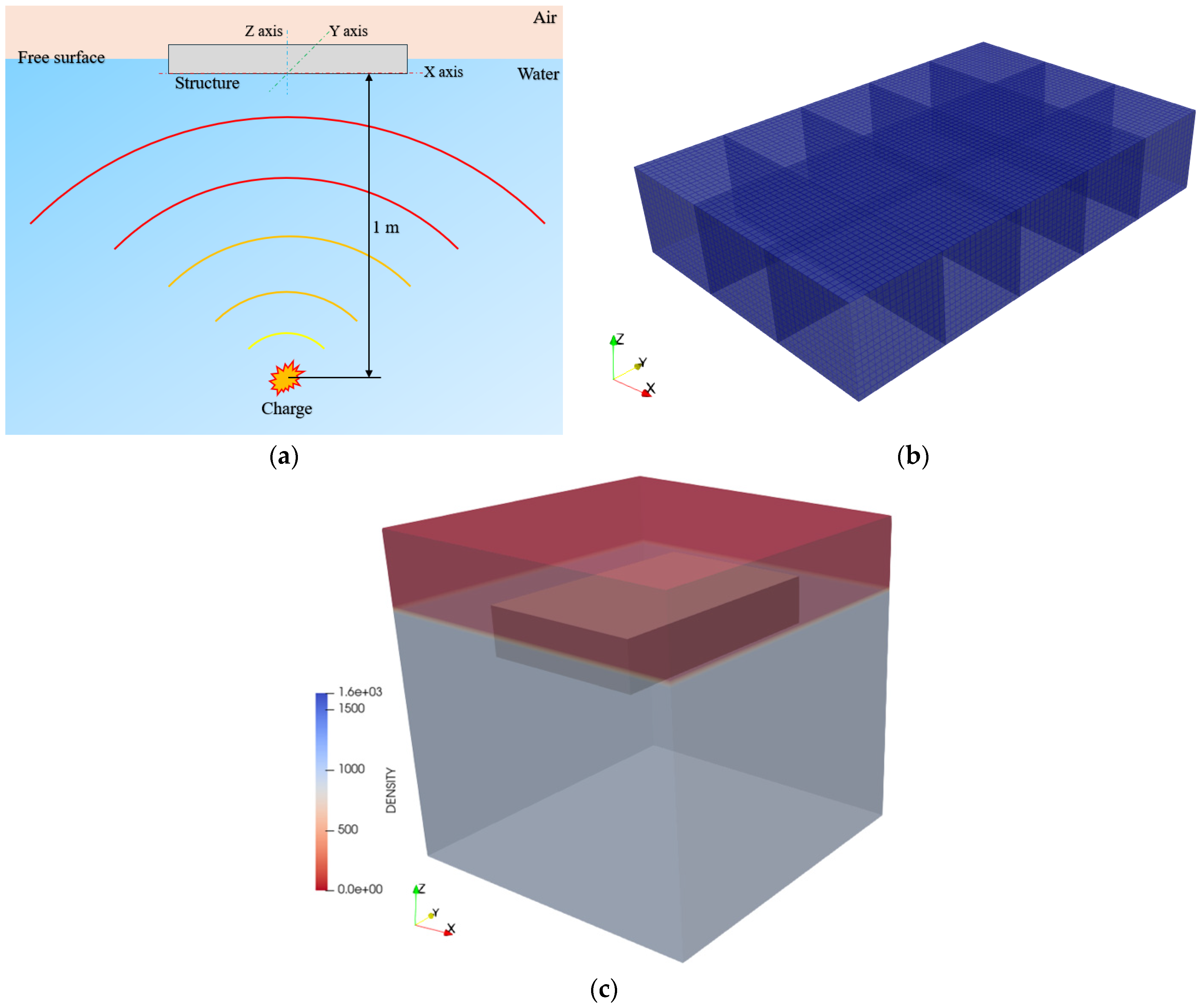
3. Case Study
3.1. UNDEX Scenario
3.2. Numerical Modelling
- Explicit modeling of added mass: in the second step, a numerical model is set up with water explicitly represented, performing a CEL simulation to account for FSI without solving the shock wave propagation.
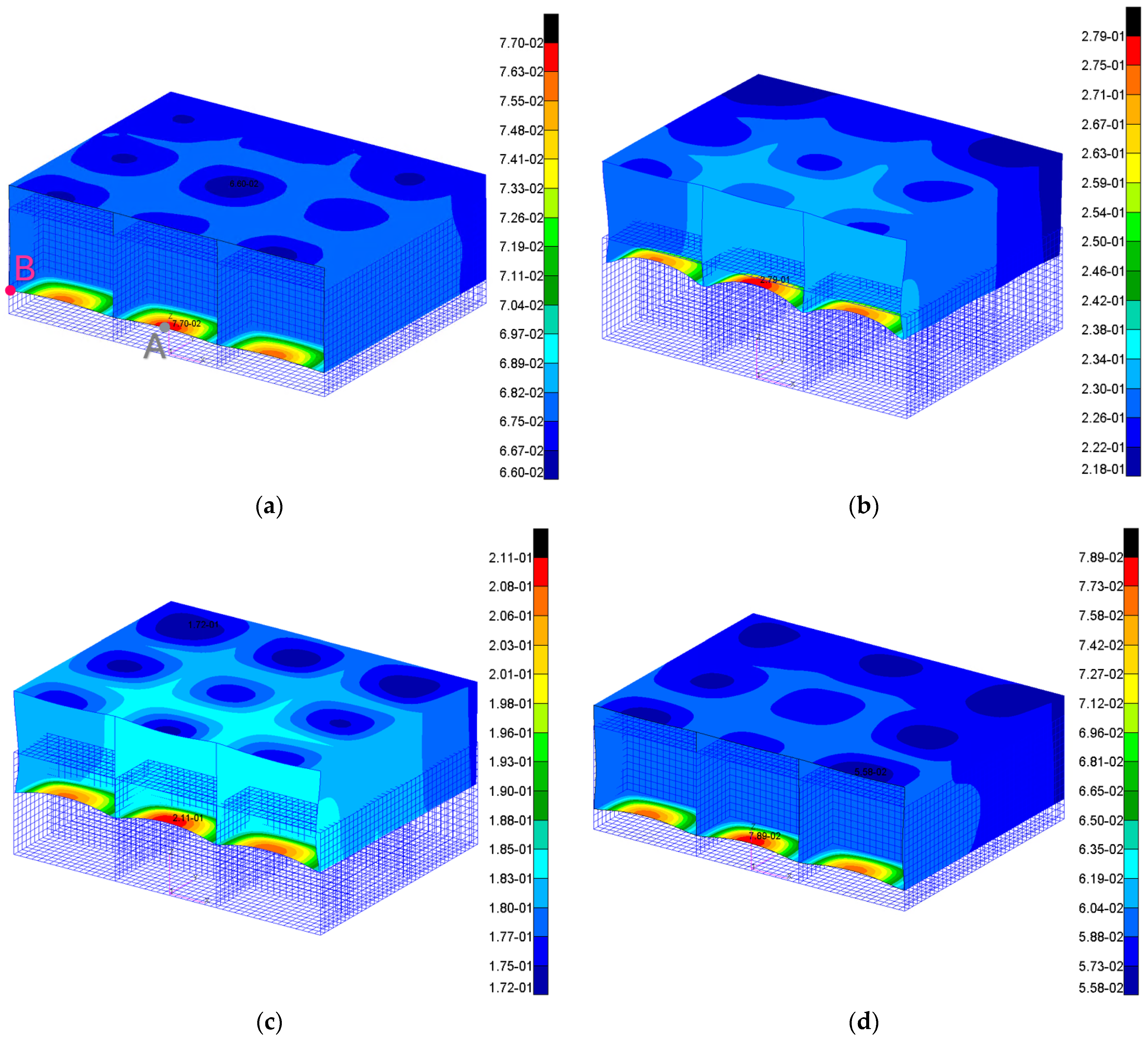
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bardiani, J.; Lomazzi, L.; Sbarufatti, C.; Manes, A. A Machine Learning-based Tool to Correlate Coupled and Uncoupled Numerical Simulations for Submerged Plates Subjected to Underwater Explosions. J. Marine. Sci. Appl. 2025. [Google Scholar] [CrossRef]
- de Camargo, F.V. Survey on experimental and numerical approaches to model underwater explosions. J. Mar. Sci. Eng. 2019, 7, 15. [Google Scholar] [CrossRef]
- Tran, P.; Wu, C.; Saleh, M.; Bortolan Neto, L.; Nguyen-Xuan, H.; Ferreira, A.J.M. Composite structures subjected to underwater explosive loadings: A comprehensive review. Compos. Struct. 2021, 263, 113684. [Google Scholar] [CrossRef]
- Ming, F.R.; Zhang, A.M.; Xue, Y.Z.; Wang, S.P. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions. Ocean Eng. 2016, 117, 359–382. [Google Scholar] [CrossRef]
- Bardiani, J.; Sbarufatti, C.; Manes, A. Transfer Learning with Deep Neural Network Toward the Prediction of the Mass of the Charge in Underwater Explosion Events. J. Mar. Sci. Eng. 2025, 13, 190. [Google Scholar] [CrossRef]
- Qiankun, J.; Gangyi, D. A finite element analysis of ship sections subjected to underwater explosion. Int. J. Impact. Eng. 2011, 38, 558–566. [Google Scholar] [CrossRef]
- Rajendran, R.; Narasimhan, K. Deformation and fracture behaviour of plate specimens subjected to underwater explosion-a review. Int. J. Impact. Eng. 2006, 32, 1945–1963. [Google Scholar] [CrossRef]
- Ren, S.F.; Zhao, P.F.; Wang, S.P.; Liu, Y.Z. Damage prediction of stiffened plates subjected to underwater contact explosion using the machine learning-based method. Ocean Eng. 2022, 266, 112839. [Google Scholar] [CrossRef]
- Li, J.; Rong, J.L. Experimental and numerical investigation of the dynamic response of structures subjected to underwater explosion. Eur. J. Mech. B/Fluids 2012, 32, 59–69. [Google Scholar] [CrossRef]
- Cole, R.H.; Weller, R. Underwater Explosions. Phys. Today 1948, 1, 35. [Google Scholar] [CrossRef]
- Wang, H.; Cheng, Y.S.; Liu, J.; Gan, L. The Fluid-Solid Interaction Dynamics between Underwater Explosion Bubble and Corrugated Sandwich Plate. Shock. Vib. 2016, 2016, 6057437. [Google Scholar] [CrossRef]
- Kong, X.S.; Gao, H.; Jin, Z.; Zheng, C.; Wang, Y. Predictions of the responses of stiffened plates subjected to underwater explosion based on machine learning. Ocean Eng. 2023, 283, 115216. [Google Scholar] [CrossRef]
- Löhner, R.; Li, L.; Soto, O.A.; Baum, J.D. An arbitrary Lagrangian–Eulerian method for fluid–structure interactions due to underwater explosions. Int. J. Numer. Methods Heat Fluid Flow 2023, 33, 2308–2349. [Google Scholar] [CrossRef]
- Sagar, H.J.; El Moctar, O. Dynamics of a cavitation bubble between oblique plates. Phys. Fluids 2023, 35, 013324. [Google Scholar] [CrossRef]
- Sigrist, J.F.; Broc, D. A versatile method to calculate the response of equipment mounted on ship hulls subjected to underwater shock waves. Finite Elem. Anal. Des. 2023, 218, 103917. [Google Scholar] [CrossRef]
- Walters, A.P.; Didoszak, J.M.; Kwon, Y.W. Explicit modeling of solid ocean floor in shallow underwater explosions. Shock. Vib. 2013, 20, 189–197. [Google Scholar] [CrossRef]
- Huang, H.; Jiao, Q.J.; Nie, J.X.; Qin, J.F. Numerical modeling of underwater explosion by one-dimensional ANSYS-AUTODYN. J. Energetic Mater. 2011, 29, 292–325. [Google Scholar] [CrossRef]
- Ding, P.; Buijk, A. Simulation of under water explosion using MSC Dytran. Ann. Arbor. 2006, 1001, 48105. [Google Scholar]
- Wang, Q. Multi-oscillations of a bubble in a compressible liquid near a rigid boundary. J. Fluid Mech. 2014, 745, 509–536. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, H.; Dong, T.; Xu, X. Dumbbell-Shaped Damage Effect of Closed Cylindrical Shell Subjected to Far-Field Side-On Underwater Explosion Shock Wave. J. Mar. Sci. Eng. 2022, 10, 1874. [Google Scholar] [CrossRef]
- DeRuntz, J.A.; Geers, T.L.; Felippa, C.A. The Underwater Shock Analysis Code (USA-Version 3): A Reference Manual; Defense Nuclear Agency: Washington, DC, USA, 1980.
- Qiu, G.; Henke, S.; Grabe, J. Application of a Coupled Eulerian-Lagrangian approach on geomechanical problems involving large deformations. Comput. Geotech. 2011, 38, 30–39. [Google Scholar] [CrossRef]
- Giuliano, D.; Lomazzi, L.; Giglio, M.; Manes, A. On Eulerian-Lagrangian methods to investigate the blast response of composite plates. Int. J. Impact. Eng. 2023, 173, 104469. [Google Scholar] [CrossRef]
- Kumar, L.; Tummalapalli, S.; Rathi, S.C.; Murthy, L.B.; Krishna, A.; Misra, S. Machine learning with word embedding for detecting web-services anti-patterns. J. Comput. Lang. 2023, 75, 101207. [Google Scholar] [CrossRef]
- Lomazzi, L.; Morin, D.; Cadini, F.; Manes, A.; Aune, V. Deep learning-based analysis to identify fluid-structure interaction effects during the response of blast-loaded plates. Int. J. Prot. Struct. 2023, 15, 722–752. [Google Scholar] [CrossRef]
- The MacNeal-Schwendler Corporation (MSC). DYTRAN User Manual. 2023. Available online: https://www.manuallib.com/file/2615765 (accessed on 20 February 2025).
- Bardiani, J.; Kyaw Oo D’Amore, G.; Sbarufatti, C.; Manes, A. Machine Learning Combined with Numerical Simulations: An Effective Way to Reconstruct the Detonation Point of Contact Underwater Explosions with Seabed Reflection. J. Mar. Sci. Eng. 2025, 13, 526. [Google Scholar] [CrossRef]
- Bardiani, J.; Giglio, M.; Sbarufatti, C.; Manes, A. On the Exploration of the Influence of Seabed Reflected Waves on Naval Structures. Eng. Proc. 2025, 85, 7. [Google Scholar] [CrossRef]
- Nestegård, A.; Ronæss, M.; Hagen, Ø.; Ronold, K.; Bitner-Gregersen, E.M. New DNV Recommended Practice DNV-RP-C205 on Environmental Conditions and Environmental Loads. In Proceedings of the Sixteenth International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 28 May 2006. [Google Scholar]
- ShipRight Design and Construction Structural Design Assessment Procedure for Primary Structure of Passenger Ships Working Together for a Safer World. 2017. Available online: https://www.academia.edu/14512983/Structural_Design_Assessment_Primary_Structure_of_Passenger_Ships_Guidance_on_direct_calculations (accessed on 20 February 2025).
- Singh, K.K.; Singh, N.K.; Jha, R. Analysis of symmetric and asymmetric glass fiber reinforced plastic laminates subjected to low-velocity impact. J. Compos. Mater. 2016, 50, 1853–1863. [Google Scholar] [CrossRef]
- Poloni, D.; Oboe, D.; Sbarufatti, C.; Giglio, M. Variable Thickness Strain Pre-Extrapolation for the Inverse Finite Element Method. Sensors 2023, 23, 1733. [Google Scholar] [CrossRef]




| Structural Element | Type | Thickness [mm] |
|---|---|---|
| Outer bottom | Plate | 15 |
| Inner bottom | Plate | 12 |
| Girder | Plate | 10 |
| Floor | Plate | 10 |
| [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | Thickness [mm] |
|---|---|---|---|---|---|---|
| 26,000 | 26,000 | 0.1 | 3800 | 2800 | 2800 | 0.25 |
| Material | MSC Dytran Model | Input Parameters |
|---|---|---|
| Fiber-reinforced composite | MAT2 (Anisotropic material) | See Table 2 |
| Water | Polynomial EOS | |
| Charge (TNT) | JWL EOS | |
| Air above the free surface | Ideal gas EOS |
| N° | Type |
|---|---|
| 1 | CEL–Floating and deformable structure |
| 2 | UEL 1°step–Rigid and fixed structure |
| 3 | UEL 2°step–Deformable structure–No added mass contribution |
| 4 | UEL 2°step–Deformable structure–Considered added mass contribution |
| N° | Type | Time | [m] | [m] | [m] |
|---|---|---|---|---|---|
| 1 | CEL–Floating and deformable grillage | 1 h 31 min | 0.077 | 0.067 | 0.010 |
| 2 | UEL 1°step–Rigid and fixed grillage | 1 h 01 min | - | - | - |
| 3 | UEL 2°step–Deformable grillage–No added mass contribution | 1 min | 0.279 | 0.229 | 0.050 |
| 4 | UEL 2°step–Deformable grillage–Considered added mass contribution | 2 min | 0.211 | 0.182 | 0.029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bardiani, J.; Kyaw Oo D’Amore, G.; Sbarufatti, C.; Manes, A. Underwater Explosion Analysis on Composite Marine Structures: A Comparison Between CEL and UEL Methods. J. Compos. Sci. 2025, 9, 177. https://doi.org/10.3390/jcs9040177
Bardiani J, Kyaw Oo D’Amore G, Sbarufatti C, Manes A. Underwater Explosion Analysis on Composite Marine Structures: A Comparison Between CEL and UEL Methods. Journal of Composites Science. 2025; 9(4):177. https://doi.org/10.3390/jcs9040177
Chicago/Turabian StyleBardiani, Jacopo, Giada Kyaw Oo D’Amore, Claudio Sbarufatti, and Andrea Manes. 2025. "Underwater Explosion Analysis on Composite Marine Structures: A Comparison Between CEL and UEL Methods" Journal of Composites Science 9, no. 4: 177. https://doi.org/10.3390/jcs9040177
APA StyleBardiani, J., Kyaw Oo D’Amore, G., Sbarufatti, C., & Manes, A. (2025). Underwater Explosion Analysis on Composite Marine Structures: A Comparison Between CEL and UEL Methods. Journal of Composites Science, 9(4), 177. https://doi.org/10.3390/jcs9040177












