Effect of Yarn-Level Fibre Hybridisation on Thermomechanical Behaviour of 3D Woven Orthogonal Flax/E-Glass Composite Laminae
Abstract
1. Introduction
2. Two-Scale Homogenisation Scheme
2.1. Material
2.2. Generation of Microstructures
2.3. Microscale RVE Model
2.4. Mesoscale RUC Model
3. Thermomechanical Analysis of Hybrid Yarns and Their 3D Woven Composite Laminae
3.1. Homogenised Thermomechanical Properties of the Hybrid Yarn
3.2. Micro-Stress in the Hybrid Yarn
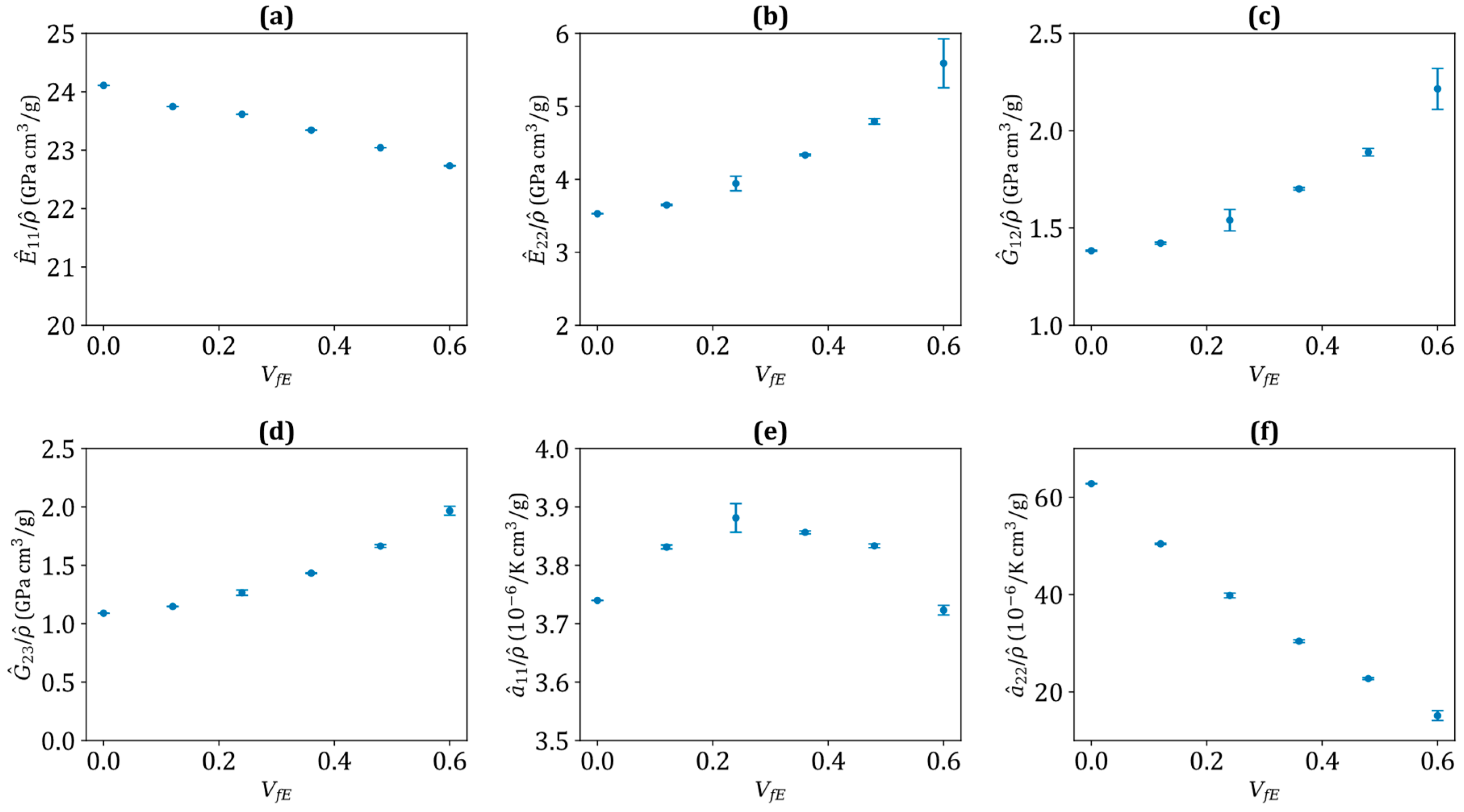
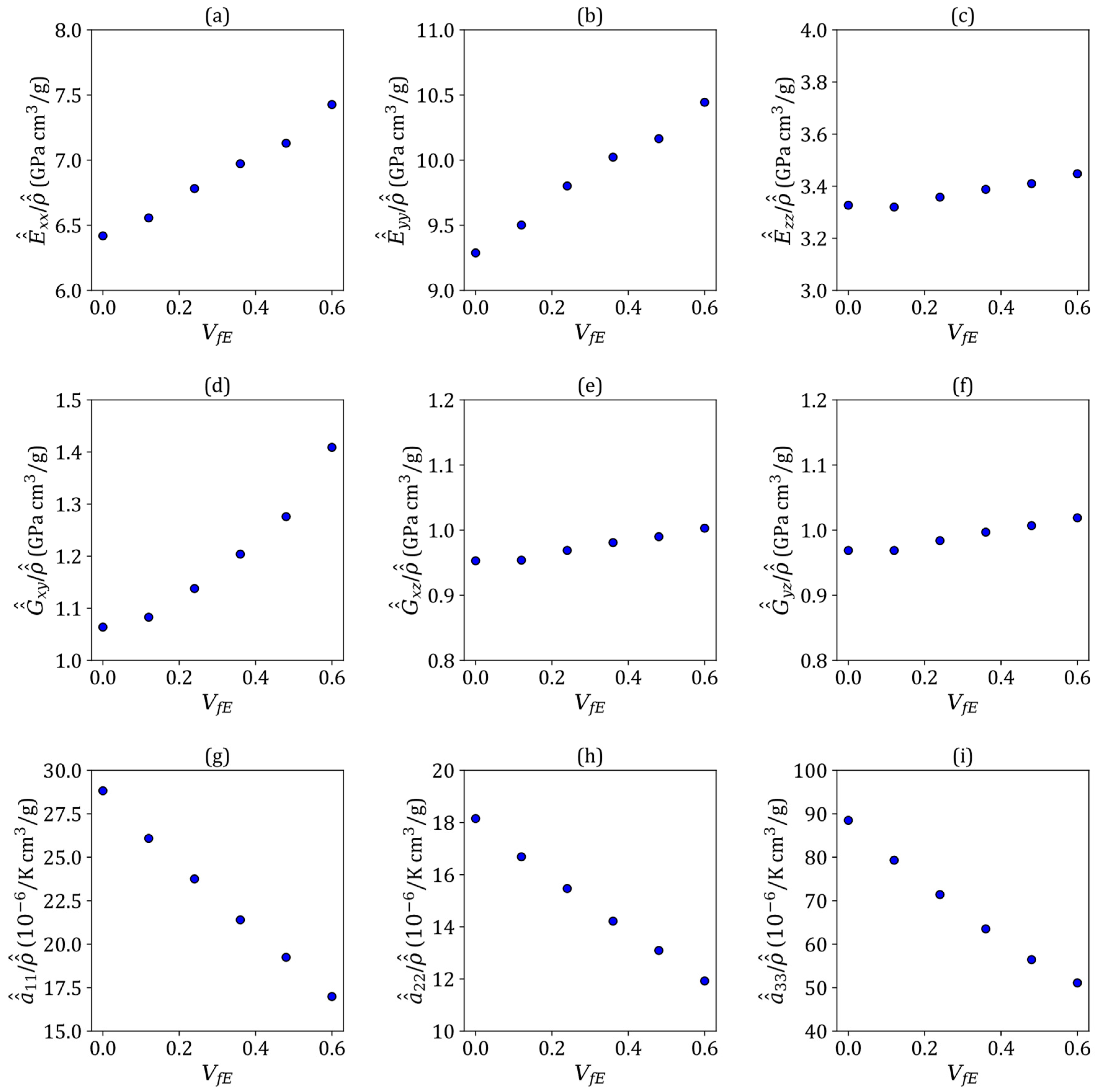
3.3. Homogenised Thermomechanical Properties of the 3D Woven Fabrics
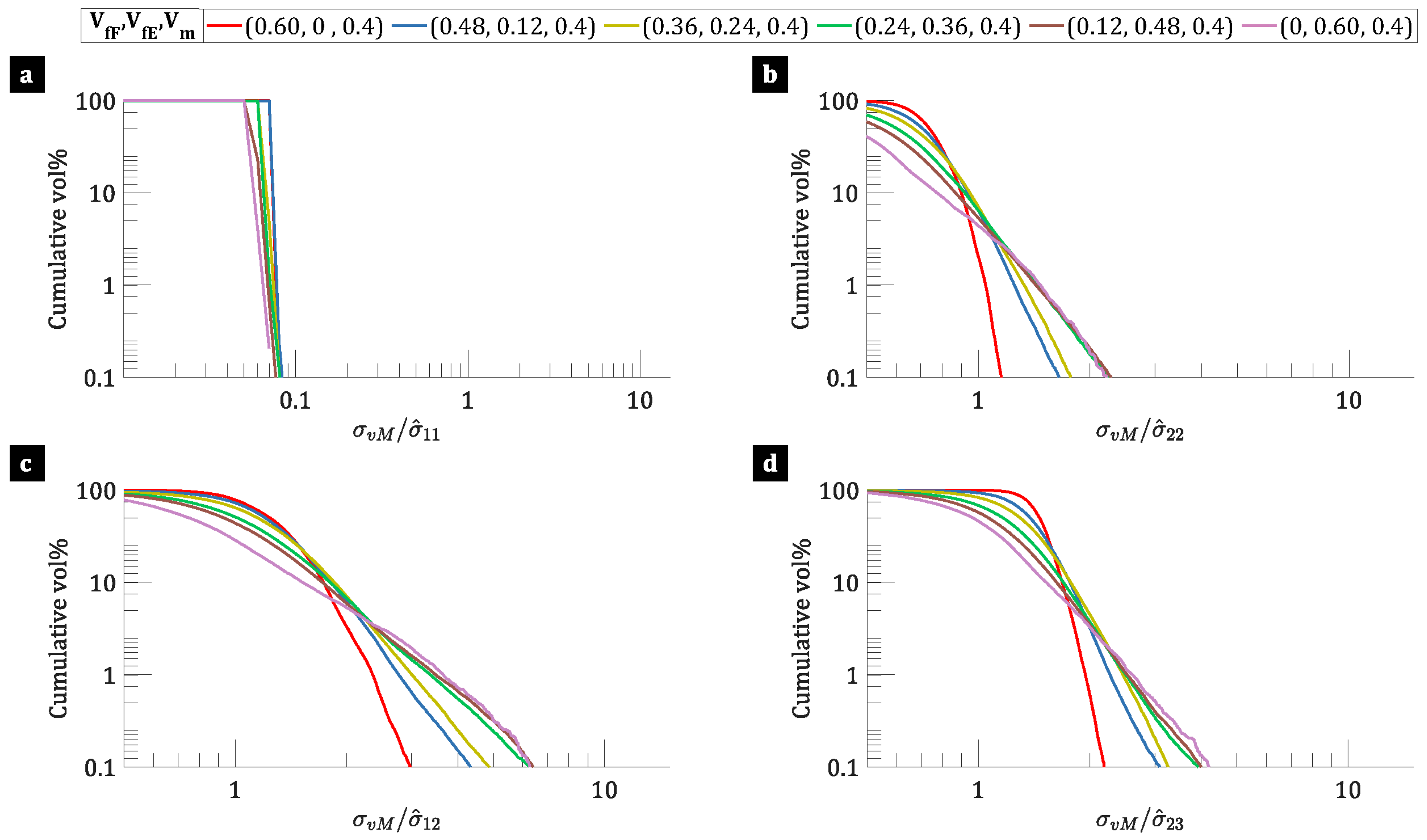
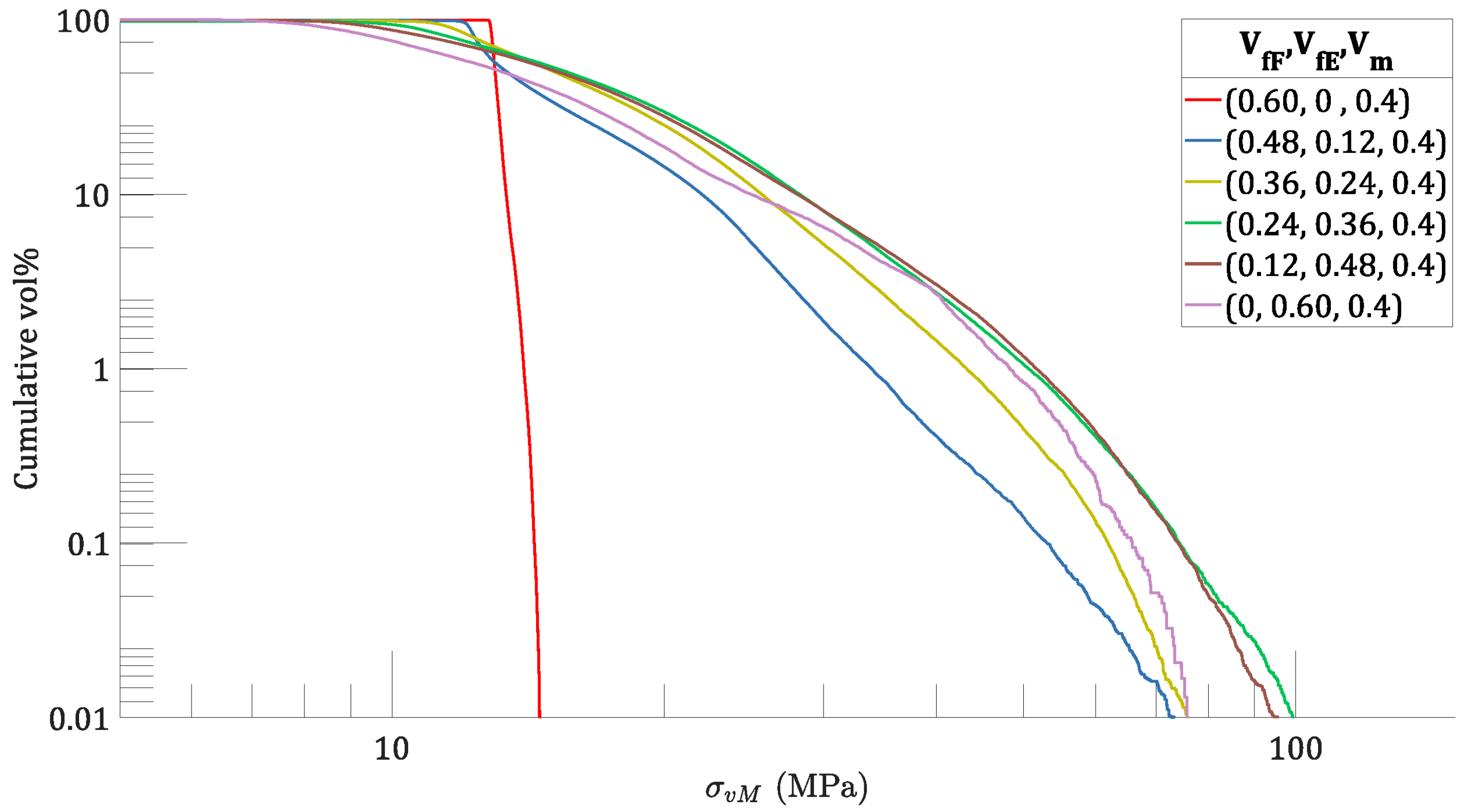
3.4. Meso-Stress in the Woven Fabrics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Sathishkumar, T.; Navaneethakrishnan, P.; Shankar, S.; Rajasekar, R.; Rajini, N. Characterization of natural fiber and composites—A review. J. Reinf. Plast. Compos. 2013, 32, 1457–1476. [Google Scholar] [CrossRef]
- Gupta, M.K.; Ramesh, M.; Thomas, S. Effect of hybridization on properties of natural and synthetic fiber-reinforced polymer composites (2001–2020): A review. Polym. Compos. 2021, 42, 4981–5010. [Google Scholar] [CrossRef]
- Nurazzi, N.M.; Asyraf, M.R.M.; Fatimah Athiyah, S.; Shazleen, S.S.; Rafiqah, S.A.; Harussani, M.M.; Kamarudin, S.H.; Razman, M.R.; Rahmah, M.; Zainudin, E.S.; et al. A Review on Mechanical Performance of Hybrid Natural Fiber Polymer Composites for Structural Applications. Polymers 2021, 13, 2170. [Google Scholar] [CrossRef]
- Ismail, S.O.; Akpan, E.; Dhakal, H.N. Review on natural plant fibres and their hybrid composites for structural applications: Recent trends and future perspectives. Compos. Part C Open Access 2022, 9, 100322. [Google Scholar] [CrossRef]
- Mohd Bakhori, S.N.; Hassan, M.Z.; Mohd Bakhori, N.; Jamaludin, K.R.; Ramlie, F.; Md Daud, M.Y.; Abdul Aziz, S.A. Physical, Mechanical and Perforation Resistance of Natural-Synthetic Fiber Interply Laminate Hybrid Composites. Polymers 2022, 14, 1322. [Google Scholar] [CrossRef]
- Jin, K.K.; Oh, J.H.; Ha, S.K. Effect of Fiber Arrangement on Residual Thermal Stress Distributions in a Unidirectional Composite. J. Compos. Mater. 2007, 41, 591–611. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, J.; Gu, B.; Sun, B. In-situ characterization and multiscale finite element analyses for thermomechanical behavior of 3D woven composites. Compos. Sci. Technol. 2023, 233, 109906. [Google Scholar] [CrossRef]
- Zhao, L.G.; Warrior, N.A.; Long, A.C. A micromechanical study of residual stress and its effect on transverse failure in polymer–matrix composites. Int. J. Solids Struct. 2006, 43, 5449–5467. [Google Scholar] [CrossRef]
- Safarabadi, M.; Shokrieh, M.M. Understanding residual stresses in polymer matrix composites. In Residual Stresses in Composite Materials; Elsevier: Amsterdam, The Netherlands, 2014; pp. 197–232. [Google Scholar]
- Lu, C.; Chen, P.; Yu, Q.; Gao, J.; Yu, B. Thermal Residual Stress Distribution in Carbon Fiber/Novel Thermal Plastic Composite. Appl. Compos. Mater. 2008, 15, 157–169. [Google Scholar] [CrossRef]
- Dhiman, S.; Potluri, P.; Katnam, K.B. Thermally induced residual stresses in orthogonal 3D woven composites: The role of binder architecture and cooling rate. In Proceedings of the AIAA SCITECH 2022 Forum: American Institute of Aeronautics and Astronautics, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Hui, X.; Xu, Y.; Wang, J.; Zhang, W. Microscale viscoplastic analysis of unidirectional CFRP composites under the influence of curing process. Compos. Struct. 2021, 266, 113786. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, Y.; Yang, G.; Tang, A.; Yang, Z.; Li, S.; Li, Y.; Song, D. Evolution of curing residual stresses in composite using multi-scale method. Compos. Part B Eng. 2018, 155, 49–61. [Google Scholar] [CrossRef]
- Zobeiry, N.; Poursartip, A. 3—The origins of residual stress and its evaluation in composite materials. In Structural Integrity and Durability of Advanced Composites; Woodhead Publishing: Cambridge, UK, 2015; pp. 43–72. [Google Scholar]
- Karadeniz, Z.H.; Kumlutas, D. A numerical study on the coefficients of thermal expansion of fiber reinforced composite materials. Compos. Struct. 2007, 78, 1–10. [Google Scholar] [CrossRef]
- Yang, L.; Yan, Y.; Ma, J.; Liu, B. Effects of inter-fiber spacing and thermal residual stress on transverse failure of fiber-reinforced polymer–matrix composites. Comput. Mater. Sci. 2013, 68, 255–262. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, Z.; Ellyin, F. Evolution of residual stresses induced during curing processing using a viscoelastic micromechanical model. J. Compos. Mater. 2001, 35, 522–542. [Google Scholar] [CrossRef]
- Zhao, L.G.; Warrior, N.A.; Long, A.C. A thermo-viscoelastic analysis of process-induced residual stress in fibre-reinforced polymer–matrix composites. Mater. Sci. Eng. A 2007, 452–453, 483–498. [Google Scholar] [CrossRef]
- Maligno, A.R.; Warrior, N.A.; Long, A.C. Finite element investigations on the microstructure of fibre-reinforced composites. Express Polym. Lett. 2008, 2, 665–676. [Google Scholar] [CrossRef]
- Maligno, A.R.; Warrior, N.A.; Long, A.C. Effects of inter-fibre spacing on damage evolution in unidirectional (UD) fibre-reinforced composites. Eur. J. Mech. A/Solids 2009, 28, 768–776. [Google Scholar] [CrossRef]
- Hui, X.; Xu, Y.; Zhang, W. Multiscale model of micro curing residual stress evolution in carbon fiber-reinforced thermoset polymer composites. Front. Mech. Eng. 2020, 15, 475–483. [Google Scholar] [CrossRef]
- Wang, M.; Hang, X. Finite Element Analysis of Residual Stress Distribution Patterns of Prestressed Composites Considering Interphases. Materials 2023, 16, 1345. [Google Scholar] [CrossRef]
- Fletcher, A.J.; Oakeshott, J.L. Thermal residual microstress generation during the processing of unidirectional carbon fibre/epoxy resin composites: Random fibre arrays. Composites 1994, 25, 806–813. [Google Scholar] [CrossRef]
- González, C.; Llorca, J. Mechanical behavior of unidirectional fiber-reinforced polymers under transverse compression: Microscopic mechanisms and modeling. Compos. Sci. Technol. 2007, 67, 2795–2806. [Google Scholar] [CrossRef]
- McLendon, W.R.; Whitcomb, J.D. Influence of thermally induced microstress and microstructural randomness on transverse strength of unidirectional composites. J. Compos. Mater. 2015, 50, 1467–1481. [Google Scholar] [CrossRef]
- He, J.; Cui, X.; Lua, J.; Liu, L. Interplay of manufacturing-induced thermal residual stresses and microvoids in damage and failure of fiber-reinforced composites. Int. J. Mech. Sci. 2023, 242, 108000. [Google Scholar] [CrossRef]
- Zhang, F.; Ye, Y.; Li, M.; Wang, H.; Cheng, L.; Wang, Q.; Ke, Y. Computational modeling of micro curing residual stress evolution and out-of-plane tensile damage behavior in fiber-reinforced composites. Compos. Struct. 2023, 322, 117370. [Google Scholar] [CrossRef]
- Parameswaranpillai, J.; Krishnasamy, S.; Siengchin, S.; Radoor, S.; Joy, R.; George, J.J.; Muthukumar, C.; Muthukumar, S.M.K.; Salim, N.V.; Hameed, N.; et al. Thermal Properties of the Natural Fiber-Reinforced Hybrid Polymer Composites: An Overview. In Natural Fiber-Reinforced Composites; Wiley-VCH: Hoboken, NJ, USA, 2022; pp. 31–51. [Google Scholar]
- Vinod, A.; Gowda, Y.; Krishnasamy, S.; Sanjay, M.R.; Siengchin, S. Thermal Properties of Hybrid Natural Fiber-Reinforced Thermoplastic Composites. In Natural Fiber-Reinforced Composites; Wiley-VCH: Hoboken, NJ, USA, 2022; pp. 17–30. [Google Scholar]
- Yang, N.; Zou, Z.; Potluri, P.; Soutis, C.; Katnam, K.B. Intra-yarn fibre hybridisation effect on homogenised elastic properties and micro and meso-stress analysis of 2D woven laminae: Two-scale FE model. Compos. Struct. 2024, 344, 118358. [Google Scholar] [CrossRef]
- Li, S.; Sitnikova, E. Representative Volume Elements and Unit Cells: Concepts, Theory, Applications and Implementation; Woodhead Publishing: Cambridge, UK, 2019. [Google Scholar]
- Gentles, F.; Anderson, J.; Thomason, J.L. Characterisation of the transverse thermoelastic properties of natural fibres used in composites. In Proceedings of the 14th European Conference on Composite Materials, ECCM14, Budapest, Hungary, 7–10 June 2010. [Google Scholar]
- Thomason, J.; Yang, L.; Gentles, F. Characterisation of the Anisotropic Thermoelastic Properties of Natural Fibres for Composite Reinforcement. Fibers 2017, 5, 36. [Google Scholar] [CrossRef]
- Saidane, E.H.; Scida, D.; Ayad, R. Thermo-mechanical behaviour of flax/green epoxy composites: Evaluation of thermal expansion coefficients and application to internal stress calculation. Ind. Crops Prod. 2021, 170, 113786. [Google Scholar] [CrossRef]
- Schapery, R.A. Thermal Expansion Coefficients of Composite Materials Based on Energy Principles. J. Compos. Mater. 1968, 2, 380–404. [Google Scholar] [CrossRef]
- Hashin, Z. Analysis of Properties of Fiber Composites With Anisotropic Constituents. J. Appl. Mech. 1979, 46, 543–550. [Google Scholar] [CrossRef]
- Chamis, C.C. Simplified composite micromechanics equations for hygral, thermal and mechanical properties. In Proceedings of the SAMPE Quarterly: Ann. Conf. of the Society of the Plastics Industry (SPI) Reinforced Plastics/Composites Inst, Houston, TX, USA, 7–11 February 1984; pp. 14–23. [Google Scholar]
- Trias, D.; Costa, J.; Turon, A.; Hurtado, J. Determination of the critical size of a statistical representative volume element (SRVE) for carbon reinforced polymers☆. Acta Mater. 2006, 54, 3471–3484. [Google Scholar] [CrossRef]
- Yang, L.; Yan, Y.; Ran, Z.; Liu, Y. A new method for generating random fibre distributions for fibre reinforced composites. Compos. Sci. Technol. 2013, 76, 14–20. [Google Scholar] [CrossRef]
- Melro, A.R.; Camanho, P.P.; Pinho, S.T. Influence of geometrical parameters on the elastic response of unidirectional composite materials. Compos. Struct. 2012, 94, 3223–3231. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, L.; Zhang, M.; Song, C. Study on the Effect of Void Defect on Mechanical Properties of Carbon Fiber Composites by Finite Element Method. J. Inst. Eng. Ser. C 2022, 103, 1433–1446. [Google Scholar] [CrossRef]
- Vallmajó, O.; Arteiro, A.; Guerrero, J.M.; Melro, A.R.; Pupurs, A.; Turon, A. Micromechanical analysis of composite materials considering material variability and microvoids. Int. J. Mech. Sci. 2023, 263, 108781. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual; Dassault Systèmes Simulia Corp: Johnston, RI, USA, 2009. [Google Scholar]
- Brown, L.P.; Long, A.C. Modeling the geometry of textile reinforcements for composites: TexGen. In Composite Reinforcements for Optimum Performance; Elsevier: Amsterdam, The Netherlands, 2021; pp. 237–265. [Google Scholar]
- Sherburn, M. Geometric and Mechanical Modelling of Textiles; University of Nottingham: Nottingham, UK, 2007. [Google Scholar]
- Scida, D.; Aboura, Z.; Benzeggagh, M.L.; Bocherens, E. A micromechanics model for 3D elasticity and failure of woven-fibre composite materials. Compos. Sci. Technol. 1999, 59, 505–517. [Google Scholar] [CrossRef]
- Zhong, Y.; Tran, L.Q.N.; Kureemun, U.; Lee, H.P. Prediction of the mechanical behavior of flax polypropylene composites based on multi-scale finite element analysis. J. Mater. Sci. 2017, 52, 4957–4967. [Google Scholar] [CrossRef]
- Swolfs, Y.; Verpoest, I.; Gorbatikh, L. Recent advances in fibre-hybrid composites: Materials selection, opportunities and applications. Int. Mater. Rev. 2019, 64, 181–215. [Google Scholar] [CrossRef]
- Huntsman. Technical Data Sheet: Araldite LY 564 & Aradur 2954. 2011. Available online: https://files.ekmcdn.com/mouldlife/resources/other/araldite-ly564-aradur-2954-eur-e-1-.pdf (accessed on 6 May 2024).
- Li, S.; Jeanmeure, L.F.C.; Pan, Q. A composite material characterisation tool: UnitCells. J. Eng. Math. 2015, 95, 279–293. [Google Scholar] [CrossRef]
- Soden, P.D.; Hinton, M.J.; Kaddour, A.S. Chapter 2.1—Lamina properties, lay-up configurations and loading conditions for a range of fibre reinforced composite laminates. In Failure Criteria in Fibre-Reinforced-Polymer Composites; Elsevier: Oxford, UK, 2004; pp. 30–51. [Google Scholar]
- Affdl, J.C.H.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Dasgupta, A.; Agarwal, R.K.; Bhandarkar, S.M. Three-dimensional modeling of woven-fabric composites for effective thermo-mechanical and thermal properties. Compos. Sci. Technol. 1996, 56, 209–223. [Google Scholar] [CrossRef]







| Constituent | (GPa) | (GPa) | (GPa) | (GPa) | () | () | Density () | Diameter () | ||
|---|---|---|---|---|---|---|---|---|---|---|
| E-glass | ||||||||||
| Flax | ||||||||||
| Epoxy |
| Lamina | Method | (GPa) | (GPa) | (GPa) | (GPa) | () | () | |
|---|---|---|---|---|---|---|---|---|
| E-glass/epoxy | RVE | 6.90 | 25.10 | |||||
| Experimental | 8.60 | 26.40 | ||||||
| Chamis | 6.46 | 21.31 |
| ( ) | (GPa) | (GPa) | (GPa) | (GPa) | () | () | () | () | |
|---|---|---|---|---|---|---|---|---|---|
| (0.60, 0, 0.4) | 32.07 | 0.32 | 4.69 | 1.84 | 1.45 | 4.97 | 83.53 | 83.56 | 1.33 |
| (0.48, 0.12, 0.4) | 34.67 | 0.30 | 5.33 | 2.08 | 1.68 | 5.59 | 73.63 | 73.01 | 1.46 |
| (0.36, 0.24, 0.4) | 37.31 | 0.29 | 6.22 | 2.43 | 2.00 | 6.13 | 62.83 | 62.87 | 1.58 |
| (0.24, 0.36, 0.4) | 39.92 | 0.27 | 7.41 | 2.91 | 2.45 | 6.59 | 52.02 | 52.19 | 1.71 |
| (0.12, 0.48, 0.4) | 42.17 | 0.26 | 8.77 | 3.46 | 3.05 | 7.02 | 41.61 | 41.57 | 1.83 |
| (0, 0.60,0.4) | 44.55 | 0.24 | 10.96 | 4.34 | 3.86 | 7.30 | 29.66 | 32.89 | 1.96 |
| Plain Weave | Method | (GPa) | (GPa) | (GPa) | (GPa) | () | () | |
|---|---|---|---|---|---|---|---|---|
| E-glass/epoxy | RUC | 18.2 | 55.8 | |||||
| Experimental | N/A | N/A | N/A |
| ( ) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | (GPa) | |||
|---|---|---|---|---|---|---|---|---|---|
| (0.60, 0,0.4) | 7.90 | 11.42 | 4.09 | 1.31 | 1.17 | 1.19 | 0.11 | 0.50 | 0.46 |
| (0.48, 0.12, 0.4) | 8.46 | 12.26 | 4.28 | 1.40 | 1.23 | 1.25 | 0.10 | 0.49 | 0.45 |
| (0.36, 0.24, 0.4) | 9.09 | 13.14 | 4.50 | 1.52 | 1.30 | 1.32 | 0.10 | 0.48 | 0.43 |
| (0.24, 0.36, 0.4) | 9.76 | 14.03 | 4.74 | 1.69 | 1.37 | 1.40 | 0.10 | 0.46 | 0.42 |
| (0.12, 0.48, 0.4) | 10.41 | 14.84 | 4.98 | 1.86 | 1.45 | 1.47 | 0.10 | 0.44 | 0.40 |
| (0, 0.60,0.4) | 11.22 | 15.77 | 5.21 | 2.13 | 1.51 | 1.54 | 0.10 | 0.42 | 0.39 |
| ( ) | () | () | () | () |
|---|---|---|---|---|
| (0.60, 0,0.4) | 35.45 | 22.32 | 108.86 | 1.23 |
| (0.48, 0.12, 0.4) | 33.65 | 21.52 | 102.32 | 1.29 |
| (0.36, 0.24, 0.4) | 31.83 | 20.73 | 95.70 | 1.34 |
| (0.24, 0.36, 0.4) | 29.96 | 19.90 | 88.94 | 1.40 |
| (0.12, 0.48, 0.4) | 28.10 | 19.12 | 82.42 | 1.46 |
| (0, 0.60,0.4) | 25.66 | 18.01 | 77.17 | 1.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, N.; Zou, Z.; Soutis, C.; Potluri, P.; Katnam, K.B. Effect of Yarn-Level Fibre Hybridisation on Thermomechanical Behaviour of 3D Woven Orthogonal Flax/E-Glass Composite Laminae. J. Compos. Sci. 2025, 9, 135. https://doi.org/10.3390/jcs9030135
Yang N, Zou Z, Soutis C, Potluri P, Katnam KB. Effect of Yarn-Level Fibre Hybridisation on Thermomechanical Behaviour of 3D Woven Orthogonal Flax/E-Glass Composite Laminae. Journal of Composites Science. 2025; 9(3):135. https://doi.org/10.3390/jcs9030135
Chicago/Turabian StyleYang, Nenglong, Zhenmin Zou, Constantinos Soutis, Prasad Potluri, and Kali Babu Katnam. 2025. "Effect of Yarn-Level Fibre Hybridisation on Thermomechanical Behaviour of 3D Woven Orthogonal Flax/E-Glass Composite Laminae" Journal of Composites Science 9, no. 3: 135. https://doi.org/10.3390/jcs9030135
APA StyleYang, N., Zou, Z., Soutis, C., Potluri, P., & Katnam, K. B. (2025). Effect of Yarn-Level Fibre Hybridisation on Thermomechanical Behaviour of 3D Woven Orthogonal Flax/E-Glass Composite Laminae. Journal of Composites Science, 9(3), 135. https://doi.org/10.3390/jcs9030135









