Comparative Analysis of Bending and Rolling Shear Performance of Poplar and Hybrid Maple–Poplar Cross-Laminated Timber (CLT)

Abstract

Cross-laminated timber (CLT) is gaining popularity as a sustainable alternative to traditional building materials. However, the decline of natural vegetation and the growth of plantation hardwoods has led the researchers to consider alternatives. This study presents a comparative analysis of bending and rolling shear performance of homogenous poplar (Populus nigra L.) CLT and hybrid CLT, with maple (Acer platanoides L.), in the outer layer and poplar in the core, compared to spruce (Picea abies (L.), H. Karst.) CLT. The CLT panels were prepared using one-component polyurethane (1C-PUR) and melamine adhesive (ME). Poplar CLT exhibited equal or better properties than spruce CLT. The outer maple layer in the hybrid CLT enhanced the global bending modulus (E_mg) and bending strength (f_m) by 74% and 37%, respectively, due to its higher modulus of elasticity better shear resistance by reducing the cross-layer stress concentrations and rolling shear failure. Additionally, both the adhesive types and wood species significantly influenced the f_m, E_mg, and rolling shear strength (f_r) independently, while their interaction effect was found to be non-significant. The experimental bending stiffness was higher than the theoretical values. The shear analogy method provided the most accurate results for bending and shear strengths, while bending stiffness was best predicted by the modified gamma method, with minor variations. The finite-element models (FEMs) also produced results with a deviation of only 10%.

1. Introduction

Global warming, climate change, rising pollution, and environmental degradation demand the use of renewable, sustainable, and low-carbon construction materials [1]. Conventional construction materials such as concrete and steel exhibit higher levels of embodied carbon, thereby contributing substantially to climate change. In response, carbon-neutral green building materials have attracted attention among researchers, particularly the use of renewable resources like lumber [2]. Cross-laminated timber (CLT) is gaining popularity as a sustainable alternative to traditional building materials because of its advantages, such as massive dimension, high prefabrication potential, reduction in construction time, seismic safety, lightweight, and ease of installation. Conventional CLT comprises panels with three to nine layers of wood, bonded orthogonally using structural adhesive [1,3]. Global production of CLT panels is projected to reach 3 million cubic metres by 2025 [4], with Europe contributing 2 million cubic metres in 2023 [5]. Traditionally, CLT panels have been made from softwoods such as spruce, pine, and fir [1,3]. However, the increasing demand for CLT and the decline in forest cover have driven researchers to explore the use of lower-grade plantation-grown hardwoods, such as poplar and other cultivated wood species, to meet these needs. Furthermore, new forest management strategies involving the cultivation of lower-grade hardwoods, such as poplar and willow, have augmented Europe’s hardwood supply [6]. Since the beginning of the 21st century, numerous studies have evaluated the suitability of various hardwoods for CLT panels in response to changing global forest composition.

Rolling shear is an inherent characteristic of CLT resulting from the perpendicular arrangement of subsequent layers and the comparatively low shear strength and modulus perpendicular to the wood [7]. Additionally, wood has significant anisotropy, indicating that its properties differ across the three mutually perpendicular axes [7]. The shear moduli in the radial-tangential (RT) plane, often referred to as the rolling shear modulus, can be up to ten times greater than the shear moduli in the longitudinal-tangential (LT) planes [8]. Softwoods are particularly more prone to rolling shear failure due to their elongated wood fibres, which are susceptible to shearing or sliding, as well as their lower shear strength along the grain [9,10]. For the hardwood species, rolling shear failure is often caused by the density variation between early and late wood, especially at the interface [10,11]. The rolling shear modulus of conventional spruce CLT varies from 100 to 141 N/mm² [8] which is reportedly lower than that of hardwood CLT panels such as beech [10,12,13], maple [14], poplar [12,15], eucalyptus [16,17]. Hardwoods are known for their superior strength and rigidity, which enhance the load-carrying capability of CLT panels by reducing the risk of rolling shear failure [12,15,16]. Additionally, hardwood CLT requires 10–15% less material than softwood CLT to achieve comparable strength [18]. However, the primary challenge with hardwood CLT is its lower bond strength and durability, as well as its tendency for increased delamination, as highlighted by various researchers [11,19].

Numerous studies have indicated the potential of hybrid or mixed species CLT composed of various wood species with differing densities and grades [10,12,13,14] or structural composites such as plywood, oriented strand board (OSB), laminated strand lumber (LSL), and laminated veneer lumber (LVL) [20] to enhance material resources and achieve high-strength structural materials. However, very limited studies are available on the suitability of poplar wood for homogeneous and hybrid CLT manufacturing with a high-density outer layer. In hybrid CLT panels, high-density outer layers enhance bending performance [14,16], whereas core layers augment shear performance [17,21,22]. Consequently, designers of hybrid CLT panels must assess the influence of the outer and core layers on ultimate load capacity and serviceability [3]. Hematabadi et al. [12] reported that low-density poplar (Populus alba) CLT exhibited reduced E_mg relative to larch and pine; however, a high-density beech (Fagus orientalis) core layer with poplar outer layers enhanced bending performance by 12.5% and rolling shear by 30%. In a similar vein, Sciomenta et al. [13] observed an increase in bending (37%) and rolling shear performance (24%) in hybrid beech-Corsican pine (Fagus sylvatica–Pinus nigra) CLT compared to the homogeneous Corsican pine CLT, attributed to the superior density and rolling shear modulus of beech wood. Furthermore, melamine–urea–formaldehyde (MUF) adhesive demonstrated enhanced performance relative to polyurethane (PUR). In a separate investigation, Lu et al. [22] indicated that hybrid poplar–Douglas fir CLT exhibited approximately 8% greater bending stiffness, whereas hybrid Douglas fir–poplar CLT showed 22% enhanced bending stiffness compared to pure poplar CLT. Yin et al. [23] observed that the high-density outer layer enhanced bending performance by 15% and rolling shear by 12% compared to low-density CLT panels made from Chinese fir. Ma et al. [14] reported that hybrid maple–spruce CLT (Acer saccharum–Picea glauca) exhibits a 28% greater modulus of elasticity compared to hybrid spruce–maple CLT while demonstrating a 24% reduction in rolling shear strength due to the lower rolling shear modulus of the core spruce wood. The core beech layer enhanced the rolling shear performance of hybrid spruce–beech CLT nearly threefold compared to spruce CLT, as reported by Aicher et al. [10], and 1.8 times greater than laminated strand lumber (LSL) [20].

Theoretical methodologies (shear analogies, modified gamma, Timoshenko beam theory, and composite theory) alongside the finite element method (FEM) are effective means of analyzing the bending performance of CLT panels [21,24]. Compared to experimental data, the shear analogy forecasts a 25% reduced bending stiffness for white ash and red maple CLT [25]. At the same time, He et al. [26] reported that the effective bending stiffness via shear analogy (EI_{eff, shear}) yielded the most precise result for local bending stiffness (EI_l). In contrast, modified gamma theory (EI_{eff, gamma}) was more accurate for global bending stiffness (EI_g). The authors further observed that FEM could evaluate the stiffness and strength of CLT panels with a range of 10–20% accuracy. Shear analogies showed higher precision for bending and rolling shear strength, whereas bending stiffness was the gamma method [17,21,24]. Huang et al. [7] reported that the composite beam theory and shear analogy technique yield precise findings for f_r in the context of out-of-plane bending; however, the modified gamma method demonstrates excellent reliability with the redesigned planar configuration. Dobeš et al. [27] noted that the FEM forecasted a maximum displacement that was 7% more than the actual values. Furthermore, FEM was shown to underestimate the maximum load capacity of thinner panels by 4%, while overestimating it by 20% for thicker panels [21]. In contrast, Navaratnam et al. [24] observed that the FEM underestimated the bending stiffness of three-layered radiata pine CLT by 5% while overestimating it by 13% for five-layered CLT.

As CLT is a structural component, its mechanical properties like E_mg, f_m, and f_r must be considered during structural design. Furthermore, designing wall, floor or roof assemblies composed of CLT panels needs consideration for the maximum compressive stress both parallel and perpendicular to the grain directions. Several studies indicated that hardwood CLTs outperformed the typical softwood CLTs in terms of mechanical properties, like load-bearing capabilities, material consumption, and the risk of rolling shear failure [12,15,16]. Still, the bond line delamination in hardwood CLTs is a major drawback. Moreover, increasing demand for CLT and expansion of plantation-grown hardwood forests, like poplar and other cultivated species necessitates the researchers to explore the feasibility of utilizing these materials in CLT manufacturing. This exploration involves analyzing their properties in homogeneous CLT panels made entirely from single species and hybrid CLT panels that combine different wood species. Selecting suitable species depends on factors such as resource availability, economic viability and compliance with established minimum performance criteria to ensure that the chosen species or combination of species meets the required structural and environmental standards.

In the Czech Republic, poplar (Populus spp.) and maple (Acer spp.), two common fast-growing species, make up around 24% of the avenue plantations [28]. Moreover, the latest iteration of EN 16351 [29] identifies poplar as the sole hardwood species for the production of CLT panels, with minimal study concerning maple [16]. Das et al. [19] showed superior bonding performance of both poplar and hybrid maple–poplar CLT, compared to spruce (Picea abies (L.) H. Karst.) CLT. This study was carried out with the that CLT from poplar, which has a density almost comparable to that of spruce, may match or surpass the conventional spruce CLT in terms of both bending and rolling shear performance. Additionally, the study also explores the potential benefits of hybrid CLT panels prepared by combining low-density poplar in the core and high-density maple in the outer layer with an expectation to achieve enhanced load-bearing capabilities, material efficiency, and reduced risk of rolling shear failure. Utilization of low-density and underutilized hardwoods in CLT production aligns with sustainability objectives by enhancing the resource base. The experimental results were compared with theoretically predicted values from three different methodologies: Timoshenko beam theory, shear analogies, and modified gamma. Additionally, finite element models (FEMs) were utilized to evaluate the bending stiffness.

2. Materials and Methods

2.1. Materials

The study included two hardwood species, poplar (Populus nigra L.) and maple (Acer platanoides L.), as well as a softwood, Norway spruce (Picea abies (L.) H. Karst.), which were obtained from a commercial provider (woodstore) in the Czech Republic, and possessed the nominal dimensions of a 150 mm width, a 3 m length, and a thickness of 30 mm. The kiln-dried lumber exhibited a moisture content of 13%, and was classified as Grade B. Low-density poplar, demonstrating a moderate load-bearing capacity akin to that of spruce, was used for both the homogeneous CLT and the core layer of hybrid CLT panels. The external layers of hybrid CLT panels were constructed from high-density maple, which exhibits exceptional mechanical qualities. Additionally, homogeneous spruce CLT was made for comparison. After the acquisition of the lumber, it was acclimatized at 20 °C and 65% relative humidity before specimen preparation. The lumber’s modulus of elasticity (MOE) was determined using the FAKOPP Ultrasound Timer UT-06/2013, produced by Fakopp Enterprise, Gfalva, Hungary. The mean density, moisture content and modulus of elasticity (MOE) values of each species have been provided in

Table 1. Mean density, moisture content (%), and modulus of elasticity (MOE) of wood.

Wood Species	Mean Density	Mean Moisture Content	Mean MOE
Poplar	398 ± 46	11.9 ± 0.6	8900 ± 849
Spruce	423 ± 36	11.7 ± 0.7	9800 ± 942
Maple	653 ± 76	12.3 ± 0.5	13,810 ± 1142

.

A single-component polyurethane adhesive (1C-PUR) (Adhesive 2010) and a liquid melamine adhesive (Plus A011), accompanied by a hardener (H011), provided by Akzo Nobel (Amsterdam, The Netherlands), were used to fabricate the CLT panels. The objective was to evaluate the impact of the adhesive on the panels’ bending and rolling shear performance. The manufacturer and product listing assert that the ME lacks formaldehyde. The 1C-PUR is a pure solid with a viscosity between 6000 and 19,000 mPas, while a liquid hardener with 65% solid content has a viscosity ranging from 1500 to 9000 mPas.

2.2. Preparation of the Three-Layered CLT Panels

During production, lamellas with visible wood defects, such as bending, knots, splitting, or fractures, were discarded to prevent material faults from affecting the final product’s quality. The lamellas were randomly picked based on their visual qualities, following the guidelines provided by Jan Brundin et al. [30]. The outer layers were devoid of any imperfections and had dimensions of 2000 mm × 75 mm × 20 mm (length × width × thickness), while the lamellas with minor permissible amounts of defects according to the standard [28], were processed for the core layer, with dimensions of 300 mm × 75 mm × 20 mm (length × width × thickness), to prepare CLT panels of 2000 mm × 300 mm × 60 mm, as shown in Figure 1. As such, a layup was followed as the mechanical properties of CLT are predominantly controlled by the outer layers while the core layer only serves as a link between the outer layers and transfers the stress while.

Using a wooden spatula, one side of the face layers was applied with glue at a rate of 180 g/m² for 1C-PUR and 300 g/m² for ME. Following the manufacturer’s instructions, the ME was applied using an adhesive-to-hardener ratio of 100:100 (weight-to-weight). Following glueing, each panel was assembled and pressed at 1 MPa pressure for 1 h at 20 °C. The production procedure did not include edge glueing since it had less influence [19]. CLT panels were kept at room temperature for nearly two days after pressing to completely cure adhesives. After trimming on both sides, CLT panels were conditioned for three weeks at 65 ± 5% RH and 20 ± 2 °C before testing.

2.3. Experimental Testing

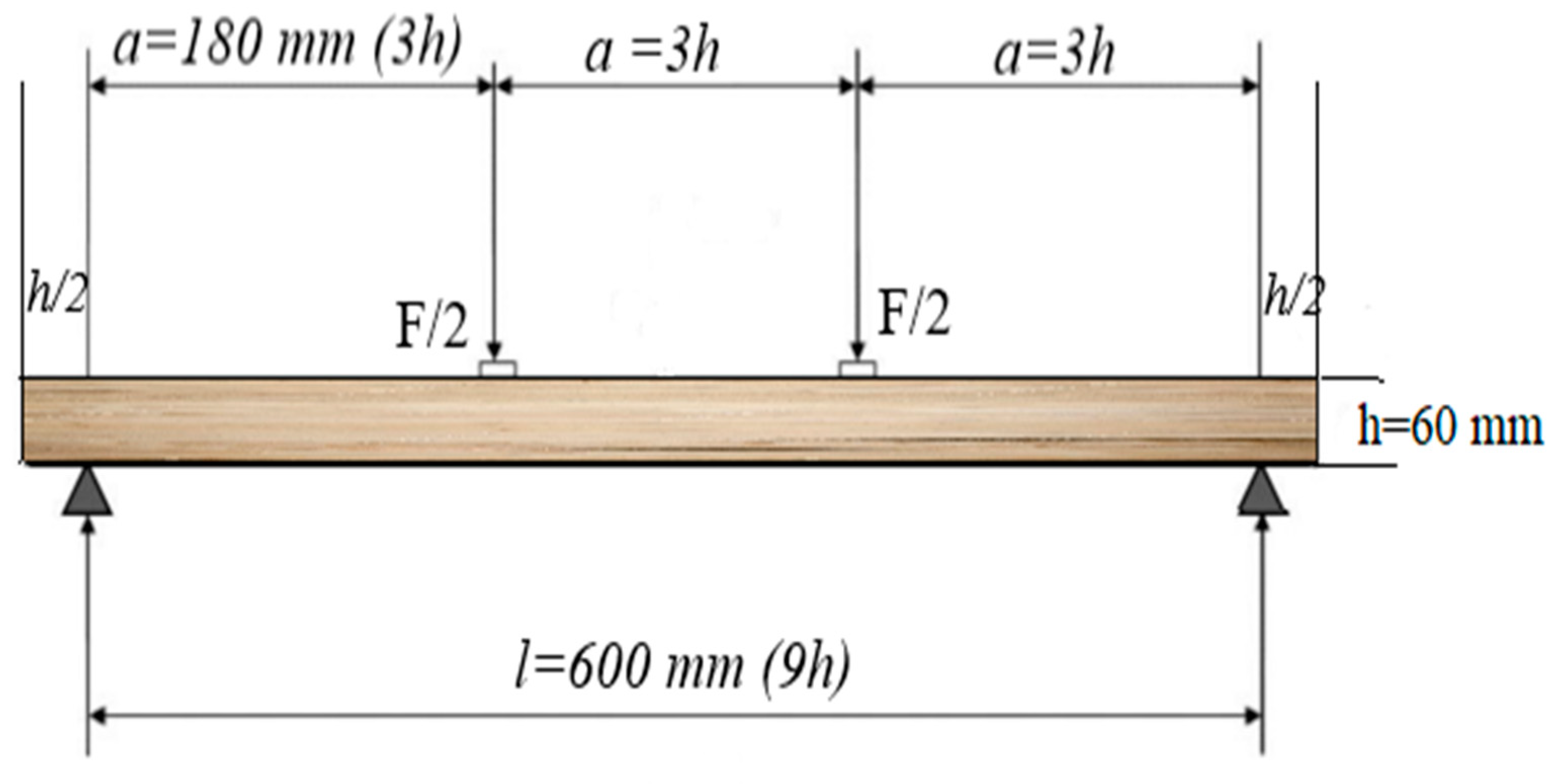
2.3.1. Bending Test

EN 16351 [29] compliance four-point bending test was conducted to evaluate the bending performance, with the span length being 18 times the thickness (h) of the panel (18 h), as shown in Figure 2, using the universal testing machine TIRA 2850 S E5, Germany (TIRA, Schalkau, Germany). Ten replicate samples, with a total of 60 specimens, were examined for each adhesive and layup. The test specimens were supported at both ends and the loading points, and were spaced six times more than the panel thickness (6 h) between the center and either end of the opposite support. The load was gradually increased, reaching a peak in about 300 ± 120 s. The extensometer linked to the testing apparatus determined the total deflection, while the connected PC recorded the load–displacement curves. Using Equation (1) [24,26], the global bending stiffness (EI_mg) was calculated as follows:

$${\mathit{E}\mathit{I}}_{\mathit{m}\mathit{g}}={\displaystyle \frac{\mathbf{3}\mathit{a}{\mathit{l}}^{\mathbf{2}}-\mathbf{4}{\mathit{a}}^{\mathbf{3}}}{\mathbf{48}(\frac{\left({\mathit{W}}_{\mathbf{2}}-{\mathit{W}}_{\mathbf{1}}\right)}{\left({\mathit{F}}_{\mathbf{2}}-{\mathit{F}}_{\mathbf{1}}\right)}-\frac{\mathbf{3}\mathit{a}}{\mathbf{5}\mathit{G}\mathit{b}\mathit{h}})}}$$

(1)

where a—loading point distance to the nearest support (mm), l—specimen length between supports (mm), h and b—panel thickness and width (mm), F₂ − F₁—increase in of load corresponds to 10% and 40% of maximum load (N), W₂ − W₁—increase in displacement proportional to load F₂ − F₁ (mm), G—shear modulus (N/mm²).

Using Equation (2), suggested by Navaratnam et al. [24], the bending strength (f_m) was calculated as follows:

$${\mathit{f}}_{\mathit{m}}={\displaystyle \frac{\mathbf{3}\mathit{F}\mathit{a}}{\mathit{b}{\mathit{h}}^{\mathbf{2}}}}$$

(2)

where f_m is the bending strength (N/mm²), and F is the maximum load (N).

2.3.2. Rolling Shear (RS) Test

Following EN 16351 [29], the RS strength was evaluated with a short-span four-point bending test was conducted over the span of nine times more than the thickness of the panel (9 h), as seen in Figure 3. Similarly to the bending test, ten replicate samples, with a total of 60 specimens, were examined for each adhesive and layup. Both loading points were positioned at a distance that was three times the panel thickness (3 h) from each end of the supports and their position ensured that they were spaced apart equally. The computer recorded the load–displacement curve throughout the test, which was conducted using the UTM Instron 5882 (Illinois ToolWorks Inc., Norwood, MA, USA) at a 10 mm/min loading rate.

Equation (3) was used, as Li et al. [21] suggested, to calculate the CLT panels’ RS strength (f_r).

$${\mathit{f}}_{\mathit{r}}={\displaystyle \frac{\mathbf{3}{\mathit{F}}_{\mathit{u}}}{\mathbf{4}\mathit{b}\mathit{h}}}$$

(3)

2.4. Statistical Analysis

The study used a randomized factorial design. A two-way analysis of variance (ANOVA) was conducted using Statistica 13 (TIBCO Software Inc., Palo Alto, CA, USA) to assess the influence of wood species and adhesive type on the bending and rolling shear properties of CLT panels. The Tukey HSD test (p < 0.05) was used to determine statistical significance between datasets.

2.5. Theoretical Calculation

This research used three widely used theoretical methods: shear analogy (SA), Timoshenko beam theory (TBT), and modified gamma (MG). According to SA, bending stiffness is the product of the rigidity of the layer and Steiner’s stiffness in proximity to the neutral axis [31]. TBT is an extended version of the Bernoulli–Euler theory and calculates the flexural stiffness of CLT with the layer’s characteristics and their arrangement while considering the effect of shear [31]. The most widely used MG approach relies only on the hypothesis of mechanically linked beams without considering shear deformation [24]. As suggested by Brandner et al. [31], Equations (4)–(6) were used to calculate the bending stiffness by all three methods.

$${\mathit{E}\mathit{I}}_{\mathit{e}\mathit{f}\mathit{f},\mathit{s}\mathit{h}\mathit{e}\mathit{a}\mathit{r}}={\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\mathit{E}}_{\mathit{i}}\mathbf{\ast }{\mathit{b}}_{\mathit{i}}\mathbf{\ast }{\displaystyle \frac{{{\mathit{h}}_{\mathit{i}}}^{\mathbf{3}}}{\mathbf{12}}}+{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\mathit{E}}_{\mathit{i}}\mathbf{\ast }{\mathit{A}}_{\mathit{i}}\mathbf{\ast }{{\mathit{Z}}_{\mathit{i}}}^{\mathbf{2}}$$

(4)

$${\mathit{E}\mathit{I}}_{\mathit{e}\mathit{f}\mathit{f},\mathit{t}\mathit{i}\mathit{m}\mathit{o}}={\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{(\mathit{E}}_{\mathit{i}}\mathbf{\ast }{\mathit{I}}_{\mathit{i}})+{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\mathit{E}}_{\mathit{i}}\mathbf{\ast }{\mathit{A}}_{\mathit{i}}\mathbf{\ast }{{\mathit{e}}_{\mathit{s}\mathit{i}}}^{\mathbf{2}}$$

(5)

$${\mathit{E}\mathit{I}}_{\mathit{e}\mathit{f}\mathit{f},\mathit{g}\mathit{a}\mathit{m}\mathit{m}\mathit{a}}={\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{(\mathit{E}}_{\mathit{i}}\mathbf{\ast }{\mathit{b}}_{\mathit{i}}\mathbf{\ast }{\displaystyle \frac{{{\mathit{h}}_{\mathit{i}}}^{\mathbf{3}}}{\mathbf{12}}})+{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{\mathit{E}}_{\mathit{i}}\mathbf{\ast }{\mathit{A}}_{\mathit{i}}\mathbf{\ast }{{\mathit{Z}}_{\mathit{i}}}^{\mathbf{2}}\mathbf{\ast }{\mathit{\gamma }}_{\mathit{i}}$$

(6)

where E_i is the MOE of the ith-layer (N/mm²), b_i and h_i are the width and thickness of the ith-layer (mm), A_i is the area of the ith-layer (mm²), Z_i is the distance between the center of ith layer to the neutral axis (mm), I_i is the moment of inertia of the ith-layer, e_si is similar to Z_i (mm), and γ_i is the connection efficiency factor.

Using Equation (7), suggested by Brandner et al. [31], the connection efficiency factor (γ_i) was calculated as follows:

$${\mathit{\gamma }}_{\mathit{i}}=\mathbf{1}{+\left({\displaystyle \frac{{\mathit{\pi }}^{\mathbf{2}}{\mathit{E}}_{\mathit{i}}{\mathit{b}}_{\mathit{i}}{\mathit{h}}_{\mathit{i}}}{{{\mathit{L}}_{\mathit{e}\mathit{f}\mathit{f}}}^{\mathbf{2}}\mathbf{\ast }(\mathit{G}{\mathbf{\ast }\mathit{b}}_{\mathit{j}}/{\mathit{h}}_{\mathit{j}})}}\right)}^{-\mathbf{1}}$$

(7)

where L_eff represents effective the specimen length, and j represents the transverse layer.

Equations (8) and (9), suggested by Li et al. [21], were used to calculate the theoretical bending strength (f_m) and rolling shear strength (τ_m) as follows:

$${\mathit{f}}_{\mathit{m}}={\displaystyle \frac{{\mathit{M}}_{\mathit{m}\mathit{a}\mathit{x}}}{{\mathit{S}}_{\mathit{e}\mathit{f}\mathit{f}}}}$$

(8)

$${\mathsf{\tau }}_{\mathit{m}}={\displaystyle \frac{{\mathit{V}}_{\mathit{m}\mathit{a}\mathit{x}}}{{\mathit{I}}_{\mathit{e}\mathit{f}\mathit{f}}}}\times {\displaystyle \frac{\mathit{Q}}{\mathit{b}}}$$

(9)

where f_m and τ_m represent theoretical bending and rolling shear strength (N/mm²), respectively; V_max and M_max represent maximum shear force (kN) and bending moment (N/mm), respectively; Q represents area moment of the specimen (mm³); S_eff represents the section modulus as calculated by EI_eff by E_{1 ×} h_i/2 [26].

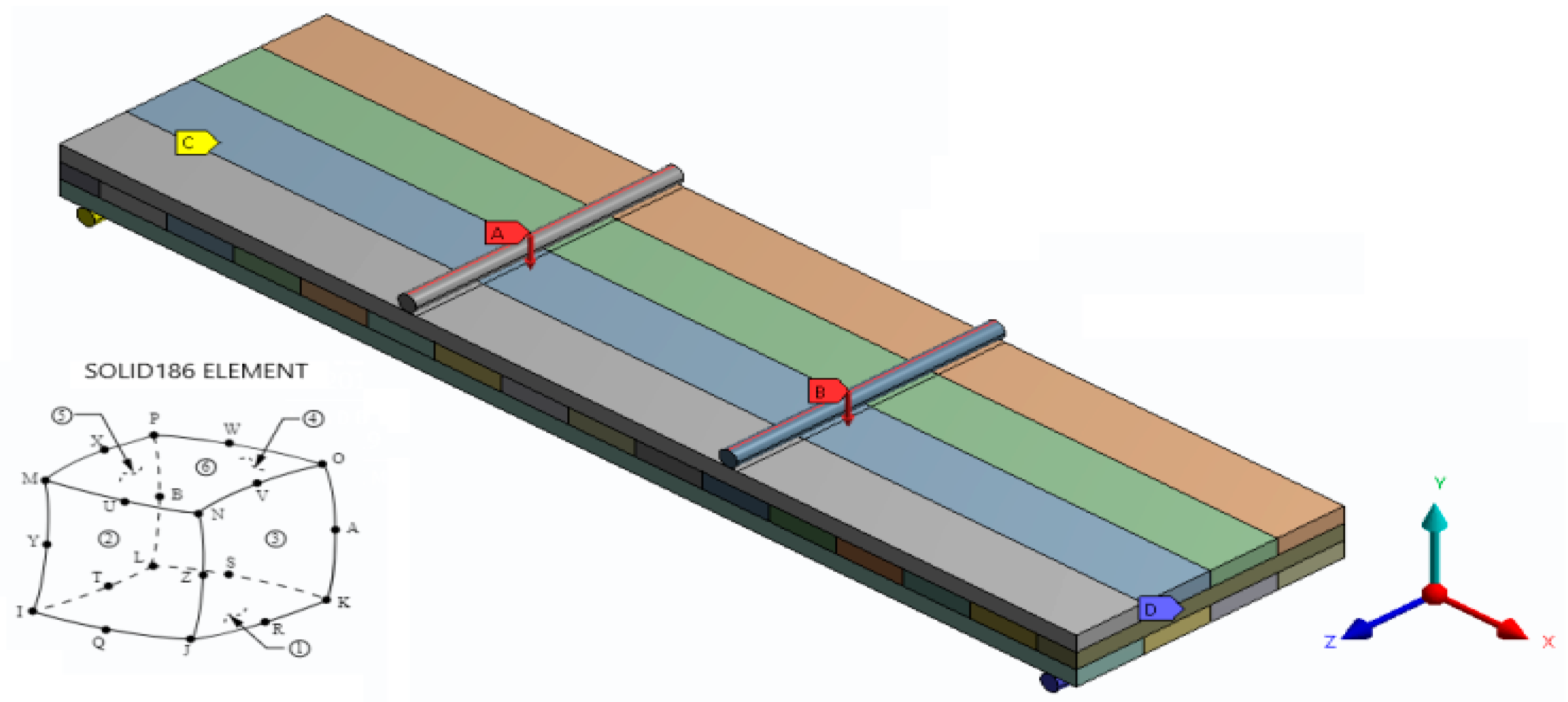
2.6. Finite Element Modelling

As a composite material, the CLT panels were modelled using ANSYS 2019 R13. The individual layers of CLT panels were simulated as an orthotropic material with varying elastic characteristics in the longitudinal, tangential, and radial axes. The model omitted wood imperfections such as knots, cracks, annular rings, and other issues. The orthotropic CLT panels’ mechanical behaviour is determined by nine distinct elastic constants, including three elastic moduli (E_L, E_R, E_T), three Poisson’s ratios (v_LR, v_LT, v_RT), and three shear moduli (G_LR, G_LT, G_RT).

Table 2. Elastic constant of the wood species at 12% moisture for modelling.

Wood	EL (N/mm2)	ER	ET	vLR (-)	vLT (-)	vRT (-)	GLR (N/mm2)	GLT	GRT
Poplar	8900	739	418	0.344	0.42	0.875	676	463	134
Spruce	9800	1080	578	0.422	0.462	0.530	950	900	98
Maple	13,810	1311	678	0.46	0.50	0.82	1013	753	255

displays the different wood properties used for the modelling.

The three-layer composite CLT panels were made of orthotopically aligned poplar layers for homogenous poplar CLT and outer maple with core poplar wood for hybrid CLT, which were joined together with polyurethane (1C-PUR) and melamine adhesive (ME) separately. The outer and core layers were connected without gaps; their faces and edges could not slide or separate. Since the outer and core layers were not edge bonded, their interaction is modelled as friction. Tangential movements are affected by friction. The coefficient of friction (f) was assumed to be 0.5 for easier numerical modelling, based on Dobeš et al.’s [27] findings that reported a coefficient of friction of 0.65 between wood and steel. The CLT panels and auxiliary components, such as steel loading rollers and supports, were represented using SOLID186 elements. All 20 element nodes have three degrees of freedom, allowing strain, deflection, hyperelasticity, creep, and stress stiffening in all three dimensions. A single homogeneous unit represents the loads and supports at both ends and the middle. This simulation employed boundary conditions like the experiment depicted in Figure 4 [27,32]. A hinged or fixed support inhibiting the displacement and roller support allowing X-axis movement were given for each CLT panel at the end, and two rollers loaded the top layer, identical to the experiment. The auto-generated shared topology was used to create the mesh. The CLT models were loaded with a load of 21,500 N for both F_A and F_B, as determined in the experiment [32].

3. Results and Discussion

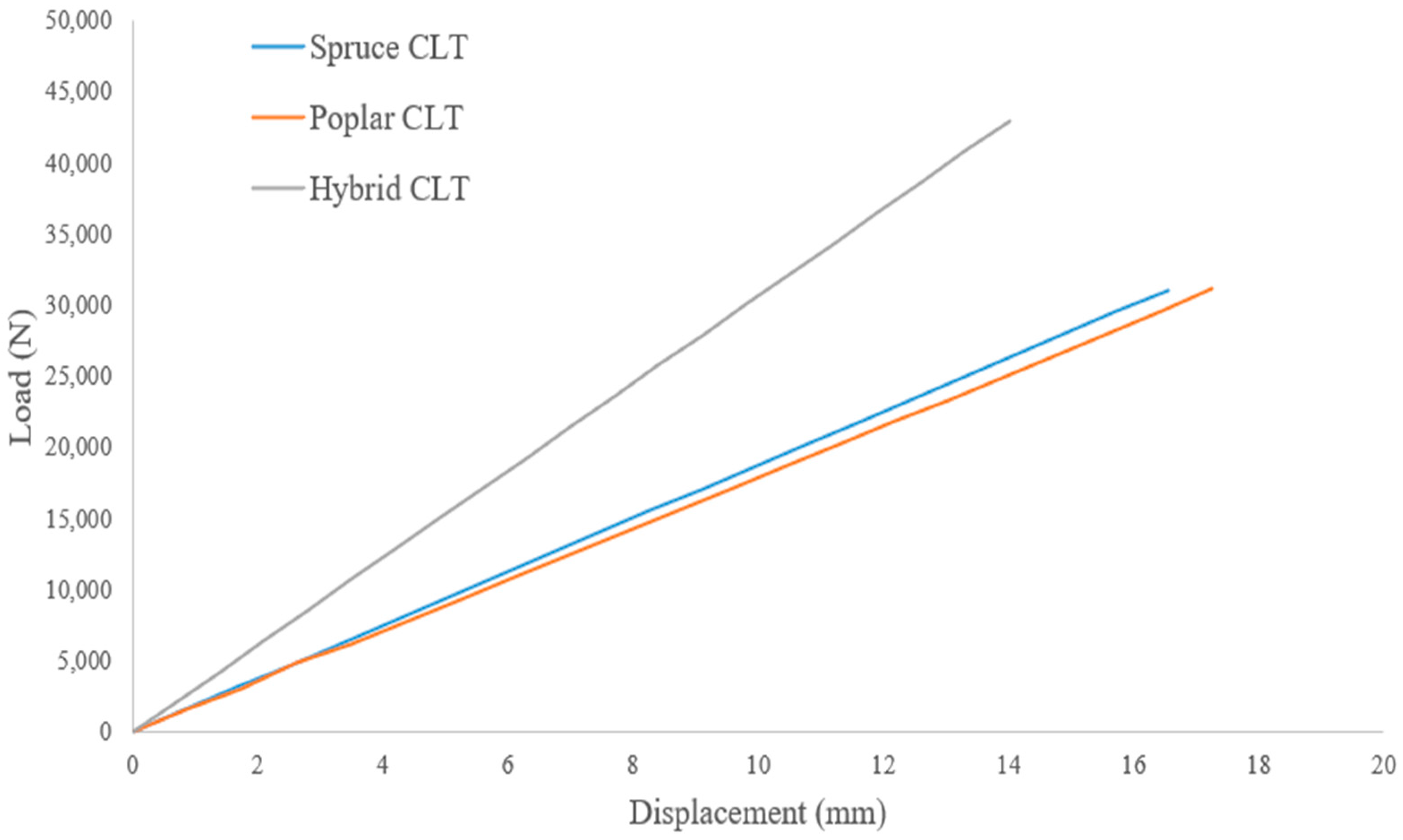
3.1. Bending Characteristics

Figure 5 illustrates the mean load versus displacement curves for homogeneous spruce, poplar, and hybrid CLT panels, incorporating both adhesive types. The samples with similar lamella types demonstrated similar load–displacement curves, characterized by a linear trend until the maximum load (F_max), followed by a reduction in force leading to brittle failure. The orthotropic characteristics of wood and their orthogonal configuration in CLT panels likely contributed to the brittle failure and subsequent reduction in maximum load [12,17]. Some specimens, particularly in hybrid CLT, exhibited varying degrees of ductility, which were attributed to the longitudinal maple layers, which supported greater loads despite the core transverse layers experiencing rolling shear failure [23]. The maximum load (F_max) of the poplar CLT panels that bonded with 1C-PUR ranged from 27,530 to 36,190 N, with an average value of 32,200 N. Conversely, the panels bonded with ME demonstrated a F_max ranging from 28,100 to 35,890 N, with a mean value of 30,890 N. Hematabadi et al. [12] reported similar results. In spruce CLT panels, the mean Fmax recorded was 32,200 N for 1C-PUR and 30,890 N for ME, which is consistent with the findings of Sikora et al. [33]. The high-density of the outer maple lamellas in hybrid CLT panels significantly enhances their load-bearing capacity compared to poplar and spruce, with mean F_max values of 43,290 N and 42,856 N for 1C-PUR and MEs, respectively [23]. Additionally, the maximum displacement (d_max) was greater in poplar CLT compared to spruce and hybrid CLT. Despite the variation in modulus of elasticity between poplar and spruce wood, poplar exhibited commendable performance regarding its load-bearing capacity. The lower density and resultant flexibility of poplar permit greater deflection (d_max) prior to failure, indicating that poplar CLT can undergo more deformation before fracturing.

Hybrid CLT demonstrated a load-bearing capability that was 33% greater than that of spruce CLT, which exhibited an approximately 11% higher value than poplar CLT. The enhanced load-bearing capacity of hybrid CLT panels can be attributed to the incorporation of a low-density core made of poplar, which may be compressed by high-density maple layers on the exterior [34]. This is partly because if two species possess similar densities, their cellular architectures are likely to exhibit significant similarities, leading to reduced variation in densification under the same pressure conditions. However, the homogenous CLT panels (poplar and spruce) demonstrate consistency in thickness, grade, and anatomical structure. Due to their uniformity, minimal densification occurred, resulting in inferior load-bearing ability compared to hybrid CLT.

Table 3. Statistical evaluation of E_mg and f_m of CLT panels.

Effect	Value	F	df	Error	p-Value
Intercept	0.000547	48,435.53	2	53	0.000000
Species	0.008594	259.36	4	106	0.000000
Adhesive	0.888103	3.34	2	53	0.043080
Species×Adhesive	0.991690	0.11	4	106	0.978501

displays the statistical analysis of wood species, adhesives, and their interactions on CLT panels’ global bending modulus of elasticity (E_mg) and bending strength (f_m). From the statistical analysis, it was observed that the effect of wood species is highly significant for both E_mg and f_m (p = 0.000), and so as well as the adhesive (p = 0.043); however, the interaction effect was insignificant (p = 0.978).

Figure 6 illustrates the E_mg and f_m as functions of adhesive and species. In poplar CLT, the mean E_mg and f_m were 7949 N/mm² and 31.10 N/mm², respectively, with 1C-PUR adhesive and 7802 N/mm² and 29.97 N/mm², respectively, with ME. Similarly, the E_mg values for spruce CLT were recorded as 8338 N/mm² and 8152 N/mm², and the f_m values of 32.01 N/mm² and 31.63 N/mm², with 1C-PUR and ME, respectively. For hybrid CLT, the E_mg values were 13,426 N/mm² and 13,276 N/mm², with the f_m values of 44.78 N/mm² and 44.33 N/mm² for 1C-PUR and ME, respectively. The results indicated a variation of only 4% in the bending performance of the CLT panels concerning the adhesive type, which is similar to the results of Ma et al. [14], who reported a roughly 5% variation in maple and hybrid maple–spruce CLT bonded with PRF and MF. The reported results of poplar CLT are nearly equivalent to those of spruce CLT, whereas the outer maple in the hybrid CLT enhanced the E_mg by 74% and the f_m by 37% due to lamella anisotropy and inherent strength. According to Niederwestberg [35], when CLT panels were loaded perpendicular to the grain, the core layer of a three-layered CLT panel with a uniform layer thickness only contributed to about 38% of the total stiffness, with a MOE ratio of 16 between the top and core layers. This might have one cause where the outer maple layer primarily contributed to bending performance. Another possible reason could be that the low-density of the core poplar may effectively absorb the compressive stresses within the elastic range, ensuring structural integrity under stress without enduring irreversible deformation [36]; conversely, the outer high-density maple improves the panel ductility, enabling more efficiency to withstand cracks and failures [2]. Nonetheless, the uniformity of the lamellas in both spruce and poplar CLT had a minimal impact on the adhesive-type changes in both E_mg and f_m. The findings of our study are consistent with earlier research on spruce CLT conducted by Sikora et al. [33] and Davis et al. [20], as well as on poplar CLT by Hematabdi et al. [12]. However, maple–poplar hybrid CLT’s performance is comparatively lower than hybrid maple–spruce CLT, as indicated by Ma et al. [14].

3.2. Rolling Shear Test

Figure 7 illustrates the impact of wood species and adhesive type on the rolling shear strength (f_r) of CLT panels. The load versus displacement curves for both bending and rolling shear exhibit similarities. Consistent with the findings of Ma et al. [14], both wood species and adhesive type were significant (p = 0.00) as individual factors in predicting f_r, whereas their interaction effect was not significant (p = 0.562). The rolling shear strength of spruce CLT bonded with 1C-PUR was 1.88 N/mm², while that of ME-bonded CLT was 2.003 N/mm². In a similar manner, the f_r of poplar CLT was measured at 2.13 N/mm² and 2.17 N/mm², whereas hybrid CLT exhibited values of 3.08 N/mm² and 3.17 N/mm² for 1C-PUR and ME, respectively. It was additionally noted that ME exhibited a higher f_r than 1C-PUR, consistent with the findings of Sciomenta et al. [13]. The formic acid hardener in ME might have catalyzed the curing process by reducing its viscosity and pH and increasing the f_r [32]. The reduced f_r in spruce CLT may be attributed to the vulnerability of softwoods to rolling shear failure or their short fibre characteristics [10,15]. Furthermore, the current CLT design approach recommends a G_RT of 50 N/mm² for spruce, whereas Karakoç et al. [37] reported a reduced G_RT of 25 N/mm² in spruce, potentially contributing to the lower f_r. Furthermore, the f_r of poplar observed in our study exceeds that of spruce CLT and the values reported by Hematabadi et al. [12]. The f_r of hybrid CLT panels was enhanced by incorporating high-density maple in the outer lamellae, as noted by Nero et al. [16], surpassing the values reported for red maple [25] and birch CLT [17]. A potential explanation may be the elevated strength-to-density ratio or the planar shear modulus of the core poplar in both poplar and hybrid CLT, which could have influenced this higher result [17]. The elevated f_r in poplar and hybrid CLT may also result from notable density fluctuations in their latewood regions [38]. Furthermore, hardwoods exhibit a higher f_r due to their shear modulus in the radial-tangential (G_RT) plane being over 40% of the G_LT, in contrast to 10% for softwoods [38].

Table 4. Global bending modulus of elasticity (E_mg), bending strength (f_m) and rolling shear strength (f_r) of the CLT panels.

Species	Adhesive	Emg	fm	fr
Poplar	MF	7802 a	29.97 a	2.17 a
	1C-PUR	7950 ab	31.10 ab	2.12 a
Spruce	MF	8152 bc	31.63 ab	2.00 b
	1C-PUR	8338 c	32.00 b	1.88 c
Hybrid	MF	13,276 d	44.33 c	3.17 d
	1C-PUR	13,426 d	44.77 c	3.08 e

Means followed by different letters are only statistically significant according to Tukey HSD (p = 0.05).

illustrates the interactions between wood species and adhesives derived from the Tukey HSD test, which was used to compare all means. According to the findings, the E_mg hybrid CLT is not statistically significant for adhesive types; however, they are significant compared to both poplar and spruce CLT. While spruce bonded with MF reported comparable findings with 1C-PUR bonded poplar, which are not statistically significant. Similar results were also obtained for f_m where hybrid CLT is not statistically significant for adhesive types. Additionally, both 1C-PUR bonded poplar and MF bonded spruce reported similar f_m values, which are not significantly different. However, for f_r, both hybrid and spruce CLT offered a significant difference, whereas it was not significant for poplar.

Several studies have demonstrated that gaps and insufficient edge-glueing adversely affect CLT’s physical and mechanical properties. Gardner et al. [39] indicated that a gap of less than 6 mm from non-edge glueing reduces CLT’s bending stiffness and shear strength, with a maximum variation in only 2%. Franzoni et al. [40] observed that narrow gaps had minimal impact on bending stiffness due to the negligible cross-layer contribution, while wider gaps considerably reduced shear stiffness. Brandner [30] indicates that edge glueing may result in irregular crack patterns on the wooden surface of face layers due to shrinkage and swelling, which can be mitigated through non-edge glueing methods. Furthermore, the gaps resulting from non-edge glueing are chiefly accountable for the panels’ stress concentration and eventual failure [39,40]. Sound and dead knots significantly affected the load-bearing capacity of the CLT panels [41]. The factors may have influenced their mechanical performance, as the chosen core lamellas were of grade B with visual grading, exhibiting acceptable defects and lacking edge glueing.

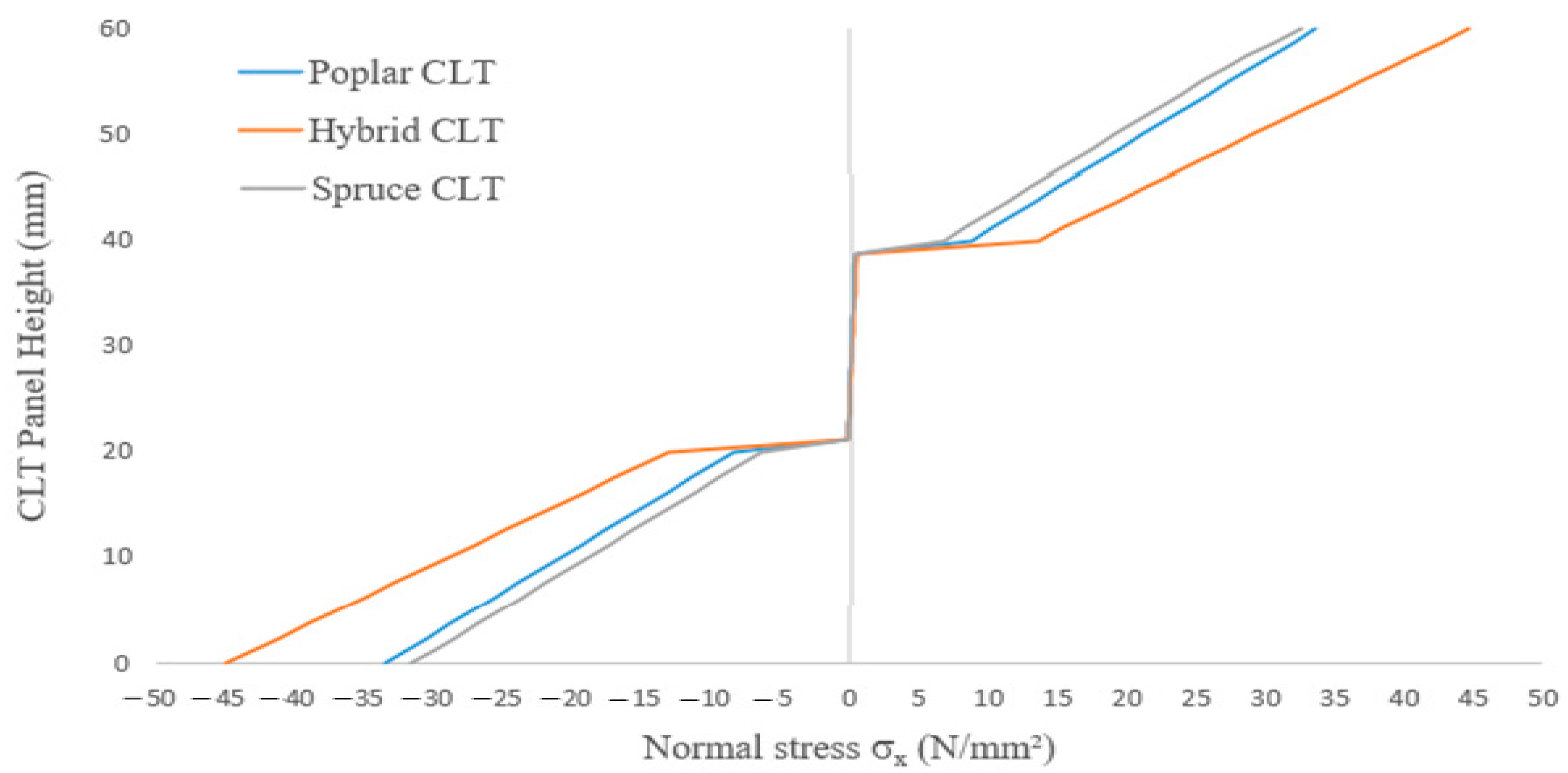
3.3. Failure Modes in Bending and Rolling Shear

Figure 8 illustrates the failures observed in bending and rolling shear tests. Most CLT panels experienced failures primarily due to rolling shear (RS) failures, including core-layer delamination and bending failure on the bottom. As stress increased, RS failure, as illustrated in Figure 8a, initiated at the beam centre and progressed toward the supports [12]. As the load on hybrid CLT increased, the low-density core of poplar caused greater deformation, which transmitted stress to the outer maple layers. This resulted in rolling shear failure and delamination between the layers. Dong et al. [42] reported analogous failure patterns. Tensile failures (Figure 8b) in the longitudinal direction may result from knots and other defects in wood fibres or the reduced load-carrying capacity of both poplar and spruce lamellas in homogeneous CLT [12,33], while the tensile strength of maple may have also played a role in hybrid CLT [38]. The midspan deflection increases with the load, resulting in stress at the supporting ends. Failure initiates at the supporting ends when the stress surpasses the bonding strength, as illustrated in Figure 8c.

3.4. Comparison of Experimental and Theoretical Data

Two global bending stiffness values were calculated for each CLT panel: one utilizing the respective shear value (EI_{mg, s}) and the other assuming an infinite shear value (EI_{mg, i}), as outlined by Li et al. [21]. The infinite shear modulus is a theoretical concept that evaluates a material’s capacity to resist deformation without shear stress and distortion. The average bending stiffness of poplar CLT was 4.46 × 10¹¹ Nmm², whereas for spruce, it was 4.82 × 10¹¹ Nmm² and 7.24 × 10¹¹ Nmm² for hybrid CLT with shear. Nevertheless, an infinite shear modulus results in a minimal variation of approximately 1% across all CLT panels, aligning with the results reported by Li et al. [21] and Navaratnam et al. [24]. The experimental bending stiffness (EI_mg) and the theoretical predictions are presented in Figure 9. Similarly to the findings of Sikora et al. [33] and He et al. [26], the experimental EI_mg exceeds all theoretical values of bending stiffness. The theoretical values exhibited a variation of only 12% in hybrid CLT, while the variation was 19% for both spruce and poplar CLT. This variation could be caused by the variation in material properties or the potential densification of the low-density poplar core layer between the high-density maple layers, contributing to the reduced variability observed in the hybrid CLT panels [42]. Dong et al. [42] reported a 7% variation in hybrid CLT–bamboo composite panels compared to homogeneous CLT panels. The results indicate that SA and TBT exhibit equivalent effective bending stiffness values, whereas MG demonstrates lower values but reports the highest accuracy with the connection efficiency factor (γ) [17,21]. The integration of the shear modulus (G) with the influence of shear deformation may have diminished the precision of the theoretical analysis method [33]. The results obtained are more precise than those reported by Crovella et al. [25], who utilized a modulus of elasticity for red maple and white ash and identified a 25% variance in their experimental findings.

Figure 10 compares the experimentally determined bending and shear strengths with the values predicted through theoretical analysis. The figure indicated that the theoretical approaches reported a lower rolling shear strength by 6.5% and an overestimation of bending strength by 4.5% compared to the experimental findings. Li et al. [21] reported similar findings, identifying a 7% variation between experimental and theoretically predicted values. The SA approach demonstrated superior accuracy in predicting the highest bending and rolling shear strength, surpassing the performance of the MG and TBM methods. The variation was primarily attributed to the differences in bending stiffness values in the theoretical calculation approach. The MG approach exhibited the lowest accuracy in evaluating bending and shear strength, which is consistent with the findings of Li et al. [21] and Sikora et al. [33]. Based on the findings, the theoretical methods demonstrate effective prediction of bending and shear strength.

Figure 11 illustrates the load–displacement curves obtained from the finite element method analysis. The FEM analysis indicated that under a load of 31,240 N, the deflection in poplar CLT was 17.26 mm. In contrast, the comparison of the experimental results with the FEM values indicated that the deflection was approximately 12% lower than the experimental measurements. The results obtained from FEM and experimental analysis indicated a variation of 11% for spruce CLT and 18% for hybrid CLT. The perfect bonding approach and removing non-edge glueing gaps during finite element modelling may account for the discrepancy between experimental values and finite element analysis [27]. The results obtained aligned with the findings of Wang et al. [32].

Figure 12 indicates that poplar CLT experiences a compressive stress of 33.61 N/mm² and a tensile stress of 33.69 N/mm² at the center of the cross-section. In contrast, spruce CLT exhibits compressive and tensile stresses of 31.53 N/mm² and 32.61 N/mm², while hybrid CLT shows 45.30 N/mm² and 45.26 N/mm² values, respectively. The figure indicates that the outer layers experienced the highest bending stress, whereas the core exhibited the lowest, consistent with the findings of Hematabadi et al. [12]. Furthermore, all three CLT layers played a role in load resistance, as indicated by FEM analysis. The discrepancy between experimental and model results may be attributed to the assumed material properties.

The bending stiffness was calculated using the FEM data and verified against the corresponding test outcomes. The global bending stiffness of poplar CLT was determined to be 4.19 × 10¹¹ Nmm², approximately 6.1% lower than the experimental value. Similarly, the bending stiffness of spruce CLT was reported as 4.43 × 10¹¹ Nmm², whereas hybrid CLT exhibited a bending stiffness of 6.47 × 10¹¹ Nmm², which is roughly 8.4% and 11% lower than the experimental value. Navaratnam et al. [24] observed a 20% discrepancy between the stiffness values generated by the FEM and the experimental results.

4. Conclusions

Bending and shear properties of poplar and maple–poplar hybrid CLT were compared to conventional spruce CLT using experimental, analytical, and FEMs. The primary findings are as follows:

◾

The hybrid CLT, involving high-density outer maple layers and a poplar core layer, resulted in significant increases in E_mg, f_m, and f_r by 74%, 37%, and 48%, respectively, compared to homogeneous poplar CLT. Additionally, the hybrid CLT also demonstrated superior performance compared to conventional spruce CLT, as well as red maple and birch CLT, in terms of rolling shear strength. The inclusion of maple lamellas in the outer layers of hybrid CLT enhanced its load-carrying capacity during bending tests.

◾

The homogenous poplar CLT exhibited E_mg, f_m, and f_r values nearly equivalent to or better than those of spruce CLT, thereby indicating its potential application in load-bearing structures and as a viable alternative for CLT production. The production of CLT presents a promising opportunity for the value-added utilization of poplar.

◾

Both the adhesive type and wood species had a significant impact on the bending strength (f_m), global bending modulus (E_mg), and rolling shear strength (f_r) independently; however, their interaction effect was not found to be significant.

◾

1C-PUR adhesive outperformed the ME in terms of global bending modulus, bending strength, and rolling shear strength.

◾

For homogeneous poplar and spruce CLT, a 19% variation in bending stiffness was observed between the theoretical and experimental values, whereas a 12% variation was noted for hybrid CLT, with the modified gamma approach yielding the most accurate results. Furthermore, the theoretical approaches indicated a 6.5% reduction in rolling shear strength and a 4.5% overestimation of bending strength, with the shear analogy yielding the most precise result.

◾

The bending stiffness of hybrid CLT, as per FEM, was approximately 11% lower than the experimental values, whereas, for both poplar and spruce CLT, the difference was between 6–8%.

In summary, the bending and rolling shear performance of both poplar hybrid CLT (maple–poplar) outperformed the traditional spruce CLT serving as a foundation for encouraging the use of low-grade poplar, and maple as the primary wood species for both homogenous and hybrid CLT production. This study was also designed to expand the market for low-value hardwood species like poplar, and maple, which are primarily used in lower value-added products.