Efficient Pb(II) Adsorption by Natural Mugaldzhar Diatomite: Isotherm, Kinetic, and Thermodynamic Analysis

Abstract

Heavy metal pollution remains one of the major environmental challenges due to the persistence and toxicity of metals such as Pb(II). This study investigates the potential of natural diatomite from Mugaldzhar, Kazakhstan, as a low-cost and sustainable sorbent for lead removal from aqueous solutions. The effects of key parameters, including sorbent dosage, particle size, contact time, temperature, and initial Pb(II) concentration, were systematically examined. Adsorption experiments revealed a maximum adsorption capacity of 74.9 mg/g at 45 °C and an initial Pb(II) concentration of 800 mg/L. The adsorption behavior followed the pseudo-second-order kinetic model, indicating a chemisorption mechanism, while isotherm analysis showed a transition from Langmuir to Freundlich type with increasing temperature. Thermodynamic data confirmed the spontaneous and endothermic nature of the process. These results demonstrate that unmodified natural diatomite exhibits high efficiency for Pb(II) removal, emphasizing its suitability as an eco-friendly and cost-effective material for water purification and environmental remediation.

1. Introduction

Heavy metal pollution is one of the most pressing environmental problems caused by industrialization and human activity. Metals such as lead (Pb), mercury (Hg), cadmium (Cd), and arsenic (As) are highly toxic and can accumulate in living organisms. Their main sources include industrial effluents, mining, vehicle emissions, pesticides, and improper waste disposal. These contaminants affect water, soil, and air quality, disrupt ecosystems, and pose serious health risks to humans [1]. Long-term exposure to heavy metals may lead to neurological disorders, kidney and liver diseases, and even cancer [2,3,4]. Therefore, developing reliable and cost-effective methods for removing heavy metals from water is an urgent environmental priority. A variety of approaches have been explored for heavy metal removal, including physicochemical, biological, and nanotechnological techniques. Among them, adsorption has proven to be one of the simplest, most effective, and economical methods [5,6,7]. It allows efficient removal of metal ions even at low concentrations and can be easily applied at both laboratory and industrial scales [8,9,10,11]. Compared to chemical or biological methods, adsorption requires less energy, produces minimal secondary waste, and allows for sorbent regeneration, making it attractive for sustainable water treatment [12,13,14,15].

Natural sorbents such as zeolites, clays, activated carbon, and diatomite are widely used for adsorption processes due to their availability and low cost [16,17,18,19,20]. Among these materials, diatomite—a sedimentary rock formed from fossilized diatom shells—is particularly interesting because of its highly porous structure, large specific surface area, and chemical stability. These properties enable it to adsorb metal ions through ion exchange, electrostatic interaction, and surface complexation [21]. In addition, diatomite is non-toxic, easily regenerated, and environmentally friendly, which further increases its practical value in water purification [22].

To enhance adsorption efficiency, many studies have focused on surface modification of diatomite. For example, Danh et al. (2023) demonstrated that manganese oxide–modified diatomite (MnO₂/diatomite) effectively removes Pb(II) ions under optimal pH conditions [23], while Mansour et al. (2025) showed that citric-acid-treated diatomite significantly improves adsorption of Pb, Cu, Al, Ni, As, and Cd ions [24]. Such modifications increase the number of active sites and alter the surface charge, leading to higher adsorption capacities [25]. However, these modification steps often increase the cost and complexity of water treatment. In this context, the use of unmodified natural diatomite remains an attractive alternative. Identifying the conditions that allow raw diatomite to achieve high adsorption performance without surface treatment is of great importance for sustainable and low-cost water purification technologies. Moreover, diatomite can also be viewed as a naturally occurring composite material composed mainly of amorphous silica with minor mineral inclusions. Its hierarchical porous framework and mechanical stability make it promising for incorporation into composite adsorption systems designed for environmental remediation.

The present study investigates the adsorption behaviour of natural diatomite from the Mugaldzhar deposit (Kazakhstan) toward Pb(II) ions in aqueous solutions. The work aims to determine the optimal conditions for adsorption and to demonstrate that raw diatomite can achieve high Pb(II) removal efficiency without modification. These results highlight the potential of Kazakhstani diatomite as a cost-effective and environmentally sustainable sorbent for heavy metal removal from wastewater.

2. Experimental

2.1. Materials

Diatomite rock was obtained from the Mugaldzhar region of Kazakhstan and subsequently ground with a mortar to a particle size of approximately 180 nm. Lead nitrate [Pb(NO₃)₂] was obtained from Labopharma (Kazakhstan) and used without further purification for the preparation of stock Pb²⁺ solutions as the model heavy metal contaminant.

2.2. Characterization of Natural Diatomite

Natural diatomite was characterized by several instrumental techniques to identify its structure and usability as an adsorbent.

Thermogravimetric analysis (TGA) was performed using a Labsys Evo analyzer (Setaram, Caluire-et-Cuire, Lyon, France) at a heating rate of 20 °C·min⁻¹ under either nitrogen atmosphere, with a gas flow rate of 20 mL·min⁻¹, to evaluate the thermal stability of the soot sample. Approximately 10 ± 0.3 mg of the sample was placed in a 100 µL alumina crucible and inserted into the instrument. Prior to the heating program, the system was held at 25 °C for 35 min under nitrogen flow to ensure thermal equilibrium within the furnace.

X-ray diffraction (XRD) analysis of the samples was carried out using a MiniFlex 300/600 diffractometer (Rigaku, Tokyo, Japan) equipped with a D/teX Ultra detector. The operating conditions were 40 kV and 15 mA with Cu Kα radiation (Kβ filter applied). The diffraction patterns were recorded in the 2θ range of 3–90° with a step size of 0.020° and a continuous scan speed of 10°/min in θ–2θ geometry. An incident slit of 1.250°, a length-limiting slit of 5.0 mm, and receiving slits of 6.0 mm were used. All measurements were performed under standard laboratory conditions.

Nitrogen adsorption–desorption analysis was performed using a static multi-purpose gas adsorption analyzer, Henan Mingguan SSA-4000 (serial no. MGSI003250205BET, Henan Mingguan, Zhengzhou, Henan, China). The samples were pre-degassed at 300 °C for 3 h prior to measurement. Nitrogen (N₂) at liquid-nitrogen temperature was used as the adsorbate, and adsorption/desorption isotherms were recorded in the standard mode. All calculations (specific surface area by the BET method) were performed using the instrument’s built-in software.

The morphology of the samples was examined using a Quanta 200i 3D scanning electron microscope (FEI, Hillsboro, OR, USA). The imaging was performed at an accelerating voltage of 30 keV with a working distance of approximately 10 mm. All measurements were carried out in high vacuum mode. The sizes of particles and pores of the powders were determined with the help of SEM images. Energy-dispersive X-ray spectroscopy (EDS) analysis was performed on a JSM-6490LA (JEOL, Akishima, Tokyo, Japan) scanning electron microscope equipped with an EDS detector. The measurements were carried out at an accelerating voltage of 10 kV with a probe current of 1.0 nA. The energy range was set from 0 to 20 keV in pulse height analyser mode (T3). Spectra were collected for 50 s live time (real time 50.2 s) with a dead time of 0% and a counting rate of approximately 81 counts per second (cps).

2.3. Batch Adsorption Experiments

All reagents employed in the batch adsorption studies were of analytical grade and therefore used without any additional purification. A stock solution of Pb(II) with an initial concentration of 1000 mg/L was prepared by dissolving Pb(NO₃)₂ in double-deionised water, and working solutions of different concentrations were obtained through dilution. Since the influence of pH was beyond the scope of this research, the Pb(II) solution was maintained at its natural pH (5.2–5.4) throughout all experiments to minimize chemical modification and to reflect natural adsorption conditions. It is well known that pH effects the adsorption capacity by affecting the degree of ionization and surface charge of the adsorbent as well as the speciation and solubility of the metal ions in solution. And changing pH manually or artificially can influence both the surface charge of the adsorbent and the ionic speciation of the adsorbate, leading to complex and non-intrinsic adsorption behaviors. Therefore, the adsorption experiments were performed without adjusting the pH of the solutions in order to preserve the inherent chemical conditions of the system and to adsorbent’s natural affinity and adsorption performance under realistic aqueous conditions.

The adsorption experiments were carried out in batch mode using a shaker set at 200 rpm, while the temperature was controlled at predetermined levels. After the designated contact period, the suspensions were filtered, and the residual Pb(II) concentration was quantified using an atomic absorption spectrometer (Analyst 800, Perkin Elmer, Waltham, MA, USA).

To assess the adsorption behaviour, the impact of various parameters was examined, including adsorbent dosage (1–10 g/L), particle size (180–700 μm), initial ion concentration (300–800 mg/L), contact time (up to 600 min), and temperature (25–45 °C). The adsorption capacity, both at a given time (q_t) and at equilibrium (q_e), was calculated according to the following equations.

$${\mathrm{q}}_{\mathrm{t}}={\displaystyle \frac{({\mathrm{C}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{t}})}{\mathrm{w}}}\times \mathrm{V}$$

(1)

$${\mathrm{q}}_{\mathrm{e}}={\displaystyle \frac{({\mathrm{C}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{e}})}{\mathrm{w}}}\times \mathrm{V}$$

(2)

In the meantime, the percent removal was obtained as follows:

$$\mathrm{A}\mathrm{d}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{p}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{\%})={\displaystyle \frac{({\mathrm{C}}_{\mathrm{i}}-{\mathrm{C}}_{\mathrm{e}})}{{\mathrm{C}}_{\mathrm{i}}}}\times 100$$

(3)

Here, C_i denotes the initial concentration of metal ions (mg/L), C_e is the concentration at equilibrium (mg/L), C_t represents the concentration at a given time t (mg/L), V is the solution volume (L), and w corresponds to the mass of the adsorbent (g).

2.4. Isotherm, Kinetic, and Thermodynamic Analysis of Adsorption Data

2.4.1. Equilibrium Modelling

Adsorption isotherms provide insight into the nature of interactions between solute molecules and the adsorbent surface, describing the relationship between adsorbate concentration in solution and the extent of its accumulation on the surface at a given temperature. Achieving an optimal correlation for the equilibrium curves is necessary to design an effective sorption system. In this work, the adsorption behaviour of heavy metals was evaluated using the Langmuir, Freundlich, Dubinin-Radushkevich (D-R), and Temkin isotherm models.

The Langmuir isotherm assumes that adsorption occurs through physical and/or chemical interactions at specific active sites on the adsorbent surface. Its linearized form can be expressed as:

$${\displaystyle \frac{{\mathrm{C}}_{\mathrm{e}}}{{\mathrm{q}}_{\mathrm{e}}}}={\displaystyle \frac{1}{{\mathrm{q}}_{\mathrm{m}}{\mathrm{K}}_{\mathrm{L}}}}+{\displaystyle \frac{{\mathrm{C}}_{\mathrm{e}}}{{\mathrm{q}}_{\mathrm{m}}}}$$

(4)

Here, q_m represents the maximum monolayer adsorption capacity (mg/g), while K_L denotes the Langmuir constant related to adsorption affinity (L/mg) [26,27]. The interaction strength between adsorbent and adsorbate can also be evaluated through the dimensionless separation factor (R_L), which is determined using the following equation:

$${\mathrm{R}}_{\mathrm{L}}={\displaystyle \frac{1}{1+{\mathrm{K}}_{\mathrm{L}}{\mathrm{C}}_{\mathrm{o}}}}$$

(5)

Here, C₀ refers to the maximum initial concentration of the adsorbate in solution (mg/L). The value of R_L reflects the nature of the adsorption process, indicating whether the isotherm is unfavourable (R_L > 1), linear (R_L = 1), favourable (0 < R_L < 1), or irreversible (R_L = 0).

Unlike the Langmuir model, the Freundlich isotherm assumes the occurrence of multilayer adsorption on a heterogeneous adsorbent surface [28]. Its linearized form is expressed as:

$$\ln {\mathrm{q}}_{\mathrm{e}}=\ln {\mathrm{K}}_{\mathrm{F}}+{\displaystyle \frac{1}{\mathrm{n}}}\ln {\mathrm{C}}_{\mathrm{e}}$$

(6)

Here, K_F(mg/g) is a constant related to the adsorption capacity, while n is an empirical parameter.

The Dubinin-Radushkevich (D-R) isotherm, originally developed to describe the sorption of subcritical vapours onto microporous solids by a pore-filling mechanism [29], has also been applied to adsorption studies of aqueous pollutants. This model assumes that the adsorption potential is not uniform but varies across a heterogeneous surface [30]. The linearized form of the D-R isotherm is given as:

$$\ln {\mathrm{q}}_{\mathrm{e}}=\ln {\mathrm{q}}_{\mathrm{m}}-\mathrm{\beta }{\mathrm{\epsilon }}^2$$

(7)

where β is a constant related to the adsorption energy (mol²/kJ²), q_m is the theoretical saturation capacity, and ε is the Polanyi potential. The Polanyi potential term can be calculated as given below:

$$\mathrm{\epsilon }=\mathrm{R}\mathrm{T}\left[1+{\displaystyle \frac{1}{{\mathrm{C}}_{\mathrm{e}}}}\right]$$

(8)

where R is the gas constant (J/mol K) and T is the absolute temperature (K). And the β constant of the D-R equation gives the mean free energy E (kJ/mol) of adsorption per molecule of the adsorbate when it is transferred to the surface of the solid from infinity in the solution, and can be calculated by the following equation:

$$\mathrm{E}={\displaystyle \frac{1}{\sqrt{2\mathrm{\beta }}}}$$

(9)

The Temkin isotherm model [31,32], which was ultimately applied in this study, accounts for the influence of indirect interactions between the adsorbent and adsorbate, as well as the heterogeneous distribution of binding energies on the sorbent surface. Its linearized expression can be written as:

$${\mathrm{q}}_{\mathrm{e}}=\mathrm{B}\ln {\mathrm{K}}_{\mathrm{T}}+\mathrm{B}\ln {\mathrm{C}}_{\mathrm{e}}$$

(10)

To explore the adsorption isotherms, the same mass of diatomite was placed in different conical flasks containing 50 mL of heavy metal ion solution at concentrations of 100, 300, 500, 600 and 800 mg/L, respectively. Adsorption was examined at three different temperatures (25, 35, and 45 °C) with a fixed contact time of 10 h.

2.4.2. Kinetic Modelling

The batch adsorption results were further analyzed using the pseudo-first-order, pseudo-second-order, intraparticle diffusion, and Elovich kinetic models to investigate the adsorption mechanism and estimate the kinetic parameters. The pseudo-first-order model, which is commonly used to describe adsorption based on solid sorption capacity, assumes that the uptake of a metal ion occurs at a single active site [33]. The linearized form of Lagergren’s pseudo-first-order rate equation is expressed as:

$$\log ({\mathrm{q}}_{\mathrm{e}}-{\mathrm{q}}_{\mathrm{t}})=\mathrm{l}\mathrm{o}\mathrm{q}({\mathrm{q}}_{\mathrm{e}})-{\displaystyle \frac{{\mathrm{k}}_1\mathrm{t}}{2.303}}$$

(11)

where k₁ is the pseudo-first-order rate constant (1/min).

The pseudo-second-order kinetic model [34], which relates adsorption rate to the square of the adsorption capacity, can be written as:

$${\displaystyle \frac{\mathrm{t}}{{\mathrm{q}}_{\mathrm{t}}}}={\displaystyle \frac{1}{{\mathrm{k}}_2{{\mathrm{q}}_{\mathrm{e}}}^2}}+{\displaystyle \frac{1}{{\mathrm{q}}_{\mathrm{e}}}}\mathrm{t}$$

(12)

Here, k₂ represents the pseudo-second-order rate constant (g/mg·min).

Since the pseudo-first- and pseudo-second-order models do not adequately describe diffusion effects or rate-limiting steps in sorbate transport, the intraparticle diffusion model [35] is often applied for this purpose. Its mathematical form is expressed as:

$${\mathrm{q}}_{\mathrm{t}}={\mathrm{k}}_{\mathrm{p}}\sqrt{\mathrm{t}}+\mathrm{C}$$

(13)

where k_p denotes the intraparticle diffusion rate constant (mg/g·min^1/2), and C corresponds to the intercept of the model plot. When intraparticle diffusion governs the adsorption process, the plot should appear linear; moreover, if the line passes through the origin, intraparticle diffusion can be considered the sole rate-controlling step. A deviation from the origin implies the presence of boundary layer resistance, indicating that diffusion within particles is not the only limiting mechanism. In such cases, other kinetic models may also contribute to the overall transport resistance of sorbate molecules [36].

The Elovich model [37] is often applied when the adsorption mechanism involves chemisorption, typically characterized by interactions between adsorbate ions and surface sites through a second-order process. Its linearized form is expressed as:

$${\mathrm{q}}_{\mathrm{t}}={\displaystyle \frac{1}{\mathrm{\beta }}}\ln (\mathrm{\alpha }\mathrm{\beta })+{\displaystyle \frac{1}{\mathrm{\beta }}}\ln \mathrm{t}$$

(14)

The adsorption kinetics were determined by immersing diatomite of the same mass in different conical flasks holding heavy metal ion solution at 45 °C. The batch adsorption operation at duty was to determine the adsorption capacity of heavy metal ions absorbed at different contact times until equilibrium had been established.

2.4.3. Thermodynamic Modelling

Thermodynamic parameters such as Gibbs free energy change (ΔG°), enthalpy change (ΔH°), and entropy change (ΔS°) are commonly evaluated to assess the influence of temperature and to determine the spontaneity of the adsorption process. The change in Gibbs free energy can be calculated using the following relation:

$$\mathrm{\Delta }{\mathrm{G}}^{\mathrm{o}}=-\mathrm{R}\mathrm{T}\ln {\mathrm{K}}_{\mathrm{L}}$$

(15)

The equilibrium constant (K_L) can be determined as:

$${\mathrm{K}}_{\mathrm{L}}={\displaystyle \frac{{\mathrm{q}}_{\mathrm{e}}}{{\mathrm{C}}_{\mathrm{e}}}}$$

(16)

The relationship among ΔG°, ΔH°, and ΔS° is expressed as follows:

$$\mathrm{\Delta }{\mathrm{G}}^{\mathrm{o}}=\mathrm{\Delta }{\mathrm{H}}^{\mathrm{o}}-\mathrm{T}\mathrm{\Delta }{\mathrm{S}}^{\mathrm{o}}$$

(17)

Equation (17) can be transformed into the following linear expression to determine the thermodynamic parameters:

$$\ln {\mathrm{K}}_{\mathrm{L}}=-{\displaystyle \frac{\mathrm{\Delta }{\mathrm{G}}^{\mathrm{o}}}{\mathrm{R}\mathrm{T}}}=-{\displaystyle \frac{\mathrm{\Delta }{\mathrm{H}}^{\mathrm{o}}}{\mathrm{R}\mathrm{T}}}+{\displaystyle \frac{\mathrm{\Delta }{\mathrm{S}}^{\mathrm{o}}}{\mathrm{R}}}$$

(18)

3. Results and Discussion

3.1. The Characteristics of Natural Diatomite

Natural diatomite is composed of multiple genera and species, displaying a range of morphologies including feathery, centric, lamellar, and needle-like forms. To gain insight into its structural and textural characteristics, the sample was examined using optical microscopy, and representative micrographs are presented in Figure 1. The mineralogical analysis of the raw diatomite revealed a complex composition, consisting primarily of diatom skeletons (frustules), along with clay minerals such as kaolinite and montmorillonite, quartz, carbonates, and organic matter. These observations highlight the heterogeneous nature of natural diatomite, which contributes to its high surface area, porosity, and potential effectiveness as an adsorbent in water purification applications.

Figure 1. Optical images of the natural diatomite sample.

From the optical microscopy images (Figure 1), the rock samples show intact, undamaged structures of diatomaceous frustules, as well as a remarkable diversity of diatom forms, morphologies, and pore architectures, which include several of the most common examples of diatom forms.

Under a nitrogen atmosphere, the diatomite thermogram (Figure 2) shows a gradual mass loss from room temperature to 1000 °C. The first step between ~50–150 °C caused about 3–4% weight loss, mainly due to the evaporation of physically adsorbed water and the release of weakly bound surface hydroxyl groups from the silica structure. From ~150 to 600 °C, a slower and continuous weight loss of ~6% is observed, mainly due to the gradual removal of silanol groups (dehydroxylation of opal-A) and the pyrolysis of minor organics under nitrogen. Above ~800 °C, the TG curve levels off, showing the high thermal stability of the silica framework. The dTG curve confirms these events with a sharp peak near 100 °C for moisture loss and weaker, broad signals between 200–600 °C linked to bound-water release and trace organics, while no major peaks appear at higher temperatures. Overall, the total mass loss (~10%) is dominated by water release, with little contribution from organics, and the high-temperature changes mainly reflect structural densification and rearrangement of the amorphous silica network, with possible polymorphic transitions. The DTA curve also showed an endothermic event below 150 °C associated with water evaporation, followed by broad thermal effects mainly after 400 °C that suggest structural rearrangements of the amorphous silica network and possible transformation into more crystalline forms such as cristobalite or tridymite.

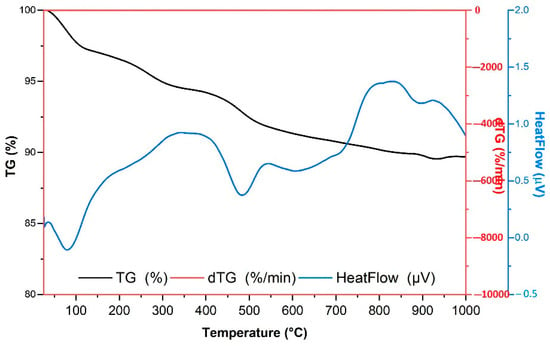
Figure 2. TG, dTG, and DTA curves of the natural diatomite sample.

Figure 3 presents the X-ray diffraction (XRD) profiles of the natural diatomite sample and the Pb²⁺-loaded diatomite after adsorption. The crystalline composition of the material is predominantly represented by the α-quartz (SiO₂) phase, with the most intense diffraction peak corresponding to an interplanar spacing of d ≈ 3.35 Å. Additional reflections at d ≈ 2.49 Å and 4.26 Å indicate the presence of an amorphous silica phase. Weak signals correspond to minor amounts of clay minerals—illite–montmorillonite and kaolinite [Al₂(Si₂O₅)(OH)₄]—confirming that the sample contains both crystalline and amorphous silica phases. The average crystallite size, calculated using the Scherrer equation, is approximately 164 nm, indicating a moderate crystalline structure of the diatomite.

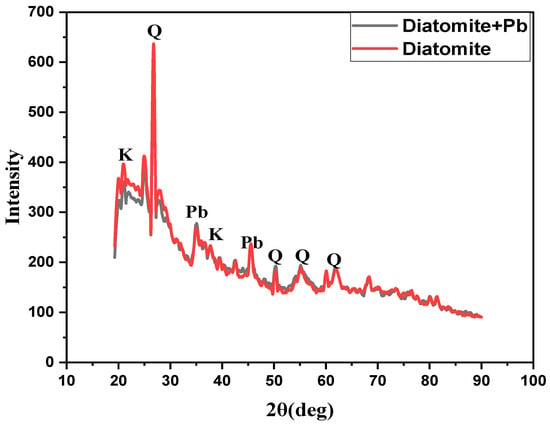
Figure 3. XRD patterns of pristine and Pb²⁺-loaded diatomite. Identified phases: α-quartz (SiO₂, PDF 01-079-6236), kaolinite (Al₂Si₂O₅(OH)₄, PDF 01-083-4643), and metallic lead (Pb, PDF 01-071-6512).

The diffraction patterns of pristine and Pb²⁺-loaded diatomite exhibit similar features, suggesting that the adsorption of lead ions does not significantly alter the crystalline structure of the material. Both samples display intense peaks of α-quartz (SiO₂, ICDD PDF 01-079-6236) at 2θ ≈ 20.9°, 26.7°, 36.6°, and 50.2°, along with weak reflections corresponding to amorphous silica. Additional peaks observed at 2θ ≈ 30.9°, 32.8°, 35.1°, 45.7°, and 54.9° are attributed to metallic lead (Pb, ICDD PDF 01-071-6512), confirming the fixation and partial reduction of Pb²⁺ ions on the diatomite surface. Peaks at 12.2° and 24.5° correspond to kaolinite (Al₂Si₂O₅(OH)₄, ICDD PDF 01-083-4643). The absence of new diffraction peaks and the lack of significant shifts in quartz reflections indicate that Pb²⁺ ions are mainly adsorbed on the surface or within the pores of diatomite, without forming new crystalline lead compounds detectable by XRD.

The specific surface area measured for natural diatomite was measured using the dynamic nitrogen adsorption–desorption method with a Sorbtometer instrument (Figure 4). The BET analysis results are summarized in Table 1. The pristine diatomite exhibited a specific surface area of 43 m² g⁻¹, with average pore diameters of 1.36 nm (adsorption) and 1.26 nm (desorption). The BET analysis was also carried out for the diatomite sample after Pb (II) adsorption to observe the changes that occurred during the batch sorption process. For the dried diatomite sample, which was used during the highest Pb (II) removal experimental conditions, the specific surface area decreased to 38 m² g⁻¹, while the average pore diameters slightly decreased to 1.20 nm (adsorption) and 1.19 nm (desorption). These reductions indicate partial pore filling and surface modification of the diatomite structure as a result of lead uptake.

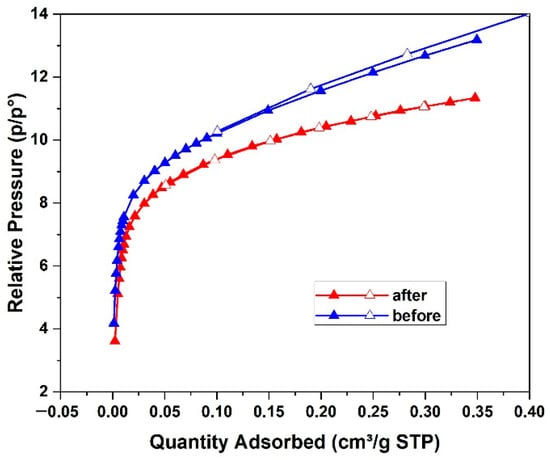
Figure 4. Nitrogen adsorption–desorption isotherms of natural diatomite before (blue), and after (red) Pb (II) removal.

Table 1. Results of the BET analysis of diatomite samples.

Samples	Specific Surface Area, m2 g−1	Average Adsorption Pore Diameter, nm	Average Desorption Pore Diameter, nm
Natural diatomite	43	1.36	1.26
Diatomite after adsorption	38	1.20	1.19

SEM analysis revealed that pristine diatomite exhibits a clean surface characterized by open pores and interconnected channels, with micropores of diverse shapes and sizes clearly visible (Figure 5). A high density of regularly ordered pores with diameters of 1–3 μm was observed, typically arranged in parallel sets and forming a honeycomb-like architecture. In addition, macropores of approximately 0.9 μm were also detected. These features highlight the heterogeneous nature of the diatomite surface, including localized clusters and partially “plugged” pores, which reflect the natural variability of its composition. After Pb²⁺ adsorption, pronounced morphological alterations were evident compared to the pristine material. Whereas the original diatomite displayed a porous and relatively smooth surface, the Pb²⁺-loaded sample exhibited partial pore filling, a rougher surface texture, and the deposition of fine particles on the pore walls and external surface. These morphological changes confirm the successful immobilization of Pb²⁺ ions within the diatomite matrix and the partial blockage of its pore system, thereby supporting its effectiveness as a sorbent for Pb²⁺ removal.

Figure 5. SEM images of diatomite samples before (a) and after (b) Pb(II) adsorption under the described experimental conditions.

To confirm the adsorption of Pb²⁺ ions on the diatomite surface, an energy-dispersive X-ray (EDX) analysis with elemental mapping was carried out. The results showed that the main elements of the pristine material are oxygen (O—58.4 wt %), silicon (Si—33.8 wt %), and aluminum (Al—4.8 wt %) (Figure 6). After Pb²⁺ adsorption, a Pb signal of about 3.0 wt % was detected, confirming the successful fixation of lead ions on the diatomite surface.

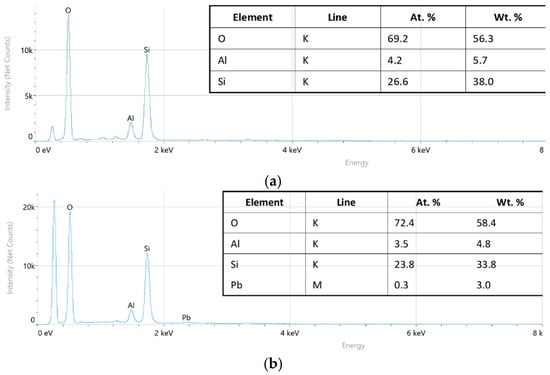
Figure 6. Energy-dispersive X-ray spectroscopy of diatomite samples before (a) and after (b) Pb(II) adsorption.

The elemental maps (SEM-mapping) reveal a uniform distribution of Si and O corresponding to the silica matrix, along with localized Pb-enriched regions indicating adsorption sites (Figure 7). These Pb-rich zones suggest that lead ions are immobilized within the pores and microstructural defects of diatomite. The obtained results are consistent with the XRD data, confirming that Pb²⁺ adsorption does not lead to the formation of new crystalline phases but occurs mainly on the sorbent surface.

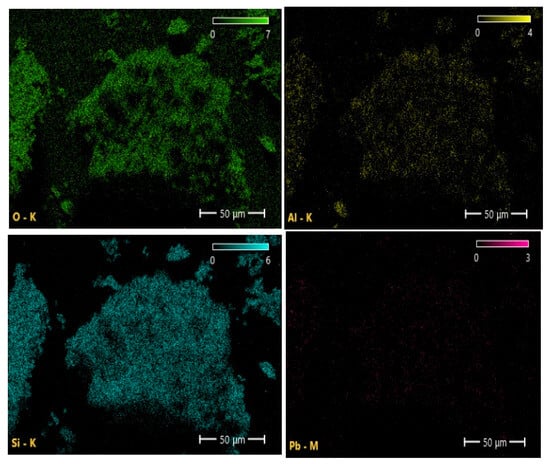
Figure 7. Elemental maps of Si, O, Al, and Pb, indicating homogeneous Si–O–Al distribution and localized Pb enrichment zones.

3.2. Pb (II) Removal from Water by Natural Diatomite

The effects of adsorbent dose and particle size on the removal efficiency and adsorption capacity of diatomite toward Pb (II) ions are illustrated in Figure 8. The results indicate that increasing the diatomite dose enhances overall Pb (II) removal efficiency by providing a greater number of active sites for adsorption. However, the amount of Pb (II) adsorbed per unit mass of diatomite (q_t) decreases at higher doses, likely due to site saturation, particle aggregation, or a reduced adsorbate-to-adsorbent ratio. Regarding the influence of particle size, the highest adsorption performance—both in terms of % removal and q_t was observed with the smallest particle size (180 μm), which offers a higher surface area-to-volume ratio. This increases the accessibility of active sites and promotes more efficient adsorption. In contrast, larger particle sizes result in reduced surface area, thereby limiting interaction with Pb (II) ions and diminishing overall adsorption efficiency.

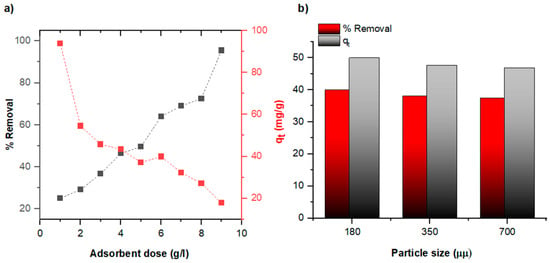
Figure 8. Pb (II) adsorption onto diatomite: (a) effect of adsorbent dosage and (b) effect of particle size (Contact time: 3 h, Initial heavy metal concentration 500 mg/L).

Figure 9 shows the adsorption capacity of diatomite over time at different initial Pb(II) concentrations (300, 500, and 800 ppm) and temperatures (25 °C, 35 °C, and 45 °C). The results indicate a rapid increase in adsorption capacity during the initial stages, followed by a plateau-like region. This behavior indicates a two-phase adsorption mechanism: an initial rapid uptake due to the abundance of available active sites, followed by a slower phase as these sites become gradually saturated. Equilibrium was nearly reached after 60 min; however, a slight increase continued with extended contact time, particularly at higher concentrations. At each temperature, higher initial Pb(II) concentrations resulted in greater adsorption capacities, reflecting an enhanced driving force for mass transfer at high ion concentrations. Conversely, the adsorption capacity increased slightly as the temperature increased from 25 °C to 45 °C across all concentration levels, suggesting that lower temperatures reduced the affinity of Pb(II) ions for the adsorbent. This temperature-dependent increase in adsorption performance may support the involvement of a chemisorption mechanism, with thermodynamic favorability increasing at elevated temperatures. The highest adsorption capacity, 74.9 mg/g, was achieved at an initial Pb(II) concentration of 800 mg/L, a temperature of 45 °C, and a contact time of 600 min.

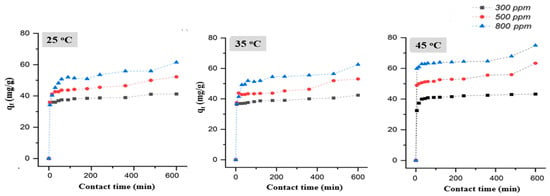
Figure 9. Effect of initial Pb(II) concentration, temperature and contact time on adsorption.

Table 2 summarizes the isotherm modeling results for Pb(II) adsorption onto diatomite across different temperatures. According to the data, the Freundlich isotherm provided a better fit at higher temperatures (35 °C and 45 °C), while the Langmuir isotherm exhibited the best fit at the lowest temperature (25 °C). Figure 10 also illustrates the temperature-dependent comparison of the Langmuir and the Freundlich isotherm models. Results indicated predominantly monolayer adsorption at lower temperatures, whereas adsorption shifted toward heterogeneous and possibly multilayer interactions at higher temperatures. Such a transition reflects the enhanced mobility of Pb²⁺ ions and the activation of diverse surface sites with increasing temperature, consistent with the endothermic nature of the process. According to the Langmuir isotherm results, the maximum adsorption capacity (q_m) of diatomite increased with increasing temperature (from 54.05 to 65.78 mg/g), also suggesting an endothermic adsorption process and an increase in adsorption efficiency at higher temperatures. Reduced kinetic energy at lower temperatures likely promotes the occupation of the most accessible active sites, consistent with the monolayer adsorption assumptions of the Langmuir model. In contrast, at the higher temperatures of the study, increased thermal energy enhances surface heterogeneity and promotes ion redistribution, and this condition may allow for multilayer adsorption or binding at lower-energy sites. The greater molecular mobility at higher temperatures enabled ions to overcome energy barriers and interact with a broader range of adsorption sites, including those with weaker affinities. Consequently, the adsorption process becomes more heterogeneous, aligning more closely with the assumptions of the Freundlich isotherm model. According to the Freundlich model, strong adsorption affinity and favorable interactions were found to exist between multilayer Pb²⁺ ions and the diatomite surface.

Table 2. Isotherm constants for adsorption at different temperatures.

Temperature	25 °C	35 °C	45 °C
Langmuir
qm (mg/g)	54.05	54.06	65.78
KL (L/mg)	0.016	0.019	0.020
R2	0.9956	0.9869	0.9911
Freundlich
KF ((mg/g) (L/mg)1/n)	9.56	11.51	8.66
N	2.25	2.45	2.15
R2	0.9922	0.9998	0.9976
Dubinin-Radushkevich
qm (mg/g)	44.80	45.50	52.15
Β	1.02 × 10−3	1.09 × 10−3	1.29 × 10−3
E	101.1	129.0	121.2
R2	0.8936	0.8882	0.8991
Temkin
B	8.79	8.84	11.40
KT	0.3416	0.9808	0.341
R2	0.9873	0.9805	0.9901

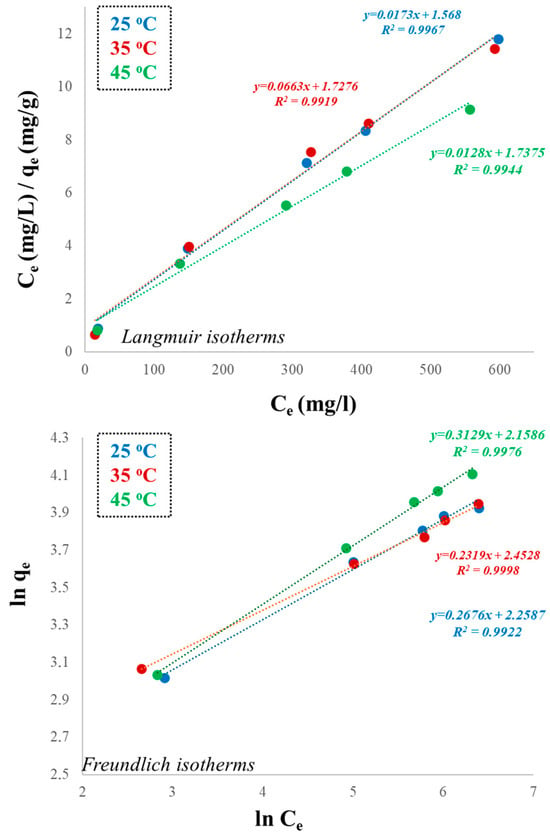
Figure 10. Temperature-dependent comparison of Langmuir and Freundlich isotherms.

To elucidate the rate and mechanism of Pb²⁺ adsorption onto diatomite, the experimental kinetic data were analyzed using common kinetic models. The kinetic analysis of Pb(II) adsorption onto diatomite revealed that the process is best described by the pseudo-second-order model as indicated by its highest regression coefficient (0.9999) (Table 3). Also, kinetic plots are given in Supplementary Material (Figure S1). This model assumes that the rate-limiting step is chemical adsorption (chemisorption), involving valence forces through the sharing or exchange of electrons between the adsorbent and the adsorbate. When chemisorption dominates, the pseudo-second-order model generally provides a more accurate fit to experimental data, as it relates the adsorption rate to the number of active sites available on the adsorbent surface rather than solely to the adsorbate concentration. The rate constant of 0.0316 g/mg·min indicates a moderate adsorption rate. From the kinetic point of view, the results point out that the adsorption of Pb²⁺ ions onto diatomite is governed by chemisorption, as found by the fit of the pseudo-second-order kinetic model, which suggests that chemical interactions between Pb²⁺ ions and the active sites on the diatomite surface control the adsorption process.

Table 3. Kinetic parameters for adsorption (at 45 °C and 800 mg/L initial heavy metal concentration).

Pseudo-First Order
k1	0.0559
qe	4.48
R2	0.8691
Pseudo-Second Order
k2	0.0316
qe	63.7
R2	0.9999
Intraparticle Diffusion
kp	0.6621
C	58.49
R2	0.9271
Elovich
A	13.051
Β	0.0372
R2	0.9951

Although the Elovich and intraparticle diffusion models yielded relatively high determination coefficients (R²), their predictive accuracy and consistency were inferior to those of the pseudo-second-order model. The highest correlation coefficient (R² = 0.9999) obtained for the pseudo-second-order model demonstrated excellent agreement with the experimental data, confirming its suitability for describing the adsorption behavior. This strong correlation further confirms that chemisorption is the dominant mechanism governing Pb(II) uptake onto the diatomite surface under the studied conditions. This strong correlation indicates that chemisorption is the dominant mechanism, where the rate-limiting step is governed by chemical interactions involving valence forces through electron sharing or exchange between the adsorbent and adsorbate, rather than by physical diffusion or simple surface adsorption.

The thermodynamic parameters of Pb(II) adsorption onto diatomite are given in Table 4. The negative values of Gibbs free energy change (ΔG°), ranging from −19.17 to −19.39 kJ/mol across the studied temperatures between 25 and 45 °C, confirmed the spontaneity of the adsorption process. Moreover, the increasing value of ΔG° with temperature suggested that spontaneity was enhanced at higher temperatures. The enthalpy change (ΔH°) was calculated to be 15.9 kJ/mol, further confirming the endothermic nature of the adsorption. Additionally, the positive entropy change value (ΔS° = +110.4 J/mol·K) implied an increase in randomness at the adsorbent–heavy metal solution interface, which may be attributed to desolvation of Pb(II) ions or structural reorganization of the adsorbent surface during binding. Overall, the thermodynamic parameters for Pb(II) adsorption onto diatomite indicate a spontaneous and endothermic process, accompanied by increasing disorder at the solid–liquid interface. These findings support a mechanism dominated by chemisorption, driven by both energetic favorability and enhanced interfacial entropy.

Table 4. Thermodynamic parameters of adsorption.

T (°C)	∆G° (kJ/mol)	∆H° (kJ/mol)	∆S° (J/mol K)	R2
20	–19.17	15.9	110.4	0.9937
30	–19.35
40	–19.39

Table 5 presents a comparison of the performance of sorbents for Pb(II) adsorption. Among the diatomite research conducted before, the highest adsorption capacity was achieved in our study. One possible reason for the higher adsorption capacity observed in this study is the origin and intrinsic characteristics of the diatomite sample, since it is well known that natural diatomites differ considerably in their mineral composition, including variations in silica content, as well as the presence of clays, organic matter, or carbonate impurities. In addition to diatomite properties such as surface area, porosity, functional groups, pretreatment methods, and adsorption conditions (pH, temperature, initial concentration), which collectively promote more effective Pb²⁺ binding. Also, a comparison with different types of adsorbents showed that diatomite is a promising adsorbent for heavy metal removal, with its practical applicability being maximized under optimized operating conditions.

Table 5. Comparison of the performance of sorbents for Pb(II) adsorption.

Adsorbent	Heavy Metal	Adsorption Capacity (mg/g)	Isotherm Fitting	Kinetic Model	Temperature Dependency	Reference
Diatomite (Turkey)	Pb(II)	26	Freundlich	Pseudo-2nd order	Endothermic	[38]
Diatomite (Iran)	Pb(II)	25.01	Langmuir	Pseudo-2nd order	Endothermic	[39]
Calcined diatomite (China)	Pb(II)	47.96	Langmuir	Pseudo-2nd order	N/A	[40]
Perlite	Pb(II)	13.39	Langmuir & Freundlich	Pseudo-2nd order	N/A	[41]
Natural calcite	Pb(II)	19.92	Langmuir	Pseudo-2nd order	Endothermic	[42]
Commercial Activated Carbon	Pb(II)	16.84	Langmuir & Freundlich	Pseudo-2nd order	Endothermic	[43]
Nano-scale zero valent iron (nZVI)	Pb(II)	50.31	Langmuir	Pseudo-2nd order	N/A	[44]
Magnetic biochar (MBC)	Pb(II)	27	Langmuir	Pseudo-2nd order	Endothermic	[45]
Diatomite (Kazakhstan)	Pb(II)	74.9	Langmuir & Freundlich	Pseudo-2nd order	Endothermic	This study

N/A: not available.

4. Conclusions

This study confirms that natural diatomite is an efficient and sustainable sorbent for the removal of Pb(II) from aqueous solutions. The adsorption performance was affected by operational factors such as adsorbent dosage, particle size, temperature, and initial Pb(II) concentration, with the maximum capacity (74.9 mg/g) obtained at 45 °C, demonstrating that higher temperatures favor the process. Kinetic and isotherm analyses indicated that chemisorption plays a dominant role, with adsorption behavior best fitted to the pseudo-second-order model and the Freundlich isotherm at elevated temperatures. Thermodynamic evaluation showed that the adsorption is both spontaneous and endothermic. Post-adsorption structural and morphological characterization revealed evidence of pore filling, roughened surface texture, and fine Pb-containing deposits on the diatomite matrix, validating its role as an effective sorbent. This study demonstrates the potential of diatomite as a naturally abundant, porous silica material for efficient heavy metal adsorption. Its low cost, environmental compatibility, and scalability make it a promising candidate for water purification applications. Although reusability was not investigated in this work, the chemical stability of diatomite suggests good regeneration potential, which should be addressed in future studies to assess its practical applicability.