Characteristics of the Mesostructure of 3D-Printed PLA/GNP Composites
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of PLA/GNP Composites
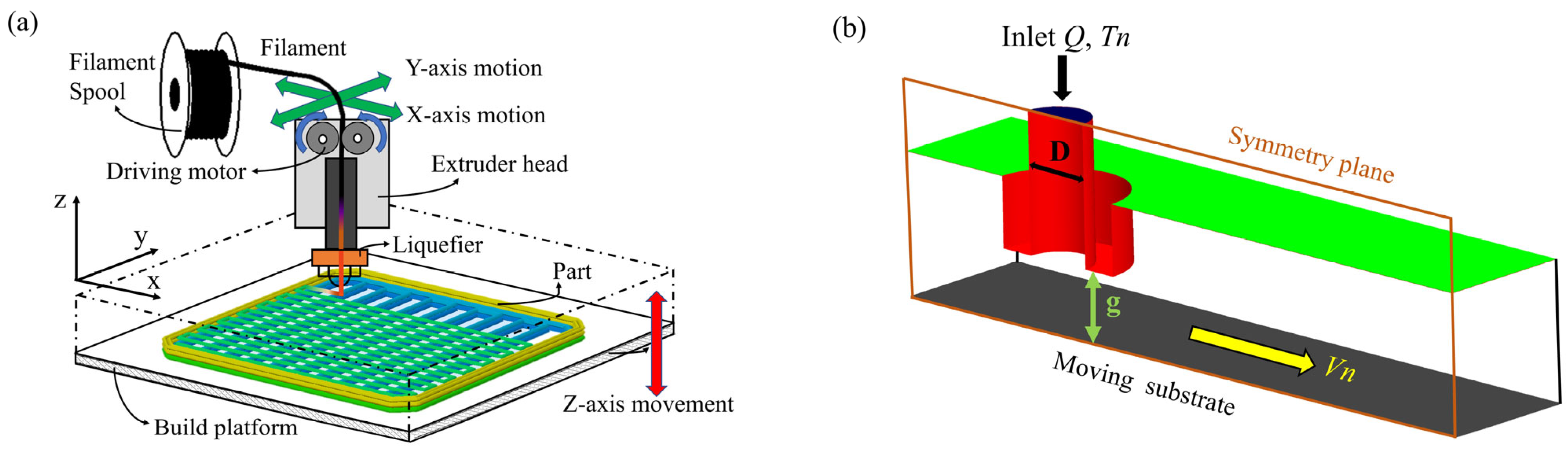
2.2. CFD Simulation of 3D-Printed PLA/GNPs
2.2.1. Governing Equations
2.2.2. Heat Transfer Model
2.2.3. Cross-WLF Rheology Model
2.2.4. Free Surface Reconstruction Based on VOF Scheme
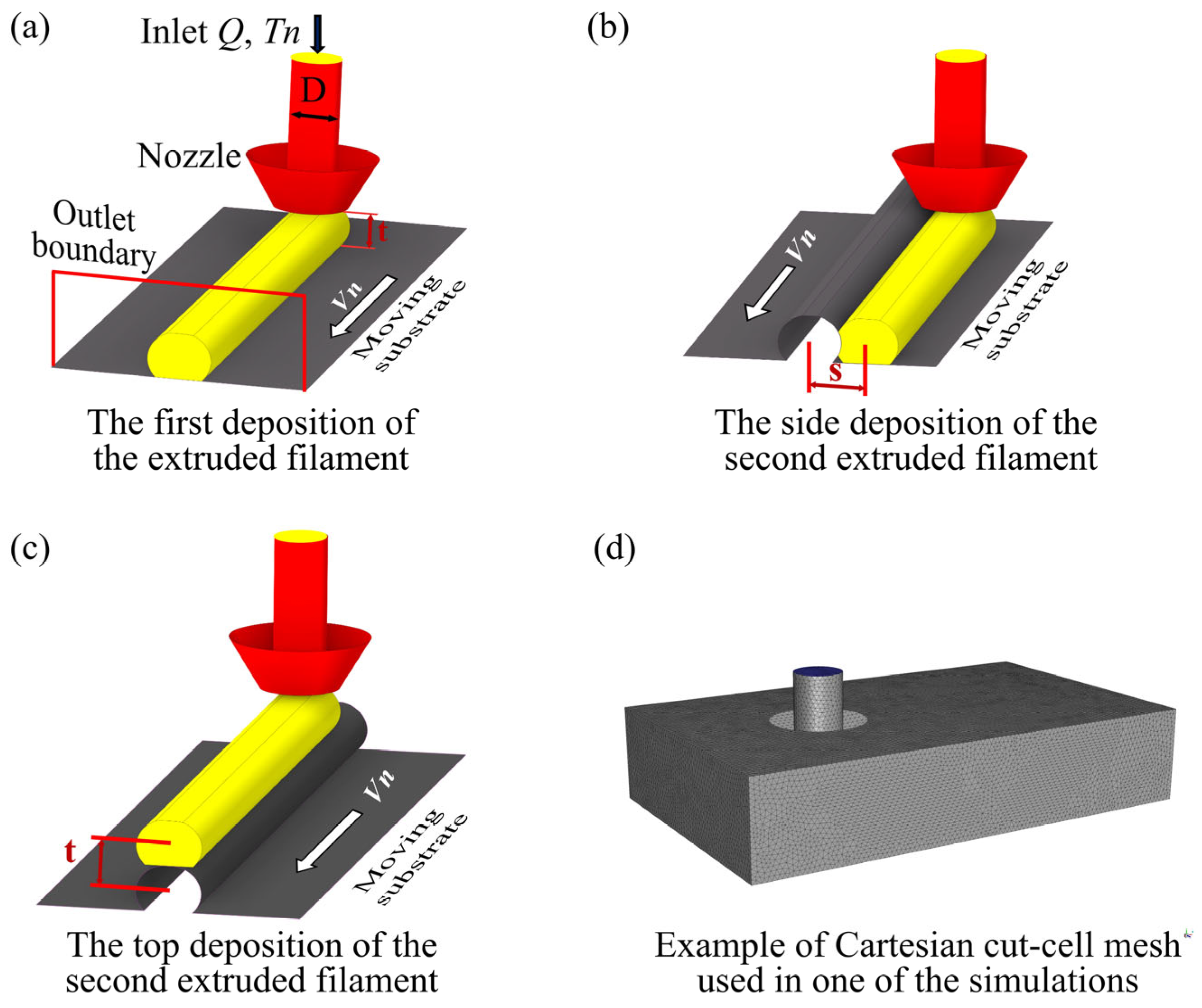
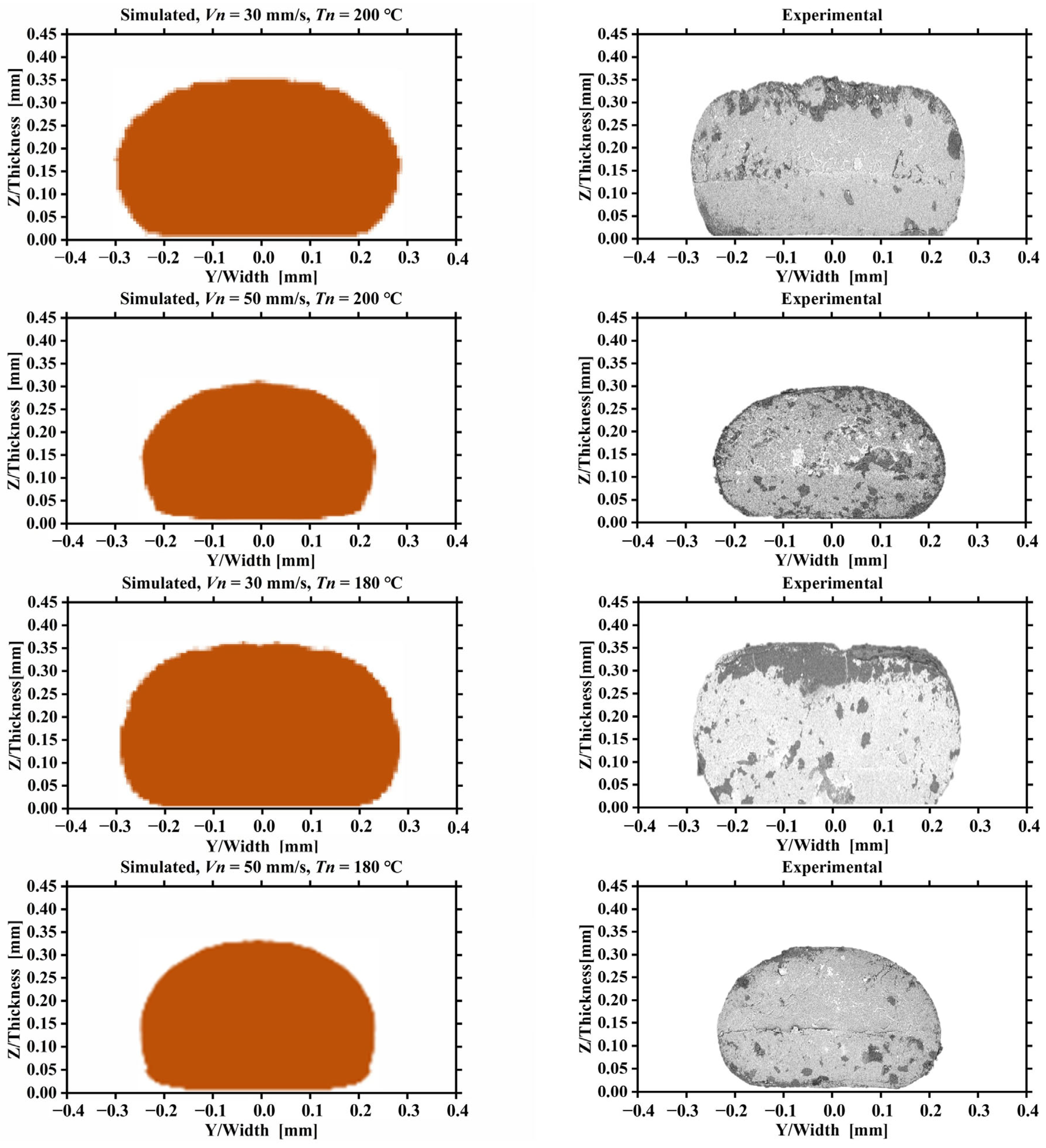
2.3. Implementation and Validation of Mesostructure Numerical Calculation
Post-Processing and Validation of Numerical Simulation
2.4. Mesostructure Characterization and Analysis Methods
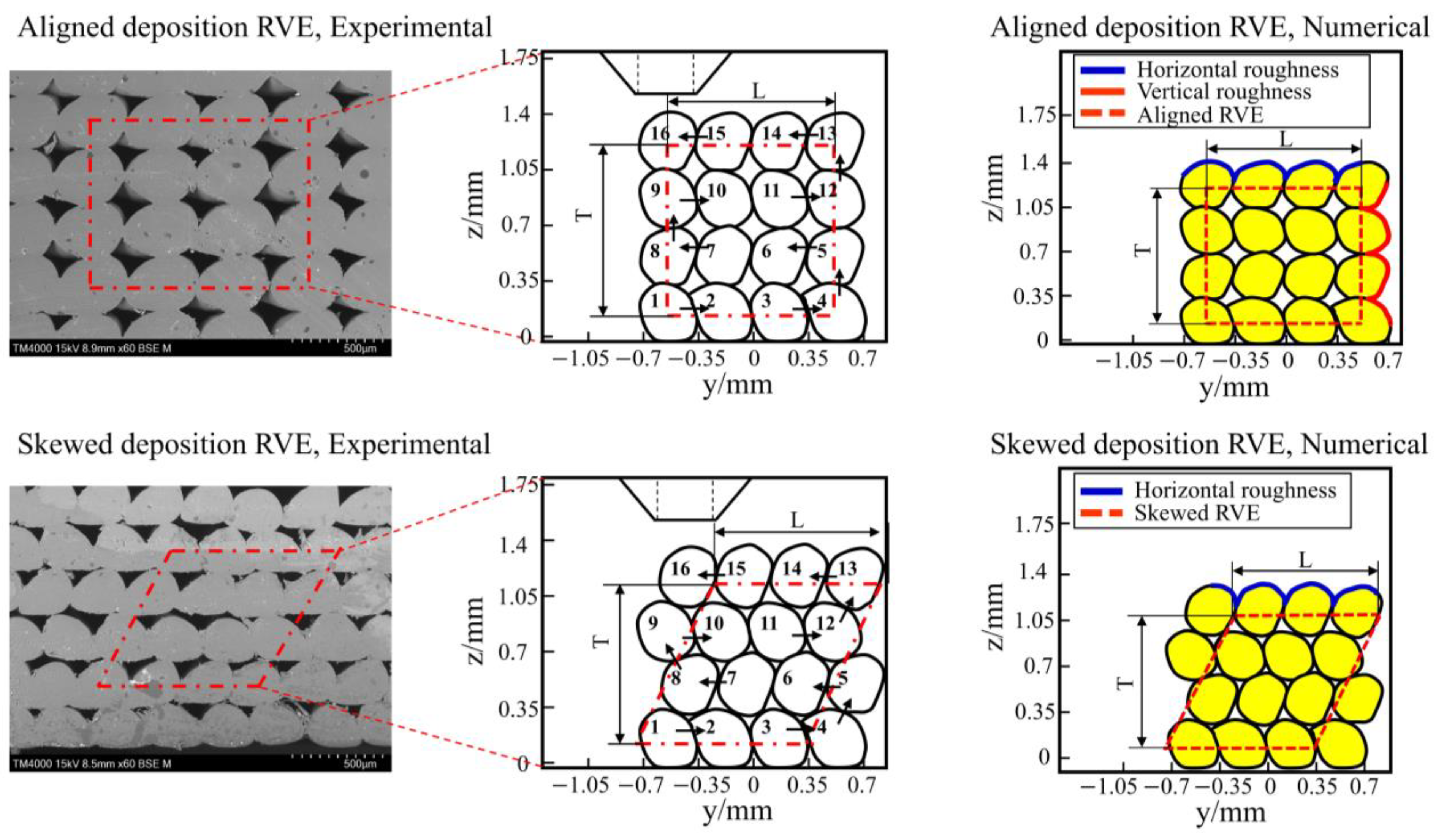
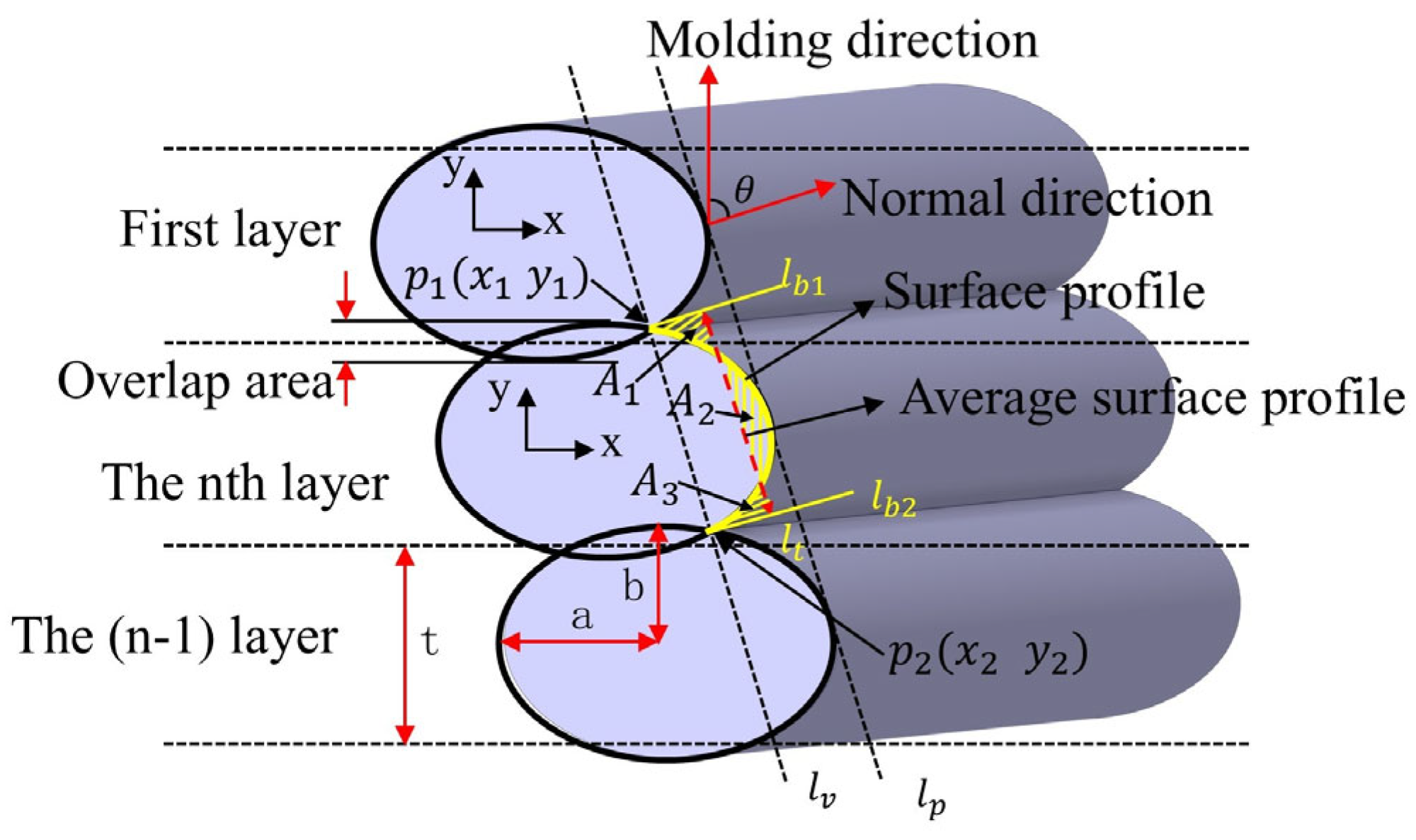
2.4.1. Characterization of Filament Cross-Sectional Morphology
2.4.2. Porosity Morphology and Analysis
2.4.3. Roughness Analysis
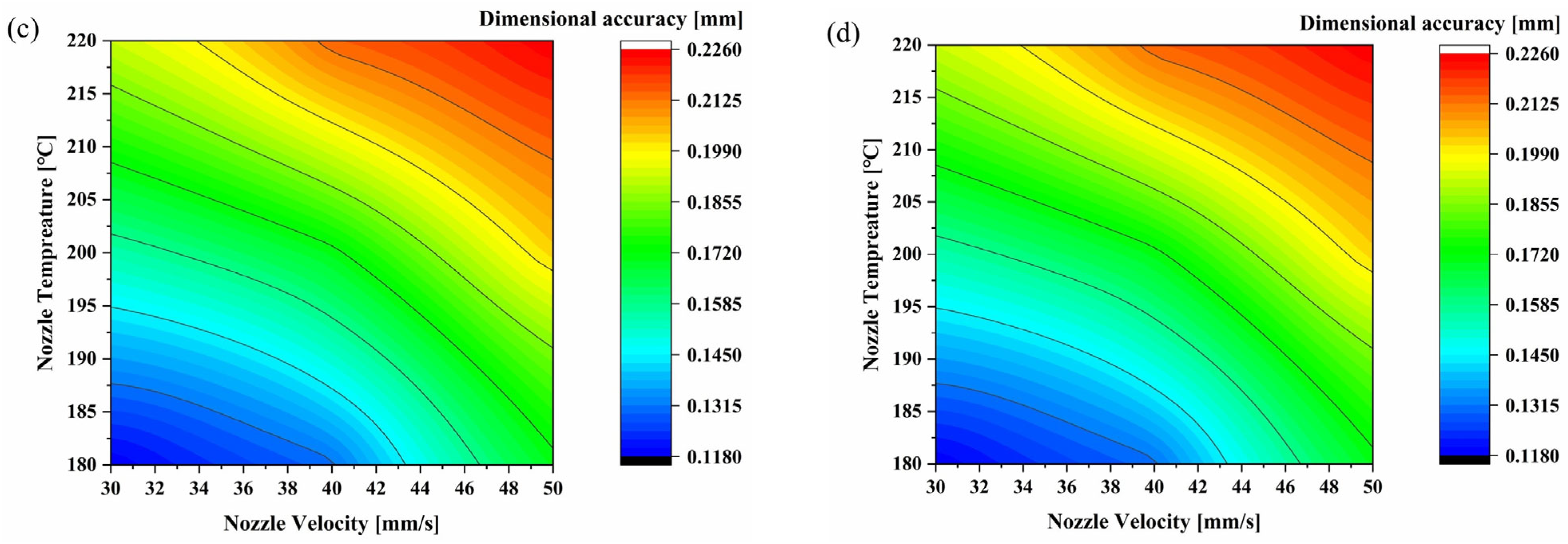
2.4.4. Dimensional Accuracy Analysis
2.4.5. Tensile Strength Analysis
3. Results and Discussion
3.1. Effect of Printing Parameters on Deposited Filament Cross-Sectional Morphology
3.2. Effect of Printing Parameters on Pore Morphology and Porosity
3.3. Effect of Printing Parameters on Roughness
3.4. Effect of Printing Parameters on Dimensional Accuracy and Tensile Strength
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cano-Vicent, A.; Tambuwala, M.M.; Hassan, S.S.; Barh, D.; Aljabali, A.A.; Birkett, M.; Arjunan, A.; Serrano-Aroca, Á. Fused deposition modelling: Current status, methodology, applications and future prospects. Addit. Manuf. 2021, 47, 102378. [Google Scholar] [CrossRef]
- Ahn, S.J.; Lee, H.; Cho, K.J. 3D printing with a 3D printed digital material filament for programming functional gradients. Nat. Commun. 2024, 15, 3605. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Tang, M.; Zhang, J.; Wang, H.; Zhou, J.; Wang, Q.; Qian, Z. Effects of rCF attributes and FDM-3D printing parameters on the mechanical properties of rCFRP. Compos. Part B Eng. 2024, 270, 111122. [Google Scholar] [CrossRef]
- Zhang, R.X.; Yu, L.; Chen, K.; Xue, P.; Jia, M.; Hua, Z. Amelioration of interfacial properties for CGF/PA6 composites fabricated by ultrasound-assisted FDM 3D printing. Compos. Commun. 2023, 39, 101551. [Google Scholar] [CrossRef]
- Faizaan, M.; Shenoy Baloor, S.; Nunna, S.; Mallya, R.; Rao Udupi, S.; Ramanath Kini, C.; Kada, S.R.; Creighton, C. A study on the overall variance and void architecture on MEX-PLA tensile properties through printing parameter optimization. Sci. Rep. 2025, 15, 3103. [Google Scholar] [CrossRef]
- Phan, D.D.; Horner, J.S.; Swain, Z.R.; Beris, A.N.; Mackay, M.E. Computational fluid dynamics simulation of the melting process in the fused filament fabrication additive manufacturing technique. Addit. Manuf. 2020, 33, 101161. [Google Scholar] [CrossRef]
- Rashid, A.A.; Koç, M. Fused filament fabrication process: A review of numerical simulation techniques. Polymers 2021, 13, 3534. [Google Scholar] [CrossRef]
- Comminal, R.; Serdeczny, M.P.; Pedersen, D.B.; Spangenberg, J. Numerical modelling of the strand deposition flow in extrusion-based additive manufacturing. Addit. Manuf. 2018, 20, 68–76. [Google Scholar] [CrossRef]
- Penumakala, P.K.; Santo, J.; Thomas, A. A critical review on the fused deposition modelling of thermoplastic polymer composites. Compos. Part. B Eng. 2020, 201, 108336. [Google Scholar] [CrossRef]
- Shah, A.K.; Palit, A.; Williams, M.A.; Wilson, P.F.; Jain, A. Microstructural alteration and its impact on the effective stiffness of short carbon fibre-reinforced PLA in fused deposition modelling. Compos. Part A Appl. Sci. Manuf. 2025, 199, 109229. [Google Scholar] [CrossRef]
- Sun, H.; Hwang, U.; Kim, S.; Sung, J.; Kim, T.; Suhr, J.; Park, I.K.; Nam, J.D. Reversible Thixotropic Rheological Properties of Graphene-Incorporated Epoxy Inks for Self-Standing 3D Printing. ACS Macro Lett. 2025, 14, 135–141. [Google Scholar] [CrossRef] [PubMed]
- dos Anjos, E.G.R.; Brazil, T.R.; de Melo Morgado, G.F.; Antonelli, E.; Rezende, M.C.; Pessan, L.A.; Moreira, F.K.V.; Marini, J.; Passador, F. Renewable PLA/PHBV blend-based graphene nanoplatelets and carbon nanotube hybrid nanocomposites for electromagnetic and electric-related applications. ACS Appl. Electron. Mater. 2023, 5, 6165–6177. [Google Scholar] [CrossRef]
- Gerdefaramarzi, R.S.; Ebrahimian, H.M.; Khodaei, M. 3D printed poly (lactic acid)/poly (ε-caprolactone)/graphene nanocomposite scaffolds for peripheral nerve tissue engineering. Arab. J. Chem. 2024, 17, 105927. [Google Scholar] [CrossRef]
- Ponnamma, D.; Yin, Y.; Salim, N.; Parameswaranpillai, J.; Thomas, S.; Hameed, N. Recent progress and multifunctional applications of 3D printed graphene nanocomposites. Compos. Part. B Eng. 2021, 204, 108493. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Z.; Huang, L.; Essa, K.; Bilotti, E.; Zhang, H.; Peijs, T.; Hao, L. Additive manufacturing high performance graphene-based composites: A review. Compos. Part A Appl. Sci. Manuf. 2025, 124, 9–22. [Google Scholar] [CrossRef]
- Park, S.; Shou, W.; Makatura, L.; Matusik, W.; Fu, K.K. 3D printing of polymer composites: Materials, processes, and applications. Matter 2022, 5, 43–76. [Google Scholar] [CrossRef]
- Milovanović, A.; Golubović, Z.; Kirin, S.; Babinský, T.; Šulák, I.; Milošević, M.; Sedmak, A. Manufacturing parameter influence on FDM polypropylene tensile properties. J. Mech. Sci. Technol. 2023, 37, 5541–5547. [Google Scholar] [CrossRef]
- Eksi, S.; Karakaya, C. Effects of Process Parameters on Tensile Properties of 3D-Printed PLA Parts Fabricated with the FDM Method. Polymers 2025, 17, 1934. [Google Scholar] [CrossRef]
- Shanmugam, V.; Babu, K.; Kannan, G.; Mensah, R.A.; Samantaray, S.K.; Das, O. The thermal properties of FDM printed polymeric materials: A review. Polym. Degrad. Stab. 2024, 228, 110902. [Google Scholar] [CrossRef]
- Li, S.; Cheng, P.; Ahzi, S.; Peng, Y.; Wang, K.; Chinesta, F.; Correia, J.P.M. Advances in hybrid fibres reinforced polymer-based composites prepared by FDM: A review on mechanical properties and prospects. Compos. Commun. 2023, 40, 101592. [Google Scholar] [CrossRef]
- Xu, X.; Ren, H.; Chen, S.; Luo, X.; Zhao, F.; Xiong, Y. Review on melt flow simulations for thermoplastics and their fiber reinforced composites in fused deposition modelling. J. Manuf. Process. 2023, 92, 272–286. [Google Scholar] [CrossRef]
- Mosleh, N.; Dariushi, S.; Esfandeh, M. An experimental and numerical investigation on mechanical properties of 3D printed continuous glass tow pre-reinforced composites. Rapid Prototyp. J. 2022, 28, 1284–1296. [Google Scholar] [CrossRef]
- Šeta, B.; Sandberg, M.; Brander, M.; Mollah, M.T.; Pokkalla, D.K.; Kumar, V.; Spangenberg, J. Numerical modelling of fibre orientation in multi-layer, isothermal material-extrusion big area additive manufacturing. Addit. Manuf. 2024, 92, 104396. [Google Scholar]
- Serdeczny, M.P.; Comminal, R.; Mollah, M.T.; Pedersen, D.B.; Spangenberg, J. Viscoelastic simulation and optimisation of the polymer flow through the hot-end during filament-based material extrusion additive manufacturing. Virtual Phys. Prototyp. 2022, 17, 205–219. [Google Scholar] [CrossRef]
- Ren, S.; Han, Z.; Xiong, Y.; Wei, H.; Xiao, J.; Wen, L.; Lei, M.; Hou, X. Crystallization-induced residual deformation evolution in thermoplastics during material extrusion and subsequent annealing. Mech. Mater. 2025, 206, 105345. [Google Scholar] [CrossRef]
- Samy, A.A.; Golbang, A.; Harkin-Jones, E.; Archer, E.; Tormey, D.; McIlhagger, A. Finite element analysis of residual stress and warpage in a 3D printed semi-crystalline polymer: Effect of ambient temperature and nozzle speed. J. Manuf. Process. 2021, 10, 70. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Serdeczny, M.P.; Comminal, R.; Pedersen, D.B.; Spangenberg, J. Numerical simulations of the mesostructure formation in material extrusion additive manufacturing. Addit. Manuf. 2019, 28, 419–429. [Google Scholar] [CrossRef]
- Qiu, W.; Xu, X.; Dong, K.; Wang, Y.; Xiong, Y. Recent advances in 4D printing of fibre-reinforced polymer composites: A review and outlook. Compos. Part. B Eng. 2024, 283, 111645. [Google Scholar] [CrossRef]
- Anerao, P.; Kulkarni, A.; Munde, Y. A review on exploration of the mechanical characteristics of 3D-printed biocomposites fabricated by fused deposition modelling (FDM). Rapid Prototyp. J. 2024, 30, 430–440. [Google Scholar] [CrossRef]
- Awasthi, P.; Banerjee, S.S. Fused Deposition Modelling of Thermoplastics Elastomeric Materials: Challenges and Opportunities. Addit. Manuf. 2021, 6, 102177. [Google Scholar]
- Wang, Y.; Lei, M.; Wei, Q.; Wang, Y.; Zhang, J.; Guo, Y.; Saroia, J. 3D printing biocompatible l-Arg/GNPs/PLA nanocomposites with enhanced mechanical property and thermal stability. J. Mater. Sci. 2022, 55, 5064–5078. [Google Scholar] [CrossRef]
- Lei, M.; Wei, Q.; Li, M.; Zhang, J.; Yang, R.; Wang, Y. Numerical simulation and experimental study the effects of process parameters on filament morphology and mechanical properties of FDM 3D printed PLA/GNPs nanocomposite. Polymers 2022, 14, 3081. [Google Scholar] [CrossRef]
- Mulbah, C.; Kang, C.; Mao, N. A review of VOF methods for simulating bubble dynamics. Prog. Nucl. Energy 2022, 154, 104478. [Google Scholar] [CrossRef]
- ISO 4287; Geometrical Product Specification (GPS)—Surface Texture: Pro-file Method—Terms, Definition and Surface Texture Parameters. International Organization for Standardization (ISO): Geneva, Switzerland, 1997.
- Bochmann, L.; Bayley, C.; Helu, M.; Transchel, R.; Wegener, K.; Dornfeld, D. Understanding error generation in fused deposition modelling. Surf. Topogr. Metrol. Prop. 2015, 3, 014002. [Google Scholar] [CrossRef]
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2014.
- Schwartz, J.J.; Hamel, J.; Ekstrom, T.; Ndagang, L.; Boydston, A.J. Not all PLA filaments are created equal: An experimental investigation. Rapid Prototyp. J. 2020, 26, 1263–1276. [Google Scholar] [CrossRef]







| Parameters | Signal | Value |
|---|---|---|
| Density of PLA/GNP nanocomposite (kg/m3) | 1300 | |
| Viscosity of PLA/GNP nanocomposite (Pa·s, range-function of T) | 20–8000 | |
| Thermal conductivity of the nanocomposite (W/mK) | 0.195 | |
| Specific heat capacity of nanocomposite (J/kg K) | 2000 | |
| Surface tension coefficient (kg/s2) | 0.04 | |
| Density of the air (kg/m3) | 0.9 | |
| Viscosity of the air (Pa·s) | 2.3 × 10−5 | |
| Thermal conductivity of the air (W/mK) | 0.034 | |
| Specific heat capacity of the air (J/kgK) | 1000 |
| Parameters | Symbol | Value | Unit |
|---|---|---|---|
| Nozzle velocity | Vn | 30, 40, 50 | mm/s |
| Nozzle temperature | Tn | 180, 200, 220 | °C |
| Air temperature | Ta | 25 | °C |
| Nozzle diameter | D | 0.4 | mm |
| Feed rate | Qfr | 5.024 | mm3/s |
| Substrate temperature | Ts | 25 | °C |
| Gap distance | g | 0.4 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, M.; Liu, P.; Niu, C.; Xu, Y.; Li, Q.; Liang, X.; Chen, H. Characteristics of the Mesostructure of 3D-Printed PLA/GNP Composites. J. Compos. Sci. 2025, 9, 585. https://doi.org/10.3390/jcs9110585
Lei M, Liu P, Niu C, Xu Y, Li Q, Liang X, Chen H. Characteristics of the Mesostructure of 3D-Printed PLA/GNP Composites. Journal of Composites Science. 2025; 9(11):585. https://doi.org/10.3390/jcs9110585
Chicago/Turabian StyleLei, Mingju, Pengfei Liu, Caiyun Niu, Yiyi Xu, Qiaowen Li, Xueru Liang, and Hongfeng Chen. 2025. "Characteristics of the Mesostructure of 3D-Printed PLA/GNP Composites" Journal of Composites Science 9, no. 11: 585. https://doi.org/10.3390/jcs9110585
APA StyleLei, M., Liu, P., Niu, C., Xu, Y., Li, Q., Liang, X., & Chen, H. (2025). Characteristics of the Mesostructure of 3D-Printed PLA/GNP Composites. Journal of Composites Science, 9(11), 585. https://doi.org/10.3390/jcs9110585





