Cyclic Loading Response and Failure Mechanism of Composite Auxetic Perforated Buckling-Restrained Braces: A Comparative Study of Q235B and LY160 Steel
Abstract
1. Introduction
2. Design of Composite Auxetic Cellular Units
2.1. Deformation Mechanism
2.2. Geometric Definition
3. Experimental Procedure
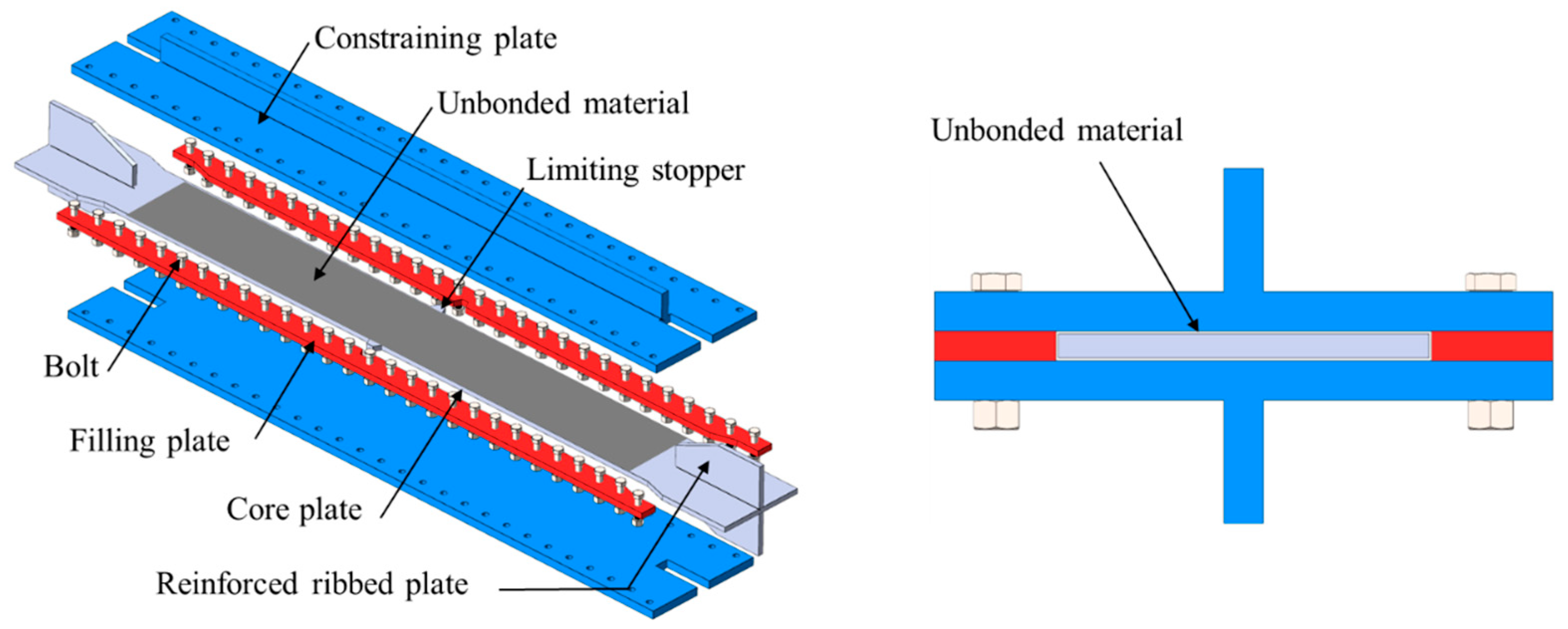
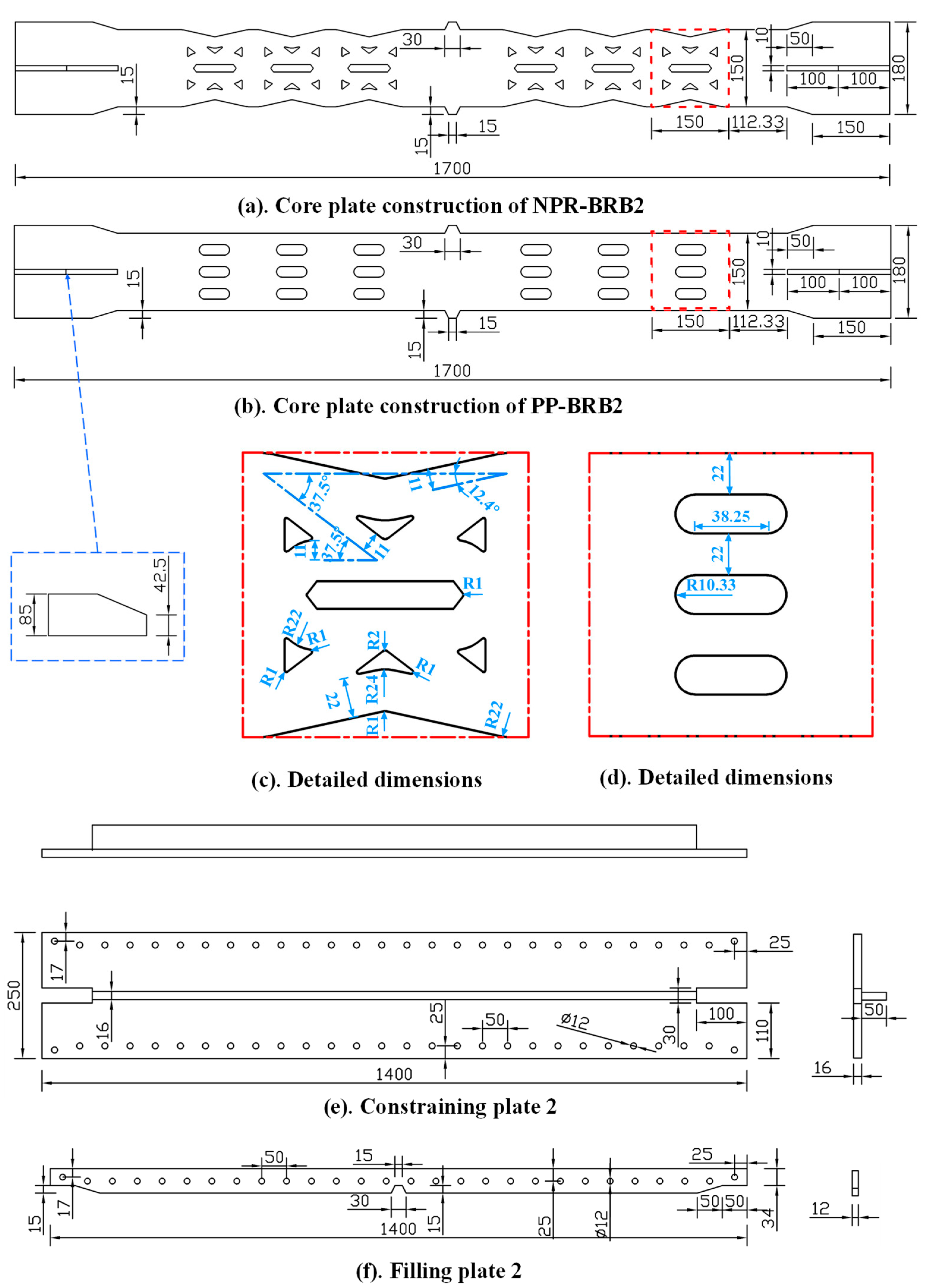
3.1. Specimen Design
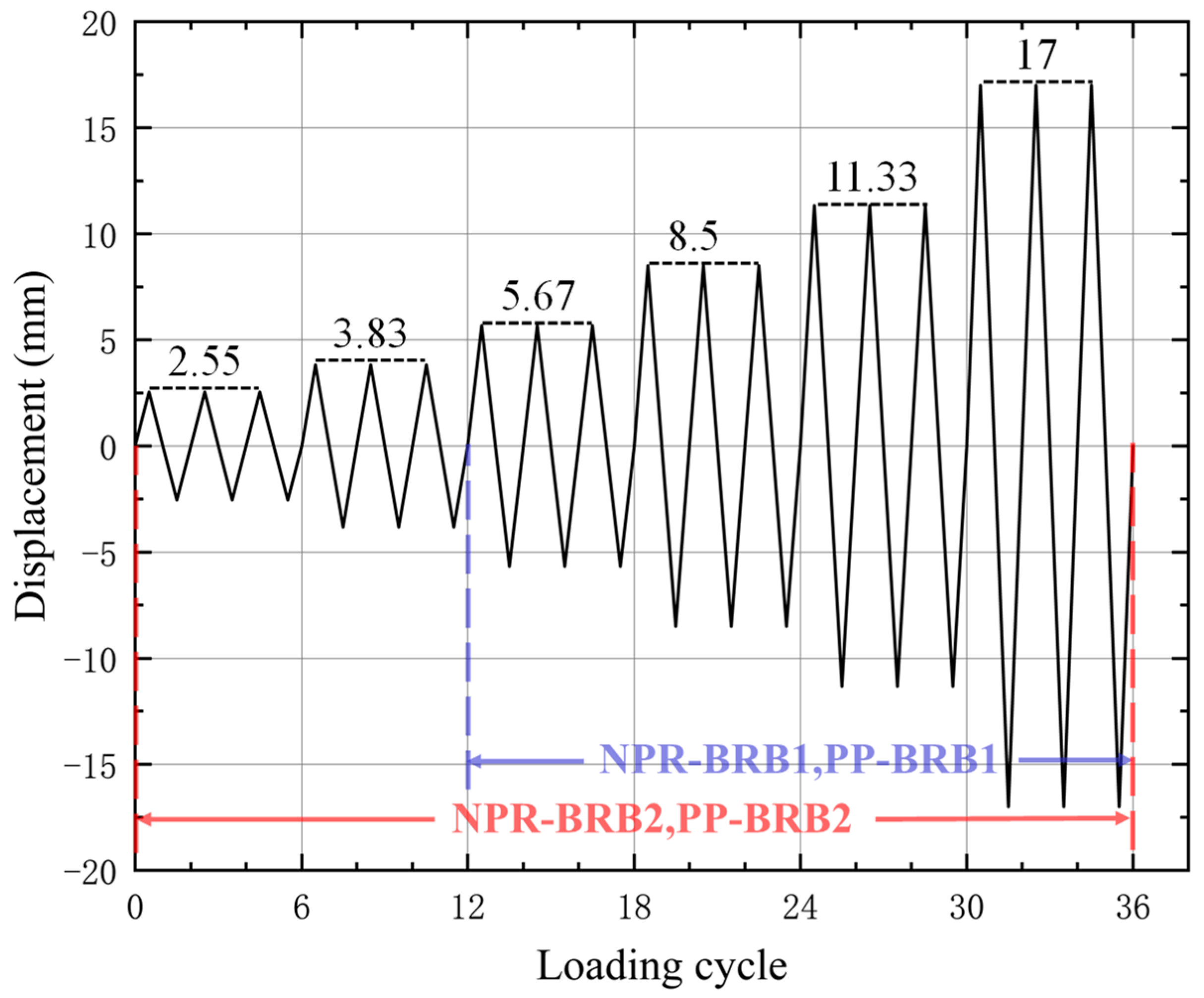
3.2. Test Setup and Loading Protocol
4. Experimental Results and Discussion
4.1. Failure Modes
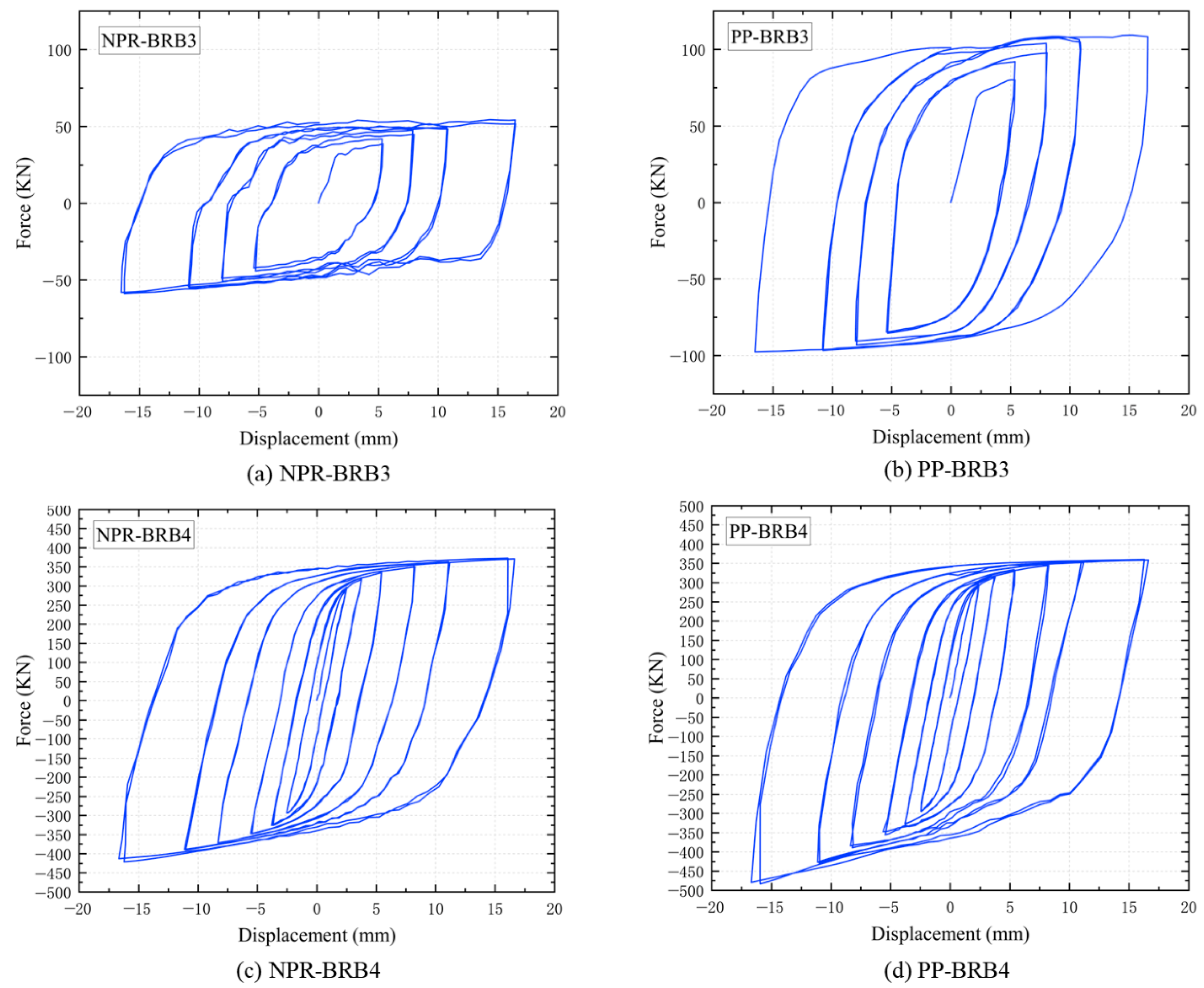
4.2. Hysteresis Curves
4.3. Compressive Strength Adjustment Factor
4.4. Ductility and Energy Dissipation Capacity
5. Numerical Simulation Study
5.1. Validation of the Numerical Model
5.2. Material Influence
5.3. Parameter Effects
5.3.1. Influence of Reentrant Angle
5.3.2. Influence of Section Weakening Ratio
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhong, J.; Zhao, C.; Liu, Y.; Ren, J.; Yang, C.; Zhang, Z. Meta-materials of Re-entrant Negative Poisson’s Ratio Structures Made from Fiber-Reinforced Plastics: A Short Review. Fibers Polym. 2024, 25, 395–406. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Shuaibu, A.S.; Deng, J.; Xu, C.; Ade-Oke, V.P.; Aiyu, A.; Momoh, D. Advancing auxetic materials: Emerging development and innovative applications. Rev. Adv. Mater. Sci. 2024, 63, 20240021. [Google Scholar] [CrossRef]
- Alderson, A. A triumph of lateral thought. Chem. Ind. 1999, 17, 384–391. [Google Scholar]
- Grima, J.N.; Caruana-Gauci, R.; Attard, D.; Gatt, R. Three-dimensional cellular structures with negative Poisson’s ratio and negative compressibility properties, Proceedings of the Royal Society A: Mathematical. Phys. Eng. Sci. 2012, 468, 3121–3138. [Google Scholar] [CrossRef]
- Mahdinejad Gorji, J.; Payganeh, G.; Moradi-Dastjerdi, R. Mechanical and energy absorption behavior of an innovative high-performance auxetic structure. Mech. Based Des. Struct. Mach. 2024, 52, 2316–2335. [Google Scholar] [CrossRef]
- Imbalzano, G.; Tran, P.; Ngo, T.D.; Lee, P.V.S. A numerical study of auxetic composite panels under blast loadings. Compos. Struct. 2016, 135, 339–352. [Google Scholar] [CrossRef]
- Tian, Z.; Shi, S.; Liao, Y.; Wang, W.; Zhang, L.; Xiao, Y. Energy Absorption Mechanisms of Riveted and Assembled Double-Trapezoidal Auxetic Honeycomb Core Structures Under Quasi-Static Loading. J. Compos. Sci. 2025, 9, 89. [Google Scholar] [CrossRef]
- Indreș, A.I.; Constantinescu, D.M.; Mocian, O.A.; Sorohan, Ș. Particularities on the Low-Velocity Impact Behavior of 3D-Printed Sandwich Panels with Re-Entrant and Honeycomb Core Topologies. J. Compos. Sci. 2024, 8, 426. [Google Scholar] [CrossRef]
- Kun, Y.; Fei, T.; Bo, W.Y.; He, H.Y. Study on impact energy absorption performance and optimization of negative Poisson’s ratio structure. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 328. [Google Scholar] [CrossRef]
- Donoghue, J.P.; Alderson, K.L.; Evans, K.E. The fracture toughness of composite laminates with a negative Poisson’s ratio. Phys. Status Solidi B 2009, 246, 2011–2017. [Google Scholar] [CrossRef]
- Bora, K.M.; Varshney, S.K.; Kumar, C.S. Rounded corner thicken strut re-entrant auxetic honeycomb: Analytical and numerical modeling. Mech. Res. Commun. 2024, 136, 104246. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wang, X.Y.; Ren, X.; Xie, Y.M.; Wu, Y.; Zhou, Y.Y.; Wang, S.L.; Han, C.Z. A novel type of tubular structure with auxeticity both in radial direction and wall thickness. Thin-Walled Struct. 2021, 163, 107758. [Google Scholar] [CrossRef]
- Luo, C.; Han, C.Z.; Zhang, X.Y.; Zhang, X.G.; Xie, Y.M. Design, manufacturing and applications of auxetic tubular structures: A review. Thin-Walled Struct. 2021, 163, 107682. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Zawistowski, M.; Poteralski, A. Parametric optimization of selected auxetic structures, Multiscale and Multidisciplinary Modeling. Exp. Des. 2024, 7, 4777–4789. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, H.; Nie, B.; Jia, F.; Gao, Q. Energy absorption characteristics of carbon fiber reinforced plastic/aluminum hybrid materials double arrow-head auxetic structure. J. Sandw. Struct. Mater. 2024, 26, 490–506. [Google Scholar] [CrossRef]
- Lu, F.; Wei, T.; Zhang, C.; Huang, Y.; Zhu, Y.; Rui, X. A novel 3D tetra-missing rib auxetic meta-structure with tension/compression-twisting coupling effect. Thin-Walled Struct. 2024, 199, 111764. [Google Scholar] [CrossRef]
- Nickabadi, S.; Sayar, M.A.; Alirezaeipour, S.; Ansari, R. Optimizing an auxetic metamaterial structure for enhanced mechanical energy absorption: Design and performance evaluation under compressive and impact loading. J. Sandw. Struct. Mater. 2024, 26, 1129–1164. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef]
- Hosseini, M.; Mazaheri, H. Mechanical behavior of graded combined auxetic-honeycomb structures. Int. J. Mech. Sci. 2024, 276, 109223. [Google Scholar] [CrossRef]
- Meng, Z.; Xu, Y.; Xie, J.; Zhou, W.; Bol, R.J.M.; Liu, Q.; Savjia, B. Unraveling the reinforcing mechanisms for cementitious composites with 3D printed multidirectional auxetic lattices using X-ray computed tomography. Mater. Des. 2024, 246, 113331. [Google Scholar] [CrossRef]
- Chen, M.; Fang, S.; Wang, G.; Xuan, Y.; Gao, D.; Zhang, M. Compressive and flexural behaviour of engineered cementitious composites based auxetic structures: An experimental and numerical study. J. Build. Eng. 2024, 86, 108999. [Google Scholar] [CrossRef]
- Bao, Y.; Wei, Z.; Jia, Z.; Wang, D.; Zhang, X.; Kang, Z. Mechanical metamaterial design with the customized low-frequency bandgap and negative Poisson’s ratio via topology optimization. Extrem. Mech. Lett. 2024, 67, 102–124. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y.; Hu, Z.; Lu, W.; Li, Z.; Gao, N.; Liu, Y. Gelatin-based metamaterial hydrogel films with high conformality for ultra-soft tissue monitoring. Nano-Micro Lett. 2023, 16, 34. [Google Scholar] [CrossRef] [PubMed]
- Pan, K.; Ding, J.; Zhang, W.; Zhao, S. The negative Poisson’s ratio ship base design and vibration isolation performance analysis. Appl. Sci. 2021, 11, 11167. [Google Scholar] [CrossRef]
- Yao, Y.; Ni, Y.; He, L.H. Rutile-mimic 3D metamaterials with simultaneously negative Poisson’s ratio and negative compressibility. Mater. Des. 2021, 200, 109440. [Google Scholar] [CrossRef]
- Ghofrani, S.; Mehrizi, A.A.; Nasrollahi, V.; Dimov, S. Novel Cardiovascular Stent Based on Hibiscus-Aestivation-Inspired Auxetic Unit Cell. Int. J. Mech. Sci. 2024, 277, 109428. [Google Scholar] [CrossRef]
- Liang, K.; Cheng, Q. A novel design of an actively deformable honeycomb structure with application to a variable thickness leading-edge wing. J. Intell. Mater. Syst. Struct. 2023, 34, 1902–1916. [Google Scholar] [CrossRef]
- Wang, W.; Xu, X.; Lu, L. Design and Optimization of Negative Poisson Ratio Thin-Walled Tube Using Sensitivity-Based Response Surface Model Methodology. Int. J. Struct. Stab. Dyn. 2023, 23, 2350036. [Google Scholar] [CrossRef]
- Nguyễn, H.; Fangueiro, R.; Ferreira, F.; Nguyen, Q. Auxetic materials and structures for potential defense applications: An overview and recent developments. Text. Res. J. 2023, 93, 5268–5306. [Google Scholar] [CrossRef]
- Uhlířová, T.; Pabst, W. Direct measurement of negative Poisson ratios of auxetic materials via the impulse excitation technique (IET). J. Eur. Ceram. Soc. 2024, 44, 2338–2345. [Google Scholar] [CrossRef]
- Hamed, A.A.; Asl, R.B.; Rahimzadeh, H. Experimental and numerical study on the structural performance of auxetic-shaped, ring-shaped and unstiffened steel plate shear walls. J. Build. Eng. 2021, 34, 101939. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Wang, P.; Liu, J.; Zhang, Z.; Wang, S.; Gao, Y.; Li, M. Dynamic damage behavior of auxetic textile reinforced concrete under impact loading. J. Build. Eng. 2024, 97, 110764. [Google Scholar] [CrossRef]
- Gan, Z.; Pham, T.M.; Thambiratnam, D.P.; Chan, T.H.; Asad, M.; Xu, S.; Zhuge, Y. High strain rate effect and dynamic compressive behaviour of auxetic cementitious composites. J. Build. Eng. 2024, 94, 110011. [Google Scholar] [CrossRef]
- Valverde-Burneo, D.; García-Troncoso, N.; Segura, I.; García-Laborda, M.; Santillán, N. Experimental and Theoretical Analysis of Auxetic Cementitious Composite: A Comparative Study with Recycled and Virgin Steel Fibers. J. Build. Eng. 2025, 101, 111822. [Google Scholar] [CrossRef]
- Luo, C.; Ren, X.; Han, D.; Zhang, X.G.; Zhong, R.; Zhang, X.Y.; Xie, Y.M. A novel concrete-filled auxetic tube composite structure: Design and compressive characteristic study. Eng. Struct. 2022, 268, 114759. [Google Scholar] [CrossRef]
- Haider, S.M.B.; Lee, D. A review on BRB and SC-BRB members in building structures. Struct. Eng. Mech. 2021, 80, 609. [Google Scholar] [CrossRef]
- Xiong, C.; Cao, Y.C.; Wang, T. Experimental and numerical studies of a core plate repairable double-stage yield buckling-restrained brace. J. Constr. Steel Res. 2024, 223, 109006. [Google Scholar] [CrossRef]
- Huang, F.; Duan, H.; Cheng, B.; Teng, N. Hysteretic performance of all-steel assembled double-cores buckling-restrained braces using Q195 low-yield core. J. Constr. Steel Res. 2021, 187, 106925. [Google Scholar] [CrossRef]
- Avci-Karatas, C.; Celik, O.C.; Ozmen Eruslu, S. Modeling of buckling restrained braces (BRBs) using full-scale experimental data. KSCE J. Civ. Eng. 2019, 23, 4431–4444. [Google Scholar] [CrossRef]
- Guoqiang, L.; Feifei, S.; Hai, G. Engineering Application of TJ-type Buckling Restrained Braces. Build. Struct. S 2009, 1, 607–610. [Google Scholar]
- Shi, Q.X.; Wang, F.; Wang, P.; Chen, K. Experimental and numerical study of the seismic performance of an all-steel assembled Q195 low-yield buckling-restrained brace. Eng. Struct. 2018, 176, 481–499. [Google Scholar] [CrossRef]
- Chen, Z.P.; Zhu, S. Cyclic tension–compression behaviors of large-dimensional superelastic shape memory alloy buckling-restrained plates. J. Struct. Eng. 2024, 150, 04024152. [Google Scholar] [CrossRef]
- Zhuge, Y.; Ma, X.; Zeng, J. Recent progress in buckling restrained braces: A review on material development and selection. Adv. Struct. Eng. 2022, 25, 1549–1564. [Google Scholar] [CrossRef]
- Jia, L.J.; Ge, H.; Xiang, P.; Liu, Y. Seismic performance of fish-bone shaped buckling-restrained braces with controlled damage process. Eng. Struct. 2018, 169, 141–153. [Google Scholar] [CrossRef]
- Jia, L.J.; Dong, Y.; Ge, H.; Kondo, K. Experimental study on high-performance buckling-restrained braces with perforated core plates. Int. J. Struct. Stab. Dyn. 2019, 19, 1940004. [Google Scholar] [CrossRef]
- Zhang, Y.; Ren, X.; Zhang, X.Y.; Huang, T.T.; Sun, L.; Xie, Y.M. A novel buckling-restrained brace with auxetic perforated core: Experimental and numerical studies. Eng. Struct. 2021, 249, 113223. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, J.; Cai, X.; Xu, Z.; Wen, Y. Cyclic behavior of ellipse and peanut-shaped perforated buckling-restrained braces. Eng. Struct. 2023, 291, 116432. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhu, Y.; Lu, F.; Yu, C.; Ren, X.; Shao, Y. A novel buckling-induced planner isotropic auxetic meta-structure and its application in BRB: A numerical study. Mech. Adv. Mater. Struct. 2024, 31, 6081–6094. [Google Scholar] [CrossRef]
- Basri, H.; Ras, A.; Hamdaoui, K. Parametric investigation of buckling restrained brace with auxetic core. J. Vib. Eng. Technol. 2024, 12, 6215–6234. [Google Scholar] [CrossRef]
- Momoh, E.O.; Jayasinghe, A.; Hajsadeghi, M.; Vinal, R. A state-of-the-art review on the application of auxetic materials in cementitious composites. Thin-Walled Struct. 2024, 196, 111447. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Y. 3D Printed Auxetic Mechanical Metamaterial with Chiral Cells and Re-entrant Cores. Sci. Rep. 2018, 8, 2397. [Google Scholar] [CrossRef]
- Naveed, A.B.; Mubashar, A.; Khan, M.K.A.; Munir, A.; Khanet, K.A. Additively manufactured hybrid auxetic structures for enhanced low frequency acoustic performance through experiments and modelling. Sci. Rep. 2025, 15, 23460. [Google Scholar] [CrossRef] [PubMed]
- Nugroho, W.T.; Dong, Y.; Pramanik, A.; Selvan, M.C.P.; Zhang, Z.; Ramakrishna, S. Additive manufacturing of re-entrant structures: Well-tailored structures, unique properties, modelling approaches and real applications. Addit. Manuf. 2023, 78, 103829. [Google Scholar] [CrossRef]
- Etemadi, E.; Hosseinabadi, M.; Taghizadeh, M.; Scarpe, F.; Hu, H. Enhancing the energy absorption capability of auxetic metamaterials through auxetic cells within re-entrant circular units. Eng. Struct. 2024, 315, 118379. [Google Scholar] [CrossRef]
- Fu, T.; Wang, X.; Hu, X.; Rabczuk, T. Impact dynamic response of stiffened porous functionally graded materials sandwich doubly-curved shells with Arc-type auxetic core. Int. J. Impact Eng. 2024, 191, 105000. [Google Scholar] [CrossRef]
- Sahoo, K.C.; Sreevidya, N.; Sakthivel, T.; Reddy, G.V.P. Effect of notch angle on creep deformation and rupture behavior of 304HCu SS. Eng. Res. Express 2024, 6, 015093. [Google Scholar] [CrossRef]
- GB/T 228-2021; Metallic Materials-Tensile Testing-Part 1: Method of a Test at Room Temperature. China Standard Press: Beijing, China, 2021. (In Chinese)
- T/CECS 817-2021; Technical Specification for the Application of Flexion Restraint Bracing. China Architecture & Building Press: Beijing, China, 2021. (In Chinese)
- Shi, G.; Gao, Y.; Wang, X.; Zhang, Y. Mechanical properties and constitutive models of low yield point steels. Constr. Build. Mater. 2018, 175, 570–587. [Google Scholar] [CrossRef]


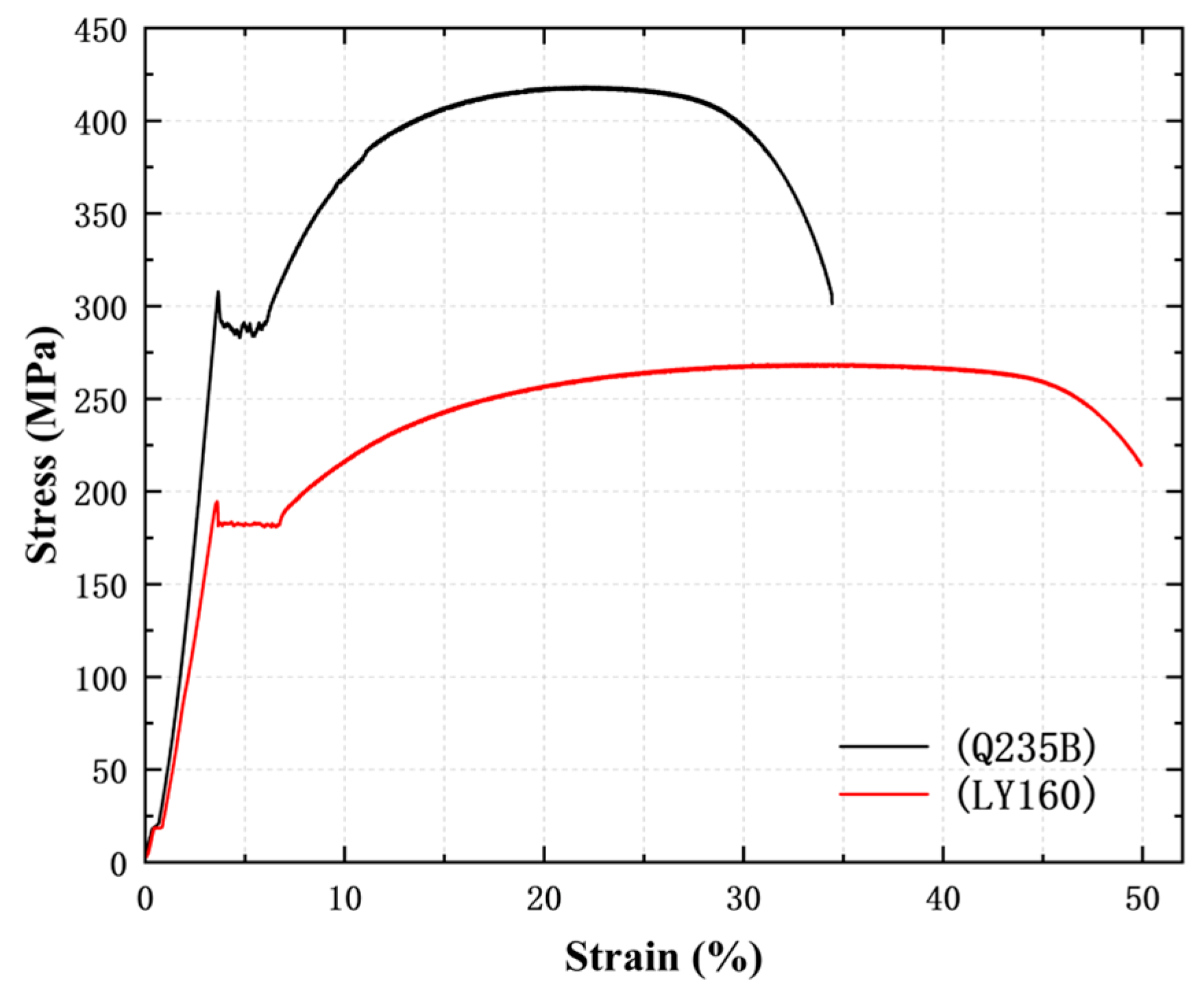









| Material | Elasticity Modulus E (MPa) | Yield Strength (MPa) | (MPa) | (%) |
|---|---|---|---|---|
| Q235B | 283.1 | 418.2 | 22.2 | |
| LY160 | 181.2 | 268.4 | 33.3 |
| Specimen | (KN) | (KN) | (KJ) | CPD | ||
|---|---|---|---|---|---|---|
| NPR-BRB1 | 65.6 | 84.46 | 22,041.6 | 1.288 | 0.469 | 219.7 |
| PP-BRB1 | 126.9 | 140.2 | 34,465.7 | 1.105 | 0.382 | 189 |
| NPR-BRB2 | 289.8 | 306.9 | 74,813.8 | 1.027 | 0.501 | 211.3 |
| PP-BRB2 | 282.5 | 321 | 76,257.7 | 1.136 | 0.458 | 215 |
| NPR-BRB3 | 59 | 52.2 | 18,530.9 | 1.130 | 0.492 | 223.6 |
| PP-BRB3 | 97.9 | 109.3 | 24,443.4 | 0.896 | 0.535 | 195.7 |
| NPR-BRB4 | 371.9 | 422.1 | 86,275.3 | 1.135 | 0.456 | 188.3 |
| PP-BRB4 | 359.5 | 484.8 | 90,451.3 | 1.292 | 0.448 | 194.5 |
| Material | b | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Q235B | 283.1 | 10 | 1.2 | 100,000 | 2500 | 7500 | 100 | 500 | 0 | - | - |
| LY160 | 181.2 | 110 | 4 | 2991 | 210 | 1180 | 180 | 1290 | 145 | 220 | 1 |
| Specimen | (°) | (°) | (°) | (%) | (KN) | (KN) | (KJ) | CPD | ||
|---|---|---|---|---|---|---|---|---|---|---|
| NPR-BRB5 | 32.5 | 10.83 | 32.95 | 52 | 214.16 | 242.32 | 1.131 | 55,297.28 | 0.486 | 264.35 |
| NPR-BRB6 | 35 | 11.67 | 32.92 | 52 | 202.69 | 233.69 | 1.153 | 54,726.16 | 0.488 | 263.35 |
| NPR-BRB7 | 37.5 | 12.4 | 29.56 | 52 | 197.59 | 220.28 | 1.115 | 50,821.51 | 0.488 | 265.66 |
| NPR-BRB8 | 40 | 13.33 | 32.64 | 52 | 195.49 | 214.95 | 1.1 | 50,136.19 | 0.493 | 266.34 |
| NPR-BRB9 | 42.5 | 14.17 | 32.4 | 52 | 191.02 | 212.49 | 1.112 | 50,461.75 | 0.566 | 306.57 |
| NPR-BRB2 | 37.5 | 12.4 | 37.5 | 41 | 295.82 | 312.09 | 1.055 | 74,620.57 | 0.501 | 215.49 |
| NPR-BRB10 | 37.5 | 12.4 | 30.23 | 47 | 238.35 | 259.14 | 1.087 | 67,023.08 | 0.513 | 251.98 |
| NPR-BRB11 | 37.5 | 12.4 | 29.64 | 57 | 168 | 172.59 | 1.027 | 42,181.93 | 0.553 | 305.33 |
| NPR-BRB12 | 37.5 | 12.4 | 30.33 | 63 | 130.74 | 124.25 | 0.95 | 30,122.11 | 0.443 | 272.65 |
| NPR-BRB13 | 37.5 | 12.4 | 29.88 | 68 | 102.25 | 80.62 | 0.788 | 20,671 | 0.489 | 247.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, X.; Wu, K.; Zhang, Z. Cyclic Loading Response and Failure Mechanism of Composite Auxetic Perforated Buckling-Restrained Braces: A Comparative Study of Q235B and LY160 Steel. J. Compos. Sci. 2025, 9, 581. https://doi.org/10.3390/jcs9110581
Chen Y, Wang X, Wu K, Zhang Z. Cyclic Loading Response and Failure Mechanism of Composite Auxetic Perforated Buckling-Restrained Braces: A Comparative Study of Q235B and LY160 Steel. Journal of Composites Science. 2025; 9(11):581. https://doi.org/10.3390/jcs9110581
Chicago/Turabian StyleChen, Yongdang, Xianjie Wang, Kechuan Wu, and Zheng Zhang. 2025. "Cyclic Loading Response and Failure Mechanism of Composite Auxetic Perforated Buckling-Restrained Braces: A Comparative Study of Q235B and LY160 Steel" Journal of Composites Science 9, no. 11: 581. https://doi.org/10.3390/jcs9110581
APA StyleChen, Y., Wang, X., Wu, K., & Zhang, Z. (2025). Cyclic Loading Response and Failure Mechanism of Composite Auxetic Perforated Buckling-Restrained Braces: A Comparative Study of Q235B and LY160 Steel. Journal of Composites Science, 9(11), 581. https://doi.org/10.3390/jcs9110581





