Behaviour Analysis of Timber–Concrete Composite Floor Structure with Granite Chip Connection
Abstract
1. Introduction
1.1. Incorporation of Granite Chunks into a Timber–Concrete Composite
1.2. Complex Behaviour of Timber–Concrete Composites
2. Materials and Methods
2.1. General Approach
2.2. Comparison of Analytical Design Methods for Timber–Concrete Composite Members with Reinforced Adhesive Layer
2.3. Design Method for a Timber–Concrete Composite Member Subjected to Bending
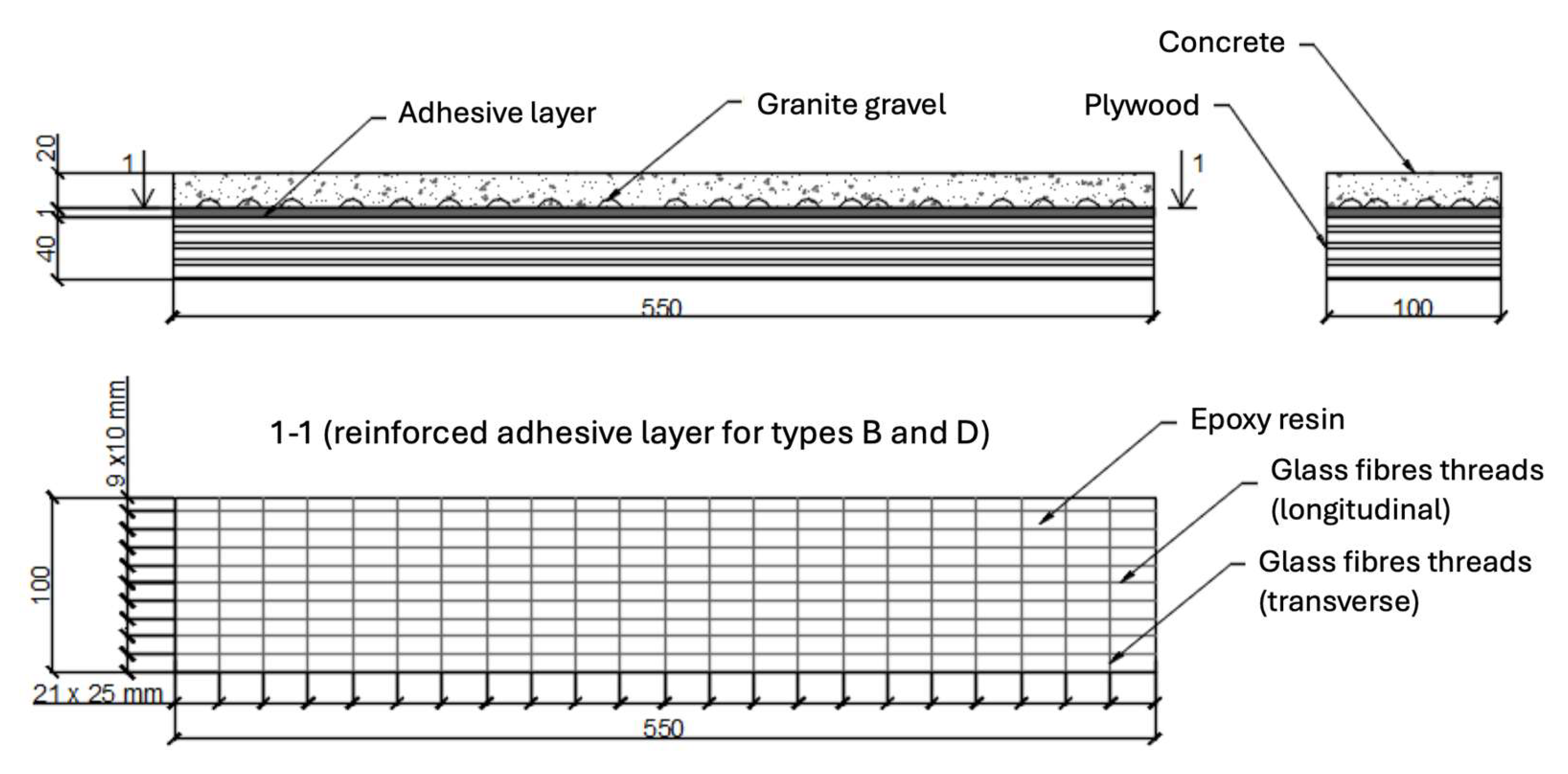
2.4. Laboratory Experiment
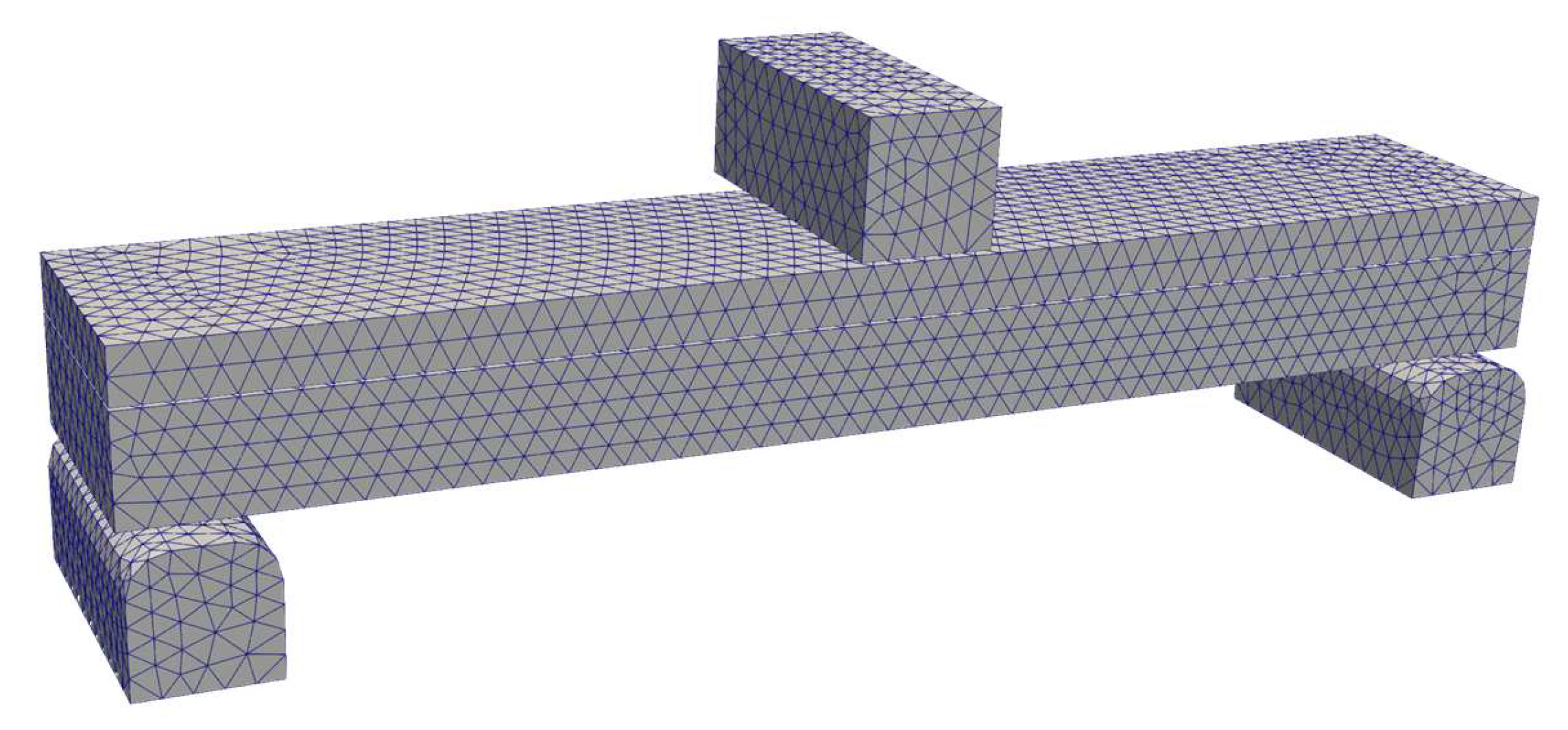
2.5. Finite Element Models
2.5.1. Concrete Material Model
2.5.2. Timber Material Model
- Transversal anisotropy for stiffness and strength.
- Multi-axial failure criteria divided in two parts—parallel to grain mode and perpendicular mode.
- Multi-axial plasticity for compression.
- Strain-hardening plasticity perpendicular to grains.
- normal stress in fibre (axial) direction.
- normal stress in radial direction.
- normal stress in tangential direction.
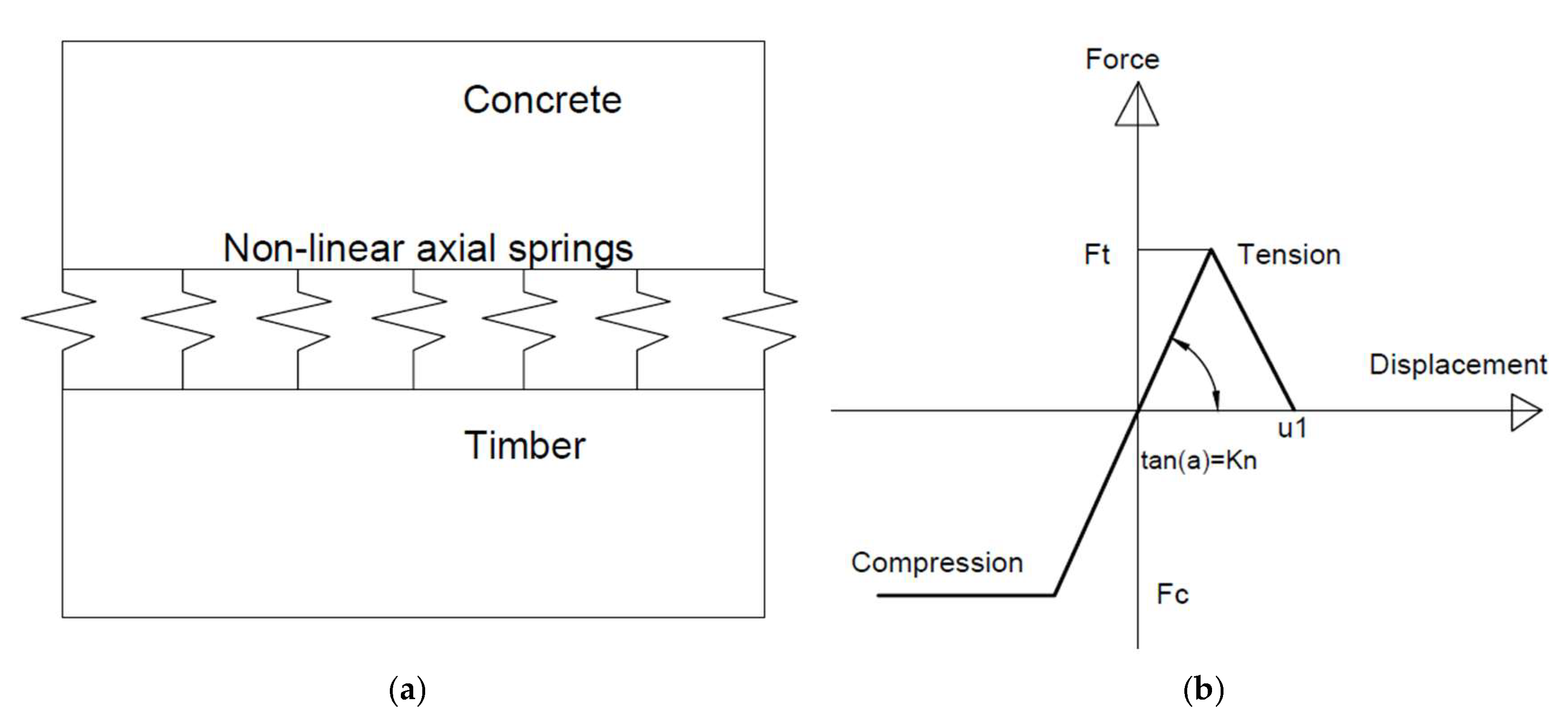
2.5.3. Cohesive Zone Element Between Timber and Concrete
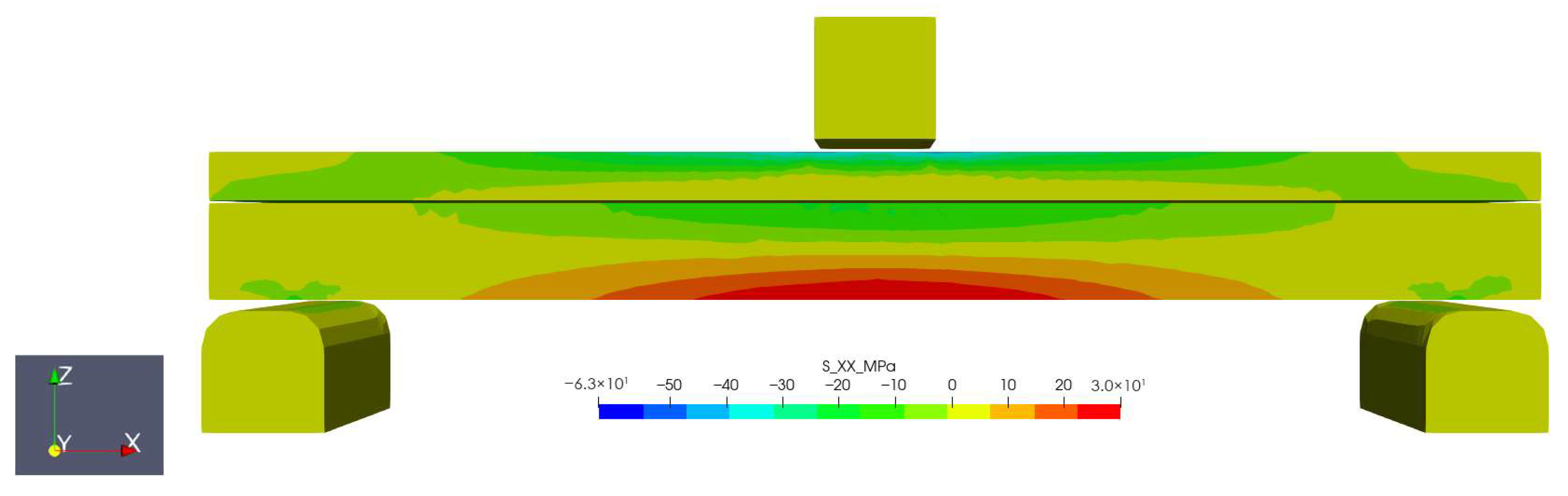
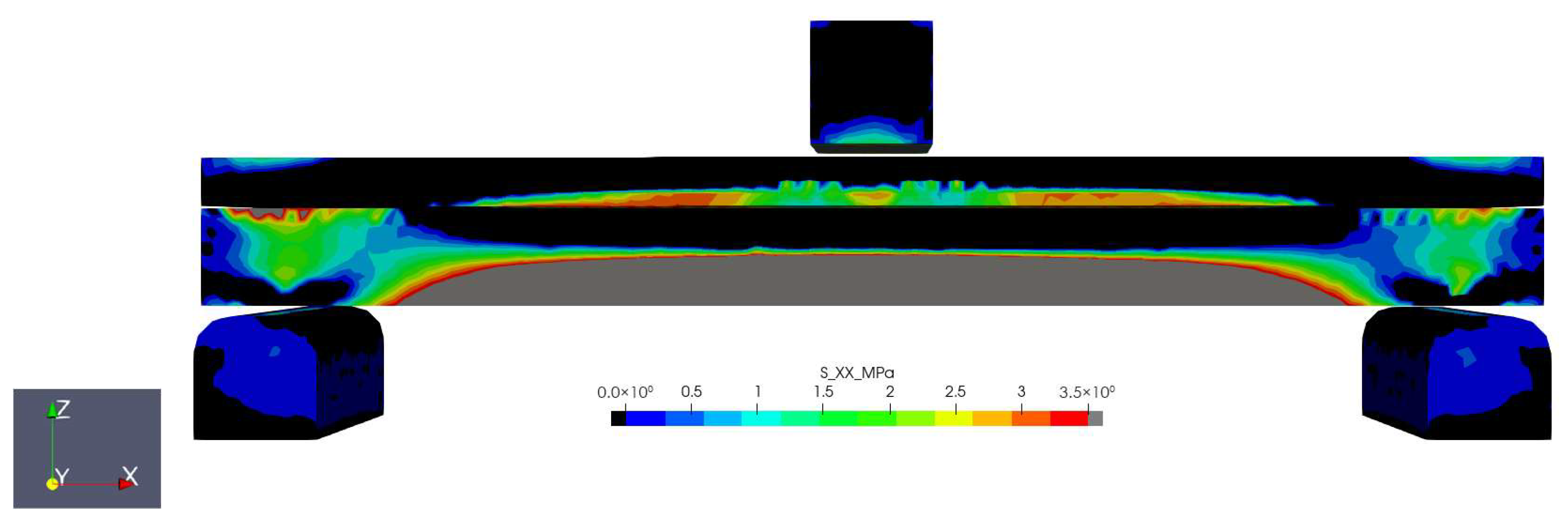
3. Results and Discussions
3.1. Influence of the Adhesive and Concrete Layer Mechanical Properties on the Behaviour of Timber–Concrete Composite Member Subjected to Flexure
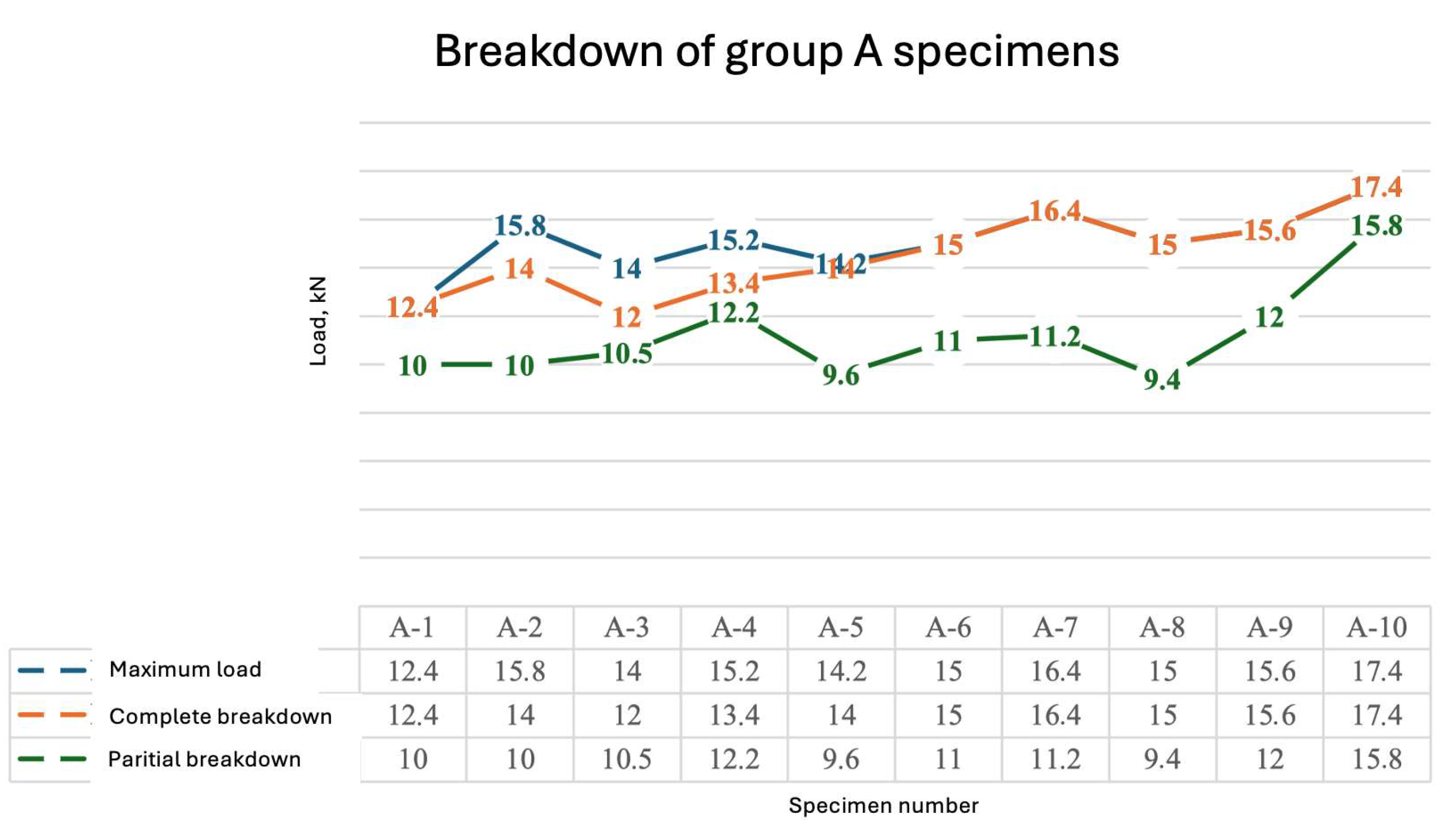
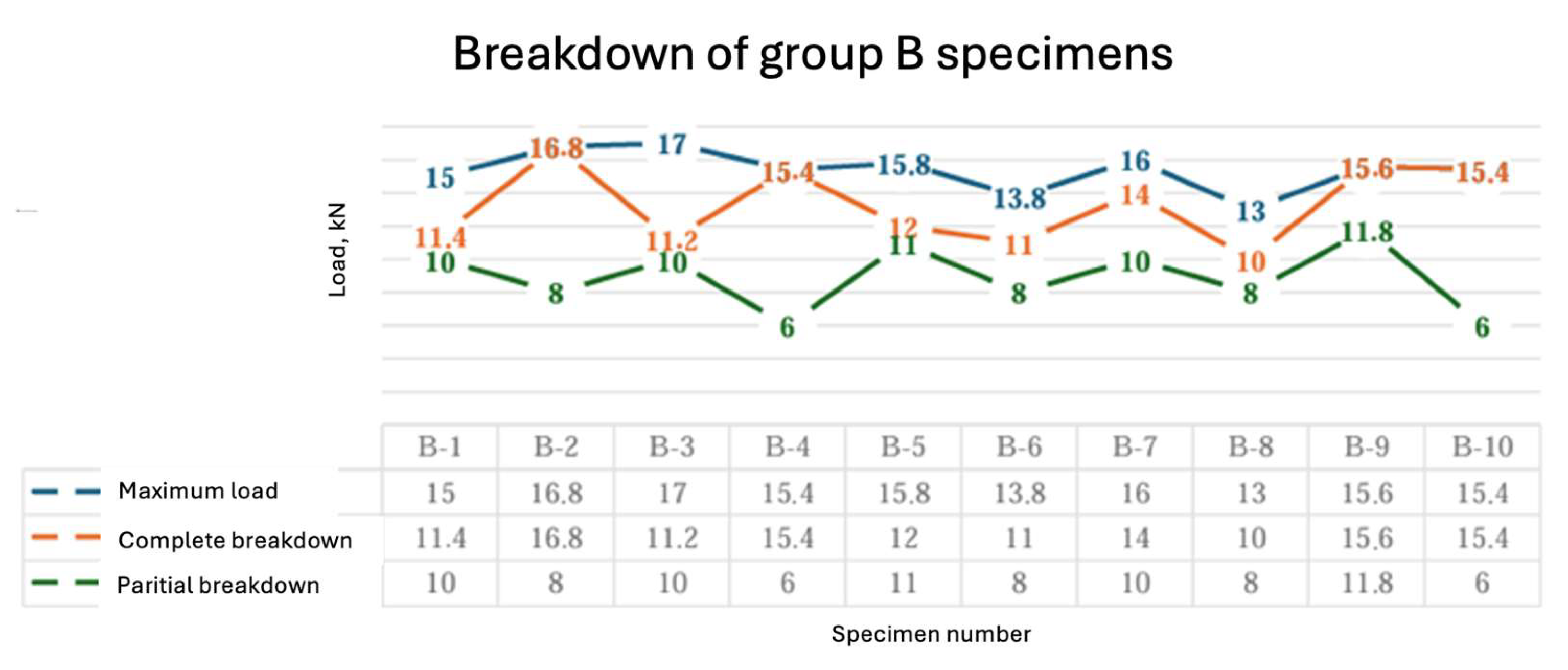
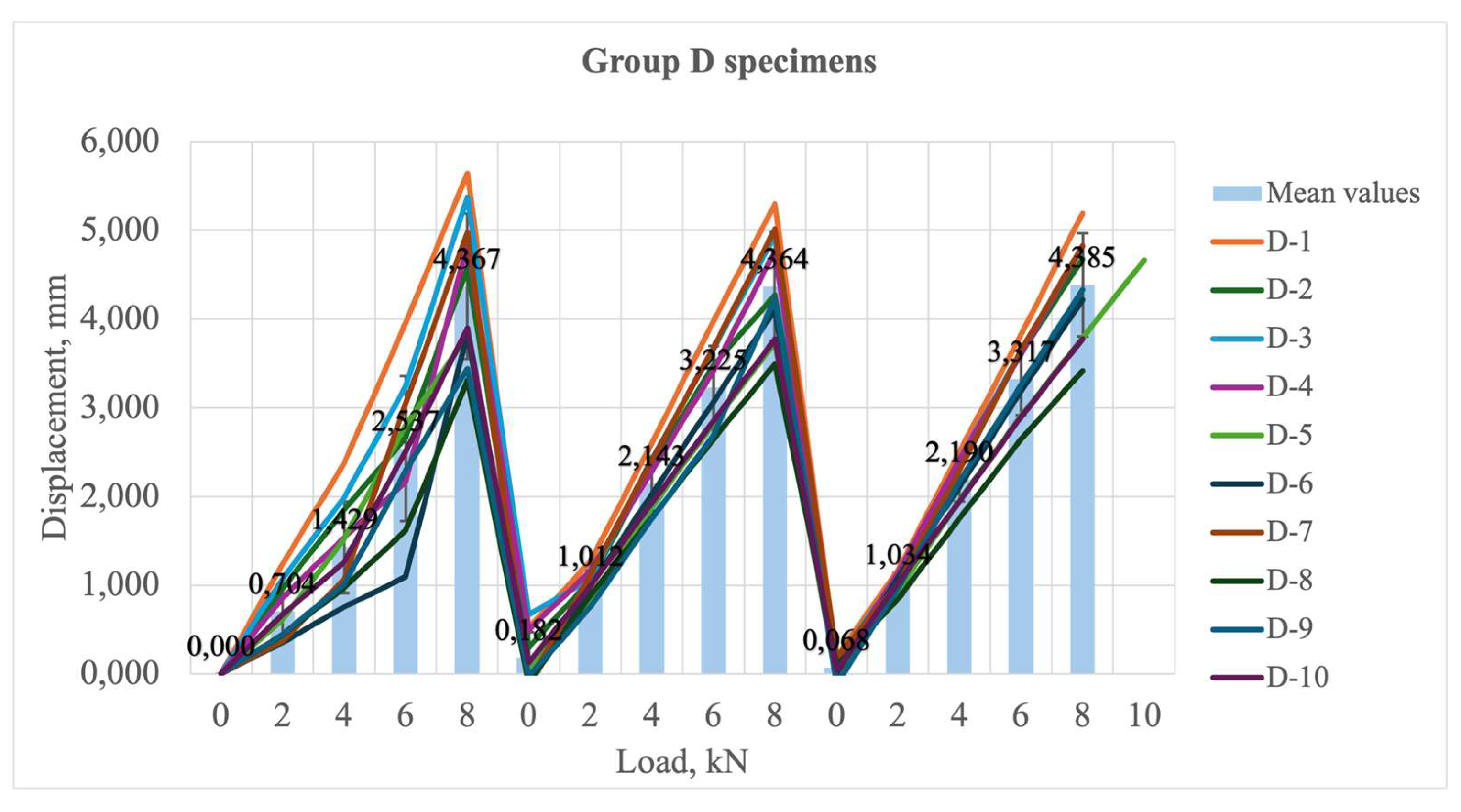
3.1.1. Description of Experimental Results
3.1.2. Comparison of Results, Obtained by Laboratorian Experiment, FEM and Analytical Analyses
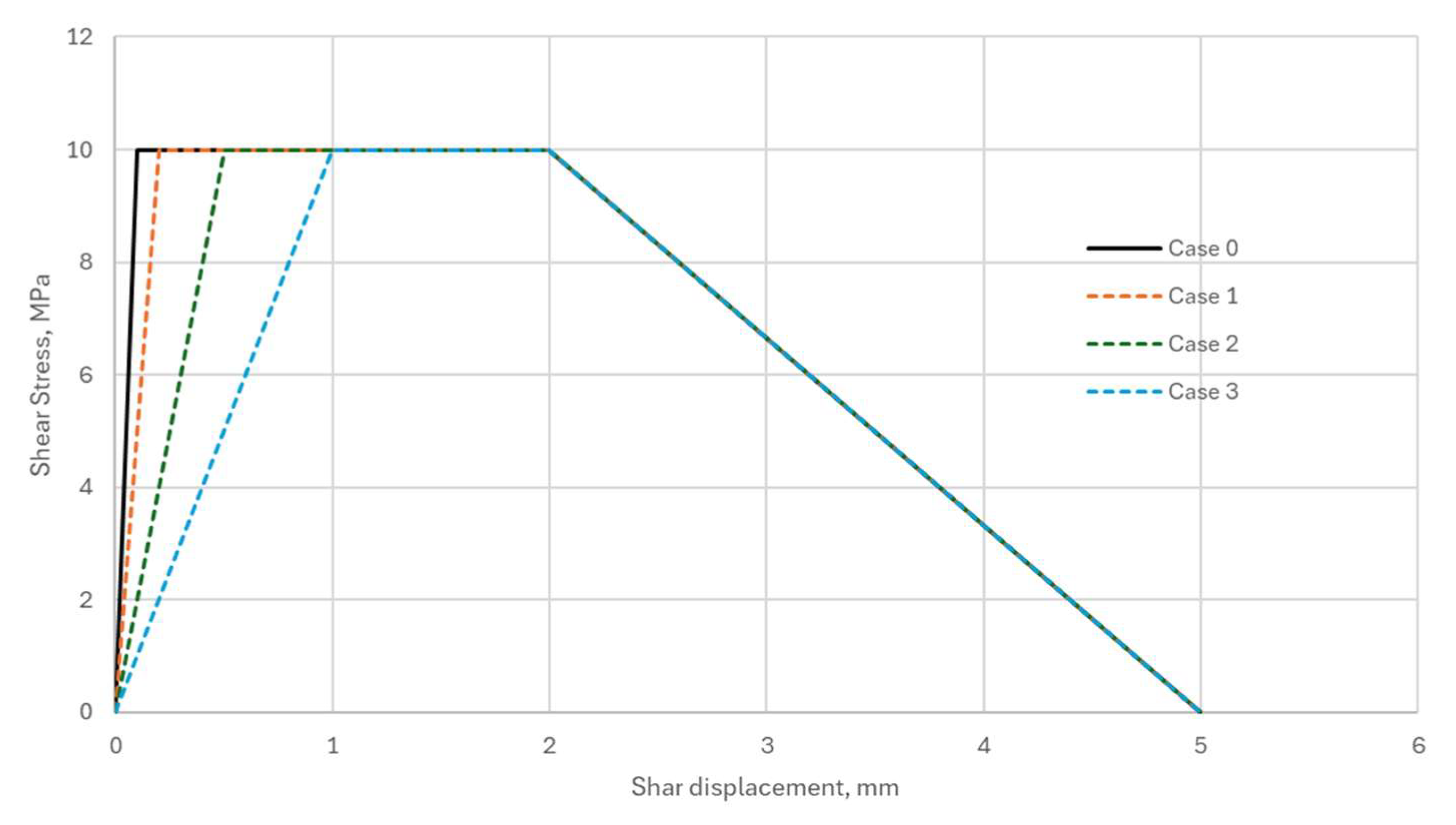
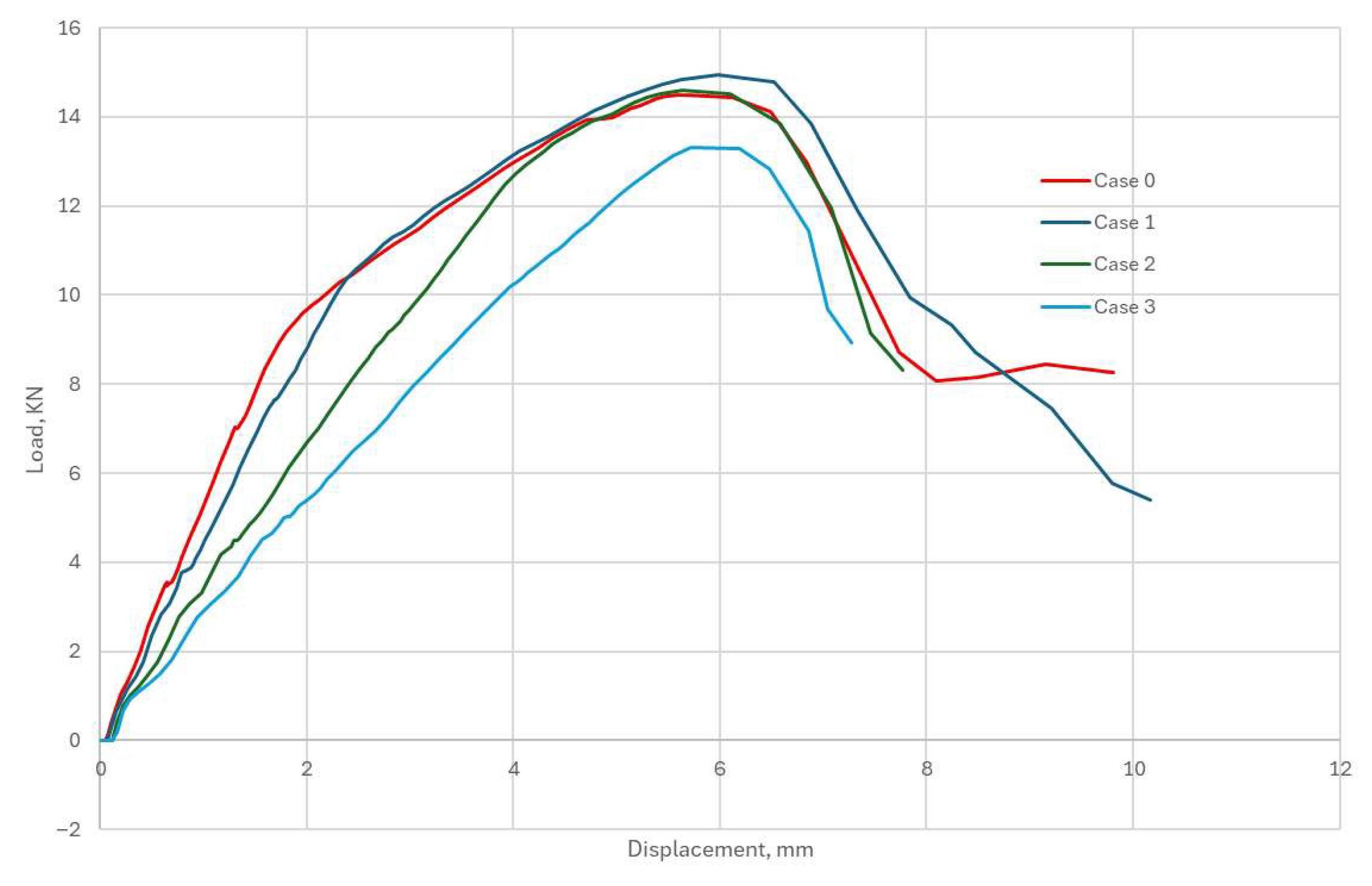
3.1.3. Influence of the Adhesive Layer Reinforcement on the Behaviour of the Timber–Concrete Members Subjected to Flexure
- Varying the number, orientation and location of reinforcement to identify the optimum configuration;
- Investigate the adhesion quality of reinforcement with different reinforcement materials in the adhesive layer to achieve a more effective composite effect.
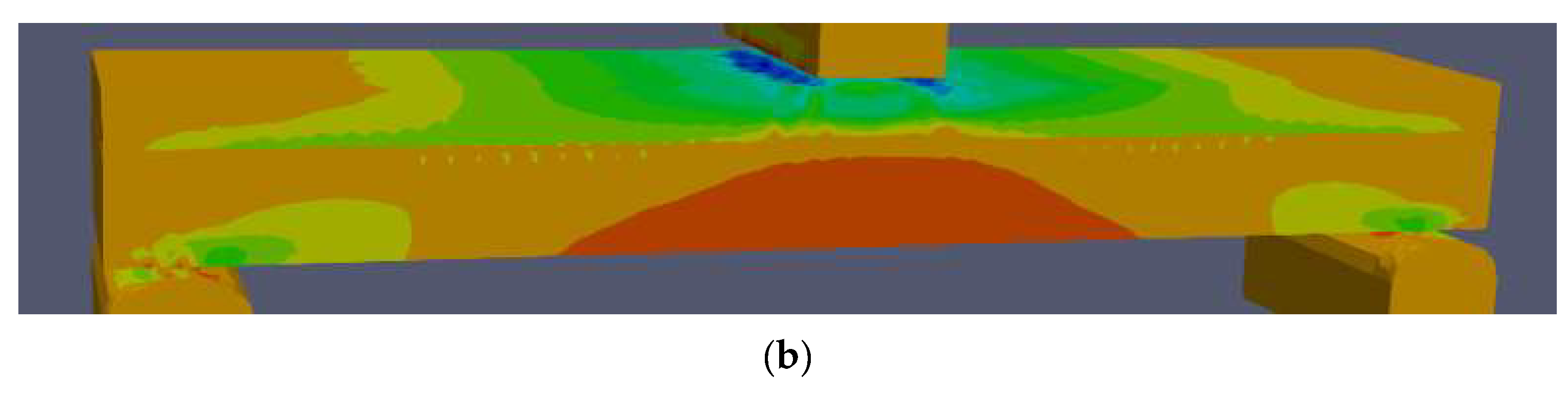
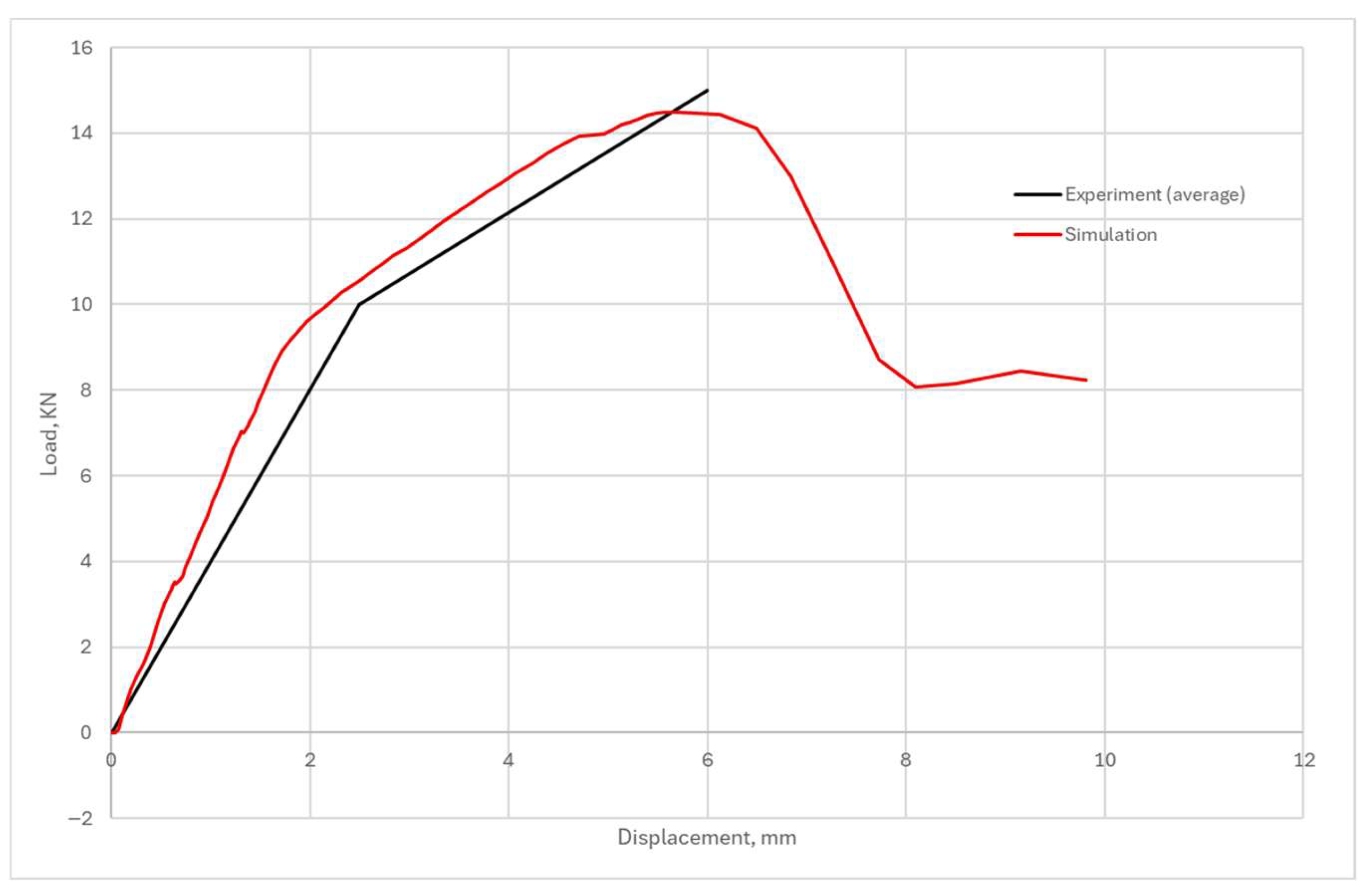
3.2. Simulation Validation with Experiments
4. Conclusions
- Applying the macro-mechanics layered material model to epoxy adhesive layers reinforced by a glass fibre yarn net, enabling vertical displacement predictions within less than 5% error compared to laboratory results.
- The introduction of an epoxy adhesive reinforcement method increased the load-bearing capacity of TCC specimens by approximately 30% compared to unreinforced specimens and simultaneously reduced the brittleness of the adhesive connection.
- Verification of the Verisim4D finite element software for modelling non-linear behaviour of the reinforced adhesive layer and concrete, achieving close agreement with experimental load-displacement curves across all three specimen types.
- Critical assessment of different analytical design methods for TCC members with reinforced adhesive layers, culminating in the selection of the layered macro-mechanics approach that best captures the mechanical interactions and slip behaviour in such composites.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Buka-Vaivade, K.; Serdjuks, D.; Podkoritovs, A.; Pakrastins, L.; Mironovs, V. Rigid Connection with Granite Chips in the Timber-Concrete Composite. Environ. Technol. Resour. Proc. Int. Sci. Pr. Conf. 2021, 3, 36–39. [Google Scholar] [CrossRef]
- Cardoso, W.; Baptista, R.C.; Machado, T.A.P.; Galdino, A.G.d.S.; Di Felice, R. Evaluation of the Incorporation of Marble and Granite Cutting Residues in Concrete for the Production of Interlocking Paving Floors. Rev. Ifes Ciência 2021, 7, 1–17. [Google Scholar] [CrossRef]
- Movaffaghi, H.; Pyykkö, J.; Yitmen, I. Value-Driven Design Approach for Optimal Long-Span Timber-Concrete Composite Floor in Multi-Storey Wooden Residential Buildings. Civ. Eng. Environ. Syst. 2020, 37, 100–116. [Google Scholar] [CrossRef]
- Shi, B.; Zhou, X.; Tao, H.; Yang, H.; Wen, B. Long-Term Behavior of Timber–Concrete Composite Structures: A Literature Review on Experimental and Numerical Investigations. Buildings 2024, 14, 1770. [Google Scholar] [CrossRef]
- Eslami, H.; Yaghma, A.; Bhagya Jayasinghe, L.; Waldmann, D. Influence of Different End-of-Life Cycle Scenarios on the Environmental Impacts of Timber-Concrete Composite Floor Systems. In Proceedings of the World Conference on Timber Engineering (WCTE 2023), Oslo, Norway, 19–22 June 2023; pp. 982–988. [Google Scholar]
- Ilgın, H.E.; Aslantamer, Ö.N. Analysis of Space Efficiency in High-Rise Timber Residential Towers. Appl. Sci. 2024, 14, 4337. [Google Scholar] [CrossRef]
- Nepal, P.; Prestemon, J.P.; Ganguly, I.; Kumar, V.; Bergman, R.D.; Poudyal, N.C. The Potential Use of Mass Timber in Mid-to High-Rise Construction and the Associated Carbon Benefits in the United States. PLoS ONE 2024, 19, e0298379. [Google Scholar] [CrossRef]
- Monteiro, S.R.S.; Dias, A.M.P.G.; Lopes, S.M.R. Transverse Distribution of Concentrated Loads in Timber–Concrete Floors: Parametric Study. Proc. Inst. Civ. Eng.-Struct. Build. 2020, 173, 340–351. [Google Scholar] [CrossRef]
- Ustinovichius, L.; Turskis, Z.; Miedziałowski, C.; Vaišnoras, M. Implementation of Wood-Framed Buildings in the Nordic Region: A MADAMOS (an Integrated Multi-Criteria Decision-Making Approach for Profitable Realisation Alternatives) Method. Buildings 2024, 14, 1020. [Google Scholar] [CrossRef]
- Pastori, S.; Salehi, M.-S.; Radl, S.; Mazzucchelli, E.S. A Fast-Calibrated Computational Fluid Dynamic Model for Timber–Concrete Composite Ventilated Façades. Buildings 2024, 14, 3567. [Google Scholar] [CrossRef]
- Gutiérrez, N.; Negrão, J.; Dias, A.; Guindos, P. Bibliometric Review of Prefabricated and Modular Timber Construction from 1990 to 2023: Evolution, Trends, and Current Challenges. Sustainability 2024, 16, 2134. [Google Scholar] [CrossRef]
- Şahin, N.; Biçer, Ö.P. Development of Cross-Laminated Timber and Current Standards in Türkiye. SETSCI Conf. Proc. 2024, 20, 32–36. [Google Scholar] [CrossRef]
- Siqueira, T.P.L.; da Glória, M.Y.R.; Martinelli, E.; Toledo Filho, R.D. Development and Validation of a Theoretical Model for Flexural Behaviour in Timber-Concrete and Bamboo-Concrete Composite Beams. Buildings 2025, 15, 2021. [Google Scholar] [CrossRef]
- Wen, B.; Tao, H.; Shi, B.; Yang, H. Dynamic Properties of Timber–Concrete Composite Beams with Crossed Inclined Coach Screw Connections: Experimental and Theoretical Investigations. Buildings 2023, 13, 2268. [Google Scholar] [CrossRef]
- Cvetković, R.; Ranković, S.; Mišulić, T.K.; Kukaras, D. Experimental Analysis of Mechanical Behaviour of Timber-Concrete Composite Beams with Different Connecting Systems. Buildings 2024, 14, 79. [Google Scholar] [CrossRef]
- Wen, B.; Shi, B.; Tao, H.; Yang, H.; Huang, B. Experimental Investigations on Vibration Performance of Timber-Concrete Composite Beams Using Lightweight Aggregate Concrete. In Proceedings of the World Conference on Timber Engineering (WCTE 2023), Oslo, Norway, 19–22 June 2023; pp. 1888–1893. [Google Scholar]
- Theoretical and Experimental Research on Slip and Uplift of the Timber-Concrete Composite Beam: BioResources. Available online: https://bioresources.cnr.ncsu.edu/ (accessed on 23 July 2025).
- Denouwé, D.D.; Messan, A.; Fournely, E.; Bouchair, A. Influence of Interlayer in Timber-Concrete Composite Structures with Threaded Rebar as Shear Connector-Experimental Study. Am. J. Civ. Eng. Archit. 2018, 6, 38–45. [Google Scholar] [CrossRef][Green Version]
- Cao, J.; Yu, D.; Zhang, J. Mechanical Properties of Timber-Concrete Connections with Steel Tube Connectors. Sustain. Struct. 2022, 2, 17. [Google Scholar] [CrossRef]
- Buka-Vaivade, K.; Serdjuks, D.; Pakrastins, L. Cost Factor Analysis for Timber–Concrete Composite with a Lightweight Plywood Rib Floor Panel. Buildings 2022, 12, 761. [Google Scholar] [CrossRef]
- Mirdad, M.A.H.; Khan, R.; Chui, Y.H. Analytical Procedure for Timber−Concrete Composite (TCC) System with Mechanical Connectors. Buildings 2022, 12, 885. [Google Scholar] [CrossRef]
- Soalih, H.A.; Demir, S. Current Practice and Recent Developments of Shear Connectors for Timber Concrete Composite Applications: A State of the Art Review. JSEAM 2023, 6, 422–440. [Google Scholar] [CrossRef]
- Sandak, A.; Brzezicki, M.; Sandak, J. 9—Trends and Perspectives in the Use of Timber and Derived Products in Building Façades. In New Materials in Civil Engineering; Samui, P., Kim, D., Iyer, N.R., Chaudhary, S., Eds.; Butterworth-Heinemann: Oxford, UK, 2020; pp. 333–374. ISBN 978-0-12-818961-0. [Google Scholar]
- Van Thai, M.; Galimard, P.; Elachachi, S.M.; Ménard, S. Multi-Objective Optimisation of Cross Laminated Timber-Concrete Composite Floor Using NSGA-II. J. Build. Eng. 2022, 52, 104285. [Google Scholar] [CrossRef]
- Shahnewaz, M.; Jackson, R.; Tannert, T. Reinforced Cross-Laminated Timber-Concrete Composite Floor Systems. Eng. Struct. 2023, 291, 116395. [Google Scholar] [CrossRef]
- Derikvand, M.; Fink, G. Bending Properties of Deconstructable Cross-Laminated Timber-Concrete Composite Floor Elements. Wood Mater. Sci. Eng. 2022, 17, 253–260. [Google Scholar] [CrossRef]
- Khorsandnia, N.; Valipour, H.R.; Crews, K. Finite Element Modeling of Timber-Concrete Composite Beams under Short-Term Loadings. In ECCOMAS 2012-European Congress on Computational Methods in Applied Sciences and Engineering, e-Book Full Papers; Vienna University of Technology: Vienna, Austria, 2012; pp. 859–867. [Google Scholar]
- Briuka, E.; Serdjuks, D.; Akishin, P.; Sahmenko, G.; Podkoritovs, A.; Ozolins, R. Behaviour Analysis of Beam-Type Timber and Timber-Concrete Composite Panels. Appl. Sci. 2024, 14, 7403. [Google Scholar] [CrossRef]
- Fu, Q.; Yanb, L.; Kasal, B. Bending Behavior of Adhesively-Bonded Engineered Wood-Concrete Composite Decks. Acta Polytech. CTU Proc. 2022, 33, 175–180. [Google Scholar] [CrossRef]
- Yeoh, D.; Fragiacomo, M.; Deam, B. Experimental Behaviour of LVL–Concrete Composite Floor Beams at Strength Limit State. Eng. Struct. 2011, 33, 2697–2707. [Google Scholar] [CrossRef]
- Clouston, P.; Bathon, L.A.; Schreyer, A. Shear and Bending Performance of a Novel Wood–Concrete Composite System. J. Struct. Eng. 2005, 131, 1404–1412. [Google Scholar] [CrossRef]
- Bogensperger, T.; Krenn, H. Ribbed Clt Elements with Cut-Backs. In Proceedings of the World Conference on Timber Engineering 2025, Brisbane, Australia, 22–26 June 2025; pp. 1104–1111. [Google Scholar]
- VeriSim4D FEM Software by InDEM. Available online: https://indem.engineering (accessed on 1 August 2025).
- EN 1995-1-1; Erocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- EN 1995-1-1. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1995.1.1.2004.pdf (accessed on 17 September 2025).
- EN 1992-1-1. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1992.1.1.2004.pdf (accessed on 17 September 2025).
- Sliseris, J.; Frolovs, G.; Rocens, K.; Goremikins, V. Optimal Design of GFRP-Plywood Variable Stiffness Plate. Procedia Eng. 2013, 57, 1060–1069. [Google Scholar] [CrossRef]
- Sliseris, J.; Andrä, H.; Kabel, M.; Wirjadi, O.; Dix, B.; Plinke, B. Estimation of Fiber Orientation and Fiber Bundles of MDF. Mater. Struct. 2016, 49, 4003–4012. [Google Scholar] [CrossRef]
- Buka-Vaivade, K.; Sliseris, J.; Serdjuks, D.; Sahmenko, G.; Pakrastins, L. Numerical Comparison of HPFRC and HPC Ribbed Slabs. IOP Conf. Ser. Mater. Sci. Eng. 2019, 660, 012054. [Google Scholar] [CrossRef]
- Gailitis, R.; Sliseris, J.; Korniejenko, K.; Mikuła, J.; Łach, M.; Pakrastins, L.; Sprince, A. Long-Term Deformation Properties of a Carbon-Fiber-Reinforced Alkali-Activated Cement Composite. Mech. Compos. Mater. 2020, 56, 85–92. [Google Scholar] [CrossRef]
- Sliseris, J.; Korjakins, A. Numerical Modeling of the Casting Process and Impact Loading of a Steel-Fiber-Reinforced High-Performance Self-Compacting Concrete. Mech. Compos. Mater. 2019, 55, 29–40. [Google Scholar] [CrossRef]
- Červenka, V.; Jendele, L.; Červenka, J. ATENA Program Documentation Part 1; Cervenka Consulting: Praha, Czech Republic, 2021. [Google Scholar]
- Walraven, J. Fib Model Code for Concrete Structures 2010: Mastering Challenges and Encountering New Ones. Struct. Concr. 2013, 14, 3–9. [Google Scholar] [CrossRef]
- Yvonne, D. Murray Manual for LS-DYNA Wood Material Model 143; US Department of Transportation: Washington, DC, USA, 2007; p. 166. [Google Scholar]
- Latvijas Finieris Group. Plywood Handbook 2022; Latvijas Finieris Group: Riga, Latvia, 2022. [Google Scholar]

















| Title of the Method | Advantages | Limitations/Disadvantages | Suitability for Adhesive Timber-to-Concrete Connections |
|---|---|---|---|
| The composite equations (governing equations of a composite beam) | Accurate model of slip and shear force distribution | Complex analysis, difficult to use without software | Average—calibration of parameters required |
| The CEREMA method | Solution for sinusoidal load, relatively simple | Suitable for simple loads, does not consider the non-linearity of the connection | Low—over-simplified |
| The semi-analytical Vh-s method | Possible analysis of the non-linear behaviour of the connection (softening phase) | Not suitable for compliant connections, iterative and complex | Average—can be used for the adhesive connections with limitations |
| The Gamma method | Simple, practical application; Can be extended by the information from EN 1995-1-1 [35] | Limited in number of layers, does not accept shear deformations along length | Average—limitations related to the multilayered structures |
| Micromechanics approach for layered material | Possibility of orthotropic layers analysis, high precision | Precise information regarding the mechanical properties of all the layers is required | High—precisely shows the effect of adhesive layer |
| Finite element method | Accurate and general method | Many input parameters that are not easy to define, less transparent results. | Very high- can consider all important mechanical effects |
| Material | Property Name | Value | Unit | Reference |
|---|---|---|---|---|
| Concrete | Grade | C30/37 | - | Calc. from compressive strength |
| Modulus of elasticity | 33 | GPa | Calc. from compressive strength | |
| Compressive strength | 40 | MPa | Exp. Measured | |
| Tensile strength | 3.5 | MPa | Calc. from compressive strength | |
| Fracture energy | 147.6 | Pa×m | Calc. from compressive strength | |
| Poissons ratio | 0.2 | - | Recommended value in EN 1992 | |
| Density | 2400.0 | kg/m3 | Exp. Measured | |
| Timber | Plywood type, grade | Riga Ply, S | - | [41] |
| Modulus of elasticity in grain direction, | 6.5 | GPa | [45] | |
| Modulus of elasticity perpendicular to grains, | 0.37 | GPa | [45] | |
| Poissons ratio in L-T and T-L plane, | 0.002 | - | [45] | |
| Poissons ratio in R-T plane, | 0.2 | - | [45] | |
| Shear modulus in L-T and L-R plane, | 0.69 | GPa | [45] | |
| Shear modulus in T-R plane, | 0.15 | GPa | [45] | |
| Tensile strength parallel to grains | 30 | MPa | [45] | |
| Compressive strength parallel to grains | 17 | MPa | [45] | |
| Tensile strength perpendicular to grains | 0.4 | MPa | [45] | |
| Compressive strength perpendicular to grains | 2.2 | MPa | [45] | |
| Rolling shear strength | 3.2 | MPa | [45] | |
| Shear strength parallel to grains | 5 | MPa | [45] | |
| Fracture energy, mode I- splitting, parallel to grains | 0.5 | MPa×cm | [44] | |
| Fracture energy, mode I- splitting, perpendicular to grains | 0.005 | MPa×cm | [44] | |
| Fracture energy, mode II- shearing, parallel to grains | 8.38 | MPa×cm | [44] | |
| Fracture energy, mode II- shearing, perpendicular to grains | 0.078 | MPa×cm | [44] | |
| B,D parameters | 30 | - | [44] | |
| Density | 800 | kg/m3 | Exp. Measured |
| Case | Initial Stiffness, MPa/mm | Displacement at Yield Point, mm | Peak Shear Stress, MPa |
|---|---|---|---|
| Case 0 | 100 | 0.1 | 10 |
| Case 1 | 50 | 0.2 | 10 |
| Case 2 | 20 | 0.5 | 10 |
| Case 3 | 10 | 1 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haijima, A.; Briuka, E.; Sliseris, J.; Serdjuks, D.; Ziverts, A.; Lapkovskis, V. Behaviour Analysis of Timber–Concrete Composite Floor Structure with Granite Chip Connection. J. Compos. Sci. 2025, 9, 538. https://doi.org/10.3390/jcs9100538
Haijima A, Briuka E, Sliseris J, Serdjuks D, Ziverts A, Lapkovskis V. Behaviour Analysis of Timber–Concrete Composite Floor Structure with Granite Chip Connection. Journal of Composites Science. 2025; 9(10):538. https://doi.org/10.3390/jcs9100538
Chicago/Turabian StyleHaijima, Anna, Elza Briuka, Janis Sliseris, Dmitrijs Serdjuks, Arturs Ziverts, and Vjaceslavs Lapkovskis. 2025. "Behaviour Analysis of Timber–Concrete Composite Floor Structure with Granite Chip Connection" Journal of Composites Science 9, no. 10: 538. https://doi.org/10.3390/jcs9100538
APA StyleHaijima, A., Briuka, E., Sliseris, J., Serdjuks, D., Ziverts, A., & Lapkovskis, V. (2025). Behaviour Analysis of Timber–Concrete Composite Floor Structure with Granite Chip Connection. Journal of Composites Science, 9(10), 538. https://doi.org/10.3390/jcs9100538







