Dynamic Mechanical Behavior of Nanosilica-Based Epoxy Composites Under LEO-like UV-C Exposure
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. UV-C Irradiation
2.3. Dynamic Mechanical Analysis
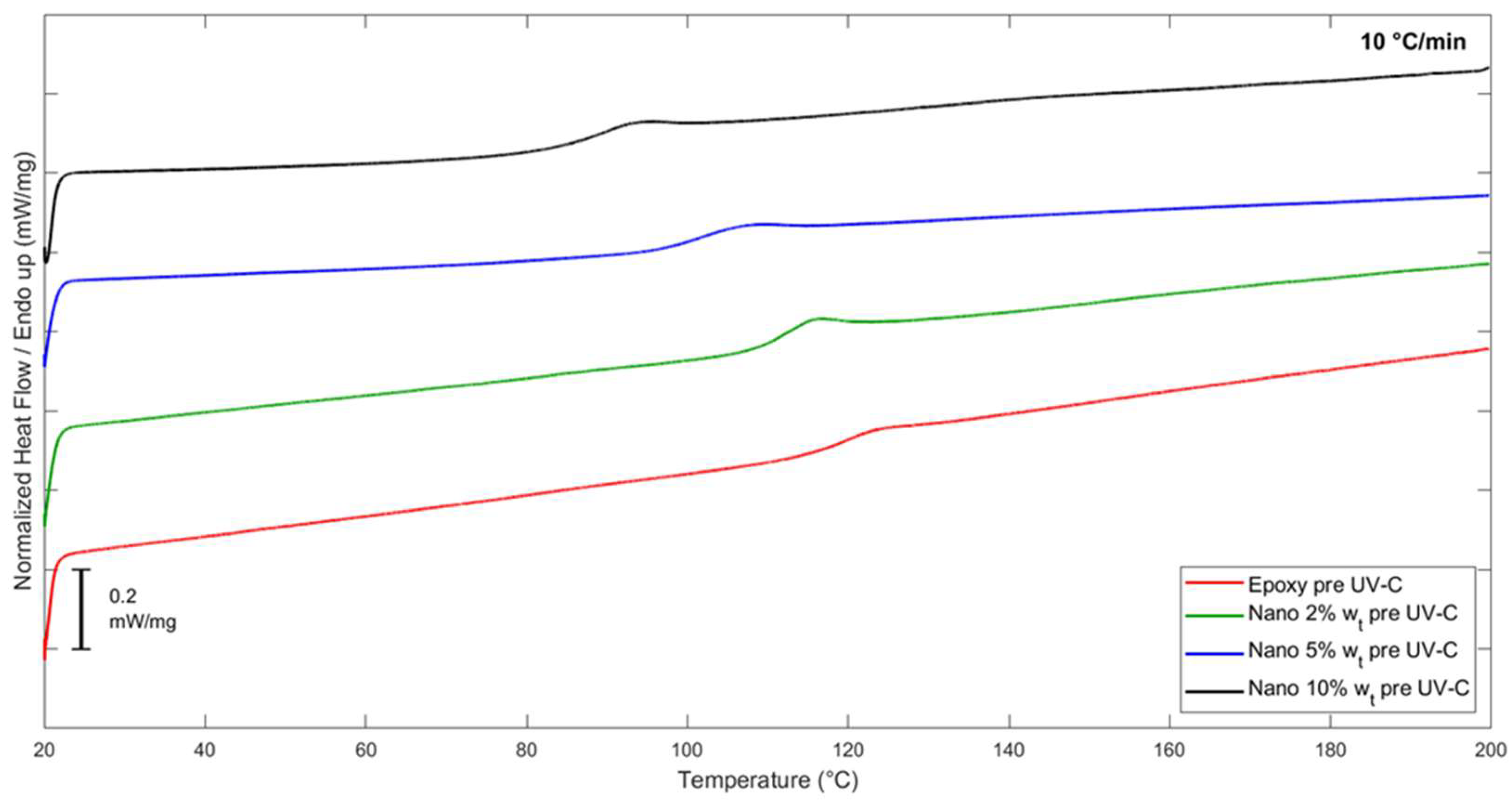
2.4. Differential Scanning Calorimetry
2.5. FTIR
3. Results
3.1. Cryogenic-Temperature Tests
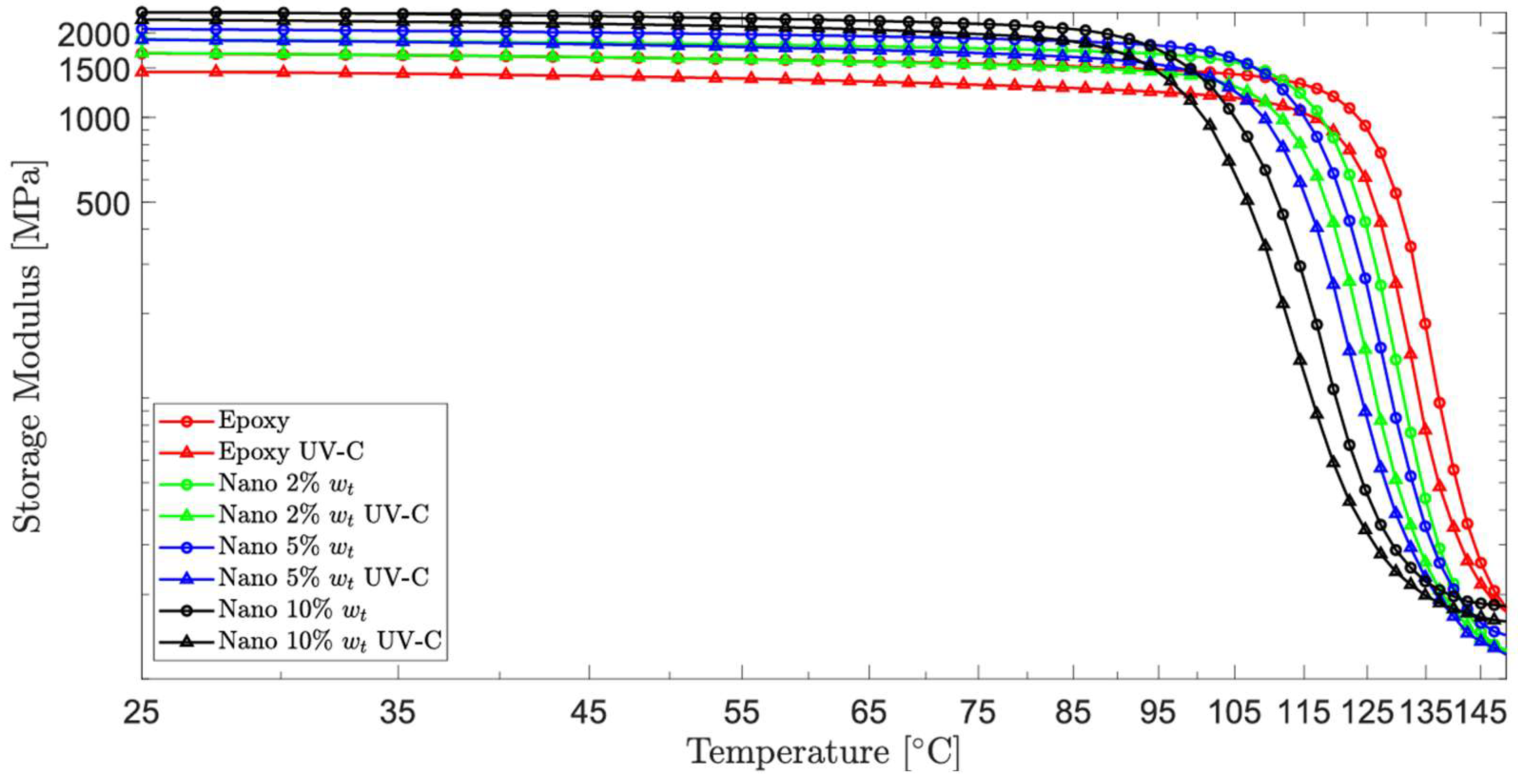
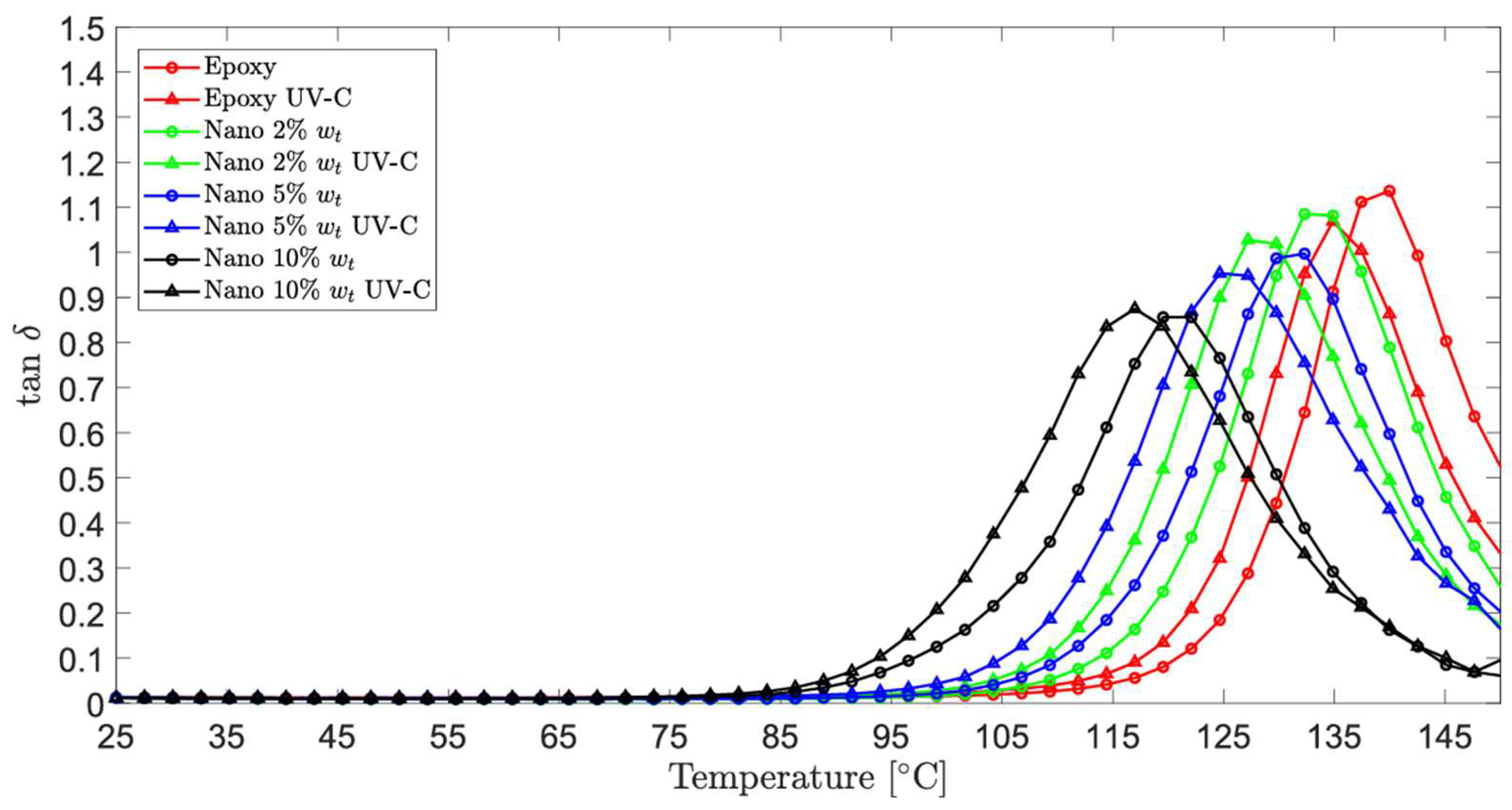
3.2. Comparative Analysis of Temperature-Dependent Behavior in UVC-Irradiated and Non-Irradiated Samples
3.3. Frequency Response of Nanosilica–Epoxy Composites
3.4. Fourier-Transform Infrared Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DMA | Dynamic Mechanical Analysis |
| DSC | Differential Scanning Calorimetry |
| FTIR | Fourier-Transform Infrared Spectroscopy |
| LEO | Low Earth Orbit |
| PMCs | Polymeric Matrix Composites |
| Tg | Temperature of glass transition |
| TTPS | Time–Temperature Superposition Principle |
| UV | Ultraviolet |
Appendix A


References
- Shimamura, H.; Miyazaki, E. Investigations into Synergistic Effects of Atomic Oxygen and Vacuum Ultraviolet. J. Spacecr. Rocket. 2009, 46, 241–247. [Google Scholar] [CrossRef]
- Lu, T.; Solis-Ramos, E.; Yi, Y.; Kumosa, M. UV degradation model for polymers and polymer matrix composites. Polym. Degrad. Stab. 2018, 154, 203–210. [Google Scholar] [CrossRef]
- Yagnamurthy, S.; Chen, Q.; Chen, C.; Chasiotis, I. Erosion yield of epoxy–silica nanocomposites at the lower earth orbit environment of the International Space Station. J. Compos. Mater. 2012, 47, 107–117. [Google Scholar] [CrossRef]
- Gordo, P.; Frederico, T.; Melicio, R.; Duzellier, S.; Amorim, A. System for space materials evaluation in LEO environment. Adv. Space Res. 2020, 66, 307–320. [Google Scholar] [CrossRef]
- Zhang, B.; Clausi, M.; Heck, B.; Laurenzi, S.; Santonicola, M.G.; Kleperis, J.; Antuzevics, A.; Reiter, G.; Aleshin, A.N.; Lobach, A.S. Changes in Surface Free Energy and Surface Conductivity of Carbon Nanotube/Polyimide Nanocomposite Films Induced by UV Irradiation. ACS Appl. Mater. Interfaces 2021, 13, 24218–24227. [Google Scholar] [CrossRef]
- Jang, J.-H.; Hong, S.-B.; Kim, J.-G.; Goo, N.-S.; Yu, W.-R. Accelerated Testing Method for Predicting Long-Term Properties of Carbon Fiber-Reinforced Shape Memory Polymer Composites in a Low Earth Orbit Environment. Polymers 2021, 13, 1628. [Google Scholar] [CrossRef] [PubMed]
- Grossman, E.; Gouzman, I. Space environment effects on polymers in low earth orbit. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2003, 208, 48–57. [Google Scholar] [CrossRef]
- Toto, E.; Laurenzi, S.; Paris, C.; Santonicola, M.G. Combined Effects of Solar Radiation and High Vacuum on the Properties of Graphene/Polysiloxane Nanocomposites in Simulated Space Environment. J. Compos. Sci. 2023, 7, 215. [Google Scholar] [CrossRef]
- Jin, S.B.; Son, G.S.; Kim, Y.H.; Kim, C.G. Enhanced durability of silanized multi-walled carbon nanotube/epoxy nanocomposites under simulated LEO space environment. Compos. Sci. Technol. 2013, 87, 224–231. [Google Scholar] [CrossRef]
- De Groh, K.K.; Banks, B.A. Atomic Oxygen Erosion Data from the MISSE 2–8 Missions. NASA Technical Memorandum, 2019. Available online: https://ntrs.nasa.gov/citations/20190025445 (accessed on 13 September 2024).
- Chen, C.; Justice, R.S.; Schaefer, D.W.; Baur, J.W. Highly dispersed nanosilica–epoxy resins with enhanced mechanical properties. Polymer 2008, 49, 3805–3815. [Google Scholar] [CrossRef]
- Sprenger, S. Nanosilica-Toughened Epoxy Resins. Polymers 2020, 12, 1777. [Google Scholar] [CrossRef]
- Ranjbar, Z.; Ashhari, S.; Jannesari, A.; Montazeri, S. Effects of nanosilica on the Anticorrosive properties of epoxy coatings. Prog. Color Color. Coat. 2013, 6, 119–128. [Google Scholar] [CrossRef]
- Prabhakaran, R. Nano composites for Space Applications. J. Aerosp. Sci. Technol. 2015, 67, 1–17. [Google Scholar]
- Lee, D.W.; Yoo, B.R. Advanced silica/polymer composites: Materials and applications. J. Ind. Eng. Chem. 2016, 38, 1–12. [Google Scholar] [CrossRef]
- Guo, Q.; Zhu, P.; Li, G.; Wen, J.; Wang, T.; Lu, D.; Sun, R.; Wong, C. Study on the effects of interfacial interaction on the rheological and thermal performance of silica nanoparticles reinforced epoxy nanocomposites. Compos. Part B: Eng. 2017, 116, 388–397. [Google Scholar] [CrossRef]
- Allahverdi, A.; Ehsani, M.; Janpour, H.; Ahmadi, S. The effect of nanosilica on mechanical, thermal and morphological properties of epoxy coating. Prog. Org. Coat. 2012, 75, 543–548. [Google Scholar] [CrossRef]
- Sprenger, S. Epoxy resin composites with surface-modified silicon dioxide nanoparticles: A review. J. Appl. Polym. Sci. 2013, 130, 1421–1428. [Google Scholar] [CrossRef]
- Chennareddy, R.; Tuwair, H.; Kandil, U.F.; ElGawady, M.; Reda Taha, M.M. UV-resistant GFRP composite using carbon nanotubes. Constr. Build. Mater. 2019, 220, 679–689. [Google Scholar] [CrossRef]
- Suliga, A.; Jakubczyk, E.M.; Hamerton, I.; Viquerat, A. Analysis of atomic oxygen and ultraviolet exposure effects on cycloaliphatic epoxy resins reinforced with octa-functional POSS. Acta Astronaut. 2018, 142, 103–111. [Google Scholar] [CrossRef]
- Tortorici, D.; Toto, E.; Santonicola, M.G.; Laurenzi, S. Effects of UV C exposure on composite materials made of recycled carbon fibers. Acta Astronaut. 2024, 220, 367–373. [Google Scholar] [CrossRef]
- Khanna, Y.P.; Turi, E.A.; Taylor, T.J.; Vickroy, V.V.; Abbott, R.F. Dynamic mechanical relaxations in polyethylene. Macromolecules 1985, 18, 1302–1309. [Google Scholar] [CrossRef]
- Wolfrum, J.; Eibl, S.; Lietch, L. Rapid evaluation of long-term thermal degradation of carbon fiber epoxy composites. Compos. Sci. Technol. 2009, 69, 523–530. [Google Scholar] [CrossRef]
- CYCOM® 823 RTM Resin System. Technical Data Sheet; Solvay: Brussels, Belgium, 2016. [Google Scholar]
- THINKY CORPORATION. Planetary Centrifugal Mixer THINKY MIXER ARE-250 Instruction Manual; THINKY CORPORATION: Tokyo, Japan, 2022. [Google Scholar]
- Kemnitz, R.A.; Cobb, G.R.; Singh, A.K.; Hartsfield, C.R. Characterization of simulated LEO space environment effects on acid-spun carbon nanotube yarns. Mater. Des. 2019, 184, 108178. [Google Scholar] [CrossRef]
- Anderson, J.B.; Smith, R.E. Natural Orbit Environment Guidelines for Use in Aerospace Vehicle Development; NASA Technical Memorandum 4527; NASA: Huntsville, AL, USA, 1994.
- Determination of the Linear Viscoelastic Region of a Polymer Using a Strain Sweep on the DMA 2980. Available online: https://www.tainstruments.com/pdf/literature/TS61.pdf (accessed on 2 March 2025).
- Ljubić, D.; Stamenović, M.; Smithson, C.; Nujkić, M.; Međo, B.; Putić, S. Time: Temperature superposition principle: Application of WLF equation in polymer analysis and composites. Zaštita Mater. 2014, 55, 395–400. [Google Scholar]
- Zarrelli, M.; Skordos, A.A.; Partridge, I.K. Thermomechanical analysis of a toughened thermosetting system. Mech. Compos. Mater. 2008, 44, 181–190. [Google Scholar] [CrossRef]
- Lange, J.; Manson, J.A.E.; Hult, A. Build-up of structure and viscoelastic properties in epoxy and acrylate resins cured below their ultimate glass transition temperature. Polymer 1996, 37, 5859–5868. [Google Scholar] [CrossRef]
- Muller-Pabel, M.; Agudo, J.A.R.; Gude, M. Measuring and understanding cure-dependent viscoelastic properties of epoxy resin: A review. Polym. Test. 2022, 114, 107701. [Google Scholar] [CrossRef]
- Woo, E.; Seferis, J.; Schaffnit, R. Viscoelastic characterization of high-performance epoxy matrix composites. Polym. Compos. 1991, 12, 273–280. [Google Scholar] [CrossRef]
- Saseendran, S.; Wysocki, M.; Varna, J. Evolution of viscoelastic behavior of a curing LY5052 epoxy resin in the rubbery state. Adv. Compos. Mater. 2017, 26, 553. [Google Scholar] [CrossRef]
- Cui, Z.; Brinson, L.C. A combination optimization method for the estimation of material parameters for viscoelastic solids. Int. J. Comput. Sci. Math. 2014, 5, 325–335. [Google Scholar] [CrossRef]
- Introduction to Fourier Transform Infrared Spectroscopy. Available online: https://www.chem.uci.edu/~dmitryf/manuals/Fundamentals/FTIR%20principles.pdf (accessed on 11 June 2024).
- Widmann, G.; Schawe, J.; Riesen, R. Interpret DMA curves, Part 1. METTLER TOLEDO. Available online: https://www.mt.com/mt_ext_files/Editorial/Generic/0/TA_UserCom15_0460929710242401_files/tauserc15e.pdf (accessed on 11 June 2024).
- Liu, Y.L.; Hsu, C.Y.; Wei, W.L.; Jeng, R.J. Preparation and thermal properties of epoxy–silica nanocomposites from nanoscale colloidal silica. Polymer 2003, 44, 5159–5167. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Zhang, Z.Q.; Moon, K.S.; Wong, C.P. Glass transition and relaxation behavior of epoxy nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 3849–3858. [Google Scholar] [CrossRef]
- Zheng, Y.; Chonung, K.; Wang, G.; Wei, P.; Jiang, P. Epoxy/nano-silica composites: Curing kinetics, glass transition temperatures, dielectric, and thermal–mechanical performances. J. Appl. Polym. Sci. 2009, 111, 917–927. [Google Scholar] [CrossRef]
- Sperling, L.H. Basic Viscoelastic Definitions and Concepts. In Sound and Vibration Damping with Polymers; American Chemical Society: Washington, DC, USA, 1990. [Google Scholar]
- Khare, K.S.; Khare, R. Effect of carbon nanotube dispersion on glass transition in cross-linked epoxy–carbon nanotube nanocomposites: Role of interfacial interactions. J. Phys. Chem. B 2016, 117, 7444–7454. [Google Scholar] [CrossRef] [PubMed]
- Najmi, L.; Hu, Z. Effects of carbon nanotubes on thermal behavior of epoxy resin composites. J. Compos. Sci. 2023, 7, 313. [Google Scholar] [CrossRef]
- Gopalakrishnamurthy, P.K.; Sandur, C. Investigation of dynamic mechanical behavior of nanosilica filled carbon-Kevlar epoxy polymer hybrid nanocomposite. Ann. De Chim. Sci. Des Mater. 2022, 46, 141–146. [Google Scholar] [CrossRef]
- Kopsidas, S.; Olowojoba, G.B. Multifunctional epoxy composites modified with a graphene nanoplatelet/carbon nanotube hybrid. J. Appl. Polym. Sci. 2021, 138, 50890. [Google Scholar] [CrossRef]
- Al Azzawi, W.; Epaarachchi, J.A.; Leng, J. Investigation of ultraviolet radiation effects on thermomechanical properties and shape memory behavior of styrene-based shape memory polymers and its composite. Compos. Sci. Technol. 2018, 165, 266–273. [Google Scholar] [CrossRef]
- Shi, Z.; Zou, C.; Zhou, F.; Zhao, J. Analysis of the mechanical properties and damage mechanism of carbon fiber/epoxy composites under UV aging. Materials 2022, 15, 2919. [Google Scholar] [CrossRef]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity, 2nd ed.; Springer: New York, NY, USA, 2008; pp. 99–157. [Google Scholar]
- Sahmetlioglu, E.; Mart, H.; Yuruk, H.; Surme, Y. Synthesis and characterization of oligosalicylaldehyde-based epoxy resins. Chem. Pap. 2006, 60, 65–68. [Google Scholar] [CrossRef]
- Gonzalez, M.G.; Cabanelas, J.C.; Baselga, J. Applications of FTIR on epoxy resins-identification, monitoring the curing process, phase separation and water uptake. In Infrared Spectroscopy-Materials Science, Engineering and Technology, 2nd ed.; IntechOpen: Rijeka, Croatia, 2012; Volume 2, pp. 261–284. [Google Scholar]
- Yin, Q.; Yang, W.; Sun, C.; Di, M. Preparation and properties of lignin-epoxy resin composite. BioResources 2012, 7, 5737–5748. [Google Scholar] [CrossRef]
- FT-IR Spectra of Pure Silica Nanoparticles. Available online: https://www.researchgate.net/figure/FT-IR-spectra-of-pure-silica-nanoparticles_fig2_295092184 (accessed on 9 April 2025).
- Panwar, K.; Jassal, M.; Agrawal, A.K. In situ synthesis of Ag–SiO2 Janus particles with epoxy functionality for textile applications. Particuology 2014, 19, 107–112. [Google Scholar] [CrossRef]
- Petreanu, I.; Niculescu, V.C.; Enache, S.; Iacob, C.; Teodorescu, M. Structural Characterization of Silica and Amino-Silica Nanoparticles by Fourier Transform Infrared (FTIR) and Raman Spectroscopy. Anal. Lett. 2022, 56, 390–403. [Google Scholar] [CrossRef]
- Gheno, G.; Ganzerla, R.; Bortoluzzi, M.; Paganica, R. Accelerated weathering degradation behavior of polyester thermosetting powder coatings. Prog. Org. Coat. 2016, 101, 90–99. [Google Scholar] [CrossRef]
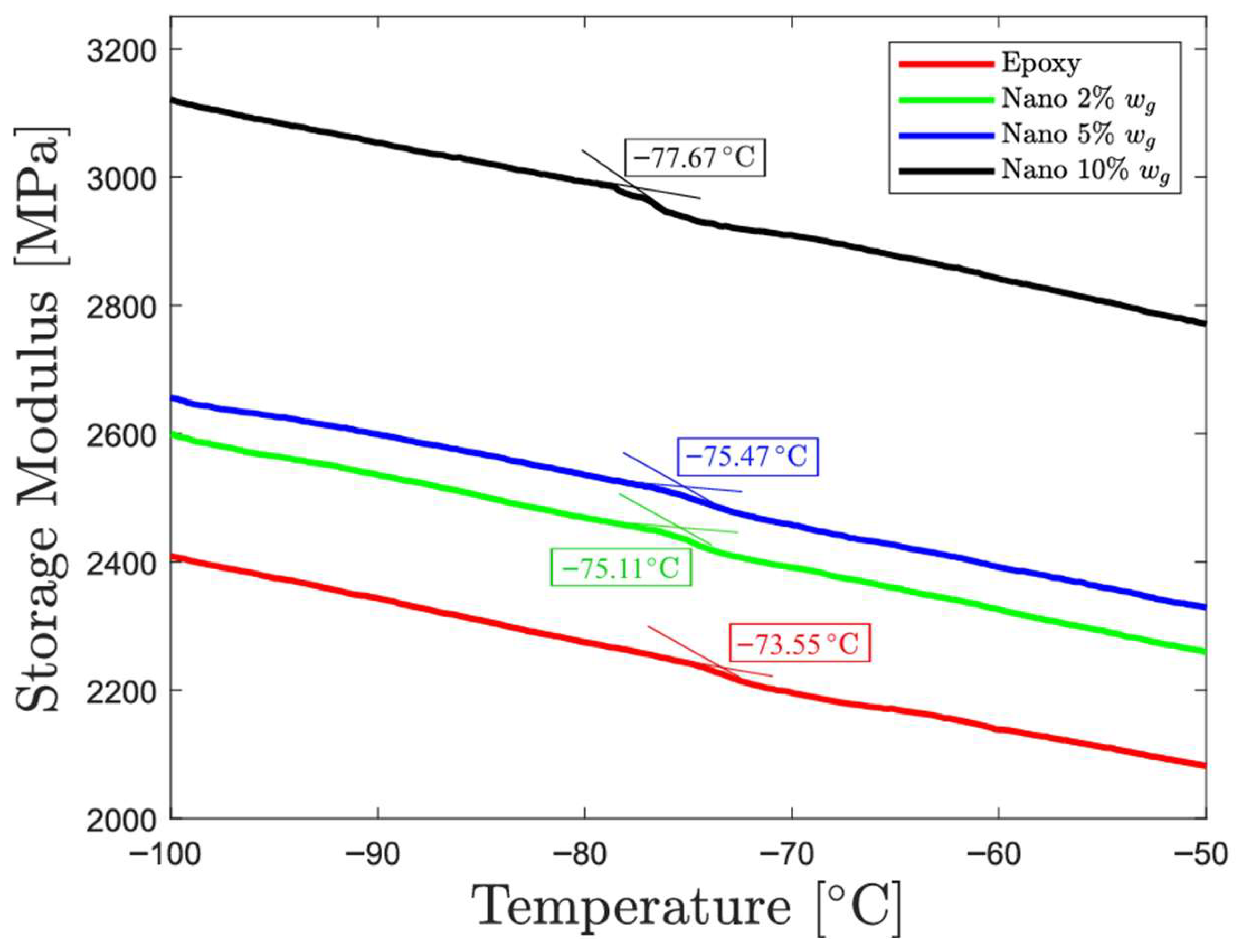
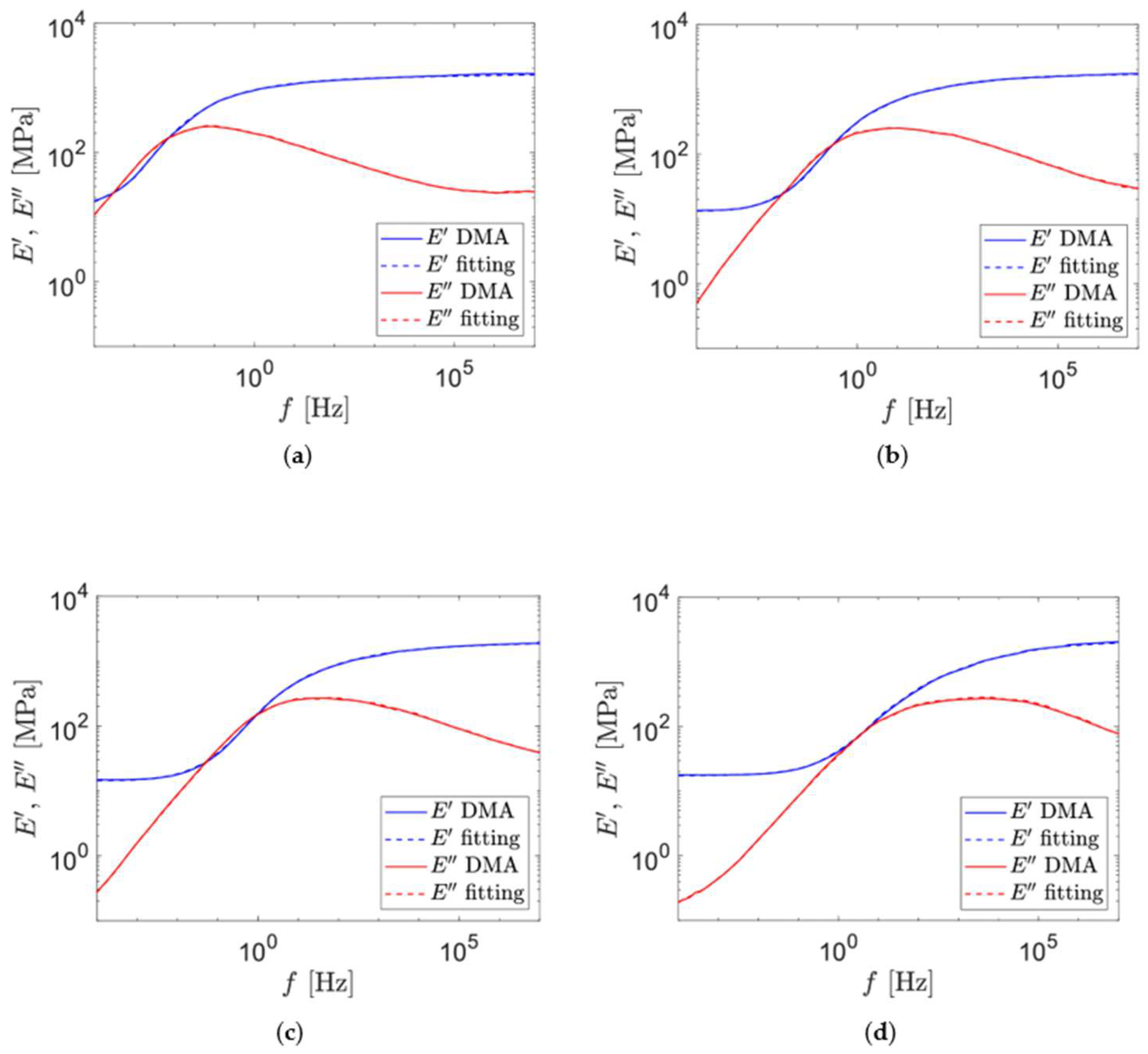


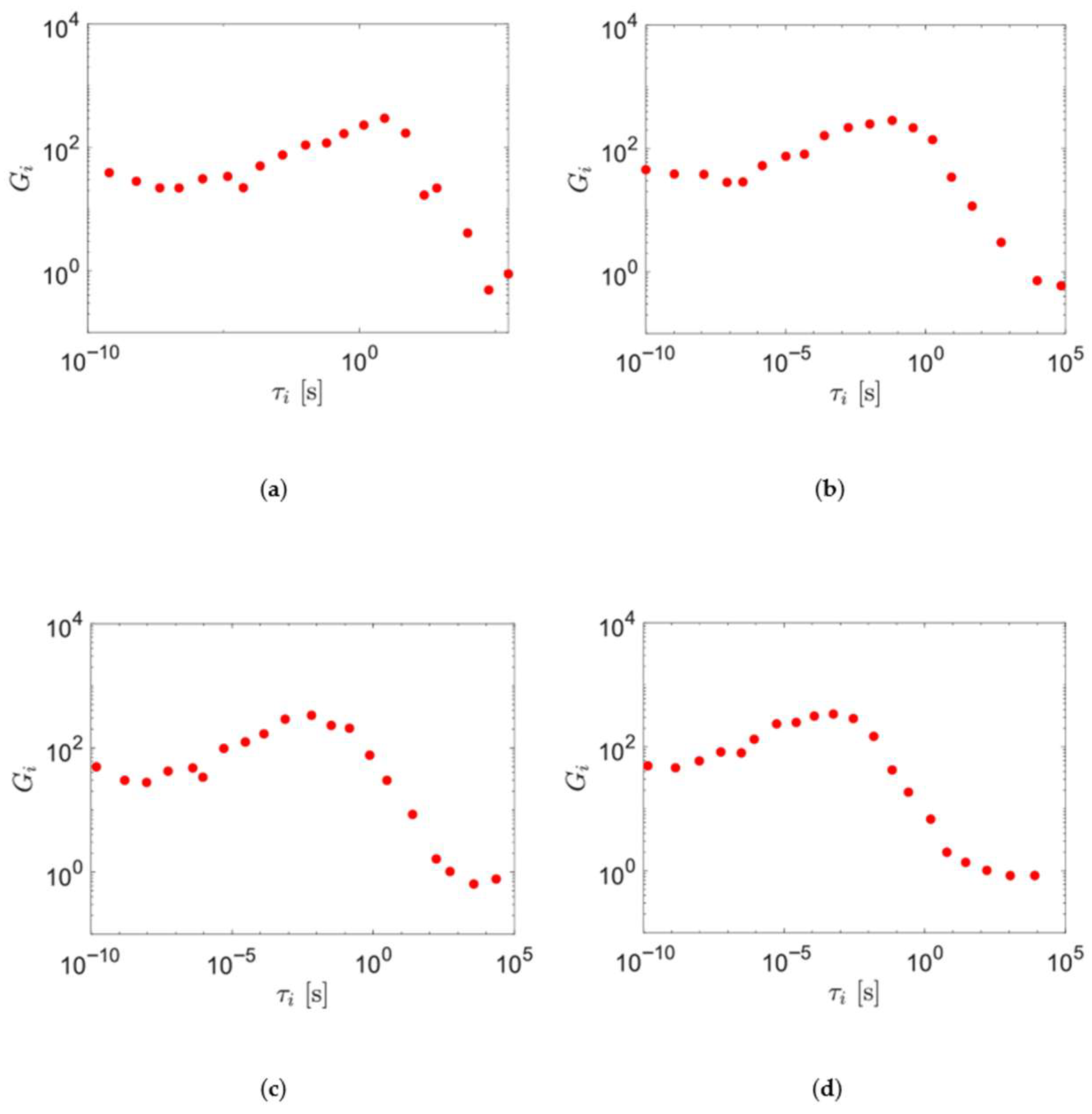


| wt% Nanosilica | Storage Modulus (MPa) at −100 °C | Storage Modulus (MPa) at 25 °C | Tβ-Relaxation (°C) |
|---|---|---|---|
| 0 | 2409.79 ± 16.54 | 1731.33 ± 8.48 | −77.69 ± 0.81 |
| 2 | 2599.79 ± 42.35 | 1887.10 ± 24.96 | −75.47 ± 0.41 |
| 5 | 2656.55 ± 69.41 | 1954.57 ± 22.18 | −75.11 ± 0.26 |
| 10 | 3121.49 ± 17.30 | 2356.99 ± 8.46 | −73.55 ± 0.79 |
| wt% Nanosilica | E′ (MPa) | Tg (Tonset) (°C) | Tg (Tpeak) (°C) | Damping Factor |
|---|---|---|---|---|
| 0 | 1689.45 ± 9.15 | 119.81 ± 0.25 | 138.73 ± 0.35 | 1.15 ± 0.07 |
| 2 | 1893.30 ± 3.31 | 110.75 ± 0.90 | 133.71 ± 0.09 | 1.10 ± 0.06 |
| 5 | 2063.70 ± 10.23 | 107.06 ± 0.25 | 131.30 ± 0.52 | 1.01 ± 0.02 |
| 10 | 2372.82 ± 9.72 | 93.14 ± 0.24 | 120.41 ± 1.21 | 0.87 ± 0.07 |
| wt% Nanosilica | E′ (MPa) Post UV-C | Tg (Tonset) (°C) Post UV-C | Tg (Tpeak) (°C) Post UV-C | Damping Factor Post UV-C |
|---|---|---|---|---|
| 0 | 1455.11 ± 4.73 | 117.49 ± 0.32 | 134.68 ± 0.56 | 1.07 ± 0.06 |
| 2 | 1694.98 ± 4.83 | 106.06 ± 0.38 | 128.46 ± 1.18 | 1.04 ± 0.01 |
| 5 | 1891.35 ± 0.43 | 102.44 ± 0.18 | 126.49 ± 0.85 | 0.97 ± 0.03 |
| 10 | 2228.95 ± 1.84 | 91.21 ± 0.76 | 116.81 ± 0.43 | 0.87 ± 0.02 |
| Wavenumber (cm−1) | Assignment |
|---|---|
| 2924 | C-H stretching |
| 1728 | C=O bond |
| 1601 | C=C stretching |
| 1508, 1491 | C=C stretching |
| 1451 | CH2 deformation |
| 1235 | C-O-H asymmetric stretching |
| 1158, 1112 | C-O stretching |
| 1038 | C-O-C stretching |
| 819 | C-O-C stretching |
| 750 | C-H out of plane bending |
| Wavenumber (cm−1) | Assignment |
|---|---|
| 3024 | C-H aromatic ring stretching |
| 2957 | C-H stretching |
| 1375 | CH3 deformation |
| 1100 | Si-O-Si symmetric stretching |
| 599 | Si-O-Si bending |
| Wavenumber (cm−1) | Assignment |
|---|---|
| 3505 | O-H stretching |
| 2961 | C-H stretching |
| 1715 | C=O bending |
| 1604 | C=C stretching |
| 1507, 1490 | C=C aromatic ring stretching |
| 1450 | CH2 deformation |
| 1158 | C-O stretching |
| 1035 | C-O-C stretching |
| 822 | C-H aromatic stretching |
| 749, 711 | C-H aromatic out of plane bending |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mancini, E.P.; Palmeri, F.; Laurenzi, S. Dynamic Mechanical Behavior of Nanosilica-Based Epoxy Composites Under LEO-like UV-C Exposure. J. Compos. Sci. 2025, 9, 529. https://doi.org/10.3390/jcs9100529
Mancini EP, Palmeri F, Laurenzi S. Dynamic Mechanical Behavior of Nanosilica-Based Epoxy Composites Under LEO-like UV-C Exposure. Journal of Composites Science. 2025; 9(10):529. https://doi.org/10.3390/jcs9100529
Chicago/Turabian StyleMancini, Emanuela Proietti, Flavia Palmeri, and Susanna Laurenzi. 2025. "Dynamic Mechanical Behavior of Nanosilica-Based Epoxy Composites Under LEO-like UV-C Exposure" Journal of Composites Science 9, no. 10: 529. https://doi.org/10.3390/jcs9100529
APA StyleMancini, E. P., Palmeri, F., & Laurenzi, S. (2025). Dynamic Mechanical Behavior of Nanosilica-Based Epoxy Composites Under LEO-like UV-C Exposure. Journal of Composites Science, 9(10), 529. https://doi.org/10.3390/jcs9100529






