Advanced Dynamic Thermal Vibration of Thick Composited FGM Cylindrical Shells with Fully Homogeneous Equation by Using TSDT and Nonlinear Varied Shear Coefficient
Abstract
1. Introduction
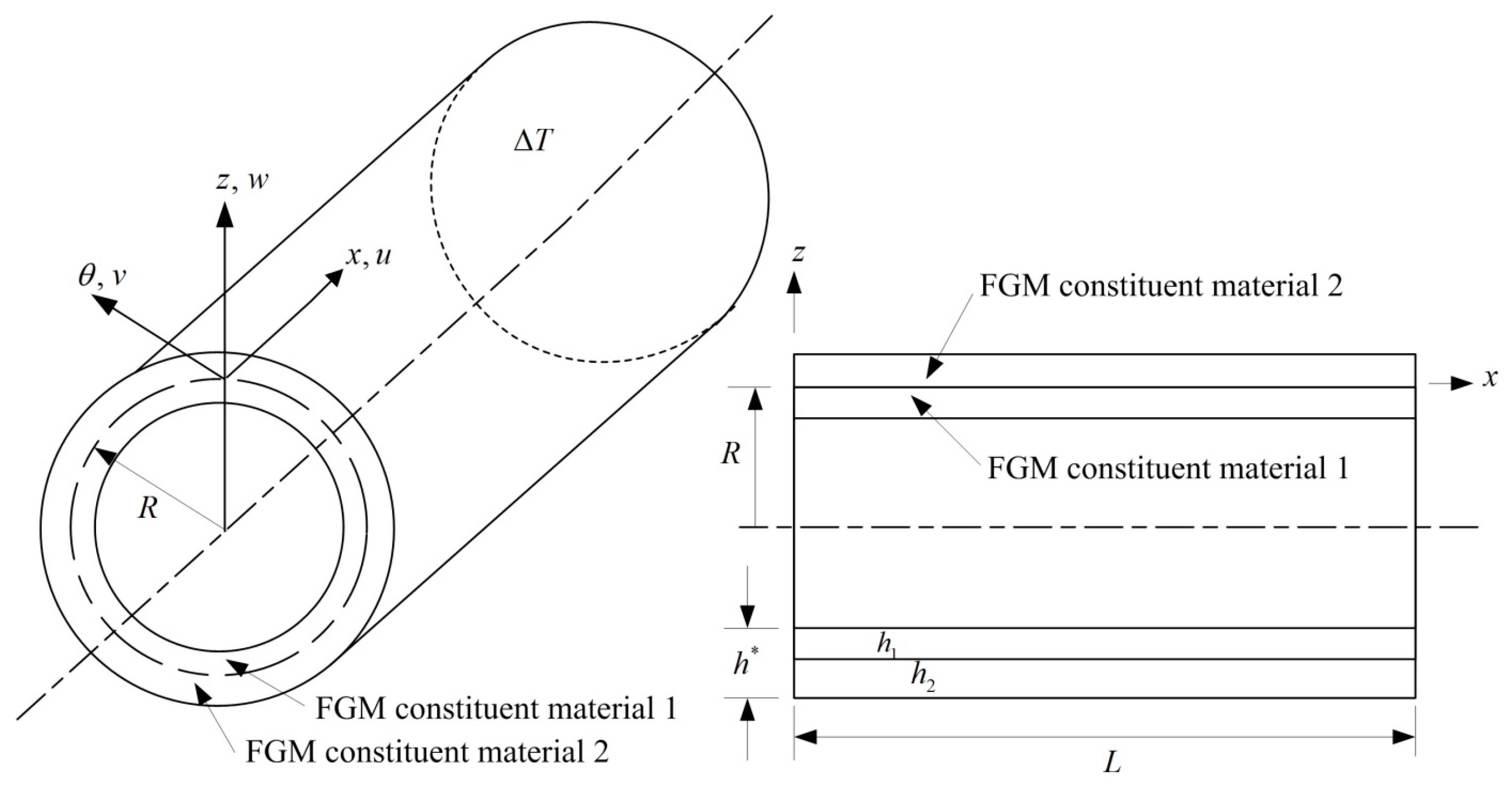
2. Formulation
2.1. Nonlinear Displacements in TSDT
2.2. Stresses in Thick FGM Shells
2.3. External Thermal Loads
2.4. Dynamic Equations of Motion
2.5. Numerical GDQ Method
3. Numerical Results
3.1. Vibration Frequency
3.2. Advanced
3.3. Dynamic Convergence of
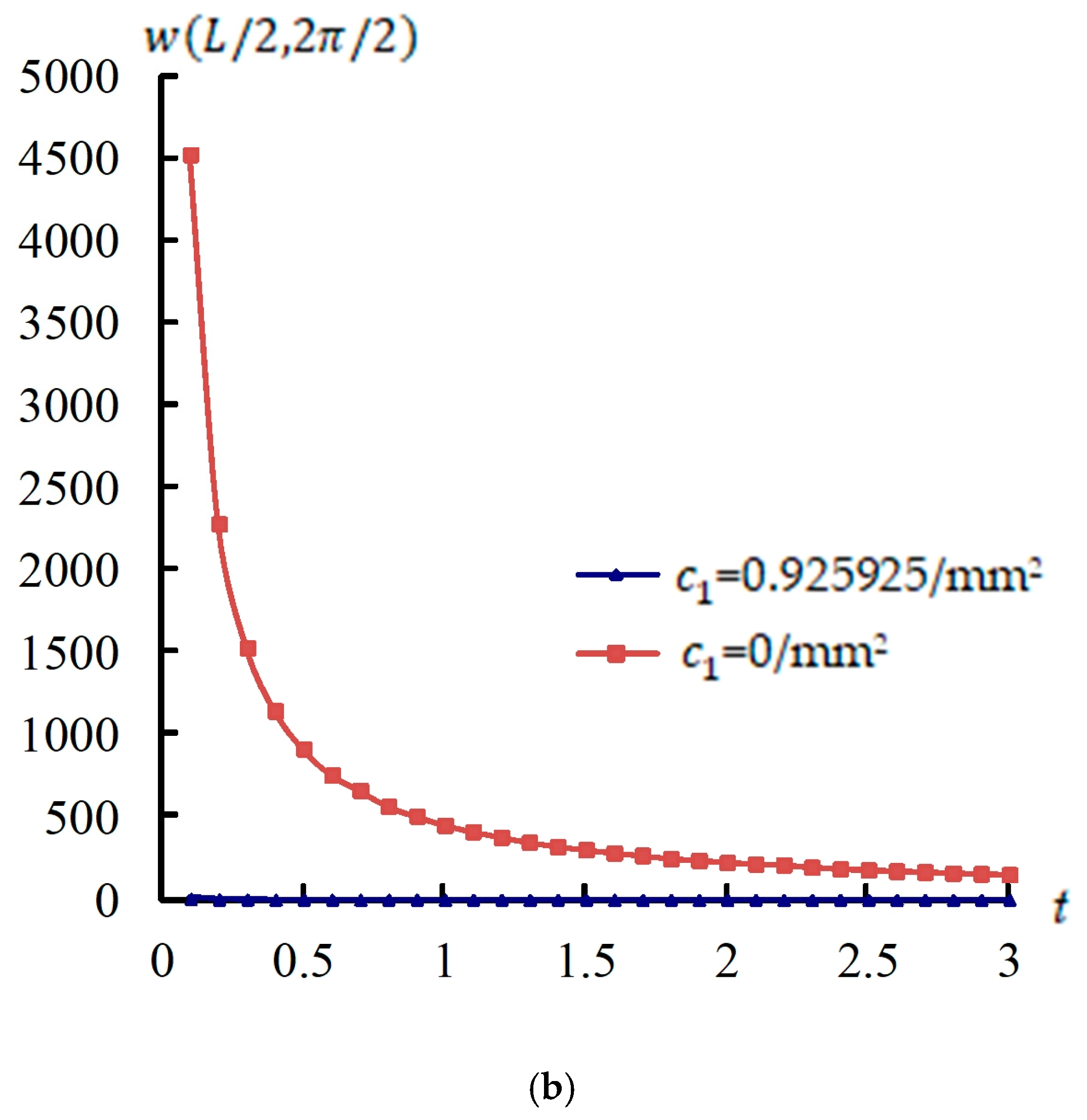
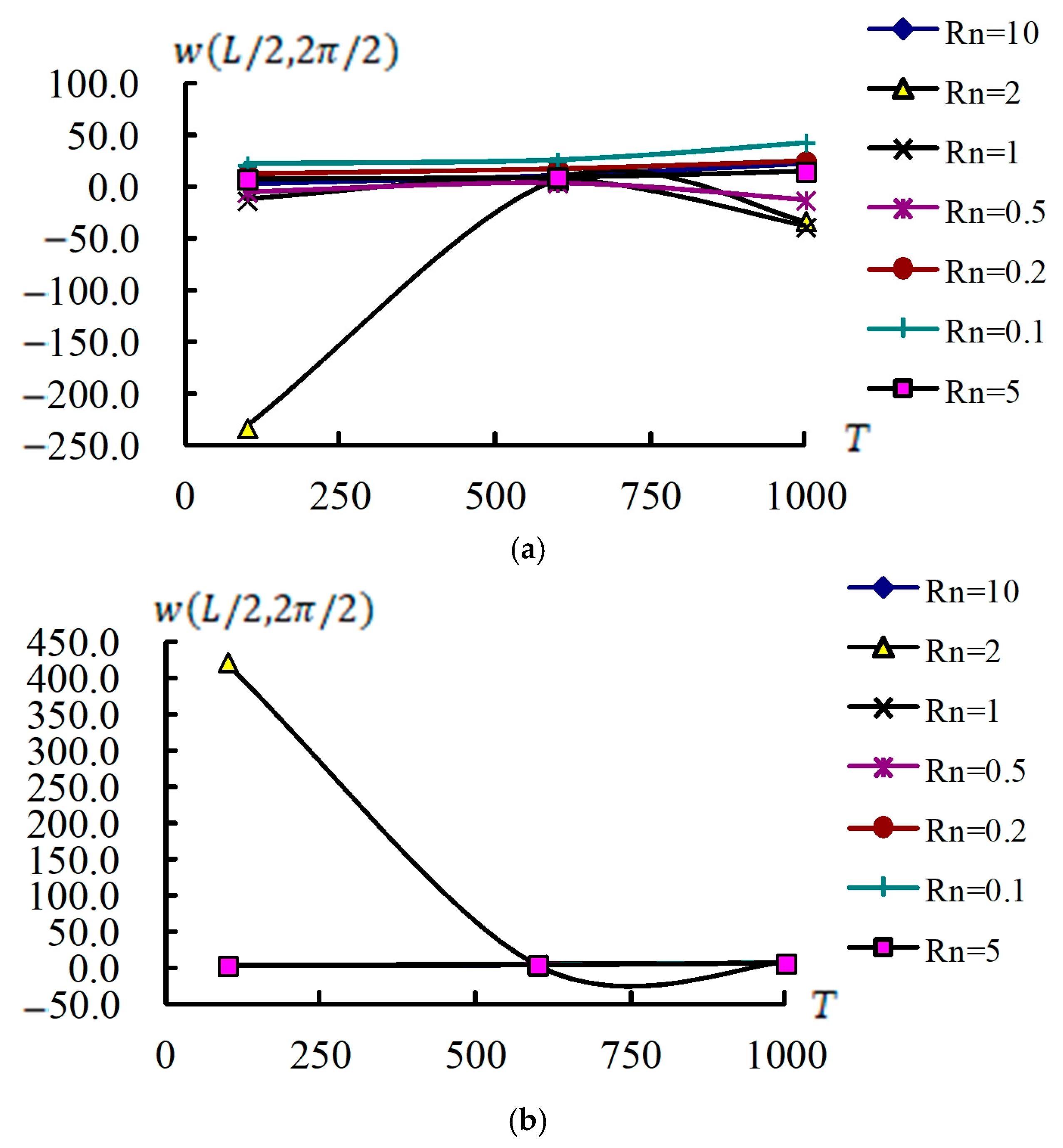
3.4. w(L/2,2π/2) Time Responses
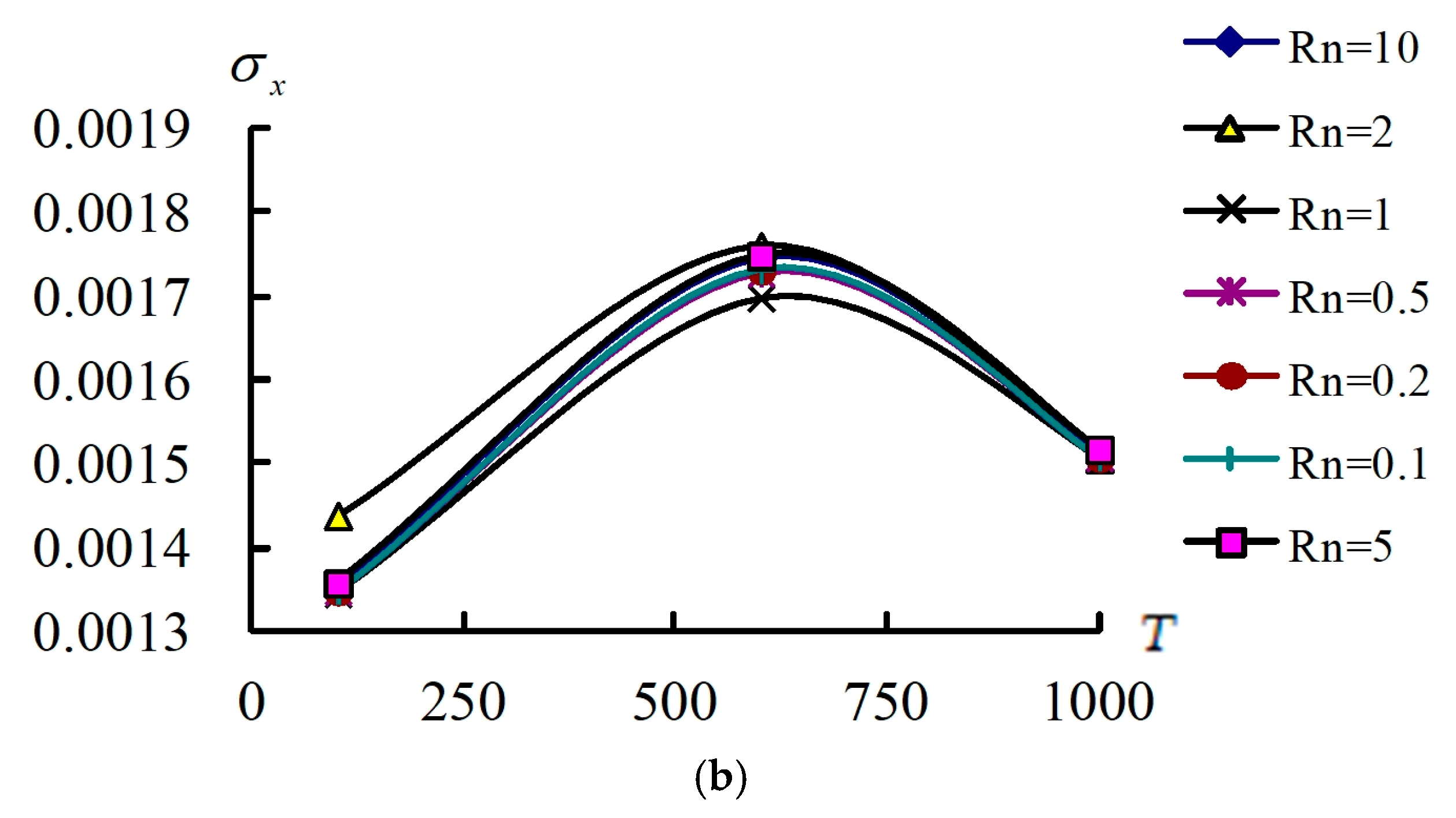
3.5. Stresses Time Responses
3.6. Compared Results
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Shahmohammadi, M.A.; Azhari, M.; Saadatpour, M.M. Free vibration analysis of sandwich FGM shells using isogeometric B-spline finite strip method. Steel Compos. Struct. 2020, 34, 361–376. [Google Scholar]
- Hajlaoui, A.; Chebbi, E.; Wali, M.; Dammak, F. Geometrically nonlinear analysis of FGM shells using solid-shell element with parabolic shear strain distribution. Int. J. Mech. Mater. Des. 2020, 16, 351–366. [Google Scholar] [CrossRef]
- Ghamkhar, M.; Naeem, M.N.; Imran, M.; Kamran, M.; Soutis, C. Vibration frequency analysis of three-layered cylinder shaped shell with effect of FGM central layer thickness. Sci. Rep. 2019, 9, 1566. [Google Scholar] [CrossRef] [PubMed]
- Moshkelgosha, E.; Askari, E.; Jeong, K.H.; Shafiee, A.A. Fluid-structure coupling of concentric double FGM shells with different lengths. Struct. Eng. Mech. 2017, 61, 231–244. [Google Scholar] [CrossRef][Green Version]
- Hajlaoui, A.; Triki, E.; Frikha, A.; Wali, M.; Dammak, F. Nonlinear dynamics analysis of FGM shell structures with a higher order shear strain enhanced solid-shell element. Lat. Am. J. Solids Struct. 2017, 14, 72–91. [Google Scholar] [CrossRef]
- Golpayegani, I.F.; Arani, E.M.; Foroughifar, A.A. Finite element vibration analysis of variable thickness thin cylindrical FGM shells under various boundary conditions. ASTM Int. 2019, 8, 491–502. [Google Scholar] [CrossRef]
- Singh, R.; Sharma, P. A review on modal characteristics of FGM structures. AIP Conf. Proc. 2019, 2148, 030037. [Google Scholar]
- Tornabene, F.; Reddy, J.N. FGM and laminated doubly-curved and degenerate shells resting on nonlinear elastic foundations: A GDQ solution for static analysis with a posteriori stress and strain recover. J. Indian Inst. Sci. 2013, 93, 635–688. [Google Scholar]
- Sepiani, H.A.; Rastgoo, A.; Ebrahimi, F.; Arani, A.G. Vibration and buckling analysis of two-layered functionally graded cylindrical shell considering the effects of transverse shear and rotary inertia. Mater. Des. 2010, 31, 1063–1069. [Google Scholar] [CrossRef]
- Reddy, J.N. Book chapter 10—Free vibration analysis of functionally graded ceramic-metal plates. In Analysis and Design of Plated Structures; Series in Civil and Structural Engineering; Woodhead Publishing: Sawston, UK, 2007; Volume 1, pp. 293–321. [Google Scholar] [CrossRef]
- Rafieea, M.; Nitzscheb, F.; Labrosse, M. Dynamics, vibration and control of rotating composite beams and blades: A critical review. Thin-Walled Struct. 2017, 119, 795–819. [Google Scholar] [CrossRef]
- Kazancı, Z. A review on the response of blast loaded laminated composite plates. Prog. Aerosp. Sci. 2016, 81, 49–59. [Google Scholar] [CrossRef]
- Teotia, M.; Soni, R.K. Applications of finite element modelling in failure analysis of laminated glass composites: A review. Eng. Fail. Anal. 2018, 94, 412–437. [Google Scholar] [CrossRef]
- D’Ottavio, M.; Polit, O. Book chapter 3—Classical, first order, and advanced theories. In Stability and Vibrations of Thin Walled Composite Structures; Woodhead Publishing: Sawston, UK, 2017; pp. 91–140. [Google Scholar]
- Sobhani Aragh, B.; Borzabadi Farahani, E.; Xu, B.X.; Ghasemnejad, H.; Mansur, W.J. Manufacturable insight into modelling and design considerations in fibre-steered composite laminates: State of the art and perspective. Comput. Methods Appl. Mech. Eng. 2021, 379, 113752. [Google Scholar] [CrossRef]
- Birman, V.; Genin, G.M. Book chapter 1.15 Linear and nonlinear elastic behavior of multidirectional laminates. In Comprehensive Composite Materials II; Elsevier: Amsterdam, The Netherlands, 2018; Volume 1, pp. 376–398. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Paroissien, E.; Lachaud, F.; Schwartz, S. Modelling load transfer in single-lap adhesively bonded and hybrid (bolted/bonded) joints. Prog. Aerosp. Sci. 2022, 130, 100811. [Google Scholar] [CrossRef]
- Kurpa, L.; Shmatko, T. Book chapter 11—Parametric vibrations of axially compressed functionally graded sandwich plates with a complex plan form. In Mechanics and Physics of Structured Media; Academic Press: Cambridge, MA, USA, 2022; pp. 213–232. [Google Scholar] [CrossRef]
- Banić, D.; Turkalj, G.; Lanc, D. A geometrically nonlinear finite element formulation for buckling analysis of shear deformable angle-ply composite beam-type structures. Comput. Struct. 2024, 301, 107427. [Google Scholar] [CrossRef]
- Benounas, S.; Belarbi, M.O.; Vinh, P.V.; Daikh, A.A.; Fantuzzi, N. Finite element model for free vibration analysis of functionally graded doubly curved shallow shells by using an improved first-order shear deformation theory. Structures 2024, 64, 106594. [Google Scholar] [CrossRef]
- Thu, T.T.T.; Anh, T.N.; Thi, H.N.; Thi, H.N. Transient response of doubly-curved bio-inspired composite shells resting on viscoelastic foundation subject to blast load using improved first-order shear theory and isogeometric approach. Def. Technol. 2024, 38, 171–193. [Google Scholar] [CrossRef]
- Hong, C.C. Thermal vibration of thick FGM spherical shells by using TSDT. Int. J. Mech. Mater. Des. 2021, 17, 367–380. [Google Scholar] [CrossRef]
- Lee, S.J.; Reddy, J.N.; Rostam-Abadi, F. Transient analysis of laminated composite plates with embedded smart-material layers. Finite Elem. Anal. Des. 2004, 40, 463–483. [Google Scholar] [CrossRef]
- Hong, C.C. Advanced frequency of thick FGM cylindrical shells with fully homogeneous equation. J. Struct. Eng. Appl. Mech. 2024, 7, 69–83. [Google Scholar] [CrossRef]






| (1/mm2) | GDQ Grids | (mm) at t = 6 s | |||
|---|---|---|---|---|---|
| = 0.5 | = 1 | = 2 | |||
| 0.925925 | 10 | 7 × 7 | 4.776584 | 4.642688 | 8.262124 |
| 9 × 9 | 4.771451 | 4.638021 | 8.254965 | ||
| 11 × 11 | 4.771457 | 4.638009 | 8.255040 | ||
| 13 × 13 | 4.771566 | 4.638039 | 8.254931 | ||
| 5 | 7 × 7 | 0.498478 | 0.463956 | 2.032378 | |
| 9 × 9 | 0.498031 | 0.463565 | 2.030849 | ||
| 11 × 11 | 0.498031 | 0.463568 | 2.030760 | ||
| 13 × 13 | 0.498026 | 0.463562 | 2.030836 | ||
| 0 | 10 | 7 × 7 | 475.2319 | 412.1400 | 421.1254 |
| 9 × 9 | 61.30657 | 64.71359 | 65.75298 | ||
| 11 × 11 | 62.15060 | 63.59567 | 66.56091 | ||
| 13 × 13 | 61.34299 | 64.75323 | 65.77515 | ||
| 5 | 7 × 7 | 2.538622 | 2.664105 | 2.716292 | |
| 9 × 9 | 2.422237 | 2.555500 | 2.597797 | ||
| 11 × 11 | 2.422514 | 2.555724 | 2.598066 | ||
| 13 × 13 | 2.422525 | 2.555730 | 2.598067 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.-C. Advanced Dynamic Thermal Vibration of Thick Composited FGM Cylindrical Shells with Fully Homogeneous Equation by Using TSDT and Nonlinear Varied Shear Coefficient. J. Compos. Sci. 2025, 9, 4. https://doi.org/10.3390/jcs9010004
Hong C-C. Advanced Dynamic Thermal Vibration of Thick Composited FGM Cylindrical Shells with Fully Homogeneous Equation by Using TSDT and Nonlinear Varied Shear Coefficient. Journal of Composites Science. 2025; 9(1):4. https://doi.org/10.3390/jcs9010004
Chicago/Turabian StyleHong, Chih-Chiang. 2025. "Advanced Dynamic Thermal Vibration of Thick Composited FGM Cylindrical Shells with Fully Homogeneous Equation by Using TSDT and Nonlinear Varied Shear Coefficient" Journal of Composites Science 9, no. 1: 4. https://doi.org/10.3390/jcs9010004
APA StyleHong, C.-C. (2025). Advanced Dynamic Thermal Vibration of Thick Composited FGM Cylindrical Shells with Fully Homogeneous Equation by Using TSDT and Nonlinear Varied Shear Coefficient. Journal of Composites Science, 9(1), 4. https://doi.org/10.3390/jcs9010004






