Determining the Advanced Frequency of Composited Functionally Graded Material Plates Using Third-Order Shear Deformation Theory and Nonlinear Varied Shear Coefficients
Abstract
1. Introduction
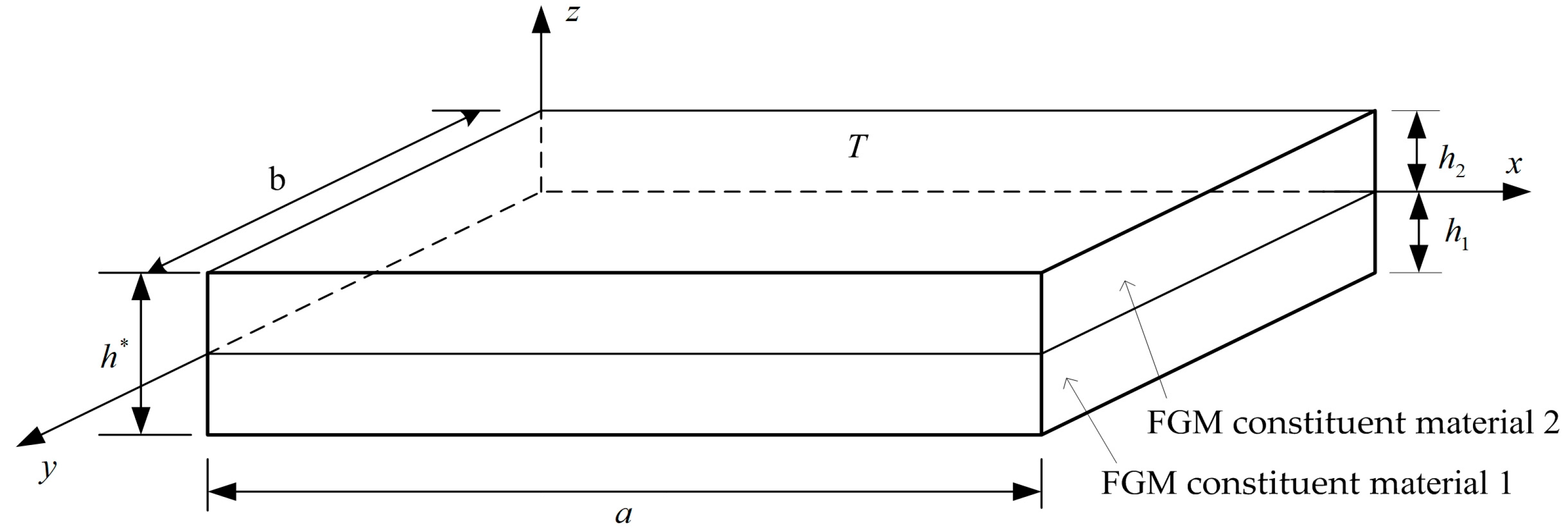
2. Formulation for the Advanced Nonlinear
3. Numerical Results
3.1. Advanced Computational Values of
3.2. Values of Non-Dimensional Frequency Parameters , and
3.3. Natural Frequency Values
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Ghumare, S.M.; Sayyad, A.S. Analytical solution using fifth order shear and normal deformation theory for FG plates resting on elastic foundation subjected to hygro-thermo-mechanical loading. Mater. Today Proc. 2020, 21, 1089–1093. [Google Scholar] [CrossRef]
- Belardi, V.G.; Fanelli, P.; Vivio, F. First-order shear deformation analysis of rectilinear orthotropic composite circular plates undergoing transversal loads. Compos. Part B 2019, 174, 107015. [Google Scholar] [CrossRef]
- Khayat, M.; Rahnema, H.; Baghlani, A.; Dehghan, S.M. A theoretical study of wave propagation of eccentrically stiffened FGM plate on Pasternak foundations based on higher-order shear deformation plate theory. Mater. Today Commun. 2019, 20, 100595. [Google Scholar] [CrossRef]
- Tu, T.M.; Quoc, T.H.; Long, N.V. Vibration analysis of functionally graded plates using the eight-unknown higher order shear deformation theory in thermal environments. Aerosp. Sci. Technol. 2019, 84, 698–711. [Google Scholar] [CrossRef]
- Duc, N.D.; Lee, J.; Nguyen-Thoi, T.; Thang, P.T. Static response and free vibration of functionally graded carbon nanotube-reinforced composite rectangular plates resting on Winkler–Pasternak elastic foundations. Aerosp. Sci. Technol. 2017, 68, 391–402. [Google Scholar] [CrossRef]
- Bui, T.Q.; Do, T.V.; Ton, L.H.T.; Doan, D.H.; Tanaka, S.; Pham, D.T.; Nguyen-Van, T.; Yu, T.; Hirose, S. On the high temperature mechanical behaviors analysis of heated functionally graded plates using FEM and a new third-order shear deformation plate theory. Compos. Part B Eng. 2016, 92, 218–241. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A simple higher-order shear deformation theory for bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 96, 165–173. [Google Scholar] [CrossRef]
- Ungbhakorn, V.; Wattanasakulpong, N. Thermo-elastic vibration analysis of third-order shear deformable functionally graded plates with distributed patch mass under thermal environment. Appl. Acoust. 2013, 74, 1045–1059. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. Free vibration response of functionally graded thick plates with shear and normal deformations effects. Compos. Struct. 2013, 96, 799–823. [Google Scholar] [CrossRef]
- Kim, Y.W. Temperature dependent vibration analysis of functionally graded rectangular plates. J. Sound Vib. 2005, 284, 531–549. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E.; Reddy, J.N. A numerical investigation on the natural frequencies of FGM sandwich shells with variable thickness by the local generalized differential quadrature method. Appl. Sci. 2017, 7, 131. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Natural frequency analysis of functionally graded orthotropic cross-ply plates based on the finite element method. Math. Comput. Appl. 2019, 24, 52. [Google Scholar] [CrossRef]
- You, Q.; Hua, F.; Huang, Q.; Zhou, X. Efficient analysis on buckling of FG-CNT reinforced composite joined conical–cylindrical laminated shells based on GDQ method under multiple loading conditions. Mech. Adv. Mater. Struct. 2024, 1–18. [Google Scholar] [CrossRef]
- Hua, F.; Fu, W.; Zhou, X. Guided wave propagation in functionally graded viscoelastic polymer composite shells reinforced with graphite particles. Waves Random Complex Media 2022, 1–27. [Google Scholar] [CrossRef]
- Moita, J.S.; Correia, V.F.; Mota Soares, C.M.; Herskovits, J. Higher-order finite element models for the static linear and nonlinear behaviour of functionally graded material plate-shell structures. Compos. Struct. 2019, 212, 465–475. [Google Scholar] [CrossRef]
- Hua, F.; Fu, W.; You, Q.; Huang, Q.; Abad, F.; Zhou, X. A refined spectral element model for wave propagation in multiscale hybrid epoxy/carbon fiber/graphene platelet composite shells. Aerosp. Sci. Technol. 2023, 138, 108321. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, L. Effect of thickness stretching on bending, buckling, and free vibration of functionally graded porous beams. Int. J. Struct. Stab. Dyn. 2024. [Google Scholar] [CrossRef]
- Civalek, Ö.; Dastjerd, S.; Akgöz, B. Buckling and free vibrations of CNT-reinforced cross-ply laminated composite plates. Mech. Based Des. Struct. Mach. 2022, 50, 1914–1931. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Vibrational characteristics of embedded microbeams lying on a two-parameter elastic foundation in thermal environment. Compos. Part B Eng. 2018, 150, 68–77. [Google Scholar] [CrossRef]
- Ramteke, P.M.; Panda, S.K. Free vibrational behaviour of multi-directional porous functionally graded structures. Arab. J. Sci. Eng. 2021, 46, 7741–7756. [Google Scholar] [CrossRef]
- Hong, C.C. Free vibration frequency of thick FGM spherical shells with simply homogeneous equation by using TSDT. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–15. [Google Scholar] [CrossRef]
- Hong, C.C. GDQ computation for thermal vibration of thick FGM plates by using fully homogeneous equation and TSDT. Thin-Walled Struct. 2019, 135, 78–88. [Google Scholar] [CrossRef]
- Lee, S.J.; Reddy, J.N.; Rostam-Abadi, F. Transient analysis of laminated composite plates with embedded smart-material layers. Finite Elem. Anal. Des. 2004, 40, 463–483. [Google Scholar] [CrossRef]
- Lee, S.J.; Reddy, J.N. Non-linear response of laminated composite plates under thermomechanical loading. Int. J. Non-Linear Mech. 2005, 40, 971–985. [Google Scholar] [CrossRef]
- Whitney, J.M. Structural Analysis of Laminated Anisotropic Plates; Technomic Publishing Company, Inc.: Lancaster, PA, USA, 1987. [Google Scholar]
- Sheen, H.S. Nonlinear thermal bending response of FGM plates due to heat condition. Compos. Part B Eng. 2007, 38, 201–215. [Google Scholar] [CrossRef]
- Hong, C.C. Advanced frequency analysis of thick FGM plates using third-order shear deformation theory with a nonlinear shear correction coefficient. J. Struct. Eng. Appl. Mech. 2022, 5, 143–160. [Google Scholar] [CrossRef]
- Hong, C.C. Advanced dynamic thermal vibration of laminated FGM plates with simply homogeneous equation by using TSDT and nonlinear varied shear coefficient. Appl. Sci. 2022, 12, 11776. [Google Scholar] [CrossRef]
- Hong, C.C. Thermal sinusoidal vibration and transient response of magnetostrictive functionally graded material plates without shear effects. Res. Appl. Mech. Eng. 2013, 2, 11–22. [Google Scholar]





| Materials | ||||||
|---|---|---|---|---|---|---|
| SUS304 | (Pa) | 201.04 | 0 | 3.079 | −6.534 | 0 |
| 0.3262 | 0 | −2.002 | 3.797 | 0 | ||
| (Kg/m3) | 8166 | 0 | 0 | 0 | 0 | |
| Si3N4 | (Pa) | 348.43 | 0 | −3.70 | 2.16 | −8.946 |
| 0.24 | 0 | 0 | 0 | 0 | ||
| (Kg/m3) | 2370 | 0 | 0 | 0 | 0 |
| (a) | ||||||||
(1/mm2) | (mm) | |||||||
| 92.592598 | 0.12 | −0.323869 | −0.324963 | −0.365392 | −0.541369 | −2.399161 | 0.802957 | 0.518229 |
| 0.925925 | 1.2 | −0.323870 | −0.324963 | −0.365392 | −0.541370 | −2.399165 | 0.802958 | 0.518229 |
| 0.231481 | 2.4 | −0.323869 | −0.324963 | −0.365392 | −0.541370 | −2.399165 | 0.802958 | 0.518229 |
| 0.037037 | 6 | −0.323869 | −0.324962 | −0.365392 | −0.541370 | −2.399163 | 0.802957 | 0.518229 |
| 0.009259 | 12 | −0.323870 | −0.324962 | −0.365392 | −0.541370 | −2.399163 | 0.802957 | 0.518229 |
| 0 | 0.12 | 0.915601 | 0.992033 | 1.175883 | 1.340146 | 1.396886 | 1.249938 | 1.099855 |
| 0 | 1.2 | 0.915601 | 0.992030 | 1.175884 | 1.340146 | 1.396886 | 1.249938 | 1.099855 |
| 0 | 2.4 | 0.915601 | 0.992030 | 1.175884 | 1.340146 | 1.396886 | 1.249938 | 1.099855 |
| 0 | 6 | 0.915600 | 0.992028 | 1.175884 | 1.340146 | 1.396886 | 1.249938 | 1.099855 |
| 0 | 12 | 0.915600 | 0.992027 | 1.175884 | 1.340146 | 1.396886 | 1.249938 | 1.099855 |
| (b) | ||||||||
(1/mm2) | (mm) | |||||||
| 92.592598 | 0.12 | −0.448521 | −0.456089 | −0.539418 | −0.922718 | 9.852672 | 0.682434 | 0.491249 |
| 0.925925 | 1.2 | −0.448522 | −0.456090 | −0.539419 | −0.922719 | 9.852635 | 0.682434 | 0.491249 |
| 0.231481 | 2.4 | −0.448522 | −0.456089 | −0.539419 | −0.922719 | 9.852635 | 0.682434 | 0.491249 |
| 0.037037 | 6 | −0.448522 | −0.456089 | −0.539418 | −0.922718 | 9.852679 | 0.682434 | 0.491249 |
| 0.009259 | 12 | −0.448522 | −0.456089 | −0.539418 | −0.922718 | 9.852675 | 0.682434 | 0.491249 |
| 0 | 0.12 | 0.899095 | 0.957858 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| 0 | 1.2 | 0.899095 | 0.957858 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| 0 | 2.4 | 0.899095 | 0.957858 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| 0 | 6 | 0.899095 | 0.957858 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| 0 | 12 | 0.899095 | 0.957858 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| (c) | ||||||||
(1/mm2) | (mm) | |||||||
| 92.592598 | 0.12 | −0.821563 | −0.861922 | −1.181502 | −4.392330 | 1.474843 | 0.583927 | 0.463616 |
| 0.925925 | 1.2 | −0.821565 | −0.861923 | −1.181503 | −4.392341 | 1.474844 | 0.583927 | 0.463617 |
| 0.231481 | 2.4 | −0.821565 | −0.861923 | −1.181503 | −4.392341 | 1.474844 | 0.583927 | 0.463617 |
| 0.037037 | 6 | −0.821564 | −0.861924 | −1.181502 | −4.392332 | 1.474843 | 0.583927 | 0.463617 |
| 0.009259 | 12 | −0.821564 | −0.861924 | −1.181503 | −4.392332 | 1.474843 | 0.583927 | 0.463617 |
| 0 | 0.12 | 0.898426 | 0.956500 | 1.087890 | 1.195721 | 1.226106 | 1.121959 | 1.019033 |
| 0 | 1.2 | 0.898426 | 0.956498 | 1.087891 | 1.195721 | 1.226106 | 1.121959 | 1.019034 |
| 0 | 2.4 | 0.898426 | 0.956498 | 1.087891 | 1.195721 | 1.226106 | 1.121959 | 1.019034 |
| 0 | 6 | 0.898425 | 0.956496 | 1.087891 | 1.195721 | 1.226106 | 1.121958 | 1.019033 |
| 0 | 12 | 0.898426 | 0.956495 | 1.087891 | 1.195721 | 1.226106 | 1.121958 | 1.019033 |
| (d) | ||||||||
(1/mm2) | (mm) | |||||||
| 92.592598 | 0.12 | −0.778697 | −0.814248 | −1.096615 | −3.535386 | 1.560072 | 0.589436 | 0.465330 |
| 0.925925 | 1.2 | −0.778699 | −0.814250 | −1.096617 | −3.535402 | 1.560071 | 0.589436 | 0.465330 |
| 0.231481 | 2.4 | −0.778699 | −0.814250 | −1.096617 | −3.535402 | 1.560071 | 0.589436 | 0.465330 |
| 0.037037 | 6 | −0.778699 | −0.814249 | −1.096615 | −3.535396 | 1.560071 | 0.589435 | 0.465330 |
| 0.009259 | 12 | −0.778699 | −0.814250 | −1.096615 | −3.535396 | 1.560071 | 0.589435 | 0.465330 |
| 0 | 0.12 | 0.899096 | 0.957861 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| 0 | 1.2 | 0.899095 | 0.957858 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| 0 | 2.4 | 0.899095 | 0.957858 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| 0 | 6 | 0.899095 | 0.957856 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| 0 | 12 | 0.899095 | 0.957856 | 1.091129 | 1.200860 | 1.232039 | 1.126363 | 1.021824 |
| (e) | ||||||||
(1/mm2) | (mm) | |||||||
| 92.592598 | 0.12 | −0.189321 | −0.185985 | −0.195625 | −0.252506 | −0.532897 | 1.590231 | 0.610227 |
| 0.925925 | 1.2 | −0.189321 | −0.185984 | −0.195625 | −0.252506 | −0.532898 | 1.590231 | 0.610227 |
| 0.231481 | 2.4 | −0.189321 | −0.185984 | −0.195625 | −0.252506 | −0.532898 | 1.590231 | 0.610227 |
| 0.037037 | 6 | −0.189321 | −0.185984 | −0.195625 | −0.252506 | −0.532897 | 1.590231 | 0.610227 |
| 0.009259 | 12 | −0.189321 | −0.185984 | −0.195625 | −0.252506 | −0.532897 | 1.590231 | 0.610227 |
| 0 | 0.12 | 0.932950 | 1.029296 | 1.276062 | 1.516531 | 1.616819 | 1.419804 | 1.206723 |
| 0 | 1.2 | 0.932949 | 1.029293 | 1.276062 | 1.516531 | 1.616820 | 1.419804 | 1.206723 |
| 0 | 2.4 | 0.932949 | 1.029293 | 1.276063 | 1.516531 | 1.616820 | 1.419804 | 1.206723 |
| 0 | 6 | 0.932948 | 1.029290 | 1.276063 | 1.516531 | 1.616819 | 1.419803 | 1.206723 |
| 0 | 12 | 0.932948 | 1.029290 | 1.276062 | 1.516531 | 1.616819 | 1.419803 | 1.206723 |
| (a) | ||||||
| mm, Nonlinear Varied | ||||||
| T = 1 K | T = 100 K | T = 300 K | T = 600 K | T = 1000 K | ||
| 5 | 0.5 | 0.001707 | 0.001072 | 0.001856 | 0.001219 | 0.001388 |
| 1 | 0.001085 | 0.001912 | 0.001196 | 0.001253 | 0.002444 | |
| 2 | 0.001128 | 0.001910 | 0.001151 | 0.002200 | 0.001543 | |
| 10 | 0.004561 | 0.001836 | 0.001866 | 0.004803 | 0.002482 | |
| 8 | 0.5 | 0.001653 | 0.002817 | 0.002974 | 0.001940 | 0.003718 |
| 1 | 0.001723 | 0.003037 | 0.003077 | 0.003345 | 0.002314 | |
| 2 | 0.001800 | 0.001836 | 0.001883 | 0.002042 | 0.002452 | |
| 10 | 0.003197 | 0.002037 | 0.002110 | 0.003614 | 0.002793 | |
| 10 | 0.5 | 0.003427 | 0.003523 | 0.003713 | 0.004119 | 0.004651 |
| 1 | 0.002150 | 0.002203 | 0.002311 | 0.002820 | 0.004904 | |
| 2 | 0.002872 | 0.002294 | 0.004005 | 0.007483 | 0.003061 | |
| 10 | 0.002479 | 0.002509 | 0.002597 | 0.004550 | 0.003445 | |
| (b) | ||||||
| mm, Nonlinear Varied | ||||||
| T = 1 K | T = 100 K | T = 300 K | T = 600 K | T = 1000 K | ||
| 5 | 0.5 | 0.034605 | 0.021141 | 0.035339 | 0.023160 | 0.029544 |
| 1 | 0.022002 | 0.037707 | 0.022780 | 0.023799 | 0.052017 | |
| 2 | 0.022863 | 0.037654 | 0.021917 | 0.041778 | 0.032853 | |
| 10 | 0.092434 | 0.036204 | 0.035525 | 0.091197 | 0.052815 | |
| 8 | 0.5 | 0.085749 | 0.142172 | 0.144959 | 0.094311 | 0.202585 |
| 1 | 0.089396 | 0.003001 | 0.149956 | 0.162600 | 0.126102 | |
| 2 | 0.093391 | 0.092694 | 0.091803 | 0.099286 | 0.133605 | |
| 10 | 0.165847 | 0.102802 | 0.102862 | 0.175707 | 0.152172 | |
| 10 | 0.5 | 0.277821 | 0.277824 | 0.282792 | 0.312856 | 0.395915 |
| 1 | 0.174300 | 0.173750 | 0.175997 | 0.214193 | 0.417443 | |
| 2 | 0.232849 | 0.180933 | 0.304987 | 0.568351 | 0.260551 | |
| 10 | 0.200992 | 0.197894 | 0.197787 | 0.345595 | 0.293273 | |
| (c) | ||||||
| Present Solution | ||||||
| mm, Nonlinear Varied | ||||||
| T = 1 K | T = 100 K | T = 300 K | T = 600 K | T = 1000 K | ||
| 5 | 0.5 | 0.098593 | 0.060234 | 0.100685 | 0.065986 | 0.084176 |
| 1 | 0.062687 | 0.107433 | 0.064904 | 0.067808 | 0.148203 | |
| 2 | 0.065139 | 0.107282 | 0.062445 | 0.119031 | 0.093604 | |
| 10 | 0.263356 | 0.103151 | 0.101216 | 0.259833 | 0.150476 | |
| 8 | 0.5 | 0.244309 | 0.405064 | 0.413005 | 0.268703 | 0.577187 |
| 1 | 0.254701 | 0.436718 | 0.427241 | 0.463265 | 0.359280 | |
| 2 | 0.266082 | 0.264097 | 0.261559 | 0.282879 | 0.380655 | |
| 10 | 0.472516 | 0.292895 | 0.293067 | 0.500611 | 0.433556 | |
| 10 | 0.5 | 0.791543 | 0.791553 | 0.805706 | 0.891361 | 1.128005 |
| 1 | 0.496600 | 0.495035 | 0.501435 | 0.610259 | 1.189342 | |
| 2 | 0.663413 | 0.515498 | 0.868943 | 1.619294 | 0.742339 | |
| 10 | 0.572648 | 0.563822 | 0.563517 | 0.984639 | 0.835567 | |
| (d) | ||||||
(1/mm2) | (mm) | |||||
| = 10,
T =
300 K, Nonlinear Varied , for SUS304/Si3N4 | Jha et al. 2013 [9], | |||||
| 0.925925 | 1.2 | 0.003713 | 0.002311 | 0.004005 | - | |
| 0.333333 | 2 | 0.007991 | 0.004971 | 0.005131 | - | |
| 0.013333 | 10 | 0.053758 | 0.055573 | 0.057577 | - | |
| 0.009259 | 12 | 0.070666 | 0.073052 | 0.075691 | - | |
| 0.006802 | 14 | 0.089049 | 0.092056 | 0.095384 | 0.0839 | |
| (e) | ||||||
(1/mm2) | (mm) | |||||
| Present Solution, = 10, T = 300 K, Nonlinear Varied | Kim 2005 [10] Forced Vibration, = 200 mm, = 0 | Duc et al. 2017 [5] CNTRC, FSDT | ||||
| UD type | ||||||
| 0.925925 | 1.2 | 0.282792 | 0.175997 | 0.304987 | - | - |
| 0.333333 | 2 | 0.608525 | 0.378548 | 0.390709 | - | - |
| 0.013333 | 10 | 4.093280 | 4.231468 | 4.384090 | 4.1165 | 3.99244 |
| 0.009259 | 12 | 5.380705 | 5.562391 | 5.763298 | - | - |
| 0.006802 | 14 | 6.780427 | 7.009404 | 7.262784 | - | - |
| (f) | ||||||
(1/mm2) | (mm) | |||||
| = 10, T = 300 K | Ungbhakorn and Wattanasakulpong 2013 [8] = 400 K | |||||
| 0.925925 | 1.2 | 0.805706 | 0.501435 | 0.868943 | - | |
| 0.333333 | 2 | 1.733756 | 1.078525 | 1.113175 | - | |
| 0.053333 | 5 | 4.123597 | 4.262512 | 4.414177 | - | |
| 0.037037 | 6 | 5.420403 | 5.603161 | 5.803643 | 5.359 | |
| 0.013333 | 10 | 11.662205 | 12.055917 | 12.490754 | - | |
| (a) | |||||||||
| (1/s) | |||||||||
| T = 1 K | T = 100 K | T = 300 K | T = 600 K | T = 1000 K | |||||
| 5 | 0.5 | 0.029227 | 0.018034 | 0.030248 | 0.019096 | 0.020672 | |||
| 1 | 0.018583 | 0.032166 | 0.019499 | 0.019623 | 0.036396 | ||||
| 2 | 0.019310 | 0.032121 | 0.018760 | 0.034448 | 0.022987 | ||||
| 10 | 0.078070 | 0.030884 | 0.030408 | 0.075196 | 0.036954 | ||||
| 10 | 0.5 | 0.058662 | 0.059249 | 0.060513 | 0.064490 | 0.069255 | |||
| 1 | 0.036803 | 0.037054 | 0.037661 | 0.044152 | 0.073021 | ||||
| 2 | 0.049166 | 0.038585 | 0.065263 | 0.117157 | 0.045576 | ||||
| 10 | 0.042439 | 0.042203 | 0.042323 | 0.071239 | 0.051300 | ||||
| (b) | |||||||||
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.030248 | 0.012079 | 0.010355 | 0.005455 | 0.003399 | 0.007451 | 0.006401 | 0.005629 | 0.005048 |
| 10 | 0.060513 | 0.042673 | 0.035361 | 0.020371 | 0.015934 | 0.031821 | 0.014847 | 0.011815 | 0.006108 |
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.019082 | 0.009523 | 0.010442 | 0.004176 | 0.007139 | 0.007156 | 0.006237 | 0.005555 | 0.005061 |
| 10 | 0.023112 | 0.030248 | 0.014602 | 0.012079 | 0.015355 | 0.010355 | 0.015735 | 0.005455 | 0.006460 |
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.008481 | 0.007713 | 0.010970 | 0.009022 | 0.007734 | 0.006781 | 0.006089 | 0.006744 | 0.001734 |
| 10 | 0.027054 | 0.023712 | 0.012403 | 0.016924 | 0.009628 | 0.011476 | 0.015462 | 0.004309 | 0.006783 |
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.010463 | 0.009661 | 0.008689 | 0.007765 | 0.007011 | 0.006711 | 0.002147 | 0.001856 | 0.001620 |
| 10 | 0.012677 | 0.019082 | 0.010558 | 0.009523 | 0.012944 | 0.010442 | 0.013141 | 0.004176 | 0.007080 |
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.005210 | 0.007929 | 0.007340 | 0.006738 | 0.006999 | 0.002301 | 0.001972 | 0.001712 | 0.001502 |
| 10 | 0.010366 | 0.015779 | 0.014532 | 0.008480 | 0.008050 | 0.017151 | 0.011124 | 0.001000 | 0.008826 |
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.006944 | 0.006693 | 0.006307 | 0.005852 | 0.005405 | 0.004941 | 0.004526 | 0.004152 | 0.003821 |
| 10 | 0.008856 | 0.008481 | 0.008063 | 0.007713 | 0.008185 | 0.010970 | 0.009856 | 0.009022 | 0.003542 |
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.005915 | 0.005753 | 0.005469 | 0.005921 | 0.005027 | 0.004625 | 0.004279 | 0.003964 | 0.003679 |
| 10 | 0.012552 | 0.008211 | 0.011614 | 0.010954 | 0.010263 | 0.009585 | 0.006448 | 0.008361 | 0.007834 |
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.005130 | 0.005009 | 0.006575 | 0.005036 | 0.004590 | 0.004284 | 0.004006 | 0.003746 | 0.003506 |
| 10 | 0.010707 | 0.010463 | 0.010102 | 0.009661 | 0.009180 | 0.008689 | 0.004282 | 0.007765 | 0.007361 |
| (1/s) | |||||||||
| n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | |
| 5 | 0.004509 | 0.007183 | 0.005173 | 0.004502 | 0.004205 | 0.003967 | 0.003743 | 0.003530 | 0.003328 |
| 10 | 0.005754 | 0.005626 | 0.005439 | 0.005199 | 0.004907 | 0.007963 | 0.007584 | 0.007228 | 0.006915 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, C.-C. Determining the Advanced Frequency of Composited Functionally Graded Material Plates Using Third-Order Shear Deformation Theory and Nonlinear Varied Shear Coefficients. J. Compos. Sci. 2024, 8, 325. https://doi.org/10.3390/jcs8080325
Hong C-C. Determining the Advanced Frequency of Composited Functionally Graded Material Plates Using Third-Order Shear Deformation Theory and Nonlinear Varied Shear Coefficients. Journal of Composites Science. 2024; 8(8):325. https://doi.org/10.3390/jcs8080325
Chicago/Turabian StyleHong, Chih-Chiang. 2024. "Determining the Advanced Frequency of Composited Functionally Graded Material Plates Using Third-Order Shear Deformation Theory and Nonlinear Varied Shear Coefficients" Journal of Composites Science 8, no. 8: 325. https://doi.org/10.3390/jcs8080325
APA StyleHong, C.-C. (2024). Determining the Advanced Frequency of Composited Functionally Graded Material Plates Using Third-Order Shear Deformation Theory and Nonlinear Varied Shear Coefficients. Journal of Composites Science, 8(8), 325. https://doi.org/10.3390/jcs8080325






