Buckling Analysis of Variable-Angle Tow Composite Plates through Variable Kinematics Hierarchical Models
Abstract
1. Introduction
2. Carrera’s Unified Formulation
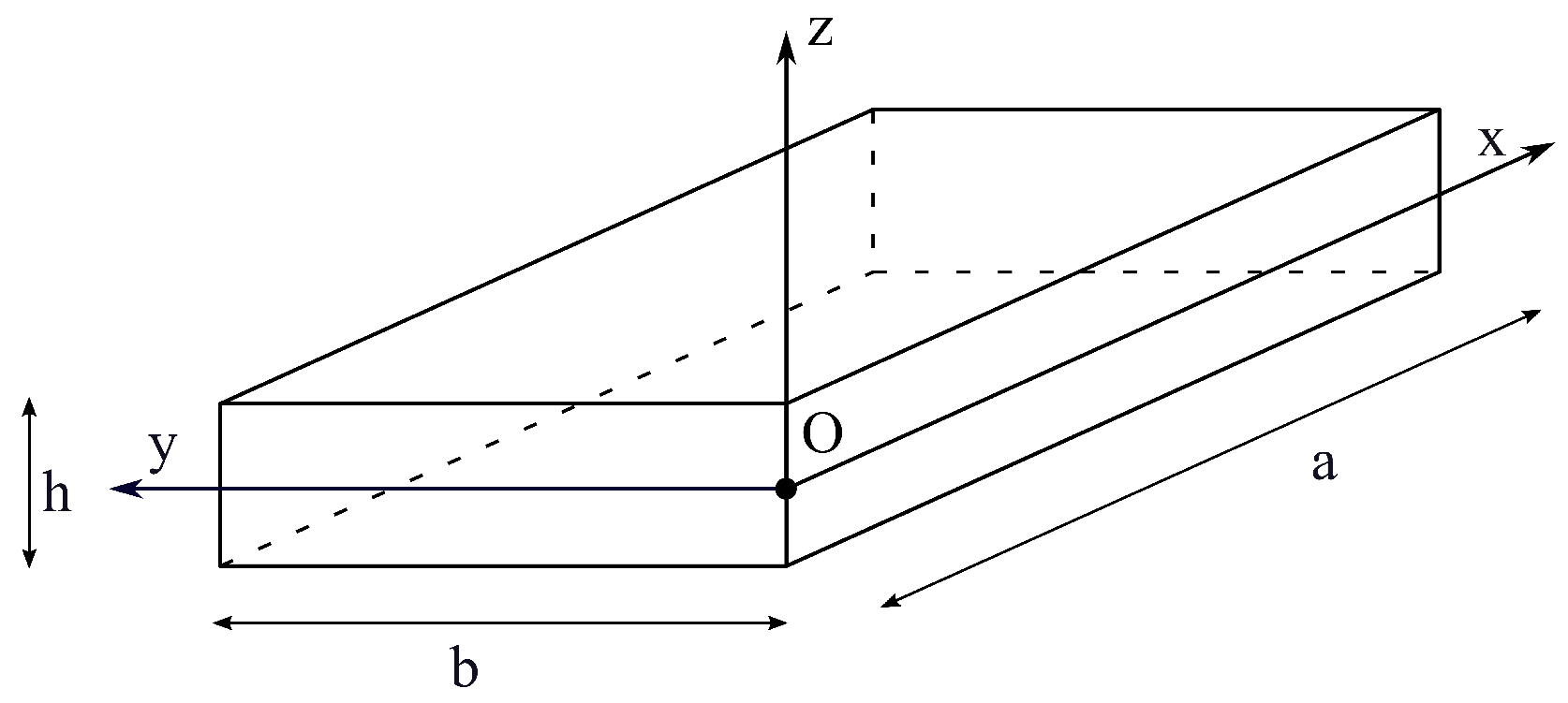
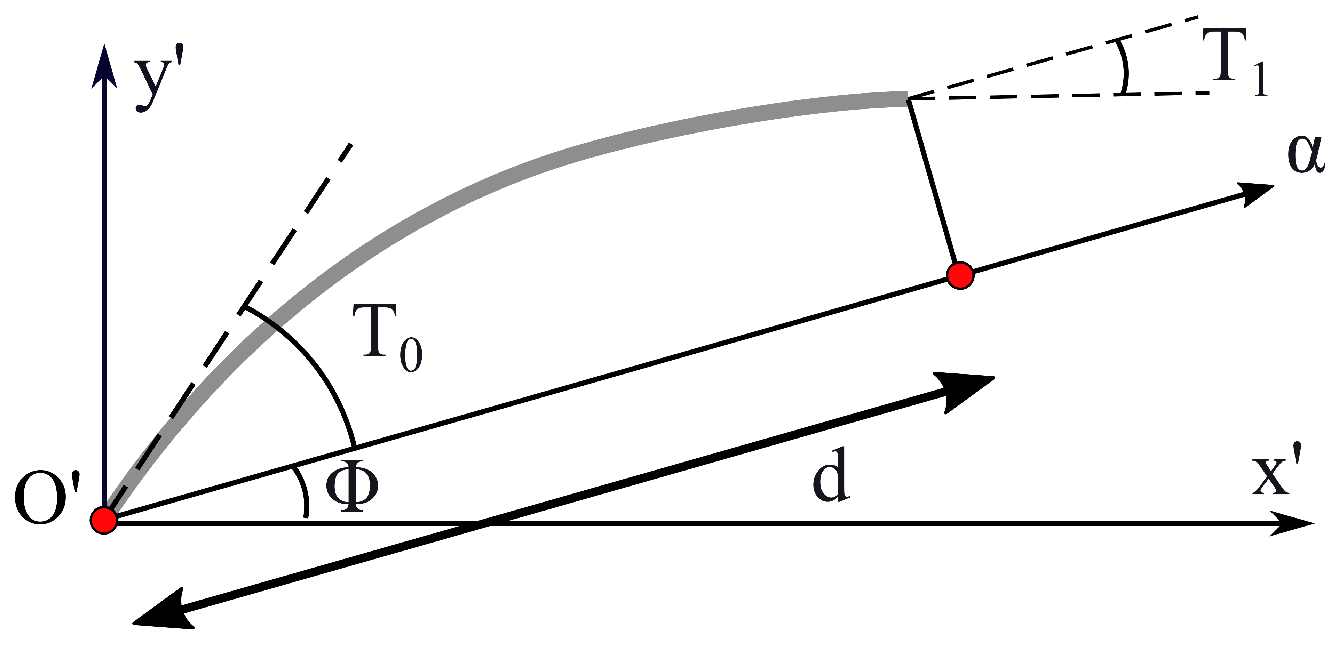
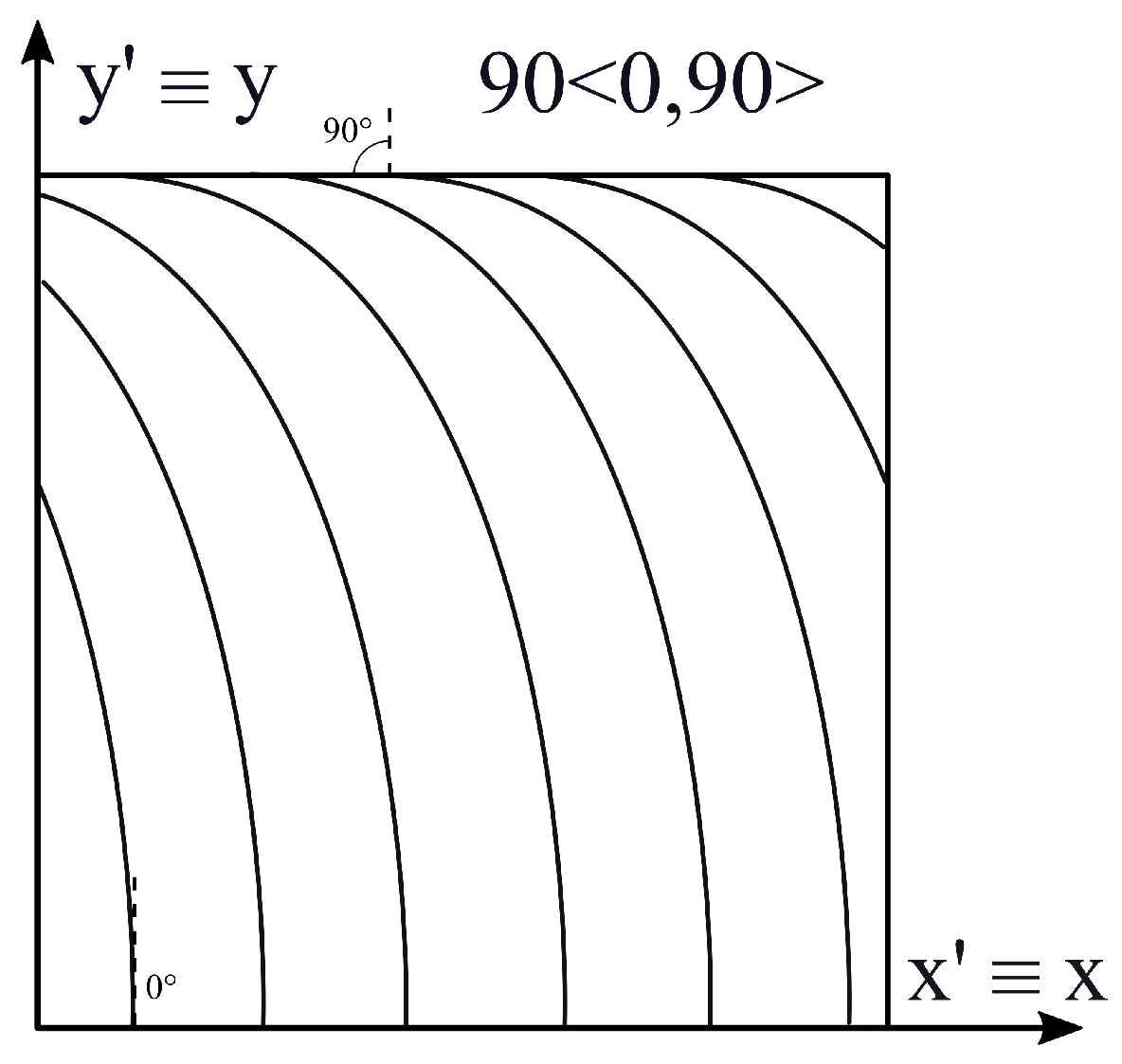
2.1. Variable-Angle Tow Composite Plates
2.2. Variational Formulation
2.2.1. Prebuckling Problem
2.2.2. Linear Buckling Problem
2.3. Kinematic Assumption and Finite Element Approximation
2.3.1. Equivalent Single-Layer Theories
2.3.2. Layer-Wise Theories
2.3.3. Finite Element Formulation
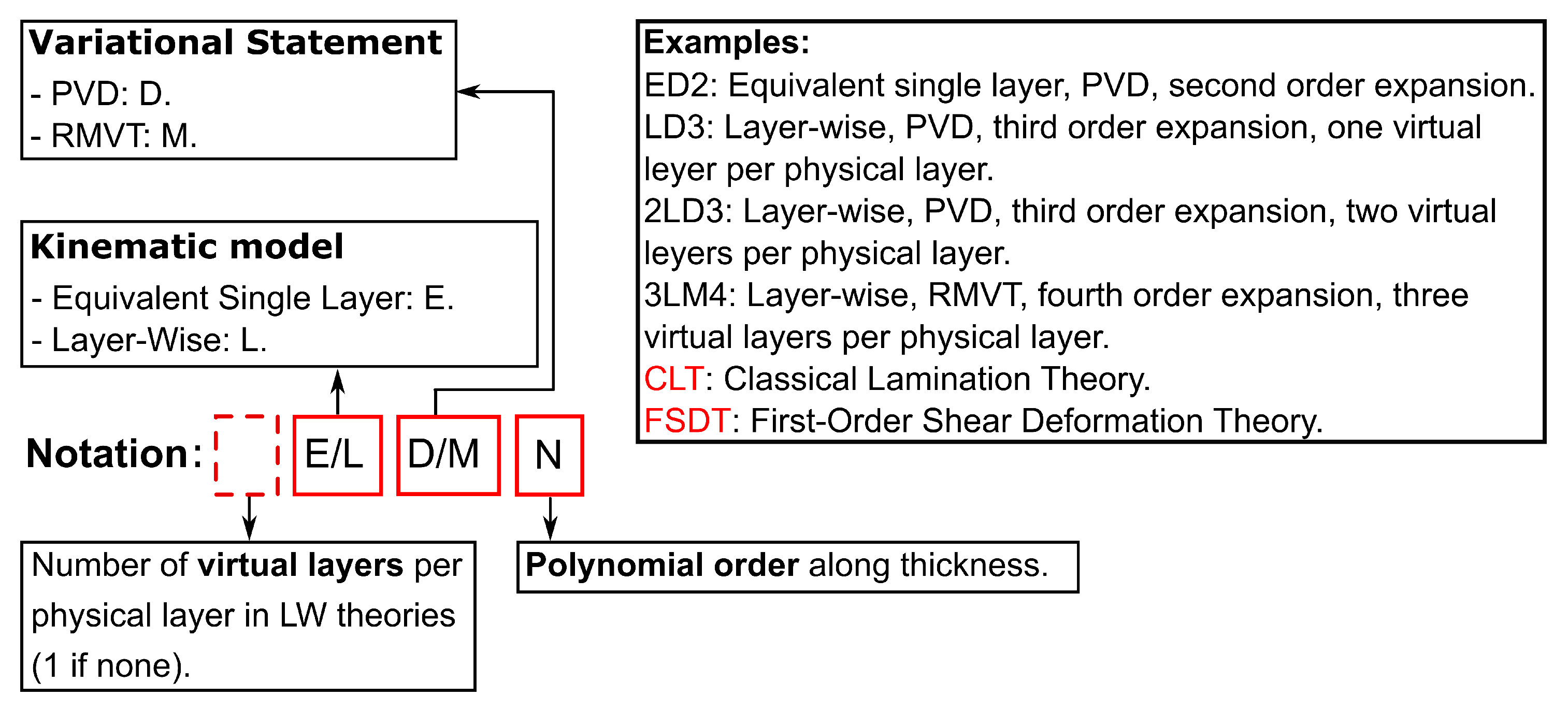
2.4. Acronym System
2.5. Stiffness Matrices Expression
3. Numerical Results
3.1. Monolayer Plate
3.2. Multilayer Plate
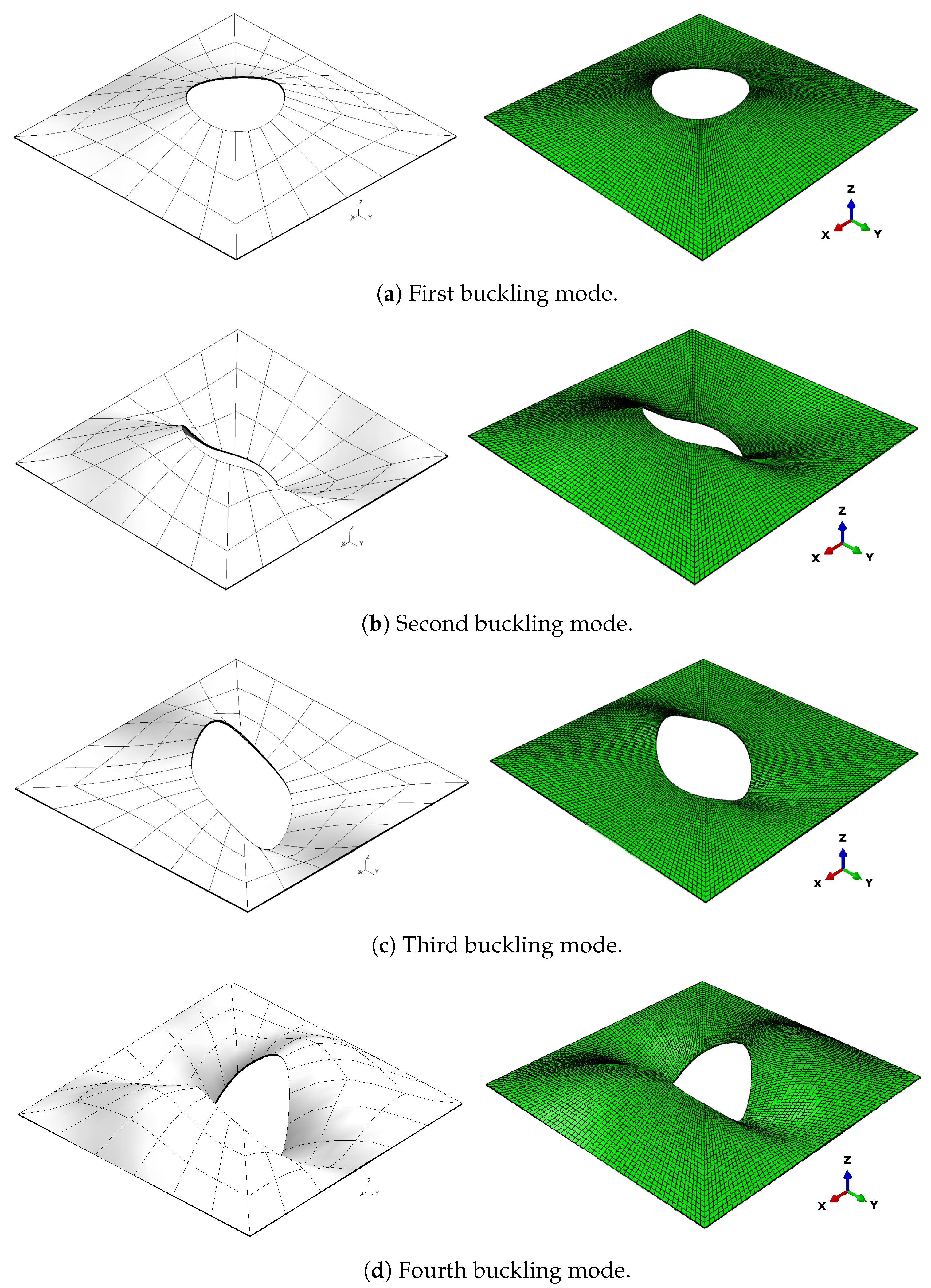
3.3. Multilayer Plate with a Central Cut-Out
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Governing Equations
Appendix B. Expression of the Fundamental Nuclei
References
- Dirk, H.J.L.; Ward, C.; Potter, K.D. The engineering aspects of automated prepreg layup: History, present and future. Compos. Part B Eng. 2012, 43, 997–1009. [Google Scholar]
- Zhuo, P.; Li, S.; Ashcroft, I.A.; Jones, A.I. Material extrusion additive manufacturing of continuous fiber reinforced polymer matrix composites: A review and outlook. Compos. Part B Eng. 2021, 224, 109143. [Google Scholar] [CrossRef]
- Hyer, M.W.; Lee, H.H. Innovative Design of Composite Structures: The Use of Curvilinear Fiber Format to Improve Buckling Resistance of Composite Plates with Central Circular Holes; Technical Report; NASA Langley Research Center: Hampton, VA, USA, 1990.
- Brampton, C.J.; Wu, K.C.; Kim, H.A. New optimization method for steered fiber composites using the level set method. Struct. Multidiscip. Optim. 2015, 52, 493–505. [Google Scholar] [CrossRef]
- Gürdal, Z.; Tatting, B.F.; Wu, C.K. Variable stiffness composite panels: Effects of stiffness variation on the in-plane and buckling response. Compos. Part A Appl. Sci. Manuf. 2008, 39, 911–922. [Google Scholar] [CrossRef]
- Oliveri, V.; Milazzo, A. A Rayleigh-Ritz approach for postbuckling analysis of variable angle tow composite stiffened panels. Comput. Struct. 2018, 196, 263–276. [Google Scholar] [CrossRef]
- Hao, P.; Yuan, X.; Liu, H.; Wang, B.; Liu, C.; Yang, D.; Zhan, S. Isogeometric buckling analysis of composite variable-stiffness panels. Compos. Struct. 2017, 165, 192–208. [Google Scholar] [CrossRef]
- Hao, P.; Liu, C.; Yuan, X.; Wang, B.; Li, G.; Zhu, T.; Niu, F. Buckling optimization of variable-stiffness composite panels based on flow field function. Compos. Struct. 2017, 181, 240–255. [Google Scholar] [CrossRef]
- Raju, G.; Wu, Z.; Kim, B.C.; Weaver, P.M. Prebuckling and buckling analysis of variable angle tow plates with general boundary conditions. Compos. Struct. 2012, 94, 2961–2970. [Google Scholar] [CrossRef]
- Sciascia, G.; Oliveri, V.; Weaver, P.M. Eigenfrequencies of prestressed variable stiffness composite shells. Compos. Struct. 2021, 270, 114019. [Google Scholar] [CrossRef]
- Chen, X.; Wu, Z.; Nie, G.; Weaver, P. Buckling analysis of variable angle tow composite plates with a through-the-width or an embedded rectangular delamination. Int. J. Solids Struct. 2018, 138, 166–180. [Google Scholar] [CrossRef]
- Wu, Z.; Raju, G.; Weaver, P.M. Framework for the buckling optimization of variable-angle tow composite plates. AIAA J. 2015, 53, 3788–3804. [Google Scholar] [CrossRef]
- Montemurro, M. An extension of the polar method to the first-order shear deformation theory of laminates. Compos. Struct. 2015, 127, 328–339. [Google Scholar] [CrossRef]
- Montemurro, M. The polar analysis of the third-order shear deformation theory of laminates. Compos. Struct. 2015, 131, 775–789. [Google Scholar] [CrossRef]
- Montemurro, M.; Catapano, A. On the effective integration of manufacturability constraints within the multi-scale methodology for designing variable angle-tow laminates. Compos. Struct. 2017, 161, 145–159. [Google Scholar] [CrossRef]
- Catapano, A.; Montemurro, M.; Balcou, J.-A.; Panettieri, E. Rapid prototyping of variable angle-tow composites. Aerotec. Missili Spaz. 2019, 98, 257–271. [Google Scholar] [CrossRef]
- Montemurro, M.; Catapano, A. A general b-spline surfaces theoretical framework for optimisation of variable angle-tow laminates. Compos. Struct. 2019, 209, 561–578. [Google Scholar] [CrossRef]
- Fiordilino, G.A.; Izzi, M.I.; Montemurro, M. A general isogeometric polar approach for the optimisation of variable stiffness composites: Application to eigenvalue buckling problems. Mech. Mater. 2021, 153, 103574. [Google Scholar] [CrossRef]
- Carrera, E. Theories and finite elements for multilayered, anisotropic, composite plates and shells. Arch. Comput. Methods Eng. 2002, 9, 87–140. [Google Scholar] [CrossRef]
- Carrera, E. Theories and finite elements for multilayered plates and shells: A unified compact formulation with numerical assessment and benchmarking. Arch. Comput. Methods Eng. 2003, 10, 215–296. [Google Scholar] [CrossRef]
- Carrera, E.; Giunta, G.; Brischetto, S. Hierarchical closed form solutions for plates bent by localized transverse loadings. J. Zhejiang-Univ.-Sci. A 2007, 8, 1026–1037. [Google Scholar] [CrossRef]
- Gaetano, G.; Salim, B.; Fabio, B.; Erasmo, C. Hierarchical theories for a linearised stability analysis of thin-walled beams with open and closed cross-section. Adv. Aircr. Spacecr. Sci. 2014, 1, 253. [Google Scholar]
- Hui, Y.; Xu, R.; Giunta, G.; De Pietro, G.; Hu, H.; Belouettar, S.; Carrera, E. Multiscale CUF-FE2 nonlinear analysis of composite beam structures. Comput. Struct. 2019, 221, 28–43. [Google Scholar] [CrossRef]
- Hui, Y.; Bai, X.; Yang, Y.; Yang, J.; Huang, Q.; Liu, X.; Huang, W.; Giunta, G.; Hu, H. A data-driven CUF-based beam model based on the tree-search algorithm. Compos. Struct. 2022, 300, 116123. [Google Scholar] [CrossRef]
- Viglietti, A.; Zappino, E.; Carrera, E. Analysis of variable angle tow composites structures using variable kinematic models. Compos. Part B Eng. 2019, 171, 272–283. [Google Scholar] [CrossRef]
- Fallahi, N.; Viglietti, A.; Carrera, E.; Pagani, A.; Zappino, E. Effect of fiber orientation path on the buckling, free vibration, and static analyses of variable angle tow panels. Facta Univ. Ser. Mech. Eng. 2020, 18, 165–188. [Google Scholar] [CrossRef]
- Fallahi, N.; Carrera, E.; Pagani, A. Application of ga optimization in analysis of variable stiffness composites. Int. J. Mater. Metall. Eng. 2021, 15, 65–70. [Google Scholar]
- Sanchez-Majano, A.R.; Pagani, A.; Petrolo, M.; Zhang, C. Buckling sensitivity of tow-steered plates subjected to multiscale defects by high-order finite elements and polynomial chaos expansion. Materials 2021, 14, 2706. [Google Scholar] [CrossRef] [PubMed]
- Pagani, A.; Sanchez-Majano, A.R. Influence of fiber misalignments on buckling performance of variable stiffness composites using layerwise models and random fields. Mech. Adv. Mater. Struct. 2022, 29, 384–399. [Google Scholar] [CrossRef]
- Demasi, L.; Ashenafi, Y.; Cavallaro, R.; Santarpia, E. Generalized unified formulation shell element for functionally graded variable-stiffness composite laminates and aeroelastic applications. Compos. Struct. 2015, 131, 501–515. [Google Scholar] [CrossRef]
- Vescovini, R.; Dozio, L. A variable-kinematic model for variable stiffness plates: Vibration and buckling analysis. Compos. Struct. 2016, 142, 15–26. [Google Scholar] [CrossRef]
- Carrera, E.; Demasi, L. Classical and advanced multilayered plate elements based upon pvd and rmvt. part 1: Derivation of finite element matrices. Int. J. Numer. Methods Eng. 2002, 55, 191–231. [Google Scholar] [CrossRef]
- Carrera, E.; Demasi, L. Classical and advanced multilayered plate elements based upon pvd and rmvt. part 2: Numerical implementations. Int. J. Numer. Methods Eng. 2002, 55, 253–291. [Google Scholar] [CrossRef]
- Giunta, G.; Iannotta, D.A.; Montemurro, M. A FEM Free Vibration Analysis of Variable Stiffness Composite Plates through Hierarchical Modeling. Materials 2023, 16, 4643. [Google Scholar] [CrossRef] [PubMed]
- Iannotta, D.A.; Giunta, G.; Montemurro, M. A mechanical analysis of variable angle-tow composite plates through variable kinematics models based on Carrera’s unified formulation. Compos. Struct. 2024, 327, 117717. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Carrera, E. On the use of the murakami’s zig-zag function in the modeling of layered plates and shells. Comput. Struct. 2004, 82, 541–554. [Google Scholar] [CrossRef]
- Bathe, K.-J. Finite Element Procedures; Klaus-Jurgen Bathe: Watertown, MA, USA, 2007. [Google Scholar]
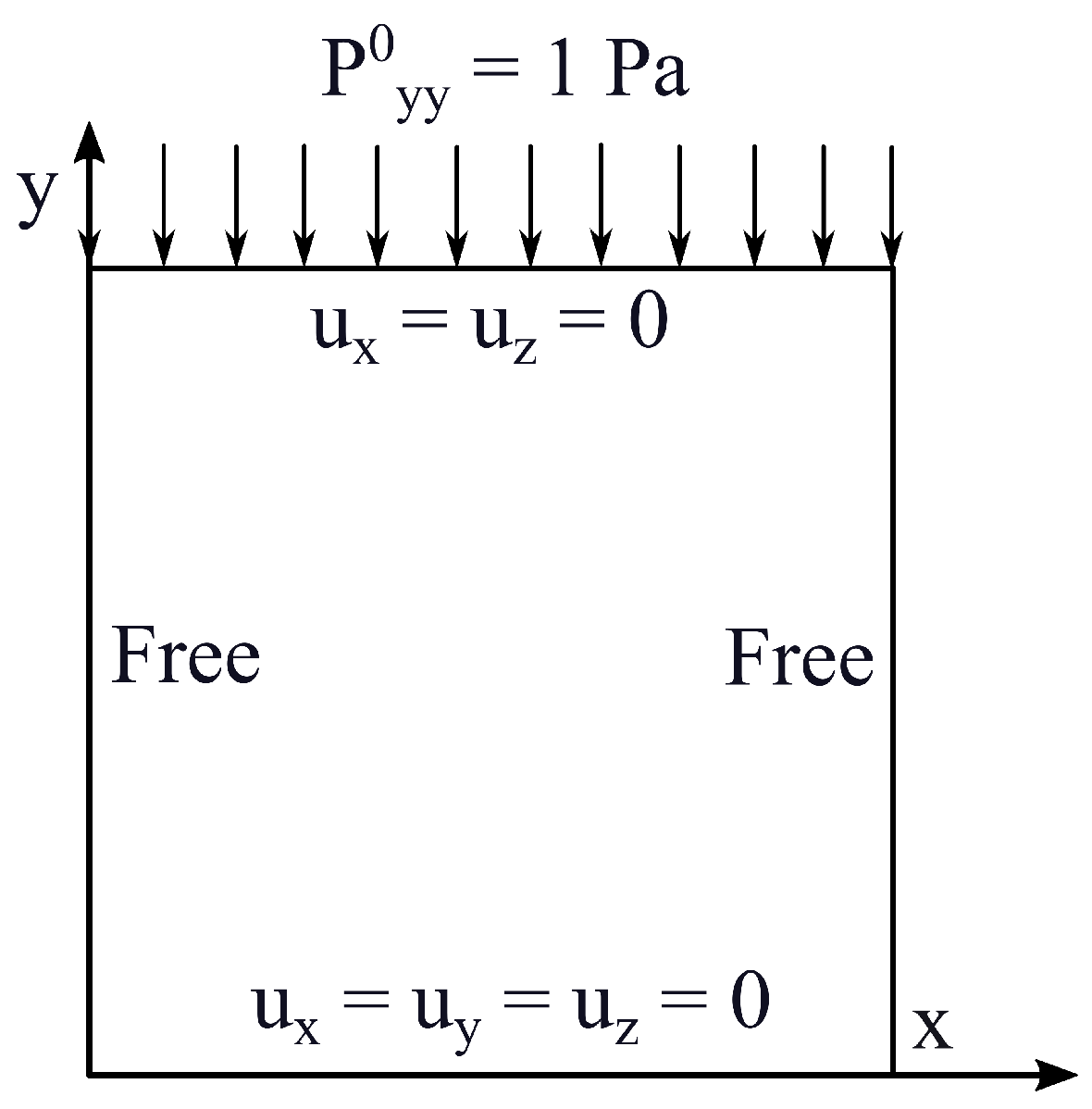
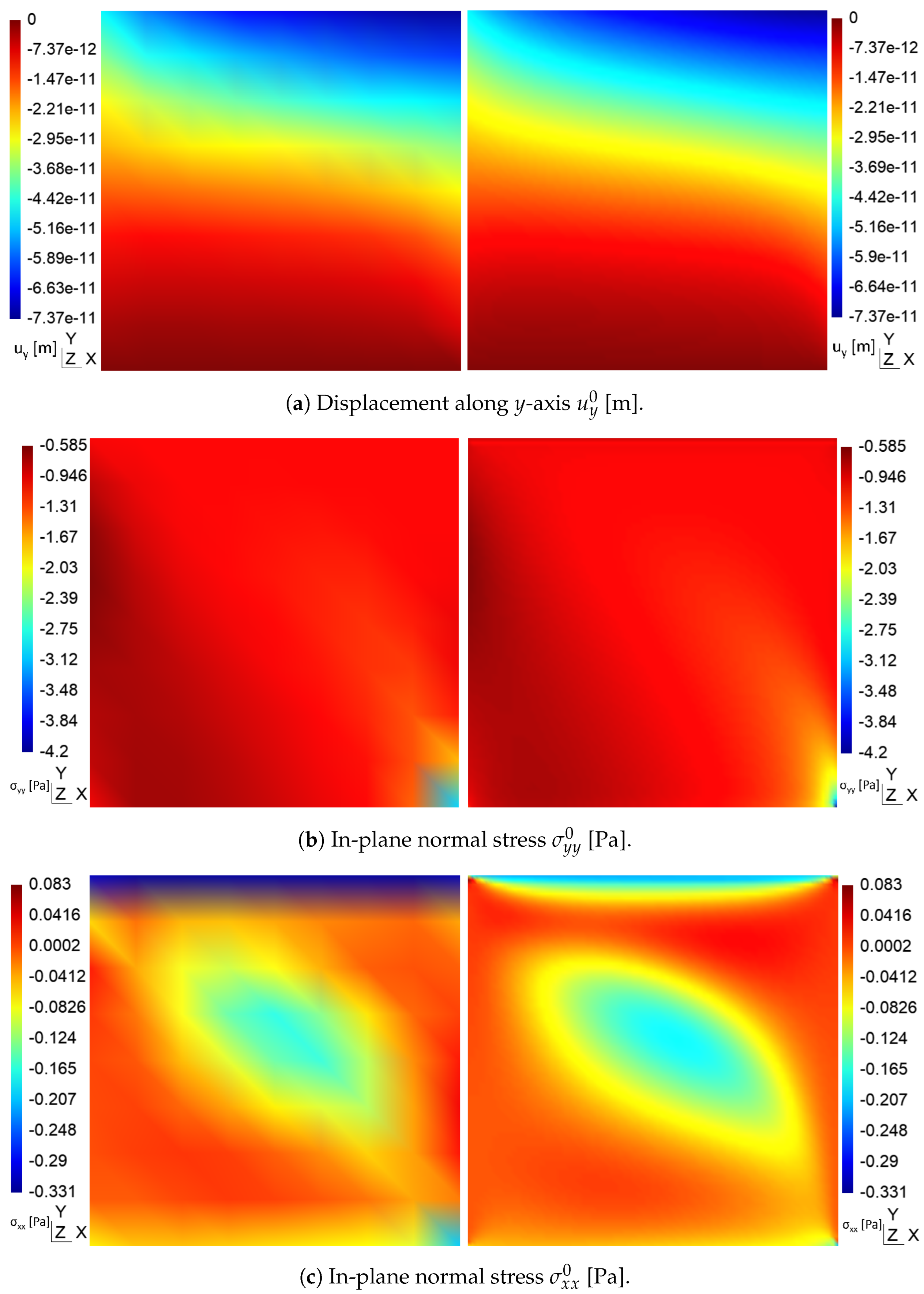
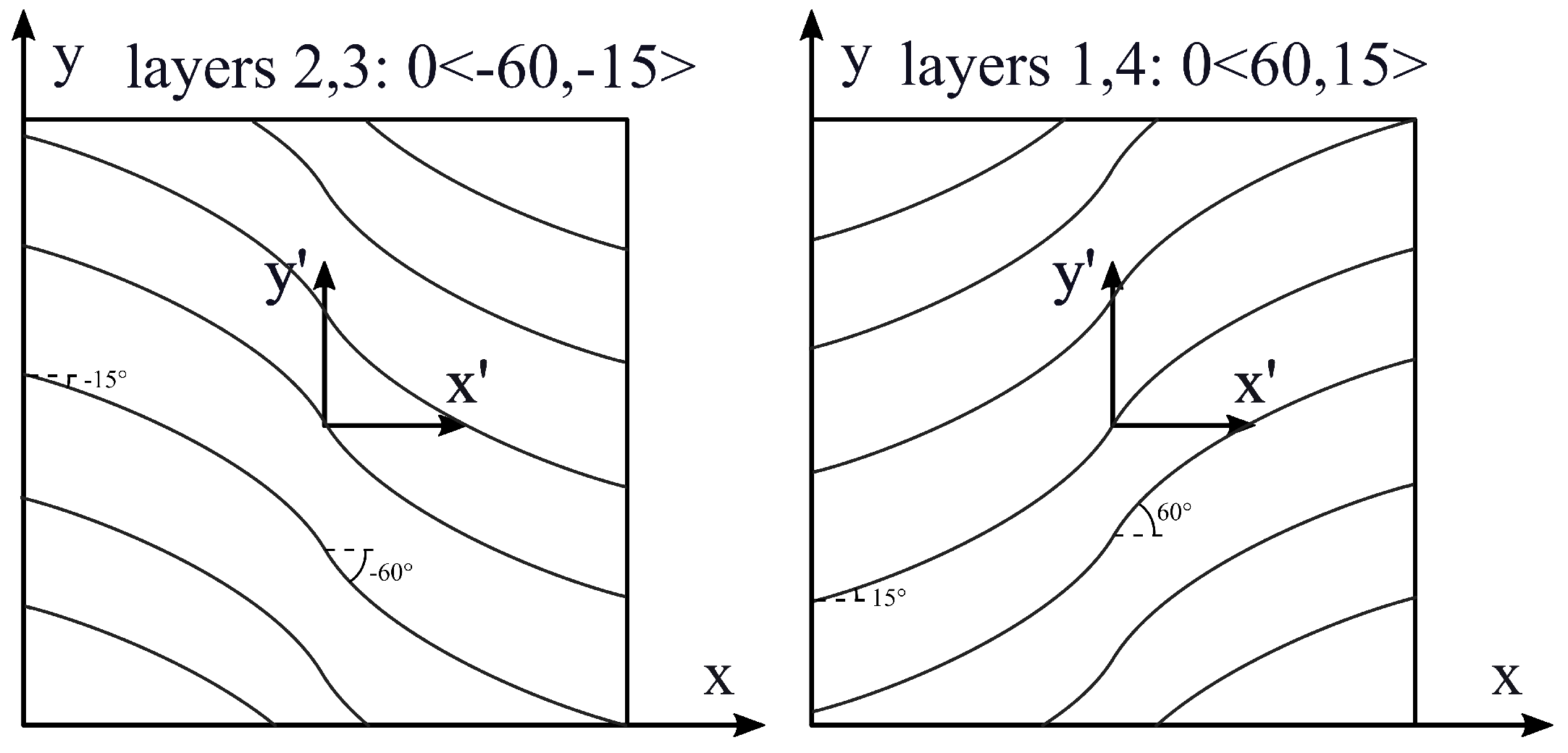
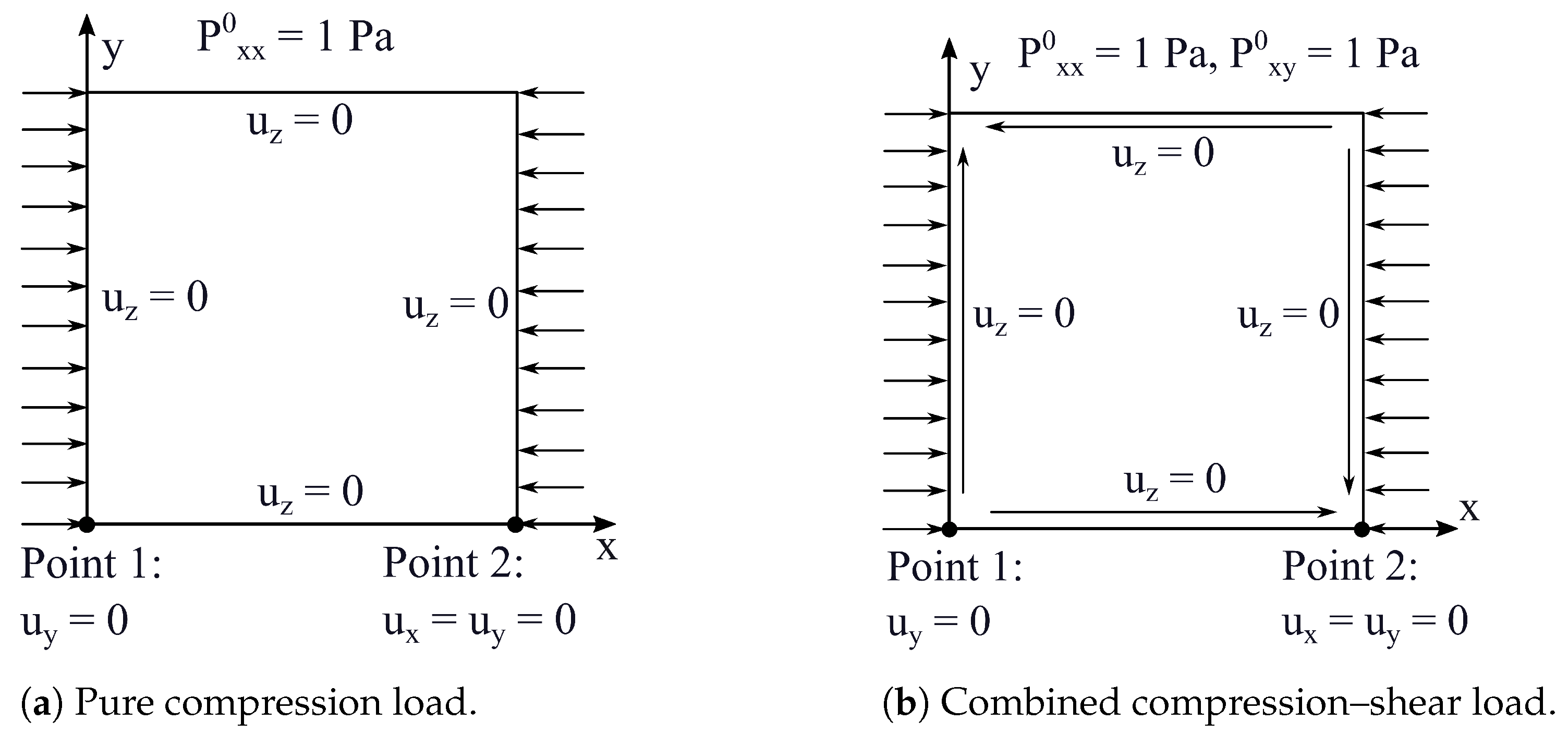
| Case | [GPa] | [GPa] | [GPa] | [GPa] | , |
|---|---|---|---|---|---|
| 1 | 50 | 10 | 5 | 5 | |
| 2, 3 | 181 |
| DOF | |||||
|---|---|---|---|---|---|
| Abaqus 3D | 1,310,499 | 28.926 | 57.366 | 85.585 | 122.498 |
| 225 | 29.901 | 57.475 | 136.926 | 170.607 | |
| 729 | 28.126 | 55.545 | 88.768 | 125.994 | |
| 1521 | 28.333 | 56.023 | 85.550 | 122.138 | |
| 2601 | 28.473 | 56.323 | 85.196 | 121.744 | |
| 3969 | 28.565 | 56.524 | 85.160 | 121.739 |
| Model | DOF |
|---|---|
| Abaqus 3D | 1,310,499 |
| 3LM4 | 22,542 |
| 3LM2 | 12,138 |
| 3LD4 | 11,271 |
| 3LD2 | 6069 |
| ED4 | 4335 |
| ED2 | 2601 |
| FSDT | 1734 |
| CLT | 1734 |
| Abaqus 3D | 28.926 | 57.366 | 85.585 | 122.498 |
| 3LM4 | 28.962 | 57.319 | 85.796 | 122.756 |
| 3LM2 | 28.958 | 57.309 | 85.788 | 122.743 |
| 3LD4 | 28.979 | 57.478 | 85.891 | 122.928 |
| 3LD2 | 28.979 | 57.479 | 85.892 | 122.929 |
| ED4 | 28.468 | 56.296 | 85.154 | 121.683 |
| ED2 | 28.473 | 56.323 | 85.196 | 121.744 |
| FSDT | 28.973 | 57.492 | 85.918 | 122.976 |
| CLT | 29.008 | 57.681 | 86.179 | 123.361 |
| Pure compression Pa | ||||
| Abaqus 3D | 13.63 | 21.57 | 35.42 | 54.46 |
| Ref. [7] | 13.63 | 21.64 | 35.41 | 54.56 |
| Ref. [26] | 13.67 | 21.68 | 35.69 | 54.60 |
| LM4 | 13.63 | 21.57 | 35.62 | 54.47 |
| LM2 | 13.63 | 21.57 | 35.62 | 54.47 |
| LD4 | 13.63 | 21.57 | 35.62 | 54.47 |
| LD2 | 13.63 | 21.57 | 35.62 | 54.47 |
| ED4 | 13.64 | 21.71 | 35.80 | 54.60 |
| ED2 | 13.67 | 21.74 | 35.85 | 54.81 |
| FSDT | 13.68 | 21.75 | 35.86 | 54.83 |
| CLT | 13.85 | 22.04 | 36.42 | 56.17 |
| Compression–shear Pa | ||||
| Abaqus 3D | 12.04 | 18.46 | 30.86 | 41.87 |
| Ref. [7] | 12.04 | 18.49 | 30.83 | 41.84 |
| LM4 | 12.05 | 18.51 | 31.03 | 42.39 |
| LM2 | 12.05 | 18.51 | 31.03 | 42.39 |
| LD4 | 12.05 | 18.51 | 31.03 | 42.39 |
| LD2 | 12.05 | 18.51 | 31.03 | 42.39 |
| ED4 | 12.07 | 18.55 | 31.14 | 42.56 |
| ED2 | 12.08 | 18.58 | 31.20 | 42.75 |
| FSDT | 12.10 | 18.59 | 31.22 | 42.73 |
| CLT | 12.26 | 18.84 | 31.75 | 43.70 |
| Pure compression Pa | ||||
| Abaqus 3D | 13.322 | 22.522 | 31.974 | 36.974 |
| LM4 | 13.294 | 22.386 | 31.352 | 37.071 |
| LM2 | 13.298 | 22.390 | 31.360 | 37.077 |
| LD4 | 13.378 | 22.534 | 31.661 | 37.280 |
| LD2 | 13.383 | 22.539 | 31.672 | 37.288 |
| ED4 | 13.369 | 22.554 | 31.763 | 37.301 |
| ED2 | 13.420 | 22.633 | 31.916 | 37.432 |
| FSDT | 13.464 | 22.658 | 31.920 | 37.486 |
| CLT | 13.539 | 22.862 | 32.353 | 37.790 |
| Compression–shear Pa | ||||
| Abaqus 3D | 11.152 | 19.396 | 23.956 | 32.302 |
| LM4 | 11.146 | 19.322 | 23.491 | 32.337 |
| LM2 | 11.149 | 19.326 | 23.496 | 32.343 |
| LD4 | 11.204 | 19.436 | 23.638 | 32.519 |
| LD2 | 11.207 | 19.440 | 23.646 | 32.526 |
| ED4 | 11.228 | 19.490 | 23.730 | 32.611 |
| ED2 | 11.253 | 19.536 | 23.808 | 32.709 |
| FSDT | 11.264 | 19.534 | 23.808 | 32.697 |
| CLT | 11.326 | 19.713 | 24.097 | 33.020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giunta, G.; Iannotta, D.A.; Kirkayak, L.; Montemurro, M. Buckling Analysis of Variable-Angle Tow Composite Plates through Variable Kinematics Hierarchical Models. J. Compos. Sci. 2024, 8, 320. https://doi.org/10.3390/jcs8080320
Giunta G, Iannotta DA, Kirkayak L, Montemurro M. Buckling Analysis of Variable-Angle Tow Composite Plates through Variable Kinematics Hierarchical Models. Journal of Composites Science. 2024; 8(8):320. https://doi.org/10.3390/jcs8080320
Chicago/Turabian StyleGiunta, Gaetano, Domenico Andrea Iannotta, Levent Kirkayak, and Marco Montemurro. 2024. "Buckling Analysis of Variable-Angle Tow Composite Plates through Variable Kinematics Hierarchical Models" Journal of Composites Science 8, no. 8: 320. https://doi.org/10.3390/jcs8080320
APA StyleGiunta, G., Iannotta, D. A., Kirkayak, L., & Montemurro, M. (2024). Buckling Analysis of Variable-Angle Tow Composite Plates through Variable Kinematics Hierarchical Models. Journal of Composites Science, 8(8), 320. https://doi.org/10.3390/jcs8080320







