Machine Learning Algorithms for Prediction and Characterization of Cohesive Zone Parameters for Mixed-Mode Fracture
Abstract
1. Introduction
2. Cohesive Zone Modeling
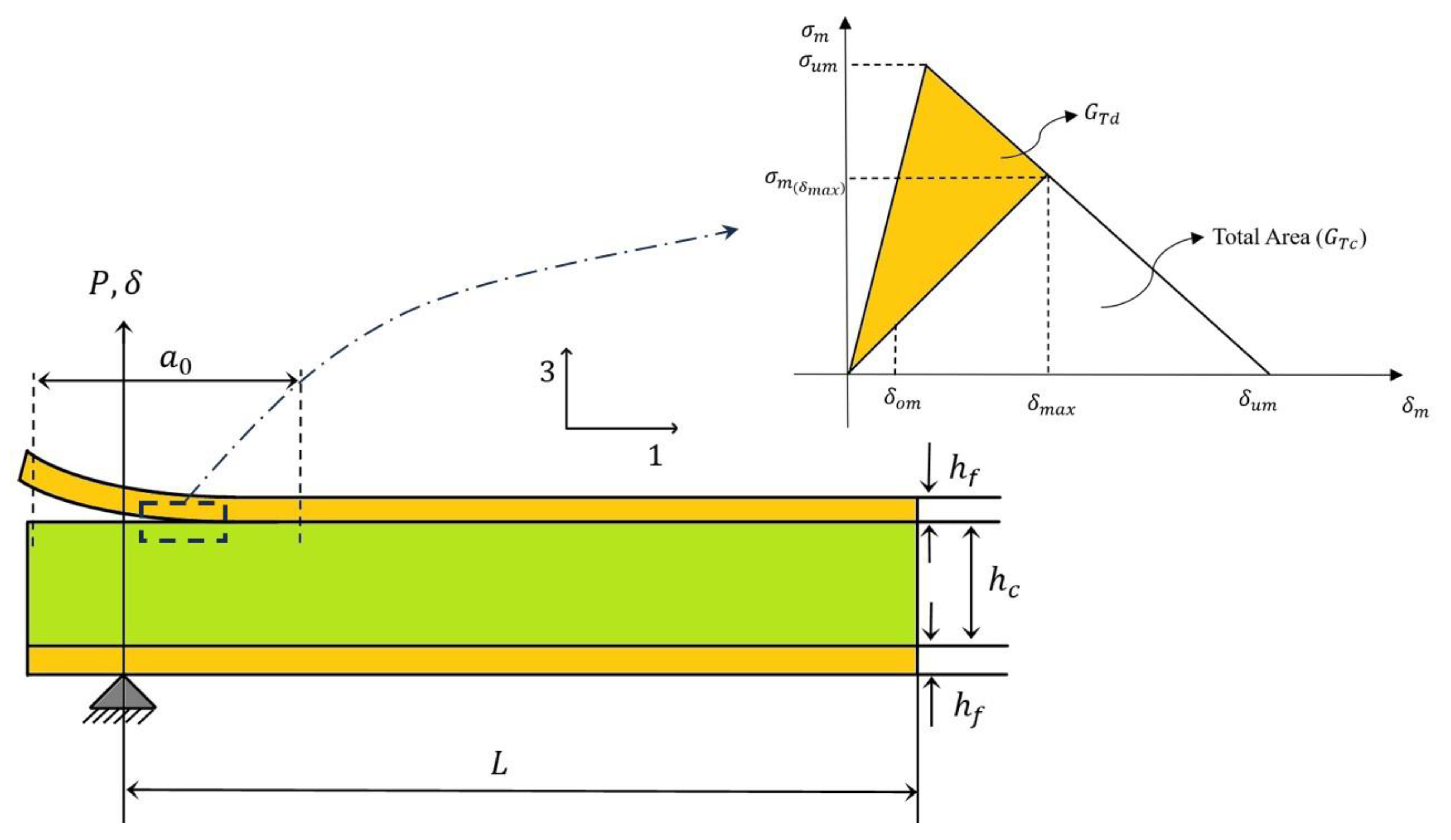
2.1. Cohesive Zone Model
2.2. Numerical Simulation of the ADCB Specimen
2.3. Geometry and Materials Properties
3. Machine Learning Algorithms
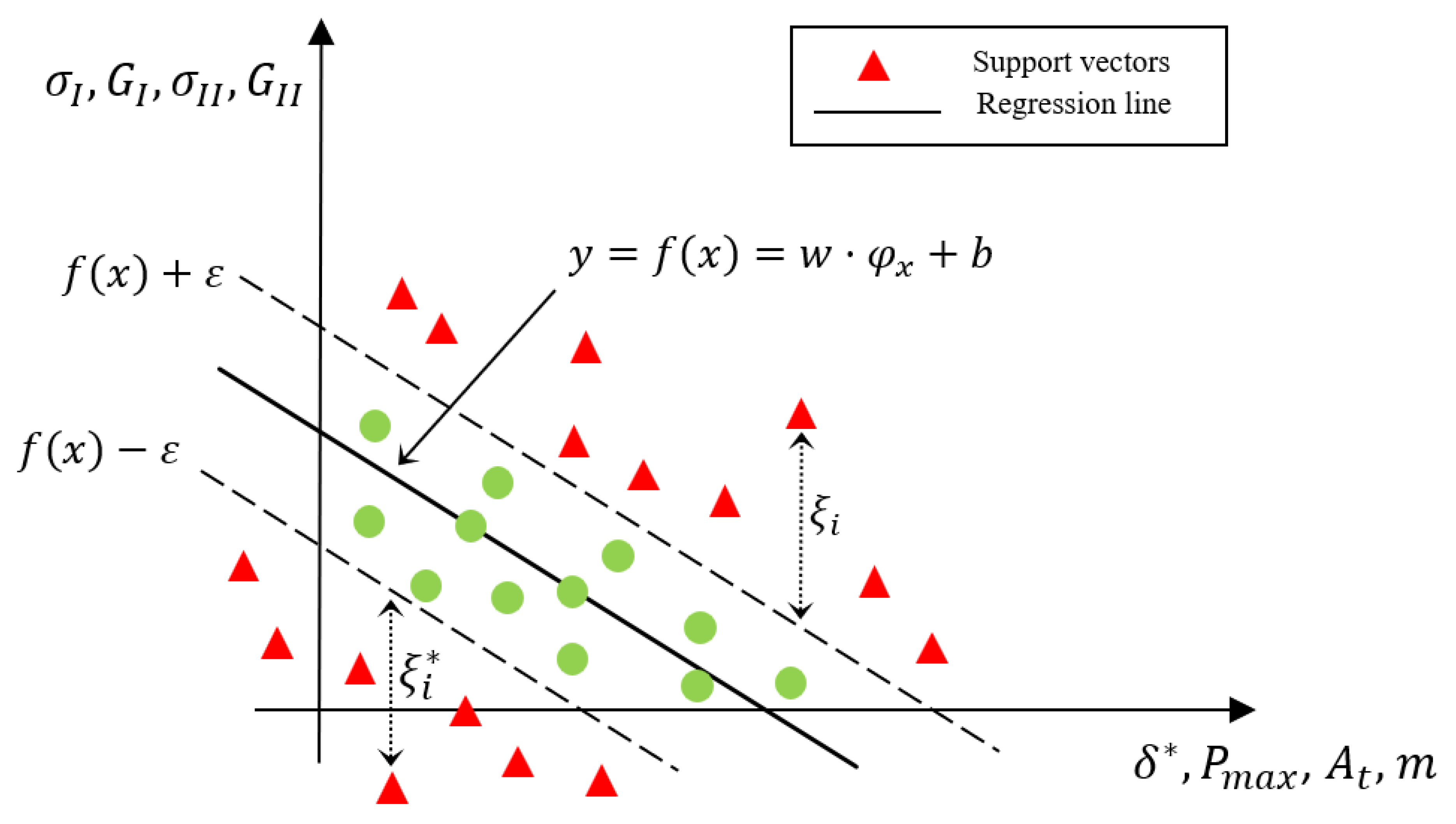
3.1. Support Vector Regression
3.2. Random Forest
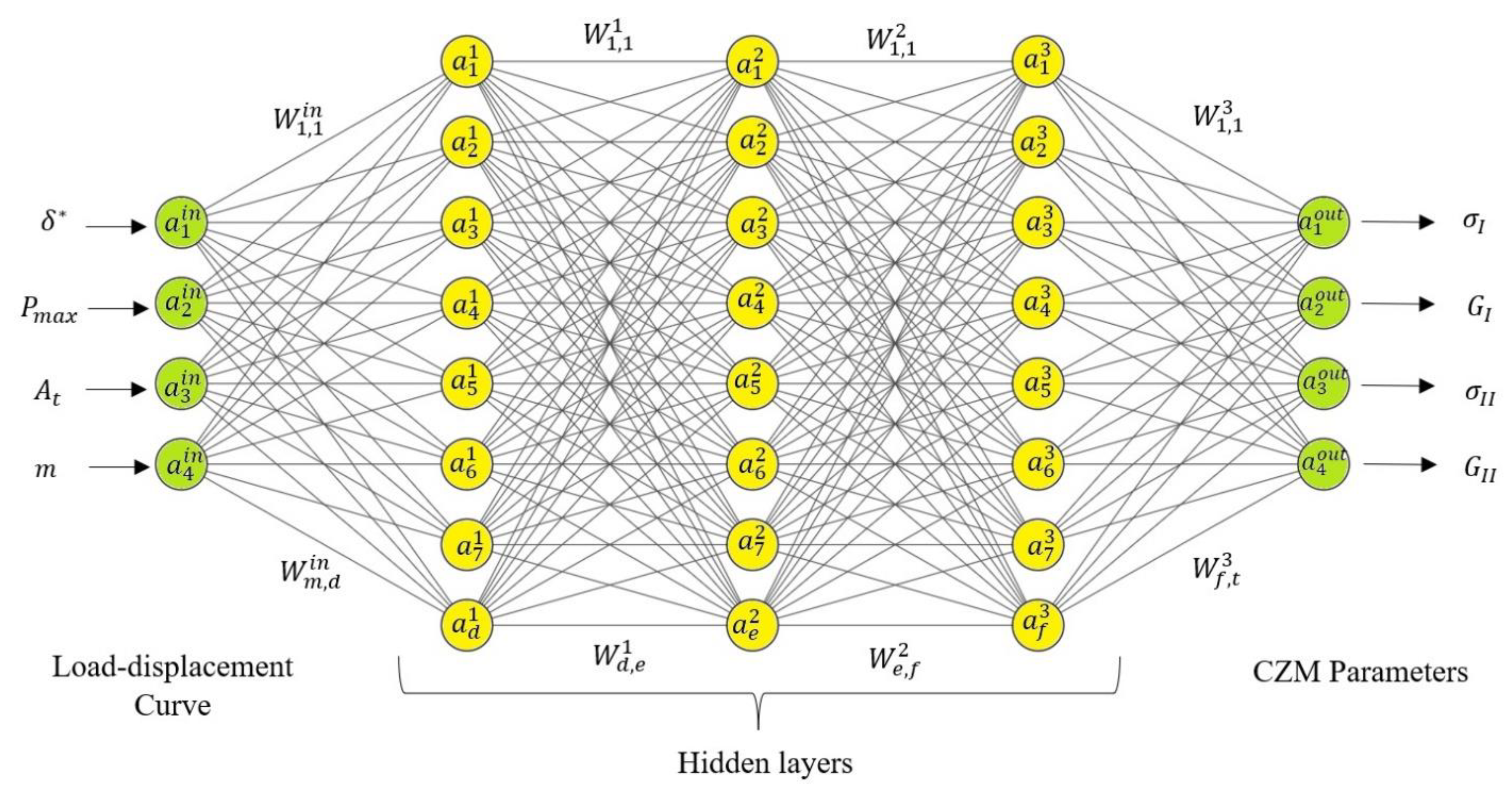
3.3. Artificial Neural Network
4. Results and Discussion
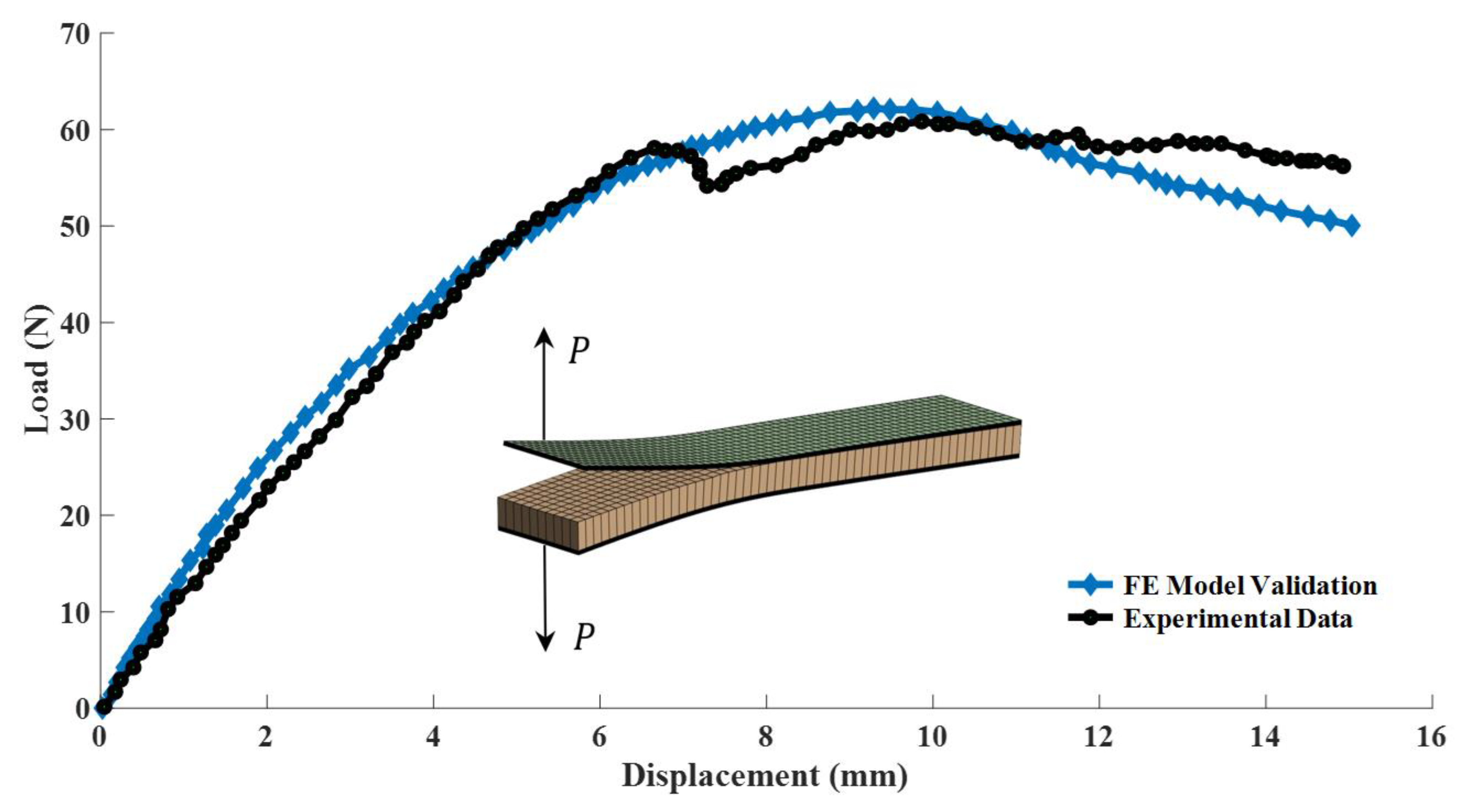
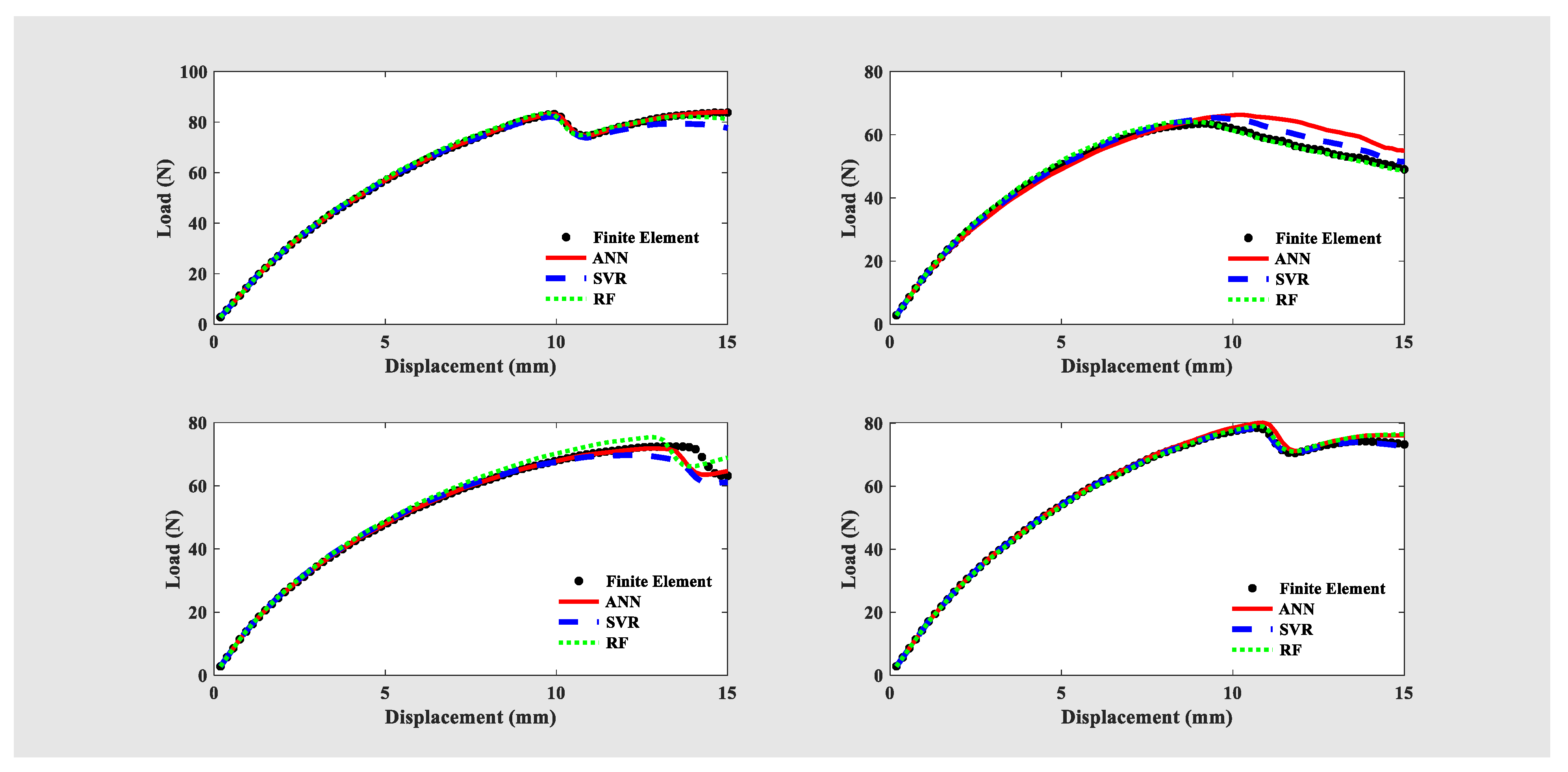
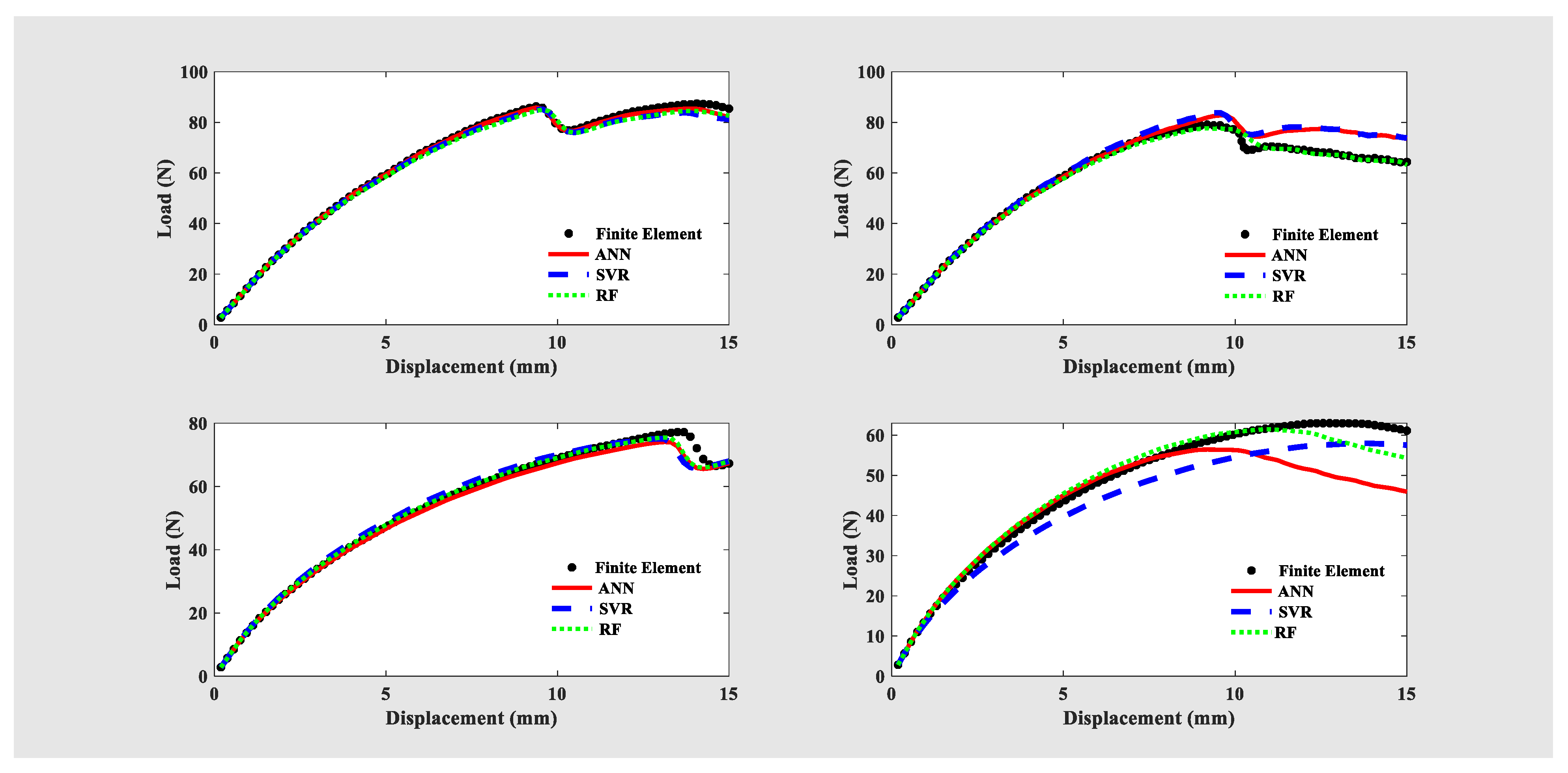
4.1. Validation of Modeling Approach
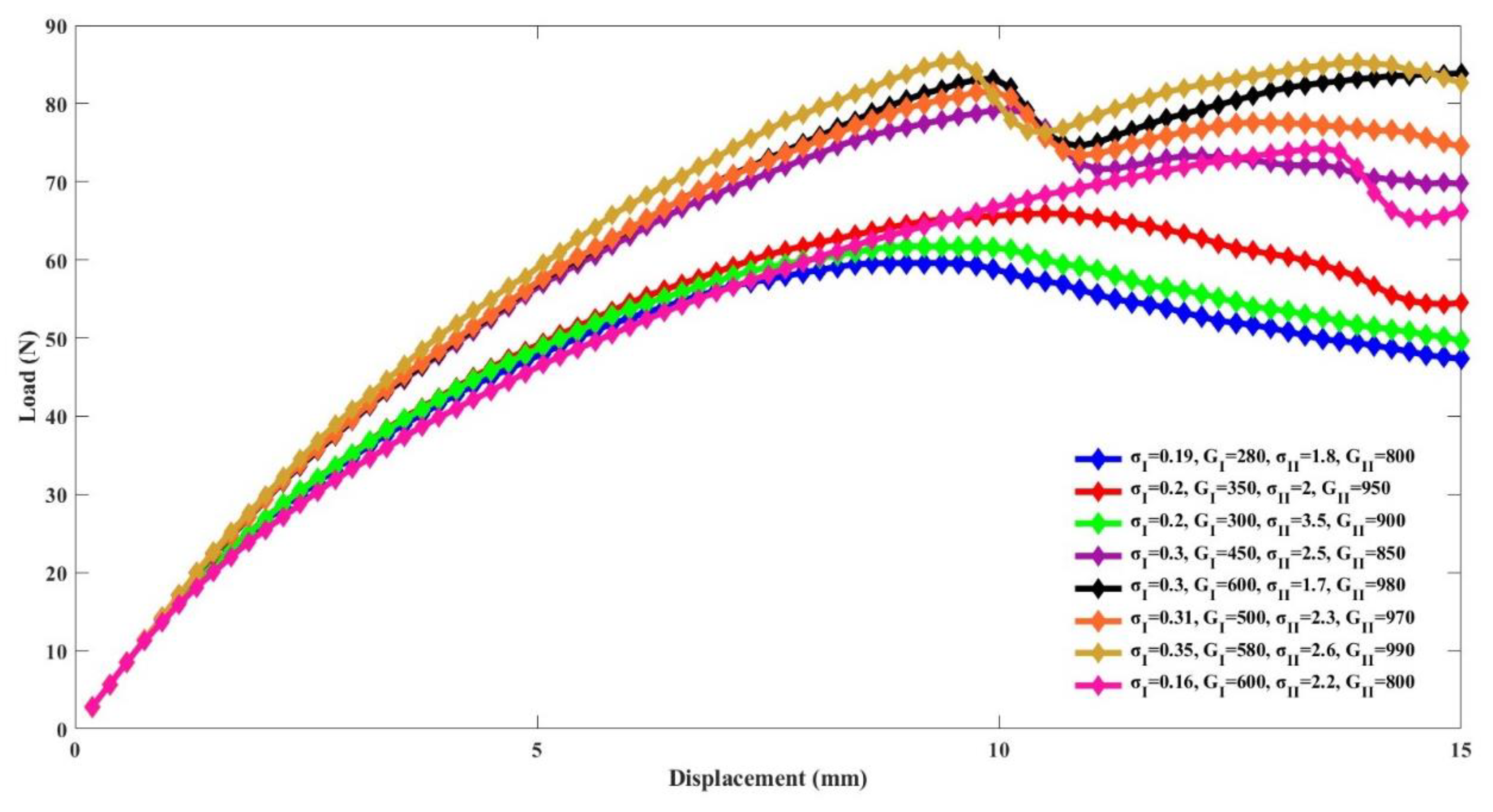
4.2. Dataset Collection for Cohesive Zone Model Parameters
4.3. Hyperparameters Tuning
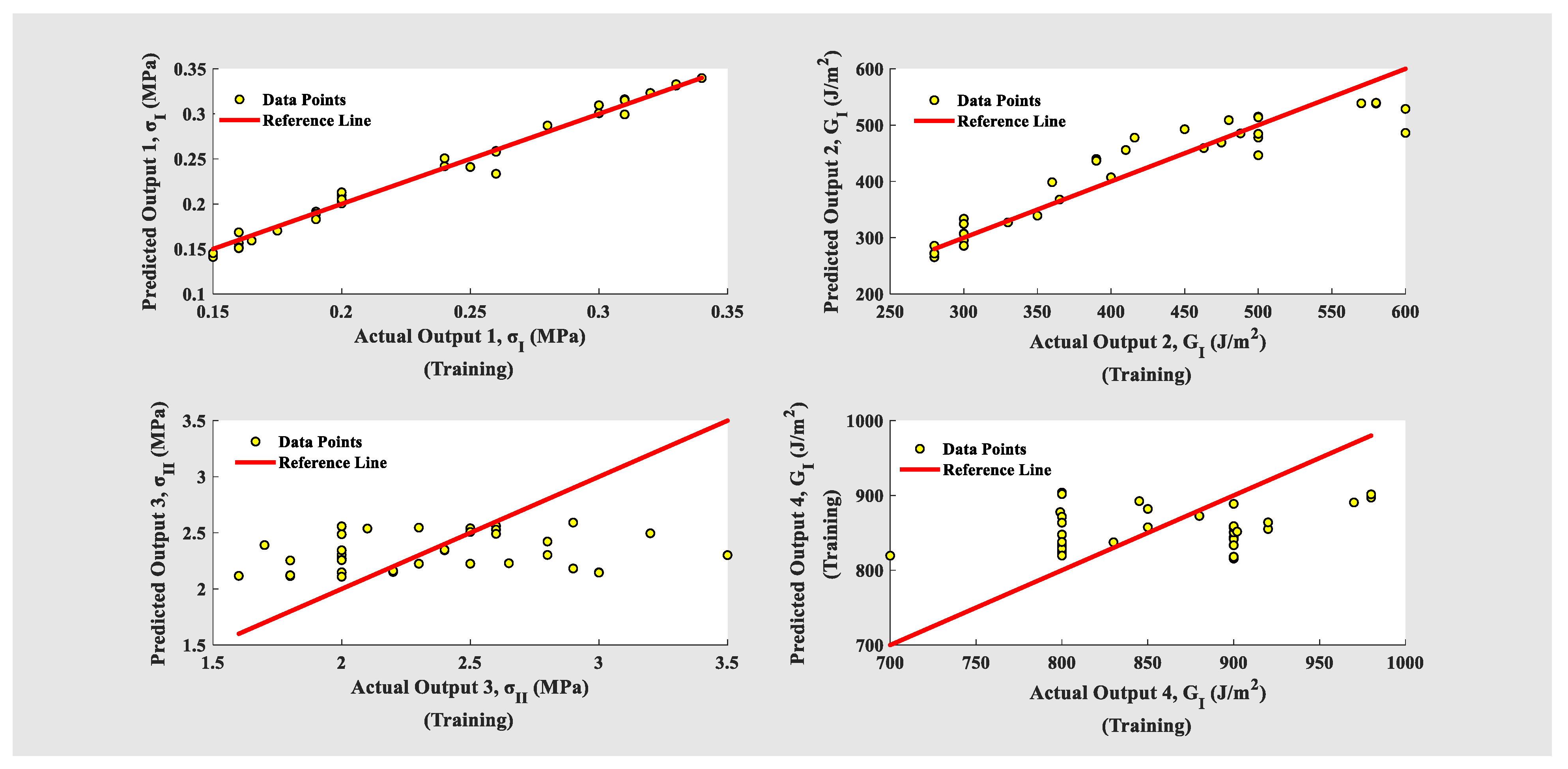
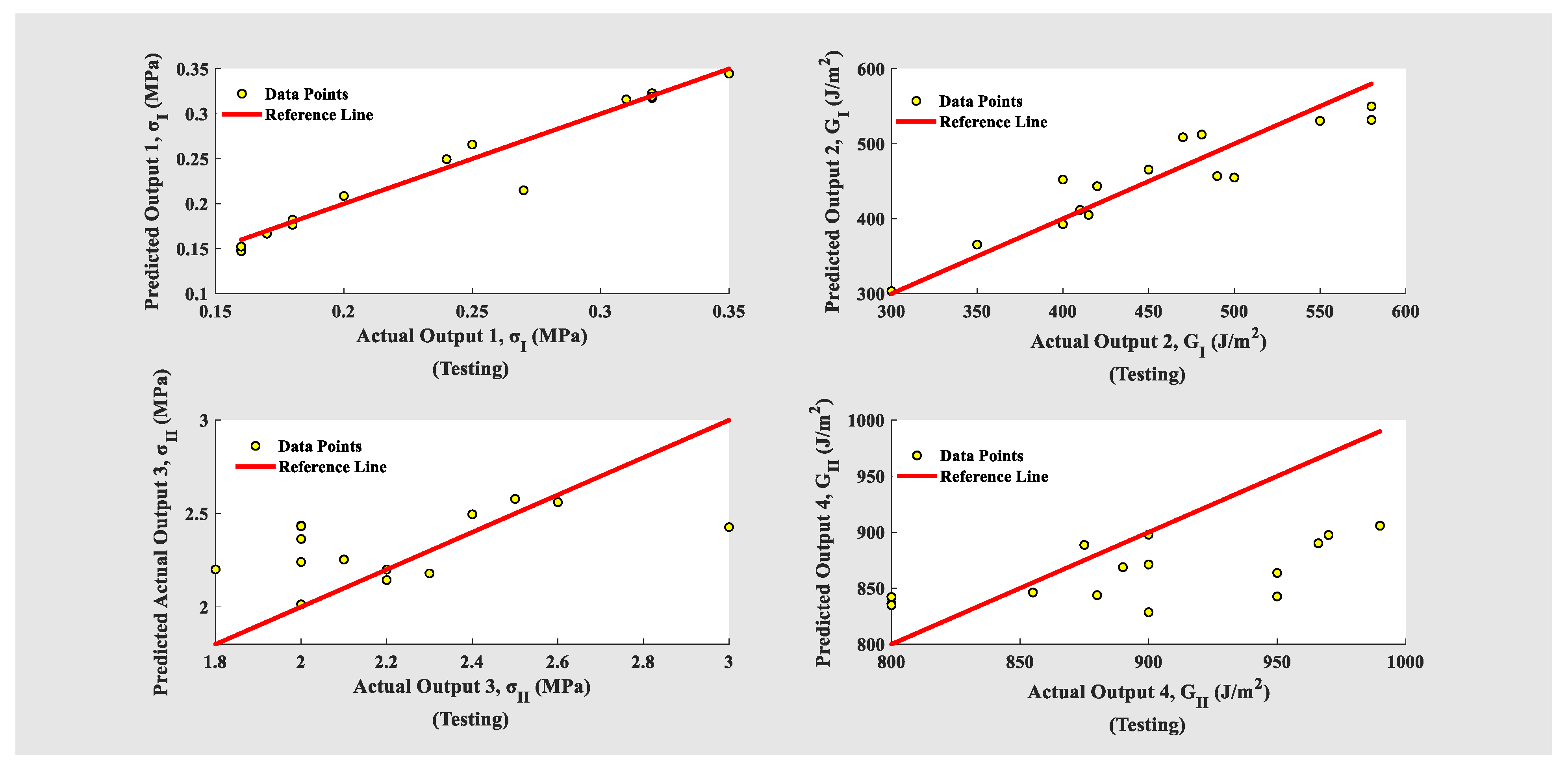
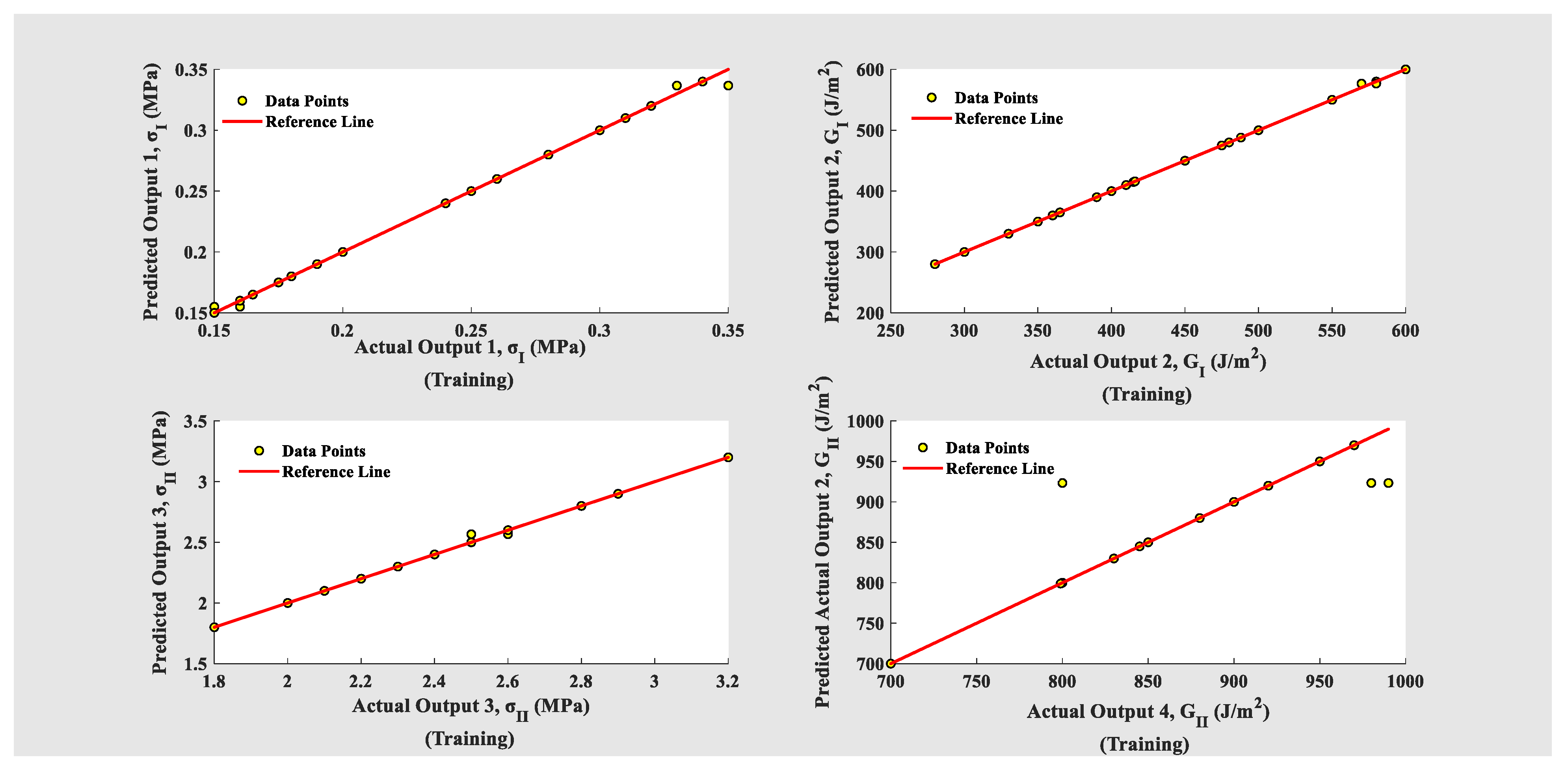
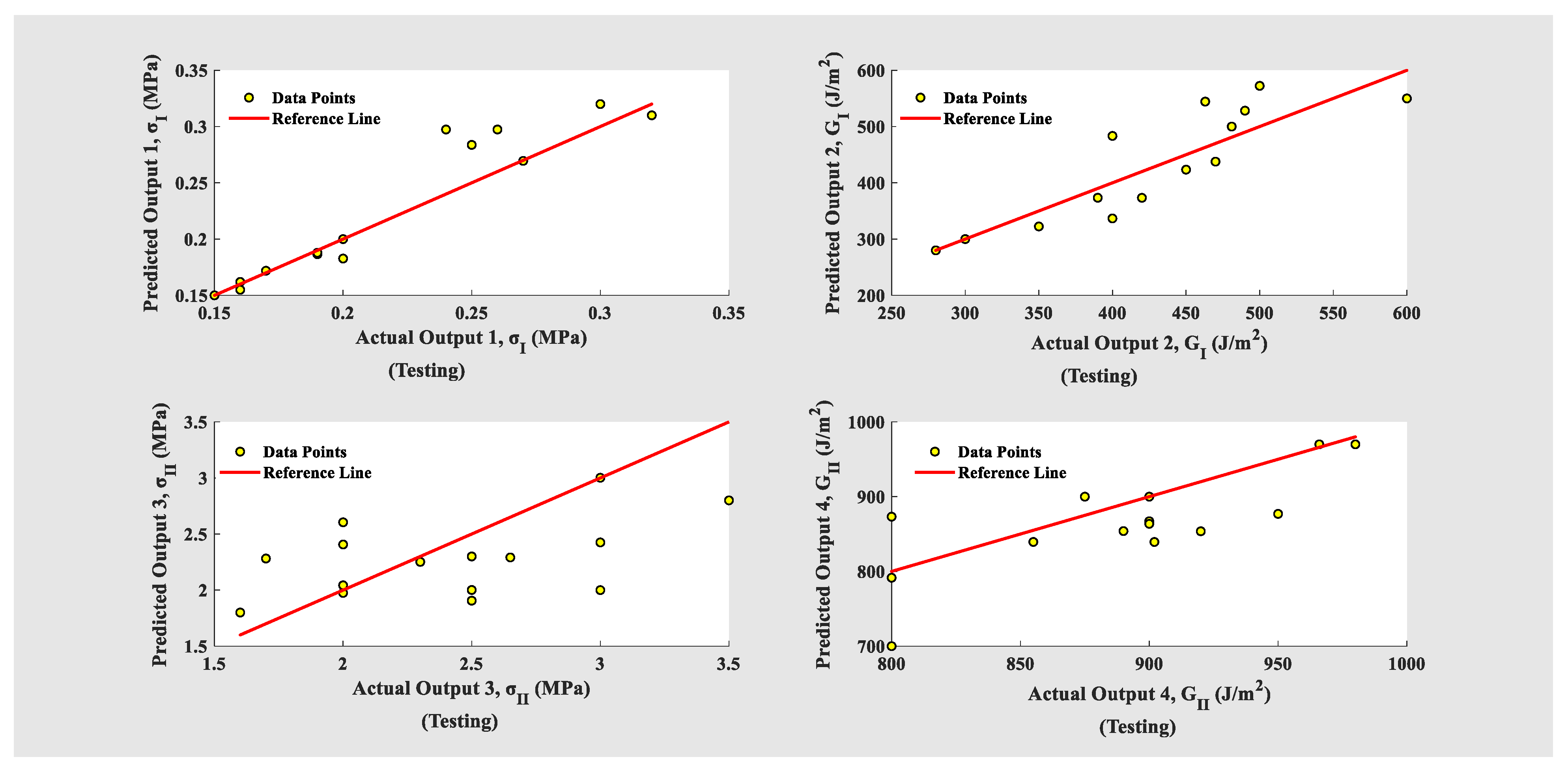
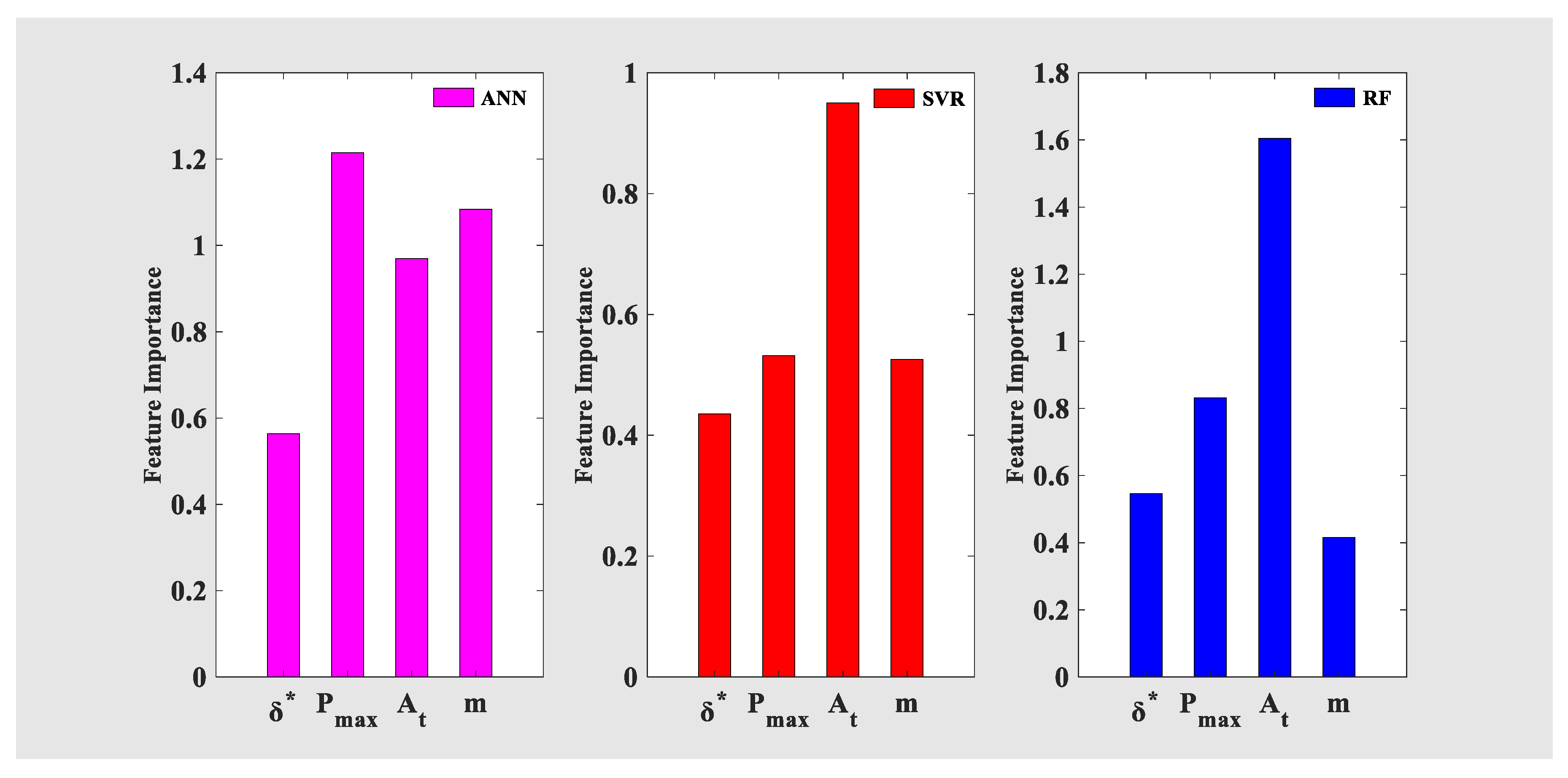
4.4. Evaluation of Machine Learning Algorithms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Y.; Zeng, X.; Deng, Y.; Wei, G. Investigation on manufacturing and low-velocity impact performance of all-composite sandwich structure with S-type foldcore. Compos. Struct. 2022, 290, 115539. [Google Scholar] [CrossRef]
- Lv, H.; Shi, S.; Chen, B.; Ma, J.; Sun, Z. Low-velocity impact response of composite sandwich structure with grid–honeycomb hybrid core. Int. J. Mech. Sci. 2023, 246, 108149. [Google Scholar] [CrossRef]
- Xue, P.; Wei, X.; Li, Z.; Xiong, J. Face-core interfacial debonding characterization model of an all-composite sandwich beam with a hexagonal honeycomb core. Eng. Fract. Mech. 2022, 269, 108554. [Google Scholar] [CrossRef]
- Abrate, S.; Ferrero, J.F.; Navarro, P. Cohesive zone models and impact damage predictions for composite structures. Meccanica 2015, 50, 2587–2620. [Google Scholar] [CrossRef]
- Cui, H. Numerical simulation of crack propagation in solid propellant with extrinsic cohesive zone model. Meccanica 2022, 57, 1617–1630. [Google Scholar] [CrossRef]
- Kumar, A.; Sain, T. Phase field-based cohesive zone approach to model delamination in fiber-reinforced polymer composites. Compos. Struct. 2024, 329, 117751. [Google Scholar] [CrossRef]
- Vereecke, J.; Bois, C.; Wahl, J.-C.; Briand, T.; Ballère, L.; Lavelle, F. Explicit modelling of meso-scale damage in laminated composites—Comparison between finite fracture mechanics and cohesive zone model. Compos. Sci. Technol. 2024, 253, 110640. [Google Scholar] [CrossRef]
- Poblete, F.R.; Mondal, K.; Ma, Y.; Dickey, M.D.; Genzer, J.; Zhu, Y. Direct measurement of rate-dependent mode I and mode II traction-separation laws for cohesive zone modeling of laminated glass. Compos. Struct. 2022, 279, 114759. [Google Scholar] [CrossRef]
- Zangoei, A.R.; Rahimi, G.H.; Gazor, M.S.; Vahidibidhendi, M.; Azarniya, O. Experimental and numerical study of delamination phenomenon in sandwich structures with hybrid corrugated core in the mode II of crack growth. J. Compos. Mater. 2023, 57, 1199–1210. [Google Scholar] [CrossRef]
- Fu, C.; Wang, X. Simulating delamination in composite laminates involving large scale fiber bridging based on the mixed-mode three-linear cohesive zone model. Theor. Appl. Fract. Mech. 2022, 117, 103164. [Google Scholar] [CrossRef]
- Rafiee, R.; Sotoudeh, S. A cohesive zone model for predicting the initiation of Mode II delamination in composites under cyclic loading. J. Reinf. Plast. Compos. 2021, 40, 179–192. [Google Scholar] [CrossRef]
- Freed, Y.; Salviato, M.; Zobeiry, N. Implementation of a probabilistic machine learning strategy for failure predictions of adhesively bonded joints using cohesive zone modeling. Int. J. Adhes. Adhes. 2022, 118, 103226. [Google Scholar] [CrossRef]
- Kouno, Y.; Imanaka, M.; Hino, R.; Omiya, M.; Yoshida, F. Estimation of fracture behavior of CFRP/CFRP adhesively bonded joints under mixed-mode conditions using a cohesive zone model. J. Adhes. Sci. Technol. 2024, 38, 1–18. [Google Scholar] [CrossRef]
- Diehl, T. On using a penalty-based cohesive-zone finite element approach, Part II: Inelastic peeling of an epoxy-bonded aluminum strip. Int. J. Adhes. Adhes. 2008, 28, 256–265. [Google Scholar] [CrossRef]
- Allix, O.; Ladevéze, P.; Corigliano, A. Damage analysis of interlaminar fracture specimens. Compos. Struct. 1995, 31, 61–74. [Google Scholar] [CrossRef]
- Needleman, A. An analysis of tensile decohesion along an interface. J. Mech. Phys. Solids 1990, 38, 289–324. [Google Scholar] [CrossRef]
- Mi, Y.; Crisfield, M.A.; Davies, G.A.O.; Hellweg, H.B. Progressive delamination using interface elements. J. Compos. Mater. 1998, 32, 1246–1272. [Google Scholar] [CrossRef]
- Donadon, M.V.; De Almeida SF, M.; Arbelo, M.A.; de Faria, A.R. A three-dimensional ply failure model for composite structures. Int. J. Aerosp. Eng. 2009, 2009, 486063. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids. J. Mech. Phys. Solids 1992, 40, 1377–1397. [Google Scholar] [CrossRef]
- Akhmet, G.; Yu, Y.; Hu, P.; Hou, W.-B.; Han, X. Analysis of the performance of adhesively bonded corrugated core sandwich structures using cohesive zone method. J. Sandw. Struct. Mater. 2020, 22, 104–124. [Google Scholar] [CrossRef]
- Airoldi, A.; Novembre, E.; Mirani, C.; Gianotti, G.; Passoni, R.; Cantoni, C. A model for damage and failure of carbon-carbon composites: Development and identification through Gaussian process regression. Mater. Today Commun. 2023, 35, 106059. [Google Scholar] [CrossRef]
- Han, X.; Cai, H.; Sun, J.; Wei, Z.; Huang, Y.; Meng, L. Behaviors of composite laminates under low-energy impact using a novel analytical framework. Int. J. Appl. Mech. 2022, 14, 2250004. [Google Scholar] [CrossRef]
- Jumel, J.; Budzik, M.K.; Shanahan, M.E. Beam on elastic foundation with anticlastic curvature: Application to analysis of mode I fracture tests. Eng. Fract. Mech. 2011, 78, 3253–3269. [Google Scholar] [CrossRef]
- Cabello, M.; Zurbitu, J.; Renart, J.; Turon, A.; Martínez, F. A non-linear hyperelastic foundation beam theory model for double cantilever beam tests with thick flexible adhesive. Int. J. Solids Struct. 2016, 80, 19–27. [Google Scholar] [CrossRef]
- Cabello, M.; Zurbitu, J.; Renart, J.; Turon, A.; Martínez, F. A general analytical model based on elastic foundation beam theory for adhesively bonded DCB joints either with flexible or rigid adhesives. Int. J. Solids Struct. 2016, 94–95, 21–34. [Google Scholar] [CrossRef]
- Ereiz, S.; Duvnjak, I.; Jiménez-Alonso, J.F. Review of finite element model updating methods for structural applications. Structures 2022, 41, 684–723. [Google Scholar] [CrossRef]
- Valoroso, N.; Sessa, S.; Lepore, M.; Cricrì, G. Identification of mode-I cohesive parameters for bonded interfaces based on DCB test. Eng. Fract. Mech. 2013, 104, 56–79. [Google Scholar] [CrossRef]
- Jaillon, A.; Jumel, J.; Lachaud, F.; Paroissien, E. Mode I cohesive zone model parameters identification and comparison of measurement techniques based on uncertainty estimation. Int. J. Solids Struct. 2020, 191, 577–587. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Wang, X.; Liang, L. Inverse parameter identification of cohesive zone model for simulating mixed-mode crack propagation. Int. J. Solids Struct. 2014, 51, 2400–2410. [Google Scholar] [CrossRef]
- Shen, B.; Paulino, G.H. Identification of cohesive zone model and elastic parameters of fiber-reinforced cementitious composites using digital image correlation and a hybrid inverse technique. Cem. Concr. Compos. 2011, 33, 572–585. [Google Scholar] [CrossRef]
- Fasikaw, K.; Tomasz, T.; Shimels, G.H.; Woldemichael, D. Artificial Intelligence in Predicting Mechanical Properties of Composi te Materials. J. Compos. Sci. 2023, 7, 364. [Google Scholar]
- Maniraj, J.; Arockiasamy, F.S.; Kumar, C.R.; Kumar, D.A.; Jenish, I.; Suyambulingam, I.; Rangappa, S.M.; Siengchin, S. Machine Learning Techniques for the Design and Optimization of Polymer Composites: A Review. E3S Web Conf. 2023, 428, 02013. [Google Scholar] [CrossRef]
- Cassola, S.; Duhovic, M.; Timo, S.; May, D. Machine learning for polymer composites process simulation–a review. Compos. Part B Eng. 2022, 246, 110208. [Google Scholar] [CrossRef]
- Wang, Y.; Soutis, C.; Ando, D.; Sutou, Y.; Narita, F. Application of deep neural network learning in composites design. Eur. J. Mater. 2022, 2, 117–170. [Google Scholar] [CrossRef]
- Ren, X.-Y.; Wang, J.; Liang, Y.-J.; Ma, L.-H.; Zhou, W. Acoustic emission detection of filament wound CFRP composite structure damage based on Mel spectrogram and deep learning. Thin-Walled Struct. 2024, 198, 111683. [Google Scholar] [CrossRef]
- Mirkhalaf, M.; Rocha, I. Micromechanics-based deep-learning for composites: Challenges and future perspectives. Eur. J. Mech. A/Solids 2024, 105, 105242. [Google Scholar] [CrossRef]
- Jin, H.; Zhang, E.; Espinosa, H.D. Recent Advances and Applications of Machine Learning in Experimental Solid Mechanics: A Review. Appl. Mech. Rev. 2023, 75, 061001. [Google Scholar] [CrossRef]
- Thai, H.-T. Machine learning for structural engineering: A state-of-the-art review. Structures 2022, 38, 448–491. [Google Scholar] [CrossRef]
- Hu, M.; Tan, Q.; Knibbe, R.; Xu, M.; Jiang, B.; Wang, S.; Li, X.; Zhang, M.-X. Recent applications of machine learning in alloy design: A review. Mater. Sci. Eng. R Rep. 2023, 155, 100746. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, Y.; Wu, C.; Fang, J.; Sun, G.; Steven, G.P.; Li, Q. Machine learning based topology optimization of fiber orientation for variable stiffness composite structures. Int. J. Numer. Methods Eng. 2021, 122, 6736–6755. [Google Scholar] [CrossRef]
- Han, S.; Ye, Q.; Hakamy, A.; Abd-Elnaiem, A.M. Numerical solution hybridized by machine-leaning-based algorithm to provide an efficient method for analyzing thermomechanical shock behavior of the circumferentially-graded graphene-plates reinforced composite sandwich panel. Mech. Adv. Mater. Struct. 2023, 31, 4399–4422. [Google Scholar] [CrossRef]
- Qiao, S.; Huang, M.; Liang, Y.; Zhang, S.; Zhou, W. Damage mode identification in carbon/epoxy composite via machine learning and acoustic emission. Polym. Compos. 2023, 44, 2427–2440. [Google Scholar] [CrossRef]
- Lavaggi, T.; Samizadeh, M.; Kermani, N.N.; Khalili, M.M.; Advani, S.G. Theory-guided machine learning for optimal autoclave co-curing of sandwich composite structures. Polym. Compos. 2022, 43, 5319–5331. [Google Scholar] [CrossRef]
- Mouloodi, S.; Rahmanpanah, H.; Burvill, C.; Gohari, S.; Davies, H.M.S. Experimental, regression learner, numerical, and artificial neural network analyses on a complex composite structure subjected to compression loading. Mech. Adv. Mater. Struct. 2021, 29, 2437–2453. [Google Scholar] [CrossRef]
- Hu, H.; Wei, Q.; Wang, T.; Ma, Q.; Jin, P.; Pan, S.; Li, F.; Wang, S.; Yang, Y.; Li, Y. Experimental and Numerical Investigation Integrated with Machine Learning (ML) for the Prediction Strategy of DP590/CFRP Composite Laminates. Polymers 2024, 16, 1589. [Google Scholar] [CrossRef] [PubMed]
- Cai, G.; Zhang, D.; Hou, J.-A.; Lau, D.; Qin, R.; Wang, W.; Zhang, W.; Wu, C.; Tam, L.-H. A machine learning prediction model for investigating vibration properties of epoxy resin under moisture conditions. Int. J. Non-linear Mech. 2024, 166, 104857. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z.; Di Caprio, F.; Gu, G.X. Machine learning for accelerating the design process of double-double composite structures. Compos. Struct. 2022, 285, 115233. [Google Scholar] [CrossRef]
- Azeem, O.A.; Pinho, S.T. A machine learning assisted multifidelity modelling methodology to predict 3D stresses in the vicinity of design features in composite structures. Int. J. Solids Struct. 2024, 301, 112946. [Google Scholar] [CrossRef]
- Monaco, E.; Rautela, M.; Gopalakrishnan, S.; Ricci, F. Machine learning algorithms for delaminations detection on composites panels by wave propagation signals analysis: Review, experiences and results. Prog. Aerosp. Sci. 2024, 146, 100994. [Google Scholar] [CrossRef]
- Balcıoğlu, H.E.; Seçkin, A. Comparison of machine learning methods and finite element analysis on the fracture behavior of polymer composites. Arch. Appl. Mech. 2021, 91, 223–239. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Jiang, B.; Wang, R.; Liu, Y.; Jia, L. Mechanical properties prediction of composite laminate with FEA and machine learning coupled method. Compos. Struct. 2022, 299, 116086. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, F.; Li, J.; Xiao, W. A hybrid support vector regression with multi-domain features for low-velocity impact localization on composite plate structure. Mech. Syst. Signal Process. 2021, 154, 107547. [Google Scholar] [CrossRef]
- Lu, S.; Jiang, M.; Wang, X.; Yu, H.; Su, C. Damage degree prediction method of CFRP structure based on fiber Bragg grating and epsilon-support vector regression. Optik 2018, 180, 244–253. [Google Scholar] [CrossRef]
- Sikdar, S.; Ostachowicz, W.; Kundu, A. Deep learning for automatic assessment of breathing-debonds in stiffened composite panels using non-linear guided wave signals. Compos. Struct. 2023, 312, 116876. [Google Scholar] [CrossRef]
- Viotti, I.D.; Gomes, G.F. Delamination identification in sandwich composite structures using machine learning techniques. Comput. Struct. 2023, 280, 106990. [Google Scholar] [CrossRef]
- Tao, C.; Zhang, C.; Ji, H.; Qiu, J. Reconstruction and Prediction of Mode-I Cohesive Law using Artificial Neural Network. Compos. Sci. Technol. 2024, 256, 110755. [Google Scholar] [CrossRef]
- Liu, X.; Athanasiou, C.E.; Padture, N.P.; Sheldon, B.W.; Gao, H. A machine learning approach to fracture mechanics problems. Acta Mater. 2020, 190, 105–112. [Google Scholar] [CrossRef]
- Qing, X.; Liao, Y.; Wang, Y.; Chen, B.; Zhang, F.; Wang, Y. Machine learning based quantitative damage monitoring of composite structure. Int. J. Smart Nano Mater. 2022, 13, 167–202. [Google Scholar] [CrossRef]
- Su, M.; Peng, H.; Yuan, M.; Li, S. Identification of the interfacial cohesive law parameters of FRP strips externally bonded to concrete using machine learning techniques. Eng. Fract. Mech. 2021, 247, 107643. [Google Scholar] [CrossRef]
- Zhao, L.; Dai, Y.; Wei, J.; Qin, F. Deep neural network aided cohesive zone parameter identifications through die shear test in electronic packaging. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 766–780. [Google Scholar] [CrossRef]
- Kohnke, P. ANSYS Theory Reference; Ansys Inc: Canonsburg, PA, USA, 2020. [Google Scholar]
- de Moura, M.F.; Moreira, R.D.; Rocha, R.J.; Oliveira, C.F. Determination of the fracture energy under mode I loading of a honey-comb/carbon-epoxy sandwich panel using the asymmetric double cantilever beam test. J. Sandw. Struct. Mater. 2022, 24, 1977–1992. [Google Scholar] [CrossRef]
- de Moura, M.; Gonçalves, J.; Silva, F. A new energy based mixed-mode cohesive zone model. Int. J. Solids Struct. 2016, 102–103, 112–119. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Lyu, F.; Fan, X.; Ding, F.; Chen, Z. Prediction of the axial compressive strength of circular concrete-filled steel tube columns using sine cosine algorithm-support vector regression. Compos. Struct. 2021, 273, 114282. [Google Scholar] [CrossRef]
- Bergmayr, T.; Höll, S.; Kralovec, C.; Schagerl, M. Local residual random forest classifier for strain-based damage detection and localization in aerospace sandwich structures. Compos. Struct. 2023, 304, 116331. [Google Scholar] [CrossRef]
- Revathy, G.; Rajendran, V.; Rashmika, B.; Kumar, P.S.; Parkavi, P.; Shynisha, J. Random Forest Regressor based superconductivity materials investigation for critical temperature prediction. Mater. Today: Proc. 2022, 66, 648–652. [Google Scholar] [CrossRef]
- Zara, A.; Belaidi, I.; Khatir, S.; Brahim, A.O.; Boutchicha, D.; Wahab, M.A. Damage detection in GFRP composite structures by improved artificial neural network using new optimization techniques. Compos. Struct. 2023, 305, 116475. [Google Scholar] [CrossRef]
- Peng, X.; Qiu, C.; Li, J.; Wu, H.; Liu, Z.; Jiang, S. Multiple-scale uncertainty optimization design of hybrid composite structures based on neural network and genetic algorithm. Compos. Struct. 2021, 262, 113371. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Pal, K.; Patel, B.V. Data classification with k-fold cross validation and holdout accuracy estimation methods with 5 different machine learning techniques. In Proceedings of the 2020 Fourth International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 11–13 March 2020; IEEE: New York, NY, USA, 2020; pp. 83–87. [Google Scholar]




| Material | Properties | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| CFRP | |||||||||
| NOMEX | |||||||||
| Mean R2 | Mean MAPE | Box Constraint | Mean R2 | Mean MAPE | |
| 0.01 | 0.5308 | 6.0558 | 0.1 | 0.4658 | 7.2371 |
| 0.02 | 0.5376 | 6.1988 | 0.7 | 0.5359 | 6.2742 |
| 0.03 | 0.5233 | 7.1526 | 1 | 0.5376 | 6.1987 |
| 0.04 | 0.5168 | 7.4750 | 2 | 0.5424 | 6.3128 |
| 0.05 | 0.5024 | 7.8319 | 3 | 0.5380 | 6.4652 |
| No. | No. of Trees | Number of Folds (%) | Mean (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 1 | 5 | 8.4952 | 9.6051 | 11.9662 | 8.6994 | 7.4333 | 9.2395 | 6.1857 | 9.9078 | 11.5513 | 11.249 | 9.4332 |
| 2 | 10 | 8.7319 | 10.6674 | 9.7386 | 8.9025 | 9.3058 | 11.1510 | 9.1339 | 7.0797 | 9.5477 | 10.2851 | 9.4544 |
| 3 | 36 | 8.4919 | 10.4474 | 8.5306 | 10.7308 | 11.5945 | 8.2028 | 8.0728 | 10.4431 | 10.0279 | 10.8345 | 9.7376 |
| 4 | 82 | 8.4929 | 11.4597 | 9.1358 | 9.6219 | 9.7889 | 8.4278 | 11.4191 | 5.7201 | 10.1255 | 7.8462 | 9.2038 |
| 5 | 140 | 8.4924 | 9.8091 | 7.1622 | 10.7415 | 7.4258 | 10.4358 | 8.9860 | 10.9316 | 9.8295 | 10.3503 | 9.4167 |
| 6 | 260 | 8.4918 | 11.4592 | 11.1199 | 7.7427 | 9.6577 | 10.3049 | 7.2246 | 9.4013 | 9.8909 | 7.2202 | 9.2517 |
| 7 | 480 | 8.4918 | 10.2073 | 8.7420 | 8.9150 | 8.7455 | 8.3842 | 11.089 | 10.9269 | 13.2572 | 13.8415 | 10.2604 |
| 8 | 650 | 8.4918 | 10.7436 | 9.9257 | 8.5966 | 12.4392 | 6.6686 | 10.0478 | 6.5755 | 11.3680 | 8.3010 | 9.3161 |
| Number | Design | Number of Folds (%) | Mean (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| 1 | (24, 136, 68) | 0.9660 | 1.0791 | 1.0517 | 0.9845 | 1.0195 | 1.1307 | 1.0552 | 1.0303 | 1.0629 | 1.0409 | 1.0321 |
| 2 | (128, 128, 64) | 1.0464 | 1.0807 | 0.9970 | 1.0213 | 1.0448 | 1.0183 | 1.0091 | 1.0912 | 1.0286 | 1.0598 | 1.0417 |
| 3 | (64, 128, 32) | 0.9523 | 1.1049 | 1.0135 | 1.0064 | 0.9675 | 1.1326 | 1.1764 | 1.0116 | 1.0382 | 1.0859 | 1.0489 |
| 4 | (64, 32, 16) | 0.9965 | 0.9698 | 1.0894 | 1.1165 | 1.0789 | 0.9931 | 1.0096 | 1.0806 | 1.2289 | 1.0737 | 1.0518 |
| 5 | (25, 14, 30) | 1.0566 | 1.2809 | 1.0140 | 1.0373 | 0.9576 | 1.1982 | 1.0863 | 0.9965 | 1.0097 | 1.0804 | 1.0718 |
| 6 | (6, 12, 18) | 1.1260 | 1.1050 | 0.9924 | 1.4297 | 0.9799 | 1.0727 | 1.0918 | 1.0369 | 1.0854 | 1.0713 | 1.0991 |
| 7 | (12, 12, 12) | 1.1769 | 1.2491 | 3.1212 | 1.2077 | 1.1493 | 1.1373 | 1.1298 | 1.0434 | 0.9577 | 1.0871 | 1.3260 |
| 8 | (4, 4, 16) | 1.0675 | 1.0979 | 2.2337 | 1.4208 | 1.0566 | 2.6262 | 1.6814 | 1.1751 | 1.0834 | 1.0336 | 1.4476 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramian, A.; Elhajjar, R. Machine Learning Algorithms for Prediction and Characterization of Cohesive Zone Parameters for Mixed-Mode Fracture. J. Compos. Sci. 2024, 8, 326. https://doi.org/10.3390/jcs8080326
Ramian A, Elhajjar R. Machine Learning Algorithms for Prediction and Characterization of Cohesive Zone Parameters for Mixed-Mode Fracture. Journal of Composites Science. 2024; 8(8):326. https://doi.org/10.3390/jcs8080326
Chicago/Turabian StyleRamian, Arash, and Rani Elhajjar. 2024. "Machine Learning Algorithms for Prediction and Characterization of Cohesive Zone Parameters for Mixed-Mode Fracture" Journal of Composites Science 8, no. 8: 326. https://doi.org/10.3390/jcs8080326
APA StyleRamian, A., & Elhajjar, R. (2024). Machine Learning Algorithms for Prediction and Characterization of Cohesive Zone Parameters for Mixed-Mode Fracture. Journal of Composites Science, 8(8), 326. https://doi.org/10.3390/jcs8080326







