Abstract
An estimate of the effect of initial damage, such as delamination in the area of a structural hole, on the static and fatigue strength of polymer composite material (PCM) based on computational mechanics methods is presented. Calculation for durability of structural elements made of PCM is conducted using Simcenter 3D—Samcef package and Specialist Durability module. A typical carbon fiber-reinforced plastic with the available physical and mechanical characteristics obtained from the tests was chosen as the study material. Fatigue characteristics of the typical carbon fiber-reinforced plastic were approximated for subsequent calculation on durability. In the durability calculation, the observed parameter is the degradation of the material stiffness under repeated loading of the investigated area. The convergence with the experimental results of the fatigue strength modeling for a defect-free sample, which is a strip with a hole, is estimated. The fatigue strength of a sample with a delamination-type defect is also compared with the fatigue strength of a damage-free sample.
1. Introduction
Generally, the operational behavior of a structure is defined by its strength, stiffness and service life [1]. Initially, knowledge of the fatigue behavior of fiber-reinforced composites was very limited and was based on a metal fatigue calculation methodology where calculation information was extracted from metal fatigue calculations using a stress-life curve or Wühler (SN) fatigue life curve.
Later, fatigue strength models were developed predicting the deterioration of the mechanical characteristics of the material during fatigue life [2,3,4]. Thus, the gradual damage of a composite with a loss of stiffness in the damaged zones leads to a continuous redistribution of stresses and a decrease in stress concentrations in its components [5,6,7,8]. In addition, measuring strength during the development of damage in the material is impractical, since only one measurement can be made for one specimen, and it is very difficult to compare the damage between two specimens [9].
Phenomenological models describing residual stiffness and progressive damage models have been considered in structural modeling problems. Although progressive damage models quantitatively consider the main mechanisms of fatigue damage, their defining equations are often cumbersome to use and the application of these models to full-scale and complex structures has a number of problems [4].
The main obstacle to the development of progressive damage models for composites is the complexity of the fatigue damage mechanisms, both in their occurrence and in the details of the evolution process [10].
The structural modeling tasks do not consider manufacturing defects which are stress concentrators and usually initiate the further growth of material damage in the PCM. At the same time, for further modeling of a structure in operation, studies of the initial damage effect are mainly carried out for impact damage previously obtained by the structure [11,12]. In this paper, the influence of local delamination caused by the sample hole tooling on static and fatigue strength is considered using a sample made of PCM with a hole subject to compression as an example.
The static and fatigue strength calculations are introduced using the Van Paepegem Material method [13] in the Simcenter 3D software package. The authors describe the creation of an experimental database, which served as the foundation for the development of the mathematical model, as well as an algorithm of its integration into the finite element analysis software. The main goal of creating the model was to accurately assess the influence of damage propagation on the fatigue strength of composite materials. This method is based on the method of damage accumulation and development, both in the material layers [14,15,16,17,18] and in the interface between them [17,19,20,21]. The calculation results were compared with experimental data that examines the effects of load spectrum reduction on the strength of a notched graphite/epoxy composite product [22].
Also, the problem of modeling manufacturing defects in PCM was considered in the study [23]. This article offers a model that predicts and analyzes the development of defects during composite reinforcements and prepreg forming. An explicit dynamic approach was used to simulate the formation of folds during the molding of textile fittings associated to a simplified behavior of shell elements made of woven cells, which is in good agreement with experimental forming. Mesoscopic F.E. analyses were used to simulate slippage between yarns. It was shown that this approach could simulate possible slippages during textile composite reinforcement forming. In [24], authors developed a multiscale model of the deformation of multilayer thin plates made of composite materials with isolated defects based on an asymptotic analysis of the general three-dimensional equations of deformable solid mechanics. Using the developed asymptotic method, the general solution of the three-dimensional equations of strain mechanics was reduced to the solution of problems for thin plates without defects and local three-dimensional problems in the vicinity of the defect with the condition of attenuation of the solution at a distance from the defect.
An example of the numerical solution of the finite element local mechanics problem for a three-layer composite plate with a defect in the middle layer was also given. It is shown that the influence of the defect on the distribution of stress fields is significantly localized in its immediate vicinity. It was established that the maximum concentration of transversal stresses is reached in the vicinity of the defect’s vertices. In [25], the extended finite element method was used to simulate crack growth in a composite material. The presence of the crack is described using special enriched functions combined with additional degrees of freedom. Two approaches were used: the cohesive segments approach and the linear elastic fracture mechanics approach. The considered methods have different laws of crack propagation: in the cohesive segments approach, the obtained fracture surface is a plane; in the case of LEFM, the uneven fracture surface is qualitatively perpendicular to the edge of the load application. Paper [26] considers the influence of technological defects of PCM parts on static strength (curvature of layers, pores, “resin pockets”) using the example of a composite flange of a sound-absorbing casing of an aircraft engine made of fiberglass plastics. The axisymmetric problem of the anisotropic elasticity theory was solved using the finite element method with a PLANE183 grid element to analyze the stress–strain state. The results obtained were compared with similar data obtained for the same flange without defects.
During the analysis, it was found that the presence of technological defects of the “resin pocket” type does not lead to a significant reduction in static strength when compared to the defect-free design. In [27], authors develop a three-stage methodology to determine the damageability and durability of PCM structures with delamination-type defects. Its stages are the calculation of macroscopic stress–strain state with defects; the calculation of microscopic stress–strain state with defects; and model building for calculation of the damageability parameter and damageability accumulation in the defect vicinity under different types of cyclic loading.
An example of the calculation of a helicopter blade structure was performed using this method, which showed the possibility of its application for modeling the damageability in complex composite structures.
The simulation of the initiation and propagation of fatigue damage has been carried out in many papers. Paper [28] presents a method for predicting crack path for brittle and quasi-brittle materials. This method used a combination of X-FEM and models with the cohesive zone. A scheme for calculating and predicting further crack propagation has been developed. Validation was carried out on the basis of experiments from other papers. Paper [29] proposes a methodology for modeling concrete cohesive fracture with the propagation of a 3D crack, as well as experimental validation of samples for 4-point bending. The number and propagation paths of cracks depended on the dimension of the model, but the strain distributions were the same in all computational cases. In addition to statics, work was also carried out on the development of a crack for calculations of cyclic fatigue. The studies in [30,31,32] combined methods for determining the propagation of a crack using the micromechanical failure of the cohesive layer CDM and X-FEM and their validation.
As demonstrated above, for damage modeling, methods based on X-FEM and various combinations with them are mainly used. However, these methods require rather high computational power due to the construction of finite element models. The mesh in the area of the already initiated crack should be very small. For modeling micro, mini or elementary samples, these methods are suitable; however, in conditions of structurally similar samples, these methods will not be usable. Also, a crack is a particular case of damage in specimens under loading. Defects can occur even at the stages of manufacturing and have a significant impact on the results of experiments.
2. Description of the Calculation Methodology
The fatigue calculation is carried out in three stages:
- Preparation of the model by the user;
The geometric model is a solid-state layer-by-layer simulation that allows the calculation of damage accumulation both in the layers and in the interface between them. This modeling approach most accurately conveys a picture of the stress–strain state of the structure but requires high computational power.
On the prepared model geometry, a mesh model with stacking corresponding to the type design is created and all material data (physical, mechanical and fatigue characteristics as well as cohesion layer characteristics) are assigned. Boundary and loading conditions are imposed on the finite-element mesh.
The material model is a typical carbon/epoxy unidirectional prepreg T300/5208 with the mechanical and strength characteristics of a monolayer (E1, E2, nu12, nu23, G12, G23). Between the layers inside the package, a damage interface is implemented with transverse and shear stiffness characteristics (K01, K01, K02S), fracture toughness (GIc, GIIc, GIIIc) and energy threshold(Y0S). The same characteristics, but with different meanings, are used in the interface between packages.
In addition, this paper specifies a manufacturing defect, such as delamination from the machining of the hole. According to the available experimental data, this delamination is between the first and second layers of the composite material package and extends 0.3 mm inside the specimen.
A specimen with geometric dimensions of 350 mm × 38 mm and a central unfilled hole with a diameter of 6.35 mm acts as a model. The material stacking has the form [45/0/−45/90]2s and corresponds to 16 layers (monolayer thickness 0.14 mm).
The model uses linear Hex solid elements with eight nodes for each layer. The interface between the layers consists of linear cohesive Hex elements. The dimension of the entire model is 85,901 elements and 183,458 nodes. The size of the element far from the region of interest is 2.5 mm; near the hole, the mesh thickens to an element size of 0.3 mm.
The specimen is subjected to a compressive load. In order to avoid a loss of stability, a rigid frame was simulated over the specimen in the form of constraints, which corresponds to the experiment described in [14]. Models with frames of 19 mm × 19 mm and 32 mm × 32 mm with specimens with and without initial damage were taken as the calculated cases. It was not necessary to simulate frames of a larger size since the specimen had a loss of stability in this place.
- Calculation using the static solver Samcef module with the Mecano module (first iteration).
For the static calculation, the Samcef and Mecano modules are used to calculate the initial damage to the material at the initial stage of loading, which will correspond to the first cycle of fatigue calculation. In the models with initial damage, the defect around the hole is laid with a thickness of 1–2 elements, which corresponds to the experimental data of 0.3 mm [23]. In the model, a defect is a specially designated area with reduced characteristics of the cohesive interface between the first and second layers. The delamination is modeled using a zone with reduced characteristics (around the hole)—here the defect is initiated. The damage interface between the layers, with its own stiffness characteristics, is responsible for the growth of the delamination.
- Fatigue analysis is performed using the Durability module;
This module periodically recalculates the stresses and strains in the model to consider the accumulation of damage and therefore the loss of stiffness of the material.
Damage accumulation is calculated using two methods:
- Model of damage accumulation in the layer under quasi-static load application;
Damage accumulation is described using the principles of continuum mechanics and fracture mechanics. This involves tracking the evolution of damage in the composite structure over time, as the load is applied. The model includes aspects such as the initiation and propagation of cracks and other types of damage, as well as the stress–strain state that develops in the composite material.
The model provides prediction of the response of composites to quasi-static loading and can be used to optimize composite material design to minimize damage and improve durability.
- Prediction of the onset of delamination-type damage.
The onset and propagation of delamination damage can be predicted using a combination of experimental testing and computational models.
One approach to predicting delamination damage is the use of finite element analysis (FEA), which involves breaking down the composite material into smaller parts and analyzing the local mechanical behavior of each part. FEA can also be used to simulate the propagation of cracks and delamination damage in the material, allowing engineers to assess potential failure modes and predict the overall strength and durability of the material under different loads and conditions.
Thus, the damage accumulation model is comprehensive for PCM and can describe what principle the failure will follow in the PCM package.
But this methodology is associated with the difficulty of determining the coefficients describing the accumulation of damage in the PCM during the operation of the structure. They are found using the results of tests for three stacks and three coefficients of cycle asymmetry. It is necessary to obtain 9 SN curves for elementary specimens of [±45]ns, [0]n, [0/90]n stacks and to consider the tensile–tensile, compression–compression and tension–compression cyclic asymmetry coefficients. The resulting curves are converted into stiffness degradation curves.
The damage summation method is based on recording the potential strain energy of the material without damage and with damage variables, such as matrix cracking, matrix-fiber delamination and fiber failure. Next, the calculation of stresses and stiffness drop for shear, transverse and longitudinal directions is carried out by determining the solving equations according to the following structure:
- Damageability is determined;
- The equivalent plastic strain is determined;
- The equivalent stresses are determined;
- The dependence of equivalent stresses on equivalent plastic strains is plotted.
The fracture is described using the three known modes of interlayer fracture: tensile, sliding shear and tearing shear. The solving equations of energy density with initial stiffness and equivalent thermodynamic force are written. It is possible to use three laws determining the onset of stratification: polynomial, bi-triangular and exponential. The bi-triangular law shows the best convergence. All laws differ in stress and displacement relationship; in bi-triangular models, this relationship is set to bilinear (Figure 1). In Simcenter 3D, the cohesive zone is defined by the interface between layers with zero thickness.
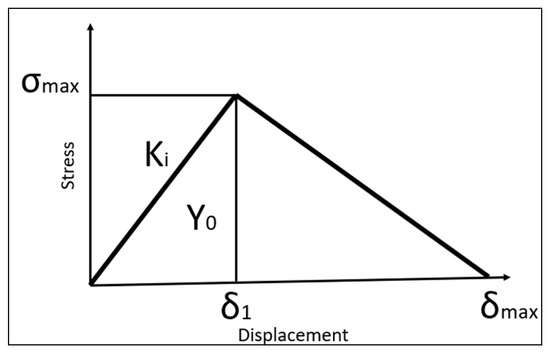
Figure 1.
Stress–Displacement relationship.
is the energy threshold, Ki is the slope from 0.0 to and means K03S.
To find the unknown material characteristics used in the delamination model, it is necessary to test the interface of specimens [45/−45], [0/0] for each modulus of failure.
The model of damage accumulation in the layer and delamination is based on testing samples for residual stiffness during the stage of determining the equivalent stresses after the loss of structural stiffness. Relationships of material damage to the number of cycles of the structure (material) are plotted for fiber, matrix (transverse direction) and shear failure. The calculation results are the coefficients of the damage accumulation equation for each of the three directions, which are considered in the fatigue solver.
3. Results of Static Calculations and Comparison with Experimental Data
During the tests of real specimens from [22], a decision was made to use 32 mm × 32 mm frames to prevent a loss of stability. As a result, the delamination zone exceeded 19 mm and in very rare cases 32 mm. The magnitude of the local stability loss near the hole significantly affected the durability of the specimen. This result indicates that the effect of the stability loss frame used in the test should be considered when comparing compressive fatigue data.
The 32 mm × 32 mm frame models with and without initial damage showed a loss of stability near the hole (Figure 2 and Figure 3).
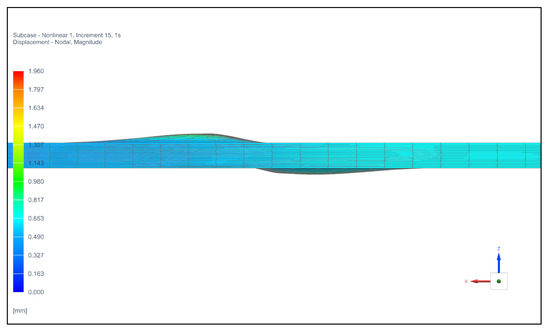
Figure 2.
Loss of stability in the area of the 32 mm × 32 mm frame hole with initial damage (displacement, mm).

Figure 3.
Loss of stability in the area of the 32 mm × 32 mm frame hole without initial damage (displacement, mm).
In the model with initial damage, defects are observed to accumulate away from the hole on layers 1 and 16 (Figure 4, Figure 5 and Figure 6). In the model without initial damage, they accumulate along the edges of the hole and go deep into the specimen.
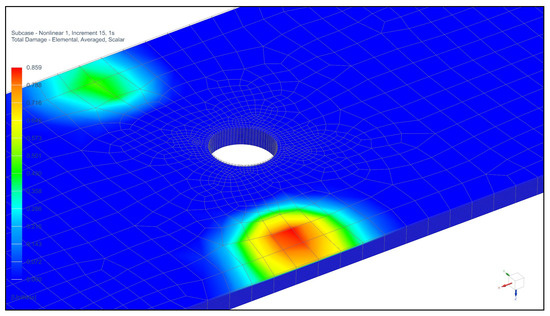
Figure 4.
Damage accumulation in a 32 mm × 32 mm specimen with a defect (total damage).

Figure 5.
Damage accumulation in a 32 mm × 32 mm specimen without a defect (total damage).
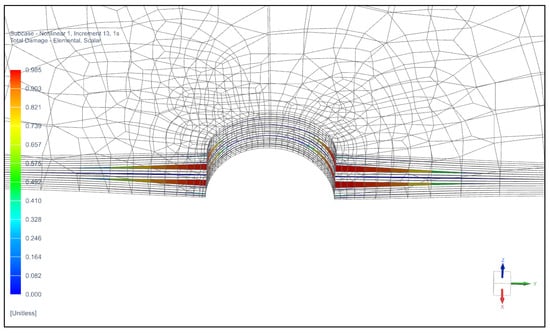
Figure 6.
Damage propagation pattern in specimen 32 mm × 32 mm without defect (total damage).
Since the plate with a 32 mm × 32 mm frame loses stability, a decision was made to specify a 19 × 19 frame, perform static and fatigue calculations and evaluate the effect of frame dimensions on the results.
Specimens with a 19 mm × 19 mm frame showed a strong discrepancy in results after static calculation (Figure 7). In the models considering the interlayer damage, a loss of stability in the area of the hole was observed (Table 1).
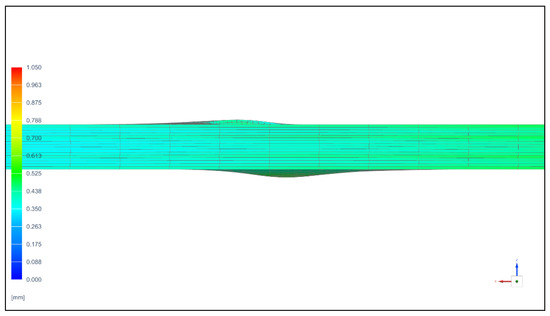
Figure 7.
Loss of stability in the area of the 19 mm × 19 mm frame hole with initial damage (displacement, mm).

Table 1.
Results of static calculations of specimens.
The damage accumulated after static calculations also diverges (Figure 8). In the sample with delamination, in addition to the damage around the hole, local defects in other layers are observed.

Figure 8.
Damage accumulation in a 19 mm × 19 mm specimen with a defect in the area of the hole (Total damage).
In order to describe material degradation, it is necessary for the damage evolution equation to account for both rupture and fatigue damage. In this paper, it is assumed that the total damage evolution is decomposed as
The damage variable is used to represent the material degradation, and when approaches one, failure occurs. represents the damage caused by monotonic loading and characterizes rupture failure similar to the conventional cohesive zone model. To simulate rupture, the material failure process is controlled by , with the material breaking when . The cohesive law governs the evolution of .
Since specimens with a 32 mm × 32 mm frame lose stability in the area of the hole, which will certainly significantly affect the results of fatigue calculations, a decision was made to use only specimens with a 19 mm × 19 mm frame in the future
4. Results of Fatigue Calculations and Comparison with Experimental Data
Specimens with a 19 mm × 19 mm frame with and without a defect are tested using the Transport Wing Standard Test (TWIST) loading program (Figure 9). The cyclogram of specimen loading is a graph of the level of load versus time that is superimposed on the applied boundary conditions of the model. The data from the Cyclogram and the SSS from the static analysis are used in the fatigue analysis. At each cycle, the load is multiplied by the coefficient from the cyclogram and applied to the model.
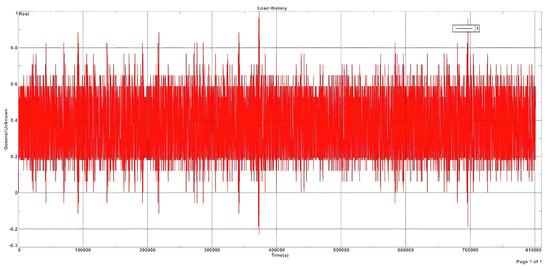
Figure 9.
Cyclogram of specimen loading by TWIST program.
Figure 10 and Figure 11 show the number of cycles to failure and stiffness reduction for specimens without initial damage. The region of interest is the area around the hole.
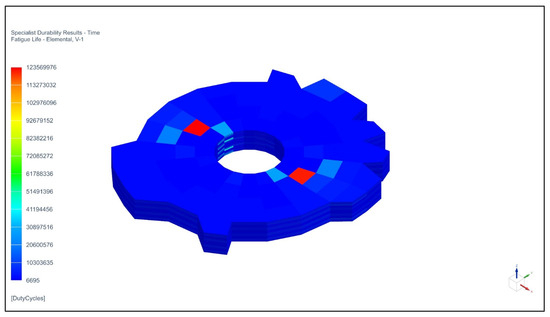
Figure 10.
Fatigue life for a 19 mm × 19 mm frame specimen without initial damage.
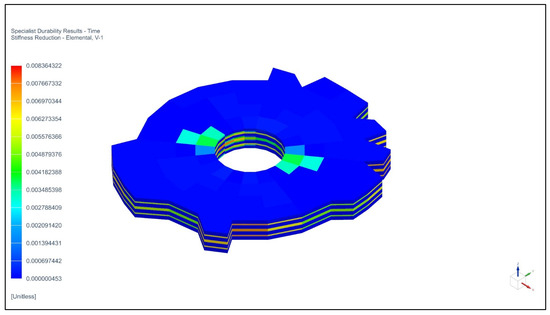
Figure 11.
Stiffness reduction of a 19 mm × 19 mm frame specimen without initial damage.
For fatigue calculations, the end-of-calculation criterion is a residual stiffness of 2% for 25% of work area elements.
As can be seen on Figure 9 and Figure 10, the minimum number of cycles to failure for 19 mm × 19 mm frame specimens without initial damage is 6695, while the maximum stiffness reduction is 0.84%, which is a satisfactory result.
From the results of the evaluation of the models after fatigue calculations with different amplitudes (Figure 12, Figure 13, Figure 14 and Figure 15), it is possible to draw conclusions about the fracture mode of the specimens.
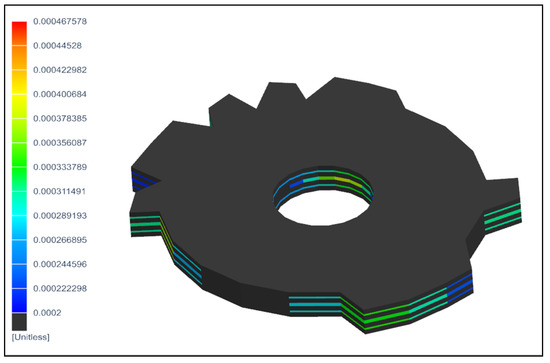
Figure 12.
State of the specimen in the reinforcement direction for , −248 MPa.
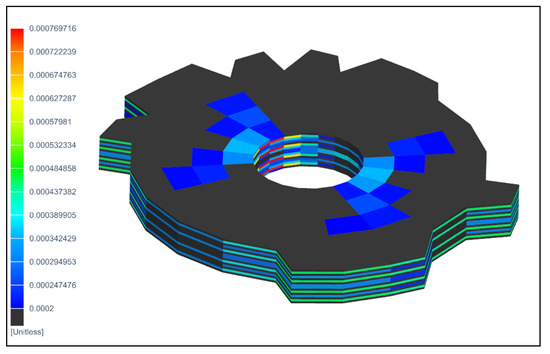
Figure 13.
State of the specimen in the reinforcement direction for , −248 MPa.
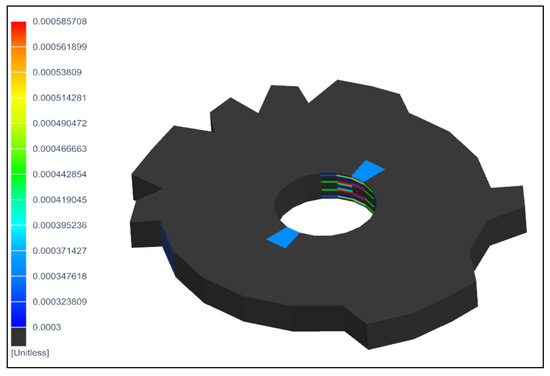
Figure 14.
State of the specimen across the reinforcement for , −248 MPa.
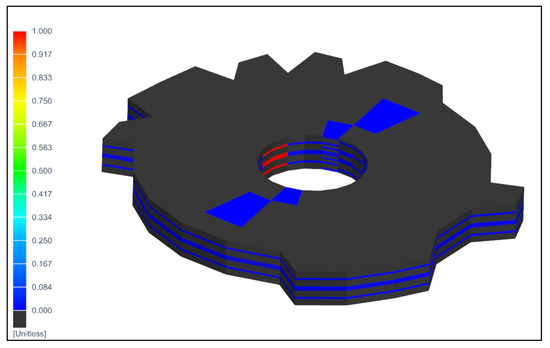
Figure 15.
State of the specimen across the reinforcement for , −248 MPa.
Destruction along the fiber D11. Both the maximum value and the damage area with a distribution over the layers change. The lower damage boundary is 0.02%. Elements with damage below the limit are shown in black.
The maximum matrix failure is cracking D22. In the presence of tensile stresses in the cycle, there is a complete failure in this mode of a part of the elements on the border of the hole. The lower damage boundary is 0.03%. Elements with damage below the boundary are shown in black.
The results of the fatigue calculation for a sample without damage are shown in Table 2 and Table 3.

Table 2.
Calculation results of durability without initial damage.

Table 3.
Comparisons of the damaged state of the specimen for programs with the same minimum and different average cycle stresses with constant amplitude.
For specimens with a 19 mm × 19 mm frame and initial damage, the minimum number of cycles to failure is 0 (Figure 16), and there is also a sharp drop in stiffness near the hole of 100% (Figure 17).
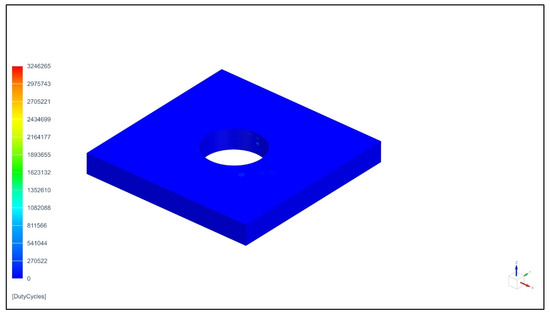
Figure 16.
Fatigue life for a 19 mm × 19 mm frame specimen with initial damage.
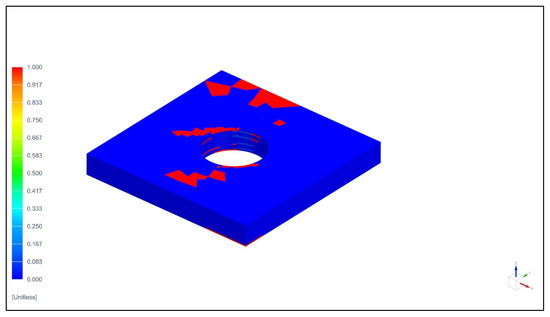
Figure 17.
Stiffness reduction of a 19 mm × 19 mm frame specimen with initial damage.
For models with initial damage, a wider area around the hole was chosen to observe the paths of material stiffness degradation.
The results of fatigue calculations for damaged specimens are shown in Table 4.

Table 4.
The results of fatigue calculations for specimens with initial damage.
According to the results of fatigue calculations for 19 mm × 19 mm frame models with and without initial damage, we can conclude that the defect obtained during operation or mechanical influences significantly affects the durability of specimens. Both in terms of the number of cycles to failure and stiffness reduction, there is a sharp drop in performance for specimens with the defect.
5. Conclusions
The method of structural damage modeling that was presented makes it possible to describe the real behavior of the structure during long-term operation in the presence and development of manufacturing defects. This method contains description of damage development in the layer and description of delamination. The calculation of damage is carried out both on the first cycle of loading (which corresponds to the static formulation of the problem) and on the long-term strength.
The simulation results of the sample without initial damage have been successfully validated with experiments, which proves the applicability of the method for fatigue calculations. The number of fatigue cycles for full TWIST, zero-compression cycles and asymmetric cycles with dominant compression showed high convergence and were applied to models with initial damage.
The method of using initial damage in the models presented in this paper is applicable to most samples of the computational–experimental pyramid, starting from microsamples and ending with structurally similar ones. This method does not require high computational power or long work with a finite element mesh.
It is shown that initial damage from machining (delamination from hole drilling) significantly affects the static and fatigue strength of the structure, so it is necessary to consider all manufacturing defects of delamination type in the composite material.
Author Contributions
Conceptualization, K.K.S. and N.O.K.; methodology, K.K.S.; software, N.O.K.; validation, K.K.S., A.E.L. and A.V.S.; formal analysis, N.O.K.; investigation, K.K.S.; resources, A.V.S.; data curation, A.E.L.; writing—original draft preparation, N.O.K.; writing—review and editing, A.E.L.; visualization, N.O.K.; supervision, K.K.S.; project administration, K.K.S.; funding acquisition, K.K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reifsnider, K.L. Life prediction analysis: Directions and divagations. In Proceedings of the Sixth International Conference on Composite Materials and Second European Conference on Composite Materials (ICCM & ECCM), Proceedings, London, UK, 20–24 July 1987; Matthews, F.L., Buskell, N.C.R., Hodgkinson, J.M., Morton, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1987; Volume 4, pp. 4.1–4.31. [Google Scholar]
- Harris, B. Fatigue Behaviour of Polymer-Based Composites and Life Prediction Methods; Nationaal Fonds voor Wetenschappelijk Onderzoek: Brussels, Belgium, 1995. [Google Scholar]
- Hahn, H.T.; Kim, R.Y. Fatigue behaviour of composite laminates. J. Compos. Mat. 1976, 10, 156–180. [Google Scholar] [CrossRef]
- Schaff, J.R.; Davidson, B.D. Life prediction methodology for composite structures. Part I—Constant amplitude and two-stress level fatigue. J. Compos. Mat. 1997, 31, 128–157. [Google Scholar] [CrossRef]
- Allen, D.H.; Highsmith, A.L.; Lo, D.C. A continuum damage mechanics model for life prediction of laminated composites. In Durability of Polymer Based Composite Systems for Structural Applications, Proceedings of the International Colloquium, Brussels, Belgium, 27–31 August 1990; Cardon, A.H., Verchery, G., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 119–128. [Google Scholar]
- Daniel, I.M.; Charewicz, A. Fatigue damage mechanisms and residual properties of graphite/epoxy laminates. Eng. Fract. Mech. 1986, 25, 793–808. [Google Scholar] [CrossRef]
- Hwang, W.; Han, K.S. Cumulative damage models and multi-stress fatigue life prediction. J. Compos. Mat. 1986, 20, 125–153. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Lessard, L.B. Progressive fatigue damage modeling of composite materials, Part I: Modeling. J. Compos. Mat. 2000, 34, 1056–1080. [Google Scholar] [CrossRef]
- Highsmith, A.L.; Reifsnider, K.L. Stiffness-reduction mechanisms in composite laminates. In Damage in Composite Materials; Reifsnider, K.L., Ed.; ASTM STP 775; American Society for Testing and Materials: West Conshohocken, PA, USA, 1982; pp. 103–117. [Google Scholar]
- Talreja, R. Fatigue damage evolution in composites—A new way forward in modeling. In Proceedings of the Second International Conference on Fatigue of Composites, Williamsburg, VA, USA, 4–7 June 2000; p. 9.1. [Google Scholar]
- Ryabov, A.A.; Voronkov, O.V.; Suhov, S.V.; Strelets, D.Y.; Slobodchikov, V.G. Numerical and experimental investigations of compressed stiffened composite panel with local impact damage. Aerosp. Syst. 2018, 1, 99–107. [Google Scholar] [CrossRef]
- Kondakov, I.; Chernov, A.; Guseva, N.; Levchenkov, M. Protective elements for lattice composite fuselage structures against low-velocity impacts. Aerosp. Syst. 2022, 5, 1–9. [Google Scholar] [CrossRef]
- Paepegem, W. Development and Finite Element Implementation of a Damage Model for Fatigue of Fibre-Reinforced Polymers; Ghent University Architectural and Engineering Press: Ghent, Belgium, 2002. [Google Scholar]
- Talreja, R. Damage mechanics of composite materials based on thermodynamics with internal variables. In Durability of Polymer Based Composite Systems for Structural Applications, Proceedings of the International Colloquium, Brussels, Belgium, 27–31 August 1990; Cardon, A.H., Verchery, G., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 65–79. [Google Scholar]
- El Mahi, A.; Berthelot, J.-M.; Brillaud, J. Stiffness reduction and energy release rate of cross-ply laminates during fatigue tests. Compos. Struct. 1995, 30, 123–130. [Google Scholar] [CrossRef]
- Ladeveze, P. A damage approach for composite structures: Theory and identification. In Mechanical Identification of Composites, Proceedings of the the European Mechine Colloquium 269, Saint-Etienne, France, 3–6 December 1990; Vautrin, A., Sol, H., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 44–57. [Google Scholar]
- Sidoroff, F.; Subagio, B. Fatigue damage modelling of composite materials from bending tests. In Proceedings of the Sixth International Conference on Composite Materials and Second European Conference on Composite Materials (ICCM & ECCM), Proceedings, London, UK, 20–24 July 1987; Matthews, F.L., Buskell, N.C.R., Hodgkinson, J.M., Morton, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1987; Volume 4, pp. 4.32–4.39. [Google Scholar]
- Kawai, M. Damage mechanics model for off-axis fatigue behavior of unidirectional carbon fiber-reinforced composites at room and high temperatures. In Proceedings of the Twelfth International Conference on Composite Materials (ICCM-12), Paris, France, 5–9 July 1999; p. 322. [Google Scholar]
- Allix, O.; Ladevèze, P. Interlaminar interface modelling for the prediction of delamination. Compos. Struct. 1992, 22, 235–242. [Google Scholar] [CrossRef]
- Prinz, R. Damage rates for interlaminar failure of fatigue CFRP laminates. In Developments in the Science and Technology of Composite Materials, Proceedings of the Fourth European Conference on Composite Materials (ECCM/4), Stuttgart, Germany, 25–28 September 1990; Füller, J., Grüninger, G., Schulte, K., Bunsell, A.R., Massiah, A., Eds.; Elsevier Applied Science: Amsterdam, The Netherlands, 1990; pp. 189–193. [Google Scholar]
- Vieillevigne, S.; Jeulin, D.; Renard, J.; Sicot, N. Modelling of the fatigue behaviour of a unidirectional glass epoxy composite submitted to fatigue loadings. In Proceedings of the International Conference on Fatigue of Composites, Proceedings, Paris, France, 3–5 June 1997; Degallaix, S., Bathias, C., Fougères, R., Eds.; La Société Française de Métallurgie et de Matériaux: Paris, France, 1997; pp. 424–430. [Google Scholar]
- Phillips, E.P. Effects of Truncation of a Predominantly Compression Load Spectrum on the Life of a Notched Graphite/Epoxy Laminate; ASTM International: West Conshohocken, PA, USA, 1979. [Google Scholar]
- Boisse, P.; Hamila, N.; Madeo, A. Modelling the development of defects during composite reinforcements and prepreg forming. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 347, 20150269. [Google Scholar] [CrossRef] [PubMed]
- Dimitrienko, Y.I.; Yurin, Y.V. Multiscale Simulation of Multilayer Thin Composite Plates with Solitary Defects. Math. Model. Numer. Methods 2016. [Google Scholar]
- Shalimov, A.S.; Tashkinov, M.A. Simulation of crack growth in porous materials using finite elements with additional degrees of freedom. Math. Model. Nat. Sci. 2018. [Google Scholar]
- Anoshkin, A.N.; Zuiko, V.; Yu Osokin, V.M.; Tretyakov, A.A.; Pisarev, P.V. Modeling of technological defects and evaluation of their influence on the static strength of composite flanges. Mater. Sci. 2016. [Google Scholar]
- Dimitrienko, Y.I.; Yuri, Y.V. Finite Element Modeling of Damage and Durability of Composite Structural Elements with Lamination-Type Defects. Math. Model. Numer. Methods 2017. [Google Scholar]
- Ferté, G.; Massin, P.; Moes, N. 3D crack propagation with cohesive elements in the extended finite element method. Comput. Methods Appl. Mech. Eng. 2016, 300, 347–374. [Google Scholar] [CrossRef]
- Kurumatani, M.; Soma, Y.; Terada, K. Simulations of cohesive fracture behavior of reinforced concrete by a fracturemechanics-based damage model. Eng. Fract. Mech. 2019, 206, 392–407. [Google Scholar] [CrossRef]
- Li, H.; Yuan, H.; Li, X. Assessment of low cycle fatigue crack growth under mixed-mode loading conditions by using a cohesive zone mode. Int. J. Fatigue 2015, 75, 39–50. [Google Scholar] [CrossRef]
- Li, H.; Yuan, H. Cohesive zone modelling of low cycle fatigue cracks in cracked and notched specimens. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 1246–1257. [Google Scholar] [CrossRef]
- Li, X.; Chen, J. An extended cohesive damage model for simulating arbitrary damage propagation in engineering materials. Comput. Methods Appl. Mech. Eng. 2017, 315, 744–759. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
