Mechanical Homogenization of Transversely Isotropic CNT/GNP Reinforced Biocomposite for Wind Turbine Blades: Numerical and Analytical Study
Abstract
1. Introduction
2. First Homogenization
2.1. Mathematical Model
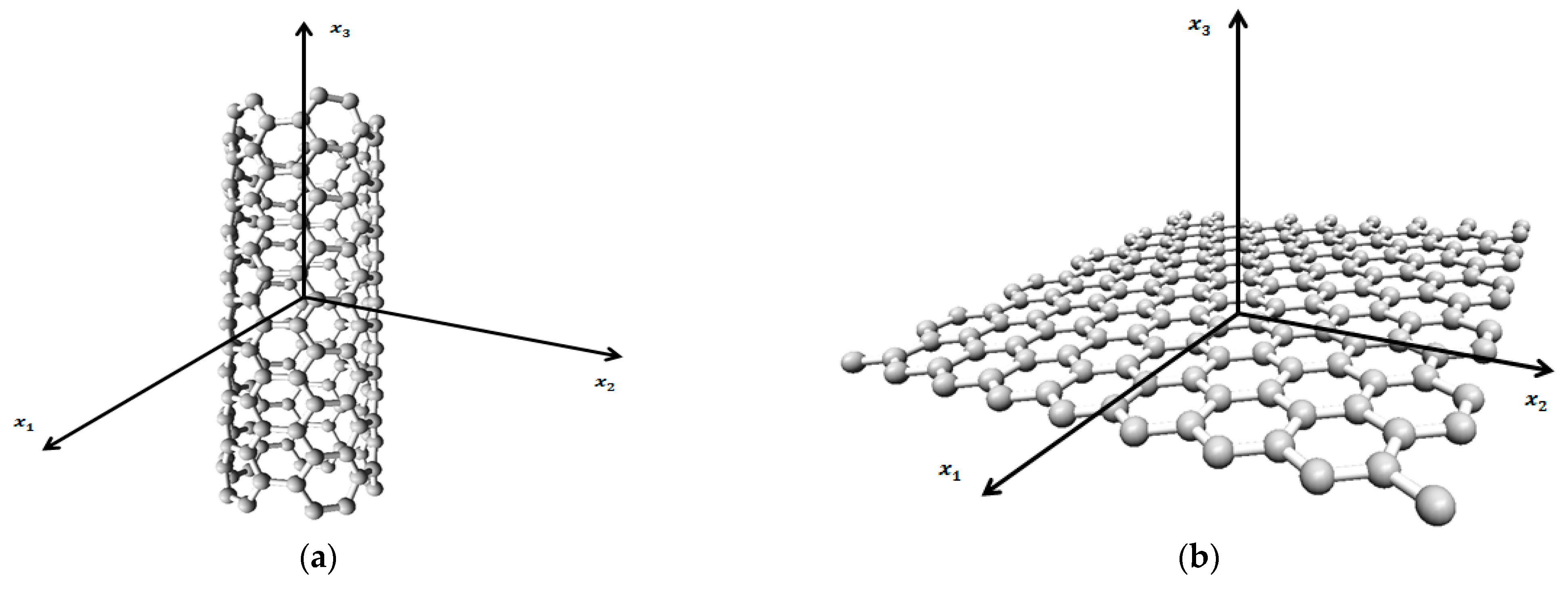
2.1.1. CNT Inclusion
2.1.2. GNP Inclusion
2.2. Numerical Model
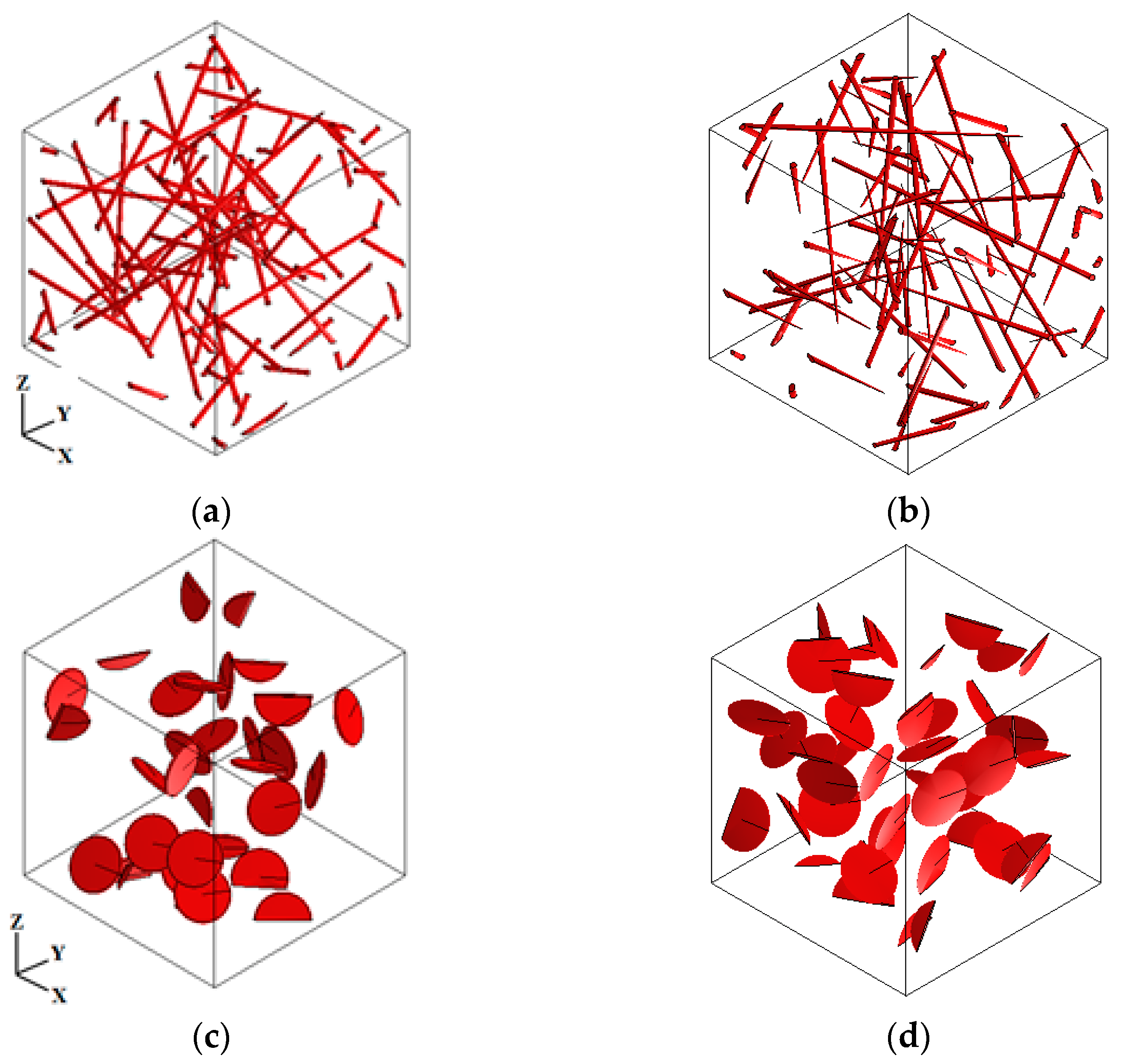
2.2.1. RVE Geometry
- -
- The CNT inclusions are considered to have an ellipsoidal (prolate) shape. GNP inclusions are considered as disc-shaped spheroidal inclusions with aligned and random orientations.
- -
- The phases are considered as perfectly bounded.
2.2.2. Materials Properties
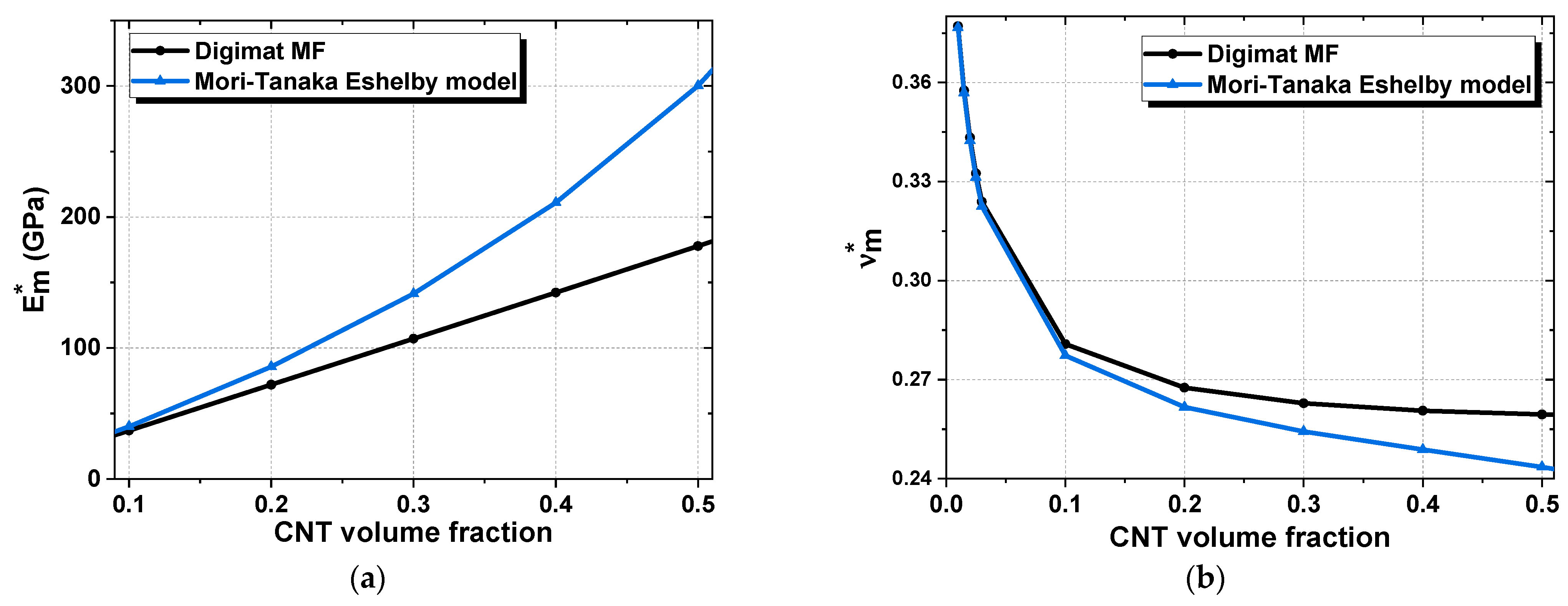
2.3. First Homogenization Results
3. Second Homogenization
3.1. Mathematical Model
3.1.1. Isotropic Fiber
- a.
- Chamis approach
- b.
- Hashin–Rosen model
- c.
- Halpin–Tsai model
- ζ = 2 L/d for calculation of the longitudinal modulus.
- ζ = 2 for calculation of the transversal modulus.
3.1.2. Transversely Isotropic Fiber
- a.
- Hahn model
- b.
- Halpin-Tsai model
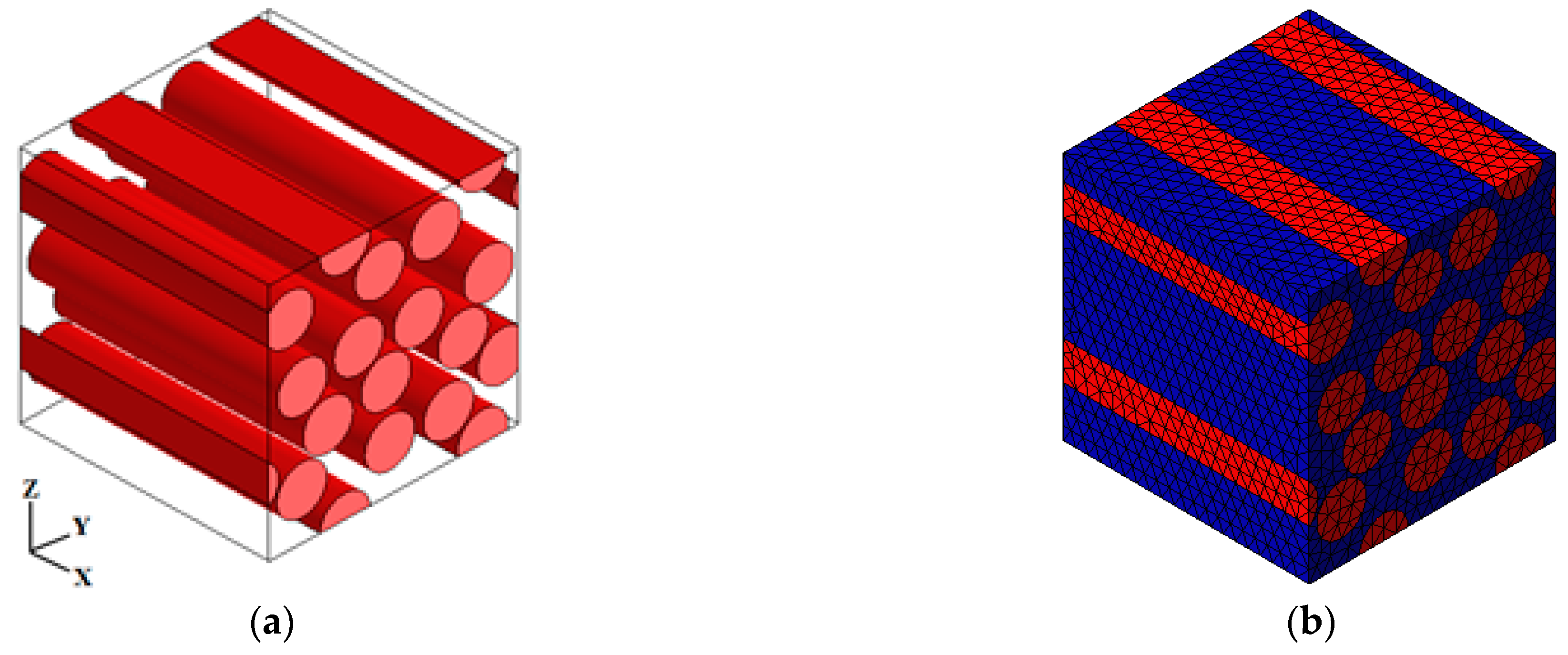
3.2. Numerical Model
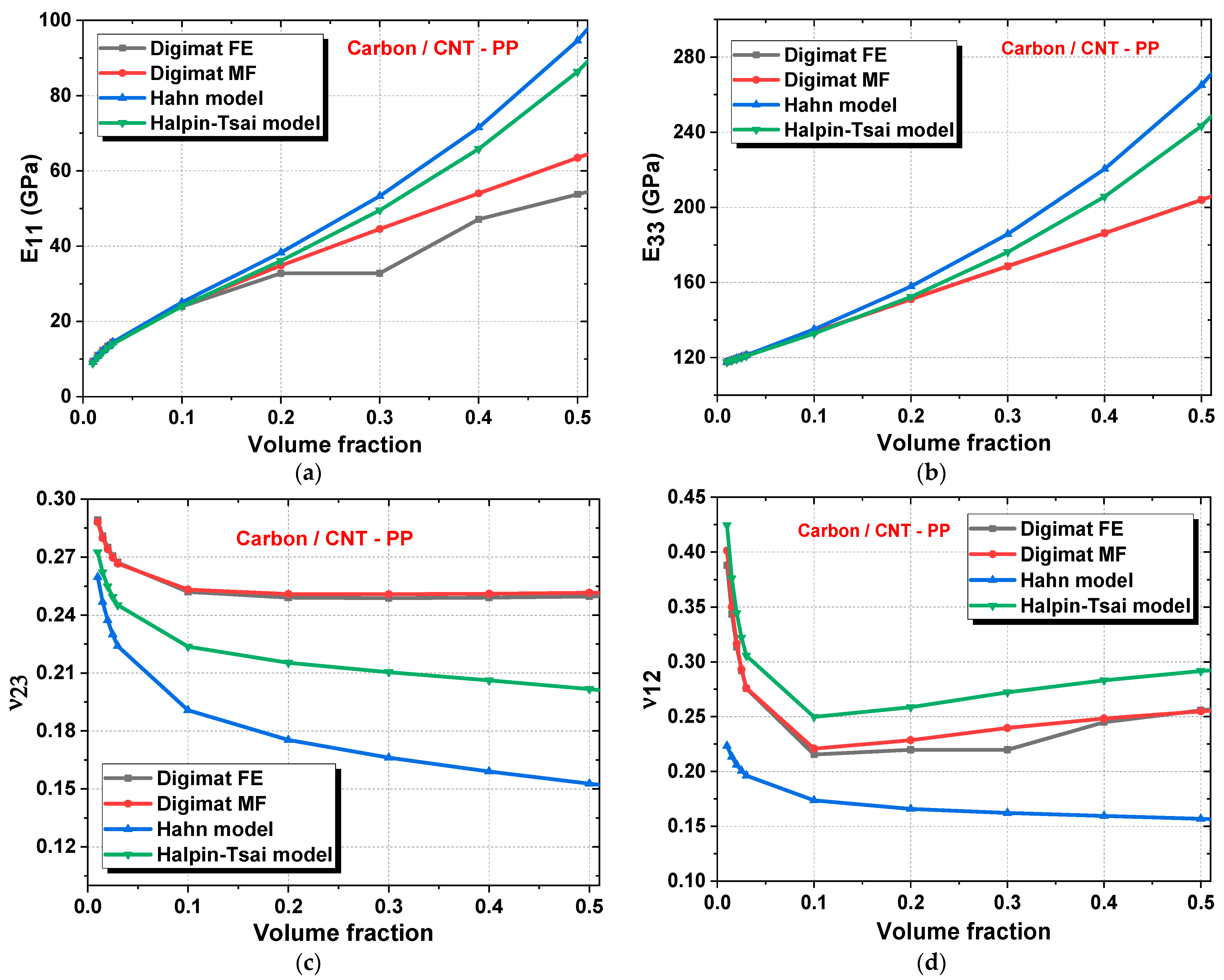
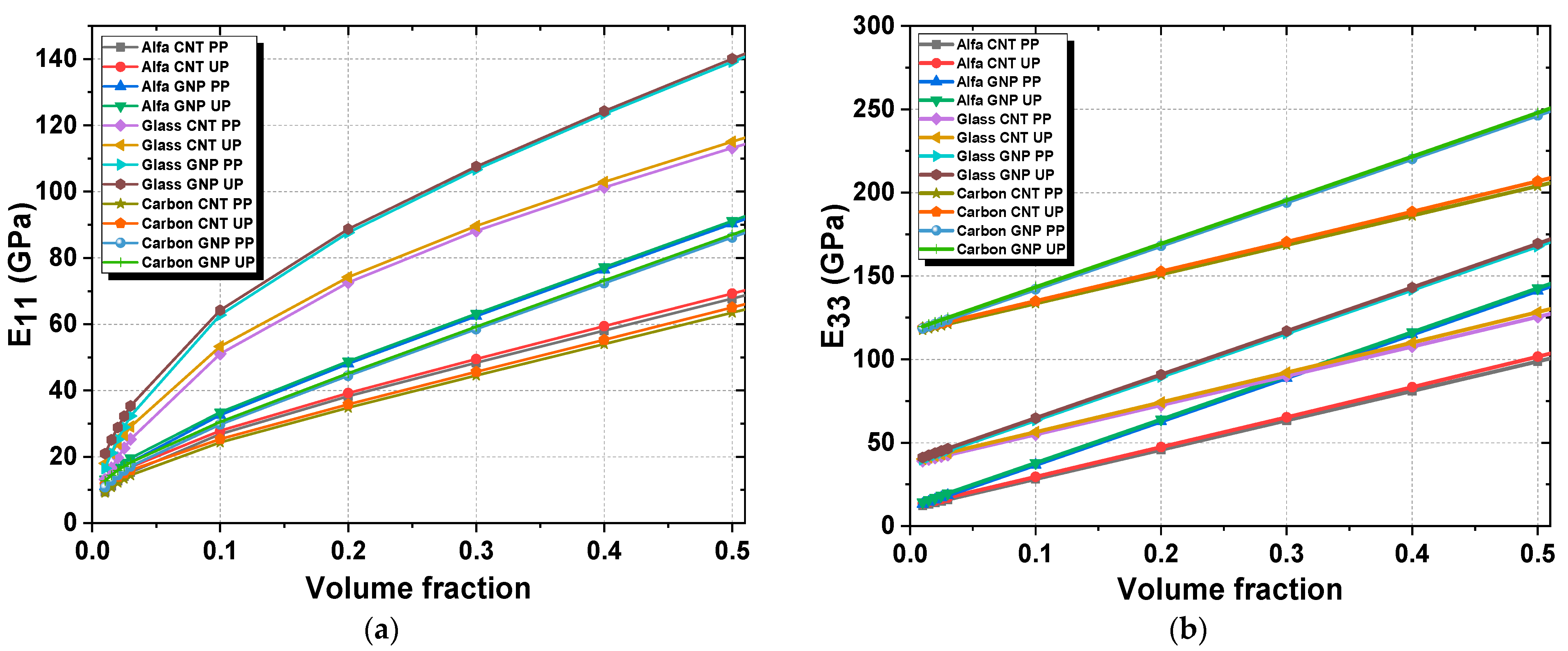
3.3. Second Homogenization Results
4. Effect of Aspect Ratio on the Mechanical Properties
5. Effect of Agglomeration on the Mechanical Properties
5.1. Agglomeration of CNTs
5.1.1. Method Comparison
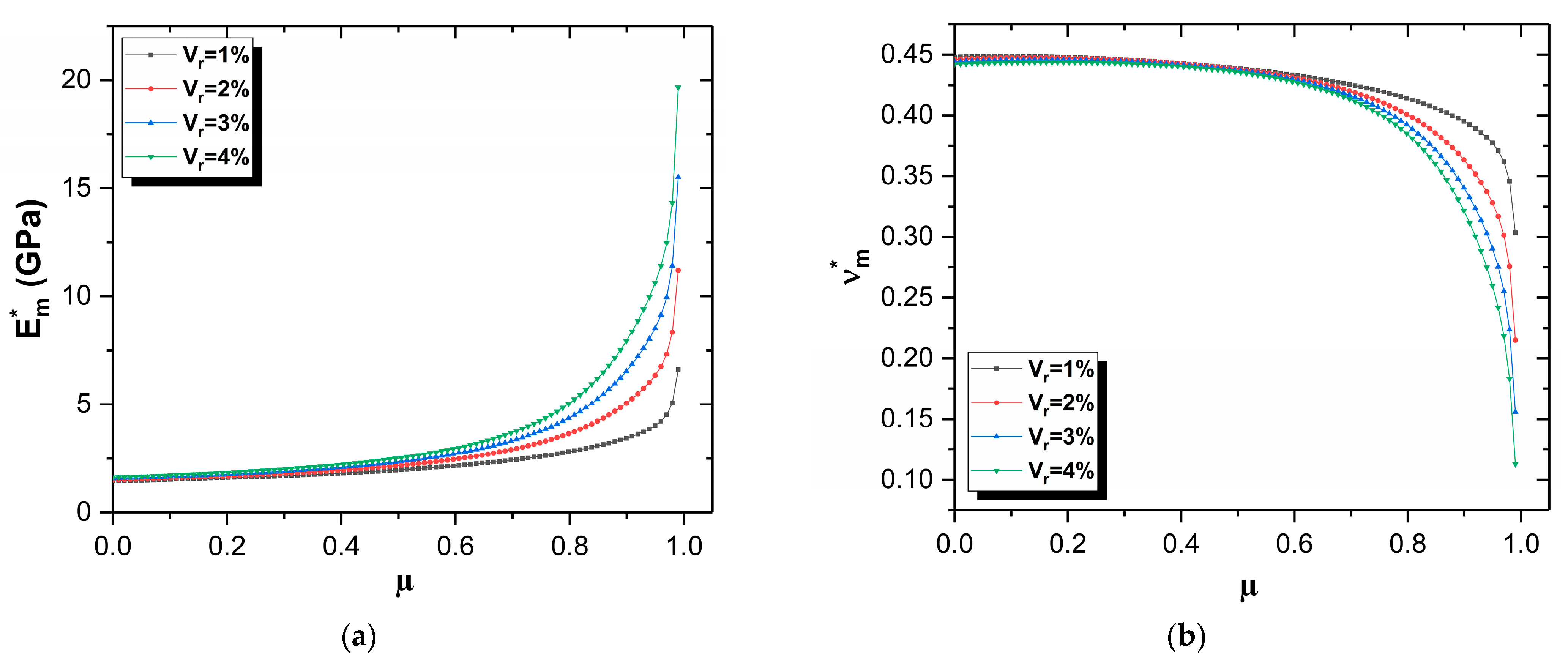
5.1.2. Results and Discussions
5.2. Agglomeration of GNPs
Results and Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Rouway, M.; Nachtane, M.; Tarfaoui, M.; Chakhchaoui, N.; Omari, L.E.H.; Fraija, F.; Cherkaoui, O. Mechanical Properties of a Biocomposite Based on Carbon Nanotube and Graphene Nanoplatelet Reinforced Polymers: Analytical and Numerical Study. J. Compos. Sci. 2021, 5, 234. [Google Scholar] [CrossRef]
- Nachtane, M.; Tarfaoui, M.; Goda, I.; Rouway, M. A review on the technologies, design considerations and numerical models of tidal current turbines. Renew Energy 2020, 157, 1274–1288. [Google Scholar] [CrossRef]
- Lamhour, K.; Rouway, M.; Tizliouine, A.; El Hachemi Omari, L.; Salhi, H.; Cherkaoui, O. Experimental study on the properties of Alfa/wool woven fabrics reinforced epoxy composite as an application in wind turbine blades. J. Compos. Mater. 2022, 56, 3253–3268. [Google Scholar] [CrossRef]
- Mahmoud Zaghloul, M.Y.; Yousry Zaghloul, M.M.; Yousry Zaghloul, M.M. Developments in polyester composite materials—An in-depth review on natural fibres and nano fillers. Compos. Struct. 2021, 278, 114698. [Google Scholar] [CrossRef]
- Nachtane, M.; Meraghni, F.; Chatzigeorgiou, G.; Harper, L.T.; Pelascini, F. Multiscale viscoplastic modeling of recycled glass fiber-reinforced thermoplastic composites: Experimental and numerical investigations. Compos. Part B Eng. 2022, 242, 110087. [Google Scholar] [CrossRef]
- Nunna, S.; Blanchard, P.; Buckmaster, D.; Davis, S.; Naebe, M. Development of a cost model for the production of carbon fibres. Heliyon 2019, 5, e02698. [Google Scholar] [CrossRef]
- Zaghloul, M.M.Y.; Zaghloul, M.Y.M.; Zaghloul, M.M.Y. Experimental and modeling analysis of mechanical-electrical behaviors of polypropylene composites filled with graphite and MWCNT fillers. Polym. Test. 2017, 63, 467–474. [Google Scholar] [CrossRef]
- García-Macías, E.; Castro-Triguero, R. Coupled effect of CNT waviness and agglomeration: A case study of vibrational analysis of CNT/polymer skew plates. Compos. Struct. 2018, 193, 87–102. [Google Scholar] [CrossRef]
- Maghsoudlou, M.A.; Barbaz Isfahani, R.; Saber-Samandari, S.; Sadighi, M. Effect of interphase, curvature and agglomeration of SWCNTs on mechanical properties of polymer-based nanocomposites: Experimental and numerical investigations. Compos. Part B Eng. 2019, 175, 107119. [Google Scholar] [CrossRef]
- Pan, Z.-Z.; Chen, X.; Zhang, L.-W. Modeling large amplitude vibration of pretwisted hybrid composite blades containing CNTRC layers and matrix cracked FRC layers. Appl. Math. Model. 2020, 83, 640–659. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Hassanzadeh-Aghdam, M.K.; Mahmoodi, M.J.; Ansari, R. Creep performance of CNT polymer nanocomposites -An emphasis on viscoelastic interphase and CNT agglomeration. Compos. Part B Eng. 2019, 168, 274–281. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.-W. On the elastic properties of carbon nanotube-based composites: Modelling and characterization. J. Phys. Appl. Phys. 2003, 36, 573–582. [Google Scholar] [CrossRef]
- Bonnet, P.; Sireude, D.; Garnier, B.; Chauvet, O. Thermal properties and percolation in carbon nanotube-polymer composites. Appl. Phys. Lett. 2007, 91, 201910. [Google Scholar] [CrossRef]
- Fidelus, J.D.; Wiesel, E.; Gojny, F.H.; Schulte, K.; Wagner, H.D. Thermo-mechanical properties of randomly oriented carbon/epoxy nanocomposites. Compos. Part Appl. Sci. Manuf. 2005, 36, 1555–1561. [Google Scholar] [CrossRef]
- Hassanzadeh-Aghdam, M.K. Evaluating the effective creep properties of graphene-reinforced polymer nanocomposites by a homogenization approach. Compos. Sci. Technol. 2021, 209, 108791. [Google Scholar] [CrossRef]
- Gao, C.; Zhan, B.; Chen, L.; Li, X. A micromechanical model of graphene-reinforced metal matrix nanocomposites with consideration of graphene orientations. Compos. Sci. Technol. 2017, 152, 120–128. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.-Z.; Koratkar, N. Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef]
- Narh, K.A.; Jallo, L.; Rhee, K.Y. The effect of carbon nanotube agglomeration on the thermal and mechanical properties of polyethylene oxide. Polym. Compos. 2008, 29, 809–817. [Google Scholar] [CrossRef]
- Alian, A.R.; El-Borgi, S.; Meguid, S.A. Multiscale modeling of the effect of waviness and agglomeration of CNTs on the elastic properties of nanocomposites. Comput. Mater. Sci. 2016, 117, 195–204. [Google Scholar] [CrossRef]
- Daghigh, H.; Daghigh, V.; Milani, A.; Tannant, D.; Lacy, T.E.; Reddy, J.N. Nonlocal bending and buckling of agglomerated CNT-Reinforced composite nanoplates. Compos. Part B Eng. 2020, 183, 107716. [Google Scholar] [CrossRef]
- Shi, D.-L.; Feng, X.-Q.; Huang, Y.Y.; Hwang, K.-C.; Gao, H. The Effect of Nanotube Waviness and Agglomeration on the Elastic Property of Carbon Nanotube-Reinforced Composites. J. Eng. Mater. Technol. 2004, 126, 250–257. [Google Scholar] [CrossRef]
- Ji, X.-Y.; Cao, Y.-P.; Feng, X.-Q. Micromechanics prediction of the effective elastic moduli of graphene sheet-reinforced polymer nanocomposites. Model. Simul. Mater. Sci. Eng. 2010, 18, 045005. [Google Scholar] [CrossRef]
- Yun, G.J.; Zhu, F.-Y.; Lim, H.J.; Choi, H. A damage plasticity constitutive model for wavy CNT nanocomposites by incremental Mori-Tanaka approach. Compos. Struct. 2021, 258, 113178. [Google Scholar] [CrossRef]
- Fazilati, J.; Khalafi, V.; Jalalvand, M. Free vibration analysis of three-phase CNT/polymer/fiber laminated tow-steered quadrilateral plates considering agglomeration effects. Thin-Walled Struct. 2022, 179, 109638. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M.; Fantuzzi, N.; Reddy, J.N. Multiscale approach for three-phase CNT/polymer/fiber laminated nanocomposite structures. Polym. Compos. 2019, 40, E102–E126. [Google Scholar] [CrossRef]
- Chamis, C.C. Simplified Composite Micromechanics Equations For Hygral, Thermal And Mechanical Properties. In Proceedings of the Ann. Conf. of the Society of the Plastics Industry (SPI) Reinforced Plastics/Composites Inst., Houston, TX, USA, 1 January 1983. [Google Scholar]
- Hashin, Z.; Rosen, B.W. The Elastic Moduli of Fiber-Reinforced Materials. J. Appl. Mech. 1964, 31, 223–232. [Google Scholar] [CrossRef]
- Halpin, J.C. Stiffness and Expansion Estimates for Oriented Short Fiber Composites. J. Compos. Mater. 1969, 3, 732–734. [Google Scholar] [CrossRef]













| CNT | 536 | 184 | 132 | 2143 | 791 |
| GNP | 850 | 6.8 | 369 | 102,000 | 102,000 |
| CNT | 421.14 | 2079.8 | 0.17164 | 0.59522 | 132 | 791 |
| GNP | 1029.204 | 102,000 | 0.004 | 0.4 | 369 | 102,000 |
| Materials | PP | UP |
|---|---|---|
| Model | Elastic | Elastic |
| Symmetry | Isotropic | Isotropic |
| Density ρ (g/cm3) | 0.9 | 1.3 |
| Young’s modulus E (GPa) | 1.4 | 3.8 |
| Poisson’s ratio v | 0.45 | 0.42 |
| Elastic Properties | CNT | GNP |
|---|---|---|
| Axial Young’s modulus (GPa) | 2079.8 | 102,000 |
| In plane Young’s modulus (GPa) | 421.14 | 1029.204 |
| In plane Poisson’s ratio | 0.59522 | 0.4 |
| Transverse Poisson’s ratio | 0.17164 | 0.004 |
| Transverse shear modulus (GPa) | 791 | 102,000 |
| In plane shear modulus (GPa) | 132 | 369 |
| Density (g/cm3) | 1.2 | 2.2 |
| Materials | Alfa | E-Glass |
|---|---|---|
| Model | Elastic | Elastic |
| Symmetry | Isotropic | Isotropic |
| Density ρ (g/cm3) | 1.52 | 2.54 |
| Young’s modulus E (GPa) | 19.4 | 73 |
| Poisson’s ratio v | 0.34 | 0.23 |
| CNT | GNP | |
|---|---|---|
| Axial Young’s modulus (GPa) | 2079.8 | 102,000 |
| In plane Young’s modulus (GPa) | 421.14 | 1029.204 |
| In plane Poisson’s ratio | 0.59522 | 0.4 |
| Transverse Poisson’s ratio | 0.17164 | 0.004 |
| Transverse shear modulus (GPa) | 791 | 102,000 |
| In plane shear modulus (GPa) | 132 | 369 |
| Density (g/cm3) | 1.2 | 2.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Bahi, A.; Rouway, M.; Tarfaoui, M.; Moumen, A.E.; Chakhchaoui, N.; Cherkaoui, O.; Omari, L.E.H. Mechanical Homogenization of Transversely Isotropic CNT/GNP Reinforced Biocomposite for Wind Turbine Blades: Numerical and Analytical Study. J. Compos. Sci. 2023, 7, 29. https://doi.org/10.3390/jcs7010029
El Bahi A, Rouway M, Tarfaoui M, Moumen AE, Chakhchaoui N, Cherkaoui O, Omari LEH. Mechanical Homogenization of Transversely Isotropic CNT/GNP Reinforced Biocomposite for Wind Turbine Blades: Numerical and Analytical Study. Journal of Composites Science. 2023; 7(1):29. https://doi.org/10.3390/jcs7010029
Chicago/Turabian StyleEl Bahi, Amine, Marwane Rouway, Mostapha Tarfaoui, Ahmed El Moumen, Nabil Chakhchaoui, Omar Cherkaoui, and Lhaj El Hachemi Omari. 2023. "Mechanical Homogenization of Transversely Isotropic CNT/GNP Reinforced Biocomposite for Wind Turbine Blades: Numerical and Analytical Study" Journal of Composites Science 7, no. 1: 29. https://doi.org/10.3390/jcs7010029
APA StyleEl Bahi, A., Rouway, M., Tarfaoui, M., Moumen, A. E., Chakhchaoui, N., Cherkaoui, O., & Omari, L. E. H. (2023). Mechanical Homogenization of Transversely Isotropic CNT/GNP Reinforced Biocomposite for Wind Turbine Blades: Numerical and Analytical Study. Journal of Composites Science, 7(1), 29. https://doi.org/10.3390/jcs7010029










