Dynamic Composite Materials Characterisation with Hopkinson Bars: Design and Development of New Dynamic Compression Systems
Abstract
1. Introduction
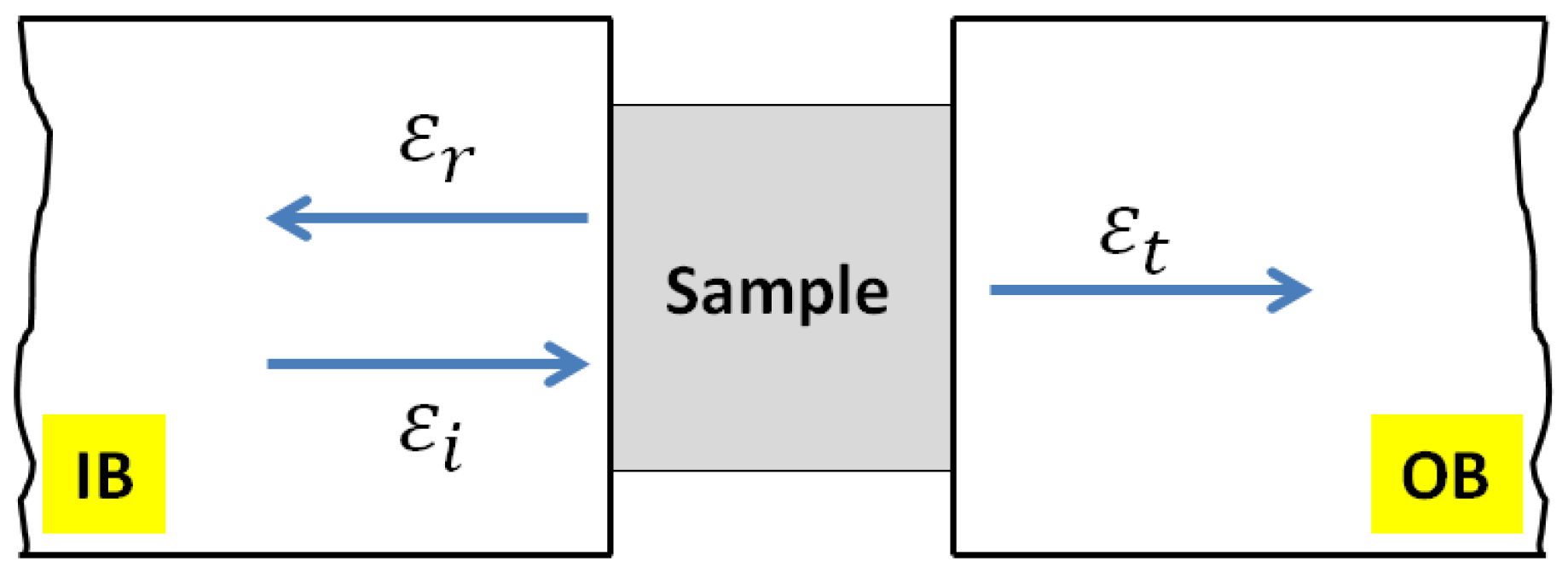
2. Hopkinson Bar Theory
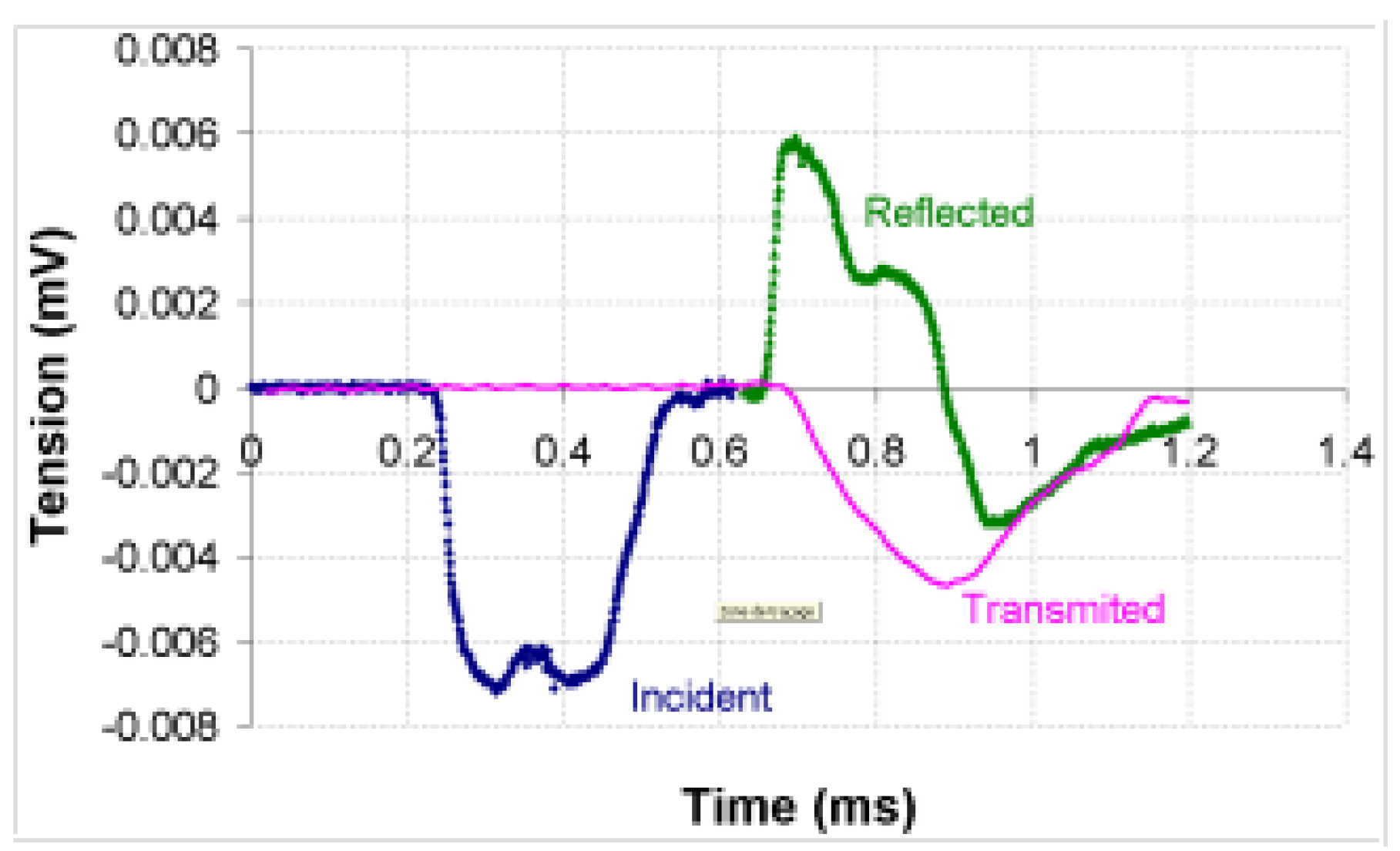
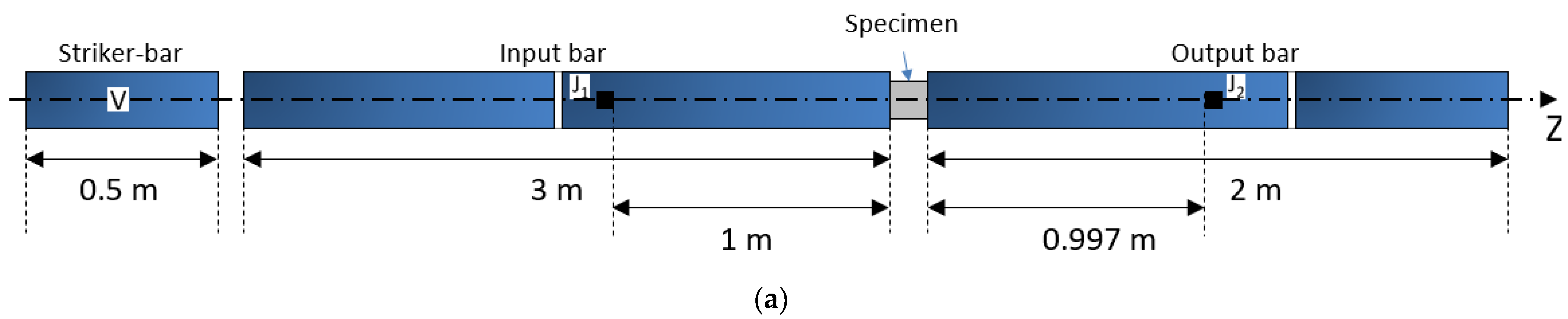
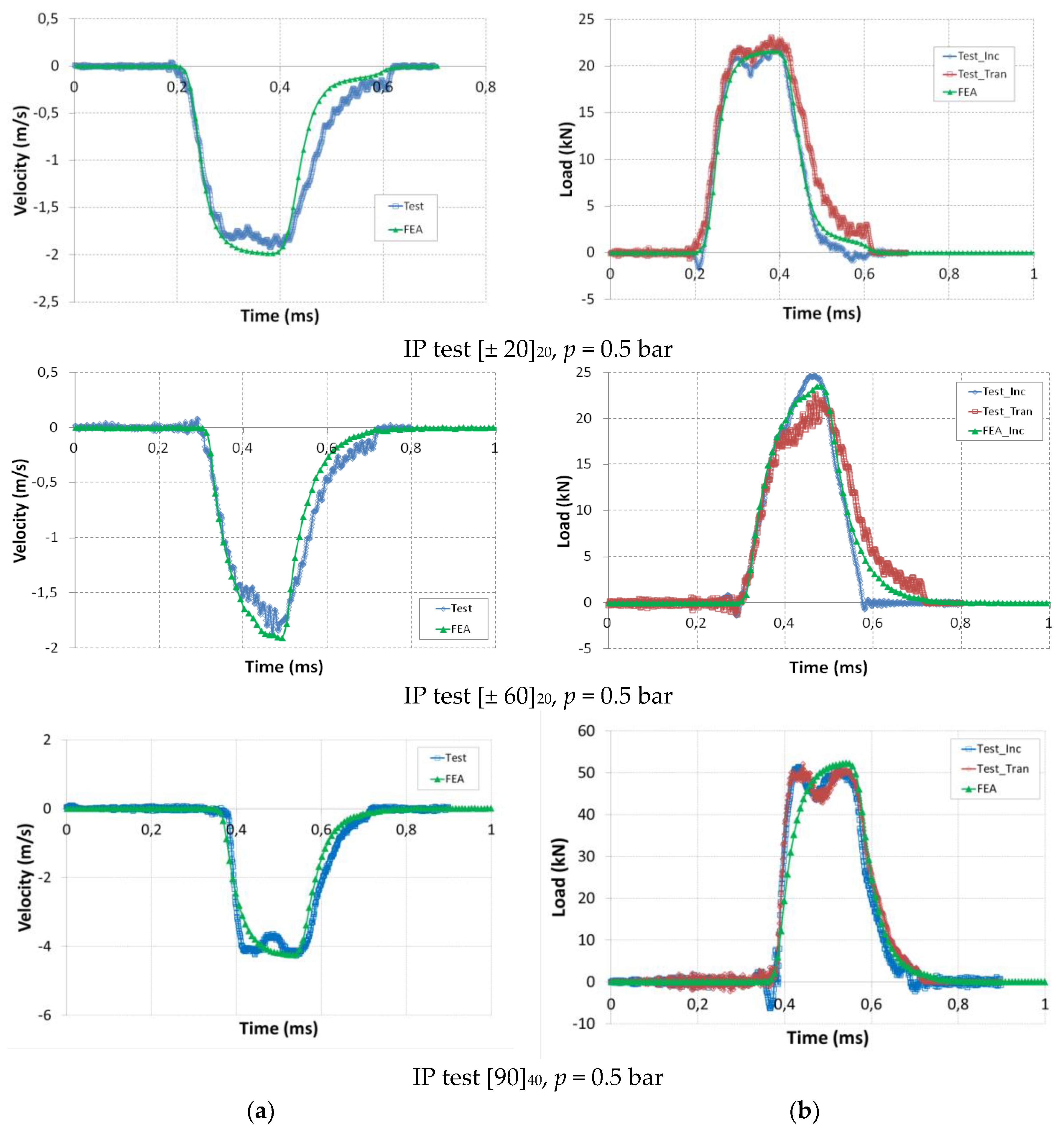
3. Experimental and Numerical Validation
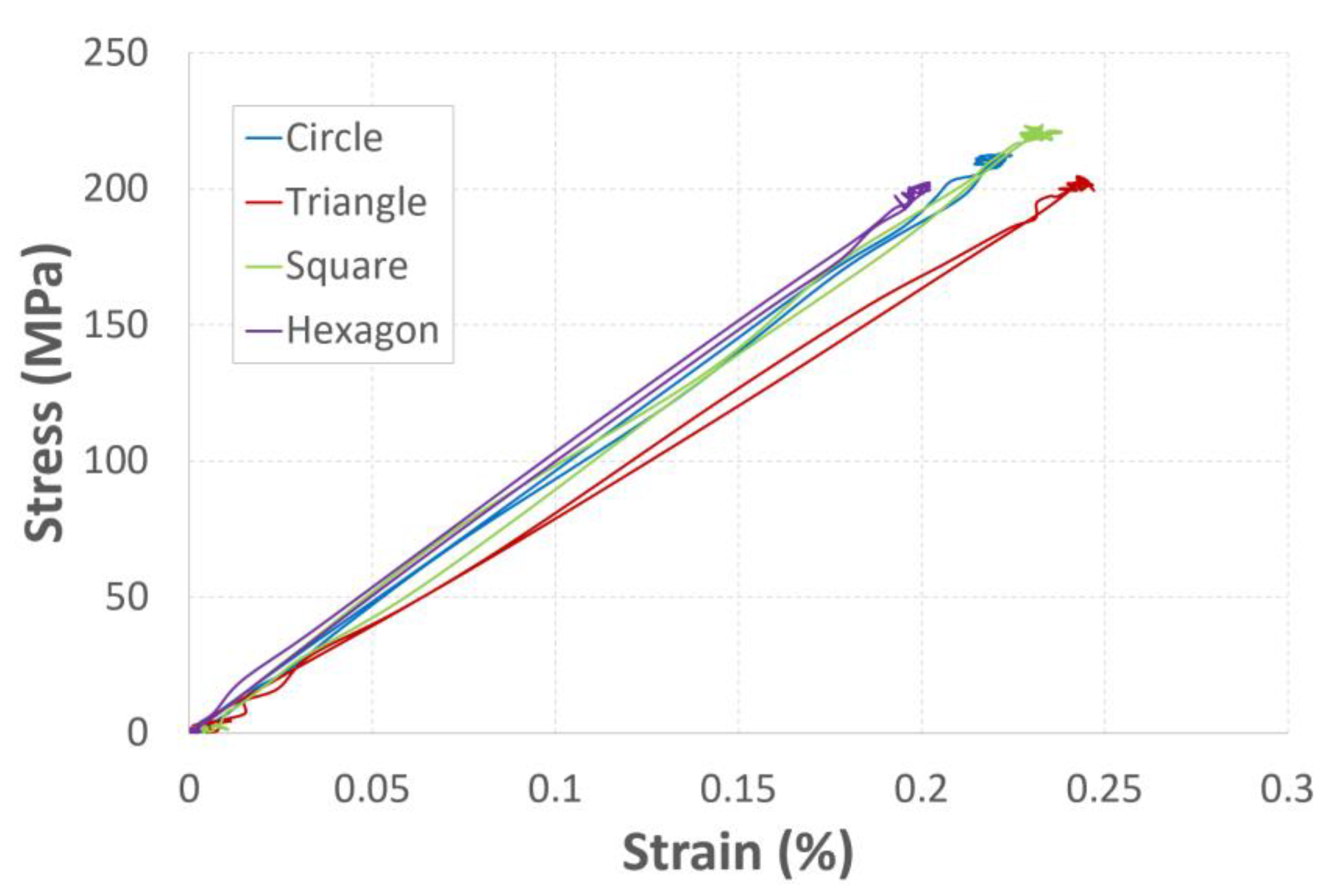
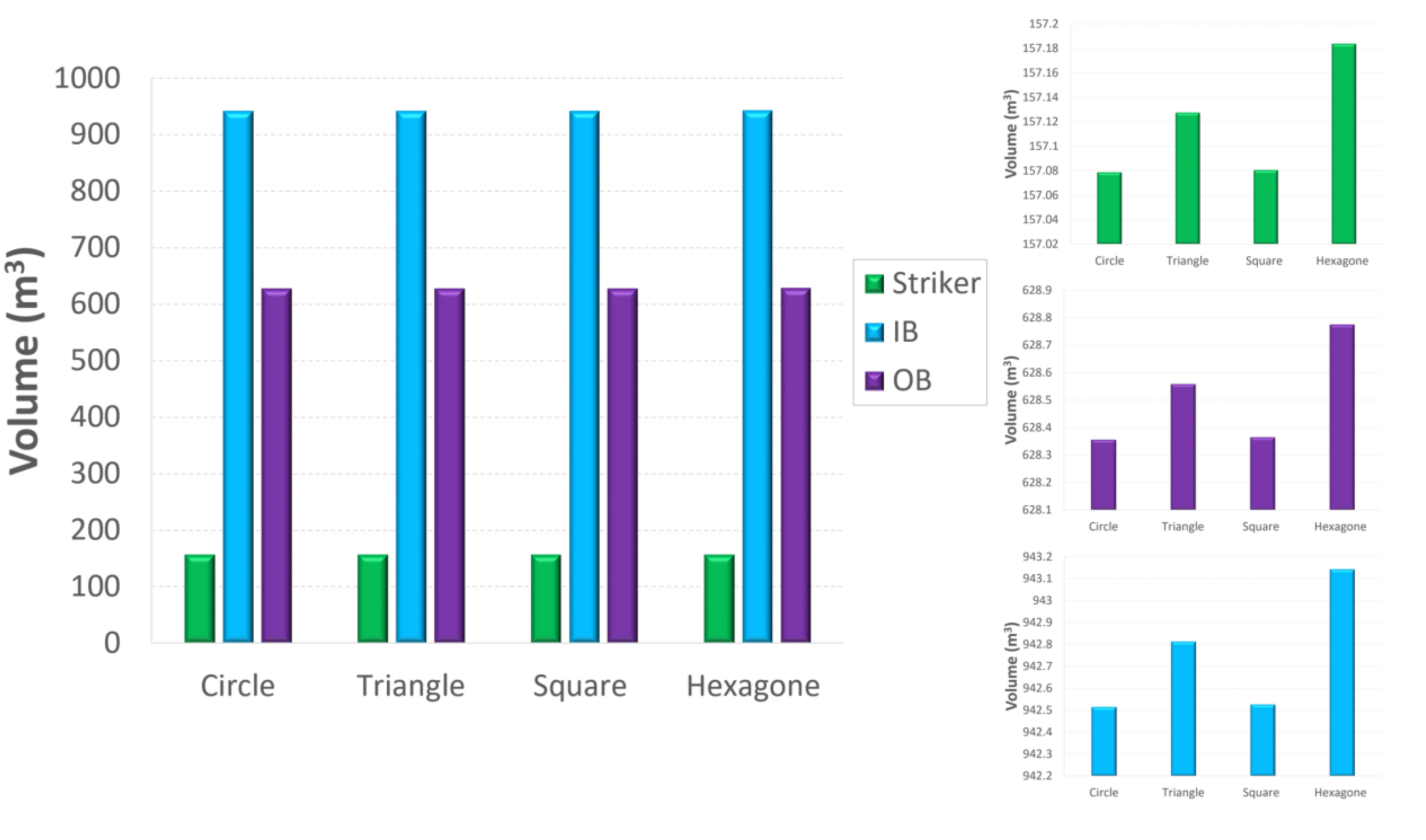
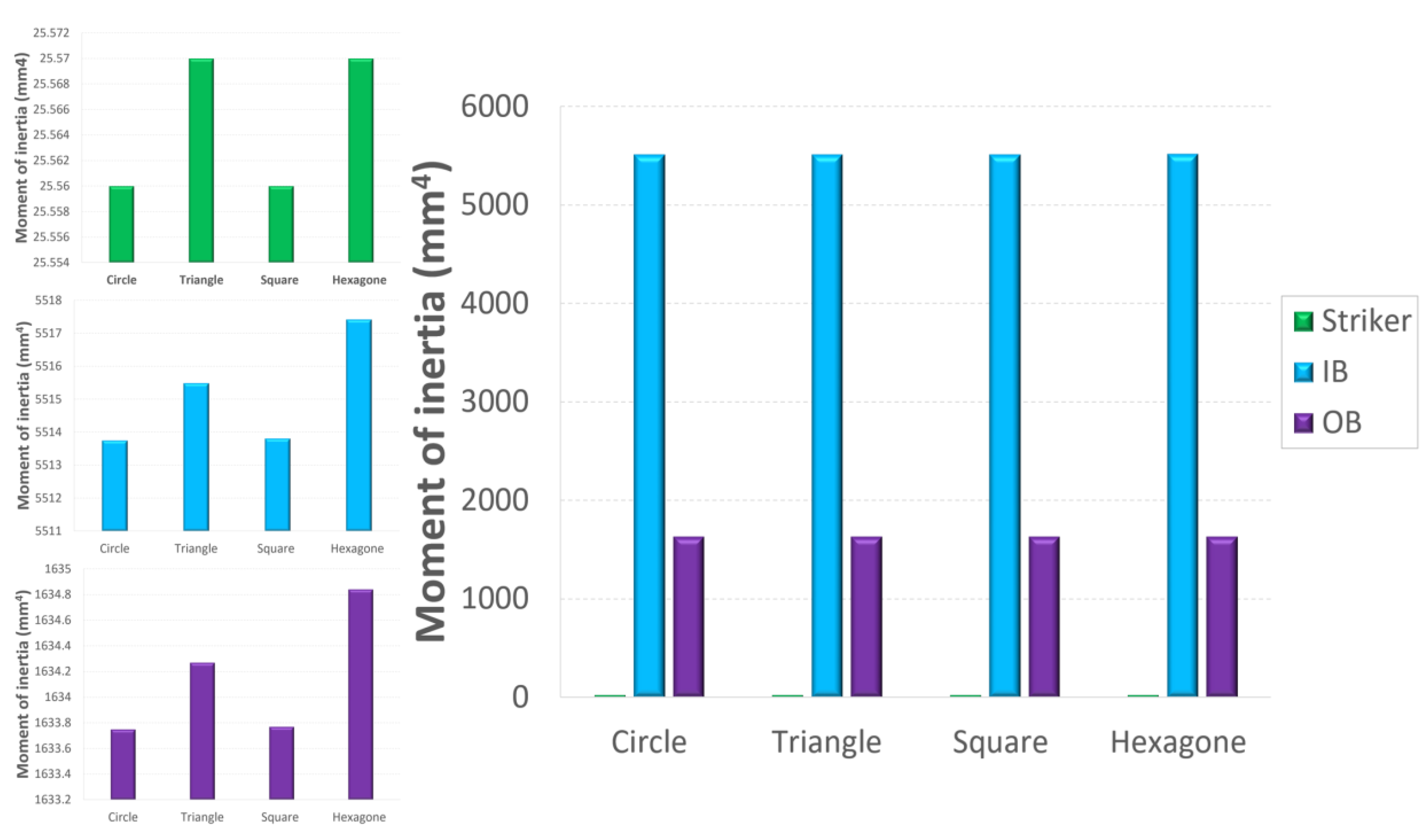
4. Parametric Study: Effect of Bar Geometry
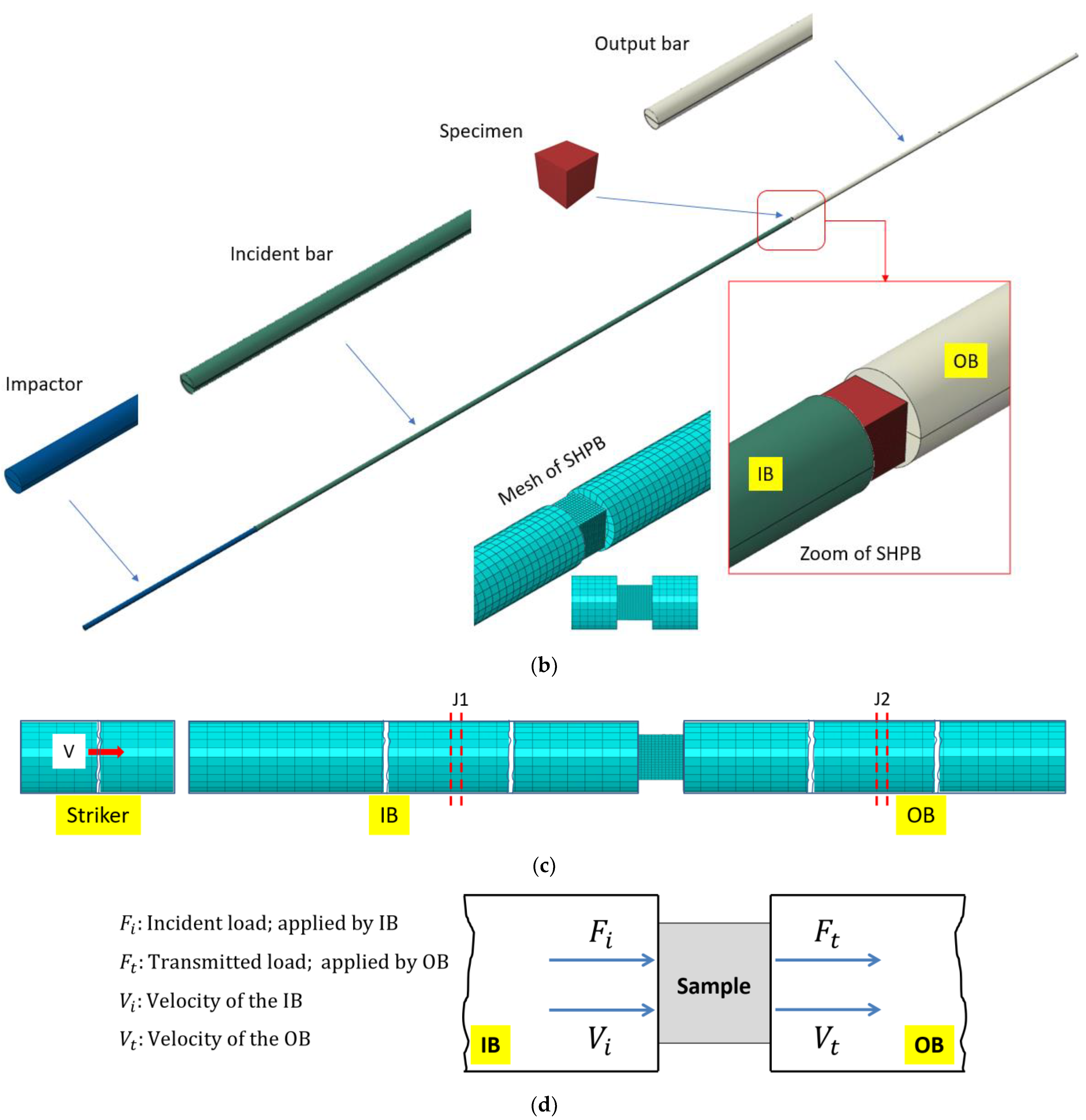
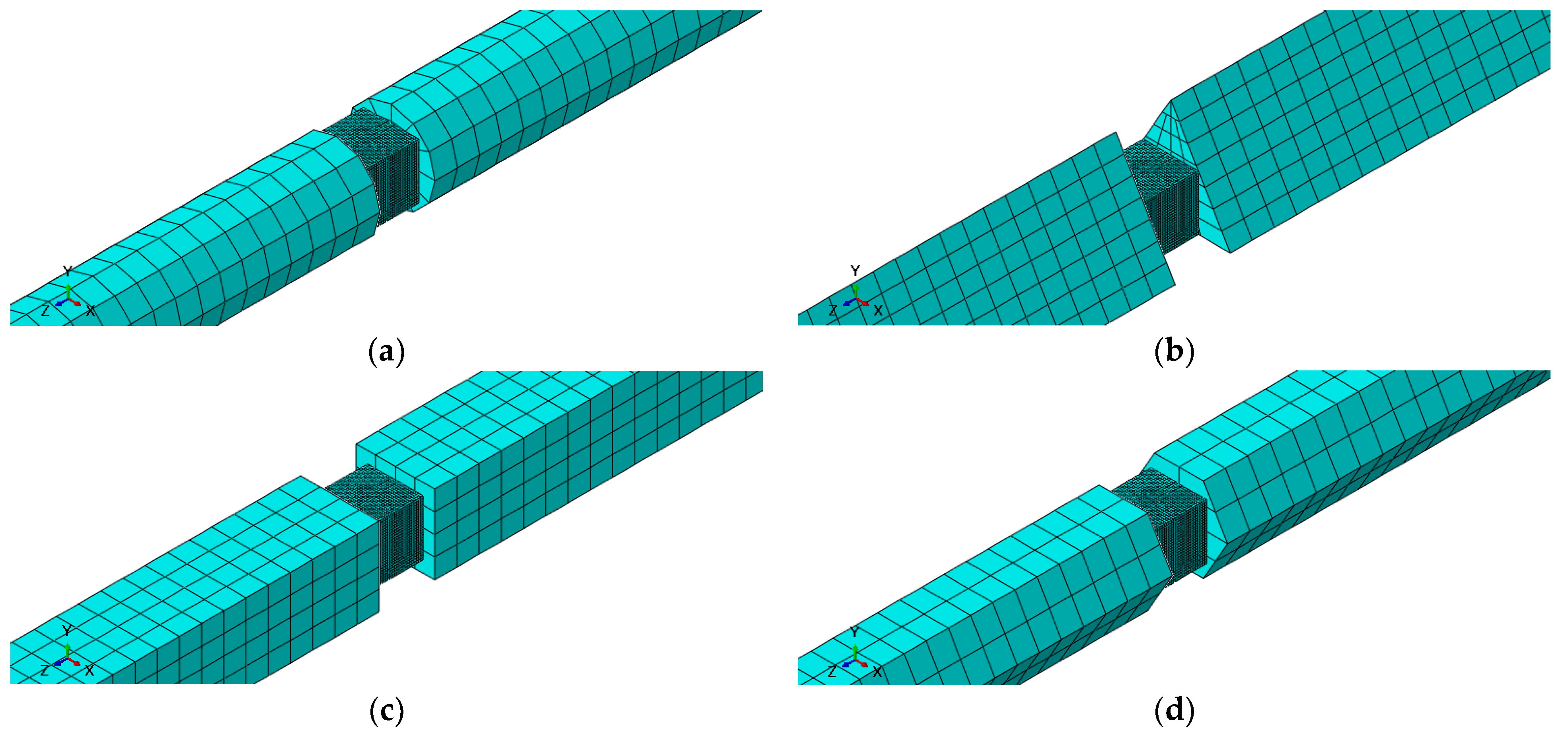
4.1. Mesh Procedure
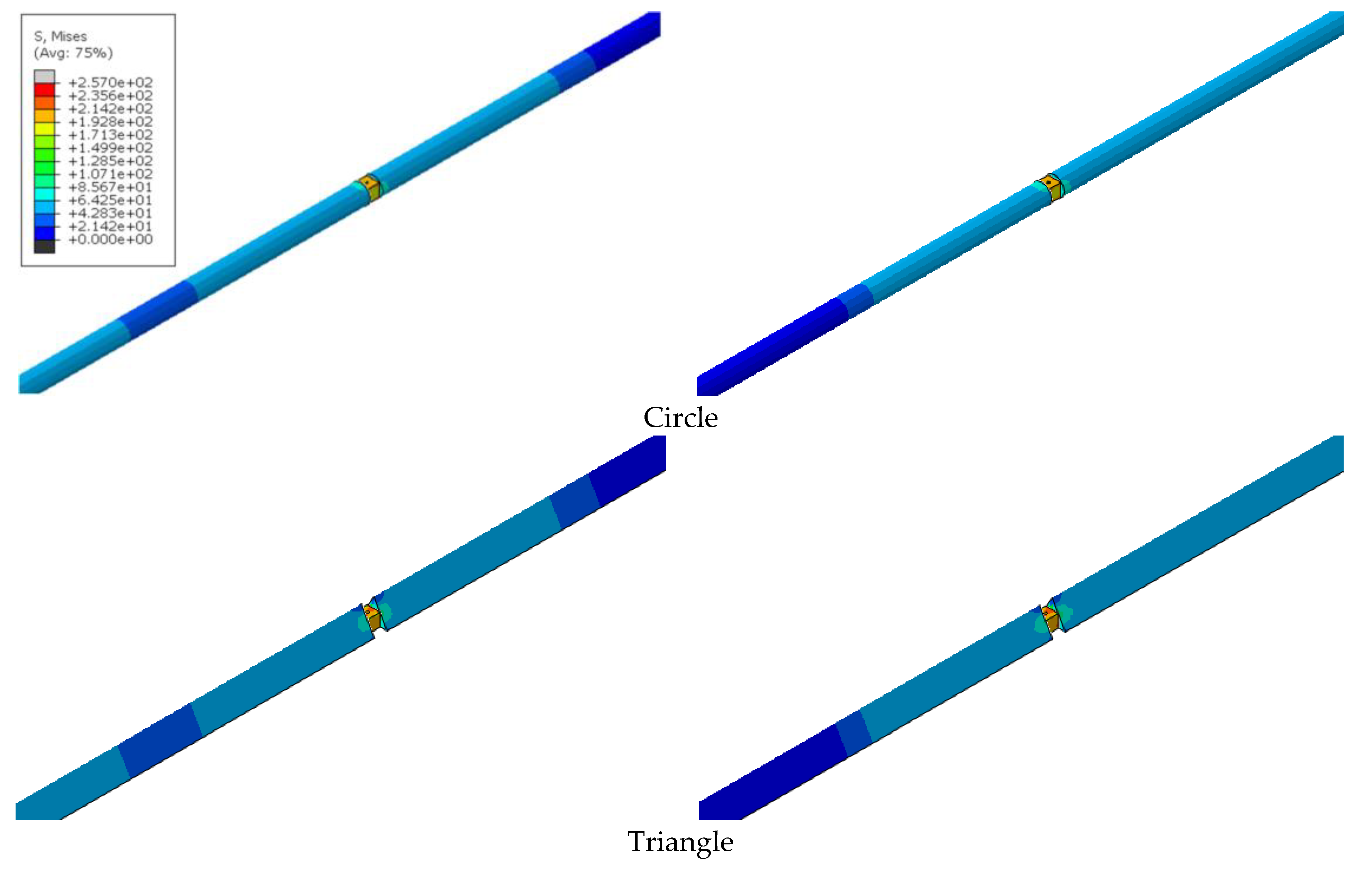
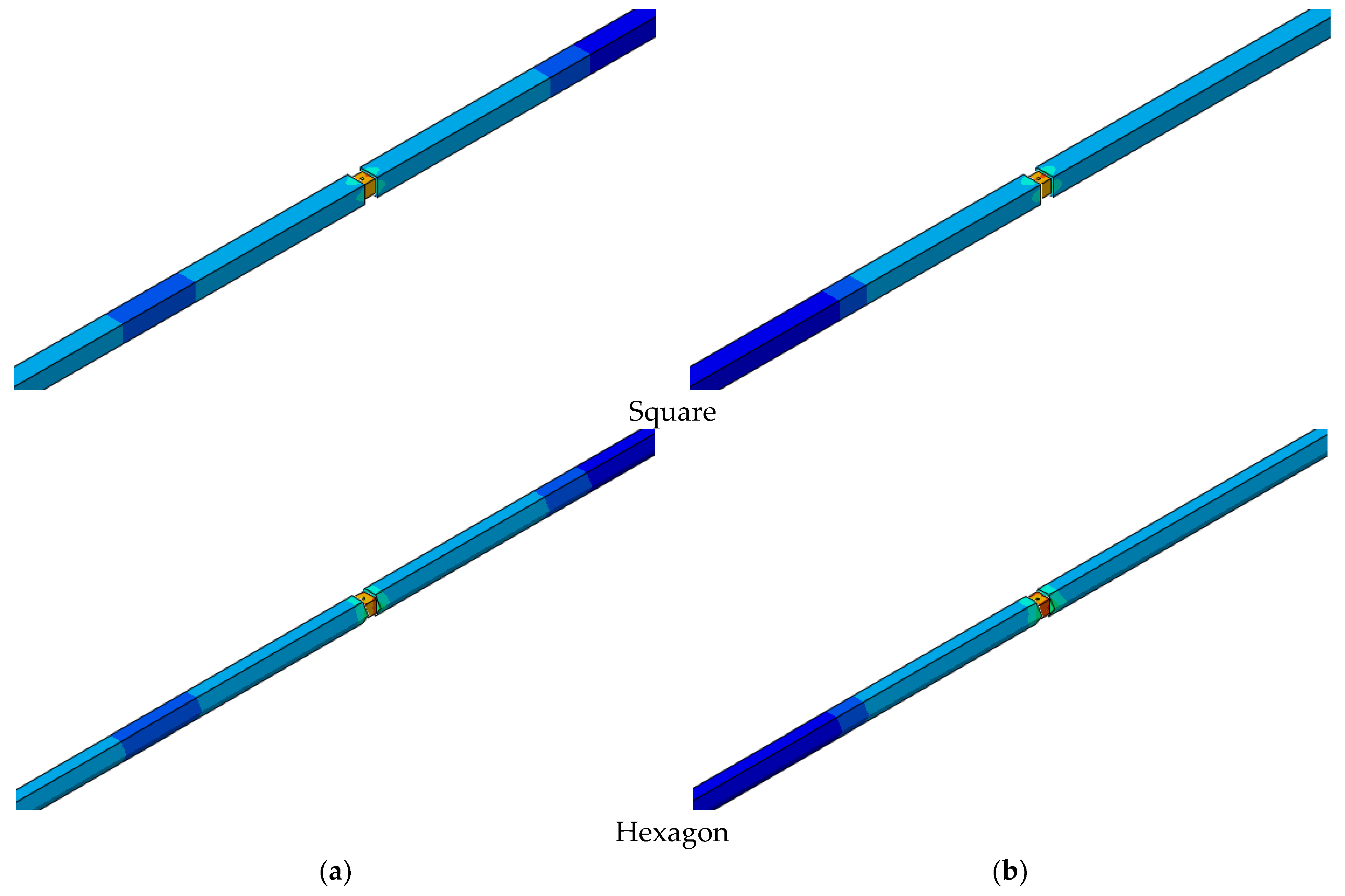
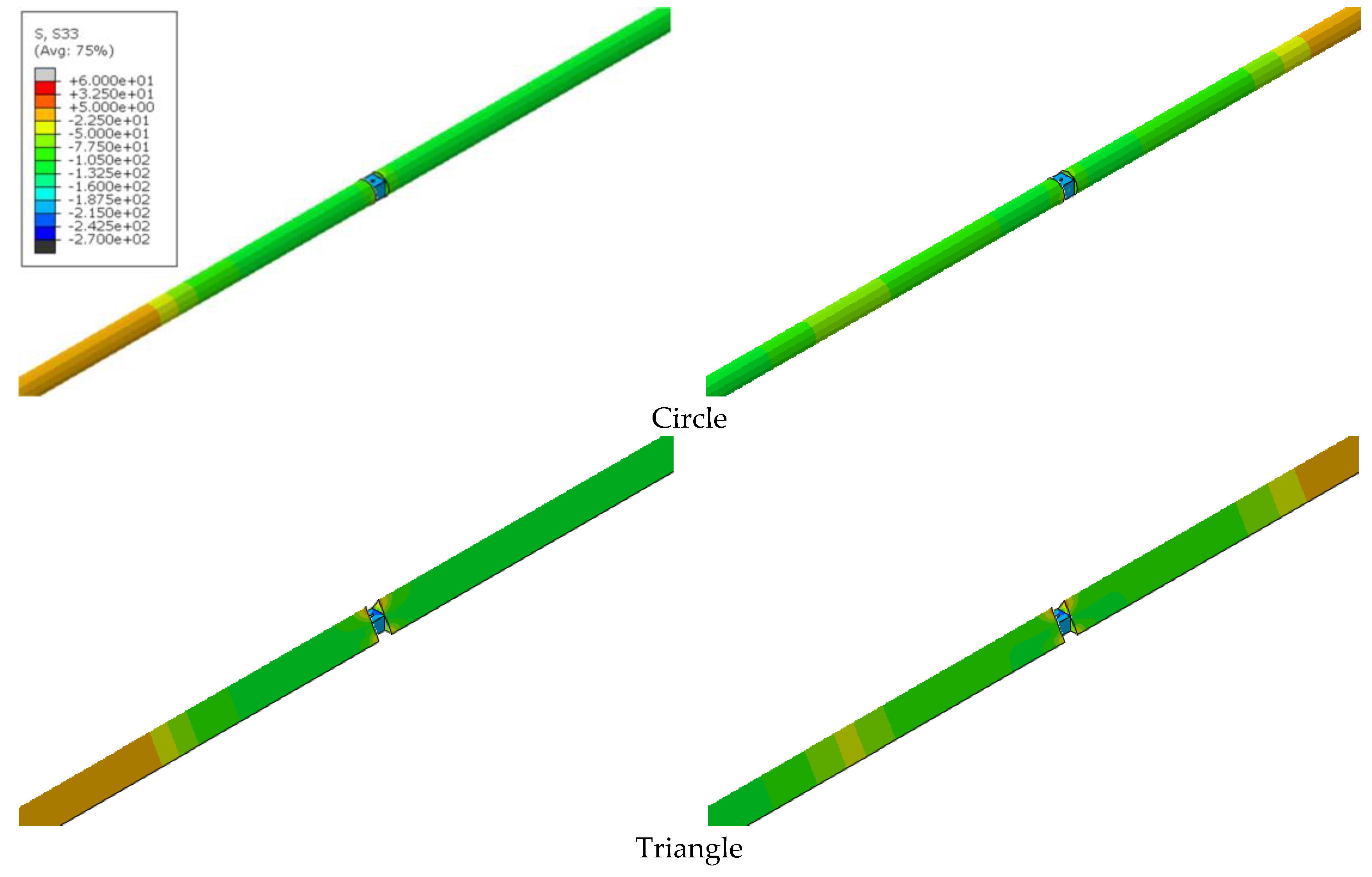
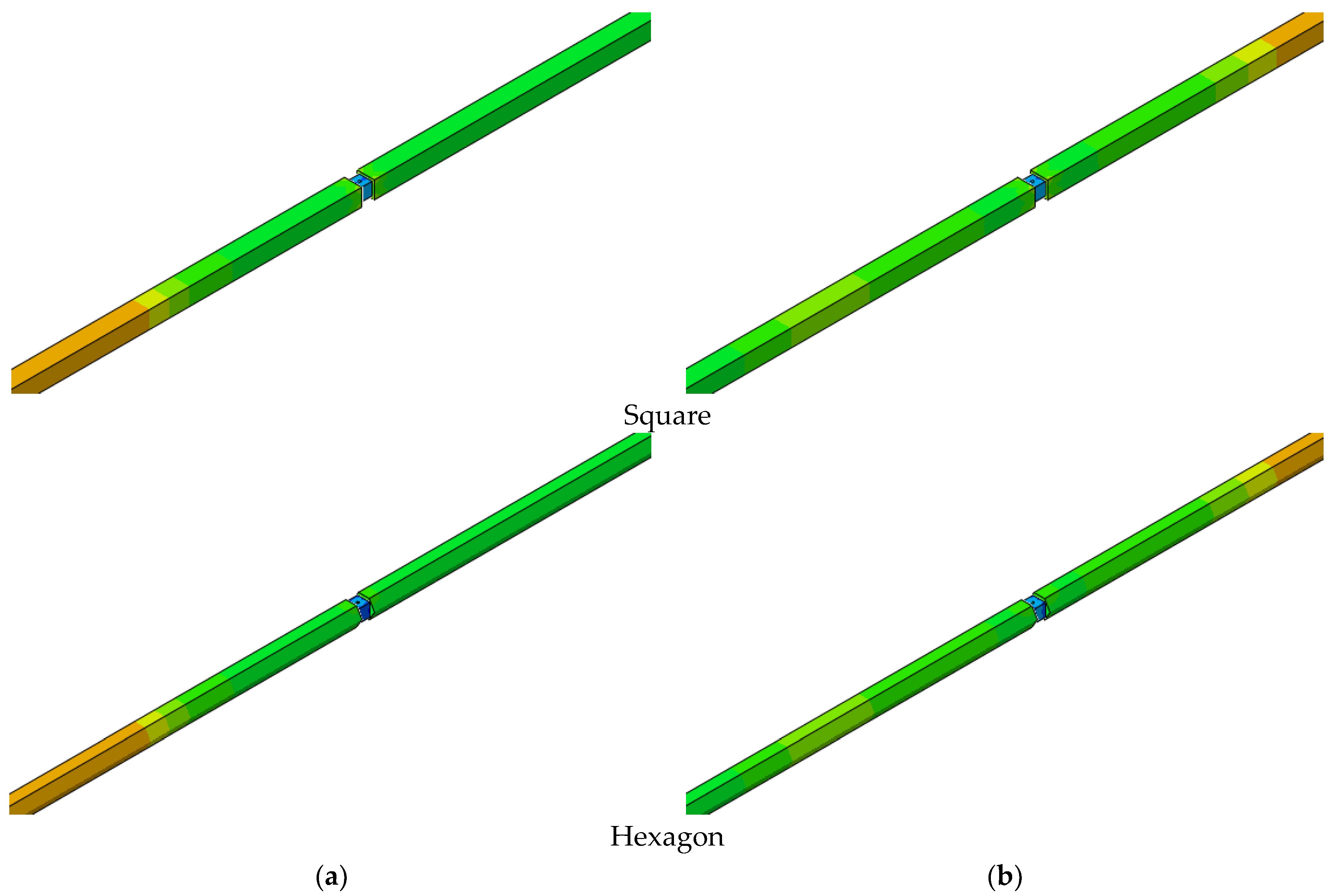
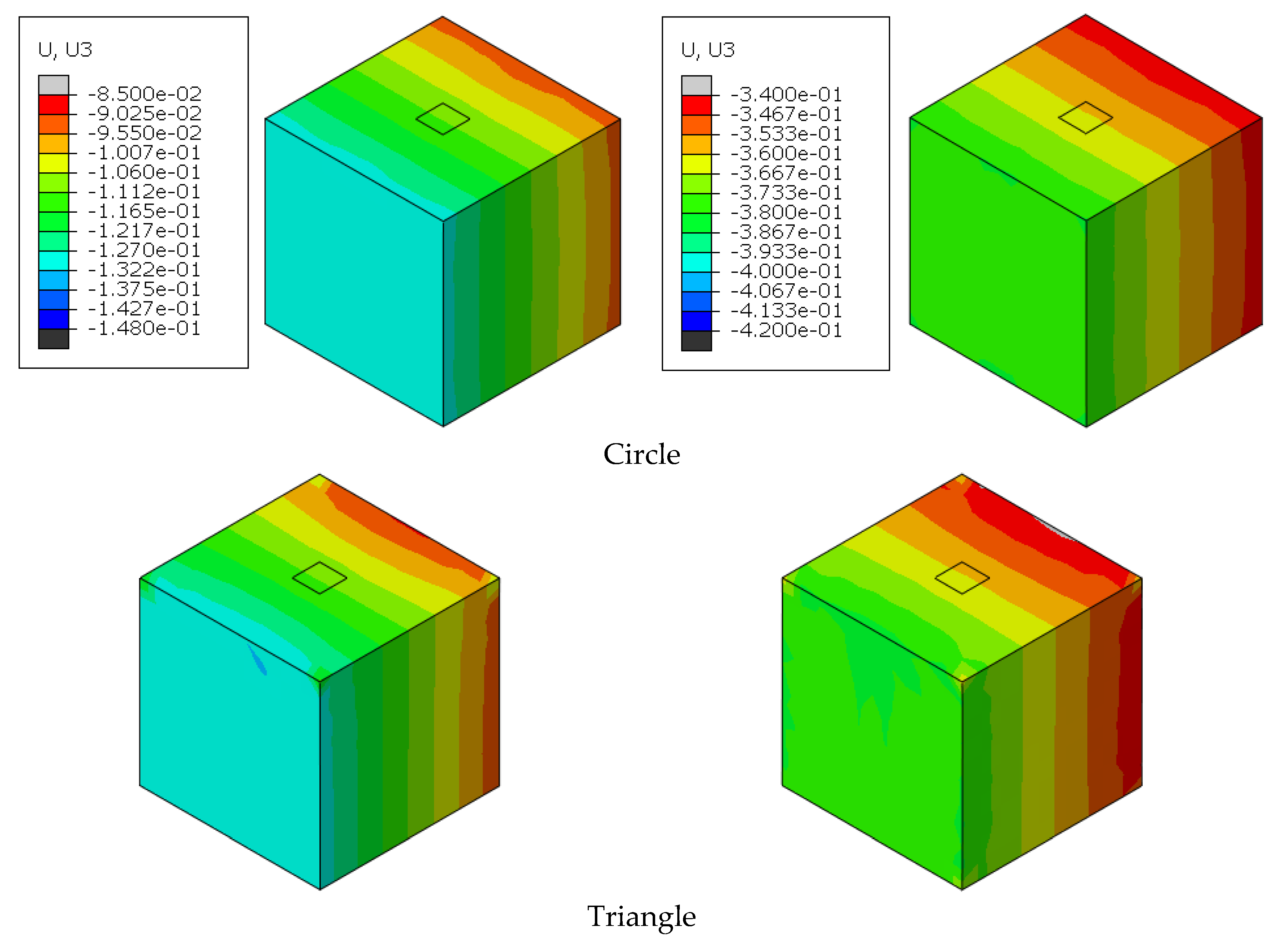
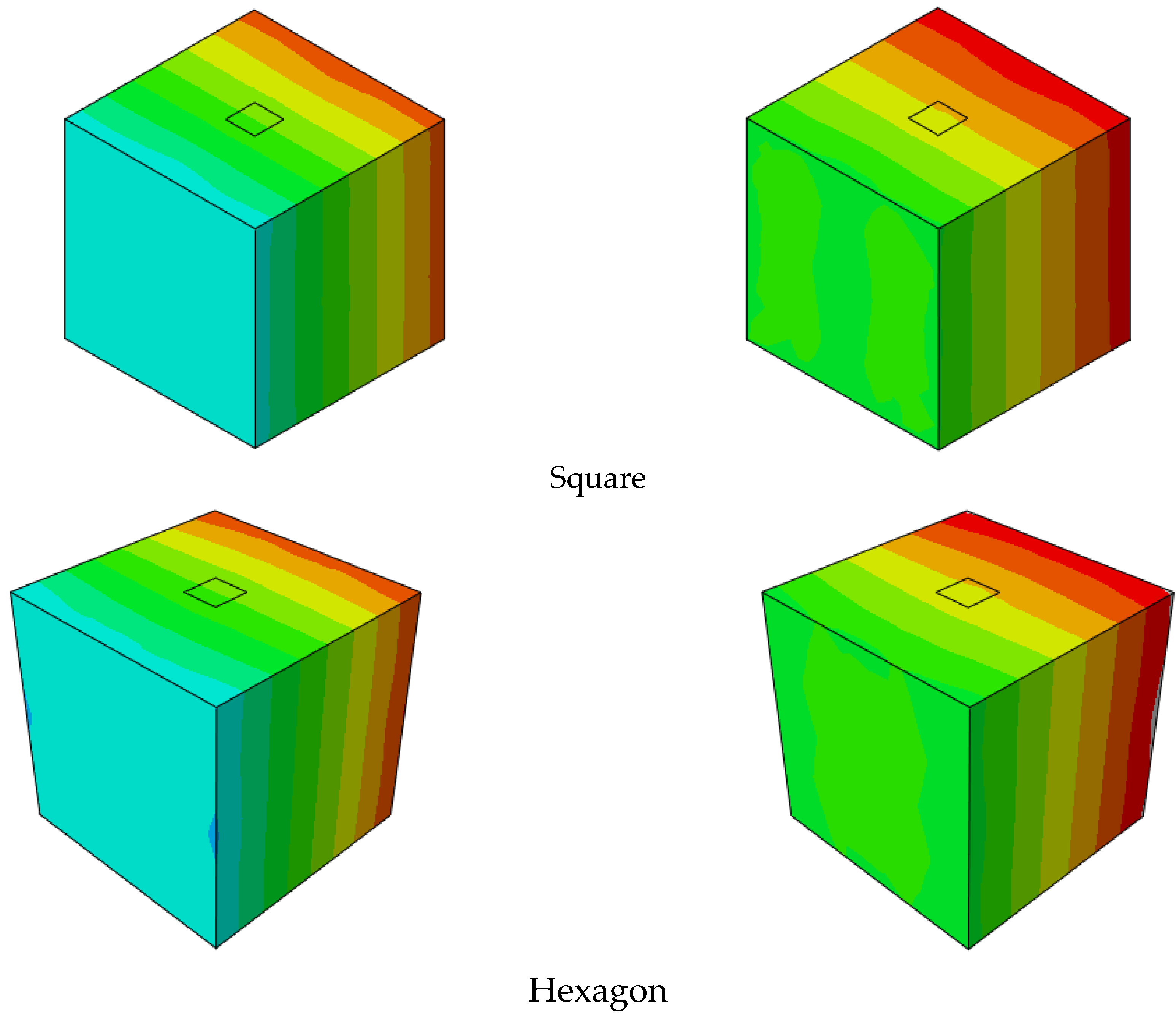
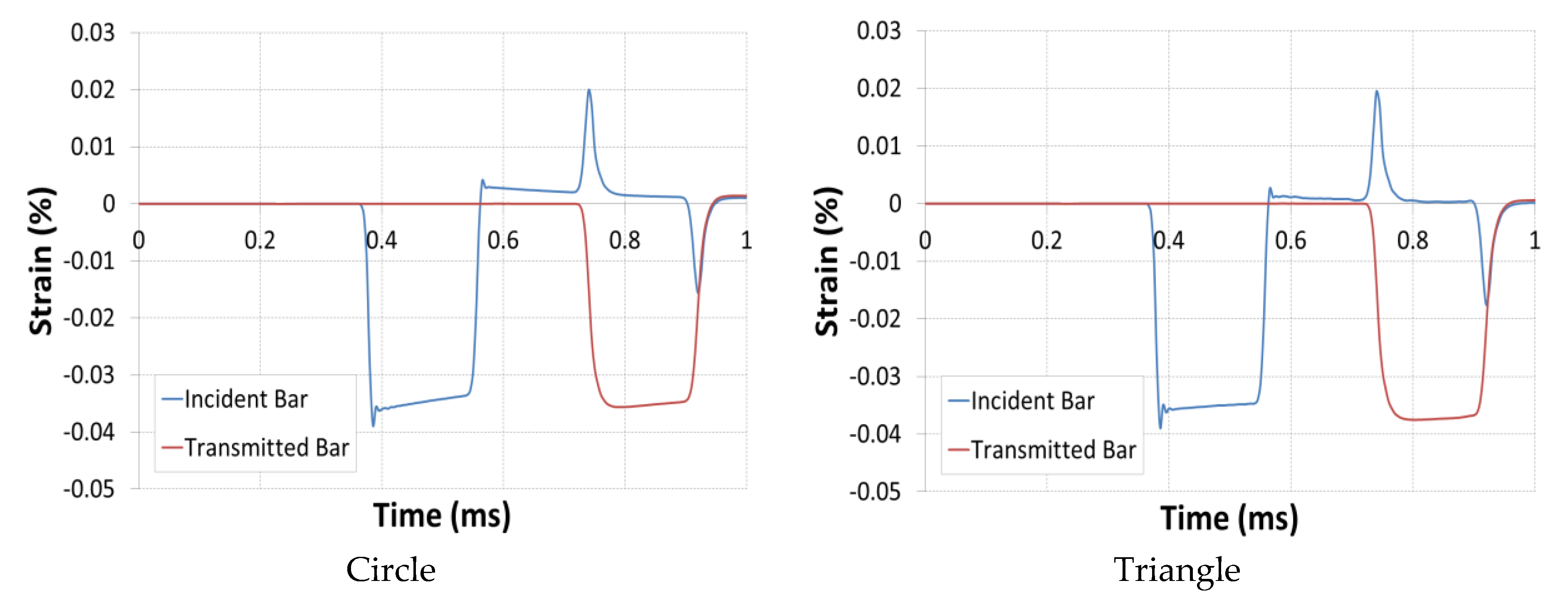
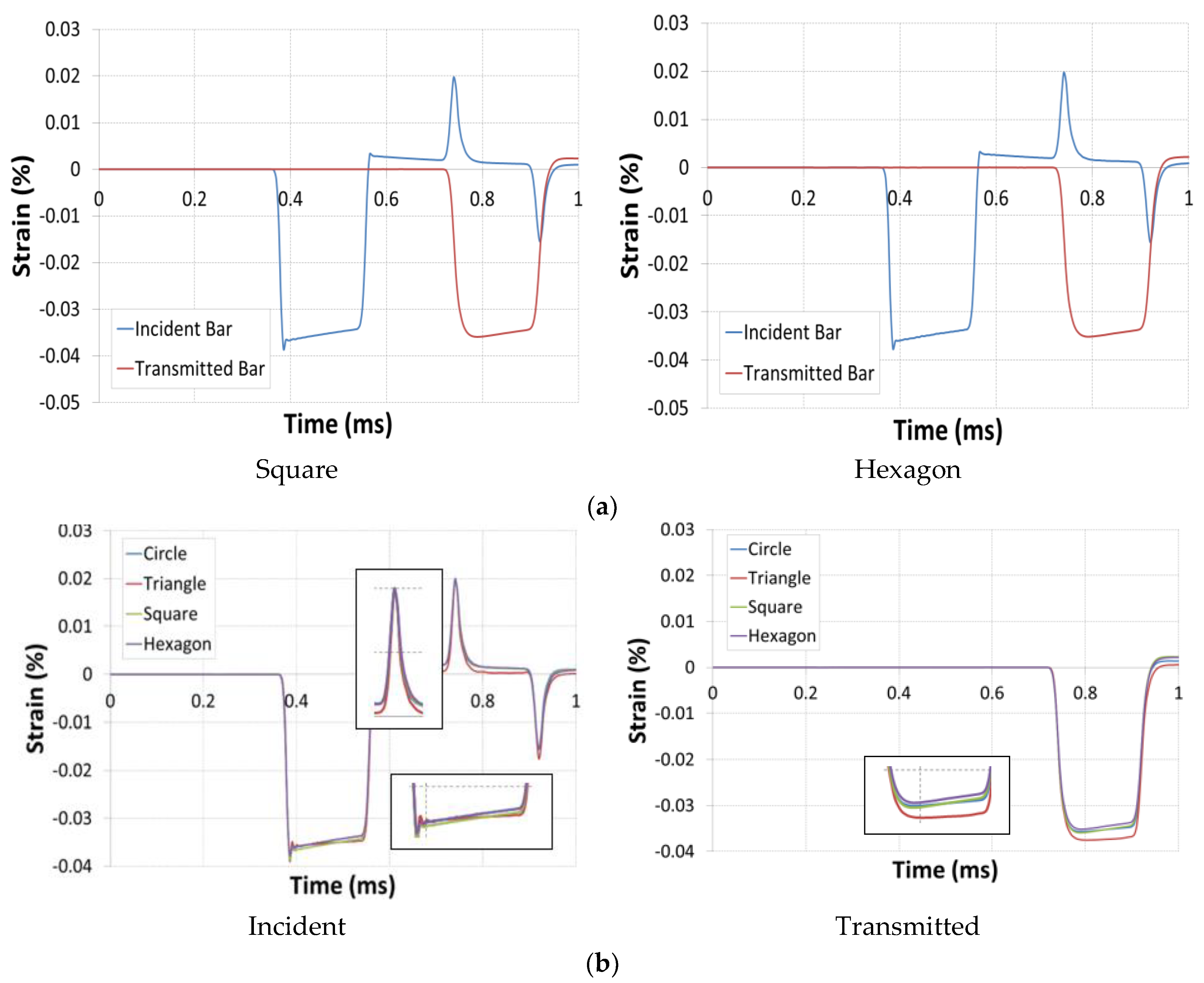
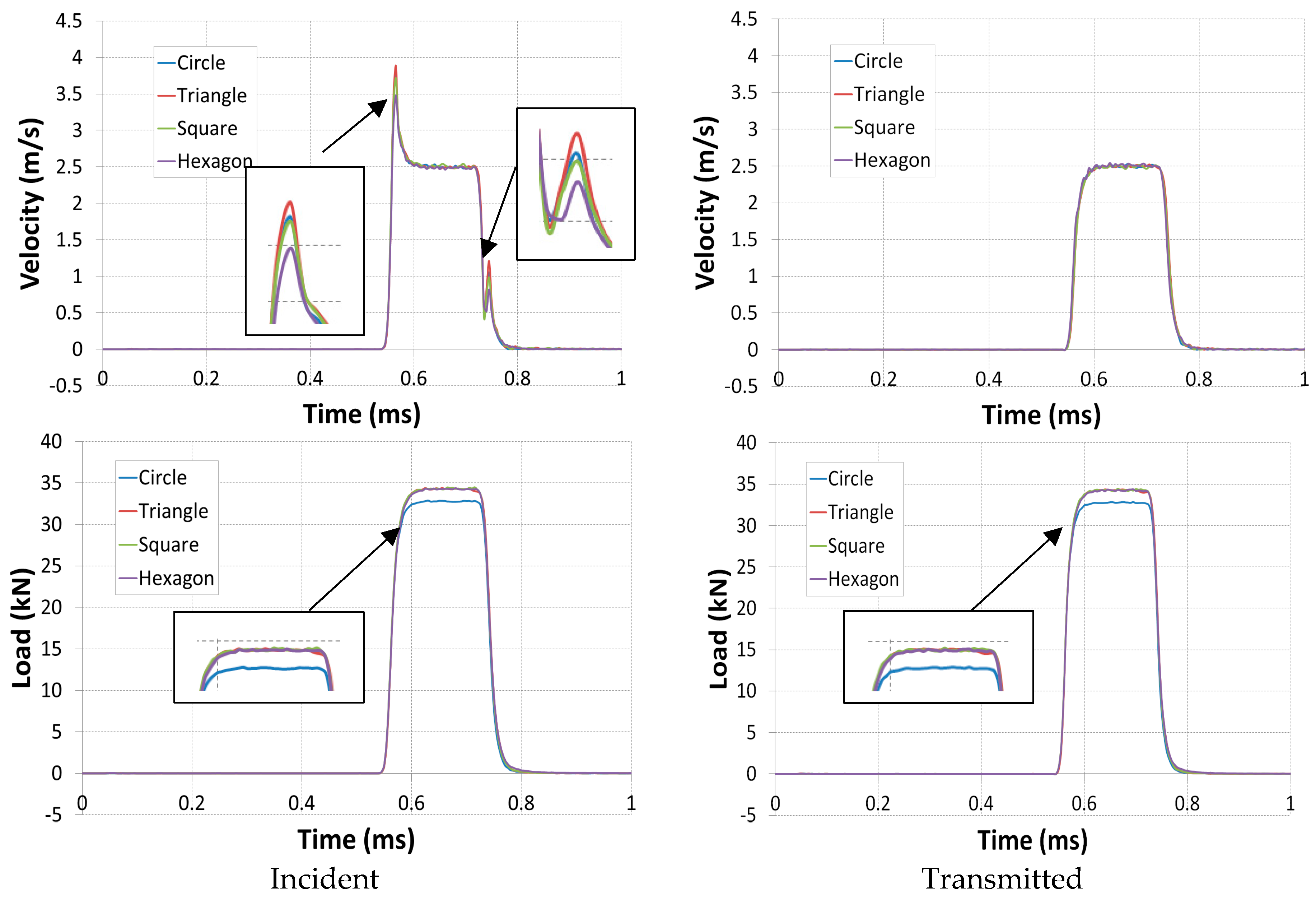
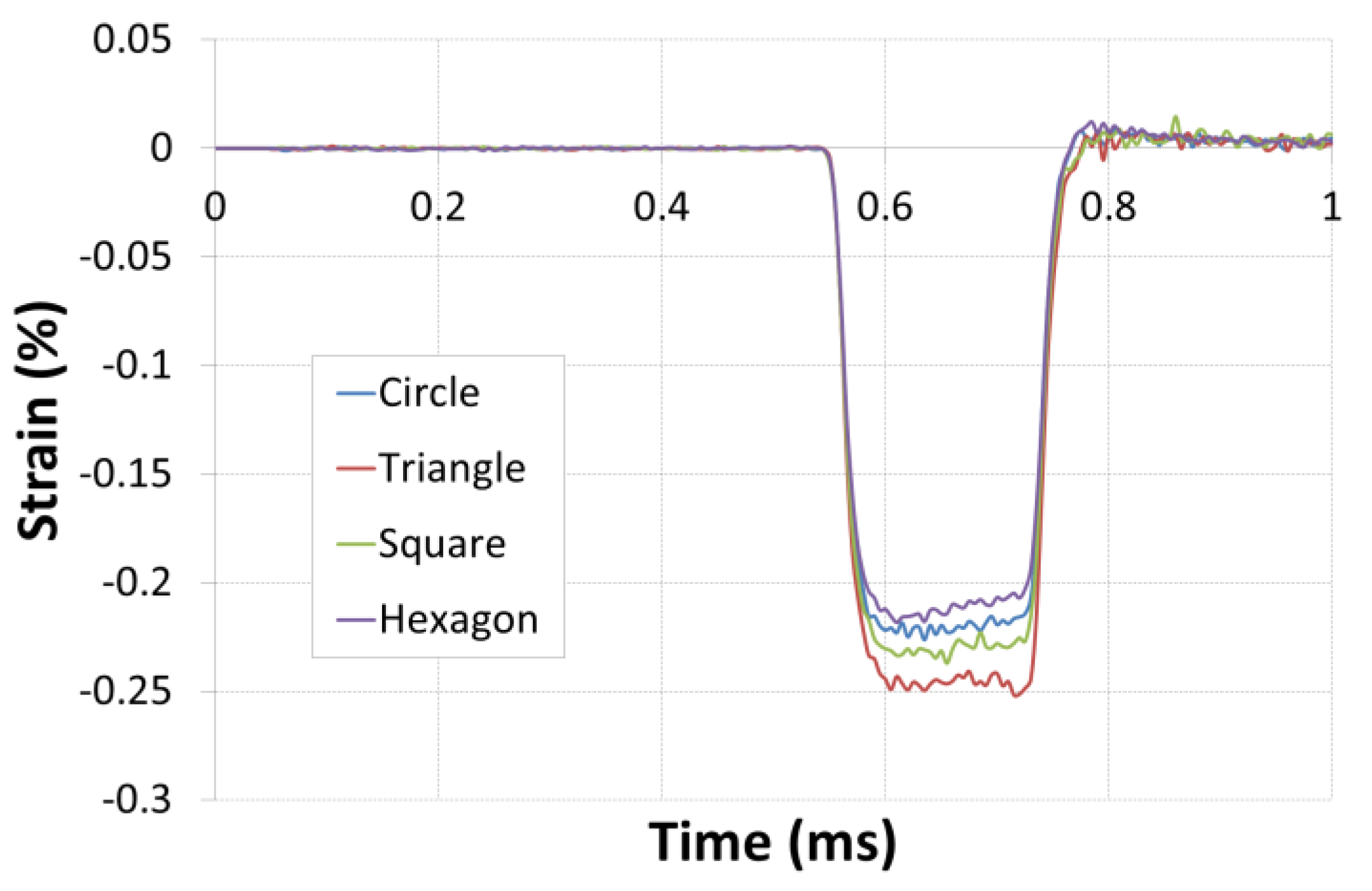
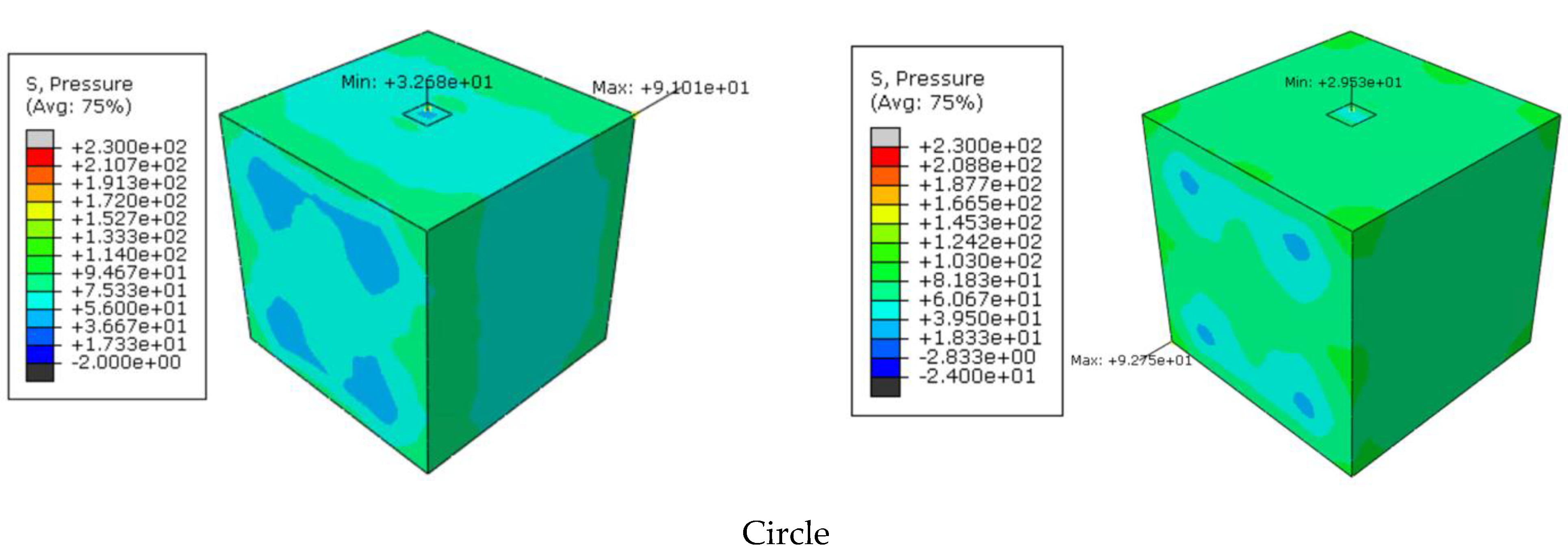
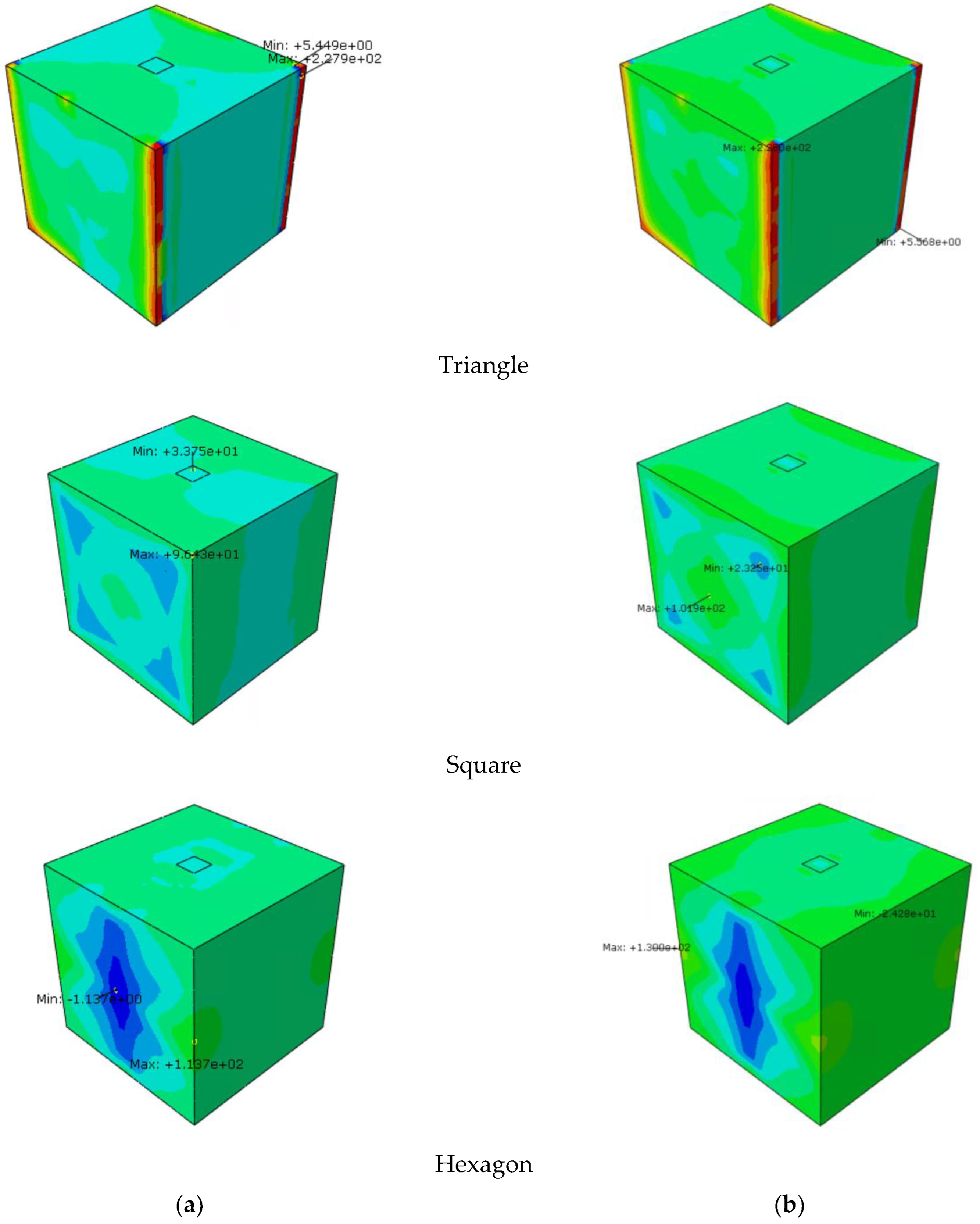
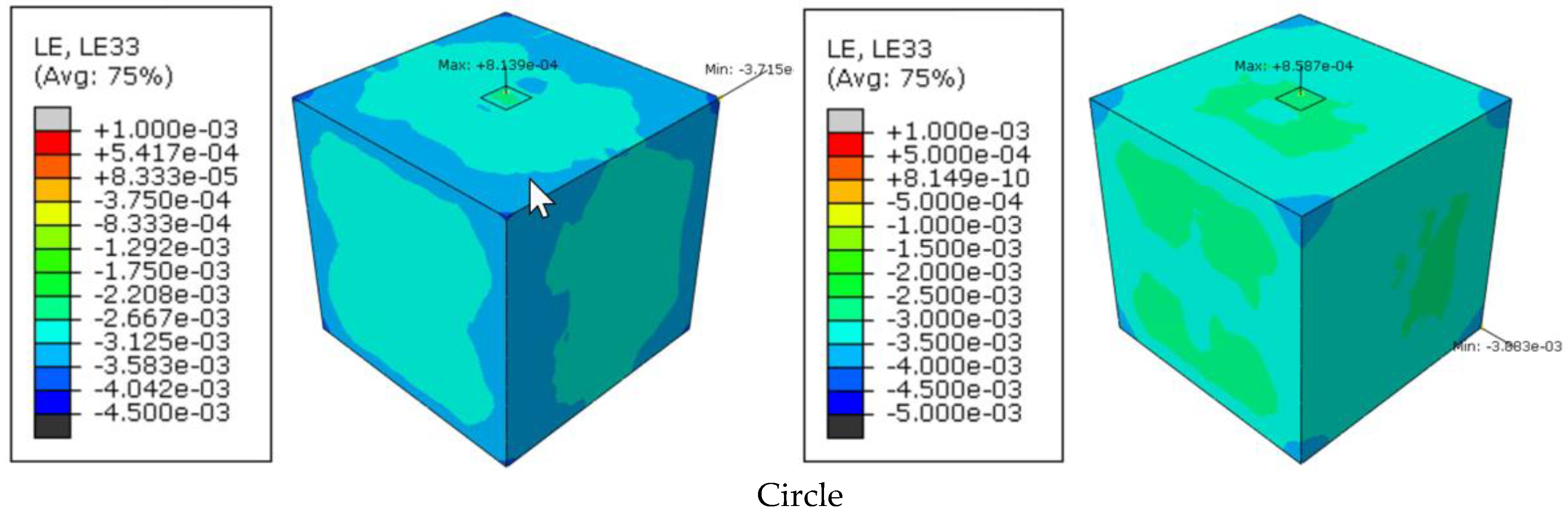
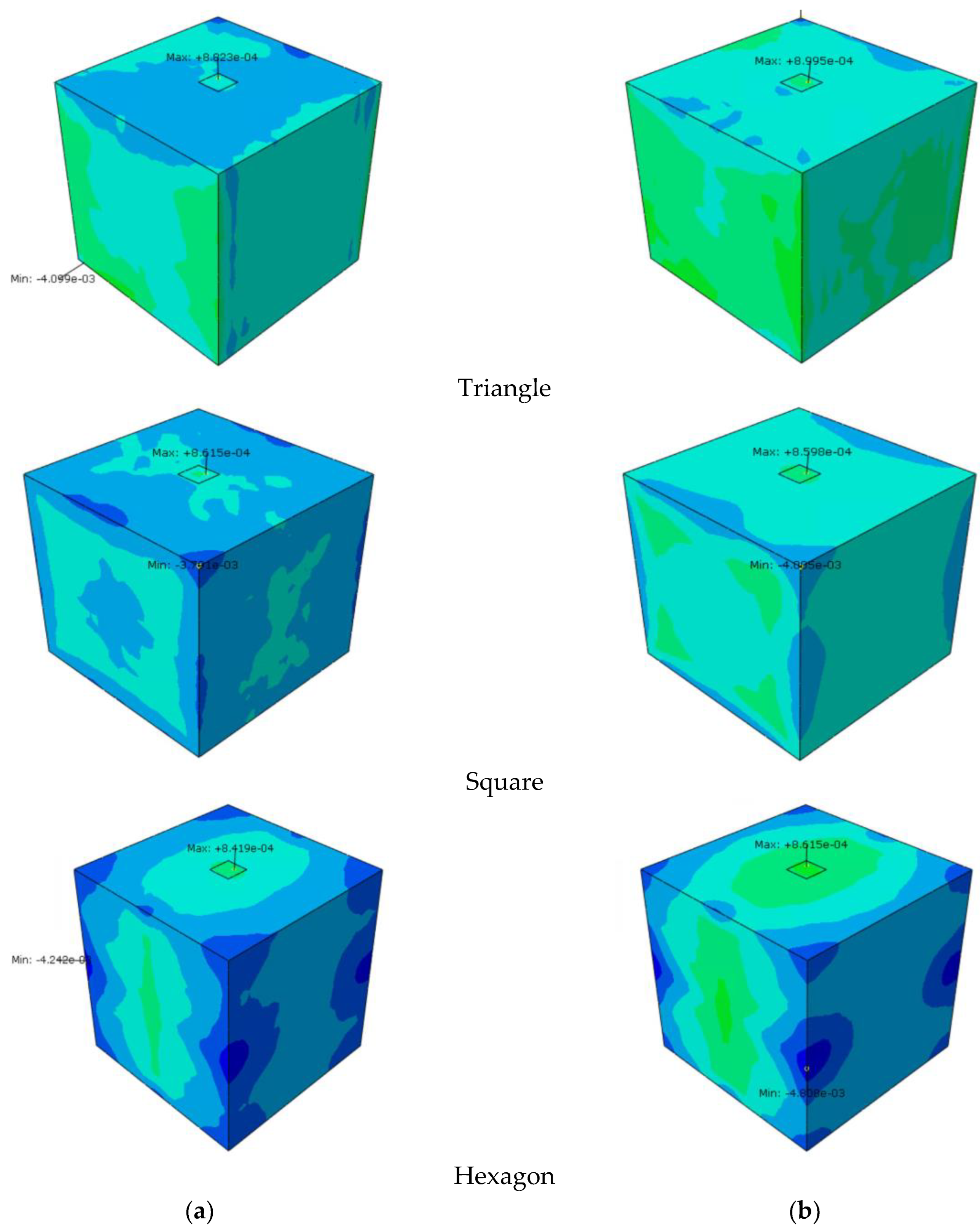
4.2. Results and Discussion
- Analysis of the incident, transmitted and reflected waves by placing skin elements of negligible thickness used to model the two gauges J1 and J2 placed, respectively, on the input and output bars. These skins were modelled using the mesh with membrane elements M3D4R (four-node quadrilateral membrane, reduced integration, hourglass control).
- The initial velocity conditions were applied to all nodes of the striker volume. The value of this velocity is fixed at V = 5 m/s.
- For initial boundary conditions, only one movement in the z-direction is allowed for the striker and the bars.
- The different physical parameters of strains, velocities, and loads are determined by the numerical model and compared for the different geometries.
- The incident “Fi” and transmitted “Ft” loads are determined, respectively, at the incident bar/sample and transmitted bar/sample interfaces.
- Similarly, the incident “Vi” and transmitted “Vt” velocities are determined, respectively, at the incident bar/sample and transmitted bar/sample interfaces.
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hopkinson, B. A Method of Measuring the Pressure Produced in the Detonation of High Explosives or by the Impact of Bullets. Philos. Trans. R. Soc. Lond. 1914, 213, 437–456. [Google Scholar]
- Davies, R.M.; Taylor, G.I. A critical study of the Hopkinson pressure bar. Philos. Trans. R. Soc. Lond. 1948, 240, 375–457. [Google Scholar] [CrossRef]
- Kolsky, H. An Investigation of the Mechanical Properties of Materials at very High Rates of Loading. Proc. Phys. Soc. Sect. B 1949, 62, 676–700. [Google Scholar] [CrossRef]
- Sassi, S.; Tarfaoui, M.; BenYahia, H. In-situ heat dissipation monitoring in adhesively bonded composite joints under dynamic compression loading using SHPB. Compos. Part B Eng. 2018, 54, 64–76. [Google Scholar] [CrossRef]
- Tarfaoui, M.; Nachtane, M.; El Moumen, A. Energy dissipation of stitched and unstitched woven composite materials during dynamic compression test. Compos. Part B Eng. 2019, 167, 487–496. [Google Scholar] [CrossRef]
- Tarfaoui, M.; Choukri, S.; Nême, A. Dynamic response of symmetric and asymmetric e-glass/epoxy laminates at high strain rates. Key Eng. Mater. 2010, 446, 73–82. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Chen, W. Pulse shaping techniques for testing elastic-plastic materials with a split Hopkinson pressure bar. Exp. Mech. 2005, 45, 186. [Google Scholar] [CrossRef]
- Qi, F. Issues of SHPB test on concrete-like material. Eng. Mech. 2014, 31, 1–14+26. [Google Scholar]
- Pankow, M.; Attard, C.; Waas, A.M. Specimen size and shape effect in split Hopkinson pressure bar testing. J. Strain Anal. Eng. Des. 2009, 44, 689–698. [Google Scholar] [CrossRef]
- Gueraiche, L.; Tarfaoui, M.; Osmani, H.; El Malki, A. A practical note for SHPB test with new algorithms for delimiting pulses. Compos. Struct. 2015, 126, 145–158. [Google Scholar]
- Song, B.; Syn, C.J.; Grupido, C.L.; Chen, W.; Lu, W.Y. A Long Split Hopkinson Pressure Bar (LSHPB) for Intermediate-rate Characterisation of Soft Materials. Exp. Mech. 2007, 48, 809. [Google Scholar] [CrossRef]
- Chihi, M.; Tarfaoui, M.; Qureshi, Y.; Benyahia, H.; Bouraoui, V. Graphene Nanofillers as a Player to Improve the Dynamic Compressive Response and Failure Behaviour of carbon/epoxy Composite. Nanotechnology 2020, 31, 425709. [Google Scholar] [CrossRef] [PubMed]
- Song, B.; Chen, W.; GE, Y.; Weerasooriya, T. Dynamic and quasi-static compressive response of porcine muscle. J. Biomech. 2007, 40, 2999–3005. [Google Scholar] [CrossRef]
- Gray, G.T.; Blumenthal, W.R. Split-Hopkinson Pressure Bar Testing of Soft Materials. Mech. Test. Eval. 2000, 8, 488–496. [Google Scholar] [CrossRef]
- Chen, W.; Subhash, G.; Ravichandran, G. Evaluation of Ceramic Specimen Geometries Used in a Split Hopkinson Pressure Bar. Dymat J. 1994, 1, 193–210. [Google Scholar]
- Rahmani, K.; Majzoobi, G.H.; Atrian, A. A novel approach for dynamic compaction of Mg-SiC nanocomposite powder using a modified Split Hopkinson Pressure Bar. Powder Metall. 2018, 61, 164–177. [Google Scholar] [CrossRef]
- Chihi, M.; Tarfaoui, M.; Qureshi, Y.; Bouraoui, C.; Benyahia, H. Effect of Carbon Nanotubes on the In-plane Dynamic Behaviour of a Carbon/Epoxy Composite under high strain rate compression using SPHB. Smart Mater. Struct. 2020, 29, 085012. [Google Scholar] [CrossRef]
- Song, B.; Chen, W.; Frew, D.J. Dynamic compressive response and failure behaviour of an epoxy syntactic foam. J. Compos. Mater. 2004, 38, 915–936. [Google Scholar] [CrossRef]
- Chen, W.; Lu, F.; Cheng, M. Tension and compression tests of two polymers under quasi-static and dynamic loading. Polym. Test. 2002, 21, 113–121. [Google Scholar] [CrossRef]
- Li, Z.; Lambros, J. Strain rate effects on the thermomechanical behaviour of polymers. Int. J. Solids Struct. 2001, 38, 3549–3562. [Google Scholar] [CrossRef]
- El-Habak, A.M.A. Mechanical behaviour of woven glass fibre-reinforced composites under impact compression load. Composites 1991, 22, 129–134. [Google Scholar] [CrossRef]
- Tarfaoui, M.; Nême, A.; Choukri, S. Damage kinetics of glass/epoxy composite materials under dynamic compression. J. Compos. Mater. 2009, 43, 1137–1154. [Google Scholar] [CrossRef]
- Arbaoui, J.; Tarfaoui, M.; Alaoui, A.E.M. Mechanical behaviour and damage kinetics of woven E-glass/vinylester laminate composites under high strain rate dynamic compressive loading: Experimental and numerical investigation. Int. J. Impact Eng. 2016, 87, 44–54. [Google Scholar] [CrossRef]
- Arbaoui, J.; Tarfaoui, M.; El Malki Alaoui, A. Dynamical characterisation and damage mechanisms of E-glass/vinylester woven composites at high strain rates compression. J. Compos. Mater. 2016, 50, 3313–3323. [Google Scholar] [CrossRef]
- Allen Ross, C.; Tedesco, W.; Kuennen, T. Effects of strain rate on concrete strength. Mater. J. 1995, 92, 37–47. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, H.J.; Li, Q.M.; Huang, F.L. Further investigation on the dynamic compressive strength enhancement of concrete-like materials based on split Hopkinson pressure bar tests. Part I: Experiments. Int. J. Impact Eng. 2009, 36, 1327–1334. [Google Scholar] [CrossRef]
- Wang, P.T.; Shah, S.P.; Naaman, A.E. High-strength concrete in ultimate strength design. J. Struct. Eng. 1978, 104, 1761–1773. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Zhou, J. Experimental and modeling study of dynamic mechanical properties of cement paste, mortar and concrete. Constr. Build. Mater. 2013, 47, 419–430. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Chen, W. Pulse shaping techniques for testing brittle materials with a split Hopkinson pressure bar. Exp. Mech. 2002, 42, 93–106. [Google Scholar] [CrossRef]
- Du, X.L.; Wang, Y. Non-linear uniaxial dynamic strength criterion for concrete. Shuili Xuebao J. Hydraul. Eng. 2010, 41, 300–309. [Google Scholar]
- Woldesenbet, E.; Vinson, J.R. Specimen Geometry Effects on High-Strain-Rate Testing of Graphite/Epoxy Composites. AIAA J. 1999, 37, 1102–1106. [Google Scholar] [CrossRef]
- Davies, E.D.H.; Hunter, S.C. The dynamic compression testing of solids by the method of the split Hopkinson pressure bar. J. Mech. Phys. Solids 1963, 11, 155–179. [Google Scholar] [CrossRef]
- Challita, G.; Othman, R. Finite-element analysis of SHPB tests on double-lap adhesive joints. Int. J. Adhes. Adhes. 2010, 30, 236–244. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Cargile, J.D. The effect of concrete target diameter on projectile deceleration and penetration depth. Int. J. Impact Eng. 2006, 32, 1584–1594. [Google Scholar] [CrossRef]
- Frew, D.J.; Hanchak, S.J.; Green, M.L.; Forrestal, M.J. Penetration of concrete targets with ogive-nose steel rods. Int. J. Impact Eng. 1998, 21, 489–497. [Google Scholar] [CrossRef]
- Lu, Y.B.; Li, Q.M. Appraisal of Pulse-Shaping Technique in Split Hopkinson Pressure Bar Tests for Brittle Materials. Int. J. Prot. Struct. 2010, 1, 363–390. [Google Scholar] [CrossRef]
- Lee, O.S.; Kim, S.H.; Han, Y.H. Thickness effect of pulse shaper on dynamic stress equilibrium and dynamic deformation behaviour in the polycarbonate using SHPB technique. J. Exp. Mech. 2006, 21, 51–60. [Google Scholar]
- Abotula, S.; Chalivendra, V. Effect of Aspect Ratio of Cylindrical Pulse shapers on Force Equilibrium in Hopkinson Pressure Bar Experiments. In Proceedings of the Society for Experimental Mechanics—SEM Annual Conference and Exposition on Experimental and Applied Mechanics, Indianapolis, IN, USA, 7–10 June 2010; Volume 3, pp. 453–461. [Google Scholar]
- Heard, W.F.; Martin, B.E.; Nie, X.; Slawson, T.; Basu, P.K. Annular Pulse Shaping Technique for Large-Diameter Kolsky Bar Experiments on Concrete. Exp. Mech. 2014, 54, 1343–1354. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Z.; Liu, D.; Zou, Y.; Yin, T. Wave shaping by special shaped striker in SHPB tests. In Advances in Rock Dynamics and Applications; CRC Press: Boca Raton, FL, USA, 2011; pp. 105–124. [Google Scholar]
- Li, X.; Zou, Y.; Zhou, Z. Numerical Simulation of the Rock SHPB Test with a Special Shape Striker Based on the Discrete Element Method. Rock Mech. Rock Eng. 2014, 47, 1693–1709. [Google Scholar] [CrossRef]
- Cloete, T.; Westhuizen, A.V.D.; Kok, S.; Nurick, G.A. Tapered striker pulse shaping technique for uniform strain rate dynamic compression of bovine bone. EDP Sci. 2009, 1, 901–907. [Google Scholar]
- Vecchio, K.S.; Jiang, F. Improved Pulse Shaping to Achieve Constant Strain Rate and Stress Equilibrium in Split-Hopkinson Pressure Bar Testing. Metall. Mater. Trans. A 2007, 38, 2655–2665. [Google Scholar] [CrossRef]
- Baranowski, P.; MbBachowski, J.; Gieleta, R.; Damaziak, K.; Mazurkiewicz, L.L.; KoBodziejczyk, D. Numerical study for determination of pulse shaping design variables in SHPB apparatus. Bulletin of the Polish Academy of Sciences. Tech. Sci. 2013, 61, 459–466. [Google Scholar]

| Panel | Thickness, (mm) | Surface (mm2) | Void Fraction (%) | Stacking Sequence | Fibre Volume Fraction (%) |
|---|---|---|---|---|---|
| A | 12.52 (0.3) | 13 × 13 | 2.00 | [±20]20 | 54.0 |
| B | 13.00 (0.1) | 13 × 13 | 1.78 | [±60]20 | 55.0 |
| C | 13.00 (0.1) | 13 × 13 | 2.26 | [90]40 | 53.5 |
| Density (kg/m3) | E1 (MPa) | E2 (MPa) | E3 (MPa) | G12 (MPa) | G13 (MPa) | G23 (MPa) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1840 | 46,217 | 16,086 | 9062 | 0.28 | 0.41 | 0.097 | 2224 | 3500 | 4540 |
| Material | Young’s Modulus E (MPa) | Poisson’s Ratio, ν | Density, (kg/m3) |
|---|---|---|---|
| Steel (striker and bars) | 182,000 | 0.32 | 7800 |
| Aluminium (sample) | 70,000 | 0.35 | 2700 |
| Shape | Dimension (mm) | Surface (mm2) | Sketch |
|---|---|---|---|
| Circle (SHPB-C) | R = 10 | 314 | 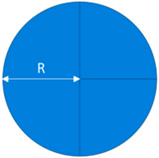 |
| Triangle (SHPB-T) | B = 26.94 H = 23.33 | 314 |  |
| Square (SHPB-S) | c = 17.7246 | 314 |  |
| Hexagon (SHPB-H) | a = 11 H = 22 V = 19.0526 | 314 |  |
| Shape | Advantage | Disadvantages |
|---|---|---|
| Circle (SHPB-C) |
|
|
| Triangle (SHPB-T) |
|
|
| Square (SHPB-S) |
|
|
| Hexagon (SHPB-H) |
|
|
| Mass (kg) | Circle | Triangle | Square | Hexagone |
|---|---|---|---|---|
| Striker | 1.23 | 1.23 | 1.23 | 1.23 |
| IB | 7.35 | 7.35 | 7.35 | 7.36 |
| OB | 4.9 | 4.9 | 4.9 | 4.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarfaoui, M. Dynamic Composite Materials Characterisation with Hopkinson Bars: Design and Development of New Dynamic Compression Systems. J. Compos. Sci. 2023, 7, 33. https://doi.org/10.3390/jcs7010033
Tarfaoui M. Dynamic Composite Materials Characterisation with Hopkinson Bars: Design and Development of New Dynamic Compression Systems. Journal of Composites Science. 2023; 7(1):33. https://doi.org/10.3390/jcs7010033
Chicago/Turabian StyleTarfaoui, Mostapha. 2023. "Dynamic Composite Materials Characterisation with Hopkinson Bars: Design and Development of New Dynamic Compression Systems" Journal of Composites Science 7, no. 1: 33. https://doi.org/10.3390/jcs7010033
APA StyleTarfaoui, M. (2023). Dynamic Composite Materials Characterisation with Hopkinson Bars: Design and Development of New Dynamic Compression Systems. Journal of Composites Science, 7(1), 33. https://doi.org/10.3390/jcs7010033






