Measurement of the Heat Transfer Properties of Carbon Fabrics via Infrared Thermal Mapping
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Measurement of the Specific Heat Capacity
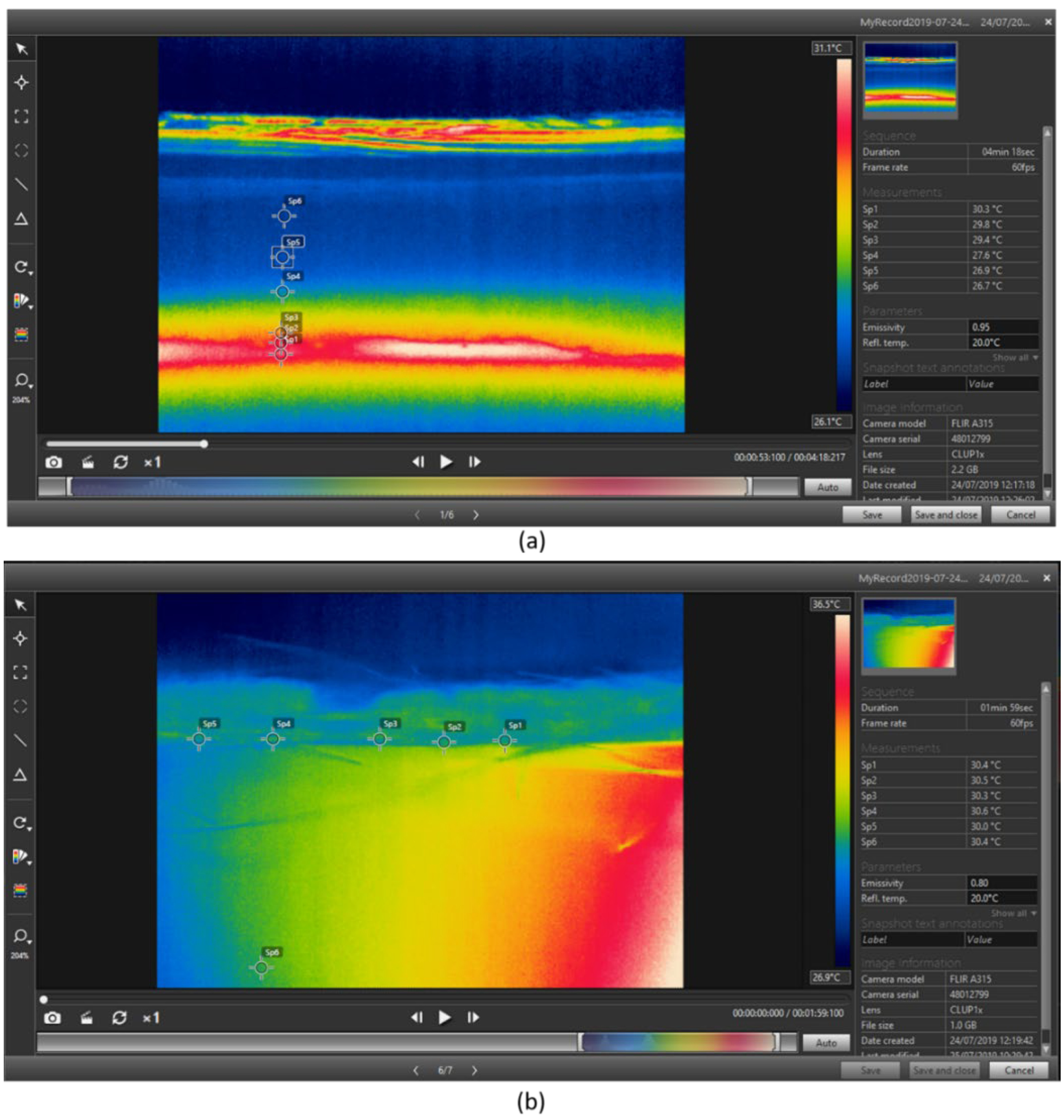
2.3. Measurement of the Thermal Conductivity
3. Results and Discussion
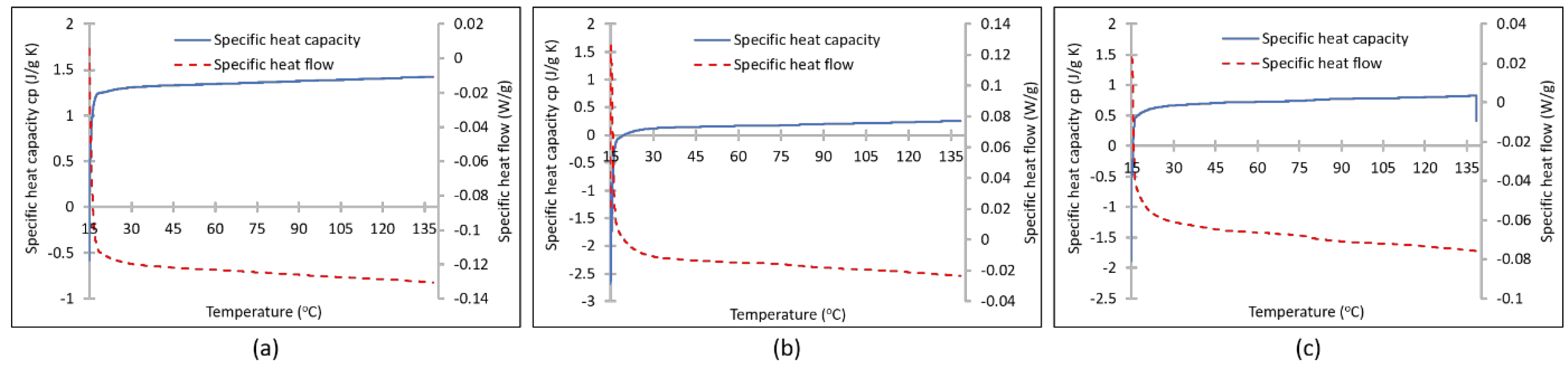
3.1. Results of Specific Heat Capacity
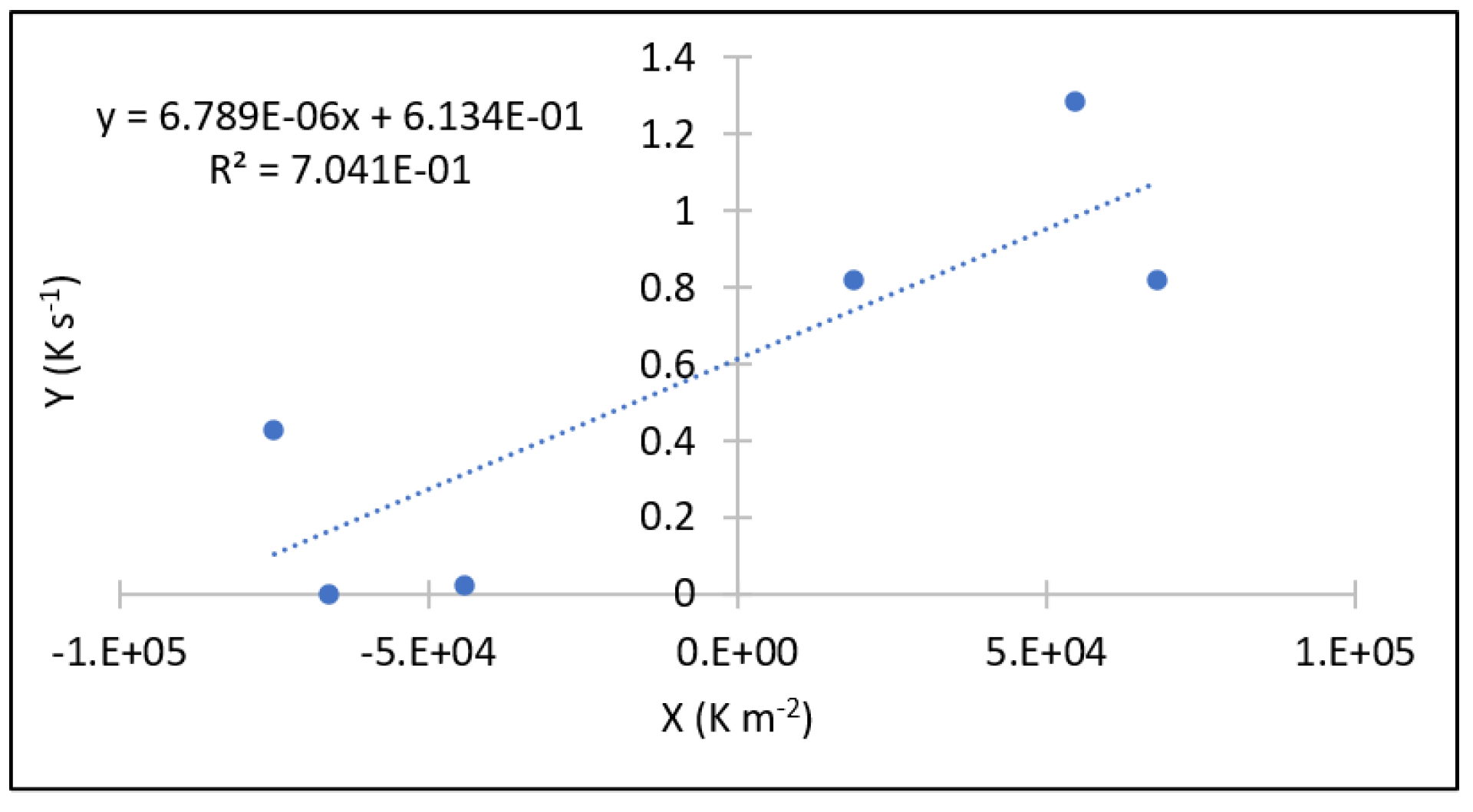
3.2. Results of Thermal Conductivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moll, P.; Ohlberg, L.; Salzer, S.; Coutandin, S.; Fleischer, J. Integrated gripping-system for heating and preforming of thermoplastic unidirectional tape laminates. Procedia CIRP 2019, 85, 266–271. [Google Scholar] [CrossRef]
- Brody, J.C.; Gillespie, J.W. The effects of a thermoplastic polyester preform binder on vinyl ester resin. J. Thermoplast. Comp. Mat. 2005, 18, 157–179. [Google Scholar] [CrossRef]
- Yoo, H.M.; Lee, J.W.; Kim, J.S.; Um, M.K. Influence of non-reactive epoxy binder on the permeability and friction coefficient of twill-woven carbon fabric in the liquid composite molding process. Appl. Sci. 2020, 10, 7039. [Google Scholar] [CrossRef]
- Schmidt, S.; Mahrholz, T.; Kühn, A.; Wierach, P. Powder binders used for the manufacturing of wind turbine rotor blades. Part 1. Characterization of resin-binder interaction and preform properties. Polym. Compos. 2018, 39, 708–717. [Google Scholar] [CrossRef]
- Kappel, E.; Albrecht, M. A controlled recipient evacuation process to form composite profiles from flat multi-angle prepreg stacks-infrastructure and C-profile verification. Adv. Manuf. Polym. Comp. Sci. 2019, 5, 140–154. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; McGregor, O.P.L.; Endruweit, A.; Elsmore, M.T.; De Focatiis, D.S.A.; Harper, L.T.; Warrior, N.A. Double diaphragm forming simulation for complex composite structures. Compos. A Appl. Sci. Manuf. 2017, 95, 346–358. [Google Scholar] [CrossRef]
- Sun, J.; Gu, Y.; Li, M.; Ma, X.; Zhang, Z. Effect of forming temperature on the quality of hot diaphragm formed C-shaped thermosetting composite laminates. J. Reinf. Plast. Comp. 2012, 31, 1074–1087. [Google Scholar] [CrossRef]
- Wakeman, M.; Rudd, C.D. Compression moulding of glass and polypropylene composites for optimised macro- and micro-mechanical properties—1 Commingled glass and polypropylene. Comp. Sci. Technol. 1998, 58, 1879–1898. [Google Scholar] [CrossRef]
- Bader, M.G.; Lekakou, C. Processing for laminated structures. In Composites Engineering Handbook; Mallick, P.K., Ed.; CRC Press: Boca Raton, FL, USA, 1997; pp. 371–479. [Google Scholar]
- Rutt, M.; Lekakou, C.; Smith, P.A.; Sordon, A.; Santoni, C.; Meeks, G.; Hamerton, I. Methods for process-related resin selection and optimisation in high-pressure resin transfer moulding. Mater. Sci. Technol. 2019, 35, 327–335. [Google Scholar] [CrossRef]
- Liu, B.; Bickerton, S.; Advani, S.G. Modelling and simulation of resin transfer moulding (RTM)—gate control, venting and dry spot prediction. Compos. A Appl. Sci. Manuf. 1996, 27, 135–141. [Google Scholar] [CrossRef]
- Xia, C.; Shi, S.Q.; Cai, L. Vacuum-assisted resin infusion (VARI) and hot pressing for CaCO3 nanoparticle treated kenaf fiber reinforced composites. Compos. B Eng. 2015, 78, 138–143. [Google Scholar] [CrossRef]
- Oromiehie, E.; Gangadhara Prusty, B.; Compston, P.; Rajan, G. Automated fibre placement based composite structures: Review on the defects, impacts and inspections techniques. Compos. Struct. 2019, 224, 110987. [Google Scholar] [CrossRef]
- Lichtinger, R.; Hörmann, P.; Stelzl, D.; Hinterhölzl, R. The effects of heat input on adjacent paths during Automated Fibre Placement. Compos. A Appl. Sci. Manuf. 2015, 68, 387–397. [Google Scholar] [CrossRef]
- Tafreshi, O.A.; Van Hoa, S.; Shadmehri, F.; Hoang, D.M.; Rosca, D. Heat transfer analysis of automated fiber placement of thermoplastic composites using a hot gas torch. Adv. Manuf. Polym. Comp. Sci. 2019, 5, 206–223. [Google Scholar] [CrossRef] [Green Version]
- Nardi, D.; Sinke, J. Design analysis for thermoforming of thermoplastic composites: Prediction and machine learning-based optimization. Compos. C Open Access 2021, 5, 100126. [Google Scholar] [CrossRef]
- Längauer, M.; Zitzenbacher, G.; Burgstaller, C.; Hochenauer, C. Enhanced infrared heating of thermoplastic composite sheets for thermoforming processes. Int. Polym. Proc. 2021, 36, 35–43. [Google Scholar] [CrossRef]
- Babeau, A.; Comas-Cardona, S.; Binetruy, C.; Orange, G. Modeling of heat transfer and unsaturated flow in woven fiber reinforcements during direct injection-pultrusion process of thermoplastic composites. Compos. A Appl. Sci. Manuf. 2015, 77, 310–318. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.L.; Crouch, I.G.; Lam, Y.C. Simulation of heat transfer and cure in pultrusion with a general-purpose finite element package. Compos. Sci. Technol. 2000, 60, 857–864. [Google Scholar] [CrossRef]
- Choo, H.L.; Martin, P.J.; Harkin-Jones, E.M.A. Measurement of heat transfer for thermoforming simulations. Int. J. Mater. Form. 2008, 1, 1027–1030. [Google Scholar] [CrossRef]
- Tranchard, P.; Samyn, F.; Duquesne, S.; Estèbe, B.; Bourbigot, S. Modelling behaviour of a carbon epoxy composite exposed to fire: Part I—characterisation of thermophysical properties. Materials 2017, 10, 494. [Google Scholar] [CrossRef] [Green Version]
- Bard, S.; Schönl, F.; Demleitner, M.; Altstädt, V. Influence of fiber volume content on thermal conductivity in transverse and fiber direction of carbon fiber-reinforced epoxy laminates. Materials 2019, 12, 1084. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kinloch, I.A.; Suhr, J.; Lou, J.; Young, R.J.; Ajayan, P.M. Composites with carbon nanotubes and graphene: An outlook. Science 2018, 362, 547–553. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lei, C.; Lekakou, C. Activated carbon–carbon nanotube nanocomposite coatings for supercapacitor applications. Surf. Coat. Technol. 2013, 232, 326–330. [Google Scholar] [CrossRef]
- Vermisoglou, E.C.; Giannakopoulou, T.; Romanos, G.; Boukos, N.; Psycharis, V.; Lei, C.; Lekakou, C.; Petridis, D.; Trapalis, C. Graphene-based materials via benzidine-assisted exfoliation and reduction of graphite oxide and their electrochemical properties. Appl. Surf. Sci. 2017, 392, 244–255. [Google Scholar] [CrossRef]
- Murugesh, A.K.; Uthayanan, A.; Lekakou, C. Electrophoresis and orientation of multiple wall carbon nanotubes in polymer solution. Appl. Phys. A 2010, 100, 135–144. [Google Scholar] [CrossRef]
- Salifu, A.A.; Nury, B.D.; Lekakou, C. Electrospinning of nanocomposite fibrillar tubular and flat scaffolds with controlled fiber orientation. Ann. Biomed. Eng. 2011, 39, 2510–2520. [Google Scholar] [CrossRef] [Green Version]
- Ashby, M.F. Chapter 11—Designing hybrid materials. In Materials Selection in Mechanical Design, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 299–340. [Google Scholar]
- Gibson, R.F. Micromechanics. In Composites Engineering Handbook; Mallick, P.K., Ed.; CRC Press: Boca Raton, FL, USA, 1997; pp. 167–202. [Google Scholar]
- Paul, B. Prediction of elastic constants of multi-phase materials. Trans. AIME 1960, 218, 36–41. [Google Scholar]
- Hind, S.; Robitaille, F. Measurement, modeling, and variability of thermal conductivity for structural polymer composites. Polym. Compos. 2010, 31, 847–857. [Google Scholar] [CrossRef]
- Clayton, W.A. Constituent and composite thermal conductivities of phenolic-carbon and phenolic-graphite ablators. In Proceedings of the AIAA/ASME 12th Structures, Structural Dynamics and Materials Conference, Anaheim, CA, USA, 19–21 April 1971; pp. 1–17. [Google Scholar]
- El-Hage, Y.; Hind, S.; Robitaille, F. Thermal conductivity of textile reinforcements for composites. J. Text. Fibrous Mater. 2018, 1, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Pope, J.; Lekakou, C. Thermoelectric polymer composite yarns and an energy harvesting wearable textile. Smart Mater. Struct. 2019, 28, 095006. [Google Scholar] [CrossRef]
- Lekakou, C.N.; Richardson, S.M. Simulation of reacting flow during filling in reaction injection molding (RIM). Polym. Eng. Sci. 1986, 26, 1264–1275. [Google Scholar] [CrossRef]
- Elsayed, Y.; Lekakou, C.; Tomlins, P. Modeling, simulations, and optimization of smooth muscle cell tissue engineering for the production of vascular grafts. Biotechnol. Bioeng. 2019, 116, 1509–1522. [Google Scholar] [CrossRef]
- Keerthi Sagar, S.N.; Sreekumar, M. Miniaturized flexible flow pump using SMA actuator. Procedia Eng. 2013, 64, 896–906. [Google Scholar] [CrossRef] [Green Version]
- Bastiurea, M.; Rodeanu Bastiurea, M.S.; Andrei, G.; Dima, D.; Murarescu, M.; Ripa, M.; Circiumaru, A. Determination of specific heat of polyester composite with graphene and graphite by differential scanning calorimetry. Tribol. Ind. 2014, 36, 419–427. [Google Scholar]
- Carvill, J. 3-Thermodynamics and heat transfer. In Mechanical Engineer′s Handbook; Elsevier: Amsterdam, The Netherlands, 1994; pp. 102–145. [Google Scholar]
- Chamis, C.C. Simplified composite micromechanics equations for strength, fracture toughnss and environmental effects. In Proceedings of the 39th Annual Conference, Reinforced Plastics/Composites Institute, New York, NY, USA, 16–19 January 1984; Society of Plastics Industry Inc.: Houston, TX, USA; pp. 1–16. [Google Scholar]
- Klett, J.W.; Edie, D.D. Flexible towpreg for the fabrication of high thermal conductivity carbon/carbon composites. Carbon 1995, 33, 1485–1503. [Google Scholar] [CrossRef]
- Ning, Q.G.; Chou, T.W. A closed-form solution of the transverse effective thermal conductivity of woven fabric composites. J. Compos. Mater. 1995, 29, 2280–2294. [Google Scholar] [CrossRef]
- Gaier, J.R.; Yodervandenberg, Y.; Berkebile, S.; Stueben, H.; Balagadde, F. The electrical and thermal conductivity of woven pristine and intercalated graphite fiber–polymer composites. Carbon 2003, 41, 2187–2193. [Google Scholar] [CrossRef] [Green Version]
- Dasgupta, A.; Agarwal, R.K.; Bhandarkar, S.M. Three-dimensional modeling of woven-fabric composites for effective thermo-mechanical and thermal properties. Compos. Sci. Technol. 1996, 56, 209–223. [Google Scholar] [CrossRef]
- Air-Thermal Conductivity, vs. Temperature and Pressure. The Engineering ToolBox. Available online: https://www.engineeringtoolbox.com/air-properties-viscosity-conductivity-heat-capacity-d_1509.html (accessed on 2 December 2021).
- Amico, S.; Lekakou, C. Flow through a two-scale porosity, oriented fibre porous medium. Transp. Porous Media 2004, 54, 35–53. [Google Scholar] [CrossRef]





| Thermal Conductivity (W m−1 K−1) | NCF300-Biaxial | Plain Weave | 4 × 4 Twill Weave | 5H Satin Weave |
|---|---|---|---|---|
| kT experimental | 0.070 ± 0.007 | 0.05 ± 0.02 | 0.04 ± 0.02 | 0.004 ± 0.003 |
| kT theoretical | 0.063 | 0.069 | 0.057 | 0.065 |
| kll experimental | 2.9 ± 0.4 | |||
| kll theoretical | 2.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kearney, P.; Lekakou, C.; Belcher, S. Measurement of the Heat Transfer Properties of Carbon Fabrics via Infrared Thermal Mapping. J. Compos. Sci. 2022, 6, 155. https://doi.org/10.3390/jcs6060155
Kearney P, Lekakou C, Belcher S. Measurement of the Heat Transfer Properties of Carbon Fabrics via Infrared Thermal Mapping. Journal of Composites Science. 2022; 6(6):155. https://doi.org/10.3390/jcs6060155
Chicago/Turabian StyleKearney, Phillip, Constantina Lekakou, and Stephen Belcher. 2022. "Measurement of the Heat Transfer Properties of Carbon Fabrics via Infrared Thermal Mapping" Journal of Composites Science 6, no. 6: 155. https://doi.org/10.3390/jcs6060155
APA StyleKearney, P., Lekakou, C., & Belcher, S. (2022). Measurement of the Heat Transfer Properties of Carbon Fabrics via Infrared Thermal Mapping. Journal of Composites Science, 6(6), 155. https://doi.org/10.3390/jcs6060155






