Analytical Solution for Static and Dynamic Analysis of Graphene-Based Hybrid Flexoelectric Nanostructures
Abstract
1. Introduction
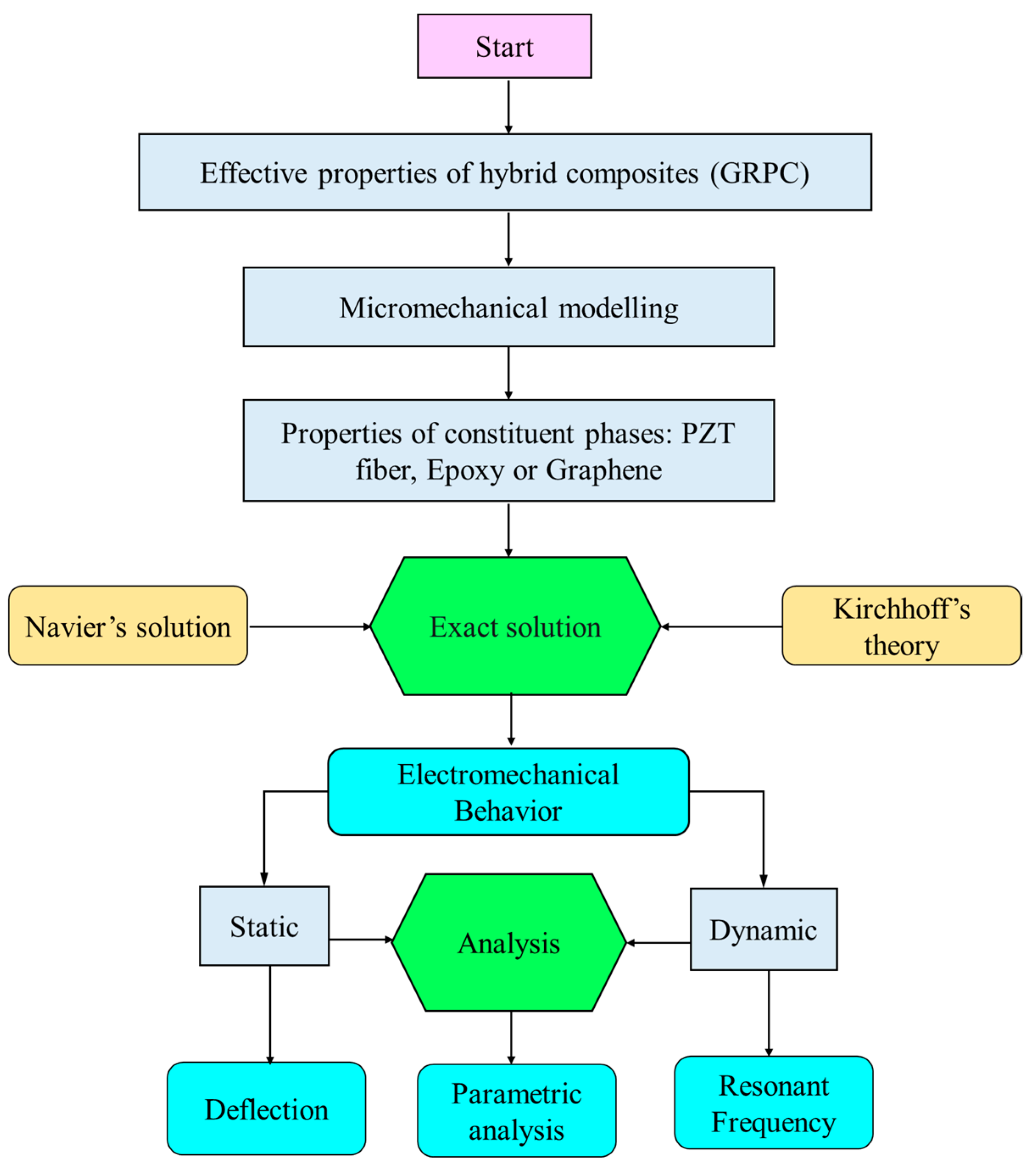
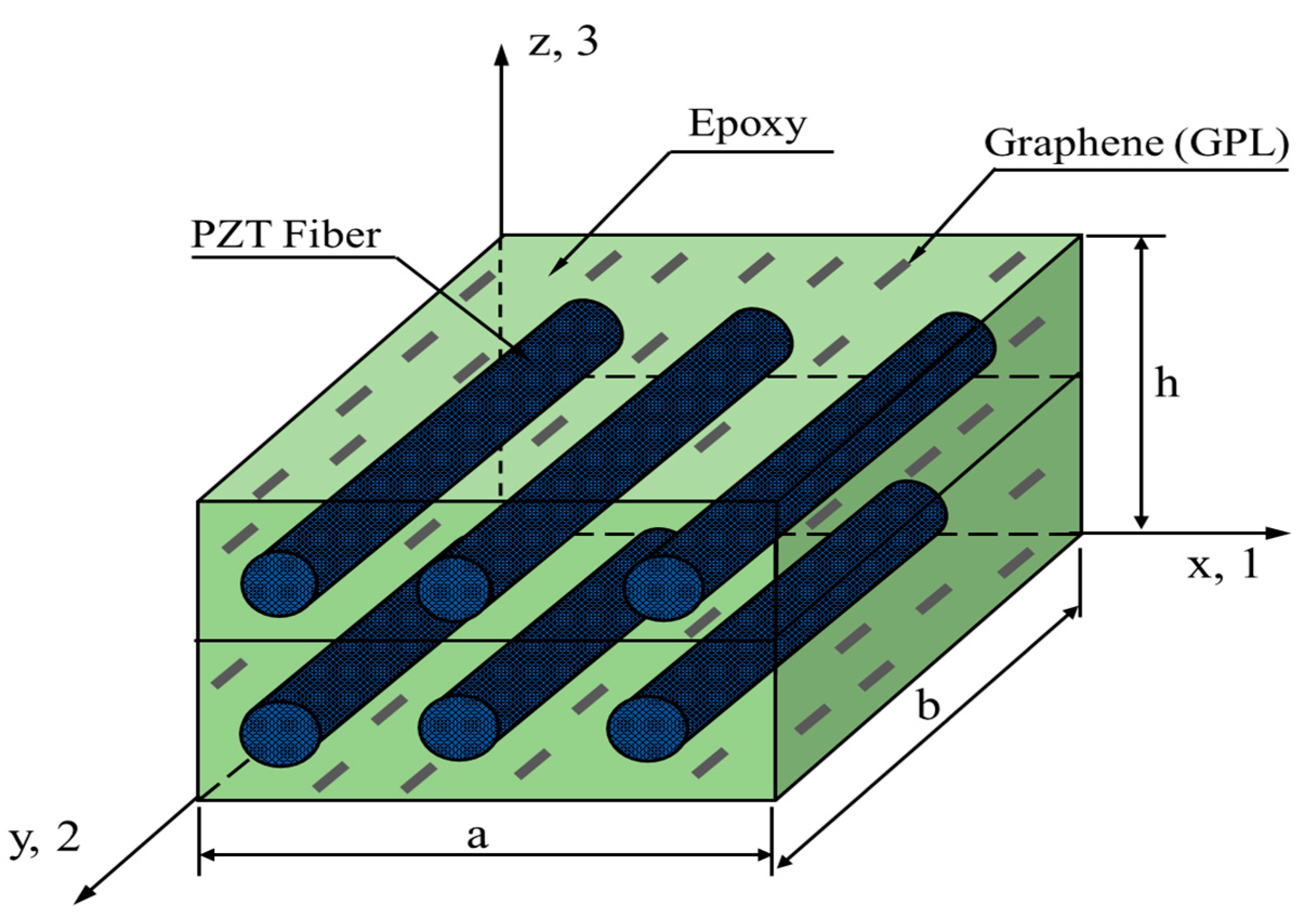
2. Materials and Methods
2.1. Assumptions of Kirchhoff’s Plate Theory
- Straight lines normal to the mid-surface (transverse normal) before deformation remain straight after deformation.
- The transverse normal are inextensible.
- The thickness of the plate does not change during a deformation.
- The transverse normal rotate in such a way that they remain normal to the middle surface after deformation.
2.2. Closed-Form Solution for Static Analysis of GRPC Plates
2.3. Closed-Form Solution for Modal Analysis Considering Free Vibration of GRPC Plates
3. Results
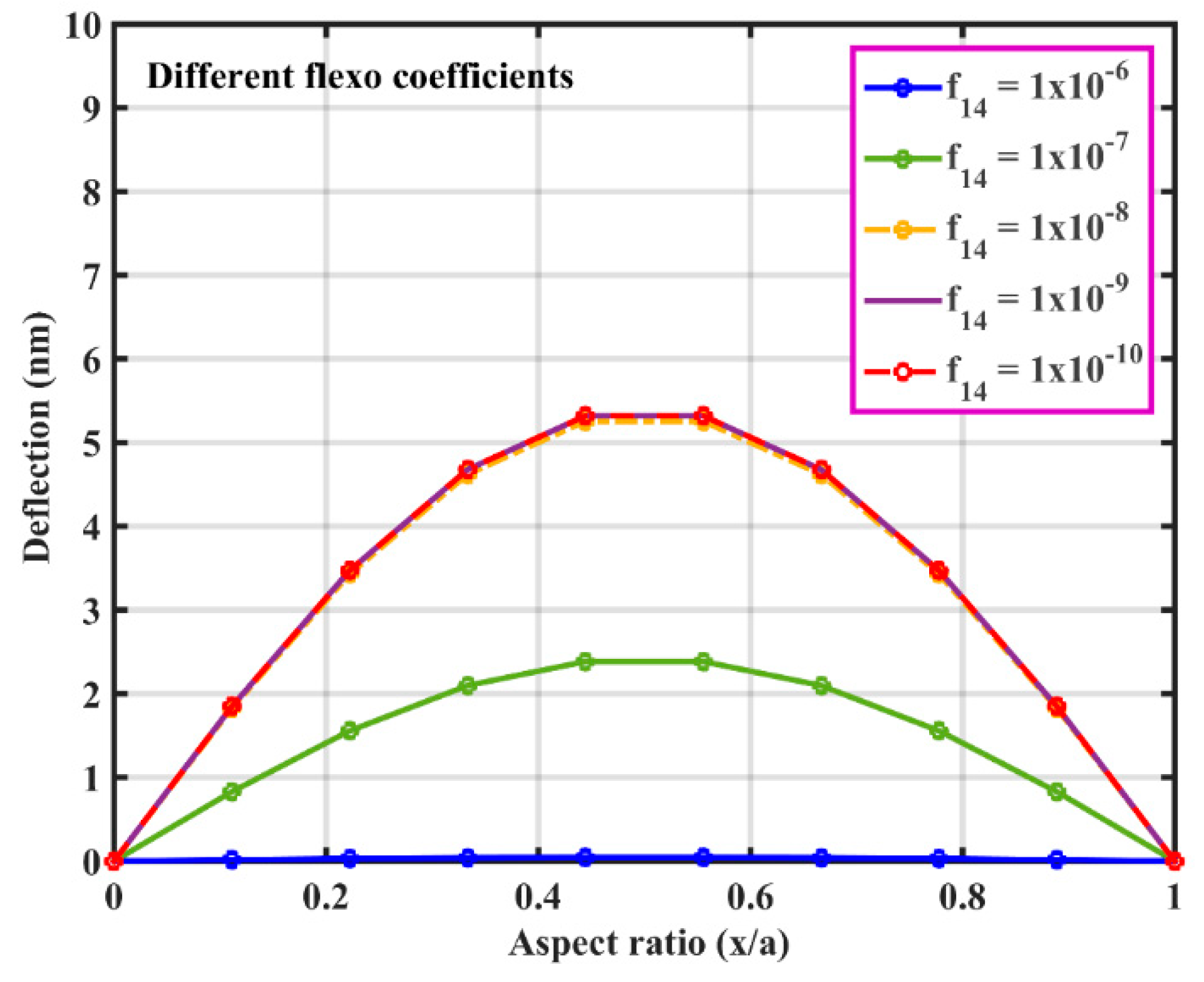
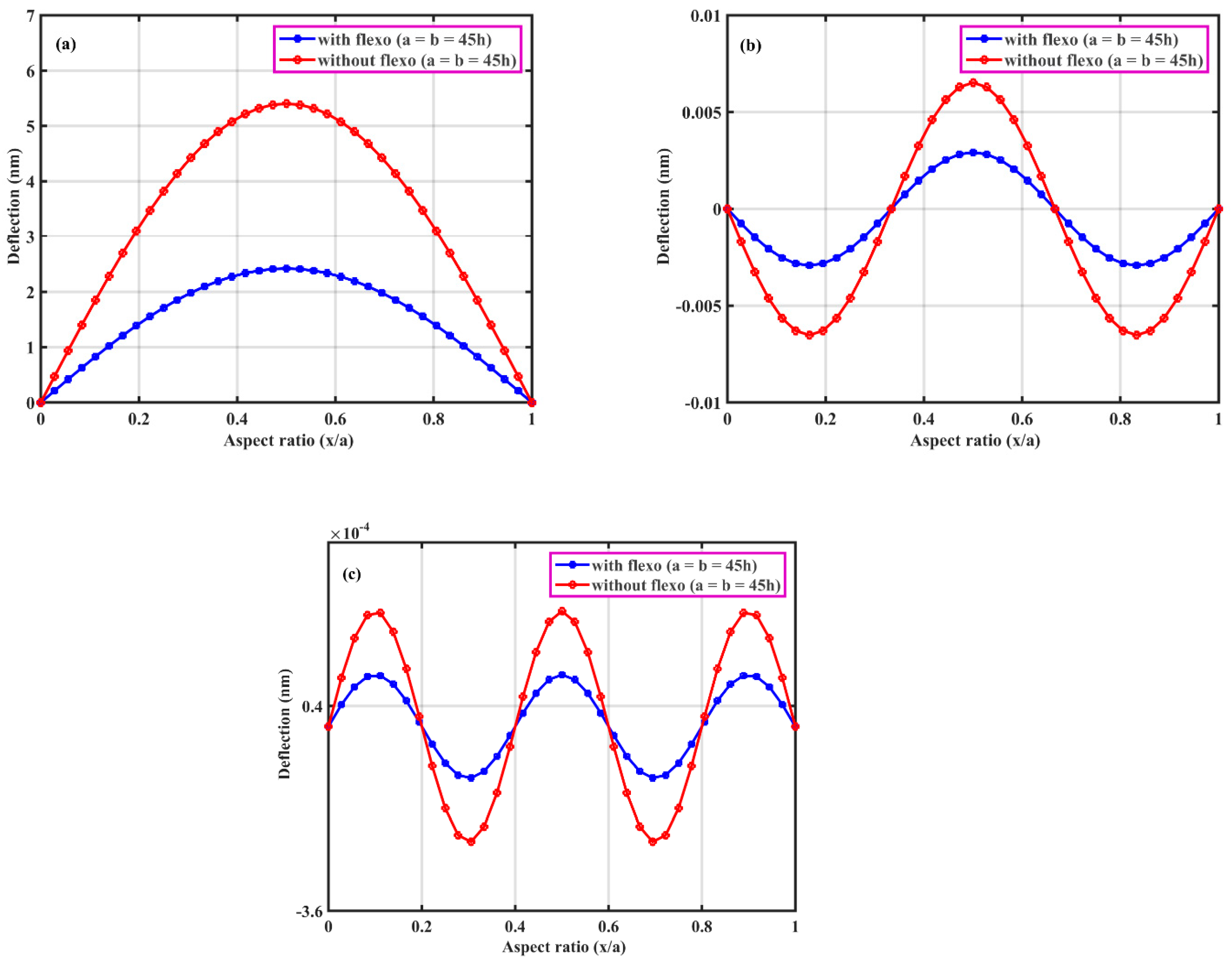
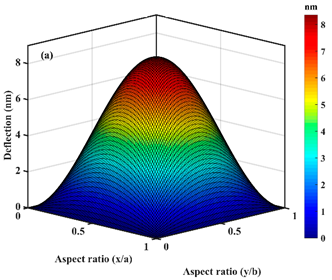
3.1. Static Deflection of Hybrid Flexoelectric GRPC Plate
3.2. Modal Analysis of Hybrid Flexoelectric GRPC Plate
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mashkevich, V.S.; Tolpygo, K.B. Electrical, Optical and Elastic Properties of Diamond Type Crystals. 1. Sov. Phys. JETP 1957, 5, 435–439. [Google Scholar]
- Ray, M.C.; Pradhan, A.K. On the use of vertically reinforced 1-3 piezoelectric composites for hybrid damping of laminated composite plates. Mech. Adv. Mater. Struct. 2007, 14, 245–261. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, L.; Sharma, P. Flexoelectricity in soft materials and biological membranes. J. Mech. Phys. Solids 2014, 62, 209–227. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Meguid, S.A.; Weng, G.J. Strain gradient polarization in graphene. Carbon 2017, 117, 462–472. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Shingare, K.B.; Rathi, A. Effect of flexoelectricity on the electromechanical response of graphene nanocomposite beam. Int. J. Mech. Mater. Des. 2019, 15, 447–470. [Google Scholar] [CrossRef]
- Ray, M.C.; Rao, K.M.; Samanta, B. Exact analysis of coupled electroelastic behaviour of a piezoelectric plate under cylindrical bending. Comput. Struct. 1992, 45, 667–677. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, L. Size effects on electromechanical coupling fields of a bending piezoelectric nanoplate due to surface effects and flexoelectricity. J. Appl. Phys. 2014, 116. [Google Scholar] [CrossRef]
- Shingare, K.B.; Kundalwal, S.I. Flexoelectric and surface effects on the electromechanical behavior of graphene-based nanobeams. Appl. Math. Model. 2020, 81, 70–91. [Google Scholar] [CrossRef]
- Shingare, K.B.; Kundalwal, S.I. Static and dynamic response of graphene nanocomposite plates with flexoelectric effect. Mech. Mater. 2019, 134, 69–84. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Shingare, K.B.; Gupta, M. Flexoelectric effect on electric potential in piezoelectric graphene-based composite nanowire: Analytical and numerical modelling. Eur. J. Mech. A Solids 2020, 84. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef]
- Chen, L.; Jin, H.; Xu, Z.; Shan, M.; Tian, X.; Yang, C.; Wang, Z.; Cheng, B. A design of gradient interphase reinforced by silanized graphene oxide and its effect on carbon fiber/epoxy interface. Mater. Chem. Phys. 2014, 145, 186–196. [Google Scholar] [CrossRef]
- Karakassides, A.; Ganguly, A.; Tsirka, K.; Paipetis, A.S.; Papakonstantinou, P. Radially Grown Graphene Nanoflakes on Carbon Fibers as Reinforcing Interface for Polymer Composites. ACS Appl. Nano Mater. 2020. [Google Scholar] [CrossRef]
- Mirabedini, A.; Ang, A.; Nikzad, M.; Fox, B.; Lau, K.T.; Hameed, N. Evolving Strategies for Producing Multiscale Graphene-Enhanced Fiber-Reinforced Polymer Composites for Smart Structural Applications. Adv. Sci. 2020, 7. [Google Scholar] [CrossRef]
- Roberts, M.W.; Clemons, C.B.; Wilber, J.P.; Young, G.W.; Buldum, A.; Quinn, D.D. Continuum Plate Theory and Atomistic Modeling to Find the Flexural Rigidity of a Graphene Sheet Interacting with a Substrate. J. Nanotechnol. 2010, 2010, 1–8. [Google Scholar] [CrossRef]
- Verma, D.; Gupta, S.S.; Batra, R.C. Vibration mode localization in single- and multi-layered graphene nanoribbons. Comput. Mater. Sci. 2014, 95, 41–52. [Google Scholar] [CrossRef]
- Hosseini, M.; Bahaadini, R.; Jamali, B. Nonlocal instability of cantilever piezoelectric carbon nanotubes by considering surface effects subjected to axial flow. JVC J. Vib. Control 2018, 24, 1809–1825. [Google Scholar] [CrossRef]
- Ray, M.C.; Bhattacharya, R.; Samantat, B. Exact Solutions for Static Analysis of Intelligent Structures. AIAA J. 1993, 31, 1684–1691. [Google Scholar] [CrossRef]
- Ray, M.C.; Pradhan, A.K. The performance of vertically reinforced 1-3 piezoelectric composites in active damping of smart structures. Smart Mater. Struct. 2006, 15, 631–641. [Google Scholar] [CrossRef]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 77, 2008–2009. [Google Scholar] [CrossRef]
- Pradhan, S.C. Buckling of single layer graphene sheet based on nonlocal elasticity and higher order shear deformation theory. Phys. Lett. A 2009, 373, 4182–4188. [Google Scholar] [CrossRef]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2016. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L. An analytical model for nanoscale unimorph piezoelectric energy harvesters with flexoelectric effect. Compos. Struct. 2016, 153, 253–261. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos. Part B 2017, 110, 132–140. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Kumar, D. Postbuckling behaviour of graphene-reinforced plate with interfacial effect. Arch. Mech. 2018, 70, 3–36. [Google Scholar]
- Lin, H.G.; Cao, D.Q.; Xu, Y.Q. Vibration, Buckling and Aeroelastic Analyses of Functionally Graded Multilayer Graphene-Nanoplatelets-Reinforced Composite Plates Embedded in Piezoelectric Layers. Int. J. Appl. Mech. 2018. [Google Scholar] [CrossRef]
- Naskar, S.; Mukhopadhyay, T.; Sriramula, S.; Adhikari, S. Stochastic natural frequency analysis of damaged thin-walled laminated composite beams with uncertainty in micromechanical properties. Compos. Struct. 2017. [Google Scholar] [CrossRef]
- Naskar, S.; Mukhopadhyay, T.; Sriramula, S. Probabilistic micromechanical spatial variability quantification in laminated composites. Compos. Part B Eng. 2018. [Google Scholar] [CrossRef]
- Naskar, S.; Mukhopadhyay, T.; Sriramula, S. Spatially varying fuzzy multi-scale uncertainty propagation in unidirectional fibre reinforced composites. Compos. Struct. 2019. [Google Scholar] [CrossRef]
- Naskar, S.; Sriramula, S. On quantifying the effect of noise in radial basis function based stochastic free vibration analysis of laminated composite beam. In Proceedings of the ECCM 2018—18th European Conference on Composite Materials, Athens, Greece, 25 June 2018. [Google Scholar]
- Karsh, P.K.; Mukhopadhyay, T.; Chakraborty, S.; Naskar, S.; Dey, S. A hybrid stochastic sensitivity analysis for low-frequency vibration and low-velocity impact of functionally graded plates. Compos. Part B Eng. 2019. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Shingare, K.B. Electromechanical response of thin shell laminated with flexoelectric composite layer. Thin-Walled Struct. 2020, 157, 107138. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Shingare, K.B.; Maware, P.P. Carbon fiber–reinforced nanocomposites: A multiscale modeling of regularly staggered carbon fibers. In Fiber-Reinforced Nanocomposites: Fundamentals and Applications; Elsevier: Amsterdam, The Netherlands, 2020; pp. 101–127. [Google Scholar]
- Shingare, K.B.; Gupta, M.; Kundalwal, S.I. Evaluation of effective properties for smart graphene reinforced nanocomposite materials. Mater. Today Proc. 2020, 23, 523–527. [Google Scholar] [CrossRef]
- Shingare, K.B.; Naskar, S. Probing the prediction of effective properties for composite materials. Eur. J. Mech. A Solids 2021, 87, 104228. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, R.; Jiang, L. A Study of the Flexoelectric Effect on the Electroelastic Fields of a Cantilevered Piezoelectric Nanoplate. Int. J. Appl. Mech. 2017, 9, 1750056. [Google Scholar] [CrossRef]
- Yan, Z.; Jiang, L.Y. Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams. J. Appl. Phys. 2013, 113, 194102. [Google Scholar] [CrossRef]
- Shu, L.; Wei, X.; Pang, T.; Yao, X.; Wang, C. Symmetry of flexoelectric coefficients in crystalline medium. J. Appl. Phys. 2011, 110. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, Second Edition. Book 2003, 2003, 858. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Strain-gradient-induced electric polarization in lead zirconate titanate ceramics. Appl. Phys. Lett. 2003, 82, 3293–3295. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectricity of barium titanate. Appl. Phys. Lett. 2006, 88, 2004–2007. [Google Scholar] [CrossRef]
- Yang, W.; Liang, X.; Shen, S. Electromechanical responses of piezoelectric nanoplates with flexoelectricity. Acta Mech. 2015, 226, 3097–3110. [Google Scholar] [CrossRef]
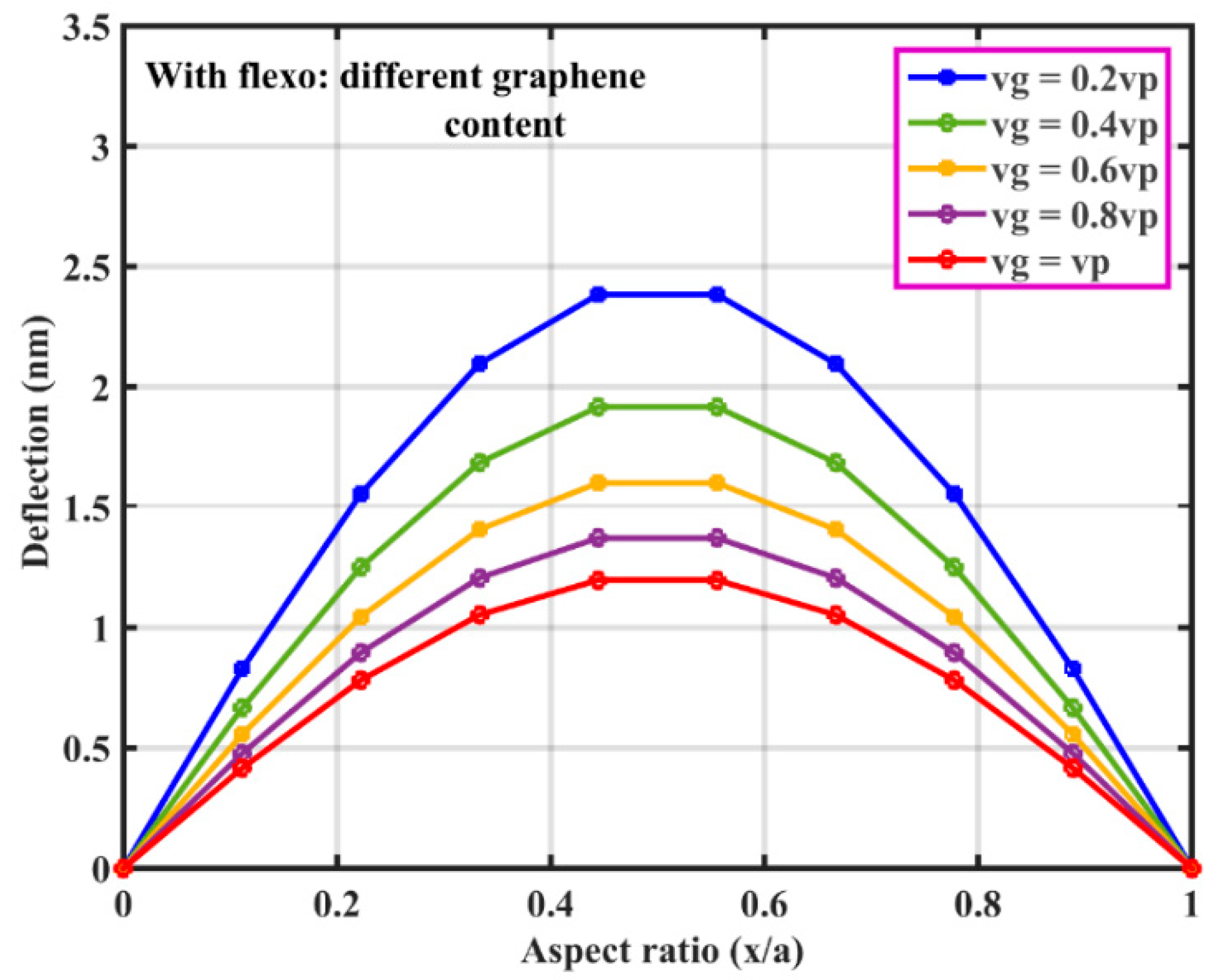
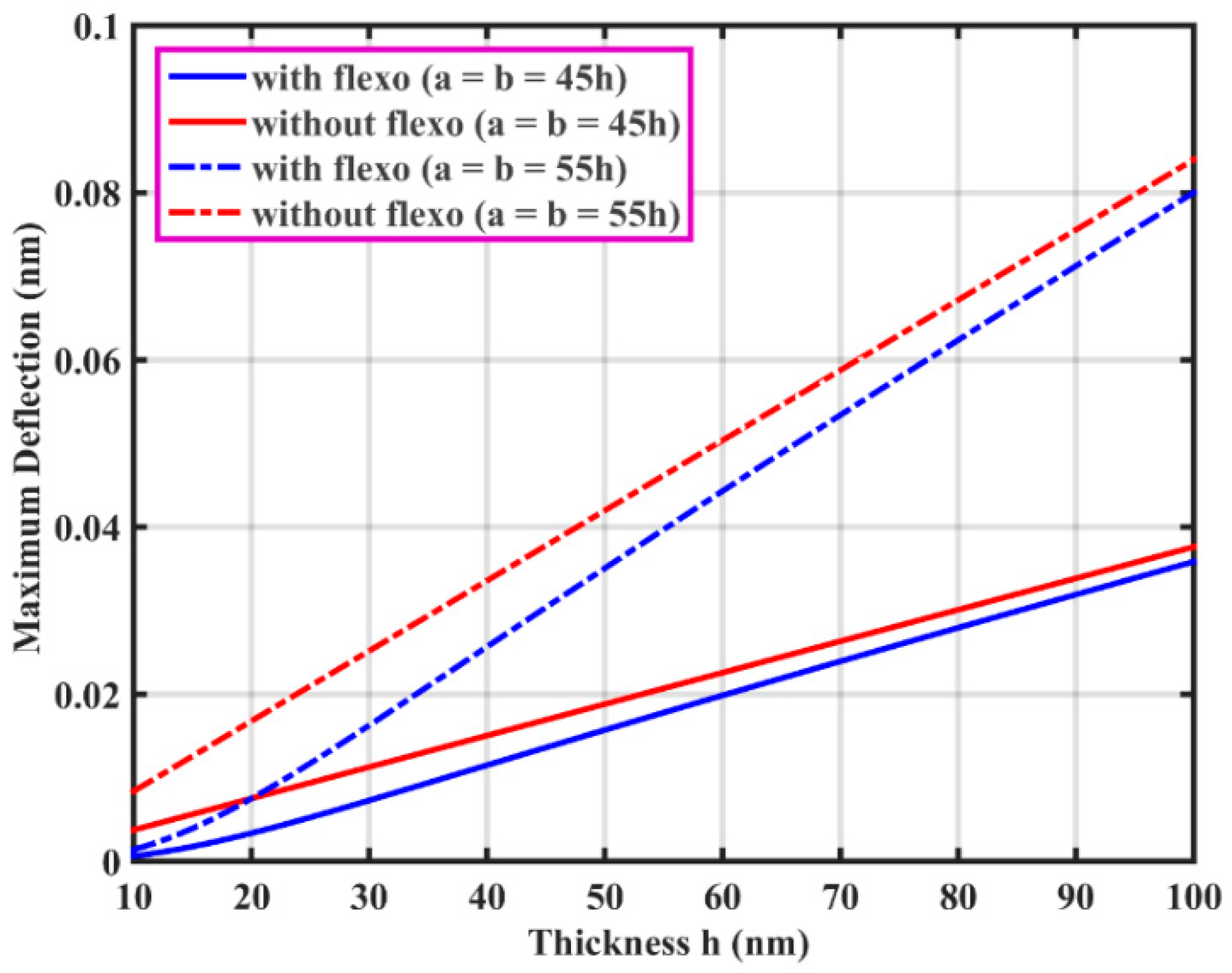
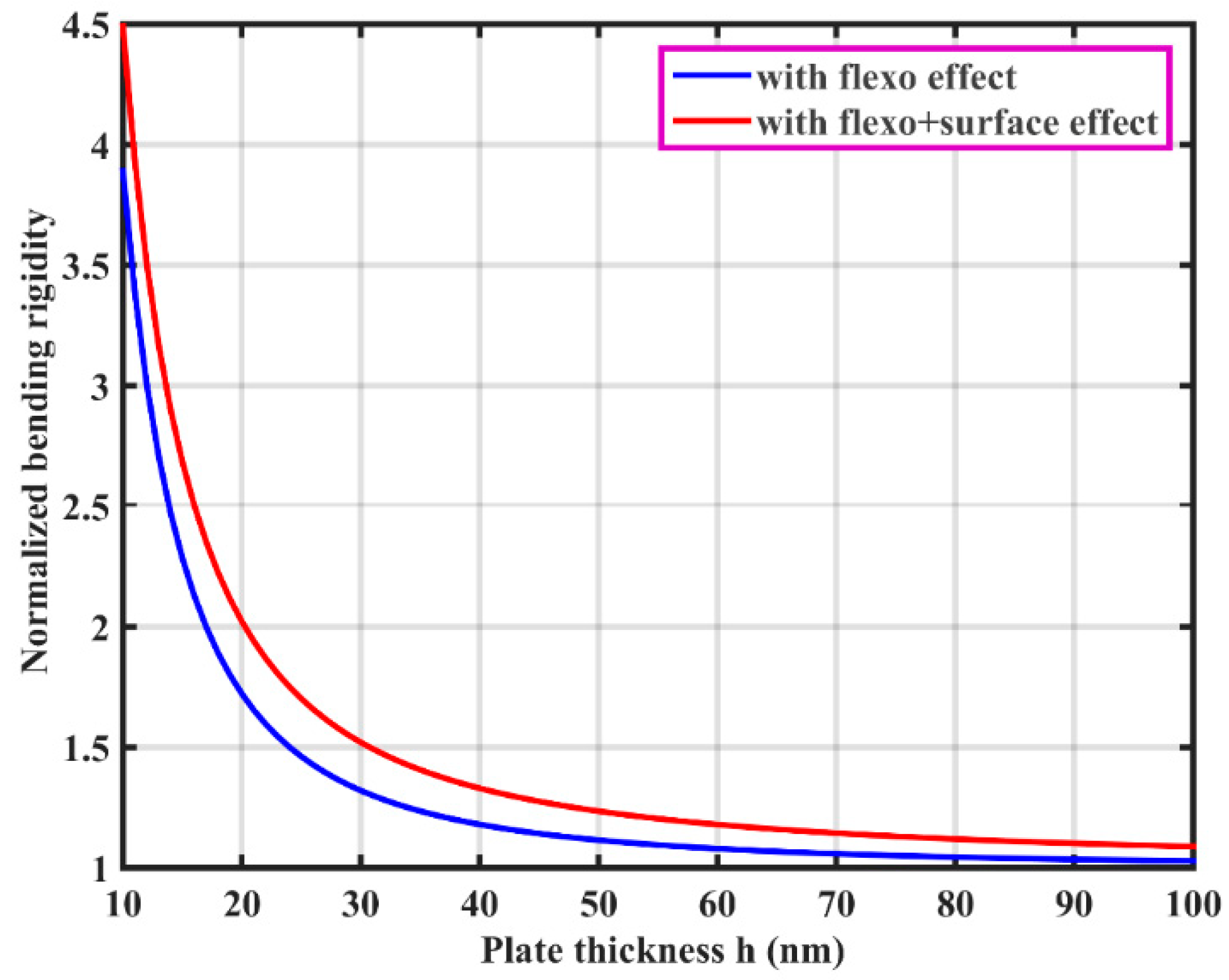
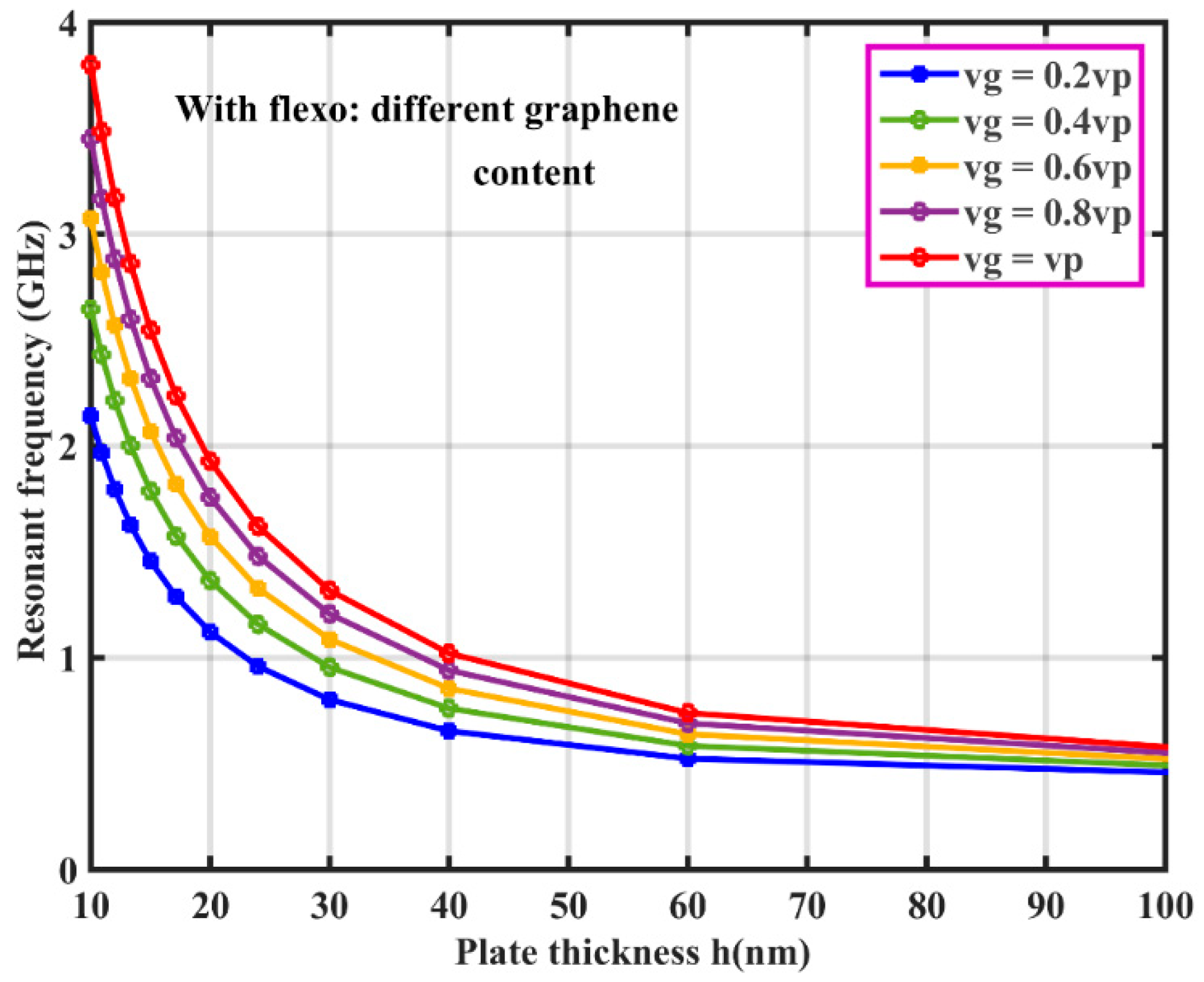
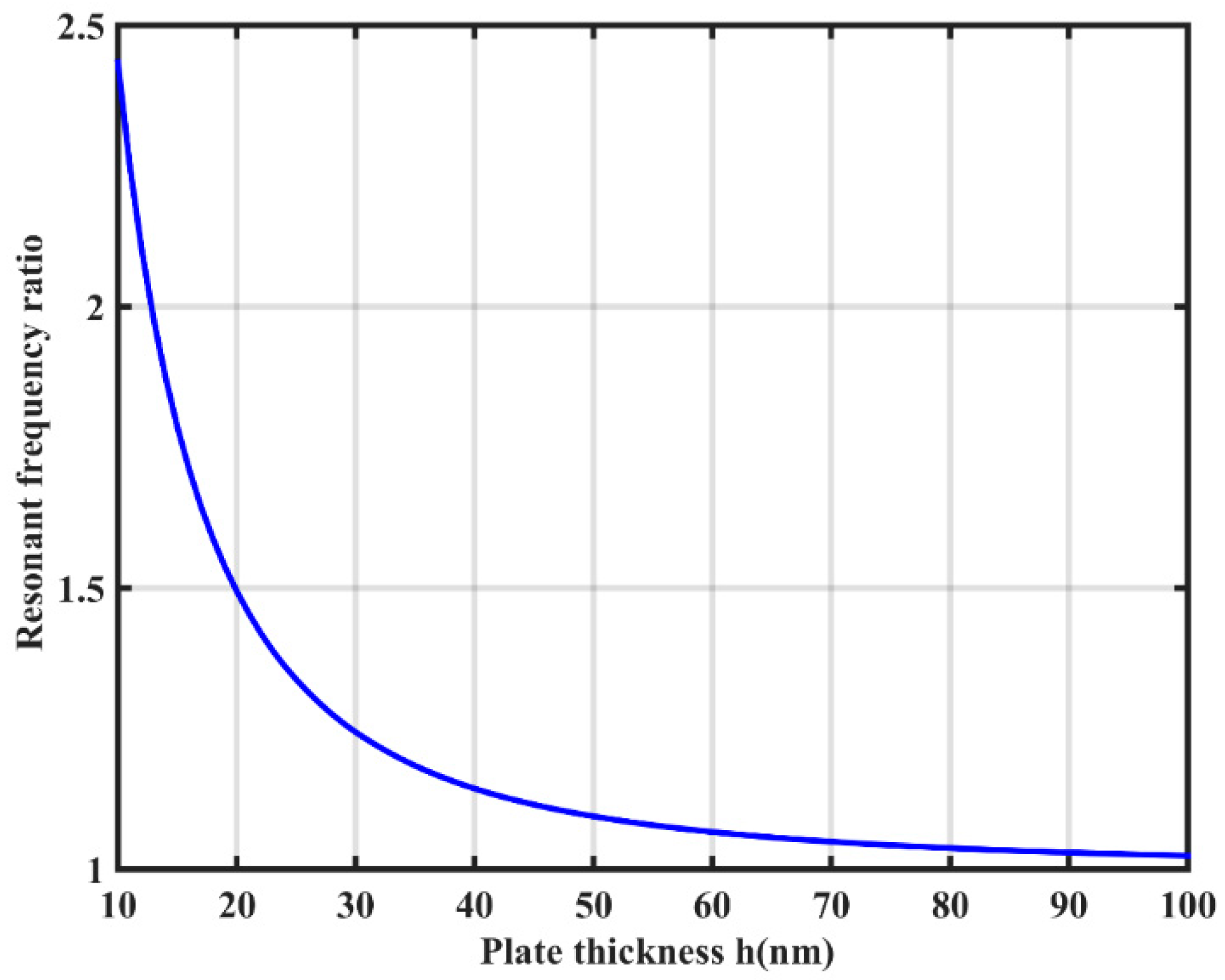
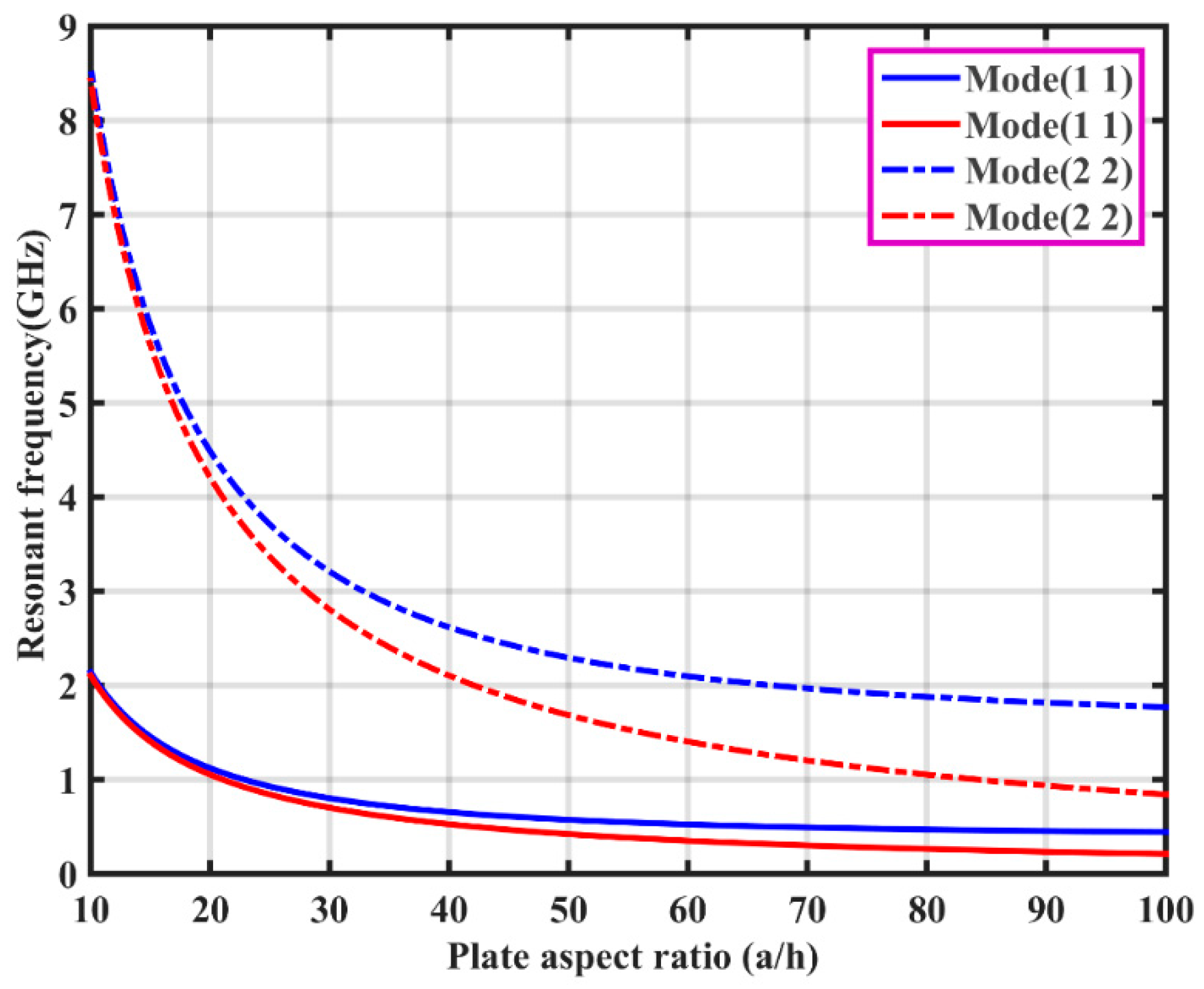
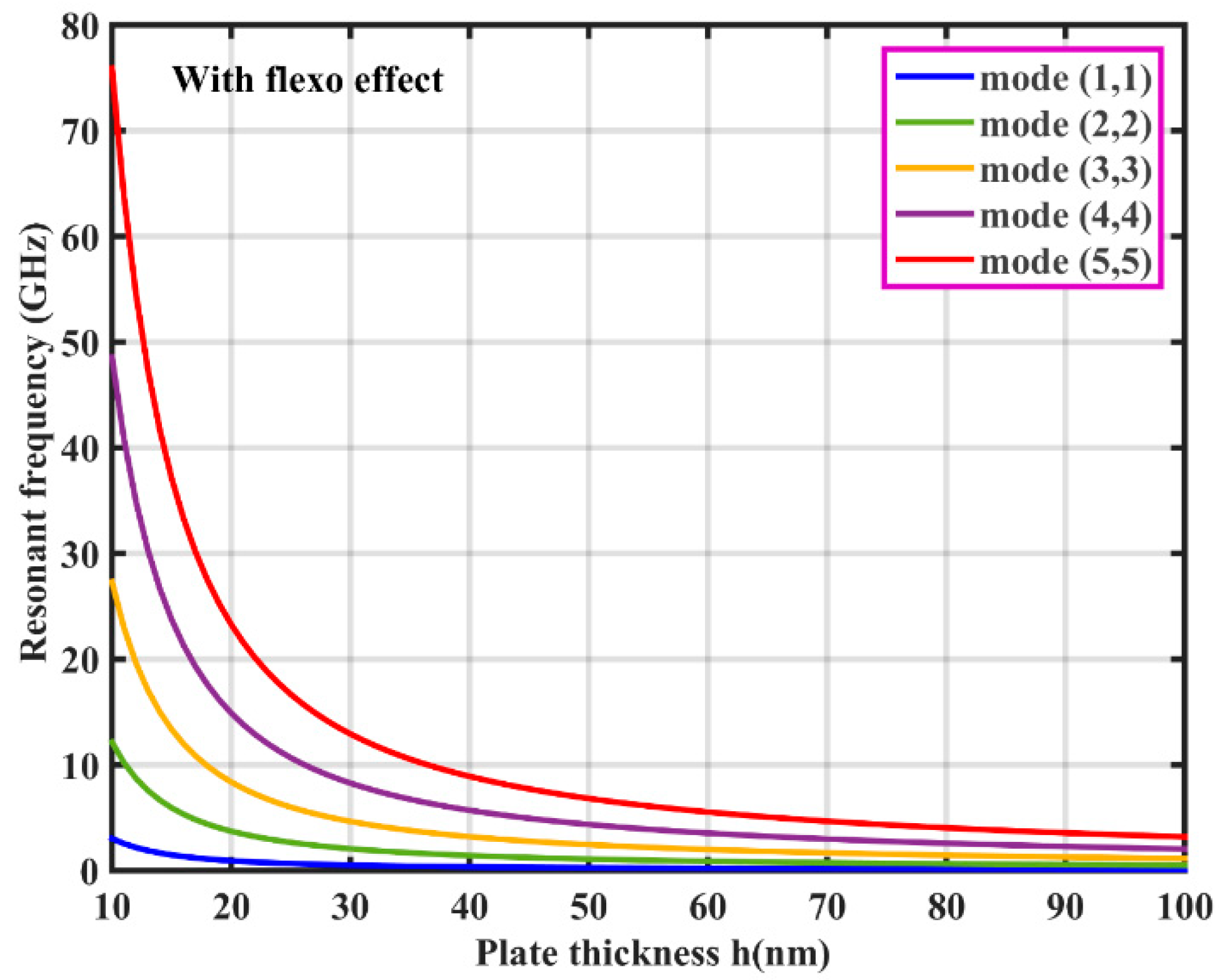
| Material | |||||
|---|---|---|---|---|---|
| GRPC | 112.43 | 3.34 | 2.03 | −6.9337 | 3.264 |
| (m, n) | Without Flexoelectric Effect | With Flexoelectric Effect |
|---|---|---|
| ; |  | 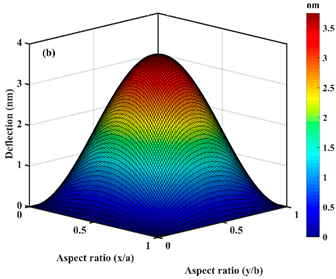 |
| ; | 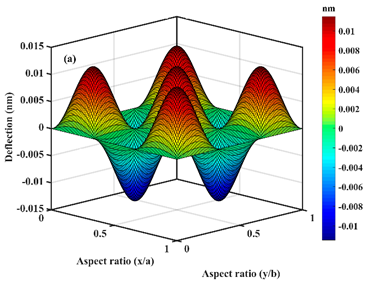 | 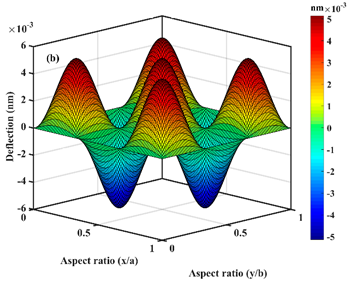 |
| Load | ||
| Point | 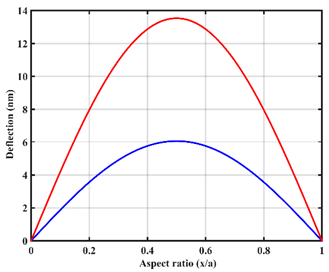 | 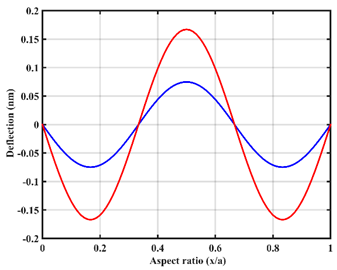 |
| In-line | 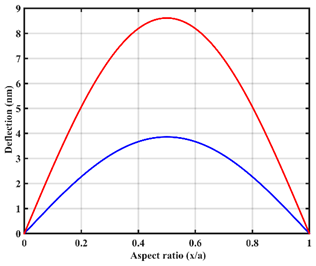 | 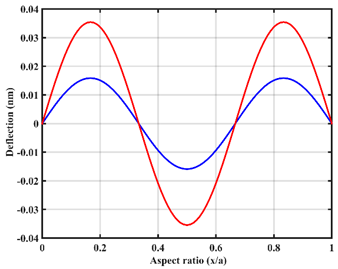 |
| UDL | 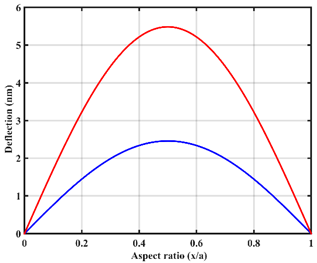 | 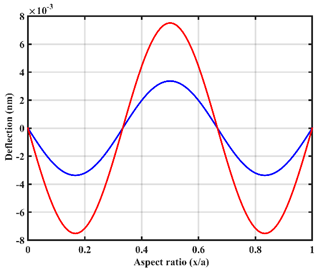 |
| UVL | 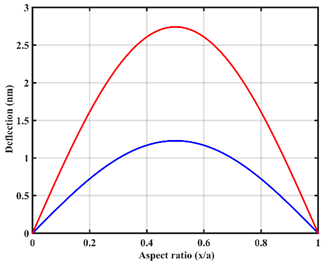 | 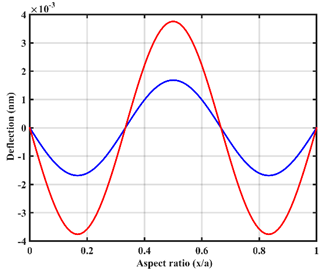 |
| Load | ||
| Point | 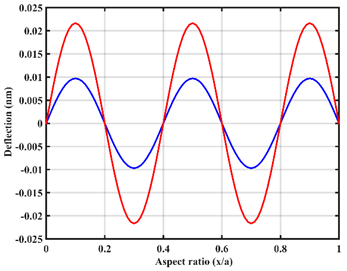 |  |
| In-line | 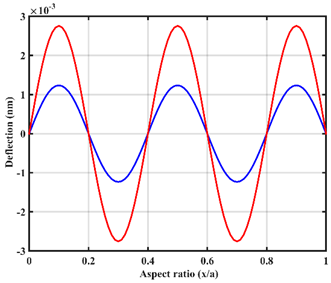 | 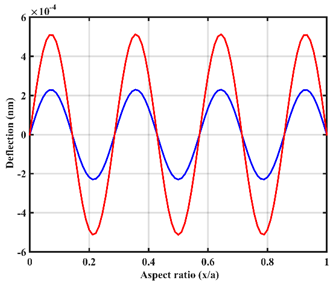 |
| UDL | 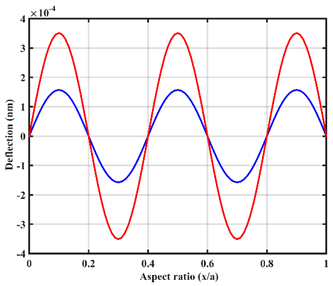 |  |
| UVL | 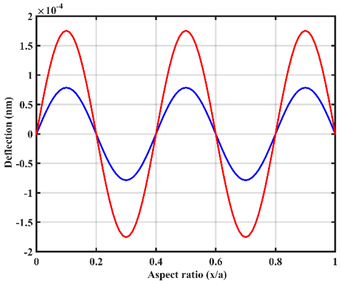 | 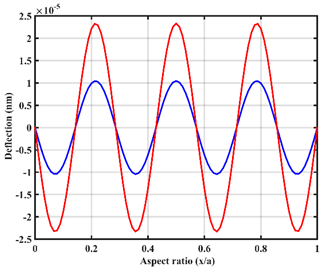 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shingare, K.B.; Naskar, S. Analytical Solution for Static and Dynamic Analysis of Graphene-Based Hybrid Flexoelectric Nanostructures. J. Compos. Sci. 2021, 5, 74. https://doi.org/10.3390/jcs5030074
Shingare KB, Naskar S. Analytical Solution for Static and Dynamic Analysis of Graphene-Based Hybrid Flexoelectric Nanostructures. Journal of Composites Science. 2021; 5(3):74. https://doi.org/10.3390/jcs5030074
Chicago/Turabian StyleShingare, Kishor Balasaheb, and Susmita Naskar. 2021. "Analytical Solution for Static and Dynamic Analysis of Graphene-Based Hybrid Flexoelectric Nanostructures" Journal of Composites Science 5, no. 3: 74. https://doi.org/10.3390/jcs5030074
APA StyleShingare, K. B., & Naskar, S. (2021). Analytical Solution for Static and Dynamic Analysis of Graphene-Based Hybrid Flexoelectric Nanostructures. Journal of Composites Science, 5(3), 74. https://doi.org/10.3390/jcs5030074







