Parameter Identification of Fiber Orientation Models Based on Direct Fiber Simulation with Smoothed Particle Hydrodynamics
Abstract
1. Introduction
1.1. Point-Wise Interaction Methods
1.2. Resolved Methods
2. Theory
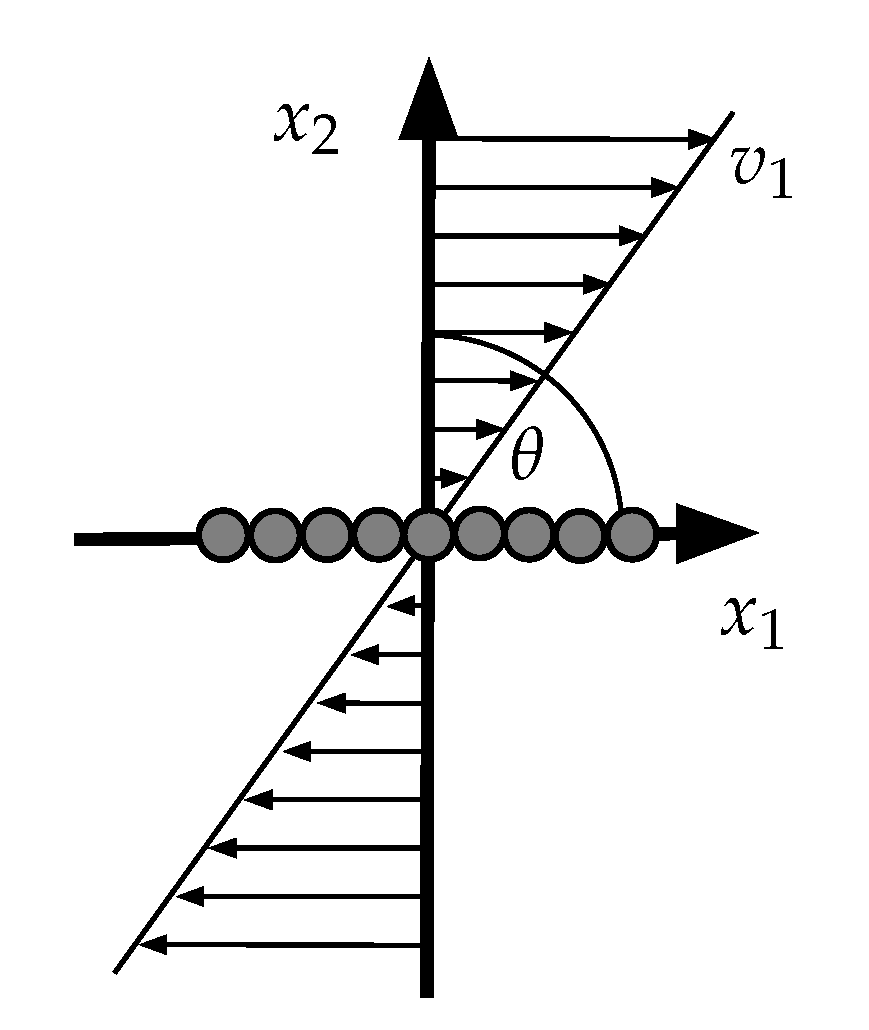
2.1. Fluid Model
2.2. Interaction between Fluid and Solid Particles
2.3. Basic Model for Flexible Fibers
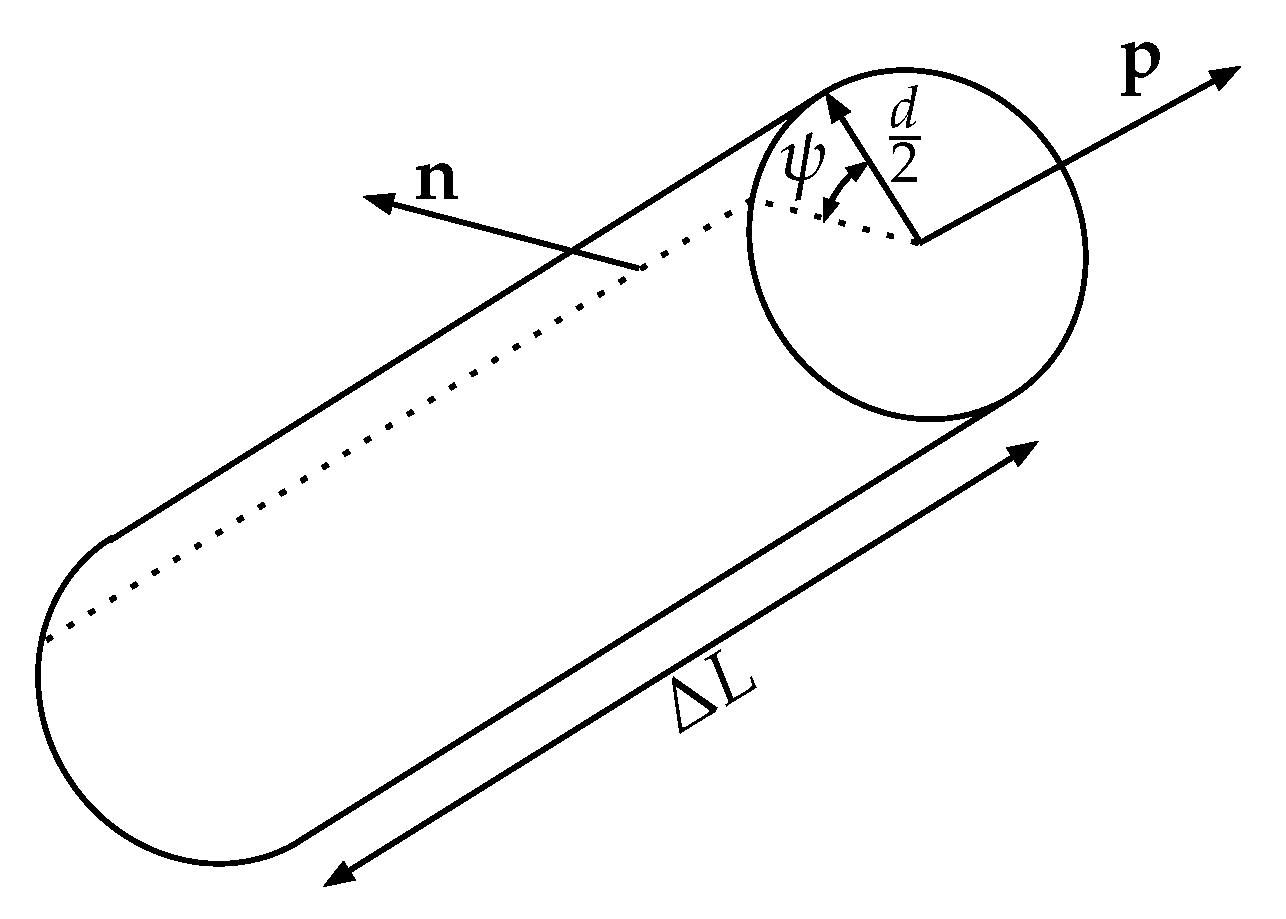
2.4. Viscous Traction at Fiber Surface
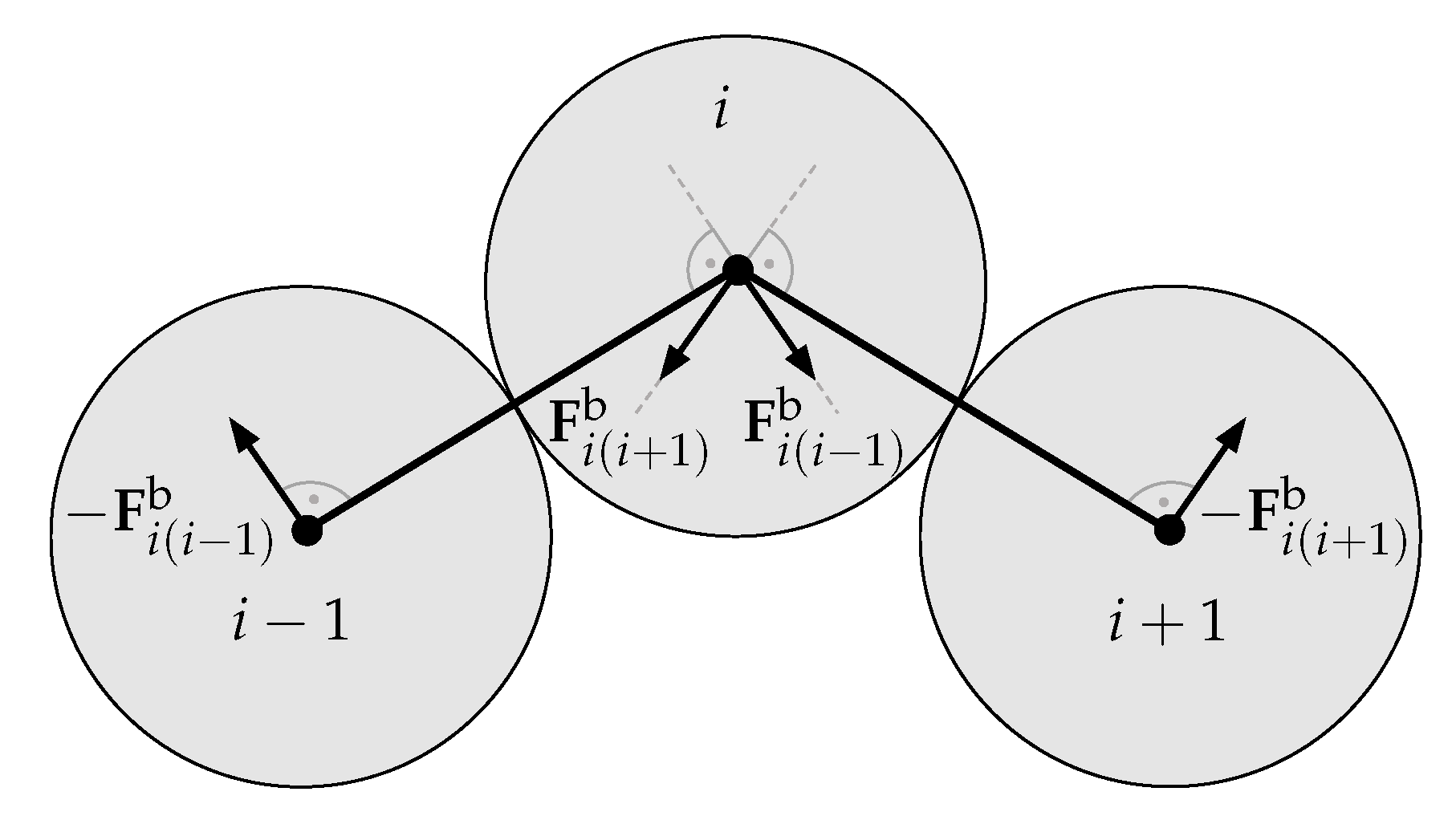
2.5. Fiber Interactions
- Surface-Surface:
- If both interacting particles are located at the center of the fiber (e.g., they have two neighbor particles each, compare Figure 4 at ), the normal direction of contact pair can be computed using the cross productof the involved fiber direction vectors and . The operator is used to conveniently denote the normalization of a vector. Solving the small linear system of equationswith its adjugate matrix leads to the solution for the distance between the fibers and the projections to source and destination vectors and , respectively.
- Surface-End and End-Surface:
- If a particle of a fiber end interacts with a central particle of another fiber, the vector between these two particles can be used to obtain the normal direction by projection. It is assumed that describes a unit vector in fiber direction at one fiber particle at position . Let be the vector from another fibers’ end particle to the point . The closest point to on a line with direction is denoted as and can be used to define the normal direction asUsing the definitions above and the fact that is the projection of to the line with direction , Equation (28) can be rewritten asThe projection on the destination fiber is given as and the contact distance is computed as .
- End-End:
- The simplest case is the interaction of two fiber ends. Here, the vector between those two particles can be simply determined bywith the corresponding distance .
2.6. Time Integration and Implementation
3. Results
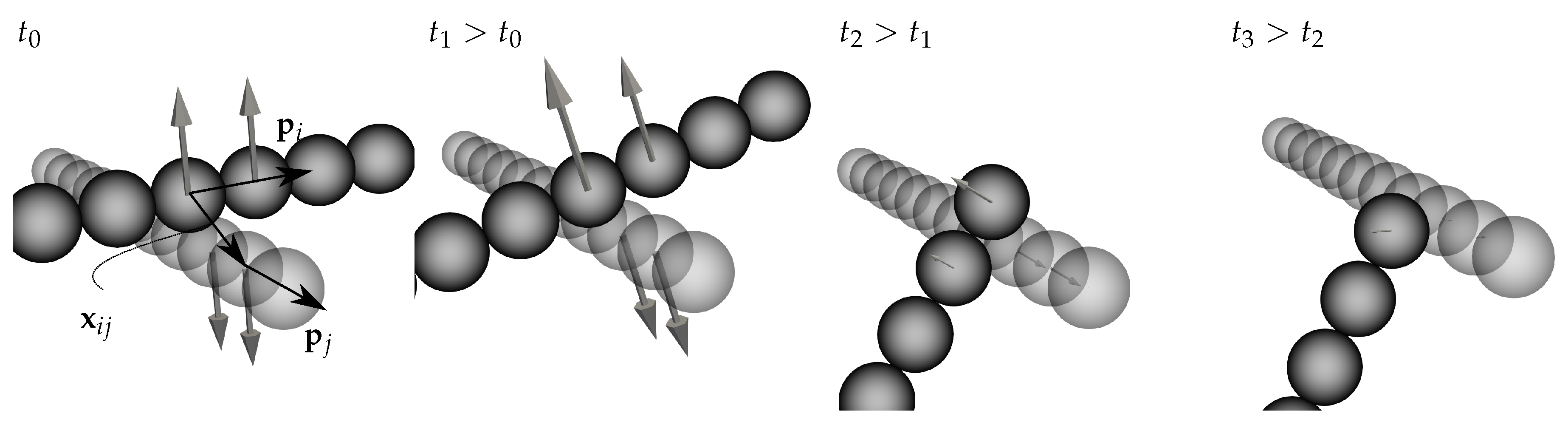
3.1. Rotation and Bending in a Simple Shear Flow
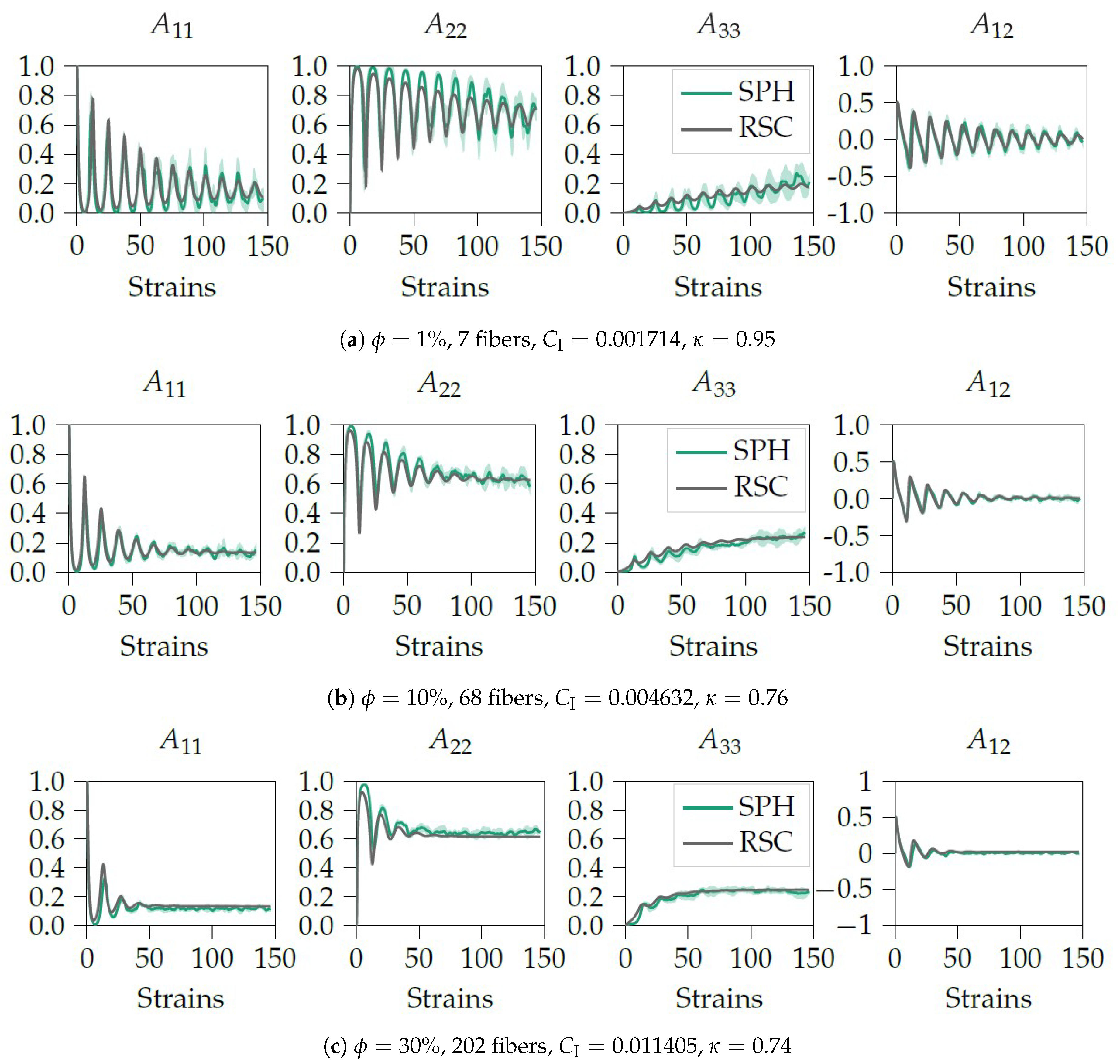
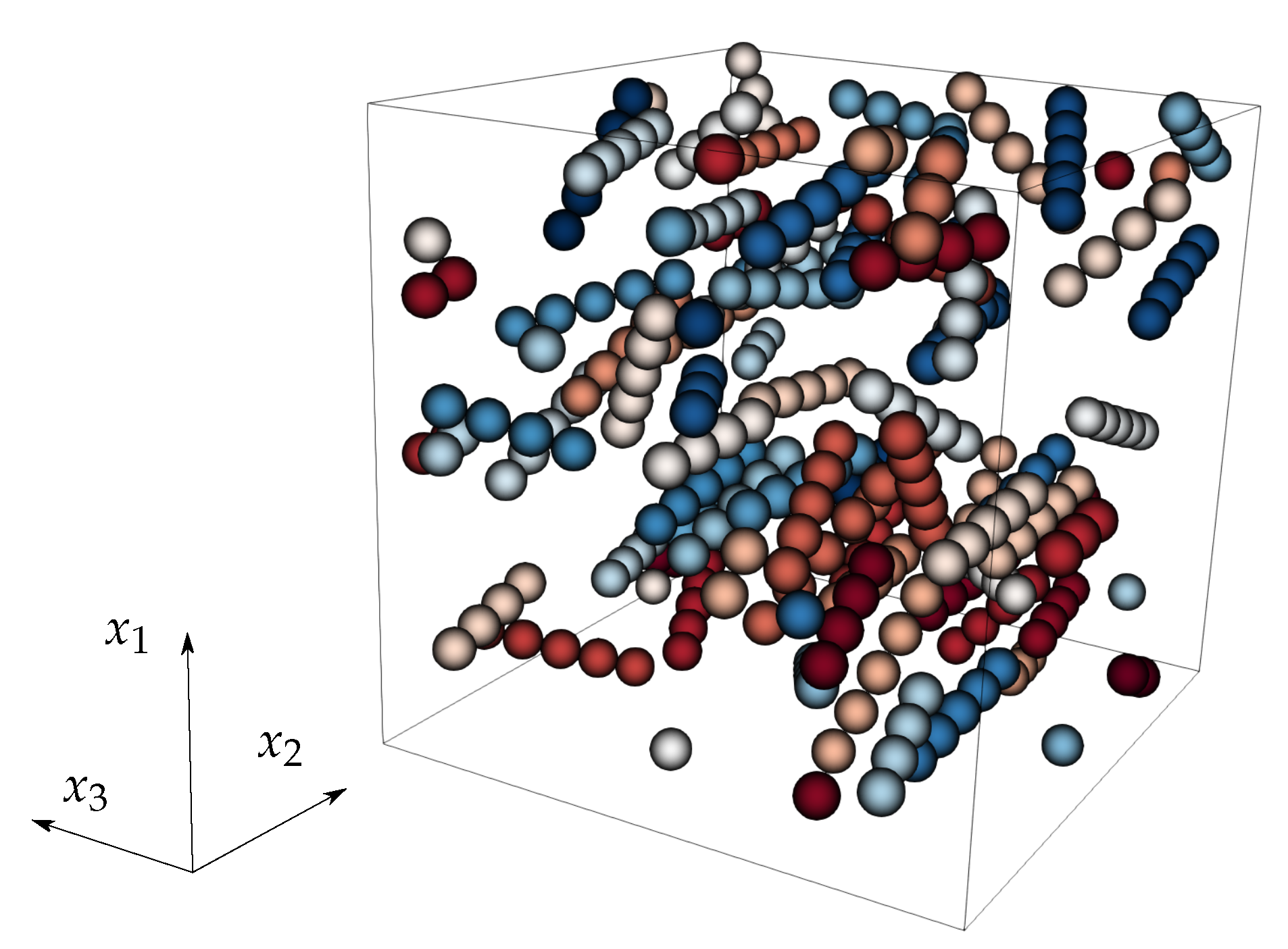
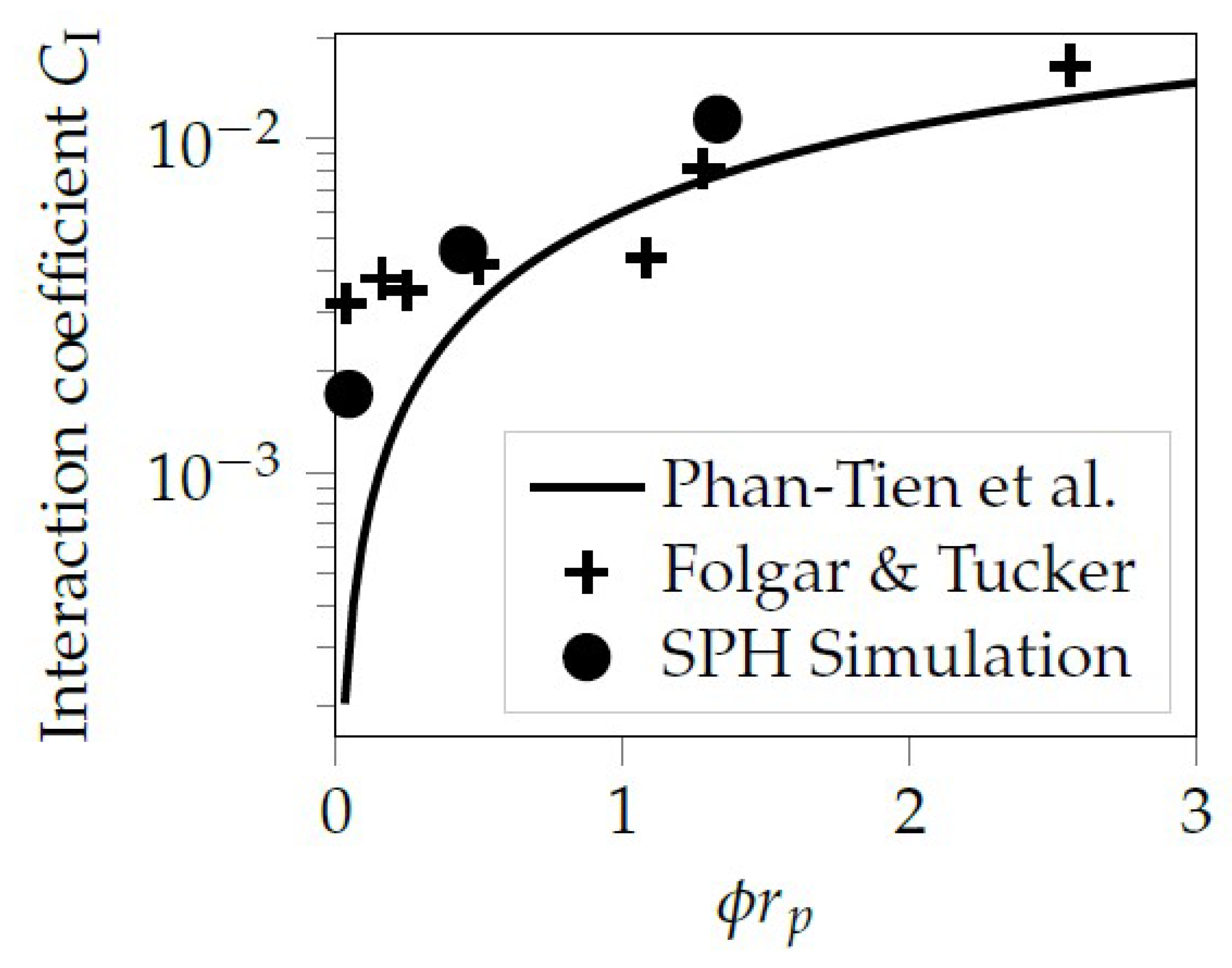
3.2. Parameter Identification for the Orientation Evolution in a Non-Dilute Short Fiber Suspensions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Evaluation of the Surface Traction Integral
References
- Kärger, L.; Bernath, A.; Fritz, F.; Galkin, S.; Magagnato, D.; Oeckerath, A.; Schön, A.; Henning, F. Development and validation of a CAE chain for unidirectional fibre reinforced composite components. Compos. Struct. 2015, 132, 350–358. [Google Scholar] [CrossRef]
- Görthofer, J.; Meyer, N.; Pallicity, T.D.; Schöttl, L.; Trauth, A.; Schemmann, M.; Hohberg, M.; Pinter, P.; Elsner, P.; Henning, F.; et al. Virtual process chain of sheet molding compound: Development, validation and perspectives. Compos. Part B Eng. 2019, 169, 133–147. [Google Scholar] [CrossRef]
- Jeffery, G.B. The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. Ser. A Contain. Pap. Mathem. Phys. Character 1922, 102, 161–179. [Google Scholar] [CrossRef]
- Folgar, F.; Tucker, C.L. Orientation Behavior of Fibers in Concentrated Suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Wang, J.; O’Gara, J.F.; Tucker, C.L. An objective model for slow orientation kinetics in concentrated fiber suspensions: Theory and rheological evidence. J. Rheol. 2008, 52, 1179–1200. [Google Scholar] [CrossRef]
- Phelps, J.H.; Tucker, C.L. An anisotropic rotary diffusion model for fiber orientation in short- and long-fiber thermoplastics. J. Non-Newt. Fluid Mech. 2009, 156, 165–176. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. An objective tensor to predict anisotropic fiber orientation in concentrated suspensions. J. Rheol. 2016, 60, 215–224. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Chung, D.H.; Kwon, T.H. Invariant-based optimal fitting closure approximation for the numerical prediction of flow-induced fiber orientation. J. Rheol. 2002, 46, 169–194. [Google Scholar] [CrossRef]
- Brady, J.F.; Bossis, G. Stokesian Dynamics. Ann. Rev. Fluid Mech. 1988, 20, 111–157. [Google Scholar] [CrossRef]
- Batchelor, G.K. Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 1970, 44, 419–440. [Google Scholar] [CrossRef]
- Hinch, E.J. The distortion of a flexible inextensible thread in a shearing flow. J. Fluid Mech. 1976, 74, 317–333. [Google Scholar] [CrossRef]
- Yamamoto, S.; Matsuoka, T. A method for dynamic simulation of rigid and flexible fibers in a flow field. J. Chem. Phys. 1993, 98, 644–650. [Google Scholar] [CrossRef]
- Yamamoto, S.; Matsuoka, T. Viscosity of dilute suspensions of rodlike particles: A numerical simulation method. J. Chem. Phys. 1994, 100, 3317–3324. [Google Scholar] [CrossRef]
- Wang, G.; Yu, W.; Zhou, C. Optimization of the rod chain model to simulate the motions of a long flexible fiber in simple shear flows. Europ. J. Mech. B/Fluid. 2006, 25, 337–347. [Google Scholar] [CrossRef]
- Meirson, G.; Hrymak, A.N. Two-dimensional long-flexible fiber simulation in simple shear flow. Polym. Compos. 2016, 37, 2425–2433. [Google Scholar] [CrossRef]
- Meirson, G.; Hrymak, A.N. Two dimensional long-flexible fiber orientation simulation in squeeze flow. Polym. Compos. 2018, 39, 4656–4665. [Google Scholar] [CrossRef]
- Skjetne, P.; Ross, R.F.; Klingenberg, D.J. Simulation of single fiber dynamics. J. Chem. Phys. 1997, 107, 2108–2121. [Google Scholar] [CrossRef]
- Joung, C.G.; Phan-Thien, N.; Fan, X.J. Direct simulations of flexible fibers. J. Non-Newt. Fluid Mech. 2001, 99, 1–36. [Google Scholar] [CrossRef]
- Ross, R.F.; Klingenberg, D.J. Dynamic simulation of flexible fibers composed of linked rigid bodies. J. Chem. Phys. 1997, 106, 2949–2960. [Google Scholar] [CrossRef]
- Lindström, S.B.; Uesaka, T. Simulation of the motion of flexible fibers in viscous fluid flow. Phys. Fluids 2007, 19, 113307. [Google Scholar] [CrossRef]
- Yamane, Y.; Kaneda, Y.; Dio, M. Numerical simulation of semi-dilute suspensions of rodlike particles in shear flow. J. Non-Newt. Fluid Mech. 1994, 54, 405–421. [Google Scholar] [CrossRef]
- Fan, X.; Phan-Thien, N.; Zheng, R. A direct simulation of fibre suspensions. J. Non-Newt. Fluid Mech. 1998, 74, 113–135. [Google Scholar] [CrossRef]
- Sundararajakumar, R.; Koch, D.L. Structure and properties of sheared fiber suspensions with mechanical contacts. J. Non-Newt. Fluid Mech. 1997, 73, 205–239. [Google Scholar] [CrossRef]
- Schmid, C.F.; Switzer, L.H.; Klingenberg, D.J. Simulations of fiber flocculation: Effects of fiber properties and interfiber friction. J. Rheol. 2000, 44, 781–809. [Google Scholar] [CrossRef]
- Sasayama, T.; Inagaki, M. Simplified bead-chain model for direct fiber simulation in viscous flow. J. Non-Newt. Fluid Mech. 2017, 250, 52–58. [Google Scholar] [CrossRef]
- Londoño-Hurtado, A.; Hernandez-Ortiz, J.P.; Osswald, T. Mechanism of fiber–matrix separation in ribbed compression molded parts. Polym. Compos. 2007, 28, 451–457. [Google Scholar] [CrossRef]
- Ramirez, D. Study of Fiber Motion in Molding Processes by Means of a Mechanistic Model. Ph.D. Thesis, University of Wisconsin Madison, Madison, WI, USA, 2014. [Google Scholar]
- Kuhn, C.; Walter, I.; Täger, O.; Osswald, T. Simulative Prediction of Fiber-Matrix Separation in Rib Filling During Compression Molding Using a Direct Fiber Simulation. J. Compos. Sci. 2017, 2, 2. [Google Scholar] [CrossRef]
- Meyer, N.; Schöttl, L.; Bretz, L.; Hrymak, A.; Kärger, L. Direct Bundle Simulation approach for the compression molding process of Sheet Molding Compound. Compos. Part A Appl. Sci. Manuf. 2020, 132, 105809. [Google Scholar] [CrossRef]
- Bian, X.; Ellero, M. A splitting integration scheme for the SPH simulation of concentrated particle suspensions. Comput. Phys. Commun. 2014, 185, 53–62. [Google Scholar] [CrossRef]
- Vázquez-Quesada, A.; Ellero, M. Rheology and microstructure of non-colloidal suspensions under shear studied with Smoothed Particle Hydrodynamics. J. Non-Newt. Fluid Mech. 2016, 233, 37–47. [Google Scholar] [CrossRef]
- Yashiro, S.; Okabe, T.; Matsushima, K. A Numerical Approach for Injection Molding of Short-Fiber- Reinforced Plastics Using a Particle Method. Adv. Compos. Mater. 2011, 20, 503–517. [Google Scholar] [CrossRef]
- Yashiro, S.; Sasaki, H.; Sakaida, Y. Particle simulation for predicting fiber motion in injection molding of short-fiber-reinforced composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1754–1764. [Google Scholar] [CrossRef]
- He, L.; Lu, G.; Chen, D.; Li, W.; Lu, C. Three-dimensional smoothed particle hydrodynamics simulation for injection molding flow of short fiber-reinforced polymer composites. Model. Simul. Mater. Sci. Eng. 2017, 25, 055007. [Google Scholar] [CrossRef]
- He, L.; Lu, G.; Chen, D.; Li, W.; Chen, L.; Yuan, J.; Lu, C. Smoothed particle hydrodynamics simulation for injection molding flow of short fiber-reinforced polymer composites. J. Compos. Mater. 2018, 52, 1531–1539. [Google Scholar] [CrossRef]
- Duong-Hong, D.; Phan-Thien, N.; Yeo, K.S.; Ausias, G. Dissipative particle dynamics simulations for fibre suspensions in newtonian and viscoelastic fluids. Comput. Method. Appl. Mech. Eng. 2010, 199, 1593–1602. [Google Scholar] [CrossRef]
- Yang, X.; Liu, M.; Peng, S. Smoothed particle hydrodynamics and element bending group modeling of flexible fibers interacting with viscous fluids. Phys. Rev. E 2014, 90, 063011. [Google Scholar] [CrossRef] [PubMed]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astronom. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astronom. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703–1759. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.; Adams, N. A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 2012, 231, 7057–7075. [Google Scholar] [CrossRef]
- Adami, S.; Hu, X.; Adams, N. A transport-velocity formulation for smoothed particle hydrodynamics. J. Comput. Phys. 2013, 241, 292–307. [Google Scholar] [CrossRef]
- Meleán, Y.; Sigalotti, L.D.G.; Hasmy, A. On the SPH tensile instability in forming viscous liquid drops. Comput. Phys. Commun. 2004, 157, 191–200. [Google Scholar] [CrossRef]
- Akinci, N.; Ihmsen, M.; Akinci, G.; Solenthaler, B.; Teschner, M. Versatile rigid-fluid coupling for incompressible SPH. ACM Trans. Graph. 2012, 31, 1–8. [Google Scholar] [CrossRef]
- Cole, I.R. Modelling CPV. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2015. [Google Scholar]
- Phan-Thien, N.; Fan, X.J.; Tanner, R.; Zheng, R. Folgar–Tucker constant for a fibre suspension in a Newtonian fluid. J. Non-Newt. Fluid Mech. 2002, 103, 251–260. [Google Scholar] [CrossRef]
- Johnson, K.L.; Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Ramachandran, P. PySPH: A reproducible and high-performance framework for smoothed particle hydrodynamics. In Proceedings of the 15th Python in Science Conference, Austin, TX, USA, 11–17 July 2016; pp. 127–135. [Google Scholar]
- Baird, D.G.; Collias, D.I. Polymer Processing: Principles and Design; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Forgacs, O.; Mason, S. Particle motions in sheared suspensions. J. Colloid Sci. 1959, 14, 457–472. [Google Scholar] [CrossRef]
- Cox, R.G. The motion of long slender bodies in a viscous fluid. Part 2. Shear flow. J. Fluid Mech. 1971, 45, 625–657. [Google Scholar] [CrossRef]
- Zhang, D.; Smith, D.E.; Jack, D.A.; Montgomery-Smith, S. Numerical Evaluation of Single Fiber Motion for Short-Fiber-Reinforced Composite Materials Processing. J. Manuf. Sci. Eng. 2011, 133, 51002. [Google Scholar] [CrossRef]
- Lees, A.W.; Edwards, S.F. The computer study of transport processes under extreme conditions. J. Phys. C Solid State Phys. 1972, 5, 1921–1928. [Google Scholar] [CrossRef]
- Pan, D.; Hu, J.; Shao, X. Lees–Edwards boundary condition for simulation of polymer suspension with dissipative particle dynamics method. Mol. Simul. 2016, 42, 328–336. [Google Scholar] [CrossRef]


| Strain | 0 | ||||
|---|---|---|---|---|---|
 |  | 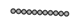 |  | 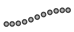 | |
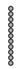 |  |  |  |  | |
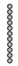 |  |  |  |  | |
 |  |  |  |  | |
 |  |  |  |  |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meyer, N.; Saburow, O.; Hohberg, M.; Hrymak, A.N.; Henning, F.; Kärger, L. Parameter Identification of Fiber Orientation Models Based on Direct Fiber Simulation with Smoothed Particle Hydrodynamics. J. Compos. Sci. 2020, 4, 77. https://doi.org/10.3390/jcs4020077
Meyer N, Saburow O, Hohberg M, Hrymak AN, Henning F, Kärger L. Parameter Identification of Fiber Orientation Models Based on Direct Fiber Simulation with Smoothed Particle Hydrodynamics. Journal of Composites Science. 2020; 4(2):77. https://doi.org/10.3390/jcs4020077
Chicago/Turabian StyleMeyer, Nils, Oleg Saburow, Martin Hohberg, Andrew N. Hrymak, Frank Henning, and Luise Kärger. 2020. "Parameter Identification of Fiber Orientation Models Based on Direct Fiber Simulation with Smoothed Particle Hydrodynamics" Journal of Composites Science 4, no. 2: 77. https://doi.org/10.3390/jcs4020077
APA StyleMeyer, N., Saburow, O., Hohberg, M., Hrymak, A. N., Henning, F., & Kärger, L. (2020). Parameter Identification of Fiber Orientation Models Based on Direct Fiber Simulation with Smoothed Particle Hydrodynamics. Journal of Composites Science, 4(2), 77. https://doi.org/10.3390/jcs4020077






