Peridynamic Mindlin Plate Formulation for Functionally Graded Materials
Abstract
1. Introduction
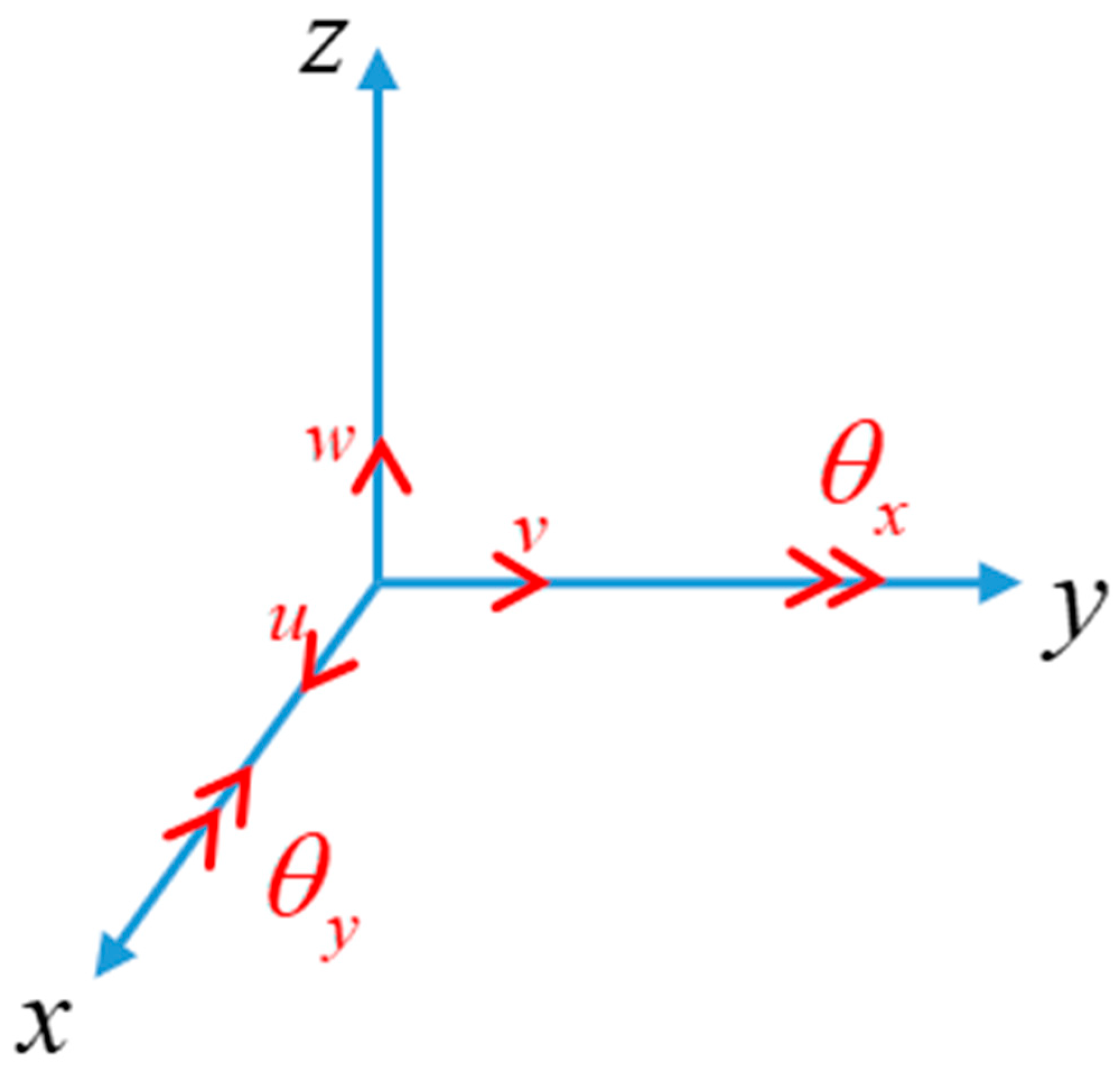
2. Classical Mindlin Plate Formulation
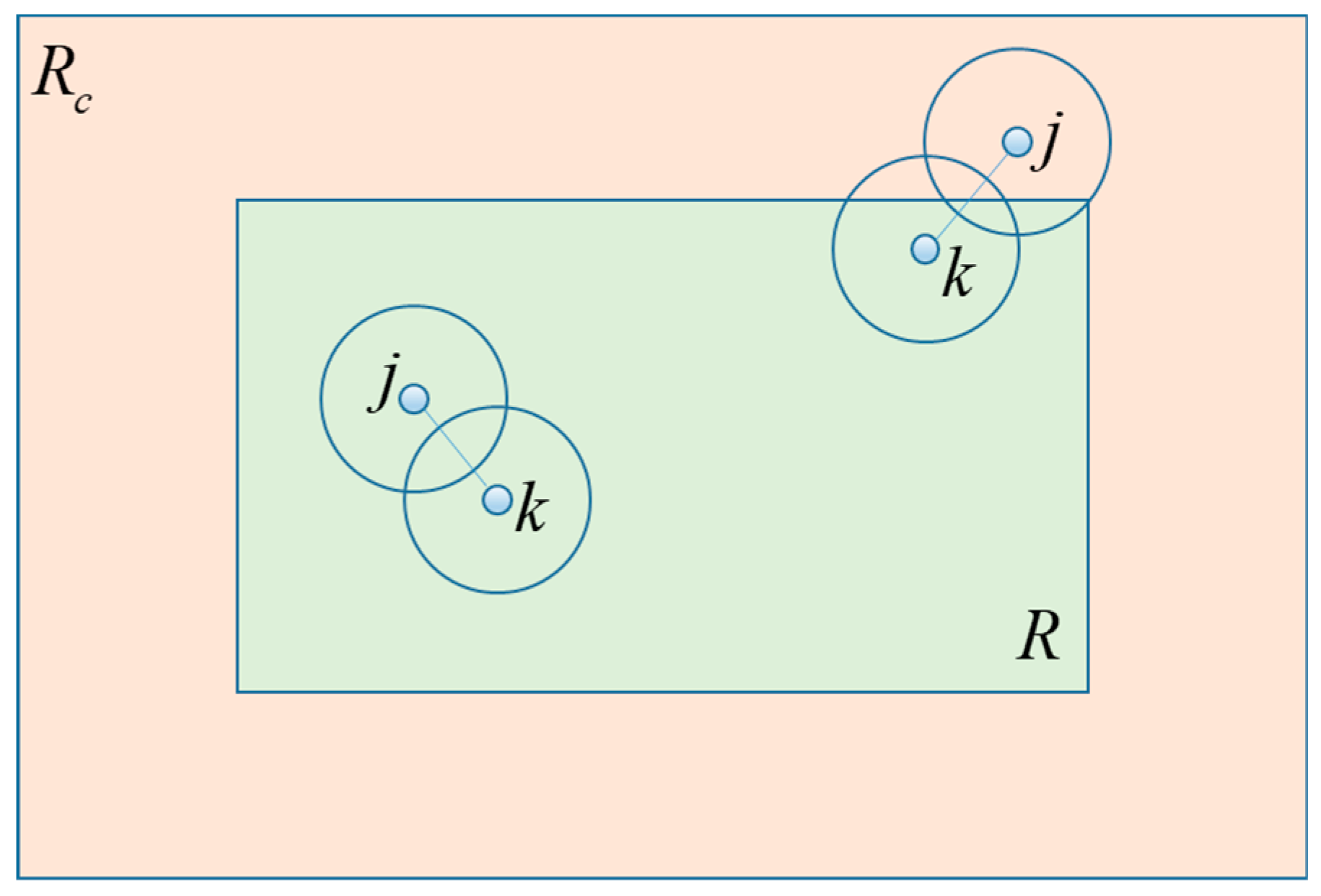
3. Peridynamic Mindlin Plate Formulation
4. Numerical Results
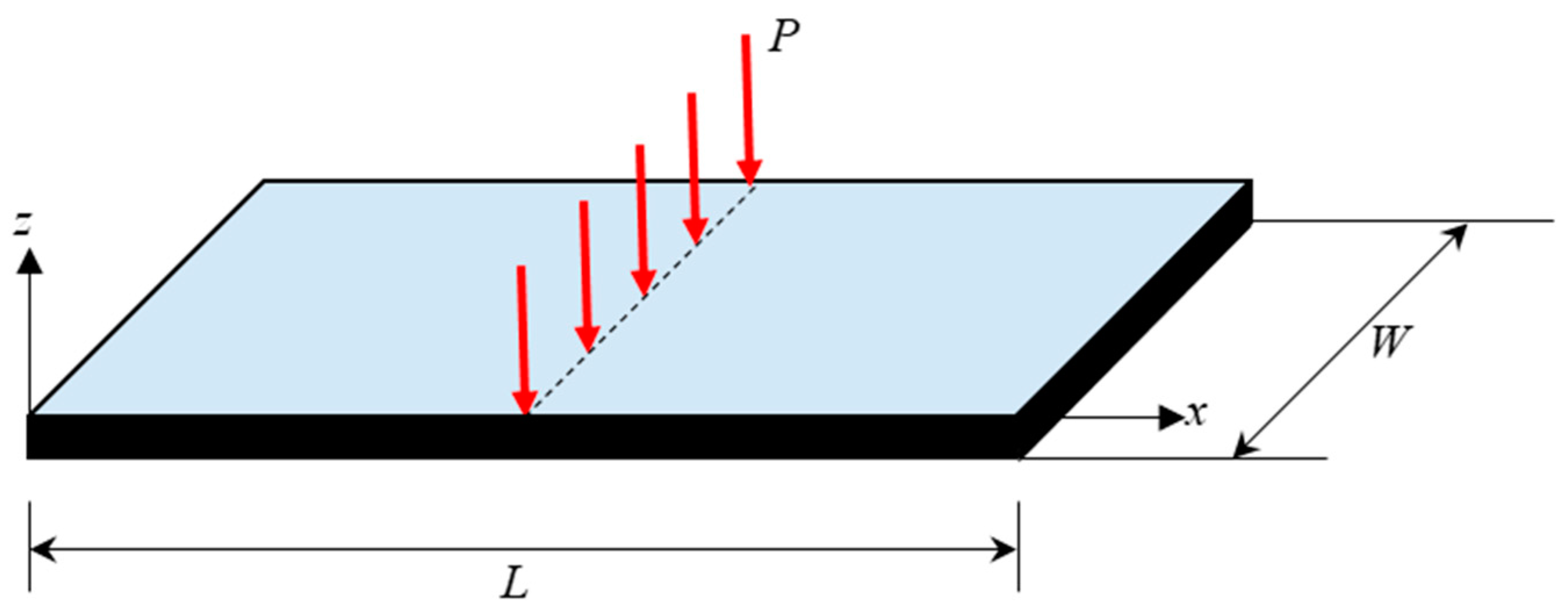
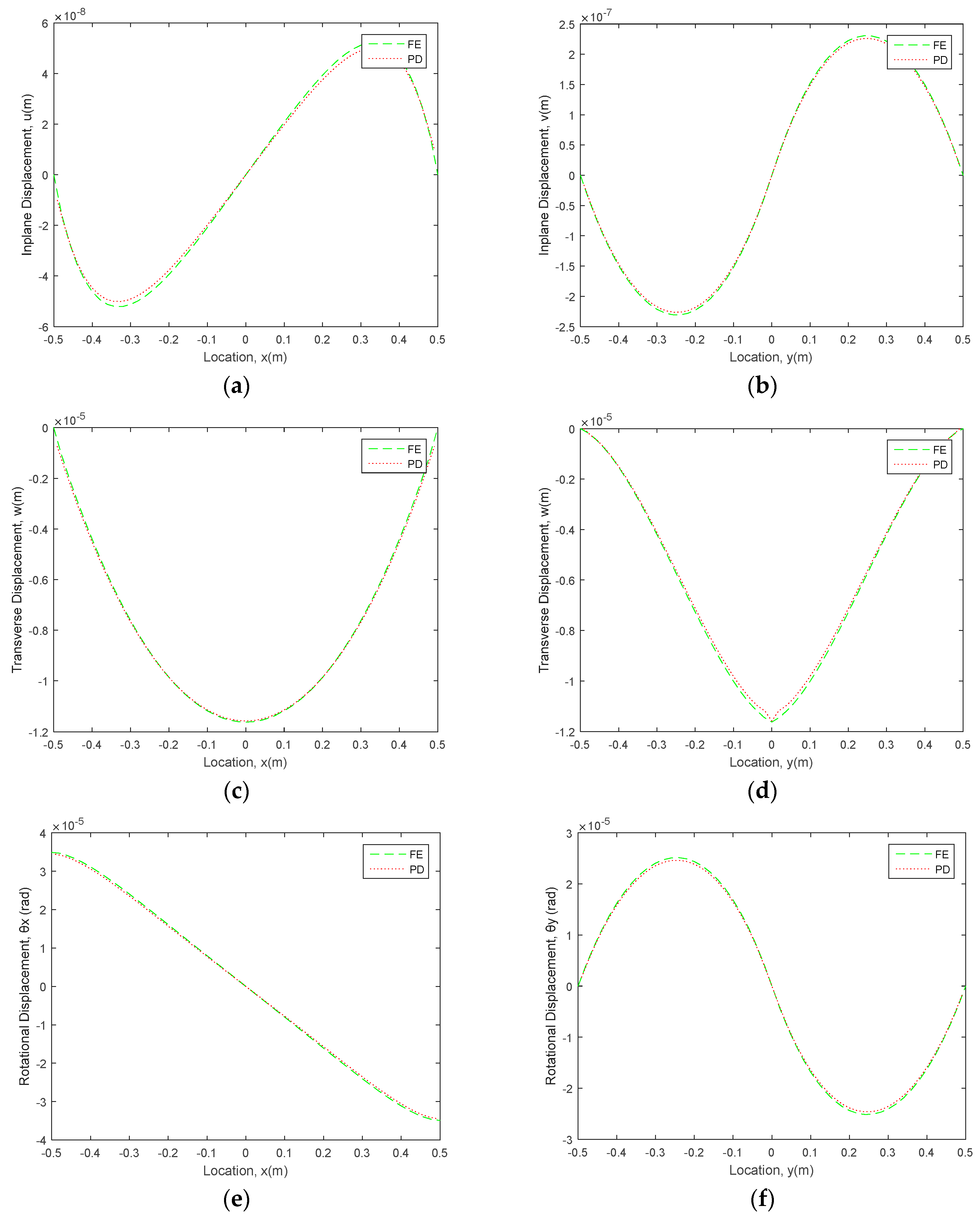
4.1. Simply Supported Functionally Graded Mindlin Plate
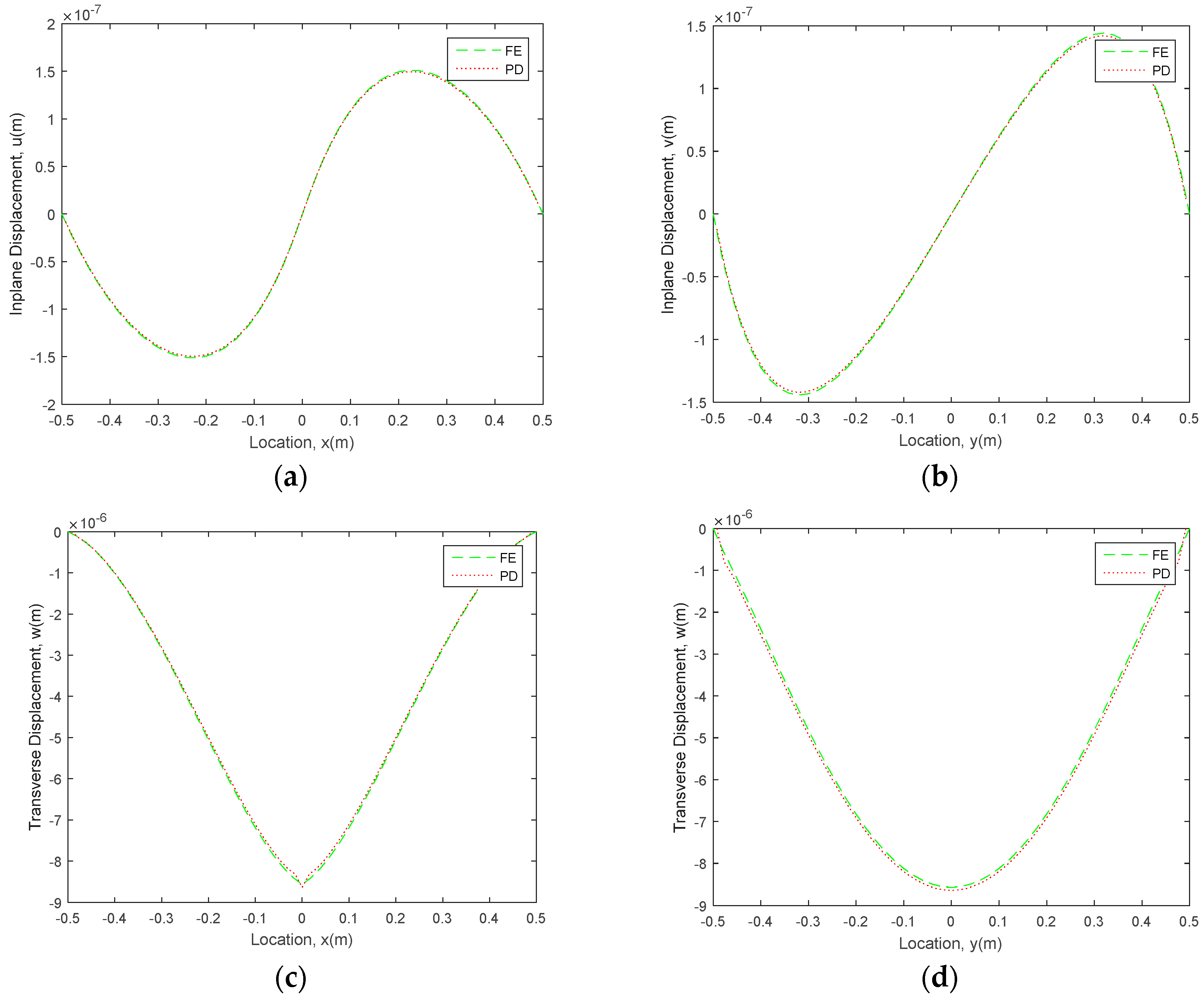
4.2. Fully Clamped Functionally Graded Mindlin Plate
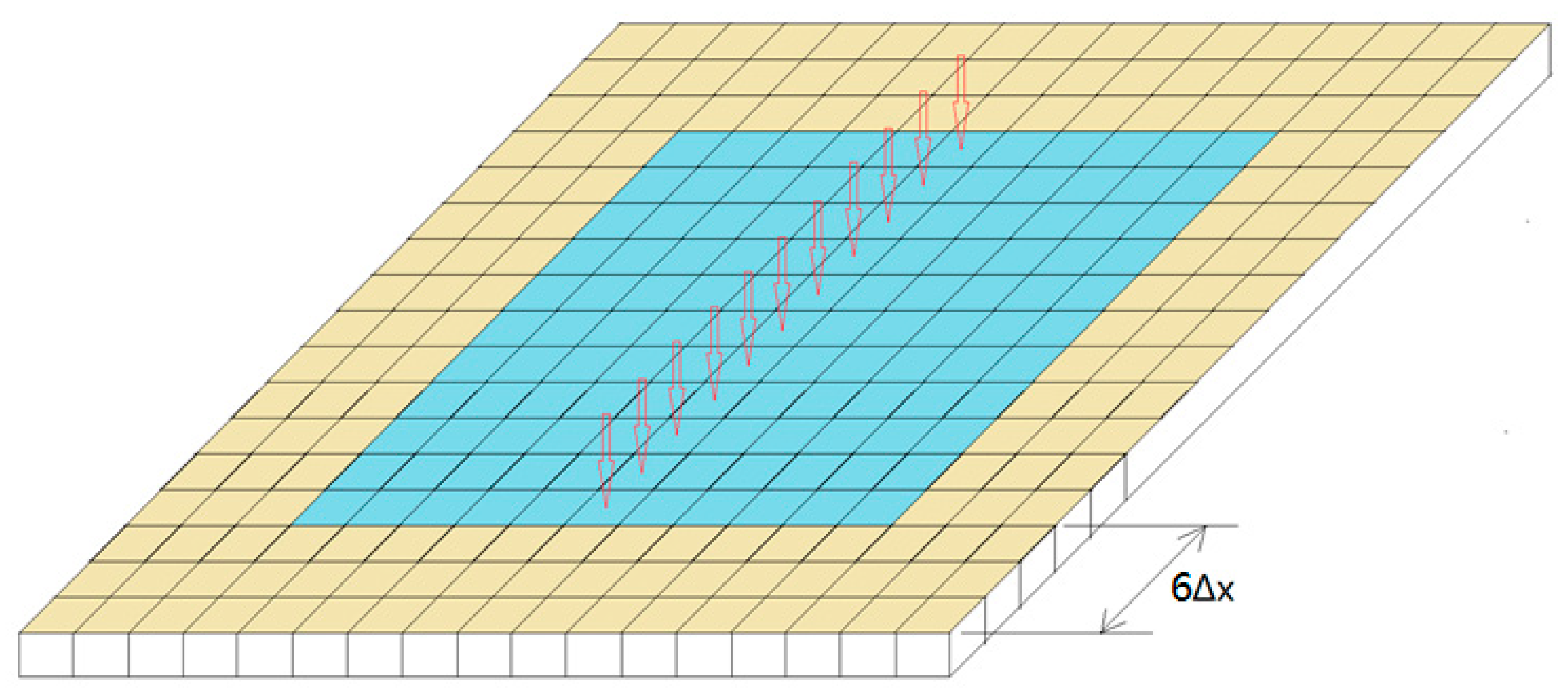
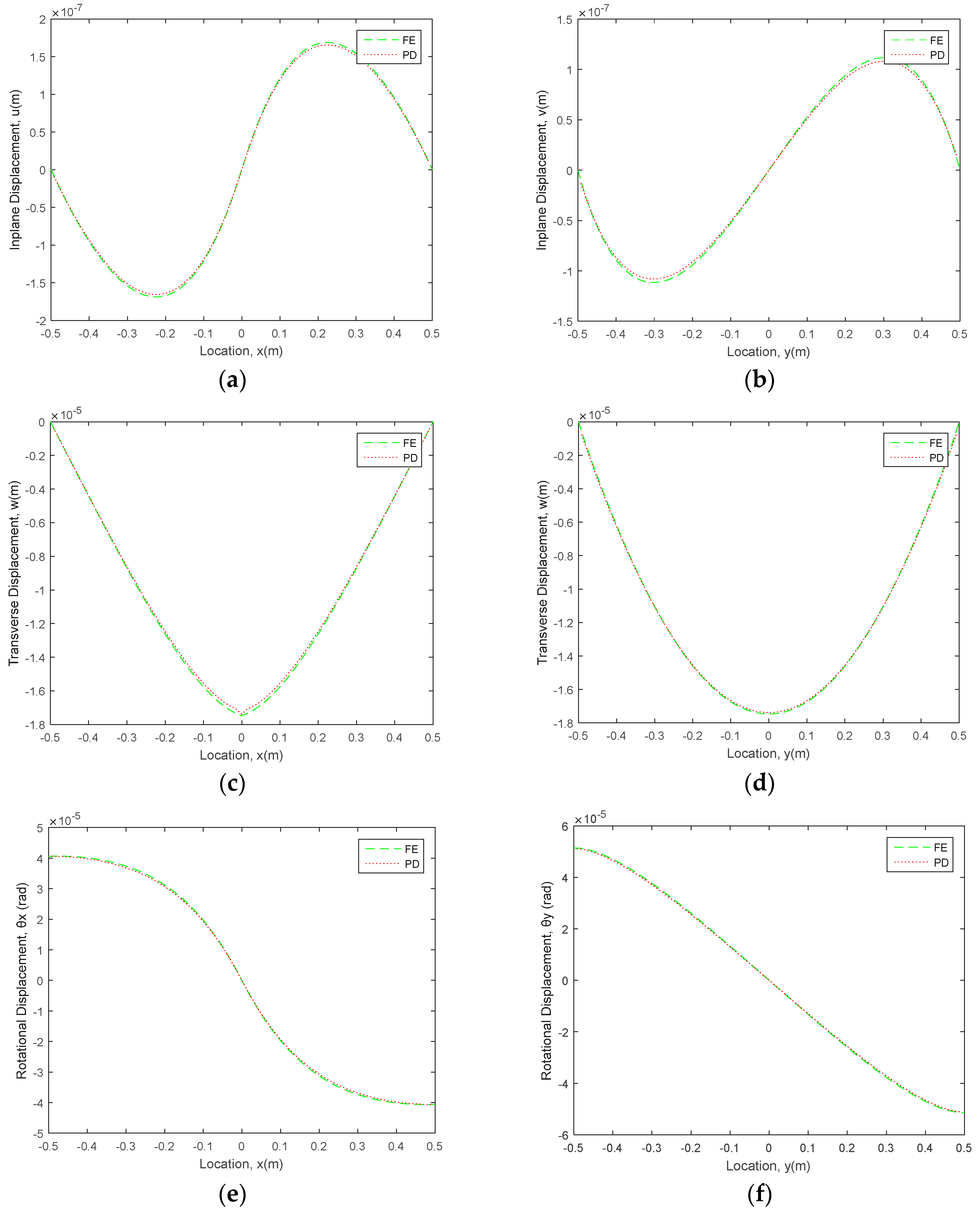
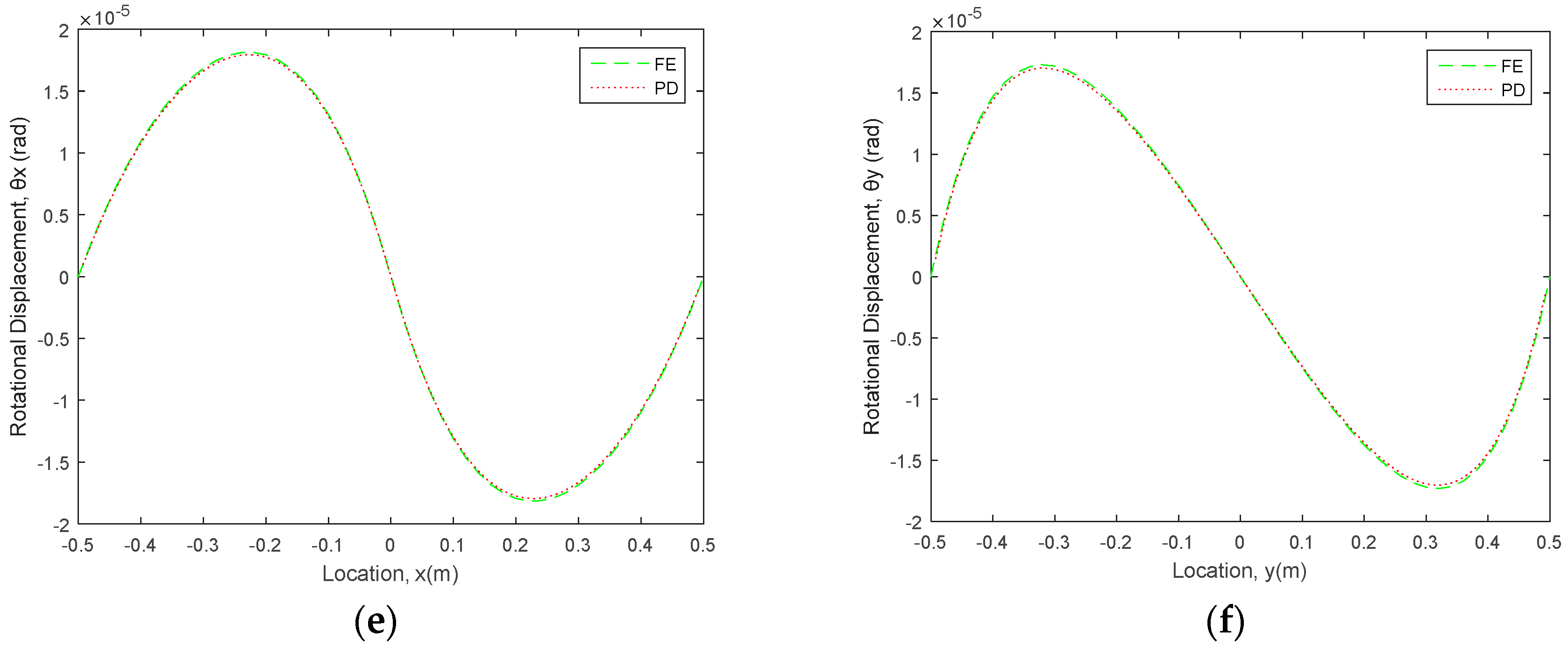
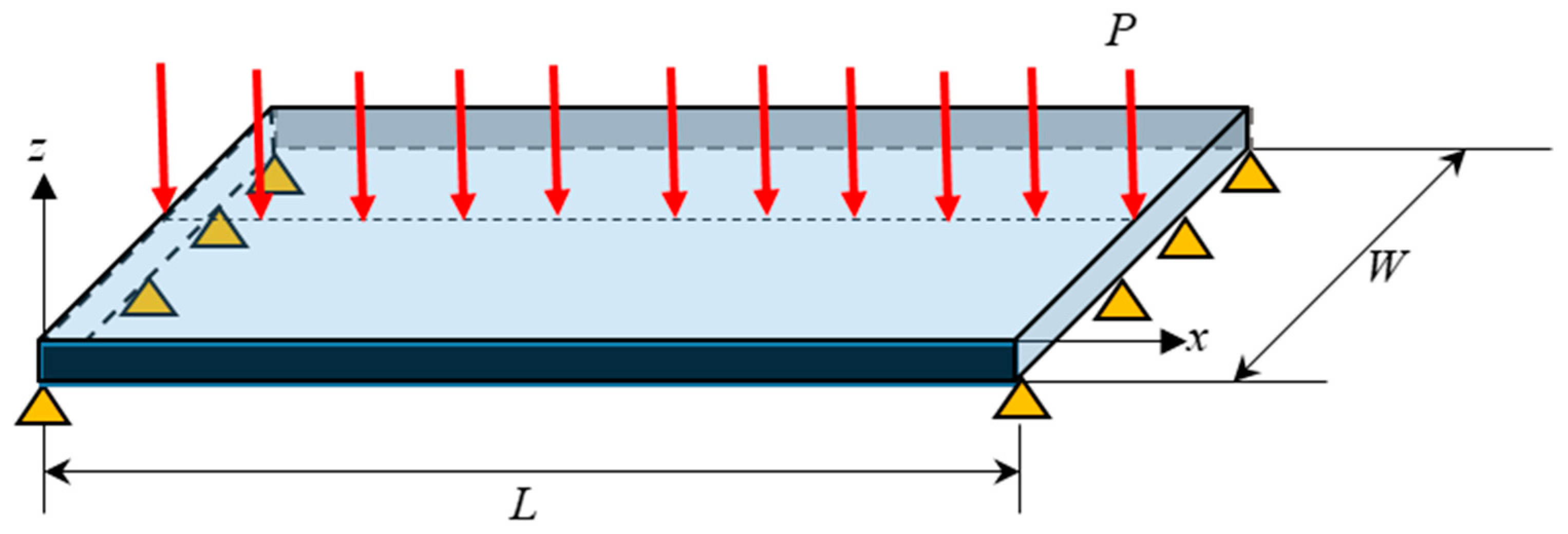
4.3. Functionally Graded Mindlin Plate Subjected to Mixed Boundary Conditions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

Appendix B
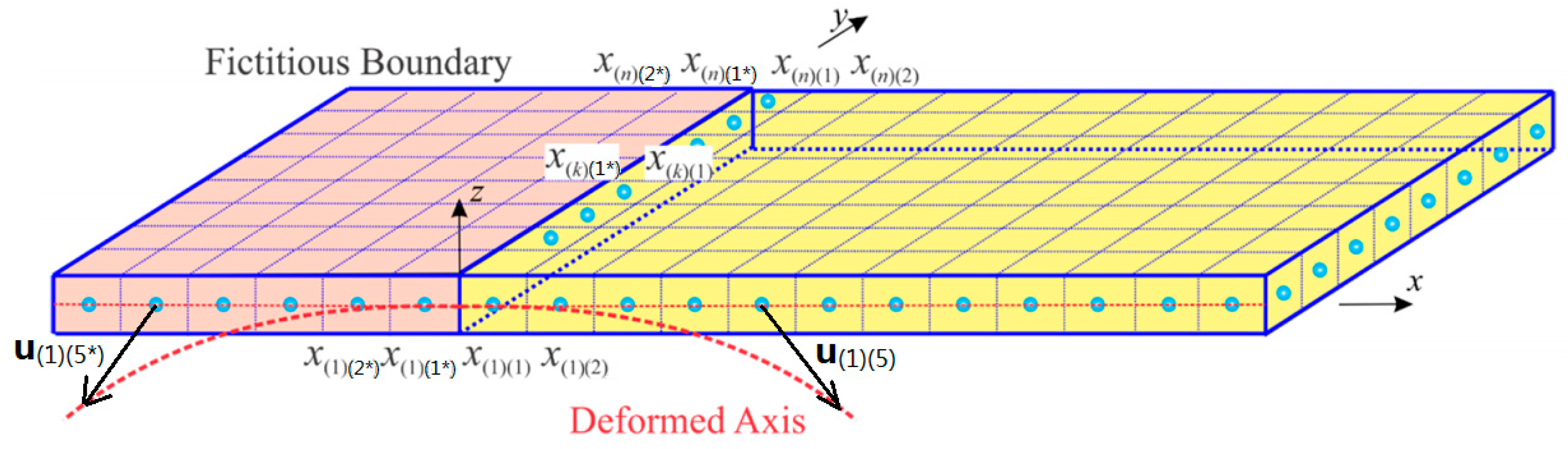
Clamped Boundary Condition
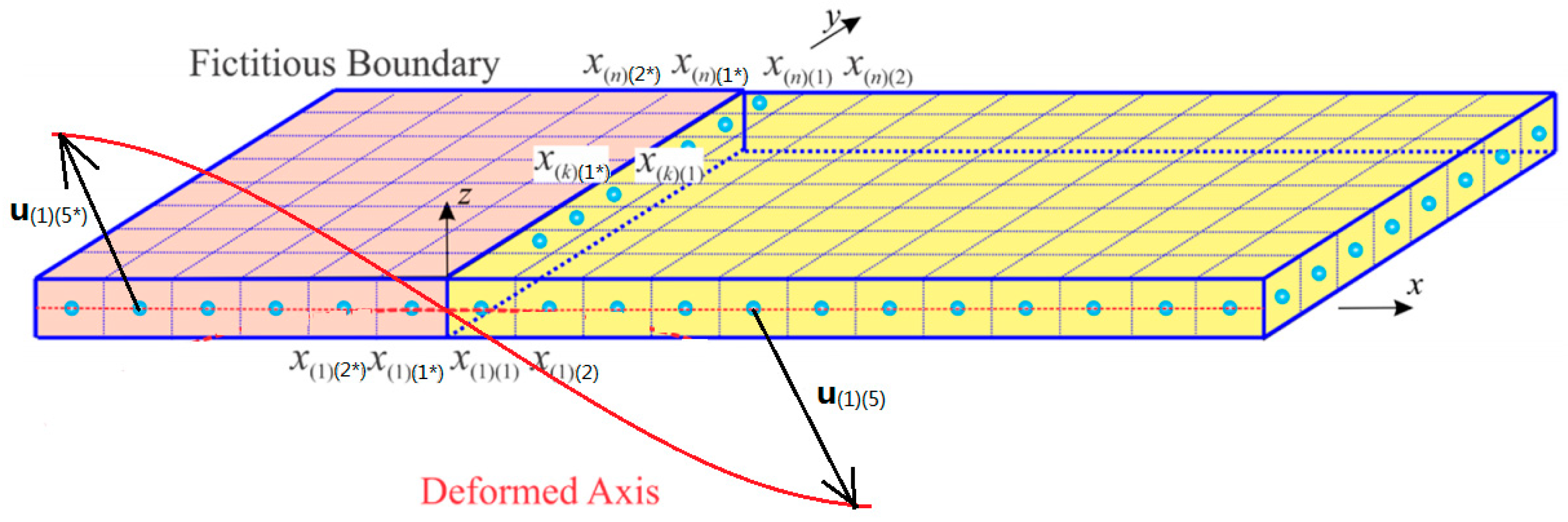
Simply Supported Boundary Condition
References
- Vel, S.; Batra, R.C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates. J. Sound Vib. 2004, 272, 703–730. [Google Scholar] [CrossRef]
- Shen, H.-S. Nonlinear bending response of functionally graded plates subjected to transverse loads and in thermal environments. Int. J. Mech. Sci. 2002, 44, 561–584. [Google Scholar] [CrossRef]
- Zenkour, A. Generalized shear deformation theory for bending analysis of functionally graded plates. Appl. Math. Model. 2006, 30, 67–84. [Google Scholar] [CrossRef]
- Bian, Z.; Chen, W.; Lim, C.W.; Zhang, N. Analytical solutions for single- and multi-span functionally graded plates in cylindrical bending. Int. J. Solids Struct. 2005, 42, 6433–6456. [Google Scholar] [CrossRef][Green Version]
- Carrera, E.; Brischetto, S.; Cinefra, M.; Soave, M. Effects of thickness stretching in functionally graded plates and shells. Compos. Part B Eng. 2011, 42, 123–133. [Google Scholar] [CrossRef]
- Ferreira, A.; Batra, R.C.; Roque, C.; Qian, L.; Martins, P. Static analysis of functionally graded plates using third-order shear deformation theory and a meshless method. Compos. Struct. 2005, 69, 449–457. [Google Scholar] [CrossRef]
- Kashtalyan, M. Three-dimensional elasticity solution for bending of functionally graded rectangular plates. Eur. J. Mech. A Solids 2004, 23, 853–864. [Google Scholar] [CrossRef]
- Xiang, S.; Kang, G.-W. A nth-order shear deformation theory for the bending analysis on the functionally graded plates. Eur. J. Mech. A Solids 2013, 37, 336–343. [Google Scholar] [CrossRef]
- Silling, S. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic States and Constitutive Modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef]
- Jenabidehkordi, A.; Rabczuk, T.; Ma, B.; Dui, G.; Yang, S.; Xin, L. The Multi-Horizon Peridynamics. Comput. Model. Eng. Sci. 2019, 121, 493–500. [Google Scholar] [CrossRef]
- Wang, X.; Kulkarni, S.S.; Tabarraei, A. Concurrent coupling of peridynamics and classical elasticity for elastodynamic problems. Comput. Methods Appl. Mech. Eng. 2019, 344, 251–275. [Google Scholar] [CrossRef]
- Ni, T.; Zaccariotto, M.; Zhu, Q.-Z.; Galvanetto, U. Static solution of crack propagation problems in Peridynamics. Comput. Methods Appl. Mech. Eng. 2019, 346, 126–151. [Google Scholar] [CrossRef]
- Chowdhury, S.R.; Roy, P.; Roy, D.; Reddy, J.N. A modified peridynamics correspondence principle: Removal of zero-energy deformation and other implications. Comput. Methods Appl. Mech. Eng. 2019, 346, 530–549. [Google Scholar] [CrossRef]
- Liu, S.; Fang, G.; Liang, J.; Fu, M.; Wang, B. A new type of peridynamics: Element-based peridynamics. Comput. Methods Appl. Mech. Eng. 2020, 366, 113098. [Google Scholar] [CrossRef]
- Diehl, P.; Prudhomme, S.; Lévesque, M. A Review of Benchmark Experiments for the Validation of Peridynamics Models. J. Peridynamics Nonlocal Model. 2019, 1, 14–35. [Google Scholar] [CrossRef]
- Katiyar, A.; Agrawal, S.; Ouchi, H.; Seleson, P.; Foster, J.T.; Sharma, M.M. A general peridynamics model for multiphase transport of non-Newtonian compressible fluids in porous media. J. Comput. Phys. 2020, 402, 109075. [Google Scholar] [CrossRef]
- Song, X.; Khalili, N. A peridynamics model for strain localization analysis of geomaterials. Int. J. Numer. Anal. Methods Géoméch. 2018, 43, 77–96. [Google Scholar] [CrossRef]
- Ozdemir, M.; Kefal, A.; Imachi, M.; Tanaka, S.; Oterkus, E. Dynamic fracture analysis of functionally graded materials using ordinary state-based peridynamics. Compos. Struct. 2020, 244, 112296. [Google Scholar] [CrossRef]
- Oterkus, E.; Madenci, E. Peridynamics for failure prediction in composites. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 20th AIAA/ASME/AHS Adaptive Structures Conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012; p. 1692. [Google Scholar]
- Yang, Z.; Oterkus, E.; Nguyen, C.T.; Oterkus, S. Implementation of peridynamic beam and plate formulations in finite element framework. Contin. Mech. Thermodyn. 2018, 31, 301–315. [Google Scholar] [CrossRef]
- Diyaroglu, C.; Oterkus, S.; Oterkus, E.; Madenci, E. Peridynamic Modeling of Diffusion by Using Finite-Element Analysis. IEEE Trans. Components Packag. Manuf. Technol. 2017, 7, 1–9. [Google Scholar] [CrossRef]
- Zhu, N.; De Meo, D.; Oterkus, E. Modelling of Granular Fracture in Polycrystalline Materials Using Ordinary State-Based Peridynamics. Materials 2016, 9, 977. [Google Scholar] [CrossRef] [PubMed]
- Imachi, M.; Tanaka, S.; Bui, T.Q.; Oterkus, S.; Oterkus, E. A computational approach based on ordinary state-based peridynamics with new transition bond for dynamic fracture analysis. Eng. Fract. Mech. 2019, 206, 359–374. [Google Scholar] [CrossRef]
- Gao, Y.; Oterkus, S. Ordinary state-based peridynamic modelling for fully coupled thermoelastic problems. Contin. Mech. Thermodyn. 2018, 31, 907–937. [Google Scholar] [CrossRef]
- Wang, H.; Oterkus, E.; Oterkus, S. Predicting fracture evolution during lithiation process using peridynamics. Eng. Fract. Mech. 2018, 192, 176–191. [Google Scholar] [CrossRef]
- Alpay, S.; Madenci, E. Crack growth prediction in fully-coupled thermal and deformation fields using peridynamic theory. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013; p. 1477. [Google Scholar]
- Diyaroglu, C.; Oterkus, E.; Oterkus, S. An Euler–Bernoulli beam formulation in an ordinary state-based peridynamic framework. Math. Mech. Solids 2017, 24, 361–376. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Z.; Mehrmashhadi, J.; Bobaru, F. A stochastic multiscale peridynamic model for corrosion-induced fracture in reinforced concrete. Eng. Fract. Mech. 2020, 229, 106969. [Google Scholar] [CrossRef]
- De Meo, D.; Diyaroglu, C.; Zhu, N.; Oterkus, E.; Siddiq, M.A. Modelling of stress-corrosion cracking by using peridynamics. Int. J. Hydrogen Energy 2016, 41, 6593–6609. [Google Scholar] [CrossRef]
- Ghajari, M.; Iannucci, L.; Curtis, P. A peridynamic material model for the analysis of dynamic crack propagation in orthotropic media. Comput. Methods Appl. Mech. Eng. 2014, 276, 431–452. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, G.; Wang, Y.; Bobaru, F. A peridynamic model for dynamic fracture in functionally graded materials. Compos. Struct. 2015, 133, 529–546. [Google Scholar] [CrossRef]
- Oterkus, E.; Guven, I.; Madenci, E. Impact damage assessment by using peridynamic theory. Open Eng. 2012, 2, 523–531. [Google Scholar] [CrossRef]
- Liu, X.; He, X.; Wang, J.; Sun, L.G.; Oterkus, E. An ordinary state-based peridynamic model for the fracture of zigzag graphene sheets. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180019. [Google Scholar] [CrossRef] [PubMed]
- Madenci, E.; Oterkus, S. Ordinary state-based peridynamics for plastic deformation according to von Mises yield criteria with isotropic hardening. J. Mech. Phys. Solids 2016, 86, 192–219. [Google Scholar] [CrossRef]
- Weckner, O.; Mohamed, N.A.N. Viscoelastic material models in peridynamics. Appl. Math. Comput. 2013, 219, 6039–6043. [Google Scholar] [CrossRef]
- Foster, J.T.; Silling, S.A.; Chen, W.W. Viscoplasticity using peridynamics. Int. J. Numer. Methods Eng. 2009, 81, 1242–1258. [Google Scholar] [CrossRef]
- Oterkus, S.; Madenci, E.; Agwai, A. Peridynamic thermal diffusion. J. Comput. Phys. 2014, 265, 71–96. [Google Scholar] [CrossRef]
- Diyaroglu, C.; Oterkus, S.; Oterkus, E.; Madenci, E.; Han, S.; Hwang, Y. Peridynamic wetness approach for moisture concentration analysis in electronic packages. Microelectron. Reliab. 2017, 70, 103–111. [Google Scholar] [CrossRef]
- Ouchi, H.; Katiyar, A.; York, J.; Foster, J.; Sharma, M.M. A fully coupled porous flow and geomechanics model for fluid driven cracks: A peridynamics approach. Comput. Mech. 2015, 55, 561–576. [Google Scholar] [CrossRef]
- Taylor, M.; Steigmann, D. A two-dimensional peridynamic model for thin plates. Math. Mech. Solids 2013, 20, 998–1010. [Google Scholar] [CrossRef]
- O’Grady, J.; Foster, J. Peridynamic beams: A non-ordinary, state-based model. Int. J. Solids Struct. 2014, 51, 3177–3183. [Google Scholar] [CrossRef]
- O’Grady, J.; Foster, J. Peridynamic plates and flat shells: A non-ordinary, state-based model. Int. J. Solids Struct. 2014, 51, 4572–4579. [Google Scholar] [CrossRef]
- Diyaroglu, C.; Oterkus, E.; Oterkus, S.; Madenci, E. Peridynamics for bending of beams and plates with transverse shear deformation. Int. J. Solids Struct. 2015, 69, 152–168. [Google Scholar] [CrossRef]
- Chowdhury, S.R.; Roy, P.; Roy, D.; Reddy, J.N. A peridynamic theory for linear elastic shells. Int. J. Solids Struct. 2016, 84, 110–132. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2014; Volume 17. [Google Scholar]
- Javili, A.; Morasata, R.; Oterkus, E.; Oterkus, S. Peridynamics review. Math. Mech. Solids 2018, 24, 3714–3739. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Oterkus, E.; Oterkus, S. Peridynamic Mindlin Plate Formulation for Functionally Graded Materials. J. Compos. Sci. 2020, 4, 76. https://doi.org/10.3390/jcs4020076
Yang Z, Oterkus E, Oterkus S. Peridynamic Mindlin Plate Formulation for Functionally Graded Materials. Journal of Composites Science. 2020; 4(2):76. https://doi.org/10.3390/jcs4020076
Chicago/Turabian StyleYang, Zhenghao, Erkan Oterkus, and Selda Oterkus. 2020. "Peridynamic Mindlin Plate Formulation for Functionally Graded Materials" Journal of Composites Science 4, no. 2: 76. https://doi.org/10.3390/jcs4020076
APA StyleYang, Z., Oterkus, E., & Oterkus, S. (2020). Peridynamic Mindlin Plate Formulation for Functionally Graded Materials. Journal of Composites Science, 4(2), 76. https://doi.org/10.3390/jcs4020076






