Bending, Free Vibration, and Buckling Analysis of Functionally Graded Porous Micro-Plates Using a General Third-Order Plate Theory
Abstract
1. Introduction
2. General Third-Order Plate Theory
2.1. Displacements and Strains
2.2. Modified Couple Stress Model
2.3. FGPM Plate Constitutive Equations
2.4. Equation of Motion
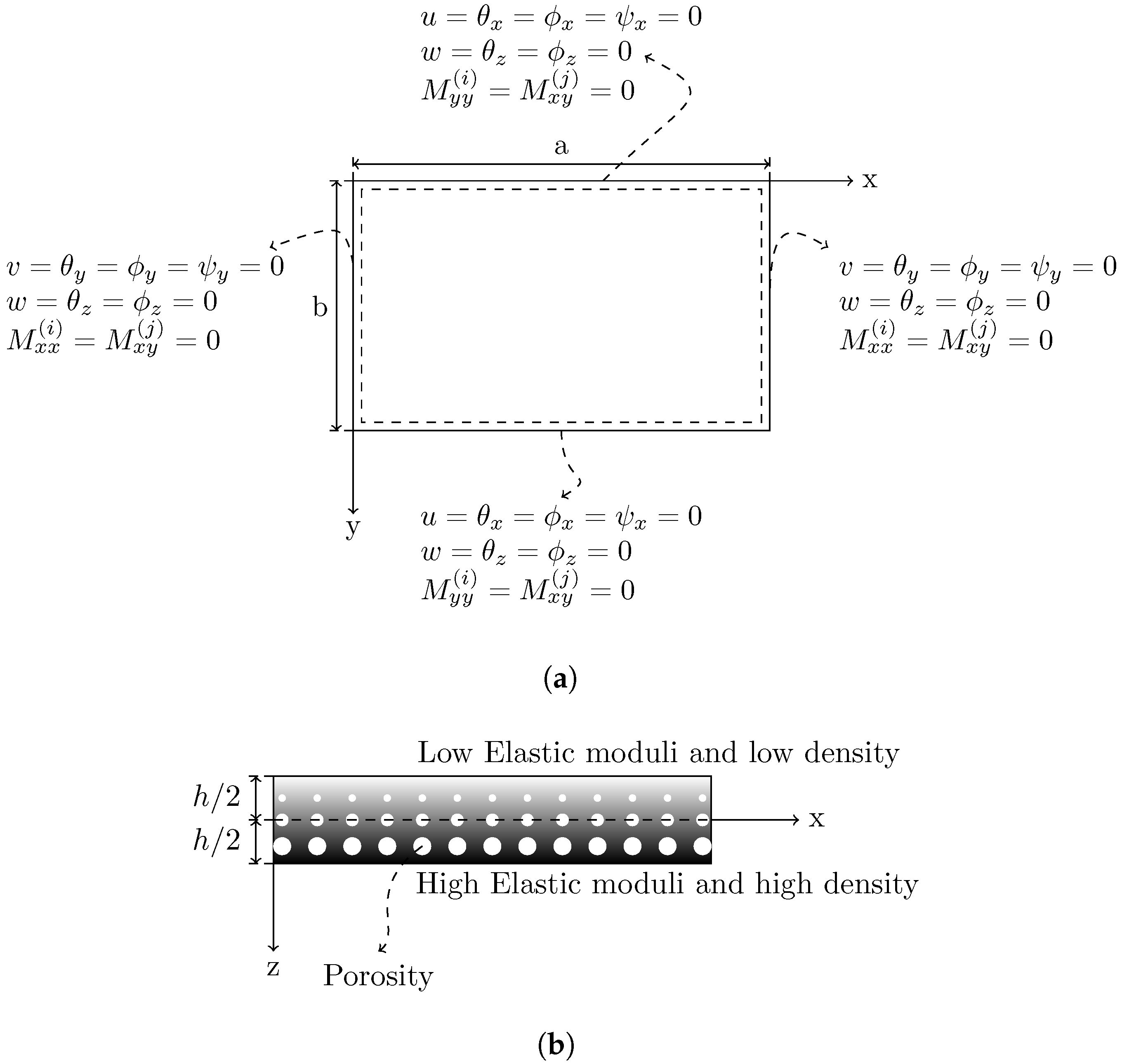
3. Solution Procedure
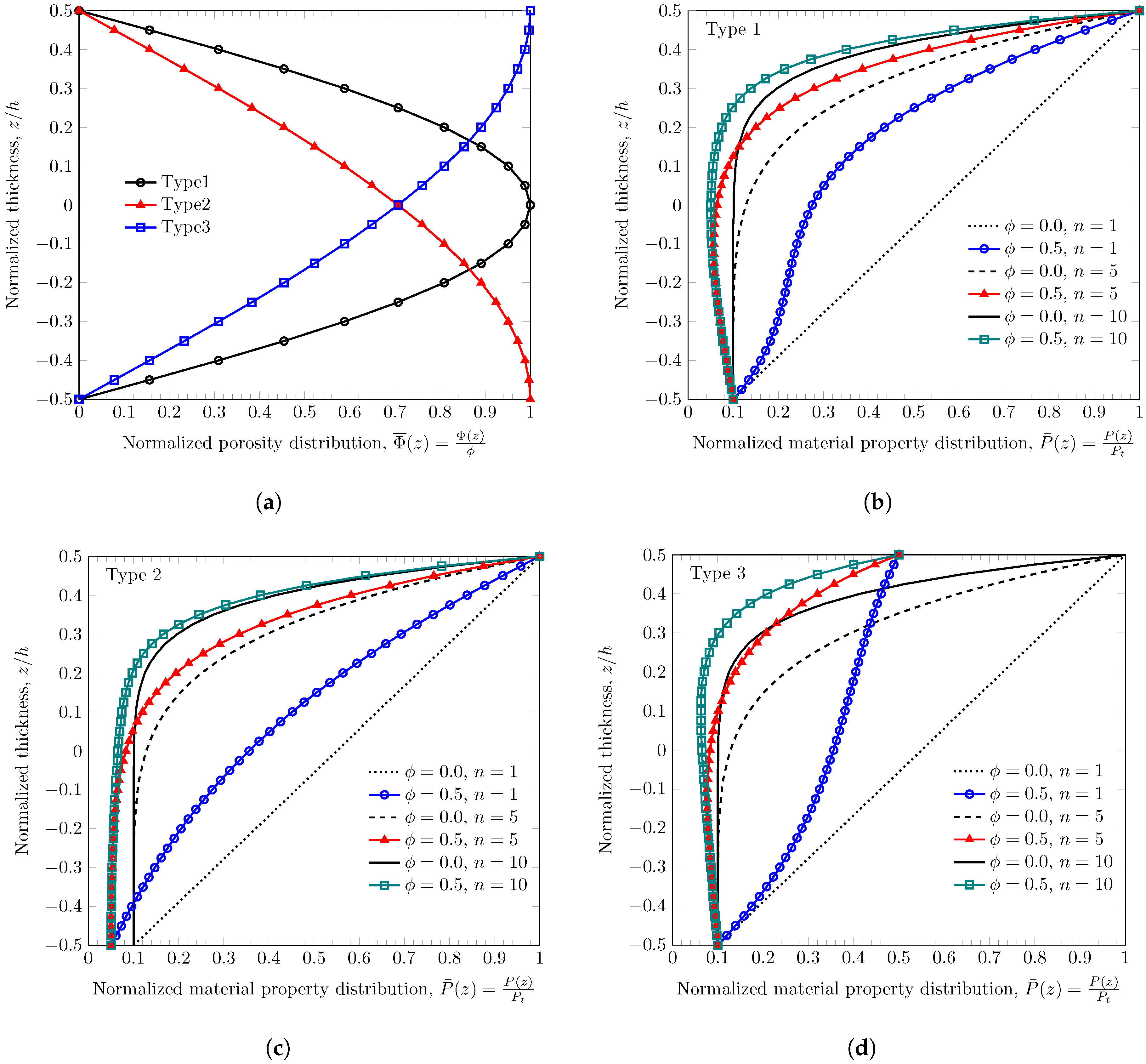
4. Numerical Results and Discussions
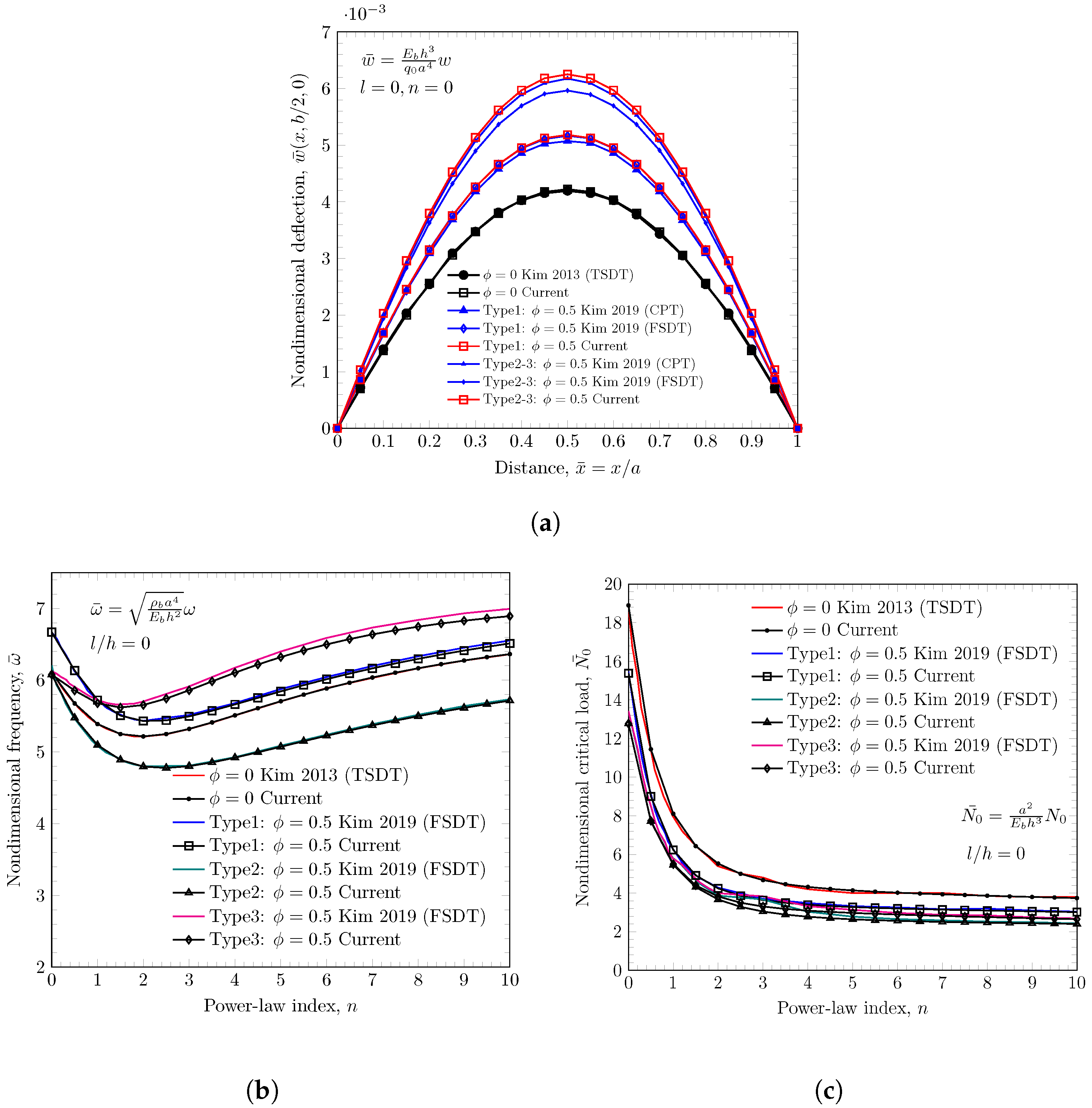
4.1. Verification
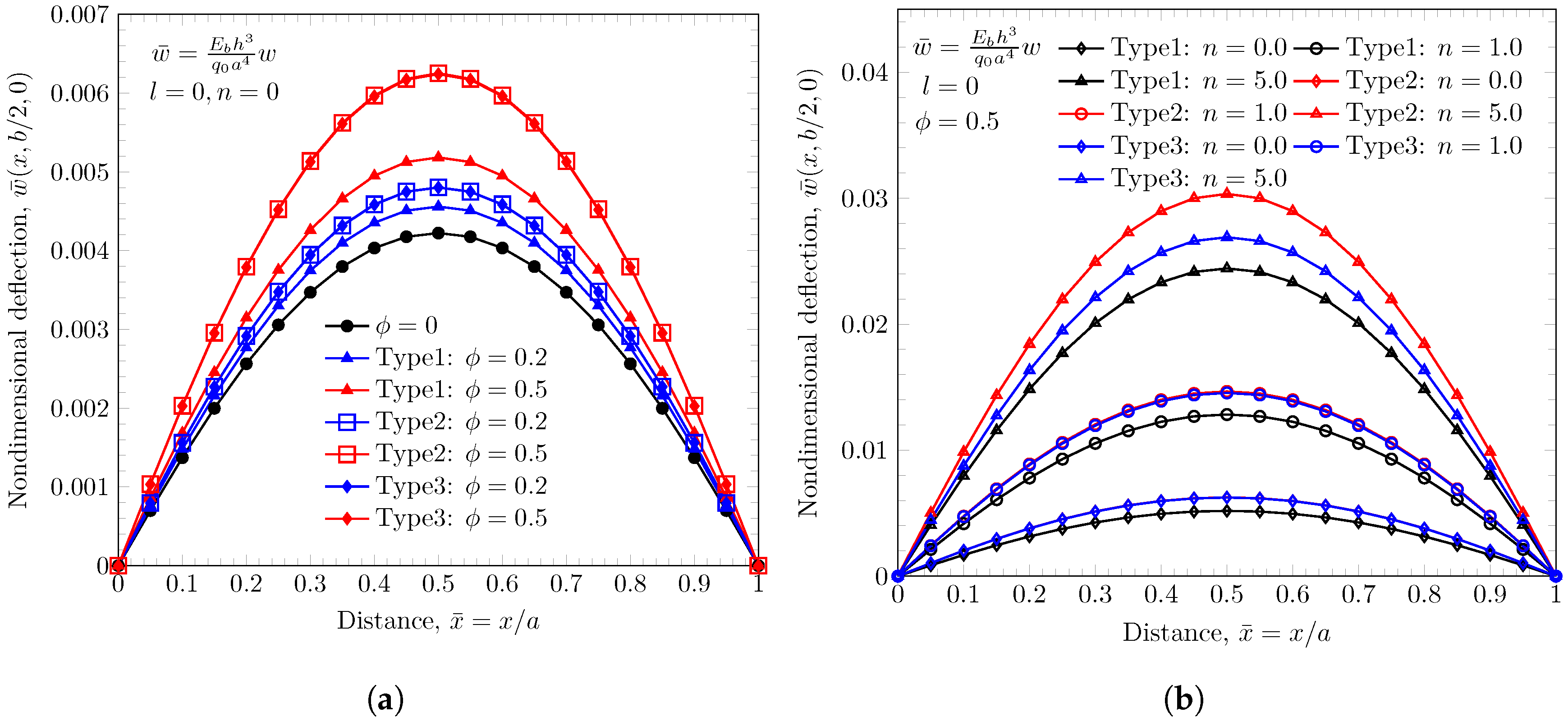
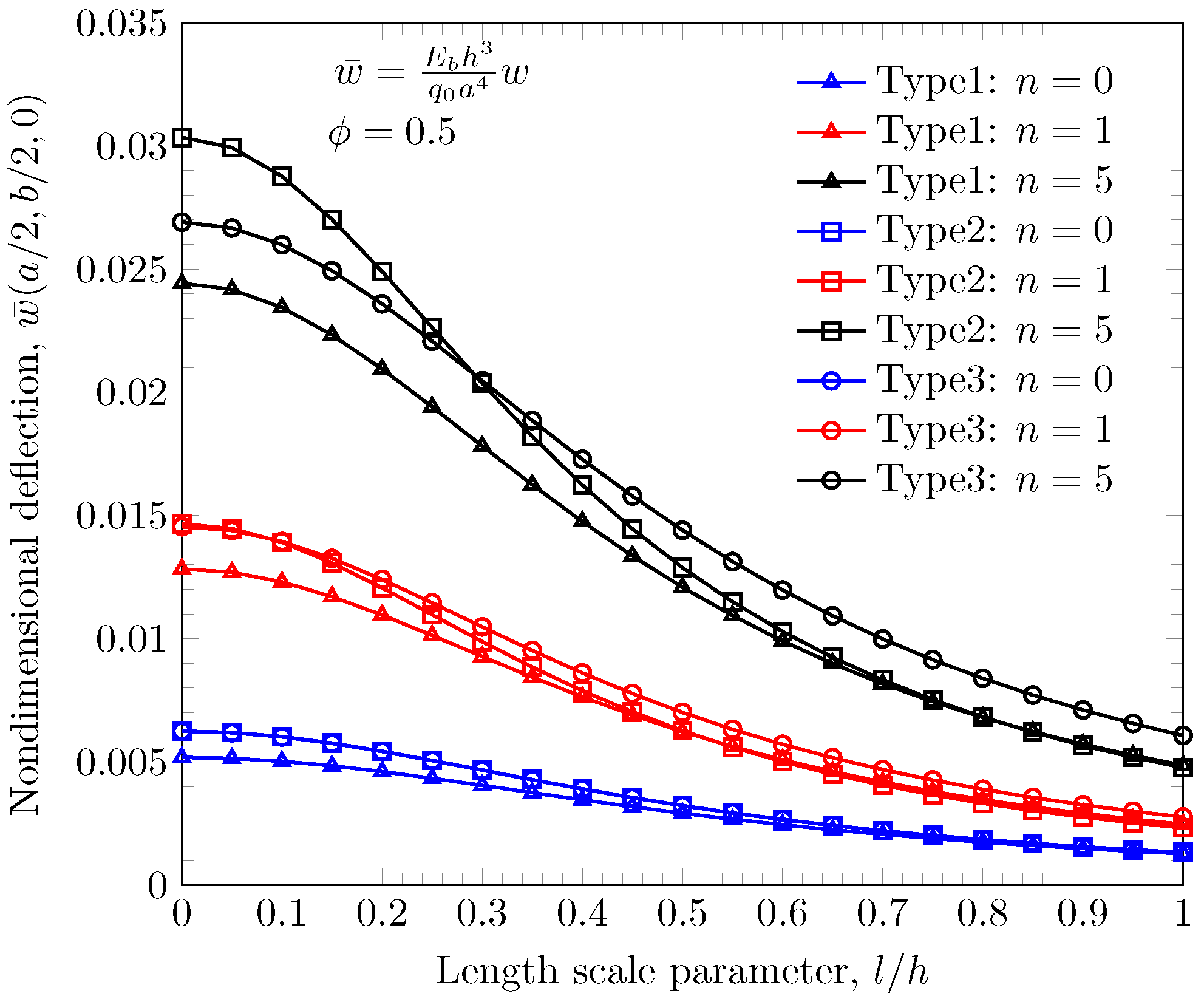
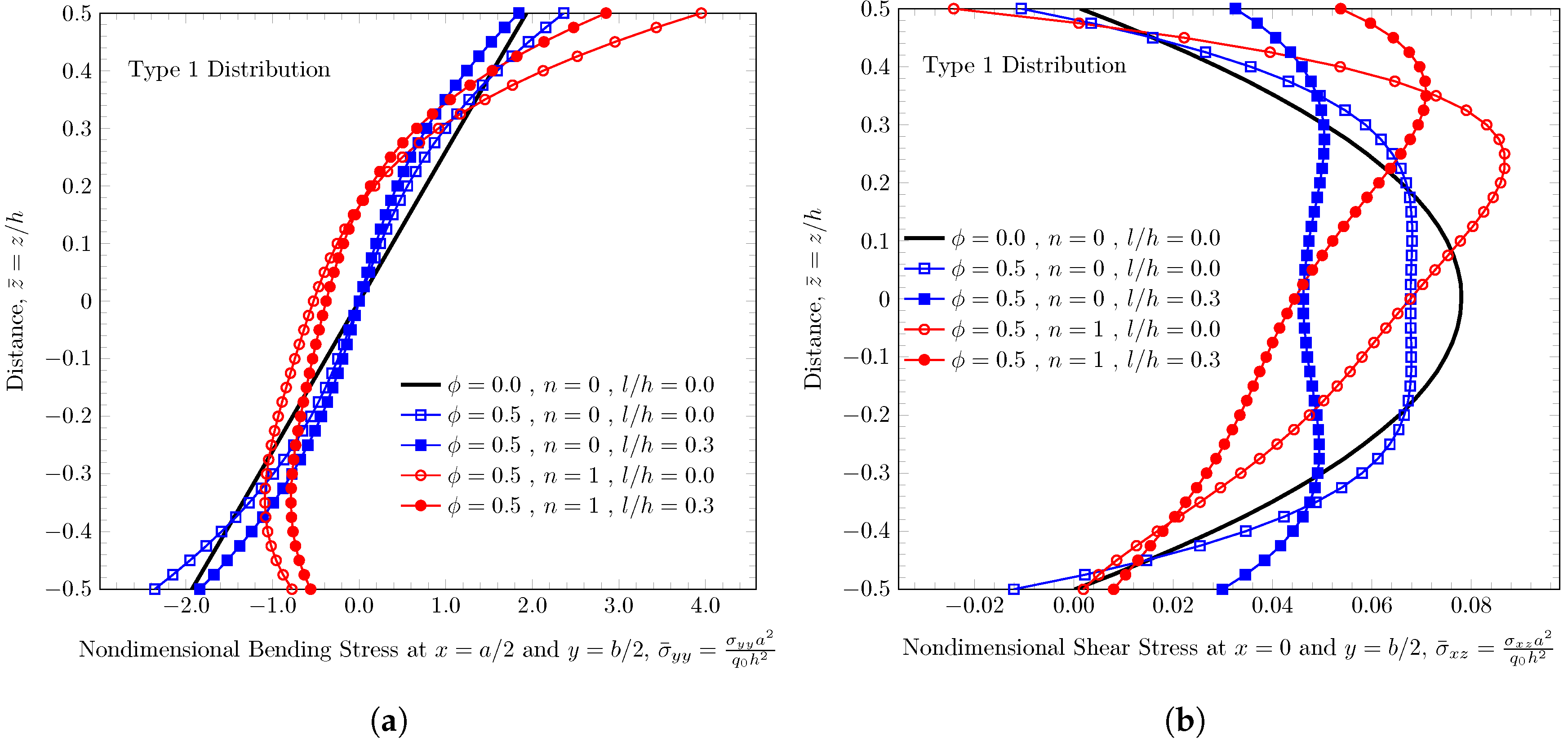
4.2. Static Bending
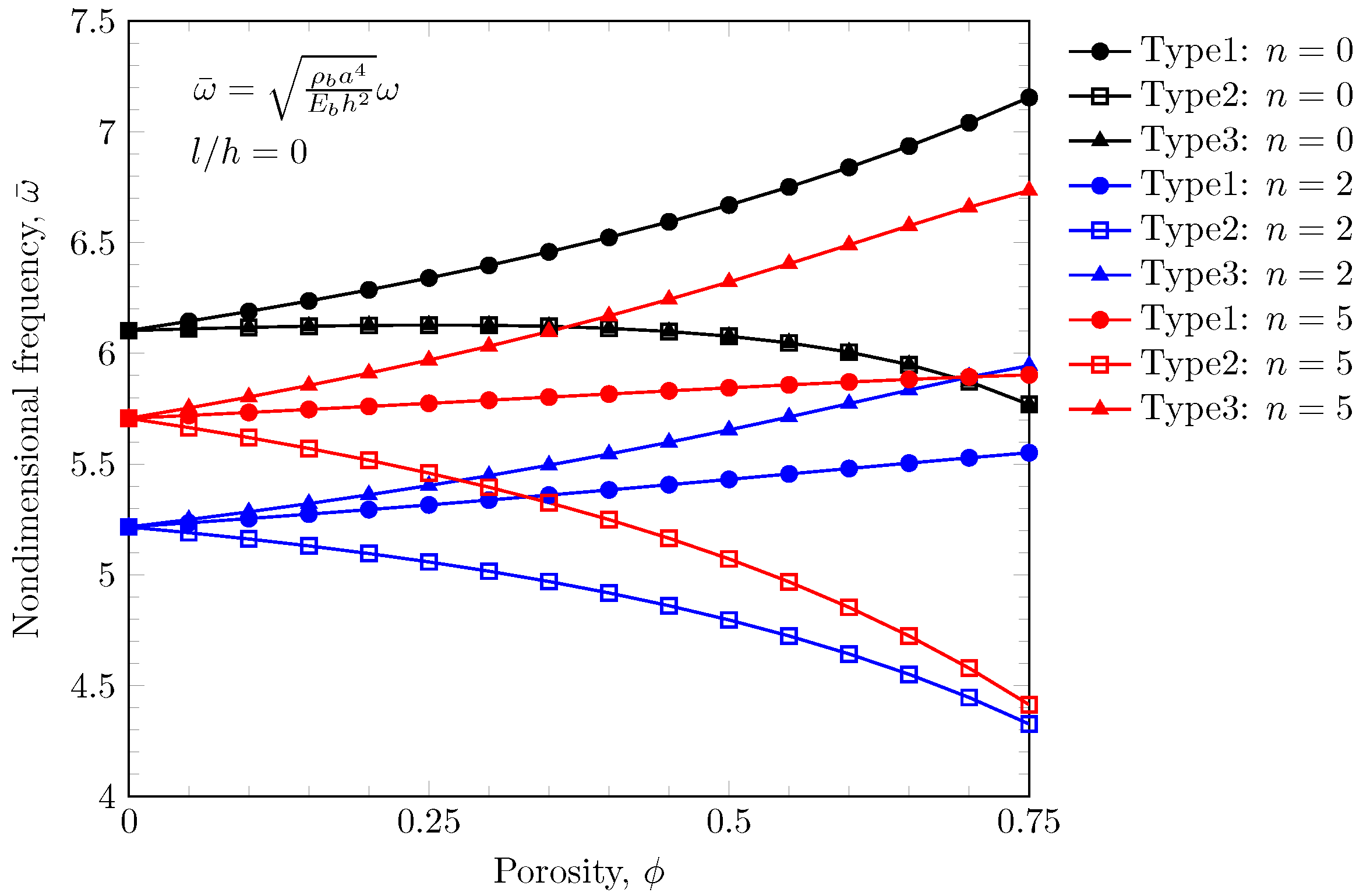
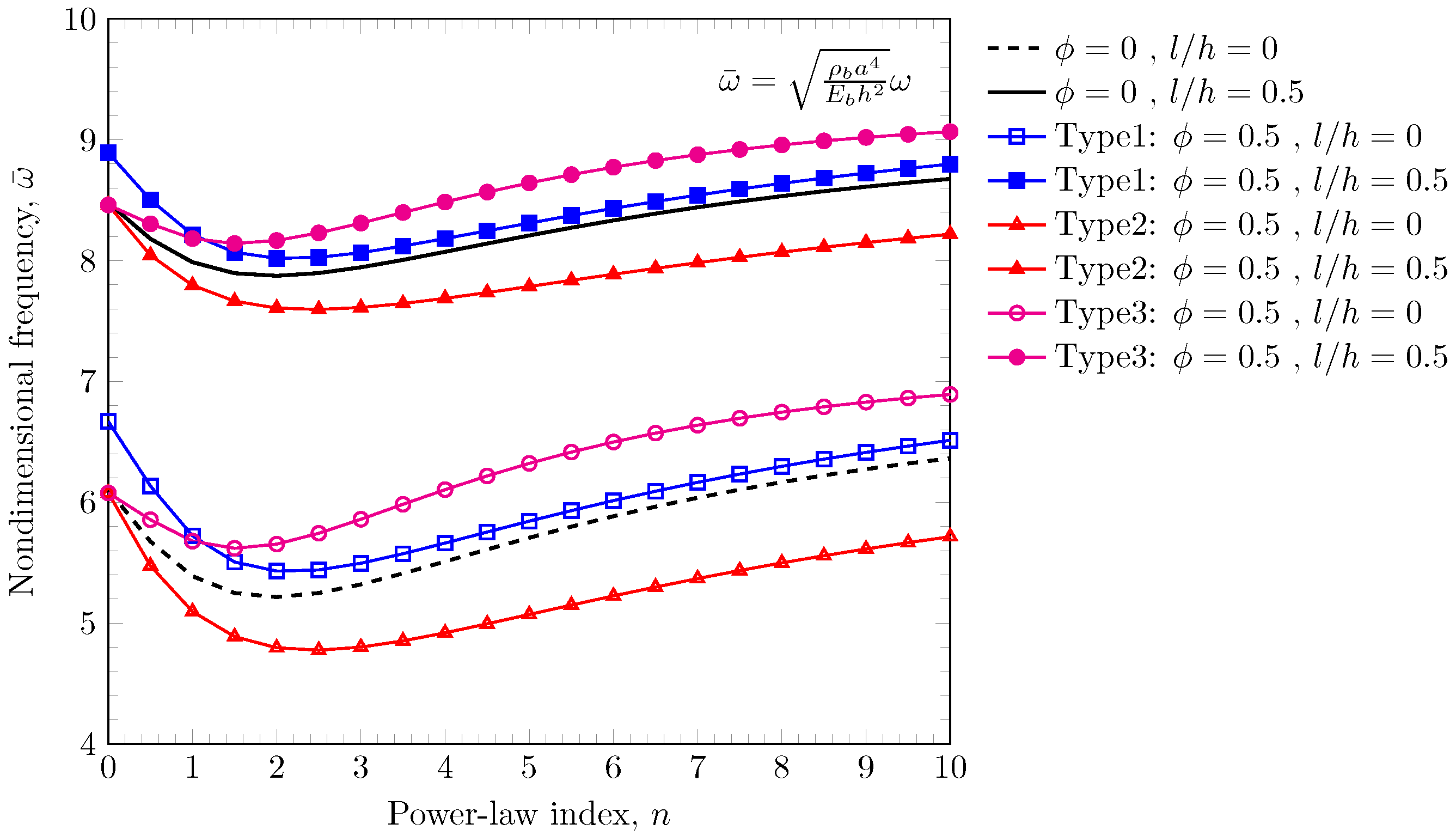
4.3. Free Vibration
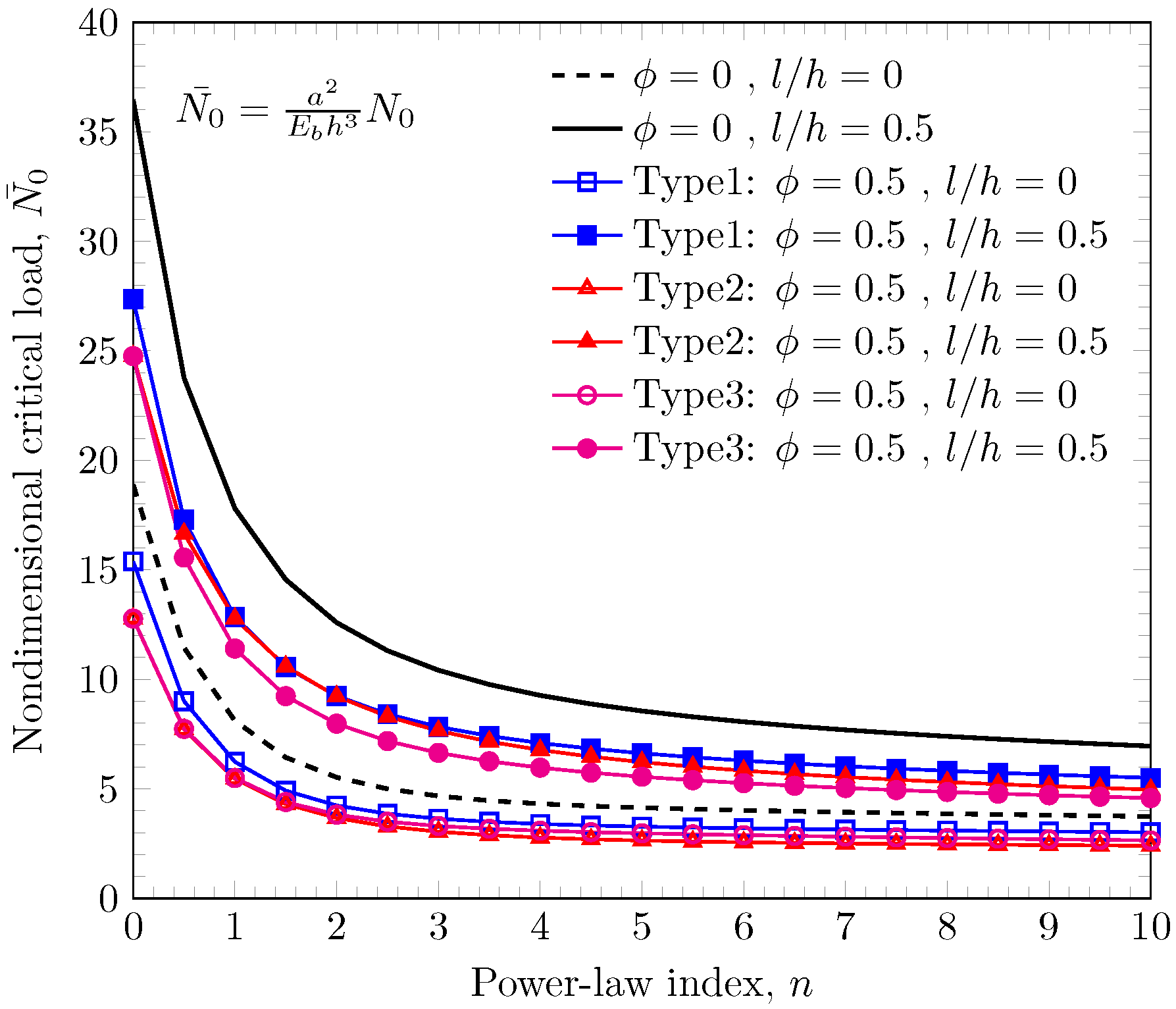
4.4. Buckling
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhushan, B. Nanotribology and nanomechanics of MEMS/NEMS and BioMEMS/BioNEMS materials and devices. In Nanotribology and Nanomechanics: An Introduction, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Fleck, N.A.; Muller, G.M.; Ashby, M.F.; Hutchinson, J.W. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Lam, D.C.; Yang, F.; Chong, A.C.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Mcfarland, A.W.; Colton, J.S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J. Micromech. Microeng. 2005, 15, 1060–1067. [Google Scholar] [CrossRef]
- Motz, C.; Schöberl, T.; Pippan, R. Mechanical properties of micro-sized copper bending beams machined by the focused ion beam technique. Acta Mater. 2005, 53, 4269–4279. [Google Scholar] [CrossRef]
- Demir, E.; Raabe, D.; Roters, F. The mechanical size effect as a mean-field breakdown phenomenon: Example of microscale single crystal beam bending. Acta Mater. 2010, 58, 1876–1886. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S. Size effect on dynamic stability of functionally graded microbeams based on a modified couple stress theory. Compos. Struct. 2011, 93, 342–350. [Google Scholar] [CrossRef]
- Liu, D.; He, Y.; Dunstan, D.J.; Zhang, B.; Gan, Z.; Hu, P.; Ding, H. Toward a further understanding of size effects in the torsion of thin metal wires: An experimental and theoretical assessment. Int. J. Plast. 2013, 41, 30–52. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 2015, 133, 54–61. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Tiersten, H.F. Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 1962, 11, 415–448. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.C.; Lam, D.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Fleck, N.A.; Hutchinson, J.W. A reformulation of strain gradient plasticity. J. Mech. Phys. Solids 2001, 49, 2245–2271. [Google Scholar] [CrossRef]
- Yang, Y.Y. Stress analysis in a joint with a functionally graded material under a thermal loading by using the Mellin transform method. Int. J. Solids Struct. 1998, 35, 1261–1287. [Google Scholar] [CrossRef]
- Neubrand, A.; Chung, T.J.; Rödel, J.; Steffler, E.D.; Fett, T. Residual stresses in functionally graded plates. J. Mater. Res. 2002, 17, 2912–2920. [Google Scholar] [CrossRef]
- Birman, V.; Byrd, L.W. Modeling and Analysis of Functionally Graded Materials and Structures. Appl. Mech. Rev. 2007, 60, 195. [Google Scholar] [CrossRef]
- Şimşek, M.; Reddy, J.N. A unified higher order beam theory for buckling of a functionally graded microbeam embedded in elastic medium using modified couple stress theory. Compos. Struct. 2013, 101, 47–58. [Google Scholar] [CrossRef]
- Reddy, J.N. Microstructure-dependent couple stress theories of functionally graded beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Javaheri, R.; Eslami, M.R. Buckling of functionally graded plates under in-plane compressive loading. J. Appl. Math. Mech. 2002, 82, 277–283. [Google Scholar] [CrossRef]
- Ma, L.S.; Wang, T.J. Nonlinear bending and post-buckling of a functionally graded circular plate under mechanical and thermal loadings. Int. J. Solids Struct. 2003, 40, 3311–3330. [Google Scholar] [CrossRef]
- Lanhe, W. Thermal buckling of a simply supported moderately thick rectangular FGM plate. Compos. Struct. 2004, 64, 211–218. [Google Scholar] [CrossRef]
- Reddy, J.; Kim, J. A nonlinear modified couple stress-based third-order theory of functionally graded plates. Compos. Struct. 2012, 94, 1128–1143. [Google Scholar] [CrossRef]
- Kim, J.; Reddy, J.N. Analytical solutions for bending, vibration, and buckling of FGM plates using a couple stress-based third-order theory. Compos. Struct. 2013, 103, 86–98. [Google Scholar] [CrossRef]
- Ansari, R.; Faghih Shojaei, M.; Mohammadi, V.; Gholami, R.; Darabi, M.A. Nonlinear vibrations of functionally graded Mindlin microplates based on the modified couple stress theory. Compos. Struct. 2014, 114, 124–134. [Google Scholar] [CrossRef]
- Zhang, B.; He, Y.; Liu, D.; Shen, L.; Lei, J. An efficient size-dependent plate theory for bending, buckling and free vibration analyses of functionally graded microplates resting on elastic foundation. Appl. Math. Model. 2015, 39, 3814–3845. [Google Scholar] [CrossRef]
- Al Jahwari, F.; Anwer, A.A.; Naguib, H.E. Fabrication and microstructural characterization of functionally graded porous acrylonitrile butadiene styrene and the effect of cellular morphology on creep behavior. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 795–803. [Google Scholar] [CrossRef]
- Al Jahwari, F.; Huang, Y.; Naguib, H.E.; Lo, J. Relation of impact strength to the microstructure of functionally graded porous structures of acrylonitrile butadiene styrene (ABS) foamed by thermally activated microspheres. Polymer 2016, 98, 270–281. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Shishkovsky, I.; Bertrand, P.; Smurov, I. Manufacturing of fine-structured 3D porous filter elements by selective laser melting. Appl. Surf. Sci. 2009, 255, 5523–5527. [Google Scholar] [CrossRef]
- Koohbor, B.; Kidane, A. Design optimization of continuously and discretely graded foam materials for efficient energy absorption. Mater. Des. 2016, 102, 151–161. [Google Scholar] [CrossRef]
- Giannitelli, S.M.; Basoli, F.; Mozetic, P.; Piva, P.; Bartuli, F.N.; Luciani, F.; Arcuri, C.; Trombetta, M.; Rainer, A.; Licoccia, S. Graded porous polyurethane foam: A potential scaffold for oro-maxillary bone regeneration. Mater. Sci. Eng. C 2015, 51, 329–335. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Li, Y.; Wang, Q.; Wen, S.; Wei, Q.; Yan, C.; Hao, L.; Liu, J.; Shi, Y. Continuous functionally graded porous titanium scaffolds manufactured by selective laser melting for bone implants. J. Mech. Behav. Biomed. Mater. 2018, 80, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Yang, J.; Kitipornchai, S. Free and forced vibrations of shear deformable functionally graded porous beams. Int. J. Mech. Sci. 2016, 108, 14–22. [Google Scholar] [CrossRef]
- Shafiei, N.; Kazemi, M. Buckling analysis on the bi-dimensional functionally graded porous tapered nano-/micro-scale beams. Aerosp. Sci. Technol. 2017, 66, 1–11. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Q.; Deng, X.; Choe, K.; Xie, F.; Shuai, C. A modified series solution for free vibration analyses of moderately thick functionally graded porous (FGP) deep curved and straight beams. Compos. Part B Eng. 2018, 165, 155–166. [Google Scholar] [CrossRef]
- Wu, D.; Liu, A.; Huang, Y.; Huang, Y.; Pi, Y.; Gao, W. Dynamic analysis of functionally graded porous structures through finite element analysis. Eng. Struct. 2018, 165, 287–301. [Google Scholar] [CrossRef]
- Shahverdi, H.; Barati, M.R. Vibration analysis of porous functionally graded nanoplates. Int. J. Eng. Sci. 2017, 120, 82–99. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Wan, Y.H.; Zhang, Y.F. Vibrations of longitudinally traveling functionally graded material plates with porosities. Eur. J. Mech. A Solids 2017, 66, 55–68. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R.; Abrishamdari, M.; Mohammadi, M.H. Natural frequencies of functionally graded plates with porosities via a simple four variable plate theory: An analytical approach. Thin-Walled Struct. 2017, 120, 366–377. [Google Scholar] [CrossRef]
- Thai, H.T.; Choi, D.H. A simple first-order shear deformation theory for the bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 101, 332–340. [Google Scholar] [CrossRef]
- Akbaş, S.D. Vibration and static analysis of functionally graded porous plates. J. Appl. Comput. Mech. 2017, 3, 199–207. [Google Scholar]
- Wang, Y.Q.; Zu, J.W. Large-amplitude vibration of sigmoid functionally graded thin plates with porosities. Thin-Walled Struct. 2017, 119, 911–924. [Google Scholar] [CrossRef]
- Cong, P.H.; Chien, T.M.; Khoa, N.D.; Duc, N.D. Nonlinear thermomechanical buckling and post-buckling response of porous FGM plates using Reddy’s HSDT. Aerosp. Sci. Technol. 2018, 77, 419–428. [Google Scholar] [CrossRef]
- Mirjavadi, S.S.; Afshari, B.M.; Barati, M.R.; Hamouda, A. Transient response of porous FG nanoplates subjected to various pulse loads based on nonlocal stress-strain gradient theory. Eur. J. Mech. A Solids 2018, 74, 210–220. [Google Scholar] [CrossRef]
- Zhao, J.; Choe, K.; Xie, F.; Wang, A.; Shuai, C.; Wang, Q. Three-dimensional exact solution for vibration analysis of thick functionally graded porous (FGP) rectangular plates with arbitrary boundary conditions. Compos. Part B Eng. 2018, 155, 369–381. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, F.; Wang, A.; Shuai, C.; Tang, J.; Wang, Q. Dynamics analysis of functionally graded porous (FGP) circular, annular and sector plates with general elastic restraints. Compos. Part B Eng. 2019, 159, 20–43. [Google Scholar] [CrossRef]
- Thang, P.T.; Nguyen-Thoi, T.; Lee, D.; Kang, J.; Lee, J. Elastic buckling and free vibration analyses of porous-cellular plates with uniform and non-uniform porosity distributions. Aerosp. Sci. Technol. 2018, 79, 278–287. [Google Scholar] [CrossRef]
- Kim, J.; Żur, K.K.; Reddy, J.N. Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates. Compos. Struct. 2019, 209, 879–888. [Google Scholar] [CrossRef]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells, 2nd ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Reddy, J.N. Energy Principles and Variational Methods in Applied Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coskun, S.; Kim, J.; Toutanji, H. Bending, Free Vibration, and Buckling Analysis of Functionally Graded Porous Micro-Plates Using a General Third-Order Plate Theory. J. Compos. Sci. 2019, 3, 15. https://doi.org/10.3390/jcs3010015
Coskun S, Kim J, Toutanji H. Bending, Free Vibration, and Buckling Analysis of Functionally Graded Porous Micro-Plates Using a General Third-Order Plate Theory. Journal of Composites Science. 2019; 3(1):15. https://doi.org/10.3390/jcs3010015
Chicago/Turabian StyleCoskun, Semsi, Jinseok Kim, and Houssam Toutanji. 2019. "Bending, Free Vibration, and Buckling Analysis of Functionally Graded Porous Micro-Plates Using a General Third-Order Plate Theory" Journal of Composites Science 3, no. 1: 15. https://doi.org/10.3390/jcs3010015
APA StyleCoskun, S., Kim, J., & Toutanji, H. (2019). Bending, Free Vibration, and Buckling Analysis of Functionally Graded Porous Micro-Plates Using a General Third-Order Plate Theory. Journal of Composites Science, 3(1), 15. https://doi.org/10.3390/jcs3010015




