Axial Response of Concrete-Filled FRP Tube (CFFT) Columns with Internal Bars
Abstract
:1. Introduction
2. Review of Codes and Design Guidelines
3. Experimental Work
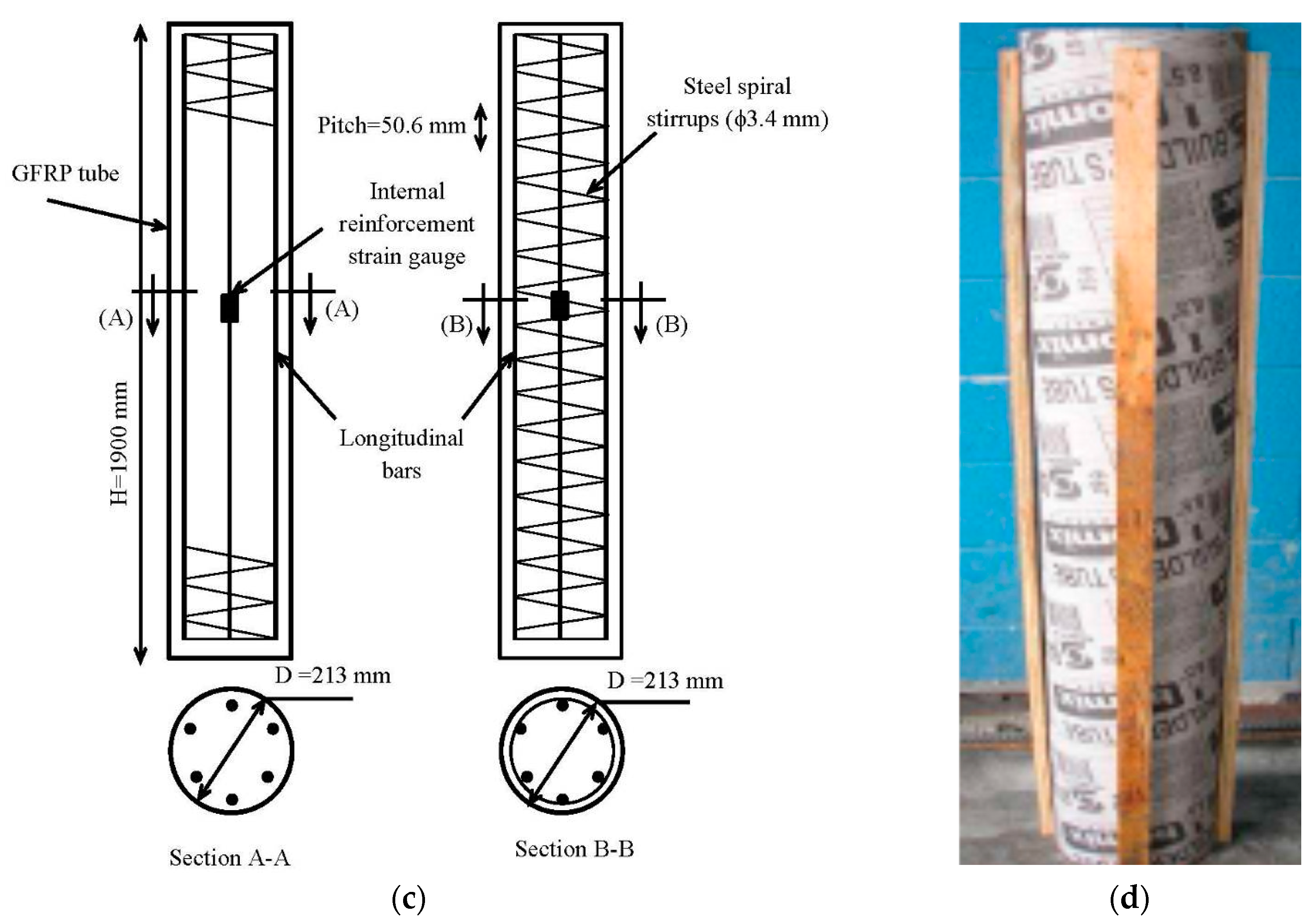
3.1. Test Matrix
3.2. Material Properties
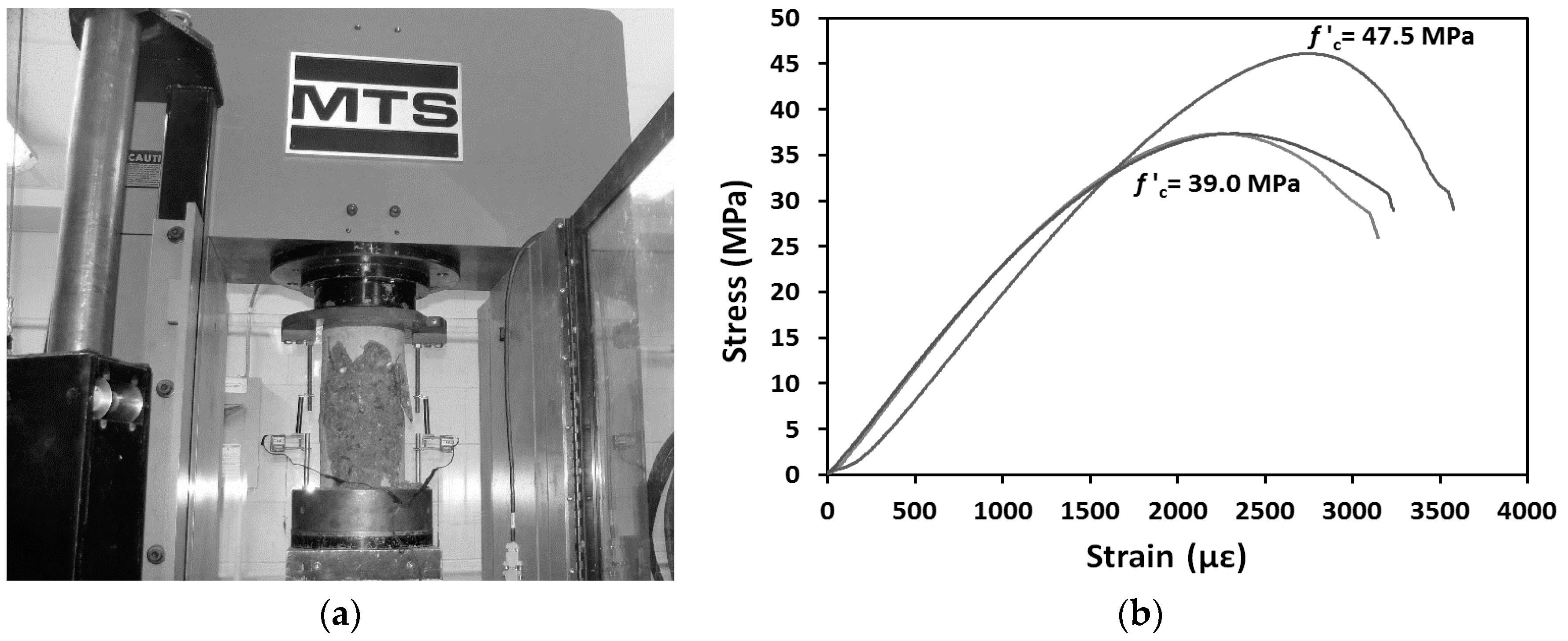
3.2.1. Concrete
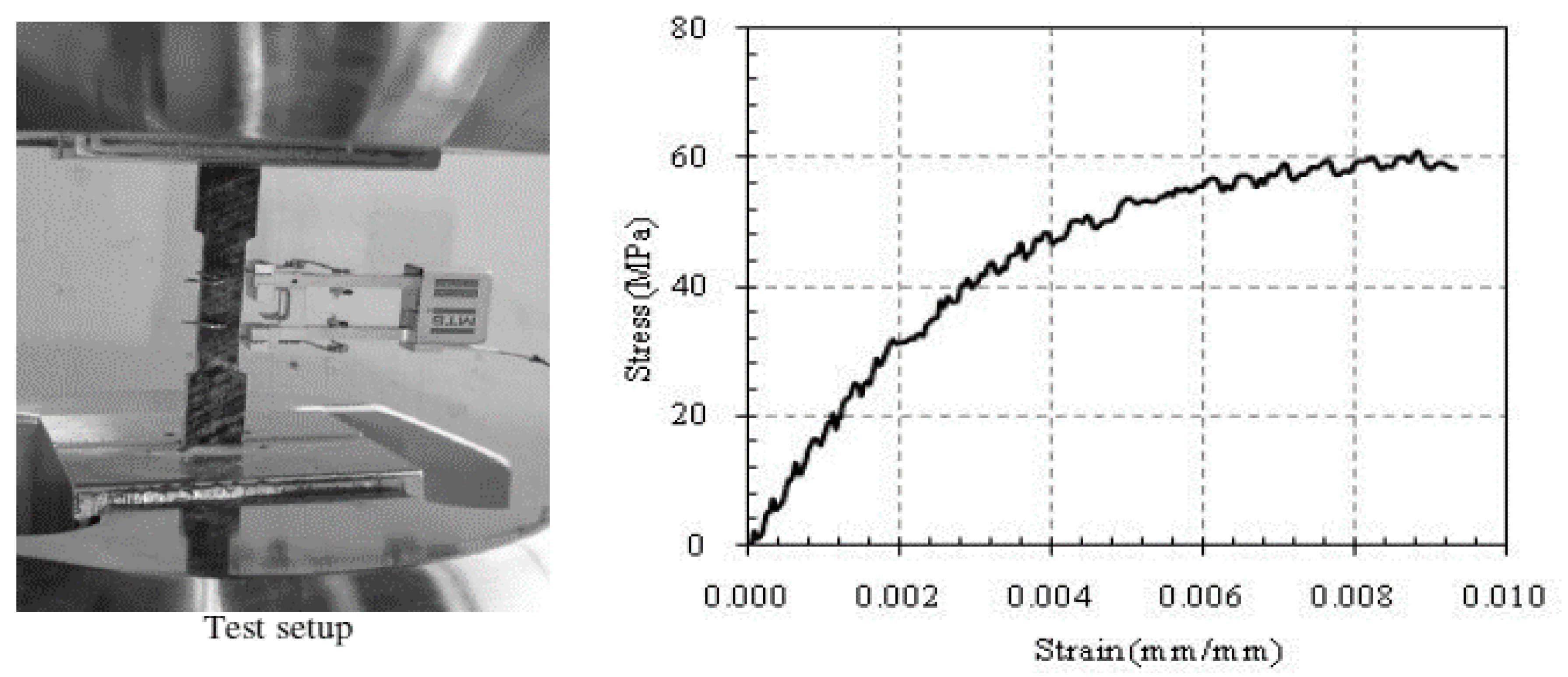
3.2.2. Steel and FRP bars
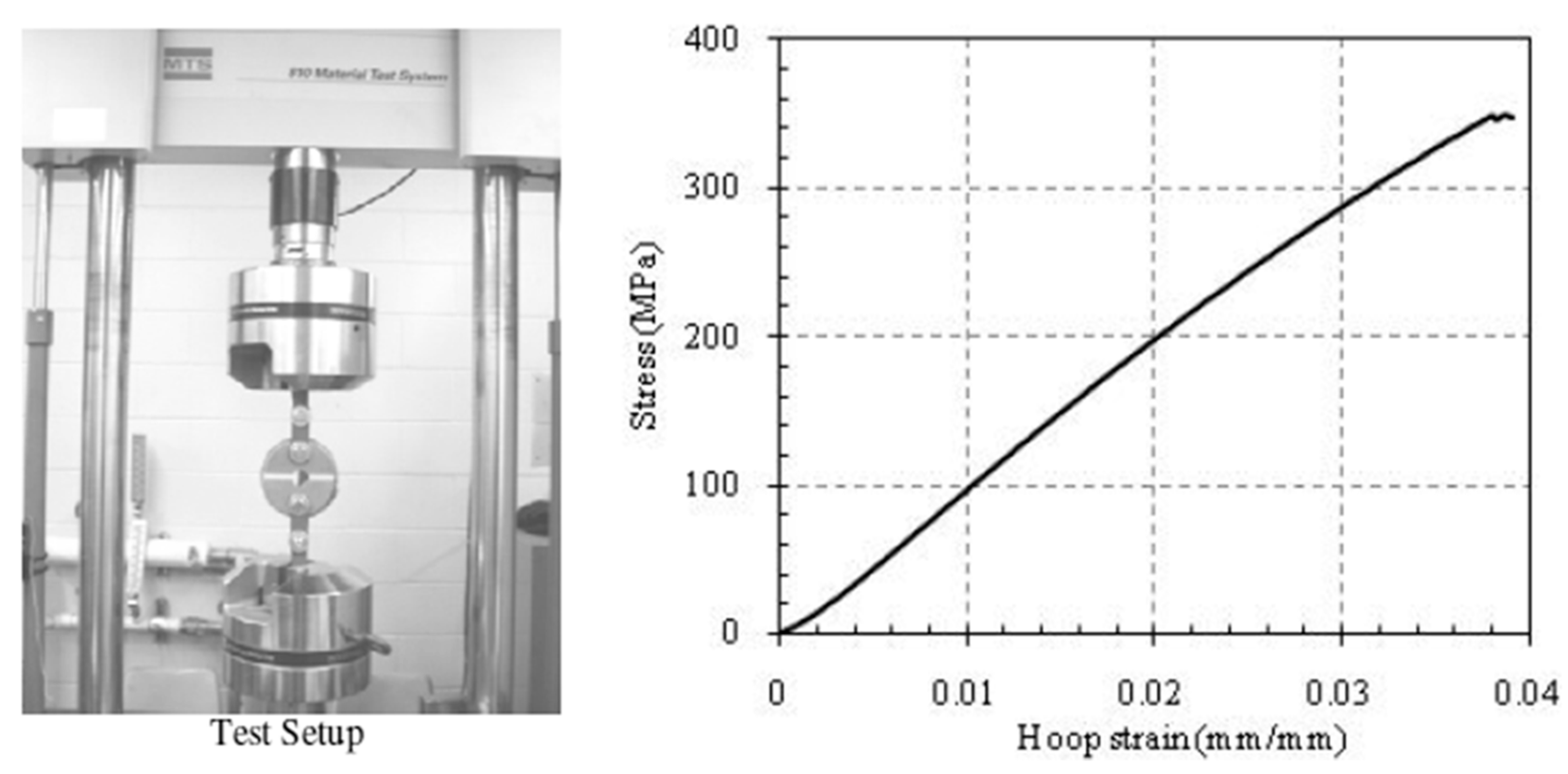
3.2.3. FRP Tubes
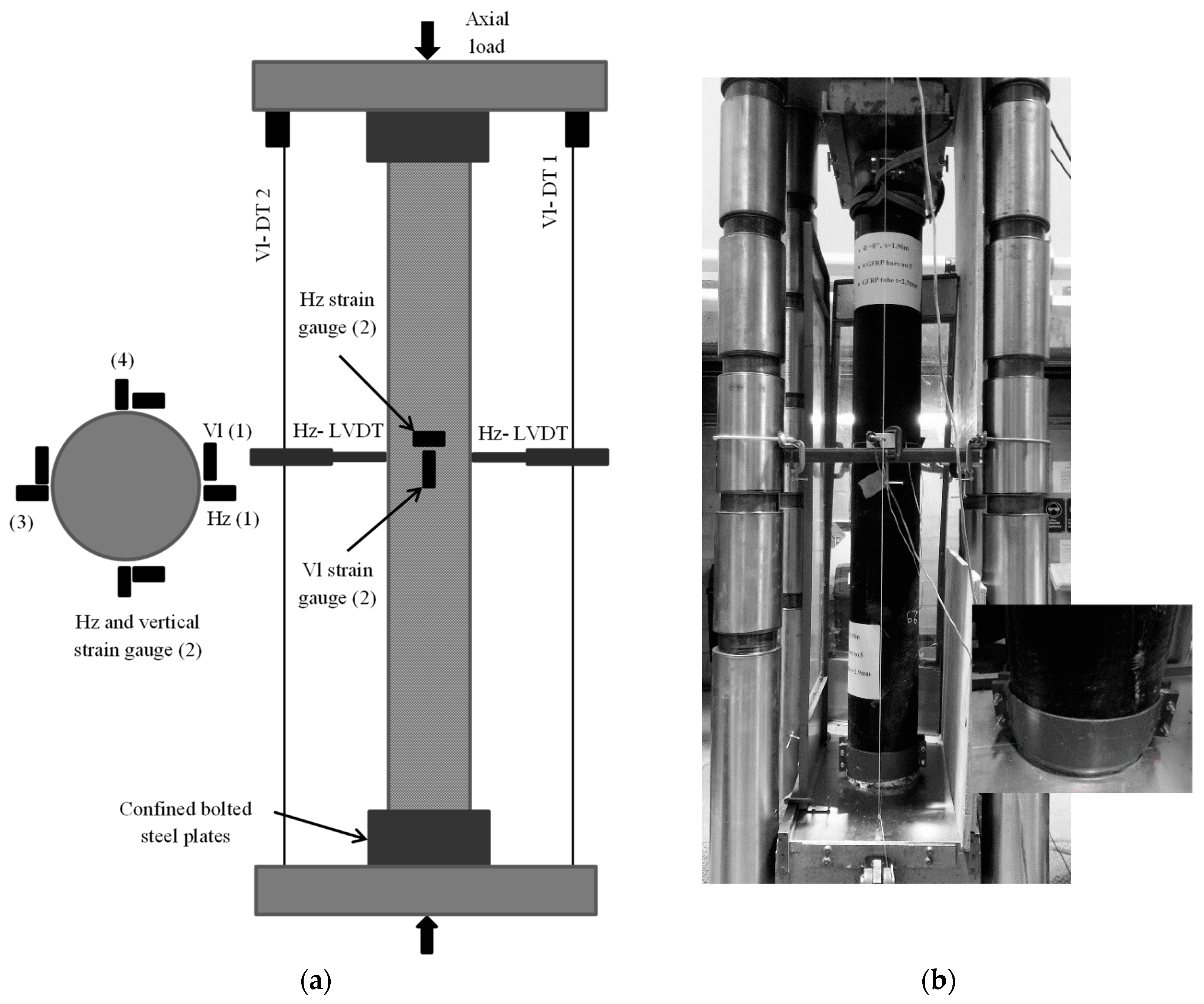
3.3. Instrumentation and Testing Procedures
4. Test Result and Discussion
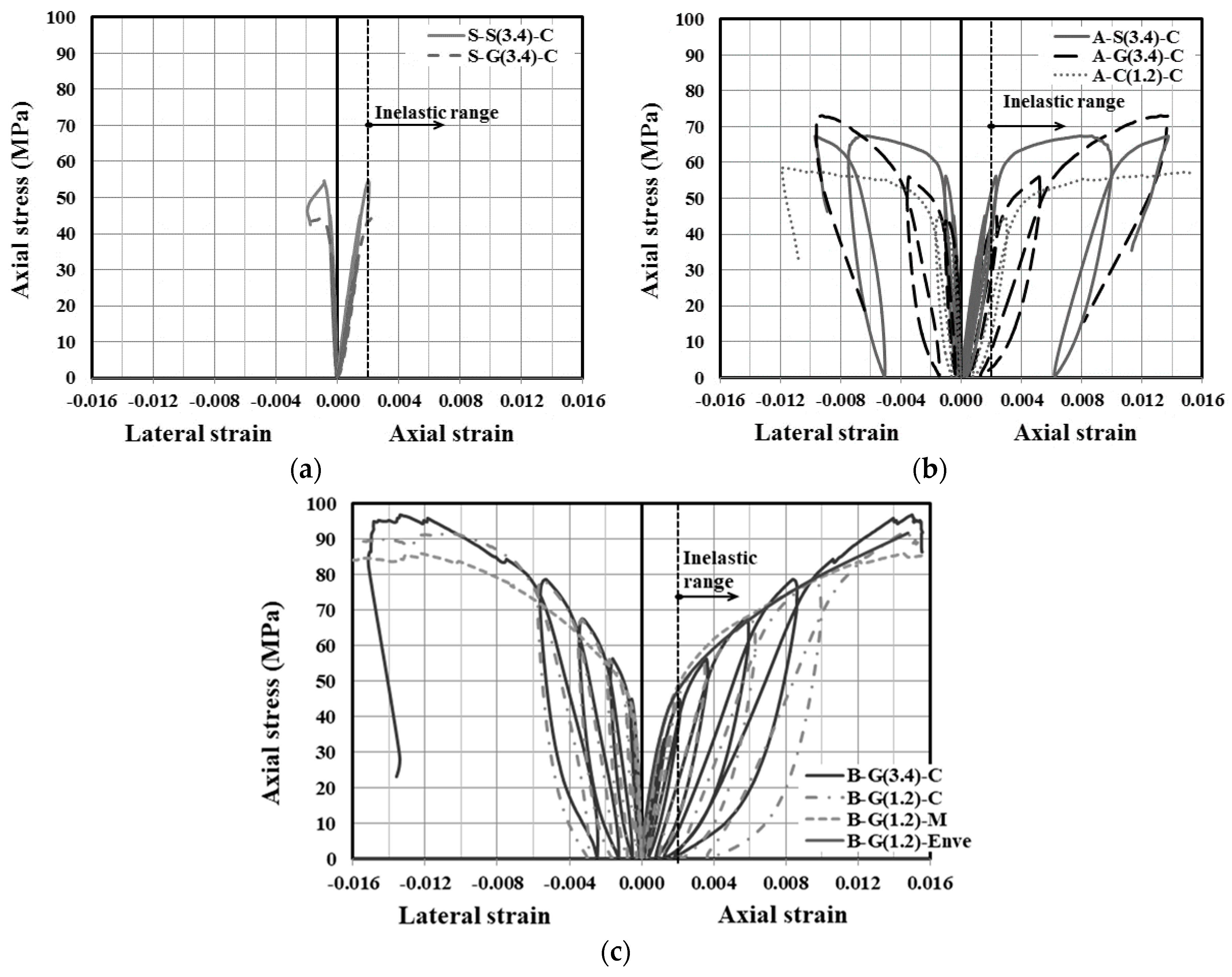
4.1. Axial and Lateral Stress-Strain Responses
4.2. Mode of Failure
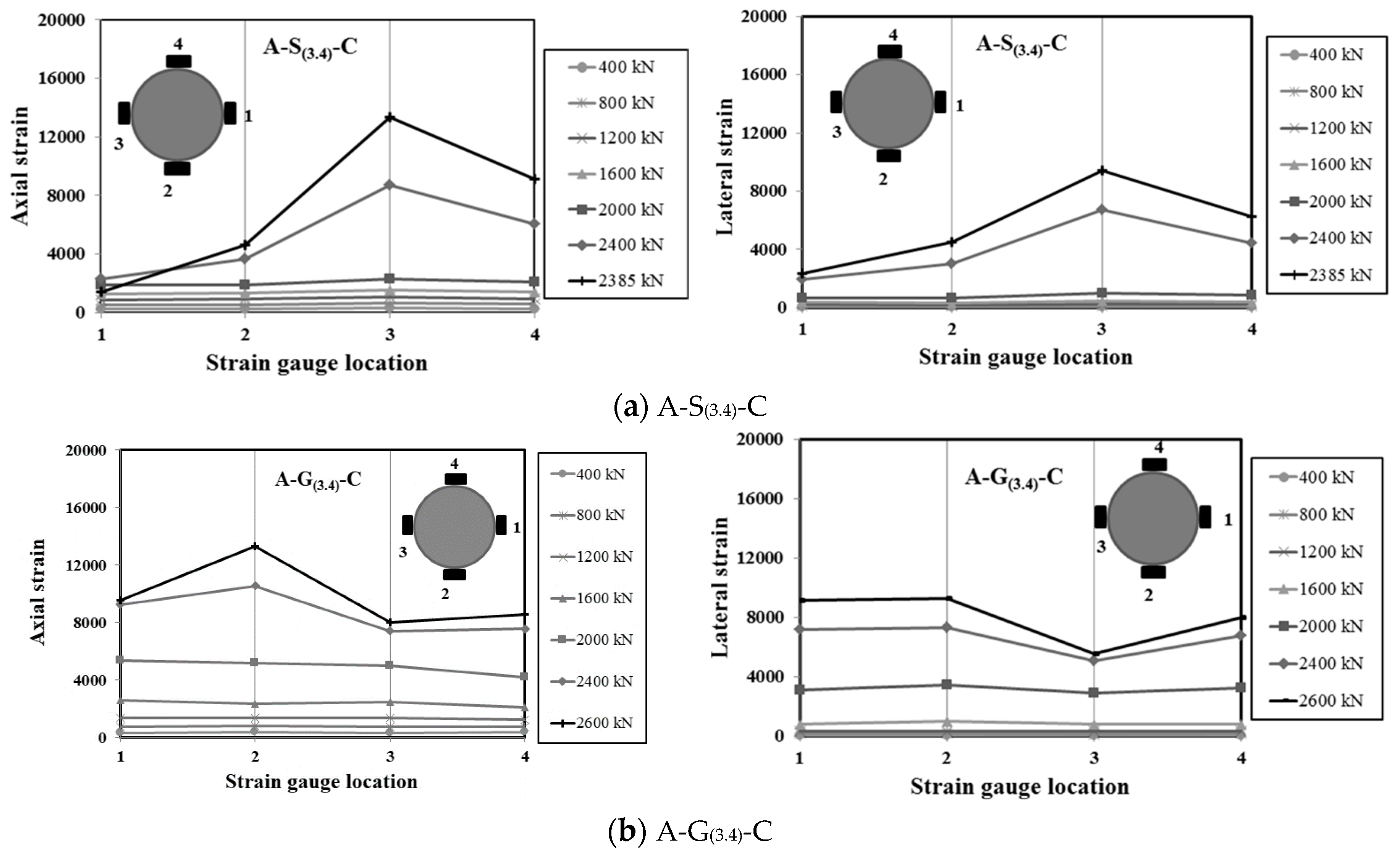
4.3. State of Stress in the GFRP Tube
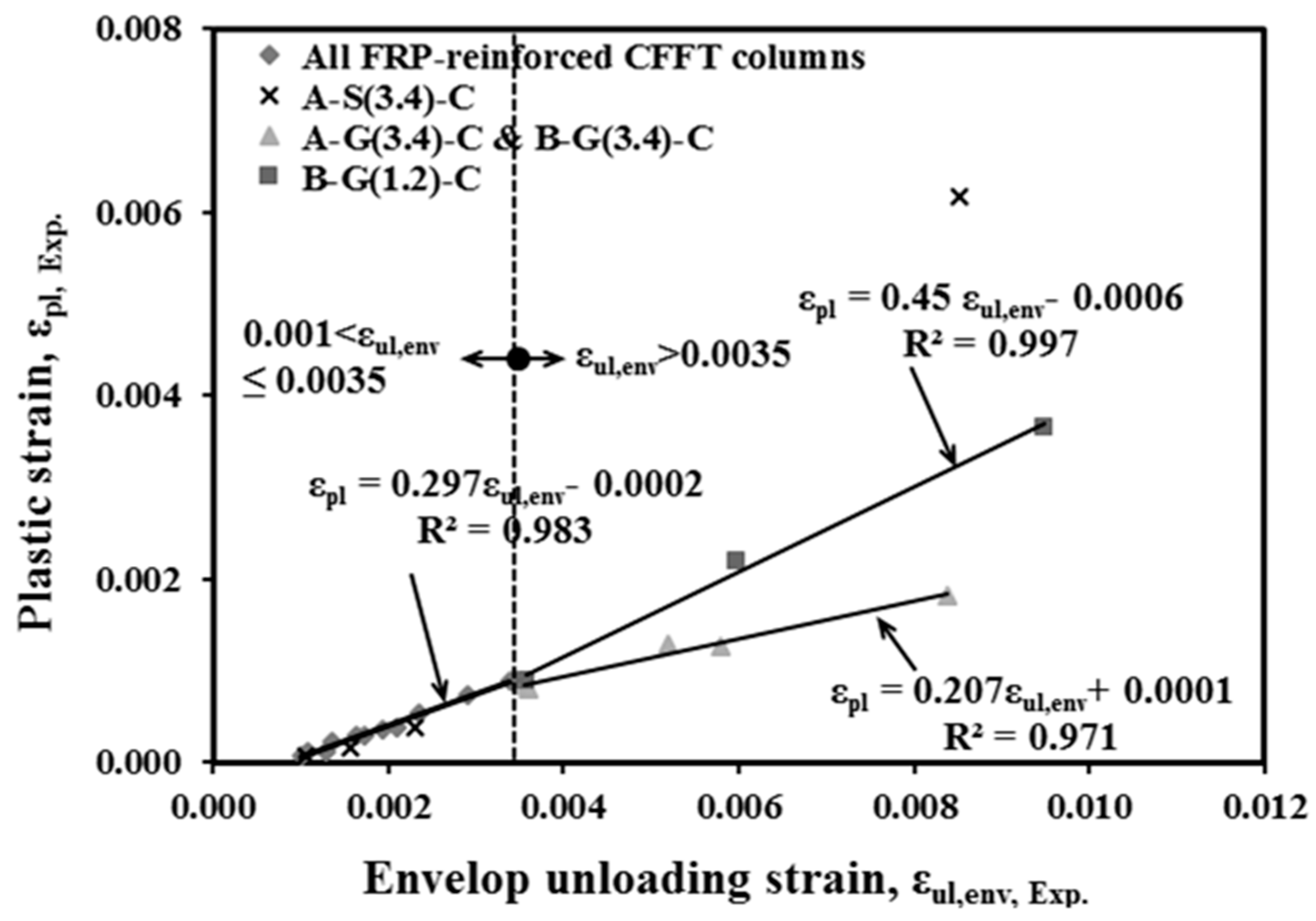
4.4. Plastic Strains
5. Comparisons of Predictions versus Experimental Results
6. Conclusions
- As expected, an increase in the FRP tube thickness (or stiffness) results in an increase in the strength and strain enhancement ratios (/ and εcc/εco).
- In general, the envelop curves for the CFFT tested specimens showed bilinear responses with a transition zone near the peak strength of the unconfined concrete (). The slope of the second branch is highly governed by GFRP tube stiffness rather than the longitudinal reinforcement amount and type.
- The FRP-reinforced CFFT columns showed lower residual plastic strains compared to that of the steel-reinforced CFFT columns after the yielding of the steel bars, when the load was removed. This can be due to the lack of yield plateau in GFRP bars which results in a much lower residual strain. As a result, the influence of internal reinforcement on cyclic loading should be considered when modelling the unloading/reloading cyclic axial stress-strain response.
- The GFRP-reinforced CFFT columns showed comparable ultimate axial strength and strain capacities compared to their counterparts reinforced with steel bars. This proves the applicability of exclusively reinforcing the CFFT columns with FRP bars and subjecting them to an axial compression load. However, a wide range of investigated parameters are necessary for a complete understanding of the behavior of FRP-reinforced CFFT columns.
- The ACI 440.R1 (2015), CSA S806 (2012), and CSA S6-06 (2010) design provisions provided higher conservative results for the GFRP-reinforced control specimens than that of the steel-reinforced specimen. This might be due to neglecting the contribution of the compressive resistance of the GFRP bars to the axial-carrying capacity.
- For FRP-reinforced CFFT columns, the CSA S806 (2012) showed better predictions based on the average with and without considering the confinement codes limits than that of the CSA S6-06 (2010) and ACI 440.2R (2008), particularly for thicker tube thickness.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- American Concrete Institute (ACI). Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; ACI 440.2R-08; American Concrete Institute: Farmington Hills, MI, USA, 2008. [Google Scholar]
- Fam, A.Z.; Rizkalla, S. Behavior of axially loaded concrete-filled circular fiber reinforced polymer tubes. ACI Struct. J. 2001, 98, 280–289. [Google Scholar]
- Fitzwilliam, J.; Bisby, L. Slenderness Effects on Circular CFRP Confined Reinforced Concrete Columns. J. Compos. Constr. 2010, 14, 280–288. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-oriented stress-strain models for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Samaan, M.; Mirmiran, A.; Shahawy, M. Modeling of concrete confined by fiber composites. J. Struct. Eng. 1998, 124, 1025–1031. [Google Scholar] [CrossRef]
- Wei, Y.Y.; Wu, Y.F. Unified stress–strain model of concrete for FRP-confined columns. Constr. Build. Mater. 2012, 26, 381–392. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, H. Compressive behavior of concrete confined by carbon fiber composite jackets. J. Mater. Civ. Eng. 2000, 12, 139–146. [Google Scholar] [CrossRef]
- Abbasnia, R.; Ahmadi, R.; Ziaadiny, H. Effect of confinement level, aspect ratio and concrete strength on the cyclic stress–strain behavior of FRP-confined concrete prisms. Compos. Part B Eng. 2012, 43, 825–831. [Google Scholar] [CrossRef]
- Abbasnia, R.; Hosseinpour, F.; Rostamian, M.; Ziaadiny, H. Cyclic and monotonic behavior of FRP confined concrete rectangular prisms with different aspect ratios. Constr. Build. Mater. 2013, 40, 118–125. [Google Scholar] [CrossRef]
- Ilki, A.; Kumbasar, N. Compressive behavior of carbon fiber composite jacketed concrete with circular and non-circular cross sections. J. Earthq. Eng. 2003, 7, 381–406. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G.; Cheung, J.G.; Xiao, Y. FRP-confined concrete under axial cyclic compression. Cem. Concr. Compos. 2006, 28, 949–958. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Stress-strain model for FRP-confined concrete under cyclic axial compression. Eng. Struct. 2009, 31, 308–321. [Google Scholar] [CrossRef]
- Mirmiran, A.; Shahawy, M.; Beitleman, T. Slenderness Limit for Hybrid FRP Concrete Columns. J. Compos. Constr. 2001, 5, 26–34. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress–strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Shao, Y.; Zhu, Z.; Mirmiran, A. Cyclic modeling of FRP confined concrete with improved ductility. Cem. Concr. Compos. 2006, 28, 959–968. [Google Scholar] [CrossRef]
- Afifi, Z.; Mohamed, M.; Benmokrane, B. Axial capacity of circular concrete columns reinforced with glass-FRP bars and spirals. J. Compos. Constr. 2014, 18, 04013017. [Google Scholar] [CrossRef]
- De Luca, A.; Matta, F.; Nanni, A. Behavior of full-scale glass fiber-reinforced polymer reinforced concrete columns under axial load. ACI Struct. J. 2010, 107, 589–596. [Google Scholar]
- Mohamed, H.; Afifi, M.; Benmokrane, B. Performance Evaluation of Concrete Columns Reinforced Longitudinally with FRP Bars and Confined with FRP Hoops and Spirals under Axial Load. J. Bridge Eng. 2014, 19, 04014020. [Google Scholar] [CrossRef]
- Sharma, U.K.; Bhargava, P.; Kaushik, S.K. Behavior of confined high strength concrete columns under axial compression. J. Adv. Concr. Technol. 2005, 3, 267–281. [Google Scholar] [CrossRef]
- Tobbi, H.; Farghaly, A.S.; Benmokrane, B. Concrete columns reinforced longitudinally and transversally with glass fiber-reinforced polymers bars. ACI Struct. J. 2012, 109, 1–8. [Google Scholar]
- Canadian Standard Association (CSA). Canadian Highway Bridge Design Cod; CAN/CSA-S6-06; Canadian Standard Association: Toronto, ON, Canada, 2010. [Google Scholar]
- Canadian Standards Association (CAN/CSA). Design of Concrete Structures; A23.3-14; Canadian Standards Association: Mississauga, ON, Canada, 2014. [Google Scholar]
- American Concrete Institute (ACI). Building Code Requirements for Structural Concrete; ACI 318-14; American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- American Concrete Institute (ACI). Guide for the Design and Construction of Concrete Reinforced with FRP Bars; ACI 440.1R-15; American Concrete Institute: Farmington Hills, MI, USA, 2015. [Google Scholar]
- Canadian Standard Association (CSA). Design and Construction of Building Components with Fibre-Reinforced Polymers; CSA-S806-12; Canadian Standards Association: Toronto, ON, Canada, 2012. [Google Scholar]
- ASTM A615/A615M-09. Standard Specification for Deformed and Plain Carbon Steel Bars for Concrete Reinforcement; ASTM: West Conshohocken, PA, USA, 2009. [Google Scholar]
- Pultrall, Inc. V-ROD Composite Reinforcing Rods Technical Data Sheet; Pultrall, Inc.: Thetford Mines, QC, Canada, 2007; Available online: www.pultrall.com (accessed on 15 July 2007).
- Masmoudi, R.; Mohamed, H. Axial behavior of slender-concrete-filled FRP tube columns reinforced with steel and carbon FRP bars. In Proceedings of the 10th International Symposium on Fiber-Reinforced Polymer Reinforcement for Concrete Structures, Tampa, FL, USA, 2–4 April 2011. [Google Scholar]
- Karimi, K.; Tait, M.; El-Dakhahkni, W. Influence of Slenderness on the behavior of a FRP-Enclosed Steel-Concrete Composite Column. J. Compos. Constr. 2012, 16, 100–109. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Akin, E. Behavior of FRP-confined normal- and high-strength concrete under cyclic axial compression. J. Compos. Constr. 2012, 16, 451–463. [Google Scholar] [CrossRef]
- Sakai, J.; Kawashima, K. Unloading and reloading stress strain model for confined concrete. J. Struct. Eng. 2006, 132, 112–122. [Google Scholar] [CrossRef]
- Xia, Y.; Xian, G.; Wang, Z.; Li, H. Static and Cyclic Compressive Properties of Self-Compacting Concrete-Filled Flax Fiber–Reinforced Polymer Tubes. J. Compos. Constr. 2016, 20, 04016046. [Google Scholar] [CrossRef]
- Mohamed, H.; Abdel Baky, H.; Masmoudi, R. Nonlinear stability analysis of CFFT columns: Experimental and Theoretical Investigations. ACI Struct. J. 2010, 107, 699–708. [Google Scholar]
- Wang, Z.; Wang, D.; Smith, S.; Lu, D. CFRP-Confined Square RC Columns. II: Experimental Investigation. J. Compos. Constr. 2012, 16, 150–160. [Google Scholar] [CrossRef]




| Code | Equation |
|---|---|
| CAN/CSA S806 (2012) | where: ke = 0.85, ϕc = 0.60, ϕs = 0.85 and ϕFRP = 0.75 |
| , where: kl = 6.7()−0.17 × kc = 1 | |
| , where: = the smaller of 0.006Ef or ϕfffu | |
| CAN/CSA S6-06 (2010) | |
| where: ke = 0.8, ϕc = 0.75, ϕs = 0.9 and ϕFRP = 0.6, α1 = 0.85–0.0015 ≥ 0.39 | |
| , where: | |
| ACI-440.2R-08 (2008) | , where: ϕ = 0.75 , where: Ѱf = 0.95, (ka) = 1 |
| , kε = 0.55, where: , |
| ID | Lateral Reinforcement Type | Longitudinal Bars | Pu (kN) | a (MPa) | / | εcc (µε) | εcc/εo | εh, Min. (µε) | εh, Aver. (µε) | εh, Max. (µε) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Type | Area | ||||||||||
| S-S(3.4)-C | ϕ3.4@50.6 | Steel | 6 M 15 | 1948 | 54.60 | 1.23 | −2510 | 1.04 | 377 | 599 | 836 |
| S-G(3.4)-C | ϕ3.4@50.6 | GFRP | 6 No. 5 | 1575 | 47.20 | 1.08 | −2711 | 1.12 | 653 | 935 | 1144 |
| S-G(3.4)-C* | ϕ3.4@50.6 | GFRP | 6 No. 5 | 1606 | 48.64 | 1.10 | −2379 | 0.99 | 270 | 457 | 605 |
| A-S(3.4)-C | A | Steel | 6 M 15 | 2402 | 67.38 | 1.53 | −13,749 | 3.83 | 2442 | 4697 | 9707 |
| A-G(3.4)-C | A | GFRP | 6 No. 5 | 2603 | 73.06 | 1.66 | −13,718 | 4.63 | 5172 | 8087 | 9610 |
| B-G(3.4)-C | B | GFRP | 6 No. 5 | 3455 | 96.97 | 2.20 | −15,578 | 5.49 | 4435 | 9745 | 15,135 |
| B-G(1.2)-C | B | GFRP | 6 No. 3 | 3272 | 91.82 | 2.08 | −15,563 | 5.96 | 11,456 | 13,787 | 16,113 |
| B-G(1.2)-M | B | GFRP | 6 No. 3 | 3068 | 86.09 | 1.95 | −15,514 | 5.15 | 3156 | 11,356 | 16,090 |
| A-C(1.2)-C | A | CFRP | 6 No. 3 | 2086 | 58.55 | 1.33 | −15,486 | 4.65 | 4190 | 8240 | 11,913 |
| A-C(1.2)-C* | A | CFRP | 6 No. 3 | 2039 | 57.23 | 1.30 | −15,475 | 5.10 | 2738 | 8024 | 12,947 |
| Reinforcement Type | Nominal Diameter (mm) | Nominal Area (mm2) | Tensile Modulus of Elasticity (GPa) | Yield Strength (MPa) | Ultimate Strength (MPa) | Ultimate Strain (%) |
|---|---|---|---|---|---|---|
| GFRP No. 3 | 9.5 | 71 | 45.4 | - | 856 | 1.89 |
| GFRP No. 5 | 15.9 | 199 | 48.2 | - | 751 | 1.60 |
| CFRP No. 3 | 9.5 | 71 | 128 | - | 1431 | 1.20 |
| Wire (mild steel) | 3.4 | 9 | 200 | 675 | 850 | 0.30 * |
| 15 M (deformed steel) | 16 | 200 | 200 | 419 | 686 | 0.21 * |
| Tube Type | d (mm) | (mm) | No. of Layers | Stacking Sequence | fFRPU (MPa) | εFRPU (%) | EFRPU (MPa) | fX (MPa) | εX (%) | EX (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 213 | 2.90 | 6 | [60°, 904°, 60°] | 548 | 1.70 | 32,260 | 55.2 | 0.62 | 8865 |
| B | 213 | 6.40 | 12 | [±60°, 902°, ±60°, 906°] | 510 | 1.69 | 30,200 | 59.2 | 0.75 | 7897 |
| ID | Ptest | ACI 440.R1 (2015) | CSA S806 (2012) | CSA S6-06 (2010) | |||
|---|---|---|---|---|---|---|---|
| PPredict | Ptest/PPredict | PPredict | Ptest/PPredict | PPredict | Ptest/PPredict | ||
| S-S(3.4)-C | 1948 | 1524 * | 1.28 * | 1439 * | 1.35 * | 1354 * | 1.44 * |
| S-G(3.4)-C | 1575 | 1097 | 1.44 | 1012 | 1.56 | 952 | 1.65 |
| S-G(3.4)-C* | 1606 | 1097 | 1.46 | 1012 | 1.59 | 952 | 1.69 |
| - | - | Average | 1.45 † | Average | 1.57 † | Average | 1.67 † |
| - | - | SD | 0.02 † | SD | 0.02 † | SD | 0.02 † |
| - | - | COV% | 1.38 † | COV% | 1.38 † | COV% | 1.38 † |
| ID | Ptest (kN) | ACI 440.2R (2008) | CSA S806 (2012) | CSA S6-06 (2010) | |||
|---|---|---|---|---|---|---|---|
| PPredict | Ptest/PPredict | PPredict | Ptest/PPredict | PPredict | Ptest/PPredict | ||
| A-S(3.4)-C | 2402 | 1998 * | 1.20 * | 1898 | 1.27 * | 1986 * | 1.21 * |
| A-G(3.4)-C | 2603 | 1571 | 1.66 | 1471 | 1.77 | 1584 | 1.64 |
| B-G(3.4)-C | 3455 | 1650 | 2.09 | 1976 | 1.75 | 1581 | 2.19 |
| B-G(1.2)-C | 3272 | 1687 | 1.94 | 2020 | 1.62 | 1616 | 2.02 |
| B-G(1.2)-M | 3068 | 1687 | 1.82 | 2020 | 1.52 | 1616 | 1.90 |
| A-C(1.2)-C | 2086 | 1606 | 1.30 | 1504 | 1.39 | 1619 | 1.29 |
| A-C(1.2)-C* | 2039 | 1606 | 1.27 | 1504 | 1.36 | 1619 | 1.26 |
| - | - | Average | 1.68 † | Average | 1.57 † | Average | 1.72 † |
| - | - | SD | 0.31 † | SD | 0.18 † | SD | 0.35 † |
| - | - | COV% | 18.4 † | COV% | 11.3 † | COV% | 20.5 † |
| ID | Ptest | ACI 440.2R (2008) | CSA S806 (2012) | CSA S6-06 (2010) | |||
|---|---|---|---|---|---|---|---|
| PPredict | Ptest/PPredict | PPredict | Ptest/PPredict | PPredict | Ptest/PPredict | ||
| A-S(3.4)-C | 2402 | 2185 | 1.10 * | 2712 | 0.89 * | 1986 | 1.21 * |
| A-G(3.4)-C | 2603 | 1758 | 1.48 | 2285 | 1.14 | 1584 | 1.64 |
| B-G(3.4)-C | 3455 | 2449 | 1.41 | 3442 | 1.00 | 2245 | 1.54 |
| B-G(1.2)-C | 3272 | 2503 | 1.31 | 3519 | 0.93 | 2295 | 1.43 |
| B-G(1.2)-M | 3068 | 2503 | 1.23 | 3519 | 0.87 | 2295 | 1.34 |
| A-C(1.2)-C | 2086 | 1797 | 1.16 | 2336 | 0.89 | 1619 | 1.29 |
| A-C(1.2)-C* | 2039 | 1797 | 1.13 | 2336 | 0.87 | 1619 | 1.26 |
| - | - | Average | 1.29 † | Average | 0.95 | Average | 1.42 |
| - | - | SD | 0.13 † | SD | 0.10 | SD | 0.14 |
| - | - | COV% | 9.8 † | COV% | 11.0 | COV% | 9.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, A.A.; Masmoudi, R. Axial Response of Concrete-Filled FRP Tube (CFFT) Columns with Internal Bars. J. Compos. Sci. 2018, 2, 57. https://doi.org/10.3390/jcs2040057
Ahmed AA, Masmoudi R. Axial Response of Concrete-Filled FRP Tube (CFFT) Columns with Internal Bars. Journal of Composites Science. 2018; 2(4):57. https://doi.org/10.3390/jcs2040057
Chicago/Turabian StyleAhmed, Asmaa Abdeldaim, and Radhouane Masmoudi. 2018. "Axial Response of Concrete-Filled FRP Tube (CFFT) Columns with Internal Bars" Journal of Composites Science 2, no. 4: 57. https://doi.org/10.3390/jcs2040057
APA StyleAhmed, A. A., & Masmoudi, R. (2018). Axial Response of Concrete-Filled FRP Tube (CFFT) Columns with Internal Bars. Journal of Composites Science, 2(4), 57. https://doi.org/10.3390/jcs2040057




