An Energetic Analysis of Apparent Hardening and Ductility in FRP Plate Debonding

Abstract

We investigate the progressive debonding of FRP reinforcements using an analytical framework based on fracture mechanics and a bilinear softening cohesive law. This study focuses on the energetic analysis of the “apparent hardening” phase observed in the force–slip ($F-\Delta$) curve. It is shown that this non-linear response is a structural phenomenon caused by stress redistribution as the softening zone develops. Full analytical expressions for all energy components (stored and dissipated) are derived, and the energy balance is established. The analysis links the amount of elastic energy stored during the hardening phase to the definitions of toughness (area under the curve) and ductility (post-peak behavior), explaining the transition from ductile to brittle failure.

1. Introduction

The need to upgrade and repair existing concrete structures represents one of the greatest challenges in modern structural engineering. The aging of infrastructure, changes in building usage, increased loading requirements, and the necessity for seismic retrofitting demand reliable and effective strengthening techniques. Fiber-reinforced polymers (FRPs) have emerged over past decades as an ideal solution, owing to their high strength-to-weight ratio, exceptional corrosion resistance, and ease of application [1,2].

However, the high performance of these advanced materials often cannot be fully exploited. Experience has demonstrated that the behavior of strengthened systems is rarely governed by the tensile strength of the FRP itself but almost always by the integrity of the bond at the FRP-to-concrete interface [3]. Debonding of the reinforcement constitutes the most common and critical failure mechanism [4]. A fundamental challenge lies in the fact that debonding is often a sudden, brittle mechanism, which can manifest without sufficient warning, thereby undermining the safety and reliability of the entire structure.

In the past, significant research has been dedicated to understanding and predicting this phenomenon [5,6]. Pioneering work led to the development of analytical models based on local bond–slip ($\tau -s$) relationships [5,7,8]. These models, particularly those adopting bilinear or curved forms with a softening branch, have been decisive in explaining the mechanics of stress transfer from FRPs to concrete. The primary outcome of these analyses has been the definition of the “Effective Anchorage Length” $\left(L_{eff}\right)$—that is, the minimum length required to mobilize the maximum possible strength of the connection [9,10]. Consequently, current design guidelines worldwide are predominantly strength-based, merely requiring the provided anchorage length to exceed the calculated $L_{eff}$ [1,2].

Nonetheless, a design philosophy focused solely on strength is inherently incomplete. In structural engineering, particularly in seismic design, ductility is not just desirable; it is a paramount requirement. A ductile failure provides clear warning through large, visible deformations and, most importantly, allows for the dissipation of vast amounts of energy, preventing catastrophic collapse [11]. It has been demonstrated, both experimentally and theoretically through size effect laws [12], that simply providing an extensive bond length (much greater than $L_{eff}$) does not guarantee better behavior. On the contrary, it can lead to a more dangerous, brittle failure, owing to the immense amount of elastic energy stored in the “loaded” system [13].

While this phenomenon has been acknowledged, a clear framework that translates these complex stability concepts into practical design rules has been lacking. In the present work, we aim to fill this gap by presenting a complete analytical framework, grounded in the principles of fracture mechanics, which explicitly addresses the stability of the debonding process [14,15,16]. Unlike classical approaches that assume a pre-existing crack, we model debonding as a progressive failure process governed by a bilinear softening cohesive law [17,18]. Recent studies have significantly expanded the application of fracture mechanics to the analysis of FRP debonding. For instance, a cohesive fracture approach was used to investigate the fundamental mechanisms of debonding [19,20]; additionally, focus has been placed on non-linear effects in compressively loaded composites, addressing the theoretical modeling of instability phenomena related to micro-cracking and their impact on macroscopic failure [21]. Furthermore, such energy-based frameworks have been recently extended to cover complex mixed-mode loading scenarios and environmental durability issues [22,23,24].

This analysis focuses on the global system response, as captured in the force–slip ($F-\Delta$) curve. Particular emphasis is placed on investigating the non-linear phase of “apparent hardening”. It is demonstrated that this “hardening” of the system—despite the fact that the interface material is locally “softening”—is a critical structural phenomenon caused by stress redistribution as the softening zone develops and activates new, intact sections of the anchorage [25].

To quantify this behavior, an extensive energy analysis is conducted. Full analytical expressions are derived for all energy components present during damage evolution—the elastic energy stored in the FBP, the energy stored in the elastic interface zone, and the energy dissipated in the softening zone. The system’s energy balance is used to explain how the energy stored during the apparent hardening phase dictates the subsequent stability. Finally, the $F-\Delta$ curve is used to quantitatively define the toughness of the system (as the total area under the curve) and its ductility (as the post-peak behavior), thus providing a deeper understanding of the safe operation of FRP strengthening systems.

2. The Analytical Model

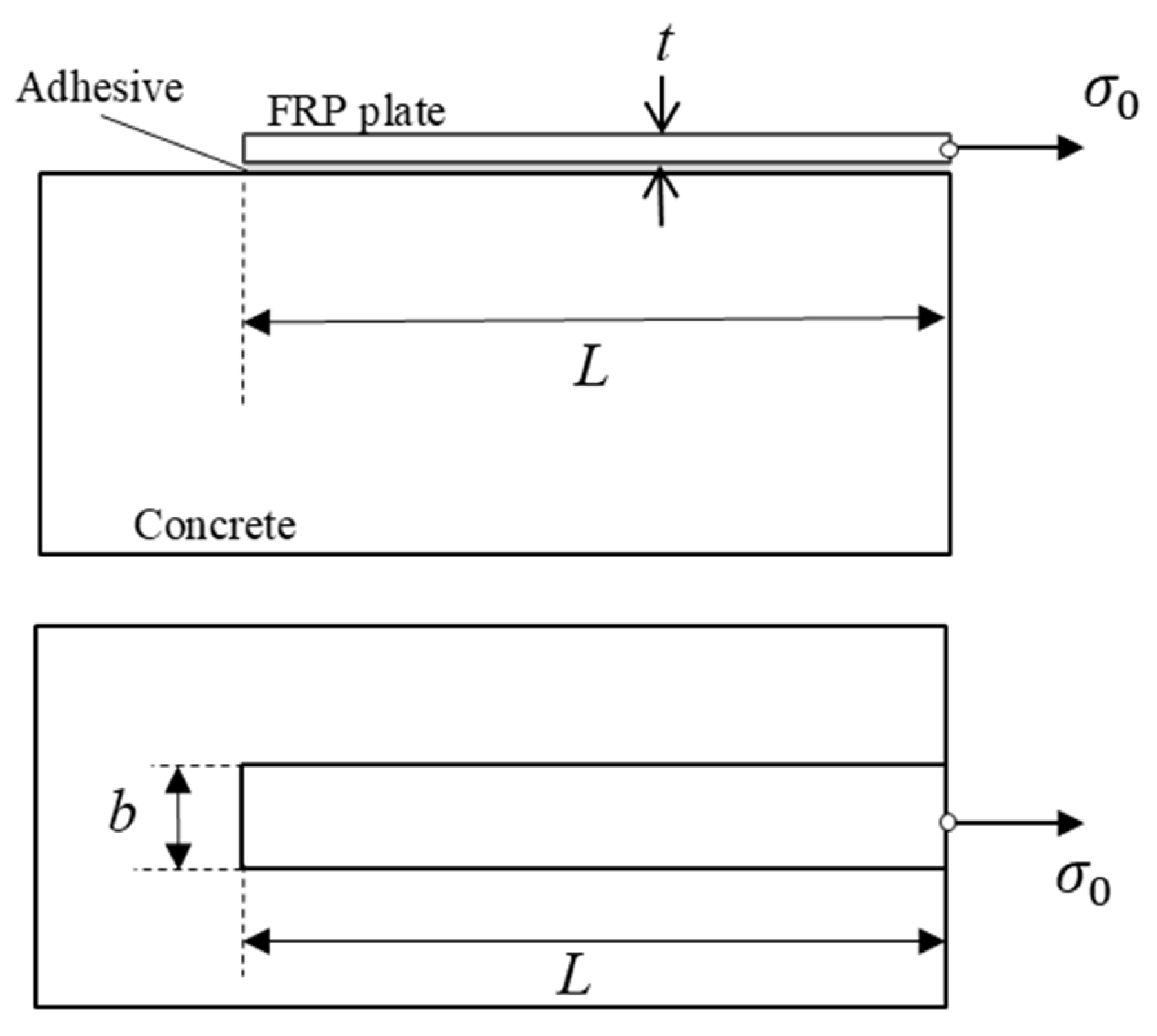
2.1. The Strengthening System

In the present paper, the strengthening system illustrated in Figure 1 is considered. The system consists of a fiber-reinforced polymer (FRP) plate bonded to a rigid, immovable concrete substrate and subjected to uniform tensile stress, ${\sigma }_0$. The FRP plate has the width $b$ and thickness $t$ and is bonded over the length $L$. The FRP behaves in a linearly elastic manner up to failure, characterized by the elastic modulus $E$ and the tensile strength $f_u$. The interfacial bond between the FRP plate and the substrate is simulated by the continuous distribution of shear springs of vanishing thickness. In the stressed analysis of the system, both the normal stresses within the FRP plate and the shear stresses along the adhesive interface are assumed to be uniform across the plate’s width $b$. Under the above simplifying assumptions, the relative stressed problem can be treated as one-dimensional with respect to an $x$-axis passing through the centroids of the FRP plate cross-sections. Since the substrate is considered a rigid and unmoved body, the axial displacement $u$ of the FRP plate coincides with the elongation $s$ of the interfacial springs, which represents the relative slip between the FRP and the substrate.

The differential equation that describes the equilibrium of an infinitesimal segment, $dx$, of the FRP plate is

$$Et{s}^{″}(x)=\tau$$

(1)

where $\tau$ is the shear stress along the adhesive interface, assuming that the slip $s$ is identical to the axial displacement of the FRP plate and applying Hooke’s law $\sigma =E{s}^{’}\left(x\right)$, with $\sigma$ being the normal stress in the FRP plate.

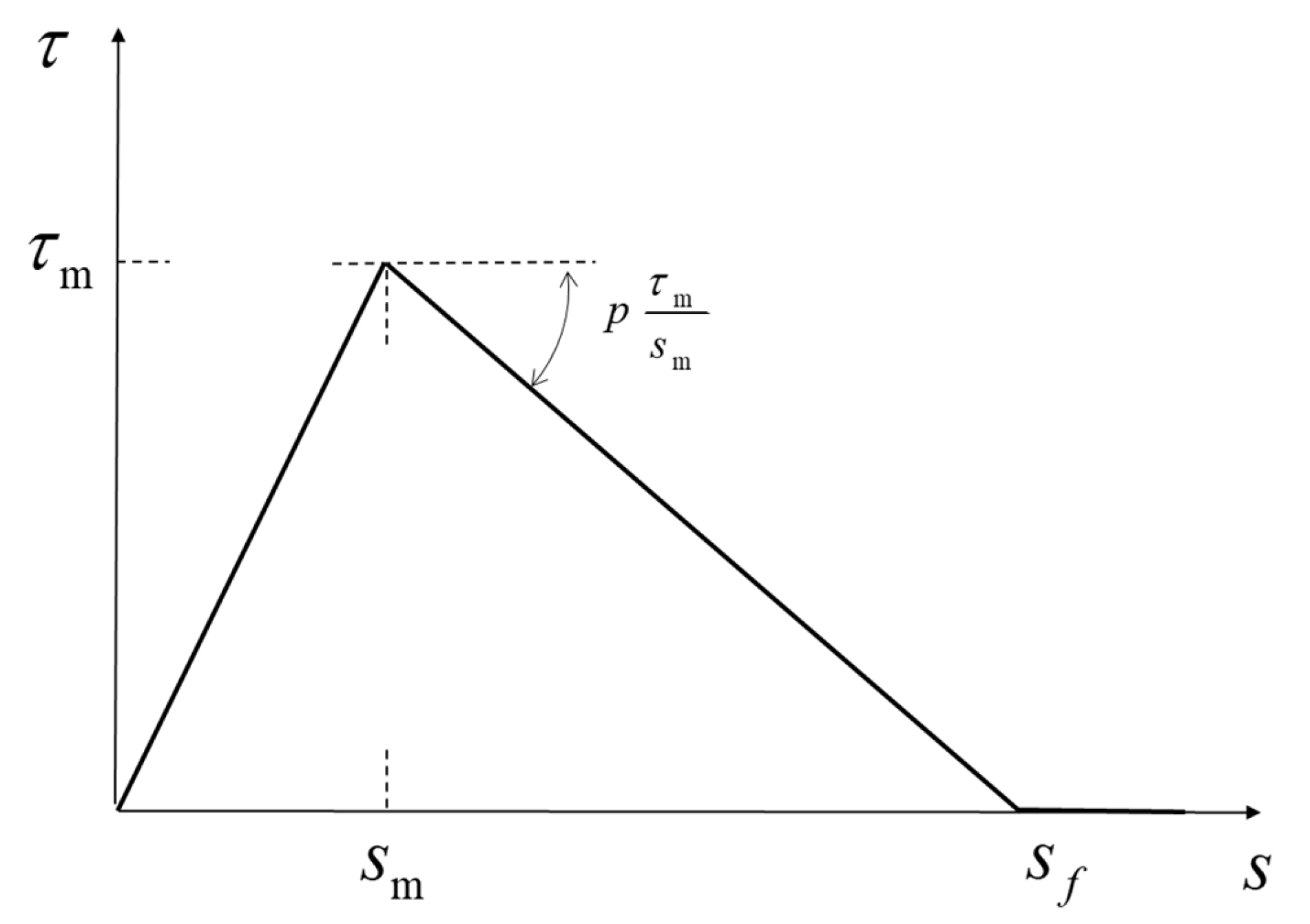
2.2. The Interface Cohesive Law and the Interface Fracture Energy

The solution to the above differential equation is contingent upon the bond slip relationship, $\tau -s$, which serves as the constitutive law for the interface and is established through experimental testing. For the present analysis, the idealized bilinear law shown in Figure 2 is adopted.

In this diagram, $\tau$ denotes the shear stress developed at the interface, while s represents the local slip. The ascending branch corresponds to the elastic response of the bond, culminating at the peak shear stress, ${\tau }_m$. The corresponding slip at this peak is denoted as $s_m$. Beyond this point, the descending (softening) branch captures the degraded response, modeling the progressive failure of the interface. The mathematical description of the bond–slip law is given by

$$\tau =\left\{\begin{array}{l}{\tau }_{m}s/s_m, s\le s_m\\ {\tau }_m(1+p-ps/s_m), s_m<s\le s_f\\ 0, s>s_f\end{array}\right.$$

(2)

where $s_f$ is the final slip and $p={s_m/(s}_f-s_m)$. When $s>s_f$, where $\tau =0$, the interface bonds have broken and a crack has formed. When the strengthening system is subjected to external loading and the resulting interfacial shear stresses remain within the ascending branch of the bond–slip diagram, the interface exhibits elastic behavior. In this regime, the absorbed energy is entirely recoverable upon unloading, and the stress state is classified as undamaged. To ensure the practical implementation of the proposed analytical framework, the identification of the characteristic parameters defining the bilinear cohesive law $({\tau }_m,s_m,s_f)$ is essential. These parameters can be derived either through standard code recommendations for conventional materials or via inverse analysis of experimental data for specific systems. For standard FRP-concrete applications, the cohesive parameters can be derived following international design recommendations. For instance, according to the CNR-DT 200 R1/2013 guidelines [26], the interfacial fracture energy is calculated as: $G_f=k_G{k}_b\sqrt{f_{cm}{f}_{ctm}}$ with $f_{cm}$ and $f_{ctm}$ being the mean values of the concrete compressive and tensile strengths, respectively; $k_G$ is a corrective factor and $k_b,$ a geometrical factor. Considering a typical application with C30 concrete $(f_{cm}=38 \mathrm{MPa}, f_{ctm}=2.9 \mathrm{MPa})$ and an FRP plate of width $b_f=b=50 \mathrm{mm}$ bonded to a concrete substrate of width $b_c=200 \mathrm{mm}$, the width factor is $k_b=\sqrt{(2-b_f/b_c)/(1+b_f/b_c)}=1.22$. Adopting the mean calibration factor $k_G=0.063 \mathrm{mm}$, the fracture energy is obtained as $G_f=0.81 \mathrm{N}/\mathrm{mm}$. Regarding the bond-slip law shape, in the absence of specific experimental data, the code suggests adopting a standard ultimate slip value of $s_f=0.25 \mathrm{mm}$. Consequently, the maximum bond stress ${\tau }_m$ is derived to satisfy the fracture energy balance $(G_f={\tau }_m{s}_f/2)$, yielding: ${\tau }_m=6.48 \mathrm{MPa}$. The elastic slip is typically assumed as a fraction of the ultimate slip or based on adhesive stiffness, e.g., $s_m=0.05 \mathrm{mm}$. For novel material systems where code provisions may not apply, the cohesive parameters should be identified experimentally. This involves performing pull-out tests and applying an inverse analysis to fit the analytical predictions to the experimental load-slip (F-Δ) curves. The authors propose utilizing the Levenberg–Marquardt (L-M) optimization algorithm to minimize the residuals between the theoretical model and test data. This rigorous calibration methodology is currently under development by the authors and is planned to be presented and validated in a future study.

The energy absorbed at the interface per unit area, i.e., the strain energy density, can be calculated from the area under the bond–slip law curve $(\tau -s$). When a portion of the interface is in the elastic region (i.e., the slip $s$ is less than the slip limit $s_m$), the absorbed energy corresponds to the area of a triangle, as shown by the shaded area in Figure 3a.

The energy density, $u_e$, is given by the following relation:

$$u_e={\displaystyle \frac{\tau s}{2}}={\displaystyle \frac{{\tau }_m{s}^2}{2s_m}}$$

(3)

When the slip $s$ exceeds the value $s_m$, a portion of the bonded surface enters the descending (softening) branch. The corresponding surface energy density, $u_d$, is represented by the total area shown in Figure 3b and is calculated as

$$u_d=G_f-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\tau }_m}{s_f-s_m}}{\left(s_f-s\right)}^2$$

(4)

where

$$G_f={\tau }_m{s}_m{\displaystyle \frac{1+p}{2p}}$$

(5)

represents the total fracture energy, that is, the energy that would have been consumed if all the interface bonds had been completely destroyed (by reaching the final slip $s_f$).

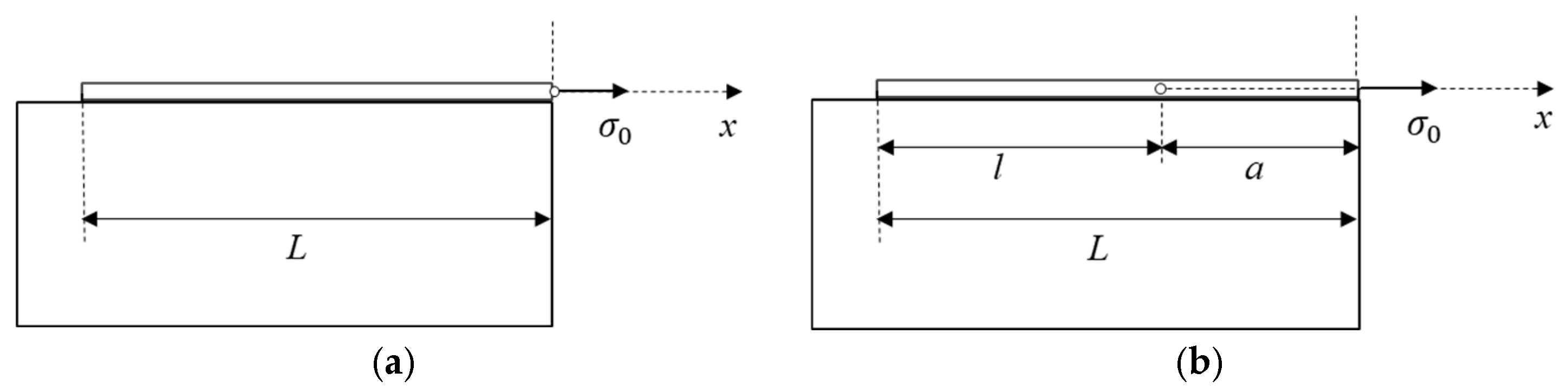
3. Analysis of Progressive Debonding

In this section, the stressed state of the strengthening system depicted in Figure 4 is analyzed considering two distinct loading cases, characterized by the behavior of the interfacial shear stresses. In the first case (see Figure 4a), the shear stresses developed along the entire interface due to the external force remain within the ascending (elastic) branch of the bond–slip diagram.

This stressed state signifies the undamaged state of the system, where the entire bond length is essentially an elastic zone, exhibiting linear elastic response. In the second case, as the external load increases further, a portion of the interface of the length a enters the descending (softening) branch, and this segment is designated as Zone II (softening/damage zone). The remaining part of the interface operates within the ascending (elastic) branch and is designated as Zone I, whose length is $l=L-a$. This stressed state, characterized by the coupling of the two zones, is referred to as the damaged state of the system (see Figure 4b). The analytical solutions to these two governing problems—the fully elastic state and the state with Zone I and Zone II coupled—is detailed in the following sections.

The analysis of the undamaged state of the system (see Figure 4a) is governed by the following differential equation and boundary conditions:

$$s^{″}(x)={\lambda }^{2}s(x), -L\le x\le 0$$

(6)

$$s^{\prime }(-L)=0, E{s}^{\prime }(0)={\sigma }_0$$

(7)

where

$${\lambda }^2={\displaystyle \frac{{\tau }_m}{Et{s}_m}}$$

(8)

Following a typical solution procedure for the above boundary value problem, the general solution for the slip distribution $s$ is

$$s(x)={\displaystyle \frac{{\sigma }_0}{\lambda E}}{\displaystyle \frac{\cosh (\lambda L+\lambda x)}{\sinh (\lambda L)}}$$

(9)

From Hooke’s law ($\sigma =E{s}^{’}$) and the interfacial bond–slip law ($\tau ={\tau }_{m}s/s_m)$, the final expressions for the normal stress in the FRP plate, $\sigma \left(x\right)$, and the shear stress at the interface, $\tau \left(x\right)$, are derived:

$$\sigma (x)={\sigma }_0{\displaystyle \frac{\sinh \lambda (L+x)}{\sinh (\lambda L)}}, \tau (x)={\sigma }_0\lambda t{\displaystyle \frac{\cosh (\lambda L+\lambda x)}{\sinh (\lambda L)}}$$

(10)

For the damaged state of the system (see Figure 4b), the governing differential equations for the two zones are

$$s_I^{″}(x)={\lambda }^2{s}_I(x),-l\le x\le 0$$

(11)

$$s_{II}^{″}(x)+p{\lambda }^2{s}_{II}(x)=p{\lambda }^2{s}_f, 0\le x\le a$$

(12)

where $l=L-a$; $s_I\left(x\right)$ and $s_{II}\left(x\right)$ are the slip functions for Zone I and Zone II, respectively. Hereinafter, the subscripts I and II will denote quantities belonging to Zone I and Zone II, respectively. The above differential equations are solved subject to the following boundary and compatibility conditions:

$$E{s}_I^{\prime }(-l)=0, s_I(0)=s_{II}(0)=s_m, E{s}_I^{\prime }(0)=E{s}_{II}^{\prime }(0)$$

(13)

The first condition states that the axial force is zero at the free end of the plate, while the remaining three ensure the continuity of slip and axial force at the common boundary. Following a standard analytical procedure, the solutions to the above differential equations that satisfy the conditions of Equation (13) are obtained in the following forms:

$$s_I(x)=s_m{\displaystyle \frac{\cosh (\lambda l+\lambda x)}{\cosh (\lambda l)}}$$

(14)

$$s_{II}(x)={\displaystyle \frac{s_m}{p}}\left[-\cos (\sqrt{p}\lambda x)+\sqrt{p}\tanh \lambda l\sin (\sqrt{p}\lambda x)\right]+s_f$$

(15)

Based on the above equations, the shears ${\tau }_I\left(x\right)$ and ${\tau }_{II}\left(x\right)$ arising in the two interface zones are calculated using the appropriate bond–slip law for each zone. It is found that

$${\tau }_I(x)={\tau }_m{\displaystyle \frac{\cosh (\lambda l+\lambda x)}{\cosh (\lambda l)}}$$

(16)

$${\tau }_{II}(x)={\tau }_m\left(\cos (\sqrt{p}\lambda x)-\sqrt{p}T\sin (\sqrt{p}\lambda x)\right)$$

(17)

where

$$T=\tanh [\lambda (L-a)]$$

(18)

Using Hooke’s law, the normal stresses ${\sigma }_I\left(x\right)$ and ${\sigma }_{II}\left(x\right)$ corresponding to the two zones of the system are found in the form

$${\sigma }_I(x)={\displaystyle \frac{E{s}_m\lambda }{\cosh (\lambda l)}}\sinh \lambda (l+x)$$

(19)

$${\sigma }_{II}(x)=E{\displaystyle \frac{\sqrt{p}}{p}}\lambda s_m\left[\sin (\sqrt{p}\lambda x)+\sqrt{p}\tanh \lambda l\cos (\sqrt{p}\lambda x)\right]$$

(20)

At the loaded end of FRP plate, the boundary condition ${\sigma }_{II}\left(a\right)={\sigma }_0$ provides

$${\sigma }_0={\displaystyle \frac{E{s}_{\mathrm{m}}\lambda }{\sqrt{p}}}\left[\sin (\sqrt{p}\lambda a)+\sqrt{p}\tanh \lambda l\cos (\sqrt{p}\lambda a)\right]$$

(21)

It is important to note that this boundary condition is not used directly in the initial analytical solution of the boundary value problem. Instead, the following condition is used: $s_I\left(0\right)=s_{II}\left(0\right)=s_m$. This condition, coupled with the stress continuity requirements at the interface between the two zones, ensures that the solution correctly models the transition of the system from the undamaged (elastic) state to the damaged (softening) state, specifically when the shear stresses reach ${\tau }_m$ and the descending branch initiates. This set of boundary and continuity conditions directly relates the length $a$ of Zone II (the softening zone) to the external stress ${\sigma }_0$, allowing for the determination of the system’s overall resistance capacity.

The undamaged (elastic) state transitions to the damaged (softening) state when the slip at the loaded end, $s\left(0\right)$, reaches the critical value $s_m$. The external stress corresponding to this transition, ${\sigma }_{0,el}$, is derived from the solution for the elastic state (from Equation (9)) by setting $s\left(0\right)=s_m$ and ${\sigma }_0={\sigma }_{0,el}$. This yields the following expression for the critical stress:

$${\sigma }_{0,el}=\lambda E{s}_m\tanh (\lambda L)$$

(22)

This critical stress satisfies the relation ${\sigma }_{{\rm I}{\rm I}}\left(0\right)={\sigma }_{0,el}$ and defines the elastic limit force of the system, $F_{el}$, via the relation $F_{el}=bt\cdot {\sigma }_{0,el}$, where $bt$ is the cross-sectional area of the FRP plate.

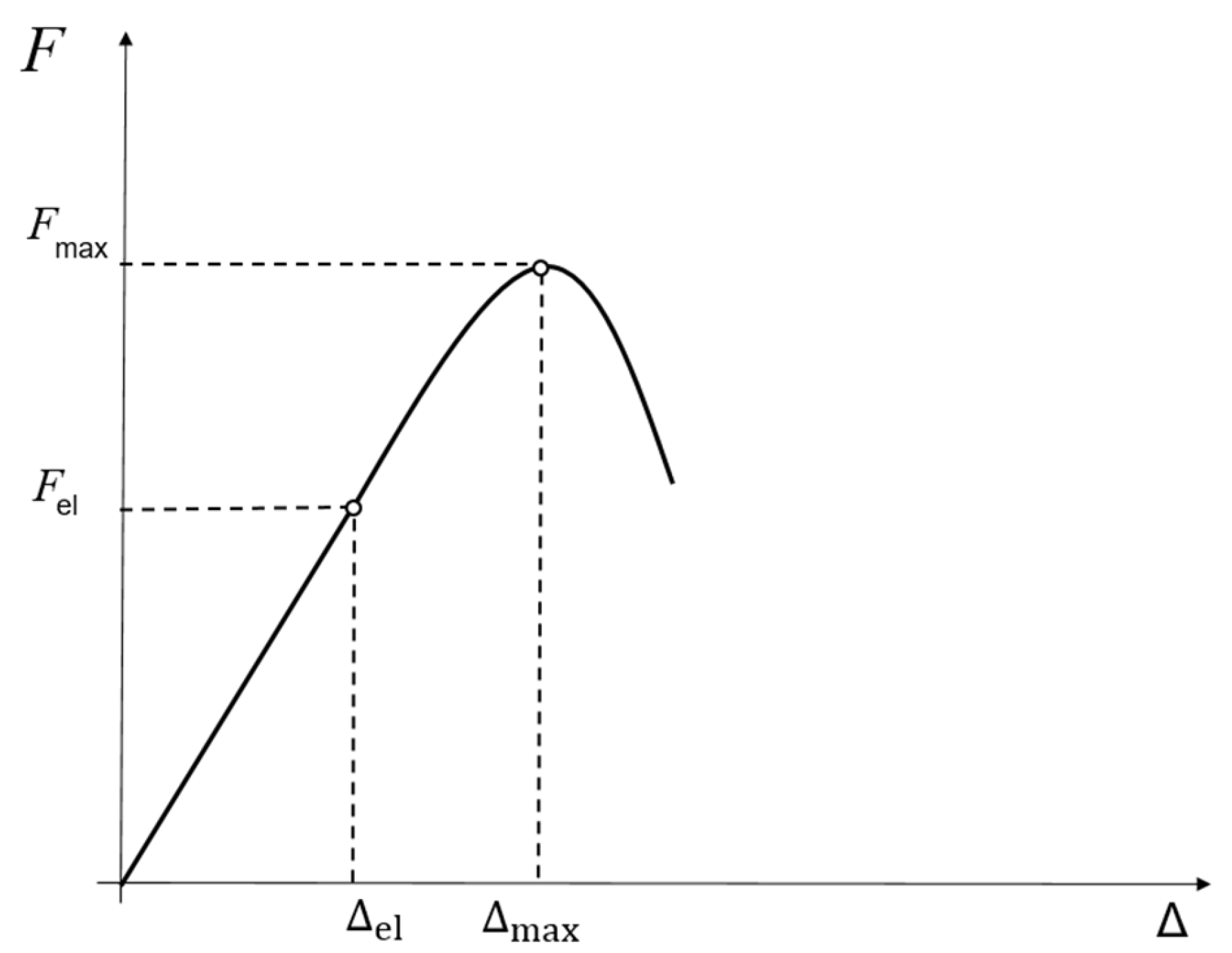
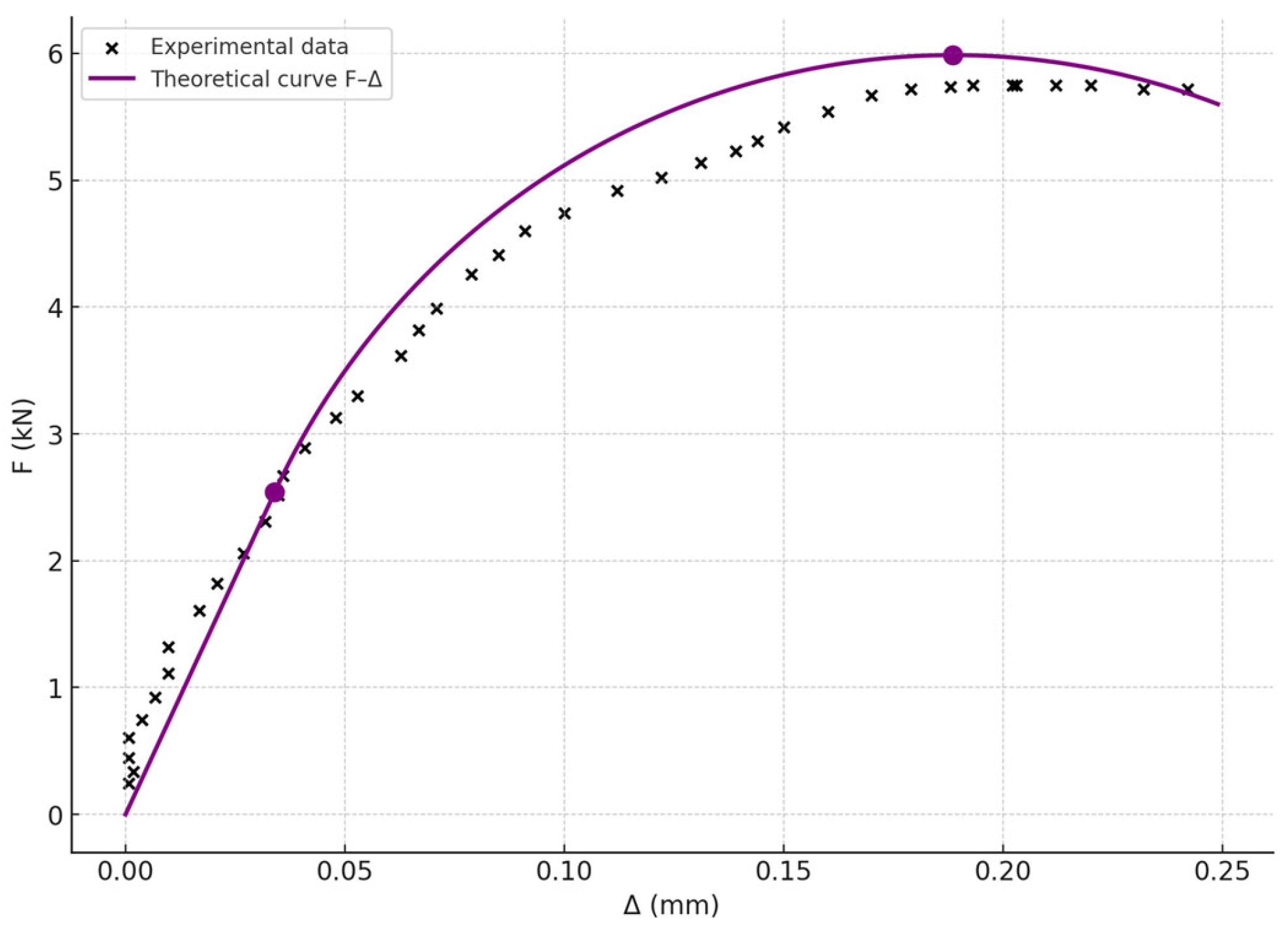
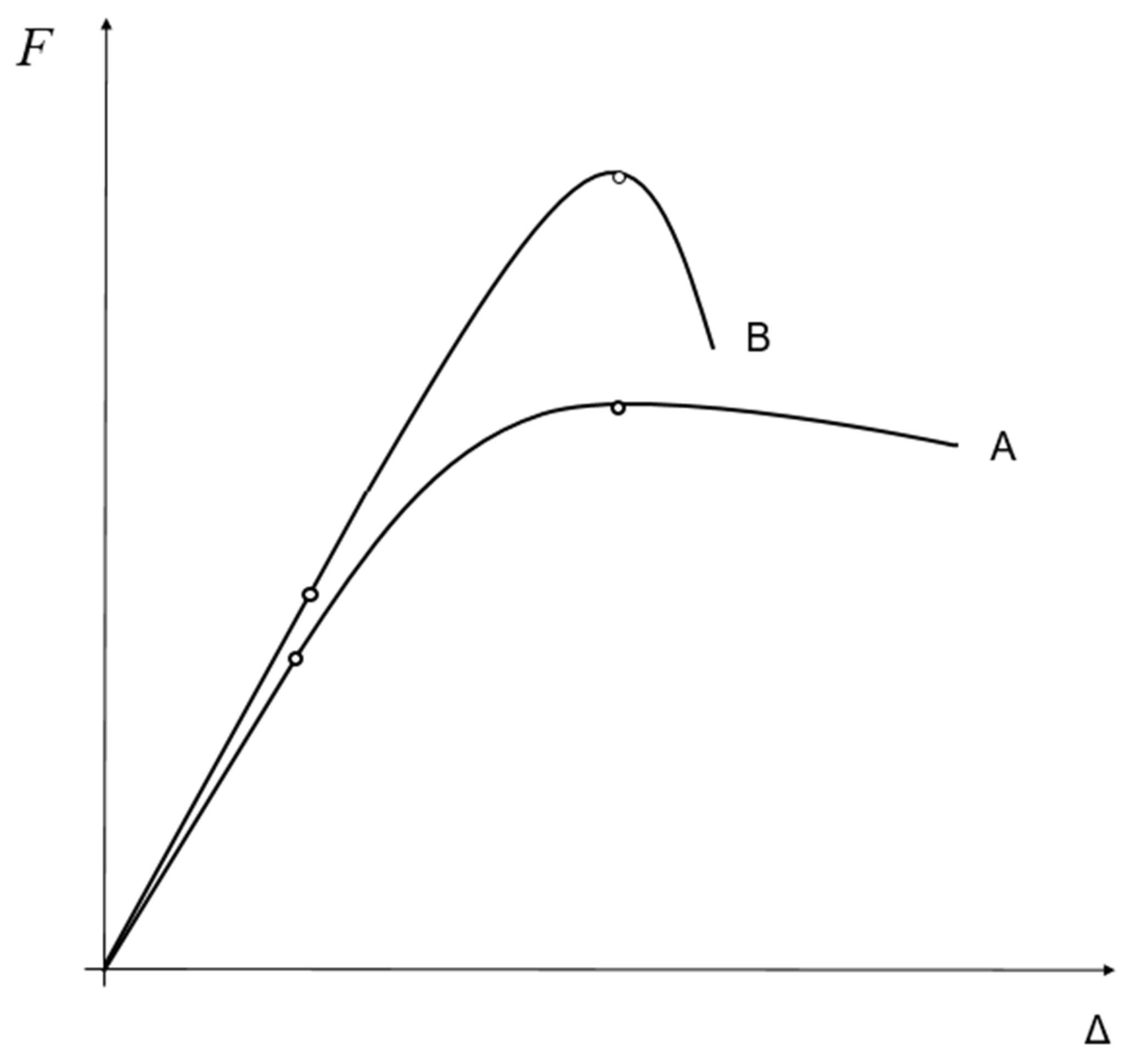
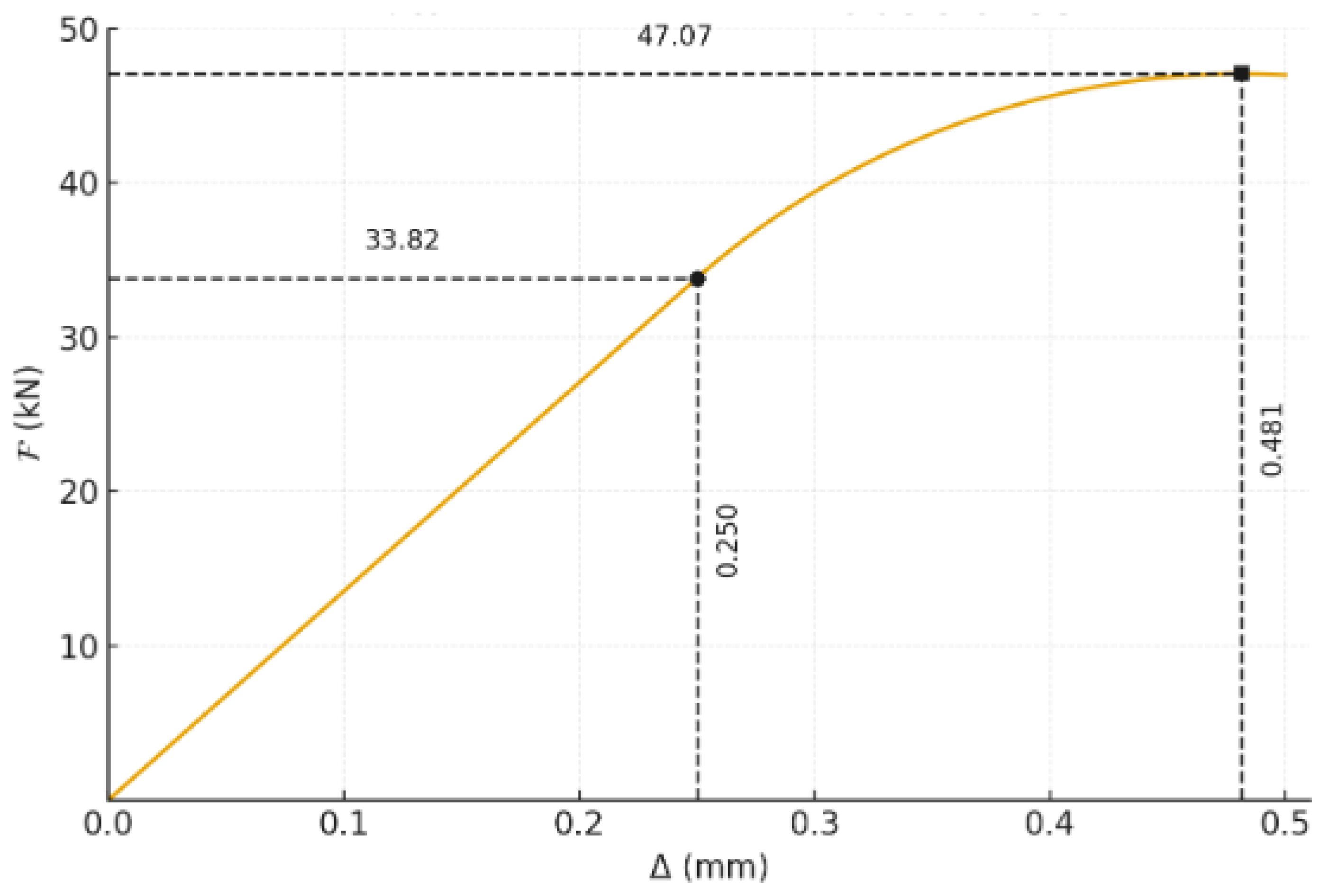
4. The Global System Response ($\mathit{F}-\mathit{\Delta }$ Curve)

The true behavior of the examined strengthening system, as can be observed in an experimental test, is captured by the global force–slip ($F-\Delta$) curve, where $F$ is the external applied force and $\Delta$ the slip of the application point. This curve is not an intrinsic material property but rather the integrated result of the interaction between the interface, the stiffness of the plate, and the anchorage geometry. The complete analytical model developed in the preceding sections allows us to theoretically construct this global $F-\Delta$ curve. The analysis of its shape—specifically its characteristic points, curvature, slope, and area—is the key to quantifying the system’s strength, stability, and ductility. A typical force–slip $F-\Delta$ curve is shown in Figure 5.

As shown in Figure 5, the global curve $F-\Delta$ consists of four distinct phases:

• The elastic phase ($a=0$) (from the onset of loading up to the point (${\Delta }_{el}$, $F_{el}$)): The $F-\Delta$ relationship is linear and is described by the elastic solution $F=bt\cdot \lambda E\mathit{tan}h(\lambda L)\Delta$, with ${\Delta }_{el}=s_m$ and $F_{el}=bt\cdot \lambda E\mathit{tan}h(\lambda L)s_m$.
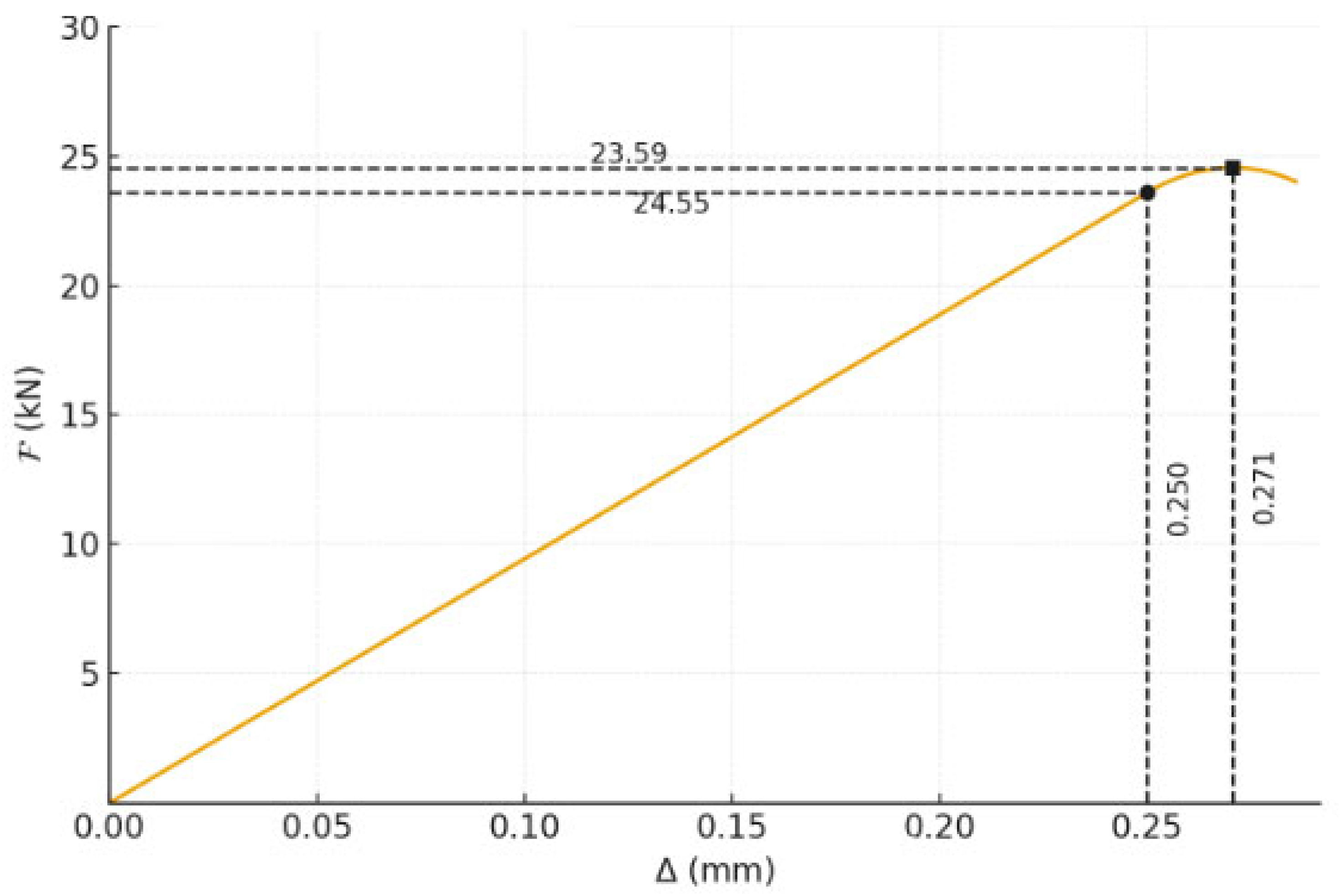
• The progressive hardening phase (from $F_{el}$ to $F_{max}$): This is the curvilinear segment between the elastic limit and the maximum force. Even though the interface material at the loaded end has already entered its softening branch, the global resistance of the system continues to increase. This apparent system “hardening” is due to stress redistribution: as the damage zone $a$ grows, it “activates” new, undamaged sections of the elastic zone (Zone I) deeper in the anchorage, which contribute to the increase in total force. The curve here is constructed parametrically via the equations $F=bt\cdot {\sigma }_{II}\left(a\right)$ and $\Delta =s_{II}\left(a\right)$.
• The peak $({\Delta }_{max}, F_{max})$: This is the point of maximum resistance. It occurs at the critical softening length $a_c$.
• The descending branch after the peak $({\Delta }_{max}, F_{max})$: After the peak, the growth of the damage zone $a$ can no longer be compensated for by the activation of new elastic segments, and the total resistance of the system begins to decrease.

The maximum value of the force, $F_{max}$, is calculated by finding the roots of its first derivative, $dF/da=0$; the latter equation has a root at $a_c$, which is found by solving the following transcendental equation:

$$\tanh [\lambda (L-a_c)]=\sqrt{p}\tan (\sqrt{p}\lambda a_c)$$

(23)

This equation can be solved numerically to yield the value of $a_c$, which corresponds to a local maximum for the force $F\left(\alpha \right)$, because the second derivative is negative at this point:

$${\displaystyle \frac{d^{2}F}{d{a}^2}}=-b{\tau }_m\lambda (1+p)\cosh [\lambda (L-a_c)]\cos (\lambda \sqrt{p}{a}_c)<0$$

(24)

For the above inequality to be valid, the following condition must hold:

$$a_c<{\displaystyle \frac{\pi }{2\lambda \sqrt{p}}}$$

(25)

The maximum value of the force, $F_{max}$, is then found by substituting $a_c$ into the expression for $F\left(a\right)$:

$$F_{\max }=btE\lambda s_m{\displaystyle \frac{(1+p)\tanh [\lambda (L-a_c)]}{\sqrt{p\left[{\tanh }^2[\lambda (L-a_c)]+p\right]}}}$$

(26)

The slip ${\Delta }_{max}$ at the plate end where the external force $F_{max}$ is applied is

$${∆}_{\max }=s_{II}(a_c)=s_m\left[{\displaystyle \frac{1+p}{p}}-{\displaystyle \frac{1}{\sqrt{p}}}{\displaystyle \frac{1-{\tanh }^2[\lambda (L-a_c)]}{\sqrt{p+{\tanh }^2[\lambda (L-a_c)]}}}\right]$$

(27)

It is obvious that

$${\Delta }_{\max }=s_{II}(a_c)<s_f(=s_m(1+p)/p)$$

(28)

The branch of the $F-\Delta$ curve after the peak (the descending branch) is the most important diagnostic tool regarding the system’s safety: it defines the mode of failure. If the descending branch is gentle, with a mild slope (a plateau), the system is stable; namely, it exhibits ductile behavior. This has enormous practical value: (i) the structure provides warning before collapse, through large, visible deformation; (ii) the structure has a high energy absorption capacity, which is critical for seismic actions; (ii) the failure is controlled and predictable. If the descending branch is steep, with a large negative slope, the system is unstable and exhibits brittle behavior, indicating a dangerous, violent failure (“snap-back”).

To initially validate the analytical model, its curve was compared with that of a published experimental load–slip response for an FRP-to-concrete bonded joint, as shown in Figure 6.

The experimental curve was taken from [27] and corresponds to a single-shear test with the reported parameters $b=25 \mathrm{m}\mathrm{m}$, $t=0.165 \mathrm{m}\mathrm{m}$, and $L=190 \mathrm{m}\mathrm{m}$ and an experimentally identified bond–slip relationship characterized by the parameters ${\tau }_m=7.2 \mathrm{M}\mathrm{P}\mathrm{a}$,${ s}_m=0.034 \mathrm{m}\mathrm{m}$, and $p=0.22$. Since the experimental curve was available only in graphical form, it was digitized using WebPlotDigitizer. Figure 6 shows the comparison between the digitized experimental curve and the analytical prediction. The analytical model captures the initial elastic stiffness, the onset of apparent hardening, the magnitude and location of the peak load, and the qualitative form of the post-peak softening branch with good accuracy. It is emphasized that the purpose of this comparison is not full experimental validation but rather demonstration that the proposed formulation reproduces the key behavioral characteristics observed in FRP plate debonding tests. A complete experimental validation is part of an ongoing research program and will be presented in future work.

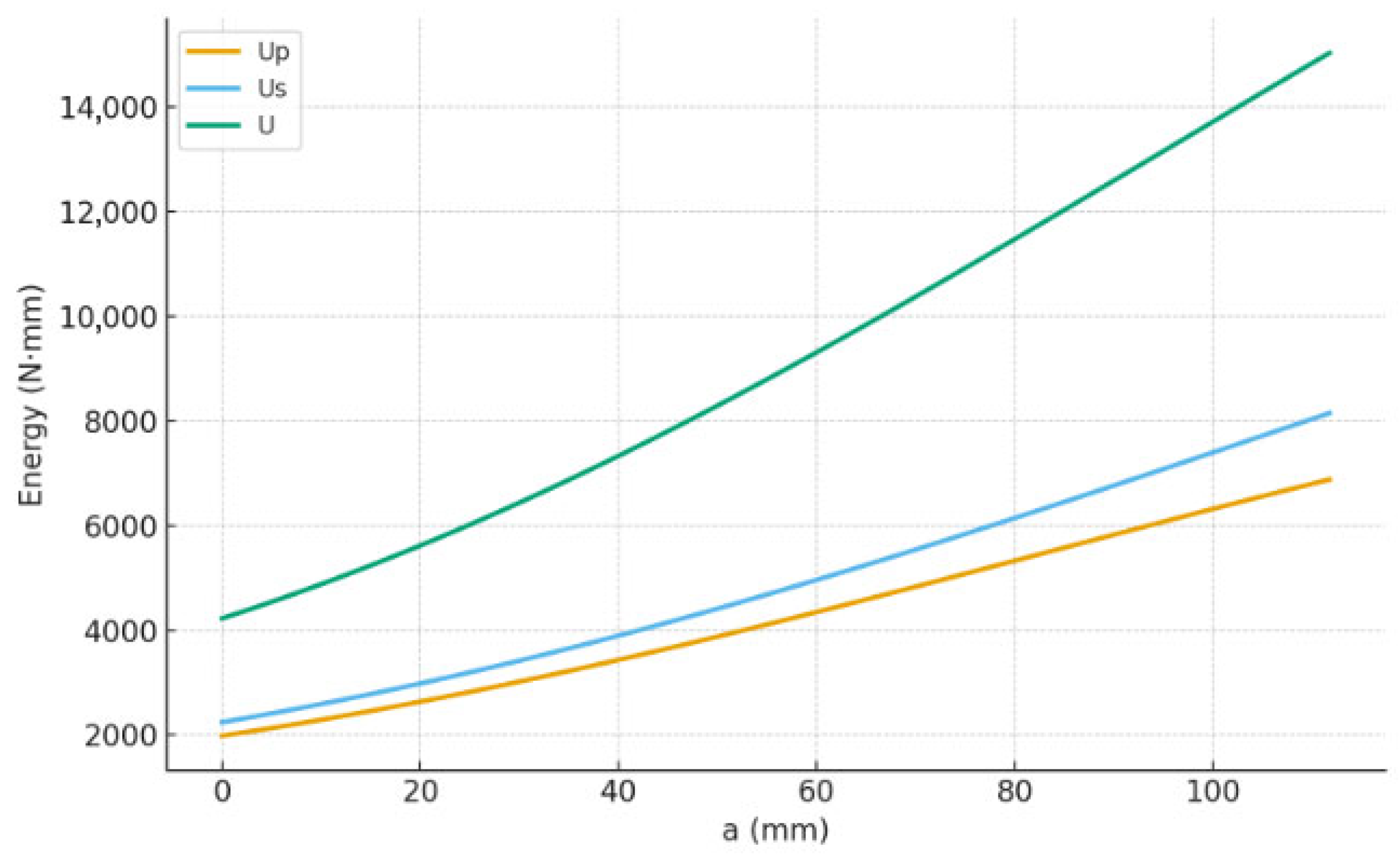
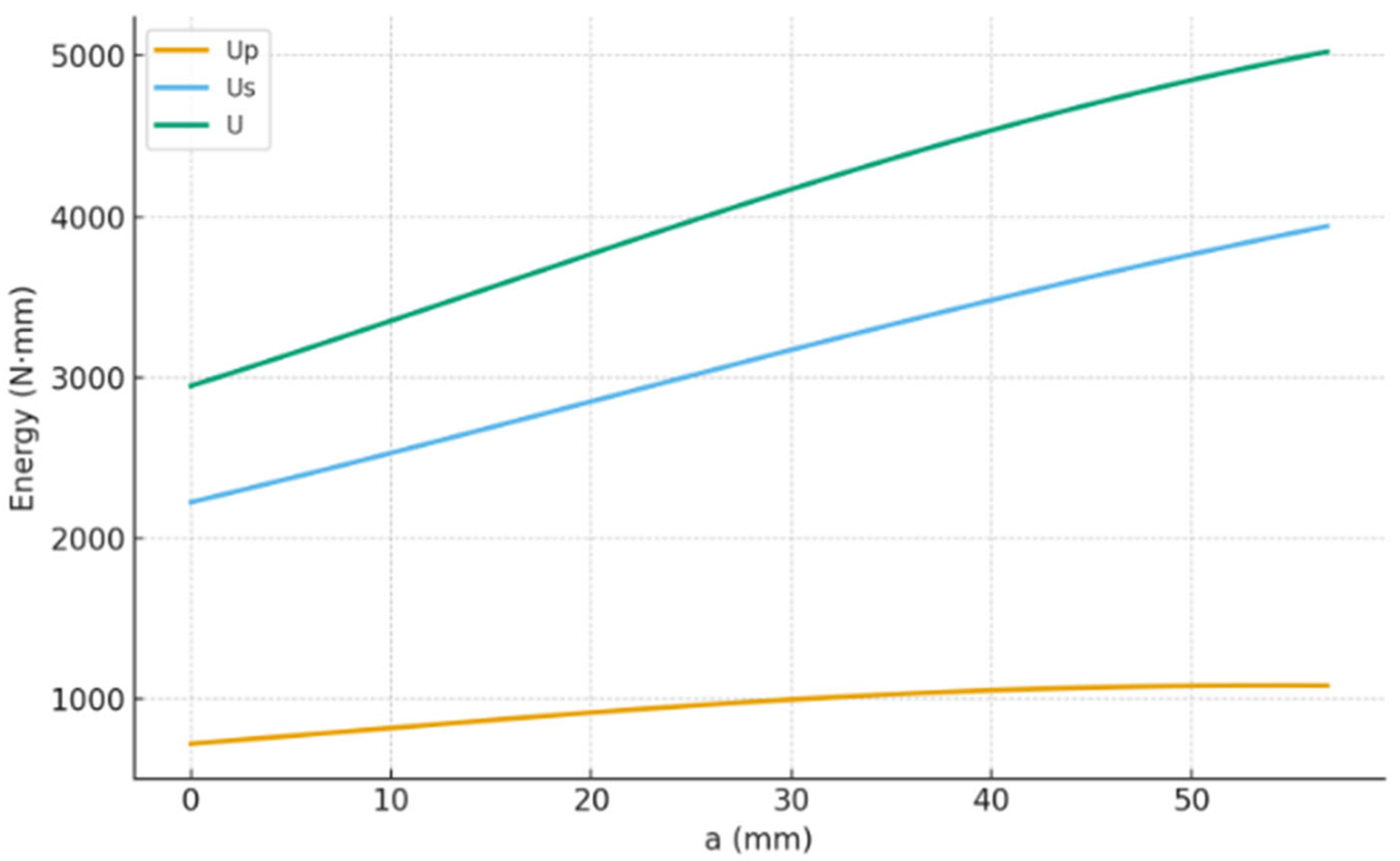
5. Energetic Analysis of Damage Evolution

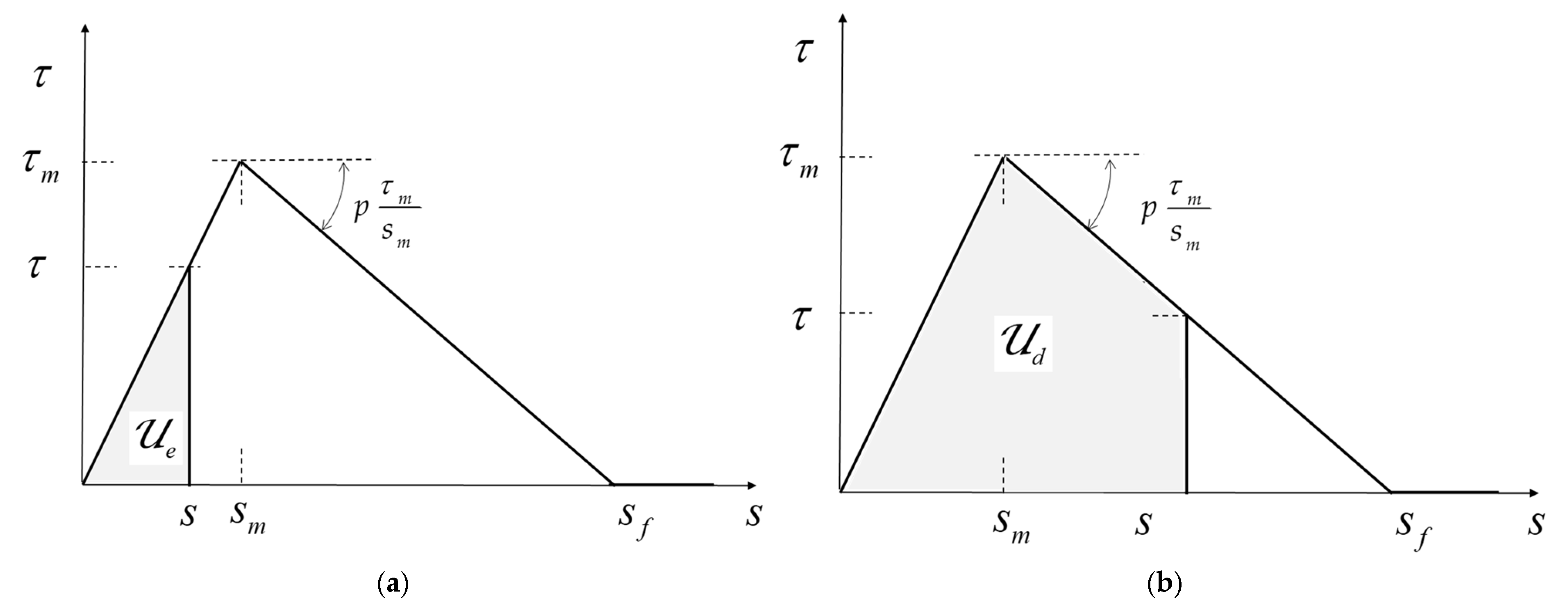
5.1. Calculation of Energy Components

Understanding the evolution of debonding requires shifting from a stress-based analysis to an energy-based one. The work performed by the external force is distributed within the system, either stored temporarily as elastic strain energy or irreversibly dissipated to create damage. This section analytically calculates the energy components and derives the system’s fundamental energy balance.

The energy components in the undamaged (elastic) state of the system are first calculated. In this case, where the entire interface is on the ascending branch, the energy absorbed by the system is entirely elastic strain energy, $U^{\left(0\right)}$, which is recoverable and consists of two parts: the energy stored in the FRP plate, $U_p^{\left(0\right)}$, and that stored in the interface, $U_s^{\left(0\right)}$. These components can be computed by integrating the energy densities along the bond length, using the solutions of the relative elastic problem. It is found that

$$U_p^{(0)}={\displaystyle \frac{{\sigma }_0^{2}bt}{4E\lambda }}\left[{\displaystyle \frac{1}{\tanh (\lambda L)}}-\lambda l[1-{\tanh }^2(\lambda L)]\right]$$

(29)

$$U_s^{(0)}={\displaystyle \frac{{\sigma }_0^{2}bt}{4E\lambda }}\left[{\displaystyle \frac{1}{\tanh (\lambda L)}}+\lambda l[1-{\tanh }^2(\lambda L)]\right]$$

(30)

The sum of the above two energy components provides the elastic energy of the undamaged state:

$$U^{(0)}={\displaystyle \frac{{\sigma }_0^{2}bt}{2E\lambda \tanh (\lambda L)}}$$

(31)

When the softening zone $a$ (Zone II) has formed, the energy state is more complex. The total absorbed energy, $U\left(a\right)$, is defined as the total work that has been expended to deform all internal components (FRP and interface); that which deforms the FRP plate is stored in it as pure elastic energy, $U_p$. This energy is calculated by integrating the strain energy densities $u_{p,I}\left(x\right)={\sigma }_I^2\left(x\right)/\left(2E\right)$ and $u_{p,II}\left(x\right)={\sigma }_{II}^2\left(x\right)/\left(2E\right)$ over both Zones I and II, respectively. It is found that

$$U_{p,I}={\displaystyle \frac{b{G}_f}{2\lambda }}{\displaystyle \frac{p}{1+p}}[T-\lambda l(1-T^2)]$$

(32)

$$U_{p,II}={\displaystyle \frac{G_{f}b}{2(1+p)}}\left[(1+p{T}^2)a-{\displaystyle \frac{1}{\lambda }}\mathrm{\Phi }(a)\right]$$

(33)

where

$$\mathrm{\Phi }(a)=(1-p{T}^2){\displaystyle \frac{\sin 2\sqrt{p}\lambda a}{2\sqrt{p}}}+T(\cos 2\sqrt{p}\lambda a-1)$$

(34)

and $T=\mathit{tan}h[\lambda (L-a)].$ The total energy $U_p(=U_{p,I}+U_{p,II})$ stored in the FRP plate is

$$U_p={\displaystyle \frac{G_{f}b}{2(1+p)}}\left[{\displaystyle \frac{p}{\lambda }}[T-\lambda l(1-T^2)]+(1+p{T}^2)a-{\displaystyle \frac{1}{\lambda }}\mathrm{\Phi }(a)\right]$$

(35)

The energy stored in the interface bond of the “healthy” Zone I, denoted by $U_{s,I}$, is purely elastic and is found by integrating the surface energy density $u_{e,I}\left(x\right)=b{\tau }_m{s}_I^2\left(x\right)/\left(2s_m\right)$ over Zone I (see Figure 3a). It is found that

$$U_{s,I}={\displaystyle \frac{b{G}_f}{2\lambda }}{\displaystyle \frac{p}{1+p}}[T+\lambda l(1-T^2)]$$

(36)

On the other hand, the energy stored in the interface bond of Zone II, denoted by $U_{s,II}$, is not purely elastic; it includes both the (small) elastic energy that remains stored in the weakened bonds and the damage energy that has already been irreversibly dissipated to cause the softening. $U_{s,II}$ can be found by integrating the surface energy density $u_{d,II}\left(x\right)=b{G}_f-b{\tau }_m{\left(s_F-s_{II}\right)}^2/\left[2\left(s_f-s_m\right)\right]$ over Zone II (Figure 3b). It is found that

$$U_{s,II}={\displaystyle \frac{G_{f}b}{2(1+p)}}\left[(1+2p-p{T}^2)a-{\displaystyle \frac{1}{\lambda }}\mathrm{\Phi }(a)\right]$$

(37)

Therefore, the total energy stored in the interface bond is

$$U_s={\displaystyle \frac{G_{f}b}{2(1+p)}}\left[{\displaystyle \frac{p}{\lambda }}[T+\lambda l(1-T^2)]+(1+2p-p{T}^2)a-{\displaystyle \frac{1}{\lambda }}\mathrm{\Phi }(a)\right]$$

(38)

The full expression for the total absorbed energy is

$$U=U_s+U_p=G_{f}ba+{\displaystyle \frac{G_{f}b}{(1+p)\lambda }}\left[pT-\mathrm{\Phi }(a)\right]$$

(39)

Figure 7 and Figure 8 show the variation in the partial energies $U_p$ and $U_s$ and in the total energy $U$ as a function of the softening length, $a$, for two representative cases of the system, which will be further analyzed below.

The endpoint of each curve corresponds to the value of $a$ at which full FRP debonding initiates. As can be demonstrated analytically, the energy stored in the interface springs is always greater than the purely elastic energy stored within the FRP itself. A more detailed discussion of these two representative cases—which correspond to two qualitatively distinct modes of system behavior—is presented in Section 6 of this study.

5.2. The Energy Balance

The system under study is non-conservative, as there is an irreversible loss of energy due to damage. The principle of virtual work (or the First Law of Thermodynamics) requires that the incremental work performed by the external force,$\delta W$, must equal the sum of the change in the total absorbed energy, $\delta U$, and the energy irreversibly dissipated to create the debonding, $\delta D$. When the system has developed a softening zone of the length $a$, an incremental change, $\delta a$, in this length induces a corresponding change, $\delta \Delta$, in the slip at the point of application of the force $F$, which is given by $\delta \Delta =s_{II}^{’}\left(a\right)\delta a$. For this increment, based on the principle of virtual work, the following relationship holds:

$$\delta W=\delta U+\delta D$$

(40)

δW is the work performed by the external force $F$ in the path $\delta \Delta$:

$$\delta W=\mathrm{F}\delta \Delta =bt\cdot {\sigma }_{II}(a)s_{II}^{\prime }(a)\delta a$$

(41)

The above relation can be written as

$$\delta W={\displaystyle \frac{dW}{da}}\delta \alpha$$

(42)

where $dW/da=bt\cdot {\sigma }_{{\rm I}{\rm I}}\left(a\right)s_{II}^{’}\left(a\right)$; using Equations (15) and (20), the latter equation provides

$${\displaystyle \frac{dW}{da}}=b{G}_f\left[1+T^2+{\displaystyle \frac{(p-1)T^2\cos (2\lambda \sqrt{p}a)+\sqrt{p}T(1+T^2)\sin (2\lambda \sqrt{p}a)}{1+p}}\right]$$

(43)

The change in the total absorbed energy, $\delta U$, is given by

$$\delta U={\displaystyle \frac{dU}{da}}\delta a$$

(44)

where $dU/da$ is calculated from Equation (39) in the form

$${\displaystyle \frac{dU}{da}}=b{G}_f\left[T^2+{\displaystyle \frac{(p-1)T^2\cos (2\lambda \sqrt{p}a)+\sqrt{p}T(1+T^2)\sin (2\lambda \sqrt{p}a)}{1+p}}\right]$$

(45)

Using the relation

$$\delta D={\displaystyle \frac{dD}{da}}\delta a$$

(46)

and taking into account Equations (43) and (45), the following is obtained:

$${\displaystyle \frac{dD}{da}}={\displaystyle \frac{dW}{da}}-{\displaystyle \frac{dU}{da}}=b{G}_f$$

(47)

In the fracture mechanics literature, the quantity

$$G={\displaystyle \frac{dW}{da}}-{\displaystyle \frac{dU}{da}}$$

(48)

is defined as the energy release rate associated with the incremental propagation, $da$, of the softening zone. Taking into account Equations (47) and (48) provides

$$G=b{G}_f$$

(49)

Equation (49) reveals that, during the propagation of the softening zone, the energy release rate is constant and equal to the energy required to create a new unit area of damage. In other words, the energy release rate (the driving force) remains exactly equal to the material’s fracture resistance ($R=b{G}_f$) throughout the entire propagation of the softening zone.

5.3. Energetic Investigation of Apparent Hardening

At this juncture, it is essential to investigate the total absorbed energy of the system, $U$, and its rate of change, $dU/da$, at the specific moment the external force reaches its maximum value. This critical state occurs when the softening zone reaches the length $a=a_c$. By substituting the maximum force condition (Equation (23)) into Equations (39) and (45), the following are obtained:

$$U(a_c)=G_{f}b{a}_c+{\displaystyle \frac{G_{f}b}{\lambda }}\tanh [\lambda (L-a_c)]{\displaystyle \frac{2{\tanh }^2[\lambda (L-a_c)]+p-1}{p+{\tanh }^2[\lambda (L-a_c)]}}$$

(50)

$${\left.{\displaystyle \frac{dU}{da}}\right|}_{a=a_c}=2b{G}_f{\tanh }^2[\lambda (L-a_c)]$$

(51)

These two equations are central to understanding the stability of the debonding process. Equation (50) provides the total energy $U\left(a_c\right)$ that has been absorbed by the entire system (both elastically stored and dissipated as damage) up to the point of peak load; this quantity represents the available “fuel” for a potential unstable failure. Equation (51) is arguably the more profound finding. It provides the rate of energy storage at the critical moment and elegantly demonstrates that the rate of energy absorption is not constant but is fundamentally linked to the remaining elastic length ($L-a_c$). As the system becomes “longer” (i.e., as $L-a_c$ increases), the $\mathit{tanh}[\lambda (L-a_c)]$ term approaches 1, and the rate of energy storage approaches its maximum possible value of $2b{G}_f$. This high rate of energy storage is precisely what “loads” the system and leads to the brittle, snap-back instability characteristic of long bond lengths.

The debonding mechanism, particularly the nature of brittle failure, can be more deeply understood by examining the asymptotic case of an infinitely long bond line $\left(L\to \infty \right).$ With this theoretical limit, Equations (35), (38), (47), and (43) lead to

$${\left.{\displaystyle \frac{d{U}_p}{da}}\right|}_{a_c,L\to \infty }={\left.{\displaystyle \frac{d{U}_s}{da}}\right|}_{a_c,L\to \infty }={\left.{\displaystyle \frac{dD}{da}}\right|}_{a_c,L\to \infty }=b{G}_f$$

(52)

$${\left.{\displaystyle \frac{dW}{da}}\right|}_{a_c,L\to \infty }=3b{G}_f$$

(53)

The above results show a perfect “energy trichotomy” as $L\to \infty .$ The rate of external work supplied to the system $(dW/da)$ is precisely partitioned into three equal streams of energy flow, all of which are equal to $b{G}_f$: (i) One part is irreversibly consumed to break the bonds at the debonding front $(dD/da).$ (ii) A second part is stored as shear strain energy in the deforming adhesive layer $(d{U}_s/da)$. (iii) The third part is stored as axial strain energy in the stretching FRP plate $(d{U}_p/da)$. This equal partitioning is the hallmark of brittle failure. The condition reveals that at the point of failure, the system spends twice as much energy on storing more potential energy $\left(dU/da=2b\cdot G_f\right)$ as it does on the actual fracture process itself $(dU/da=b\cdot G_f)$. This massive rate of energy storage is the engine of instability, leading to the accumulation of a vast reservoir of elastic energy within the system. Once the peak load is reached, this stored energy is released catastrophically, driving the debonding process forward in an uncontrolled and violent manner, which manifests as a snap-back instability. This analysis provides a clear, energy-based explanation for the brittle nature of well-anchored, long bonded joints.

6. Ductility and Toughness

The performance of the global system response, as captured by the force–slip $F-\Delta$ curve, can be quantitatively and qualitatively characterized. Toughness is defined as the total energy absorption capacity and is quantified as the total area under the $F-\Delta$ curve. A large area corresponds to a system with high toughness. However, toughness alone does not describe the safety or stability of failure; that role belongs to ductility. In the context of this stability analysis, ductility is defined not simply by the deformation capacity but by the behavior after the peak load ($F_{max}$) is reached. Ductile behavior is characterized by a gentle descending branch, a “plateau”, which provides warning before collapse and allows for controlled energy dissipation. Conversely, a lack of ductility (brittleness) manifests as a sharp, vertical drop in load (“snap-back”), indicating violent and dangerous failure. In Figure 9, the curve A represents the global response of a ductile system, whereas curve B represents that of a brittle one.

The energy analysis from the previous section provides a fundamental explanation for this difference. Brittle “snap-back” failure is not a failure of strength but one of stability. It is caused by the excess stored elastic energy accumulated in the system (primarily in the FRP) during the apparent hardening phase. If the system is “energy-rich” when it reaches $F_{max}$, this stored energy is released violently, as the dissipated fracture energy of the interface is insufficient to “brake” the unstable damage propagation. Thus, a system can exhibit high toughness (a large area before the peak) but zero ductility (a violent failure at the peak).

The qualitative observation of a “sharp drop” must be quantified. A robust approach is to define a critical slope, $K_{cr}$, as a fraction of the system’s initial elastic stiffness, $K_{in}$, namely,

$$K_{cr}=-\gamma K_{in}$$

(54)

where $\gamma$ is a coefficient defining the limit of acceptable brittleness (e.g., $\gamma =0.1$). For the strengthening system examined, $K_{in}$ is the slope of the linear part of the force–slip curve, given by

$$K_{in}=\lambda Ebt\tanh (\lambda L)$$

(55)

A system is considered brittle if the slope of the force–slip curve, $K\left(a\right)$, is less than or equal to the critical slope $K_{cr}$ at a certain point neighboring the peak value, say at the point $a=a_c+\delta a_c$ (where $\delta a_c$ is a suitably chosen value, e.g., $\delta a_c=0.02a_c$):

$$K(a_c+\delta a_c)\le K_{cr}$$

(56)

In the opposite case, $K(a_c+\delta a_c)>K_{cr}$, the system is considered ductile. For the non-linear part of the force–slip curve, the slope $K\left(a\right)$ at the point corresponding to $a=a_c+\delta a_c$ is given by the following relation:

$$K(a_c+\delta a_c)={\left.{\displaystyle \frac{dF}{d\Delta }}\right|}_{a=a_c+\delta {\alpha }_c}={\left.{\displaystyle \frac{dF/da}{d\Delta /da}}\right|}_{a=a_c+\delta {\alpha }_c}$$

(57)

By taking into account the parametric expressions $F\left(a\right)$ and $\Delta \left(a\right)$, Equation (57) provides

$$K(a_c+\delta a_c)=\lambda Ebt{\displaystyle \frac{\sqrt{p}\tanh [\lambda (L-a_c-\delta a_c)]-p\tan [\lambda \sqrt{p}(a_c+\delta a_c)]}{\tanh [\lambda (L-a_c-\delta a_c)]\tan [\lambda \sqrt{p}(a_c+\delta a_c)]+\sqrt{p}}}$$

(58)

The above brittleness criterion was applied numerically to two representative cases, and the results are shown in Figure 10 and Figure 11.

The curve shown in Figure 10 is plotted for the following parameters: $p=1$; $E=250 \mathrm{GPa}$; ${\tau }_m=5 \mathrm{MPa}$; $s_m=0.25 \mathrm{mm}$; $L=350 \mathrm{mm}$; $b=50 \mathrm{mm}$; $t=1.5 \mathrm{mm}$. For these values, it is found that $a_c=111.764 \mathrm{mm}$. By choosing $\delta a_c=0.02a_c$, the slope of the curve at the position $a_c+\delta a_c=113.999 \mathrm{mm}$ is calculated using Equation (58), resulting in $K(a_c+\delta a_c)=-10.835 \mathrm{kN}/\mathrm{mm}$. For the above numerical values of parameters, Equation (55) provides $K_{cr}=-13.529 \mathrm{kN}/\mathrm{mm}.$ Since $K(a_c+\delta a_c)>K_{cr}$, according to the adopted criterion, the response is ductile.

The curve shown in Figure 11 is plotted for the following parameters: $p=3$; $E=190 \mathrm{GPa}$; ${\tau }_m=5 \mathrm{MPa}$; $s_m=0.25 \mathrm{mm}$; $L=128 \mathrm{mm}$; $b=50 \mathrm{mm}$; $t=1.5 \mathrm{mm}$. Similarly, it is found that $a_c=56.773 \mathrm{mm}$, $K\left(a_c+\delta a_c\right)=-125.183 \mathrm{kN}/\mathrm{mm}$, and $K_{cr}=-9.434 \mathrm{kN}/\mathrm{mm}$. Since $K(a_c+\delta a_c)<K_{cr}$, the response is brittle.

7. Conclusions and Discussion

In this paper, we presented a complete analytical framework for investigating the progressive debonding of FRP reinforcements, grounded in the principles of fracture mechanics and the use of a bilinear softening cohesive law. The objective was to gain a deeper understanding of the global system response, with an emphasis on the energetic analysis of non-linear behavior and failure stability. The main conclusions of the research can be summarized as follows:

• The non-linear “apparent hardening” phase observed in the $F-\Delta$ curve is not an intrinsic material property. It was demonstrated to be a structural phenomenon caused by stress redistribution. As the softening zone $\left(a\right)$ steadily develops, it “activates” new, intact sections of the elastic anchorage zone, allowing the system to take on increasing load.
• The apparent hardening phase terminates when the maximum force, $F_{max}$, is reached. This occurs at a specific, critical length of the softening zone $\left(a_c\right)$, at which point the rate of strength loss from damage overcomes the rate of strength gain from redistribution.
• We developed a complete energy balance, deriving analytical expressions for all energy components. The analysis confirmed that the progressive failure consistently follows fracture mechanics principles, maintaining the condition $G=R$ throughout the propagation.
• The energetic analysis revealed the critical “dual” nature of the hardening phase. While this phase allows for load increase, it is simultaneously the period during which the system stores vast amounts of elastic energy (primarily in the FRP), acting as an “engine” for potential unstable failure.
• We demonstrated a clear distinction between toughness (the total area of the curve) and ductility (defined as the stability of the post-peak failure, i.e., the capacity for a gentle “plateau”). It was proven that brittle, violent “snap-back” failure is the result of the uncontrolled release of excess stored elastic energy. This occurs when the interface’s energy dissipation capacity is insufficient to manage the “engine” of stored energy.

The analytical framework developed in this work is based on several simplifying assumptions. The concrete substrate is idealized as rigid and undeformable, meaning that local cracking and substrate compliance are not explicitly modeled. The interface behavior is described by a one-dimensional bilinear softening cohesive law under pure shear, without accounting for mixed-mode effects, cyclic degradation, or rate dependency. The FRP plate is treated as prismatic and linearly elastic, and the stress transfer is assumed to be uniform across the plate width. These assumptions allow for closed-form solutions and a transparent energetic interpretation but may limit the applicability of the model to more complex geometries or loading conditions. Future work will focus on extending the model to include substrate deformability, mixed-mode cohesive laws, and three-dimensional stress transfer. The authors are also conducting an experimental campaign aimed at comprehensively validating the proposed energetic framework.

In conclusion, this work demonstrates that a design approach based solely on strength ${(F}_{max})$ is insufficient. Understanding the system’s energetic state, particularly the elastic energy stored during the apparent hardening phase, is fundamental to designing FRP strengthening systems that are not only strong but also safe, ductile, and tough.