Stochastic Optimization of Quality Assurance Systems in Manufacturing: Integrating Robust and Probabilistic Models for Enhanced Process Performance and Product Reliability
Abstract
1. Introduction
2. Literature Review
2.1. Traditional Quality Assurance Methods
2.2. Stochastic Optimization in Manufacturing
2.3. Robust Optimization Techniques
2.4. Probabilistic Models for Uncertainty
2.5. Integrated Models in QA Systems
3. Materials and Methods
3.1. Stochastic Optimization Framework
3.2. Mathematical Formulation of the Model
- ▪
- production rate (units per hour).
- ▪
- Inspection interval (time between inspections).
- ▪
- Machine settings (e.g., temperature, speed).
3.2.1. Constraint
- 1.
- The total cost of the manufacturing process cannot exceed the budget:
- 2.
- The production time must not exceed the available production window:
- 3.
- The manufacturing resources, such as materials and machinery, must be used efficiently and within their limits:
3.2.2. Uncertainty Models
- ▪
- is the scale parameter.
- ▪
- is the period of interest.
- ▪
- is the shape parameter that dictates the nature of failure over time, .
- ▪
- is the specification limit (desired material property).
- ▪
- is the actual material property.
- ▪
- is the standard deviation of material variation.
- ▪
- represents the cumulative distribution function of the standard normal distribution.
3.2.3. Optimization Problem
3.3. Unique Variant of Genetic Algorithm
- Initialization:
- Fitness Evaluation:
- Selection, Crossover, and Mutation:
- ○
- Selection: The best solutions are chosen for reproduction based on fitness.
- ○
- Crossover: Paired solutions exchange components to generate offspring.
- ○
- Mutation: Random changes are introduced to maintain diversity and avoid local optima.
- Termination:
3.4. Robust Optimization Approach
3.5. Probabilistic Models for Process Reliability
3.6. Case Study/Application
4. Results and Discussion
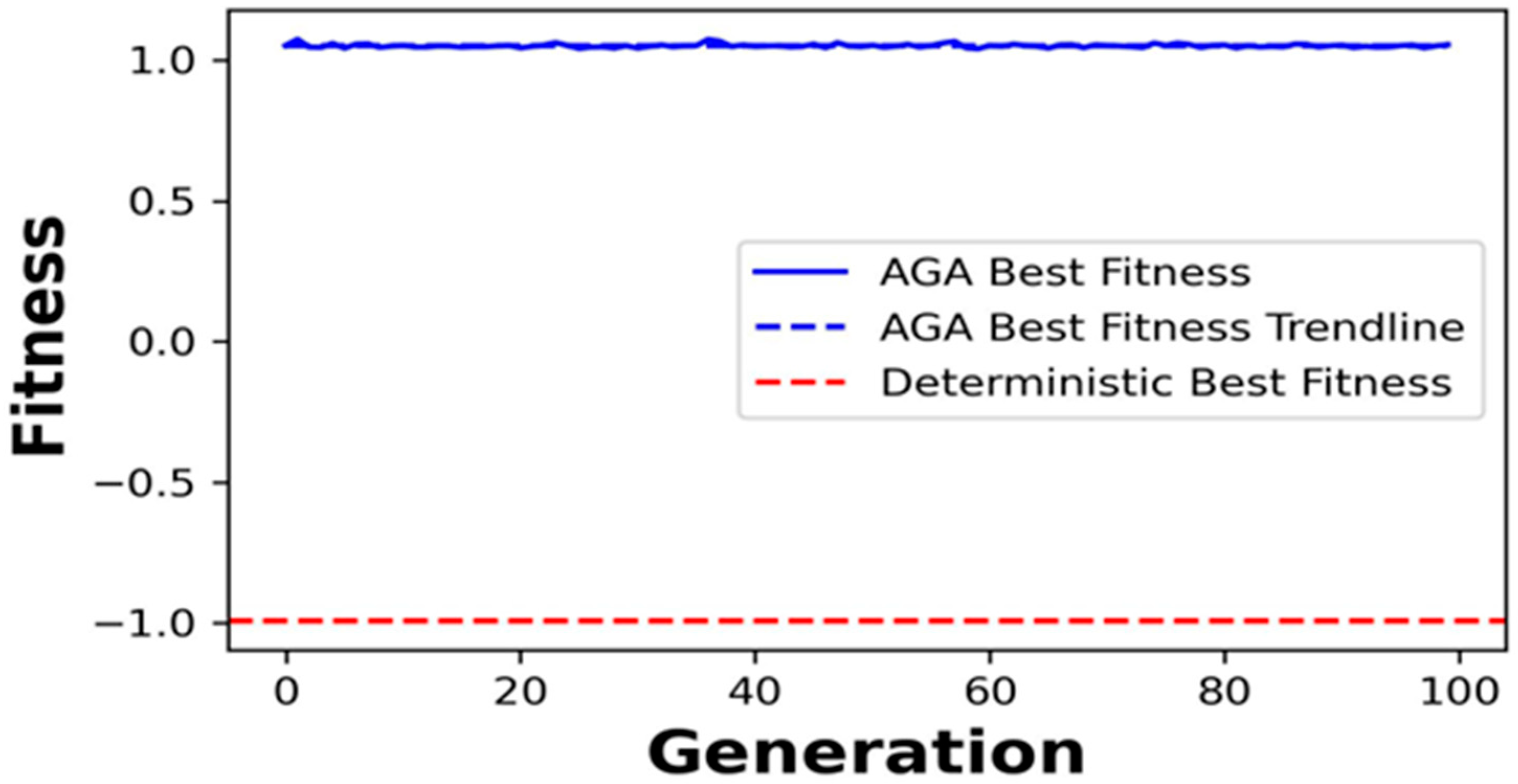
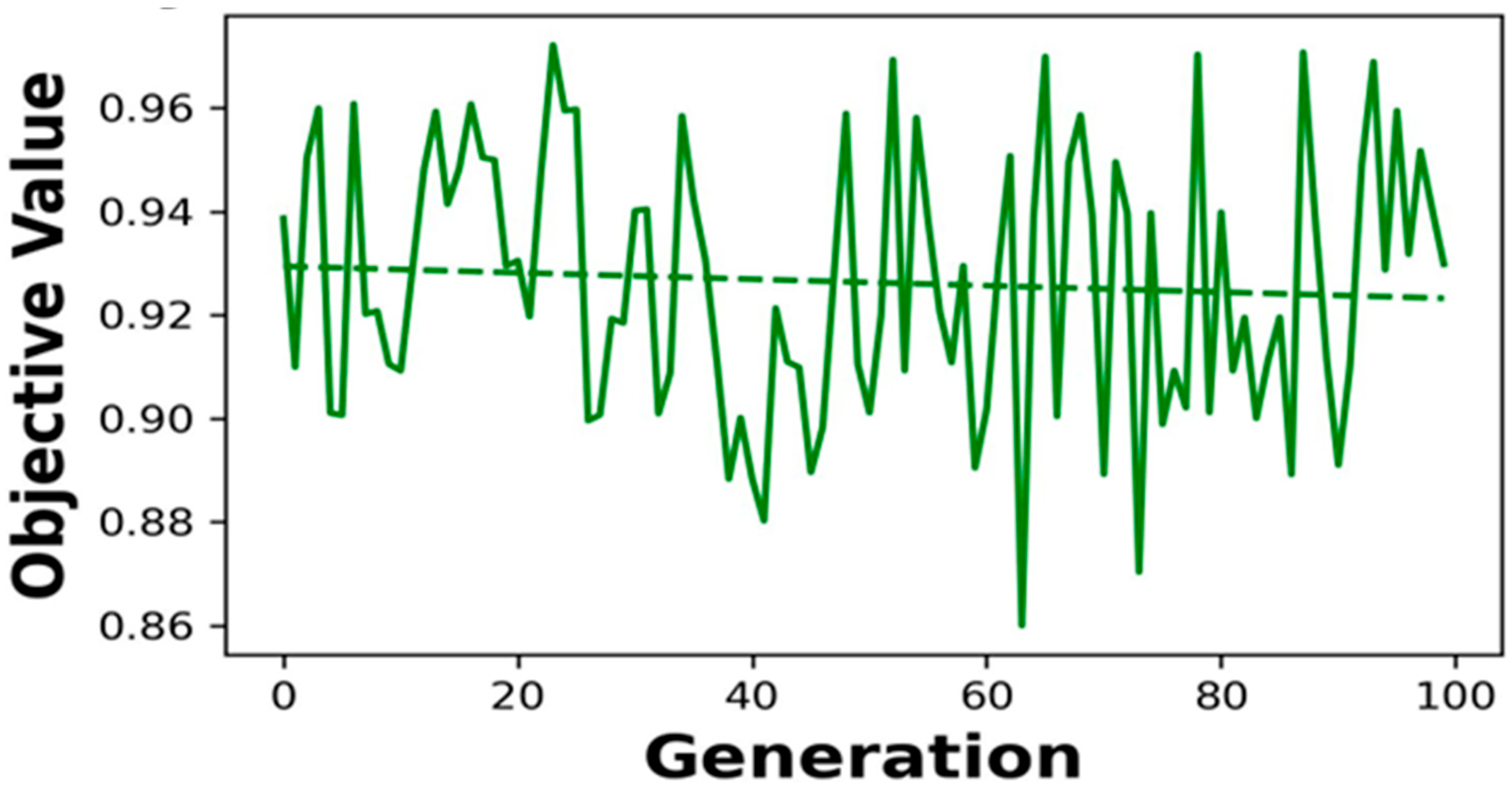
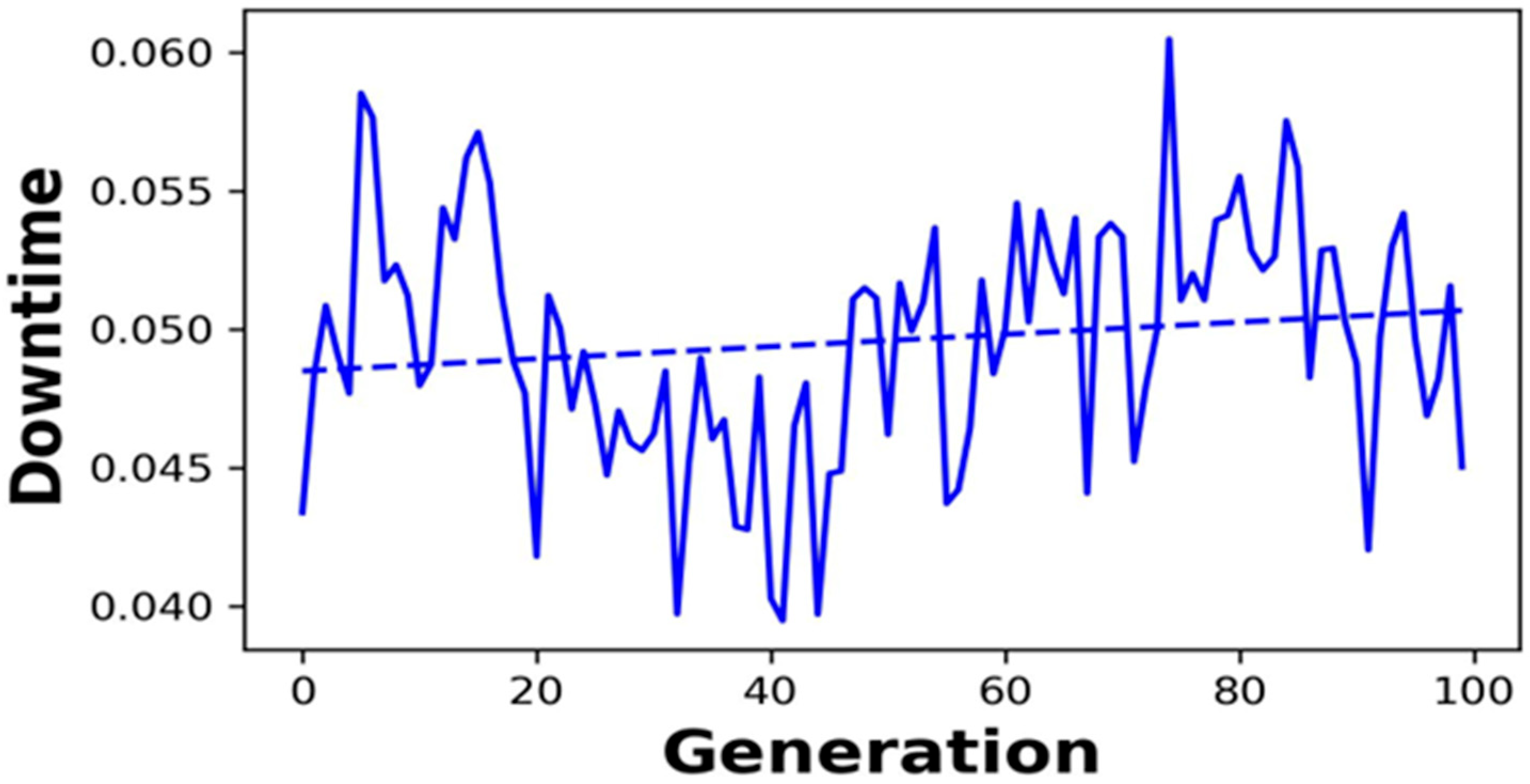
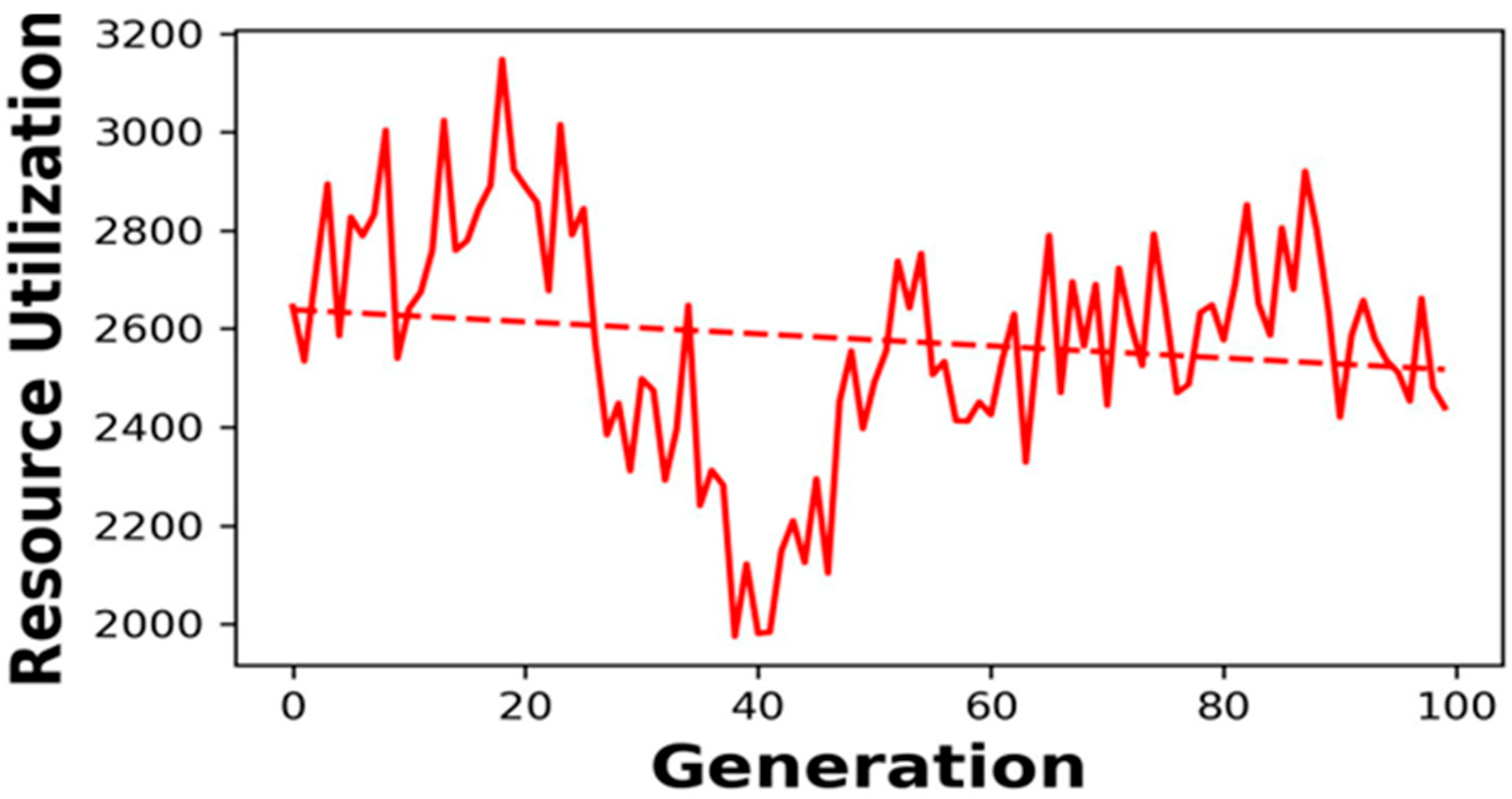
4.1. Optimization Results
4.2. Impact on Process Performance
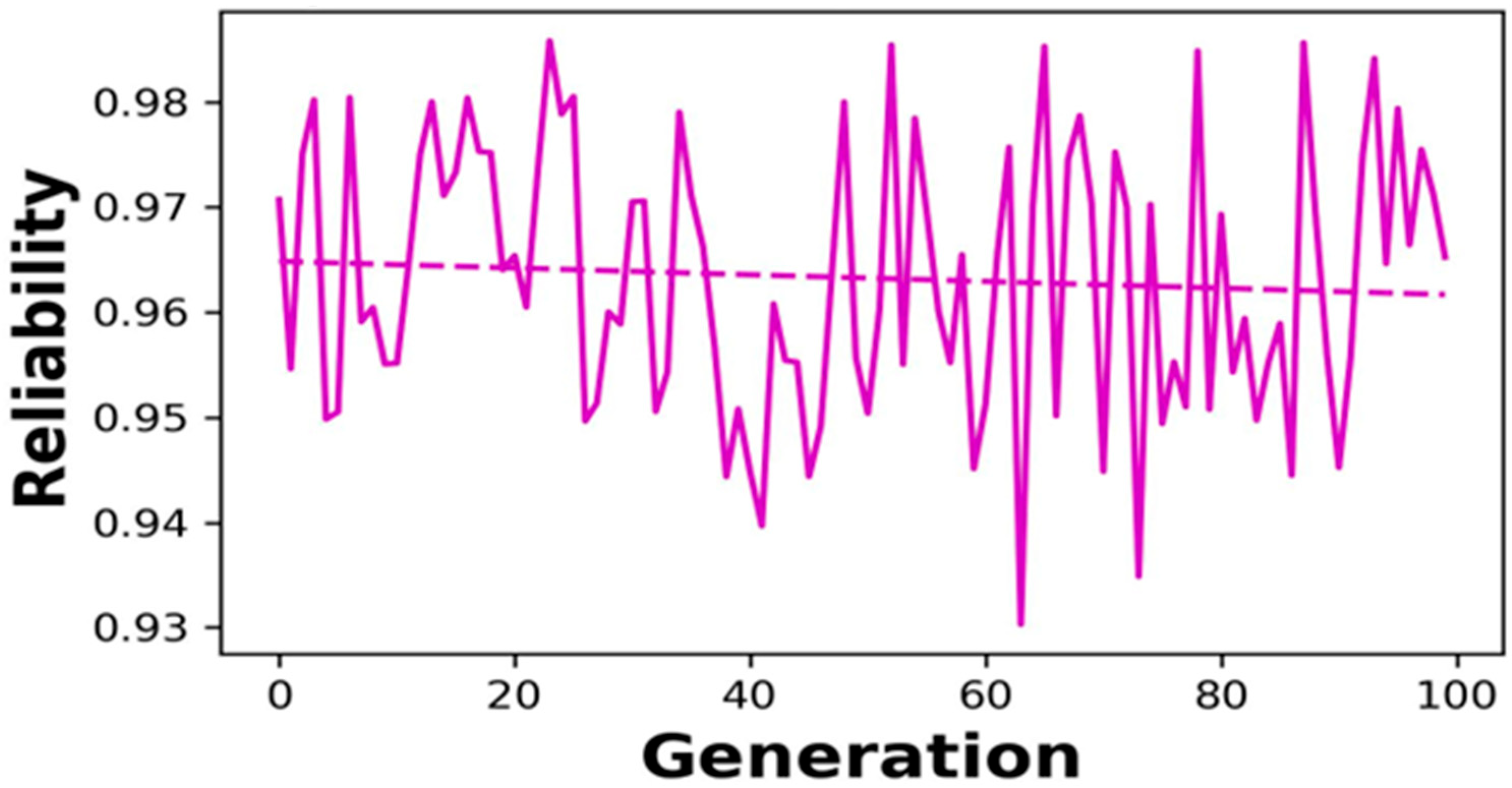
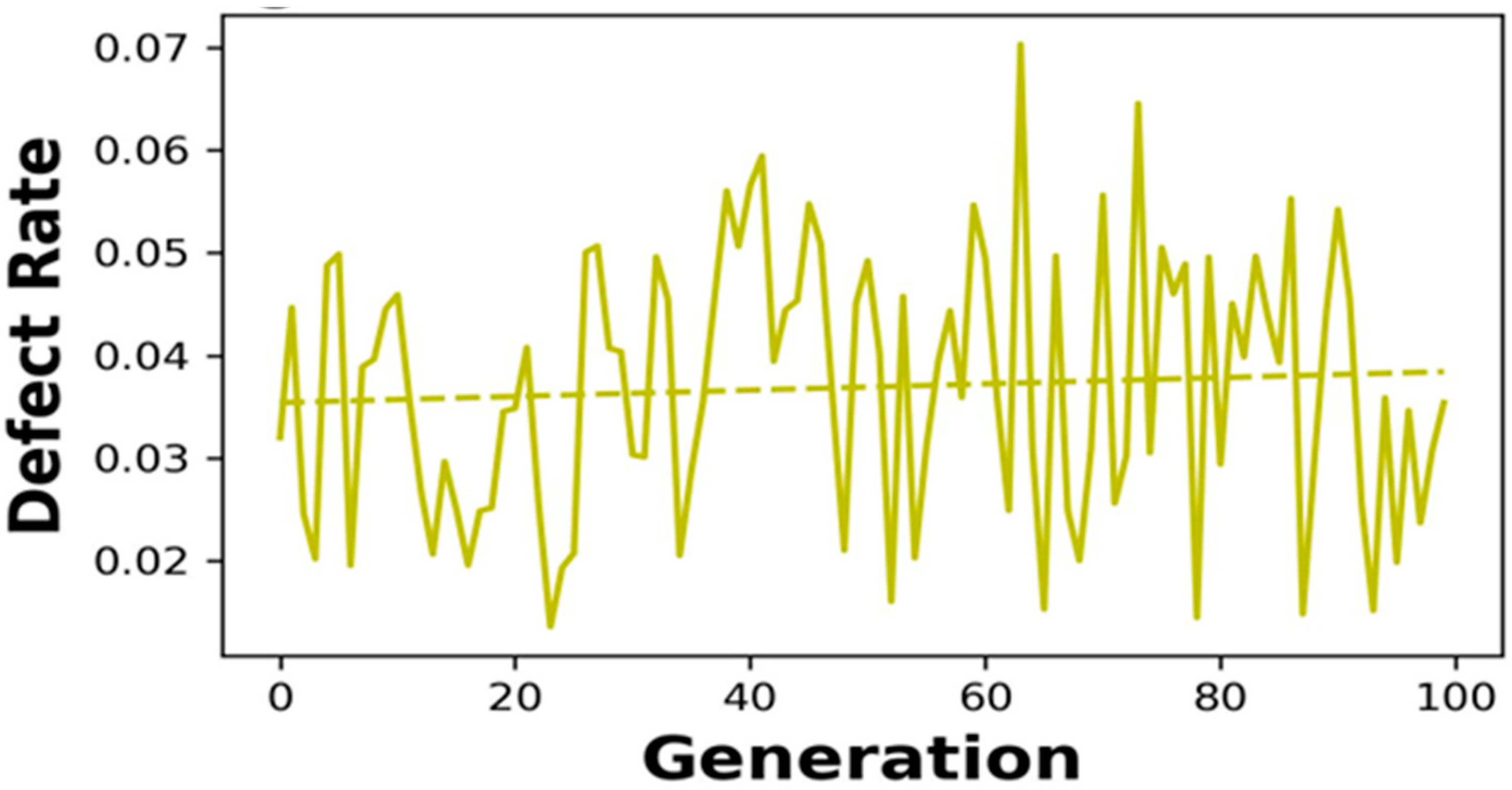
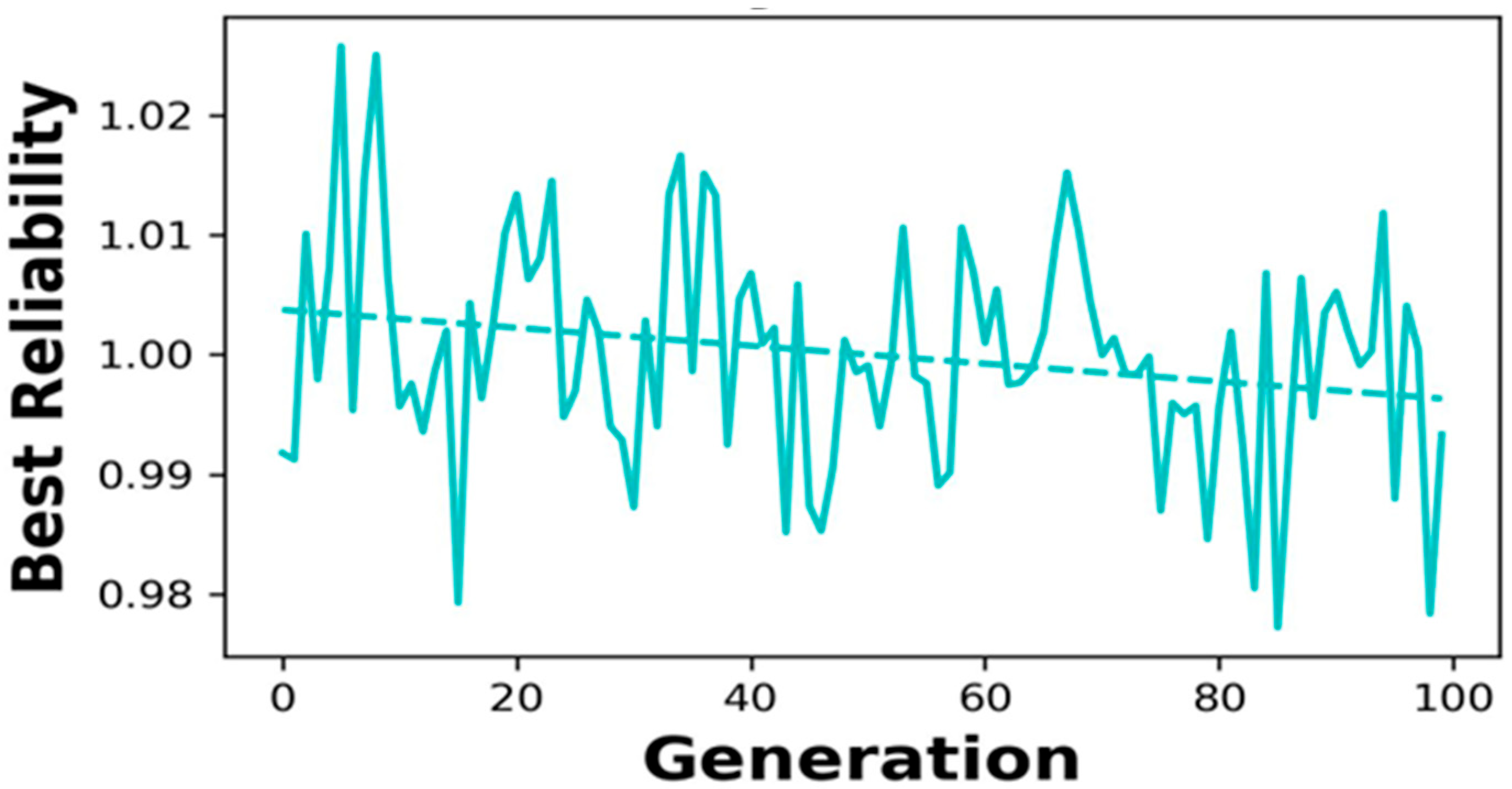
4.3. Product Reliability Analysis
4.4. Comparison with Traditional Approaches
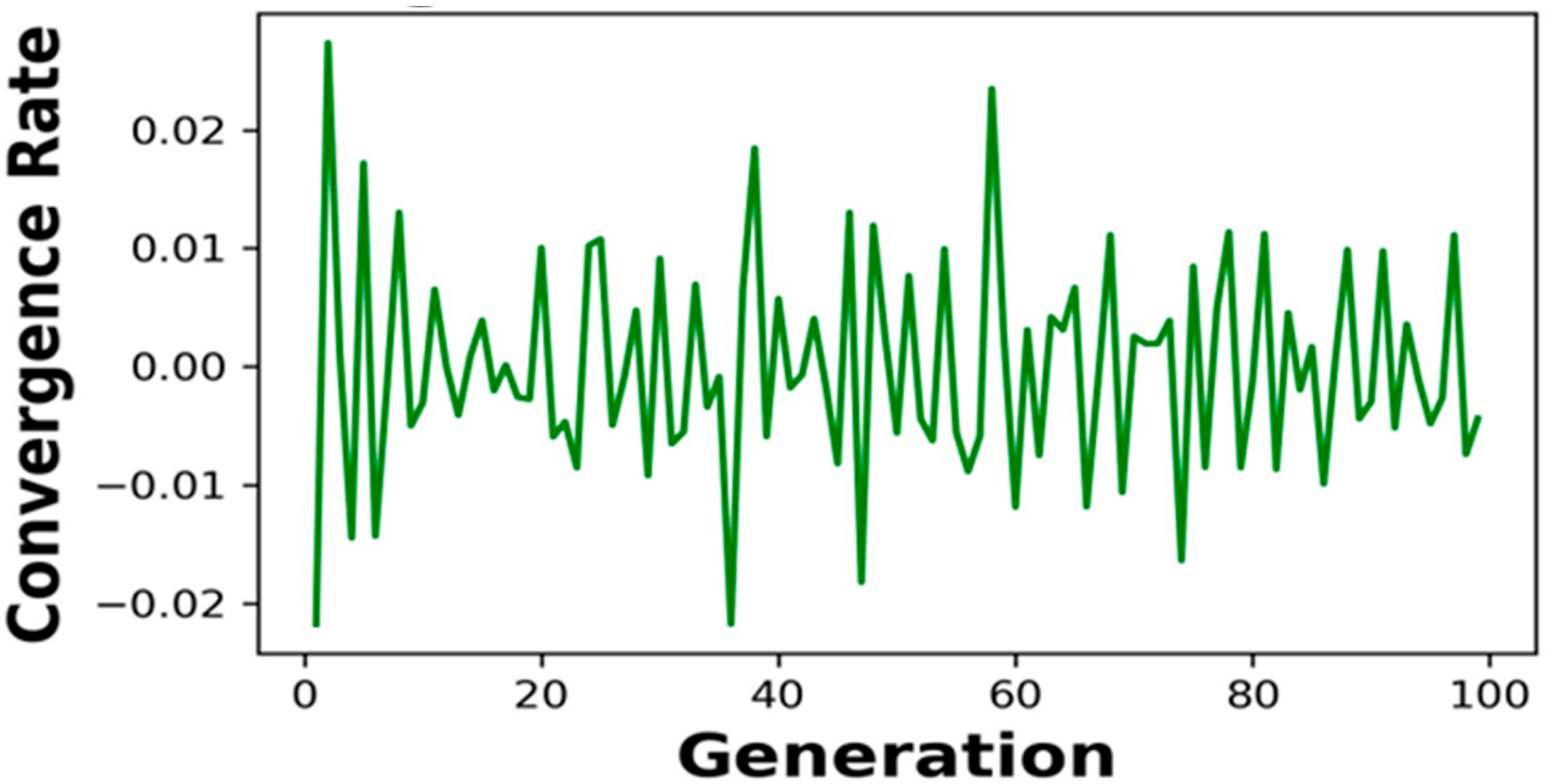
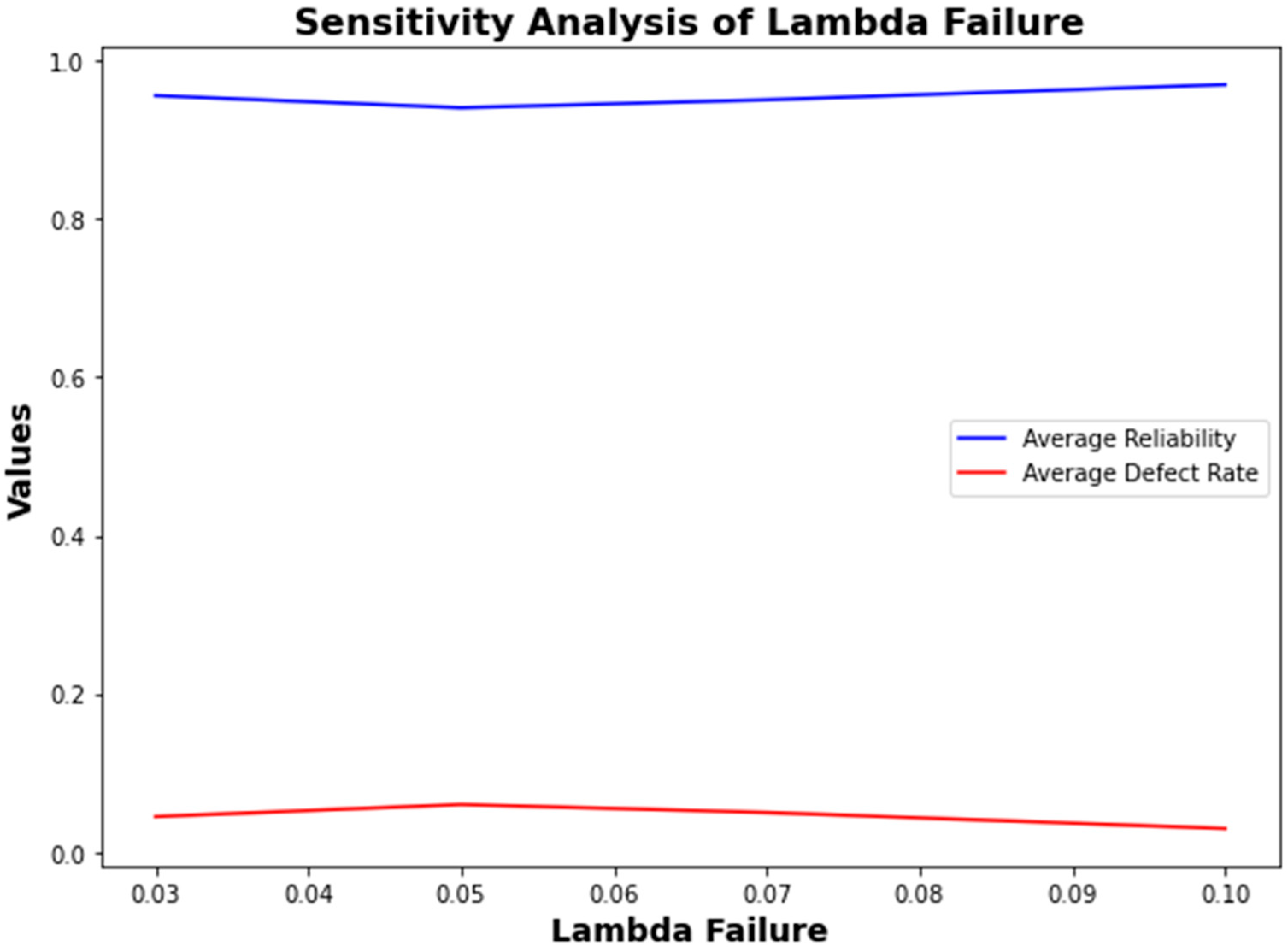
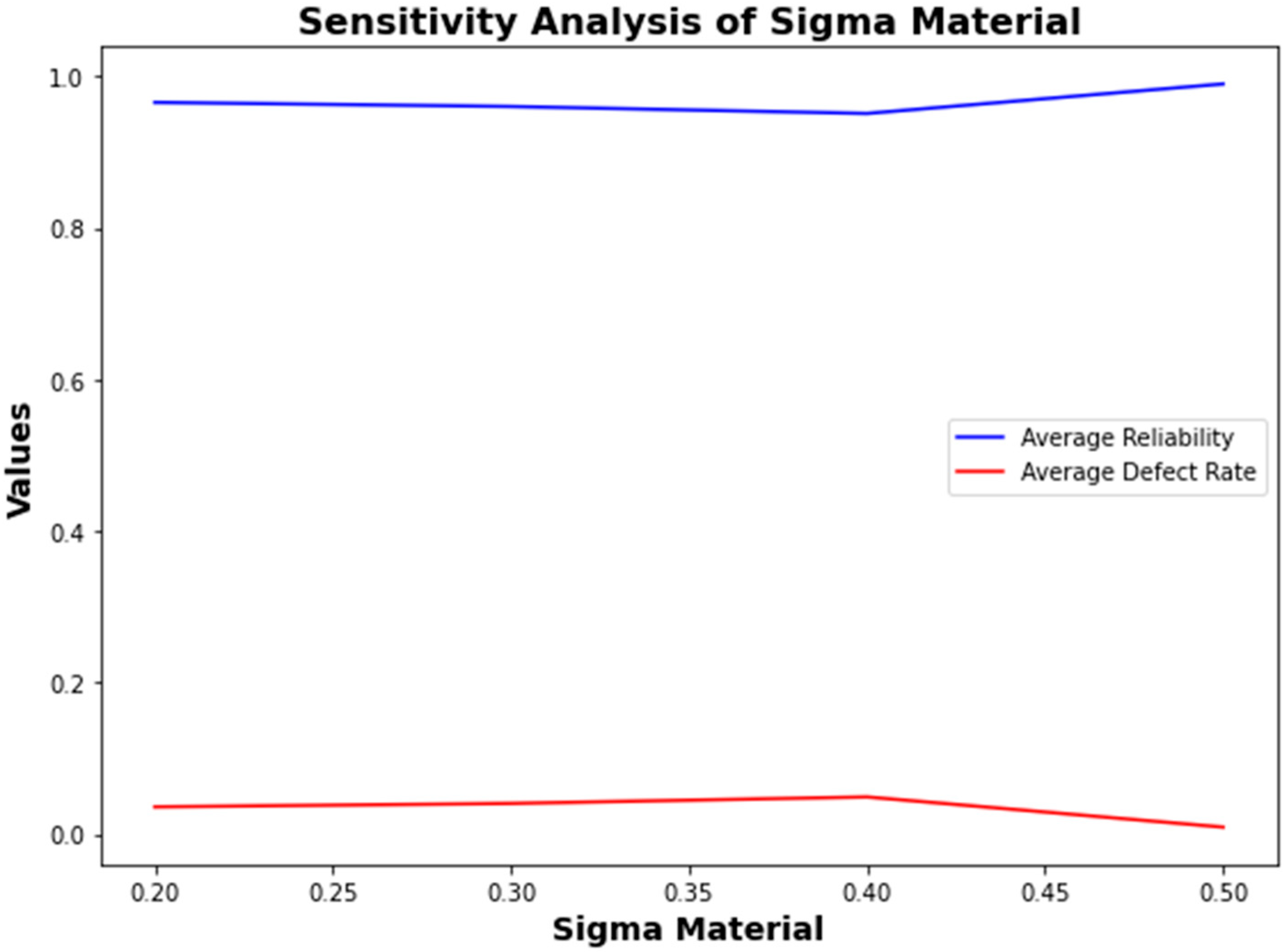
4.5. Sensitivity Analysis
5. Conclusions
5.1. Sensitivity Analysis
5.2. Contribution to the Field
- ▪
- The research presents a novel method for handling process variations while maintaining product dependability.
- ▪
- Manufacturers who implement these models gain the ability to respond to real-time uncertainties, which leads to better decision-making.
- ▪
- The research demonstrates its practical application through solar panel production, as this industry requires high product quality and reliability standards.
5.3. Practical Implications
- ▪
- These models improve decision-making by enabling companies to forecast and control production process-related risks.
- ▪
- Production scheduling in automotive manufacturing is optimized through its use when supply chain conditions change.
- ▪
- The reliability and yield of products in electronics and semiconductor production increase through their implementation when material qualities remain uncertain.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qamar, S.Z.; Al-Hinai, N.; Márquez, F.P.G. Quality Control and Quality Assurance: Techniques and Applications; BoD–Books on Demand: 2024. Available online: https://www.intechopen.com/books/13152 (accessed on 16 May 2025).
- Korshunov, G.; Petrushevskaya, A. Modeling of digital manufacturing of electronics production and product quality assurance. J. Phys. Conf. Ser. (JPCS) 2018, 150–159. [Google Scholar]
- Markulik, Š.; Sinay, J.; Pačaiová, H. Quality assurance in the automotive industry and industry 4.0. In Smart Technology Trends in Industrial and Business Management; Springer International Publishing: Cham, Switzerland, 2019; pp. 217–225. [Google Scholar]
- Trinks, S. Real Time Quality Assurance and Defect Detection in Industry 4.0. Proceedings 2021, 1613, 0073. [Google Scholar]
- Chandra, S.; Stanford, D.; Fletcher, E.; Walker, L.A. Raw Materials Production and Manufacturing Process Control Strategies. In The Science and Regulations of Naturally Derived Complex Drugs; Springer International Publishing: Cham, Switzerland, 2019; pp. 175–190. [Google Scholar]
- Wang, Y.; Li, D.; Nie, C.; Gong, P.; Yang, J.; Hu, Z.; Li, B.; Ma, M. Research progress on the wear resistance of key components in agricultural machinery. Materials 2023, 16, 7646. [Google Scholar] [CrossRef] [PubMed]
- Feng, D.; Gong, Q.; Wang, H.; Yi, S.; Cai, Y. Rest Breaks Arrange Based on Empirical Studies of Productivity in Manufacturing Industry. Asian Econ. Financ. Rev. 2019, 9, 1043. [Google Scholar]
- Malaki, A. A Study of the Effects of Operational Time Variability in Assembly Lines with Linear Walking Workers; School of Engineering in Jönköping University: Jonkoping, Sweden, 2012. [Google Scholar]
- Liu, C.; Yang, Y.; Liu, X. A holistic sustainability framework for remanufacturing under uncertainty. J. Manuf. Syst. 2024, 76, 540–552. [Google Scholar] [CrossRef]
- Hasan, K.; Yousuf, S.B.; Tushar, M.S.H.K.; Das, B.K.; Das, P.; Islam, M.S. Effects of different environmental and operational factors on the PV performance: A comprehensive review. Energy Sci. Eng. 2022, 10, 656–675. [Google Scholar] [CrossRef]
- Duan, F.; Eslami, M.; Okati, M.; Jasim, D.J.; Mahmood, A.K. Hybrid stochastic and robust optimization of a hybrid system with fuel cell for building electrification using an improved arithmetic optimization algorithm. Sci. Rep. 2025, 15, 1779. [Google Scholar] [CrossRef] [PubMed]
- Peinado-Guerrero, M.A.; Villalobos, J.R.; Phelan, P.E.; Campbell, N.A. Stochastic framework for peak demand reduction opportunities with solar energy for manufacturing facilities. J. Clean. Prod. 2021, 313, 127891. [Google Scholar] [CrossRef]
- Basciftci, B.; Ahmed, S.; Gebraeel, N.Z.; Yildirim, M. Stochastic optimization of maintenance and operations schedules under unexpected failures. IEEE Trans. Power Syst. 2018, 33, 6755–6765. [Google Scholar] [CrossRef]
- Alkan, B.; Vera, D.A.; Ahmad, M.; Ahmad, B.; Harrison, R. Complexity in manufacturing systems and its measures: A literature review. Eur. J. Ind. Eng. 2018, 12, 116–150. [Google Scholar] [CrossRef]
- Schlenkrich, M.; Seiringer, W.; Altendorfer, K.; Parragh, S.N. Enhancing Rolling Horizon Production Planning Through Stochastic Optimization Evaluated by Means of Simulation. arXiv 2024, arXiv:2402.14506. [Google Scholar]
- Yazdi, M. Maintenance strategies and optimization techniques. In Advances in Computational Mathematics for Industrial System Reliability and Maintainability; Springer: Berlin/Heidelberg, Germany, 2024; pp. 43–58. [Google Scholar]
- Leva, M.C.; Caimo, A.; Duane, R.; Demichela, M.; Comberti, L. Task complexity, and operators’ capabilities as predictor of human error: Modeling framework and an example of application. In Safety and Reliability–Safe Societies in a Changing World; CRC Press: Boca Raton, FL, USA, 2018; pp. 493–499. [Google Scholar]
- Zadeh, M.S.N.; Shoushtari, F.; Talebi, M. Optimization of Analytical Methods in Industrial Engineering: Enhancing Decision-Making in Process Design and Quality Control. Int. J. Ind. Eng. Constr. Manag. (IJIECM) 2024, 2, 27–40. [Google Scholar]
- Szipka, K. Modelling and Management of Uncertainty in Production Systems: From Measurement to Decision. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Wolniak, R.; Grebski, W. The usage of Statistical Process Control (SPC) in Industry 4.0 conditions. Zesz. Nauk. Politech. Śląskiej. Organ. I Zarządzanie 2023, 190, 259–268. [Google Scholar] [CrossRef]
- Tegegne, D.A.; Kitaw, D.; Berhan, E. Advances in statistical quality control chart techniques and their limitations to cement industry. Cogent Eng. 2022, 9, 2088463. [Google Scholar] [CrossRef]
- Goswami, A.; Dutta, H.N. Time series approaches to statistical process control. Int. J. Innov. Res. Comput. Sci. Technol. 2013, 1, 33–37. [Google Scholar]
- Amaratunga, T.; Dobranowski, J. Systematic review of the application of lean and six sigma quality improvement methodologies in radiology. J. Am. Coll. Radiol. 2016, 13, 1088–1095. e1087. [Google Scholar] [CrossRef] [PubMed]
- Antony, J.; Sony, M.; Dempsey, M.; Brennan, A.; Farrington, T.; Cudney, E.A. An evaluation into the limitations and emerging trends of Six Sigma: An empirical study. TQM J. 2019, 31, 205–221. [Google Scholar] [CrossRef]
- Antony, J.; Sony, M. An empirical study into the limitations and emerging trends of Six Sigma in manufacturing and service organisations. Int. J. Qual. Reliab. Manag. 2020, 37, 470–493. [Google Scholar] [CrossRef]
- Taher, M.A.; Bashar, M.A. The Impact of Lean Manufacturing Concepts on Industrial Processes’ Efficiency and Waste Reduction. Int. J. Progress. Res. Eng. Manag. Sci. 2024, 4, 338–349. [Google Scholar]
- Rojas, T.; Mula, J.; Sanchis, R. Quantitative modelling approaches for lean manufacturing under uncertainty. Int. J. Prod. Res. 2024, 62, 5989–6015. [Google Scholar] [CrossRef]
- Golari, M.; Fan, N.; Jin, T. Multistage stochastic optimization for production-inventory planning with intermittent renewable energy. Prod. Oper. Manag. 2017, 26, 409–425. [Google Scholar] [CrossRef]
- Govindan, K.; Cheng, T. Advances in stochastic programming and robust optimization for supply chain planning. Comput. Oper. Res. 2018, 100, 262–269. [Google Scholar] [CrossRef]
- Bozorgi-Amiri, A.; Khorsi, M. A dynamic multi-objective location–routing model for relief logistic planning under uncertainty on demand, travel time, and cost parameters. Int. J. Adv. Manuf. Technol. 2016, 85, 1633–1648. [Google Scholar] [CrossRef]
- Rizqi, Z.; Khairunisa, A. Integration of deterministic and probabilistic inventory methods to optimize the balance between overstock and stockout. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; p. 012060. [Google Scholar]
- Alsharif, H.; Jalili, M.; Hasan, K.N. Power system frequency stability using optimal sizing and placement of Battery Energy Storage System under uncertainty. J. Energy Storage 2022, 50, 104610. [Google Scholar] [CrossRef]
- Goda, D.R.; Yerram, S.R.; Mallipeddi, S.R. Stochastic Optimization Models for Supply Chain Management: Integrating Uncertainty into Decision-Making Processes. Glob. Discl. Econ. Bus. 2018, 7, 123–136. [Google Scholar] [CrossRef]
- Gabrel, V.; Murat, C.; Thiele, A. Recent advances in robust optimization: An overview. Eur. J. Oper. Res. 2014, 235, 471–483. [Google Scholar] [CrossRef]
- Simchi-Levi, D.; Wang, H.; Wei, Y. Increasing supply chain robustness through process flexibility and inventory. Prod. Oper. Manag. 2018, 27, 1476–1491. [Google Scholar] [CrossRef]
- Rabbani, M.; Manavizadeh, N.; Hosseini Aghozi, N.S. Robust optimization approach to production system with failure in rework and breakdown under uncertainty: Evolutionary methods. Assem. Autom. 2015, 35, 81–93. [Google Scholar] [CrossRef]
- Bertocci, F.; Grandoni, A.; Fidanza, M.; Berni, R. A guideline for implementing a robust optimization of a complex multi-stage manufacturing process. Appl. Sci. 2021, 11, 1418. [Google Scholar] [CrossRef]
- Grešová, E.; Svetlík, J. Mathematical modeling of the manufacturing sector’s dominant part as a base for automation. Appl. Sci. 2021, 11, 3295. [Google Scholar] [CrossRef]
- Nannapaneni, S.; Mahadevan, S.; Rachuri, S. Performance evaluation of a manufacturing process under uncertainty using Bayesian networks. J. Clean. Prod. 2016, 113, 947–959. [Google Scholar] [CrossRef]
- Xiong, M.; Chen, L.; Ming, J. Quantify uncertainty by estimating the probability density function of the output of interest using mlmc based bayes method. Discret. Contin. Dyn. Syst. Ser. B 2023, 28, 707–721. [Google Scholar] [CrossRef]
- Sun, H.; Zhao, S.; Peng, F.; Yan, R.; Zhou, L.; Zhang, T.; Zhang, C. In-situ prediction of machining errors of thin-walled parts: An engineering knowledge based sparse Bayesian learning approach. J. Intell. Manuf. 2024, 35, 387–411. [Google Scholar] [CrossRef]
- Gunjan, S.B.; Srinivasu, D. A new approach for product reliability prediction by considering the production factory lifecycle information. Reliab. Eng. Syst. Saf. 2025, 258, 110915. [Google Scholar] [CrossRef]
- Lu, M.; Shen, Z.J.M. A review of robust operations management under model uncertainty. Prod. Oper. Manag. 2021, 30, 1927–1943. [Google Scholar] [CrossRef]
- Khakifirooz, M.; Fathi, M.; Wu, K. Development of smart semiconductor manufacturing: Operations research and data science perspectives. IEEE Access 2019, 7, 108419–108430. [Google Scholar] [CrossRef]
- Fenton, N.; Neil, M.; Marquez, D. Using Bayesian networks to predict software defects and reliability. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2008, 222, 701–712. [Google Scholar] [CrossRef]
- Kumar, J.; Yadav, G.; Agrawal, B. A Hybrid Stochastic Optimization Model for Lot Sizing and Scheduling Problem. Cuest. De Fisioter. 2025, 54, 2007–2018. [Google Scholar]
- Duan, C.; Deng, C.; Li, N. Reliability assessment for CNC equipment based on degradation data. Int. J. Adv. Manuf. Technol. 2019, 100, 421–434. [Google Scholar] [CrossRef]
- Li, S.; Chen, Z.; Liu, Q.; Shi, W.; Li, K. Modeling and analysis of performance degradation data for reliability assessment: A review. IEEE Access 2020, 8, 74648–74678. [Google Scholar] [CrossRef]

| Parameter | Description | Value/Range |
|---|---|---|
| Production Rate | The number of units produced per day. | 1500 to 2500 units per day |
| Inspection Interval | Time between inspections | 0.5 to 2 h |
| Machine Setting | Machine settings | 200 to 500 (representing machine settings) |
| Weibull Distribution | Scale parameter for the Weibull distribution, representing failure rate. | 0.1 (scale parameter) |
| Weibull Distribution | Shape parameter for the Weibull distribution, influencing failure behavior. | 1.5 (shape parameter) |
| Material Quality | Standard deviation of material quality variation | 0.3 (standard deviation) |
| Population Size | The number of individuals in the genetic algorithm population. | 200 (population size) |
| Max Generations | The maximum number of generations for the genetic algorithm. | 100 (generational limit) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afolabi, K.; Akintayo, B.; Babatunde, O.; Kareem, U.A.; Ogbemhe, J.; Ighravwe, D.; Oludolapo, O. Stochastic Optimization of Quality Assurance Systems in Manufacturing: Integrating Robust and Probabilistic Models for Enhanced Process Performance and Product Reliability. J. Manuf. Mater. Process. 2025, 9, 250. https://doi.org/10.3390/jmmp9080250
Afolabi K, Akintayo B, Babatunde O, Kareem UA, Ogbemhe J, Ighravwe D, Oludolapo O. Stochastic Optimization of Quality Assurance Systems in Manufacturing: Integrating Robust and Probabilistic Models for Enhanced Process Performance and Product Reliability. Journal of Manufacturing and Materials Processing. 2025; 9(8):250. https://doi.org/10.3390/jmmp9080250
Chicago/Turabian StyleAfolabi, Kehinde, Busola Akintayo, Olubayo Babatunde, Uthman Abiola Kareem, John Ogbemhe, Desmond Ighravwe, and Olanrewaju Oludolapo. 2025. "Stochastic Optimization of Quality Assurance Systems in Manufacturing: Integrating Robust and Probabilistic Models for Enhanced Process Performance and Product Reliability" Journal of Manufacturing and Materials Processing 9, no. 8: 250. https://doi.org/10.3390/jmmp9080250
APA StyleAfolabi, K., Akintayo, B., Babatunde, O., Kareem, U. A., Ogbemhe, J., Ighravwe, D., & Oludolapo, O. (2025). Stochastic Optimization of Quality Assurance Systems in Manufacturing: Integrating Robust and Probabilistic Models for Enhanced Process Performance and Product Reliability. Journal of Manufacturing and Materials Processing, 9(8), 250. https://doi.org/10.3390/jmmp9080250







