Single, Multi-, and Many-Objective Optimization of Manufacturing Processes Using Two Novel and Efficient Algorithms with Integrated Decision-Making

Abstract

Manufacturing processes are inherently complex, multi-objective in nature, and highly sensitive to process parameter settings. This paper presents two simple and efficient optimization algorithms—Best–Worst–Random (BWR) and Best–Mean–Random (BMR)—developed to solve both constrained and unconstrained optimization problems of manufacturing processes involving single, multi-, and many-objectives. These algorithms are free from metaphorical inspirations and require no algorithm-specific control parameters, which often complicate other metaheuristics. Extensive testing reveals that BWR and BMR consistently deliver competitive, and often superior, performance compared to established methods. Their multi- and many-objective extensions, named MO-BWR and MO-BMR, respectively, have been successfully applied to tackle 2-, 3-, and 9-objective optimization problems in advanced manufacturing processes such as friction stir processing (FSP), ultra-precision turning (UPT), laser powder bed fusion (LPBF), and wire arc additive manufacturing (WAAM). To aid in decision-making, the proposed BHARAT can be integrated with MO-BWR and MO-BMR to identify the most suitable compromise solution from among a set of Pareto-optimal alternatives. The results demonstrate the strong potential of the proposed algorithms as practical tools for intelligent decision-making in real-world manufacturing applications.

1. Introduction

Manufacturing is the backbone of industrial development, contributing significantly to economic growth, employment, and technological progress. The effectiveness of manufacturing processes is critically influenced by process parameters such as temperature, forces, speed, feed rate, and material flow. These parameters directly impact product quality, energy efficiency, dimensional accuracy, surface finish, and overall productivity. The challenge lies in selecting and fine-tuning these parameters to achieve optimal process performance while minimizing costs and resource wastage. Traditional parameter selection methods, such as trial-and-error or empirical approaches, often result in suboptimal outcomes and extended development cycles. As modern manufacturing embraces digitalization and Industry 4.0, there is a growing need for intelligent and data-driven optimization techniques that can adaptively respond to process complexity and dynamic variability.

Process parameter optimization involves formulating objectives and constraints, developing suitable models, and applying optimization algorithms to identify the best parameter combinations. The number of objectives considered for optimization may be one (i.e., single objective), or more than one (i.e., multiple objectives). Most manufacturing processes have more than one conflicting objectives, such as

• Maximize metal removal rate ↔ Minimize surface roughness
• Maximize efficiency ↔ Minimize cost
• Maximize hardness ↔ Minimize energy consumption

Optimization problems involving four or more objectives are referred to as many-objective optimization problems. For example, for parameters optimization of a wire arc additive manufacturing process, objectives such as the following may be considered:

• Maximize width ↔ Maximize hardness ↔ Minimize substrate distortion ↔ Minimize interlayer waiting time, etc.

In multi- and many-objective scenarios—common in real-world manufacturing—trade-offs must be handled judiciously to ensure balanced solutions across conflicting objectives. Multi- and many-objective optimization methods help identify trade-offs and generate Pareto-optimal solutions, offering flexibility to decision-makers.

Process parameter optimization has spurred a wave of research integrating statistical methods, metaheuristic algorithms, artificial intelligence (AI), and hybrid frameworks. Many researchers have used population-based advanced optimization algorithms (also called metaheuristics) and AI tools for the parameter optimization of different manufacturing processes. Numerous studies have focused on enhancing energy efficiency and optimizing performance in both conventional and advanced manufacturing processes, particularly machining, using a range of traditional and modern optimization techniques [1,2,3,4,5,6,7]. The inherent complexity and variability of additive manufacturing (AM) have driven the growing adoption of artificial intelligence (AI)-based and multi-objective optimization approaches [8,9,10,11,12,13]. In the context of welding processes, recent reviews have highlighted the use of hybrid optimization strategies to improve modeling accuracy and process control [14,15,16]. Additionally, surrogate modeling has emerged as a promising approach for reducing the computational costs associated with high-fidelity simulations [17,18]. While relevant details can be found in the existing literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18], they are not elaborated here due to space limitations.

This paper focuses on the application of metaheuristics (also called advanced optimization algorithms) for the optimization of various manufacturing processes. Metaheuristics are particularly useful because of their ability to adapt in complex, high-dimensional landscapes. These heuristic approaches iteratively refine a population of candidate solutions, effectively exploring and exploiting the search space to achieve convergence toward global optima.

The popularity of metaheuristics stems from their numerous strengths—flexibility, independence from gradient information, suitability for multi-objective optimization, global exploration capabilities, and ease of customization [19,20]. However, despite these strengths, metaheuristics also face several limitations that should not be overlooked. One significant drawback is the lack of theoretical guarantees for achieving global optimality in most cases. Additionally, they may exhibit convergence issues, especially when dealing with highly complex, nonlinear, or large-scale optimization problems. Another critical concern is the often considerable dependency on the proper tuning of algorithm-specific parameters, which, if misconfigured, can lead to poor convergence behavior or unnecessarily high computational costs. For example, genetic algorithm (GA) requires tuning of the selection method, crossover and mutation methods, and probabilities; particle swarm optimization (PSO) requires tuning of cognitive and social coefficients and inertia weight; and ant colony algorithm (ACO) requires tuning of pheromone evaporation rate, pheromone and heuristics importances, etc. Although a few parameter-less or parameter-light methods—such as the Jaya algorithm and the Rao family of algorithms—have been developed to overcome this challenge, the majority of metaheuristics still require careful parameter calibration to perform effectively and efficiently [21,22,23]. Improper calibration may lead to suboptimal convergence or excessive computational overhead.

Over the past decade, the landscape of metaheuristics has witnessed an overwhelming influx of novel algorithms, many of which are metaphor-inspired. These include inspirations from natural events, animal behaviors, astronomical phenomena, physical processes, and even cultural practices. While this creativity is commendable, a concerning trend has emerged—many algorithms are developed by loosely associating mathematical models with arbitrary metaphors. Often, these associations lack scientific justification, with the metaphor serving as nothing more than a decorative framework [24,25,26]. Given these observations, the specific objectives of the present work are as follows:

• To establish that effective optimization techniques can be developed without relying on metaphor-based analogies.
• To present two straightforward, metaphor-independent, and parameter-free optimization algorithms—BWR and BMR—along with their multi-objective extensions.
• To assess the convergence behavior and solution precision of the proposed algorithms across single-, multi-, and many-objective optimization problems related to various manufacturing processes, with the aim of identifying potential improvements in outcomes.
• To apply the recently introduced BHARAT (Best Holistic Adaptable Ranking of Attributes Technique) for identifying the most appropriate compromise solution from a Pareto-optimal set in manufacturing process optimization.

The next section describes the proposed algorithms.

2. Materials and Methods: BWR and BMR Algorithms

2.1. Proposed Algorithms for Solving Single-Objective Constrained Optimization Problems

This section delineates the procedural framework of the two newly developed optimization algorithms—Best–Worst–Random (BWR) and Best–Mean–Random (BMR). Both methods operate without relying on metaphorical analogies or algorithm-specific control parameters, focusing instead on simple arithmetic-based search strategies within a population of candidate solutions.

2.1.1. Best–Worst–Random (BWR) Algorithm

Let the objective function be optimized and denoted as f(x), where the goal is either minimization or maximization. Assume that the problem consists of m design variables (indexed by v = 1,2,…,m) and a population of c candidate solutions (or individuals, where k = 1,2,…,c), evolving through iterative updates indexed by i. Each design variable is constrained within predefined bounds: a lower bound L_v and an upper bound H_v. The algorithm begins by randomly generating an initial population of solutions. If any variable exceeds its permissible range, it is clipped to its respective boundary value.

Next, the feasibility of each candidate is checked against the problem’s constraints. If any constraints are violated, appropriate penalty functions are imposed. These penalties +may be static, dynamic, or any other user-defined function. For constraint violation g_j(x), a typical penalty is p_j(x) = g_j(x)². The penalized objective, denoted M(x), is calculated as follows:

• M(x) = f(x) + ∑p_j(x) for minimization
• M(x) = f(x) − ∑p_j(x) for maximization

The best solution is the one with the most favorable objective (e.g., the lowest M(x) in minimization), while the worst represents the least favorable. Let S_j,k,i is the vth variable’s value for the kth population in the ith iteration. Also, let the best, worst, mean, and random values of the vth variable during the ith iteration are S_v,b,i, S_v,w,i, S_v,m,i, and S_v,r,i, respectively. Additionally, let n1, n2, n3, and n4 be randomly generated numbers from a uniform distribution in [0, 1], and F be a random factor (either 1 or 2). The candidate solution is updated using the following rules:

Modify the values of S_j,k,i and compute the new values. The new value S’_v,k,i is computed using Equation (1), if n₄ > 0.5.

S’_v,k,i = S_v,k,i + n_1,v,i (S_v,b,i − F × S_v,r,i) − n_2,v,i (S_v,w,i − S_v,r,i)

(1)

Else, S’_v,k,i = H_v − (H_v − L_v)n₃

(2)

Based on the S’_v,k,i values, check the constraints g_j(x), apply the penalties if applicable, and compute M(x). Compare the new values of M(x) with the corresponding previous values of M(x) during the ith iteration and retain the solutions yielding improved M(x) values for the next iteration.

This process continues until a predefined termination criterion—typically, a maximum number of iterations or function evaluations—is met. Upon completion, the algorithm reports the optimal variable values and corresponding objective functions.

2.1.2. Best–Mean–Random (BMR) Algorithm

The Best–Mean–Random (BMR) algorithm follows a structure very similar to the BWR method, with one key modification in the solution update mechanism. Instead of leveraging the worst solution, the BMR algorithm incorporates the mean value of the population in the updated equation.

S’_v,k,i = S_v,k,i + n_1,v,i (S_v,b,i − F × S_v._m,i) + n_2,v,i (S_v,b,i − S_v,r,i), if n₄ > 0.5

(3)

Else, use Equation (2).

All subsequent steps—penalty evaluation, objective comparison, and population update—remain identical to those in the BWR algorithm.

Figure 1 shows the flowchart that illustrates the generic process of both the BWR and BMR algorithms.

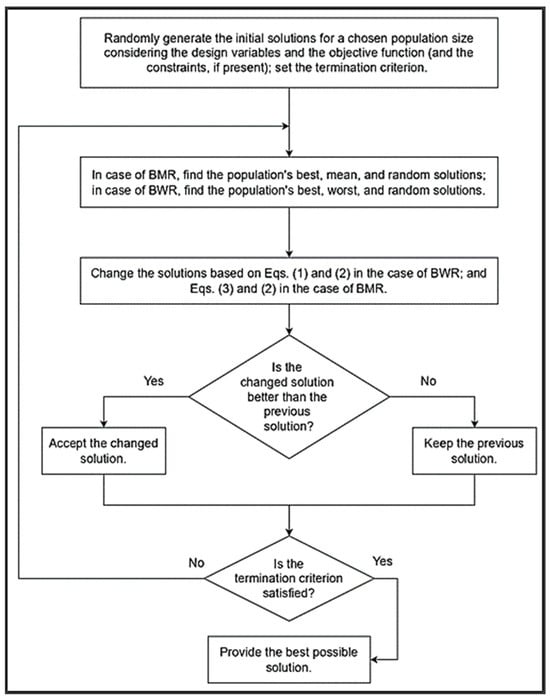
Figure 1. Generic flowchart of the BWR and BMR algorithms.

2.1.3. Demonstration of the BWR and BMR Algorithms on a Constrained Benchmark Function

Demonstration of the BWR Algorithm

To illustrate the efficacy and internal mechanics of the proposed BWR and BMR algorithms, a well-established benchmark problem—the constrained Himmelblau function—is employed.

The Himmelblau function is defined as Equation (4):

f(x): Minimize (x₁² + x₂ − 11)² + (x₁ + x₂² − 7) ²

(4)

Subject to the constraints given by Equations (5) and (6),

g₁(x) = 26 − (x₁ − 5) ² − x₂²

(5)

g₂(x) = 20 − 4 × x_{1 −} x₂

(6)

The variable bounds are given by Equation (7):

−5 ≤ x₁,x₂ ≤ 5.

(7)

The known global minimum of this constrained problem is f(x) = 0.

Step 1: The given objective function has two design variables, x1 and x2. A population size of 5 is considered for demonstration. The termination criterion is considered to be 1000 iterations. The solutions are randomly generated and are given in Table 1.

Table 1. Randomly generated initial population.

Solution	x1	x2	f(x)	g1(x)	p1	g2(x)	p2	M(x)
1	1.05763	1.85684	70.61647	7.009864	0	13.91264	0	70.61647 (best)
2	4.46747	0.27845	91.34434	25.63888	0	1.85167	0	91.34434
3	4.82116	−4.67009	442.7301	4.158276	0	5.38545	0	442.7301 (worst)
4	3.02432	3.64295	89.60672	8.825604	0	4.25977	0	89.60672
5	3.10156	4.08945	171.8241	5.672324	0	3.50431	0	171.8241

Step 2: The best value M(x) of the objective function considering the constraints are identified and shown in Table 1. The best values of x1 and x2 and M(x) are identified and indicated in bold. The worst value of M(x) of the objective function is 442.7301, and it corresponds to solution 3. The worst values of x1 and x2 and M(x) are identified and indicated in italics in Table 1.

Step 3: The best value M(x) of the objective function considering the constraints corresponds to solution 1, as it is a minimization problem. Let the random numbers generated for x1 be n₁ = 0.42, n₂ = 0.93, n₃ = 0.74, and the random numbers generated for x2 be n₁ = 0.75, n₂ = 0.35, n₃ = 0.68. The random number n₄ is a randomly generated number during an iteration, and its value decides to use either Equation (1) or Equation (2) for modifying the values of x1 and x2. Let the value of n₄ be 0.67 during the first iteration, which is greater than 0.5. Using Equations (1) and (2), the values of x1 and x2 are modified. For example, during the first iteration for candidate solution 1 that interacts randomly with candidate solution 4, the new (i.e., modified) values of x1 and x2 are computes as follows:

S’_x1,1,1 = 1.05763 + 0.42 × (1.05763 − 1 × 3.02432) − 0.93 × (4.82116 − 3.02432) = −1.43944

S’_x2,1,1 = 1.85684 + 0.75 × (1.85684 − 1 × 3.64295) − 0.35 × (−4.67009 − 3.64295) = 3.42682

The modified values of x1 and x2, the corresponding f(x), g1(x), p1, g2(x), p2, and M(x) are also computed and are given in Table 2. In this iteration, the new values of x1 and x2 for the candidate solutions 1, 2, 3, 4, and 5 are calculated considering the candidate solutions 4, 5, 1, 2, and 3, respectively, as the random solutions to interact.

Table 2. Modified values of the variables, constraints, penalties, and objective function (first iteration) obtained using the BWR algorithm.

Solution	x1	x2	f(x)	g1(x)	p1	g2(x)	p2	M(x)
1	−1.43944	3.426822	41.17727	−27.2095	740.3572	22.33094	0	781.5345
2	2.009791	1.669832	32.84193	14.27032	0	10.291	0	32.84193
3	1.321077	−2.38566	135.4995	6.774131	0	17.10136	0	135.4995
4	1.263256	6.558732	1397.911	−30.9802	959.7739	8.388247	0	2357.685
5	1.520877	8.984648	5661.864	−66.8282	4466.006	4.931843	0	10127.87

Step 4: The new values of M(x) in Table 2 are compared with the corresponding previous values of M(x) in Table 1 during the first iteration. The best M(x) values are retained, and the corresponding population is given in Table 3.

Table 3. Updated values of the variables, constraints, penalties, and objective function (first iteration) obtained using the BWR algorithm.

Solution	x1	x2	f(x)	g1(x)	p1	g2(x)	p2	M(x)
1	1.05763	1.85684	70.61647	7.009864	0	13.91264	0	70.61647
2	2.009791	1.669832	32.84193	14.27032	0	10.291	0	32.84193 (best)
3	1.321077	−2.38566	135.4995	6.774131	0	17.10136	0	135.4995
4	3.02432	3.64295	89.60672	8.825604	0	4.25977	0	89.60672
5	3.10156	4.08945	171.8241	5.672324	0	3.50431	0	171.8241 (worst)

It can be seen that the best value at the end of the first iteration is 32.84193 and the worst value is 171.8241. This shows the improvement in the best solution compared to the randomly generated initial population.

Step 5: Now, considering Table 3 as input, the second iteration can be carried out as the termination criterion is not reached, and so on. The second iteration results are not produced here for space limitations.

Step 6: Suppose the termination criterion of 1000 iterations is reached; the final results at the end of the 1000th iteration are as given in Table 4.

Table 4. Updated values of the variables, constraints, penalties, and objective function (1000th iteration) obtained using the BWR algorithm.

Solution	x1	x2	f(x)	g1(x)	p1	g2(x)	p2	M(x)
1	3.584428	−1.848126	0	20.580586	0	7.510414	0	0
2	3.584428	−1.848126	0	20.580586	0	7.510414	0	0
3	3.584428	−1.848126	0	20.580586	0	7.510414	0	0
4	3.584428	−1.848126	0	20.580586	0	7.510414	0	0
5	3.584428	−1.848126	0	20.580586	0	7.510414	0	0

It can be seen that the optimum solution of 0 is achieved by the proposed BWR algorithm with the optimum values of x1 = 3.584428 and x2 = −1.848126. The convergence graph is shown in Figure 1. The convergence is rapid, with the best result attained by iteration 159 (for a population size of 5), as illustrated in the convergence plot (Figure 2). The number of iterations required to reach 95% optimality is 40.

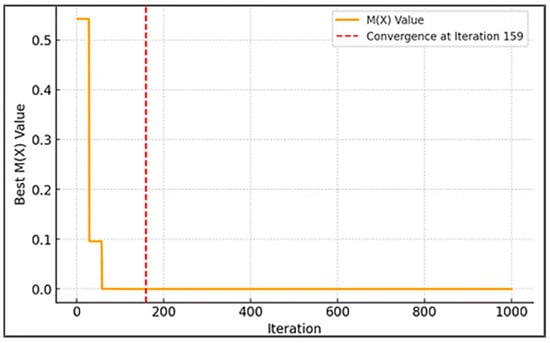
Figure 2. Convergence graph for the BWR algorithm for the constrained Himmelblau function.

Demonstration of BMR Algorithm

Now, to demonstrate the proposed BMR optimization algorithm, the same constrained Himmelblau function is considered. For comparing its performance with that of the BWR algorithm, the initial population generated in Table 1 is considered and the new values of x1 and x2 are calculated using Equation (3) (or Equation (2), if the values cross the bounds). The mean value of x1 is 3.294428, and the mean value of x2 is 1.03952 (from Table 1). Considering the same random interactions of candidate solutions 1–5 with 4, 5, 1, 2, and 3 like in the BWR algorithm, the new values of the population are given in Table 5. For example, during the first iteration for candidate solution 1 that interacts randomly with candidate solution 4, the new (i.e., modified) values of x1 and x2 are calculated using the BMR algorithm as follows:

S’_x1,1,1 = 1.05763 + 0.42 × (1.05763 − 1 × 3.294428) + 0.93 × (1.05763 − 3.02432) = −1.71085

S’_x2,1,1 = 1.85684 + 0.75 × (1.85684 − 1 × 1.03952) + 0.35 × (1.85684 − 3.64295) = 1.844692

Table 5. Modified values of the variables, constraints, penalties, and objective function (first iteration) obtained using the BMR algorithm.

Solution	x1	x2	f(x)	g1(x)	p1	g2(x)	p2	M(x)
1	−1.71085	1.844692	66.96631	−22.4384	503.4797	24.9987	0	570.446
2	1.62716	0.110027	96.67338	14.61184	0	13.38133	0	96.67338
3	3.881705	−4.0571	178.0028	8.289356	0	8.530281	0	178.0028
4	−1.08629	4.808377	251.1433	−34.1634	1167.136	19.53677	0	1418.279
5	−1.33798	6.986866	1643.435	−62.9863	3967.268	18.36505	0	5610.704

The modified values of x1 and x2, the corresponding f(x), g1(x), p1, g2(x), p2, and M(x) are also computed and are given in Table 5.

The new values of M(x) in Table 5 are compared with the corresponding previous values of M(x) in Table 1 during the first iteration. The best M(x) values are retained, and the corresponding population is given in Table 6.

Table 6. Updated values of the variables, constraints, penalties, and objective function (first iteration) using the BMR algorithm.

Solution	x1	x2	f(x)	g1(x)	p1	g2(x)	p2	M(x)
1	1.05763	1.85684	70.61647	7.009864	0	13.91264	0	70.61647 (best)
2	4.46747	0.27845	91.34434	25.63888	0	1.85167	0	91.34434
3	3.881705	−4.0571	178.0028	8.289356	0	8.530281	0	178.0028 (worst)
4	3.02432	3.64295	89.60672	8.825604	0	4.25977	0	89.60672
5	3.10156	4.08945	171.8241	5.672324	0	3.50431	0	171.8241

It can be seen that the best value at the end of the first iteration using BMR algorithm is 70.61647 and the worst value is 178.0028. This shows the improvement in the worst solution compared to the randomly generated worst solution of 442.7301, given in Table 1.

Now, considering Table 6 as input, the second generation can be carried out, and so on. Suppose 1000 iterations are carried out with the same population size of 5; the final results at the end of the 1000th iteration are exactly the same as those given in Table 4. The BMR algorithm also obtained the optimum solution of 0 with the optimum values of x1 = 3.584428 and x2 = −1.848126. The convergence graph for the BMR algorithm is shown in Figure 3. However, the BMR algorithm converged faster, reaching the optimal solution by iteration 121, whereas the BWR reached it by iteration 159. The number of iterations required to reach 95% optimality is 25.

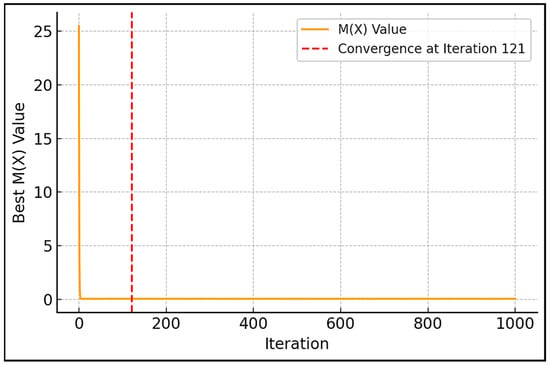
Figure 3. Convergence graph for the BMR algorithm for the constrained Himmelblau function.

To comprehensively evaluate the performance of the proposed BWR and BMR algorithms, a benchmark suite of 12 constrained engineering optimization problems is selected. These problems were recently addressed by Ghasemi et al. [27] using a metaphor-based technique known as the Flood Algorithm (FLA). Their study involved comparisons with more than 30 optimization algorithms, including methods such as the real-coded genetic algorithm (RCGA), comprehensive learning particle swarm optimization (CLPSO), self-adaptive differential evolution (SADE), ensemble of parameters and mutation strategies in DE (EPSDE), adaptive unified DE (AUDE2), fully informed PSO (FIPSO), orthogonal learning PSO (OLPSO), static heterogeneous PSO (SHPSO), artificial bee colony (ABC), genetic algorithm (GA), gray wolf optimization (GWO), whale optimization algorithm (WOA), and memory-guided sine–cosine algorithm (MG-SCA), among others. These encompassed a wide range of nature-inspired, swarm-based, and hybrid optimization strategies.

For brevity and to avoid redundancy, the mathematical formulations, decision variables, constraints, and bounds of these 12 problems are not reproduced here, as they are thoroughly documented in the original work by Ghasemi et al. [27]. In the present study, the BMR and BWR algorithms are applied to the same set of problems using identical experimental conditions, including 30 independent runs per problem, as employed by Ghasemi et al. [27] for the FLA and the other comparison algorithms. Since the FLA [27] has already claimed superiority over the other algorithms, their results have been omitted from Table 7. It is considered sufficient to evaluate the performance of the BWR and BMR algorithms by comparing them directly with the FLA [27].

Table 7. Statistical measures obtained using the BWR and BMR algorithms and FLA [27] for 12 constrained single-objective engineering design problems.

Statistical Measures	BWR	BMR	FLA [27]	Remarks
1. Welded beam optimization
Best	1.6979	1.6981	1.7248523	BWR achieved the best result with extremely low variance.
Mean	1.6979	1.7010	1.7248527
Worst	1.6979	1.7032	1.7248536
Standard deviation	2.7043 × 10−10	1.5674 × 10−3	3.08 × 10−6
2. Three-bar truss optimization
Best	1.085211 × 102	1.085211 × 102	2.6389584 × 102	BMR and BWR produced identical results, outperforming FLA.
Mean	1.085211 × 102	1.085211 × 102	2.6389584 × 102
Worst	1.085211 × 102	1.085211 × 102	2.6389584 × 102
Standard deviation	1.8346 × 10−14	1.4504 × 10−14	7.10 × 10−5
3. Cantilever beam optimization
Best	1.3351	1.3351	1.339956	Both proposed algorithms converged to 1.3351, better than FLA.
Mean	1.3351	1.3351	1.339958
Worst	1.3351	1.3351	1.339963
Standard deviation	1.5367 × 10−14	1.9342 × 10−11	6.48 × 10−7
4. Gear train optimal design
Best	7.3856 × 10−25	4.287642 × 10−22	2.700857 × 10−12	BWR achieved a near-zero best result versus FLA.
Mean	7.1755 × 10−21	3.4497 × 10−18	8.7526 × 10−10
Worst	4.3061 × 10−20	3.4131 × 10−17	1.4069 × 10−9
Standard deviation	1.121 × 10−20	8.21 × 10−18	2.76 × 10−9
5. Tension/compression spring optimization
Best	0.012648	0.012648	0.012665	All methods achieved similar best values, but BWR and BMR achieved good consistency.
Mean	0.012648	0.012648	0.012666
Worst	0.012648	0.012648	0.012667
Standard deviation	8.0429 × 10−14	8.0429 × 10−14	6.29 × 10−7
6. Pressure vessel optimization
Best	4.840545 × 102	4.840545 × 102	6.059714 × 103	BMR/BWR reached values dramatically better than FLA.
Mean	4.840545 × 102	4.840545 × 102	6.06021 × 103
Worst	4.840545 × 102	4.840545 × 102	6.09052 × 103
Standard deviation	1.6409 × 10−13	1.6409 × 10−13	3.86
7. Speed reducer optimization
Best	2.35748 × 103	2.35748 × 103	2.99447 × 103	Both proposed methods achieved better results.
Mean	2.35748 × 103	2.35748 × 103	2.994471 × 103
Worst	2.35748 × 103	2.35748 × 103	2.994473 × 103
Standard deviation	9.2825 × 10−13	9.2825 × 10−13	2.09 × 10−4
8. I-beam vertical deflection
Best	0.0016369	0.0016369	0.013074	BMR and BWR achieved better results, outperforming FLA.
Mean	0.0016369	0.0016369	0.01307445
Worst	0.0016369	0.0016369	0.01307579
Standard deviation	6.6394 × 10−19	6.6394 × 10−19	6.91 × 10−06
9. Tubular column optimal design
Best	10.3168	10.3168	26.4995	BMR and BWR achieved better results, outperforming FLA.
Mean	10.3168	10.3168	26.4995
Worst	10.3168	10.3168	26.51003
Standard deviation	9.2825 × 10−13	9.2825 × 10−13	1.41 × 10−4
10. Piston lever optimal design
Best	7.585	7.585	8.412698	BMR and BWR achieved better results, outperforming FLA.
Mean	7.585	7.585	23.821251
Worst	7.585	7.585	167.232196
Standard deviation	2.054 × 10−14	2.054 × 10−14	47.2
11. Corrugated bulkhead optimal design
Best	6.5795	6.5795	6.842958	BMR and BWR achieved better results, outperforming FLA.
Mean	6.5795	6.5795	6.8429676
Worst	6.5795	6.5795	6.8432916
Standard deviation	2.7195 × 10−15	2.7195 × 10−15	1.25 × 10−5
12. Car side impact optimization
Best	22.2857	22.2857	22.84297	BMR and BWR achieved better results. The results of FLA were less accurate, with more variability.
Mean	22.2857	22.2857	22.88914
Worst	22.2857	22.2857	23.17638
Standard deviation	1.0534 × 10−14	1.0534 × 10−14	7.38 × 10−3

The results obtained from the BMR and BWR algorithms are presented in Table 7, with the best-performing values highlighted in bold. Given that the FLA [27] has already demonstrated its superiority over a broad set of optimization algorithms, only the FLA results are retained for comparison in Table 7. This ensures clarity and conciseness while providing a sufficient basis for evaluating the relative performance of the proposed algorithms.

The results now show that the proposed metaphor-free BMR and BWR algorithms consistently outperformed FLA across all 12 problems, thereby surpassing not only FLA itself but also the entire set of algorithms that FLA had previously outperformed. The BWR and BMR algorithms consistently outperformed in all statistical metrics (best, mean, worst, and standard deviation), often with perfect or near-zero variance, indicating superior convergence stability. The key strengths demonstrated by BMR and BWR in this context include exceptional accuracy, stable performance across multiple independent runs, and zero or near-zero standard deviations, confirming robustness. Hence, the BWR and BMR algorithms are considered in this paper for solving real-life constrained manufacturing optimization tasks. For detailed results and comparisons of the benchmark functions, readers are referred to the preprint by Rao and Shah [28] available on arXiv.

It may be noted that the proposed BWR and BMR algorithms are metaphor-less and algorithm-specific control parameter-less. The Jaya algorithm and the three Rao algorithms [23] also possess these features. Hence, Table 8 is presented below to present the novel features of the proposed BWR and BMR algorithms and to differentiate them from the Jaya and Rao algorithms.

Table 8. Differences between the Jaya, Rao, BWR, and BMR algorithms.

Feature	Jaya	Rao-1/2/3	BWR	BMR
Search mechanism type	Directional (toward best, away from worst)	Directional arithmetic (best/worst/random)	Hybrid arithmetic with random fallback and flexible direction control	Hybrid arithmetic with best–mean–guided search
Novel equation logic	Linear directional	Various forms of directional logic	New combination: (best − F × rand), (worst − rand) difference, fallback to random sampling	(Best − F × mean) and (best − rand) combination, fallback to random sampling
Handling of random influence	Indirect (via coefficients)	Rao-2/3 use random individuals	Direct: random solution is explicitly part of the update rule	Same
Fallback sampling	None	None	Yes: if n4 ≤ 0.5, fallback to S’v,k,i = Hv − (Hv − Lv)n3	Same as BWR
Diversity mechanism	Moderate via random numbers r1, r2	Rao-2/3 add more diversity via randomness	Very strong, due to combination of best/worst/random directions	Strong, but more controlled than BWR
Exploration–exploitation balance	Balanced	Rao-3 is most exploratory	Highly exploratory, but still exploits best	More exploitative, smoother convergence via mean-based guidance
Design simplicity	High (1-line update rule)	High (1-line update rule)	Slightly complex, but still parameter-free and metaphor-free	Same
Robustness to local optima	Moderate	Moderate	Strong: fallback randomness + direction mix help escape traps	Good, but more conservative due to mean-based bias
Risk of premature convergence	Moderate	Moderate	Low	Low

The generalized pseudocodes of the BWR and BMR algorithms are given below in Algorithm 1.

Algorithm 1. Generalized pseudocodes of the BWR and BMR algorithms.

1: Begin BWR/BMR Algorithm 2: Initialize: 3:     -Number of variables: m 4:     -Population size: c 5:     -Maximum iterations: max_iter 6:     -Variable bounds: Lv and Hv for v = 1 to m 7:     -Algorithm mode: “BWR” or “BMR” 8:     -Optimization goal: “min” or “max” 9: Generate initial population: 10:     For k = 1 to c: 11:       For v = 1 to m: 12:             Sv,k,0 ← random value in [Lv, Hv] 13: Evaluate initial population: 14:     For each individual k: 15:           Compute objective f(x_k) 16:           For each violated constraint gj(x_k): 17:             Compute penalty pj(x_k) = gj(x_k)^2 18:           Compute penalized objective M(x_k): 19:               If goal = “min”: M(x_k) = f(x_k) + ∑ pj(x_k) 20:               If goal = “max”: M(x_k) = f(x_k) − ∑ pj(x_k) 21: Set iteration i = 0 22: Repeat until i = max_iter: 23:     Identify: 24:            - Best solution Sv,b,i: 25:               If goal = “min”: lowest M(x) 26:               If goal = “max”: highest M(x) 27:            - Worst solution Sv,w,i: 28:               If goal = “min”: highest M(x) 29:               If goal = “max”: lowest M(x) 30:            - Mean vector Sv,m,i (mean of each variable across population) 31:            - Random solution Sv,r,i (randomly selected from population) 32:     For each individual k = 1 to c: 33:          For each variable v = 1 to m: 34:             Generate random numbers: n1, n2, n3, n4 ∈ [0, 1], F ∈ {1, 2} 35:               If n4 > 0.5: 36:                  If mode = “BWR”: 37:                       S'v,k,i = Sv,k,i + n1 * (Sv,b,i − F * Sv,r,i) 38:                                           - n2 * (Sv,w,i - Sv,r,i) 39:                  Else if mode = “BMR”: 40:                       S'v,k,i = Sv,k,i + n1 * (Sv,b,i − F * Sv,m,i) 41:                                           + n2 * (Sv,b,i - Sv,r,i) 42:             Else: 43:                  S'v,k,i = Hv − (Hv − Lv) * n3 44:             Enforce bounds: 45:                  If S'v,k,i < Lv then S'v,k,i = Lv 46:                  If S'v,k,i > Hv then S'v,k,i = Hv 47:     Evaluate new solution S'_k: 48:            Compute f(S'_k) 49:            For each violated constraint gj(S'_k): 50:               Compute pj(S'_k) = gj(S'_k)^2 51:         Compute M(S'_k): 52:             If goal = “min”: M(S'_k) = f(S'_k) + ∑ pj(S'_k) 53:             If goal = “max”: M(S'_k) = f(S'_k) − ∑ pj(S'_k) 54:         Compare with previous M(x_k): 55:             If (goal = “min” and M(S'_k) < M(x_k)) or 56:                  (goal = “max” and M(S'_k) > M(x_k)): 57:                  Accept S'_k as new solution 58: Increment i ← i + 1 59: Return best solution and its objective value 60: End Algorithm

3. Materials and Methods: MO-BWR and MO-BMR Algorithms

This section is divided into two sub-sections. The first Section 3.1, describes the multi- and many-objective versions of the BWR and BMR algorithms, and the second Section 3.2, describes the multi-attribute decision-making aspects involved in selecting the best compromise Pareto-optimal solution from among the available non-dominated solutions.

3.1. Multi-Objective and Many-Objective Optimization Using BWR and BMR Algorithms

The multi- and many-objective versions of BWR and BMR are named MO-BWR and MO-BMR, respectively. These algorithms consist of features like elite seeding, fast non-dominated sorting, constraint repairing, penalty application (if constraint repairing does not work), local exploration, and edge boosting features. The procedural steps are briefly given in Table 9.

Table 9. Procedural steps of the MO-BWR and MO-BMR algorithms.

Step No.	Step Title	Description
1	Start	Begin the algorithm.
2	Initialize population	Generate initial population of solutions within variable bounds.
3	Perform elite seeding	Include high-quality or historically good solutions into initial population.
4	Apply fast non-dominated sorting	Rank individuals into fronts based on Pareto dominance and calculate crowding distance.
5	Check and repair constraints	Attempt to fix any constraint violations in the individuals (first approach).
6	Apply penalties	If violations remain, apply penalties to the objective functions (fallback approach).
7	Calculate objective function values	Evaluate all objective functions for each individual.
8	Apply edge boosting	Enhance exploration near the Pareto front boundaries (extremes).
9	Apply local exploration	Explore small neighborhoods around elite or promising solutions for refinement.
10	Update population using MO-BWR or MO-BMR	Generate new solutions using the update rule of MO-BWR or MO-BMR.
11	Termination criterion met?	Check if the maximum number of iterations or evaluations has been reached.
12	If No, return to Step 5	If not terminated, repeat the process starting from constraint checking.
13	If Yes, report Pareto-optimal solutions	End the algorithm and output the final set of non-dominated solutions.

The generalized pseudocodes of the MO-BWR and MO-BMR algorithms are given below in Algorithm 2.

Algorithm 2. The generalized pseudocodes of the MO-BWR and MO-BMR algorithms.

1: Begin MO-BWR/MO-BMR Algorithm 2: Step 1: Initialization 3:     -Define: 4:           •Design variables and bounds Lv, Hv (for v = 1 to m) 5:           •Objective functions f1(x), f2(x),…, fM(x) 6:           •Constraints gj(x) ≤ 0 (inequality), hj(x) = 0 (equality) 7:           •Algorithm-specific mode: “MO-BWR” or “MO-BMR” 8:           •Optimization goal: “min” or "max" for each objective 9:           •Population size: c 10:           •Max iterations: max_iter 11: Step 2: Initialize Population 12:     -Generate c random candidate solutions x_k ∈ [Lv, Hv] 13: Step 3: Elite Seeding 14:     -Add elite solutions (extremes or known good solutions) to population 15: Step 4: Fast Non-dominated Sorting 16:     -For each solution p: 17:           Sp ← ∅, np ← 0 18:           For each q ≠ p: 19:                If p < q: Sp ← Sp ∪ {q} 20:                If q < p: np ← np + 1 21:     -First front F0 ← {p|np = 0}; assign rank = 0 22:     -Repeat for subsequent fronts: 23:           For p ∈ Fi: For q ∈ Sp: 24:                nq ← nq − 1; if nq = 0 → Fi+1 ← Fi+1 ∪ {q} 25:     -Assign Pareto ranks to all individuals 26:     Crowding Distance Assignment (per front): 27:           -For each objective m: 28:                •Sort individuals in front by fm 29:                •Set di = ∞ for boundaries 30:                •For interior i = 2 to N−1: 31:                     di += (fm(i+1) − fm(i−1)) / (fm_max − fm_min) 32: Step 5: Constraint Repair 33:     -For each solution x: 34:           •Clip variables: x_v ← min(max(x_v, Lv), Hv) 35:           •Apply inequality repair (resample, projection, etc.) 36:           •Apply equality repair (tolerance, solver, projection) 37:           •If still infeasible → proceed to penalty 38: Step 6: Apply Penalties 39:     -For infeasible solutions: 40:           •Compute penalty pj(x) = gj(x)^2 or |hj(x)|^2 41:           •Modify objectives: 42:                If goal = “min”: f’(x) = f(x) + ∑ pj(x) 43:                If goal = “max”: f’(x) = f(x) − ∑ pj(x) 44: Step 7: Objective Function Evaluation 45:     -Compute f1(x), f2(x),…, fM(x) for all individuals 46: Step 8: Edge Boosting 47:     -Identify edge solutions Xmin,j and Xmax,j for each objective j 48:     -Filter non-dominated edge solutions 49:     -Perturb each: x’ = x + δ ⋅ sign(r) ⋅ (Hv − Lv) 50:        where δ ∈ [0.01, 0.1], r ∼ U(−1, 1) 51:     -Insert boosted solutions into population 52: Step 9: Local Exploration 53:     -For elite/promising solutions: 54:           •Apply small perturbations to explore neighborhood 55:           •Add refined candidates to the population 56: Step 10: Population Update (MO-BWR / MO-BMR) 57:     -For each individual k and each variable v: 58:           Generate n1, n2, n3, n4 ∈ [0, 1], F ∈ {1, 2} 59:           If n4 > 0.5: 60:                If mode = "MO-BWR": 61:                     S’_v,k = S_v,k + n1*(S_v,b − F*S_v,r) − n2*(S_v,w − S_v,r) 62:                If mode = "MO-BMR": 63:                     S’_v,k = S_v,k + n1*(S_v,b − F*S_v,m) + n2*(S_v,b − S_v,r) 64:           Else: 65:                S’_v,k = Hv − (Hv − Lv) * n3 66:           Enforce bounds: S’_v,k = min(max(S’_v,k, Lv), Hv) 67: Step 11: Check Termination Criterion 68:     -If i ≥ max_iter or other stopping criteria met: 69:           Go to Step 13 70: Step 12: Loop 71:     -Replace population with selected next-generation candidates 72:     -i ← i + 1 73:     -Go to Step 5 74: Step 13: Report Pareto-optimal Set 75:     -Return non-dominated front with associated objective vectors 76: End MO-BWR/MO-BMR Algorithm

The total complexity of both MO-BWR and MO-BMR algorithms is the same and is equal to O(I⋅(M.c² + c⋅(m+t_f+t_p))), where M is the number of objectives, I is the number of iterations, c is the population size, m is the number of design variables, t_f is the time to evaluate the objective and constraints per individual, and t_p is the time for penalty calculation (assumed to be proportional to the number of constraints). This reflects quadratic complexity from Pareto sorting, linear complexity in variables and evaluations, and suitability for small to medium population sizes, or scalable with faster sorting variants like the NSGA-III algorithm. In the case of the BWR and BMR algorithms, the total computational complexity is the same and is equal to O(I⋅c⋅(m + t_f + t_p)), because the only difference between them lies in the update rule (using worst vs. mean), which does not affect asymptotic complexity.

Validation of the MO-BWR and MO-BMR Algorithms for ZDT Functions

To demonstrate the effectiveness of the proposed MO-BWR and MO-BMR algorithms, the standard Zitzler–Deb–Thiele (ZDT) benchmark functions were utilized. These functions are described below.

ZDT1:

f1(x) = x1

(8)

g(x) = 1 + 9 × (1/(n − 1)) × Σ xi for i = 2 to n

(9)

f2(x) = g(x) × [1 − sqrt(f1(x)/g(x))]

(10)

ZDT2:

f1(x) = x1

(11)

g(x) = 1 + 9 × (1/(n − 1)) × Σ xi for i = 2 to n

(12)

f2(x) = g(x) × [1 − (f1(x)/g(x))^2]

(13)

ZDT3:

f1(x) = x1

(14)

g(x) = 1 + 9 × (1/(n − 1)) × Σ xi for i = 2 to n

(15)

f2(x) = g(x) × [1 − sqrt(f1(x)/g(x)) − (f1(x)/g(x)) × sin(10π × f1(x))]

(16)

ZDT4:

f1(x) = x1

(17)

g(x) = 1 + 10 × (n − 1) + Σ [xi^2 − 10 × cos(4π × xi)] for i = 2 to n

(18)

f2(x) = g(x) × [1 − sqrt(f1(x)/g(x))]

(19)

ZDT6:

f1(x) = 1 − exp(−4 × x1) × sin^6(6π × x1)

(20)

g(x) = 1 + 9 × (Σ xi for i = 2 to n)^(0.25)/(n − 1)

(21)

f2(x) = g(x) × [1 − (f1(x)/g(x))^2]

(22)

The application of the MO-BWR and MO-BMR algorithms to the ZDT benchmark problems was carried out using 40,000 function evaluations. The same number of function evaluations were used for comparing the results of non-dominated sorting genetic algorithm III (NSGA-III) for each problem. The number of runs conducted was 30. The codes for the MO-BWR and MO-BMR algorithms were written in Python version 3.12.3 on a laptop with an AMD Ryzen 5 5600H processor and 16 GB DDR4 RAM. The Pymoo library was used for benchmark functions and their true fronts, as well as the NSGA-III.

ZDT1: The optimal Pareto front is as shown in Figure 4.

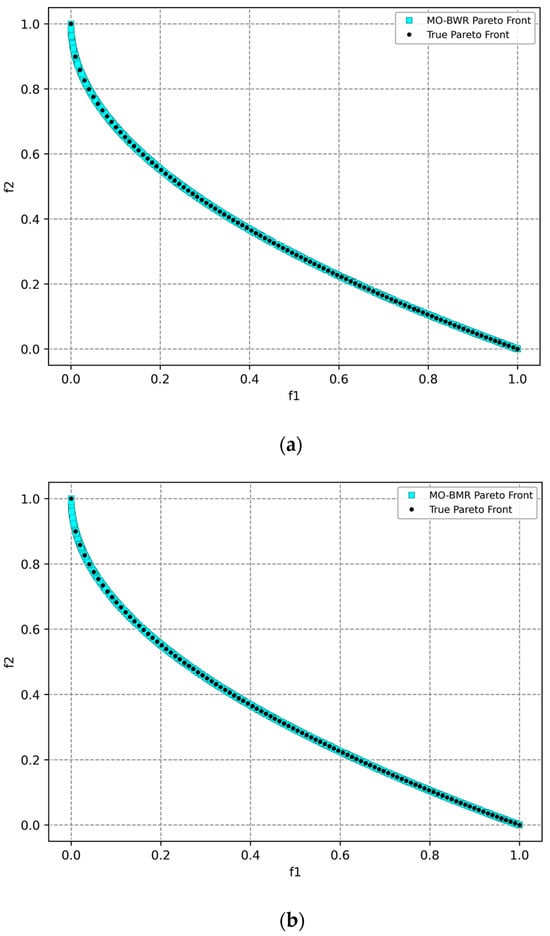
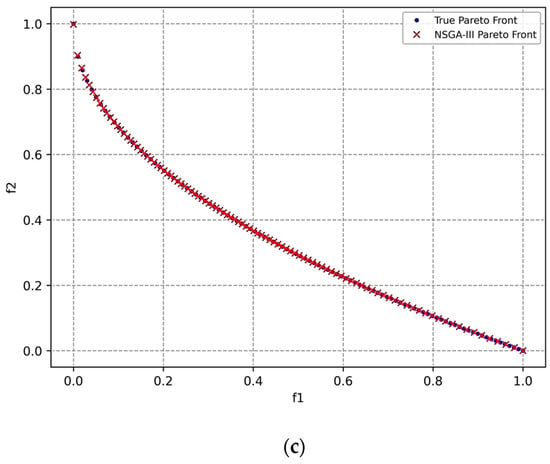
Figure 4. Pareto front obtained for the ZDT1 function using (a) the MO-BWR algorithm, (b) the MO-BMR algorithm, and (c) NSGA-III.

Then, the following performance metrics were computed, taking the true front as the reference front.

• GD (generational distance): The average distance from the obtained front to the reference Pareto front (ideal value = 0).
• IGD (inverted GD): The average distance from the reference front to the obtained front (ideal value = 0).
• Spacing: Standard deviation of distances between consecutive solutions; measures uniformity of solution distribution (the lower the better).
• Hypervolume: Volume (area in 2D) dominated by the front up to a reference point; combines convergence and diversity (the higher the better).

Table 10 shows the mean performance metrics along with the standard deviation (std. dev.) values after conducting 30 runs of MO-BWR, MO-BMR, and NSAGA-III with reference to the true front.

Table 10. Mean performance metrics of the algorithms for ZDT1 with reference to the true front after 30 runs.

Algorithm	GD		IGD		Spacing		Hypervolume
	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.
MO-BWR	0.005128	1.1805 × 10−4	0.000549	1.6931 × 10−4	0.0005928	2.4024 × 10−5	0.875832	2.7768 × 10−4
MO-BMR	0.005051	7.3743 × 10−5	0.000435	3.2228 × 10−5	0.000633	1.9272 × 10−5	0.876091	1.7750 × 10−5
NSGA-III	0.003548	5.0038 × 10−5	0.003543	6.8238 × 10−5	0.010218	4.3086 × 10−4	0.871460	5.9923 × 10−5

The MO-BMR is best in IGD and HV, showing excellent coverage and quality. A low standard deviation in HV implies consistent performance. MO-BWR is best in spacing, suggesting a very uniform distribution of points. It is slightly behind MO-BMR in IGD and HV. It shows good performance across all metrics. NSGA-III is best in GD, indicating strong convergence, but only in specific regions. It is not good in IGD and spacing, highlighting non-uniform and incomplete front coverage. Hypervolume is lower than both MO-BMR and MO-BWR.

ZDT2: The optimal Pareto front is as shown in Figure 5.

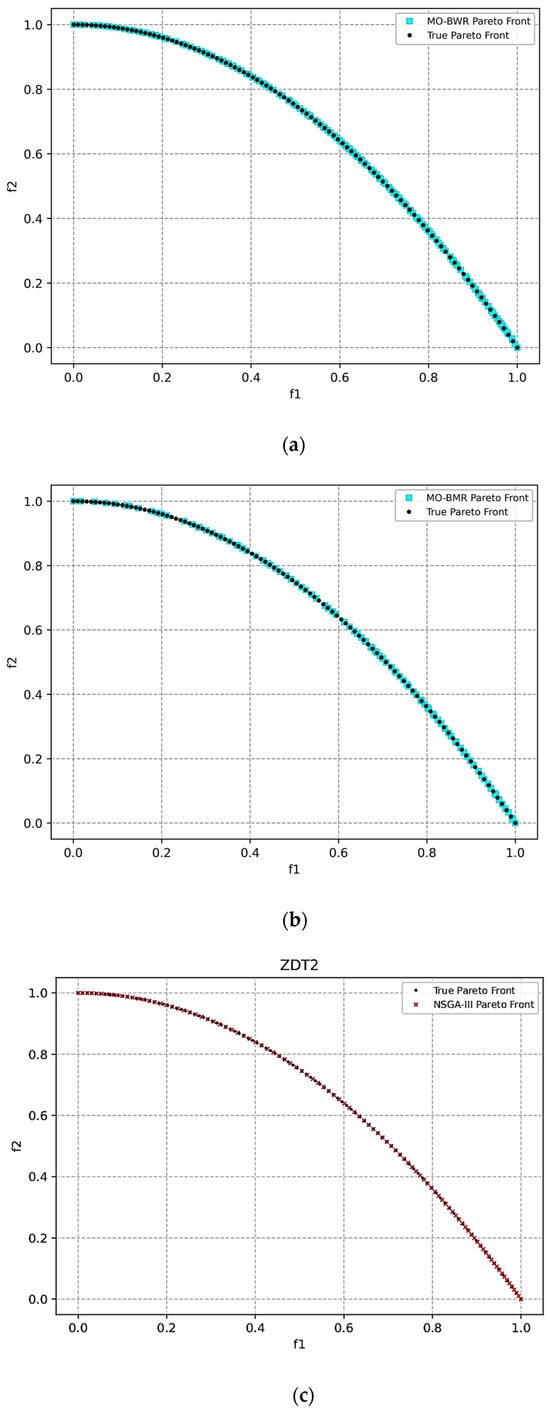
Figure 5. Pareto front obtained for the ZDT2 function using (a) the MO-BWR algorithm, (b) the MO-BMR algorithm, and (c) NSGA-III.

Table 11 shows the mean performance metrics after conducting 30 runs of MO-BWR, MO-BMR, and NSGA-III with reference to the true front.

Table 11. Mean performance metrics of the algorithms for ZDT2 with reference to the true front after 30 runs.

Algorithm	GD		IGD		Spacing		Hypervolume
	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.
MO-BWR	0.004021	5.1599 × 10−4	0.018096	9.1079 × 10−2	0.000821	5.6432 × 10−4	0.527392	7.5723 × 10−3
MO-BMR	0.004121	6.2991 × 10−4	0.002203	8.3148 × 10−3	0.001060	7.2644 × 10−4	0.539351	1.6764 × 10−3
NSGA-III	0.003609	1.5771 × 10−5	0.003438	1.6013 × 10−5	0.004172	2.9634 × 10−5	0.538386	2.4044 × 10−5

MO-BMR is best in IGD and hypervolume, indicating excellent coverage and diversity. MO-BWR is best in spacing, but significantly not good in IGD, likely due to poor spread across the front in some runs. NSGA-III is best in GD, and low variance shows high consistency. However, it is weak in spacing, suggesting clustering or non-uniformity of solutions. It has a competitive hypervolume, though slightly lower than MO-BMR.

ZDT3: The optimal Pareto front is as shown in Figure 6.

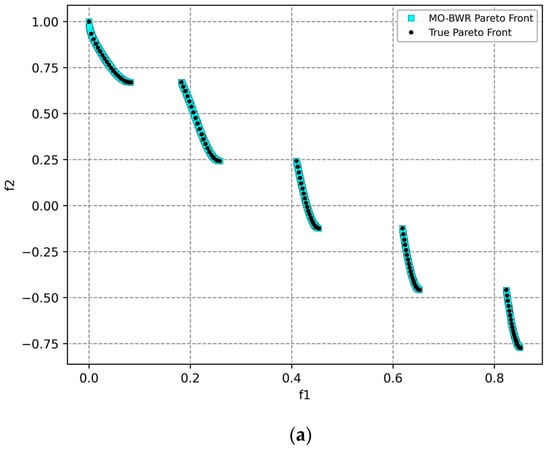
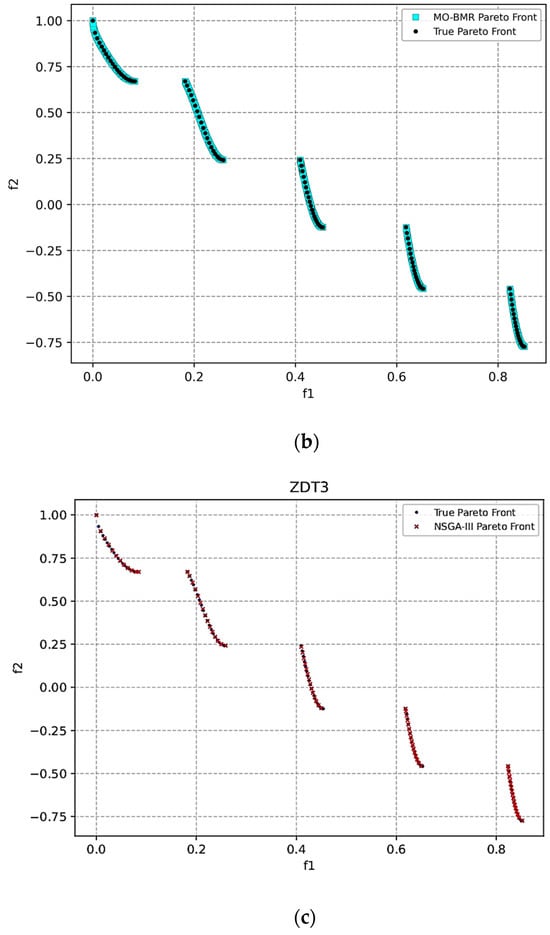
Figure 6. Pareto front obtained for the ZDT3 function using (a) the MO-BWR algorithm, (b) the MO-BMR algorithm, and (c) NSGA-III.

Table 12 shows the mean performance metrics after conducting 30 runs of MO-BWR, MO-BMR, and NSAGA-III with reference to the true front.

Table 12. Mean performance metrics of the algorithms for ZDT3 with reference to the true front after 30 runs.

Algorithm	GD		IGD		Spacing		Hypervolume
	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.
MO-BWR	0.003869	3.2657 × 10−4	0.003187	2.8226 × 10−3	0.0012825	3.4899 × 10−4	0.72128	6.9315 × 10−3
MO-BMR	0.003633	2.5603 × 10−4	0.001671	2.2589 × 10−3	0.0008835	3.3653 × 10−4	0.72463	5.4288 × 10−3
NSGA-III	0.002818	5.8555 × 10−5	0.003709	1.0524 × 10−4	0.007505	1.7482 × 10−4	0.724230	7.6240 × 10−5

The discontinuous nature of ZDT3 challenges diversity maintenance. MO-BMR is best in IGD, spacing, and hypervolume, showing excellent front coverage, distribution, and trade-off handling. It is slightly behind NSGA-III in GD, but overall is most balanced performer. MO-BWR shows moderate performance across all metrics. NSGA-III is best in GD, meaning strong localized convergence. However, it is not good in IGD and spacing, indicating non-uniformity and incomplete front coverage. Hypervolume is good, but slightly lower than MO-BMR.

ZDT4: The optimal Pareto front is as shown in Figure 7.

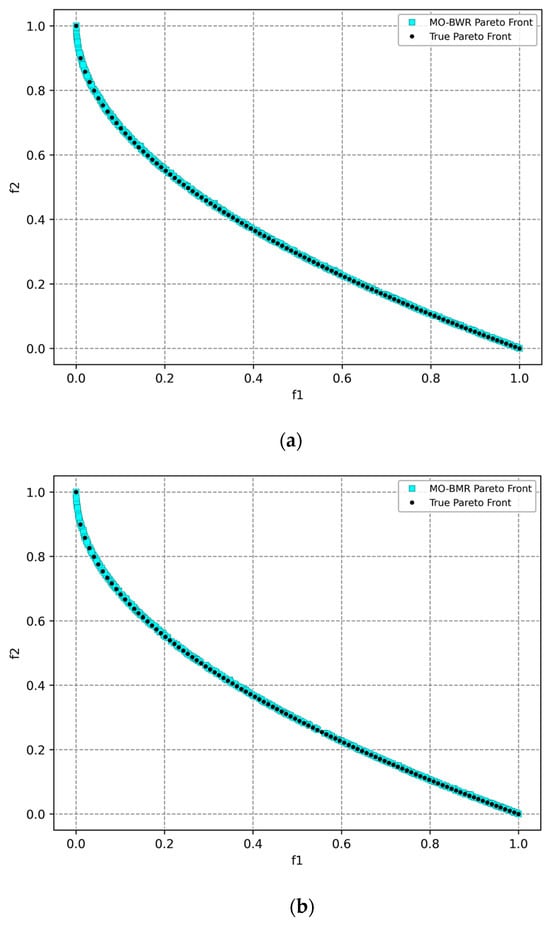
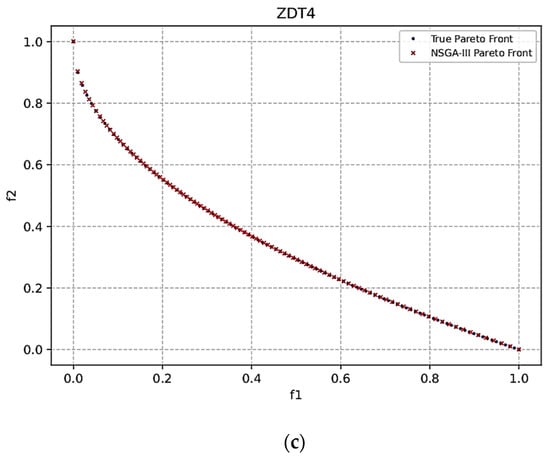
Figure 7. Pareto front obtained for the ZDT4 function using (a) the MO-BWR algorithm, (b) the MO-BMR algorithm, and (c) NSGA-III.

Table 13 shows the mean performance metrics after conducting 30 runs of MO-BWR, MO-BMR, and NSAGA-III with reference to the true front.

Table 13. Mean performance metrics of the algorithms for ZDT4 with reference to the true front after 30 runs.

Algorithm	GD		IGD		Spacing		Hypervolume
	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.
MO-BWR	0.005478	1.5433 × 10−4	0.002180	1.5306 × 10−4	0.001852	8.3442 × 10−5	0.872858	2.9916 × 10−4
MO-BMR	0.005676	2.9654 × 10−4	0.002498	3.6697 × 10−4	0.001803	1.1073 × 10−4	0.872257	6.4334 × 10−4
NSGA-III	0.004254	6.5069 × 10−4	0.005634	1.3859 × 10−3	0.010484	4.8832 × 10−4	0.867990	5.2656 × 10−3

MO-BWR is best in IGD and highest HV, indicating strong convergence and diverse spread along the true front. It is very close to MO-BMR in spacing and GD and offers a well-balanced performance across all metrics. MO-BMR has slightly better spacing than MO-BWR and close in GD and HV, second-best performer overall. NSGA-III achieves the best GD, showing strong convergence in localized regions. However, it does not have good IGD and spacing, implying poor distribution and incomplete front coverage.

The ZDT5 function involves binary numbers; hence, many researchers have not considered it while verifying their algorithms on the ZDT functions. Hence, the ZDT5 function is not considered here.

ZDT6: The optimal Pareto front is as shown in Figure 8.

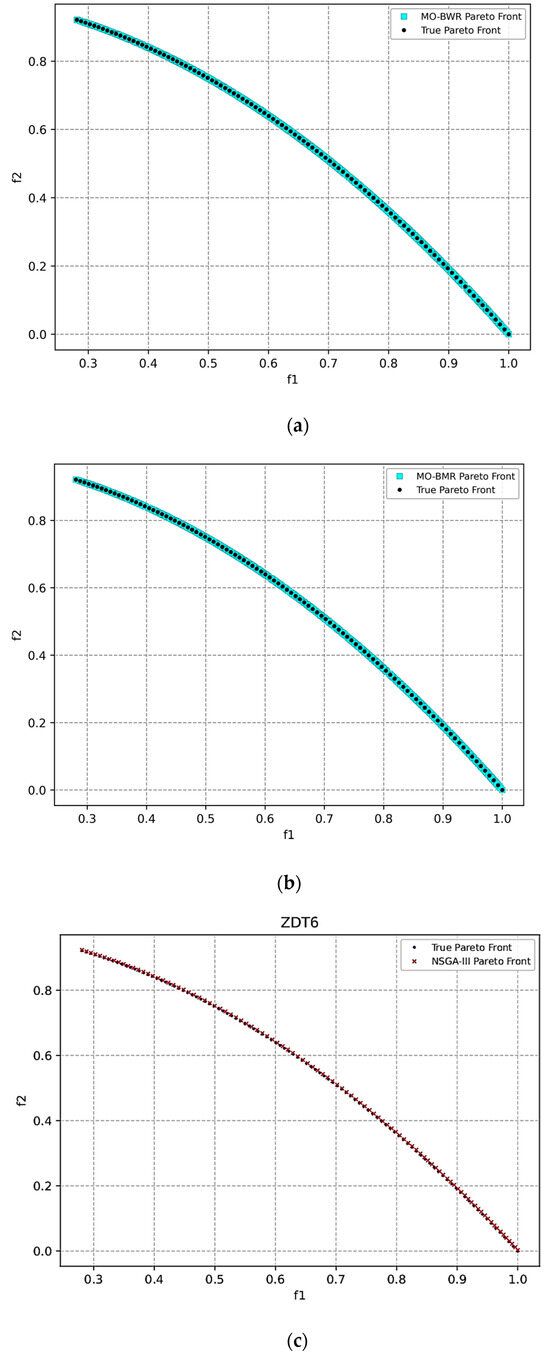
Figure 8. Pareto front obtained for the ZDT6 function using (a) the MO-BWR algorithm, (b) the MO-BMR algorithm, and (c) NSGA-III.

Table 14 shows the mean performance metrics after conducting 30 runs of MO-BWR, MO-BMR, and NSAGA-III with reference to the true front.

Table 14. Mean performance metrics of the algorithms for ZDT6 with reference to the true front after 30 runs.

Algorithm	GD		IGD		Spacing		Hypervolume
	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.	Mean	Std. Dev.
MO-BWR	0.006370	4.1160 × 10−3	0.000418	2.8515 × 10−5	0.054858	7.5815 × 10−2	0.615821	1.7178 × 10−5
MO-BMR	0.007295	4.1911 × 10−3	0.000424	2.8036 × 10−5	0.068319	7.3691 × 10−2	0.615820	1.8577 × 10−5
NSGA-III	0.004303	1.4614 × 10−4	0.004245	1.3982 × 10−4	0.002476	1.0359 × 10−4	0.607590	3.2857 × 10−4

MO-BWR achieves lowest IGD, indicating better coverage and diversity across the true front. It has the highest hypervolume, suggesting the overall best trade-off between convergence and diversity. It performs reasonably well on GD, though slightly behind NSGA-III. MO-BMR is slightly inferior to MO-BWR in all metrics. It is very close in hypervolume, but lags in IGD and spacing. NSGA-III is best in GD and spacing, indicating precise and uniformly spaced solutions near the front. However, its IGD is significantly worse than MO-BWR/BMR, showing poorer coverage of the entire front.

The following observations can be made based on the algorithms’ performance on the ZDT functions.

• GD: NSGA-III is best in GD.
• IGD: MO-BMR is best in 3 cases (ZDT1–ZDT3); MO-BWR is best in ZDT4 and ZDT6.
• Spacing: MO-BWR is best in ZDT1 and ZDT2. MO-BMR is best in ZDT3 and ZDT4. NSGA-III is best in ZDT6.
• Hypervolume: MO-BMR is best in ZDT1–ZDT3; MO-BWR is best in ZDT4 and ZDT6.

MO-BMR shows the most consistent and balanced performance. MO-BWR is also strong in spacing and HV, particularly in ZDT4 and ZDT6. NSGA-III dominates GD, but underperforms in IGD and spacing.

It may be noted from the above discussion that the MO-BWR and MO-BMR algorithms could successfully attempt the standard multi-objective benchmark functions of ZDT group. Similarly, it may be shown that these algorithms can solve the other multi-objective benchmark functions. However, it has already been shown that the BWR and BMR algorithms have been successfully applied to various standard benchmark functions [28] and engineering design problems, and hence there may not be any further need to attempt the benchmark functions. The main aim of the paper is to attempt the multi- and many-objective optimization problems of the manufacturing processes.

It may be noted that the Pareto-optimal solutions are non-dominated type, and each solution is considered a good solution. However, if the decision-maker wishes to give different levels of importance to the objectives, he or she can do it by following a multi-attribute decision-making (MADM) method. Numerous MADM methods have been proposed in the literature. Recently, an MADM method, named BHARAT, has been proposed by Rao [29]. BHARAT is very simple to implement and provides a rational way of assigning weights of importance to the objectives and logically ranks the objectives.

The next sub-section describes BHARAT for selecting the best compromise Pareto-optimal solution out of the available non-dominated Pareto solutions.

3.2. Selection of Best Compromise Pareto-Optimal Solution Using BHARAT for Decision-Making

The Best Holistic Adaptable Ranking of Attributes Technique (BHARAT) was developed by Rao [29] in 2024. The method can be used in single or group decision-making scenarios. It prioritizes simplicity, clarity, and consistency over computational complexity. The steps of BHARAT for multi- or many-objective optimization problems are given below.

Step 1: Define the decision-making problem

• Identify the alternative Pareto-optimal solutions.
• Specify which objectives are beneficial (higher is better) or non-beneficial (lower is better).

Step 2: Assign weights to the objectives

• Rank the objectives based on importance.
• Convert ranks into weights using R-method.

Step 3: Normalize the data of the objectives for the alternative Pareto solutions

• For beneficial objectives (Equation (23)):

xji^normalized = xji/xi^best

(23)

• For non-beneficial objectives (Equation (24)):

xji^normalized = xi^best/xji

(24)

Step 5: Compute total score by (Equation (25))

• For each alternative, compute

$$\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{j}=\sum _{\mathrm{i}=1}^{\mathrm{m}}\mathrm{w}\mathrm{i}\cdot {\mathrm{x}\mathrm{j}\mathrm{i}}^{\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d}}$$

(25)

Step 6: Rank the alternative Pareto-optimal solutions

Higher total score ⇒ better alternative.

The following sections present the application of the BWR and BMR algorithms for single-objective optimization of manufacturing processes, as well as the use of MO-BWR and MO-BMR algorithms for addressing multi- and many-objective optimization problems. Additionally, BHARAT is employed to identify the best compromise solution from the set of Pareto-optimal solutions.

4. Results and Discussion on Application of Proposed Algorithms for the Optimization of Manufacturing Processes

Optimizing manufacturing processes is a high-dimensional, multi-objective, constrained, and nonlinear problem with inherent stochasticity and practical limitations. This complexity justifies the need for advanced metaheuristics, multi-objective frameworks, constraint-handling techniques, and decision-making tools. Hence, the proposed BWR and BMR algorithms are used for the optimization of manufacturing processes, and their applications are described in this section.

4.1. Single-Objective Optimization of Manufacturing Processes Using the BWR and BMR Algorithms

Now, to demonstrate the applicability of the proposed BWR and BMR algorithms for single-objective optimization of manufacturing processes, two case studies are considered.

4.1.1. Optimization of a Friction Stir Processing (FSP) Process

Friction Stir Processing (FSP) is a solid-state surface modification technique derived from friction stir welding. It is primarily used to refine microstructures, homogenize material properties, and incorporate reinforcements into metallic materials without melting them. Figure 9 shows the surface composite produced by the FSP. A rotating tool with a shoulder and pin is plunged into the surface of a metal workpiece. The tool rotates and traverses along the surface while applying downward force. The frictional heat generated softens the material around the pin, causing severe plastic deformation and dynamic recrystallization. As the tool moves, it stirs and refines the material structure, often producing ultrafine grains.

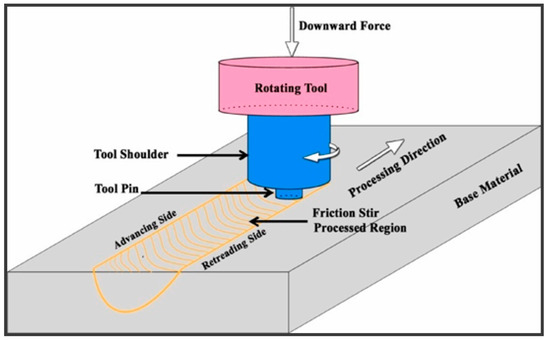
Figure 9. Surface composite produced using FSP [15].

Mohankumar et al. [16] conducted a multi-fidelity, machine learning-driven metaheuristic optimization of friction stir processing (FSP) aimed at improving the performance of hybrid surface composites (HSCs). The optimization of FSP parameters is crucial for reducing wear loss and enhancing the tribological characteristics of HSCs. In this study, a genetic algorithm (GA) was integrated with response surface methodology (RSM) to optimize the FSP process parameters for AZ31 magnesium alloy surface composites reinforced with yttria-stabilized zirconia (YSZ) and alumina (Al₂O₃) particles.

AZ31 magnesium alloy was selected as the base material for the friction stir processing (FSP) experiments, with dimensions of 120 × 70 × 5 mm. To produce the hybrid surface composite via friction stir processing, a combination of two ceramic reinforcements—alumina (Al₂O₃) and yttria-stabilized zirconia (YSZ)—was used. The axial down force applied during the process was controlled indirectly by precisely adjusting the tool’s plunge depth and vertical feed rate. The tool featured a 25 mm shoulder diameter, a 2.7 mm long pin, and a 5.7 mm pin diameter, ensuring efficient stirring of the material and uniform distribution of the reinforcement within the matrix.

A central composite design (CCD) was used, incorporating three key factors—tool rotational speed (TRS), tool traverse speed (TTS), and tool axial force (TAF)—each of which varied across five levels. Twenty experiments were conducted with different combinations of TRS, TTS, and TAF. The data thus obtained facilitated the development of a predictive empirical model for wear loss using the response surface methodology (RSM). Analysis of variance (ANOVA) confirmed the model’s statistical reliability. The genetic algorithm (GA) identified optimal FSP parameters as TRS = 1324.736 rpm, TTS = 123.676 mm/min, and TAF = 12.336 kN, resulting in a minimized wear loss of 2.953 mg. Equation (26) describes the mathematical model of wear loss. The bounds of the variables are described in Equation (27).

Minimize wear loss = f(x) = 44.79626 − 0.040091 × TRS − 0.11481 × TTS
−1.32800 × TAF + 0.000057 × TRS × TTS + 0.000316 × TRS × TAF − 0.001725 ×
TTS × TAF + 0.000011 × TRS² + 0.000245 × TTS² + 0.04551 × TAF²

(26)

The bounds of the variables are

900 rpm ≤ TRS ≤ 1500 rpm, 60 mm/min ≤ TTS ≤ 160 mm/min, and 6 kN ≤
TAF ≤ 16 kN.

(27)

The BWR and BMR algorithms are now applied to the friction stir processing to find the optimum values of the parameters (TRS, TTS, and TAF) that give the minimum wear loss. Mohankumar et al. [16] employed a genetic algorithm (GA) to determine the optimal parameters for this problem, using a population size of 100 and 150 iterations, resulting in a total of 15,000 function evaluations. In contrast, to demonstrate the efficiency and effectiveness of the proposed BMR and BWR algorithms in achieving comparable or superior results, the present study utilizes a smaller population size of 25 and 150 iterations, amounting to only 3750 function evaluations.

The optimum value of wear loss (i.e., f(x)) obtained by both the BMR and BWR algorithms is f(x) = 2.95332 mm with the optimal values of TRS = 1324.85 rpm, TTS = 124.02 mm/min, TAF = 12.408 kN. The value of wear loss obtained by the GA used by Mohankumar et al. [16] was f(x) = 2.95338 mm with the optimal values of TRS = 1324.736 rpm, TTS = 123.676 mm/min, and TAF = 12.336 kN. The optimum wear loss value obtained by the BMR and BWR algorithms is slightly better than that given by the GA. Furthermore, unlike the GA used by Mohankumar et al. [16], the BMR and BWR algorithms do not need to tune any algorithm-specific parameters and require a very small number of function evaluations to reach the optimal solution.

Figure 10 shows the convergence graph of the BWR and BMR algorithms. The convergence of the BWR algorithm is faster, and the global optimum value of f(x) = 2.95332 is achieved by both algorithms.

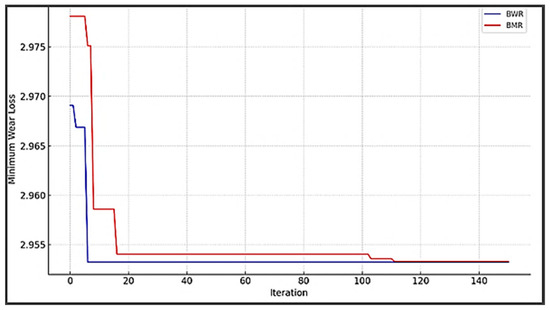
Figure 10. Convergence behavior of the BWR and BMR algorithms (FSP process).

Both the BMR and BWR algorithms consistently converged to wear loss value of 2.95332 mm, indicating good robustness and reliability. Final convergence curves of both algorithms are extremely close, indicating comparable efficiency. Multiple reruns of 30 of both BWR and BMR resulted in very similar optimal regions. This implies low randomness-induced variance and good repeatability. Both BWR and BMR are effective optimizers for this wear loss minimization problem.

Figure 11 shows the 3D response surface plots for wear loss. These 3D response surfaces illustrate how wear loss varies with changes in the process parameters (TRS, TTS, and TAF) based on the final iteration of the population.

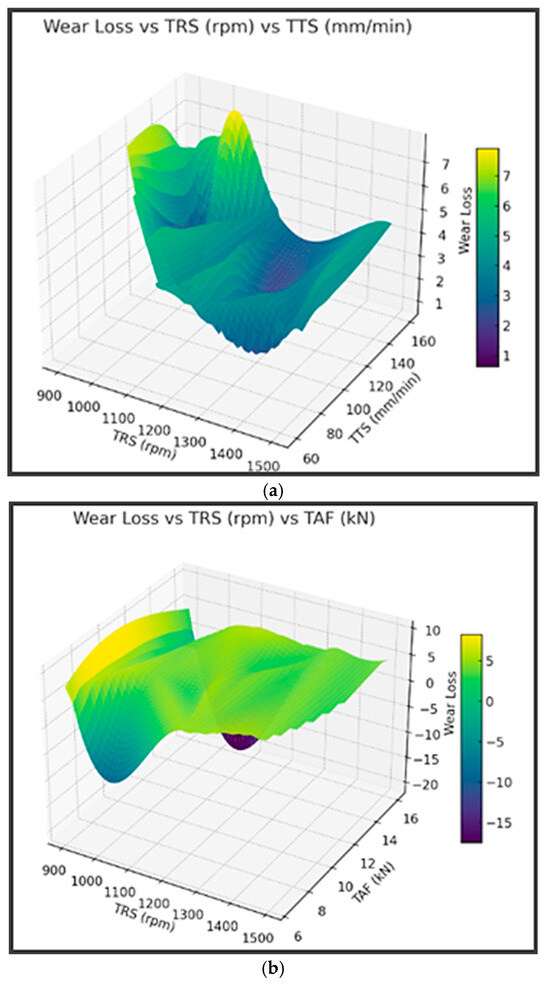
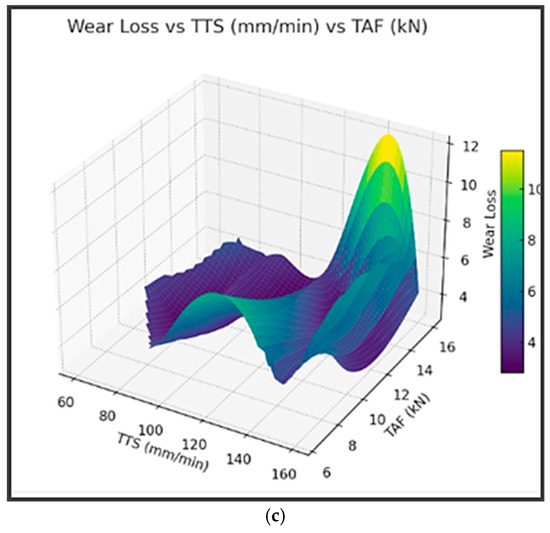
Figure 11. Response surface plots for wear loss in the FSP process (a) wear loss vs. TRS vs. TTS; (b) wear loss vs. TRS vs. TAF; and (c) wear loss vs. TTS vs. TAF.

It can be observed from Figure 11a that as tool rotational speed (TRS) increases and tool traverse speed (TTS) remains moderate to low, wear loss decreases. Very low TTS values result in higher wear. The optimal region appears to lie at high TRS (around 1400–1500 rpm) and moderate TTS (around 80–100 mm/min). A high spindle speed improves material mixing and bonding in FSP, while too fast a traverse speed may reduce heat input, increasing wear. Also, it can be observed from Figure 11b that the wear loss decreases with increasing TRS and a moderate level of TAF (Tool Axial Force). Very high TAF increases wear loss due to excessive pressure or heat. Wear loss is lowest at high TRS and TAF between 9–12 kN. Axial force must be optimized, not maximized. High TRS helps reduce wear, but excessive force causes damage due to overheating or material expulsion.

Furthermore, it can be observed from Figure 11c that wear loss is minimized in the mid-range of both TTS and TAF (TTS ≈ 80–100 mm/min, TAF ≈ 9–12 kN). Either too low or too high TTS/TAF increases wear loss. There is a sensitive interaction between tool movement speed and the downward force applied; both should be balanced to ensure uniform plastic flow and minimal material damage. Higher spindle speeds and TRS consistently reduce wear loss. Too low or too high values of TTS and TAF will increase wear loss. All three parameters (i.e., TRS, TTS, and TAF) must be carefully tuned in combination, rather than individually optimized.

4.1.2. Optimization of an Ultra-Precision Turning Process

Ultra-precision turning (UPT) plays a vital role in modern manufacturing by enabling the production of components with exceptional dimensional accuracy, superior surface finish, and tight tolerances. While it follows the principles of conventional turning, it is conducted under specialized conditions to achieve significantly higher precision. Though applicable to standard structural materials, there is a growing need to machine hardened steels like AISI D2. In this context, optimizing ultra-precision turning using cubic boron nitride (CBN) tools becomes increasingly important for achieving high-quality machining outcomes.

Tura et al. [5] studied the performance of ultra-precision CBN turning of AISI D2 and determined the optimal process parameters that yield the highest-quality results. Key process variables such as cutting speed (v_c), feed (f), and depth of cut (a_p) were systematically varied and tested to evaluate their effects on output responses, including surface roughness (R_a) and cutting force (F_c). A full factorial design of experiments was employed to capture the behavior of the process under various conditions. To identify the best combination of machining parameters, a hybrid optimization approach was implemented using genetic algorithm–response surface methodology (GA-RSM) alongside Taguchi–gray relational analysis (GRA). The results demonstrated that the combined GA-RSM and Taguchi-GRA successfully identified the optimal conditions, minimizing surface roughness and cutting forces.

The two objective functions—minimization of surface roughness (R_a) and minimization of cutting force (F_c)—are represented by Equations (28) and (29), respectively. The bounds of the variables are described by Equation (30).

Surface roughness (R_a) = 0.839 − 0.00258 × v_c − 6.72 × f −10.4 × a_p + 0.000010 × v_c × v_c
+ 49.20 × f × f + 40.8 × a_p × a_p + 0.0129 × v_c × f + 0.0164 × v_c × a_p + 82.5 × f × a_p −0.425
× v_c × f × a_p

(28)

Cutting force (F_c) = −5.2 + 0.026 × v_c + 357 × f + 695 × a_p + 0.000087 × v_c × v_c −
262 × f × f − 1667 × a_p × a_p − 1.77 × v_c × f −1.77 × v_c × a_p + 2141 × f × a_p + 19.6 × v_c ×
f × a_p

(29)

The bounds of the variables are

75 m/min ≤ v_c ≤ 175 m/min, 0.025 mm ≤ f ≤ 0.125 mm, and 0.06 mm ≤ a_p ≤ 0.1 mm

(30)

Now, the two objectives are individually solved using BWR and BMR algorithms, to demonstrate how these algorithms perform on individual objective functions. Tura et al. [5] used a population size of 1000 and 600 iterations (i.e., function evaluations = 1000 × 600 = 600,000). However, the present work used only a population size of 50 and 500 iterations (i.e., function evaluations = 50 × 500 = 25,000) to show the efficiency of the BWR and BMR algorithms.

First, the surface roughness (R_a) objective is solved individually. Figure 12 shows the convergence graph of the BWR and BMR algorithms for the surface roughness objective function of the ultra-precision turning process. The minimum value of surface roughness (R_a) obtained by both the algorithms is 0.2048 µm, corresponding to the optimal parameter values of v_c = 85.08 m/min, f = 0.025 mm, and a_p = 0.0961 mm.

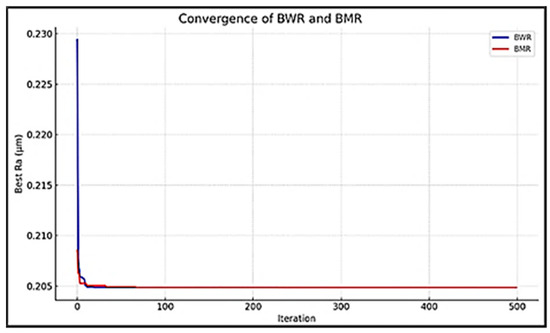
Figure 12. Convergence behavior of the BWR and BMR algorithms for the surface roughness objective function of the ultra-precision turning process.

The BWR algorithm shows a smooth and stable decrease in R_a across iterations. The intial convergence is modest, reflecting BWR’s explorative nature due to its use of the worst solution for diversity. It reaches the same final R_a (0.2048 µm), but with slightly more iterations than BMR. Its strengths are stability and exploration. The BMR algorithm shows faster improvement in the initial 100–200 iterations, due to the use of population mean rather than the worst solution. It quickly locks onto the optimal region and remains stable. It converges to 0.2048 µm, but in fewer iterations. Its strengths are speed and efficiency. However, it may be slightly more exploitative.

Next, the cutting force (F_c) objective is solved individually. Figure 13 shows the convergence graph of the BWR and BMR algorithms for F_c objective function of the ultra-precision turning process. The minimum value of F_c obtained by both the algorithms is 28.5022 N, corresponding to the optimal parameter values of v_c = 175 m/min, f = 0.025 mm, and a_p = 0.06 mm. Figure 11 shows the convergence behavior of the BWR and BMR algorithms for the surface roughness objective function of the ultra-precision turning process.

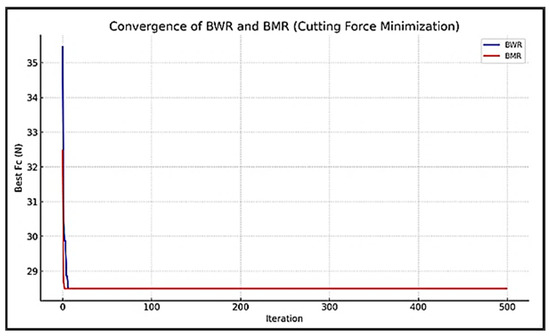
Figure 13. Convergence behavior of the BWR and BMR algorithms for cutting force objective function of the ultra-precision turning process.

The BWR algorithm shows a steady and consistent improvement in cutting force (F_c) over iterations. It is a moderate descent in the early iterations, reflecting balanced exploration and exploitation. It approaches the minimum F_c gradually, stabilizing after about 350 iterations, and exhibits robust and stable convergence, making it reliable for diverse search spaces. The BMR algorithm demonstrates a faster rate of improvement in the initial 100–200 iterations. By using the population mean instead of the worst individual, BMR accelerates convergence by focusing more on promising regions. It converges rapidly and levels off, reaching optimal F_c sooner than BWR.

In this second example of the optimization of an ultra-precision turning process, the two objectives (i.e., R_a and F_c) are optimized independently, considering them as individual single-objective functions. It can be observed that the values of the optimum variables (i.e., v_c, f, and a_p) to give a minimum value of R_a will not lead to the minimum vale of F_c. However, in real practice, both the objectives of R_a and F_c are to be considered simultaneously for optimization to find the optimal values of variables that will satisfy both objectives. Then that problem comes under the multi-objective optimization domain, and that will be attempted in the next section. The response surface plots will also be described considering both the objectives simultaneously. The results of MO-BWR and MO-BMR will be compared in the next section with those of Tura et al. [5] obtained using GA.

4.2. Multi-Objective Optimization of Manufacturing Processes Using MO-BWR and MO-BMR Algorithms

Now, to demonstrate the application potential of the proposed MO-BWR and MO-BMR algorithms, two examples of manufacturing processes are presented.

4.2.1. Multi-Objective Optimization of an Ultra-Precision Turning Process with 2 Objectives

In Section 4.1.2, two objectives of an ultra-precision turning process are presented. The two objectives are minimizing the surface roughness (R_a) and minimizing the cutting force (F_c). The two objective functions are expressed by Equations (28) and (29), and the bounds of the three input parameters v_c, f, and a_p are given by Equation (30). In Section 4.1.2, the two objectives were optimized individually. The minimum value of surface roughness (R_a) obtained by both the algorithms is 0.2048 µm, corresponding to the optimal parameter values of v_c = 85.08 m/min, f = 0.025 mm, and a_p = 0.0961 mm. The minimum value of F_c obtained by both the algorithms is 28.5022 N, corresponding to the optimal parameter values of v_c = 175 m/min, f = 0.025 mm, and a_p = 0.06 mm.

However, in actual practice, both the objective functions have to be attempted simultaneously to find the real optimum values of variables. For this purpose, the MO-BWR and MO-BMR algorithms are applied to find out the optimum values of parameters v_c, f, and a_p. Tura et al. [5] applied GA using a population size of 1000 and 600 iterations (i.e., function evaluations = 1000 × 600 = 600,000). However, the present work used only a population size of 50 and 500 iterations (i.e., function evaluations = 50 × 500 = 25,000) to show the efficiency of the MO-BWR and MO-BMR algorithms. Both MO-BWR and MO-BMR produced 50 non-dominated solutions.

Now, a composite Pareto front that includes all the best solutions of MO-BWR and MO-BWR is formed. This is a non-dominated frontier formed by merging both elite-boosted runs, giving the best trade-off solutions from both MO-BWR and MO-BMR strategies. Table 15 gives the set of 87 non-dominated optimal solutions given by the MO-BWR and MO-BMR algorithms (after removing all the duplicate solutions of the algorithms). Of the 87 non-dominated optimal solutions, 43 belong to MO-BWR and 44 belong to MO-BMR. The scores given in the last two columns are the weighted sums of the normalized objectives computed by summing up the products of multiplication of the normalized data of the objectives with the corresponding weights, as explained in Section 3.2.

Table 15. Eighty-seven non-dominated and deduplicated optimal solutions provided by the composite front (MO-BWR + MO-BMR) for the ultra-precision turning process.

S. No.	vc (m/min)	f (mm)	ap (mm)	Cutting Force (Fc)	Surface Roughness (Ra)	Algorithm	Fc Normalized	Ra Normalized	Scores (w1 = w2)	Scores *
1	82.5146	0.06869	0.084941	48.77625	0.205342	MO-BWR	0.584345	1	0.792173	0.833738
2	87.65448	0.043902	0.099332	47.03139	0.206413	MO-BWR	0.606025	0.994816	0.80042	0.8393
3	142.5948	0.03732	0.078693	32.45698	0.262183	MO-BWR	0.878152	0.783204	0.830678	0.821183
4	170.4245	0.09032	0.088298	40.95659	0.217929	MO-BWR	0.695912	0.942247	0.819079	0.843713
5	95.62711	0.087538	0.087968	30.4742	0.282167	MO-BWR	0.935289	0.727735	0.831512	0.810757
6	128.4696	0.037554	0.066472	33.17086	0.257288	MO-BWR	0.859253	0.798105	0.828679	0.822564
7	157.7395	0.079976	0.098504	34.72216	0.248188	MO-BWR	0.820864	0.827365	0.824115	0.824765
8	150.6527	0.037117	0.076792	31.96358	0.265644	MO-BWR	0.891708	0.773	0.832354	0.820483
9	110.2862	0.118883	0.099391	41.71953	0.216229	MO-BWR	0.683185	0.949654	0.81642	0.843066
10	106.5982	0.066563	0.063097	29.01916	0.30825	MO-BWR	0.982185	0.666156	0.824171	0.792568
11	148.9515	0.073364	0.074663	30.96368	0.275678	MO-BWR	0.920504	0.744863	0.832683	0.815119
12	160.7854	0.083216	0.095444	35.27169	0.244372	MO-BWR	0.808075	0.840287	0.824181	0.827402
13	123.568	0.053707	0.092931	34.29471	0.251533	MO-BWR	0.831095	0.816364	0.82373	0.822256
14	122.3099	0.07769	0.076815	42.29568	0.214273	MO-BWR	0.673879	0.958323	0.816101	0.844545
15	171.1275	0.051762	0.069634	36.53362	0.237197	MO-BWR	0.780163	0.865704	0.822934	0.831488
16	111.8499	0.118245	0.069415	42.84905	0.212657	MO-BWR	0.665176	0.965606	0.815391	0.845434
17	86.4442	0.091479	0.092805	36.09876	0.239526	MO-BWR	0.789561	0.857288	0.823424	0.830197
18	150.1235	0.027705	0.098648	36.99275	0.235162	MO-BWR	0.77048	0.873197	0.821838	0.83211
19	172.6602	0.051346	0.099421	43.39992	0.211171	MO-BWR	0.656733	0.972398	0.814566	0.846132
20	172.7808	0.093105	0.075713	46.0215	0.206804	MO-BWR	0.619323	0.992935	0.806129	0.84349
21	97.46171	0.077537	0.090784	31.17589	0.273196	MO-BWR	0.914238	0.751631	0.832934	0.816674
22	98.88902	0.045924	0.064763	39.71683	0.22343	MO-BWR	0.717635	0.919046	0.81834	0.838482
23	82.77052	0.082945	0.07797	38.52695	0.227795	MO-BWR	0.739798	0.901437	0.820618	0.836781
24	168.7994	0.122149	0.099617	28.79286	0.313298	MO-BWR	0.989904	0.655423	0.822664	0.789215
25	131.9472	0.085684	0.060651	29.77035	0.293457	MO-BWR	0.957402	0.699735	0.828568	0.802802
26	113.9237	0.09971	0.097957	33.96684	0.254308	MO-BWR	0.839118	0.807455	0.823286	0.82012
27	139.1268	0.040213	0.083598	29.49237	0.298589	MO-BWR	0.966425	0.68771	0.827068	0.799196
28	123.5313	0.080344	0.080491	44.30492	0.20906	MO-BWR	0.643319	0.98222	0.812769	0.84666
29	132.5555	0.064135	0.060767	30.23996	0.285661	MO-BWR	0.942534	0.718833	0.830684	0.808313
30	92.14646	0.054101	0.072166	37.37609	0.232907	MO-BWR	0.762578	0.881649	0.822113	0.834021
31	77.73176	0.090404	0.099483	33.51954	0.255033	MO-BWR	0.850315	0.80516	0.827737	0.823222
32	146.0835	0.084423	0.080193	29.44741	0.299456	MO-BWR	0.967901	0.685718	0.82681	0.798591
33	83.96344	0.061304	0.08945	37.6698	0.231471	MO-BWR	0.756632	0.887121	0.821876	0.834925
34	113.4191	0.082938	0.071663	45.59268	0.207014	MO-BWR	0.625148	0.991925	0.808537	0.845214
35	122.4451	0.049228	0.069718	39.14991	0.224807	MO-BWR	0.728027	0.913417	0.820722	0.839261
36	172.3149	0.042695	0.062543	31.58076	0.268994	MO-BWR	0.902517	0.763373	0.832945	0.819031
37	126.618	0.059577	0.098903	29.20329	0.304349	MO-BWR	0.975992	0.674694	0.825343	0.795213
38	135.978	0.109039	0.064395	35.77703	0.24201	MO-BWR	0.796661	0.848489	0.822575	0.827758
39	84.92093	0.055488	0.076715	30.11297	0.287844	MO-BWR	0.946508	0.713381	0.829945	0.806632
40	141.3104	0.025764	0.085915	31.58811	0.268924	MO-BWR	0.902307	0.763571	0.832939	0.819065
41	76.27219	0.069146	0.095886	29.20153	0.304385	MO-BWR	0.976051	0.674614	0.825332	0.795189
42	76.61654	0.035583	0.065652	29.82173	0.292552	MO-BWR	0.955752	0.701901	0.828827	0.803441
43	128.786	0.058334	0.089644	38.07831	0.229507	MO-BWR	0.748515	0.894711	0.821613	0.836233
44	89.92673	0.091467	0.090632	28.50217	0.320205	MO-BMR	1	0.641284	0.820642	0.78477
45	93.125	0.068078	0.073053	46.58091	0.206564	MO-BMR	0.611885	0.994086	0.802986	0.841206
46	94.59569	0.117306	0.089165	48.49687	0.206289	MO-BMR	0.587712	0.995411	0.791561	0.832331
47	169.8609	0.027899	0.093272	44.84957	0.20827	MO-BMR	0.635506	0.985941	0.810724	0.845767
48	79.0169	0.063944	0.07762	38.07141	0.229637	MO-BMR	0.74865	0.894203	0.821427	0.835982
49	113.324	0.114012	0.07555	29.78578	0.293184	MO-BMR	0.956905	0.700388	0.828647	0.802995
50	134.6341	0.100428	0.094615	38.82434	0.226513	MO-BMR	0.734132	0.906536	0.820334	0.837574
51	155.097	0.055781	0.092302	31.17347	0.273223	MO-BMR	0.914309	0.751556	0.832932	0.816657
52	81.0543	0.086283	0.094765	41.90427	0.2158	MO-BMR	0.680174	0.951542	0.815858	0.842995
53	139.0823	0.095378	0.086477	34.30859	0.250005	MO-BMR	0.830759	0.821355	0.826057	0.825117
54	83.16833	0.083512	0.078462	42.7116	0.213442	MO-BMR	0.667317	0.962052	0.814685	0.844158
55	137.9514	0.049391	0.078518	31.39718	0.270814	MO-BMR	0.907794	0.758243	0.833019	0.818063
56	122.6898	0.059028	0.083245	31.83915	0.266668	MO-BMR	0.895193	0.770032	0.832612	0.820096
57	141.8947	0.119346	0.067901	34.86518	0.247241	MO-BMR	0.817497	0.830535	0.824016	0.82532
58	99.6543	0.032536	0.075408	43.87067	0.20992	MO-BMR	0.649686	0.978196	0.813941	0.846792
59	101.6422	0.025705	0.061126	35.6438	0.242218	MO-BMR	0.799639	0.847759	0.823699	0.828511
60	168.5812	0.091376	0.062048	30.78513	0.27792	MO-BMR	0.925842	0.738854	0.832348	0.813649
61	97.46991	0.031347	0.084025	35.20114	0.24499	MO-BMR	0.809695	0.838167	0.823931	0.826778
62	169.12	0.117058	0.097332	32.95827	0.259613	MO-BMR	0.864796	0.790957	0.827877	0.820493
63	96.24646	0.040264	0.086851	37.21413	0.233675	MO-BMR	0.765897	0.878754	0.822325	0.833611
64	77.2859	0.118486	0.099235	34.07363	0.253171	MO-BMR	0.836488	0.811082	0.823785	0.821244
65	76.6078	0.123062	0.093838	30.13665	0.287284	MO-BMR	0.945764	0.714772	0.830268	0.807169
66	105.1484	0.072012	0.080786	33.38403	0.257032	MO-BMR	0.853767	0.798899	0.826333	0.820846
67	130.8655	0.049676	0.063571	29.1643	0.30516	MO-BMR	0.977297	0.672902	0.825099	0.79466
68	145.5078	0.101072	0.094603	32.5434	0.261673	MO-BMR	0.87582	0.78473	0.830275	0.821166
69	157.803	0.069365	0.08797	39.95646	0.221552	MO-BMR	0.713331	0.926837	0.820084	0.841435
70	83.13232	0.098434	0.082122	29.97337	0.289955	MO-BMR	0.950917	0.708188	0.829552	0.80528
71	119.8624	0.108749	0.071643	39.61857	0.223674	MO-BMR	0.719414	0.918043	0.818729	0.838591
72	86.86083	0.095021	0.097429	33.58461	0.254583	MO-BMR	0.848668	0.806584	0.827626	0.823418
73	163.5401	0.088529	0.082487	29.50355	0.298382	MO-BMR	0.966059	0.688186	0.827123	0.799335
74	172.5431	0.124975	0.085125	43.04325	0.211849	MO-BMR	0.662175	0.969288	0.815732	0.846443
75	140.3676	0.115604	0.097518	28.98734	0.308942	MO-BMR	0.983263	0.664663	0.823963	0.792103
76	141.1801	0.106489	0.069595	36.37571	0.238035	MO-BMR	0.78355	0.862658	0.823104	0.831015
77	143.599	0.102693	0.090062	41.49185	0.216971	MO-BMR	0.686934	0.946405	0.816669	0.842617
78	84.15055	0.122265	0.090752	43.55305	0.210698	MO-BMR	0.654424	0.974583	0.814503	0.846519
79	174.2642	0.07437	0.095702	36.81714	0.235944	MO-BMR	0.774155	0.870303	0.822229	0.831844
80	99.59887	0.058682	0.076477	30.37304	0.283644	MO-BMR	0.938404	0.723944	0.831174	0.809728
81	108.5955	0.056718	0.087075	40.4103	0.220071	MO-BMR	0.70532	0.933073	0.819196	0.841972
82	138.9037	0.056048	0.092796	40.60726	0.21916	MO-BMR	0.701899	0.936953	0.819426	0.842931
83	76.38247	0.074612	0.060667	28.72557	0.314854	MO-BMR	0.992223	0.652184	0.822203	0.7882
84	158.3087	0.076846	0.080552	28.67459	0.318921	MO-BMR	0.993987	0.643866	0.818926	0.783914
85	158.6905	0.101805	0.084081	28.88603	0.311185	MO-BMR	0.986711	0.659873	0.823292	0.790608
86	94.60775	0.048346	0.074215	29.46864	0.299045	MO-BMR	0.967204	0.68666	0.826932	0.798878
87	78.05427	0.046381	0.060139	32.10442	0.264559	MO-BMR	0.887796	0.776169	0.831982	0.82082

The row highlighted in red indicates the best compromise solution for equal weightages of F_c and R_a. * For a weightage of 0.4 to F_c and 0.6 to R_a. The row highlighted in blue indicates the best compromise solution for a weightage of 0.4 to F_c and 0.6 to R_a.

The graphs showing the Pareto fronts (i.e., non-dominated solutions) for the MO-BWR and MO-BMR algorithms are shown in Figure 14.

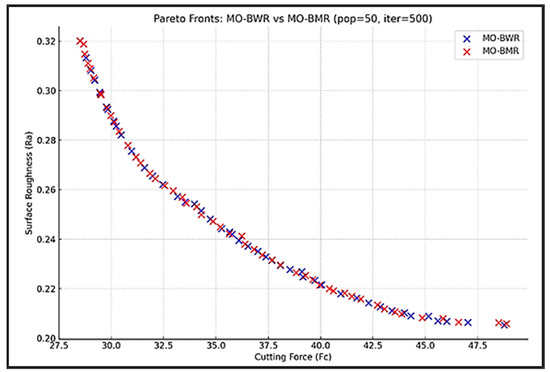
Figure 14. Pareto fronts obtained by MO-BWR and MO-BMR algorithms for the ultra-precision turning process.

It can be observed from Figure 14 that both MO-BWR and MO-BMR generate a wide spread of solutions, covering a diverse trade-off space between R_a and F_c. The MO-BWR front appears more populated toward low R_a regions, suggesting that it performs better in minimizing surface roughness. The MO-BMR front extends deeper into low F_c regions, indicating stronger performance in minimizing cutting force. MO-BWR solutions tend to cluster around high F_c but very low R_a—suitable for surface finish–critical applications. MO-BMR solutions tend to cluster around moderate R_a and low F_c—preferable for energy-efficient or tool-wear–sensitive scenarios.

Now, the composite Pareto front is considered for reference. The composite Pareto front includes all the best solutions of MO-BWR and MO-BWR. This is a non-dominated frontier formed by merging both elite-boosted runs, giving the best trade-off solutions from both the MO-BWR and MO-BMR strategies. Figure 15 shows the composite Pareto front and the Pareto fronts of MO-BWR and MO-BMR algorithms. However, the Pareto fronts of MO-BWR and MO-BMR algorithms are not visible, as they are completely covered by the composite front.

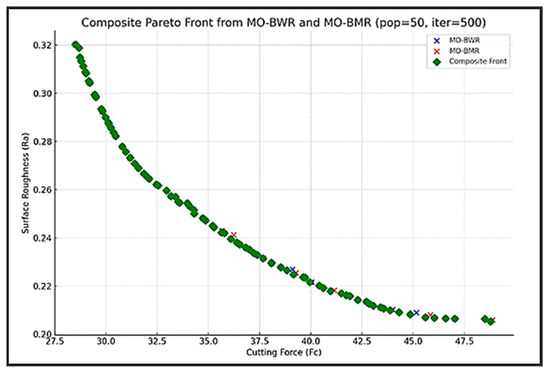
Figure 15. Pareto front obtained by using th composite front for the ultra-precision turning process.

The entire composite front (consisting of 87 unique solutions), after removing the duplicate solutions, is shared between MO-BWR and MO-BMR—they converged to the same set of non-dominated solutions.

The composite front formed from both MO-BWR and MO-BMR is necessary to capture all truly non-dominated trade-offs. The composite front offers the best trade-offs and flexibility. The focus is on balanced optimization.

Figure 16 shows the response surface plots for R_a and F_c in the ultra-precision turning process.

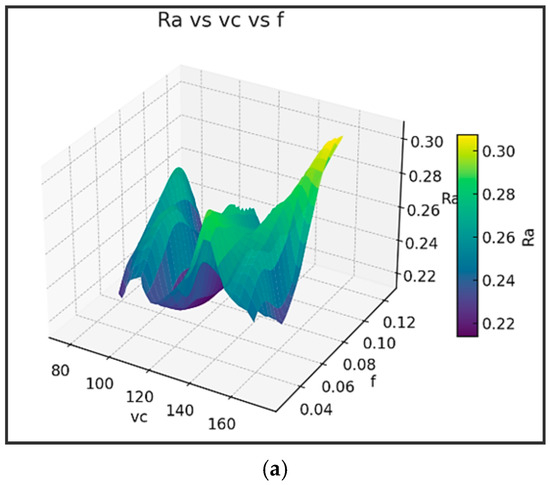
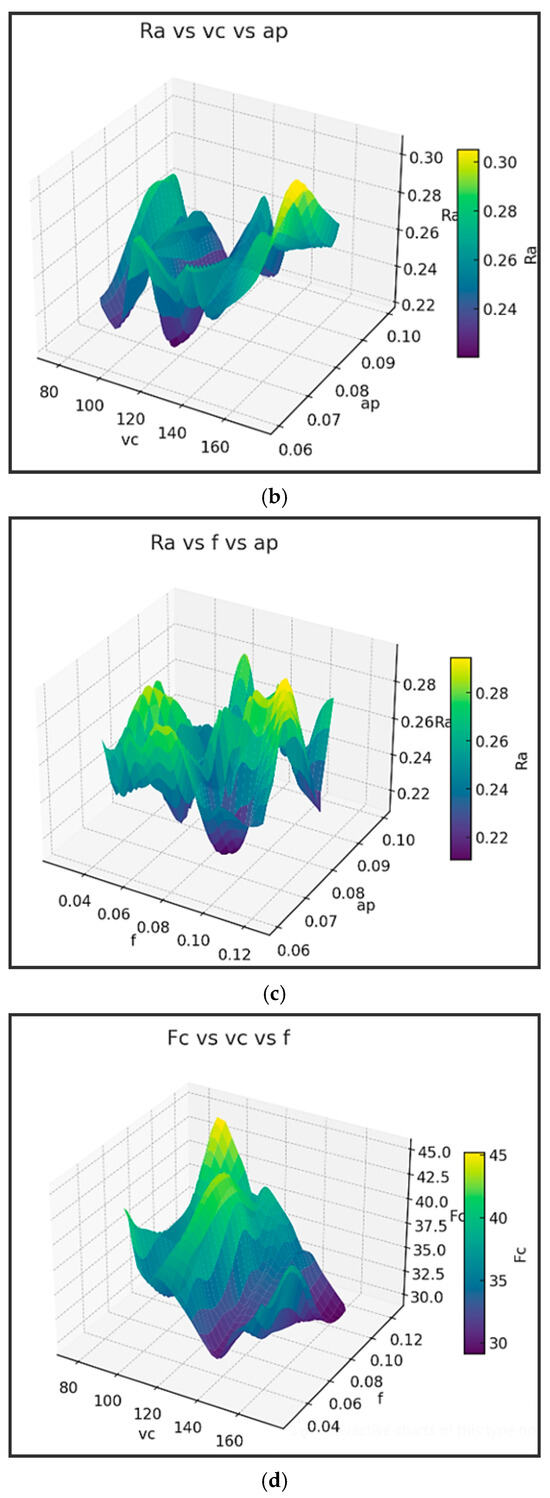
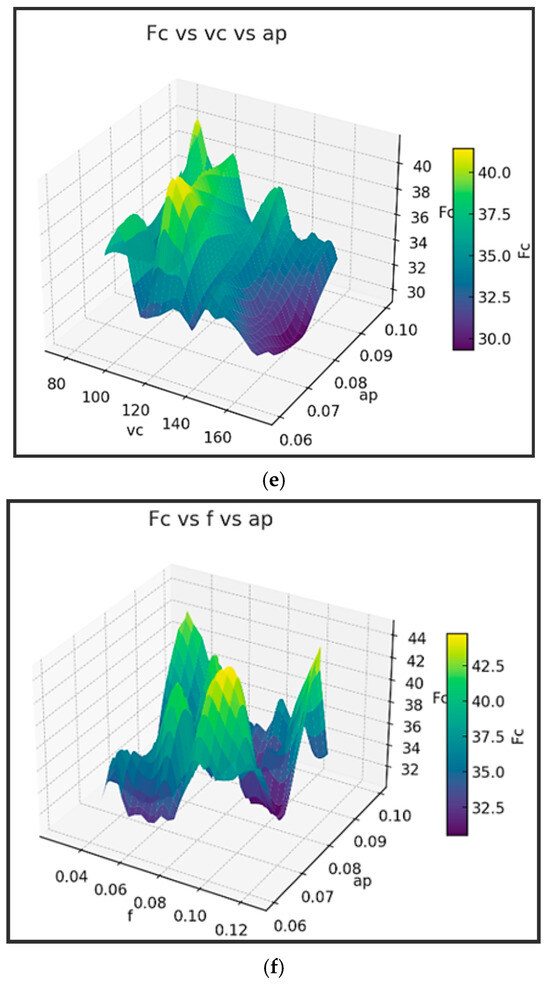
Figure 16. Response surface plots for R_a and F_c in the ultra-precision turning process (a) R_a vs. v_c vs. f; (b) R_a vs. v_c vs. a_p; (c) R_a vs f vs. a_p; (d) F_c vs. v_c vs. f; (e) F_c vs v_c vs a_p; and (f) F_c vs. f vs. a_p.

It can be observed from Figure 16a that R_a decreases with increasing vc (cutting speed), especially at a low feed. Low f (feed) is critical for achieving minimal R_a—even more influential than v_c. The surface is relatively steep along the f-axis, confirming that R_a is highly sensitive to feed. Figure 16b shows that a higher a_p (depth of cut) leads to lower Ra, particularly when combined with high v_c. The R_a surface is smooth and gently sloped along the v_c-axis, suggesting a moderate influence of cutting speed. The interaction between a_p and v_c can be exploited for surface finish improvement. Figure 16c shows that R_a is minimized when both f and a_p are small, especially when a_p is around 0.06–0.07 mm. The plot confirms a strong nonlinear interaction—a small increase in feed can sharply increase R_a, especially at a higher a_p.

Further, it can be observed from Figure 16d that F_c increases significantly with f, regardless of v_c. Higher v_c tends to slightly reduce F_c, but this effect is minor compared to the feed’s impact. The plot surface is nearly flat along v_c but sharply rises with f—again confirming feed is the most dominant factor. Figure 16e shows that a_p has a strong and direct influence on F_c—higher depth causes much higher cutting forces. F_c is minimized at low a_p and moderate-to-high v_c. Smoother gradients suggest a controllable interaction between v_c and a_p. Figure 16f shows that F_c spikes sharply with increasing f and a_p. It indicates a multiplicative effect: simultaneously increasing both parameters leads to a steep rise in F_c.

• The parameter v_c’s effect on R_a is moderate, slight on F_c, and optimal for both the objectives.
• The effect of f on R_a is very strong, and it is strong on F_c and to be kept low to minimize both the objectives.
• The effect of ap on R_a is moderate, and very strong on F_c, and low a_p is optimal for Fc and moderate a_p is optimal for R_a.

Choosing the Best Compromise Pareto-Optimal Solution from the Non-Dominated Solutions for the Ultra-Precision Turning Process

BHARAT is applied to find the best compromise Pareto-optimal solution out of the 87 non-dominated solutions of the composite front. The objective values of F_c and R_a are normalized and shown in Table 13. If the decision-maker assigns equal weightages to the objectives R_a and F_c (i.e., w_Ra = w_Fc = 0.5), then the scores (i.e., weighted sums) will be as shown in the last but one column of Table 13. For the equal weights of importance of the objectives, the optimal solution suggested is solution number 55 with optimal parameters of v_c = 137.9514 m/min, f = 0.049391 mm, and a_p = 0.078518 mm, giving an F_c of 31.39718 N and R_a of 0.270814 µm.

However, let the decision-maker assign a rank of 1 to R_a and 2 to Fc. Then, using BHARAT [28], a weightage of 0.6 is assigned to R_a and 0.4 to F_c. Application of these weights obtained by BHARAT to the normalized data of R_a and F_c leads to the scores, as shown in the last column of Table 13. From the scores given in the last column, the optimal solution suggested is solution number 58 with optimal parameters of v_c = 99.6543 m/min, f = 0.032536 mm, and a_p = 0.075408 mm, giving F_c of 43.87067 N and R_a of 0.20992 µm. Thus, based on the preferences of the decision-maker (or process planner).

The solutions provided by the MO-BWR and MO-BMR algorithms are compared with the solutions provided by Tura et al. [5] using the GA. It is surprising to note that Tura et al. [5] could obtain only 16 Pareto optimal solutions using the GA with a population size of 1000 and 600 iterations! The MO-BWR and MO-BMR algorithms provided many non-dominated solutions that are better than those provided by the GA [5]. The Pareto front given by GA [5] is shown in Figure 17.

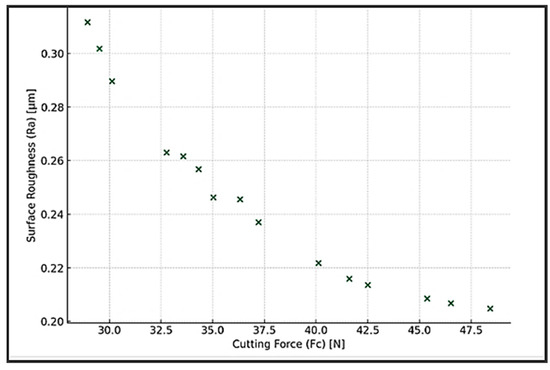
Figure 17. Pareto front obtained by using GA for the ultra-precision turning process.

Table 16 shows the performance metrics, which reveal that both MO-BWR and MO-BMR algorithms perform better than the GA of Tura et al. [5] and are equally capable of solving this problem. The Pareto front given by GA [5] is inferior to the fronts given by MO-BWR and MO-BMR in terms of GD, IGD, coverage, spacing, spread, and hypervolume.

Table 16. Performance metrics of MO-BWR, MO-BMR, and GA [5] with reference to the composite front for the ultra-precision turning process.

Algorithm	GD	IGD	Coverage	Spacing	Spread	Hypervolume
MO-BWR	0.00096	0.00548	0.4942	0.01494	0.649423	21.361
MO-BMR	0.00113	0.00513	0.5057	0.00816	0.614505	21.290
GA [5]	0.994	0.4707	0.1829	0.45580	0.77200	2.4205

Also, Tura et al. [5] applied grey relational analysis (GRA) method directly to the experimental data and suggested the optimal parameter values of v_c = 175 m/min, f = 0.025 mm, and a_p = 0.06 mm for the simultaneous optimization of R_a and F_c. However, that is not a correct judgment. Those optimal parameter values may give a minimum value of F_c as 28.5022 N, but substituting those values in the expression for R_a (i.e., Equation (25)) gives a high R_a value of 0.320205 µm. However, this set of non-dominated solutions (28.5022, 0.320205) is already included in solution no. 44 of the composite front of MO-BWR and MO-BMR given in Table 14. Moreover, giving equal weightages of 0.5 each to F_c and R_a in the present work (which was implicitly done by Tura et al. [5] in their GRA approach) does not choose solution no. 44 (i.e., F_c = 28.5022 N and R_a = 0.320205 µm) as the best compromise. It is considered one of the non-dominated solutions only. Solution no. 55, which offers F_c = 31.39718 N and R_a = 0.270814 µm, corresponding to the optimal parameter values of v_c = 137.9514 m/min, f = 0.049391 mm, and a_p = 0.078518 mm is more logical to consider as the best compromise Pareto-optimal solution considering F_c and R_a simultaneously.

It may be noted that in the GRA method used by Tura et al. [5], different distinguishing coefficient values yield selection of different alternative non-dominated solutions, and it becomes unclear which solution is to be considered finally. Furthermore, GRA involves a lot of computations. However, the proposed BHARAT is simple and takes into account the decision maker’s preferences to assign the weights to the attributes. The computational process used in BHARAT is simple and more convenient to evaluate and find the best compromise Pareto-optimal solution. The results of this investigation could help the decision-makers (i.e., process planners) on the shop floor to set the optimal input parameters to perform the ultra-precision turning process.

4.2.2. Multi-Objective Optimization of a Laser Powder Bed Fusion (LPBF) Process with 3-Objectives

Laser Powder Bed Fusion (LPBF) is an advanced additive manufacturing (AM) technology that utilizes lasers to produce intricate, high-performance parts. However, its layer-by-layer fabrication approach typically results in extended build times, high energy consumption, and increased CO₂ emissions. With the manufacturing sector increasingly prioritizing energy efficiency and environmental sustainability, minimizing the energy footprint of LPBF has become crucial. Nonetheless, there remains a scarcity of research dedicated to optimizing LPBF process parameters in a way that effectively balances energy usage with the quality of the fabricated components.

To address this, Zeng et al. [12] introduced a hybrid optimization framework that integrated Response Surface Methodology (RSM), Multi-Objective Particle Swarm Optimization (MOPSO), and the technique for order preference by similarity to the ideal solution (TOPSIS) method within a multi-attribute decision-making (MADM) approach. The goal was to determine an ideal set of process parameters—laser power (LP), scanning speed (SS), and hatching space (HS)—that could maximize relative density and surface finish while minimizing energy use. Specific energy consumption (SEC) was chosen as the metric to evaluate energy usage in LPBF operations. The study began with a central composite design (CCD) to structure the experiments and develop predictive models for SEC, surface roughness (R_a), and relative density (RD) using RSM. The influence of key process variables on each response was assessed using ANOVA and visualized through 3D surface plots to confirm model validity. Next, the MOPSO algorithm was employed to derive a set of Pareto-optimal solutions based on dominance principles. These solutions were then evaluated using the CRITIC (Criteria Importance Through Inter-criteria Correlation) method for objective weighting, and TOPSIS was applied to rank the solutions for optimality. The results indicated that all response models are highly reliable, with R² values exceeding 0.94.

The regression models for specific energy consumption (Equation (31)), surface roughness (Equation (32)), and relative density (Equation (33)) have been developed and are given below.

SEC = 317.216578 + 0.292832LP − 0.12473SS − 1585.474184HS − 0.000029LP × SS −
0.345833LP × HS + 0.399375SS × HS − 0.000322LP² + 0.000028SS² + 4557.88999HS²

(31)

R_a =289.96777 − 0.457769LP − 0.138148SS − 3384.98787HS − 0.000125LP × SS +
0.836188SS × HS + 0.001058LP² + 0.000046SS² + 14605.925994HS²

(32)

RD =69.509238 − 0.074212LP + 0.024394SS + 646.565648HS + 0.000017LP × SS −
0.20625SS × HS + 0.000108LP² − 0.000006SS² − 2601.997516HS²

(33)

The input parameter bounds for Laser Power (LP), Scanning Speed (SS), and Hatching Space (HS) are defined by Equation (34) as follows:

250 ≤ LP ≤ 310 (W), 1000 ≤ SS ≤ 1400 (mm/s), and 0.07 ≤ HS ≤ 0.09 (mm).

(34)

The objectives SEC and R_a are to be minimized and the objective RD is to be maximized. Zeng et al. [12] attempted to solve this multi-objective problem with 3 objectives using a MOPSO algorithm. The population size was taken as 200, and 500 to 3000 iterations were tried. However, to prove that the proposed MO-BWR and MO-BMR algorithms can solve this problem with fewer function evaluations, a population size of 50 and 500 iterations are used in the present work.

Table 17 gives the set of 86 non-dominated Pareto-optimal solutions given by the MO-BWR and MO-BMR algorithms (after removing all the duplicate solutions of the algorithms). Of the 86 non-dominated optimal solutions, 40 belong to MO-BWR and 46 belong to MO-BMR.

Table 17. Eighty-six non-dominated and deduplicated optimal solutions provided by the composite front (MO-BWR + MO-BMR) for the LPBF process.

S. No.	LP (W)	SS (mm/s)	HS (mm)	SEC (MJ/kg)	Ra (µm)	RD (%)	Algorithm
1	294.5688	1297.126	0.084856	183.3719	7.338862	98.48985	MO-BWR
2	298.0238	1392.765	0.08746	180.2786	9.979872	97.89908	MO-BWR
3	310	1400	0.09	179.621	11.25476	97.77915	MO-BWR
4	306.2874	1375.249	0.088762	180.4361	10.06246	97.98463	MO-BWR
5	291.0662	1273.775	0.083689	184.3564	6.831356	98.59859	MO-BWR
6	277.4228	1182.818	0.079141	188.661	6.199666	98.83672	MO-BWR
7	273.2119	1154.746	0.077737	190.1405	6.437013	98.85061	MO-BWR
8	296.4886	1333.049	0.085959	182.0979	8.198046	98.29372	MO-BWR
9	274.6762	1164.508	0.078225	189.618	6.331355	98.84897	MO-BWR
10	288.3128	1255.418	0.082771	185.1649	6.53145	98.67042	MO-BWR
11	282.499	1216.66	0.080833	186.9721	6.184623	98.7826	MO-BWR
12	286.1805	1340.507	0.084046	182.2562	8.017168	98.28101	MO-BWR
13	295.4339	1400	0.087518	180.0328	10.20202	97.81936	MO-BWR
14	278.6032	1190.688	0.079534	188.2591	6.169724	98.82778	MO-BWR
15	280.0524	1200.349	0.080017	187.7732	6.154879	98.81378	MO-BWR
16	288.5969	1257.312	0.082866	185.0801	6.55836	98.66357	MO-BWR
17	284.971	1255.12	0.082097	185.3203	6.506528	98.6689	MO-BWR
18	290.7518	1305.013	0.084251	183.2595	7.362046	98.45579	MO-BWR
19	296.2807	1333.054	0.085917	182.1062	8.187615	98.29425	MO-BWR
20	297.2659	1315.106	0.085755	182.6473	7.825797	98.39286	MO-BWR
21	293.2921	1288.614	0.084431	183.7251	7.137522	98.53174	MO-BWR
22	297.599	1317.327	0.085866	182.5599	7.891735	98.38008	MO-BWR
23	284.9665	1233.11	0.081655	186.1885	6.284345	98.74153	MO-BWR
24	284.1876	1321.752	0.083272	182.9445	7.57615	98.38481	MO-BWR
25	303.8837	1400	0.089688	179.5753	11.02432	97.71626	MO-BWR
26	280.811	1205.406	0.08027	187.5223	6.156738	98.80513	MO-BWR
27	282.8996	1309.695	0.082774	183.4037	7.331268	98.44564	MO-BWR
28	286.6495	1244.33	0.082217	185.6681	6.392532	98.70799	MO-BWR
29	300.8818	1339.212	0.086961	181.7218	8.609867	98.24473	MO-BWR
30	297.9618	1319.745	0.085987	182.4652	7.965002	98.36597	MO-BWR
31	302.1182	1351.74	0.087458	181.2885	9.029413	98.16178	MO-BWR
32	280.4331	1202.888	0.080144	187.647	6.154985	98.80955	MO-BWR
33	275.3356	1168.904	0.078445	189.3855	6.291824	98.84712	MO-BWR
34	302.4884	1349.922	0.087496	181.3274	9.006495	98.17227	MO-BWR
35	292.7606	1285.071	0.084254	183.874	7.059242	98.54842	MO-BWR
36	300.9154	1339.436	0.086972	181.7135	8.617856	98.24326	MO-BWR
37	308.7741	1400	0.09	179.5942	11.22792	97.75902	MO-BWR
38	289.0799	1260.532	0.083027	184.9366	6.606242	98.65162	MO-BWR
39	292.9929	1286.619	0.084331	183.8087	7.093061	98.54119	MO-BWR
40	278.8556	1192.371	0.079619	188.1738	6.165402	98.82558	MO-BWR
41	273.6923	1157.948	0.077897	189.9682	6.399636	98.85044	MO-BMR
42	307.3408	1394.759	0.089367	179.8644	10.80376	97.83411	MO-BMR
43	283.2342	1221.561	0.081078	186.7361	6.207013	98.77137	MO-BMR
44	295.9056	1400	0.088471	179.7365	10.53812	97.73029	MO-BMR
45	289.6617	1264.411	0.083221	184.765	6.667482	98.63674	MO-BMR
46	285.8275	1238.85	0.081943	185.9209	6.335625	98.72493	MO-BMR
47	277.6427	1184.285	0.079214	188.5857	6.192873	98.83522	MO-BMR
48	300.7437	1338.291	0.086915	181.7562	8.577159	98.25077	MO-BMR
49	290.9339	1272.893	0.083645	184.3946	6.814952	98.60232	MO-BMR
50	308.3067	1400	0.09	179.5838	11.21852	97.75144	MO-BMR
51	303.8491	1358.994	0.08795	181.0015	9.365628	98.10769	MO-BMR
52	302.3758	1400	0.089157	179.7038	10.80006	97.75064	MO-BMR
53	293.3393	1288.929	0.084446	183.7119	7.144636	98.53024	MO-BMR
54	285.3878	1235.919	0.081796	186.0572	6.308372	98.73356	MO-BMR
55	290.6889	1271.259	0.083563	184.4654	6.785097	98.60915	MO-BMR
56	308.1696	1387.797	0.08939	180.016	10.64711	97.88318	MO-BMR
57	296.1545	1313.792	0.085451	182.7595	7.731362	98.40582	MO-BMR
58	298.3207	1322.138	0.086107	182.3719	8.038978	98.35179	MO-BMR
59	294.2428	1294.952	0.084748	183.4614	7.285663	98.5008	MO-BMR
60	291.0793	1273.862	0.083693	184.3526	6.832987	98.59822	MO-BMR
61	297.8571	1319.047	0.085952	182.4924	7.943707	98.37006	MO-BMR
62	307.2901	1400	0.09	179.5605	11.19969	97.7351	MO-BMR
63	301.8463	1345.642	0.087282	181.4838	8.844421	98.20172	MO-BMR
64	285.6801	1237.868	0.081893	185.9665	6.326242	98.72786	MO-BMR
65	303.6311	1357.54	0.087877	181.0532	9.306663	98.11823	MO-BMR
66	286.569	1243.794	0.08219	185.6927	6.386617	98.70969	MO-BMR
67	296.2964	1308.642	0.085432	182.9044	7.641122	98.42906	MO-BMR
68	293.9236	1292.824	0.084641	183.5496	7.234764	98.51135	MO-BMR
69	296.3873	1309.249	0.085462	182.8802	7.657983	98.42572	MO-BMR
70	290.2456	1268.304	0.083415	184.5942	6.732857	98.62126	MO-BMR
71	276.3174	1175.449	0.078772	189.0425	6.242234	98.84308	MO-BMR
72	278.015	1186.767	0.079338	188.4587	6.18264	98.83251	MO-BMR
73	303.8583	1400	0.09	179.477	11.15224	97.68159	MO-BMR
74	276.7127	1178.085	0.078904	188.9055	6.225397	98.84103	MO-BMR
75	303.842	1358.947	0.087947	181.0032	9.363711	98.10803	MO-BMR
76	302.6819	1351.213	0.087561	181.2806	9.056286	98.16326	MO-BMR
77	301.7362	1344.908	0.087245	181.5108	8.817109	98.2067	MO-BMR
78	293.2867	1400	0.087936	179.8261	10.36886	97.74983	MO-BMR
79	285.1786	1400	0.084321	180.7664	9.446672	97.97881	MO-BMR
80	298.7719	1325.146	0.086257	182.2555	8.134097	98.33368	MO-BMR
81	287.6646	1251.098	0.082555	185.3597	6.473535	98.68558	MO-BMR
82	290.2232	1268.155	0.083408	184.6007	6.730279	98.62186	MO-BMR
83	294.4781	1394.104	0.086866	180.3396	9.838753	97.90036	MO-BMR
84	304.1035	1360.69	0.088034	180.9414	9.435141	98.09529	MO-BMR
85	306.2928	1375.285	0.088764	180.4349	10.06407	97.98434	MO-BMR
86	309.431	1396.207	0.08981	179.7424	11.06175	97.81206	MO-BMR

The Pareto fronts of the MO-BWR and MO-BMR algorithms and the composite front are shown in Figure 18.

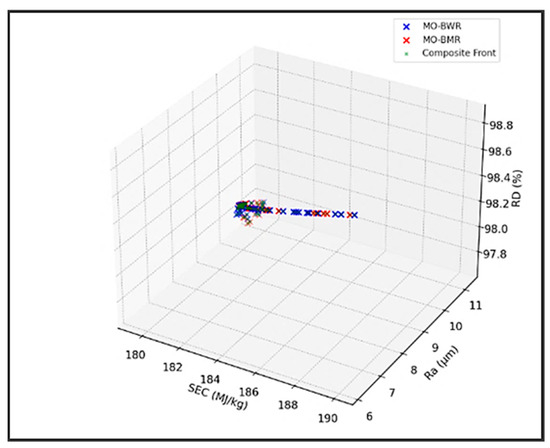
Figure 18. Pareto fronts obtained using the MO-BWR and MO-BMR algorithms for the LPBF process.

The performance metrics of the MO-BWR, MO-BMR, and MOPSO with reference to the composite front are given in Table 17. Zeng et al. [12] conducted various trials of MOPSO with a population size of 200 and 500, 1000, 1500, 2000, 2500, and 3000 iterations. The authors presented only two performance metrics (i.e., hypervolume and spacing). The better values obtained by them were for 1500 iterations. Hence, those values are kept in Table 18. However, it can be seen that the proposed MO-BWR and MO-BMR algorithms produced much better hypervolume and spacing values compared to the MOPSO algorithm used by Zeng et al. [12]. MO-BMR has better IGD and coverage than MO-BWR, showing closer proximity to the composite front. The MO-BWR achieves higher hypervolume, suggesting better extreme solutions. Composite front expectedly has ideal metrics: GD = 0, IGD = 0, Coverage = 1.

Table 18. Performance metrics of the MO-BWR, MO-BMR, and GA with reference to the composite front for the laser powder bed fusion (LPBF) process.

Algorithm	GD	IGD	Coverage	Spacing	Spread	Hypervolume
MO-BWR	0	0.01975	0.465	0.02345	0.7325	0.17313
MO-BMR	0	0.01263	0.535	0.02679	0.74999	0.14664
MOPSO	-	-	-	0.07981	-	0.11745

Thus, the proposed MO-BWR and MO-BMR algorithms are proved superior to MOPSO used by Zeng et al. [12] for the tri-objective optimization of LPBF process. These algorithms enable the effective selection of LPBF parameters that strike a balance between part quality and energy efficiency, offering a practical tool for engineers aiming to support sustainable advancement in additive manufacturing technologies.

Choosing the Best Compromise Pareto-Optimal Solution from the Non-Dominated Solutions for the LPBF Process

Zeng et al. [12] used the CRITIC method for computing the weights of the three objectives SEC, R_a, and RD. The weights thus obtained were used in the TOPSIS method to choose the best compromise Pareto-optimal solution out of the 200 solutions obtained by them. The authors reported the optimal parameters as follows: LP of 300.8W, SS of 1353.9 mm/s, and HS of 0.085mm, which leads to an SEC of 180.75 MJ/kg, R_a of 8.341 um, and RD of 98.65%. Zeng et al. [12] did not mention the numerical values of those weights anywhere in their paper. Furthermore, they did not provide all 200 MOPSO solutions to verify the optimal solution suggested by them. For fair comparison in multi-attribute decision-making (MADM), the same weights are to be used by the other MADM methods, such as BHARAT. However, as the 200 solutions data of MOPSO and the CRITIC weights are not available in Zeng et al. [12], and hence, a comparison is not possible with the CRITIC-TOPSIS method used by Zeng et al. [12].

Now, BHARAT is applied to find the best compromise Pareto-optimal solution out of the 87 non-dominated solutions of the composite front obtained by the combination of MO-BWR and MO-BMR. The objective values of SEC, R_a, and RD are normalized and shown in Table 18. If the decision-maker assigns equal weightages to the objectives SEC, R_a, and RDR (i.e., w_SEC = w_Ra = w_RD) then an average rank of 2 is assigned to each of SEC, R_a and RD (i.e., average of 1, 2, and 3 ranks). Then, using the table given in [28], BHARAT assigns an average weightage of 0.33333 to each of the three objectives. The scores (i.e., weighted sums) are shown in the last but one column of Table 19.

Table 19. LPBF process input parameters, normalized data of the objectives, and the scores of the non-dominated solutions.

Soln. No.	LP (W)	SS (mm/s)	HS (mm)	SEC Normalized	Ra Normalized	RD Normalized	Scores (Equal Weights)	Scores *
1	294.5688	1297.126	0.084856	0.97876	0.838669	0.99635	0.937917	0.940937
2	298.0238	1392.765	0.08746	0.995554	0.616729	0.990374	0.867544	0.880248
3	310	1400	0.09	0.999198	0.546869	0.989161	0.845068	0.860568
4	306.2874	1375.249	0.088762	0.994685	0.611667	0.99124	0.865855	0.878545
5	291.0662	1273.775	0.083689	0.973533	0.900975	0.99745	0.95731	0.9576
6	277.4228	1182.818	0.079141	0.95132	0.992776	0.999859	0.981309	0.975788
7	273.2119	1154.746	0.077737	0.943918	0.95617	1	0.966686	0.961458
8	296.4886	1333.049	0.085959	0.985607	0.750774	0.994366	0.91024	0.917086
9	274.6762	1164.508	0.078225	0.946519	0.972127	0.999983	0.972867	0.967433
10	288.3128	1255.418	0.082771	0.969282	0.942345	0.998177	0.969925	0.968311
11	282.499	1216.66	0.080833	0.959913	0.995191	0.999312	0.984795	0.980263
12	286.1805	1340.507	0.084046	0.984751	0.767712	0.994238	0.915558	0.921766
13	295.4339	1400	0.087518	0.996913	0.6033	0.989568	0.863252	0.876621
14	278.6032	1190.688	0.079534	0.953351	0.997594	0.999769	0.983561	0.978133
15	280.0524	1200.349	0.080017	0.955818	1	0.999627	0.985139	0.979938
16	288.5969	1257.312	0.082866	0.969726	0.938478	0.998108	0.968761	0.967331
17	284.971	1255.12	0.082097	0.968469	0.945954	0.998162	0.970852	0.969026
18	290.7518	1305.013	0.084251	0.97936	0.836028	0.996006	0.937122	0.940329
19	296.2807	1333.054	0.085917	0.985562	0.75173	0.994372	0.910546	0.917355
20	297.2659	1315.106	0.085755	0.982643	0.786486	0.995369	0.92149	0.926743
21	293.2921	1288.614	0.084431	0.976878	0.862327	0.996774	0.945317	0.947313
22	297.599	1317.327	0.085866	0.983113	0.779915	0.99524	0.919413	0.924946
23	284.9665	1233.11	0.081655	0.963953	0.979399	0.998897	0.98074	0.977233
24	284.1876	1321.752	0.083272	0.981046	0.812402	0.995288	0.929569	0.933802
25	303.8837	1400	0.089688	0.999453	0.5583	0.988525	0.848751	0.863966
26	280.811	1205.406	0.08027	0.957097	0.999698	0.99954	0.985435	0.980403
27	282.8996	1309.695	0.082774	0.97859	0.839538	0.995903	0.938001	0.941012
28	286.6495	1244.33	0.082217	0.966655	0.962823	0.998557	0.976002	0.973382
29	300.8818	1339.212	0.086961	0.987647	0.714863	0.993871	0.898785	0.907076
30	297.9618	1319.745	0.085987	0.983623	0.77274	0.995097	0.917144	0.922982
31	302.1182	1351.74	0.087458	0.990008	0.681648	0.993032	0.88822	0.897938
32	280.4331	1202.888	0.080144	0.956461	0.999983	0.999585	0.985333	0.980213
33	275.3356	1168.904	0.078445	0.947681	0.978234	0.999965	0.975284	0.969792
34	302.4884	1349.922	0.087496	0.989795	0.683382	0.993138	0.888763	0.898391
35	292.7606	1285.071	0.084254	0.976087	0.87189	0.996943	0.948297	0.949875
36	300.9154	1339.436	0.086972	0.987692	0.714201	0.993856	0.898574	0.906894
37	308.7741	1400	0.09	0.999347	0.548176	0.988957	0.845485	0.860979
38	289.0799	1260.532	0.083027	0.970479	0.931676	0.997987	0.966704	0.965594
39	292.9929	1286.619	0.084331	0.976434	0.867732	0.99687	0.947002	0.948762
40	278.8556	1192.371	0.079619	0.953783	0.998293	0.999747	0.983931	0.978534
41	273.6923	1157.948	0.077897	0.944774	0.961755	0.999998	0.968833	0.963526
42	307.3408	1394.759	0.089367	0.997846	0.569698	0.989717	0.852412	0.866966
43	283.2342	1221.561	0.081078	0.961126	0.991601	0.999198	0.983965	0.979703
44	295.9056	1400	0.088471	0.998556	0.584059	0.988667	0.857085	0.87135
45	289.6617	1264.411	0.083221	0.97138	0.923119	0.997836	0.964102	0.963388
46	285.8275	1238.85	0.081943	0.965341	0.971471	0.998729	0.978504	0.975433
47	277.6427	1184.285	0.079214	0.9517	0.993865	0.999844	0.981793	0.976283
48	300.7437	1338.291	0.086915	0.98746	0.717589	0.993932	0.899651	0.907828
49	290.9339	1272.893	0.083645	0.973331	0.903143	0.997488	0.957978	0.958171
50	308.3067	1400	0.09	0.999405	0.548636	0.98888	0.845632	0.861124
51	303.8491	1358.994	0.08795	0.991577	0.657177	0.992484	0.880404	0.891147
52	302.3758	1400	0.089157	0.998738	0.569893	0.988872	0.852493	0.867219
53	293.3393	1288.929	0.084446	0.976948	0.861469	0.996759	0.945049	0.947082
54	285.3878	1235.919	0.081796	0.964633	0.975668	0.998816	0.979696	0.976398
55	290.6889	1271.259	0.083563	0.972958	0.907117	0.997557	0.959201	0.959216
56	308.1696	1387.797	0.08939	0.997006	0.57808	0.990213	0.855091	0.869231
57	296.1545	1313.792	0.085451	0.982039	0.796092	0.9955	0.924535	0.929394
58	298.3207	1322.138	0.086107	0.984126	0.76563	0.994954	0.914894	0.921033
59	294.2428	1294.952	0.084748	0.978282	0.844793	0.996461	0.939836	0.942592
60	291.0793	1273.862	0.083693	0.973553	0.90076	0.997447	0.957244	0.957544
61	297.8571	1319.047	0.085952	0.983477	0.774812	0.995139	0.9178	0.923549
62	307.2901	1400	0.09	0.999535	0.549558	0.988715	0.845928	0.861419
63	301.8463	1345.642	0.087282	0.988942	0.695905	0.993436	0.892752	0.901848
64	285.6801	1237.868	0.081893	0.965104	0.972912	0.998758	0.978915	0.975767
65	303.6311	1357.54	0.087877	0.991294	0.661341	0.992591	0.881733	0.892299
66	286.569	1243.794	0.08219	0.966527	0.963715	0.998574	0.976262	0.973596
67	296.2964	1308.642	0.085432	0.981261	0.805494	0.995735	0.927488	0.93193
68	293.9236	1292.824	0.084641	0.977812	0.850737	0.996568	0.941696	0.944195
69	296.3873	1309.249	0.085462	0.981391	0.803721	0.995702	0.926929	0.931447
70	290.2456	1268.304	0.083415	0.972279	0.914156	0.99768	0.961362	0.961058
71	276.3174	1175.449	0.078772	0.9494	0.986006	0.999924	0.978434	0.972898
72	278.015	1186.767	0.079338	0.952341	0.99551	0.999817	0.982546	0.977061
73	303.8583	1400	0.09	1	0.551896	0.988174	0.846682	0.8622
74	276.7127	1178.085	0.078904	0.950089	0.988673	0.999903	0.979545	0.974007
75	303.842	1358.947	0.087947	0.991568	0.657312	0.992488	0.880447	0.891184
76	302.6819	1351.213	0.087561	0.990051	0.679625	0.993047	0.887565	0.897353
77	301.7362	1344.908	0.087245	0.988795	0.698061	0.993486	0.893438	0.902443
78	293.2867	1400	0.087936	0.998059	0.593593	0.988864	0.860163	0.874043
79	285.1786	1400	0.084321	0.992867	0.651539	0.991181	0.87852	0.889711
80	298.7719	1325.146	0.086257	0.984755	0.756676	0.994771	0.912058	0.918577
81	287.6646	1251.098	0.082555	0.968263	0.950776	0.998331	0.972447	0.970426
82	290.2232	1268.155	0.083408	0.972244	0.914506	0.997686	0.961469	0.961149
83	294.4781	1394.104	0.086866	0.995217	0.625575	0.990387	0.870384	0.882762
84	304.1035	1360.69	0.088034	0.991907	0.652336	0.992359	0.878858	0.889808
85	306.2928	1375.285	0.088764	0.994691	0.61157	0.991237	0.865824	0.878518
86	309.431	1396.207	0.08981	0.998523	0.556411	0.989494	0.848134	0.863217

The row highlighted in red indicates the best compromise solution. * For a weightage of 0.452 to SEC, 0.301 to R_a, and 0.247 to RD.

For the equal weights of importance of the three objectives, solution number 26 with optimal parameters of LP = 280.811 W, SS = 1205.406 mm/s, and HS = 0.08027 mm gave an SEC of 187.5223 MJ/kg, R_a of 6.156738 µm, and RD of 98.80513%. This optimal solution is much better than that proposed by Zeng et al. [12] using the CRITIC-TOPSIS method in terms of R_a and RD objectives of the LPBF process.

Now, to demonstrate further, using BHARAT, let the decision-maker assign a rank of 1 to SEC, 2 to R_a, and 3 to RD. Then, using BHARAT [29], a weightage of 0.452 is assigned to SEC, a weightage of 0.301 is assigned to Ra, and 0.247 is assigned to RD. Application of these weights obtained by BHARAT to the normalized data of SEC, R_a, and RD leads to the scores, as shown in the last column of Table 18. From the scores given in the last column, solution number 26 with optimal parameters of LP = 280.811 W, SS = 1205.406 mm/s, and HS = 0.08027 mm giving SEC of 187.5223 MJ/kg, R_a of 6.156738 µm, and RD of 98.80513% is suggested as the best compromise Pareto-optimal solution. This is the same as that obtained by assigning equal weights to the objectives in this particular example.

Zeng et al. [12] applied the CRITIC method to determine the objective weights for three objectives and subsequently used these weights within the TOPSIS framework to identify the best compromise solution. However, it is important to note that the CRITIC method derives weights solely from the objective data without incorporating the preferences of decision-makers. As a result, evaluating and ranking alternative non-dominated solutions using such data-driven weights may lack practical relevance, since the real-world importance of objectives—reflected in the decision-maker’s judgments—is not considered [29]. Additionally, the TOPSIS method involves complex computations that become increasingly cumbersome, with a larger number of objectives and non-dominated alternatives. Moreover, the rankings produced by TOPSIS can vary depending on the normalization technique employed. In contrast, the proposed BHARAT is straightforward, explicitly incorporates decision-maker preferences in assigning attribute weights, and utilizes a simple normalization process, making it more practical and user-friendly for evaluating and identifying the best solution.

4.3. Many-Objective Optimization of Wire Arc Additive Manufacturing (WAAM) Process with 9 Objectives Using MO-BWR and MO-BMR Algorithms

To showcase the broader applicability of the MO-BWR and MO-BMR algorithms in addressing many-objective optimization problems within manufacturing processes, a case study is presented involving the optimization of shape and performance in wire arc additive manufacturing (WAAM) with in-situ rolling of Ti–6Al–4V ELI (Extra Low Interstitial) alloy. Additive manufacturing (AM) offers a promising alternative, using energy sources like lasers, electron beams, or electric arcs, with powder or wire feedstock, to fabricate complex, high-performance metal parts suitable for aerospace applications [13]. Among AM methods, Wire Arc Additive Manufacturing (WAAM) stands out for its high deposition rates, cost-effectiveness, and ability to produce dense components—advantages that make it a strong complement to laser and electron beam methods.

Fu et al. [13] advanced the study by considering a wider range of process parameters and simultaneously optimizing multiple performance metrics, including hardness and grain size. Figure 19 presents a schematic of the WAAM setup for titanium alloy, incorporating integrated in situ rolling. The process was executed on a three-axis motion platform using an EWM Tetrix 551 DC TIG welding system following a predefined toolpath. During deposition, the roller moved synchronously with the welding torch, applying pressure to each layer as it was deposited. The operation took place within a sealed chamber filled with high-purity argon (99.999%), maintaining an oxygen concentration below 100 ppm and water vapor content under 20 ppm to ensure an inert environment. The substrate was a hot-rolled and mill-annealed Ti–6Al–4V plate with dimensions of 150 mm × 20 mm × 11 mm. To facilitate deposition, an electromagnetic coil positioned beneath the clamping plate was used to preheat the substrate. Before the building, the substrate surface was mechanically ground to remove oxide layers and rust, followed by ethanol cleaning for degreasing. A standardized coordinate system was used to define orientation: X-axis for deposition direction, Y-axis for overlap, and Z-axis for build height. Figure 20 demonstrates the result—a well-formed, smooth, multi-pass, multi-layer deposition.

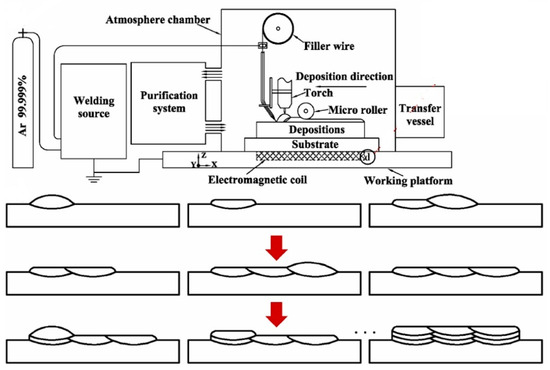
Figure 19. WAAM process with in situ rolling [13]. Reproduced with permission from Elsevier.

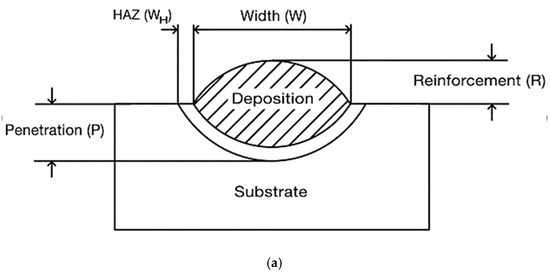
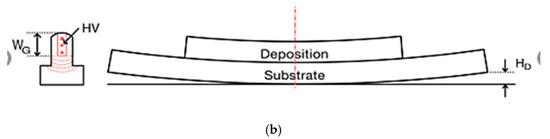
Figure 20. (a) Measurement of geometric features based on a single-pass, six-layer deposition, and (b) measurement of grain size, hardness, and substrate distortion based on the same configuration [13]. Reproduced with permission from Elsevier.

Figure 20a shows the measurement of geometric features based on a single-pass, six-layer deposition and Figure 20a shows the measurement of grain size, hardness, and substrate distortion based on the same single-pass, six-layer configuration [13].

Fu et al. [13] determined the parameter ranges determined through iterative experimentation, followed by the design of an experimental matrix using response surface methodology (RSM) to reduce the need for extensive numerical simulations. Once the response data were collected through precise measurement techniques, predictive models for the parameters were developed. Multi-objective optimization was then performed, taking into account both the forming efficiency and the requirements of the subsequent in situ rolling process. Additionally, strategies for offset and deformation control were comprehensively integrated to optimize both the geometry and the mechanical properties of Ti–6Al–4V ELI components produced via WAAM with in situ rolling.

The process parameters considered were wire feed rate (w) varying from 2 to 3 m/min, travelling speed (v) varying from 100 to 300 mm/min, current (I) varying from 150 to 210 A, and interlayer temperature (T) varying from 40 to 180 °C. The 9 objectives (i.e., output parameters) were width (W) in mm, reinforcement (R) in mm, the W/R ratio, penetration (P) in mm, substrate distortion (HD) in mm, width of heat-affected zone (WH) in mm, interlayer waiting time (t) in minutes, average grain size (WG) in mm, and Vickers hardness (HV). The following RSM models (Equations (35)–(43)) were developed by conducting 27 experiments for W, R, W/R, P, HD, WH, t, WG, and HV, respectively.

Maximize W = 5.45218 − 7.43333w − 0.0322589v + 0.170628I − 0.0189683T +
0.000057417ν² − 0.000517589I² + 0.0433333wI − 0.000151111vI + 0.0000861904νT

(35)

Maximize R = 8.29110 + 0.614342w − 0.0230509ν − 0.0478277I + 0.00294998T +
0.0000322826ν² + 0.0000910714I² + 0.0000306958νI − 0.0000154689νT

(36)

Maximize W/R = −0.942386 − 1.46253w + 0.0134285v + 0.0509107I − 0.0126195T −
0.0000472198ν² + 0.0000640758νT

(37)

Minimize P = 10.4437 − 4.42714w + 0.00864167v − 0.0514444I − 0.026381T +
0.621667w² + 0.0000117917v² + 0.000262963I² + 0.0114286wT − 0.0000991667νI

(38)

Minimize HD = 2.45044 + 0.105w − 0.000756667ν − 0.0139306I − 0.0026131T −
0.0000144833ν² + 0.00005νI

(39)

Minimize WH = −10.6536 + 2.82048w+0.01065v + 0.0754167I + 0.0114728T−
0.256667w² − 0.000103241I² + 0.0000330782T² − 0.0063333wI − 0.00642857wT−
0.0000625vI

(40)

Minimize t = −14.238 − 0.140705ν + 0.331506I + 0.0514755T + 0.000260673ν² +
0.000997212T² − 0.00202897IT

(41)

Minimize WG = 18.275 − 3.29283w − 0.0230842v − 0.115857I + 0.0000268647v² +
0.000227847I² + 0.00336028wv + 0.0152783wI

(42)

Maximize HV = 261.29 − 102.514w − 0.0285042v + 1.61902I + 0.5885T − 0.00038565ν² −
0.00737986I² − 0.00101366T² + 0.475wI + 0.130357wT + 0.00141667vI − 0.00376983IT

(43)

Fu et al. [13] reported that the wire feed rate (w) had the most significant impact on bead width (W) and reinforcement (R); the travel speed (v) most strongly influenced weld geometry (WG); the current (I) had the greatest effect on penetration (P); and the interlayer temperature (T) primarily affected interlayer waiting time (t). Optimization was performed using the response optimizer in Minitab 16, which yielded the optimal parameter settings as w = 2.5 m/min, v = 187 mm/min, I = 178 A, and T = 93 °C.

The MO-BWR and MO-BMR algorithms are now applied to this many-objective problem. A population size of 25 and 1000 iterations are considered for each of the MO-BWR and MO-BMR algorithms. After removing duplicate solutions, a composite front consisting of 45 non-dominated Pareto solutions is produced, as shown in Table 20. The last column indicates by which algorithm that particular solution is obtained.

Table 20. Non-dominated solutions of the composite Pareto front for the WAAM process.

Sol. No.	w (m/min)	v (mm/min)	I (A)	T (°C)	W (mm)	R (mm)	W/R	HD (mm)	P (mm)	WH (mm)	t (min)	WG (mm)	HV	Algorithm
1	2.818703	300	210	180	10.36607	1.614854	6.593775	0.970123	2.15361	1.925674	1.507523	2.089273	310.7585	MO-BWR
2	3	300	197.2258	177.4123	10.08171	1.750182	5.661189	0.98226	2.028551	1.760866	1.918132	1.965956	317.5822	MO-BWR
3	2.303987	264.5601	190.9868	114.1133	9.38862	1.47578	6.153255	1.046083	1.405539	2.042564	4.735318	1.416462	317.2538	MO-BWR
4	2.813185	300	210	129.841	10.01133	1.696268	6.270632	1.100614	1.857963	1.749381	4.799513	2.084176	318.1942	MO-BWR
5	2.561381	219.7272	160.8703	116.8477	8.661273	2.053726	4.34293	1.074895	1.012806	1.73674	2.25096	1.510778	312.1739	MO-BWR
6	2.745718	235.4119	176.1238	75.89464	9.416863	1.962127	4.73993	1.179217	1.026767	1.810543	8.000353	1.511253	312.0007	MO-BWR
7	3	300	210	179.294	10.66337	1.727427	6.32396	0.991004	2.374163	1.712472	1.519041	2.256737	314.6359	MO-BWR
8	2.748172	243.8514	165.8206	176.3616	8.632016	1.947594	4.477126	0.944204	1.357402	1.946123	2.680961	1.461855	314.1654	MO-BWR
9	2.314259	245.0643	162.0716	180	8.489775	1.711166	4.934086	0.895974	0.996726	2.221124	3.04739	1.454875	314.2899	MO-BWR
10	3	300	210	180	10.66823	1.726233	6.328622	0.989159	2.379743	1.715347	1.507523	2.256737	314.5114	MO-BWR
11	2.762538	219.3451	154.3542	175.0584	7.960011	2.234424	3.80047	0.962861	1.296453	1.793053	3.356387	1.504007	311.0032	MO-BWR
12	3	285.2807	210	180	10.88715	1.733516	6.367992	0.970516	2.457489	1.751777	1.332924	2.2167	313.8744	MO-BWR
13	2.31648	136.2894	172.3182	163.2944	11.50557	2.493257	4.76093	0.668577	1.550795	2.212107	6.455877	1.960963	307.8013	MO-BWR
14	2.511164	278.4013	172.6575	154.3487	8.586153	1.641734	5.059301	0.975746	1.114287	2.036094	1.661921	1.423823	316.362	MO-BWR
15	2.354565	269.065	168.4278	142.9129	8.422783	1.61838	5.043794	0.991699	1.021581	2.01153	1.495046	1.393392	316.7595	MO-BWR
16	2.607657	299.2594	194.4423	158.3394	9.42465	1.549743	5.970852	0.987715	1.478982	2.047501	2.142764	1.641999	315.496	MO-BWR
17	2.091253	172.2958	203.5145	88.91519	12.11915	1.702644	7.131629	0.795513	2.467079	2.228803	12.46922	1.780678	306.5517	MO-BWR
18	3	300	210	98.39973	10.1061	1.864194	5.789796	1.202389	1.734709	1.601429	9.421497	2.256737	322.206	MO-BWR
19	2.571429	157.2472	180.6837	54.66237	12.16113	2.276294	5.300512	1.004062	1.457206	1.936768	15.73393	1.80429	306.4403	MO-BWR
20	3	300	207.6267	167.8229	10.49146	1.748209	6.127389	1.018441	2.215548	1.683316	1.866862	2.197089	317.0997	MO-BWR
21	2.632026	300	178.0029	180	8.822313	1.605217	5.2378	0.916304	1.29678	2.126548	2.586101	1.508519	314.8213	MO-BWR
22	3	300	210	153.8647	10.48819	1.77042	6.156045	1.057453	2.173149	1.630911	2.596691	2.256737	318.4453	MO-BWR
23	2.002385	214.3243	151.6898	159.4164	8.434648	1.844037	4.738226	0.929069	0.930972	1.973806	2.35011	1.719146	316.8136	MO-BMR
24	2.270291	187.5849	171.8159	103.9534	10.32418	1.963074	5.279564	0.983606	1.31553	1.882708	5.386565	1.625206	314.5496	MO-BMR
25	2	100	150	59.90768	11.99557	2.956964	4.267669	0.943806	1.559576	1.213567	12.4542	2.653121	303.4715	MO-BMR
26	2.243395	168.3193	177.141	80.93606	11.31095	2.032747	5.568967	0.959941	1.550992	1.89214	9.796241	1.730469	312.4244	MO-BMR
27	2	100	150	40	12.2016	2.929032	4.391334	0.995826	1.629727	1.175336	15.50487	2.653121	299.839	MO-BMR
28	2.843885	174.8635	189.4094	60.26374	12.27906	2.23426	5.360341	1.033853	1.527296	1.962982	15.48282	1.826076	308.752	MO-BMR
29	2.848919	125.5623	171.682	120.2145	12.12586	2.911937	4.023228	0.798299	1.671441	1.751047	7.842215	1.918966	305.8172	MO-BMR
30	2	100	150	100.4509	11.57598	3.01385	4.015818	0.837862	1.41671	1.372498	8.685364	2.653121	308.3849	MO-BMR
31	2	100	150	55.26882	12.04358	2.950456	4.296485	0.955927	1.575923	1.202316	13.09443	2.653121	302.6969	MO-BMR
32	2.320394	179.6348	174.5737	87.9225	10.78323	2.02128	5.342614	0.99711	1.386551	1.869023	7.862378	1.662348	313.0594	MO-BMR
33	2.339365	206.7433	169.2361	84.20741	9.671962	1.909795	5.062956	1.0924	1.165188	1.788133	6.407877	1.540132	313.6725	MO-BMR
34	2.18829	135.8313	161.3727	56.71957	11.49776	2.474543	4.803455	1.009953	1.418766	1.57043	12.51199	2.060709	305.6406	MO-BMR
35	2.975673	176.4709	187.4048	178.5959	11.72321	2.346528	4.911416	0.754542	2.34383	1.942407	4.267159	1.814076	311.0404	MO-BMR
36	2.205123	243.5285	193.7983	73.13805	9.772465	1.487255	6.387063	1.107686	1.648011	1.972556	11.54153	1.423697	317.0739	MO-BMR
37	2.299112	192.8962	168.8354	71.05031	10.06287	1.976611	5.10549	1.097726	1.2301	1.756825	8.642141	1.606124	312.0201	MO-BMR
38	2.01236	131.8126	150	51.6215	10.88743	2.578765	4.485263	1.074471	1.460838	1.241318	11.07411	2.323767	304.7633	MO-BMR
39	2	196.4328	150	74.7033	8.808041	2.010263	4.582482	1.141404	1.243417	1.381917	4.581912	1.843079	312.3699	MO-BMR
40	2.434474	191.5794	171.0531	79.71003	10.2227	2.043906	5.017674	1.076872	1.198254	1.80315	7.85314	1.600627	311.7078	MO-BMR
41	2.328331	178.2878	171.2623	76.56281	10.64912	2.070033	5.173089	1.040482	1.313476	1.80115	8.918504	1.674699	311.6704	MO-BMR
42	2.499101	256.1821	157.8395	98.67959	7.706554	1.900902	4.154009	1.133597	0.88677	1.69549	2.336214	1.462814	310.457	MO-BMR
43	2.472294	221.6406	164.991	112.3709	8.972931	1.943525	4.676072	1.067212	1.047586	1.795778	2.835898	1.497988	314.0251	MO-BMR
44	2.129402	169.3066	161.8202	72.2414	10.34109	2.132161	4.97373	1.057593	1.333022	1.610003	8.260241	1.819405	311.5544	MO-BMR
45	2.770009	107.4838	187.8571	55.87982	14.80134	2.809084	5.147828	0.739238	1.923917	2.050337	20.61707	2.210007	299.6161	MO-BMR

The values shown in blue are the best values of the corresponding objectives.

Table 21 shows the performance metrics.

Table 21. Performance metrics of the algorithms for the WAAM process with reference to the true front.

Algorithm	GD	IGD	Coverage	Spacing	Spread	Hypervolume
MO-BWR	0	0.288	0.485	0.248	0.676	0.457
MO-BMR	0	0.273	0.515	0.233	0.676	0.457
Composite	0	0	1	0.206	0.66	0.914

Choosing the Best Compromise Pareto-Optimal Solution from the Non-Dominated Solutions for the WAAM Process

Now, to find out the “best compromise” non-dominated pareto solution, considering all the 9 objectives simultaneously, BHARAT is used. Let the decision-maker assign equal importance to all the objectives. In fact, the objective W/R is not required as the objectives W and R are already considered the objectives. Probably, that was why Fu et al. [13] did not consider W/R and considered only the remaining 8 objectives in the multi-objective optimization carried out by them. Hence, here also, only 8 objectives are considered for decision-making using BHARAT. Then, their average rank will be 4.5 (i.e., average of 1, 2, 3, 4, 5, 6, 7, and 8). The corresponding average weight from the BHARAT table [29] is 0.125 for each of these 9 objectives. Table 22 shows the normalized data of the 8 objectives and the BHARAT scores considering equal weightages to all the objectives (scores are shown in the last but one column).

Table 22. Normalized data of the objectives and the scores of the non-dominated solutions for the WAMM process.

Sol. No.	W	R	HD	P	WH	t	WG	HV	Scores (Eq. Wt.)	Scores *
1	0.700346	0.535811	0.689167	0.41176	0.61035	0.884182	0.666927	0.964472	0.682877	0.783785
2	0.681135	0.580713	0.680651	0.437144	0.667476	0.694908	0.70876	0.98565	0.679555	0.768411
3	0.634309	0.489666	0.639124	0.630911	0.575422	0.281486	0.983713	0.98463	0.652407	0.743824
4	0.67638	0.562824	0.607458	0.477281	0.671858	0.277721	0.668557	0.987549	0.616204	0.725702
5	0.585168	0.681429	0.621993	0.875558	0.676748	0.592158	0.922301	0.968864	0.740527	0.799747
6	0.636217	0.651037	0.566967	0.863653	0.649162	0.166608	0.922011	0.968327	0.677998	0.758268
7	0.720432	0.573163	0.674646	0.373508	0.686339	0.877477	0.617436	0.976505	0.687438	0.786791
8	0.583191	0.646215	0.708085	0.653284	0.603937	0.497182	0.953167	0.975045	0.702513	0.768717
9	0.573581	0.567768	0.746201	0.889683	0.529163	0.437399	0.95774	0.975432	0.709621	0.773803
10	0.720761	0.572767	0.675904	0.372633	0.685189	0.884182	0.617436	0.976119	0.688124	0.787418
11	0.53779	0.741385	0.694365	0.683997	0.655494	0.397131	0.926453	0.965231	0.700231	0.762433
12	0.735551	0.575183	0.688888	0.360844	0.670939	1	0.628588	0.974142	0.704267	0.801948
13	0.777333	0.827266	1	0.571816	0.53132	0.206467	0.710565	0.955293	0.697508	0.798709
14	0.580093	0.54473	0.685195	0.795818	0.57725	0.802039	0.978627	0.981863	0.743202	0.799676
15	0.569055	0.536981	0.674173	0.868036	0.584299	0.891561	1	0.983096	0.7634	0.813596
16	0.636743	0.514207	0.676892	0.599581	0.574035	0.622058	0.848595	0.979175	0.681411	0.766378
17	0.818787	0.56494	0.840434	0.359441	0.52734	0.106897	0.782506	0.951415	0.61897	0.753871
18	0.682783	0.618542	0.55604	0.511192	0.73393	0.141477	0.617436	1	0.607675	0.716003
19	0.821624	0.755278	0.665872	0.608541	0.606854	0.084717	0.772266	0.95107	0.658278	0.773964
20	0.708818	0.580058	0.656471	0.400248	0.698226	0.713992	0.634199	0.984152	0.672021	0.771074
21	0.596048	0.532614	0.729645	0.683825	0.552697	0.515419	0.923682	0.977081	0.688876	0.760739
22	0.708597	0.587428	0.632252	0.408057	0.720662	0.513317	0.617436	0.988328	0.64701	0.752206
23	0.569857	0.611854	0.71962	0.95252	0.595467	0.567175	0.810514	0.983264	0.726284	0.786323
24	0.697516	0.651351	0.67972	0.674078	0.62428	0.247454	0.857363	0.976238	0.676	0.767899
25	0.810438	0.981125	0.708384	0.568597	0.968497	0.107026	0.52519	0.941855	0.701389	0.810322
26	0.764184	0.674468	0.696477	0.571744	0.621168	0.136065	0.80521	0.969642	0.65487	0.762816
27	0.824358	0.971857	0.671379	0.544122	1	0.085968	0.52519	0.930582	0.694182	0.807856
28	0.829591	0.741331	0.646684	0.580614	0.59875	0.086091	0.763052	0.958244	0.650545	0.76764
29	0.81924	0.966185	0.837502	0.530542	0.671219	0.169968	0.726116	0.949136	0.708738	0.811532
30	0.78209	1	0.797956	0.625936	0.856348	0.153468	0.52519	0.957105	0.712261	0.813141
31	0.813682	0.978966	0.699401	0.562699	0.97756	0.101793	0.52519	0.939451	0.699843	0.809829
32	0.72853	0.670664	0.670515	0.639551	0.628851	0.169532	0.838207	0.971613	0.664683	0.764201
33	0.653452	0.633673	0.612026	0.761053	0.657298	0.208013	0.904722	0.973515	0.675469	0.760184
34	0.776805	0.821057	0.661988	0.625029	0.748417	0.106532	0.676171	0.948588	0.670573	0.778553
35	0.792037	0.778582	0.88607	0.378342	0.605093	0.312368	0.7681	0.965346	0.685742	0.788114
36	0.660242	0.493473	0.603579	0.538085	0.595844	0.115489	0.978714	0.984072	0.621187	0.725081
37	0.679862	0.655842	0.609056	0.720893	0.669012	0.154235	0.867549	0.968387	0.665605	0.757251
38	0.735571	0.855638	0.622238	0.607028	0.946845	0.120364	0.599626	0.945865	0.679147	0.780641
39	0.595084	0.667008	0.585749	0.713172	0.850511	0.29091	0.756013	0.969473	0.67849	0.754514
40	0.69066	0.678171	0.620851	0.740051	0.651824	0.169731	0.870528	0.967418	0.673654	0.764873
41	0.71947	0.68684	0.642564	0.675132	0.652548	0.149456	0.832025	0.967302	0.665667	0.763611
42	0.520666	0.630722	0.589784	1	0.693213	0.570549	0.952542	0.963536	0.740126	0.788757
43	0.606224	0.644865	0.62647	0.846489	0.6545	0.470018	0.930175	0.97461	0.719169	0.785998
44	0.698659	0.707454	0.632168	0.665233	0.730021	0.161366	0.76585	0.966941	0.665962	0.761151
45	1	0.932058	0.904413	0.460919	0.57324	0.064652	0.630492	0.92989	0.686958	0.822776

* For a weightage of 0.1718 each to W, R, and HV; and 0.0969 each to the remaining objectives. The row highlighted in red indicates the best compromise solution.

The width (W) is a beneficial objective (i.e., the maximum value is required). Hence, the value of 14.80134 corresponding to solution no. 45 is assigned 1. The other values under the W column are divided by 14.80134 to get the normalized data for W. A similar procedure is followed for other beneficial objectives such as R and HV. The objective substrate distortion (HD) is a non-beneficial objective (i.e., minimum value is required). Hence, the value of 0.668577 corresponding to solution 13 is assigned 1. To get the normalized data of HD for the other solutions in the HD column, this value of 0.668577 is divided by the corresponding HD values of the solutions. A similar procedure is followed for the other non-beneficial objectives such as P, WH, t, and WG. The scores given in the last two columns are computed by summing up the products of multiplication of the normalized data of the objectives with the corresponding weights (as explained in Section 3.2). For example, if all 8 objectives are considered equally important, then an average weight of 0.125 is assigned to each of the objectives. Then, the score of 0.682877 for solution no. 1 is obtained as 0.125 × 0.700346 + 0.125 × 0.535811 + 0.125 × 0.689167 + 0.125 × 0.41176 + 0.125 × 0.61035 + 0.125 × 0.884182 + 0.125 × 0.666927 + 0.125 × 0.964472 = 0.682877. A similar procedure can be followed to calculate the scores of different objectives given different weights. The best compromise solution is the one with the highest score.

Just for more demonstration of BHARAT, let the decision-maker assign equal importance to W, R, and HV. Then, their average rank will be 2 (i.e., average of 1, 2, and 3). The corresponding average weight from the BHARAT table [28] is 0.1718 for each of these 3 objectives. Let the decision-maker consider the remaining objectives of HD, P, WH, t, and WG as secondary and consider them equally important among themselves. Then, their average rank will be 6 (i.e., average of 4, 5, 6, 7, and 8). The corresponding average weight from the BHARAT table [29] is 0.0969 for each of these 5 objectives. The last column of Table shows the scores of the non-dominated solutions using these weights and the normalized data of the non-dominated solutions. By coincidence, this solution is the same as that obtained by assigning equal weights (and unequal weights) to the objectives in this particular example.

From the scores given in the last two columns, solution number 15 with optimal parameters of w = 2.354565 m/min, v = 269.065 mm/min, I = 168.4278 A, and T = 142.9129 °C is suggested as the optimal input parameters for the WAMM process considered. Fu et al. [13] conducted an optimal analysis using the response optimizer in Minitab 16 and reported the optimum parameters as w = 2.5 m/min, v = 187 mm/min, I = 178 A, and T = 93 °C. A comparison of the results is given in Table 23.

Table 23. Comparison of the results for the WAMM process.

Solution	W (mm)	R (mm)	HD (mm)	P (mm)	WH (mm)	t (min)	WG (mm)	HV
Fu et al. [13]	10.8	2.04	0.63 (1.0066) *	1.37	1.9	7.4	1.01 (1.632) *	312.95
Present work	8.422783	1.61838	0.991699	1.021581	2.01153	1.495046	1.393392	316.7595

* Corrected values after substituting the Fu [26]’s optimal input parameters in the respective objective functions. The bold values indicate comparatively better values of the objectives.

It can be observed that out of the 8 objectives, the present work using MO-BWR and MO- BMR algorithms provides 5 objectives comparatively better than those given by Fu et al. [13]. Thus, solution no. 15 is proved to be the best compromise Pareto-optimal solution for the considered many-objective optimization problem of the WAMM process.

Table 24 presents a comparison of the MO-BWR and MO-BMR algorithms with reference to certain criteria.

Table 24. General comparison of the MO-BWR and MO-BMR algorithms.

Criterion	MO-BWR	MO-BMR
Computational load	Moderate (dominated by sorting & crowding)	Moderate (same)
Convergence speed	Fast in early stages	Consistent and stable
Convergence stability	Moderate to good (depends on worst solution)	Very good (mean guidance is more reliable)
Exploration ability	Higher	Moderate
Suitability	Multimodal, constrained, or rugged landscapes	Smooth, continuous, or stable

The next section provides conclusions of the present work.

5. Conclusions

In this work, two new optimization algorithms—Best–Worst–Random (BWR) and Best–Mean–Random (BMR)—are proposed, and their capabilities are demonstrated across diverse manufacturing optimization problems. These algorithms are designed to be simple and efficient, operating without metaphorical inspirations or algorithm-specific control parameters that often accompany other metaheuristics.

• The BWR and BMR algorithms are applied to single-objective optimization scenarios involving friction stir processing and ultra-precision turning. The BWR and BMR algorithms demonstrated faster convergence and higher-quality solutions with fewer function evaluations—indicating computational efficiency.
• The multi- and many-objective versions—MO-BWR and MO-BMR—are tested on two- and three-objective optimization problems in the ultra-precision turning and laser powder bed fusion process. The many-objective capabilities of these algorithms are also assessed through a nine-objective problem based on the wire arc additive manufacturing process. When compared with prominent algorithms like GA, PSO, etc., the proposed methods demonstrated excellent solution diversity and convergence behavior.
• The BWR and BMR algorithms and their multi-objective variants show that competitive performance can be achieved without added complexity, offering transparent, interpretable, robust, and versatile tools for optimizing manufacturing processes.
• A key aspect of this study is the integration of BHARAT, a structured MADM tool that, along with the R-method, identifies the most suitable compromise solution from the Pareto-optimal set. This becomes particularly valuable in many-objective problems, where visual interpretation becomes infeasible.
• The results suggest broad applicability of these algorithms to real-world, high-dimensional, and constrained/unconstrained manufacturing challenges. Their potential extends to process optimization in additive manufacturing, tool path planning, welding parameter tuning, multi-axis machining, and thermal processing, as well as their possible integration with machine learning models for data-driven manufacturing.