Influence of Temperature on the Forming Limits of High-Strength Low Alloy, and Dual-Phase Steels

Abstract

High-strength steels (HSS) appear as a good alternative to common steels to reduce vehicle weight, thus reducing fuel consumption. Despite the excellent mechanical behavior towards its lower weight, its application in industry is still limited, as manufacturing such materials suffers from limitations, especially regarding formability. The literature shows springback to be the most common problem. Among the parameters that can be studied to minimize this problem, the temperature appears, according to the literature, to be one of the most influential parameters in minimizing springback. However, the consequence of the temperature increase on the forming limits of materials is not completely understood. This study proposes to determine the consequences of the use of the temperature rise technique in the forming limits of high-strength steels. Two different steels were studied (HSLA 350/440 and DP 350/600). To evaluate the formability, the Nakazima method was used (practical). Finite element models were made which describe the material as well as Nakazima experimental behavior. To predict the forming limit strains via the numerical method, the thickness gradient criterion was applied. The practical and computational results were compared to validate the finite element model. Four different temperature ranges were analyzed. In general, it was found that 400 °C has a negative impact on the forming limits of both steels. This negative effect was found to be due to the alloying elements, such as silicon and manganese, present in the alloy. These alloying elements take part in the increase and decrease in resistance coefficient at the elevated temperature. For HSLA 350/440 steel, the forming limit strain decreased with an increase in temperature up to 600 °C and then increased at 800 °C; whereas for DP 350/600 steel, the forming limit strain decreased till 400 °C and then increased for 600 °C and 800 °C. Another factor which might have contributed to the behavior of the DP steel is the interaction of hard martensite with soft ferrite phase.

1. Introduction

The challenges in the industrial application of high-strength steels refer primarily to conformability, joining of sheets, tool life, and springback. The latter is pointed out in the literature as the problem more pertinent to the mass production of structural components using these materials. The difficulty in predicting and controlling the springback may imply the need for project adjustments to the geometry of the tool, adjustments to the process parameters, and control of the forming temperature during production [1,2]. Regarding the influence of temperature on the springback of metals subjected to forming operations, the literature indicates that the relationship between the factors is more prominent, and higher temperatures used in the operations reduce the problem of the springback effect [3,4,5,6,7,8].

In contrast, the effect of the temperature increase within the forming limits of metals is not completely understood. While for certain materials, the increase in temperature increases the forming limits, in other cases, damages are found with respect to conformability [9,10,11,12,13,14,15,16,17,18,19,20,21].

The need to predict failures is found to be the utmost critical necessity in sheet metal stamping. To check the forming limits of materials, ref. [22] introduced the concept of the forming limit curve (FLC), defined on the axes of minor and major principal strains in the sheet plane. The forming limit of a sheet metal is defined as the state in which a localized thinning (necking) on the sheet starts during forming, essentially leading to a fracture/failure. The two principal strains, ε₁ and ε₂, measured at various component points in the imminence of failure, result in a curve (forming limit curve—FLC) separating the failure and safe conditions. The concept of FLC was extended to the domain of deformations between states of uniaxial stretching to deep drawing to biaxial stretching.

Ref. [23] proposed a single testing method to determine the limit strain from uniaxial stretching to equibiaxial stretching and then compared their results with those obtained by other known tests, such as Bulge and Erichsen. With single tooling, it is possible to reproduce the states of uniaxial and biaxial deformation through the deformation imposed via a hemispherical punch in rectangular metal sheets that vary in width and are fixed by a die and blank holder.

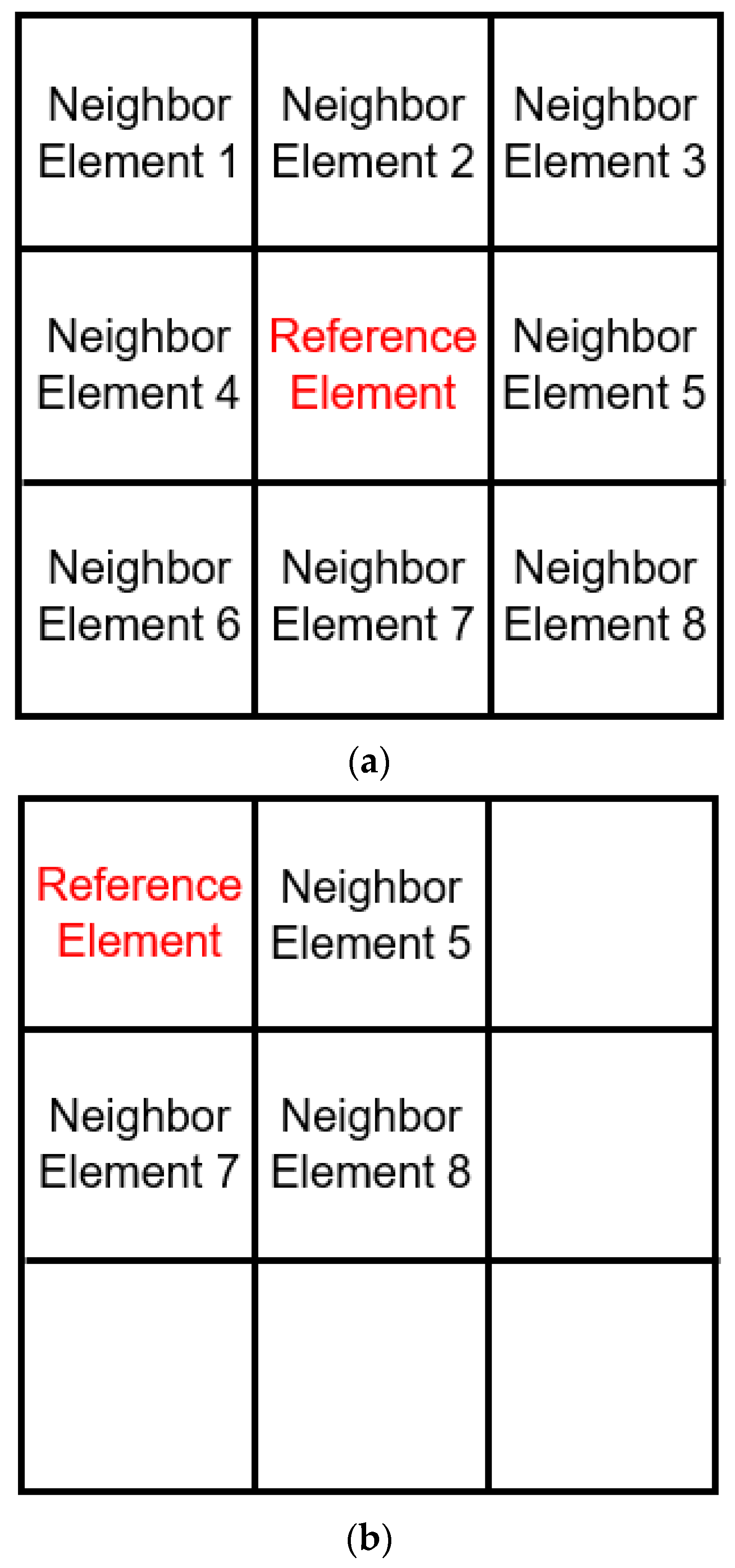
The first simulation work of forming sheet metal dates back to the 1930s [24]. However, in recent decades, through simulation based on the finite element method, the process has gained ground as a very useful tool in component designs obtained via forming. In sheet metal stamping, numerical analysis has contributed a lot to reducing the time and cost of development of tools. In the case of numerical tests predicting forming limits, such as the Nakazima test, one of the challenges is to develop a computer routine that can predict the onset of necking. Developed by [25,26], the thickness gradient criterion (TGC) correlates each of the elements of the finite element mesh with each of its neighbors. When the thickness ratio between two elements reaches a critical gradient (0.92), it is determined that necking occurred.

The present study investigates the effects of four temperature levels within the forming limits of two high-strength steels. As mentioned, limited literature is available on the temperature effect on the forming limit strain of high-strength steels, and the decrease or increase in forming limits at those temperatures is not completely understood. For this, the Nakazima method was performed experimentally and numerically modeled using the finite element software Abaqus (6-13) at room temperature and at elevated temperatures. The TGC was used to predict the onset of necking in the mathematical model. The remaining sections in the paper are laid out as follows. Section 2 provides the materials investigated and the experimental and numerical technique studied to investigate the effect of temperature on the forming limit strain of high-strength steels. Section 3 details the outcome result of the experiments and numerical analyses. It also deepens the discussion of the obtained results. Section 4 concludes and summarizes the work.

2. Materials and Methods

2.1. Materials

Two high-strength steels have been used in practical experiments and computational models. One of the materials is a conventional high-strength steel (HSLA 350/440), and the other is an advanced high-strength steel (DP 350/600). Their chemical compositions and mechanical properties are detailed in

Table 1. Chemical composition of the steels.

Material	C	Si	Mn
HSLA 350/440	0.14	0.40	2.10
DP 350/600	0.08	0.03	0.60

and

Table 2. Mechanical properties of the steels.

Material	t (mm)	YS (MPa)	TS (MPa)	Uniform EL (%)	Total EL (%)	E (GPa)
HSLA 350/440	1.4	356	449	14.8	20.8	206
DP 350/600	1.5	395	620	14.9	20.0	206

t—thickness; YS—yield strength; TS—tensile strength; EL—elongation; E—modulus of elasticity.

.

For both steels, tensile tests were performed at four different temperatures, which was published in [27]. The aim was to obtain data that would be able to describe the mechanical behavior of the materials at the range of temperatures used in this study. The range of temperature studied are room temperature (RT@30 °C), 400 °C, 600 °C, and 800 °C. The tests were experimentally conducted at uniform temperature at all temperature levels. These data were then used to feed the computational models constructed in Abaqus for this study.

2.2. Practical Experiments (Nakazima Method)

The FLCs were obtained through the use of Nakazima tooling, shown in Figure 1. For practical experiments, only two temperature levels were studied: room temperature (30 °C) and 400 °C. A set of 8 specimens (Figure 2) were tested for each of the two temperatures, totaling 32 test specimens (two different steels). For each condition, three tests were replicated. For elevated temperature experiments, the following steps were followed: (1) a set of three blanks were wrapped in a carbon blanket to prevent oxidation and the temperature drastically dropping and placed in an oven for 600 °C and preserved for 10 min for temperature homogenization; (2) the removal of the sample after the sample reached a temperature of 600 °C; (3) the placing of the sample on the test tool; (4) the punch was moved to deform the sample (during this step, the sample temperature was measured using thermocouple, which is called the “initial temperature”); and (5) the experiment was aborted after the decrease in force was observed on the computer screen (during this moment, the temperature of the sample was recorded, which is called the “final temperature”). The recorded initial and final temperatures of the samples are presented in the results section.

To analyze the forming limits, tests/simulations were carried out. Twelve tests were performed, varying the material and temperatures for both practical and computational methods, as shown in

Table 3. Test details for forming limit analysis (H—HSLA; D—DP; E—Experiment; C—Computational).

Sample Name	Temperature (°C)	Material	Method
H-RT-E	RT	HSLA 350/440	Nakazima (Experiment)
H-400-E	400	HSLA 350/440	Nakazima (Experiment)
D-RT-E	RT	DP 350/600	Nakazima (Experiment)
D-400-E	400	DP 350/600	Nakazima (Experiment)
H-RT-C	RT	HSLA 350/440	FEA (Computational)
H-400-C	400	HSLA 350/440	FEA (Computational)
H-600-C	600	HSLA 350/440	FEA (Computational)
H-800-C	800	HSLA 350/440	FEA (Computational)
D-RT-C	RT	DP 350/600	FEA (Computational)
D-400-C	400	DP 350/600	FEA (Computational)
D-600-C	600	DP 350/600	FEA (Computational)
D-800-C	800	DP 350/600	FEA (Computational)

.

For determination of the forming limit, square (4 mm × 4 mm) mesh impressions were made on the samples using the scratching technique with the height tracer equipment. The electrochemical printing technique, recommended by [28], was found ineligible due to the degradation of the mesh suffered at high temperatures. The parameters of blank holder force and punch speed were set at 12 MPa and 1.107 mm/s, respectively. The pressure applied through the blank holder was enough to completely restrain the material during the test. After the test, the sliding of the material was checked by analyzing the square grids, and no scratch or sliding marks were observed. All quads were measured on each of the specimens generated, which apparently had significant deformation imposed by the punch (such as necking and near-crack conditions), as shown in the example (Figure 3). The curves were then plotted such that none of the near-crack points went below the plotted FLC.

2.3. Numerical Simulation and Limit Criterion

Through Abaqus (6-13) software, the simulation set up to obtain the FLC was investigated with an approximate three-dimensional model (Figure 4). The bodies that make up the model of the stamping tool (die, punch, and blank holder) were considered non-deformable rigid bodies. The metal sheet is considered a deformable body, using the S4R shell element constituting the finite element mesh.

The average thickness of the sheets measured experimentally were detailed in the model. To define the mechanical properties of materials, the stress–strain curves were used for each temperature (30 °C, 400 °C, 600 °C, and 800 °C) defined in this study. The flow criterion used was von-Mises with isotropic hardening. Taking advantage of the axisymmetric relationship of the problem, only a quarter of the sheet was tested to reduce simulation computational time. The parameters used in the practical experiments, such as blank holder force and punch speed, was reproduced in the simulations.

All samples were meshed with 4 mm × 4 mm square elements, and the number of elements used in each sample is detailed in

Table 4. Number of elements for each geometry considered for finite element analysis.

Sample	Geometry (mm × mm)	Number of Elements
1	200 × 200	2500
2	200 × 175	2200
3	200 × 150	1900
4	200 × 125	1550
5	200 × 100	1250
6	200 × 75	950
7	200 × 50	650
8	200 × 25	300

. To predict the necking/failure, the thickness gradient criterion (TGC) was employed. This method follows the ratio of thickness of a neck element to the thickness of all neighboring elements (Equation (1)). Once the thickness ratio reaches to the critical thickness ratio of less than 0.92 (Equation (2)), the necking/failure has occurred at the region [25,26,29,30,31].

$${\mathrm{R}}_{\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{k}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}}=\frac{\mathrm{C}\mathrm{u}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{t}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{k}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{o}\mathrm{f} \mathrm{n}\mathrm{e}\mathrm{c}\mathrm{k} \mathrm{e}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}{\mathrm{C}\mathrm{u}\mathrm{r}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{t}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{k}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{o}\mathrm{f} \mathrm{n}\mathrm{e}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{r} \mathrm{e}\mathrm{l}\mathrm{e}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}$$

(1)

$${\mathrm{R}}_{\mathrm{t}\mathrm{h}\mathrm{i}\mathrm{c}\mathrm{k}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}}\le {\mathrm{R}}_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}}$$

(2)

To check the thickness ratio of each element (reference element) with its neighboring element at each time frame of the simulation, a dynamic spreadsheet was developed for each geometry. This spreadsheet conducted the calculation for each element thickness ratio relation with its neighboring element, as illustrated in Figure 5 and Figure 6.

As an example, if the sheet is divided into nine elements, as illustrated in Figure 5a, each element would be taken as a reference element at an instant. If the central element (highlighted) is taken as the critical element, then its thickness would be compared at each increment of the stamping simulation with the thicknesses of the other eight neighboring elements. If, in any of these comparisons, the relationship ratio between the thicknesses was less than 0.92 (like shown in Figure 6, note all commas in this figure represent a decimal point), it would be considered that during this increase in operation, the phenomenon of necking occurred; the values of the largest and smallest deformation during this increment of simulation would be taken, and the forming limit curve would be built. When the reference element is located on the edges of the sheet, as illustrated in Figure 5b, the existence of only three neighboring elements were considered for calculation.

3. Results and Discussion

The results obtained from the applied aforementioned methodologies are explained in this section. The material tensile stress–strain curve shown in Figure 7 and Figure 8 were used to feed and describe the material in the computational models for each of the four-temperature ranges. The strain hardening exponent “n” and strength coefficient “K” are also calculated from the tensile curves and are presented in Figure 9 and Figure 10. To obtain “n” and “K” values, the engineering stress–strain curves were converted to true stress–strain curves. Then, the true stress–strain curves were plotted on the log–log scale to find the straight-line slope, which is called the strain hardening exponent, n. 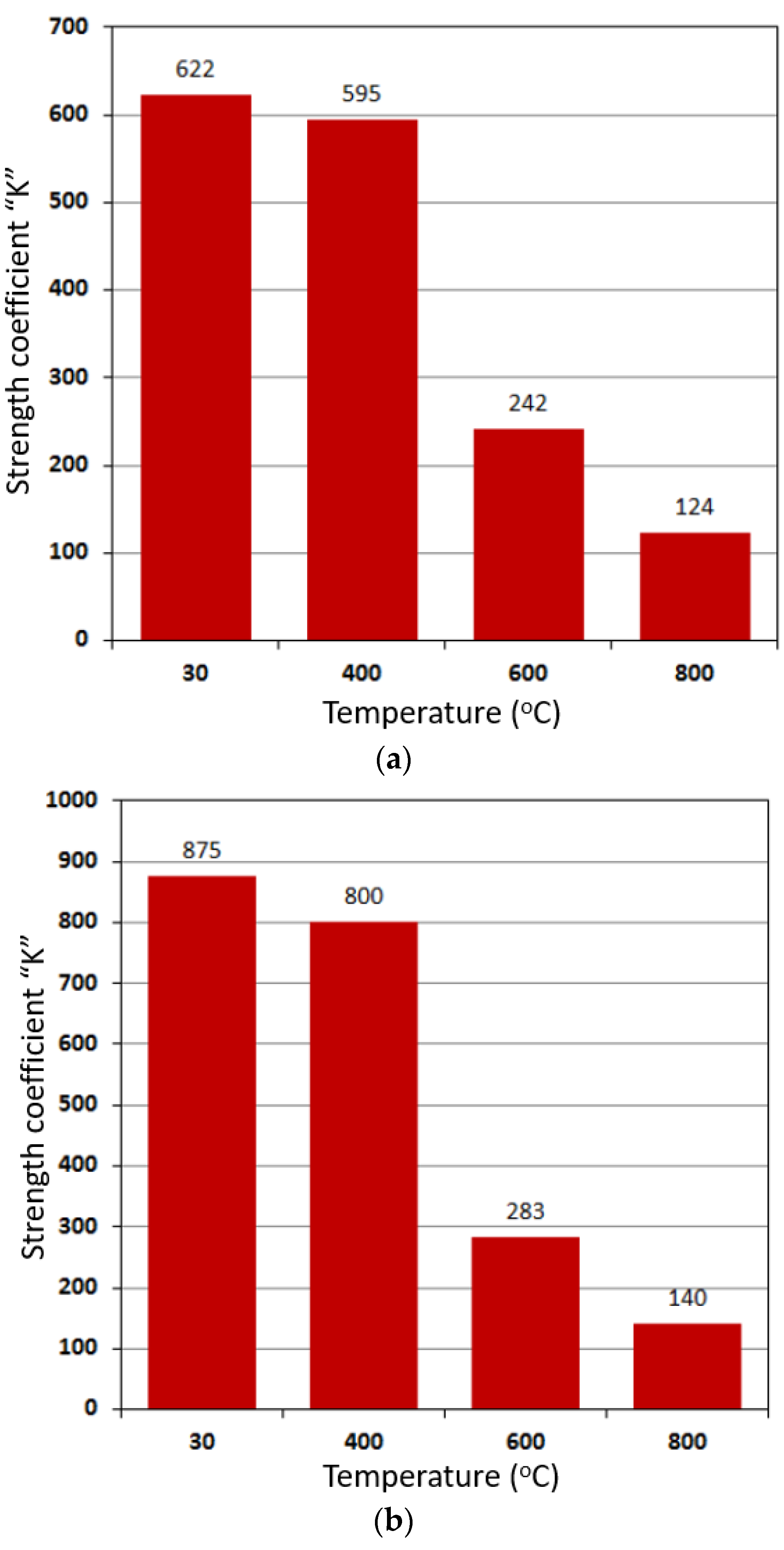The strength coefficient K will be determined from the y-intercept on the stress axis. From Figure 9, it can be observed that the strain hardening for both materials suddenly drops to very low value at 600 °C. However, at other tested temperatures, the value is very similar. At 800 °C, the strain hardening of DP steel shows a slight increase in the trend. For both steels, the strength coefficient shows a slight drop from 30 °C to 400 °C (Figure 10). However, this value shows a sudden drop of 59% for HSLA and 64% for DP steel from 400 °C to 600 °C and then about 50% from 600 °C to 800 °C.

The temperatures of the sheet metal at the start and end of the punch movement during the experiments were measured using thermocouple and are detailed in

Table 5. Parameters used during Nakazima tests.

Sample Name	Material	Geometry (mm × mm)	Initial Temperature (°C)	Final Temperature (°C)
H-RT-E-1	HSLA 350/440	200 × 200	RT	RT
H-RT-E-2	HSLA 350/440	200 × 175	RT	RT
H-RT-E-3	HSLA 350/440	200 × 150	RT	RT
H-RT-E-4	HSLA 350/440	200 × 125	RT	RT
H-RT-E-5	HSLA 350/440	200 × 100	RT	RT
H-RT-E-6	HSLA 350/440	200 × 75	RT	RT
H-RT-E-7	HSLA 350/440	200 × 50	RT	RT
H-RT-E-8	HSLA 350/440	200 × 25	RT	RT
H-400-E-1	HSLA 350/440	200 × 200	430	300
H-400-E-2	HSLA 350/440	200 × 175	420	245
H-400-E-3	HSLA 350/440	200 × 150	385	230
H-400-E-4	HSLA 350/440	200 × 125	400	270
H-400-E-5	HSLA 350/440	200 × 100	430	265
H-400-E-6	HSLA 350/440	200 × 75	385	225
H-400-E-7	HSLA 350/440	200 × 50	400	200
H-400-E-8	HSLA 350/440	200 × 25	395	220
D-RT-E-1	DP 350/600	200 × 200	RT	RT
D-RT-E-2	DP 350/600	200 × 175	RT	RT
D-RT-E-3	DP 350/600	200 × 150	RT	RT
D-RT-E-4	DP 350/600	200 × 125	RT	RT
D-RT-E-5	DP 350/600	200 × 100	RT	RT
D-RT-E-6	DP 350/600	200 × 75	RT	RT
D-RT-E-7	DP 350/600	200 × 50	RT	RT
D-RT-E-8	DP 350/600	200 × 25	RT	RT
D-400-E-1	DP 350/600	200 × 200	410	285
D-400-E-2	DP 350/600	200 × 175	370	270
D-400-E-3	DP 350/600	200 × 150	410	280
D-400-E-4	DP 350/600	200 × 125	430	320
D-400-E-5	DP 350/600	200 × 100	400	275
D-400-E-6	DP 350/600	200 × 75	430	310
D-400-E-7	DP 350/600	200 × 50	420	235
D-400-E-8	DP 350/600	200 × 25	390	265

. Note that the experiments were performed only at room temperature (30 °C) and 400 °C. It can be seen that the starting temperatures were approximately 400 °C. The measured temperature is not accurate due to the fact that heat is lost in placing the sample in the punch–die set, making sure the followed procedure is safe for personnel and equipment. The table also shows the end temperature of the sheet metal. This measurement was taken when the computer shows that the drop in force means that instability occurred in the sheet metal. The drop in temperature is due to the contact with cold die and punch as well as the convection to the atmosphere. Figure 11 shows the experimental deformed samples of HSLA 350/440 and DP 350/600 at room temperature (RT) and at 400 °C.

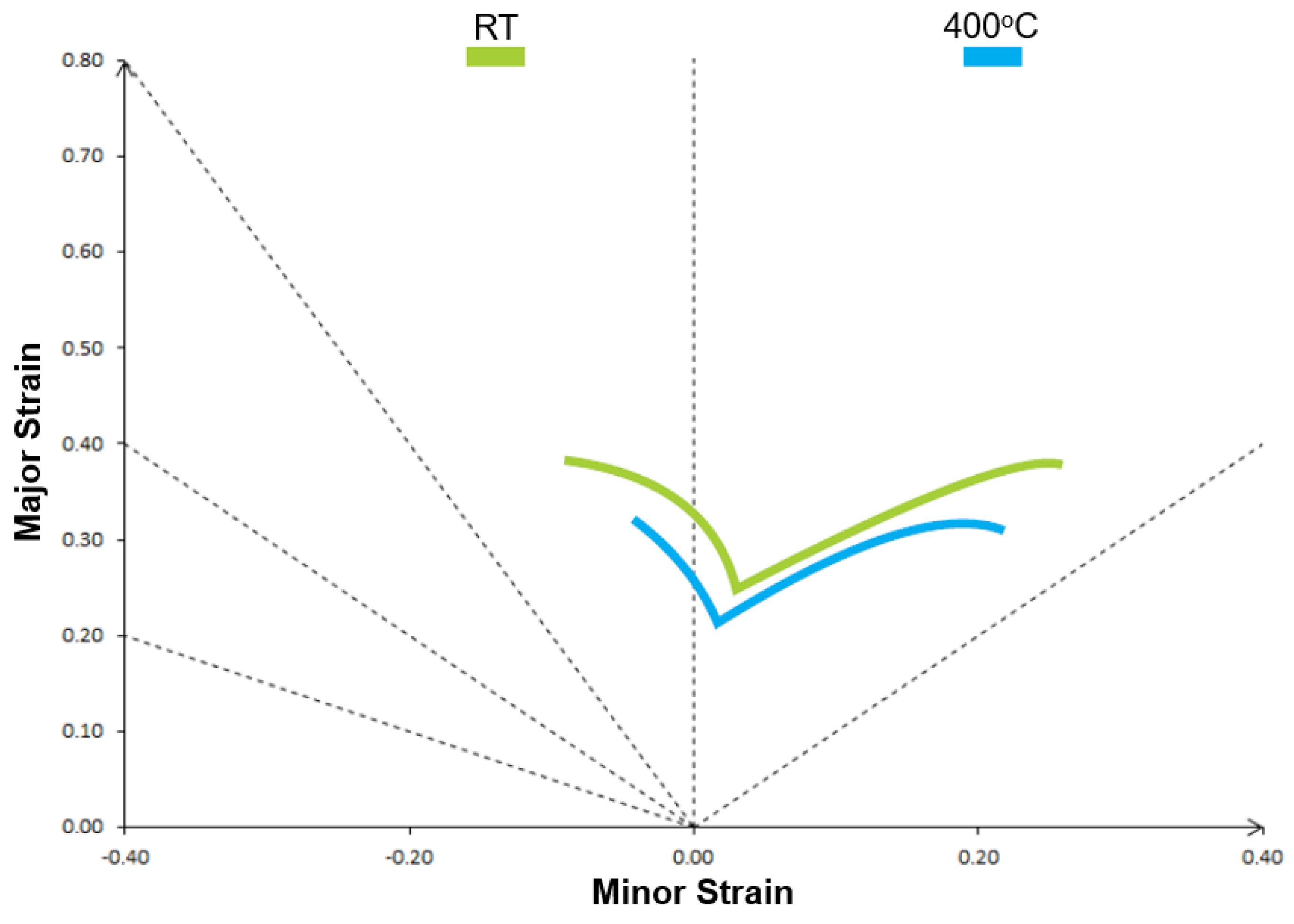
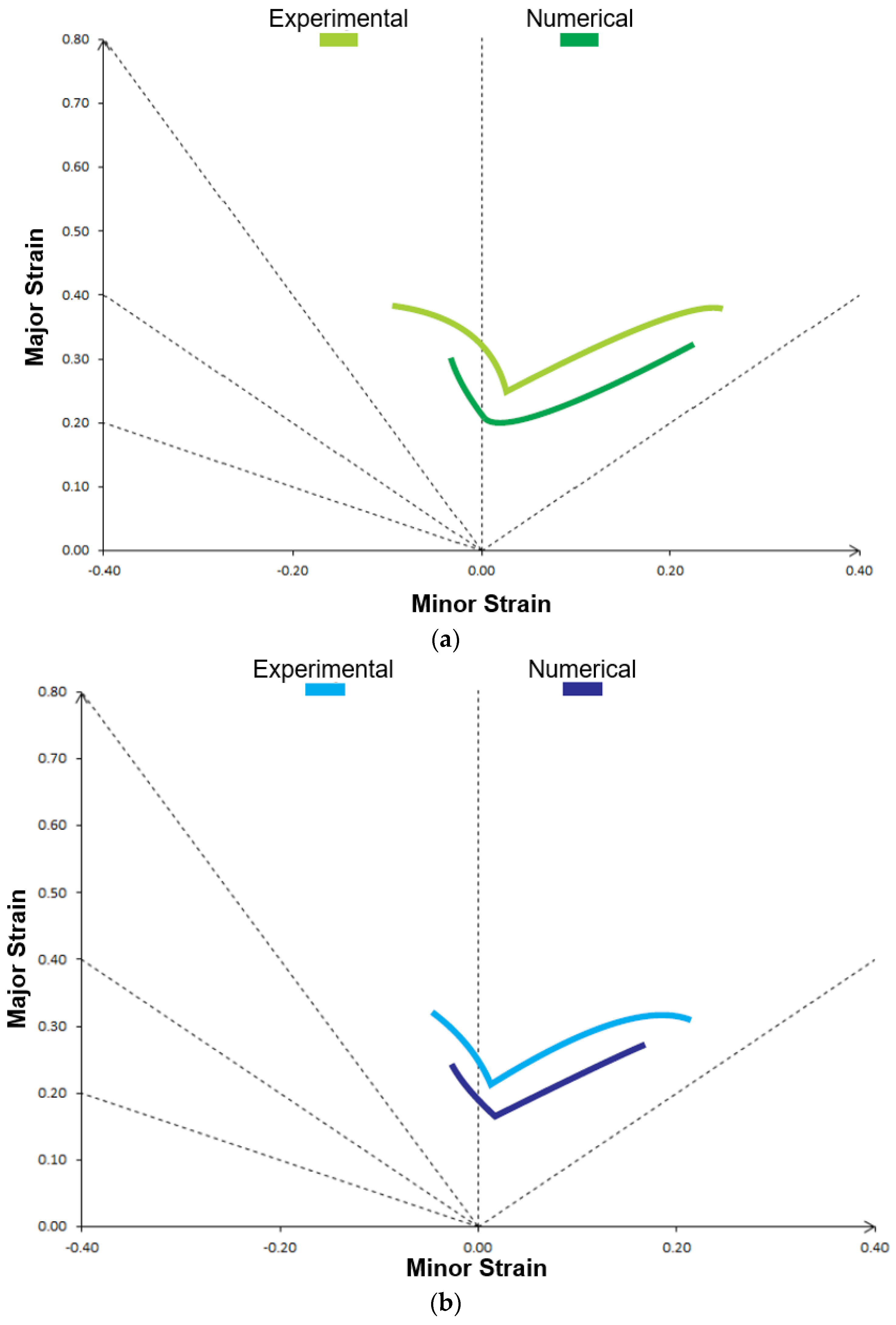
In Figure 12, the two curves shown are plotted on the same graph in order to visually compare the difference in the behavior of the material at the two temperatures (RT and 400 °C) studied. It can be noted that the limits are very close for uniaxial and biaxial deformation modes, but the Figure shows significant difference at plane strain. Figure 13a,b shows the comparison of experimental and numerical forming limits for HSLA steel at RT and 400 °C. It can be observed that the trend shows a good match, except at biaxial strain deformation.

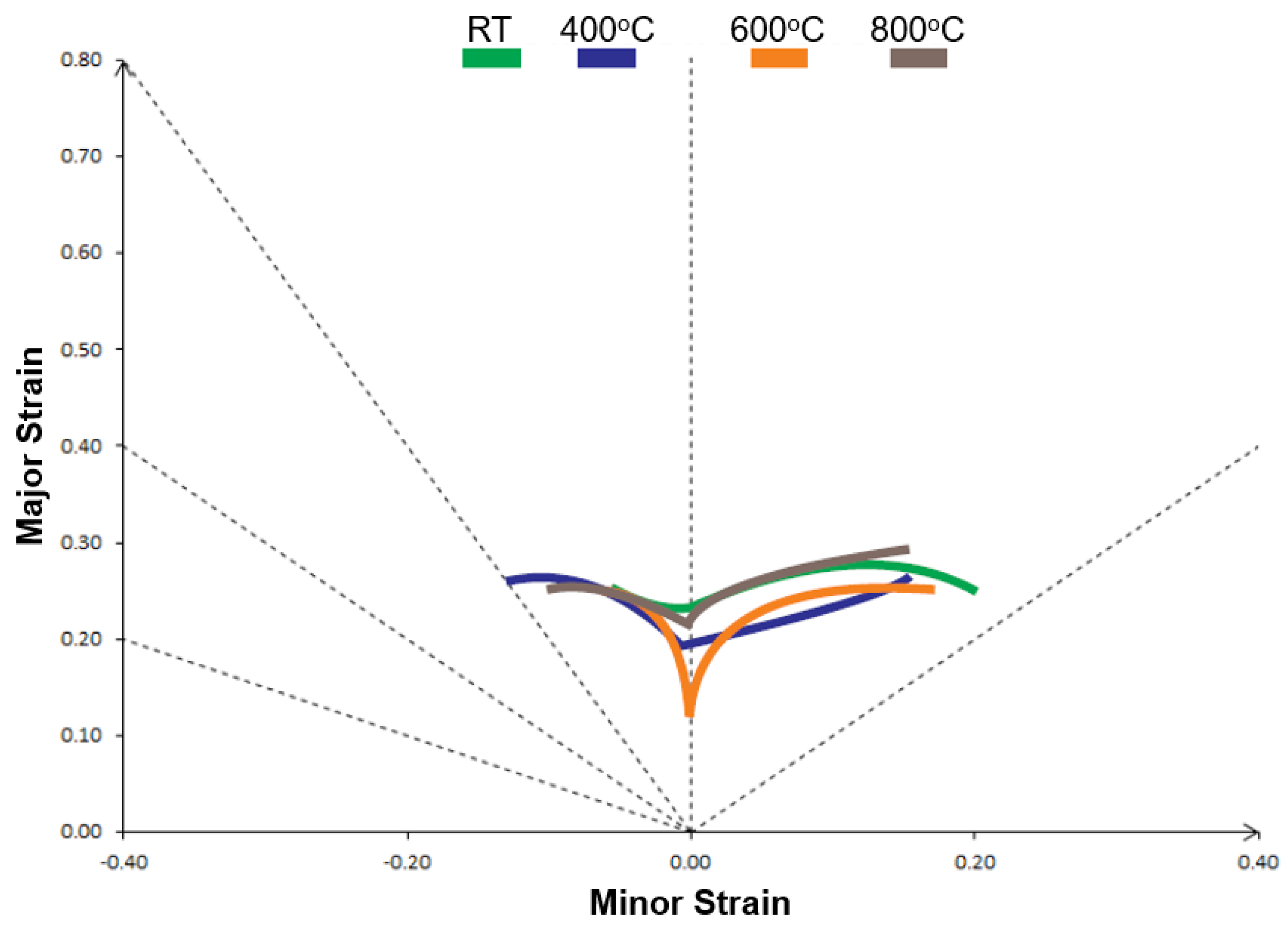
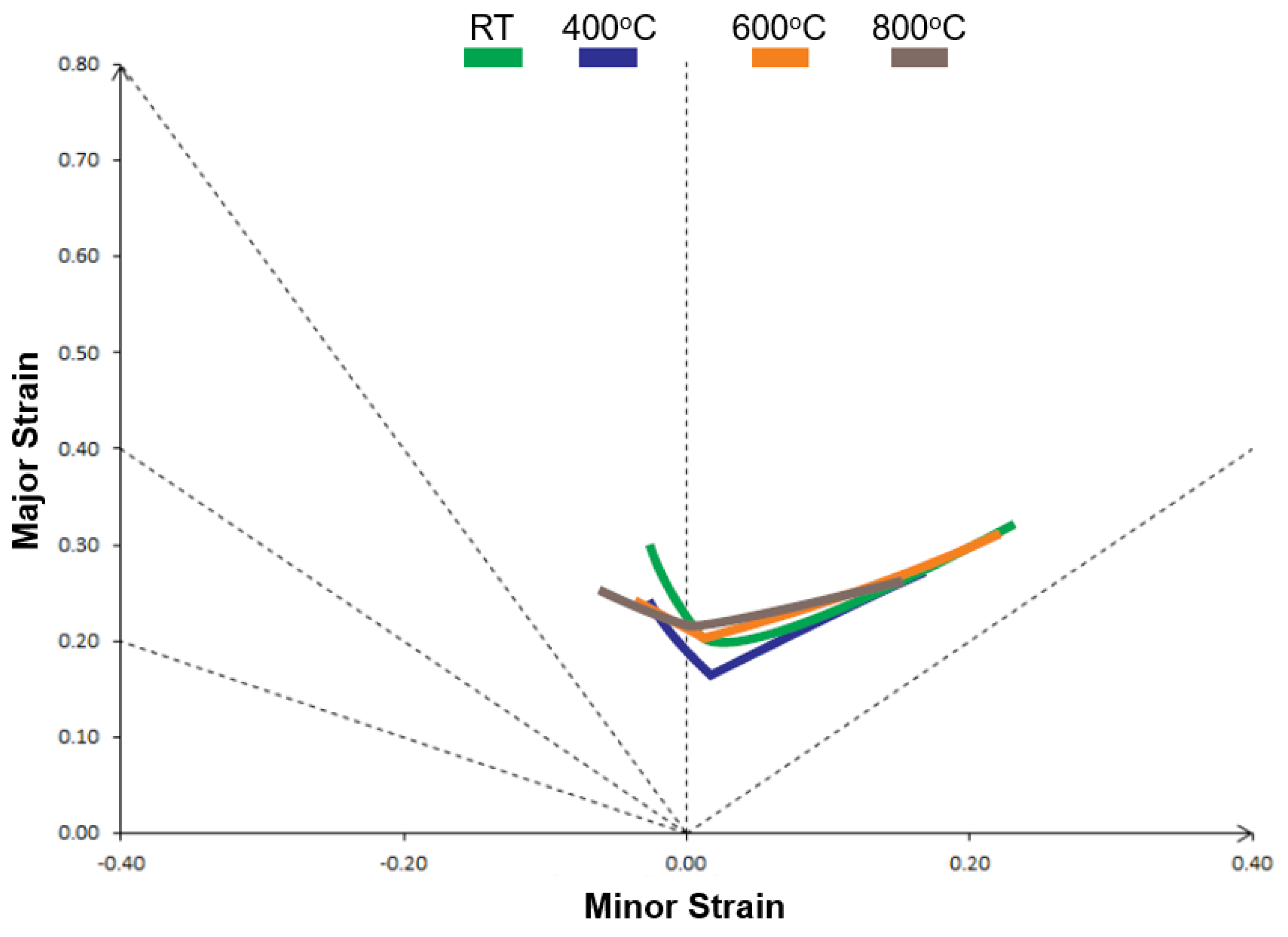
When the four predicted FLC curves from the simulations are compared (Figure 14), it is noted that there is a decrease in the forming limits at the biaxial strain deformation at 400 °C and 600 °C, compared with the curve at 30 °C. For the plane strain state, this same trend is observed with the addition of a sharp drop in the curve representing the test at 600 °C. In the uniaxial strain state, the four curves are presented as much closer. The curve for the simulation prediction at 800 °C approaches all aspects of the FLC of 30 °C.

In terms of a quantitative comparison, three reference points were taken. In addition to the point on the central axis, which represents the plan strain deformation, the other two extreme deformations, i.e., the uniaxial and biaxial points of both curves, were also compared. The values indicated in

Table 6. Experimental limit strains in HSLA350/440 steel.

Temperature (°C)	Uniaxial	Plane	Biaxial
RT	0.288	0.237	0.333
400	0.265	0.157	0.319

corresponds to the largest deformation at the major strain axis.

For HSLA 350/440 steel experiments (Figure 12 and Table 6), a significant decrease in the forming limit supported by the material when subjected to the plane strain state was demonstrated (about 34%) when tested at temperature 400 °C compared with tests at room temperature. In contrast, when the other two strain states analyzed, the decreases observed were small—approximately 8% in uniaxial and 4% in biaxial. This may be disregarded in consideration of possible measurements errors.

Therefore, the trend found agrees with the experiments by Goud et al. [11]; their experiments also experienced a significant drop in the forming limits for the plane strain deformation as the temperature increased from 150 °C to 300 °C, whereas the trend reversed at 450 °C. According to [11], two possible causes may be responsible for this behavior. The first possibility would be related to the impact of temperature on the mechanical resistance of the material, with the resistance coefficient decreasing up to a temperature of 300 °C, and at 450 °C, it increased. This phenomenon was explained by the presence of silicon and other elements that would increase the density shift due to the dynamic deformation regime for the highest temperature level of 450 °C. For comparison, [11] has 0.83% silicon and 0.39% manganese in their alloy. In this study, HSLA 350/440 steel has 0.4% silicon and 2.1% manganese. The second explanation presented by [11] would be related to the effect of temperature on the coefficient of sensitivity to the strain rate. As this coefficient is directly associated with the strain hardening coefficient, Goud et al.’s [11] study had “n” varied as follows: 0.304 at RT, 0.274 at 150 °C, 0.289 at 300 °C, and 0.261 at 450 °C. In the present study, for HSLA 350/440, the “n” varied as shown in Figure 9a.

As seen in the experiments for RT and 400 °C, the limit strains are relatively close in uniaxial and biaxial deformation. A similar trend was observed in the simulated results (Figure 14 and

Table 7. Numerical limit strains in HSLA350/440 steel.

Temperature (°C)	Uniaxial	Plane	Biaxial
RT	0.253	0.233	0.276
400	0.235	0.193	0.262
600	0.247	0.117	0.239
800	0.239	0.214	0.286

). In the plane strain mode, the limit at 400 °C shows a drop of 17% and 50% at 600 °C when compared to the limit strains at 30 °C. In the uniaxial deformation mode, the difference is negligible, and in the biaxial strain mode, the drop represents around 13%. The numerical forming limits for 800 °C are very similar, in all aspects, to the 30 °C limit strain, with no difference greater than 10%. Therefore, the results from the numerical simulation also show an effect of temperature at the plane strain deformation mode.

According to experimental tests (Figure 15 and

Table 8. Experimental limit strains in DP350/600 steel.

Temperature (°C)	Uniaxial	Plane	Biaxial
RT	0.365	0.225	0.346
400	0.315	0.211	0.301

), a decrease in the FLC of the DP 350/600 occurred at a temperature of 400 °C (compared with tests at room temperature). In the three strain states, decreases are similar, i.e., in the order of 6% to 14%. Figure 16a,b shows the comparison of experimental limits strains with the numerical prediction of the necking. It is observed that the curves do not closely agree; however, the experimental tensile stress–strain data do not provide an accurate replication of the micro deformation at the microstructure level, i.e., the interaction of the hard martensite phase with the softer ferrite phase.

When the numerical FLC’s are compared (Figure 17 and

Table 9. Numerical limit strains in DP350/600 steel.

Temperature (°C)	Uniaxial	Plane	Biaxial
RT	0.299	0.176	0.261
400	0.212	0.149	0.256
600	0.234	0.211	0.251
800	0.226	0.197	0.247

), the biggest difference in the biaxial strain state between the curves is just over 5%. In the uniaxial strain state, the second highest limit is the FLC at 600 °C (about 22% below the FLC at 30 °C), followed by the FLC at 800 °C (about 24% lower) and 400 °C, with about 29% below the curve at 30 °C. For the plane strain state, the two highest temperature curves taken exceed the FLC at 30 °C, and at 400 °C, the curve shows a limit of about 15% less than 30 °C. If similar reasoning applied as explained by Goud et al. [11], the effect of temperature would be a decrease in the limit strain on the plane strain deformation at 400 °C and then an increase to the similar value at room temperature. It is worth noting that DP 350/600 steel consist of 0.03% silicon and 0.6% manganese. Other reasoning may be related to the interaction of the hard and soft phases at higher temperature. At 400 °C, which is still lot lower than the eutectoid temperature, the deformation may be affected by the softer phase of ferrite, martensite may have held it strength, and due to higher strength difference, the material may have failed earlier than expected; while for 600 °C and 800 °C, they are just below and above the eutectoid temperature, where the martensite is about to change the phase, and the strength of this phase is comparatively less different than the softer ferrite phase; thus it has gained formability and shown higher limit strains.

4. Conclusions

This paper investigated the effect of temperature on the forming limit strain of HSLA 350/440 and DP 350/600 high-strength steels. For this, Nakazima tooling was used for the experiments. Two temperature levels were tested in the experiments. Further simulations were performed on Abaqus by modeling the same experimental setting. In addition to the two temperatures considered for the experiment, two additional higher temperature levels were simulated. The forming limit were analyzed by using the square grid for the experiments and the thickness gradient criterion for the simulations. The results are as follows. The experimentally obtained forming limits (via the Nakazima method) showed that the impact of the increase in temperature is negative with respect to the forming limits at room temperature for both steels. Simulating computational models predicting the forming limits via the thickness gradient method shows that the predicted curves have lower forming limits than those built with the experiments. For both steels, the proportion of this reduction was equivalent. This fact is probably due to the difficulty in predicting the necking during practical experiments, or the constitutive model being unable to capture the deformation mechanics at the micro level. However, the computer model was able to predict a similar trend to that observed in the experiments; i.e., a temperature of 400 °C provides the negative effect. These results also corelate with the discussion provided in the published literature. It can also be hypothesized that the hard martensite and soft ferrite phase interaction is low at 400 °C; however, it improved with the increase in temperature to 600 °C and 800 °C towards uniform formability. Temperatures of 600 °C and 800 °C are near to the eutectoid line where phase transformation initiates, and this may be the reason for the better interaction of the two phases contributing to uniform deformation. Thus, the impact of temperature cannot be generalized to provide the negative effect at higher temperatures. In the case of HSLA 350/440, the FLC at 800 °C proved to be very close to the FLC at room temperature, while 600 °C is very close to FLC at 400 °C. In the case of the DP 350/600, both curves at higher temperature levels were significantly above the FLC constructed for 400 °C.