A Selective Integration-Based Adaptive Mesh Refinement Approach for Accurate and Efficient Welding Process Simulation
Abstract
:1. Introduction
2. Concept and Implementation of Adaptive Mesh Refinement
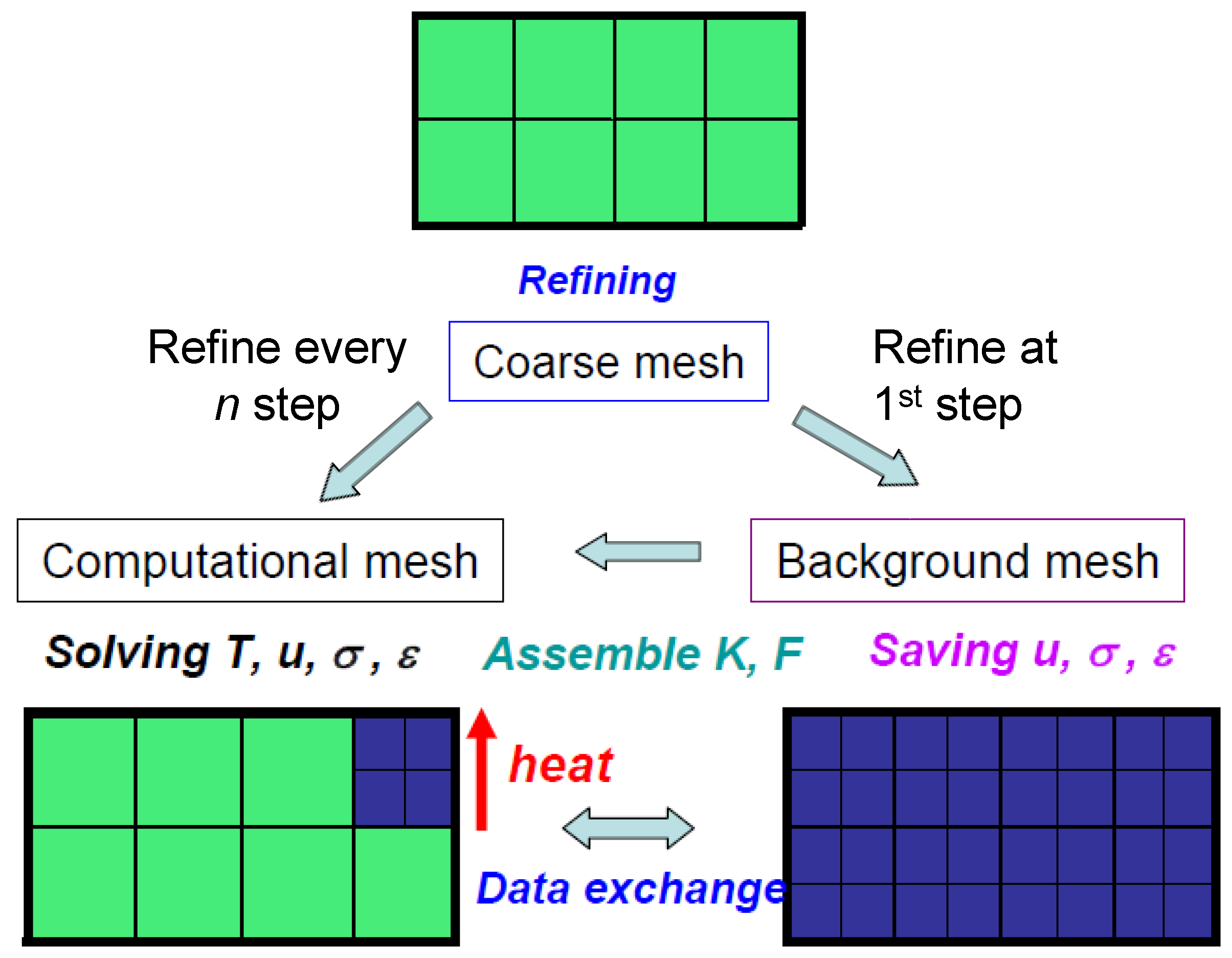
2.1. Basic Concept
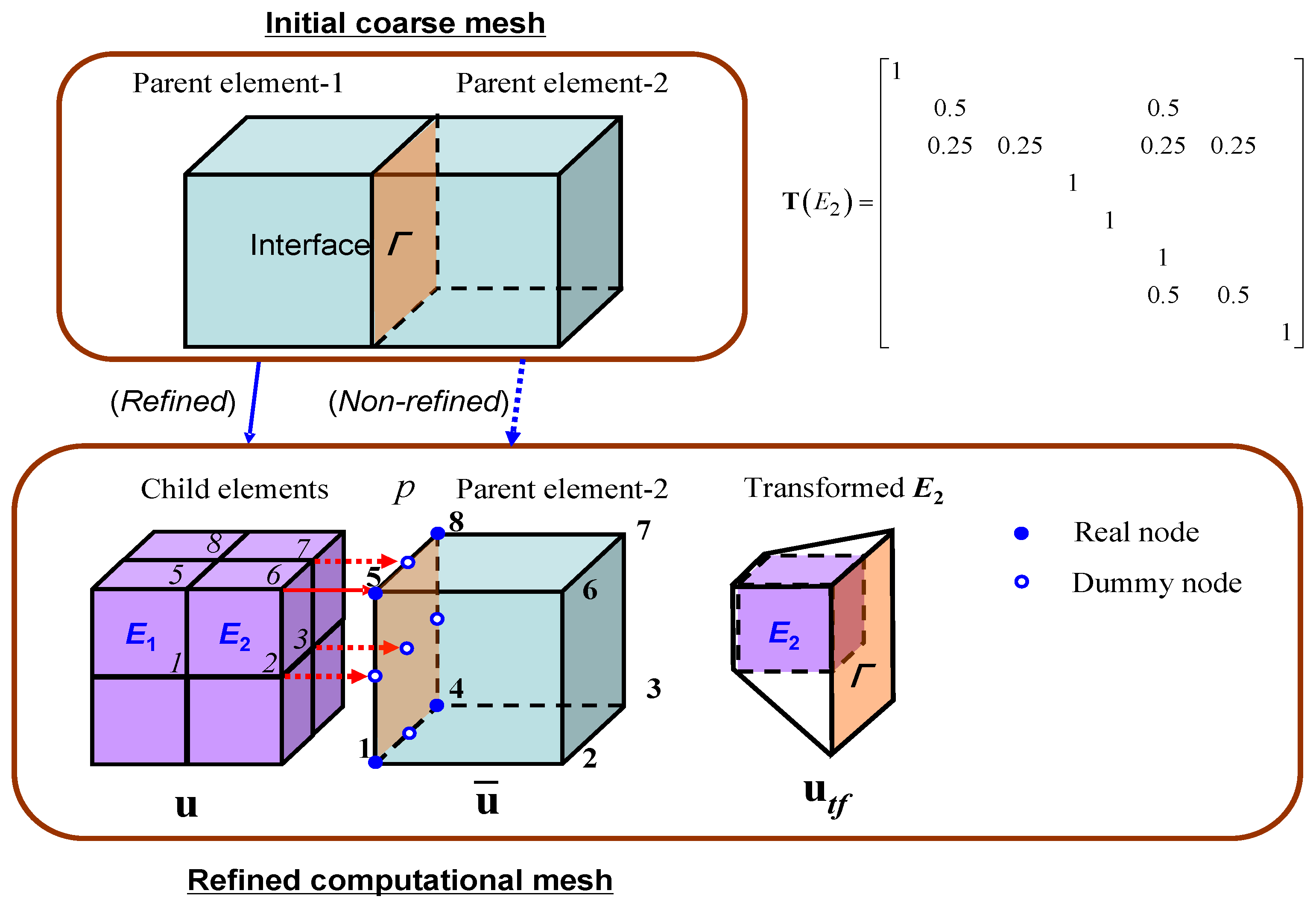
2.2. Interface Connection
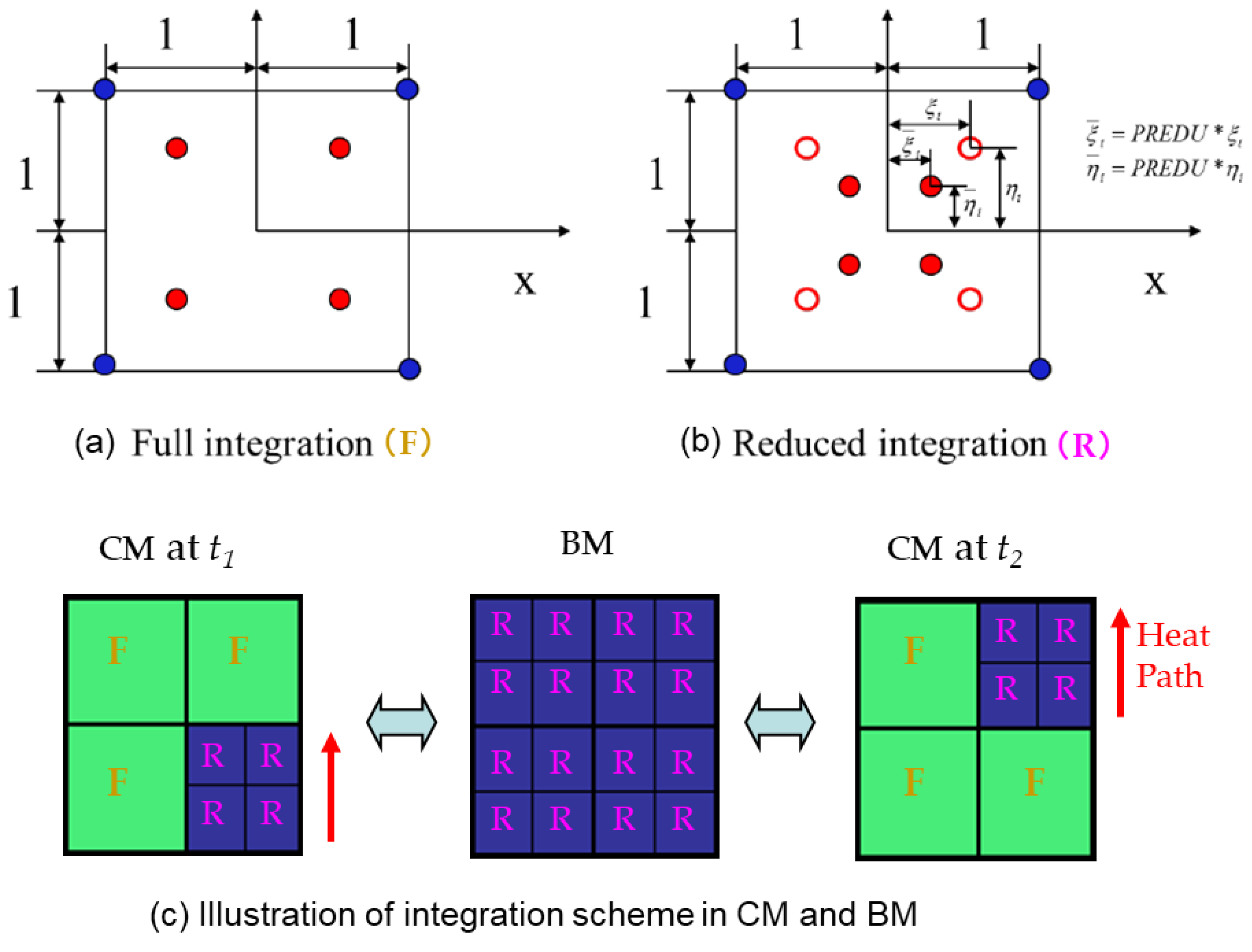
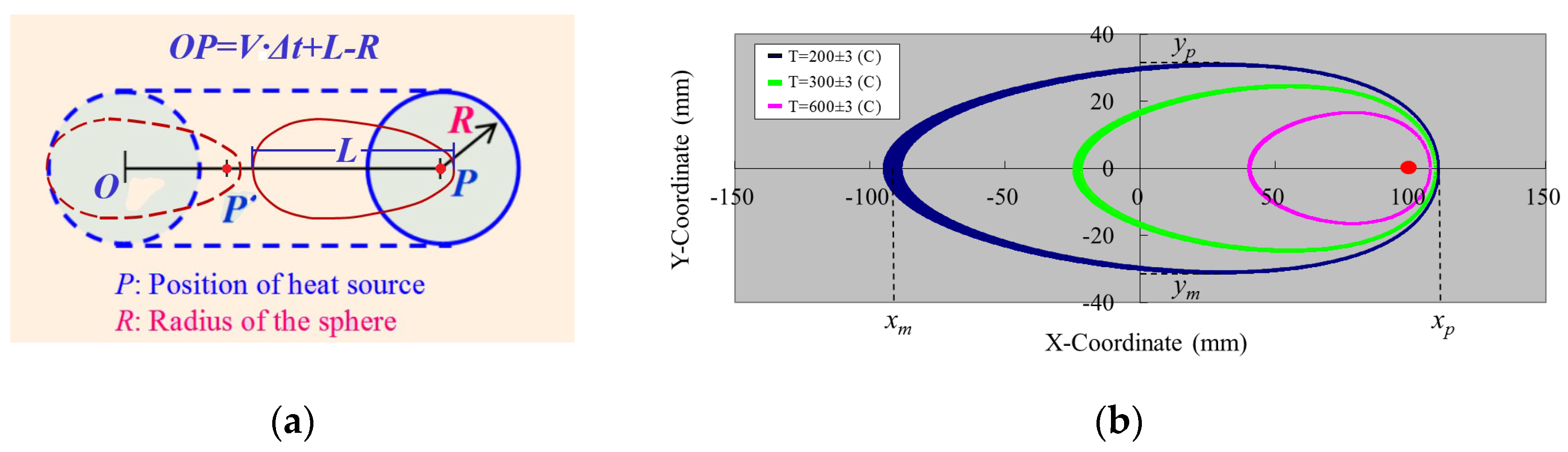
2.3. Selective Integration and Refinement Control
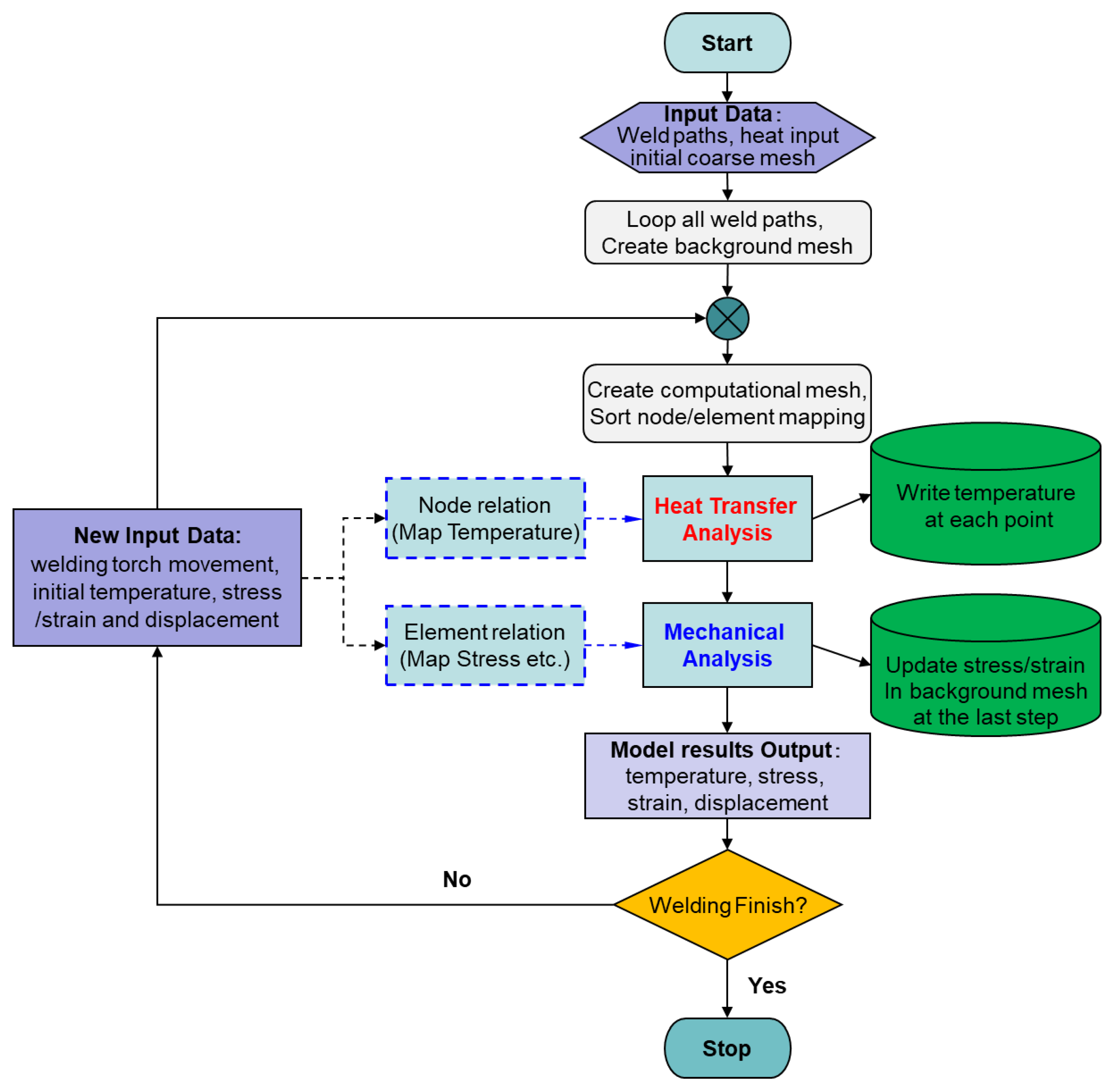
2.4. Computational Flowchart
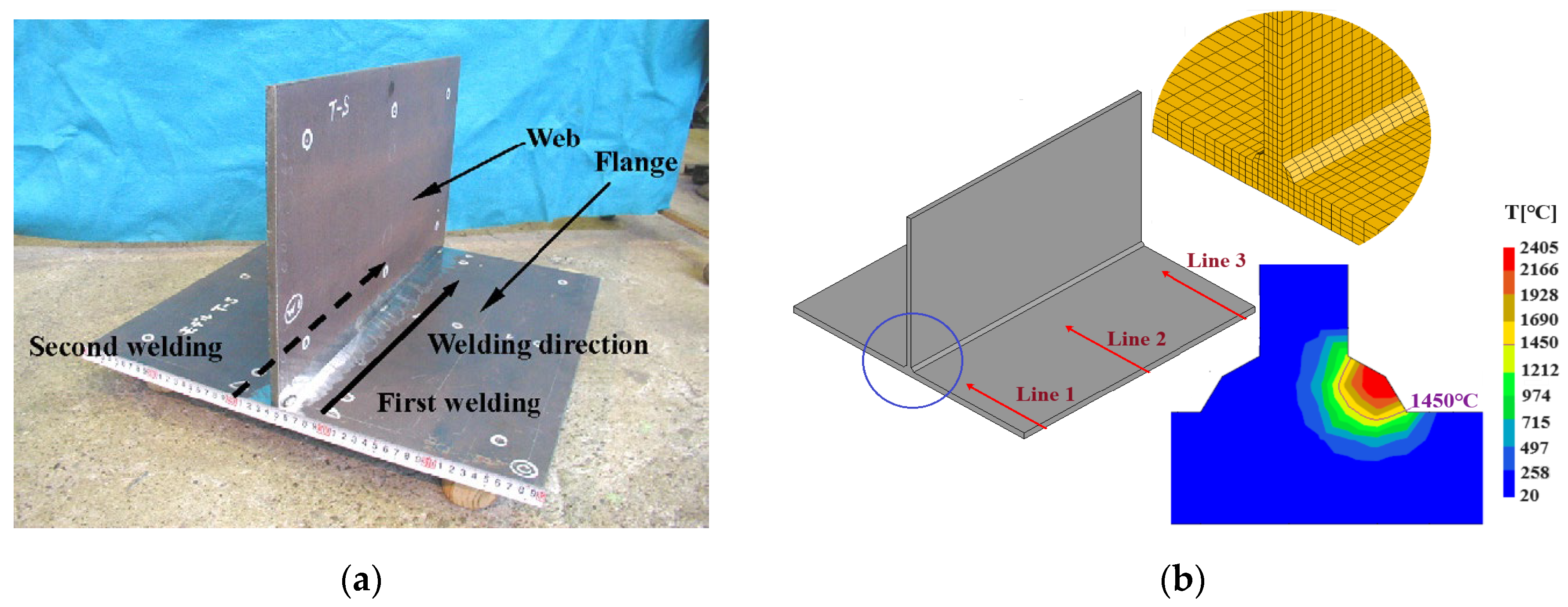
3. Validation of N-AMR by Simulation of Fillet Welding Joints
3.1. Accuracy of Conventional FEM
3.2. Study on a Larger-Size Fillet Joint
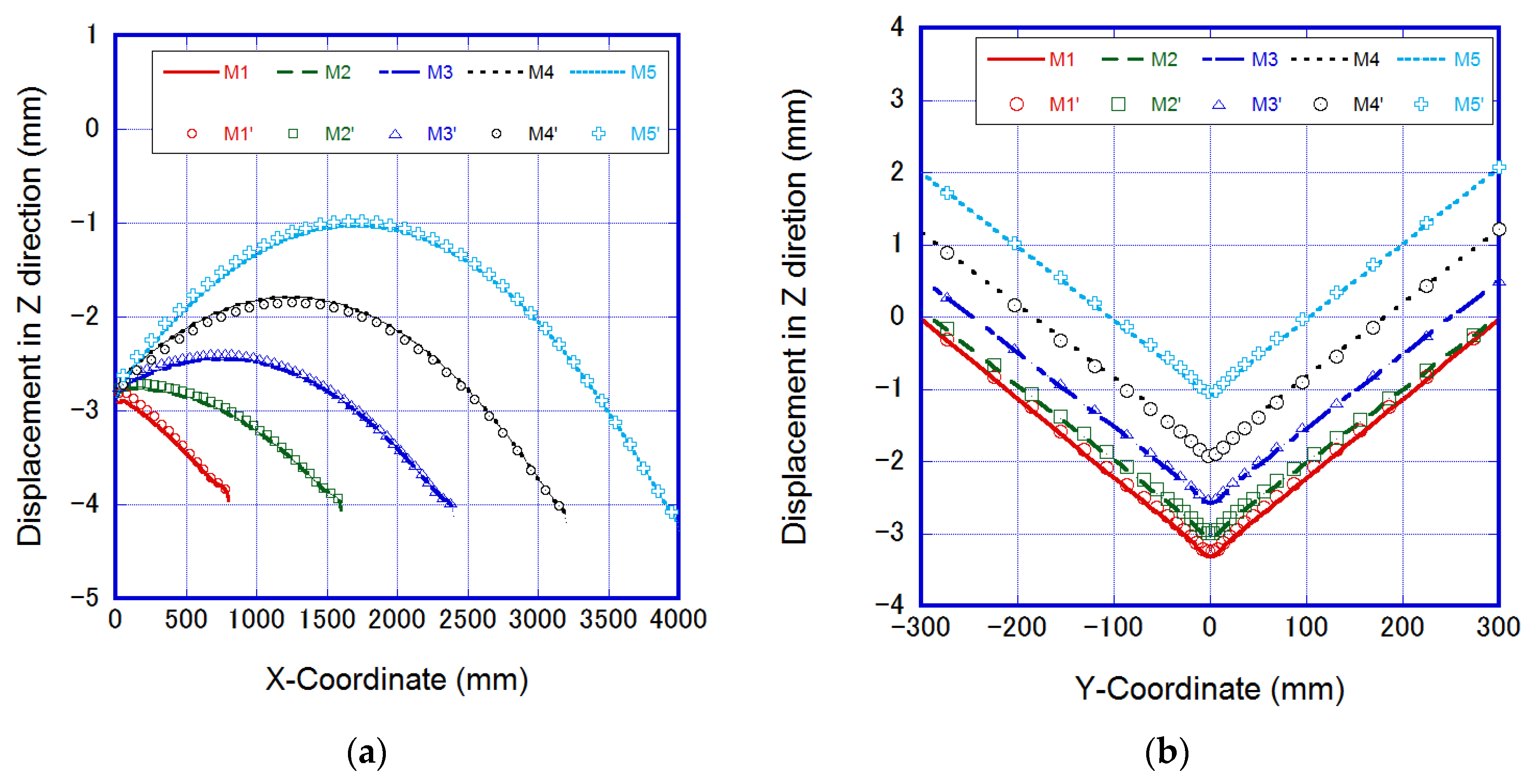
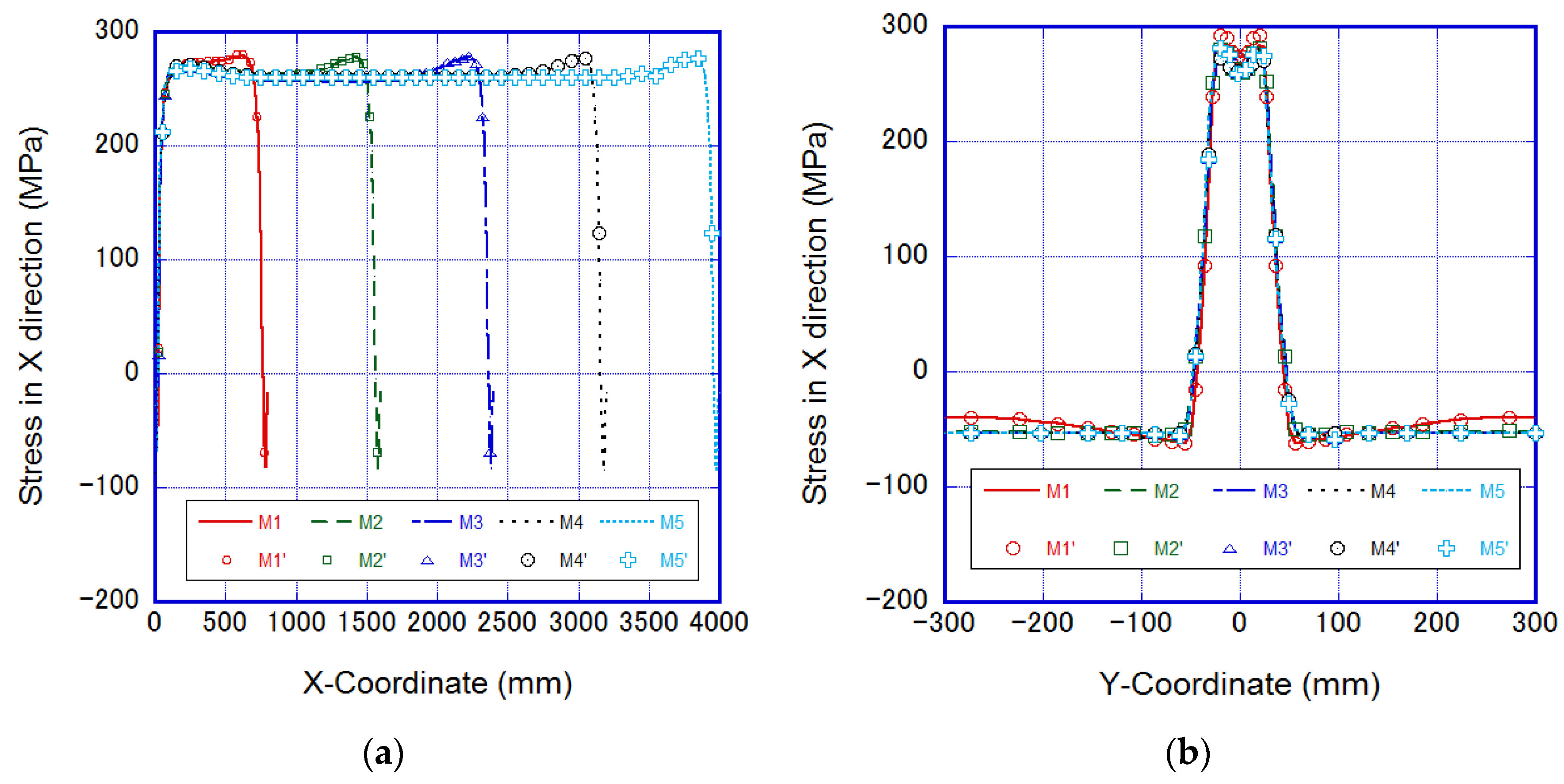
4. Results and Discussion
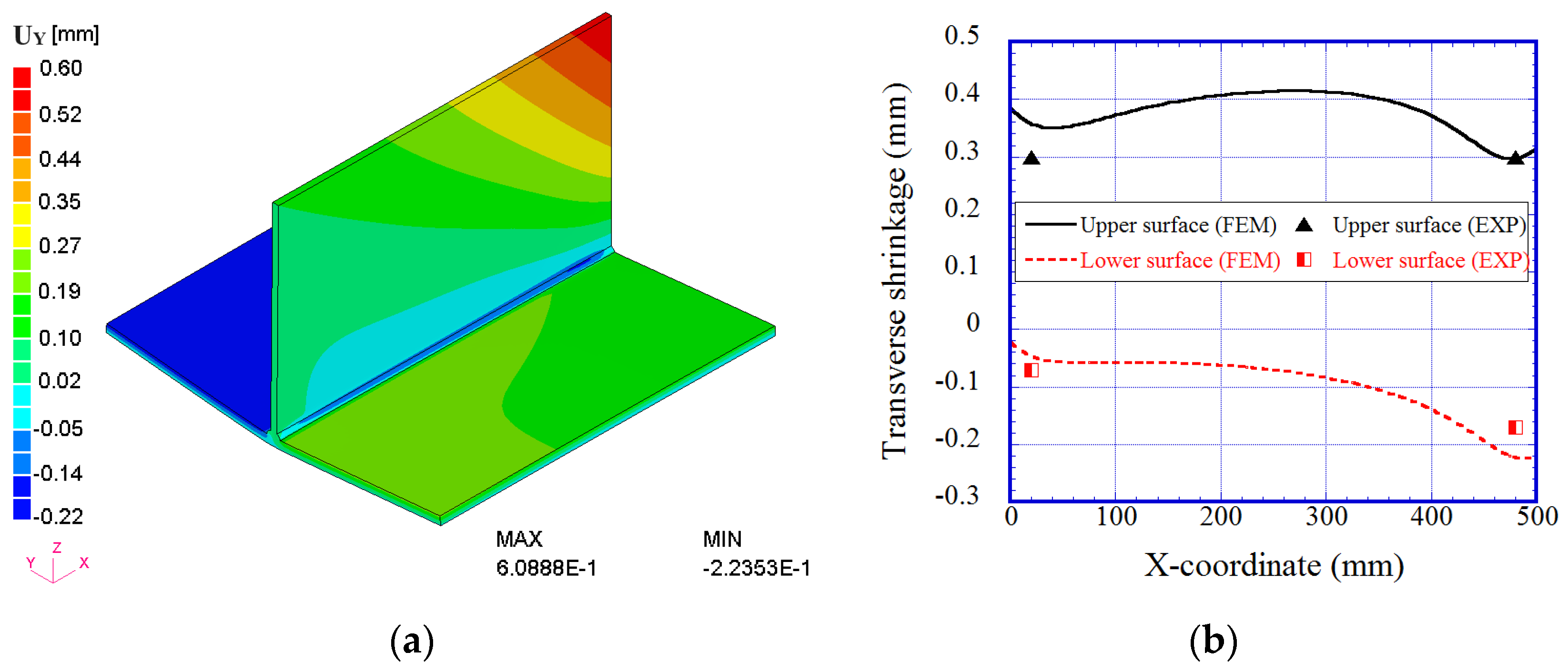
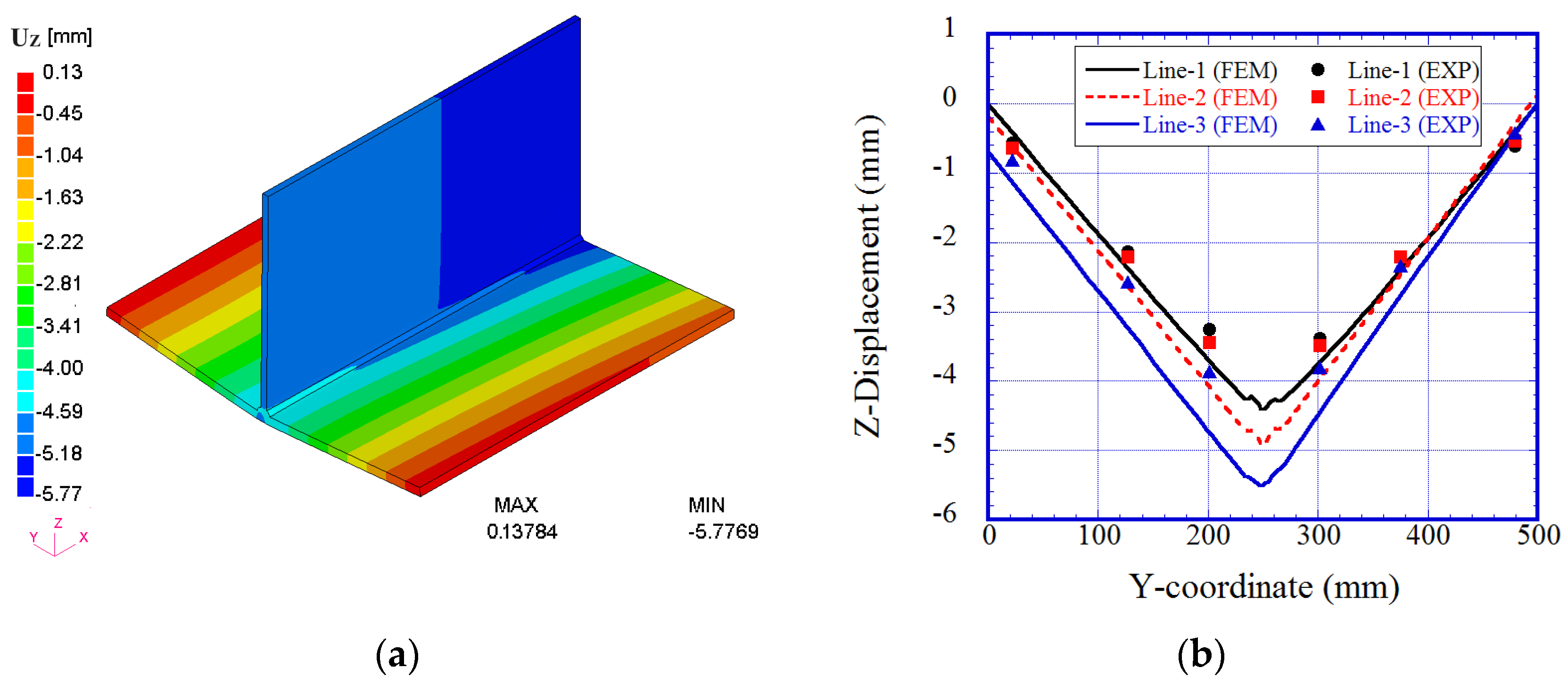
4.1. Accuracy Validation of Novel AMR
4.2. Performance of Models in Different Scales
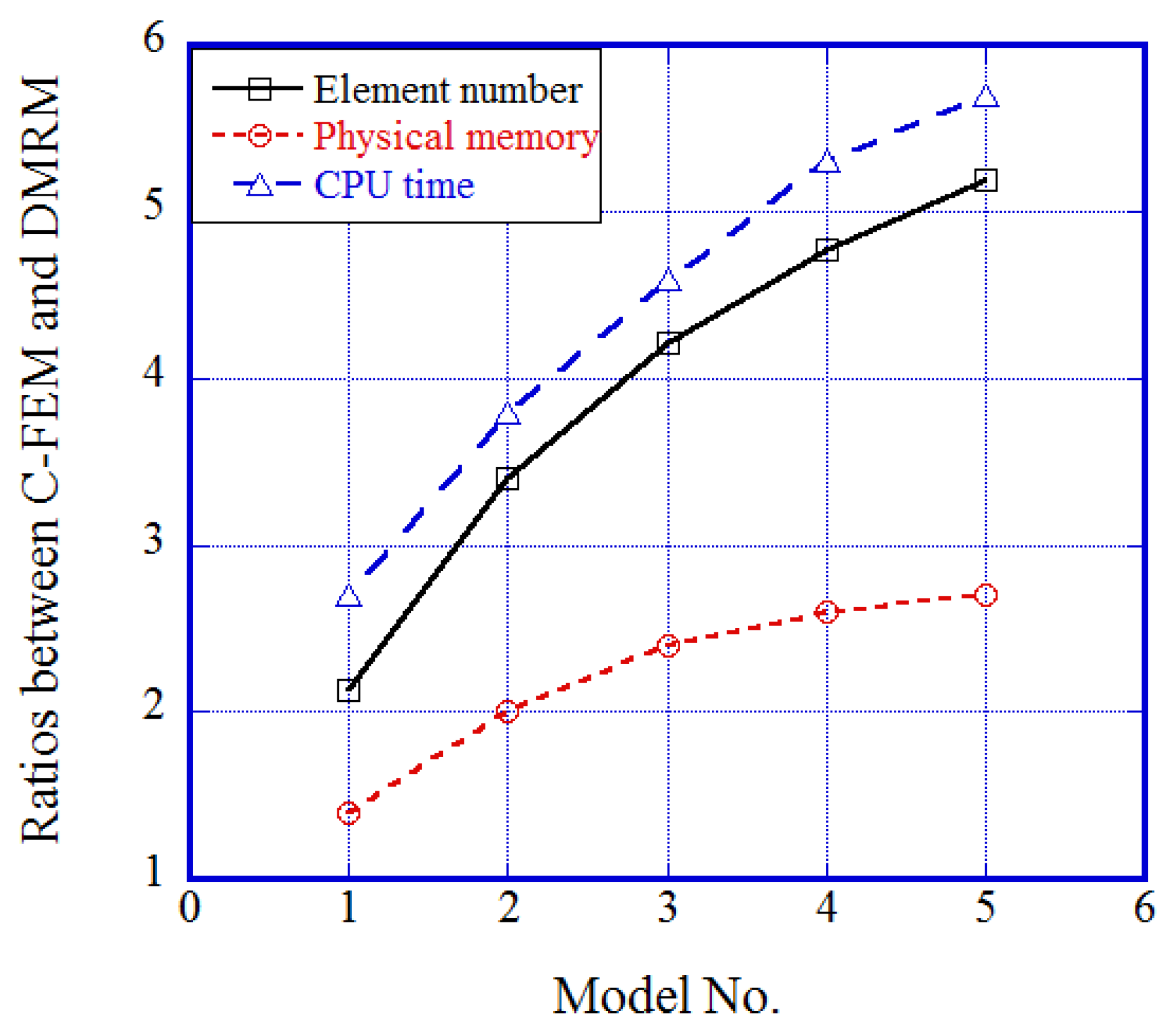
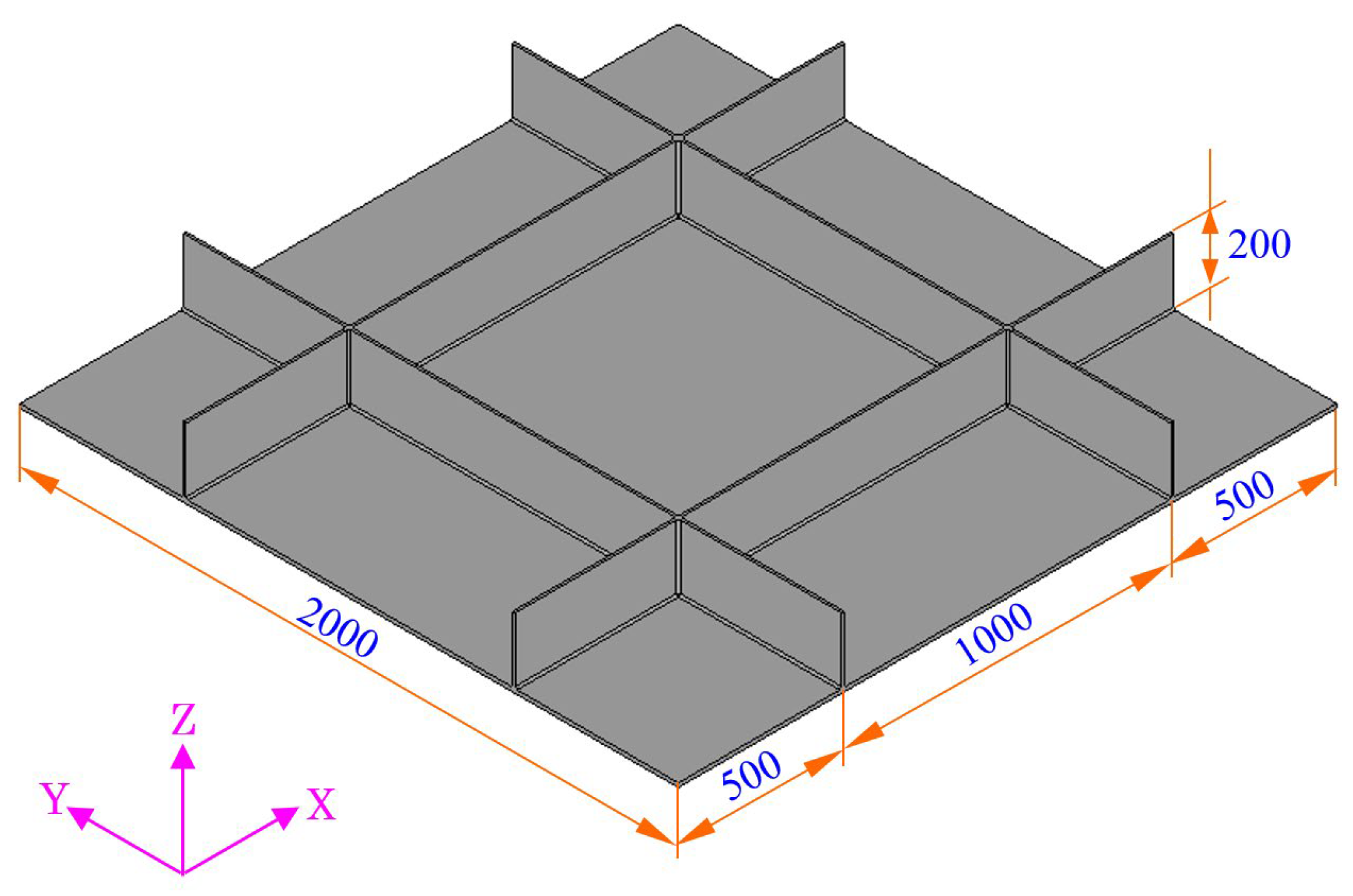
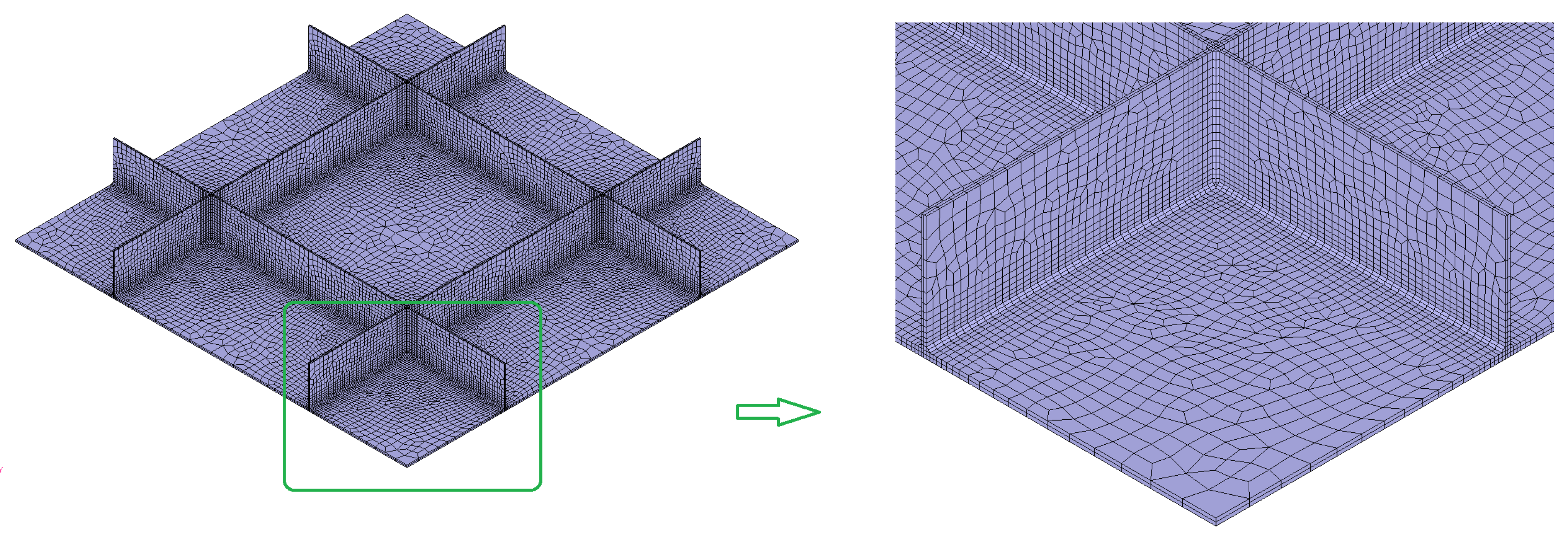
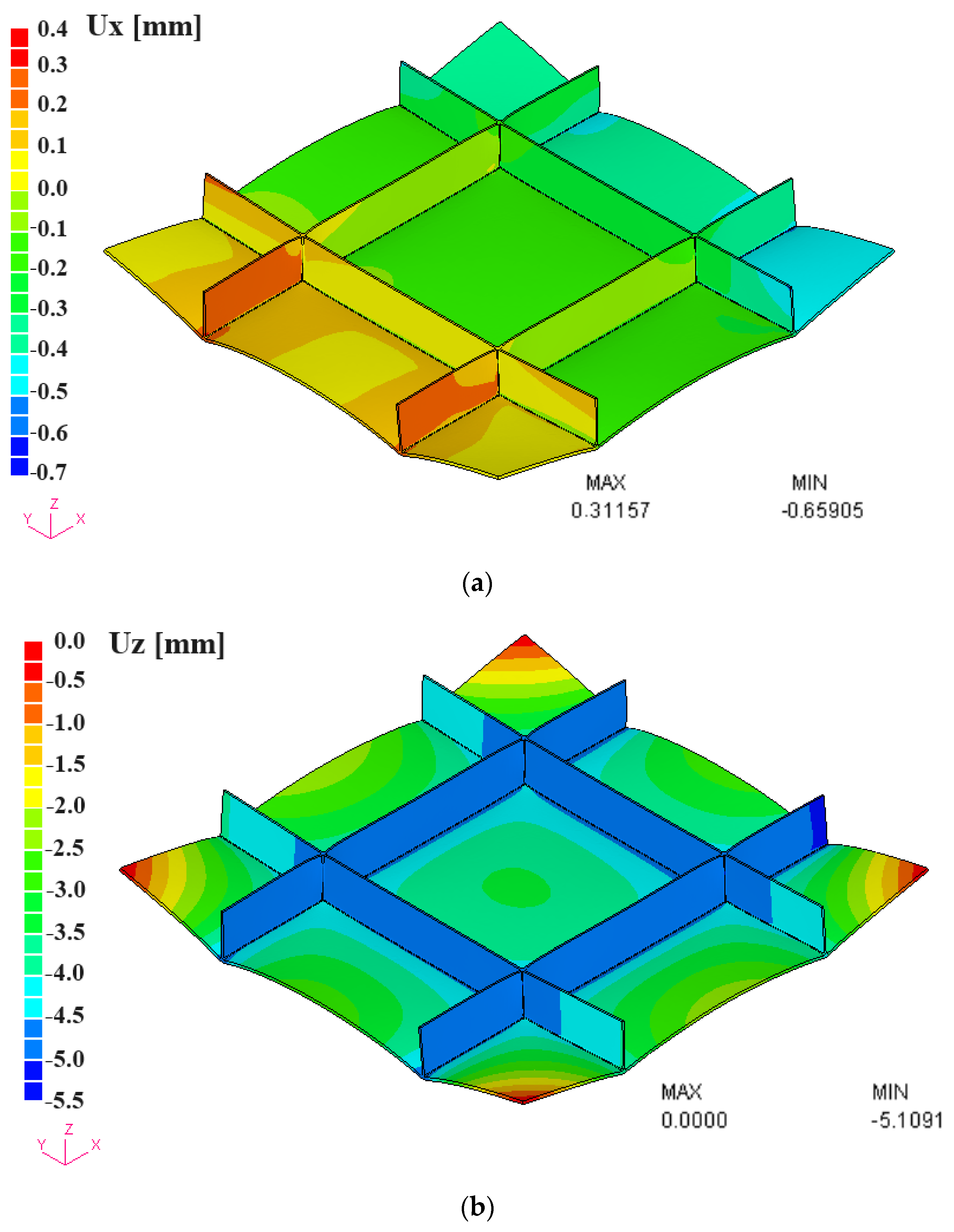
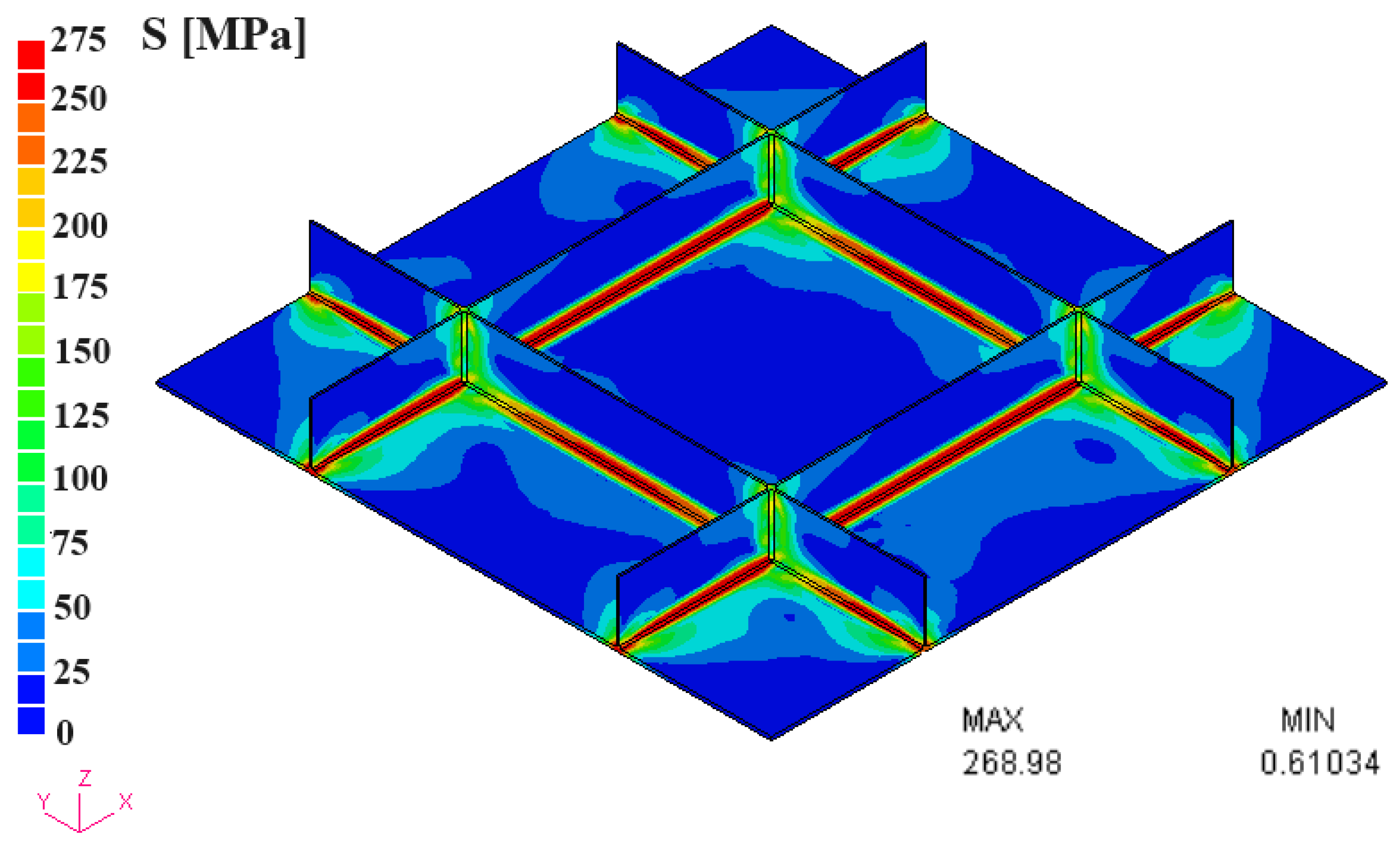
4.3. Application to a Large Stiffened Structure
5. Conclusions and Outlook
- (1)
- A novel adaptive mesh refinement (N-AMR) approach has been developed based on a selective integration scheme with reduced integration for the refined region and full integration for the coarsen region, respectively.
- (2)
- Via the introduction of a background mesh, the solution on each fine element is kept and updated to ensure the accuracy of the full model, rather than losing resolution during the mesh coarsening in ordinary AMR.
- (3)
- Since the global matrix and incremental displacements are always solved on the computational mesh, the proposed method brings a great reduction of computational time and memory cost.
- (4)
- Transient temperature, distortions, and residual stresses are compared between conventional FEM and the proposed approach. Simulation results have confirmed the accuracy of N-AMR, and the computation speed has been improved by 5.7 times in the case of a welding joint with a length of 4 m.
- (5)
- The acceleration factor increased to 7.1 for the welding simulation of a structure with a weld length of about 9 m. It can be anticipated that more savings in computational cost and physical memory can be achieved if a larger-scale structure is analyzed by the developed method. Moreover, the new AMR, developed in-house, can improve the prediction accuracy compared with traditional AMR, which is very important for engineering applications.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goldak, J.A.; Akhlaghi, M. Computational Welding Mechanics; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- O’Meara, N.; Francis, J.A.; Smith, S.D.; Withers, P.J. Development of Simplified Empirical Phase Transformation Model for Use in Welding Residual Stress Simulations. In Proceedings of the ASME 2014 Pressure Vessels and Piping Conference, PVP2014-29100, Anaheim, CA, USA, 20–24 July 2014. [Google Scholar] [CrossRef]
- Yang, Y.P. Recent Advances in Prediction of Weld Residual Stress and Distortion—Part 2. Weld. J. 2021, 100, 193–205. [Google Scholar] [CrossRef]
- Romanin, L.; Ferro, P.; Berto, F. A simplified non-linear numerical method for the assessment of welding induced deformations. Mar. Struct. 2021, 78, 102982. [Google Scholar] [CrossRef]
- Ma, N.; Deng, D.; Osawa, N.; Rashed, S.; Murakawa, H.; Ueda, Y. Welding Deformation and Residual Stress Prevention, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2022. [Google Scholar] [CrossRef]
- Ueda, Y.; Yamakawa, T. Analysis of Thermal Elastic-plastic Stress and Strain during Welding by Finite Element Method. Trans. Jpn. Weld. Soc. 1971, 2, 186–196. [Google Scholar]
- Andersson, B.A.B. Thermal stresses in a submerged-arc welded joint considering phase transformations. J. Eng. Mater. Technol. Trans. ASME 1978, 100, 356–362. [Google Scholar] [CrossRef]
- Ueda, Y.; Kim, Y.C.; Garatani, K.; Yamakita, T.; Bang, H.S. Mechanical Characteristics of Repair Welds in Thick Plate (Report I): Distributions of Three-dimensional Welding Residual Stresses and Plastic Strains and Their Production Mechanisms. Trans. JWRI 1986, 15, 359–368. [Google Scholar]
- Tekriwal, P.; Stitt, M.; Mazumder, J. A Three-dimensional Transient Finite Element Model for TIG Welding. In A Report of the Materials Engineering-Mechanical Behavior; College of Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1986; p. 130. [Google Scholar]
- Karlsson, R.I.; Josefson, B.L. Three-dimensional finite element analysis of temperatures and stresses in a single-pass butt-welded pipe. J. Press. Vessel. Technol. 1990, 112, 76–84. [Google Scholar] [CrossRef]
- Atluri, S.N.; Shen, S. The meshless local Petrov-Galerkin (mlpg) method: A simple & less-costly alternative to the finite element and boundary element methods. Comput. Model. Eng. Sci. 2002, 3, 11–52. [Google Scholar] [CrossRef]
- Sladek, J.; Sladek, V.; Atluri, S.N. Meshless local petrov-galerkin method for heat conduction problem in an anisotropic medium. Comput. Model. Eng. Sci. 2004, 6, 309–318. [Google Scholar] [CrossRef]
- Beygi, R.; Marques, E.; da Silva, L.F.M. Thermomechanical Analysis in Welding. In Computational Concepts in Simulation of Welding Processes; Springer Briefs in Applied Sciences and Technology; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Nishikawa, H.; Serizawa, H.; Murakawa, H. Actual application of FEM to analysis of large scale mechanical problems in welding. Sci. Technol. Weld. Join. 2007, 12, 147–152. [Google Scholar] [CrossRef]
- Rong, Y.; Xu, J.; Huang, Y.; Zhang, G. Review on finite element analysis of welding deformation and residual stress. Sci. Technol. Weld. Join. 2018, 23, 198–208. [Google Scholar] [CrossRef]
- Shibahara, M.; Itoh, S.; Okada, T.; Ikushima, K.; Nishikawa, S. Prediction of residual stress in multi-pass welded joint using idealized explicit FEM. In Proceedings of the ASME 2012 Pressure Vessels and Piping Conference, Toronto, ON, Canada, 15–19 July 2012; pp. 667–675. [Google Scholar]
- Ma, N. An accelerated explicit method with GPU parallel computing for thermal stress and welding deformation of large structure models. Int. J. Adv. Manuf. Technol. 2016, 87, 195–211. [Google Scholar] [CrossRef]
- Hamide, M.; Massoni, E.; Bellet, M. Adaptive mesh technique for thermal-metallurgical numerical simulation of arc welding processes. Int. J. Numer. Methods Eng. 2010, 73, 624–641. [Google Scholar] [CrossRef]
- Hu, R.; Pang, S.; Chen, X.; Liang, L.; Shao, X. An octree-based adaptive mesh refinement method for three-dimensional modeling of keyhole mode laser welding. Int. J. Heat Mass Transf. 2017, 115, 258–263. [Google Scholar] [CrossRef]
- Lindgren, L.-E.; Haggblad, H.A.; McDillb, J.M.J.; Oddy, A.S. Automatic remeshing for three-dimensional finite element simulation of welding. Comput. Methods Appl. Mech. Eng. 1997, 147, 401–409. [Google Scholar] [CrossRef]
- Runnemalm, H.; Hyun, S. Three-dimensional welding analysis using an adaptive mesh scheme. Comput. Methods Appl. Mech. Eng. 2000, 189, 515–523. [Google Scholar] [CrossRef]
- Duranton, P.; Devauxa, J.; Robin, V.; Gilles, P.; Bergheau, J.M. 3D modelling of multipass welding of a 316L stainless steel pipe. J. Mater. Process. Technol. 2004, 153–154, 457–463. [Google Scholar] [CrossRef]
- Lindgren, L.E. Finite element modeling and simulation of welding. Part 3: Efficiency and integration. J. Therm. Stress. 2001, 24, 305–334. [Google Scholar] [CrossRef]
- Shi, Q.; Lu, A.; Zhao, H.; Wu, A.P. Development and application of the adaptive mesh technique in the three-dimensional numerical simulation of the welding process. J. Mater. Process. Technol. 2002, 121, 167–172. [Google Scholar] [CrossRef]
- Huang, H.; Murakawa, H. Dynamic mesh refining and iterative substructure method for fillet welding thermo-mechanical analysis. Comput. Model. Eng. Sci. 2015, 106, 187–201. [Google Scholar] [CrossRef]
- Rykalin, N.N. Berechnung der Wärmevorgänge Beim SchweiBen (Calculation of Heat Processes during Welding); Verlag Technik: Berlin, Germany, 1957. [Google Scholar]
- Radaj, D. Heat Effects of Welding: Temperature Field, Residual Stress, Distortion; Springer: Berlin/Heidelberg, Germany, 1992; pp. 54–55. [Google Scholar]
- Chen, B.Q.; Hashemzadeh, M.; Guedes Soares, C. Numerical and experimental studies on temperature and distortion patterns in butt-welded plates. Int. J. Adv. Manuf. Technol. 2014, 72, 1121–1131. [Google Scholar] [CrossRef]
- Seles, K.; Peric, M.; Tonkovic, Z. Numerical simulation of a welding process using a prescribed temperature approach. J. Constr. Steel Res. 2018, 145, 49–57. [Google Scholar] [CrossRef]
- Deng, D.; Liang, W.; Murakawa, H. Determination of welding deformation in fillet-welded joint by means of numerical simulation and comparison with experimental measurements. J. Mater. Process. Technol. 2007, 183, 219–225. [Google Scholar] [CrossRef]
- Li, C.; Denlinger, E.R.; Gouge, M.F.; Irwin, J.E.; Michaleris, P. Numerical verification of an octree mesh coarsening strategy for simulating additive manufacturing processes. Addit. Manuf. 2019, 30, 100903. [Google Scholar] [CrossRef]

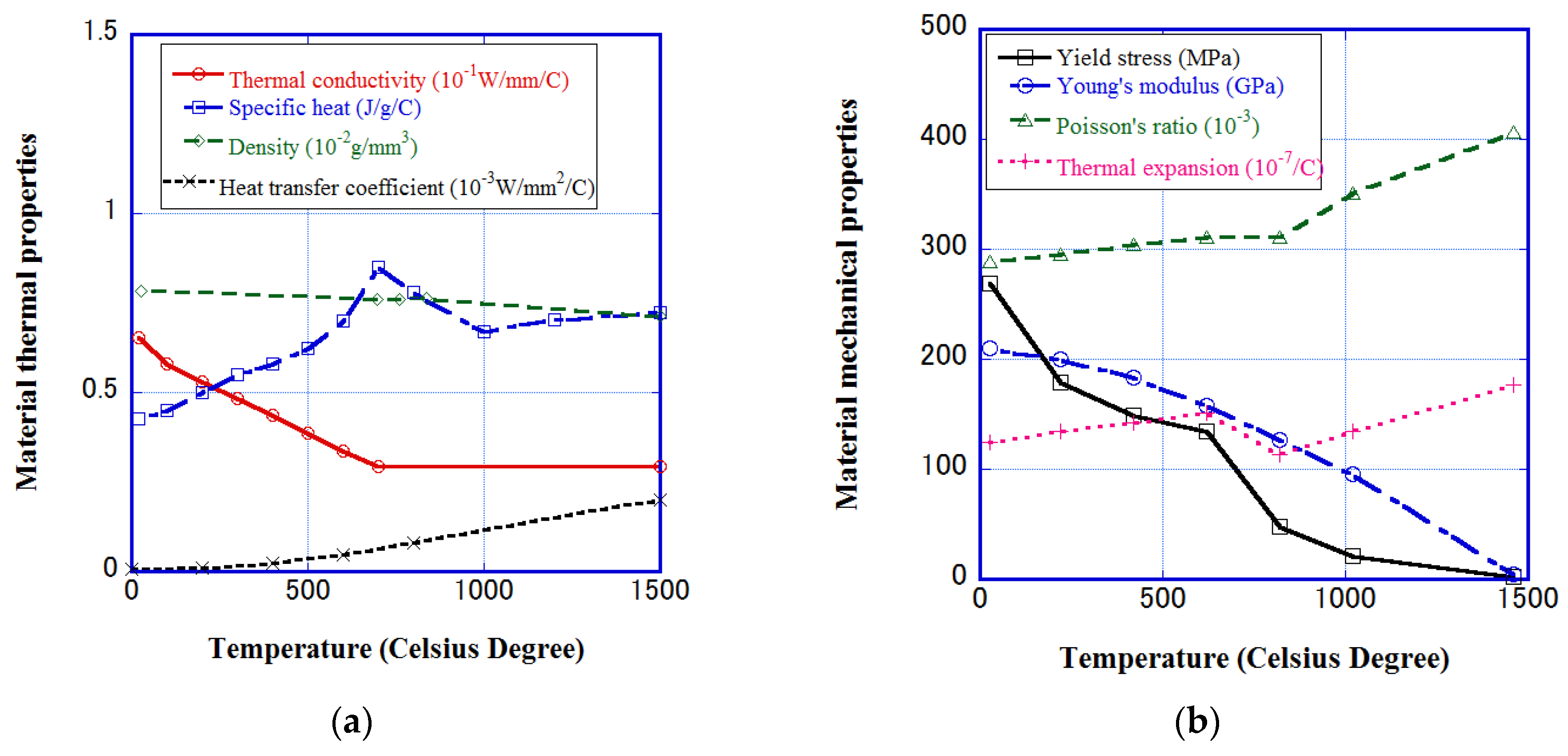
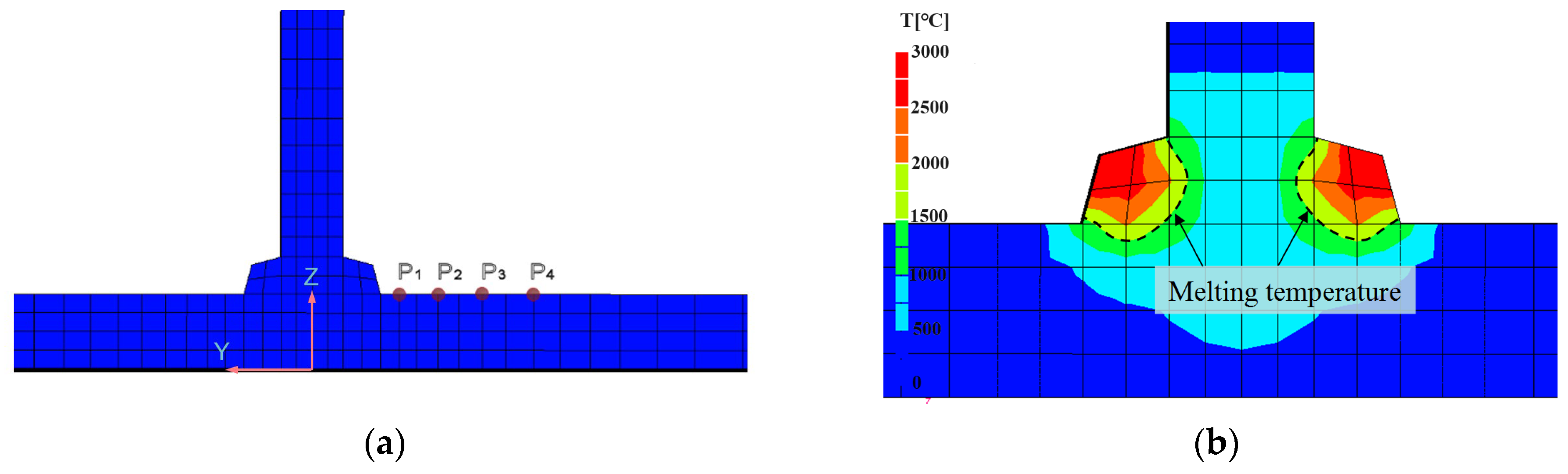
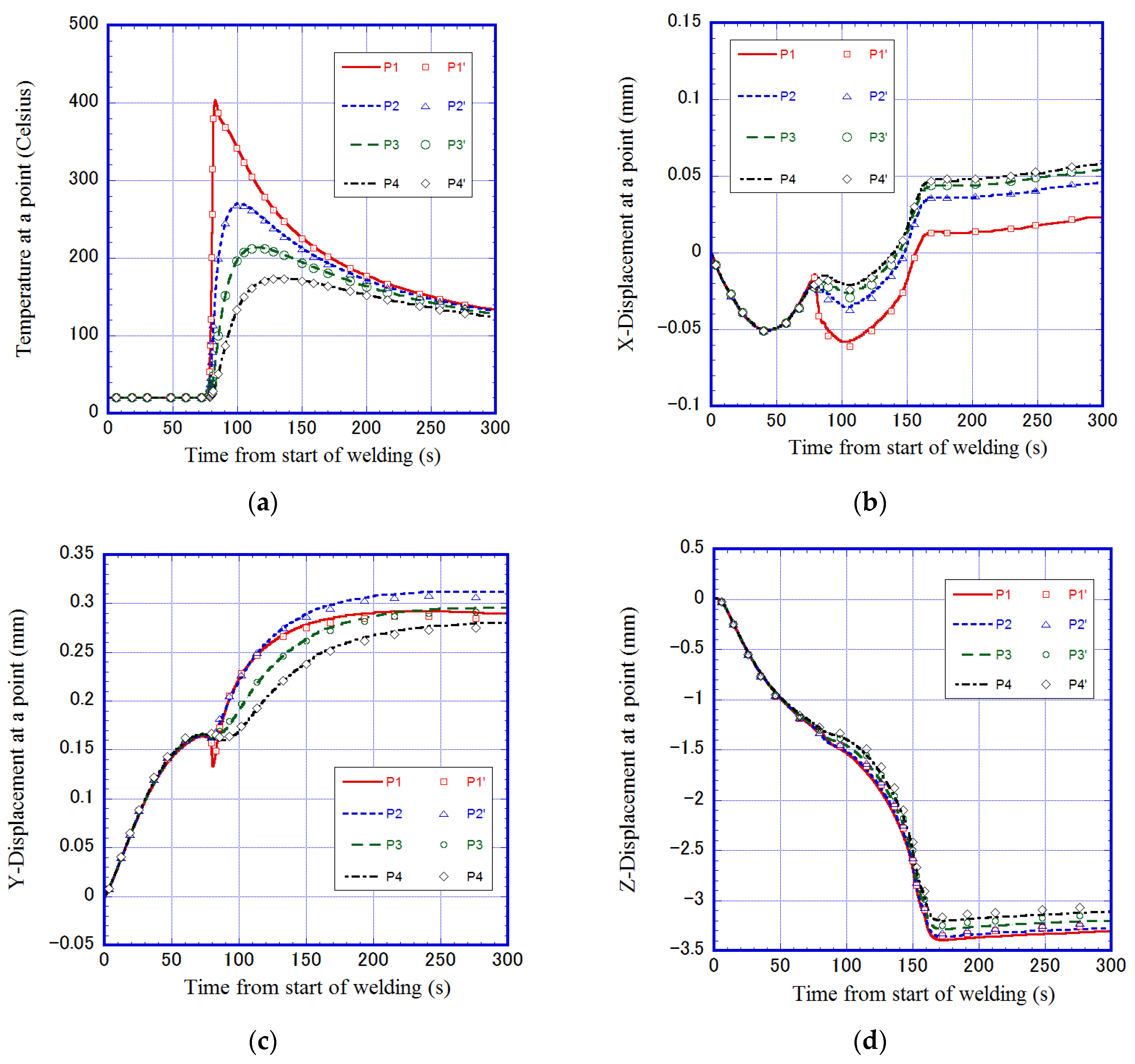
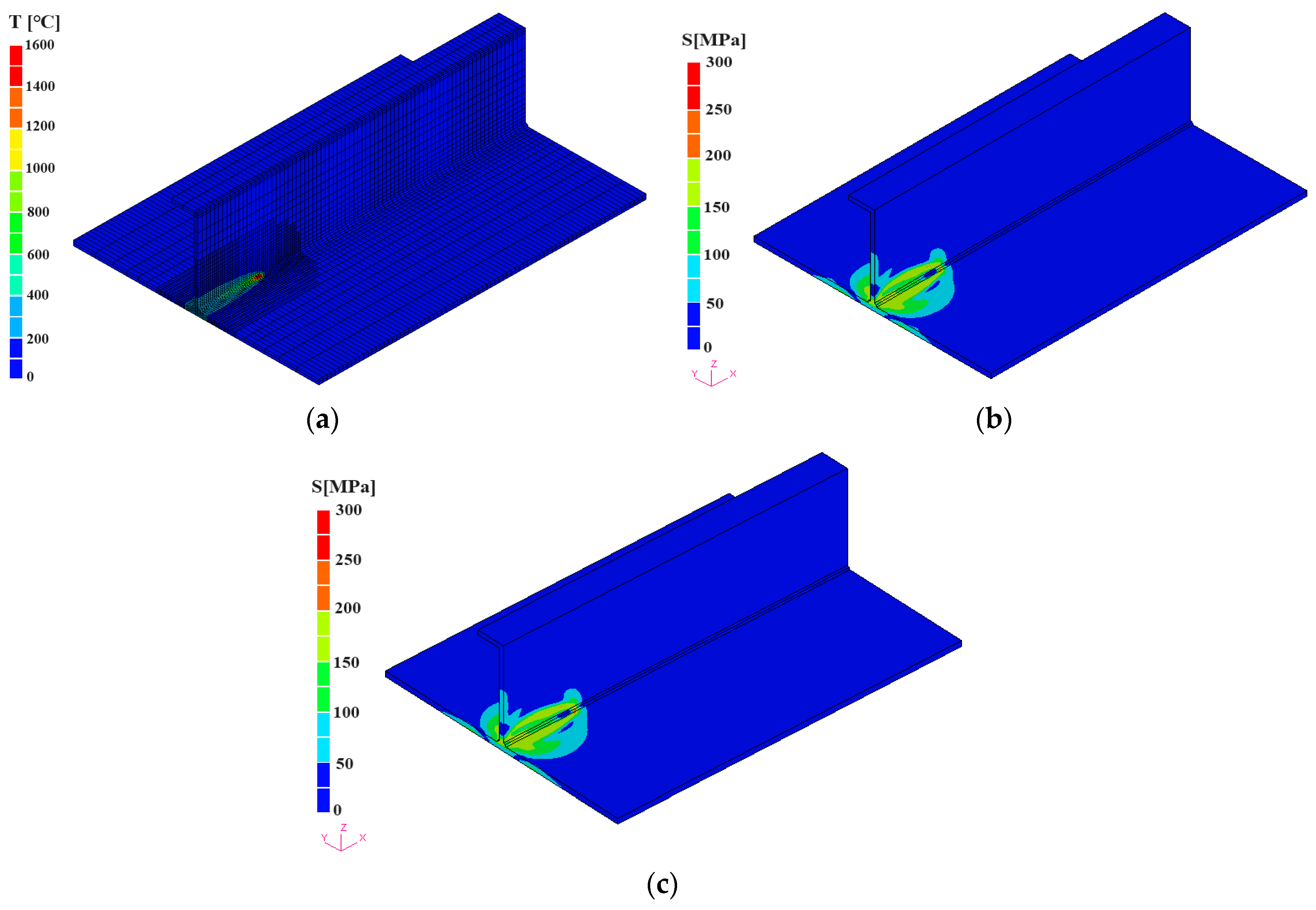
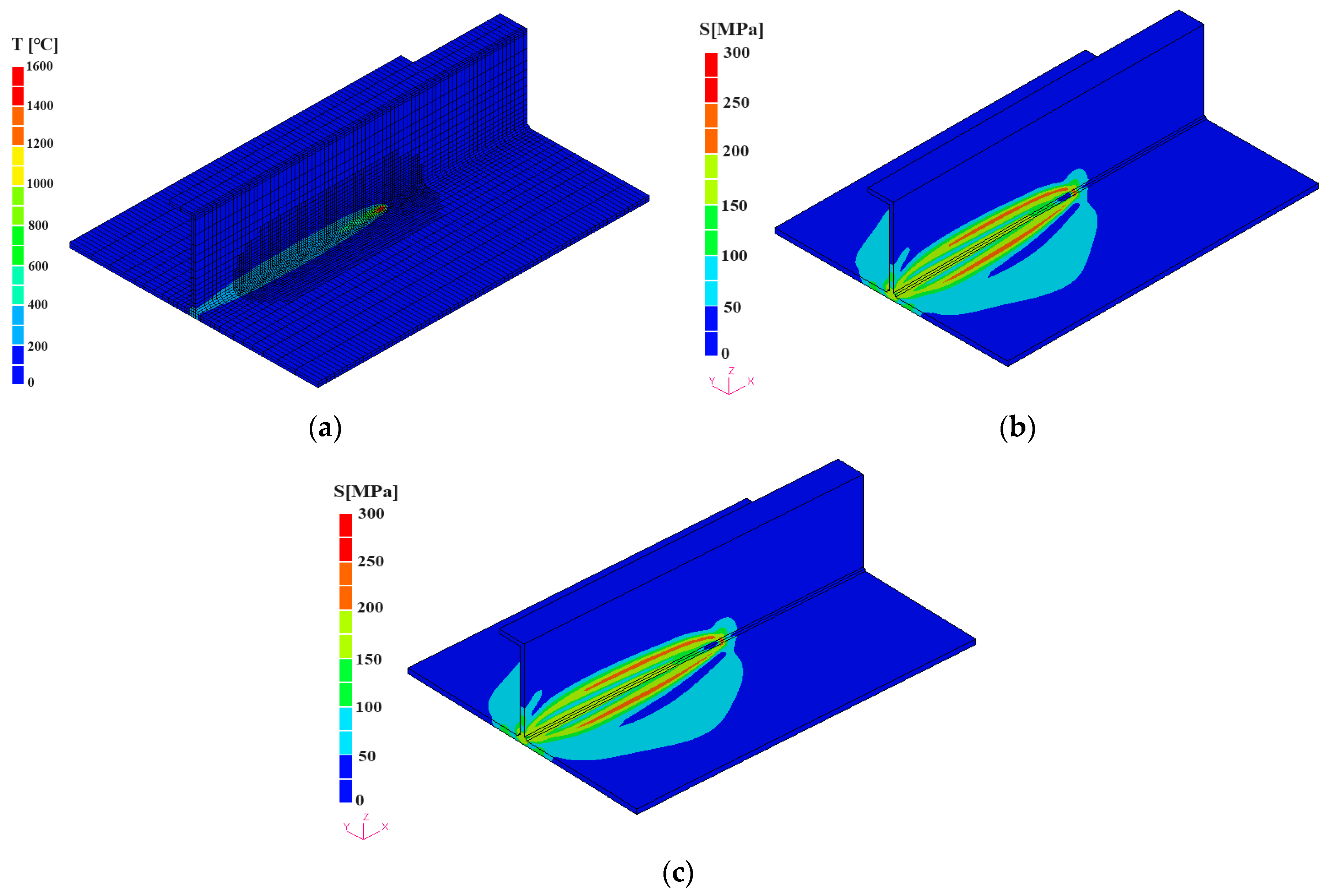

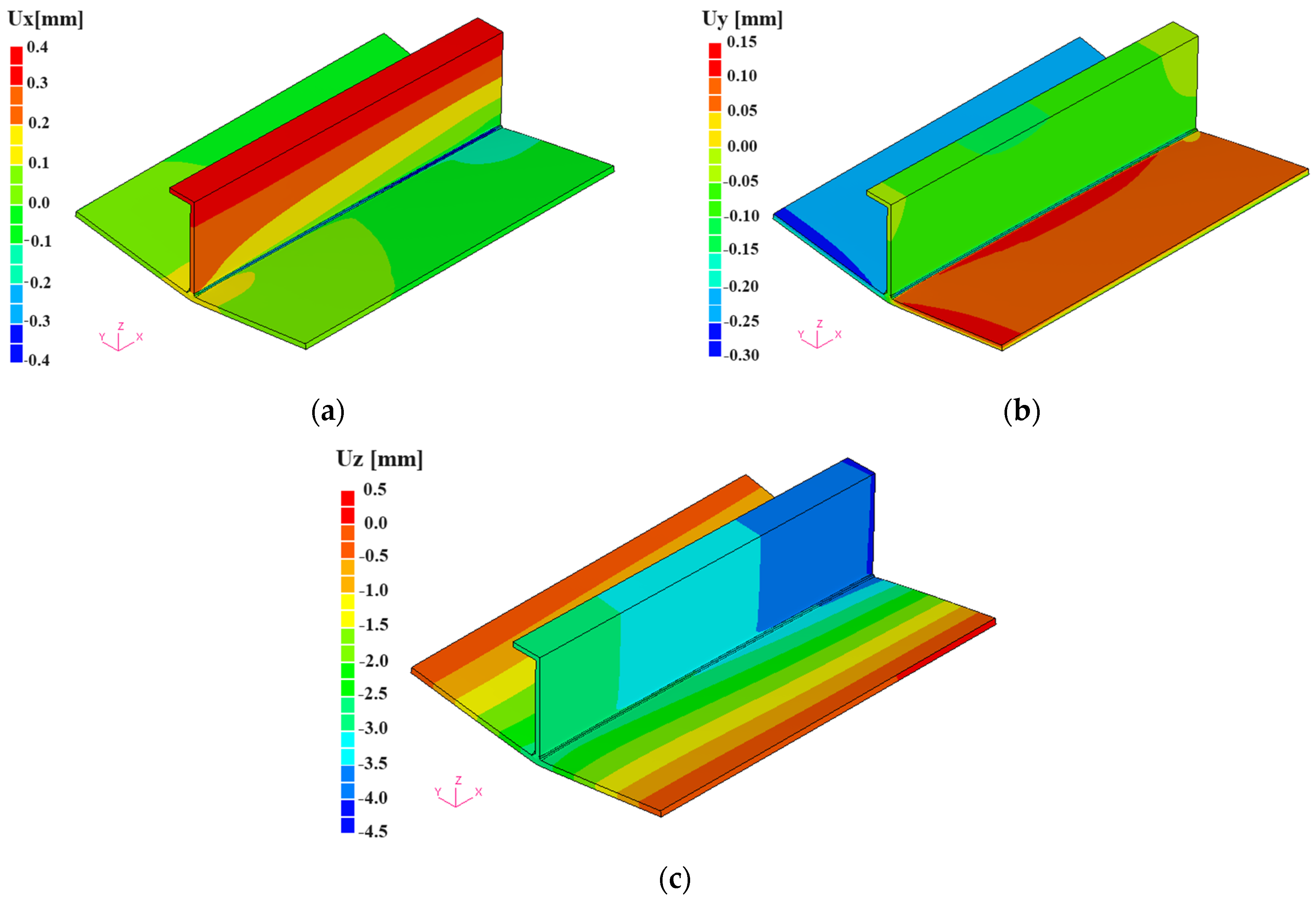
| Flange Plate mm × mm × mm | Stiffener Plate mm × mm × mm | Fillet Size mm | Voltage (V) | Current (A) | Velocity (cm/min) |
|---|---|---|---|---|---|
| 800 × 600 × 12 | 800 × 210 × 10 | 6 | 26 | 150 | 30 |
| Model No. | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|
| Length (mm) | 800 | 1600 | 2400 | 3200 | 4000 |
| Nodes | 82,593 | 164,673 | 246,753 | 328,833 | 410,913 |
| Elements | 65,280 | 130,560 | 195,840 | 261,120 | 326,400 |
| Model No. | M1 | M2 | M3 | M4 | M5 | |
|---|---|---|---|---|---|---|
| C-FEM | Clock time (h) | 13.0 | 40.1 | 77.9 | 139.2 | 199.4 |
| Memory cost (GB) | 2.2 | 4.3 | 6.7 | 8.9 | 11.2 | |
| N-AMR | Clock time (h) | 4.8 | 10.6 | 17.1 | 26.2 | 35.3 |
| Memory cost (GB) | 1.6 | 2.1 | 2.8 | 3.4 | 4.2 | |
| C-FEM/N-AMR | Ratio of time | 2.7 | 3.8 | 4.6 | 5.3 | 5.7 |
| Ratio of memory | 1.4 | 2.0 | 2.4 | 2.6 | 2.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Murakawa, H. A Selective Integration-Based Adaptive Mesh Refinement Approach for Accurate and Efficient Welding Process Simulation. J. Manuf. Mater. Process. 2023, 7, 206. https://doi.org/10.3390/jmmp7060206
Huang H, Murakawa H. A Selective Integration-Based Adaptive Mesh Refinement Approach for Accurate and Efficient Welding Process Simulation. Journal of Manufacturing and Materials Processing. 2023; 7(6):206. https://doi.org/10.3390/jmmp7060206
Chicago/Turabian StyleHuang, Hui, and Hidekazu Murakawa. 2023. "A Selective Integration-Based Adaptive Mesh Refinement Approach for Accurate and Efficient Welding Process Simulation" Journal of Manufacturing and Materials Processing 7, no. 6: 206. https://doi.org/10.3390/jmmp7060206
APA StyleHuang, H., & Murakawa, H. (2023). A Selective Integration-Based Adaptive Mesh Refinement Approach for Accurate and Efficient Welding Process Simulation. Journal of Manufacturing and Materials Processing, 7(6), 206. https://doi.org/10.3390/jmmp7060206





