Insights into Temperature Simulation and Validation of Fused Deposition Modeling Processes
Abstract
:1. Introduction
1.1. Overview of Extrusion-Based 3D Printing
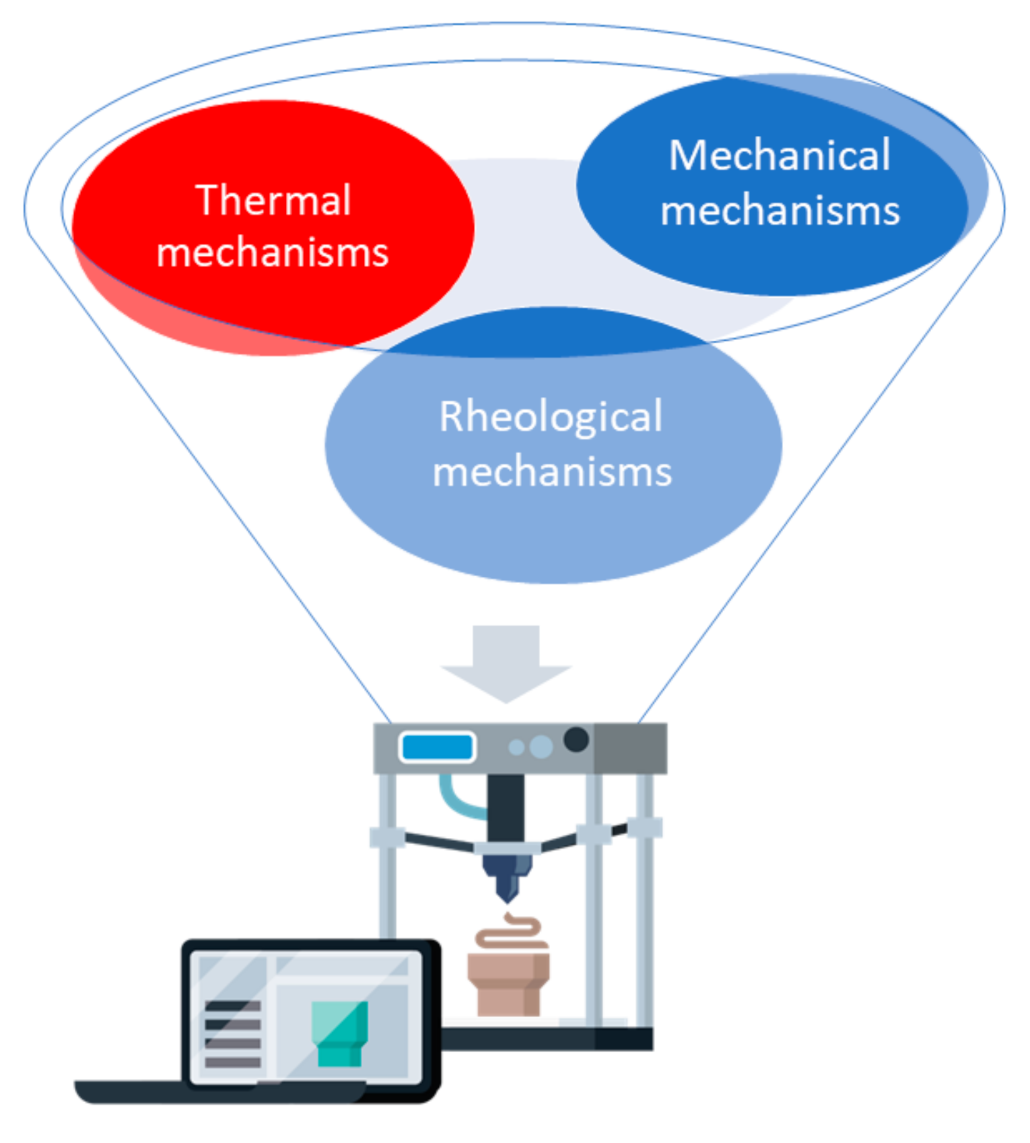
1.2. Numerical Study of Thermal Processes in 3D Printing
1.3. Summary
2. Materials and Methods
2.1. Materials and Experimental Method
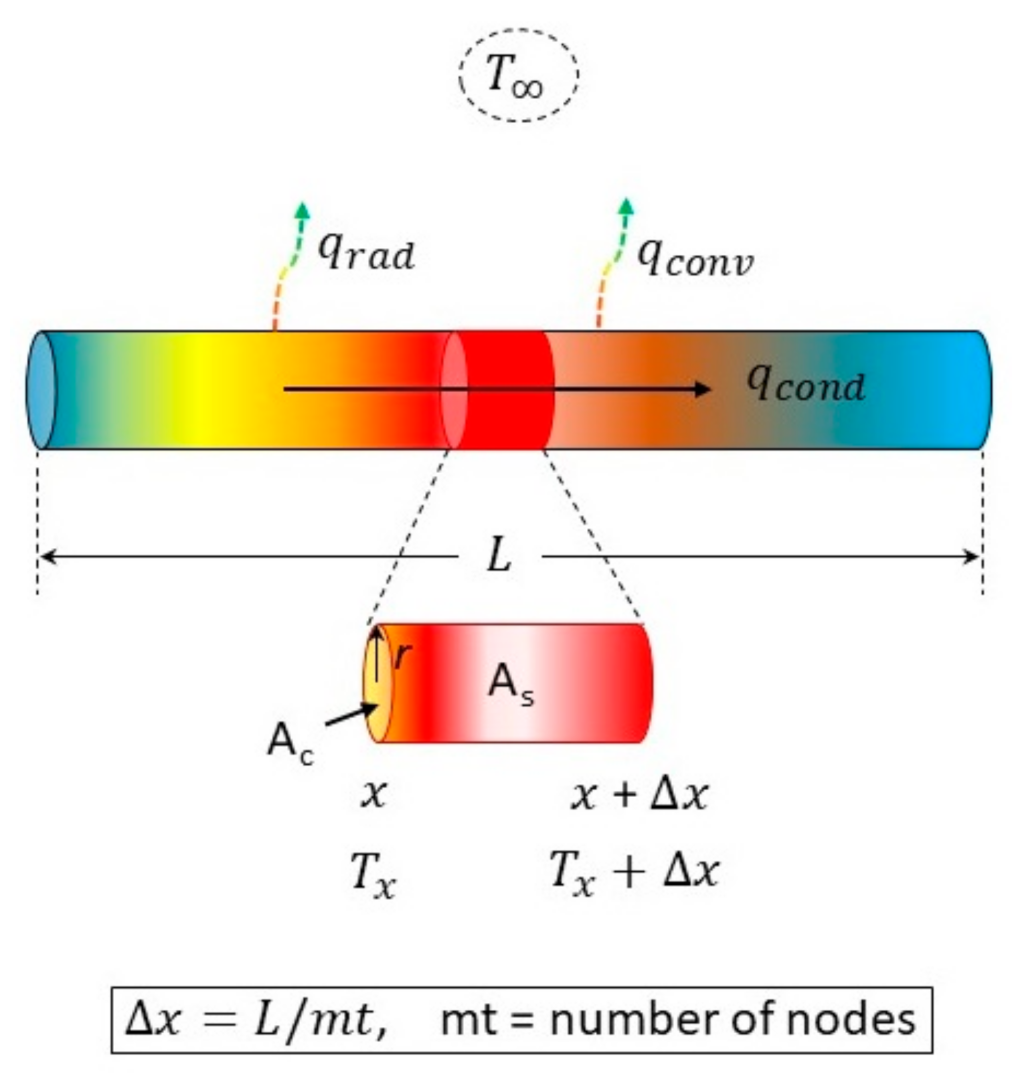
2.2. Numerical Approach
3. Results
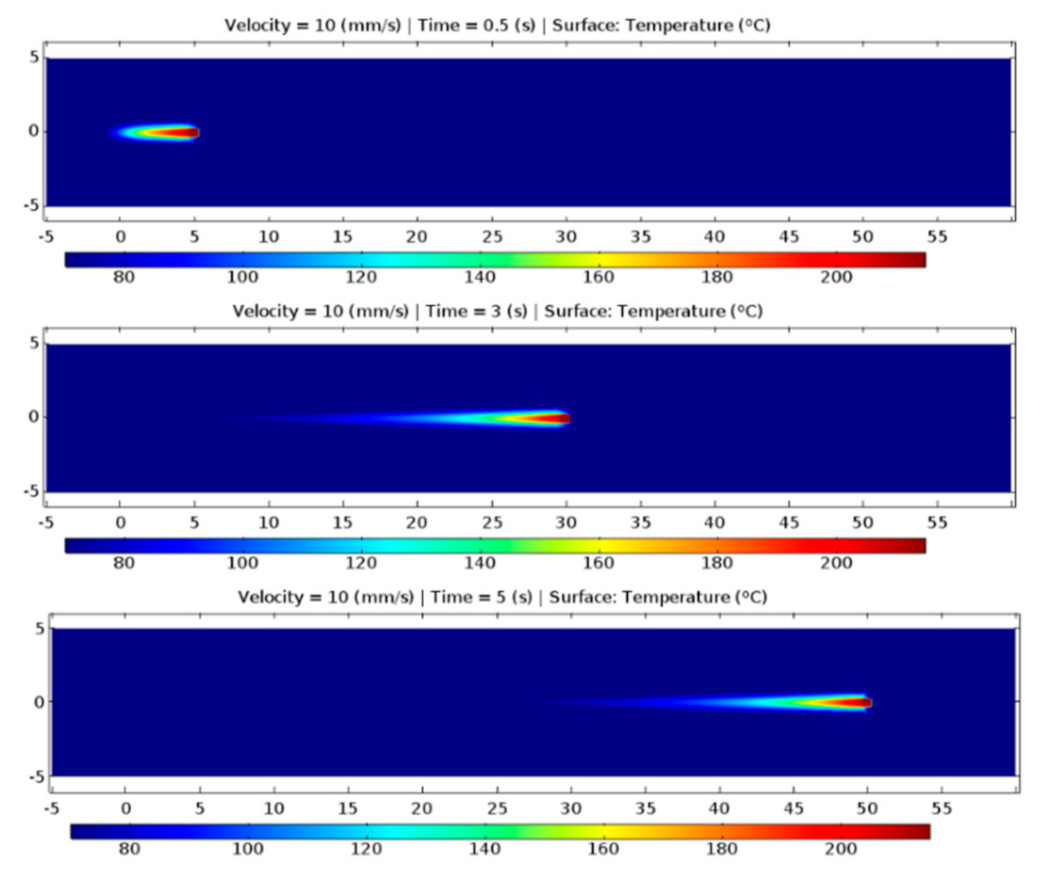
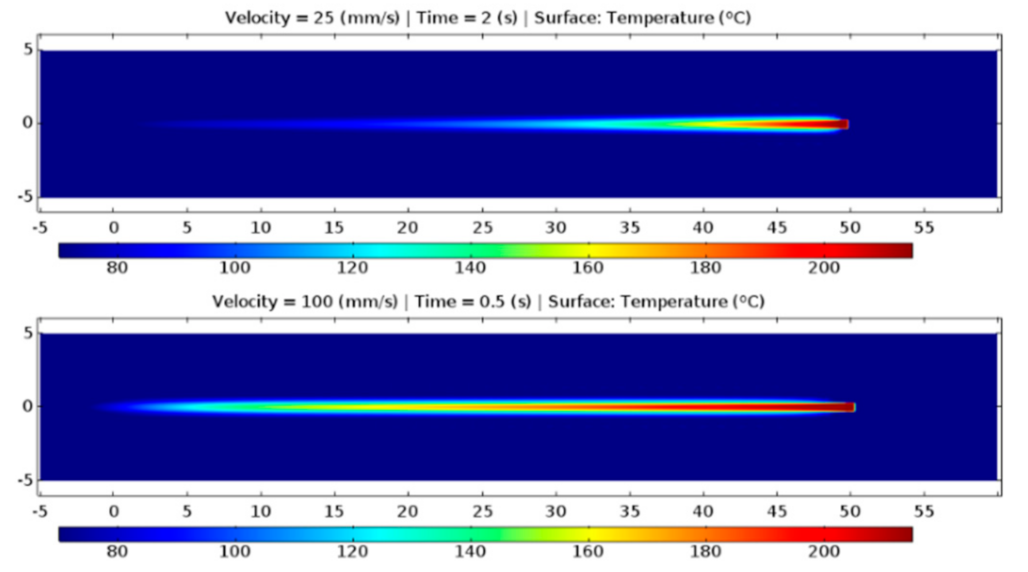
3.1. Numerical Models
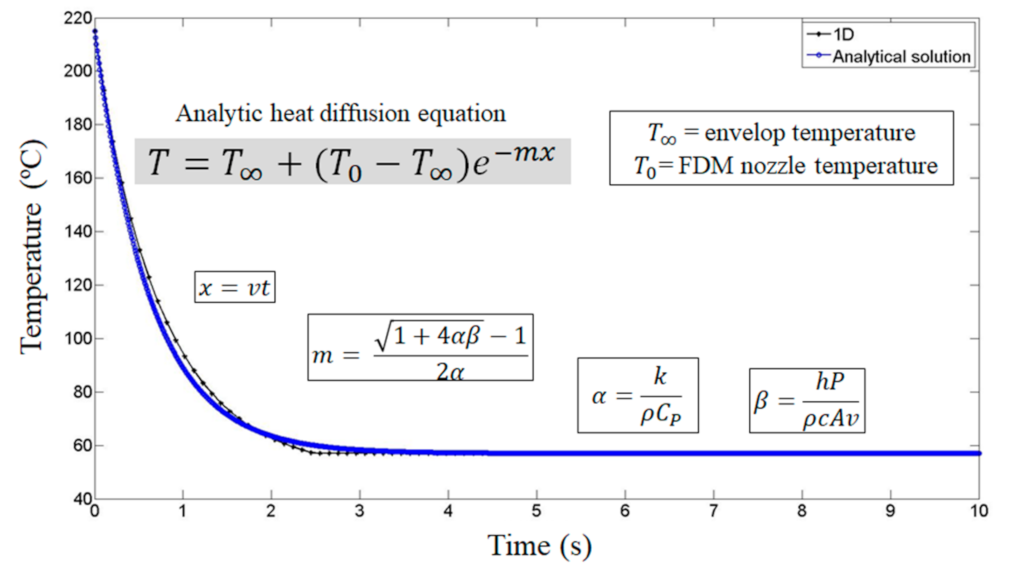
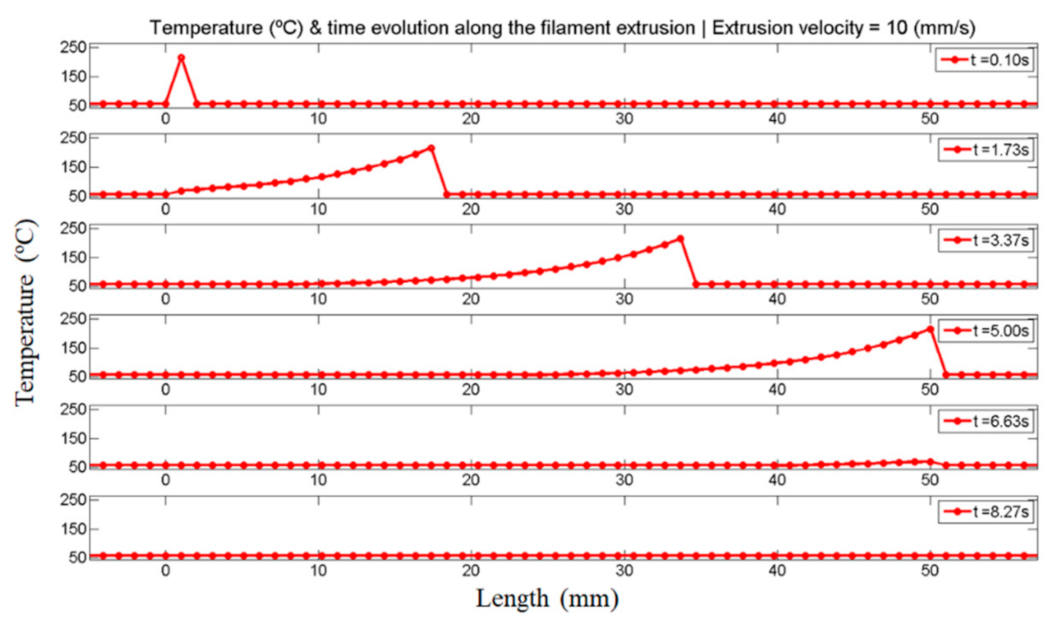
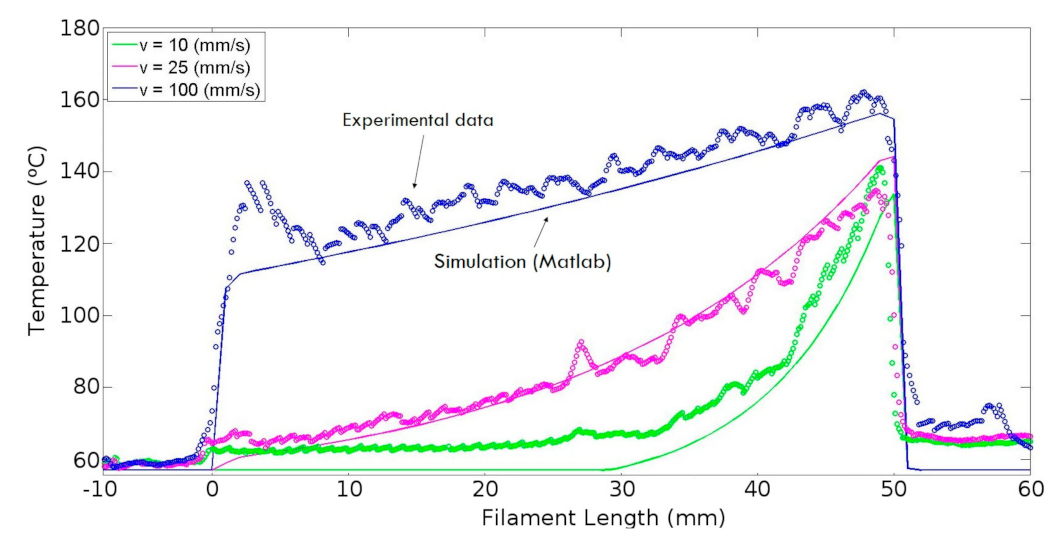
3.1.1. MATLAB Simulation
3.1.2. COMSOL Multiphysics Simulation
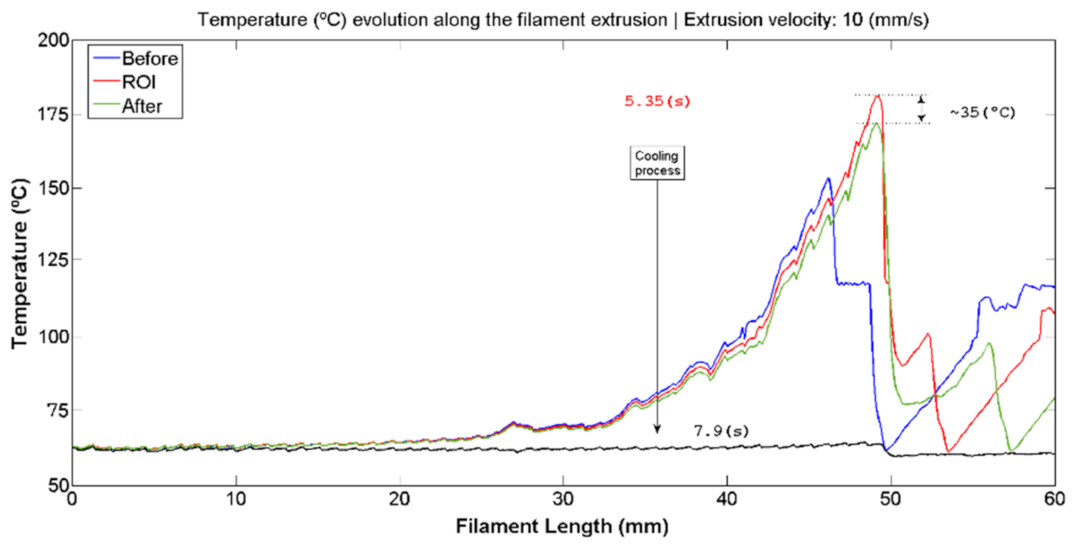
3.2. Experimental Infrared Analysis
3.3. Overall Remarks
4. Discussion
5. Conclusions
- Through the use of infrared thermal equipment, thermal gradients and critical spots in the extruded piece or part can be experimentally perceived; however, only those present at the surface are observed.
- For a better perception of the whole process, and to realize the interior of the parts, and for respective processing optimization, numerical tools are fundamental.
- The present model is highly simplified,; nevertheless, with the establishment of optimized simulation mechanisms of the printing process (mimicking what experimentally is observed), it is possible to challenge the current printers and determine to what extent these are suitable to print complex objects and optimize those in almost real-time, and according to the limitations of each specific printer, before going to the printing line.
- By measuring the discrepancy between the output of a concrete printer and the expected theoretical/simulation output, one has an expectancy of the performance for a printer. This will allow for the development of printing strategies, for that same printer, that will best approximate the expected outcome.
- The acknowledgement and prediction of the temperature and thermal behavior during the printing of an object can help in the search for the best heat source velocity, feed rate, filament or nozzle diameter, composition of the material blend and other parameters, by comparing with those created using the tool path (G-code), thus reducing the thermal gradients and bonding diffusivity of the extruded material, in order to create the object/part with best mechanical properties. These will result in part with better geometry and less residue during fabrication.
- It is thus expected that improvement of the features of the product will ultimately preserve natural resources and promote environmental and economic benefits by obtaining cleaner and environmentally friendly solutions for material processing.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hull, C. On Stereolithography. Virtual Phys. Prototyp. 2012, 7, 177. [Google Scholar] [CrossRef]
- Raja, S.; Agrawal, A.P.; Patil, P.; Thimothy, P.; Capangpangan, R.Y.; Singhal, P.; Wotango, M.T. Optimization of 3D Printing Process Parameters of Polylactic Acid Filament Based on the Mechanical Test. Int. J. Chem. Eng. 2022, 2022, 5830869. [Google Scholar] [CrossRef]
- Jandyal, A.; Chaturvedi, I.; Wazir, I.; Raina, A.; Ul Haq, M.I. 3D Printing—A Review of Processes, Materials and Applications in Industry 4.0. Sustain. Oper. Comput. 2022, 3, 33–42. [Google Scholar] [CrossRef]
- Subramani, R.; Kaliappan, S.; Sekar, S.; Patil, P.P.; Usha, R.; Manasa, N.; Esakkiraj, E.S. Polymer Filament Process Parameter Optimization with Mechanical Test and Morphology Analysis. Adv. Mater. Sci. Eng. 2022, 2022, 8259804. [Google Scholar] [CrossRef]
- Godec, D.; Gonzalez-Gutierrez, J.; Nordin, A.; Pei, E.; Ureña Alcázar, J. (Eds.) A Guide to Additive Manufacturing. In Springer Tracts in Additive Manufacturing, 1st ed.; Springer International Publishing: Cham, Switzerland, 2022; ISBN 978-3-031-05862-2. [Google Scholar]
- Jaisingh Sheoran, A.; Kumar, H. Fused Deposition Modeling Process Parameters Optimization and Effect on Mechanical Properties and Part Quality: Review and Reflection on Present Research. Mater. Today Proc. 2020, 21, 1659–1672. [Google Scholar] [CrossRef]
- What Are the Advantages and Disadvantages of 3D Printing?—TWI. Available online: https://www.twi-global.com/technical-knowledge/faqs/what-is-3d-printing/pros-and-cons#Consof3DPrinting (accessed on 9 March 2021).
- Turner, B.N.; Strong, R.; Gold, S.A. A Review of Melt Extrusion Additive Manufacturing Processes: I. Process Design and Modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Li, Q.; Kucukkoc, I.; Zhang, D.Z. Production Planning in Additive Manufacturing and 3D Printing. Comput. Oper. Res. 2017, 83, 1339–1351. [Google Scholar] [CrossRef]
- Zhang, Y.; Shapiro, V. Linear-Time Thermal Simulation of as-Manufactured Fused Deposition Modeling Components. J. Manuf. Sci. Eng. Trans. ASME 2018, 140, 071002. [Google Scholar] [CrossRef]
- Jornadas CICECO 2018—Universidade de Aveiro News. Available online: https://www.ua.pt/pt/noticias/0/54604 (accessed on 9 March 2021).
- 3D Printed Violin: 6 Most Amazing Projects|All3DP. Available online: https://all3dp.com/2/3d-printed-violin-6-most-amazing-projects/ (accessed on 9 March 2021).
- Choi, J.H.; Kang, E.T.; Lee, J.W.; Kim, U.S.; Cho, W.S. Materials and Process Development for Manufacturing Porcelain Figures Using a Binder Jetting 3D Printer. J. Ceram. Process. Res. 2018, 19, 43–49. [Google Scholar]
- Chen, Z.; Li, Z.; Li, J.; Liu, C.; Lao, C.; Fu, Y.; Liu, C.; Li, Y.; Wang, P.; He, Y. 3D Printing of Ceramics: A Review. J. Eur. Ceram. Soc. 2019, 39, 661–687. [Google Scholar] [CrossRef]
- Tosto, C.; Bragaglia, M.; Nanni, F.; Recca, G. Fused Filament Fabrication of Alumina/Polymer Filaments for Obtaining Ceramic Parts after Debinding and Sintering Processes. Materials 2022, 15, 7399. [Google Scholar] [CrossRef] [PubMed]
- Revelo, C.F.; Colorado, H.A. 3D Printing of Kaolinite Clay Ceramics Using the Direct Ink Writing (DIW) Technique. Ceram. Int. 2018, 44, 5673–5682. [Google Scholar] [CrossRef]
- Santos, T.; Ramani, M.; Devesa, S.; Batista, C.; Franco, M.; Duarte, I.; Costa, L.; Ferreira, N.; Alves, N.; Pascoal-faria, P. A 3D-Printed Ceramics Innovative Firing Technique: A Numerical and Experimental Study. Materials 2022, 16, 6236. [Google Scholar] [CrossRef] [PubMed]
- Camarero-Espinosa, S.; Moroni, L. Janus 3D Printed Dynamic Scaffolds for Nanovibration-Driven Bone Regeneration. Nat. Commun. 2021, 12, 1031. [Google Scholar] [CrossRef] [PubMed]
- Pattanashetti, N.A.; Viana, T.; Alves, N.; Mitchell, G.R.; Kariduraganavar, M.Y. Development of Novel 3D Scaffolds Using BioExtruder by Varying the Content of Hydroxyapatite and Silica in PCL Matrix for Bone Tissue Engineering. J. Polym. Res. 2020, 27, 87. [Google Scholar] [CrossRef]
- Arif, Z.U.; Khalid, M.Y.; Noroozi, R.; Sadeghianmaryan, A.; Jalalvand, M.; Hossain, M. Recent Advances in 3D-Printed Polylactide and Polycaprolactone-Based Biomaterials for Tissue Engineering Applications. Int. J. Biol. Macromol. 2022, 218, 930–968. [Google Scholar] [CrossRef]
- Lee, C.Y.; Liu, C.Y. The Influence of Forced-Air Cooling on a 3D Printed PLA Part Manufactured by Fused Filament Fabrication. Addit. Manuf. 2019, 25, 196–203. [Google Scholar] [CrossRef]
- Most Used 3D Printing Technologies 2020|Statista. Available online: https://www.statista.com/statistics/560304/worldwide-survey-3d-printing-top-technologies/ (accessed on 9 March 2021).
- Kokkinis, D.; Schaffner, M.; Studart, A.R. Multimaterial Magnetically Assisted 3D Printing of Composite Materials. Nat. Commun. 2015, 6, 8643. [Google Scholar] [CrossRef]
- Dey, A.; Roan Eagle, I.N.; Yodo, N. A Review on Filament Materials for Fused Filament Fabrication. J. Manuf. Mater. Process. 2021, 5, 69. [Google Scholar] [CrossRef]
- Xia, H.; Lu, J.; Tryggvason, G. Fully Resolved Numerical Simulations of Fused Deposition Modeling. Part II—Solidification, Residual Stresses and Modeling of the Nozzle. Rapid Prototyp. J. 2018, 24, 973–987. [Google Scholar] [CrossRef]
- Xia, H.; Lu, J.; Dabiri, S.; Tryggvason, G. Fully Resolved Numerical Simulations of Fused Deposition Modeling. Part I: Fluid Flow. Rapid Prototyp. J. 2018, 24, 463–476. [Google Scholar] [CrossRef]
- Alic, A. Physics of 3D Printing; Ljubljana, Slovenia, 2017. Available online: https://www.scribd.com/document/480834295/Amina-Alic-seminar-1b-pdf (accessed on 26 October 2020).
- Blanco, I. A Brief Review of the Applications of Selected Thermal Analysis Methods to 3D Printing. Thermo 2022, 2, 74–83. [Google Scholar] [CrossRef]
- Zhang, Y.; Chou, Y. Three-Dimensional Finite Element Analysis Simulations of the Fused Deposition Modelling Process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2006, 220, 1663–1671. [Google Scholar] [CrossRef]
- Bellehumeur, C.; Li, L.; Sun, Q.; Gu, P. Modeling of Bond Formation between Polymer Filaments in the Fused Deposition Modeling Process. J. Manuf. Process. 2004, 6, 170–178. [Google Scholar] [CrossRef]
- Marques, B.M.; Andrade, C.M.; Neto, D.M.; Oliveira, M.C.; Alves, J.L.; Menezes, L.F. Numerical Analysis of Residual Stresses in Parts Produced by Selective Laser Melting Process. Procedia Manuf. 2020, 47, 1170–1177. [Google Scholar] [CrossRef]
- Zhang, Y.; Chou, K. A Parametric Study of Part Distortions in Fused Deposition Modelling Using Three-Dimensional Finite Element Analysis. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2008, 222, 959–967. [Google Scholar] [CrossRef]
- Ji, L.; Zhou, T. Finite Element Simulation of Temperature Field in Fused Deposition Modeling. Adv. Mater. Res. 2010, 97-101, 2585–2588. [Google Scholar] [CrossRef]
- Yardimci, M.A.; Güçeri, S. Conceptual Framework for the Thermal Process Modelling of Fused Deposition. Rapid Prototyp. J. 1996, 2, 26–31. [Google Scholar] [CrossRef]
- Sun, Q.; Rizvi, G.M.; Bellehumeur, C.T.; Gu, P. Effect of Processing Conditions on the Bonding Quality of FDM Polymer Filaments. Rapid Prototyp. J. 2008, 14, 72–80. [Google Scholar] [CrossRef]
- Li, L.; Sun, Q.; Bellehumeur, C.; Gu, P. Investigation of Bond Formation in FDM Process. Trans. North Am. Manuf. Res. Inst. SME 2019, 31, 400–407. [Google Scholar]
- Pokluda, O.; Bellehumeur, C.T.; Vlachopoulos, J. Modification of Frenkel’s Model for Sintering. AIChE J. 1997, 43, 3253–3256. [Google Scholar] [CrossRef]
- Costa, S.F.; Duarte, F.M.; Covas, J.A. Estimation of Filament Temperature and Adhesion Development in Fused Deposition Techniques. J. Mater. Process. Technol. 2017, 245, 167–179. [Google Scholar] [CrossRef]
- Costa, S.F.; Duarte, F.M.; Covas, J.A. Thermal Conditions Affecting Heat Transfer in FDM/FFE: A Contribution towards the Numerical Modelling of the Process. Virtual Phys. Prototyp. 2015, 10, 35–46. [Google Scholar] [CrossRef]
- FLIR Photometry Form: FLIR DG001U-E. pp. 1-56.
- FLIR Advanced Thermal Solutions DCOO2U-L SC5000 User Manual.
- Rahman, M.; Schott, N.R.; Sadhu, L.K. Glass Transition of ABS in 3D Printing. In Proceedings of the COMSOL Conference, Boston, MA, USA, 5–7 October 2016; pp. 1–5. [Google Scholar]
- Incropera, F.P.; DeWitt, D.P.; Bergman, L.T.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Chapra, S.C. Applied Numerical Methods with MATLAB for Engineers and Scientists, 3rd ed.; Lange, M., Massar, P.E., Buczek, L., Eds.; Raghothaman Srinivasan: New York, NY, USA, 2012; ISBN 978-0-07-339796-2. [Google Scholar]
- McIlroy, C.; Olmsted, P.D. Disentanglement Effects on Welding Behaviour of Polymer Melts during the Fused-Filament-Fabrication Method for Additive Manufacturing. Polymer 2017, 123, 376–391. [Google Scholar] [CrossRef]
- Li, W.; Ghazanfari, A.; Leu, M.C.; Landers, R.G. Extrusion-on-Demand Methods for High Solids Loading Ceramic Paste in Freeform Extrusion Fabrication. Virtual Phys. Prototyp. 2017, 12, 193–205. [Google Scholar] [CrossRef]
- Kosky, P.; Balmer, R.; Keat, W.; Wise, G. (Eds.) Mechanical Engineering. In Exploring Engineering—An Introduction to Engineering and Design; Academic Press: Waltham, MA, USA, 2013; Chapter 12; pp. 259–281. ISBN 9780124158917. [Google Scholar]



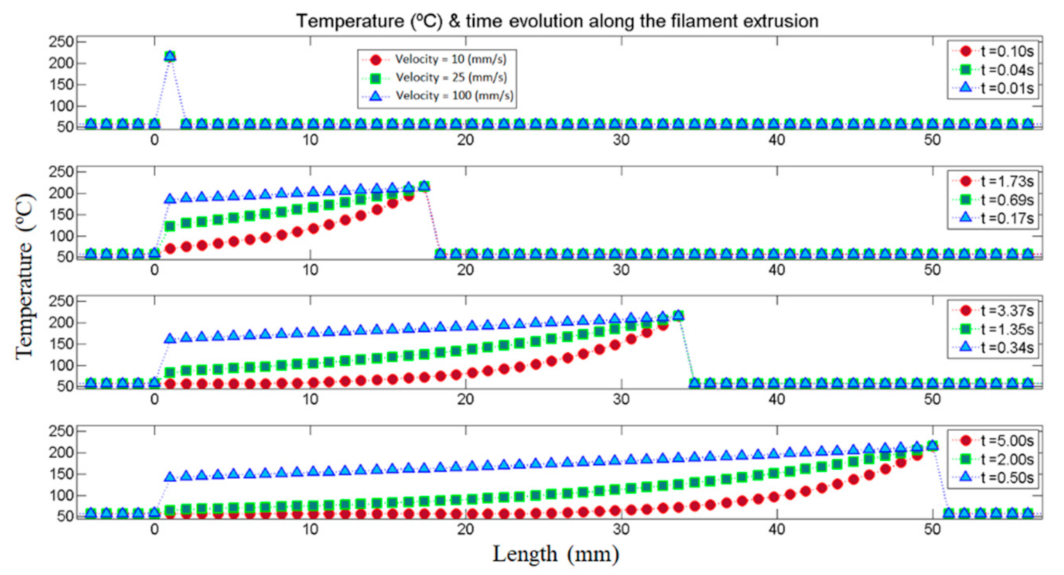
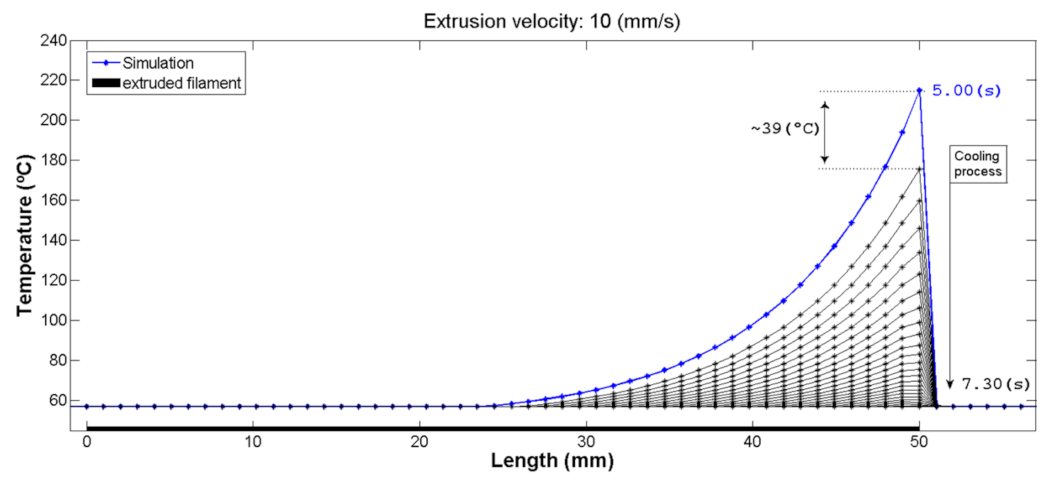
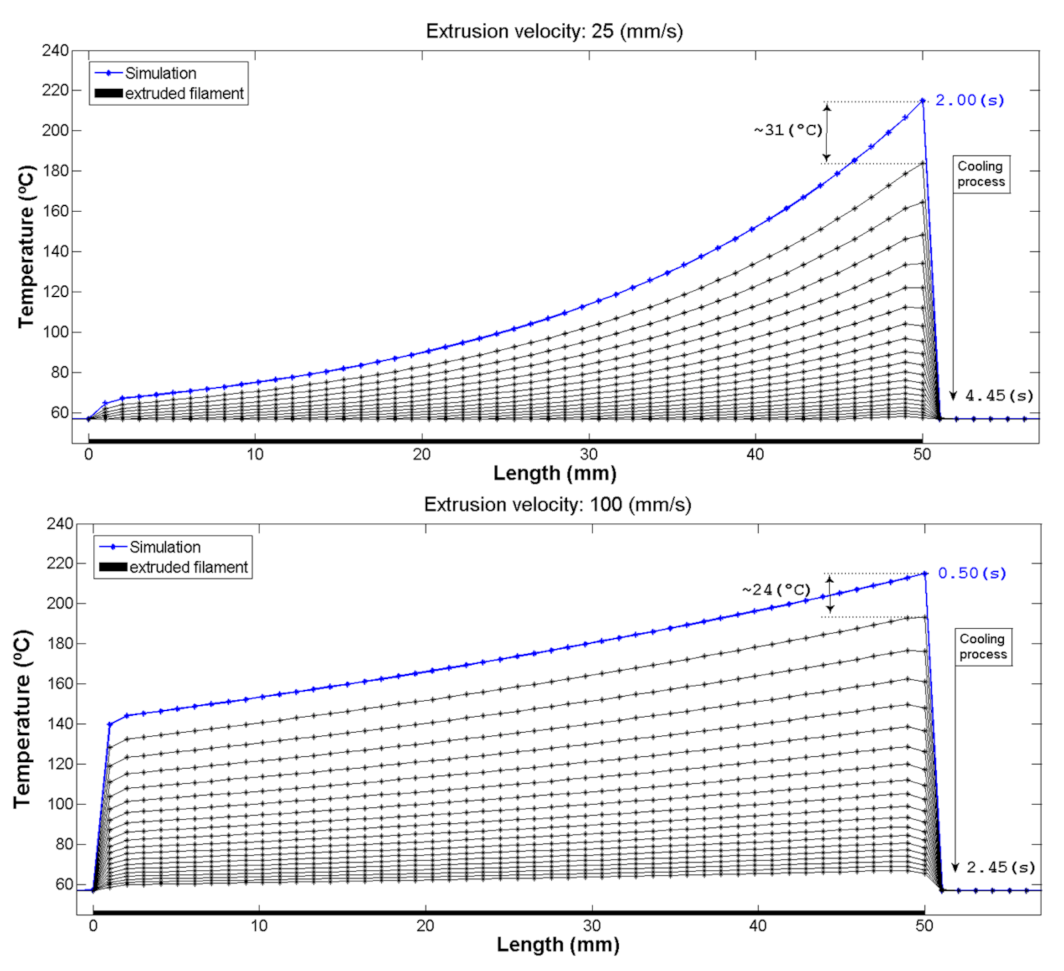
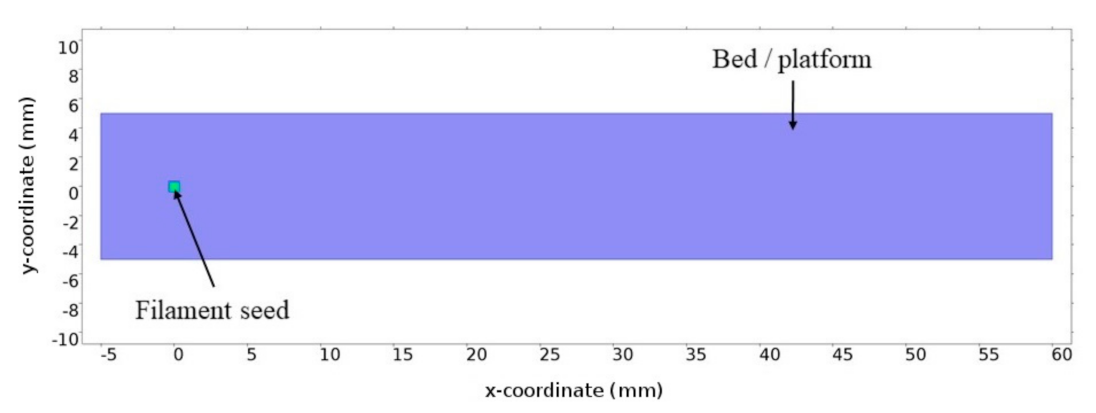



| Material | Density ρ (kg/m3) | Specific Heat CP (J/kg·K) | Thermal Conductivity (W/m·K) | Length L (mm) | Thickness ϕ (mm) | Height h (mm) |
|---|---|---|---|---|---|---|
| ABS | 1050 | 2080 | 0.177 | 50 | ~0.7 | ~0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, T.; Belbut, M.; Amaral, J.; Amaral, V.; Ferreira, N.; Alves, N.; Pascoal-Faria, P. Insights into Temperature Simulation and Validation of Fused Deposition Modeling Processes. J. Manuf. Mater. Process. 2023, 7, 189. https://doi.org/10.3390/jmmp7060189
Santos T, Belbut M, Amaral J, Amaral V, Ferreira N, Alves N, Pascoal-Faria P. Insights into Temperature Simulation and Validation of Fused Deposition Modeling Processes. Journal of Manufacturing and Materials Processing. 2023; 7(6):189. https://doi.org/10.3390/jmmp7060189
Chicago/Turabian StyleSantos, Tiago, Miguel Belbut, João Amaral, Vitor Amaral, Nelson Ferreira, Nuno Alves, and Paula Pascoal-Faria. 2023. "Insights into Temperature Simulation and Validation of Fused Deposition Modeling Processes" Journal of Manufacturing and Materials Processing 7, no. 6: 189. https://doi.org/10.3390/jmmp7060189
APA StyleSantos, T., Belbut, M., Amaral, J., Amaral, V., Ferreira, N., Alves, N., & Pascoal-Faria, P. (2023). Insights into Temperature Simulation and Validation of Fused Deposition Modeling Processes. Journal of Manufacturing and Materials Processing, 7(6), 189. https://doi.org/10.3390/jmmp7060189








