Identification of the Optimal Blank Holder Force through In-Line Measurement of Blank Draw-In in a Deep Drawing Process
Abstract
:1. Introduction
2. Materials and Methods
- First, experimental tests were carried out to assess the blank draw-in acquisition system’s capabilities to determine the optimal design conditions and to examine how alterations in lubrication conditions impact the quality indices of the stamped component.
- Second, a Finite Element (FE) model of the deep drawing process was developed and then calibrated using experimental results. The calibrated FE model was employed to perform numerical simulation plans aimed at establishing the process knowledge in form of database. Database were used to develop surrogate models for estimating the friction coefficient acting at the blank–tool interface and the blank holder force, both of which assure the satisfaction of the part quality indices.
- Finally, for the validation of the control strategy, the numerical model was used as a digital twin of the physical press machine. Specifically, the adjusted value of the blank holder force was set in the numerical model, while the blank draw-in and the part quality indices were measured to check the correspondence with the expected draw-in and the fulfilment of quality criteria.
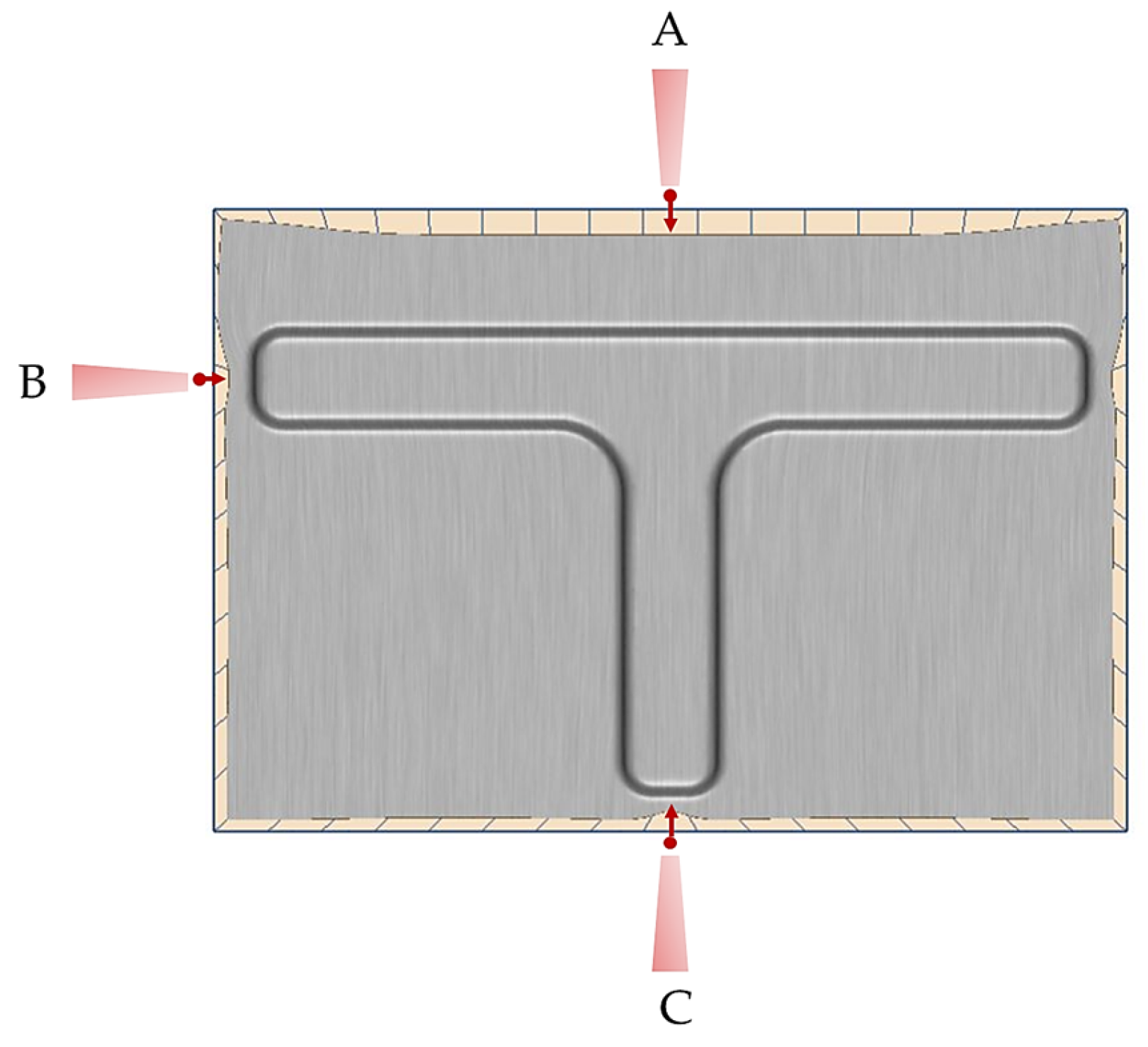
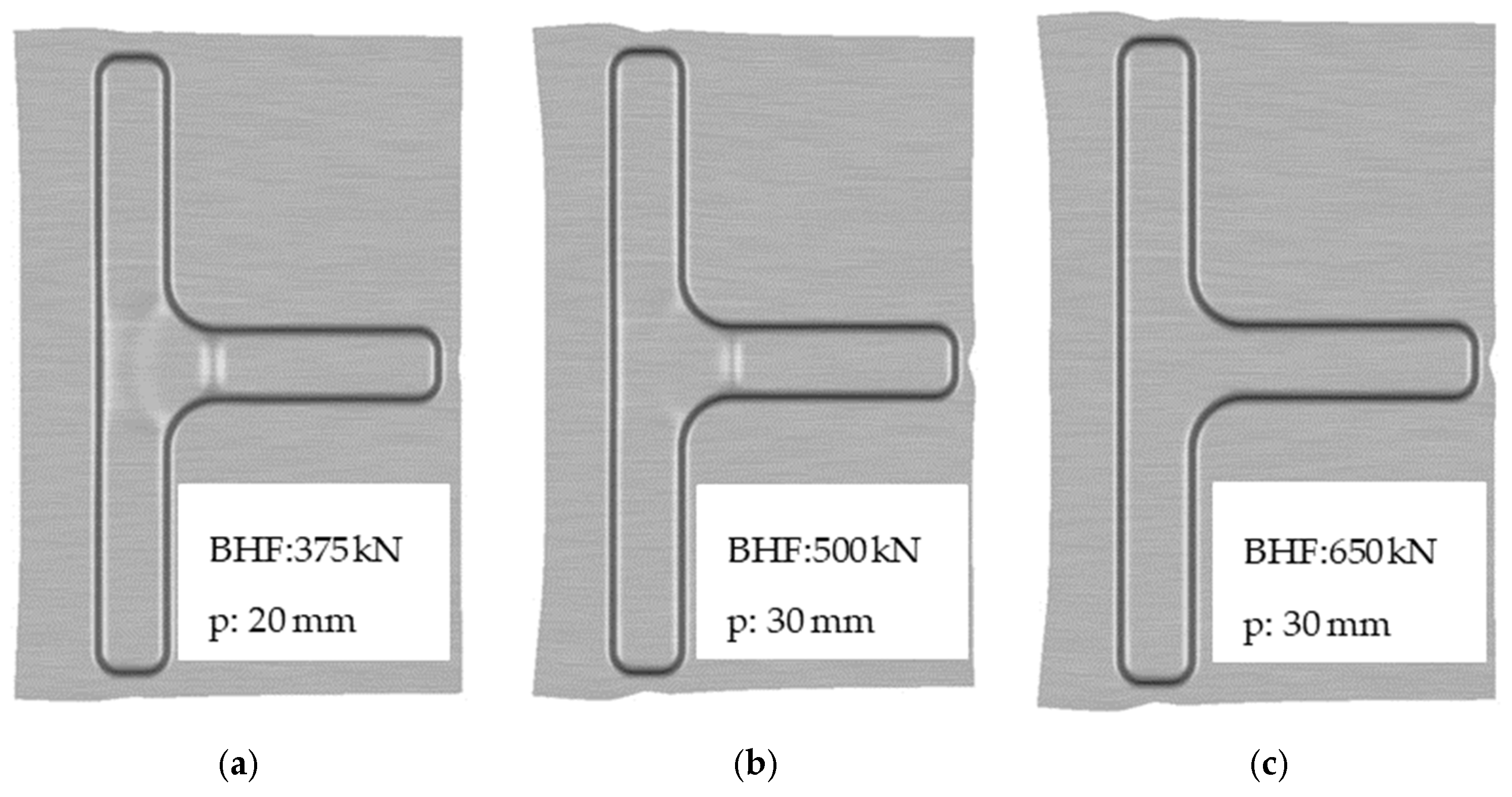
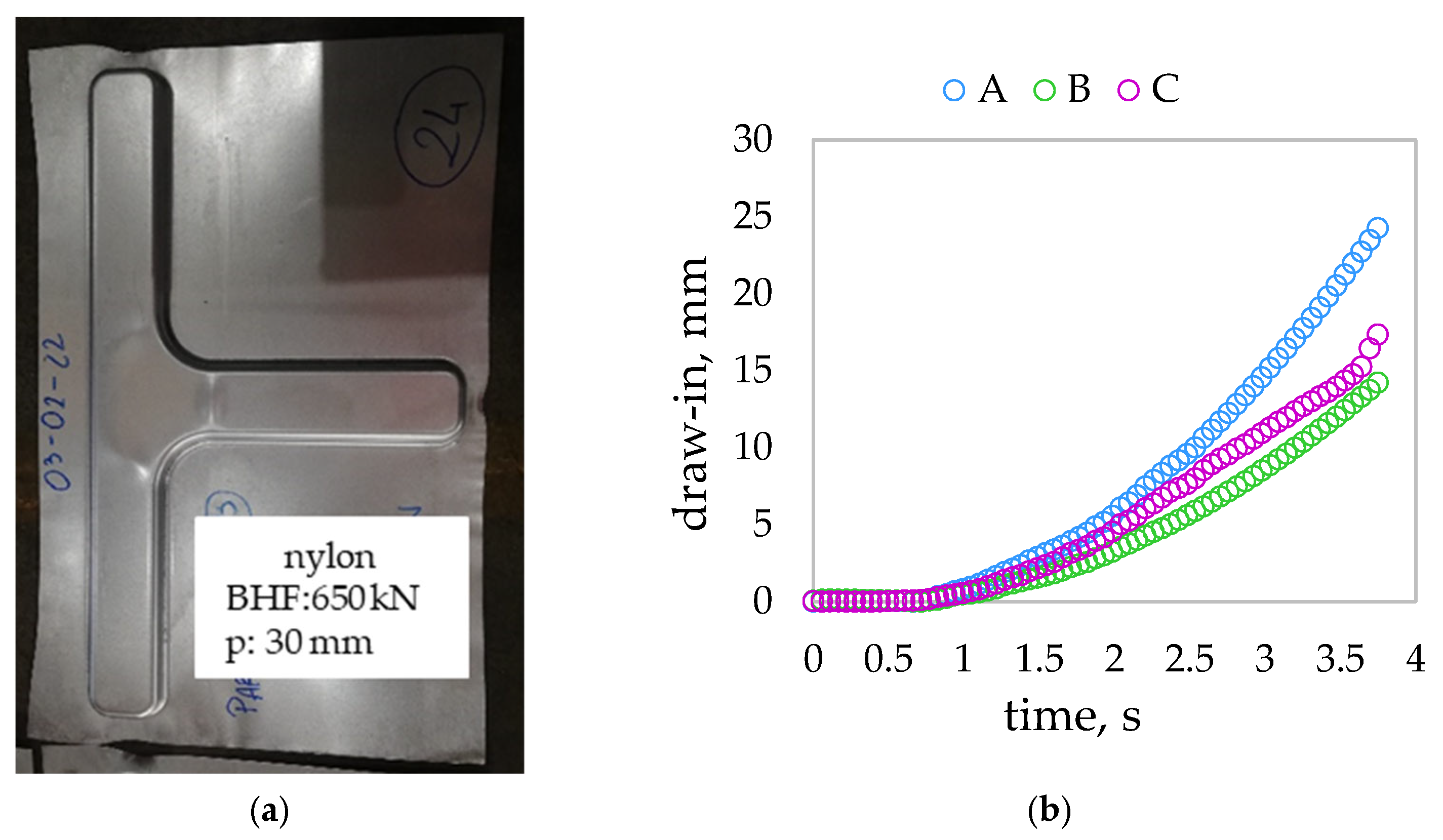
2.1. Experimental Deep Drawn Test
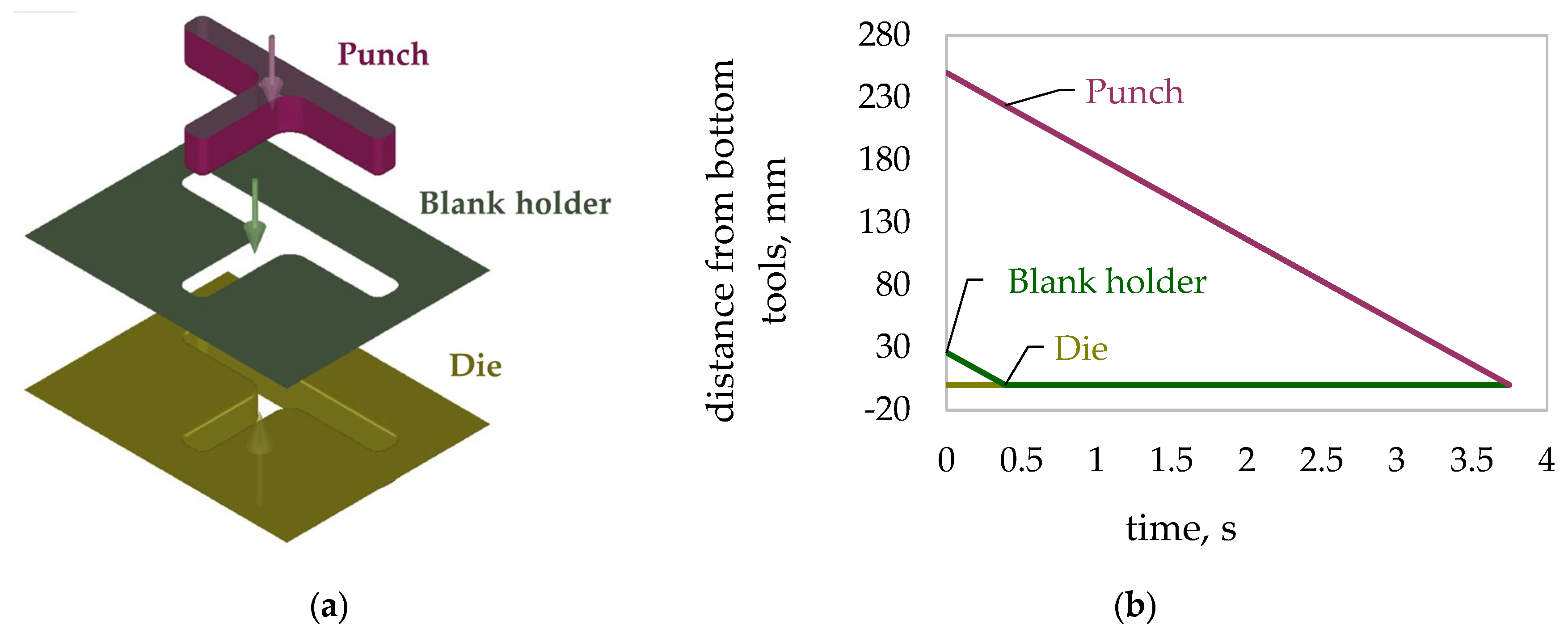
2.2. FE Modelling of the Process
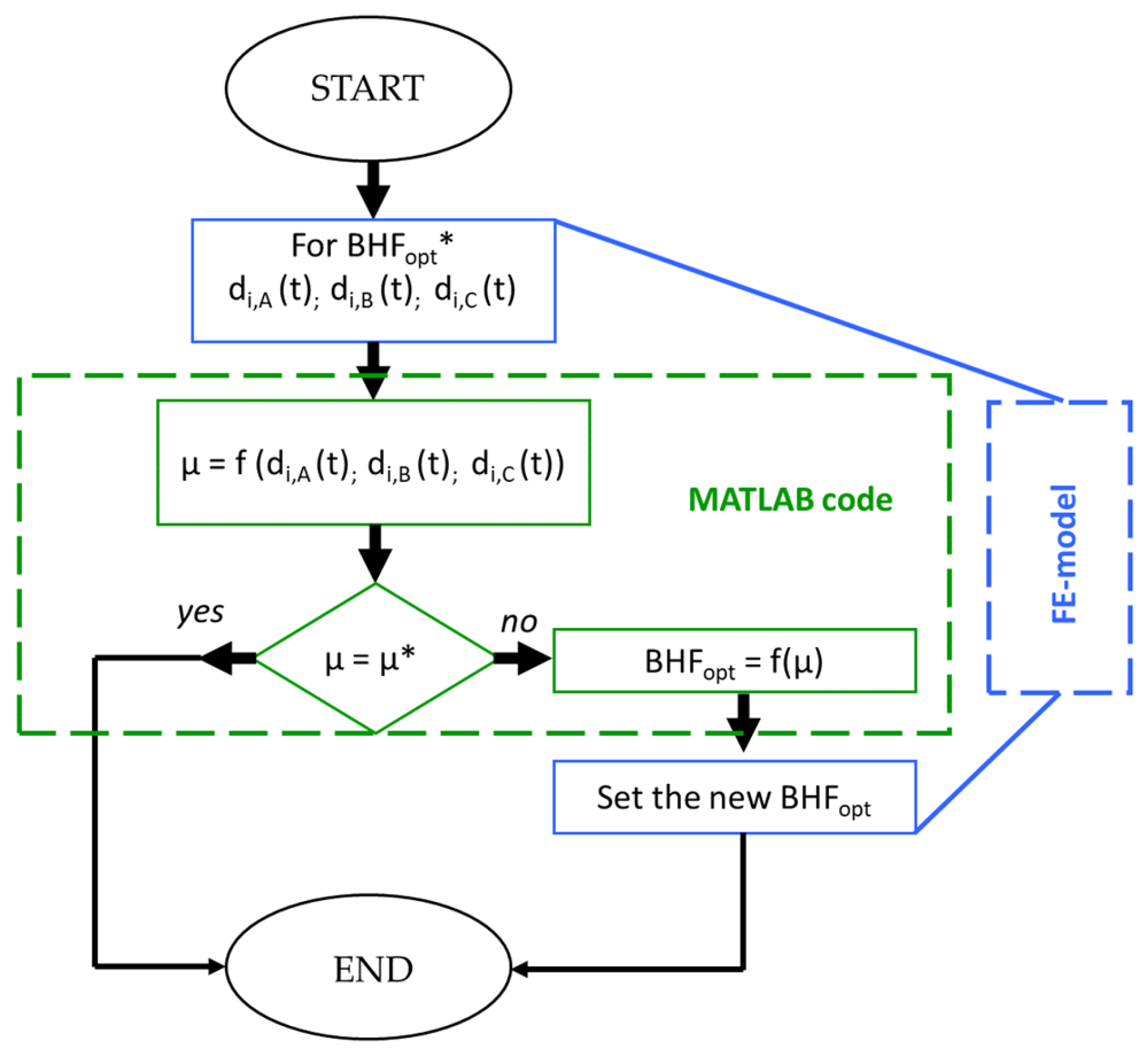
2.3. Surrogate Models and Numerical Implementation of the Control Logic
3. Results and Discussion
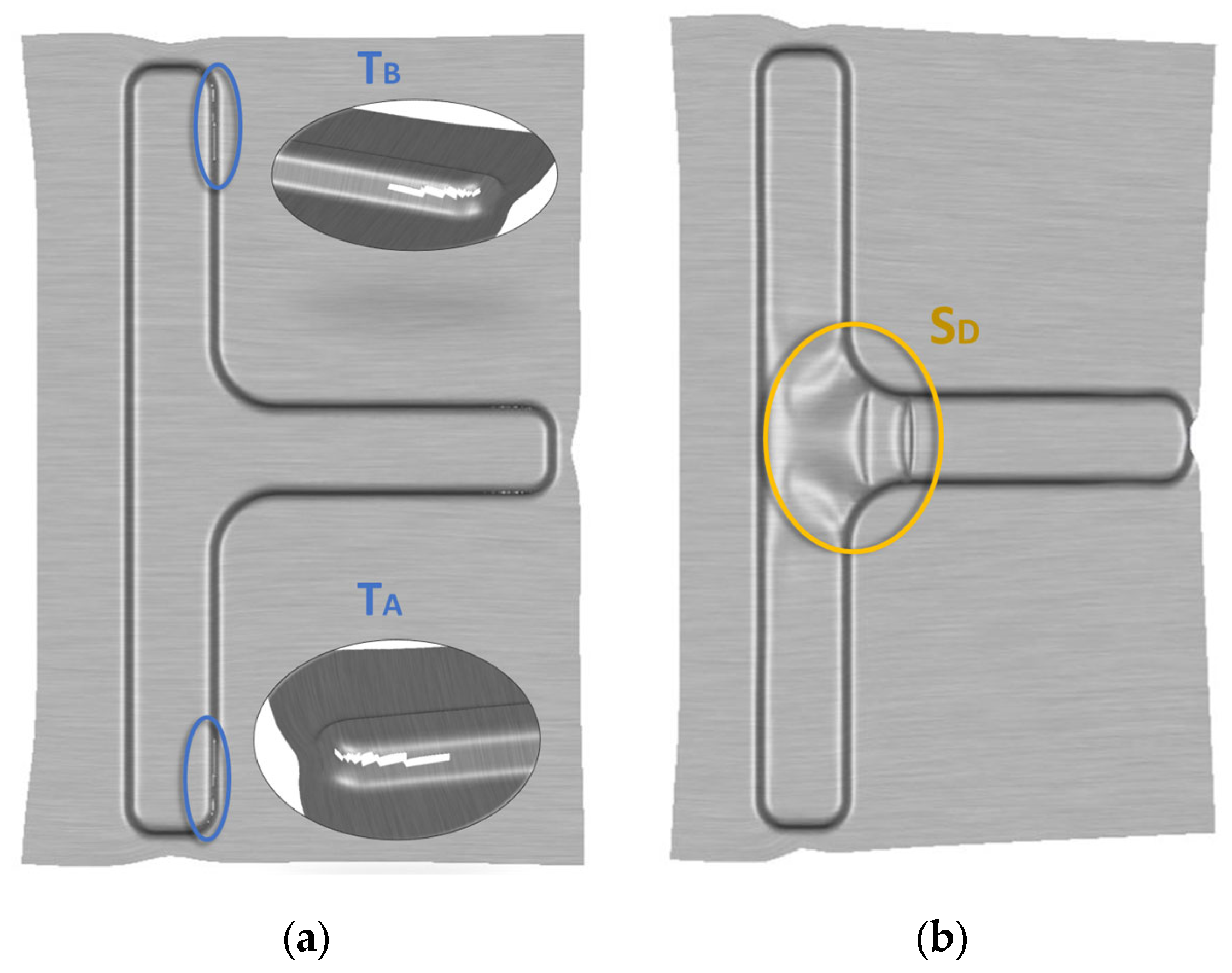
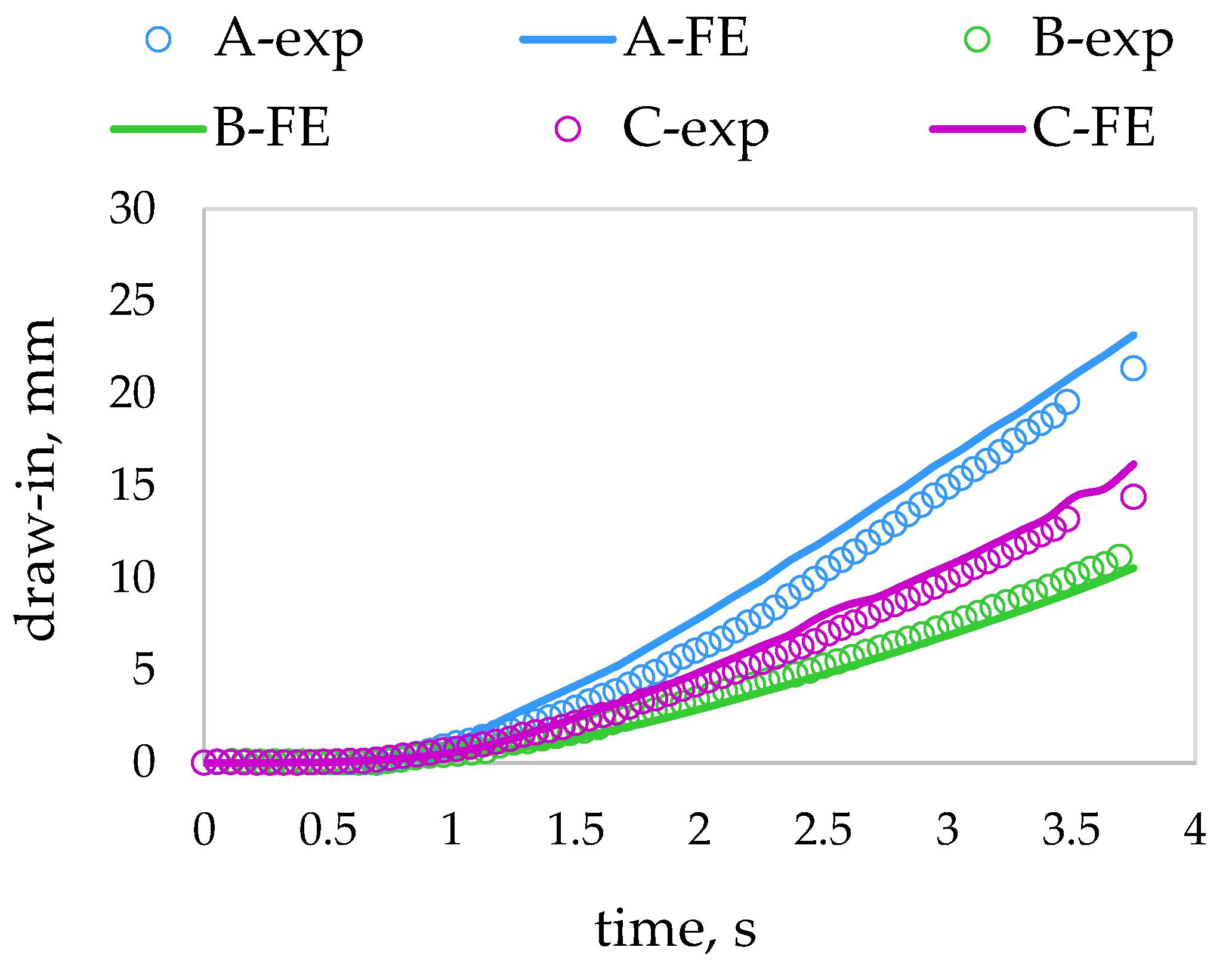
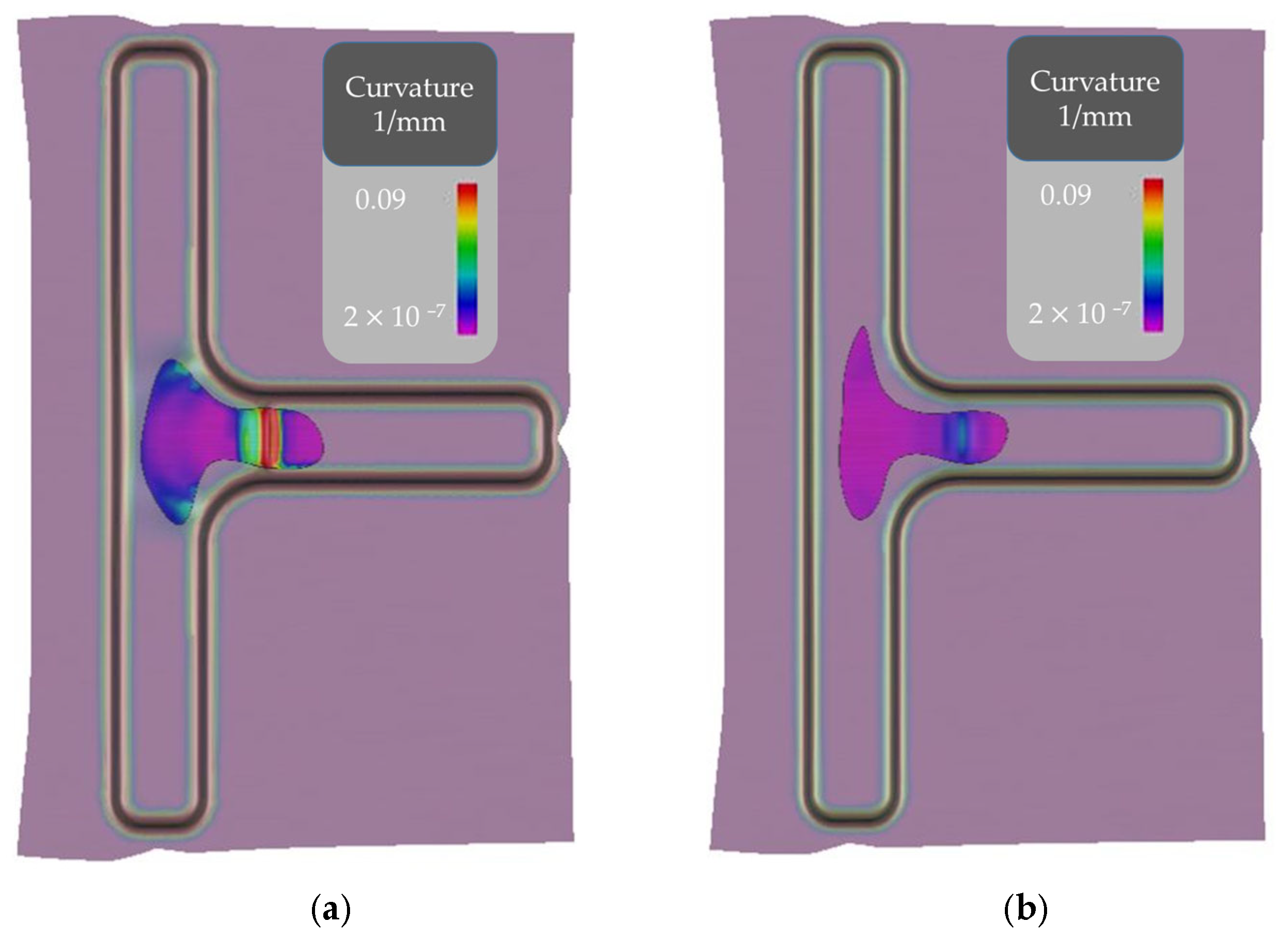
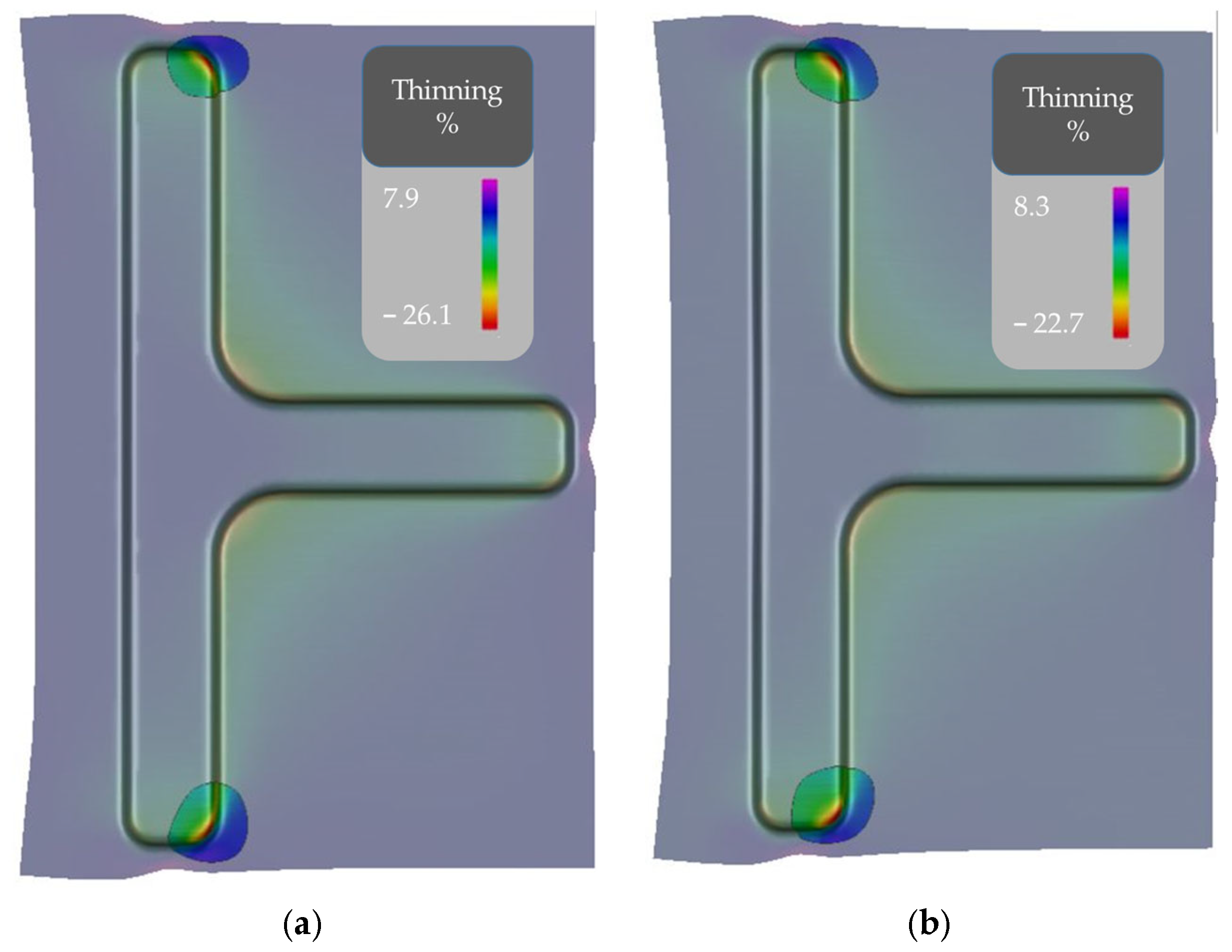
3.1. Experimental Results and Comparison with FE Results
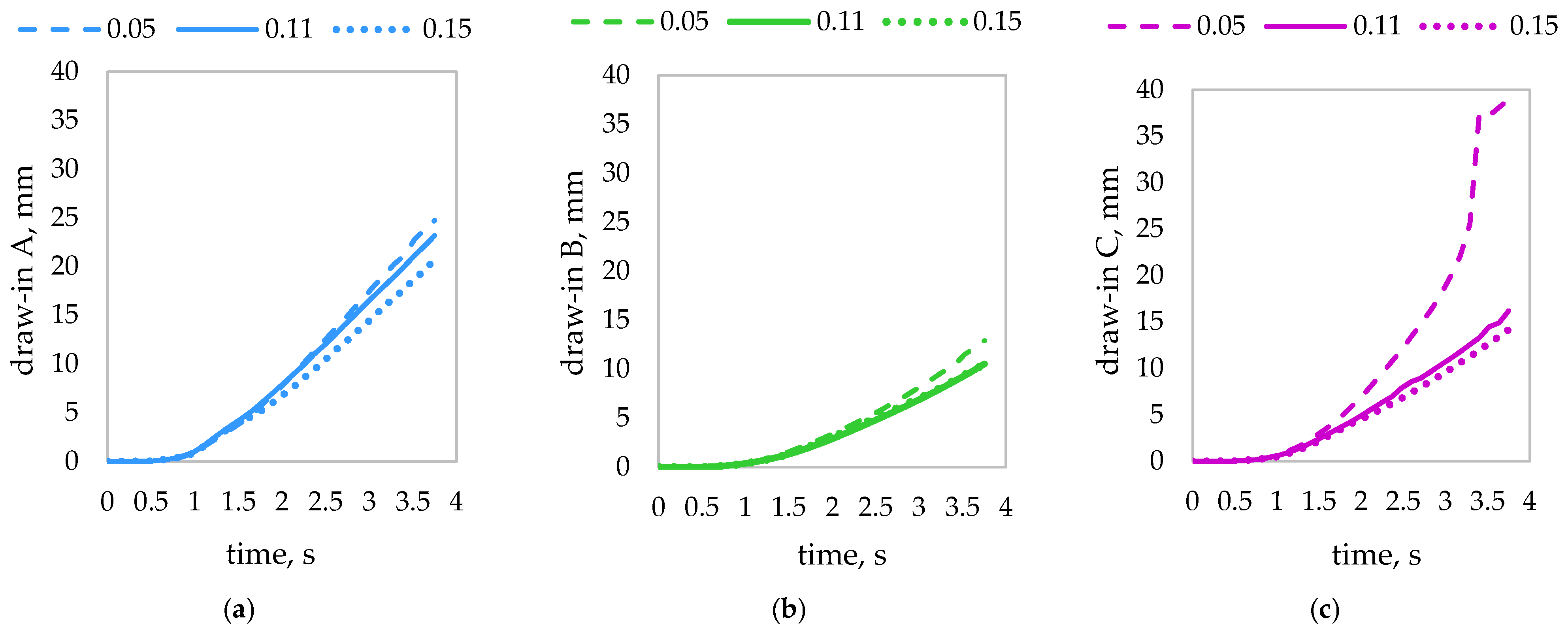
3.2. FE Results for Establishing the Surrogate Models
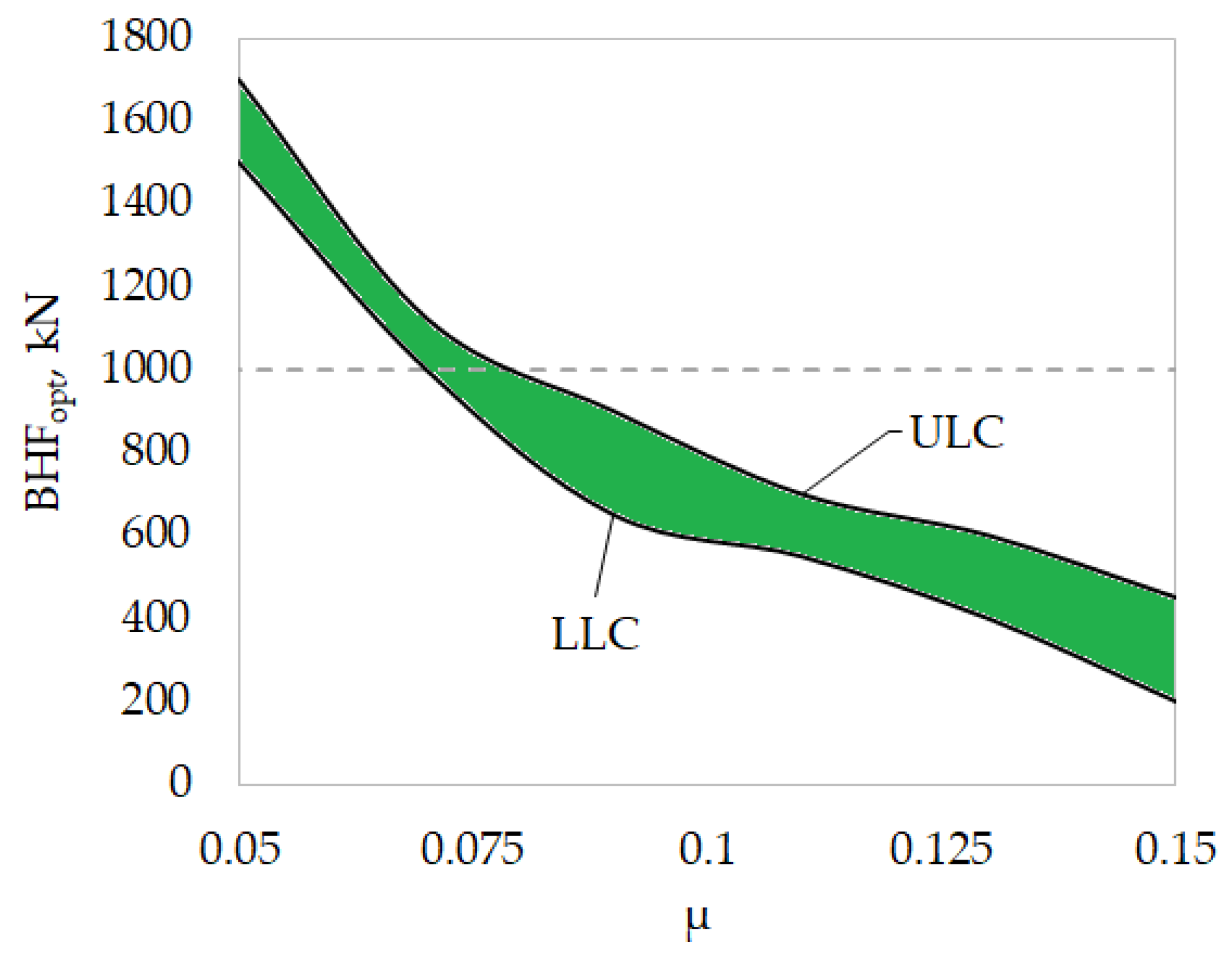
3.3. FE-Results by Adopting the Control Methodology
4. Conclusions
- Verifying the robustness of this type of control by introducing other fluctuations into the system, such as material properties;
- Implementing the designed control on a physical press and developing a machine learning method for self-learning and self-updating. This means that the control system improves its efficiency by exploiting data acquired during each deep drawing operation, thereby expanding the initial database obtained from numerical simulations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, K.; Korkolis, Y.P. Industry 4.0 in stamping: A wrinkling indicator for reduced-order modeling of deep-drawing processes. Procedia Manuf. 2020, 51, 864–869. [Google Scholar] [CrossRef]
- Psarommatis, F.; Sousa, J.; Mendonça, J.P.; Kiritsis, D. Zero-defect manufacturing the approach for higher manufacturing sustainability in the era of industry 4.0: A position paper. Int. J. Prod. Res. 2022, 60, 73–91. [Google Scholar] [CrossRef]
- Awasthi, A.; Saxena, K.K.; Arun, V. Sustainable and smart metal forming manufacturing process. Mater. Today-Proc. 2021, 44, 2069–2079. [Google Scholar] [CrossRef]
- Muñiz, L.; Trinidad, J.; Garcia, E.; Peinado, I.; Montes, N.; Galdos, L. On the Use of Advanced Friction Models for the Simulation of an Industrial Stamping Process including the Analysis of Material and Lubricant Fluctuations. Lubricants 2023, 11, 193. [Google Scholar] [CrossRef]
- Fischer, P.; Heingärtner, J.; Duncan, S.; Hora, P. On part-to-part feedback optimal control in deep drawing. J. Manuf. Process 2020, 50, 403–411. [Google Scholar] [CrossRef]
- Wiebenga, J.; Atzema, E.; An, Y.; Vegter, H.; Boogaard, A.v.D. Effect of material scatter on the plastic behavior and stretchability in sheet metal forming. J. Mater. Process Technol. 2014, 214, 238–252. [Google Scholar] [CrossRef]
- Harsch, D.; Heingärtner, J.; Renkci, Y.; Hora, P. Influence of scattering material properties on the robustness of deep drawing processes. In 10th Forming Technology Forum. Model Based Control for Smart Forming Processes; University of Twente: Enschede, The Netherland, 2017. [Google Scholar]
- Fischer, P.; Harsch, D.; Heingärtner, J.; Renkci, Y.; Hora, P. Inline feedback control for deep drawing applications. IOP Conf. Ser. Mater. Sci. Eng. 2016, 159, 012006. [Google Scholar] [CrossRef]
- Grüebler, R.; Hora, P. Temperature dependent friction modeling for sheet metal forming. Int. J. Mater. Form. 2009, 2, 251–254. [Google Scholar] [CrossRef]
- Marretta, L.; Ingarao, G.; Di Lorenzo, R. Design of sheet stamping operations to control springback and thinning: A multi-objective stochastic optimization approach. Int. J. Mech. Sci. 2010, 52, 914–927. [Google Scholar] [CrossRef]
- Gao, X.; Hong, Z.; Feng, Y.; Wang, T.; Li, Y.; Tan, J. A 6-sigma robust optimization method for stamping forming of automobile covering parts based on residual error and radial basis interpolation. J. Mech. Sci. Technol. 2021, 35, 4627–4642. [Google Scholar] [CrossRef]
- Bici, M.; Campana, F.; Cimolin, F.; Rizzo, L. Robust die compensation in sheet metal design through the integration of dual response surface and shape function optimization. Math. Probl. Eng. 2019, 2019, 7357135. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Z.; Deng, L.; Wang, X.; Long, J.; Jiang, X.; Jin, J.; Xia, J. A Review of the Intelligent Optimization and Decision in Plastic Forming. Materials 2022, 15, 7019. [Google Scholar] [CrossRef]
- Choudhari, C.S.; Khasbage, S.S. Experimental investigation of forming parameters for square cup deep drawing process. Mater. Today-Proc. 2021, 44, 4261–4267. [Google Scholar] [CrossRef]
- Feng, Y.; Hong, Z.; Gao, Y.; Lu, R.; Wang, Y.; Tan, J. Optimization of variable blank holder force in deep drawing based on support vector regression model and trust region. Int. J. Adv. Manuf. Tech. 2019, 105, 4265–4278. [Google Scholar] [CrossRef]
- Atul, S.T.; Babu, M.L. A review on effect of thinning, wrinkling and spring-back on deep drawing process. Proc. Inst. Mech. Eng. B-J. Eng. 2019, 233, 1011–1036. [Google Scholar] [CrossRef]
- Fischer, P.; Heingärtner, J.; Renkci, Y.; Hora, P. Experiences with inline feedback control and data acquisition in deep drawing. Procedia Manuf. 2018, 15, 949–954. [Google Scholar] [CrossRef]
- Fischer, P.; Harsch, D.; Heingärtner, J.; Renkci, Y.; Hora, P. Implementation of feedback control in kitchen sink production. IOP Conf. Ser. Mater. Sci. Eng. 2018, 418, 012110. [Google Scholar] [CrossRef]
- Fischer, P.; Harsch, D.; Heingärtner, J.; Renkci, Y.; Hora, P. A knowledge-based control system for the robust manufacturing of deep drawn parts. Procedia Eng. 2017, 207, 42–47. [Google Scholar] [CrossRef]
- Palmieri, M.E.; Lorusso, V.D.; Tricarico, L. Robust optimization and Kriging metamodeling of deep-drawing process to obtain a regulation curve of blank holder force. Metals 2021, 11, 319. [Google Scholar] [CrossRef]
- Endelt, B.; Tommerup, S.; Danckert, J. A novel feedback control system–Controlling the material flow in deep drawing using distributed blank-holder force. J. Mater. Process Tech. 2013, 213, 36–50. [Google Scholar] [CrossRef]
- Endelt, B.; Nielsen, K.B.; Danckert, J. New framework for on-line feedback control of a deep-drawing operation. J. Mater. Process Tech. 2006, 177, 426–429. [Google Scholar] [CrossRef]
- Brun, M.; Ghiotti, A.; Simonetto, E.; Bruschi, S.; Filippi, S. Variable blank holder pressure by magneto-rheological actuators in deep drawing. Proc. CIRP 2023, 119, 932–937. [Google Scholar] [CrossRef]
- Cavone, G.; Bozza, A.; Carli, R.; Dotoli, M. MPC-based process control of deep drawing: An industry 4.0 case study in automotive. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1586–1598. [Google Scholar] [CrossRef]
- Siegert, K.; Ziegler, M.; Wagner, S. Closed loop control of the friction force. Deep drawing process. J. Mater. Process Tech. 1997, 71, 126–133. [Google Scholar] [CrossRef]
- Lo, S.W.; Yang, T.C. Closed-loop control of the blank holding force in sheet metal forming with a new embedded-type displacement sensor. Int. J. Adv. Manuf. Tech. 2004, 24, 553–559. [Google Scholar] [CrossRef]
- Hsu, C.W.; Ulsoy, A.G.; Demeri, M.Y. Development of process control in sheet metal forming. J. Mater. Process Tech. 2002, 127, 361–368. [Google Scholar] [CrossRef]
- Palmieri, M.E.; Tricarico, L. Control of draw-in in the deep-drawing process by regulating the force on the blank holder. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1238, 012071. [Google Scholar] [CrossRef]
- Tricarico, L.; Palmieri, M.E. Robust Design of Deep Drawing Process through In-Line Feedback Control of the Draw-In. Appl. Sci. 2023, 13, 1717. [Google Scholar] [CrossRef]
- Chen, K.; Carter, A.J.; Korkolis, Y.P. Flange wrinkling in deep-drawing: Experiments, simulations and a reduced-order model. J. Manuf. Mater. Process 2022, 6, 76. [Google Scholar] [CrossRef]
- Available online: https://automotive.arcelormittal.com/products/flat/drawing_steels/drawing (accessed on 1 September 2023).
- Available online: https://www.esb-group.com/en/products-din-en/cold-rolled-steel/ (accessed on 1 September 2023).
- AutoForm, R10; AutoForm Engineering GmbH: Freienbach, Switzerland, 2019.
- Kleijnen, J.P.C. Kriging metamodeling in simulation: A review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef]



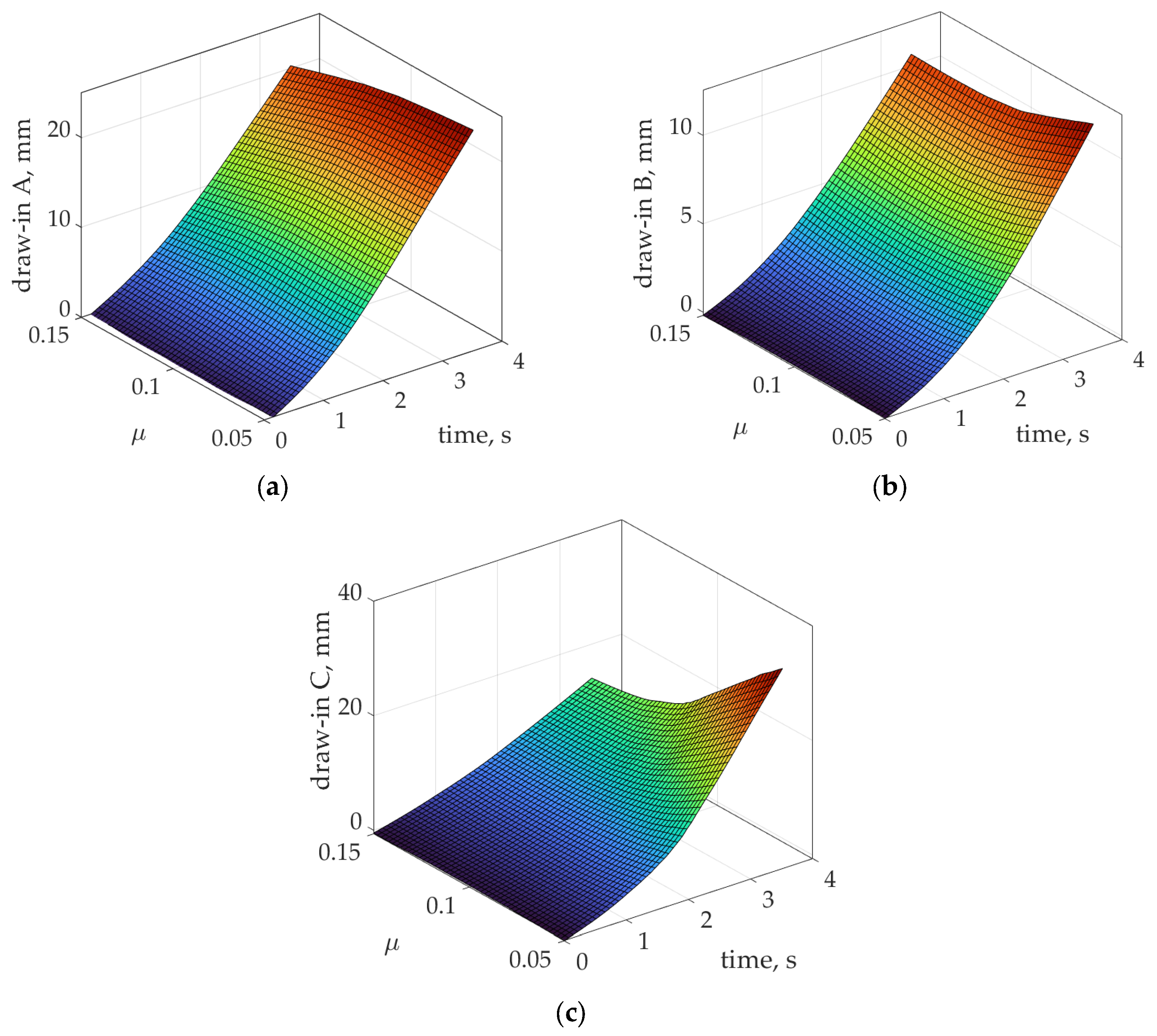

| di,A | di,B | di,C | |
|---|---|---|---|
| p00 | −3.55 | 0.85 | 3.43 |
| p10 | 5.16 | 1.52 | 6.62 |
| p01 | 54.4 | −28.03 | −131.1 |
| p20 | 0.89 | 0.65 | 1.63 |
| p11 | −13.86 | −5.1 | −61.35 |
| p02 | −239.3 | 156.8 | 869.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palmieri, M.E.; Nono Dachille, A.; Tricarico, L. Identification of the Optimal Blank Holder Force through In-Line Measurement of Blank Draw-In in a Deep Drawing Process. J. Manuf. Mater. Process. 2023, 7, 190. https://doi.org/10.3390/jmmp7060190
Palmieri ME, Nono Dachille A, Tricarico L. Identification of the Optimal Blank Holder Force through In-Line Measurement of Blank Draw-In in a Deep Drawing Process. Journal of Manufacturing and Materials Processing. 2023; 7(6):190. https://doi.org/10.3390/jmmp7060190
Chicago/Turabian StylePalmieri, Maria Emanuela, Andrea Nono Dachille, and Luigi Tricarico. 2023. "Identification of the Optimal Blank Holder Force through In-Line Measurement of Blank Draw-In in a Deep Drawing Process" Journal of Manufacturing and Materials Processing 7, no. 6: 190. https://doi.org/10.3390/jmmp7060190
APA StylePalmieri, M. E., Nono Dachille, A., & Tricarico, L. (2023). Identification of the Optimal Blank Holder Force through In-Line Measurement of Blank Draw-In in a Deep Drawing Process. Journal of Manufacturing and Materials Processing, 7(6), 190. https://doi.org/10.3390/jmmp7060190




