Abstract
There has been significant interest in additively manufactured lattice structures in recent years due to their enhanced mechanical and multi-physics properties, making them suitable candidates for various applications. This study presents a multi-parameter implicit equation model for designing body-centred cubic (BCC) lattice structures. The model is used in conjunction with a multi-objective genetic algorithm (MOGA) approach to maximise the stiffness of the BCC lattice structure while minimising von-Mises stress within the structure under a specific loading condition. The selected design from the MOGA at a specific lattice density is compared with the classical BCC lattice structure and the designs generated by a single-objective genetic algorithm, which focuses on maximising stiffness or minimising von-Mises stress alone. By conducting a finite element analysis on the optimised samples and performing mechanical testing on the corresponding 3D-printed specimens, it was observed that the optimised lattice structures exhibited a substantial improvement in mechanical performance compared to the classical BCC model. The suitability of multi-objective and single-objective optimisation approaches for designing lattice structures was further investigated by comparing the corresponding designs in terms of their stiffness and maximum von-Mises stress values. The results from the numerical analysis and experimental testing demonstrate the significance of the application of an appropriate optimisation strategy for designing lattice structures for additive manufacturing.
1. Introduction
Additive manufacturing (AM) has opened up a great potential for geometric design freedom, paving the way for the creation of a new generation of lightweight and efficient materials and with diverse applications [1,2]. This potential has been further augmented by the advancement of computer-aided design (CAD) and optimisation techniques tailored for AM, which have enabled the realisation of energy-efficient structures. Examples of such techniques include lattice (cellular) structure design and topology optimisation specifically developed for additive manufacturing, as evidenced by various studies [1,3,4,5,6].
Cellular structures can be found in natural materials, including bone, wood, sponge, and coral, with unique properties, such as their lightweight nature, high strength-to-weight ratio, and high surface area-to-volume ratio. More recently, lattice structures have been designed and engineered to serve specific purposes, such as impact absorption, acoustic or vibrational damping, heat transmission, and thermal isolation [7,8,9]. Complex lattice structures can only be fabricated through additive manufacturing technologies, such as digital light processing (DLP), fused deposition modelling (FDM), and laser powder bed fusion (L-PBF) [10].
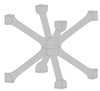
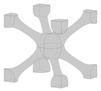
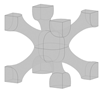
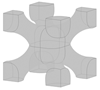
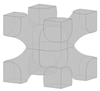
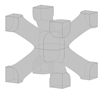
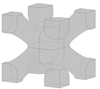
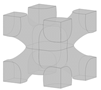
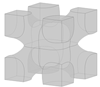
Different types of lattice structures can be grouped into two main families, including strut-based lattice structures and surface-based lattice structures [6,11]. The unit cell of a strut-based lattice structure consists of spatially distributed strut networks that are connected at certain nodes to create a truss-like structure, with examples including body-centred cubic (BCC), face-centred cubic (FCC), and octet structures. In contrast, surface-based lattice structures have unit cells constructed from surfaces. Triply periodic minimal surface (TPMS) lattices are a subset of surface-based lattices structures with their unit cells defined mathematically as the iso-surface of a given function. Examples include the Schwarz-P, diamond, and gyroid TPMS lattice structures [6]. Offering a diverse range of properties, both types of lattice structures have found numerous applications in various fields, including automotive [12], aerospace [13,14], sporting [15], biomedical [13,16], and pharmaceutical [17] industries. The focus of the current study is on the design and optimisation of BCC lattice structures which have been widely used in designs for AM. An important feature of this type of strut-based lattice structure is that the strut members are positioned at a 45° angle (as can be seen in Figure 1a) making the lattice structure self-supporting and suitable for fabrication through different AM processes [12].
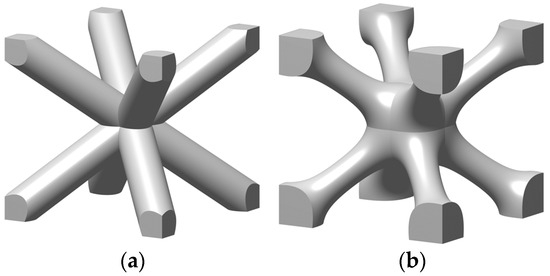
Figure 1.
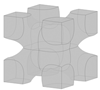
(a) Classical model of a BCC lattice unit cell with cylindrical members of uniform thickness at a 45° angle; (b) example of a shape-optimised BCC unit cell.
Tao et al. [18] and Xiao et al. [19] developed equations of implicit surfaces to represent unit cells of lattice structures similar to TPMS equations. The unit cell can be modified by varying the parameters of the implicit equation to control and tune the properties of lattice structures, such as the porosity and mechanical response. In order to achieve the desired response for a specific application, it is important to use optimisation techniques to design lattice structures that offer the best possible performance at minimal weight and are also manufacturable through AM [6]. Topology optimisation techniques [20] can be utilised to find the best material distribution, member connectivity, or position of the holes within a lattice unit cell [21]. In contrast, shape optimisation techniques aim to determine the best shape for a structure, while topology, i.e., the connectivity of the strut members within the unit cell, remains unchanged throughout the optimisation process [22,23] as demonstrated in Figure 1b for a BCC structure. Parametric shape optimisation is a subset of shape optimisation that specifically focuses on varying a predefined set of geometric parameters to optimise the design’s performance. In parametric shape optimization, the design space is constrained to a set of parameters that control the geometry, such as dimensions, angles, curves, filet radius, and other geometric attributes [24,25].
Tancogne-Dejean and Mohr [26] compared the performance of BCC structures composed of beams of a uniform thickness with the performance of BCC structures composed of tapered beams in terms of stiffness and specific energy absorption properties. Through a numerical analysis, they found a relation between the input design parameters and the lattice mechanical performance. Zhao et al. [27] used a parametric design approach to reduce the stress concentration at nodes and improve the mechanical properties of tapered BCC structures. Their simulation results showed a significant reduction in the anisotropy of the BCC lattice structure and an increase in the elastic modulus of the structure when constant-thickness cylindrical members of the BCC structure were replaced by parametrically designed tapered beams. Furthermore, they used an optimisation strategy to simultaneously optimise the lattice density distribution within a structure under a specified loading condition and the strut geometry of BCC lattice structures. In another work, Zhao et al. [28] applied their optimisation strategy for the design of BCC lattice structures with hollow prismatic struts. Bai et al. [29] proposed a strut thickness grading approach applied to BCC lattice structures to improve their mechanical properties. Through compression tests performed on lattice specimens produced through L-PBF, it was observed that BCC lattices with strut thickness grading exhibited up to 38% greater stiffness and 34% greater strength compared to the classical BCC lattices with the same density. Lee et al. [30] developed a generative machine learning algorithm for the shape optimisation of BCC lattice structures based on neural network and genetic optimisation techniques. Their design showed greater stiffness and strength values than those of a classical model of BCC structure when compared against the same relative density of .
The use of implicit surfaces has been a strong tool for designing complicated lattice structures, such as TPMS structures. However, strut-based lattice structures, such as BCC, are mainly designed using conventional CAD or through parametric equations. Such representations can be used in conjunction with an optimisation approach to perform a size optimisation on the lattice structure [31], e.g., to optimise the thickness of the struts of a classical BCC lattice or the tapered angle of a tapered BCC lattice [27]. However, it does not provide sufficient design freedom in relation to the shape optimisation of the lattice unit cell. Furthermore, most research in this area focuses on the optimisation of the lattice unit cell only for a single objective.
This study focuses on the design and optimisation of BCC structures as a type of strut-based lattice structures frequently studied in the literature. The simple topology of the BCC unit cell makes it well-suited for applying our proposed design and optimisation approach. This facilitates the evaluation of the efficiency of the proposed approach while benefiting from established benchmarks corresponding to earlier research within the same domain. A novel aspect of the current study is the presentation of the BCC lattice structure through an innovative implicit equation providing a high degree of design freedom for modifying the shape of the unit cell, which is driven by a parametric optimisation approach. Moreover, a multi-objective genetic algorithm (MOGA) tool is utilised to optimise the shape of the BCC unit cell simultaneously for two objectives: maximising the stiffness of the lattice structure and minimising the maximum von-Mises stress within the structure when it is under displacement loading. The unit cell geometry achieved from the multi-objective optimisation is compared with those of the single-objective optimisation corresponding to the maximum stiffness and minimum von-Mises stress designs. All designs are fabricated through the DLP process and undergo compression testing. The numerical and experimental results are compared and discussed.
The remainder of the manuscript is structured as follows: it commences with the introduction of the design methodology section, encompassing implicit surface modelling, finite element modelling, and genetic algorithm-based optimisation. The subsequent section covers the additive manufacturing of the designed samples and the mechanical testing setup. Then, a comprehensive Results and Discussion section is presented, leading to a summary and conclusion.
2. Design Methodology
The presented approach for the efficient design of BCC lattice structures involves the utilisation of an implicit model of the structure using a multi-parameter implicit equation implemented within the Surfer program (IMAGINARY) (Figure 2). The developed implicit equation was then exported into MATLAB® for the finite element analysis of the lattice structures and the optimisation of the geometry through single-/multi-objective genetic algorithm optimisations. Figure 3 presents a flowchart of the proposed lattice design approach.
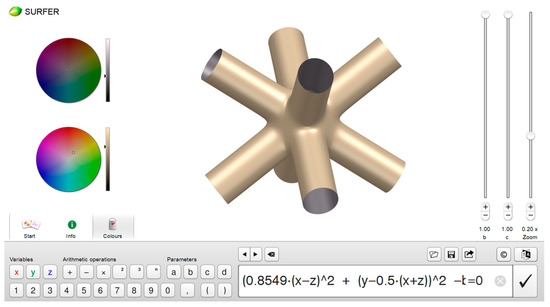
Figure 2.
Software interface of Surfer (developed by IMAGINARY).
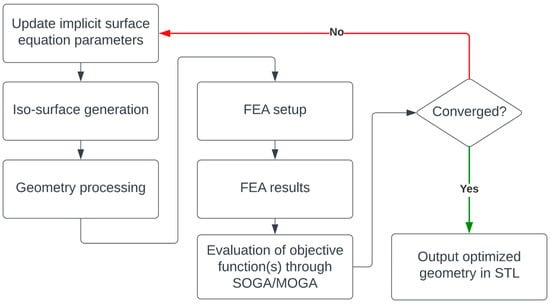
Figure 3.
Schematic of the proposed optimisation process.
2.1. Implicit Surface Model of BCC Structure
Implicit surfaces can represent complex and irregular shapes more easily than explicit representations and can be of benefit for the representation of complex lattice structures. Our study employed implicit modelling primarily to facilitate the introduction of new design variables, which can be programmed to attain the optimal configuration of a lattice structure with respect to the specific objectives. To develop the implicit model of a BCC lattice unit cell, initially, an implicit equation of a cylinder representing a strut member of the lattice unit cell was utilised, as shown in Equation (1), where is the center of the base circle of the cylinder. A BCC unit cell was constructed from four cylindrical members; therefore, the implicit equation of cylinder was repeated (multiplied) four times to represent a BCC structure, as presented in Figure 4 and Equation (2):
where is the parameter that controls the strut radius, is the parameter that controls the fillet radius at the nodes, is a constant equal to , and . This equation was developed assuming that the size of the unit cell was equal to 10 units; however, the constructed geometry could be rescaled to match a desired cell size.
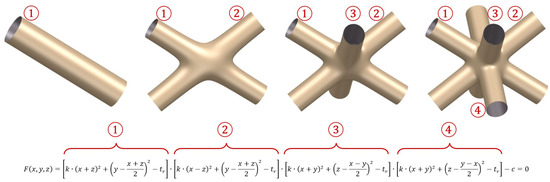
Figure 4.
Demonstration of the approach for merging implicit surfaces by multiplying equations of individual cylinders.
The developed implicit equation was then exported into MATLAB® to create iso-surfaces representing the corresponding lattice geometry. In order to achieve symmetric features on both sides of the strut members within a lattice, the construction process began with the creation of a single strut member. This was accomplished by mirroring the geometry of a strut, which was defined by Equation (2), around the outer end of the strut. A symmetrical model is important to avoid sharp corners on both sides of the strut, i.e., the same filet radius defined for the struts merging at the centre of the cell was defined for the opposite sides of the struts located at the corners of the unit cell. The unit cell was subsequently tessellated in a 3D space, with a spatial distribution defined by the parameters nx, ny, and nz representing the number of unit cells along the , , and , respectively. In this work, was set for creating test samples for the numerical analysis and experimental validation, as demonstrated in Figure 5. The generated iso-surface model of the BCC lattice structure was then converted into a STL model for further finite element analysis (FEA), optimisation, and 3D printing. The process included extracting surface points corresponding to the iso-surface model. Subsequently, these surface points were triangulated to produce a triangular mesh, which could be saved as an STL file.
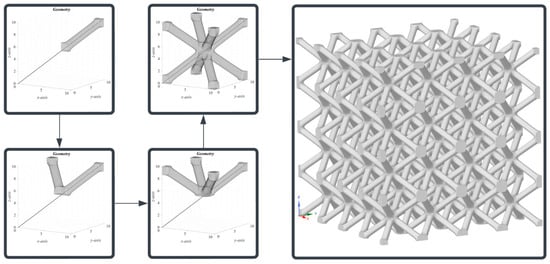
Figure 5.
The procedure used for the construction of the proposed implicit surface-based BCC lattice unit cell and tessellation into a lattice structure.
Table 1 shows various design configurations achieved by varying the design variable , while keeping constant at 0.1. It can be seen that increasing beyond a specific value significantly influences the resulting configuration, allowing control over the minimum strut thickness through the variable. Since the geometry of the proposed BCC structure was defined using an implicit equation, there was a certain range of design variables, which enabled the generation of a valid geometry. For instance, when , the implicit equation did not form a valid surface model. Thus, an experimental relation was derived to establish the lower bound of in relation to as . This ensured a minimum value of for a valid iso-surface, which enabled the generation of the corresponding STL model. Table 2 presents various design configurations achieved by adjusting the design variable while adhering to the assigned lower band values for . Increasing led to a higher relative density of the lattice unit cell, which in turn had a significant impact on the stiffness and stress distribution within the BCC lattice structure. Similarly, was expected to have a significant impact on these factors. To achieve the desired design objectives and find the optimal configuration for the lattice structure, the implementation of a multi-objective shape optimisation strategy became essential.

Table 1.
Different design variants of the proposed implicit-based BCC lattice structure achieved by increasing while keeping constant at 0.1.

Table 2.
Different design variants of the proposed implicit-based BCC lattice structure achieved by increasing while assigning lower band values to from .
2.2. Finite Element Analysis
A finite element (FE) model of the lattice structures employing a tetrahedral mesh was developed in MATLAB® using the MATLAB PDE toolbox. The boundary conditions corresponding to the FE model are presented in Figure 6. The bottom surface of the lattice structure model was fixed in the vertical (z-axis) direction, while it was allowed to move freely (frictionless) in the x-y horizontal plane. The top surface of the lattice was subject to a displacement loading of 2 mm downward (-z-axis), producing an overall strain of . A static structural FEA was performed to study the linear elastic behaviour of lattice structures under uni-axial compression. The total reaction force on the top surface of the lattice geometry was derived from FEA. The reaction force was divided by the face area (40 × 40 mm) of the lattice sample to calculate the overall stress generated, which was then divided by the applied strain to find the elastic modulus of the lattice model. The relative elastic modulus of the lattice was calculated by dividing the elastic modulus of the lattice by the Young’s modulus of the building material (), i.e., . The von-Mises stress () was also calculated across the lattice structure for the further investigation of the performance of different designs.
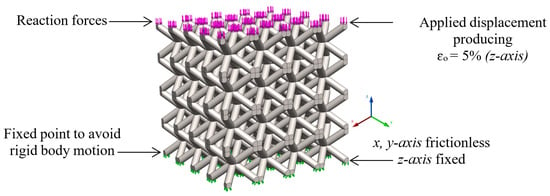
Figure 6.
Boundary conditions applied to a lattice structure and the resultant reaction forces on the top surface of the lattice.
The tetrahedral mesh used in this study for all samples had a maximum element size of 0.2 mm providing a balance between the computation cost and numerical accuracy. Figure 7 demonstrates a sample of the BCC structure with such a mesh density. To investigate the accuracy of the FEA results for the given element size, a mesh sensitivity analysis was performed on the BCC structure with a relative density of 18%. Figure 8 shows the convergence plot associated with the maximum von-Mises stress () for different mesh densities. It can be seen from the convergence plot that when a maximum element size of 0.2 mm (which corresponds to the total number of elements = 20,000 in this case) was utilised, the maximum von-Mises stress () exhibits less than a 1% deviation from the converged value of .
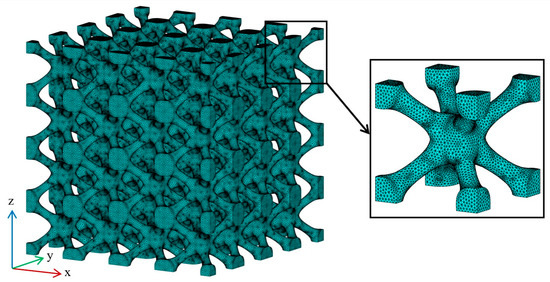
Figure 7.
Demonstration of FE mesh used for the BCC sample with 18% relative density.
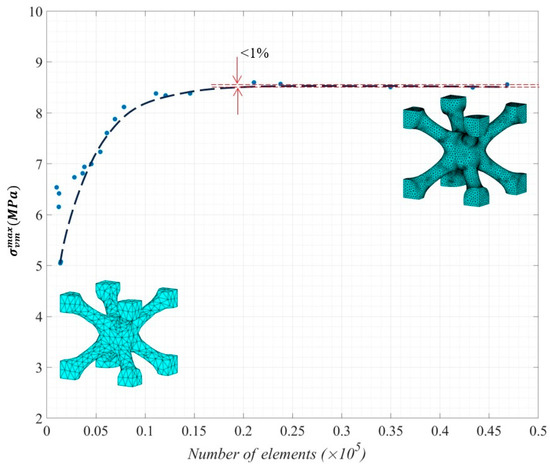
Figure 8.
Convergence of max von-Mises stress () at different mesh densities.
2.3. Preliminary Investigation of the Effect of Design Variables on the Mechanical Response of the Lattice
To investigate the effect of design variables and on the relative density ( of the lattice as well as its mechanical response to external loads, the domain of the design variables was discretized into a 30 × 30 grid, and the lattice structure corresponding to each grid point was constructed through the methodology presented in Section 2.1. These lattice structures were then saved in an STL file format for further analysis. The relative density of each design was calculated by dividing the volume of the solid region within the lattice by the volume of the whole cubic domain. Furthermore, FEA was performed on each lattice structure subjected to the boundary conditions presented in Section 2.2 to calculate the von-Moses stress and relative modulus .
Figure 9a presents the relationship between two design variables ( and ) and the relative density of the corresponding lattice structure. As can be expected, increasing the value of each design variable can lead to an increase in of the constructed lattice structure. Figure 9b presents the effects of and on the relative modulus of the constructed lattice structure. It can be seen that increasing each design variable has a positive effect on increasing .
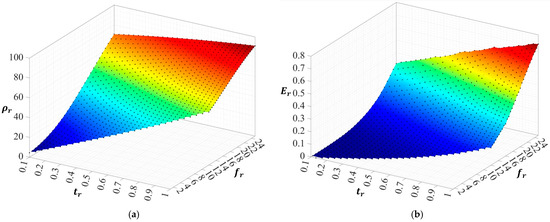
Figure 9.
(a) The relation between tr, fr, and ρr. (b) The relationship between tr, fr, and Er.
Figure 10 presents the measurements of and for the 900 different lattice designs. Figure 10a displays the measurements across the full density range, while Figure 10b focuses on the relative density range of 0–30%. The Ashby–Gibson power-law model [32], commonly used for analysing the properties of cellular structures, was employed to establish the density–stiffness relationship. It can be seen from Figure 10a that the power-law model does not fit well for the data points covering the full density range. However, when the model is applied to relative densities within the 0–30% range, the best fit curve aligns well with the data points. This particular density range has been suggested in the literature as the effective range for the implementation of Ashby–Gibson power-law model in the analysis of cellular structures [33]. From Figure 10a, it can also be seen that the variation in , which serves as an indicator of stiffness, is primarily related to the density of the lattice. However, Figure 10b highlights the presence of data points with different stiffness values at the same density. This observation suggests that factors other than density, though potentially not significant, can influence the stiffness of the lattice structure when variables vary at the same density.
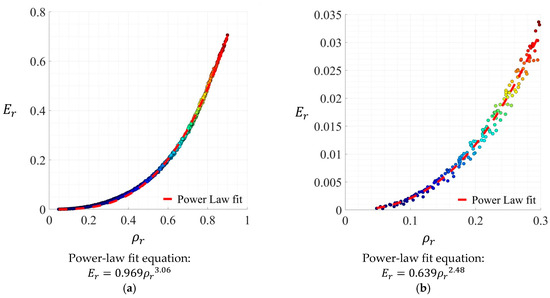
Figure 10.
Demonstration of stiffness–density (-) relationship obtained from 900 different designs and the corresponding best fit equations (a) covering the full relative density range, and (b) focusing on the 0–30% relative density range.
Figure 11 presents the datapoints corresponding to for BCC lattice structures with respect to the design variables (Figure 11a) and relative density (Figure 11b). The von-Mises stress vs. design variables plot presented in Figure 11a does not provide sufficient clarity on the relationship between , tr, and fr, due to the scattered distribution of data points within the 3D plot. From Figure 11b, it can be seen that, in general, as increases, so does (it should be noted that the results are obtained under displacement loading, where the applied displacement remains constant for all lattice samples; however, the reaction force varies, resulting in different stress levels within the lattice structures). However, compared to the stiffness–density data presented earlier in Figure 10, the stress–density data appears more scattered over a wider range. This indicates the importance of carefully adjusting the design variables to achieve the desired response from the lattice structure. In any case, the preliminary investigation of the effect of design variables on lattice structure properties demonstrates the significance and necessity of the implementation of an appropriate optimisation strategy for the design of the lattice structure, particularly for multi-objective optimisation problems, for instance, when the lattice structure is designed for maximum stiffness and minimum von-Mises stress with a target volume fraction (relative density) constraint. This was further investigated in the following section.
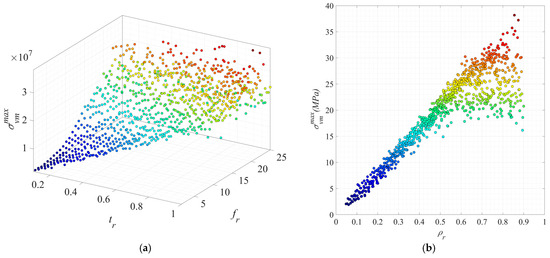
Figure 11.
Data points corresponding to 900 different designs of the BCC lattice structure presenting (a) the relationship between the maximum von-Mises stress and design variables (tr, fr), and (b) the maximum von-Mises stress–relative density (-) relationship.
2.4. Parametric Shape Optimisation of BCC Structures through the Multi-Objective Genetic Algorithm
The genetic algorithm (GA) invented in 1970s by John Holand [34] is a computational method rooted in the principles of natural evolution. These fundamental principles encompass selection, mutation, and crossover, guided by the survival of the fittest criterion. The GA, as an evolutionary algorithm, involves the definition of an objective function, which is either maximised or minimised across successive generations, primarily driven by the fittest individuals that possess superior genetic traits. Given its ability to tackle complex optimisation problems, for instance, where there is a high chance of falling into a local minima during the optimisation process, or when the problem involves optimising multiple conflicting objectives, the GA serves as a strong tool in the pursuit of optimal solutions [35]. The GA has been implemented in several previous studies focused on the design of AM, such as the optimisation of auxetic metamaterials [23] and the material optimisation of biomedical composite devices [36].
This work employed a multi-objective genetic algorithm (MOGA) approach [37] available in MATLAB® to optimise two or more objectives simultaneously. MOGA begins by a random creation of an initial population of candidate solutions (individuals or chromosomes), which are then evaluated in terms of their performance (fitness) based on the objective functions of the problem. A non-dominated sorting technique is then used to rank the chromosomes based on their dominance relationship. Selection operators, such as tournament or roulette wheel selections, are used by MOGA to choose the best fit chromosomes. It also uses genetic operators, including crossover and mutation, to create offspring for the next generation. The offspring, along with some individuals from the population at present, replaces the previous generation, and the process is repeated until a termination criterion, such as a maximum number of generations or achieving a desired level of convergence, is met. Throughout the evolutionary process, MOGA maintains a set of non-dominated solutions, the solutions that cannot be improved in any objective without sacrificing the performance of another, known as the Pareto front. This set represents the trade-off between conflicting objectives offering decision makers a diverse set of solutions to choose from, based on their preferences.
In this work, MOGA was implemented to find the best design variables and , which can optimise the two objective functions of the problem. Objective 1 (Equation (3)) was to maximise the stiffness of the BCC lattice structure (the relative modules ) and objective 2 (Equation (4)) was to minimise the maximum value of the von-Mises stress () within the lattice structure:
In this study, it was assumed that the optimised solutions were manufacturable, taking into account the selected material, AM process, and geometric properties of the cells, including the cell size, which was an important consideration if the unit cell was not self-supporting for AM. However, to extend the applicability of the proposed optimisation approach for AM, additional manufacturing constraints, such as minimum strut thickness and minimum/maximum relative density, must be incorporated into the optimisation problem to further refine the search domain.
To perform MOGA, the population size was set to 100, the number of generations was set to 200, the number of pairs of chromosomes to cross over was 20, and the number of chromosomes to be mutated was two. Convergence was achieved when the best solutions across generations remained relatively unchanged or changed only minimally. Figure 12a presents the Pareto front corresponding to the optimisation of the two objective functions through MOGA. For reference, Figure 12b demonstrates the distribution of objectives corresponding to the 900 different designs studied in Section 2.3. Comparing the two graphs presented in Figure 12, it can be seen that MOGA is able to identify designs with high values for objective 1 () and low values for objective 2 (). It can also be seen that the Pareto front offers a diverse set of solutions representing a trade-off between the two objective functions and .
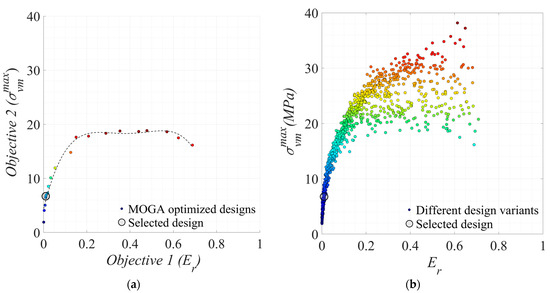
Figure 12.
(a) MOGA Pareto front presenting a set of optimised solutions with respect to objective 1 () and objective 2 (); (b) distribution of objectives corresponding to the 900 different designs studied in Section 2.3.
Figure 13a shows the - graph for the set of solutions presented by the Pareto front. The graph reveals a diverse range of designs, encompassing relative densities that range from 0 to 1. This provides designers with the flexibility to choose solutions based on their preference in relation to the relative density. Poisson’s ratio, defined as the negative of the ratio of transverse strain to axial strain, is another important property affecting the behaviour of cellular structure. Figure 13b demonstrates the Poisson’s ratio of the MOGA solutions presented by the Pareto front. It can be seen that the Poisson’s ratio of the designs exhibits a range of 0.45–0.5 at lower relative densities. However, as the relative density increases towards 1, the Poisson’s ratio decreases and falls within the range of 0.25–0.3, reaching the value of the Poisson’s ratio for the bulk material.
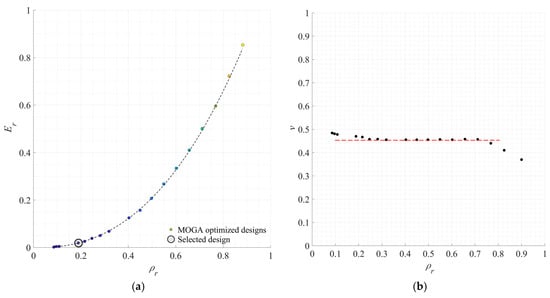
Figure 13.
(a) Stiffness–density (-) graph for the set of solutions presented by the MOGA Pareto front; (b) Poisson’s ratio () against relative density for the set of solutions presented by the MOGA Pareto front.
From the set of optimised solutions achieved from MOGA, a solution with a relative density of was selected for further analysis, including mechanical testing. This relative density was within the valid range for the implementation of the Ashby–Gibson power law and was also within the same range as the BCC structures studied in the literature, Refs. [28,30], allowing for a meaningful comparison to be performed with the results presented in previous studies on BCC structures.
2.5. Single-Objective Genetic Algorithm Optimisation (SOGA)
Following the results obtained from the multi-objective optimisation using MOGA in the previous section, this section presents the designs optimised for each single objective and compares them with those simultaneously optimised for the two objectives through MOGA. The single-objective optimisation was performed through standard GA at a relative density constraint of . To limit the search space within the specified range of the relative density, the range of the design variables were adjusted as and . The implementation of SOGA involved two runs. The first run focused on maximising objective 1 (or minimising ), exclusively. In the second run, the objective was to minimise objective 2 , exclusively. Figure 14 presents the evolution histories of the two objective functions associated with the two separate runs. It can be seen that they both converge within 20 generations. A great improvement in the mean objective can be observed in both runs of SOGA. From Figure 14a, it can be seen that the mean value of reduces from approximately 105 in the first generation of designs converging to around 91 within the evolutionary process. This corresponds to an average of 0.0095 at the first generation converging to . A similar trend can be observed in Figure 14b for the minimisation of objective 2 through SOGA. The average decreases from approximately 8.3 MPa in the initial generation to around 6.66 MPa as the evolutionary process progresses.
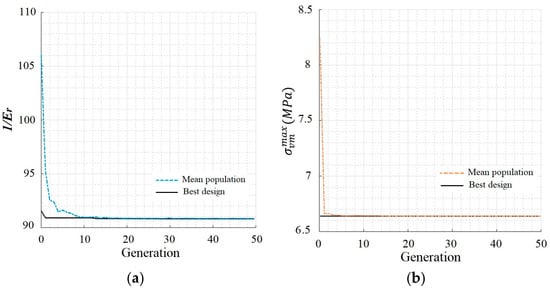
Figure 14.
Evolution histories corresponding to two runs of SOGA: (a) maximising objective 1 (minimising ) exclusively, and (b) minimising objective 2 , exclusively.
2.6. Numerical Comparison of the Solutions
FEA was performed on the BCC structures optimised through MOGA () and SOGA ( denoting stiffness-optimised BCC and denoting -optimised BCC), as well as the classical BCC structure () to compare the performance of different designs in terms of and at the relative density of . The numerical results are summarised in Table 3.

Table 3.
Performance comparison of different BCC structures optimised through MOGA and SOGA as well as the classical model of BCC.
From Table 3 it can be seen that all three structures optimised through MOGA and SOGA (, , and ) have superior performances compared to , in terms of both and . Comparing the optimised designs in terms of stiffness, it can be seen that and have very similar values of , which is slightly higher than that of . Similarly, comparing them against , it can be seen that the design optimised for the von-Mises stress () has a smaller value of compared to the other two optimised designs. Overall, the optimised designs for the BCC structure show a significant enhancement of the mechanical performance when compared with the classical model of BCC. The comparison of the numerical results corresponding to and underscores the effectiveness of the optimisation strategy. However, the three optimised designs appear very similar in shape and also performance (two almost identical), indicating that optimising one objective of this multi-objective problem can positively impact the improvement of the second objective. This was further investigated in the following sections though the additive manufacturing of the samples and subsequent mechanical testing.
3. Additive Manufacturing and Mechanical Testing
The BCC lattice specimens studied earlier were printed through the DLP process using a Phrozen Mini 8k printer with an XY print resolution of 22 µm. Three samples for each design were printed for further testing to ensure experiment repeatability. The slicing software ChituBox V1.9.3 was used to generate machine-readable files. The print settings included a bottom-layer exposure time of 35 s, other-layer exposure time of 10 s, and a layer thickness of 0.1 mm. A high-resolution transparent photopolymer resin (UV DLP Crystal Clear by Photocentric) [38] with a curing wavelength of was utilised for the 3D printing of the specimens. The printed specimens were not UV-cured after printing to avoid the non-homogeneous penetration of the UV light into the lattice structures during post-processing, which can create non-homogenous material properties across the lattice volume. Instead, a longer exposure time per layer (10 s) during the print process was used to maintain homogenous properties across the lattice. Using the same print settings, solid cubes 10 mm in size were also printed to evaluate the density and mechanical properties of the bulk material. From the mass and volume measurements obtained from the solid cubes, the density of the bulk material was calculated as 1188 kg/m3.
Table 4 presents the 3D-printed samples of the different BCC structures, including , , , and , along with their experimentally measured mass and relative density values. Using the experimental measurement of the density of bulk material, the intended design mass for the BCC samples at could be calculated as 14.22 g. However, the data presented in Table 4 show a discrepancy of up to 23% between the mass/relative density values of the BCC lattice designs and the corresponding values of the 3D-printed specimens. This can be attributed to the geometric overgrowth during the DLP 3D-printing process, which was observed and discussed in the literature [39]. Geometric overgrowth is caused by UV-light scattering effects, which depend on different factors, such as layer thickness, layer exposure time, and exposure intensity. Since the lattice structure has a complex geometry with a high surface to volume ratio, the deviation from the original design geometry is more pronounced compared to simpler shapes, such as cubes. Despite the observed design-to-build discrepancy in the mass, it was noteworthy that the relative densities of all 3D-printed specimens were about , providing a sufficient level of accuracy for the performance comparison of different 3D-printed specimens, as discussed in the following section.

Table 4.
The comparison between the theoretical masses and the 3D-printed specimens.
In order to assess the mechanical performance of the DLP-printed BCC structures and compare it with the numerically evaluated results presented in Section 2, a compression test was executed on the entire set of printed samples. All the specimens were tested along the build direction. The compression test was conducted using an Instron 3367 machine, equipped with a 30 kN load cell, in accordance with the ASTM D1621-16 standard [40]. A uniform compression rate of 0.1 mm/s was applied to each individual sample. Throughout the compression process, the reaction force and corresponding displacement were recorded through the employment of the load cell and a displacement gauge, respectively. The data were then collected and managed using the Bluehill® computer program, which captured readings at a frequency of 20 readings per second. To visually document the deformation induced by the compression plate of the machine, a high-speed, high-resolution camera capable of capturing 60 frames per second and performing high-definition video recording was utilised. An illustrative depiction of a BCC structure undergoing compression testing is presented in Figure 15.

Figure 15.
(a) Demonstration of a BCC lattice specimen during compression test and (b) different stages of the compression test presented from left to right.
During the compression testing of the specimens, the force values were systematically documented in a spreadsheet alongside their respective displacements. These force values were subsequently divided by the face area of the cubic lattice sample (40 × 40 mm2) under compression, resulting in the computation of global stress values (σ). Plotting these stress values (σ) against the strain (ε) induced by the compression test machine facilitated the determination of the Young’s modulus of the lattice material (), based on the slope of the linear elastic region within the stress–strain curve. Similarly, following ASTM D695-15 [41], the Young’s modulus () of solid samples sized 10.0 mm × 10.0 mm × 10.0 mm was calculated. These solid samples were 3D-printed using the same material and settings as those used for the lattice samples. This process yielded the stress–strain curves depicted in Figure 16, from which a Young’s modulus of MPa was computed for the bulk material. Parallel to the numerical calculations presented in Section 2, the experimental relative modulus values () for each lattice structure were deduced, employing the formula .
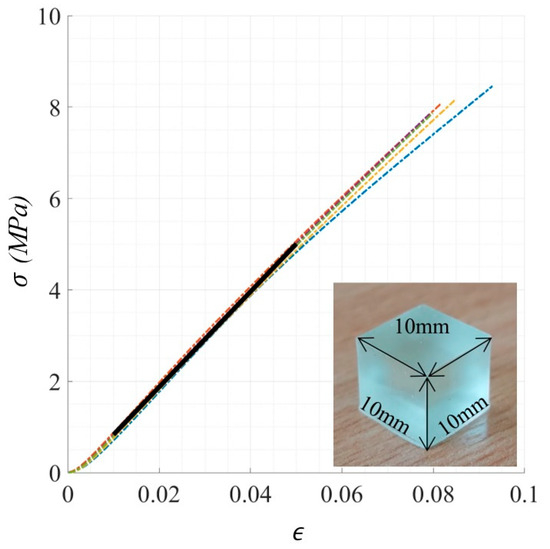
Figure 16.
Stress–strain plots corresponding to five solid samples fabricated through the DLP process resulting in an average Young’s modulus of 104.3 MPa.
The numerical model developed for FEA and the optimisation of BCC lattice structures applied a 5% strain to calculate the elastic modulus of the lattice structure. As the simulations were based on the linear FEA model neglecting large deformations, the magnitude of the applied strain did not affect the magnitude of the calculated elastic modulus for the specimen. However, when investigating the results of the compression testing of the lattice structures, it was observed that the specimens subjected to a 5% strain underwent large deformations. Consequently, the elastic modulus was determined within a smaller strain range of 1–2% to account for this behaviour. The initial strain range of 0–1% was omitted from the calculations to mitigate potential impacts arising from uneven sample surfaces during the experimental measurements.
Based on the literature, it is well-established that solid samples produced through AM can exhibit varying mechanical properties, which partly depend on their orientations during fabrication and testing processes [42]. Similarly, DLP-printed solid specimens have been observed to display anisotropic behaviour in stiffness and strength tests [43]. However, the literature reports suggest that the compressive behaviour of AM lattice structures is not influenced by build orientation in the same manner as AM solid structures [42]. In this study, all samples were tested along the build orientation. Nevertheless, future studies can take into account material anisotropy when studying the mechanical properties of DLP-printed lattice structures.
4. Results and Discussion
This section presents the results and discussions related to the compression testing of BCC lattice specimens, followed by additional comments on the broader application of the proposed method in lattice structure design for AM.
4.1. Comparison of Different Designs
Figure 17 illustrates the stress–strain plots corresponding to the compression test of a set of four different BCC structures, including , , , and . The stiffness of the lattice structures presented in terms of was directly related to the slope of the curves in the linear elastic region, which is calculated and demonstrated in Figure 18. From the comparison of the stiffness values presented in this figure, it can be observed that the experimental values of are slightly smaller than their corresponding numerical values, despite the fact that the experimental tests were performed on the lattices with a slightly larger mass (due to print inaccuracies) in comparison to their intended designs. The observed discrepancy can be attributed to various factors, including the influence of surface roughness effects, which become more prominent in samples with a high surface-to-volume ratio, such as lattice structures. These factors prevent the experimental performance from achieving the numerically estimated values. This emphasises the need for the consideration of size effects in the design and optimisation of lattice structures for AM in the future research. It is important to note that the similarity between the numerical and experimental values observed for MOGA and stiffness-optimised solutions in Figure 18 did not inherently establish the accuracy of the experimental measurements. This was due to the fact that the experiments were conducted on samples with slightly higher relative densities. Consequently, to address this concern, a MOGA solution with a relative density of 22% (similar to the relative density of the printed lattice samples) was investigated. Through FEA, a relative modulus of was calculated, which notably exceeded the value obtained from the experimental measurements .
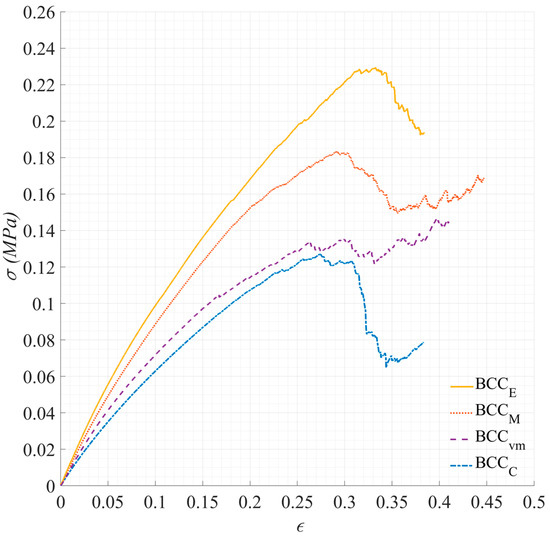
Figure 17.
Stress–strain plots associated with the compression testing of a set of samples containing BCCC, BCCM, BCCE, and BCCvm specimens.
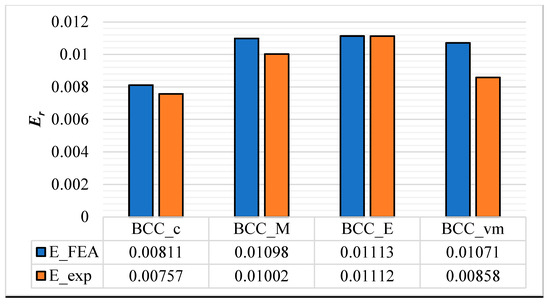
Figure 18.
Comparison of the stiffness of different BCC structures. Relative elastic modulus () calculated numerically () and experimentally () used as an indicator of stiffness. The experimental results are based on the average measurements obtained from three fabricated samples for each distinct design configuration.
The second important thing that can be observed from Figure 18 is that the experimental measurements of for the set of four BCC structures results in the same stiffness ranking as that for the numerical measurements, i.e., and have higher values of stiffness within this set of four samples, followed by , while ranks at the bottom. This demonstrates the correlation between the experimental and numerical results with respect to the stiffness. The experimental evaluation of the von-Mises stress in different lattice samples would not be as straightforward as the procedure used for the stiffness measurement and is beyond the scope of this study. However, by looking at the peaks of the stress–strain plots presented in Figure 17, it can be observed that all plots corresponding to the optimised samples have higher values of maximum stress compared to the classical model of the BCC structure, indicating the effectiveness of the proposed design and optimisation approach in improving the strength of the lattice structures.
4.2. Insights into the Failure Modes of DLP-Printed BCC Lattices
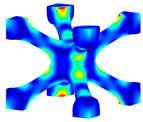
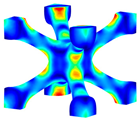
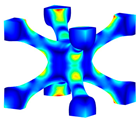
Following the compression testing, a further examination of the lattice structures was conducted to determine the mode of failure within the structures. Figure 19 presents the findings from this observation, comparing the failure mode of a classical BCC structure () with the one for an optimised BCC structure, e.g., . The observations were performed on three levels: lattice structure, unit cell, and strut levels. The observation of the failure mode at the lattice structure level for the classical BCC structure (Figure 19a) indicated the shear failure mode for this structure. This mode was observed in all three samples of the classical BCC structure repeated for testing and was reported in the literature [27]. By observing the failure of the classical BCC structure at the unit cell (Figure 19b) and strut (Figure 19c) levels further, it can be noticed that the failure starts from the nodes that are under high levels of von-Mises stress due to stress concentration. This non-uniform distribution of stress and concentration at the nodes can be observed from the von-Mises stress contour of presented Table 3. Figure 19d–f shows the failure mode of the optimised BCC at the lattice structure, unit cell, and strut levels, respectively. It can be observed that failure occurs in the middle of the struts, where the struts have their minimum thickness. This failure mode occurred due to bending, as discussed in [27]. When the filet radius at the nodes is increased while keeping the relative density constant, it leads to a reduction in the stress concentration effects and can subsequently enhance the strength of the lattice structure. However, to maintain a constant relative density while increasing the fillet radius, the diameter of the struts in the middle must be proportionally reduced, resulting in failure occurring at the middle of the struts. As can be seen in Figure 17, the optimised BCC structures require higher levels of global stress to reach the failure point. This can be attributed to a more uniform distribution of stress within the optimised lattice structures, as is evident from the corresponding von-Mises stress contours presented in Table 3.

Figure 19.
Failure modes of classical and optimised BCC structures: (a) classical BCC at lattice structure level, (b) classical BCC at unit cell level, (c) classical BCC at strut level, (d) optimised BCC at lattice structure level, (e) optimised BCC at unit cell level, (f) optimised BCC at strut level.
4.3. Further Remarks on the Generalisation of the Lattice Structure Design for AM
The primary objective of this study was to apply an innovative design approach based on implicit geometry modelling and GA optimisation on the design of BCC lattice structures intended for manufacturing through the DLP process. However, a more comprehensive design workflow for AM can be considered, aligned with the presented approach, to broaden its scope and encompass the design of diverse lattice structures for various AM processes [44,45].
An initial problem statement identifying the design space followed by a preliminary macroscale FEA or topology optimisation performed on the design space can provide insights into the mesoscale design requirements and objectives. An important step towards achieving the generalisation of the proposed approach would be the extension of the implicit modelling to other types of strut-based lattice unit cells through the development of an implicit equation representing the geometry of the corresponding unit cell. Moreover, following the selection of an appropriate material and an AM process, AM constraints and considerations need to be integrated into the proposed parametric optimisation approach as design constraints. Such design constraints can be related to geometrical features, which affect the self-supporting aspect of a unit cell, minimum feature size, and/or maximum/minimum relative densities. To achieve the utmost precision in accordance with the input geometry, it is essential to fine-tune the AM process parameters in alignment with the chosen build material and lattice geometry. Depending on the selected AM process, material anisotropy effects corresponding to the build material can also be taken into account when evaluating the response of the designed lattice structures associated with certain loading conditions and design objectives. The design workflow can also benefit from the development of appropriate testing equipment for evaluating the response of additively manufactured lattice structures. Efficient metrological measurements of the 3D-printed specimens should be considered to evaluate the design-to-build discrepancy. A clear understanding of this discrepancy would be advantageous in design and optimization stages to provide insights into the potential adjustments needed to compensate for the discrepancy in forthcoming print iterations.
5. Summary and Conclusions
This study introduced a design and optimisation methodology for the parametric shape optimisation of BCC lattice structures based on an implicit modelling scheme integrated with single-/multi-objective genetic algorithm optimisations. Stiffness responses associated with a classical BCC structure as well as single-objective and multi-objective optimised BCC structures were investigated and compared through FEA and mechanical testing. The distribution of the stress and the maximum value of the von-Mises stress were also studied numerically in different BCC structures.
When comparing the relative elastic modulus () values of various BCC structures with identical relative densities, it was observed that the optimised BCC structures exhibited an improved stiffness response compared to the conventional BCC structure. Specifically, at a relative density of , the numerical analysis and experimental measurements indicated an estimated improvement in of up to 57% and 83%, respectively. Furthermore, it was observed that the stress concentration was significantly reduced by implementing the proposed shape optimisation approach. At the relative density of , up to a 25% reduction in the maximum von-Mises stress in a BCC structure was observed upon the application of the proposed design and optimisation strategies. The experimental results further confirm these numerical findings, demonstrating that the optimised BCC structures subjected to a compression test exhibit higher maximum stress values compared to the classical BCC structure.
This research effectively implemented the multi-objective GA (MOGA) for the parametric shape optimisation of lattice structures involving multiple objectives. The range of solutions provided by MOGA allowed for flexibility in choosing a preferred design from a variety of optimised designs with different relative densities. The research also studied the use of single-objective GA (SOGA) optimisation for the design of BCC lattices at a particular relative density. Although SOGA seeks the best design associated with a single objective, the results for the second objective are still comparable to those obtained from MOGA. This evidently depends on the objectives included in the problem and whether they are in conflict with each other. In cases where conflicting objectives are present, the application of MOGA proves advantageous.
In this study, a high-resolution DLP process was utilised for the additive manufacturing of the designed BCC structures. While the process showed excellent capabilities in the fabrication of lattices with a high resolution, a noticeable design-to-build discrepancy was observed between the mass of the fabricated samples and their intended designs. This phenomenon has been discussed in the literature, attributing it to geometric overgrowth triggered by the scattering effects of UV light. These effects also have the potential to impact the shape of printed samples, leading to deviations from the original CAD model. A thorough exploration of the shape of 3D-printed lattice specimens can offer insights into these geometric discrepancies. Future research can greatly benefit from incorporating manufacturing-related effects into the design process to mitigate the design-to-build discrepancy. However, achieving this goal necessitates considering numerous process-related factors during the design phase, thereby increasing the complexity of the design and optimisation approach.
Overall, the application of implicit modelling in conjunction with a GA-based optimisation strategy was determined as a robust and promising approach for designing and optimising lattice structures for additive manufacturing. Future research should expand the application of the presented implicit modelling technique to design various types of lattice structures with desired structural responses, which can be tailored through the GA optimisation.
Author Contributions
Conceptualization, H.M.A.A. and M.A.; Formal analysis, H.M.A.A.; Methodology, H.M.A.A. and M.A.; Software, H.M.A.A.; Supervision, M.A.; Validation, H.M.A.A.; Writing—original draft, H.M.A.A. and M.A.; Writing—review and editing, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the Faculty of Computing, Engineering and Media at De Montfort University.
Data Availability Statement
Raw data from this paper are available upon request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brackett, D.; Ashcroft, I.; Hague, R. Topology optimization for additive manufacturing. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2011; pp. 348–362. [Google Scholar]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for additive manufacturing: Trends, opportunities, considerations, and constraints. CIRP Ann. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Abdi, M.; Ashcroft, I.; Wildman, R. High resolution topology design with iso-XFEM. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 4–6 August 2014; pp. 1288–1303. [Google Scholar]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef]
- Aremu, A.; Brennan-Craddock, J.; Panesar, A.; Ashcroft, I.; Hague, R.; Wildman, R.; Tuck, C. A voxel-based method of constructing and skinning conformal and functionally graded lattice structures suitable for additive manufacturing. Addit. Manuf. 2017, 13, 1–13. [Google Scholar] [CrossRef]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for additive manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Fleck, N.A.; Deshpande, V.S.; Ashby, M.F. Micro-architectured materials: Past, present and future. Proc. R. Soc. A Math. Phys. Eng. Sci. 2010, 466, 2495–2516. [Google Scholar] [CrossRef]
- Syam, W.P.; Jianwei, W.; Zhao, B.; Maskery, I.; Elmadih, W.; Leach, R. Design and analysis of strut-based lattice structures for vibration isolation. Precis. Eng. 2018, 52, 494–506. [Google Scholar] [CrossRef]
- Catchpole-Smith, S.; Sélo, R.R.J.; Davis, A.W.; Ashcroft, I.A.; Tuck, C.J.; Clare, A. Thermal conductivity of TPMS lattice structures manufactured via laser powder bed fusion. Addit. Manuf. 2019, 30, 100846. [Google Scholar] [CrossRef]
- Ryan, G.; Pandit, A.; Apatsidis, D.P. Fabrication methods of porous metals for use in orthopaedic applications. Biomaterials 2006, 27, 2651–2670. [Google Scholar] [CrossRef]
- Echeta, I.; Feng, X.; Dutton, B.; Leach, R.; Piano, S. Review of defects in lattice structures manufactured by powder bed fusion. Int. J. Adv. Manuf. Technol. 2020, 106, 2649–2668. [Google Scholar] [CrossRef]
- Abdi, M.; Ashcroft, I.; Wildman, R.D. Design optimisation for an additively manufactured automotive component. Int. J. Powertrains 2018, 7, 142–161. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Bici, M.; Brischetto, S.; Campana, F.; Ferro, C.G.; Seclì, C.; Varetti, S.; Maggiore, P.; Mazza, A. Maggiore and A. Mazza. Development of a multifunctional panel for aerospace use through SLM additive manufacturing. Procedia CIRP 2018, 67, 215–220. [Google Scholar] [CrossRef]
- Weeger, O.; Boddeti, N.; Yeung, S.K.; Kaijima, S.; Dunn, M.L. Digital design and nonlinear simulation for additive manufacturing of soft lattice structures. Addit. Manuf. 2019, 25, 39–49. [Google Scholar] [CrossRef]
- Mahmoud, D.; Elbestawi, M.A. Lattice structures and functionally graded materials applications in additive manufacturing of orthopedic implants: A review. J. Manuf. Mater. Process. 2017, 1, 13. [Google Scholar] [CrossRef]
- Fina, F.; Goyanes, A.; Madla, C.M.; Awad, A.; Trenfield, S.J.; Kuek, J.M.; Patel, P.; Gaisford, S.; Basit, A.W. 3D printing of drug-loaded gyroid lattices using selective laser sintering. Int. J. Pharm. 2018, 547, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 325–332. [Google Scholar]
- Xiao, X.; Xie, L.; Tang, R.; Liu, J.; Song, P.; Zhu, X.; Zhao, J.; Jiang, C.; Yang, S.; Wu, P. Improved compressive properties of lattice structure based on an implicit surface hybrid optimization design method via selective laser melting. Metals 2022, 12, 1477. [Google Scholar] [CrossRef]
- Abdi, M.; Ashcroft, I.; Wildman, R. An X-FEM based approach for topology optimization of continuum structures. In Proceedings of the Simulation and Modeling Methodologies, Technologies and Applications: International Conference, SIMULTECH 2012, Rome, Italy, 28–31 July 2012; pp. 277–289. [Google Scholar]
- Wang, Y.; Luo, Z.; Zhang, N.; Qin, Q. Topological shape optimization of multifunctional tissue engineering scaffolds with level set method. Struct. Multidiscip. Optim. 2016, 54, 333–347. [Google Scholar] [CrossRef]
- Bertolino, G.; Montemurro, M.; De Pasquale, G. Multi-scale shape optimisation of lattice structures: An evolutionary-based approach. Int. J. Interact. Des. Manuf. (IJIDeM) 2019, 13, 1565–1578. [Google Scholar] [CrossRef]
- Ali, H.M.A.; Abdi, M.; Zahedi, S.A.; Sung, Y. Design of a programmable particle filtering medium using a novel auxetic metamaterial. Smart Mater. Struct. 2023, in press. [CrossRef]
- Kim, J.J.; Kim, H.Y. Shape design of an engine mount by a method of parametric shape optimization. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 1997, 211, 155–159. [Google Scholar] [CrossRef]
- Bauer, J.; Priesnitz, K.; Schemmann, M.; Brylka, B.; Böhlke, T. Parametric shape optimization of biaxial tensile specimen. Pamm 2016, 16, 159–160. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Stiffness and specific energy absorption of additively-manufactured metallic BCC metamaterials composed of tapered beams. Int. J. Mech. Sci. 2018, 141, 101–116. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.Z.; Li, Z.; Zhang, T.; Zhou, H.; Ren, Z. Design, mechanical properties, and optimization of BCC lattice structures with taper struts. Compos. Struct. 2022, 295, 115830. [Google Scholar] [CrossRef]
- Zhao, M.; Li, X.; Zhang, D.Z.; Zhai, W. Design, mechanical properties and optimization of lattice structures with hollow prismatic struts. Int. J. Mech. Sci. 2023, 238, 107842. [Google Scholar] [CrossRef]
- Bai, L.; Yi, C.; Chen, X.; Sun, Y.; Zhang, J. Effective design of the graded strut of BCC lattice structure for improving mechanical properties. Materials 2019, 12, 2192. [Google Scholar] [CrossRef]
- Lee, S.; Zhang, Z.; Gu, G.X. Generative machine learning algorithm for lattice structures with superior mechanical properties. Mater. Horiz. 2022, 9, 952–960. [Google Scholar] [CrossRef]
- Chang, P.S.; Rosen, D.W. The size matching and scaling method: A synthesis method for the design of mesoscale cellular structures. Int. J. Comput. Integr. Manuf. 2013, 26, 907–927. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. The structure and properties of cellular solids. Pergamon Oxford.(2) Wamer M. Edw. SF Europhys. Letts 1988, 5, 623–628. [Google Scholar]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A.; Wildman, R.D.; Hague, R.J.M. A mechanical property evaluation of graded density al-Si10-mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Coello, C.A. An updated survey of GA-based multiobjective optimization techniques. ACM Comput. Surv. (CSUR) 2000, 32, 109–143. [Google Scholar] [CrossRef]
- He, Y.; Abdi, M.; Trindade, G.F.; Begines, B.; Dubern, J.F.; Prina, E.; Hook, A.L.; Choong, G.Y.; Ledesma, J.; Tuck, C.J.; et al. Exploiting generative design for 3D printing of bacterial biofilm resistant composite devices. Adv. Sci. 2021, 8, 2100249. [Google Scholar] [CrossRef]
- Murata, T.; Ishibuchi, H. MOGA: Multi-objective genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Perth, Australia, 29 November–1 December 1995; pp. 289–294. [Google Scholar]
- PhotoCentric3D, “UV DLP Crystal Clear”, Technical Data, Jan. Available online: https://photocentricgroup.com/product/uv-dlp-crystal-clear-resin/ (accessed on 24 February 2023).
- Mitteramskogler, G.; Gmeiner, R.; Felzmann, R.; Gruber, S.; Hofstetter, C.; Stampfl, J.; Ebert, J.; Wachter, W.; Laubersheimer, J. Light curing strategies for lithography-based additive manufacturing of customized ceramics. Addit. Manuf. 2014, 1, 110–118. [Google Scholar] [CrossRef]
- ASTM D1621-16; Standard Test Method for Compressive Properties of Rigid Cellular Plastics. ASTM International: West Conshohocken, PA, USA, 2004. Available online: https://global.ihs.com/doc_detail.cfm?gid=MMDTFBAAAAAAAAAA&input_doc_number=ASTM%20D1621 (accessed on 1 February 2023).
- ASTM D695-15; Standard Test Method for Compressive Properties of Rigid Plastics. ASTM International: West Conshohocken, PA, USA, 2015. Available online: http://www.astm.org/Standards/D695 (accessed on 1 February 2023).
- Jenkins, S.N.; Oulton, T.H.; Hernandez-Nava, E.; Ghadbeigi, H.; Todd, I.; Goodall, R. Anisotropy in the mechanical behavior of Ti6Al4V electron beam melted lattices. Mech. Res. Commun. 2019, 100, 103400. [Google Scholar] [CrossRef]
- Monzón, M.; Ortega, Z.; Hernández, A.; Paz, R.; Ortega, F. Anisotropy of photopolymer parts made by digital light processing. Materials 2017, 10, 64. [Google Scholar] [CrossRef]
- Savio, G.; Meneghello, R.; Concheri, G. Optimization of lattice structures for additive manufacturing technologies. In Advances on Mechanics, Design Engineering and Manufacturing, Proceedings of the International Joint Conference on Mechanics, Design Engineering & Advanced Manufacturing (JCM 2016), Catania, Italy, 14–16 September 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 213–222. [Google Scholar]
- Savio, G.; Meneghello, R.; Concheri, G. Geometric modeling of lattice structures for additive manufacturing. Rapid Prototyp. J. 2018, 24, 351–360. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).