New Input Factors for Machine Learning Approaches to Predict the Weld Quality of Ultrasonically Welded Thermoplastic Composite Materials

Abstract

Thermoplastic composites (TCs) enjoy high popularity in the field of engineering. Due to this popularity, there is a growing need to assemble this material with the help of fast and efficient joining processes. One joining process, which has seen increased use, is the process of ultrasonic welding. To make reliable statements about the quality of the joined material, some kind of quality assurance has to be made. In terms of ultrasonic spot welding, there are already some documented approaches for observing or predicting the joining quality, but some of these most promising parameters for quality assurance are difficult to measure in the process of continuous ultrasonic welding. This is why new parameters are investigated for their potential to improve the prediction of ultrasonic-welded TCs’ quality. Thermography and sound emission data have been found to have a correlation with the produced weld quality and are fed into different machine learning algorithms. Despite the relatively small dataset, trained algorithms reach binary classification rates of over 90%, indicating that the newly discovered parameters show the potential to improve the quality assurance of ultrasonic-welded TCs in the future. This improvement may enable the establishment of the ultrasonic welding of TCs in manufacturing.

1. Introduction

Thermoplastic composites (TCs) are increasingly used in the aerospace and automotive industries [1,2,3,4,5]. Outside of the engineering sectors, TCs have demonstrated an increase in popularity in the sports sector [3]. The advantages of a thermoplastic matrix over a thermoset matrix include shorter cycle times, weldability, unlimited storage times for the semi-finished products, and higher specific strength [1,6,7] and stiffness [1,6,8]. In addition to these mechanical properties, TCs are low in weight in comparison to other construction materials, for example, metal [6,8] (TCs—i.e., 1.59 g cm⁻³ [9], in comparison to aluminum—2.7 g cm⁻³). Since there is already a high demand for TC structures in the market, fast and efficient manufacturing processes are necessary in order to cover the demand and generate economic growth. Especially when considering aero-structures, there is a need to reduce the production cost of part suppliers in order to stay competitive [10]. For example, some composite parts for aircraft are still riveted together [10], which could be avoided by using other, faster joining techniques that, additionally, have the advantage of using no extra material for the joining process.

One of these joining techniques is the process of ultrasonic welding (UW). UW can be divided into two sub-categories: ultrasonic spot welding (SPW) and continuous ultrasonic welding (CUW). In the process of spot welding, single-spot welds are performed in order to join two welding parts. If a joining area is larger than one single spot weld, it is possible to align spot welds together so that they form a semi-continuous seam. Better suited for continuous welds is the process of CUW, which is faster and leads to more evenly shaped seams. Despite these differences, both welding techniques rely on the same physical principles: Using a converter, an electrical current is transformed into a mechanical oscillation [8,11,12]. This mechanical oscillation is transferred with a horn into the parts for welding [8,11]. The mechanical oscillation results in heat generation through internal damping [13] (surface friction and intermolecular friction [14]) in the welding zone. In an optimized process, an energy director (ED) may be placed in the welding zone since the use of a differently shaped ED influences the resulting welding quality in a positive way [11,15].

If it is possible to reliably monitor and predict the created joint of an ultrasonic welding process, the fast and cost-efficient [8] technique of ultrasonic welding has the potential to revolutionize the manufacturing process of TC-composed design parts. This work presents a qualitative investigation of different welding process parameters regarding their use as input parameters for an machine learning (ML) algorithm, which learns to predict welding quality in a reliable way.

In the following section, different approaches to monitoring and predicting the welding quality of ultrasonically welded thermoplastic composites will be introduced. An investigation of non destructive testing (NDT) methods for quality assurance follows. Subsequently to this investigation, the NDT methods are evaluated as fitting or not-fitting input parameters for an ML algorithm by training ML approaches with the collected and processed data. Finally, a conclusion is drawn and further challenges are explained.

1.1. Quality Assurance in Ultrasonic Welding

Several research groups are already investigating the topic of monitoring, influencing, and predicting the quality of ultrasonic-welded TCs. One approach, described by Li et al., is to predict the weld quality by building a wave transmission model of the welding process [14]. Using this technique of modeling, the researchers achieved error rates in the quality class prediction of 2–42%. Another study shows that power and displacement data of the sonotrode can be investigated in order to deduce a statement about the produced welding quality [16]. In addition, there are many other parameter studies that investigate the interplay of different welding parameters (e.g., weld energy, humidity, amplitude, welding force, process times) and the resulting weld quality [8,12,14,15,16,17,18,19]. All of the mentioned studies mainly focus on the investigation and understanding of the welding process itself. Through a deeper understanding of the process and the interplay of recordable welding parameters, predictions of the resulting welding quality can already be made on a rudimentary level.

With the help of artificial intelligence (AI) approaches, some research is conducted regarding training an ML algorithm to predict welding quality. One advantage of using ML techniques is that there is no deeper understanding of the system required as long as the training data contain information that enables the algorithm to learn and approximate the correlation between input and output data. In general, the use of ML can reduce computational costs and is sometimes faster than detailed calculations of physical principles; i.e., it is possible to approximate partial differential equations by overfitting an ML algorithm so that the solution to an equation does not have to be solved iteratively [20]. One research group tried to make quality predictions of ultrasonic spot-welded composites [21]. For the training process of the algorithm, the process parameters’ annealing temperature, surface condition, welding energy, plunging speed, and trigger force were selected. In parallel to their ML approach, they made quality predictions with a finite element model (FEM). Both attempts led to solutions that are able to predict the quality of a weld with a relative error smaller than 5%. In comparison to the ML algorithm, the FEM approach seemed to be more expensive regarding its computational costs [21]. Additionally to the prediction error, it was discovered that the quality predictions deviate from the experimental results when passing a weld energy of 800 $\mathrm{J}$ [21]. This indicates that the model has borders in which it is able to operate sufficiently and that have to be recognized when using it. The input parameters power, time, clamping force, and clamp displacement were used by Wang et al. to train a long short-term memory (LSTM) algorithm to predict one out of three quality classes [22]. During testing, the authors achieved a prediction accuracy of 97.5% [22]. Li et al. trained an ML algorithm with information about the duration of the different welding states of a forming weld and the corresponding net acoustic wave energy (total energy consumed by the welding system [14]) of each state [23]. In one of their approaches, an artificial neural network was trained to predict the failure load while a random forest (RF) algorithm was used to make assumptions about the welding quality classes [23]. The neural network achieved relative errors of 7.1% (between prediction and experimental results), while the random forest made quality predictions with an accuracy of 96.7%. In our own research, it was shown that the quality prediction of CUW using an AI approach may also be possible [24]. Building on this evaluation, a bigger trial with nearly 500 samples was conducted [25,26]. Neural networks with a prediction accuracy of around 72% were trained as a result of these experiments [25,26]. All algorithms that were used for the experiments can be classified as deep learning algorithms. More specifically, fully connected neural networks and a combination of a fully connected neural network with a one-dimensional convolutional neural network were used. The welding parameters of the applied welding force, amplitude output, power output, welding speed, pressure of the consolidation unit, layer thickness of the ED, number of EDs, and the position of a sample in the welded seam were selected for training and testing data [25,26].

Since there seems to be a gap in prediction quality between the ML approaches for spot welding and the ML approaches for continuous welding, the question of how this gap can be explained surfaces. Görick put forward the hypothesis that it may be possible that the number of data for training the algorithm was too small or that the data used for training did not correlate strongly enough with the welding quality, which means that the process is not represented in a detailed enough manner with the input data used [26]. In comparison with other training attempts [22], the number of data seems sufficient and the input data have a similar content as the data described previously for the quality prediction in spot welding. Nevertheless, one mentioned input parameter that has a significant influence on the welding quality is the horn displacement data [16]. However, this parameter is difficult to measure for the CUW process due to the continuity of the process. In order to produce a continuous welding seam, the sonotrode moves over the length of the material. Below the sonotrode, the melting of the material occurs, which means that at all points in time, the status of the material is static. Since the material below the sonotrode is always in the same state, it is not possible to measure the displacement of the sonotrode with common measuring equipment. This leads to the conclusion that some of the important factors for predicting the weld quality cannot be recorded in the same way as for spot welding because the continuous process is static when the conditions under the horn are observed. This is also true for the other recorded data mentioned above. An additional challenge when addressing the process of CUW is the difficulty of describing it as a whole. Simulations of the welding process have an unknown grade of uncertainty, with the exception of the fact that a full-scale simulation would only come with high computational costs of the model [21]. The challenges described above lead to the conclusion that it is necessary to find other input parameters that show a causal correlation with the welding quality in order to be able to train an ML algorithm and achieve high reliability in the quality prediction of continuous ultrasonic welded parts. In the following section, the research for possible new input parameters is described, followed by an experimental study that investigates the correlation of these new input parameters with the welding quality. Due to the fact that new input parameters for an ML algorithm should be evaluated and the conduction of spot welding trials is simpler than CUW experiments, the experimental study described herein will be conducted with spot welding only.

1.2. Parameter Research

Our approach to finding new input parameters is to investigate the material transitions during the welding, investigate the finished transition as a result of the welding process, or investigate a combination of both parameters. In order to find the right measurement methods and sensors, different NDT methods are evaluated. Through the use of these techniques, it may be possible to evaluate what is happening underneath the horn rather than investigating parameters that describe the welding signal before it has entered the welding samples. Two of the NDT methods, which carry the most potential to support the task defined, will be described in more detail in this section.

1.2.1. Thermography

The first method for evaluation is thermography. In thermography, infrared radiation is measured and can be displayed as black-and-white or colored images, where the temperature is mapped over a color scheme. One application field of thermography is medicine. Here, thermography is used to make images of breasts in order to detect whether a patient has breast cancer [27]. For the interpretation of the thermal images, AI algorithms are documented as a useful technique [27]. Another example of the use of thermography in diagnostic medicine is the use of thermal images and AI to determine different stages of cellulite [28].

In the field of engineering, thermography is mainly documented as being helpful with quality inspection. One of the less complicated applications is to inspect the state of electrical wiring by observing whether irregular heating patterns are formed when equipment is running with electricity [29]. Furthermore, research has been conducted by exciting metal plates and observing their heating patterns, which develop because cracks in the material heat up differently than material without cracks [30]. With the technique of lock-in thermography (in the cited literature, excitation with halogen lamps), it is possible not only to detect sub-surface defects in steel plates but also to make assumptions about their size and depth in the examined material [31]. Besides the investigation of metals, it is also possible to investigate composite materials with thermography. It is possible to look for defects in composite materials such as glass fibre reinforced polymers (GFRP) [4,32] or carbon fibre reinforced polymers (CFRP) [33,34] and to evaluate the quality of the adhesive bonding of two reinforced glass fiber samples [35]. In the work of Marani et al. [4], the possibility of detecting artificially created holes in GFRP structures is demonstrated, while Montanini and Freni [32] describe the detection limits and opportunities of thermography on GFRP structures. Both research teams used halogen lamps as an excitation source with the technique of lock-in thermography. In the field of CFRP materials, Yang et al. [33] used ultrasonic infrared thermography to examine defects and their sizes in aerospace composites, while Mian et al. showed the possibility of visualizing fatigue defects with the technique of infrared sonic imaging [34]. The research group of Junyan et al. conducted lock-in thermography and pulse thermography to detect defects and, in parallel, simulated their experimental tests with heat transfer models [36]. In their simulations, they discovered that smaller errors (approximately 1–2 $\mathrm{m}\mathrm{m}$ in diameter) result in almost three times weaker signals than larger defects that are approx. 6 $\mathrm{m}\mathrm{m}$ in diameter (defects 0.5 $\mathrm{m}\mathrm{m}$ under the surface, a statement that depends on the excitation time) [36]. They define weaker signals as the contrast in a simulated signal. Their experimental results reveal that it is possible to detect defects in composite materials but that there seem to be limitations regarding defect depth and the quality of defect resolution [36].

In most applications, some kind of excitation energy (e.g., ultrasound or light), which is damped in different ways regarding whether a defect exists in a structure or not, leads to heat patterns that can be used for defect detection and can also provide information about the depth of an existing defect [37]. In ultrasonic lock-in thermography, the different heating patterns of a structure can be measured, and phase images can be calculated, making it possible to investigate defects [38]. The technique of ultrasonic thermography is suggested as an NDT technique for a wide range of possible application fields [38], and the fact that polymers have a high emissivity of infrared radiation [37] makes thermography an interesting option for the observation of ultrasonic welding. Despite the wide use of thermography, there are also a few drawbacks to the technique mentioned. Through the literature research, it was discovered that the resolution of the thermal images can become a problem, especially if the errors are becoming smaller [31] or lay deeper in the material [36]. Regarding the resolution of thermal images, some experiments regarding improving the data acquired by thermal measurements have already been conducted [33]. However, these experiments focus on improving images with rather large defects [33].

The principle of exciting a structure and looking at the thermal response works fine for large and medium-sized defects but seems to lack in detail when it comes to smaller defects. Nevertheless, the methods and opportunities of thermography seem to be promising for the prediction of ultrasonic welds’ quality, and we therefore formulate the hypothesis that the internal shape of the welding zone (defects, cavities, unevenness, and irregularities) may result in different heating patterns or different temperatures of the welding part in general, which may correlate with the quality of the weld. In the recorded temperature data, the influence of developed cavities (even if not seen directly) could be present in the mean temperature of the welding zone. Based on this hypothesis, the ability of thermographic information as input data for ML algorithms will be investigated qualitatively.

1.2.2. Acoustic Signals

Included in the field of acoustic signals is the field of acoustic emission (AE). AE is described by Rizzo as a passive method to monitor transient stress waves that are generated by the rapid release of energy from localized sources [39]. In comparison to other NDT technologies, in AE, detected signals originate not from an external source but from within the observed structures [39]. AE signals can develop during crack initialization or propagation [39,40,41] in materials (e.g., concrete [40] or composite structures [41]) or as a result of friction between two (cracked) surfaces [41]. Another potential source of AE signals is melting and other material phase changes [42,43,44,45]. Based on the variety of sources for AE signals, this kind of signal offers the possibility for real-time process monitoring [39,41,46,47]. It is already described in the literature that measuring AE signals has the potential to detect and localize cracks [39,40,41].

AE is already applied in a wide range of tasks and is described as being used to supervise different processes and materials: measuring the AE signals of machines and classifying the signals gives the opportunity to supervise machines and diagnose occurring failures [48]. In addition, it is possible to identify the failure mechanism of observed materials [41]. Choi and Takahashi describe how crack information in short-fiber-reinforced thermoplastics can be mapped to different failure mechanisms [49], while Garrett et al. show that an AI algorithm is able to binary-classify crack length in sheet-metal structures (98.4% accuracy in binary classification) with AE signals as input data [50]. Not only for crack evaluation but also for the monitoring of the quality of additive manufacturing, AE can be used [47] because processes such as additive manufacturing or laser welding carry information about material changes [51]. Arul et al. mentioned that the changes in an AE signal during drilling processes can be used to monitor the sharpness of the drill and evaluate the optimal point of time for a tool change [1]. In addition to the monitoring of drilling processes, in the literature, it is described how AE signals can be useful for the quality monitoring of welding processes [46,52,53]. One research team conducted gas metal-arc welding and used a combination of AE signals and other welding input parameters to predict the weld quality [52]. In this research, features like mean square, mean signal level, and absolute energy from the time-driven data and features like counts, amplitude, frequency centroid, and peak frequency from the hit-driven data were used as relevant data [52]. It is worth mentioning that the author described how these parameters are only a few options of many when it comes to feature selection from the measured AE signals [52]. This statement indicates that the choice of feature extraction for acoustic signals seems to be based on experience and domain understanding. In addition, Zhang et al. used time-driven AE signals as a passive NDT method to describe the gas tungsten-arc welding process and make a statement about weld quality [46]. In the context of their paper, weld quality is defined as the existence or non-existence of holes (burned through defects) in the welding part [46].

The aforementioned literature leads us to the hypothesis that the technique of measuring AE signals for evaluation processes seems to have a high potential for quality assurance in the industry. As mentioned above, phase changes can result in acoustic emission [42,43,44,45], which leads us to the idea of measuring acoustic signals during the welding process in order to make assumptions about the weld quality. Different acoustic signals may appear during the welding process, which may correlate with different material developments in the welding zone. One possible problem in using highly sensitive AE sensors is that the welding process takes place under high energies and at a welding frequency of 20 kHz. This may create such violent emissions that it saturates the sensors and will not allow for the detection of small changes in the acoustic signal. Therefore, it was decided not to use highly sensitive and expensive AE sensors but rather to use common microphones that measure air-coupled sound. It has to be noted that, so far, we have used the term acoustic emission due to the need for correct citation. To avoid confusion with the field of classic AE detection, we furthermore use the term sound emission (SE), since that is the more accurate term for our signals. We therefore form the hypothesis that, during the UW air-coupled sound signals are generated that make it possible to draw conclusions about the weld quality produced. This hypothesis is investigated qualitatively in the experiments described in this work.

2. Materials and Methods

2.1. Experimental Setup

Carbon fiber plates built of T700G fibers embedded in a low-melt polyaryletherketone (LM-PAEK) matrix from Toray were used. The plates have a size of $1800\times 1200$ $\mathrm{m}{\mathrm{m}}^2$, are 1.68 $\mathrm{m}\mathrm{m}$ thick, and have a ${[0/90]}_{3s}$ layup. They were water-jet-cut into smaller samples with a size of $156\times 25.4$ $\mathrm{m}{\mathrm{m}}^2$. Holes were drilled in the plates to fix the samples on an aluminum anvil. The hole furthest from the welding zone had a radius of 2.1 $\mathrm{m}\mathrm{m}$, while the hole closer to the welding zone is a long hole with a radius of 2.1 $\mathrm{m}\mathrm{m}$ and a length of 0.3 $\mathrm{m}\mathrm{m}$. The long hole brings one degree of freedom into the system and makes it easier to mount the sample on the anvil (see Figure 1). The bottom samples are prepared for welding by fixing two ED sheets consisting of LM-PAEK with a hand sonotrode to the samples’ surface. Each ED has a thickness of 100 $\mathrm{\mu }\mathrm{m}$. For each weld, one sample with EDs and one sample without EDs were placed on the anvil and fixed with screws (2.972 $\mathrm{N}\mathrm{m}$, which resulted in a holding force of approx. 3.9 $\mathrm{k}\mathrm{N}$) in place. Through positioning the samples on the anvil, an overlap of the samples of $12.7\times 25.4$ $\mathrm{m}{\mathrm{m}}^2$ was created. Since the upper sample has to be positioned horizontally for the welding process, a shorter welding sample with the same thickness is placed below the upper sample. The ultrasonic signal for the welding process was produced using a Branson generator with a frequency of 20 kHz. A rectangularly shaped horn measuring $25\times 13$ $\mathrm{m}\mathrm{m}$ (radius at the edges of 1 $\mathrm{m}\mathrm{m}$) is used to transfer the welding signal into the specimen. At the beginning of the experiments, test welds were conducted, followed by 81 welds for which a design of experiment (DOE) was created. For the experiments described, a total of 87 welds were created. The DOE had the parameters of amplitude in percentages in the range of 92–100, welding time in $\mathrm{m}\mathrm{s}$ in the range of 700–1200, and welding force in $\mathrm{N}$ in the range of 800–1200. For all experiments, the holding time after welding was set to 2 $\mathrm{s}$ at a holding force of 1650 $\mathrm{N}$. Applied amplitudes, welding power, and welding forces and pressures were recorded with the help of a bus system provided by Beckhoff and the software TwinCat-Scope. The parameters for further evaluation came from a thermography camera (FLIR A35) and two microphones (Knowles Electronics, tested frequency response by the manufacturer—1 $\mathrm{Hz}$–10 kHz)—which are additionally implemented and controlled by the welding system. For the air-coupled sound measurement, the signals of the attached microphones were scanned with a frequency of 50 kHz in order to fulfill the Nyquist criteria. The microphones were placed at a distance of approx. 110 $\mathrm{m}\mathrm{m}$ to the welding zone and were recorded during the entire joining process. The joining process hereby refers to the process of applying the ultrasonic signal for melting the material (welding process) and the process of applying pressure for the consolidation of the material in the aftermath (consolidation process). After the first trials, the integrity of the recorded acoustic datasets outside of the manufacturer’s stated range was evaluated, and it was found that they behaved normally. Based on this normal response, they were used for all trials. The thermography camera was positioned at a height of approx. 110 $\mathrm{m}\mathrm{m}$ and a horizontal distance of approx. 40 $\mathrm{m}\mathrm{m}$ while the mount for the camera had an angle of view of 25° down on the welding zone. The camera is triggered by the welding system 500 $\mathrm{m}\mathrm{s}$ after the consolidation process is finished (2.5 $\mathrm{s}$ after the welding process) to acquire one image of the upper welding plate. The thermography camera has two sensor gain modes, the HighGainMode (−25 to + 135 °C) and the LowGainMode (−40 to +550 °C) [54]. Since the thermographic image was recorded 2.5 $\mathrm{s}$ after the welding process took place, temperatures lower than 135 °C were expected, and the HighGainMode was selected in order to obtain a maximum resolution for the measurement.

For these experiments, quality is defined as the lab-shear-strength (LSS) value. The LSS value was measured using a Zwick/Roell (Retroline 1475, ZwickRoell GmbH & Co. KG, Germany, Ulm) testing machine. The tests were performed with clamps (ZwickRoell GmbH & Co. KG, Germany, Ulm) that were able to create a holding force of 20 $\mathrm{k}\mathrm{N}$ and had a traverse speed of 1.3 mm min⁻¹.

2.2. Data Processing and Analysis Steps

This section describes how the data were processed for use in correlation analysis and training of ML algorithms. For all transformation and processing steps, Python 3 was used. Additionally, the libraries Pandas, Numpy, scipy, sklearn, and matplotlib were used for data analysis, machine learning, and visualization.

2.2.1. Acoustic Signals

Sound measurements were conducted using the TwinCat system. To archive sampling rates of 50 MSps, the ELM3602-0000 measuring clamp was used. The system maps the provided voltage range in a defined number of measuring steps, so the measured values are unitless. To change the measured values into voltage values, all data have to be transformed using factor multiplication. The two measurements were recorded using two different channels ($c{h}_1$ and $c{h}_2$). The microphone attached to $c{h}_2$ records a stronger signal, which is why the data processing steps are explained with an example measurement of $c{h}_2$. It is not clear why the microphones have a difference in the recorded signal intensity since they have a similar measuring range recorded in their data sheets, and further investigations have to be conducted to explain the observed measuring characteristics. fast Fourier transformation (FFT) was used to investigate the sound signals. The FFT was conducted with the help of the scipy library (rfft() method). When visualizing the results of the FFT, peaks at the beginning of the spectrum were observed. These peaks were caused by the offset of the signal and were not of interest for the following investigations. This is why the FFT visualization in Figure 2 starts at 1 kHz. The cut-off makes it possible for smaller peak frequencies up to 25 kHz to be investigated in one single graph (see Figure 2). Visualizing the whole signal of a joining process reveals significant noise in the FFT results. This is why, in Figure 2A, two signals of a differently processed data sample are displayed. The first signal (blue) is the result of the FFT analysis of the joining process, while the red signal is the FFT of the welding process only. As described above, welding refers to the actual heating and melting process, while joining describes the whole process of welding and consolidation. Since the FFT of the welding process seems to be less noisy and the welding process is the time in which the material transforms and is supposed to have characteristic sound signatures, offering the opportunity to make quality assumptions, only the signal of the welding process is used for the FFT analysis. An algorithm is designed that processes all the recorded data and shortens them automatically to the time duration of the weld process. For this automatic shortening process, the border between welding and consolidation is defined as a drop in the power signal recorded using the welding system. This drop has an index for each measurement that has to be multiplied by the value of 50 in order to obtain the right border for each individual measurement. The multiplication of the index by 50 is necessary because the internal system records data with a speed of 1 $\mathrm{sample}/\mathrm{m}\mathrm{s}$, while the microphones record with a speed of 50 $\mathrm{samples}/\mathrm{m}\mathrm{s}$. In addition to the separation of the welding sound data from the joining sound data, a moving average with a window of size 50 is calculated from the results of the FFT. This technique reduces the noise further and smooths the curve of the analysis (see Figure 2B). After the data are filtered, the function find_peaks() from the scipy library is used to detect peaks beginning at a height of 0.1 for $c{h}_1$ data and a height of 4 for $c{h}_2$ data. Based on the transformation method of FFT, the resulting data only carry information about the proportion of a frequency in a measured signal. This leads to the fact that the results can only be compared in a relative way. The minimum distance between two peaks is set to 50 data points. In Figure 2B, a red line shows at which level the peaks are detected. All data samples are processed according to the steps described before. A data frame that stores all detected peaks of all measurements (frequency and corresponding value) is created by processing all data samples. The detected peaks have to be binned in order to perform a correlation analysis. For the binning process, 2 kHz wide, half-open interval groups are chosen:

$$\begin{array}{c}[1,3),[3,5),[5,7),[7,9),[9,11),[11,13),[13,15),[15,17),[17,19),[19,21),[21,23),[23,25)\end{array}$$

Some of the measurements have more than one peak value in a bin. Equally dimensioned data are needed for the correlation analysis so only the maximal peak values for each measurement in each bin are selected for further investigations. The welding process took place at a frequency of 20 $\mathrm{k}\mathrm{Hz}$, and there is a peak in the FFT results at this frequency, which is why the 20 $\mathrm{k}\mathrm{Hz}$ bin ($[19,21)$) is of the highest interest. If the values of this bin are plotted against the measured LSS value of the samples, a non-linear connection between peak intensity and the LSS value is visible (Figure 3). In addition, around a peak height of 100, the welding quality seems to settle between 37 $\mathrm{M}\mathrm{Pa}$ and 45 $\mathrm{M}\mathrm{Pa}$. The observable non-linear connection leads to the conclusion that it may be necessary to calculate a Spearman correlation coefficient (corr coef) instead of a Pearson corr coef because it is a ranked coefficient and measures non-linear correlations [55]. The correlation coefficients calculated from 50 or more samples are listed in

Table 1. Spearman correlation coefficients of $c{h}_1$ and $c{h}_2$ measurements with p-value and number of samples. Only corr coef calculated with samples size ≥ 50 are listed.

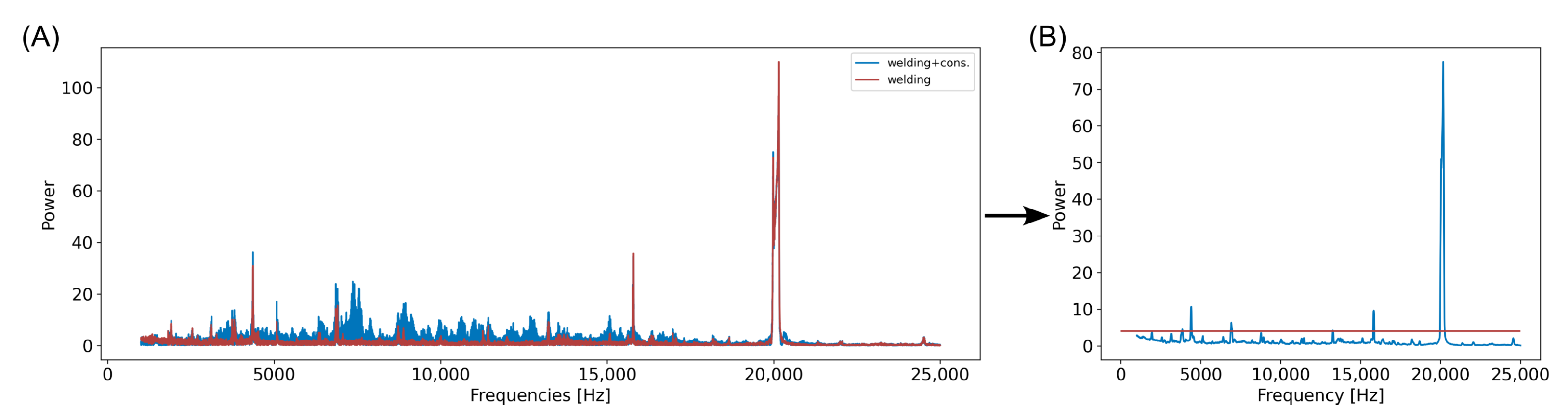
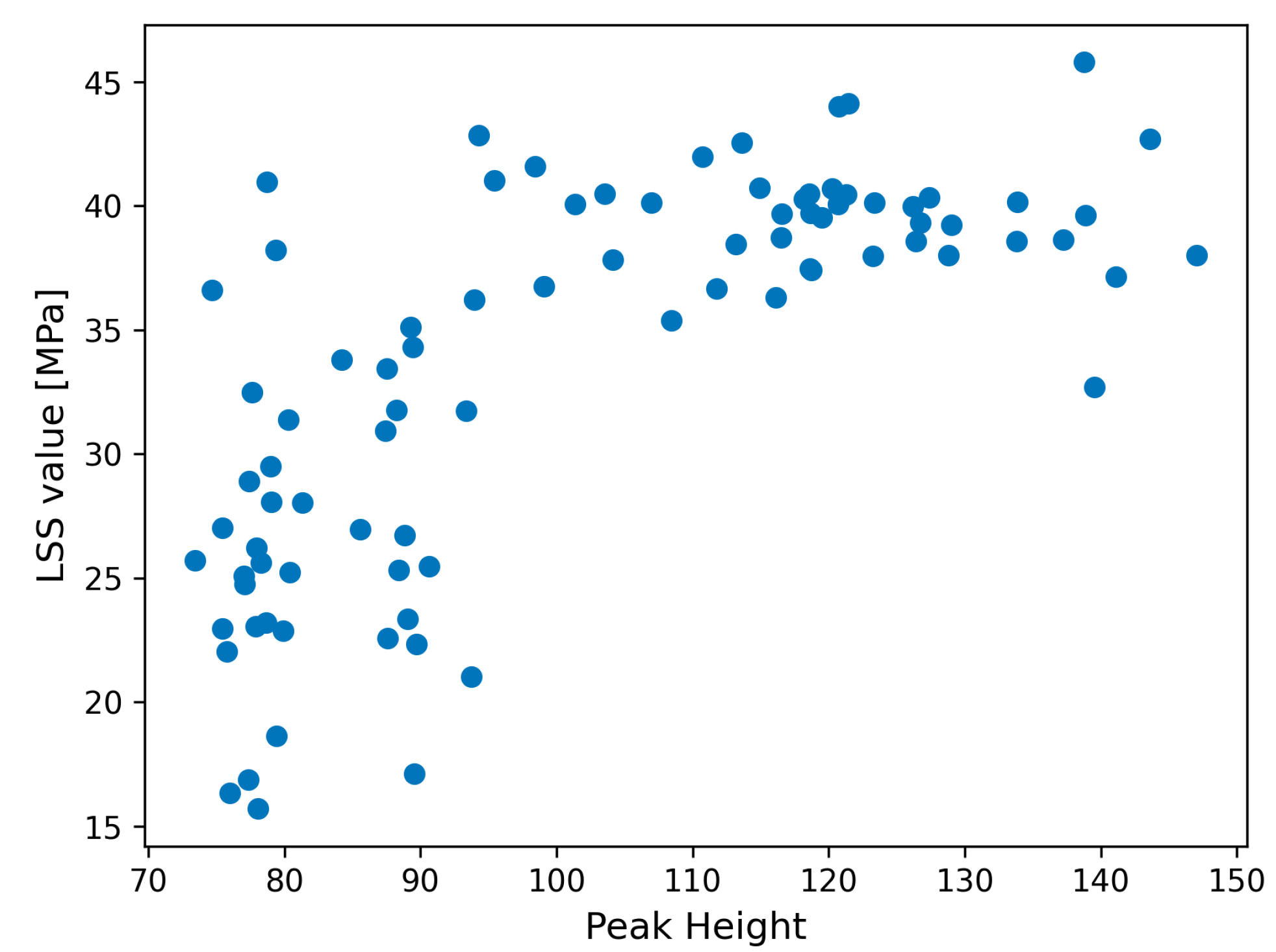
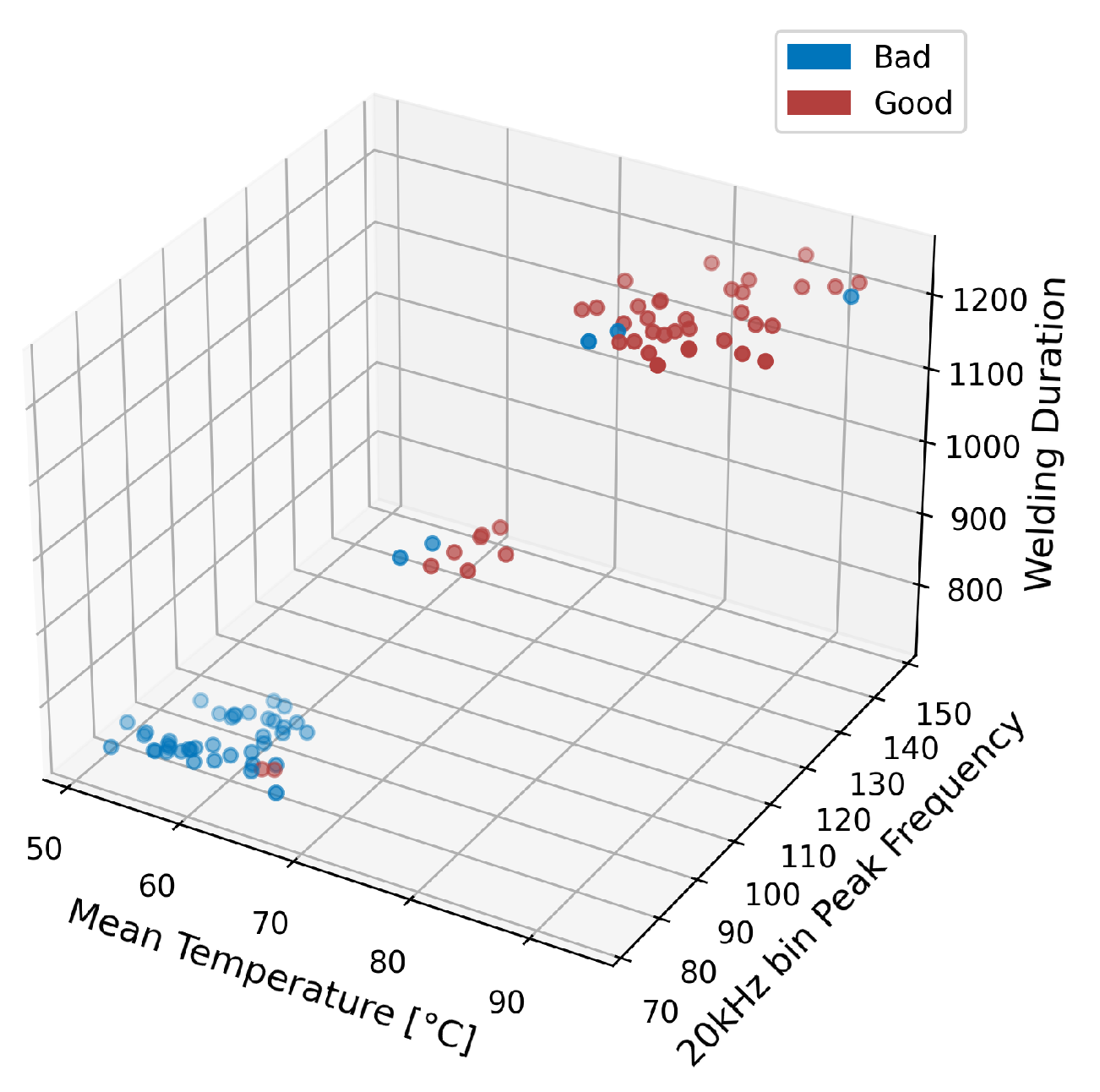
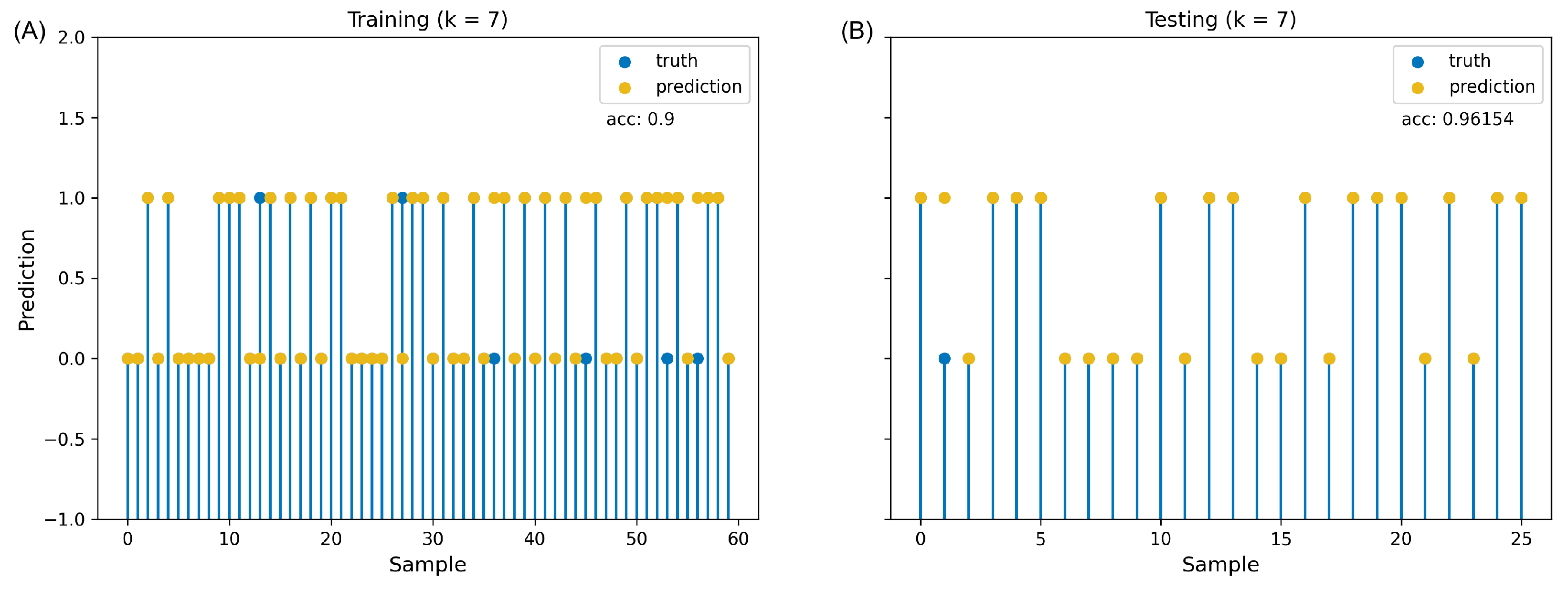
Channel	Frequ. Bin (kHz)	Corr Coef	p-Value	Num. of Samples
$c{h}_1$	$[1,3)$	0.698	$5.53\times {10}^{-14}$	87
	$[3,5)$	0.259	0.015	87
	$[5,7)$	−0.332	0.012	57
	$[15,17)$	0.182	0.187	54
	$[19,21)$	0.601	$7.42\times {10}^{-10}$	87
$c{h}_2$	$[1,3)$	0.225	0.059	71
	$[3,5)$	0.376	0.001	75
	$[5,7)$	0.288	0.021	64
	$[9,11)$	−0.166	0.198	62
	$[15,17)$	0.253	0.039	67
	$[19,21)$	0.7	$4.62\times {10}^{-14}$	87

.

All values in Table 1 are rounded at a decimal precision of ${10}^{-3}$. A list of all calculated coefficients can be found in Appendix A. The correlation coefficient values provide information about the intensity of the correlation between the two investigated variables. In detail, correlation coefficients can be interpreted as weak correlation if the absolute value is smaller than 0.5, medium correlation if the absolute value is equal to or higher than 0.5 and smaller than 0.8, and strong correlation if the absolute value is equal to or larger than 0.8 [55]. Since the Spearman correlation coefficient measures monotonicity [56], the $H_0$ hypothesis is that the data have no monotonic relationship. For all tests, the $\alpha$ value is at a level of 0.05. Five correlation coefficients were calculated with 50 data points or more for $c{h}_1$ data. Two of these (2 kHz and 20 kHz center frequency bin) show medium correlation. The corresponding p-values are also below the $\alpha$-value, which leads to the rejection of $H_0$, and correlation is assumed. All the other correlation values are too small, or $H_0$ could not be rejected. In the $c{h}_2$ data, the 20 kHz center frequency bin shows a medium correlation coefficient with a p-value below the defined $\alpha$, which hints at a potential medium correlation. It has to be mentioned that the library states that the p-value calculation is only accurate for sample sizes of more than 500 [56]. As a consequence, only bins storing data with medium correlation and with a p-value smaller than $1\times {10}^{-8}$ are used to create the dataset for training an ML algorithm.

2.2.2. Thermography

The thermography data are recorded in the mono16 format, resulting in grayscale images with a bit depth of 16 bits. The bit values stored in these images are in a specific camera value range. In order to obtain the temperature in °C, the first two leading bits have to be bit-masked off. The images have a bit depth of 14 bits after the bit-masking process. Furthermore, the values have to be transformed using the following formula [57]:

$$T_{\left[k\right]}=\frac{B}{ln\left(\frac{R}{S-O}+F\right)}$$

(1)

Except for pixel value S, all other values are parameters internal to the camera, which can be extracted from the camera registry. After this transformation, the calculated values are shifted from Kelvin to °C. The $320\times 256$-pixel images show not only the welding zone but also the surrounding welding area and some thermal reflections (see Figure 4) because the camera has some distance to the welding zone. To extract only the measurement of the welding zone, an region of interest (ROI) is cut from each transformed measurement. Here, each image is cropped with the same parameters because the camera is on a fixed position for all welding experiments. After cutting the ROI, each image has dimensions of $89\times 62$ pixels. It has to be mentioned that the data are visualized only for a better understanding and for the purpose of investigation; the actual analysis steps are conducted with pickle files (one file for each image). Similarly to the processing of the sound data, the temperature values for each image are binned (10 °C range per bin). The bins for the temperature data are half-open intervals:

$$\begin{array}{c}(23.999,34.0],(34.0,44.0],(44.0,54.0],(54.0,64.0],(64.0,74.0],(74.0,84.0],(84.0,94.0],\\ (94.0,104.0],(104.0,114.0],(114.0,124.0],(124.0,134.0],(134.0,144.0],(144.0,154.0],\\ (154.0,164.0],(164.0,174.0],(174.0,inf]\end{array}$$

Each pixel of an image is sorted into a bin during the binning process. A temperature deviation can be displayed according to the number of pixels in a bin (see Figure 5). If the LSS values are ordered and plotted above the binned temperature values for each sample, it seems that there is an LSS border value at which the share of the warmer pixels in an image is increasing (beginning at sample number 40; see Figure 5). In addition, for each image, the mean temperature can be calculated and plotted against the LSS value of the connected sample. Similarly to the data of the sound measurement, the data seem to have a non-linear connection (see Figure 6). Furthermore, similarly to the sound data, there is a border (around a mean temperature of ≥70 ${}^{°}\mathrm{C}$) at which the quality level steadies itself between 37 MPa and 45 MPa. This leads to the need for the Spearman correlation coefficient again. For the mean temperature of a recorded image against the LSS value of the produced sample, a correlation coefficient of approx. 0.762 with a corresponding p-value of approx. $1.529\times {10}^{-17}$ is calculated. The p-value against an $\alpha$ of 0.05 leads to the rejection of $H_0$, and correlation can be assumed.

2.3. Machine Learning

In order to train machine learning algorithms and see if they respond positively to the given data, one dataset for training and testing is created. Regarding the sound data, only the frequency bins showing the highest correlation are chosen. This means that for $c{h}_1$ the peak amplitude values of the bin with a center frequency of 2 kHz and for $c{h}_2$ the bin with a center frequency of 20 kHz are included in the dataset. In addition, the correlation analysis of the mean temperature shows a medium correlation, which is why it will also be included in the dataset. The parameters recorded by the internal welding system are also analyzed, and correlation coefficients are calculated. This analysis is not described in detail in this work because most parameters are already well known. The welding time shows a medium correlation in the investigations (Spearman correlation coefficient of about 0.70 with a p-value of $4.34\times {10}^{-14}$) and is included in the data frame. To summarize the description above, the following parameters are taken as inputs for training ML algorithms:

• Duration of welding (number of measured data points of one parameter);
• Mean temperature of a thermal image;
• Peak amplitude of the FFT of the 2 kHz bin of $c{h}_1$ data;
• Peak amplitude of the FFT of the 20 kHz bin of $c{h}_2$ data.

A dataset for training with these parameters is referred to as a full data frame, while a dataset with missing $c{h}_1$ data is referred to as a reduced data frame.

One thermal image is recorded with errors and is therefore eliminated from the analysis, which leads to a data frame for ML with 86 data points instead of 87. The corresponding LSS value is added to each sample, and a label is created. For the trials described here, the samples are divided into good and bad welds, where good is defined as an LSS value of ≥37 MPa and bad as the values below. When the selected parameters (without $c{h}_1$) are visualized with the corresponding LSS value, groups are formed (see Figure 7). For this visualization, the 20 kHz bin of $c{h}_2$ is selected because it is the welding frequency, and not only correlation but also causality is assumed. The groups’ build during the visualization primarily consists of either good or bad welds, which indicates that the selected data could be suitable for ML. For ML approaches, the library sklearn is used. More specifically, the options for k-nearest-neighbour (KNN), RF, and support vector machine (SVM) are trained and tested. RF additionally provides the option to investigate the importance of the input parameters for the predictions of the algorithm. Training for all algorithms was performed with the same randomly selected 70% of the data. The other 30% are used for testing the resulting model. The dataset before separation in test and training data is balanced and contains around 48.84% of samples with the label good welding.

3. Results

The goal of this work was to validate whether the newly investigated parameters of the welding process not only correlate with the measured welding quality but also carry the potential to train artificial intelligence algorithms to predict welding quality. To investigate this hypothesis, three different ML approaches were tested. The goal was to investigate how the algorithms respond to the provided data. Based on the fact that the dataset is relatively small, it was not the goal of this work to develop an algorithm that can be used in a production environment for quality assurance.

The first algorithm that is used for the evaluation of the new input parameters is the KNN approach. The algorithm is set up to evenly weigh all k neighbors and use the Euclidean distance for distance calculation. For the classification, seven (k = 7) neighbors are selected. The KNN algorithm is provided with welding time (represented by the number of the measured welding force data points), mean temperature, maximal peaks of the 2 kHz bin of $c{h}_1$, and the maximal peaks of the 20 kHz bin of $c{h}_2$ as input parameters, and a training accuracy of 90% and a testing accuracy of 96.15% are achieved. The results of this investigation can be seen in Figure 8. The 20 kHz bins seem to be causally explainable, and the question arises of whether the KNN algorithm can be trained without the data from $c{h}_1$. This training leads to the same accuracies as if the $c{h}_1$ data were included in the training and testing data.

The second investigated algorithm is the RF approach. For the RF, 25 estimators (trees) are used. The algorithm is trained and tested with the same input data as the KNN algorithm. During the training and testing processes, accuracies of 100% and 96.15% are reached, respectively. Without the data from $c{h}_1$, the algorithm achieves the same results. During different runs, it is observed that the importance of the factors changes randomly, which is why no results about the individual importance are listed in this work.

Using SVM leads to training accuracies of 91.67% and testing accuracies of 100%, independent of whether the full or reduced dataset is fed into the algorithm.

4. Discussion

For the analyses described, datasets of a spot welding process are measured and preprocessed, and features from these signals are selected. It has to be mentioned that, in data measurement, the topic of discretization of a continuous signal is always present. This can be, for example, a floor, when measuring acoustic signals. The measuring rate of 50 kHz makes it possible to measure the sound range of the generated welding signal and slightly above it. However, the welding process may generate other signals in much higher frequency ranges, which cannot be measured with the described approach. Instead of expensive AE sensors, relatively cheap microphones are used to measure the sound during the welding. These microphones have a response range from 1 Hz to 10 kHz defined by the manufacturer. The recorded sound data have changing peak amplitudes at 20 kHz, which correlate with the LSS value of the welds. This indicates that the microphones record reliable data in these frequency ranges, and a qualitative statement about the use of sound emission data can be made. Nevertheless, it may be advisable to upgrade the measuring system with microphones specifically designed for higher frequencies around 20 kHz. The use of a recording unit with a maximal frequency of 50 kHz may cut off some frequencies worth measuring, but the described results show that it does not seem to be necessary to cover more frequency ranges. In terms of thermography, the surrounding environment may have an influence when acquiring the thermal images. This influence is reduced by cropping the ROI of each image, but it is not certain that some infrared radiation is measured that is not related to welding. The welding structures are excited by the welding process itself, so an extra excitation, as described in the chapter about thermography, is not necessary. When preprocessing data in general, it is worth mentioning that every data-processing step may result in a reduction in information. Regardless of the risk of losing information through preprocessing, the steps taken are necessary to shape the data and to conduct a correlation analysis. Even if some information is lost, the algorithms seem to learn, and a correlation between thermography and LSS values is shown. The described data processing is one way of working with the data. The literature hints at the fact that there are always several other data-processing methods, since future selection offers a significant range of possibilities [52]. Nevertheless, the goal of this work is to examine the potential of the newly discovered parameters for the ultrasonic welding process and does not consist in finding the best data processing/feature extraction process leading to the selected methods. For future applications, it has to be investigated which form of data is preferable. It may be advisable to use the raw image data of the thermography camera rather than manually extracting features. One advantage of the raw image data is that it additionally allows for the investigation of the heat pattern over the entire area at once, possibly allowing even more information about the heating pattern to be extracted. For the process of continuous ultrasonic welding, this information is more complex to obtain since a sequence of images has to be cropped and stitched together. The range of sensitivity (gain mode) has to be re-evaluated since the setup of the thermography camera did restrict the recorded information (cut-off at approx. 170 °C). The measured temperatures exceeded the range of the sensor mode, and the measured temperature data may have lost some of their accuracy while leaving the calibrated temperature space. Since this paper is about a qualitative analysis of the option to use thermography, it is of no concern for the experiments described here, but the use of another sensor mode to measure the entire occurring temperature range has to be considered.

The dataset size for all investigations is below 100 samples, which is relatively small. Through the small number of testing and training data, the algorithms show differing performance with respect to different random seeds for the separation of testing and training data. Other publications use similarly sized datasets to train and test their ML algorithms [22]. The border that divides the welds into good and bad samples is chosen manually. It is not clear whether the algorithm is able to separate good from bad samples if another border is selected. For future algorithms, it may be advisable to test some regression instead of classification, but a much bigger dataset would be needed. More data will be needed to train a reliable ML algorithm. Even if the results cannot be used for ML quality assurance in the industry yet, and even if the borders that define good and bad welds are fixed at the moment, the algorithms seem to respond to the given data in a positive way, and the new parameters, namely sound and thermography, show great potential.

In this study, all samples were measured during spot-welding, and a transition between spot-welding and continuous welding has to be made. Further experiments have to be conducted in order to investigate whether the described results can be applied in the same way to CUW. Additional data-processing steps have to be evaluated. For the sound data, another problem may occur. During the spot welding, all stages associated with the welding process (melting material, material flow, etc.) [16] happen sequentially at one welding position. In CUW, the different stages happen simultaneously because the process is continuous. It is not clear whether this phenomenon pollutes the signal in a way that makes it impossible to analyze it properly.

5. Conclusions

The prediction of ultrasonic-welded TCs’ quality based on process parameters that are used to start the welding process has the disadvantage of not representing the process as a whole. This is because these parameters do not carry information about the melting and connection process itself but only describe which parameters are introduced to the welding process. As an example, if there are small impurities in the welding zone, these impurities are not likely to be represented in the recorded parameters that initialize the welding process (e.g., the welding pressure).

In this work, the parameters of sound and thermography were investigated and evaluated for their potential to help monitor the welding quality. These two parameters have the characteristics of being recorded during (for sound) or after (for thermography) the welding in order to be able to describe the result of a welding process using parameters not involved in the process. Both parameters are investigated during spot-welding experiments but also have the potential to be used in the process of continuous ultrasonic welding. This is a substantial advantage in comparison to the parameter of sonotrode displacement that is used in the literature [16], since the displacement is difficult to measure during CUW. Both new parameters were processed, and features are extracted from the data in order to conduct correlation analysis and data visualization. Through visualization of the extracted information of sound and thermography data, a non-linear correlation was found. In the thermography and sound data, thresholds can be defined to separate good welds from bad welds. The visual observations were supported by the calculation of the Spearman correlation coefficient, with both parameters showing a correlation close to 0.7. To further confirm the potential of the discovered parameters, ML algorithms were trained to check for a positive response. All three approaches (KNN, RF, and SVM) responded positively to the data and showed classification accuracies greater than 90%, even if the dataset was comparatively small. Not using the peak frequency of $c{h}_1$ data of 2 kHz does not lead to weaker accuracies in training or in testing, which is why it is assumed that the important frequency is in the 20 kHz bin. In order to use the new parameters in CUW, it may be necessary to develop different data-processing steps than those described. This transfer may be possible when using the technique of wavelet transformation, since CUW has not only a time component but also a coordinate dependency. However, this hypothesis has to be investigated further. The usefulness of the newly described parameters has to be further evaluated by producing bigger datasets, but the presented results indicate that the parameters show great potential.

The discovered parameters seem to offer the possibility of simplifying the quality assurance of ultrasonically welded parts and help to clear the way for the further use of this technology across broad industry sectors. A patent for the sound parameter is already pending. Since the parameters of sound and thermography have a border at which the quality seems to stagnate between 37 MPa and 45 MPa, further investigations into techniques that not only seem to correlate with the LSS value of a sample but can display the actual shape of the welding zone and produce quality assumptions based on the shape of the created connection are advisable. This could create the possibility of differentiating weld quality in more detail. Instead of merely predicting good and bad welds, it may be possible to predict actual LSS values. In future experiments, not only could the LSS value be used as a definition of quality but also visual inspections of the welding area could also be used.