Study of SLA Printing Parameters Affecting the Dimensional Accuracy of the Pattern and Casting in Rapid Investment Casting
Abstract
1. Introduction
2. Materials and Methods
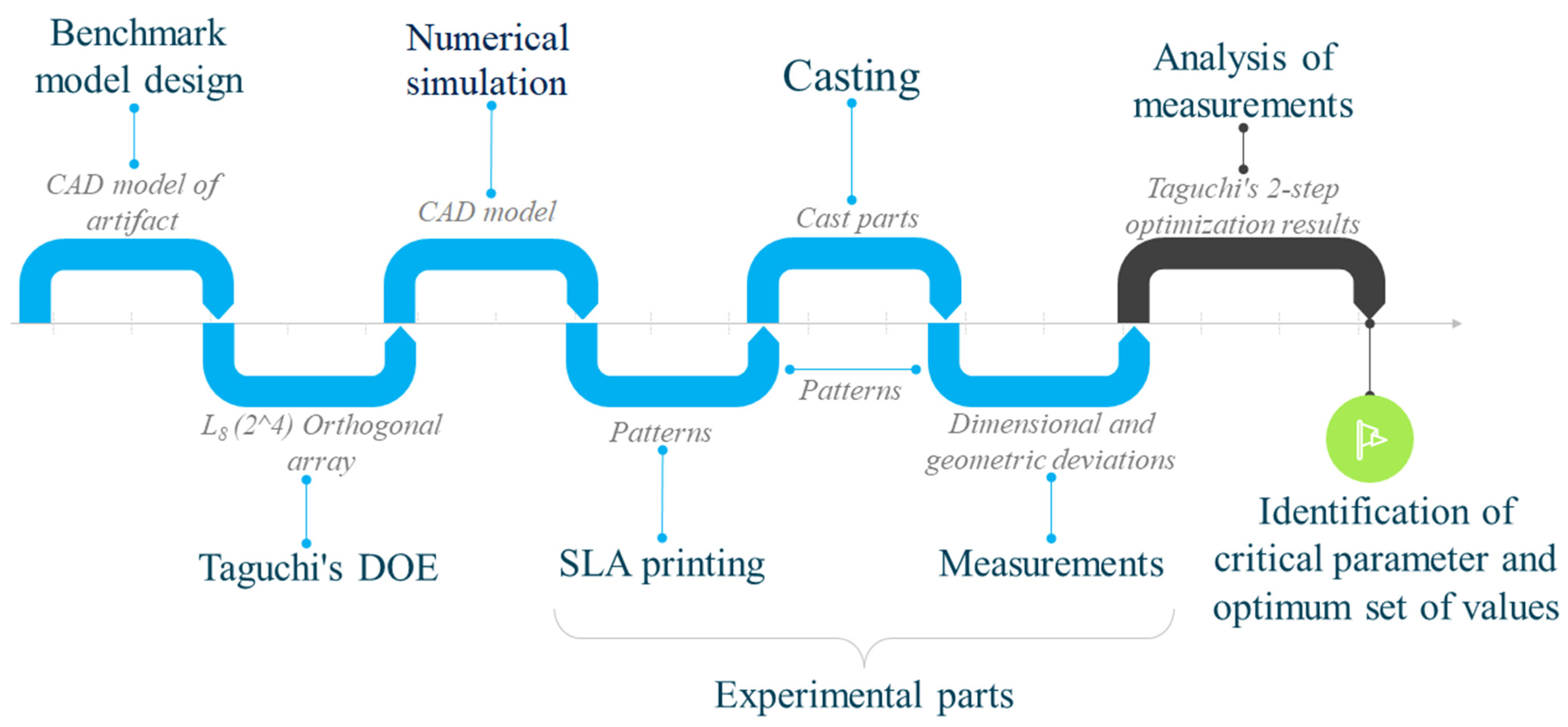
2.1. Methodology
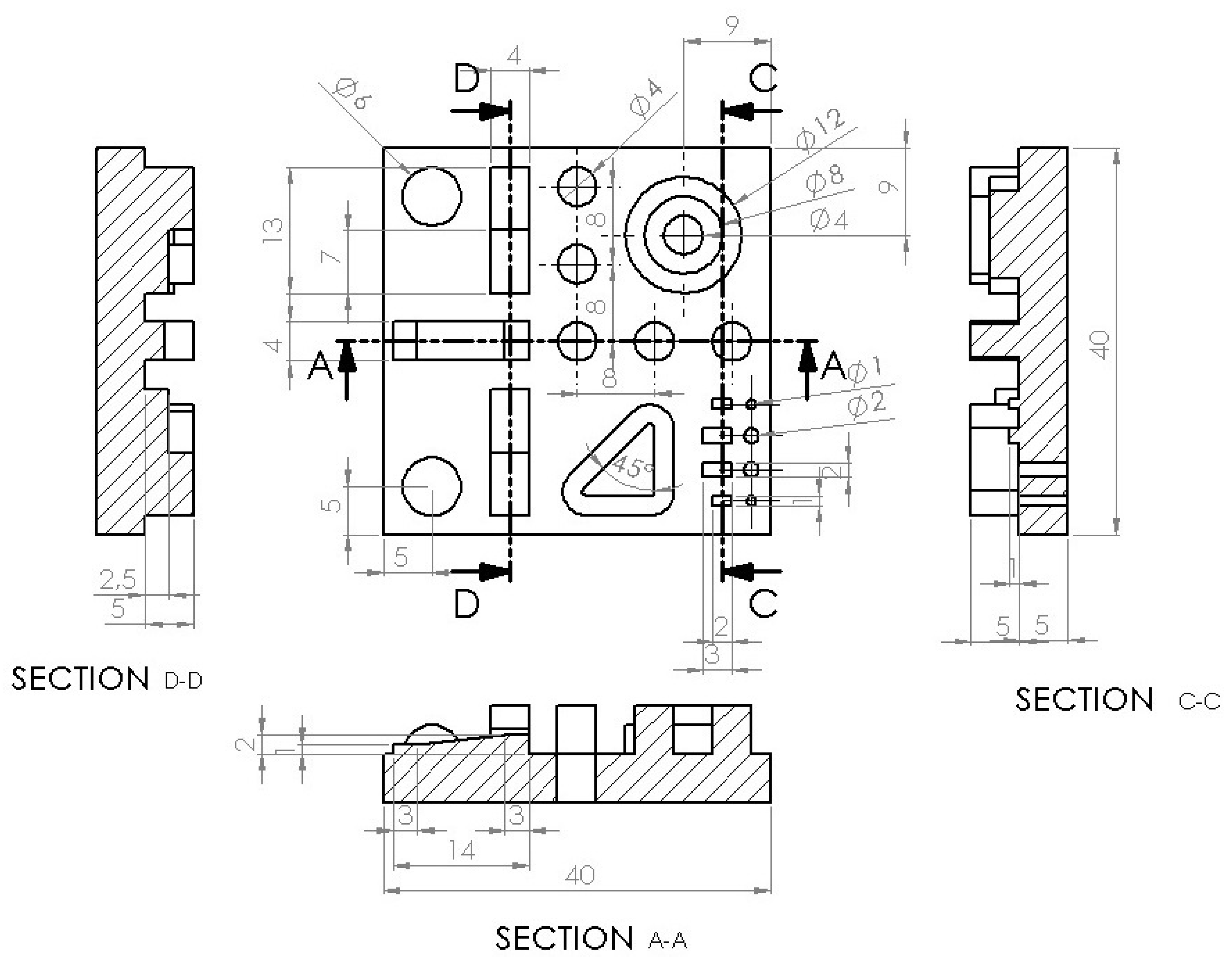
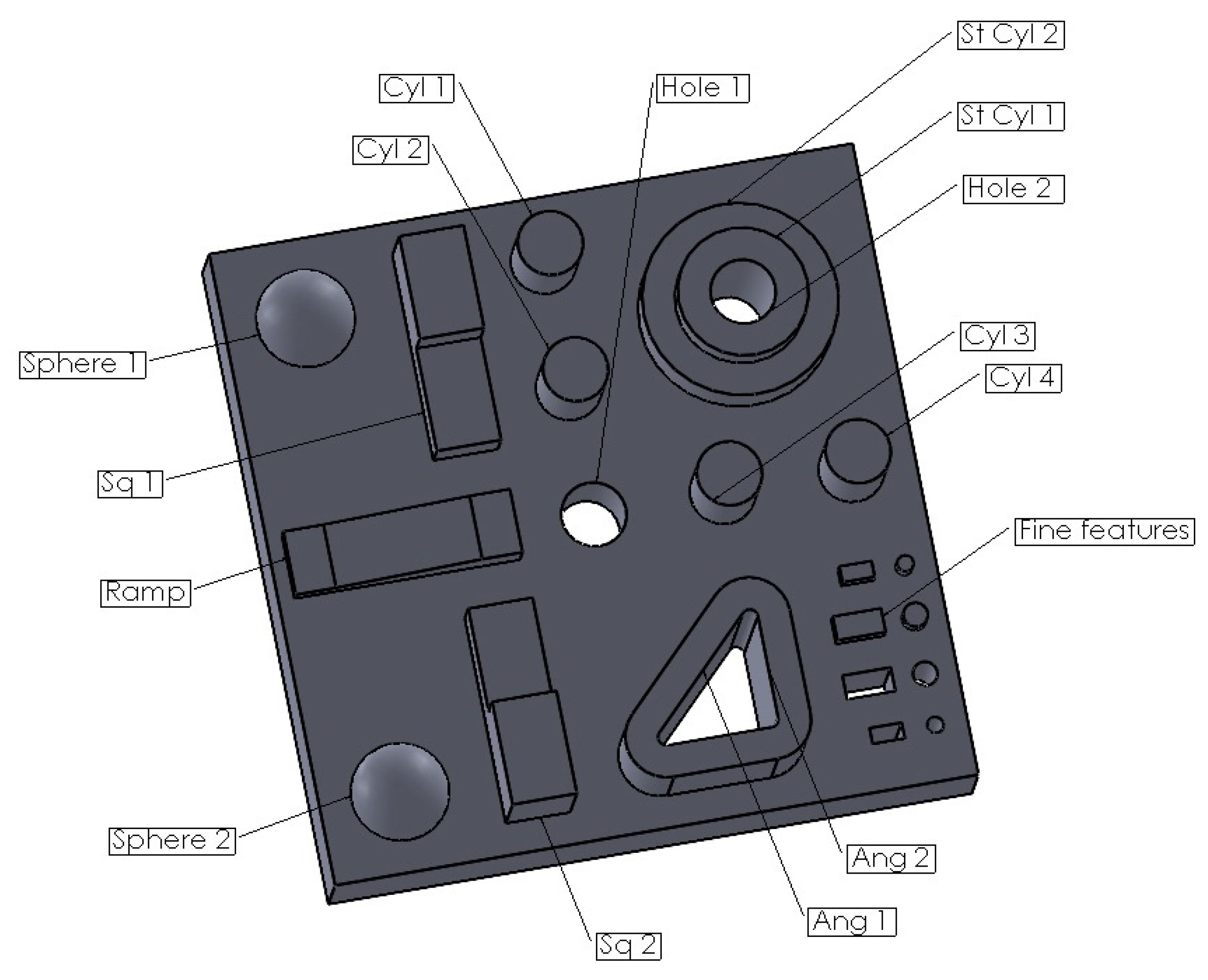
2.1.1. Benchmark Model Design
2.1.2. Taguchi’s Design of Experiments
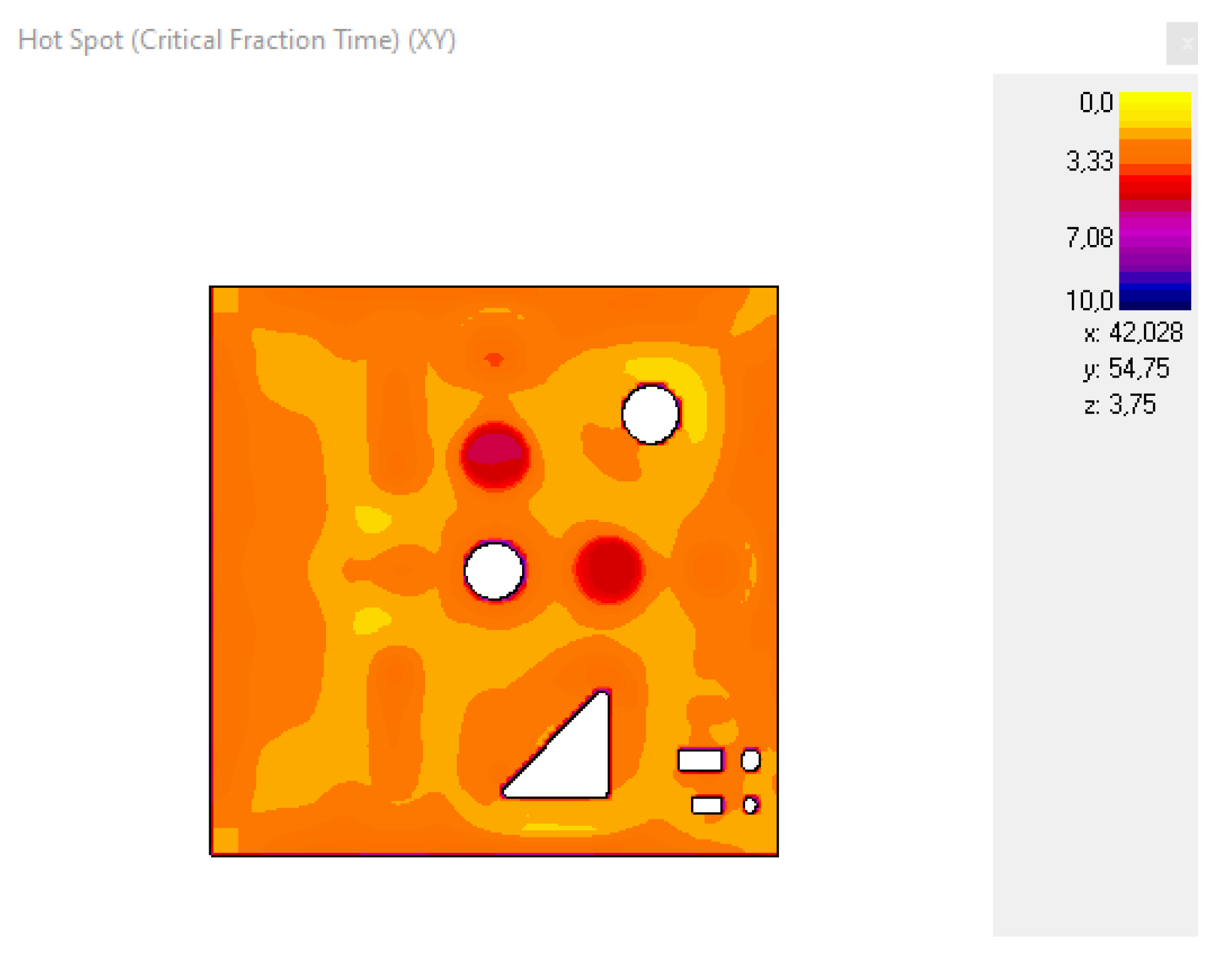
2.1.3. Numerical Simulation
2.1.4. Experimental part I. SLA Printing
2.1.5. Experimental Part II. Casting
2.1.6. Measurements
2.1.7. Analysis of Measurements
2.1.8. Identification of Critical Parameters and Optimum Set of Values
3. Results and Discussion
3.1. Experimental Results
3.1.1. Printing Results
3.1.2. Casting Results
3.2. Measurement and Analysis
3.2.1. Printed Patterns
Dimensional Accuracy
Geometric Characteristics
3.2.2. Casting
Dimensional Accuracy
Geometric Characteristics
4. Conclusions
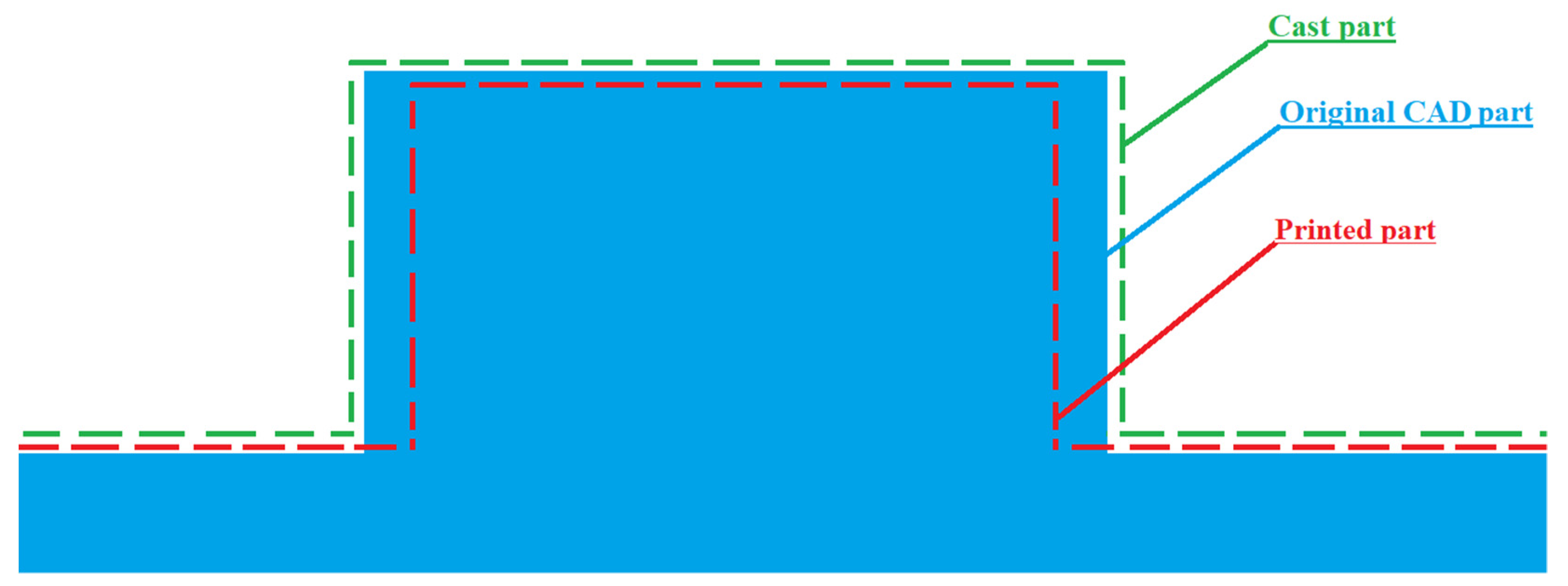
- The most impactful critical factor affecting the dimensional accuracy and geometric characteristics of both the Castable Wax printed patterns and Al cast parts was the Build angle, and the second most impactful factor was the Layer thickness according to the S/N ratio ranking of parameters based on the “Smaller-the-better” scheme. The optimum values for these critical parameters to achieve good dimensional and geometric accuracies in printed and cast parts were the same, 0 deg build angle and 0.25 μm layer thickness. These values were found using Castable Wax, and differ from what is reported in the literature, where it is stated that 45 deg angle gives the best accuracy for other photopolymers.
- The measurement results of both printed patterns and cast parts revealed that dimensional deviations increase with increased diameter in cylindrical features. Holes had larger dimensional deviations than boss cylinders and were undersized by 1.9% and 4% in printed and cast parts, respectively.
- Accuracy in height (Z direction) of the rectangular features were better than the accuracy in X-Y directions. In Z direction deviations were 0.7% and 0.1% in printed and cast parts, respectively, while in X-Y directions average deviations were 1.25% and 2.1% in printed and cast parts, respectively. Circular features had deviations 1.3% more than rectangular features in patterns, and had deviations 13% less than rectangular features in cast parts.
- Staircase effects on printed patterns were replicated in the cast parts showing the ability of the casting process to cast the small deviations on the surface. Fine features with diameters and width less than 2 mm were not cast properly.
- On average, the geometric characteristics had twice as many deviations as the dimensional characteristics. The most accurate geometric characteristic was the sphere roundness both in printed and cast parts, showing 0.011 mm and 0.016 mm deviations in average, respectively. The angularity was the least accurate geometric characteristic, showing 0.23 mm and 0.42 mm deviations in printed and cast parts, correspondingly.
- Form 3 LF SLA printer had 0.1 mm dimensional accuracy in average for printed Castable Wax parts.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

| Feature | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| D.4_Cyl 1-4 | 2 | 1 | 3 | 4 |
| D.4_Hole 1-2 | 1 | 2 | 3 | 4 |
| D.6_Sph 1-2 | 4 | 1 | 2 | 3 |
| D.8_Step Cyl 1 | 4 | 2 | 1 | 3 |
| D.12_Step Cyl 2 | 3 | 1 | 2 | 4 |
| L.6.5_Sq 1-2 | 4 | 1 | 2 | 3 |
| W.4_Sq 1-2 | 4 | 1 | 2 | 3 |
| H.2.5_Sq 1-2 | 3 | 1 | 4 | 2 |
| H.5_Sq 1-2 | 4 | 1 | 2 | 3 |
| Sum | 29 | 11 | 21 | 29 |
| Ranking of sums | 3 | 1 | 2 | 3 |
| Characteristics | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| Flatness | 1 | 2 | 4 | 3 |
| Conc_Step cyl 1-2 | 1 | 2 | 3 | 4 |
| Round_Sphere 1-2 | 3 | 2 | 1 | 4 |
| Angle | 3 | 1 | 2 | 4 |
| Parall_Sq 1-2 | 4 | 1 | 3 | 2 |
| Perpend_Sq 1-2 | 4 | 1 | 2 | 3 |
| Y.36_Cyl 1 | 3 | 2 | 1 | 4 |
| Y.28_Cyl 2 | 4 | 3 | 1 | 2 |
| X.28_Cyl 3 | 1 | 2 | 4 | 3 |
| X.36_Cyl 5 | 1 | 2 | 3 | 4 |
| Sum | 25 | 18 | 24 | 33 |
| Ranking of sums | 3 | 1 | 2 | 4 |
| Feature | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| D.4_Cyl 1-4 | 4 | 1 | 3 | 2 |
| D.4_Hole 1-2 | 1 | 2 | 3 | 4 |
| D.6_Sph 1-2 | 3 | 1 | 2 | 4 |
| D.8_Step Cyl 1 | 3 | 1 | 4 | 2 |
| D.12_Step Cyl 2 | 2 | 1 | 3 | 4 |
| L.6.5_Sq 1-2 | 3 | 1 | 2 | 4 |
| W.4_Sq 1-2 | 4 | 1 | 2 | 3 |
| H.2.5_Sq 1-2 | 1 | 3 | 2 | 4 |
| H.5_Sq 1-2 | 2 | 1 | 4 | 3 |
| Sum | 23 | 12 | 25 | 30 |
| Ranking of sums | 2 | 1 | 3 | 4 |
| Characteristics | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| Flatness_ | 1 | 3 | 2 | 4 |
| Conc_Step cyl 1-2 | 1 | 4 | 2 | 3 |
| Round_Sphere 1-2 | 3 | 2 | 4 | 1 |
| Angle | 4 | 1 | 2 | 3 |
| Parall_Sq 1-2 | 4 | 1 | 2 | 3 |
| Perpend_Sq 1-2 | 4 | 1 | 3 | 2 |
| Y.36_Cyl 1 | 3 | 1 | 4 | 2 |
| Y.28_Cyl 2 | 2 | 3 | 4 | 1 |
| X.28_Cyl 3 | 4 | 3 | 2 | 1 |
| X.36_Cyl 5 | 1 | 4 | 3 | 2 |
| Sum | 27 | 23 | 28 | 22 |
| Ranking of sums | 3 | 2 | 4 | 1 |
References
- Berman, S. Investment Castings | What Are Investment Castings Used for? 2017. Available online: https://www.ferralloy.com/investment-castings-applications/ (accessed on 4 May 2022).
- Mukhtarkhanov, M.; Perveen, A.; Talamona, D. Application of Stereolithography Based 3D Printing Technology in Investment Casting. Micromachines 2020, 11, 946. [Google Scholar] [CrossRef] [PubMed]
- Pattnaik, S.; Jha, P.K.; Karunakar, D.B. A review of rapid prototyping integrated investment casting processes. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2014, 228, 249–277. [Google Scholar] [CrossRef]
- Cheah, C.M.; Chua, C.K.; Lee, C.W.; Feng, C.; Totong, K. Rapid prototyping and tooling techniques: A review of applications for rapid investment casting. Int. J. Adv. Manuf. Technol. 2005, 25, 308–320. [Google Scholar] [CrossRef]
- Prakash, C.; Singh, S.; Kopperi, H.; Ramakrihna, S.; Mohan, S. Comparative job production based life cycle assessment of conventional and additive manufacturing assisted investment casting of aluminium: A case study. J. Clean. Prod. 2021, 289, 125164. [Google Scholar] [CrossRef]
- Lee, C.; Chua, C.K.; Cheah, C.M.; Tan, L.H.; Feng, C. Rapid investment casting: Direct and indirect approaches via fused deposition modelling. Int. J. Adv. Manuf. Technol. 2004, 23, 93–101. [Google Scholar]
- Kumar, P.; Ahuja, I.; Singh, R. Application of fusion deposition modelling for rapid investment casting—A review. Int. J. Mater. Eng. Innov. 2012, 3, 204–227. [Google Scholar] [CrossRef]
- Chua, C.; Feng, C.; Lee, C.W.; Ang, G.Q. Rapid investment casting: Direct and indirect approaches via model maker II. Int. J. Adv. Manuf. Technol. 2005, 25, 26–32. [Google Scholar] [CrossRef]
- Greenbaum, P.; Khan, S. Direct investment casting of rapid prototype parts: Practical commercial experience. In Proceedings of the 2nd European Conference on Rapid Prototyping, Nottingham, UK, 15–16 July 1993. [Google Scholar]
- Arnold, C.; Monsees, D.; Hey, J.; Schweyen, R. Surface quality of 3D-printed models as a function of various printing parameters. Materials 2019, 12, 1970. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Park, W.; Cho, H.; Zhang, W.; Leu, M. A neural network approach to the modelling and analysis of stereolithography processes. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2001, 215, 1719–1733. [Google Scholar] [CrossRef]
- Garcia, E.A.; Ayranci, C.; Qureshi, A.J. Material property-manufacturing process optimization for form 2 vat-photo polymerization 3D Printers. J. Manuf. Mater. Processing 2020, 4, 12. [Google Scholar] [CrossRef]
- Islam, M.; Gomer, H.; Sacks, S. Comparison of dimensional accuracies of stereolithography and powder binder printing. Int. J. Adv. Manuf. Technol. 2016, 88, 3077–3087. [Google Scholar] [CrossRef]
- Mucci, V.; Arenas, G.F.; Duchowicz, R.; Cook, W.D.; Vallo, C. Influence of Thermal Expansion on Shrinkage During Photopolymerization of Dental Resins Based on bis-GMA/TEGDMA. Dent. Mater. Off. Publ. Acad. Dent. Mater. 2008, 25, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Foteinopoulos, P.; Papacharalampopoulos, A.; Stavropoulos, P. On thermal modeling of Additive Manufacturing processes. CIRP J. Manuf. Sci. Technol. 2018, 20, 66–83. [Google Scholar] [CrossRef]
- Park, G.; Kim, S.; Heo, S.; Koak, J.; Seo, D. Effects of Printing Parameters on the Fit of Implant-Supported 3D Printing Resin Prosthetics. Materials 2019, 12, 2533. [Google Scholar] [CrossRef] [PubMed]
- Unkovskiy, A.; Bui, P.H.-B.; Schille, C.; Geis-Gerstorfer, J.; Huettig, F.; Spintzyk, S. Objects build orientation, positioning, and curing influence dimensional accuracy and flexural properties of stereolithographically printed resin. Dent. Mater. 2018, 34, e324–e333. [Google Scholar] [CrossRef] [PubMed]
- Hada, T.; Kanazawa, M.; Iwaki, M.; Arakida, T.; Soeda, Y.; Katheng, A.; Otake, R.; Minakuchi, S. Effect of Printing Direction on the Accuracy of 3D-Printed Dentures Using Stereolithography Technology. Materials 2020, 13, 3405. [Google Scholar] [CrossRef] [PubMed]
- Alharbi, N.; Osman, R.; Wismeijer, D. Factors influencing the dimensional accuracy of 3d-printed full-coverage dental restorations using stereolithography technology. Int. J. Prosthodont. 2016, 29, 503–510. [Google Scholar] [CrossRef] [PubMed]
- McCarty, M.; Chen, S.; English, J.; Kasper, F. Effect of print orientation and duration of ultraviolet curing on the dimensional accuracy of a 3-dimensionally printed orthodontic clear aligner design. Am. J. Orthod. Dentofac. Orthop. 2020, 158, 889–897. [Google Scholar] [CrossRef] [PubMed]
- Rubayo, D.; Phasuk, K.; Vickery, J.; Morton, D.; Lin, W. Influences of build angle on the accuracy, printing time, and material consumption of additively manufactured surgical templates. J. Prosthet. Dent. 2021, 126, 658–663. [Google Scholar] [CrossRef] [PubMed]
- Favero, C.; English, J.; Cozad, B.; Wirthlin, J.; Short, M.; Kasper, F. Effect of print layer height and printer type on the accuracy of 3-dimensional printed orthodontic models. Am. J. Orthod. Dentofac. Orthop. 2017, 152, 557–565. [Google Scholar] [CrossRef] [PubMed]
- Piedra-Cascón, W.; Krishnamurthy, V.; Att, W.; Revilla-León, M. 3D printing parameters, supporting structures, slicing, and post-processing procedures of vat-polymerization additive manufacturing technologies: A narrative review. J. Dent. 2021, 109, 103630. [Google Scholar] [CrossRef]
- Resende, C.D.; Quirino Barbosa, T.; Moura, G.; Rizzante, F.P.; Mendonça, G.; Zancopé, K.; das Neves, F.D. Cost and effectiveness of 3-dimensionally printed model using three different printing layer parameters and two resins. J. Prosthet. Dent. 2021, in press. [Google Scholar] [CrossRef] [PubMed]
- Loflin, W.; English, J.; Borders, C.; Harris, L.; Moon, A.; Holland, J.; Kasper, F. Effect of print layer height on the assessment of 3D-printed models. Am. J. Orthod. Dentofac. Orthop. 2019, 156, 283–289. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Li, P.; Chu, F.; Shen, G. Influence of the three-dimensional printing technique and printing layer thickness on model accuracy. J. Orofac. Orthop. / Fortschr. Der Kieferorthopädie 2019, 80, 194–204. [Google Scholar] [CrossRef] [PubMed]
- Mantada, P.; Mendricky, R.; Safka, J. Parameters influencing the precision of various 3d printing technologies. MM Sci. J. 2017, 2017, 2004–2012. [Google Scholar] [CrossRef]
- Khaledi, A.-A.; Farzin, M.; Akhlaghian, M.; Pardis, S.; Mir, N. Evaluation of the marginal fit of metal copings fabricated by using 3 different CAD-CAM techniques: Milling, stereolithography, and 3D wax printer. J. Prosthet. Dent. 2020, 124, 81–86. [Google Scholar] [CrossRef]
- Piangsuk, T.; Dawson, D.; El-Kerdani, T.; Lindquist, T. The Accuracy of Post and Core Fabricated with Digital Technology. J. Prosthodont. 2022. online ahead of print. [Google Scholar] [CrossRef]
- Cheng, P.; Khan, S. Dimensional accuracy and surface finish of investment casting parts by indirect additive manufacturing from fused filament fabrication. IOP Conf. Ser. Mater. Sci. Eng. 2018, 429, 012100. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, R.; Ahuja, I. Investigations on dimensional accuracy of the components prepared by hybrid investment casting. J. Manuf. Processes 2015, 20, 525–533. [Google Scholar] [CrossRef]
- Wu, H.; Li, D.; Tang, Y.; Guo, N.; Cui, F.; Sun, B. Rapid casting of hollow turbine blades using integral ceramic moulds. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 695–702. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Foteinopoulos, P.; Papapacharalampopoulos, A. On the Impact of Additive Manufacturing Processes Complexity on Modelling. Appl. Sci. 2021, 11, 7743. [Google Scholar] [CrossRef]
- Foteinopoulos, P.; Esnault, V.; Komineas, G.; Papacharalampopoulos, A.; Stavropoulos, P. Cement-based additive manufacturing: Experimental investigation of process quality. Int. J. Adv. Manuf. Technol. 2020, 106, 4815–4826. [Google Scholar] [CrossRef]
- Gargiulo, E.P. Stereolithography process accuracy: User experience. In Proceedings of the 1st European Conference on Rapid Prototyping, Nottingham, UK, 6–7 July 1992; pp. 187–207. [Google Scholar]
- Mahesh, M.; Wong, Y.; Fuh JY, H.; Loh, H.T. Benchmarking for comparative evaluation of RP systems and processes. Rapid Prototyp. J. 2004, 10, 123–135. [Google Scholar] [CrossRef]
- Mahmood, S.; Talamona, D.; Goh, K.L.; Qureshi, A.J. Fast Deviation Simulation for “Fused Deposition Modelling” Process. In Proceedings of the 14th CIRP CAT 2016—CIRP Conference Computer Aided Tolerancing, Procedia CIRP, Gotherburg, Sweden, 18–20 May 2016; pp. 327–332. [Google Scholar] [CrossRef][Green Version]
- Moylan, S.; Slotwinski, J.; Cooke, A.; Jurrens, K.; Alkan Donmez, M. An Additive Manufacturing Test Artifact. J. Res. Natl. Inst. Stand. Technol. 2014, 119, 429–459. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Li, D.; Zhou, W. Process parameters appraisal of fabricating ceramic parts based on stereolithography using the Taguchi method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 1249–1258. [Google Scholar] [CrossRef]
- Wang, J.; Sama, S.; Lynch, P.; Manogharan, G. Design and Topology Optimization of 3D-Printed Wax Patterns for Rapid Investment Casting. Procedia Manuf. 2019, 34, 683–694. [Google Scholar] [CrossRef]
- Kabnure, B.; Shinde, V.; Patil, D. Quality and yield improvement of ductile iron casting by simulation technique. Mater. Today Proc. 2020, 27, 111–116. [Google Scholar] [CrossRef]
- Browne, D.; O’Mahoney, D. Interface heat transfer in investment casting of aluminum alloys. Metall. Mater. Trans. A 2001, 32, 3055–3063. [Google Scholar] [CrossRef]
- Bagalkot, A.; Pons, D.; Symons, D.; Clucas, D. The Effects of Cooling and Shrinkage on the Life of Polymer 3D Printed Injection Moulds. Polymers 2022, 14, 520. [Google Scholar] [CrossRef]
- Zhou, J.G.; Herscovici, D.; Chen, C.C. Parametric process optimization to improve the accuracy of rapid prototyped stereolithography parts. Int. J. Mach. Tools Manuf. 2000, 40, 363–379. [Google Scholar] [CrossRef]
- Using Castable Wax Resin. n.d. Available online: https://support.formlabs.com/s/article/Using-Castable-Wax-Resin?language=en_US (accessed on 6 September 2022).
- Ultra-Vest® MAXX™ Investments. 2022. Available online: https://www.ransom-randolph.com/_files/ugd/cc5f22_4044309c88244e85a19f95210a1b53e1.pdf (accessed on 27 August 2022).
- Castable Wax: Jewelry Pattern Burnout Process. 2022. Available online: https://manufat.com/download/Formlabs_Castable_Wax_Usage_Guide.pdf (accessed on 27 August 2022).
- Stefanescu, D. Science and Engineering of Casting Solidification, 2nd ed.; Springer: New York, NY, USA, 2008; p. 67. [Google Scholar]
- Ye, R. Decreasing Shrinkage in Metal Die-Casting. 3ERP Prototyping. 2022. Available online: https://www.3erp.com/blog/decreasing-shrinkage-metal-die-casting/#:~:text=Solidification%20shrinkage%20is%20the%20next,4%25%20or%203%25%20respectively (accessed on 4 April 2022).
- Methods and Formulas for Analyze Taguchi Design. n.d. Available online: https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistical-modeling/doe/how-to/taguchi/analyze-taguchi-design/methods-and-formulas/methods-and-formulas/ (accessed on 1 September 2022).
- Mahmood, S.; Qureshi, A.; Talamona, D. Taguchi based process optimization for dimension and tolerance control for fused deposition modelling. Addit. Manuf. 2018, 21, 183–190. [Google Scholar] [CrossRef]
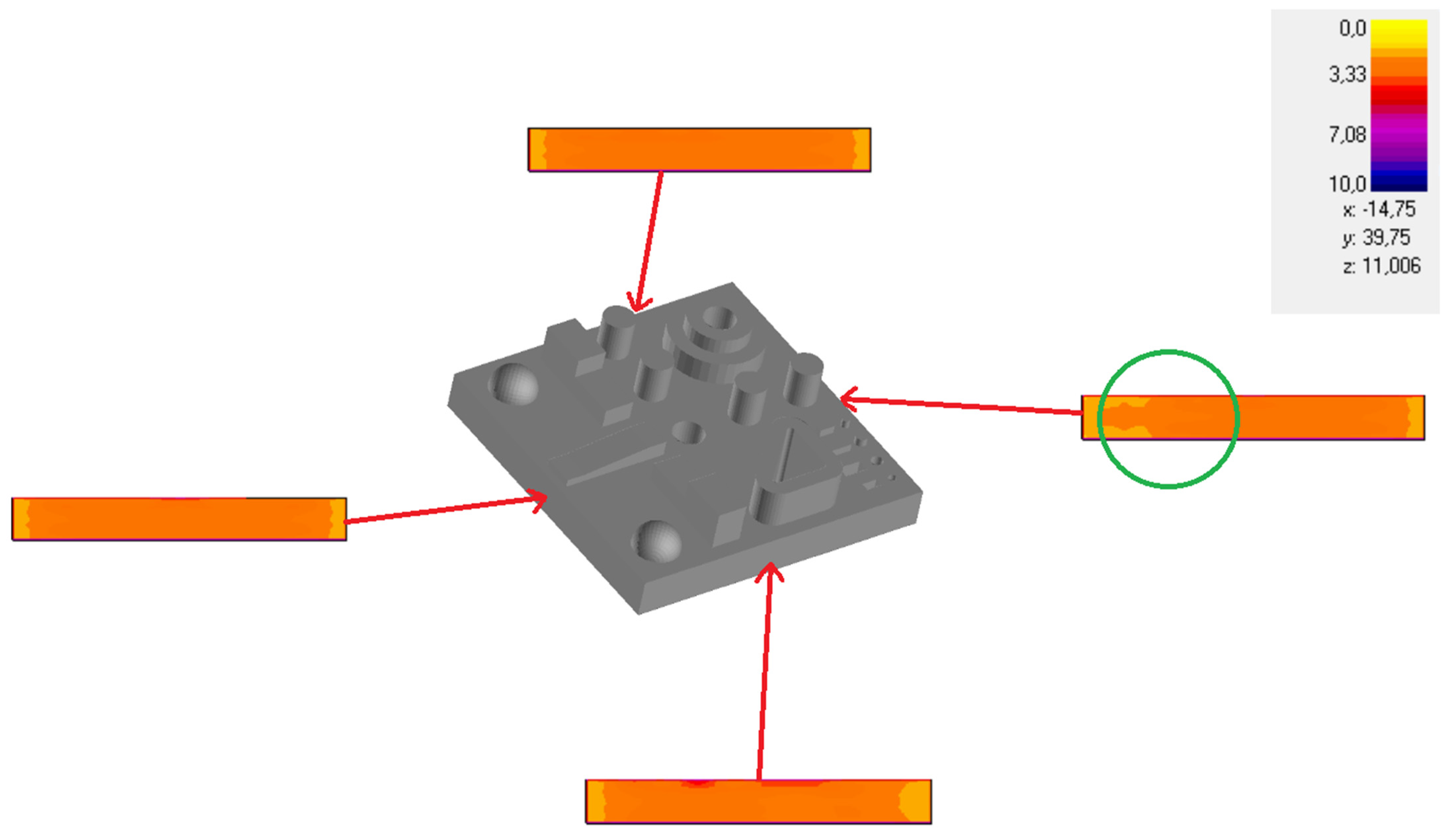
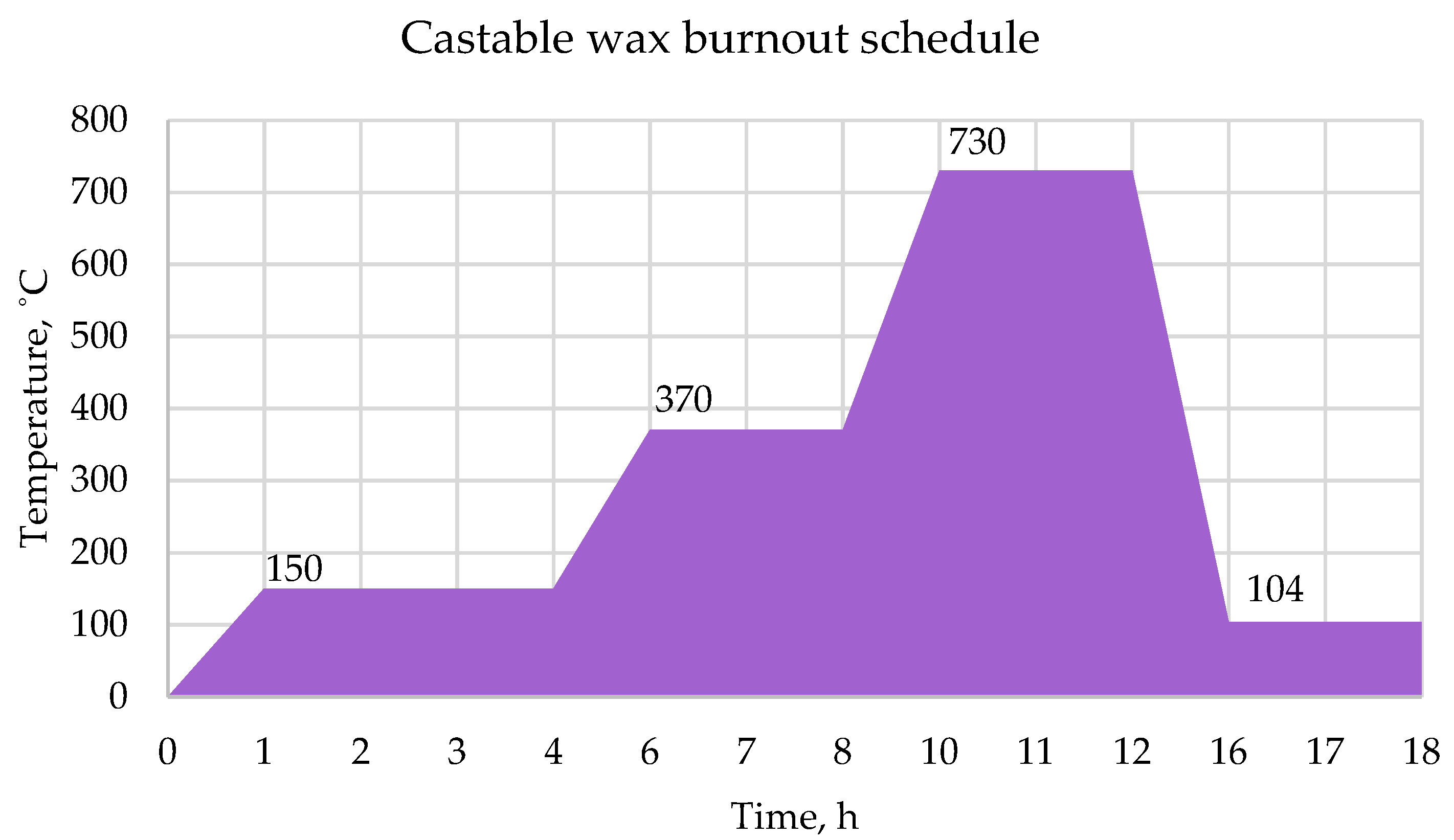



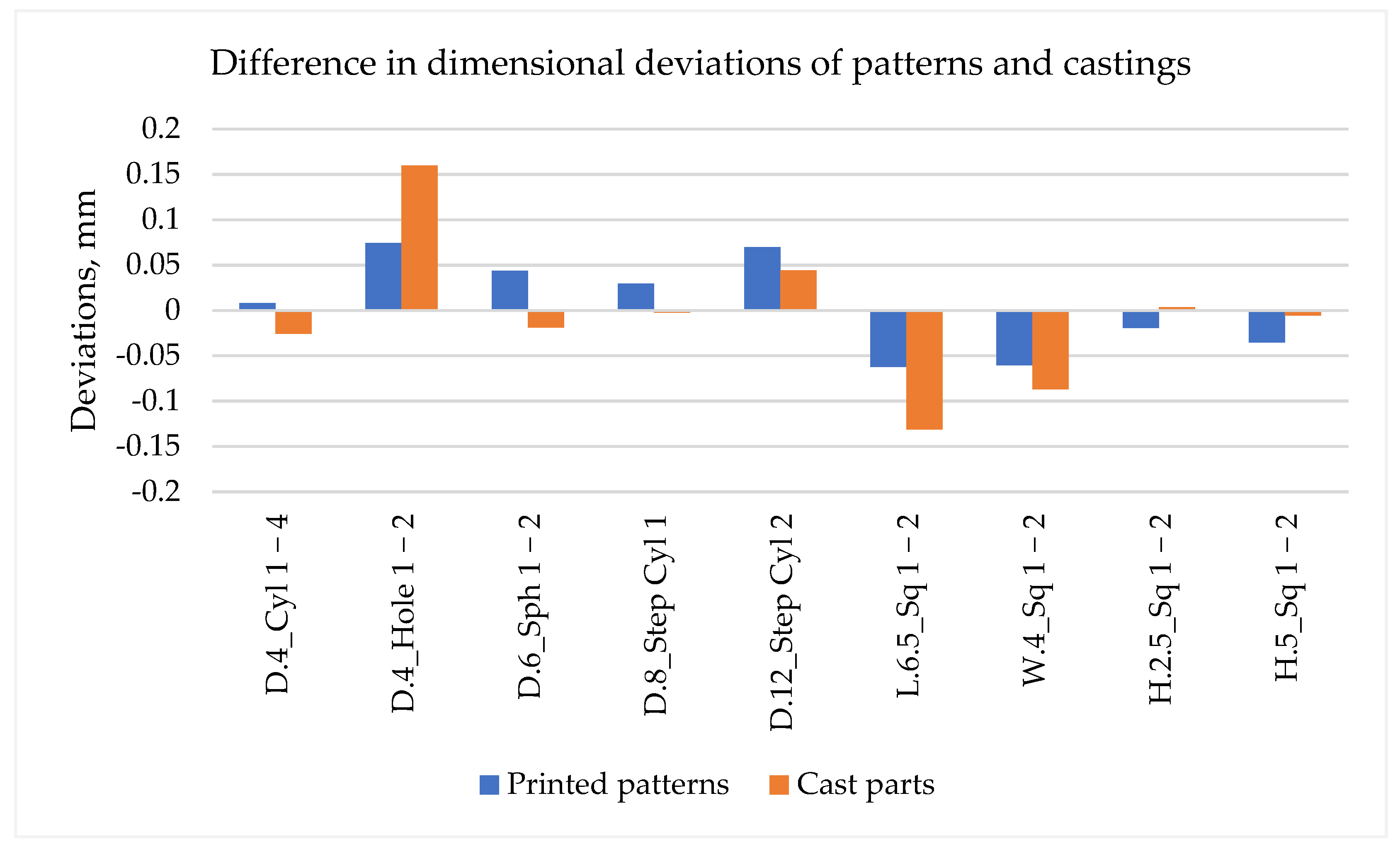
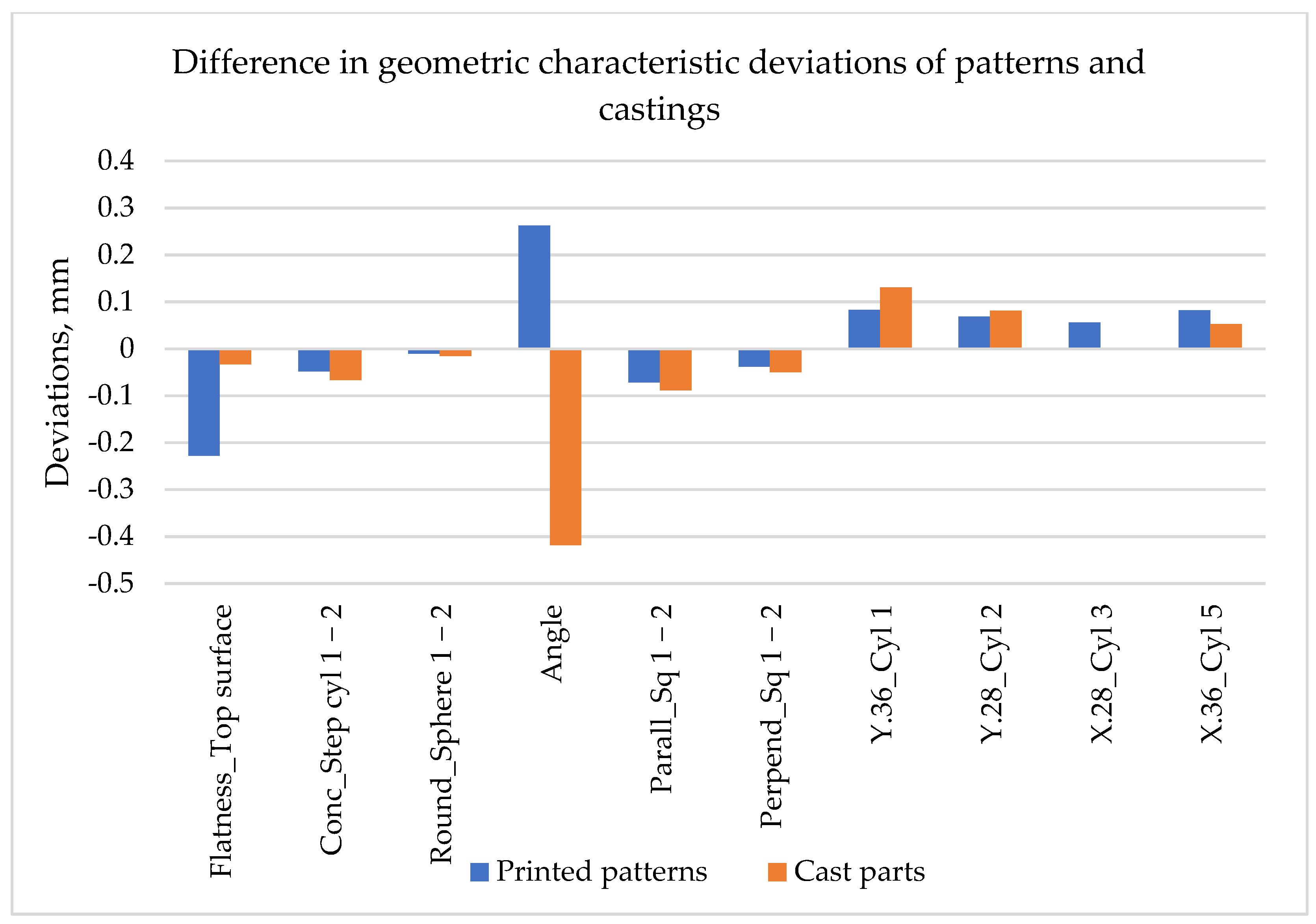
| Source | AM Method | Study Focus | Findings |
|---|---|---|---|
| Lee et al. [11] Mucci et al. [13] Islam et al. [14] | SLA | The effect of Laser exposure time on the dimensional accuracy of printed part | Increased printing speed leads to less laser exposure time and causes poor polymerization, resulting in poor accuracy and surface finish |
| Arnold et al. [10] Unkovskiy et al. [17] | SLA | The effect of Printing direction/positioning on the build platform on the dimensional accuracy of printed part | No significant effect on the dimensional accuracy Recommended to build the part far from the platform edges |
| Arnold et al. [10] Park et al. [16] Unkovskiy et al. [17] Hada et al. [18] Alharbi et al. [19] McCarty et al. [20] Rubayo et al. [21] | SLA | The effect of Build angle on the dimensional accuracy of printed part | 45° gives better dimensional accuracy; 0° consumes less time but more material, and vice versa for 90° |
| Piedra-Cascón et al. [12] Park et al. [16] Favero et al. [22] Dias Resende et al. [24] Loflin et al. [25] Zhang et al. [26] | SLA | The effect of Layer thickness on the dimensional accuracy of printed part | Small difference between 25, 50, and 100 μm layer thicknesses in terms of dimensional accuracy; 100 μm was mostly recommended due to faster printing time |
| Khaledi et al. [28] Piangsuk et al. [29] | SLA | The dimensional accuracy of milled and RIC parts | Compared the SLA assisted RIC copings with milled copings. Parts produced by using of SLA showed dimensional stability of patterns and cast parts over milled parts. |
| Cheng et al. [30] Kumar et al. [31] Kumar et al. [7] | FDM | The dimensional accuracy of RIC parts | Post processing of FDM printed patterns does not significantly affect the dimensional accuracy of cast parts. 90° orientation in FDM is best for dimensional accuracy of cast parts. |
| Parameters | Level 1 | Level 2 |
|---|---|---|
| A: Layer thickness (μm) | 25 | 50 |
| B: Build angle (deg) | 0 | 45 |
| C: Support density | 0.75 | 1 |
| D: Support touchpoint size (mm) | 0.5 | 0.6 |
| # | A | B | C | D |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 | 2 |
| 3 | 1 | 2 | 1 | 2 |
| 4 | 1 | 2 | 2 | 1 |
| 5 | 2 | 1 | 1 | 2 |
| 6 | 2 | 1 | 2 | 1 |
| 7 | 2 | 2 | 1 | 1 |
| 8 | 2 | 2 | 2 | 2 |
| Casting Material | Mold Material | |
|---|---|---|
| Al 518 | Silica Sand | |
| Thermal conductivity, [W/m/K] | 96.17 | 0.59 |
| Specific heat, [J/kg/K] | 962.3 | 1075.3 |
| Density, [kg/m3] | 2574 | 1521 |
| Casting temperature, [C] | 700 | 104 |
| Solidification temperature, [C] | 437 | - |
| Mesh Size | CFS Time | Difference | HS | Difference |
|---|---|---|---|---|
| 1 mm | 0.063 | --- | 1.642 | --- |
| 0.5 mm | 0.068 | 7.9% | 1.819 | 10.8% |
| 0.25 mm | 0.071 | 4.4% | 1.75 | 3.8% |
| Form 3 LF SLA Printer | Castable Wax V1 FLCWPU01 | ||
|---|---|---|---|
| Build volume: | 145 × 145 × 185 mm | Tensile Modulus: | 220 MPa |
| Laser Spot Size: | 85 microns | Elongation at Break: | 13% |
| Operating temperature: | 35 °C | Ash Content (TGA): | 0.0–0.1% |
| Laser specifications: | Class 1 Laser Product Wavelength 405 nm laser | Wax content: | 20% |
| Casting Parameters | Parameter Values |
|---|---|
| Casting temperature | 700 °C |
| Temperature of the mold prior to casting | 104 °C |
| Pouring speed | 2.5 cm/s |
| Height of the ladle above the pouring basin | 2.5 cm |
| Time before quenching | 1 h |
| Dimensional Accuracy | Geometric Characteristics | ||
|---|---|---|---|
| Dimension | Features | Characteristic | Features |
| Diameter | Cyl 1-4 | Flatness | Top surface |
| Hole 1-2 | Concentricity | St cyl 1-2 and Hole 2 | |
| St cyl 1-2 | Parallelism | Sq 1-2 | |
| Sphere 1-2 | Perpendicularity | Sq 1-2 and Top surface | |
| Width | Sq 1-2 | Roundness | Sphere 1-2 |
| Length | Sq 1-2 | Angularity | Ang 1-2 |
| Height | Sq 1-2 | Positioning | Cyl 1-4 |
| Dimension | Features | Nominal Value | Average Measured Value | Range | Average Deviation | |
|---|---|---|---|---|---|---|
| Max | Min | |||||
| Diameter | D.4_Cyl 1-4 | 4 | 3.9921 | 4.0713 | 3.9357 | 0.0079 |
| D.4_Hole 1-2 | 4 | 3.9257 | 4.0361 | 3.7726 | 0.0743 | |
| D.6_Sph 1-2 | 6 | 5.9566 | 6.0345 | 5.8824 | 0.0434 | |
| D.8_Step Cyl 1 | 8 | 7.9705 | 8.0045 | 7.9177 | 0.0295 | |
| D.12_Step Cyl 2 | 12 | 11.9302 | 11.9765 | 11.8688 | 0.0698 | |
| Length | L.6.5_Sq 1-2 | 6.5 | 6.5698 | 6.6548 | 6.4771 | −0.0623 |
| Width | W.4_Sq 1-2 | 4 | 4.0606 | 4.2667 | 4.0049 | −0.0606 |
| Height | H.2.5_Sq 1-2 | 2.5 | 2.5194 | 2.6772 | 2.4763 | −0.0194 |
| H.5_Sq 1-2 | 5 | 5.0353 | 5.1989 | 4.9628 | −0.0353 | |
| Feature | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| D.4_Cyl 1-4 | 1 | 2 | 4 | 3 |
| D.4_Hole 1-2 | 1 | 2 | 4 | 3 |
| D.6_Sph 1-2 | 4 | 1 | 3 | 2 |
| D.8_Step Cyl 1 | 4 | 3 | 1 | 2 |
| D.12_Step Cyl 2 | 3 | 1 | 2 | 4 |
| L.6.5_Sq 1-2 | 2 | 1 | 4 | 3 |
| W.4_Sq 1-2 | 3 | 1 | 2 | 4 |
| H.2.5_Sq 1-2 | 3 | 1 | 4 | 2 |
| H.5_Sq 1-2 | 2 | 3 | 1 | 4 |
| Sum | 23 | 15 | 25 | 27 |
| Ranking of sums | 2 | 1 | 3 | 4 |
| Feature | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| D.4_Cyl 1-4 | 1 | 1 | 2 | 1 |
| D.4_Hole 1-2 | 1 | 2 | 2 | 2 |
| D.6_Sph 1-2 | 1 | 1 | 1 | 1 |
| D.8_Step Cyl 1 | 1 | 2 | 2 | 1 |
| D.12_Step Cyl 2 | 1 | 1 | 2 | 2 |
| L.6.5_Sq 1-2 | 2 | 2 | 1 | 1 |
| W.4_Sq 1-2 | 1 | 2 | 2 | 1 |
| H.2.5_Sq 1-2 | 1 | 1 | 1 | 2 |
| H.5_Sq 1-2 | 2 | 1 | 2 | 1 |
| Level 1 | 7 | 5 | 3 | 6 |
| Level 2 | 2 | 4 | 6 | 3 |
| Optimum level | 1 | 1 | 2 | 1 |
| Characteristics | Features | Nominal Value | Average Measured Value | Range | Average Deviation | |
|---|---|---|---|---|---|---|
| Max | Min | |||||
| Flatness | Top surface | 0 | 0.2277 | 5.0597 | 0.0050 | −0.2277 |
| Concentricity | Conc_Step cyl 1-2 | 0 | 0.0486 | 0.1350 | 0.0117 | −0.0486 |
| Roundness | Round_Sphere 1-2 | 0 | 0.0106 | 0.0630 | 0.0003 | −0.0106 |
| Angularity | Angle | 45 | 44.7374 | 46.2236 | 43.4469 | 0.2626 |
| Parallelism | Parall_Sq 1-2 | 0 | 0.0720 | 0.2747 | 0.0264 | −0.0720 |
| Perpendicularity | Perpend_Sq 1-2 | 0 | 0.0385 | 0.1489 | 0.0109 | −0.0385 |
| Position | Y.36_Cyl 1 | 36 | 35.9170 | 36.0424 | 35.7923 | 0.0830 |
| Y.28_Cyl 2 | 28 | 27.9317 | 28.0421 | 27.8041 | 0.0683 | |
| X.28_Cyl 3 | 28 | 27.9442 | 27.9953 | 27.8437 | 0.0558 | |
| X.36_Cyl 5 | 36 | 35.9183 | 35.9851 | 35.8161 | 0.0817 | |
| Characteristics | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| Flatness | 1 | 4 | 2 | 3 |
| Conc_Step cyl 1-2 | 1 | 2 | 3 | 4 |
| Round_Sphere 1-2 | 3 | 2 | 1 | 4 |
| Angle | 2 | 1 | 4 | 3 |
| Parall_Sq 1-2 | 4 | 1 | 3 | 2 |
| Perpend_Sq 1-2 | 3 | 1 | 2 | 4 |
| Y.36_Cyl 1 | 4 | 2 | 1 | 3 |
| Y.28_Cyl 2 | 4 | 3 | 1 | 2 |
| X.28_Cyl 3 | 1 | 2 | 3 | 4 |
| X.36_Cyl 5 | 1 | 3 | 2 | 4 |
| Sum | 24 | 21 | 22 | 33 |
| Ranking of sums | 3 | 1 | 2 | 4 |
| Characteristics | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| Flatness_ | 2 | 1 | 2 | 1 |
| Conc_Step cyl 1-2 | 1 | 1 | 1 | 2 |
| Round_Sphere 1-2 | 1 | 2 | 1 | 2 |
| Angle | 2 | 1 | 1 | 1 |
| Parall_Sq 1-2 | 1 | 2 | 2 | 1 |
| Perpend_Sq 1-2 | 1 | 2 | 1 | 1 |
| Y.36_Cyl 1 | 2 | 1 | 1 | 2 |
| Y.28_Cyl 2 | 2 | 1 | 1 | 2 |
| X.28_Cyl 3 | 1 | 1 | 1 | 2 |
| X.36_Cyl 5 | 1 | 1 | 1 | 2 |
| Level 1 | 6 | 7 | 8 | 4 |
| Level 2 | 4 | 3 | 2 | 6 |
| Optimum level | 1 | 1 | 1 | 2 |
| Parameters | Dimensional Accuracy | Geometric Accuracy | ||
|---|---|---|---|---|
| Level | Value | Level | Value | |
| A: Layer thickness, (μm) | 1 | 25 | 1 | 25 |
| B: Build angle, (deg) | 1 | 0 | 1 | 0 |
| C: Support density | 2 | 1 | 1 | 0.75 |
| D: Touchpoint size | 1 | 0.5 | 2 | 0.6 |
| Dimension | Features | Nominal Value | Average Measured Value | Range | Average Deviation | |
|---|---|---|---|---|---|---|
| Max | Min | |||||
| Diameter | D.4_Cyl 1-4 | 4 | 4.0257 | 4.0909 | 3.9767 | −0.0257 |
| D.4_Hole 1-2 | 4 | 3.8405 | 3.9346 | 3.5713 | 0.1595 | |
| D.6_Sph 1-2 | 6 | 6.0191 | 6.1160 | 5.9109 | −0.0191 | |
| D.8_Step Cyl 1 | 8 | 8.0027 | 8.0337 | 8.0242 | −0.0027 | |
| D.12_Step Cyl 2 | 12 | 11.9557 | 11.9967 | 11.8967 | 0.0443 | |
| Length | L.6.5_Sq 1-2 | 6.5 | 6.6315 | 6.7482 | 6.6723 | −0.1315 |
| Width | W.4_Sq 1-2 | 4 | 4.0868 | 4.2519 | 4.0146 | −0.0868 |
| Height | H.2.5_Sq 1-2 | 2.5 | 2.4964 | 2.5752 | 2.4288 | 0.0036 |
| H.5_Sq 1-2 | 5 | 5.0057 | 5.1148 | 5.0060 | −0.0057 | |
| Feature | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| D.4_Cyl 1-4 | 4 | 1 | 2 | 3 |
| D.4_Hole 1-2 | 1 | 2 | 3 | 4 |
| D.6_Sph 1-2 | 2 | 1 | 4 | 3 |
| D.8_Step Cyl 1 | 1 | 3 | 2 | 4 |
| D.12_Step Cyl 2 | 2 | 1 | 3 | 4 |
| L.6.5_Sq 1-2 | 4 | 1 | 3 | 2 |
| W.4_Sq 1-2 | 4 | 1 | 2 | 3 |
| H.2.5_Sq 1-2 | 1 | 4 | 3 | 2 |
| H.5_Sq 1-2 | 2 | 1 | 4 | 3 |
| Sum | 21 | 15 | 26 | 28 |
| Ranking of sums | 2 | 1 | 3 | 4 |
| Feature | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| D.4_Cyl 1-4 | 2 | 2 | 1 | 2 |
| D.4_Hole 1-2 | 1 | 1 | 1 | 1 |
| D.6_Sph 1-2 | 1 | 2 | 2 | 2 |
| D.8_Step Cyl 1 | 1 | 1 | 1 | 2 |
| D.12_Step Cyl 2 | 1 | 1 | 2 | 2 |
| L.6.5_Sq 1-2 | 2 | 2 | 2 | 1 |
| W.4_Sq 1-2 | 1 | 2 | 2 | 1 |
| H.2.5_Sq 1-2 | 1 | 1 | 2 | 2 |
| H.5_Sq 1-2 | 2 | 1 | 2 | 1 |
| Level 1 | 6 | 5 | 3 | 4 |
| Level 2 | 3 | 4 | 6 | 5 |
| Optimum level | 1 | 1 | 2 | 2 |
| Characteristics | Features | Nominal Value | Average Measured Value | Range | Deviation | |
|---|---|---|---|---|---|---|
| Max | Min | |||||
| Flatness | Top surface | 0 | 0.0331 | 0.0903 | 0.0167 | −0.0331 |
| Concentricity | Conc_Step cyl 1-2 | 0 | 0.0667 | 0.2579 | 0.0090 | −0.0667 |
| Roundness | Round_Sphere 1-2 | 0 | 0.0155 | 0.0450 | 0.0002 | −0.0155 |
| Angularity | Angle | 45 | 45.4182 | 46.9586 | 44.1689 | −0.4182 |
| Parallelism | Parall_Sq 1-2 | 0 | 0.0888 | 0.2271 | 0.0241 | −0.0888 |
| Perpendicularity | Perpend_Sq 1-2 | 0 | 0.0501 | 0.1041 | 0.0188 | −0.0501 |
| Position | Y.36_Cyl 1 | 36 | 35.8697 | 36.0996 | 35.6304 | 0.1303 |
| Y.28_Cyl 2 | 28 | 27.9194 | 28.1344 | 27.6950 | 0.0806 | |
| X.28_Cyl 3 | 28 | 27.9983 | 28.1442 | 27.8335 | 0.0017 | |
| X.36_Cyl 5 | 36 | 35.9477 | 36.0956 | 35.7895 | 0.0523 | |
| Characteristics | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| Flatness_ | 1 | 3 | 2 | 4 |
| Conc_Step cyl 1-2 | 2 | 4 | 3 | 1 |
| Round_Sphere 1-2 | 3 | 2 | 4 | 1 |
| Angle | 3 | 1 | 2 | 4 |
| Parall_Sq 1-2 | 4 | 1 | 3 | 2 |
| Perpend_Sq 1-2 | 3 | 1 | 4 | 2 |
| Y.36_Cyl 1 | 3 | 1 | 4 | 2 |
| Y.28_Cyl 2 | 2 | 3 | 4 | 1 |
| X.28_Cyl 3 | 4 | 1 | 3 | 2 |
| X.36_Cyl 5 | 1 | 4 | 3 | 2 |
| Sum | 26 | 21 | 32 | 21 |
| Ranking of sums | 2 | 1 | 3 | 1 |
| Characteristics | A: Layer Thickness | B: Build Angle | C: Support Density | D: Touchpoint Size |
|---|---|---|---|---|
| Flatness | 2 | 2 | 1 | 2 |
| Conc_Step cyl 1-2 | 2 | 1 | 1 | 1 |
| Round_Sphere 1-2 | 2 | 2 | 1 | 2 |
| Angle | 1 | 2 | 1 | 2 |
| Parall_Sq 1-2 | 1 | 1 | 2 | 1 |
| Perpend_Sq 1-2 | 2 | 1 | 2 | 2 |
| Y.36_Cyl 1 | 1 | 1 | 1 | 1 |
| Y.28_Cyl 2 | 1 | 1 | 1 | 1 |
| X.28_Cyl 3 | 1 | 2 | 2 | 2 |
| X.36_Cyl 5 | 1 | 2 | 2 | 2 |
| Level 1 | 6 | 5 | 6 | 4 |
| Level 2 | 4 | 5 | 4 | 6 |
| Optimum level | 1 | 1 or 2 | 1 | 2 |
| Parameters | Dimensional Accuracy | Geometric Accuracy | ||
|---|---|---|---|---|
| Level | Value | Level | Value | |
| A: Layer thickness, (μm) | 1 | 25 | 1 | 25 |
| B: Build angle, (deg) | 1 | 0 | 1 | 0 |
| C: Support density | 2 | 1 | 1 | 0.75 |
| D: Touchpoint size | 2 | 0.6 | 2 | 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badanova, N.; Perveen, A.; Talamona, D. Study of SLA Printing Parameters Affecting the Dimensional Accuracy of the Pattern and Casting in Rapid Investment Casting. J. Manuf. Mater. Process. 2022, 6, 109. https://doi.org/10.3390/jmmp6050109
Badanova N, Perveen A, Talamona D. Study of SLA Printing Parameters Affecting the Dimensional Accuracy of the Pattern and Casting in Rapid Investment Casting. Journal of Manufacturing and Materials Processing. 2022; 6(5):109. https://doi.org/10.3390/jmmp6050109
Chicago/Turabian StyleBadanova, Nazym, Asma Perveen, and Didier Talamona. 2022. "Study of SLA Printing Parameters Affecting the Dimensional Accuracy of the Pattern and Casting in Rapid Investment Casting" Journal of Manufacturing and Materials Processing 6, no. 5: 109. https://doi.org/10.3390/jmmp6050109
APA StyleBadanova, N., Perveen, A., & Talamona, D. (2022). Study of SLA Printing Parameters Affecting the Dimensional Accuracy of the Pattern and Casting in Rapid Investment Casting. Journal of Manufacturing and Materials Processing, 6(5), 109. https://doi.org/10.3390/jmmp6050109






