FE-Simulation Based Design of Wear-Optimized Cutting Edge Roundings
Abstract
:1. Introduction
2. Materials and Methods
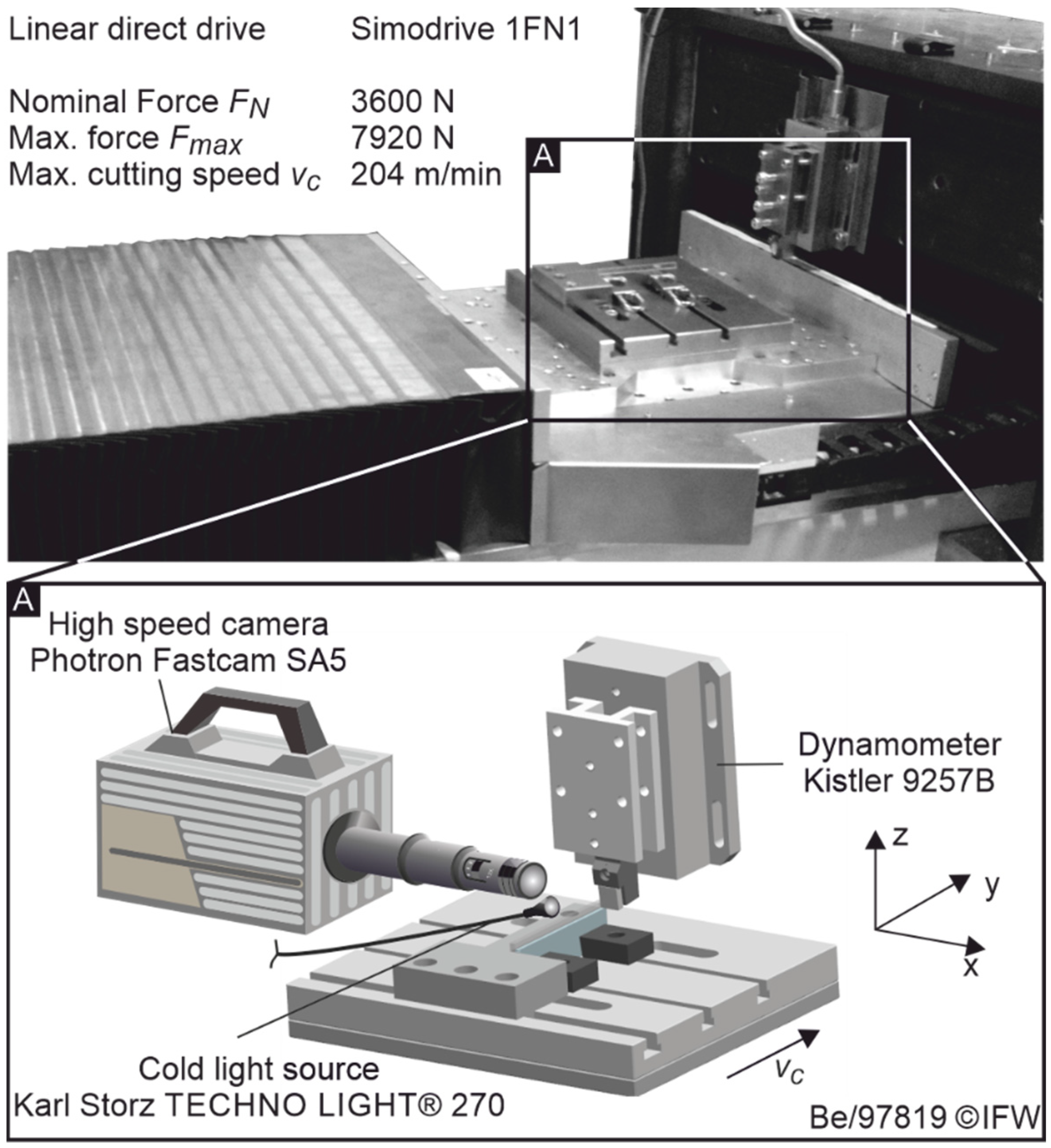
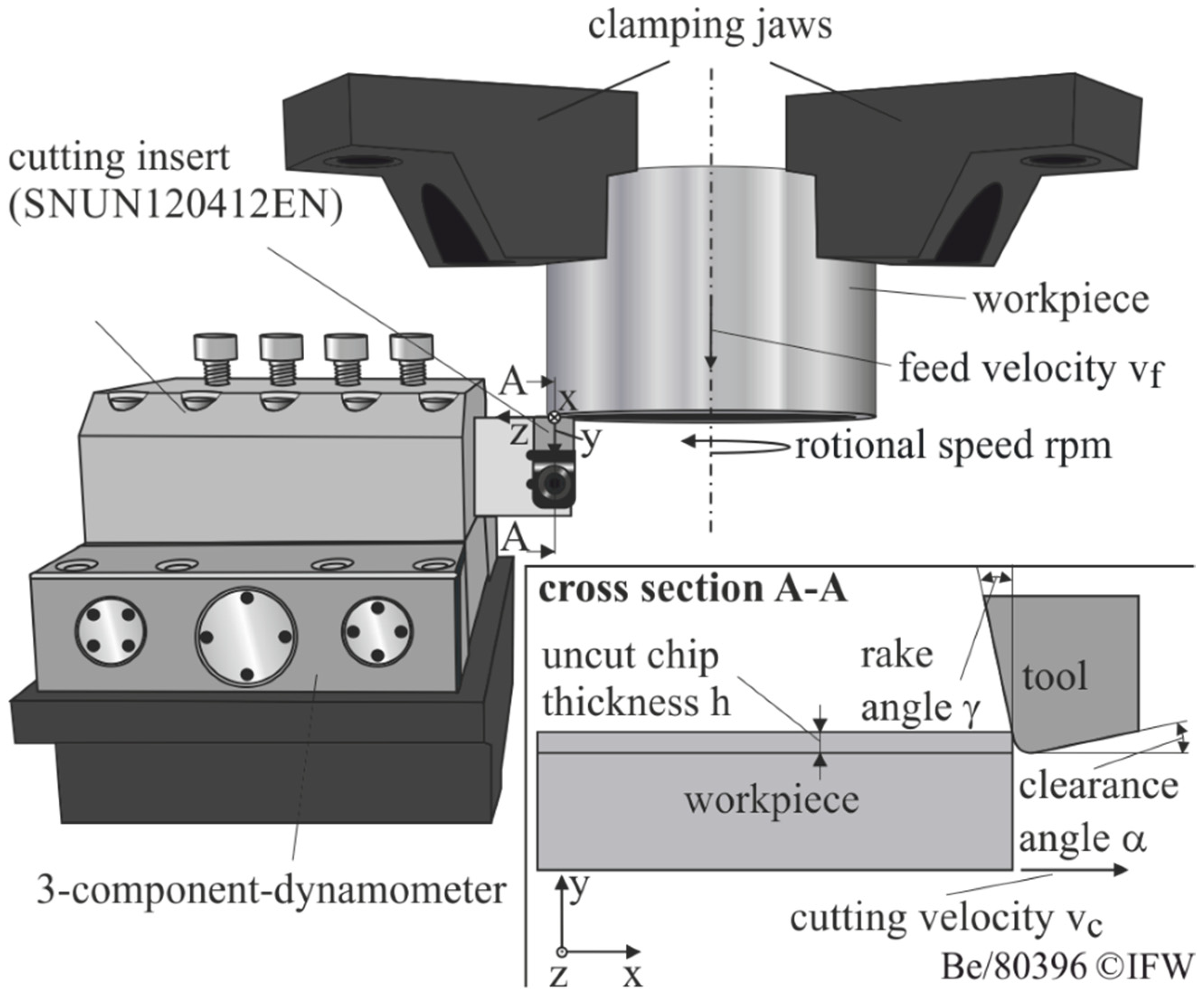
2.1. Experimental Setup
2.1.1. Planing
2.1.2. Turning
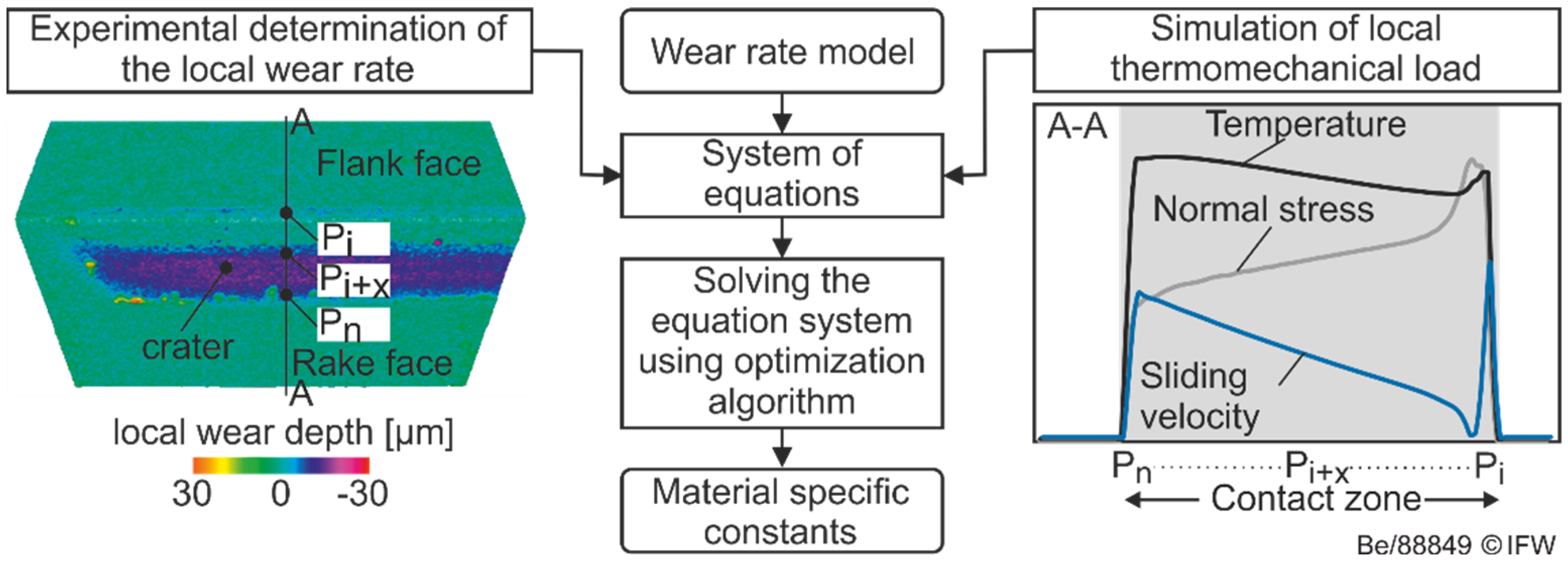
2.2. Simulation Setup
3. Results
3.1. Experimental Results
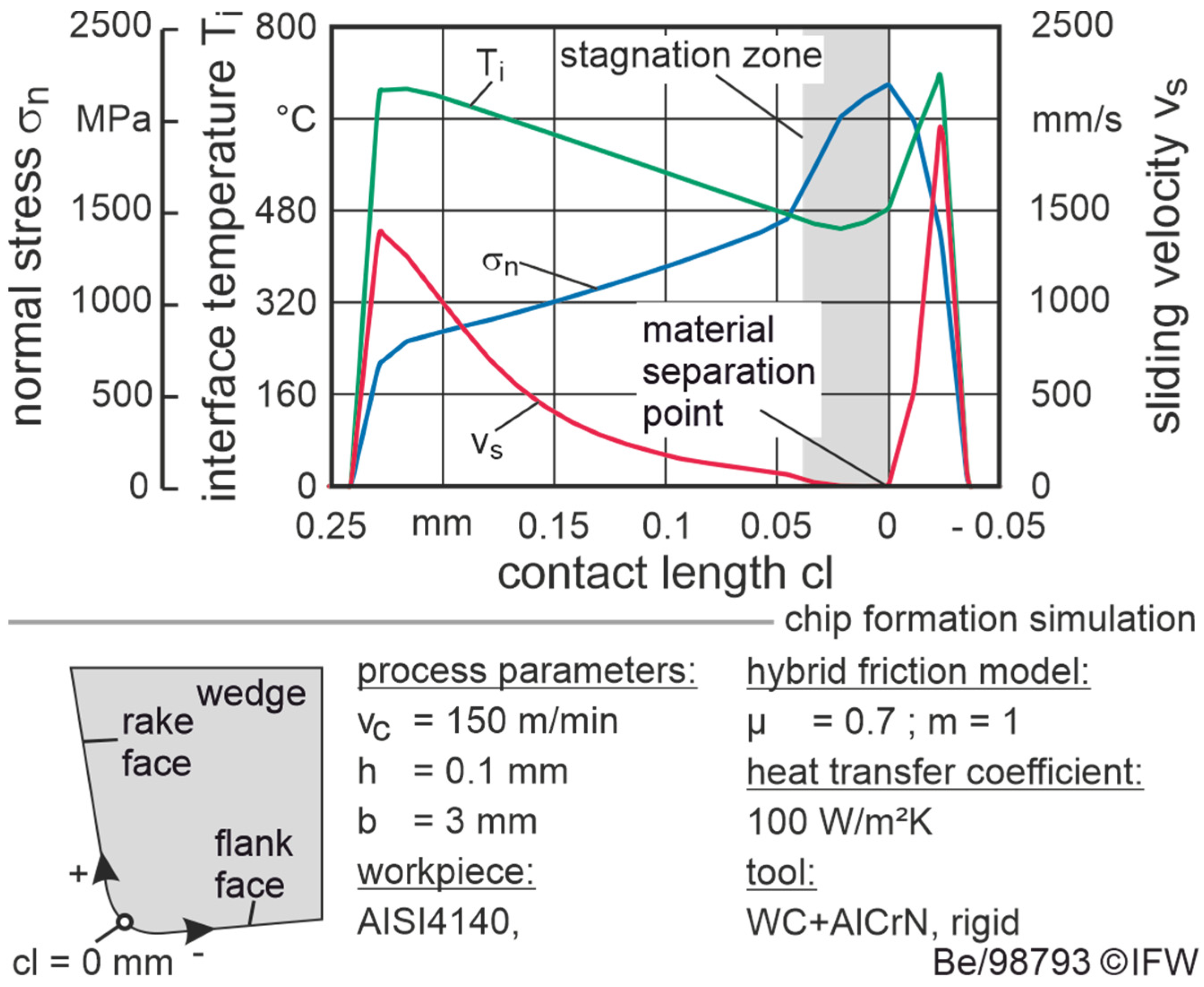
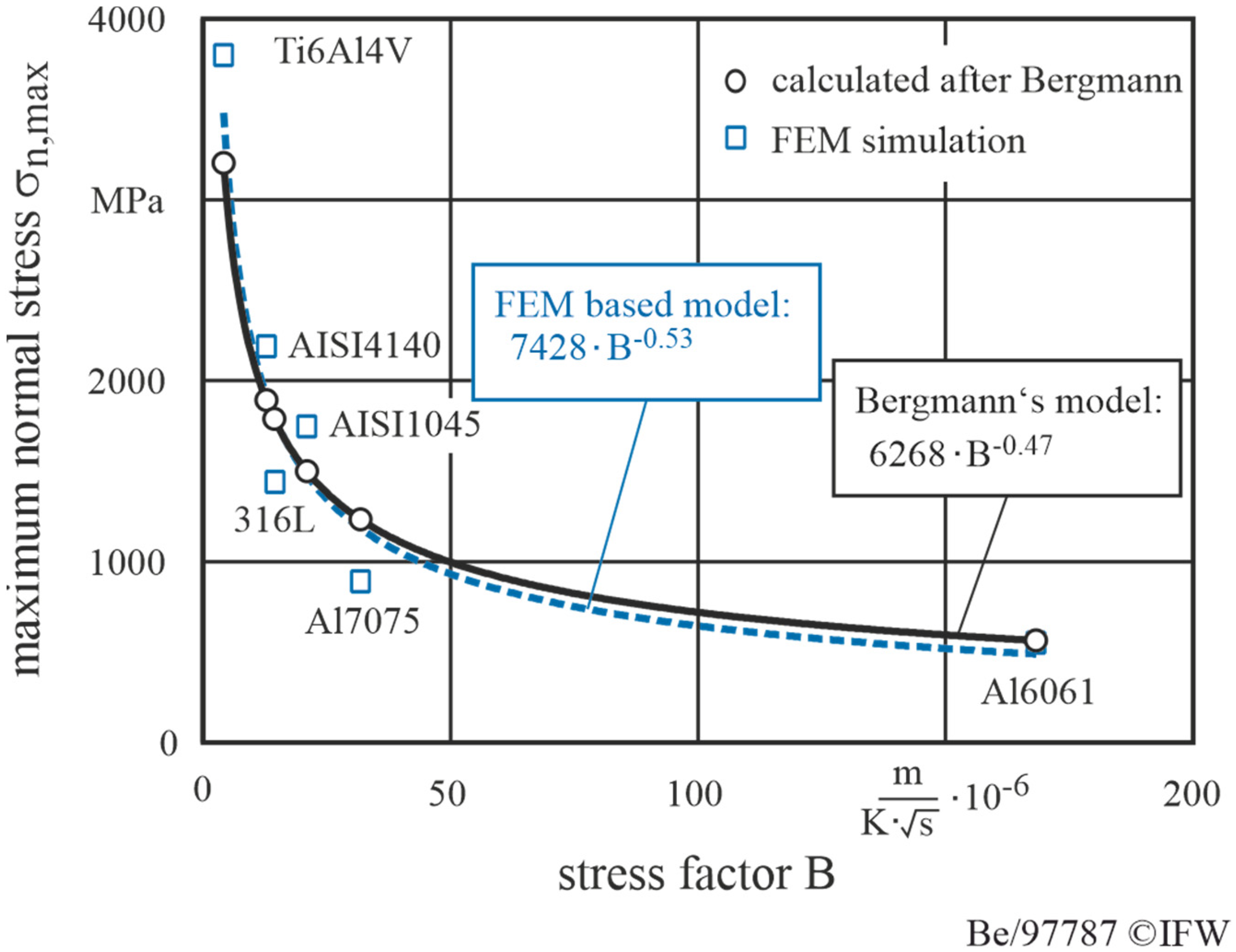
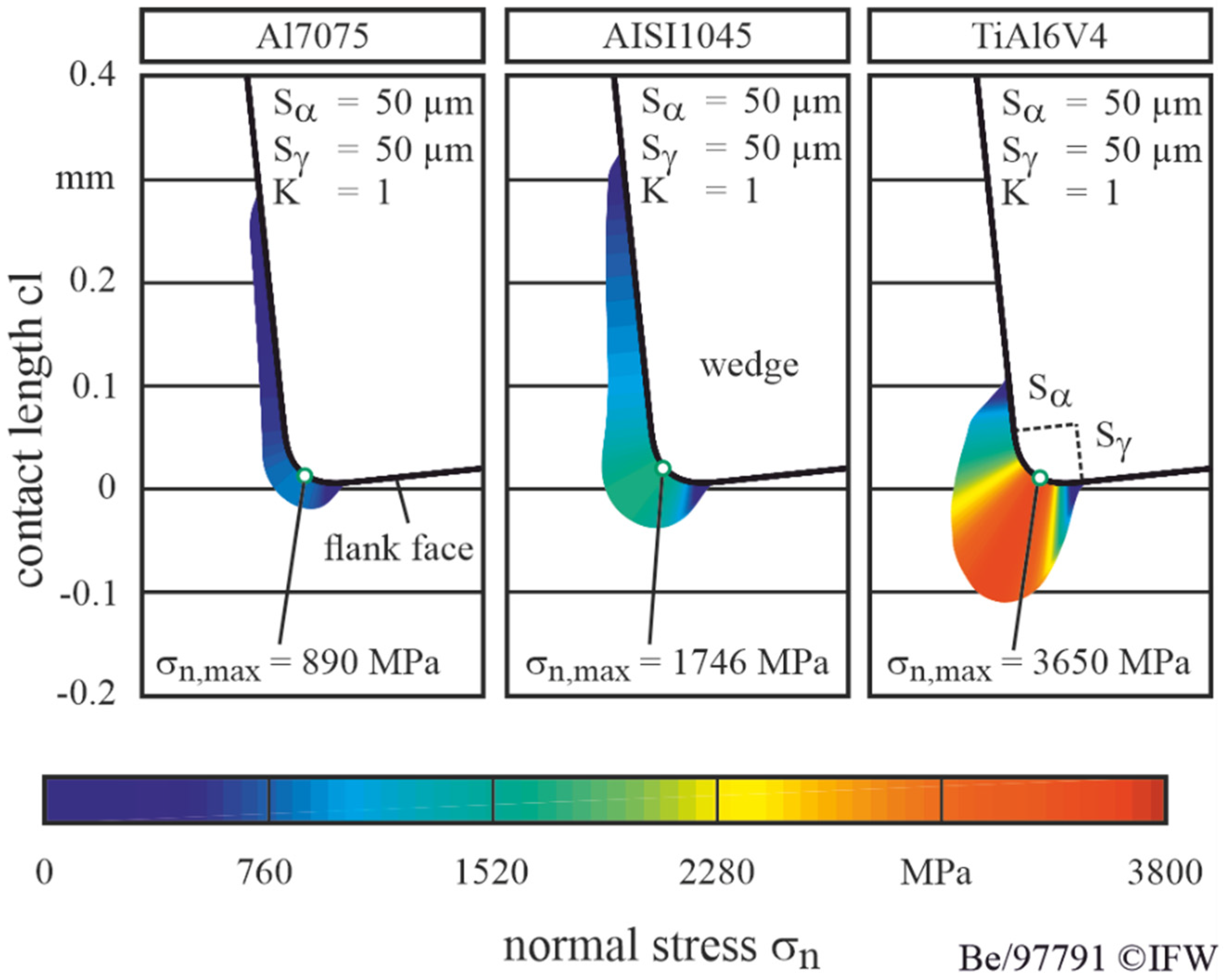
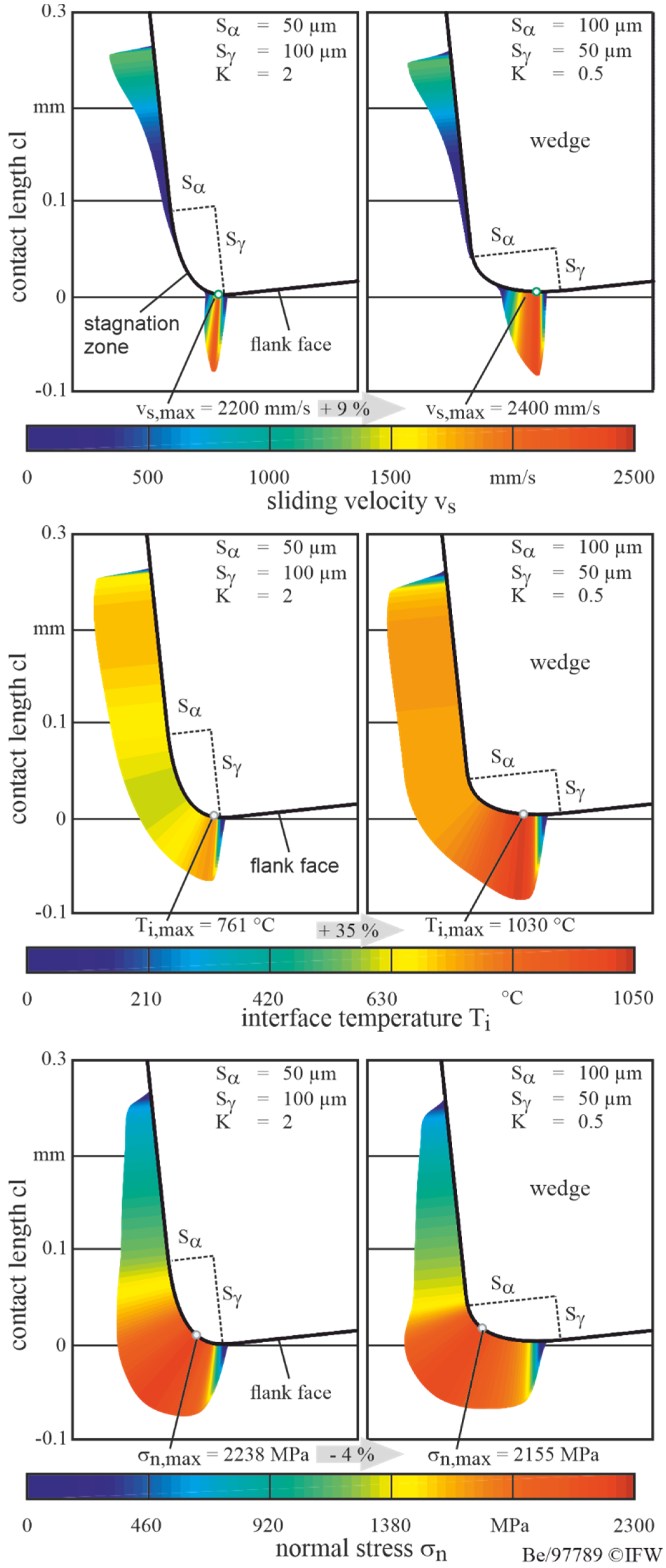
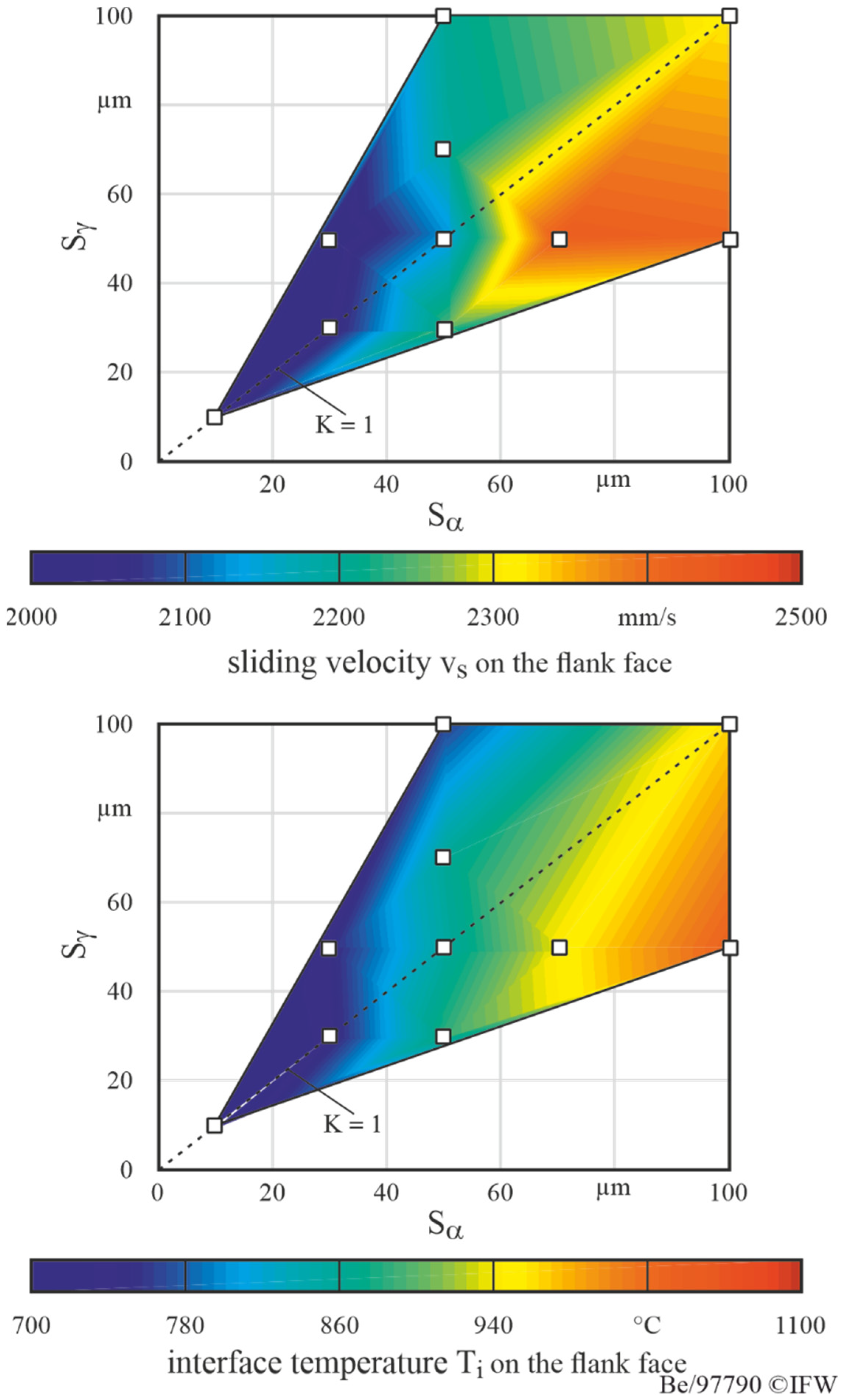
3.2. Simulation Results
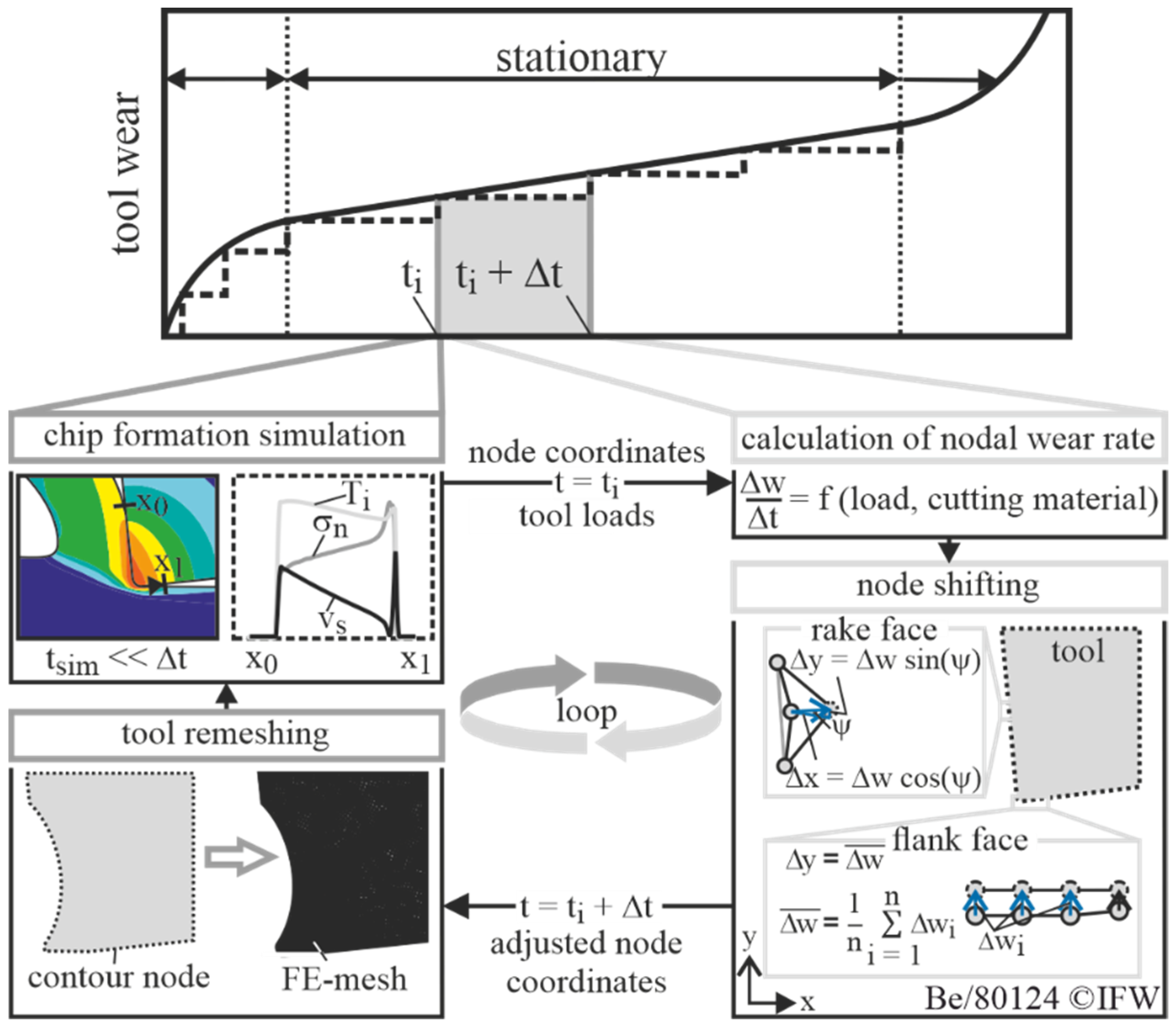
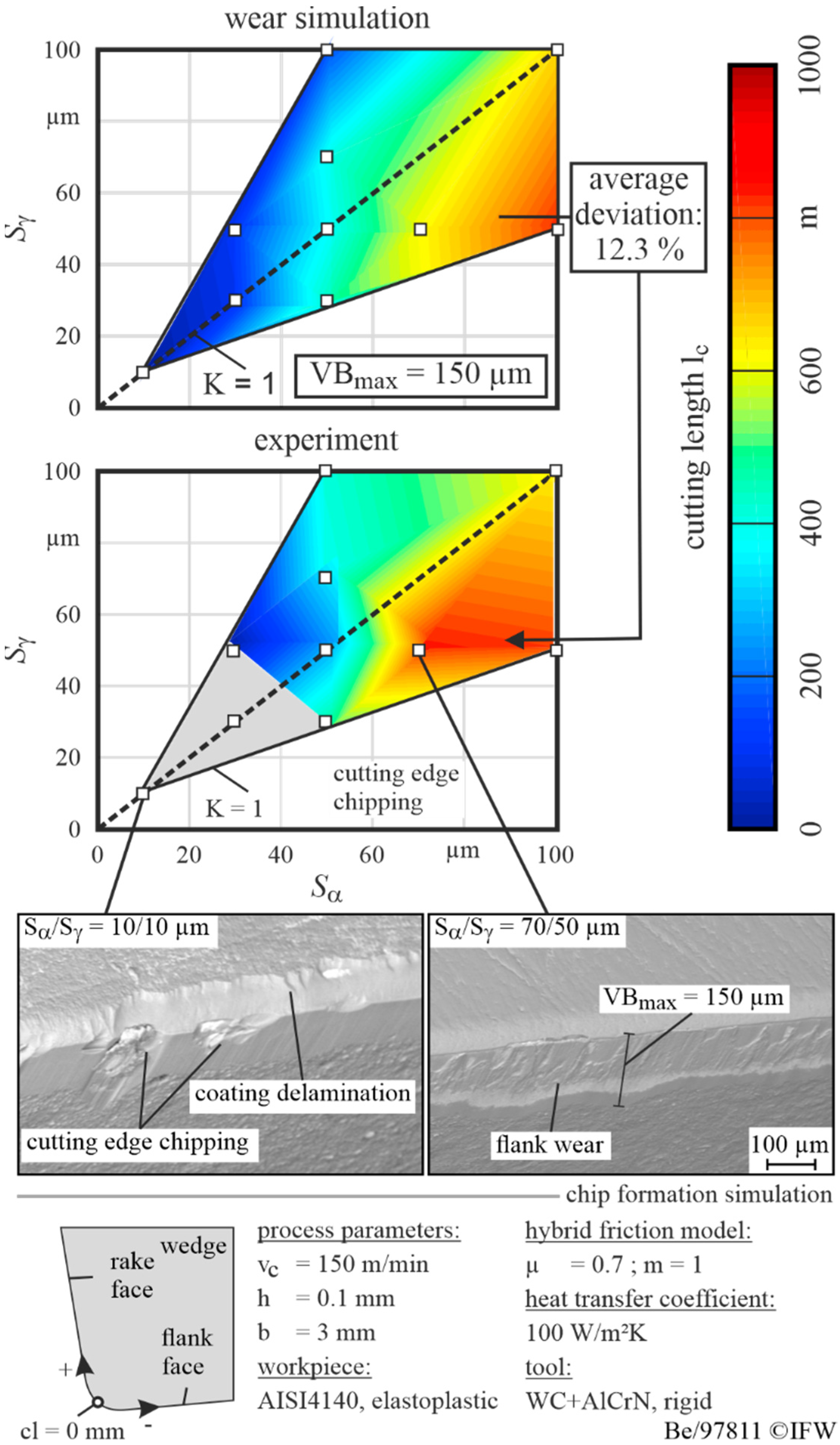
4. Wear Simulation of Rounded Cutting Edges
5. Conclusions
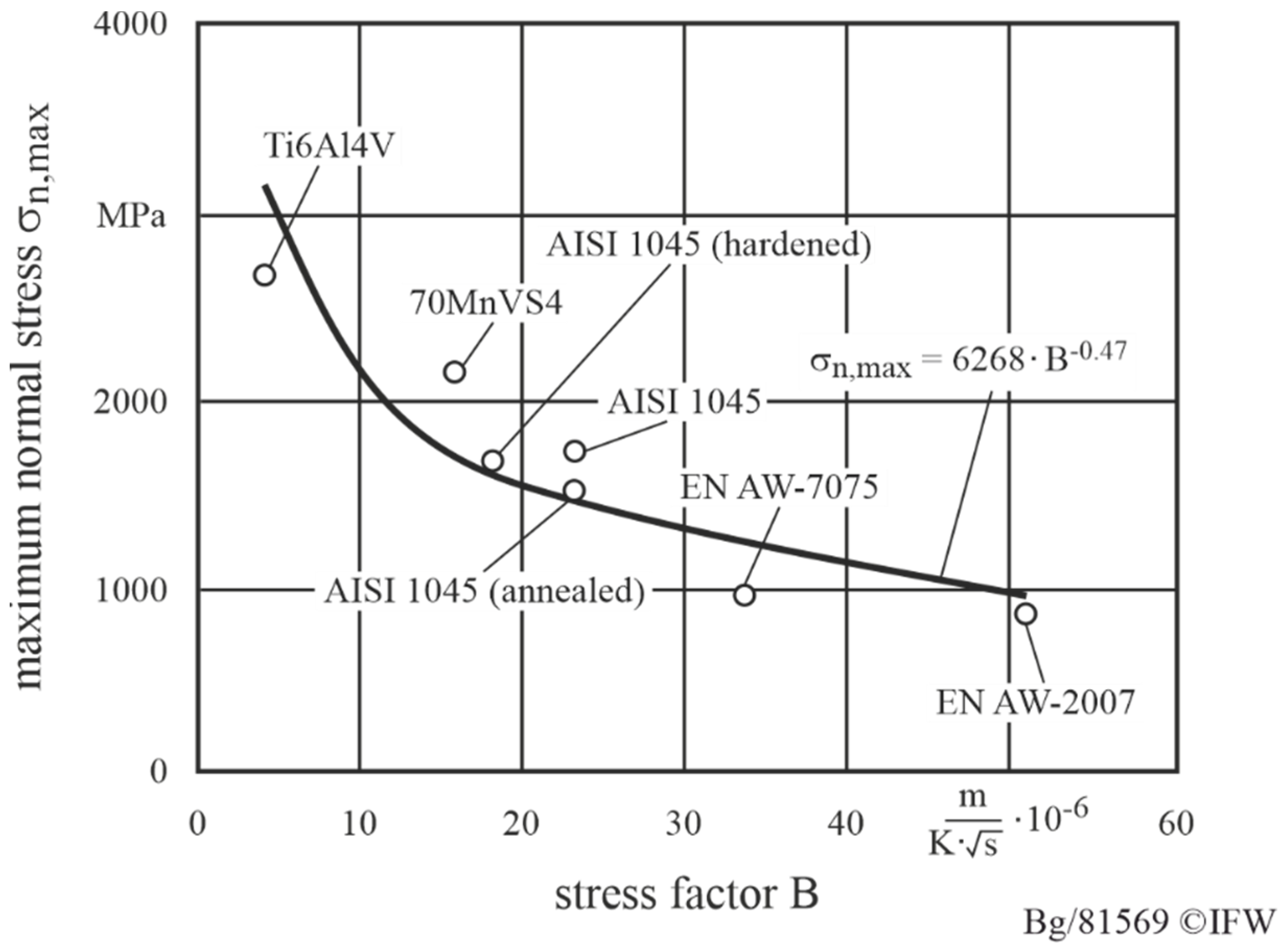
- With regard to the maximum normal stresses, Bergmann’s findings regarding the relationship between the workpiece properties and the normal stresses were confirmed.
- The latter is an essential input variable for common wear rate models for the simulative calculation of tool wear.
- Friction is the main influencing factor on temperature, relative sliding speed and contact length, which significantly influences the wear calculation.
- The use of adapted friction and material models in combination with the discretization of the operating time allows a precise prediction of tool wear.
- A combined approach of a parameterized chip formation simulation and tool wear model allows the calculation of tool wear depending on the used cutting edge rounding.
- As a result, the wear-optimized cutting edge rounding can be determined and evaluated during experimental investigations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Denkena, B.; Biermann, D. Cutting Edge Geometries. CIRP Ann. Manuf. Technol. 2014, 63, 631–653. [Google Scholar] [CrossRef]
- Denkena, B.; Reichstein, M.; Brodehl, J.; de Leon Garcia, L. Surface Preparation, Coating and Wear Performance of Geometrical Defined Cutting Edges. Manuf. Eng. 2005, 5, 43–51. [Google Scholar]
- Wyen, C.-F.; Wegener, K. Influence of cutting edge radius on cutting forces in machining titanium. CIRP Ann. 2010, 59, 93–96. [Google Scholar] [CrossRef]
- Özel, T.; Altan, T. Determination of workpiece flow stress and friction at the chip tool contact for high-speed cutting. Int. J. Mach. Tools Manuf. 2000, 47, 133–152. [Google Scholar] [CrossRef]
- Ulutan, D.; Lazoglu, I.; Dinc, C. Three-dimensional temperature predictions in machining processes using finite difference method. J. Mater. Process. Technol. 2009, 209, 1111–1121. [Google Scholar] [CrossRef]
- Albrecht, P. New Developments in the Theory of the Metal-Cutting Process. The Ploughing Process in Metal Cutting. Trans. ASME 1960, 82, 348–357. [Google Scholar]
- Denkena, B.; Lucas, A.; Bassett, E. Effects of the cutting edge microgeometry on tool wear and its thermo-mechanical load. CIRP Ann. 2011, 60, 73–76. [Google Scholar] [CrossRef]
- Karpat, Y.; Özel, T. Mechanics of high speed cutting with curvilinear edge tools. Int. J. Mach. Tools Manuf. 2008, 48, 195–208. [Google Scholar] [CrossRef]
- Shaw, M.C. Metal Cutting Principles, 2nd ed.; Oxford University Press: New York, NY, USA, 2005. [Google Scholar]
- Biermann, D.; Terwey, I. Cutting edge preparation to improve drilling tools for HPC processes. CIRP J. Manuf. Sci. Technol. 2008, 1, 76–80. [Google Scholar] [CrossRef]
- Aurich, J.C.; Zimmermann, M.; Leitz, L. The preparation of cutting edges using a marking laser. Prod. Eng. 2011, 5, 17–24. [Google Scholar] [CrossRef]
- Shatla, M.; Kerk, C.; Altan, T. Process modeling in machining. Part II: Validation and applications of the determined flow stress data. Int. J. Mach. Tools Manuf. 2001, 41, 1659–1680. [Google Scholar] [CrossRef]
- Bassett, E. Belastungsspezifische Auslegung und Herstellung von Schneidkanten für Drehwerkzeuge. Ph.D. Thesis, Leibniz Universität Hannover, Hanovra, Germany, 2014. [Google Scholar]
- Denkena, B.; Köhler, J.; Mesfin, M. Influence of the cutting edge rounding on the chip formation process. Prod. Eng. 2012, 6, 329–338. [Google Scholar] [CrossRef]
- Heckmann, L. Systematische Analyse der Schneidkantenarchitektur Mithilfe der Finite-Elemente-Methode. Ph.D. Thesis, Universität Kassel, Kassel, Germany, 2010. [Google Scholar]
- Usui, E.; Shirakashi, T.; Kitagawa, T. Analytical prediction of cutting tool wear. Wear 1984, 100, 129–151. [Google Scholar] [CrossRef]
- Yen, Y.-C.; Söhner, J.; Lilly, B.; Altan, T. Estimation of toolwear in orthogonal cutting using the finite element analysis. Int. J. Mach. Sci. Technol. 2004, 146, 82–91. [Google Scholar]
- Tiffe, M.; Aßmuth, R.; Saelzer, J.; Biermann, D. Investigation on cutting edge preparation and FEM assisted optimization of the cutting edge micro shape for machining of nickel-base alloy. Prod. Eng. 2019, 13, 459–467. [Google Scholar] [CrossRef]
- Beblein, S.; Breidenstein, B.; Denkena, B. On the thermal insulation effect of PVD-AlCrN-coated cutting tools in continuous turning of AISI 4140. In Proceedings of the 13th International Conference “THE-A-Coatings” in Manufacturing Engineering 2017, Thessaloniki, Greece, 5–6 October 2017; pp. 53–61. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strain, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Beblein, S.; Breidenstein, B.; Denkena, B.; Pusch, C.; Hoche, M.; Oechsner, M. Thermomechanical coating load in dependence of fundamental coating properties. Procedia CIRP 2017, 58, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Usui, E.; Hirota, A.; Masuko, M. Analytical Prediction of Three Dimensional Cutting Process–Part 3: Cutting Temperature and Crater Wear of Carbide Tool. Trans. ASME 1978, 100, 222–228. [Google Scholar] [CrossRef]
- Bergmann, B.; Grove, T. Basic principles for the design of cutting edge roundings. CIRP Ann. Manuf. Technol. 2018, 67, 73–78. [Google Scholar] [CrossRef]
- Amor, R.B. Thermomechanische Wirkmechanismen und Spanbildung bei der Hochgeschwindigkeitszerspanung. Ph.D. Thesis, Universität Hannover, Hannover, Germany, 2003. [Google Scholar]
- Baehr, H.D.; Stephan, K. Wärmeleitung und–Diffusion. In Wärme-Und Stoffübertragung; Springer: Berlin, Germany, 2013; Volume 8, pp. 121–311. [Google Scholar]
- Bergmann, B. Grundlagen zur Auslegung der Schneidkantenverrundung. Ph.D. Thesis, Leibniz Universität Hannover, Hannover, Germany, 2017. [Google Scholar]
- Zorev, N.N.; Uteschew, M.H. Untersuchung der Kontaktspannungen auf den Arbeitsflächen des Werkzeugs mit einer Schneidenabrundung. Ann. CIRP 1971, 20, 31–32. [Google Scholar]
- Cockroft, M.G.; Latham, D.J. Ductility and the workability of metals. J. Inst. Met. 1968, 96, 33–39. [Google Scholar]
- Breidenstein, B.; Denkena, B.; Heckemeyer, A.; Beblein, S. Correlation between coating properties and thermal load of CrAlN-coated cutting tools. Defect Diffus. Forum 2020, 404, 53–60. [Google Scholar] [CrossRef]
- Denkena, B.; Krödel, A.; Beblein, S. A novel approach to determine the velocity dependency of the friction behavior during machining by means of digital particle image velocimetry (DPIV). Int. J. Manuf. Sci. Technol. 2021, 32, 81–90. [Google Scholar] [CrossRef]
- Binder, M.; Klocke, F.; Lung, D. Tool wear simulation of complex shaped coated cutting tools. Wear 2015, 330–331, 600–607. [Google Scholar] [CrossRef]
- Binder, M.; Klocke, F.; Doebbeler, B. An advanced numerical approach on tool wear simulation for tool and process design in metal cutting. Simul. Model. Pract. Theory 2017, 70, 65–82. [Google Scholar] [CrossRef]
- Binder, M. Mechanismenbasierte Verschleißsimulation zur Integrierten Werkzeug-und Prozessauslegung. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 2017. [Google Scholar]
- Yen, Y.-C.; Söhner, J.; Weule, H.; Schmidt, J.; Altan, T. Estimation of tool wear of carbide tool in orthogonal cutting using the FEM simulation. Int. J. Mach. Sci. Technol. 2002, 6, 467–486. [Google Scholar] [CrossRef]
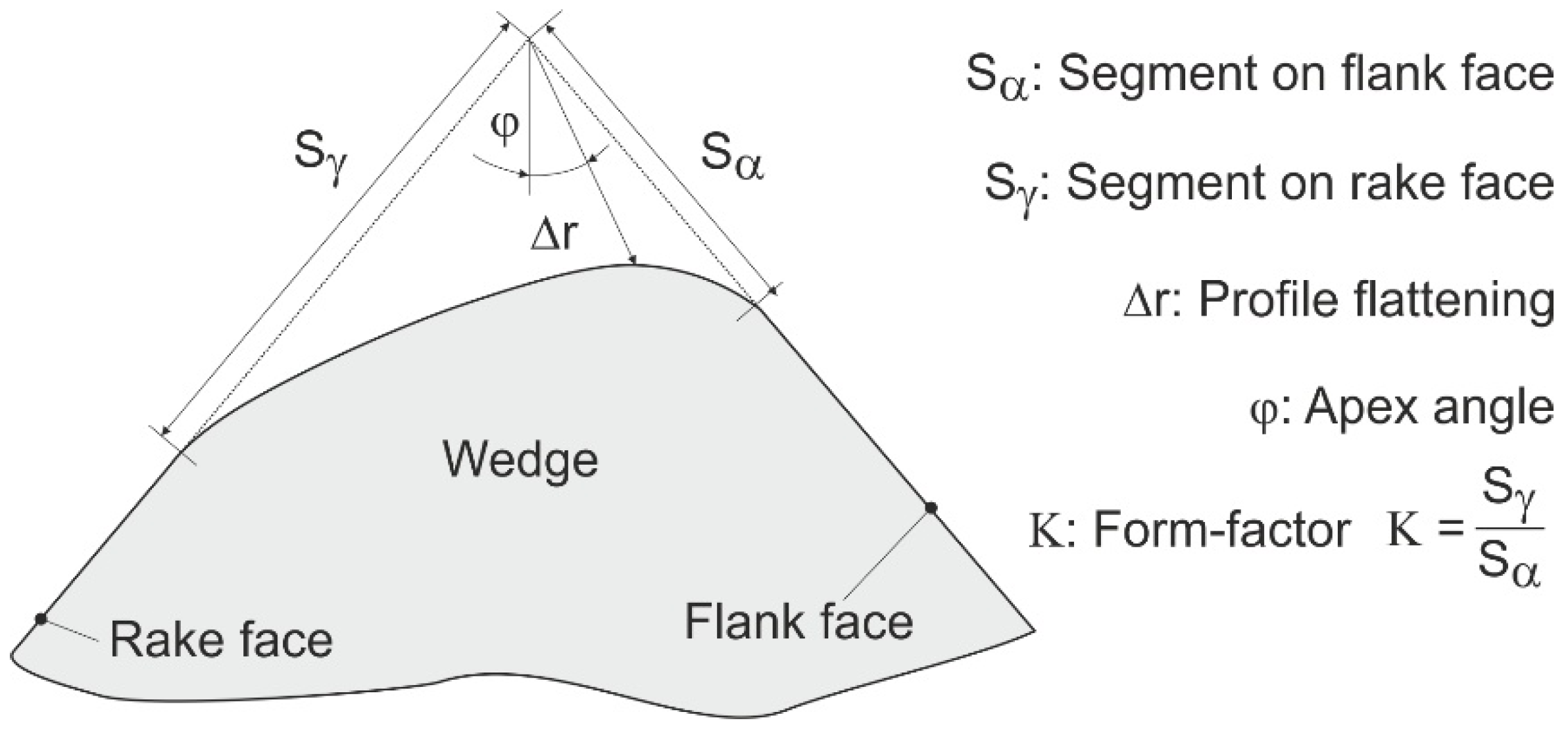


| Cutting Edge Segment | K = 1 | K > 1 | K < 1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sα | 10 | 30 | 50 | 100 | 30 | 50 | 70 | 50 | 70 | 100 |
| Sγ | 10 | 30 | 50 | 100 | 50 | 70 | 100 | 30 | 50 | 70 |
| Workpiece | Tensile Strength (MPa) | Young’s Modulus (GPa) | Poisson’s Ratio | Thermal Expansion (10−6 °C) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 20 °C | 500 °C | 1000 °C | 20 °C | 500 °C | 1000 °C | constant | 20 °C | 500 °C | 1000 °C | |
| Al7075T6 | 540 | 540 | 540 | 68.9 | 68.9 | 68.9 | 0.3 | 22 | 22 | 22 |
| TiAl6V4 | 940 | 855 | 723 | 117 | 90 | 63 | 0.31 | - | - | - |
| AISI4140 | 655 | 594 | 540 | 212 | 175 | 125 | 0.3 | 11.9 | 14.5 | 14.9 |
| Al6061 | 260 | 260 | 260 | 68.9 | 68.9 | 68.9 | 0.3 | - | - | - |
| 316L | 640 | 595 | 550 | 305 | 261 | 227 | 0.3 | 6.6 | 6.8 | 7.4 |
| AISI1045 | 565 | 504 | 445 | 212 | 175 | 125 | 0.3 | 11.9 | 14.5 | 15.1 |
| Workpiece | Thermal Conductivity (W/m·K) | Emissivity | Vol. Heat Capacity (10−6 °C) | ||||
|---|---|---|---|---|---|---|---|
| 20 °C | 500 °C | 1000 °C | constant | 20 °C | 500 °C | 1000 °C | |
| Al7075T6 | 180 | 180 | 180 | 0.7 | 2.4 | 2.4 | 2.4 |
| TiAl6V4 | 7.0 | 13.5 | 17.9 | 0.7 | 2.4 | 2.9 | 4.2 |
| AISI4140 | 41.7 | 36.7 | 34.1 | 0.7 | 3.6 | 5.3 | 6.1 |
| Al6061 | 180 | 180 | 180 | 0.25 | 2.4 | 2.4 | 2.4 |
| 316L | 14 | 21 | 26 | 0.7 | 3.6 | 4.3 | 5.4 |
| AISI1045 | 51.5 | 38.1 | 26.8 | 0.75 | 3.6 | 5.3 | 4.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergmann, B.; Denkena, B.; Beblein, S.; Picker, T. FE-Simulation Based Design of Wear-Optimized Cutting Edge Roundings. J. Manuf. Mater. Process. 2021, 5, 126. https://doi.org/10.3390/jmmp5040126
Bergmann B, Denkena B, Beblein S, Picker T. FE-Simulation Based Design of Wear-Optimized Cutting Edge Roundings. Journal of Manufacturing and Materials Processing. 2021; 5(4):126. https://doi.org/10.3390/jmmp5040126
Chicago/Turabian StyleBergmann, Benjamin, Berend Denkena, Sascha Beblein, and Tobias Picker. 2021. "FE-Simulation Based Design of Wear-Optimized Cutting Edge Roundings" Journal of Manufacturing and Materials Processing 5, no. 4: 126. https://doi.org/10.3390/jmmp5040126
APA StyleBergmann, B., Denkena, B., Beblein, S., & Picker, T. (2021). FE-Simulation Based Design of Wear-Optimized Cutting Edge Roundings. Journal of Manufacturing and Materials Processing, 5(4), 126. https://doi.org/10.3390/jmmp5040126






