A Review on Strain Gradient Plasticity Approaches in Simulation of Manufacturing Processes
Abstract
1. Introduction
- What is an enhanced continuum mechanics model?
- Why such models are required for the simulation of manufacturing operations?
- Which enhanced models of continuum mechanics can be used to simulate manufacturing operations?
- Which contributions can be found in literature that already used enhanced model to simulate manufacturing operations?
2. Challenges in Manufacturing Processes Simulations
- Strain localization in a length scale whose order of magnitude is the same as grain size, therefore violating the limit of validity of material homogeneity;
- Mesh-size hypersensitivity when introducing material softening in the behavior law during the analysis;
- Proper material characterization at high temperatures and high strain rates developing during manufacturing processes;
- The complex material behavior at the tool-workpiece contact location.
2.1. Strain Localization and Mesh-Size Dependency
2.2. Material Characterization at High Temperatures and High Strain Rates
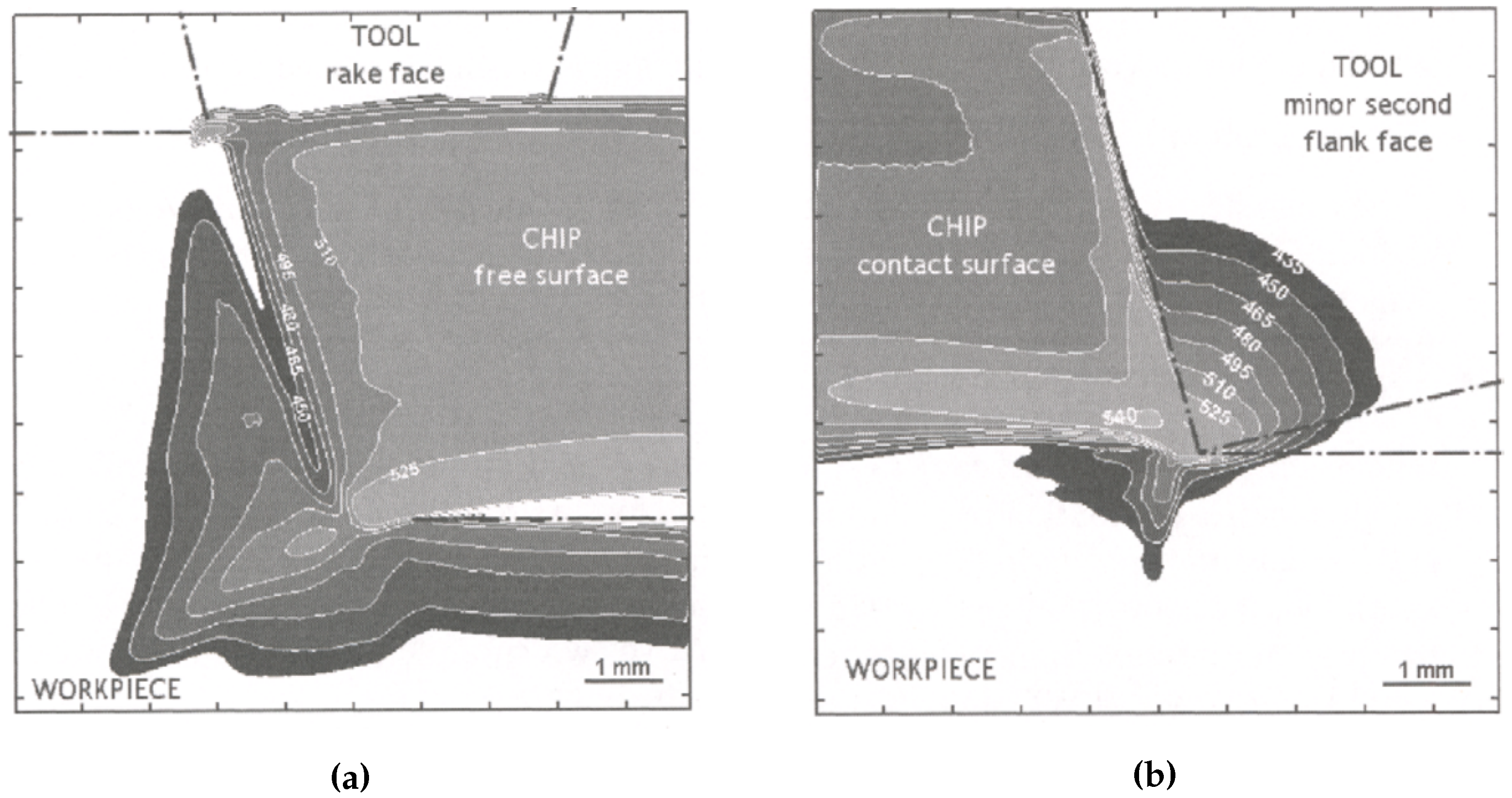
2.3. Tool-Workpiece Contact
3. Historical Excursus of SGPTs in Literature
3.1. Aifantis’ Theory
3.2. Gradient of the Local Spin Vector—Fleck and Hutchinson 1993
3.3. Second Gradient of Displacement—Fleck and Hutchinson 1997
3.4. Gradient of the Cumulative Plastic Strain—Fleck and Hutchinson 2001
3.5. Irrotational Plastic Flow and Burgers Tensor—Gurtin and Anand 2005
3.6. The Common Framework—Gudmundson 2004
3.7. Dislocations-Enriched SGT
3.8. Gradient of Micro-Structure Rotation—Cosserat Media
3.9. Gradient of Micro-Structure Deformation—Micromorphic Media
4. Reported Applications of SGPTs in Manufacturing Processes Simulation
4.1. Scalar SGPT Applied to Flat Punch Molding
4.2. SGPT Used to Model Rolling at Small Scale
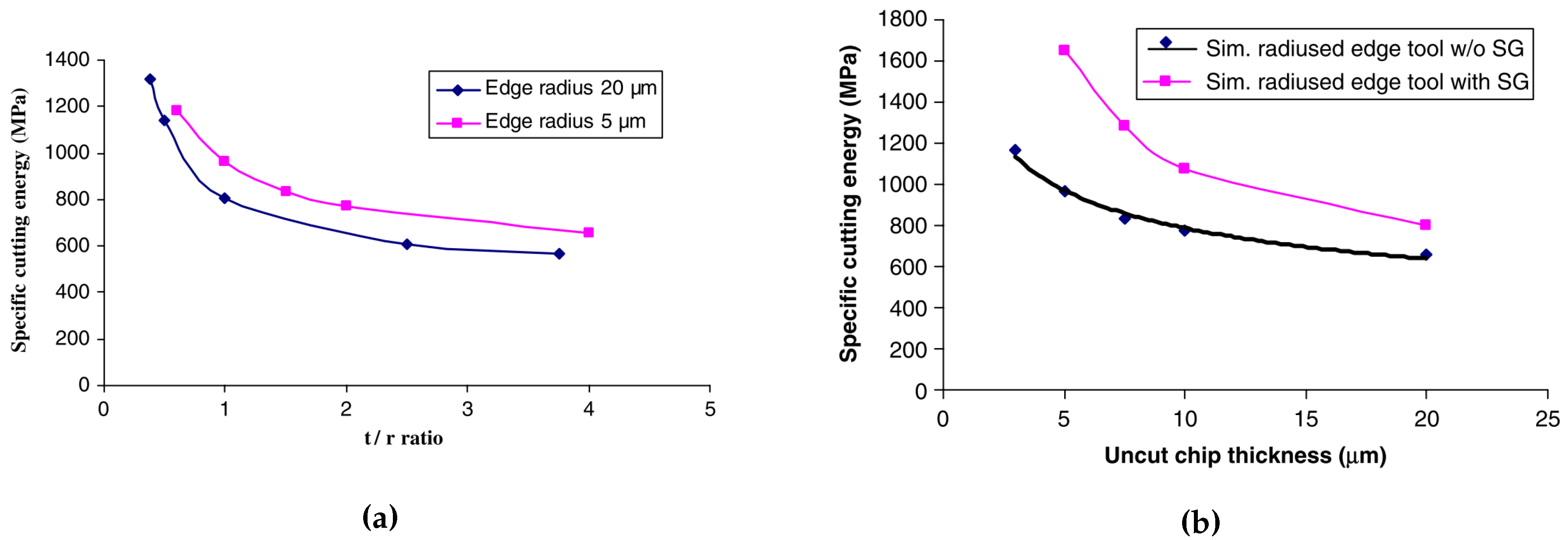
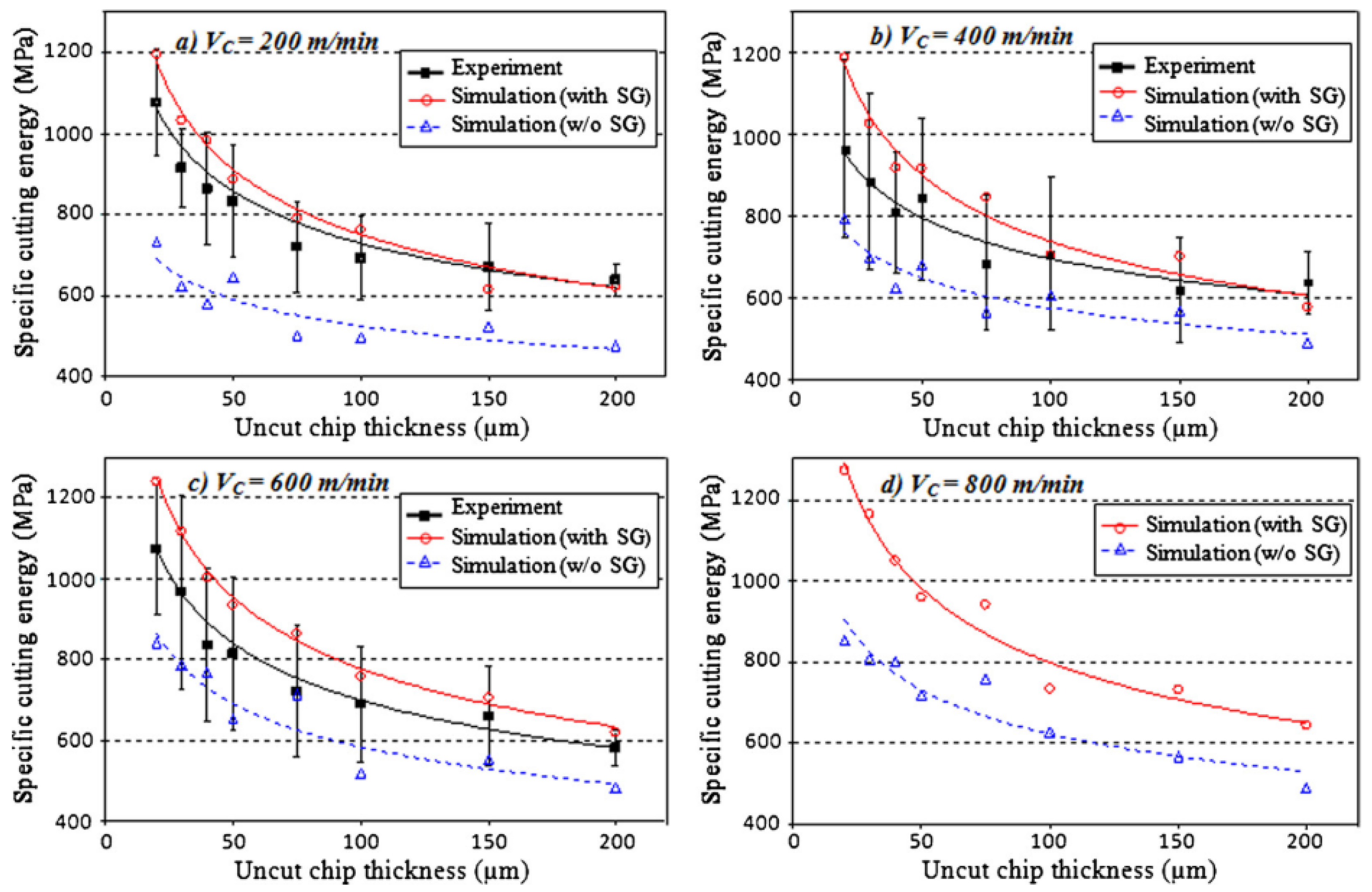
4.3. MSGT Applied to Orthogonal Cutting
4.4. Micromorphic Media Applied to Forming
5. Conclusions
- The forces/moments used to shear/shape the continuum localize in areas that are comparable to the grain size of the metal; in this case a further hardening due to the dislocations movement must be properly captured by adopting a SGPT;
- The velocity with which the continuum is deformed might induce material to behave viscously, and this must be covered by a proper design of the material behavior;
- The temperature developed during the process might be relatively high, and this imposes to considerate the thermal behavior (often adiabatic) that are taken into account by the definition of a thermodynamically-consistent description of the continuum;
- Implementation-wise if the plastic deformation is expected to occur at the boundaries, a higher degree theory is favorable.
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Notation
Appendix B. Methodology Used to Prepare the Review
References
- Joshi, S.S.; Melkote, S.N. An Explanation for the Size-Effect in Machining Using Strain Gradient Plasticity. J. Manuf. Sci. Eng. 2004, 126, 679. [Google Scholar] [CrossRef]
- Royer, R.; Darnis, P.; Laheurte, R.; Gérard, A.; Cahuc, O. Finite strain gradient plasticity theory for high speed machining. Procedia Eng. 2011, 10, 2312–2317. [Google Scholar] [CrossRef][Green Version]
- Voyiadjis, G.Z.; Deliktas, B. Formulation of strain gradient plasticity with interface energy in a consistent thermodynamic framework. Int. J. Plast. 2009, 25, 1997–2024. [Google Scholar] [CrossRef]
- Wu, J.; Liu, Z. Modeling of flow stress in orthogonal micro-cutting process based on strain gradient plasticity theory. Int. J. Adv. Manuf. Technol. 2010, 46, 143–149. [Google Scholar] [CrossRef]
- Huang, J.; Kalaitzidou, K.; Sutherland, J.W.; Milligan, W.W.; Aifantis, E.C.; Sievert, R.; Forest, S. Gradient Plasticity: Implications to Chip Formation in Machining. In Proceedings of the 4th International ESAFORM Conference on Material Forming, Liege, Belgium, 23–25 April 2001; pp. 527–530. [Google Scholar]
- Laheurte, R.; Cahuc, O.; Darnis, P.; Gerard, A. Behaviour law for cutting process. Int. J. Adv. Manuf. Technol. 2006, 29, 17–23. [Google Scholar] [CrossRef]
- Cahuc, O.; Darnis, P.; Laheurte, R. Mechanical and Thermal Experiments in Cutting Process for New Behaviour Law. Int. J. Form. Process. 2007, 10, 235–269. [Google Scholar] [CrossRef]
- Liu, K.; Melkote, S.N. Finite element analysis of the influence of tool edge radius on size effect in orthogonal micro-cutting process. Int. J. Mech. Sci. 2007, 49, 650–660. [Google Scholar] [CrossRef]
- Wang, X.B. Adiabatic Shear Localization for Steels Based on Johnson–Cook Model and Second- and Fourth-Order Gradient Plasticity Models. J. Iron Steel Res. Int. 2007, 14, 56–61. [Google Scholar] [CrossRef]
- Demir, E. A Taylor-based plasticity model for orthogonal machining of single-crystal FCC materials including frictional effects. Int. J. Adv. Manuf. Technol. 2009, 40, 847–856. [Google Scholar] [CrossRef]
- Jing, X.B.; Lin, B.; Zhang, D.W. Modeling and analysis of factors of size effect in micro-cutting: The tool geometry and the depth of cutting. In Proceedings of the 2013 International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO 2013), Suzhou, China, 26–30 August 2013; pp. 314–318. [Google Scholar] [CrossRef]
- Molinari, A.; Musquar, C.; Sutter, G. Adiabatic shear banding in high speed machining of Ti-6Al-4V: Experiments and modeling. Int. J. Plast. 2002, 18, 443–459. [Google Scholar] [CrossRef]
- Ye, G.G.; Chen, Y.; Xue, S.F.; Dai, L.H. Critical cutting speed for onset of serrated chip flow in high speed machining. Int. J. Mach. Tools Manuf. 2014, 86, 18–33. [Google Scholar] [CrossRef]
- Dixit, U.S.; Joshi, S.N.; Davim, J.P. Incorporation of material behavior in modeling of metal forming and machining processes: A review. Mater. Des. 2011, 32, 3655–3670. [Google Scholar] [CrossRef]
- Tang, B.; Xiang, L.; Cheng, L.; Liu, D.; Kou, H.; Li, J. The formation and evolution of shear bands in plane strain compressed nickel-base superalloy. Metals 2018, 8, 141. [Google Scholar] [CrossRef]
- Calamaz, M.; Coupard, D.; Girot, F. A new material model for 2D numerical simulation of serrated chip formation when machining titanium alloy Ti-6Al-4V. Int. J. Mach. Tools Manuf. 2008, 48, 275–288. [Google Scholar] [CrossRef]
- List, G.; Sutter, G.; Bi, X.F.; Molinari, A.; Bouthiche, A. Strain, strain rate and velocity fields determination at very high cutting speed. J. Mater. Process. Technol. 2013, 213, 693–699. [Google Scholar] [CrossRef]
- Lee, S.; Hwang, J.; Ravi Shankar, M.; Chandrasekar, S.; Compton, W.D. Large strain deformation field in machining. Metall. Mater. Trans. A: Phys. Metall. Mater. Sci. 2006, 37, 1633–1643. [Google Scholar] [CrossRef]
- Chinesta, F.; Ladeveze, P.; Cueto, E. A Short Review on Model Order Reduction Based on Proper Generalized Decomposition. Arch. Comput. Methods Eng. 2011, 18, 395–404. [Google Scholar] [CrossRef]
- Fleck, N.A.; Hutchinson, J.W. Strain Gradient Plasticity. Adv. Appl. Mech. 1997, 33, 295–361. [Google Scholar] [CrossRef]
- Stölken, J.S.; Evans, A.G. A microbend test method for measuring the plasticity length scale. Acta Mater. 1998, 46, 5109–5115. [Google Scholar] [CrossRef]
- Begley, M.R.; Hutchinson, J.W. The mechanics of size-dependent indentation. J. Mech. Phys. Solids 1998, 46, 2049–2068. [Google Scholar] [CrossRef]
- Poole, W.; Ashby, M.; Fleck, N. Micro-hardness of annealed and work-hardened copper polycrystals. Scr. Mater. 1996, 34, 559–564. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Ma, Q.; Clarke, D.R. Size dependent hardness of silver single crystals. J. Mater. Res. 1995, 10, 853–863. [Google Scholar] [CrossRef]
- González, D.; Alkorta, J.; Martínez-Esnaola, J.M.; Gil Sevillano, J. Numerical analysis of the indentation size effect using a strain gradient crystal plasticity model. Comput. Mater. Sci. 2014, 82, 314–319. [Google Scholar] [CrossRef]
- Stelmashenko, N.A.; Walls, M.G.; Brown, L.M.; Milman, Y.V. Microindentations on W and Mo oriented single crystals: An STM study. Acta Metall. Mater. 1993, 41, 2855–2865. [Google Scholar] [CrossRef]
- Panteghini, A.; Bardella, L. On the Finite Element implementation of higher-order gradient plasticity, with focus on theories based on plastic distortion incompatibility. Comput. Methods Appl. Mech. Eng. 2016, 310, 840–865. [Google Scholar] [CrossRef]
- Han, C.S.; Ma, A.; Roters, F.; Raabe, D. A Finite Element approach with patch projection for strain gradient plasticity formulations. Int. J. Plast. 2007, 23, 690–710. [Google Scholar] [CrossRef]
- Dahlberg, C.F.; Faleskog, J. An improved strain gradient plasticity formulation with energetic interfaces: Theory and a fully implicit finite element formulation. Comput. Mech. 2013, 51, 641–659. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 2011, 48, 1962–1990. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Anand, L. A theory of strain-gradient plasticity for isotropic, plastically irrotational materials. Part II: Finite deformations. Int. J. Plast. 2005, 21, 2297–2318. [Google Scholar] [CrossRef]
- Liu, D.; Dunstan, D.J. Material length scale of strain gradient plasticity: A physical interpretation. Int. J. Plast. 2017, 98, 156–174. [Google Scholar] [CrossRef]
- Al-Rub, R.K.A.; Voyiadjis, G.Z. Determination of the Material Intrinsic Length Scale of Gradient Plasticity Theory. Int. J. Multiscale Comput. Eng. 2005, 2, 377–400. [Google Scholar] [CrossRef]
- Duan, D.M.; Wu, N.Q.; Slaughter, W.S.; Mao, S.X. Length scale effect on mechanical behavior due to strain gradient plasticity. Mater. Sci. Eng. A 2001, 303, 241–249. [Google Scholar] [CrossRef]
- Aifantis, E.C. Strain gradient interpretation of size effects. Int. J. Fract. 1999, 95, 299–314. [Google Scholar] [CrossRef]
- Liu, D.; He, Y.; Dunstan, D.J.; Zhang, B.; Gan, Z.; Hu, P.; Ding, H. Toward a further understanding of size effects in the torsion of thin metal wires: An experimental and theoretical assessment. Int. J. Plast. 2013, 41, 30–52. [Google Scholar] [CrossRef]
- Liu, D.; He, Y.; Dunstan, D.J.; Zhang, B.; Gan, Z.; Hu, P.; Ding, H. Anomalous plasticity in the cyclic torsion of micron scale metallic wires. Phys. Rev. Lett. 2013, 110, 1–5. [Google Scholar] [CrossRef]
- Ehrler, B.; Hou, X.D.; Zhu, T.T.; P’Ng, K.M.; Walker, C.J.; Bushby, A.J.; Dunstan, D.J. Grain size and sample size interact to determine strength in a soft metal. Philos. Mag. 2008, 88, 3043–3050. [Google Scholar] [CrossRef]
- Dunstan, D.J.; Ehrler, B.; Bossis, R.; Joly, S.; P’Ng, K.M.; Bushby, A.J. Elastic Limit and Strain Hardening of Thin Wires in Torsion. Phys. Rev. Lett. 2009, 103, 1–4. [Google Scholar] [CrossRef]
- Fleck, N.A.; Muller, G.M.; Ashby, M.F.; Hutchinson, J.W. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Fleck, N.A.; Hutchinson, J.W. A reformulation of strain gradient plasticity. J. Mech. Phys. Solids 2001, 49, 2245–2271. [Google Scholar] [CrossRef]
- Dahlberg, C.F.; Boåsen, M. Evolution of the length scale in strain gradient plasticity. Int. J. Plast. 2019, 112, 220–241. [Google Scholar] [CrossRef]
- Zhang, X.; Aifantis, K. Interpreting the internal length scale in strain gradient plasticity. Rev. Adv. Mater. Sci. 2015, 41, 72–83. [Google Scholar]
- Yuan, H.; Chen, J. Identification of the intrinsic material length in gradient plasticity theory from micro-indentation tests. Int. J. Solids Struct. 2001, 38, 8171–8187. [Google Scholar] [CrossRef]
- Abu Al-Rub, R.K.; Voyiadjis, G.Z. Analytical and experimental determination of the material intrinsic length scale of strain gradient plasticity theory from micro- and nano-indentation experiments. Int. J. Plast. 2004, 20, 1139–1182. [Google Scholar] [CrossRef]
- De Borst, R.; Mühlhaus, H.B. Gradient-dependent plasticity: Formulation and algorithmic aspects. Int. J. Numer. Methods Eng. 1992, 35, 521–539. [Google Scholar] [CrossRef]
- Benallal, A.; Berstad, T.; Børvik, T.; Hopperstad, O.S. Uniqueness, loss of ellipticity and localization for the time-discretized, rate-dependent boundary value problem with softening. Int. J. Numer. Methods Eng. 2010, 84, 864–882. [Google Scholar] [CrossRef]
- Wcisło, B.; Pamin, J.; Kowalczyk-Gajewska, K.; Menzel, A. Numerical analysis of ellipticity condition for large strain plasticity. AIP Conf. Proc. 2018, 1922. [Google Scholar] [CrossRef]
- Jirásek, M.; Rolshoven, S. Localization properties of strain-softening gradient plasticity models. Part I: Strain-gradient theories. Int. J. Solids Struct. 2009, 46, 2225–2238. [Google Scholar] [CrossRef]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Ration. Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Chambon, R.; Caillerie, D.; El Hassan, N. One-dimensional localisation studied with a second grade model. Eur. J. Mech. A/Solids 1998, 17, 637–656. [Google Scholar] [CrossRef]
- Qiu, X.; Huang, Y.; Wei, Y.; Gao, H.; Hwang, K.C. The flow theory of mechanism-based strain gradient plasticity. Mech. Mater. 2003, 35, 245–258. [Google Scholar] [CrossRef]
- Nguyen, G.D.; Korsunsky, A.M.; Belnoue, J.P. A nonlocal coupled damage-plasticity model for the analysis of ductile failure. Int. J. Plast. 2015, 64, 56–75. [Google Scholar] [CrossRef]
- Lele, S.P.; Anand, L. A large-deformation strain-gradient theory for isotropic viscoplastic materials. Int. J. Plast. 2009, 25, 420–453. [Google Scholar] [CrossRef]
- Mediavilla, J.; Peerlings, R.H.; Geers, M.G. An integrated continuous-discontinuous approach towards damage engineering in sheet metal forming processes. Eng. Fract. Mech. 2006, 73, 895–916. [Google Scholar] [CrossRef]
- Brepols, T.; Wulfinghoff, S.; Reese, S. Gradient-extended two-surface damage-plasticity: Micromorphic formulation and numerical aspects. Int. J. Plast. 2017, 97, 64–106. [Google Scholar] [CrossRef]
- Saanouni, K.; Hamed, M. Micromorphic approach for finite gradient-elastoplasticity fully coupled with ductile damage: Formulation and computational aspects. Int. J. Solids Struct. 2013, 50, 2289–2309. [Google Scholar] [CrossRef]
- Peerlings, R.H.J.; De Borst, R.; Brekelmans, W.A.M.; De Vree, J.H.P. Gradient Enhanced Damage for Quasi-brittle Materials. Int. J. Numer. Methods Eng. 1996, 39, 3391–3403. [Google Scholar] [CrossRef]
- Sabet, S.A.; de Borst, R. Structural softening, mesh dependence, and regularisation in non-associated plastic flow. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 2170–2183. [Google Scholar] [CrossRef]
- Mazière, M.; Forest, S. Strain gradient plasticity modeling and finite element simulation of Lüders band formation and propagation. Contin. Mech. Thermodyn. 2013, 27, 83–104. [Google Scholar] [CrossRef]
- Ling, C.; Forest, S.; Besson, J.; Tanguy, B.; Latourte, F. A reduced micromorphic single crystal plasticity model at finite deformations. Application to strain localization and void growth in ductile metals. Int. J. Solids Struct. 2018, 134, 43–69. [Google Scholar] [CrossRef]
- Forest, S. Micromorphic Approach for Gradient Elasticity, Viscoplasticity, and Damage. J. Eng. Mech. 2009, 135, 117–131. [Google Scholar] [CrossRef]
- Peirs, J.; Verleysen, P.; Degrieck, J.; Coghe, F. The use of hat-shaped specimens to study the high strain rate shear behaviour of Ti-6Al-4V. Int. J. Impact Eng. 2010, 37, 703–714. [Google Scholar] [CrossRef]
- Marchand, A.; Duffy, J. An experimental study of the formation process of adiabatic shear bands in a structural steel. J. Mech. Phys. Solids 1988, 36, 251–283. [Google Scholar] [CrossRef]
- Rahmaan, T.; Zhou, P.; Butcher, C.; Worswick, M.J. Strain rate and thermal softening effects in shear testing of AA7075-T6 sheet. EPJ Web Conf. 2018, 183, 02037. [Google Scholar] [CrossRef]
- Chen, G.; Ren, C.; Yang, X.; Jin, X.; Guo, T. Finite element simulation of high-speed machining of titanium alloy (Ti-6Al-4V) based on ductile failure model. Int. J. Adv. Manuf. Technol. 2011, 56, 1027–1038. [Google Scholar] [CrossRef]
- Astakov, V. (Ed.) Tribology and Interface Engineering Series. In Tribology of Metal Cutting, 1st ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2006; Chapter 3; pp. 124–219. [Google Scholar] [CrossRef]
- Zorev, N. Inter-relationship between shear processes occurring along tool face and shear plane in metal cutting. Int. Res. Prod. Eng. 1963, 49, 143–152. [Google Scholar]
- Shirakashi, T.; Usui, E. Friction Characteristics on Tool Face in Metal Machining. J. Jpn. Soc. Precis. Eng. 1973, 39, 966–972. [Google Scholar] [CrossRef]
- Childs, T.H. Friction modelling in metal cutting. Wear 2006, 260, 310–318. [Google Scholar] [CrossRef]
- Bahi, S.; Nouari, M.; Moufki, A.; Mansori, M.E.; Molinari, A. Hybrid modelling of sliding-sticking zones at the tool-chip interface under dry machining and tool wear analysis. Wear 2012, 286–287, 45–54. [Google Scholar] [CrossRef]
- Bahi, S.; Nouari, M.; Moufki, A.; El Mansori, M.; Molinari, A. A new friction law for sticking and sliding contacts in machining. Tribol. Int. 2011, 44, 764–771. [Google Scholar] [CrossRef]
- Ackroyd, B.; Chandrasekar, S.; Compton, W.D. A Model for the Contact Conditions at the Chip-Tool Interface in Machining. J. Tribol. 2003, 125, 649. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlinear Theory of Continuous Media; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Gurtin, M.E. An Introduction to Continuum Mechanics; Academic Press: Cambridge, MA, USA, 1981; p. 265. [Google Scholar]
- Forest, S.; Sievert, R. Nonlinear microstrain theories. Int. J. Solids Struct. 2006, 43, 7224–7245. [Google Scholar] [CrossRef]
- Aifantis, E.C. On the Microstructural Origin of Certain Inelastic Models. J. Eng. Mater. Technol. 1984, 106, 326. [Google Scholar] [CrossRef]
- Aifantis, E.C. The physics of plastic deformation. Int. J. Plast. 1987, 3, 211–247. [Google Scholar] [CrossRef]
- Gudmundson, P. A unified treatment of strain gradient plasticity. J. Mech. Phys. Solids 2004, 52, 1379–1406. [Google Scholar] [CrossRef]
- Steinmann, P. Views on multiplicative elastoplasticity and the continuum theory of dislocations. Int. J. Eng. Sci. 1996, 34, 1717–1735. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Anand, L. Thermodynamics applied to gradient theories involving the accumulated plastic strain: The theories of Aifantis and Fleck and Hutchinson and their generalization. J. Mech. Phys. Solids 2009, 57, 405–421. [Google Scholar] [CrossRef]
- Toupin, R.A. Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal. 1964, 17, 85–112. [Google Scholar] [CrossRef]
- Fleck, N.; Hutchinson, J. A phenomenological theory for strain gradient effects in plasticity. J. Mech. Phys. Solids 1993, 41, 1825–1857. [Google Scholar] [CrossRef]
- Smyshlyaev, V.; Fleck, N. The role of strain gradients in the grain size effect for polycrystals. J. Mech. Phys. Solids 1996, 44, 465–495. [Google Scholar] [CrossRef]
- Fleck, N.; Willis, J. A mathematical basis for strain-gradient plasticity theory—Part I: Scalar plastic multiplier. J. Mech. Phys. Solids 2009, 57, 161–177. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Generalizing J2 flow theory: Fundamental issues in strain gradient plasticity. Acta Mech. Sin. Xuebao 2012, 28, 1078–1086. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Anand, L. A theory of strain-gradient plasticity for isotropic, plastically irrotational materials. Part I: Small deformations. J. Mech. Phys. Solids 2005, 53, 1624–1649. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Y.; Nix, W.; Hutchinson, J. Mechanism-based strain gradient plasticity—I. Theory. J. Mech. Phys. Solids 1999, 47, 1239–1263. [Google Scholar] [CrossRef]
- Huang, Y.; Gao, H.; Nix, W.D.; Hutchinson, J.W. Mechanism-based strain gradient plasticity—II. Analysis. J. Mech. Phys. Solids 2000, 48, 99–128. [Google Scholar] [CrossRef]
- Taylor, G.I. Plastic Strain in Metals. J. Inst. Met. 1938, 62, 307–325. [Google Scholar]
- Nye, J.F. Some geometrical relations in dislocated crystals. Acta Metall. 1953, 1, 153–162. [Google Scholar] [CrossRef]
- Ashby, M.F. The deformation of plastically non-homogeneous materials. Philos. Mag. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Niordson, C.F.; Hutchinson, J.W. On lower order strain gradient plasticity theories. Eur. J. Mech. A/Solids 2003, 22, 771–778. [Google Scholar] [CrossRef]
- Menzel, A.; Steinmann, P. On the continuum formulation of higher gradient plasticity for single and polycrystals. J. Mech. Phys. Solids 2000, 48, 1777–1796. [Google Scholar] [CrossRef]
- Wulfinghoff, S.; Böhlke, T. Equivalent plastic strain gradient enhancement of single crystal plasticity: Theory and numerics. Proc. R. Soc. Math. Phys. Eng. Sci. 2012, 468, 2682–2703. [Google Scholar] [CrossRef]
- Wulfinghoff, S.; Bayerschen, E.; Böhlke, T. A gradient plasticity grain boundary yield theory. Int. J. Plast. 2013, 51, 33–46. [Google Scholar] [CrossRef]
- Cosserat, E.; Cosserat, F. Theorie des Corps Deformables. Nature 1909, 81, 67. [Google Scholar] [CrossRef]
- Koiter, W.T. Couple Stresses in the Theory of Elasticity, I & II. Philos. Trans. R. Soc. Lond. 1964, 67, 17–44. [Google Scholar]
- Khoei, A.R.; Yadegari, S.; Biabanaki, S.O. 3D finite element modeling of shear band localization via the micro-polar Cosserat continuum theory. Comput. Mater. Sci. 2010, 49, 720–733. [Google Scholar] [CrossRef]
- De Borst, R. Simulation of strain localization: A reappraisal of the cosserat continuum. Eng. Comput. 1991, 8, 317–332. [Google Scholar] [CrossRef]
- Eringen, A.C.; Suhubi, E.S. Nonlinear theory of simple micro-elastic solids-I. Int. J. Eng. Sci. 1964, 2, 189–203. [Google Scholar] [CrossRef]
- Eringen, A.C. Microcontinuum Field Theories: I. Foundations and Solids, 1st ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Dillard, T.; Forest, S.; Ienny, P. Micromorphic continuum modelling of the deformation and fracture behaviour of nickel foams. Eur. J. Mech. A/Solids 2006, 25, 526–549. [Google Scholar] [CrossRef]
- Anand, L.; Aslan, O.; Chester, S.A. A large-deformation gradient theory for elastic-plastic materials: Strain softening and regularization of shear bands. Int. J. Plast. 2012, 30–31, 116–143. [Google Scholar] [CrossRef]
- Poh, L.H.; Peerlings, R.H.J.; Geers, M.G.D.; Swaddiwudhipong, S. An implicit tensorial gradient plasticity model - Formulation and comparison with a scalar gradient model. Int. J. Solids Struct. 2011, 48, 2595–2604. [Google Scholar] [CrossRef]
- Peerlings, R.H.J. On the role of moving elastic-plastic boundaries in strain gradient plasticity. Model. Simul. Mater. Sci. Eng. 2007, 15. [Google Scholar] [CrossRef][Green Version]
- Acharya, A.; Bassani, J.L. On Non-Local Flow Theories that Preserve the Classical Structure of Incremental Boundary Value Problems. In IUTAM Symposium on Micromechanics of Plasticity and Damage of Multiphase Materials. Solid Mechanics and its Applications; Springer: Dordrecht, The Netherlands, 1996. [Google Scholar] [CrossRef]
- Bassani, J.L. Incompatibility and a simple gradient theory of plasticity. J. Mech. Phys. Solids 2001, 49, 1983–1996. [Google Scholar] [CrossRef]
- Guha, S.; Sangal, S.; Basu, S. Numerical investigations of flat punch molding using a higher order strain gradient plasticity theory. Int. J. Mater. Form. 2014, 7, 459–467. [Google Scholar] [CrossRef]
- Shu, J.Y.; Fleck, N.A. The prediction of a size effect in micro-indentation. Int. J. Solids Struct. 1998, 35, 1363–1383. [Google Scholar] [CrossRef]
- Nielsen, K.L.; Niordson, C.F.; Hutchinson, J.W. Rolling at small scales. J. Manuf. Sci. Eng. Trans. ASME 2016, 138, 1–10. [Google Scholar] [CrossRef]
- Fleck, N.A.; Willis, J.R. A mathematical basis for strain-gradient plasticity theory. Part II: Tensorial plastic multiplier. J. Mech. Phys. Solids 2009, 57, 1045–1057. [Google Scholar] [CrossRef]
- Liu, K. Process Modeling of Micro-Cutting Including Strain Gradient Effects. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, December 2005. [Google Scholar]
- Liu, K.; Melkote, S.N. Material strengthening mechanisms and their contribution to size effect in micro-cutting. J. Manuf. Sci. Eng. Trans. ASME 2006, 128, 730–738. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Y. Taylor-based nonlocal theory of plasticity. Int. J. Solids Struct. 2001, 38, 2615–2637. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data from metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Taylor, G.I.; Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. A Math. Eng. Sci. 1934, 143, 307–326. [Google Scholar] [CrossRef]
- Asad, M.; Mabrouki, T.; Rigal, J.F. Finite-element-based hybrid dynamic cutting model for aluminium alloy milling. Proc. Inst. Mech. Eng. Part B: J. Eng. Manuf. 2010, 224, 1–13. [Google Scholar] [CrossRef]
- Asad, M. Elaboration of Concepts and Methodologies to Study Peripheral Down-Cut Milling Process from Macro-To-Micro Scales. Ph.D. Thesis, Institute National des Sciences AppliquéEs de Lyon, Villeurbanne, France, September 2010. [Google Scholar]
- Mabrouki, T.; Courbon, C.; Zhang, Y.; Rech, J.; Nélias, D.; Asad, M.; Hamdi, H.; Belhadi, S.; Salvatore, F. Some insights on the modelling of chip formation and its morphology during metal cutting operations. Comptes Rendus—Mec. 2016, 344, 335–354. [Google Scholar] [CrossRef]
- Diamantopoulou, E.; Liu, W.; Labergere, C.; Badreddine, H.; Saanouni, K.; Hu, P. Micromorphic constitutive equations with damage applied to metal forming. Int. J. Damage Mech. 2017, 26, 314–339. [Google Scholar] [CrossRef]


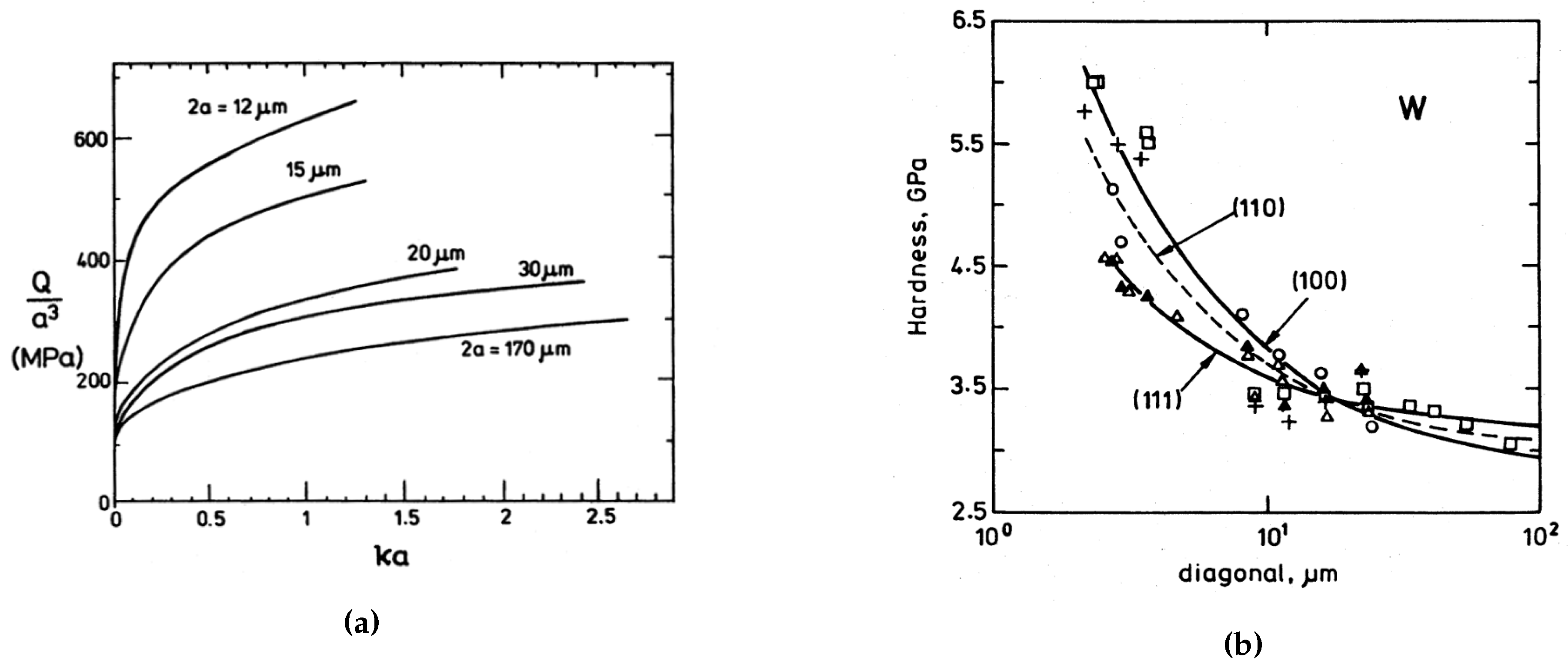
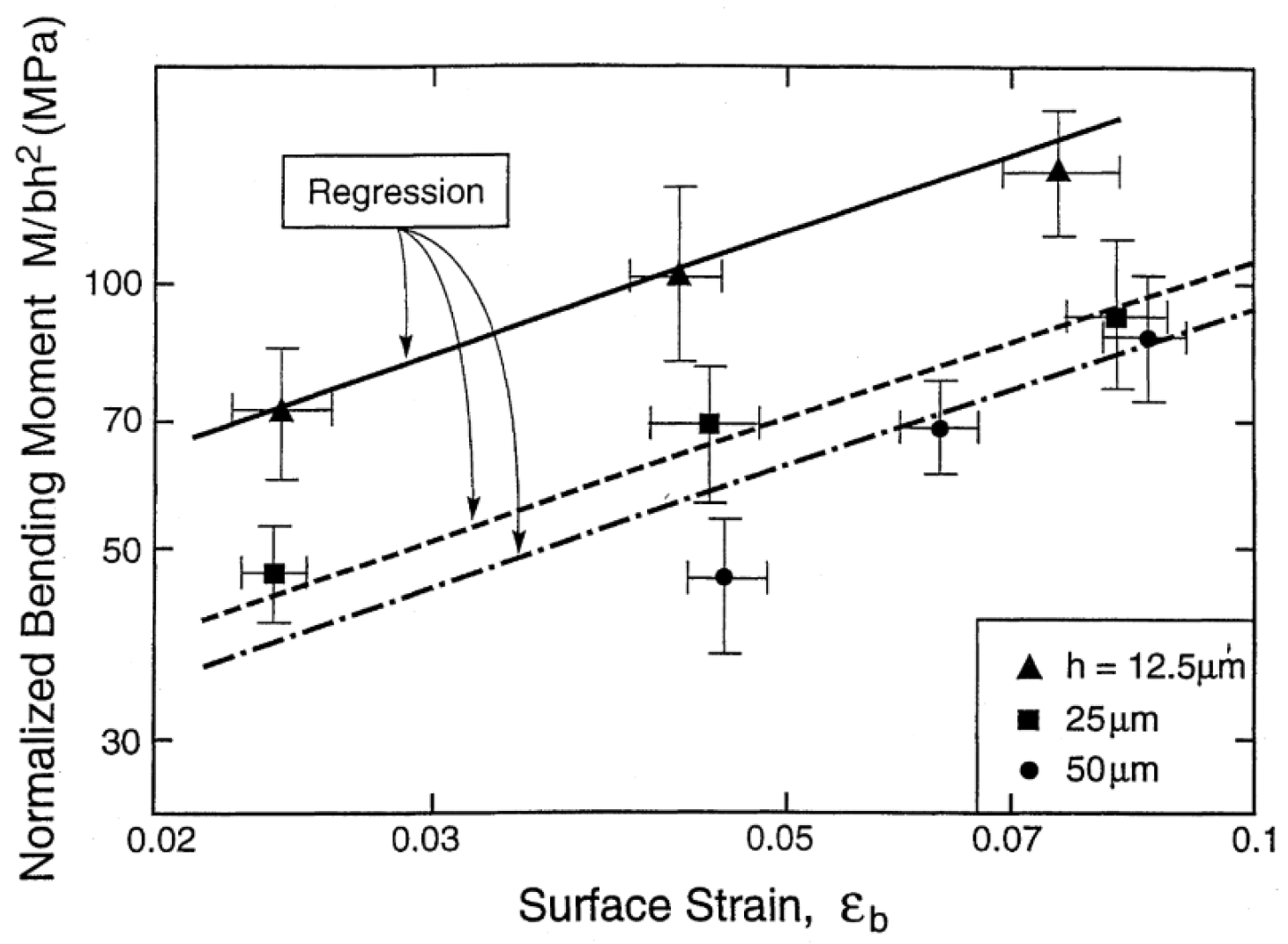

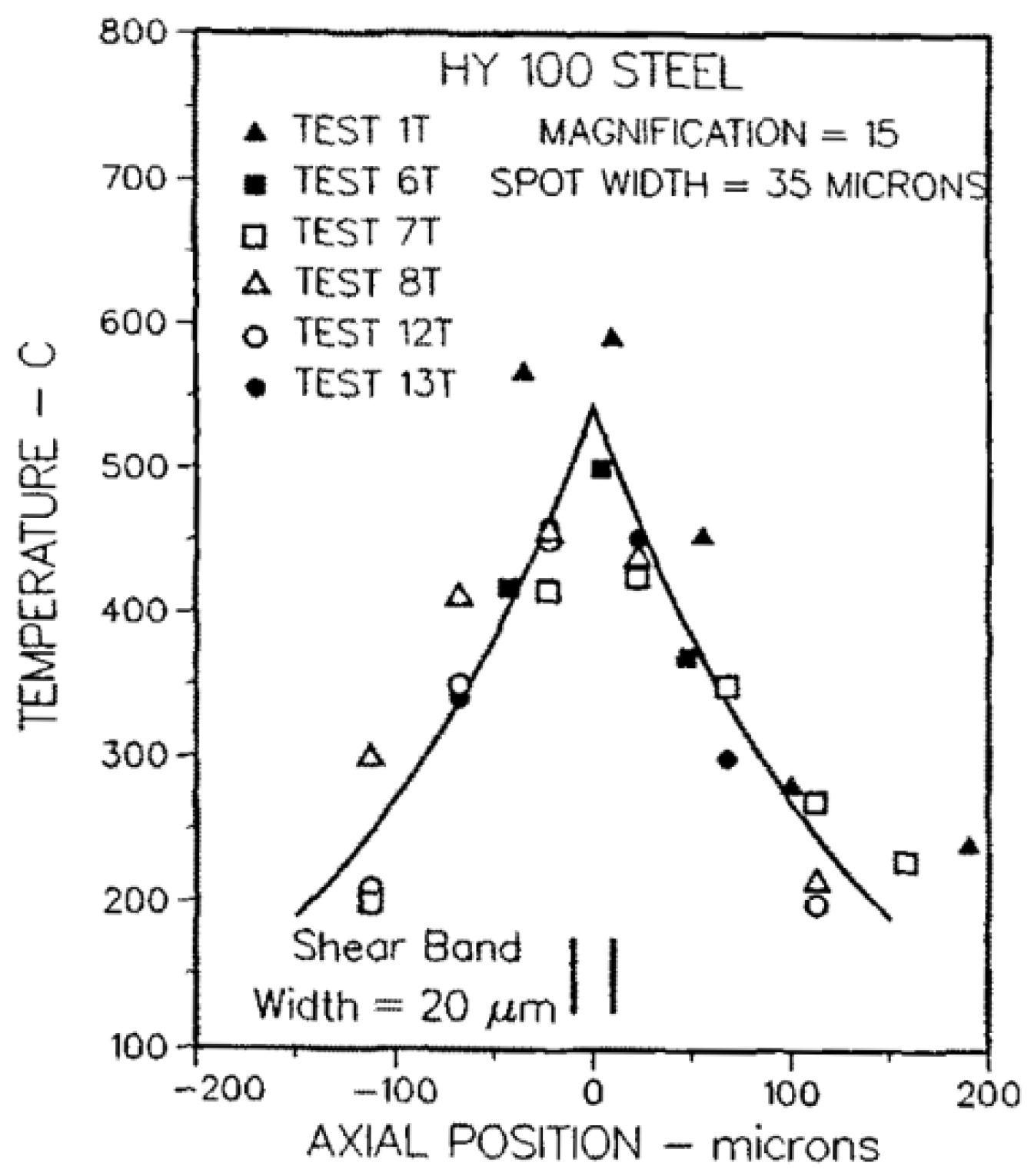
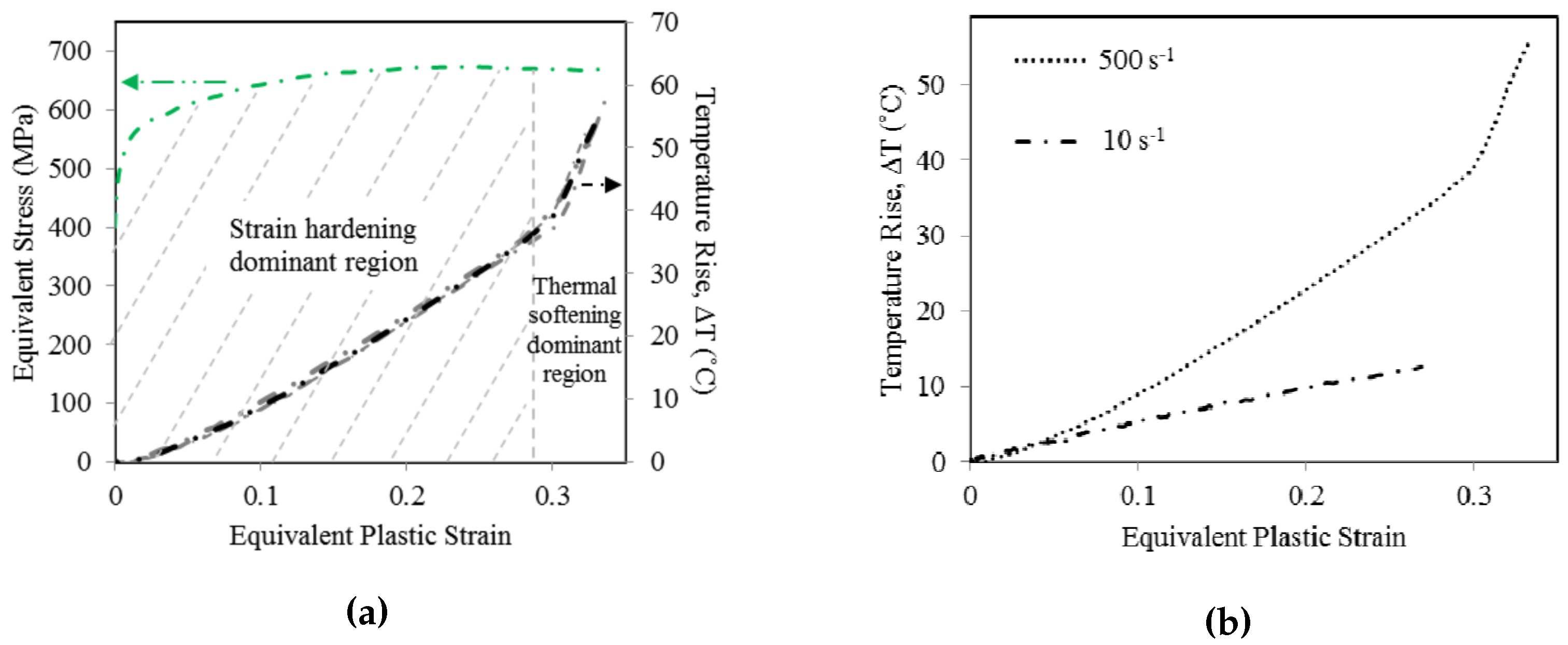

| Name | # d.o.f. | # Charact. Lengths | Additional Feature | Higher Order/Higher Grade |
|---|---|---|---|---|
| Aifantis [36,79,80] | 3 | 1/2 | Higher Grade | |
| Fleck1993 [85] | 3 | 2 | Higher Grade | |
| Fleck1997 [20] | 3 | 6 | Higher Grade | |
| Fleck2001 [42] | 3 | 1 | Higher Grade | |
| Gurtin [89] | 3 | 2 | Higher Grade | |
| Gudmundson [81] | 3 | 6 | Higher Grade | |
| Gao [90,91] | 3 | 1 | Higher Grade | |
| Cosserat [99] | 6 | 3 | Higher Order | |
| Micromorphic [103] | 12 | 2 | Higher Order |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, R.; Girot Mata, F.A.; Forest, S.; Jacquin, D. A Review on Strain Gradient Plasticity Approaches in Simulation of Manufacturing Processes. J. Manuf. Mater. Process. 2020, 4, 87. https://doi.org/10.3390/jmmp4030087
Russo R, Girot Mata FA, Forest S, Jacquin D. A Review on Strain Gradient Plasticity Approaches in Simulation of Manufacturing Processes. Journal of Manufacturing and Materials Processing. 2020; 4(3):87. https://doi.org/10.3390/jmmp4030087
Chicago/Turabian StyleRusso, Raffaele, Franck Andrés Girot Mata, Samuel Forest, and Dimitri Jacquin. 2020. "A Review on Strain Gradient Plasticity Approaches in Simulation of Manufacturing Processes" Journal of Manufacturing and Materials Processing 4, no. 3: 87. https://doi.org/10.3390/jmmp4030087
APA StyleRusso, R., Girot Mata, F. A., Forest, S., & Jacquin, D. (2020). A Review on Strain Gradient Plasticity Approaches in Simulation of Manufacturing Processes. Journal of Manufacturing and Materials Processing, 4(3), 87. https://doi.org/10.3390/jmmp4030087






