Experimental and Numerical Investigation of the Influence of Process Parameters in Incremental Sheet Metal Forming on Residual Stresses
Abstract
1. Introduction
2. Materials and Method
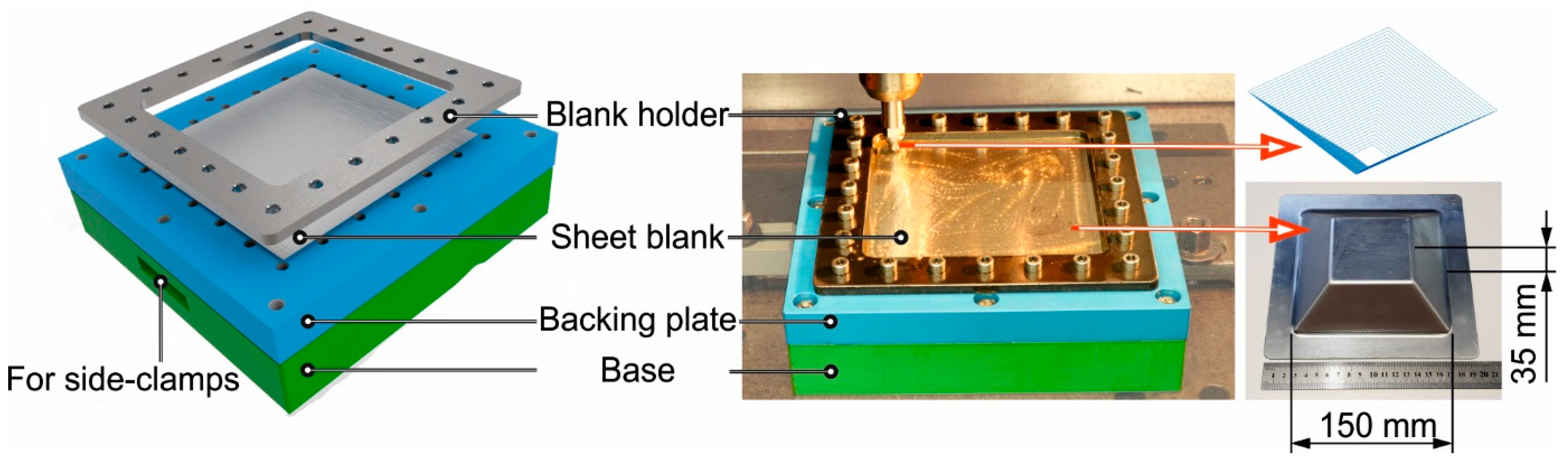
2.1. Experimental Set-Up of SPIF
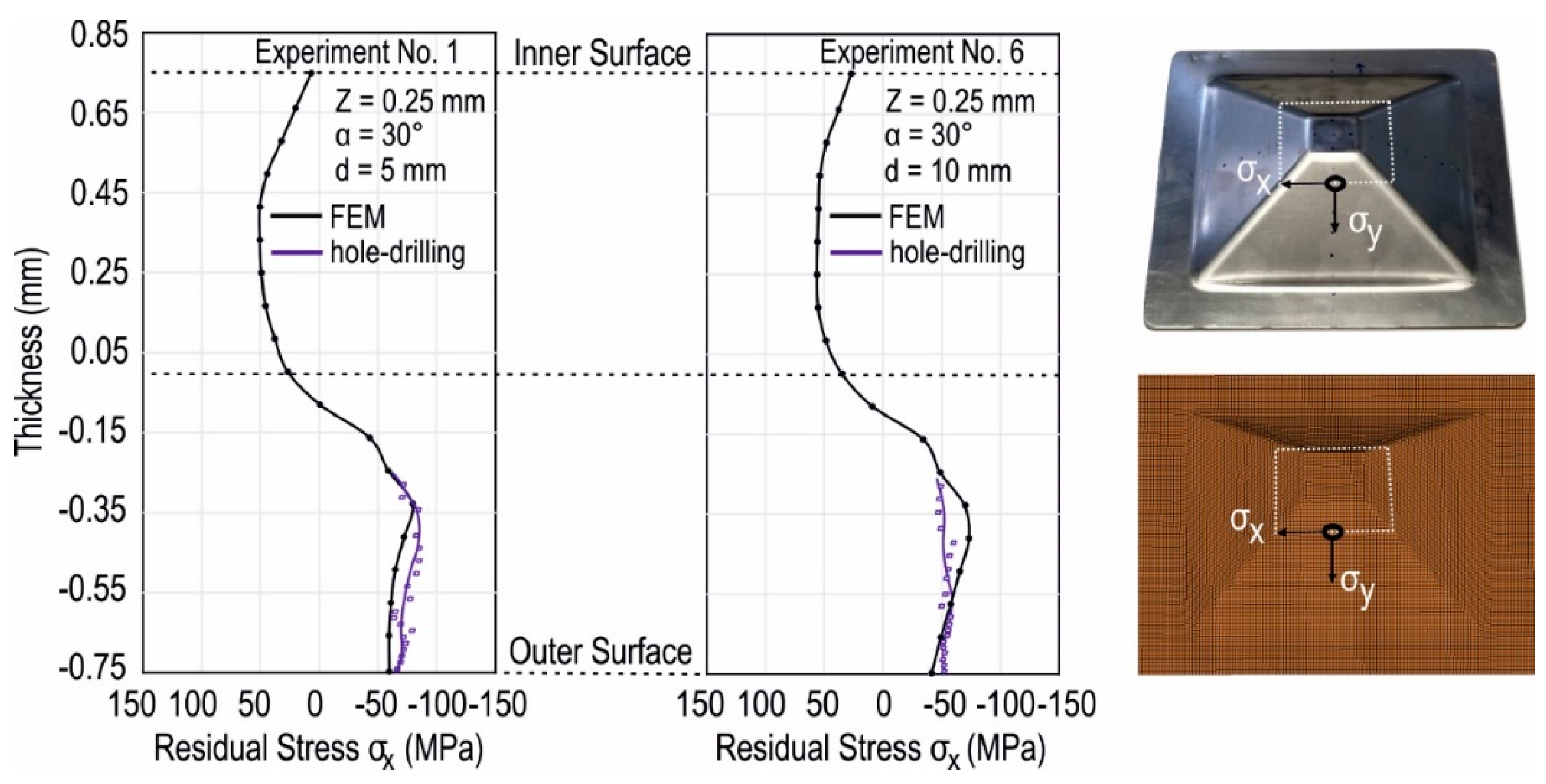
2.2. Hole-Drilling-Method
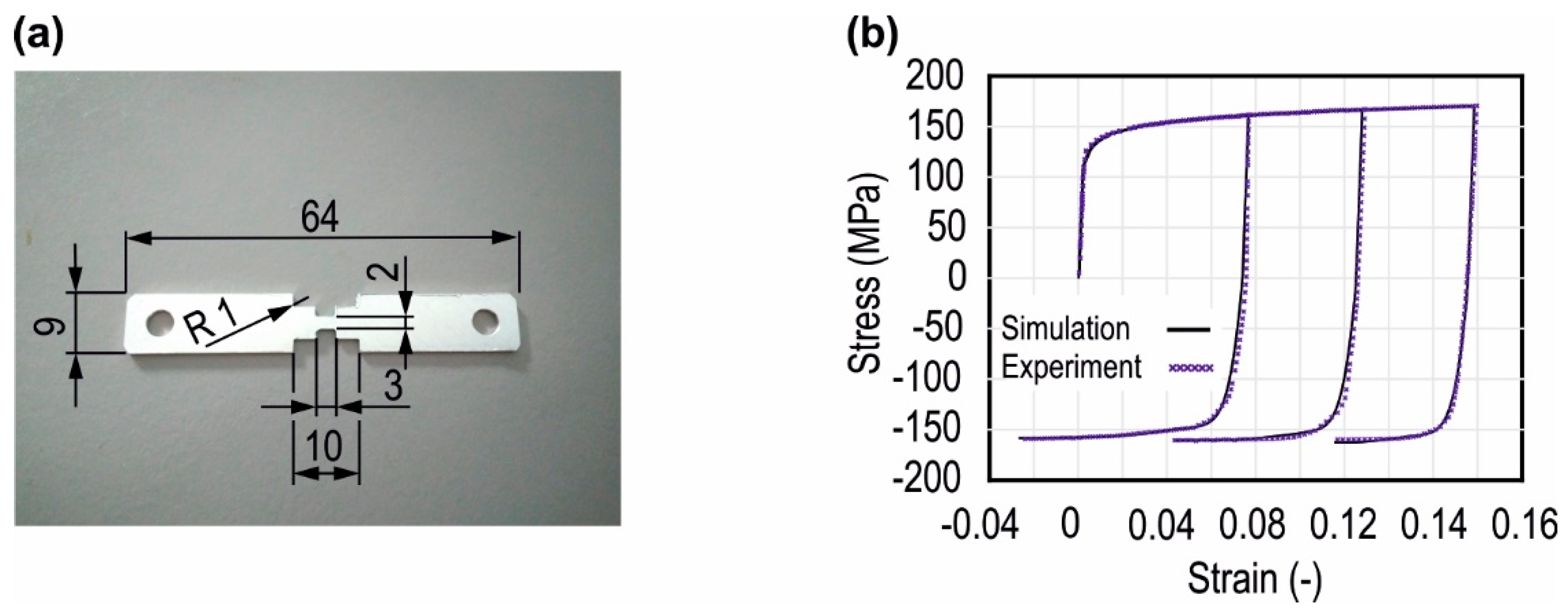
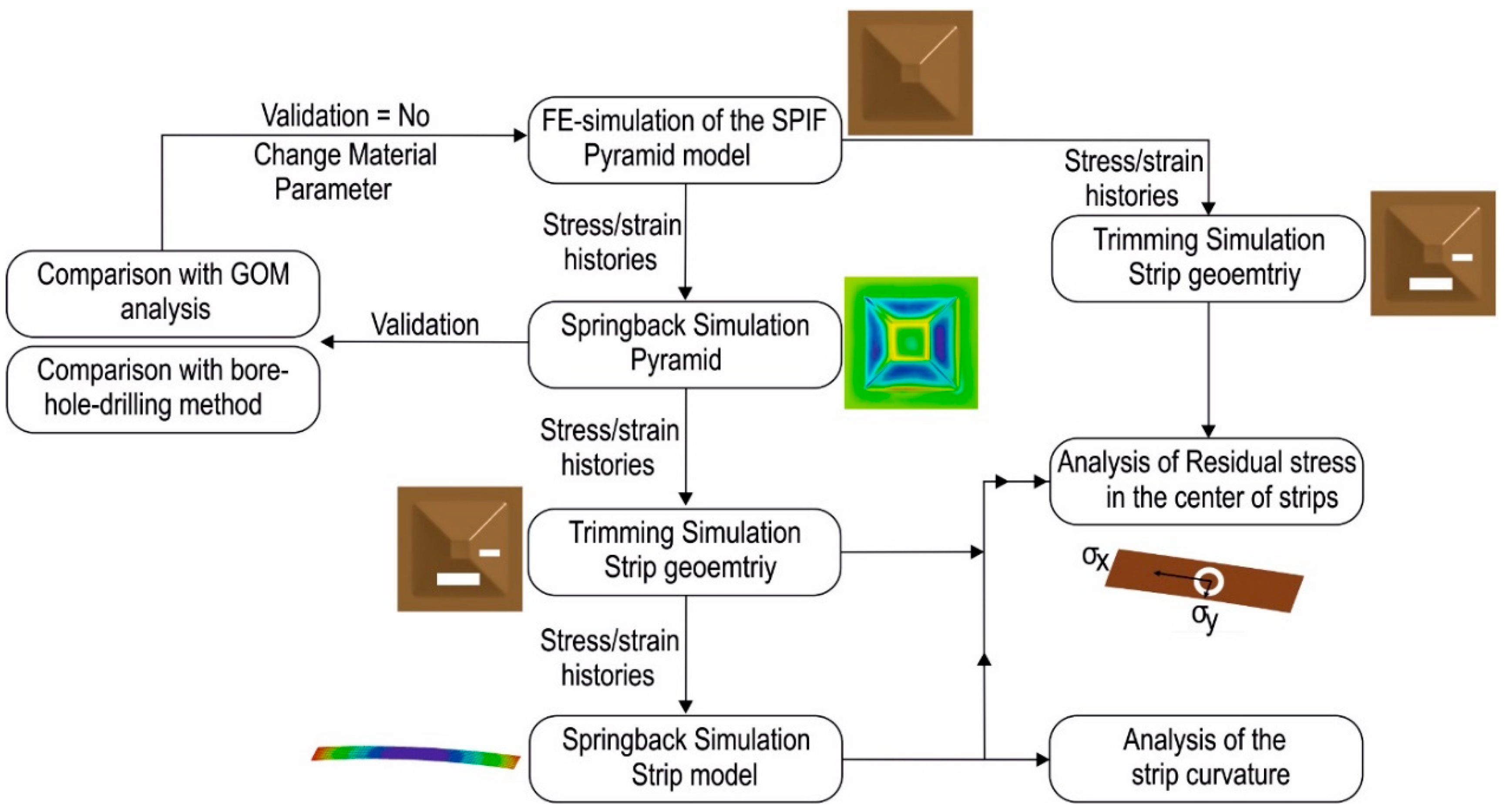
2.3. The Finite Element (FE) Model of the SPIF Process
2.4. Solution Procedure
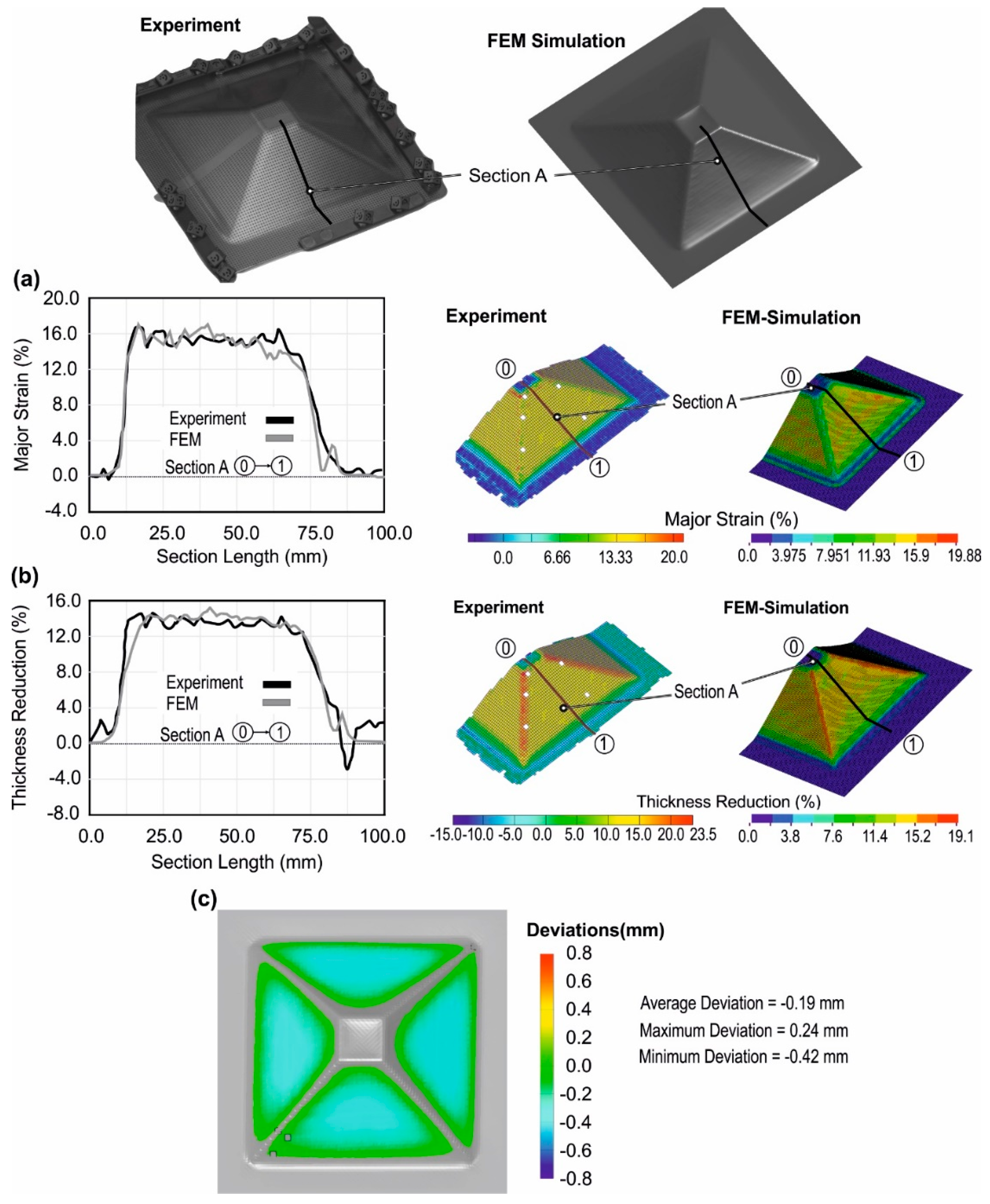
3. Results and Discussions
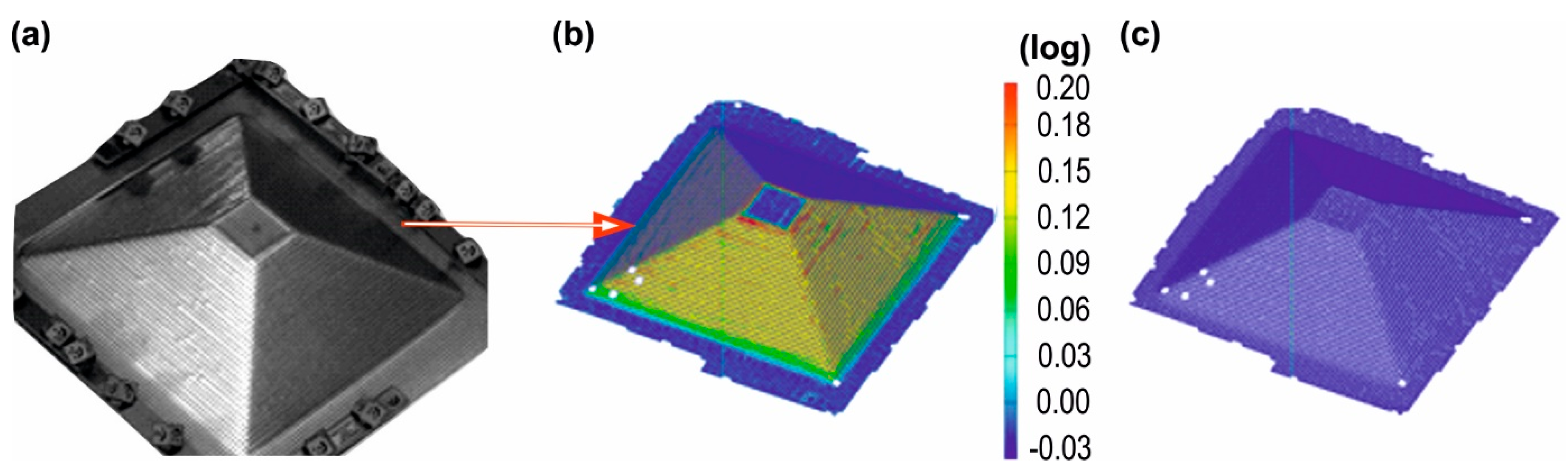
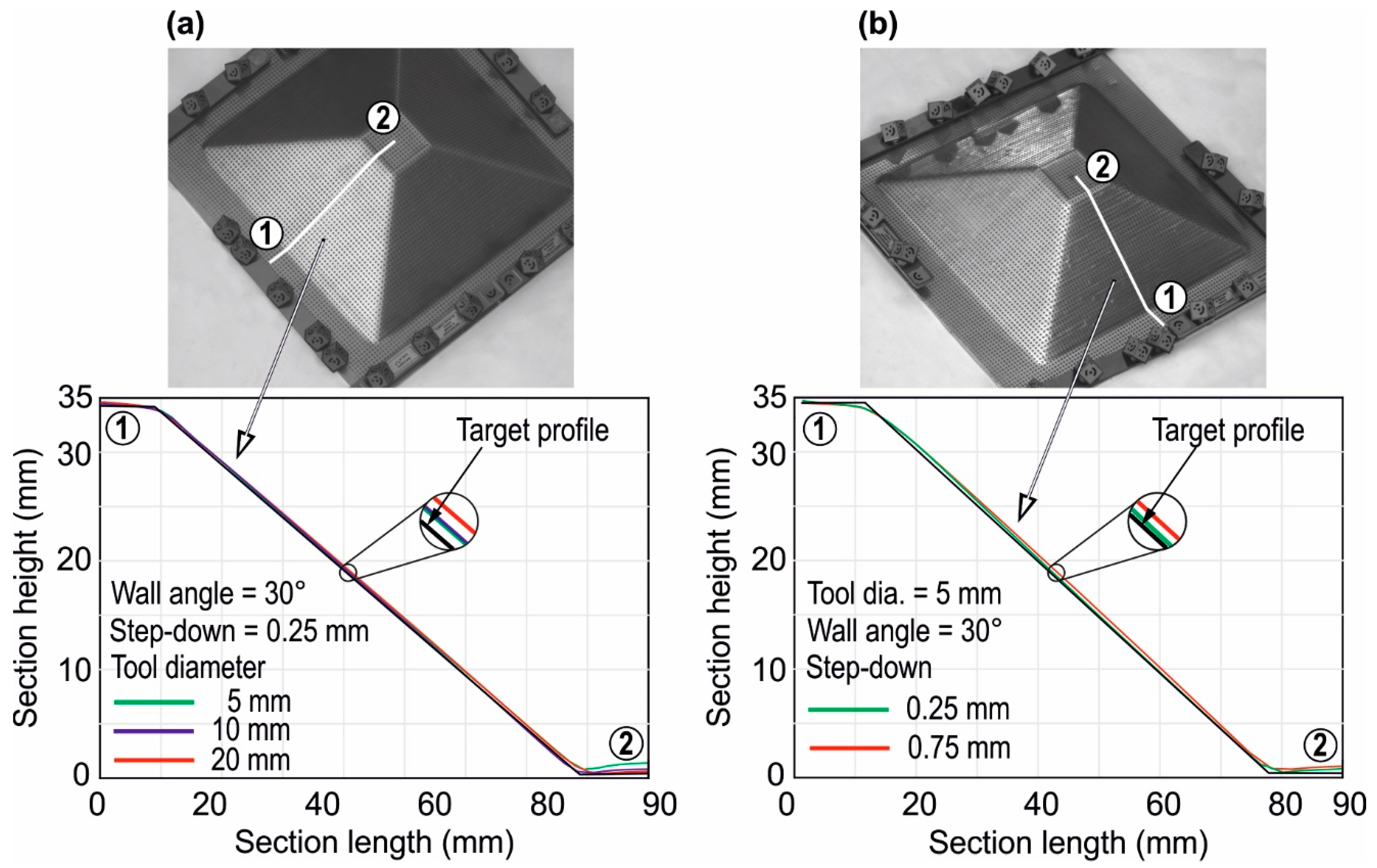
3.1. Validation of the Numerical Simulation
3.2. Influence of Process Parameters on Residual Stresses
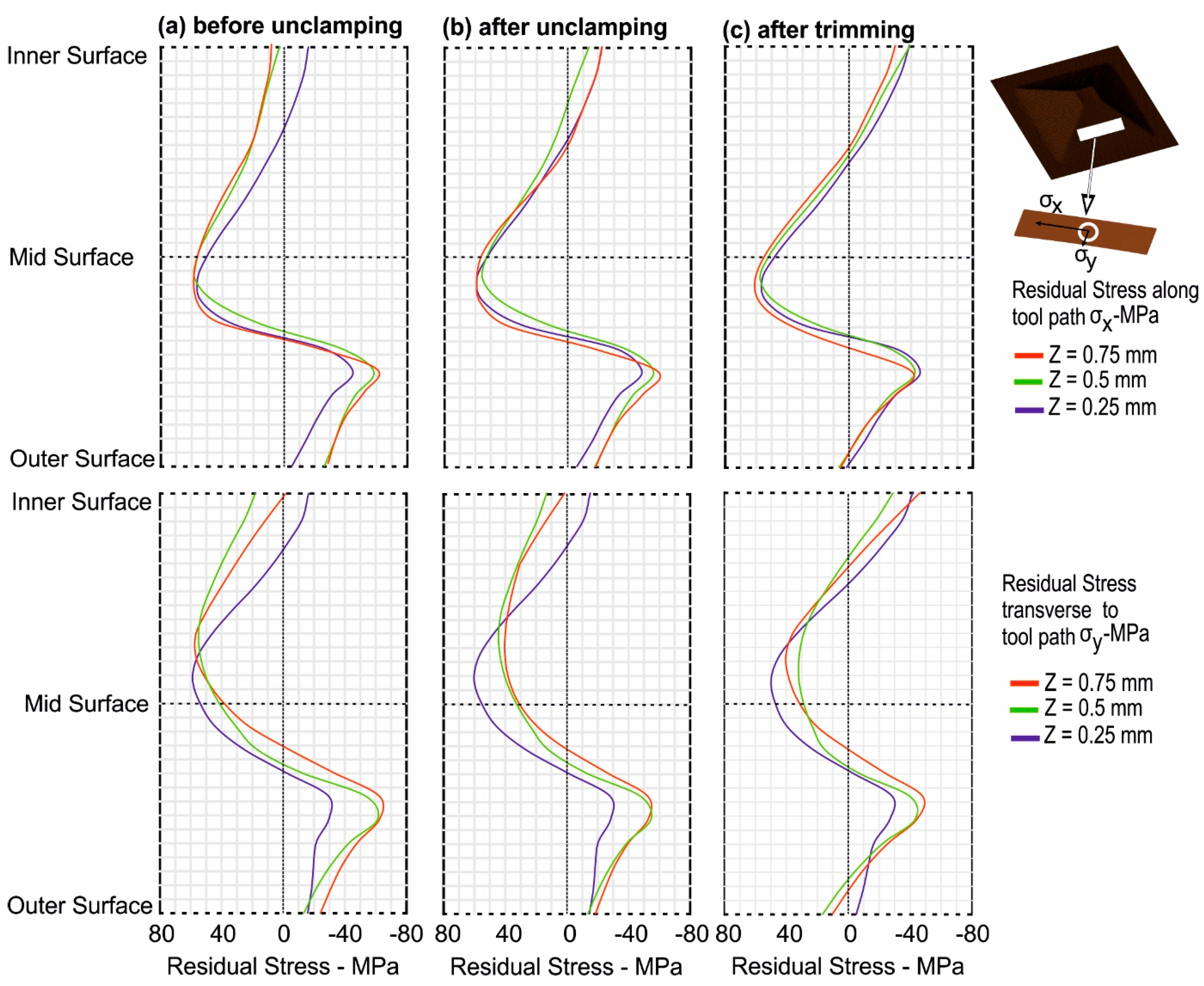
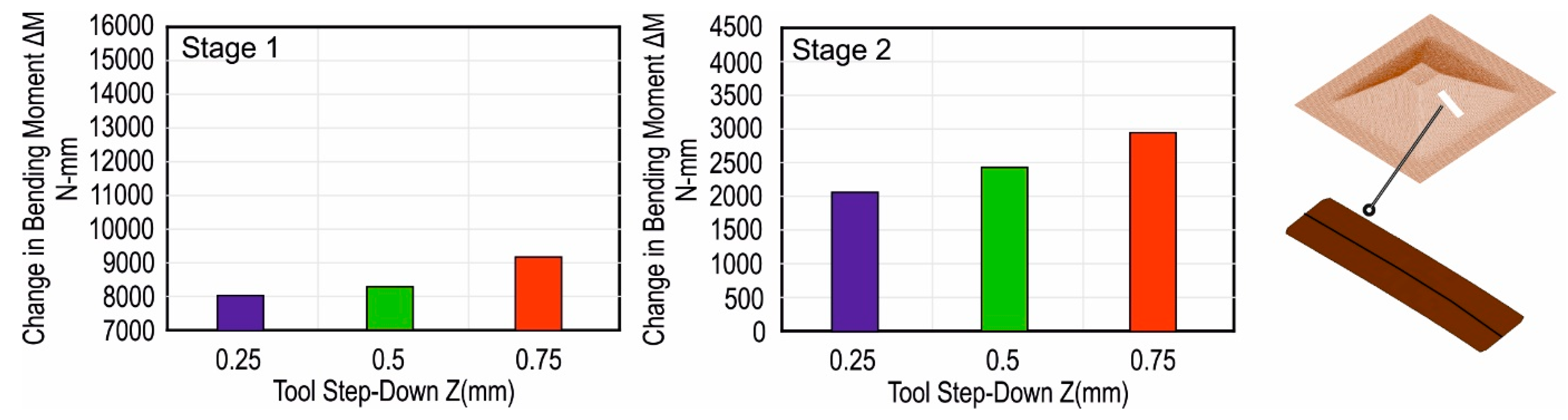
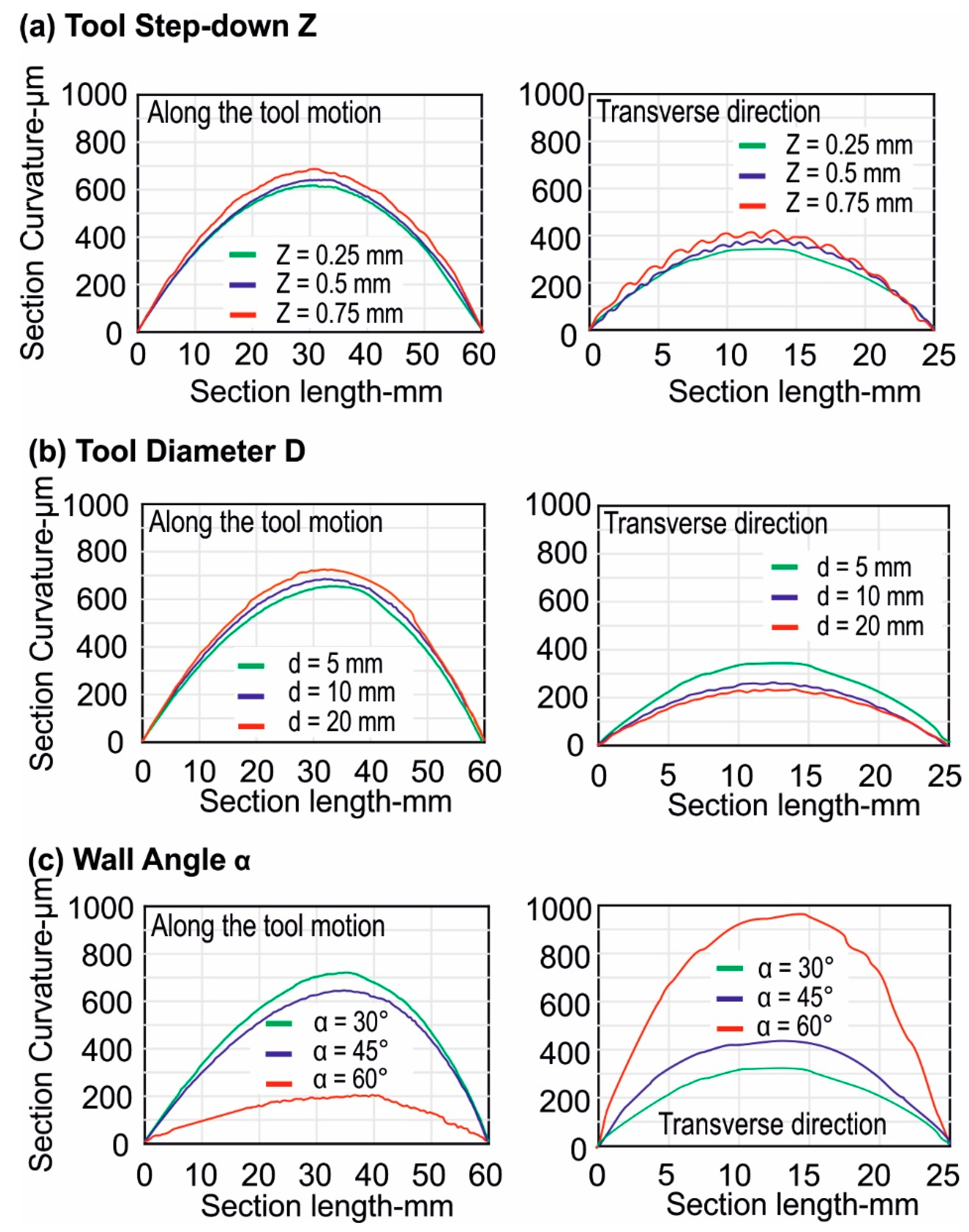
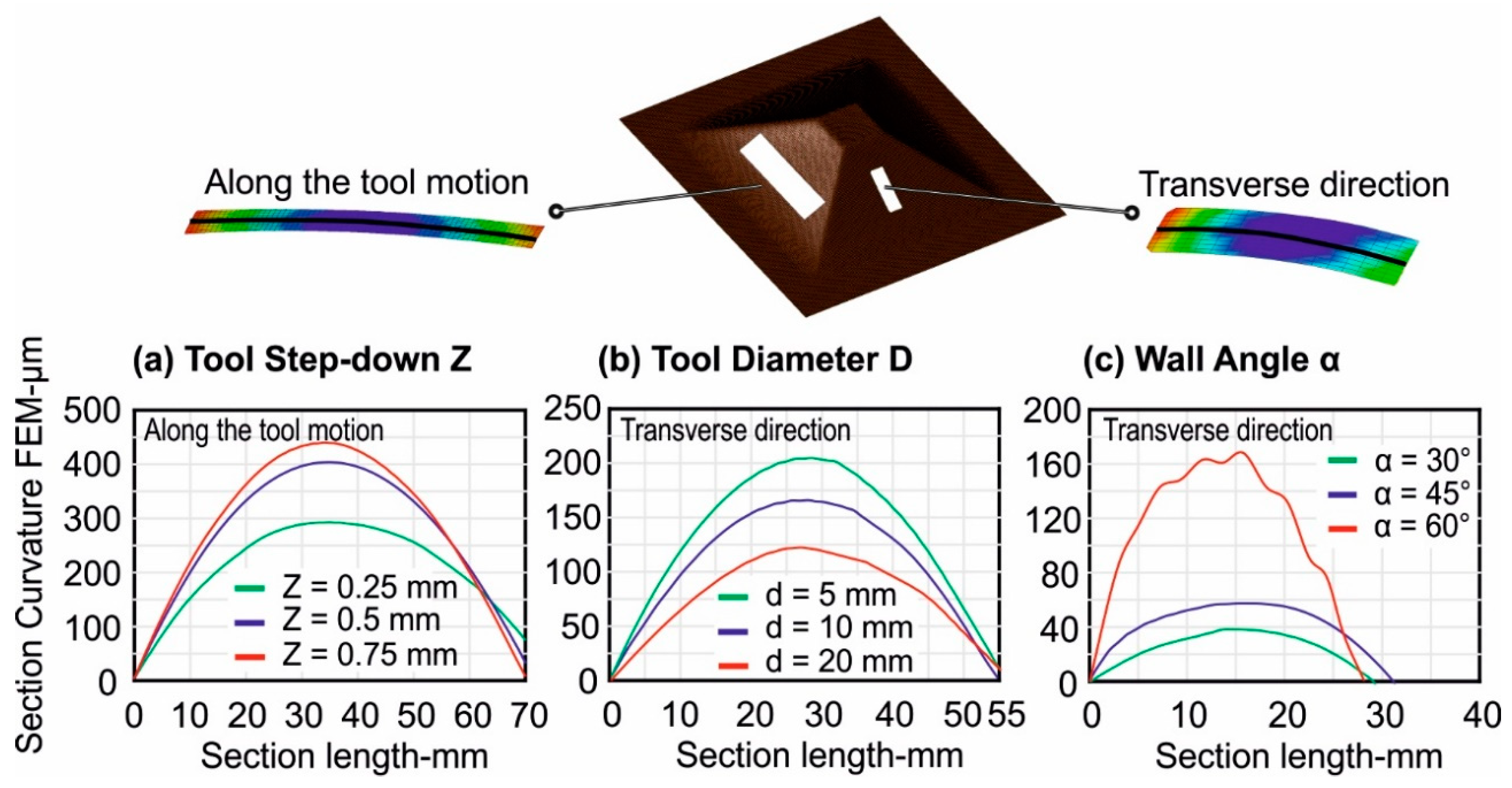
3.2.1. Tool Step-Down
- By increasing the tool step-down, the magnitude of the compressive residual stresses on the non-contact surface increased more compared to tensile stresses on the tool contact side as indicated by the ‘before unclamping’ state.
- For larger tool step-down values, the magnitude of the residual stresses changed more upon unclamping in the transverse direction of the tool motion.
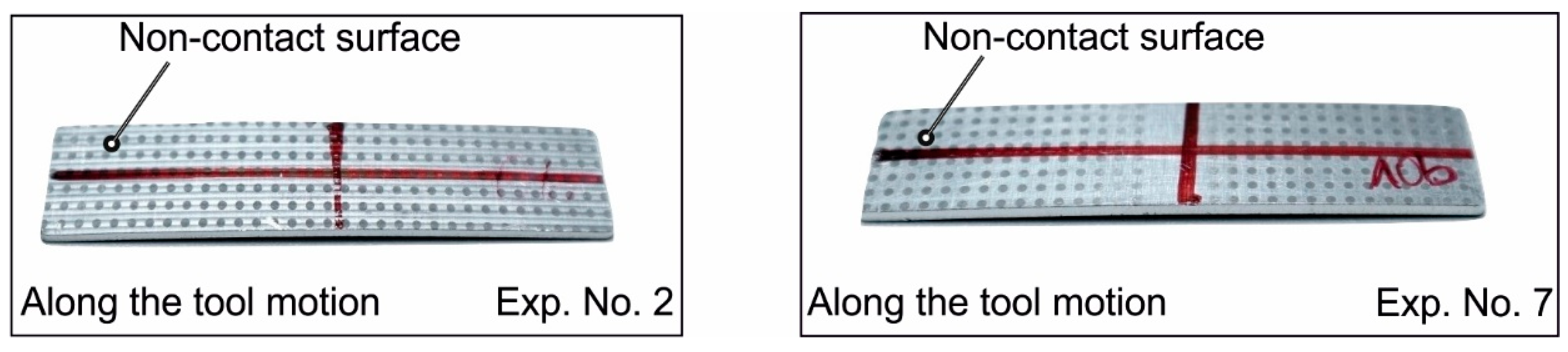
- The change in the magnitude of the residual stresses was greater upon trimming compared to unclamping. There was also a significant change in the magnitude of the residual stresses for outer and inner surfaces. The final state of the residual stress after trimming for the inner surface was compression, similar to the initial unclamped state, i.e., before unclamping and vice-versa for the outer surface.
- The bending moment change was highest with the largest tool step-down and vice-versa. Therefore, the geometric deviations will be highest with the largest tool step-down.
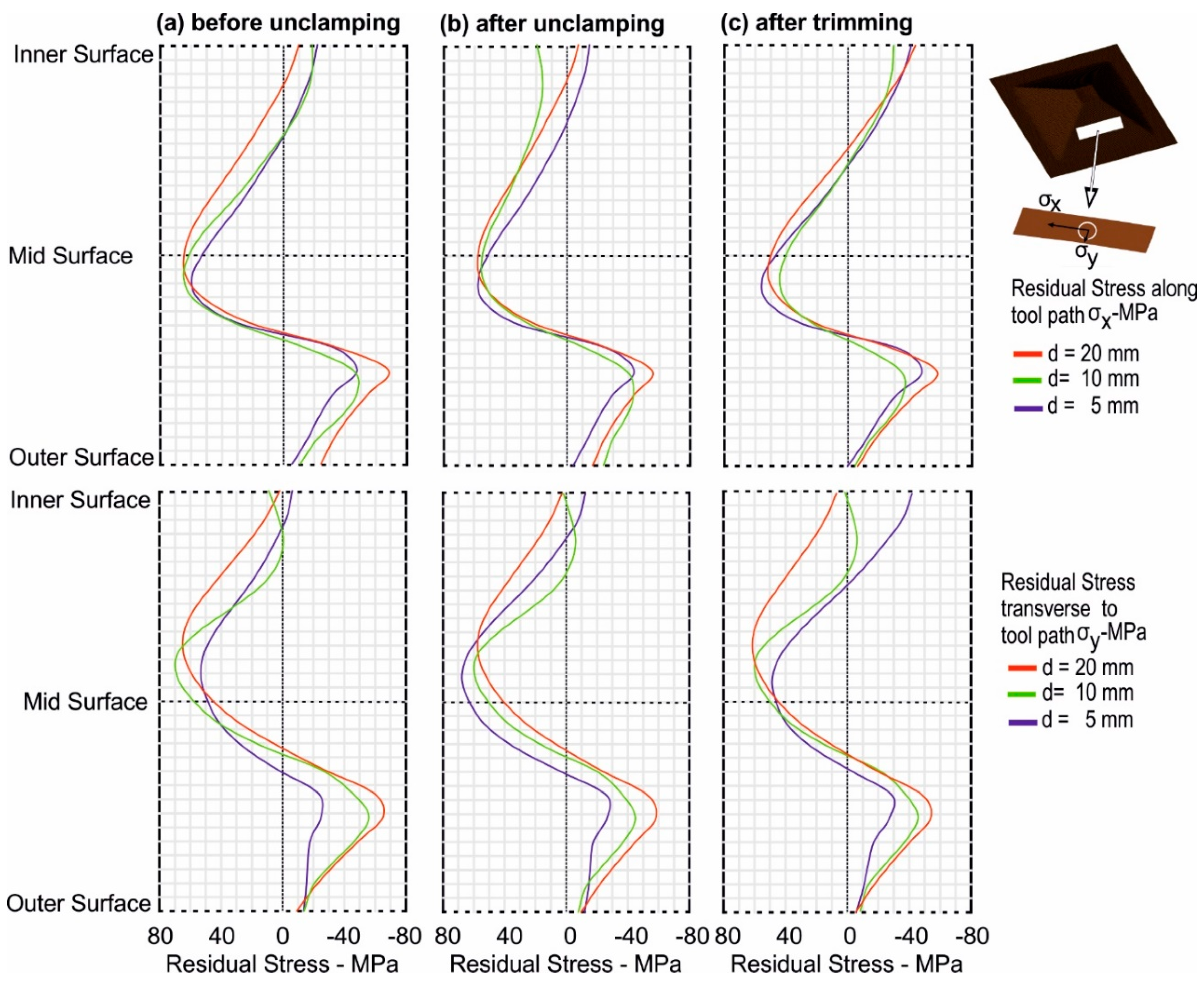
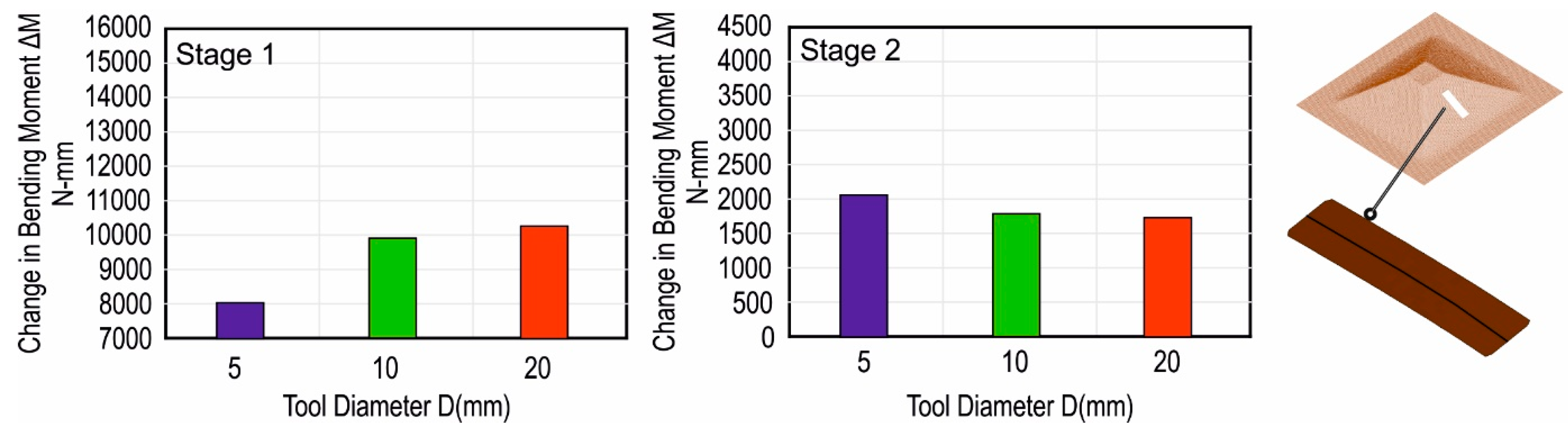
3.2.2. Tool Diameter
- In the initial clamped state, the magnitude of the residual stresses, by increasing the tool diameter, increased both in tension and compression.
- The ‘before unclamping’ state indicates that the residual stress, by increasing the tool diameter, increased more pronouncedly in the transverse direction of the tool motion.
- A notable change in the transverse direction in the magnitude and state of the residual stresses occurred upon unclamping, represented by ‘after unclamping’ in Figure 11, and this change was largest with the largest tool diameter.
- Upon trimming, the respective change in the magnitude of the residual stresses was slightly larger with the smallest tool diameter.
- The change in the bending moment was highest with the largest tool diameter upon unclamping in the transverse direction.
- The change in the bending moment was highest with the smallest tool diameter upon trimming in the transverse direction.
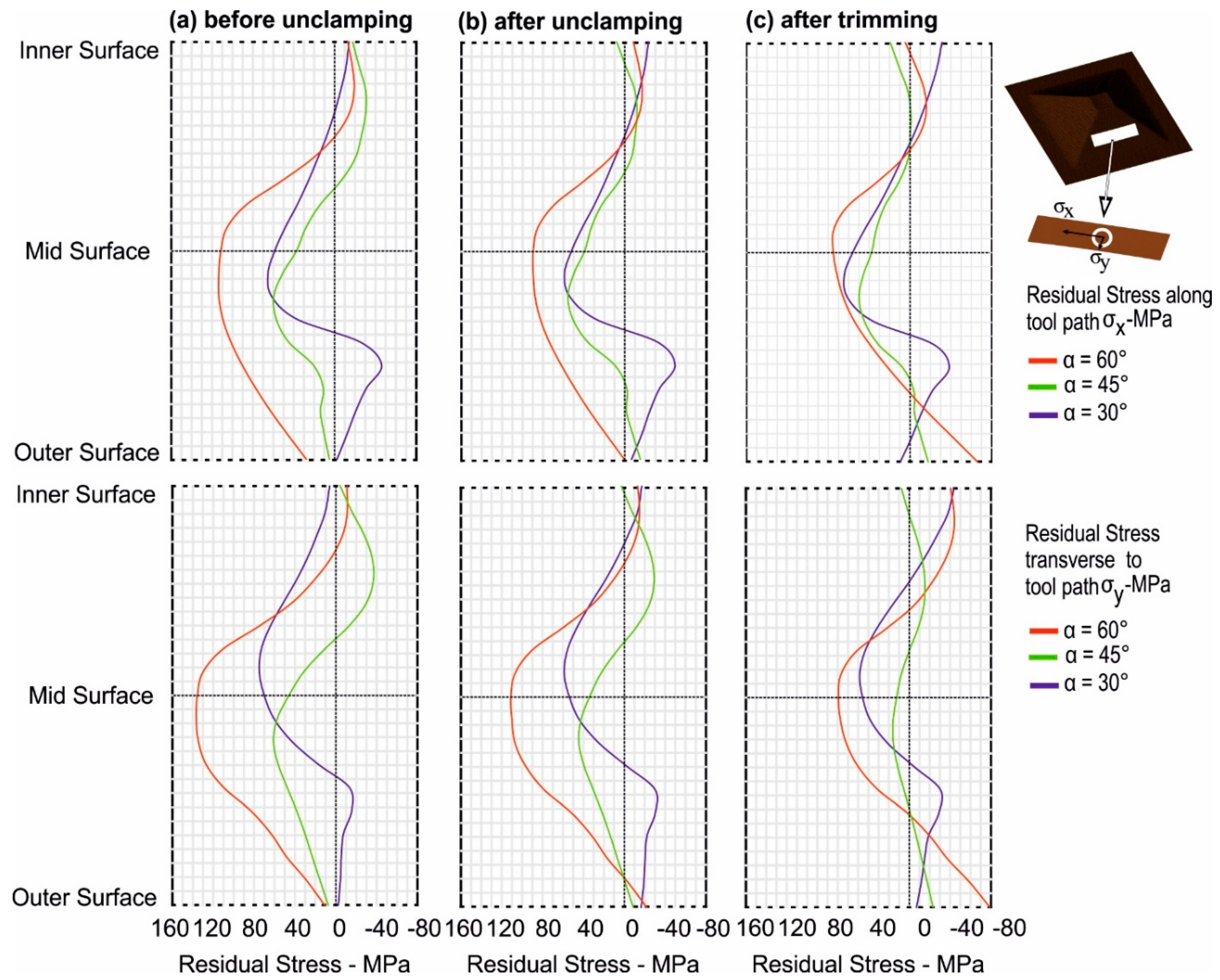
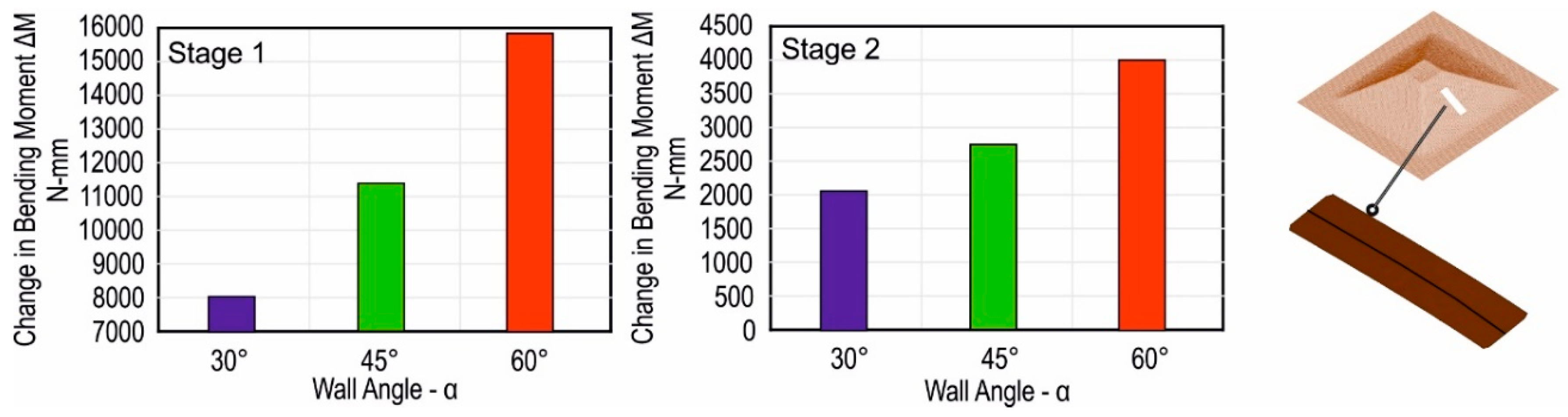
3.2.3. Wall Angle
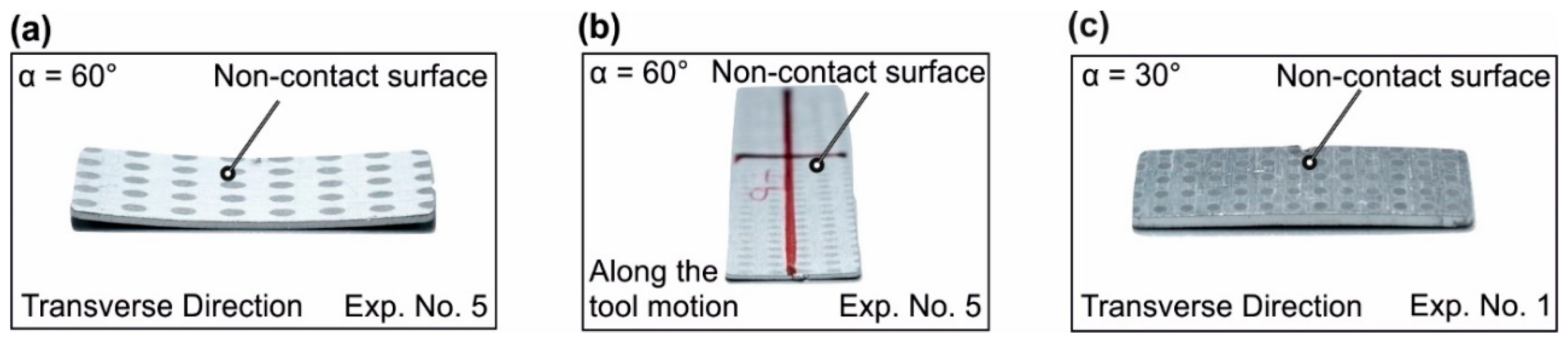
- In contrast to tool diameter and tool step-down, by increasing the wall angle, the through thickness distribution of the residual stresses changed to tension.
- The magnitude of the residual stresses was higher in the transverse direction.
- A significant change in the magnitude of the residual stress occurred upon trimming, and this was highest with the largest wall angle.
- The change in the bending moment was highest with the largest wall angle, and this change is significant as compared to the other process parameters, i.e., tool diameter and wall angle.
3.3. Residual Stresses vs. Geometrical Accuracy
4. Conclusions
- (1)
- The magnitude of the residual stresses in the clamped state increased when the tool diameter, tool step-down, and the wall angle increased. Upon unclamping, the respective change in the magnitude of the residual stresses and the bending moments was highest with the greatest tool-diameter and tool step-down. Upon trimming, the change in the magnitude of the residual stresses and bending moments was greatest with the highest tool step-down value. However, the change in the magnitude of the residual stresses and bending moment was highest with the smallest tool diameter in the transverse direction of the tool motion. Moreover, for greater wall angles, the respective change in the magnitude of residual stresses and bending moment was highest and occurred significantly in the transverse direction of the tool motion.
- (2)
- The widely known fact from the literature that a smaller tool step-down and a smaller tool diameter have a positive effect on geometrical accuracy is explained in terms of residual stress. This is because, during unclamping, the greatest changes in the magnitude of the residual stresses occurred with the greatest tool step-down and tool diameter. During unclamping, these changes in the magnitude of the residual stresses were directly proportional to the elastic portion of the deformation. The elastic portion of the deformation, which was recovered upon unclamping, increased when the tool step-down and tool diameter increased. Hence, geometrical accuracy in the unclamped state increases when tool step-down and tool diameter decrease.
- (3)
- However, upon trimming, the largest changes in the magnitude of the residual stresses occurred with the smallest tool diameter was significant in the transverse direction of the tool motion. Hence, geometric deviations were largest with the smallest tool diameter in the trimmed state.
- (4)
- In contrast to tool diameter and tool step-down, the state of the residual stresses in the trimmed state with the greater wall angles was such that it caused the strips to curl toward the tool contact face, opposite to other process parameters.
- (5)
- The most significant parameter for the effect on the residual stresses and geometrical accuracy is the wall angle. The geometrical accuracy decreased significantly in the transverse direction when the wall angle was increased. However, this parameter is usually fixed, and its value depends on the geometry of the part to be formed. The other two parameters, i.e., tool diameter and tool step-down, also have a considerable effect on residual stress and geometrical accuracy.
- (6)
- The effect of changing process parameters on the residual stresses was more evident in the transverse direction of the tool motion.
Author Contributions
Funding
Acknowledgement
Conflicts of Interest
References
- Jeswiet, J.; Micari, F.; Hirt, G.; Bramley, A.; Duflou, J.; Allwood, J. Asymmetric Single Point Incremental Forming of Sheet Metal. CIRP Ann. 2005, 54, 88–114. [Google Scholar] [CrossRef]
- Emmens, W.; Boogaard, A.V.D.; Boogaard, T.V.D. An overview of stabilizing deformation mechanisms in incremental sheet forming. J. Mater. Process. Technol. 2009, 209, 3688–3695. [Google Scholar] [CrossRef]
- Bambach, M.; Araghi, B.T.; Hirt, G. Strategies to improve the geometric accuracy in asymmetric single point incremental forming. Prod. Eng. 2009, 3, 145–156. [Google Scholar] [CrossRef]
- Allwood, J.M.; King, G.P.F.; Duflou, J.; Allwood, J. A structured search for applications of the incremental sheet-forming process by product segmentation. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2005, 219, 239–244. [Google Scholar] [CrossRef]
- Totten, G.E. Handbook of Residual Stress and Deformation of Steel; ASM International: Almere, The Netherlands, 2002. [Google Scholar]
- Holweger, W.; Walther, F.; Loos, J.; Wolf, M.; Schreiber, J.; Dreher, W.; Kern, N.; Lutz, S. Non-destructive subsurface damage monitoring in bearings failure mode using fractal dimension analysis. Ind. Lubr. Tribol. 2012, 64, 132–137. [Google Scholar] [CrossRef]
- Huber, N.; Heerens, J. On the effect of a general residual stress state on indentation and hardness testing. Acta Mater. 2008, 56, 6205–6213. [Google Scholar] [CrossRef]
- Kim, S.-J.; Kim, D.; Lee, K.; Cho, H.-H.; Han, H.N. Residual-stress-induced grain growth of twinned grains and its effect on formability of magnesium alloy sheet at room temperature. Mater. Charact. 2015, 109, 88–94. [Google Scholar] [CrossRef]
- Allwood, J.M.; Braun, D.; Music, O. The effect of partially cut-out blanks on geometric accuracy in incremental sheet forming. J. Mater. Process. Technol. 2010, 210, 1501–1510. [Google Scholar] [CrossRef]
- Tanaka, S.; Nakamura, T.; Hayakawa, K.; Motomura, K. Residual Stress in Sheet Metal Parts Made by Incremental Forming Process. AIP Conf. Proc. 2007, 908, 775–780. [Google Scholar]
- Radu, C.; Herghelegiu, E.; Tampu, N.C.; Cristea, I.; Tampu, C. The Residual Stress State Generated by Single Point Incremental Forming of Aluminum Metal Sheets. Appl. Mech. Mater. 2013, 371, 148–152. [Google Scholar] [CrossRef]
- Radu, C.; Tampu, C.; Cristea, I.; Chirita, B. The Effect of Residual Stresses on the Accuracy of Parts Processed by SPIF. Mater. Manuf. Process. 2013, 28, 572–576. [Google Scholar] [CrossRef]
- Jiménez, I.; López, C.; Martinez-Romero, O.; Mares, P.; Siller, H.R.; Diabb, J.; Sandoval-Robles, J.A.; Elías-Zúñiga, A. Investigation of residual stress distribution in single point incremental forming of aluminum parts by X-ray diffraction technique. Int. J. Adv. Manuf. Technol. 2017, 91, 2571–2580. [Google Scholar] [CrossRef]
- Singh, A.; Agrawal, A. Investigation of surface residual stress distribution in deformation machining process for aluminum alloy. J. Mater. Process. Technol. 2015, 225, 195–202. [Google Scholar] [CrossRef]
- Shi, X.; Hussain, G.; I Butt, S.; Song, F.; Huang, D.; Liu, Y. The state of residual stresses in the Cu/Steel bonded laminates after ISF deformation: An experimental analysis. J. Manuf. Process. 2017, 30, 14–26. [Google Scholar] [CrossRef]
- Behera, A.K.; Ou, H. Effect of stress relieving heat treatment on surface topography and dimensional accuracy of incrementally formed grade 1 titanium sheet parts. Int. J. Adv. Manuf. Technol. 2016, 87, 3233–3248. [Google Scholar] [CrossRef]
- Maqbool, F.; Bambach, M. Revealing the Dominant Forming Mechanism of Single Point Incremental Forming (SPIF) by Splitting Plastic Energy Dissipation. Procedia Eng. 2017, 183, 188–193. [Google Scholar] [CrossRef]
- Mohammadi, A.; Vanhove, H.; Van Bael, A.; Seefeldt, M.; Duflou, J.R. The effect of laser radiation on the residual stress levels of single point incrementally formed (SPIF) parts. In Proceedings of the International Workshop on Thermal Forming and Welding Distortion, Bremen, Germany, 9–10 April 2014. [Google Scholar]
- Ambrogio, G.; Cozza, V.; Filice, L.; Micari, F. An analytical model for improving precision in single point incremental forming. J. Mater. Process. Technol. 2007, 191, 92–95. [Google Scholar] [CrossRef]
- Micari, F.; Ambrogio, G.; Filice, L. Shape and dimensional accuracy in Single Point Incremental Forming: State of the art and future trends. J. Mater. Process. Technol. 2007, 191, 390–395. [Google Scholar] [CrossRef]
- Maeda, A.; Jin, Y.; Kuboki, T. Light press of sheet metal edge for reducing residual stress generated by laser cutting considering mechanical properties and intensity of residual stress. J. Mater. Process. Technol. 2015, 225, 178–184. [Google Scholar] [CrossRef]
- Rendler, N.J.; Vigness, I. Hole-drilling strain-gage method of measuring residual stresses. Exp. Mech. 1966, 6, 577–586. [Google Scholar] [CrossRef]
- Niku-Lari, A.; Flavenot, J.; Lu, J. Measurement of residual-stress distribution by the incremental hole-drilling method. J. Mech. Work. Technol. 1985, 11, 167–188. [Google Scholar] [CrossRef]
- Bambach, M.; Taleb-Araghi, B.; Hirt, G.; Reimers, W. Error control in explicit finite element simulation of incremental sheet metal forming. In Proceedings of the 7th International Conference and Workshop on 3D Sheet Metal Forming Processes (Numisheet2008), Interlaken, Switzerland, 1–5 September 2008. [Google Scholar]
- Chaboche, J.L.; Rousselier, G. On the Plastic and Viscoplastic Constitutive Equations—Part I: Rules Developed with Internal Variable Concept. J. Press. Vessel Technol. 1983, 105, 153–158. [Google Scholar] [CrossRef]
- Henrard, C.; Bouffioux, C.; Eyckens, P.; Sol, H.; Duflou, J.R.; Van Houtte, P.; Van Bael, A.; Duchêne, L.; Habraken, A.M. Forming forces in single point incremental forming: Prediction by finite element simulations, validation and sensitivity. Comput. Mech. 2010, 47, 573–590. [Google Scholar] [CrossRef]
- Bambach, M.; Hirt, G. Performance Assessment of Element Formulations and Constitutive Laws for the Simulation of Incremental Sheet Forming (ISF). Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.485.6511&rep=rep1&type=pdf (accessed on 10 April 2019).
- Maqbool, F.; Bambach, M. Dominant deformation mechanisms in single point incremental forming (SPIF) and their effect on geometrical accuracy. Int. J. Mech. Sci. 2018, 136, 279–292. [Google Scholar] [CrossRef]
- Maqbool, F.; Bambach, M. A Modular Tooling Set-Up for Incremental Sheet Forming (ISF) with Subsequent Stress-Relief Annealing under Partial Constraints. In Proceedings of the AIP Conference, Dublin, Ireland, 26–28 April 2017. [Google Scholar]


| Experiment No. | Tool Diameter (D/mm) | Wall Angle α | Tool Step-Down (Z/mm) |
|---|---|---|---|
| 1 | 5 | 30° | 0.25 |
| 2 | 5 | 30° | 0.5 |
| 3 | 5 | 30° | 0.75 |
| 4 | 5 | 45° | 0.25 |
| 5 | 5 | 60° | 0.25 |
| 6 | 10 | 30° | 0.25 |
| 7 | 20 | 30° | 0.25 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maqbool, F.; Bambach, M. Experimental and Numerical Investigation of the Influence of Process Parameters in Incremental Sheet Metal Forming on Residual Stresses. J. Manuf. Mater. Process. 2019, 3, 31. https://doi.org/10.3390/jmmp3020031
Maqbool F, Bambach M. Experimental and Numerical Investigation of the Influence of Process Parameters in Incremental Sheet Metal Forming on Residual Stresses. Journal of Manufacturing and Materials Processing. 2019; 3(2):31. https://doi.org/10.3390/jmmp3020031
Chicago/Turabian StyleMaqbool, Fawad, and Markus Bambach. 2019. "Experimental and Numerical Investigation of the Influence of Process Parameters in Incremental Sheet Metal Forming on Residual Stresses" Journal of Manufacturing and Materials Processing 3, no. 2: 31. https://doi.org/10.3390/jmmp3020031
APA StyleMaqbool, F., & Bambach, M. (2019). Experimental and Numerical Investigation of the Influence of Process Parameters in Incremental Sheet Metal Forming on Residual Stresses. Journal of Manufacturing and Materials Processing, 3(2), 31. https://doi.org/10.3390/jmmp3020031





