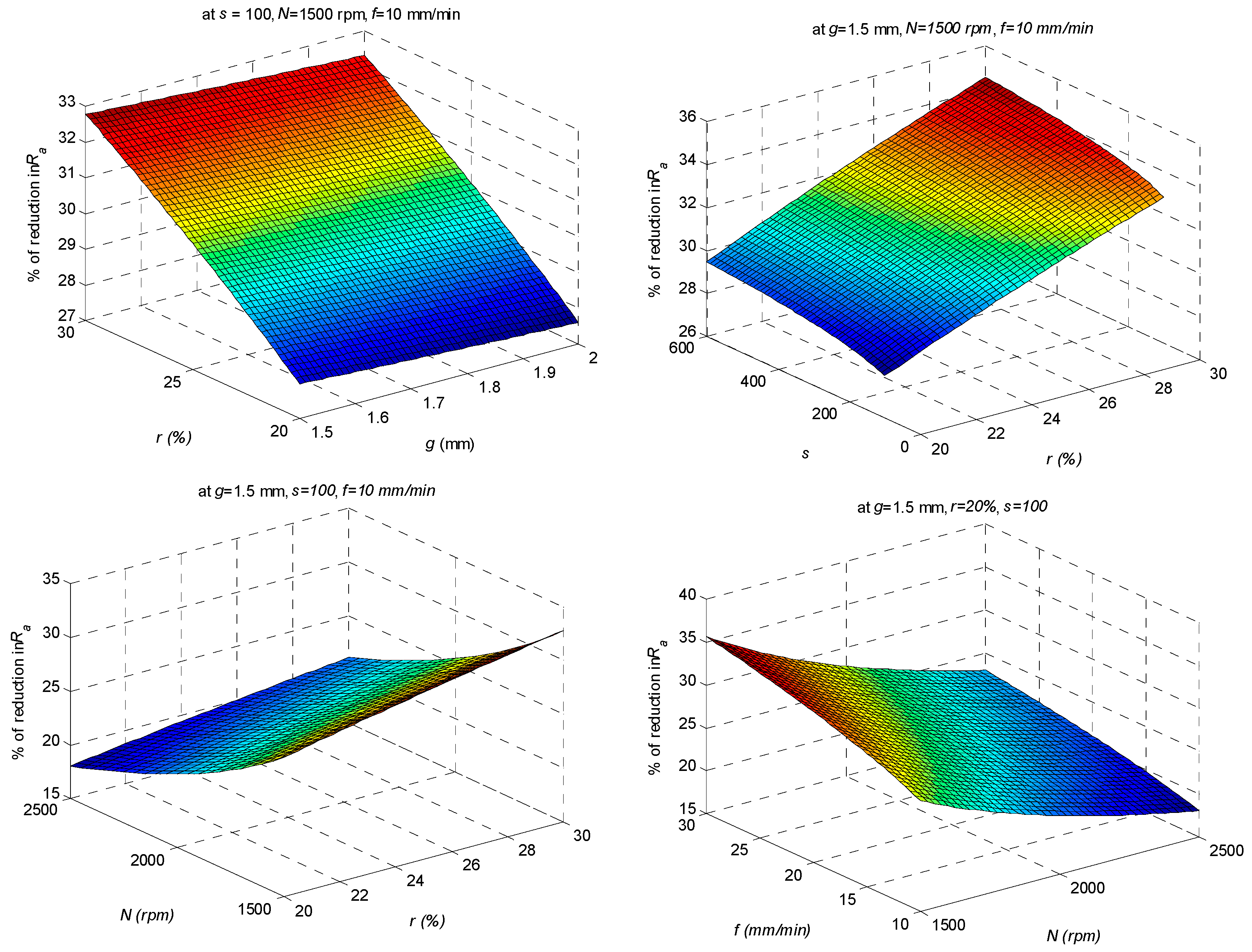
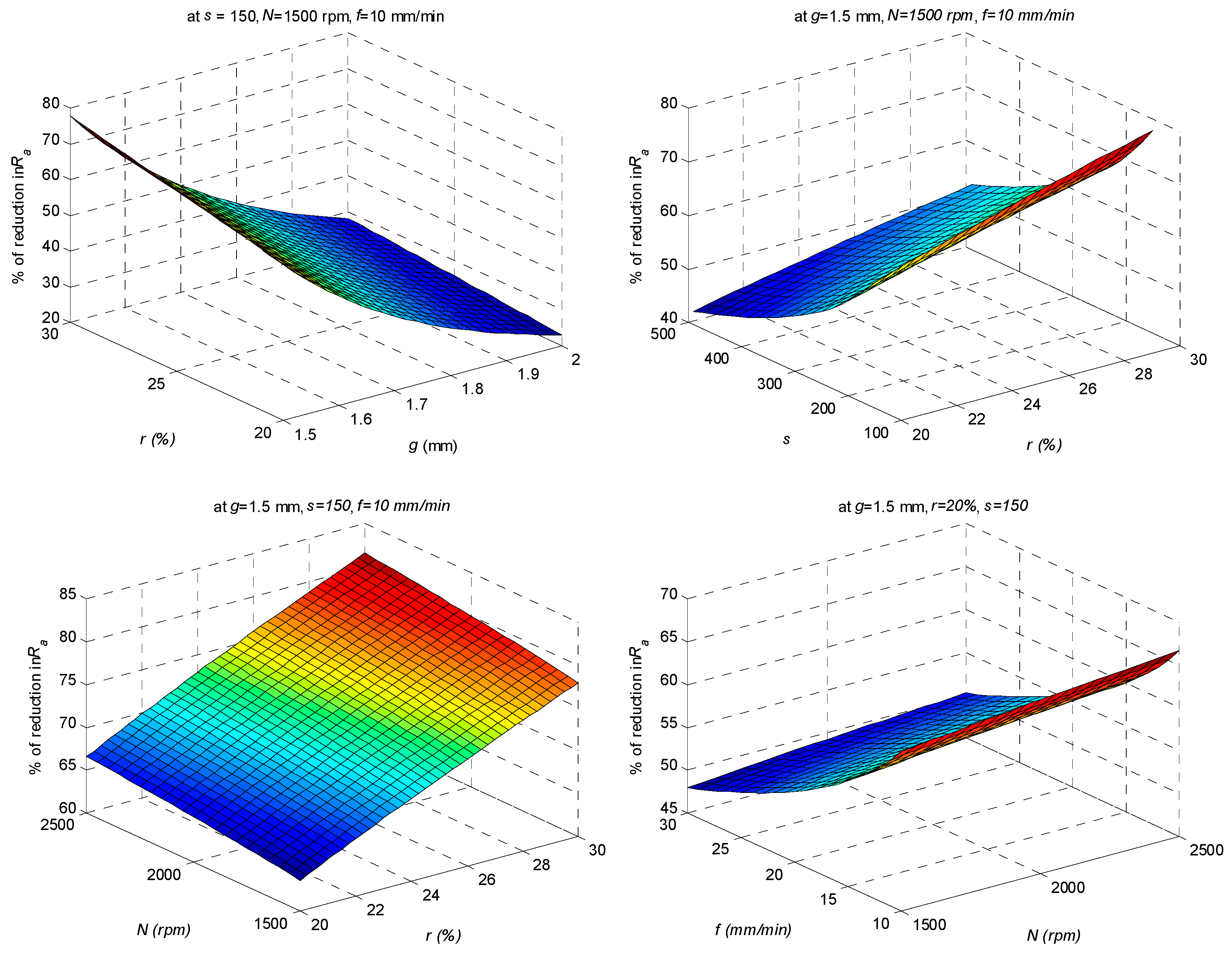
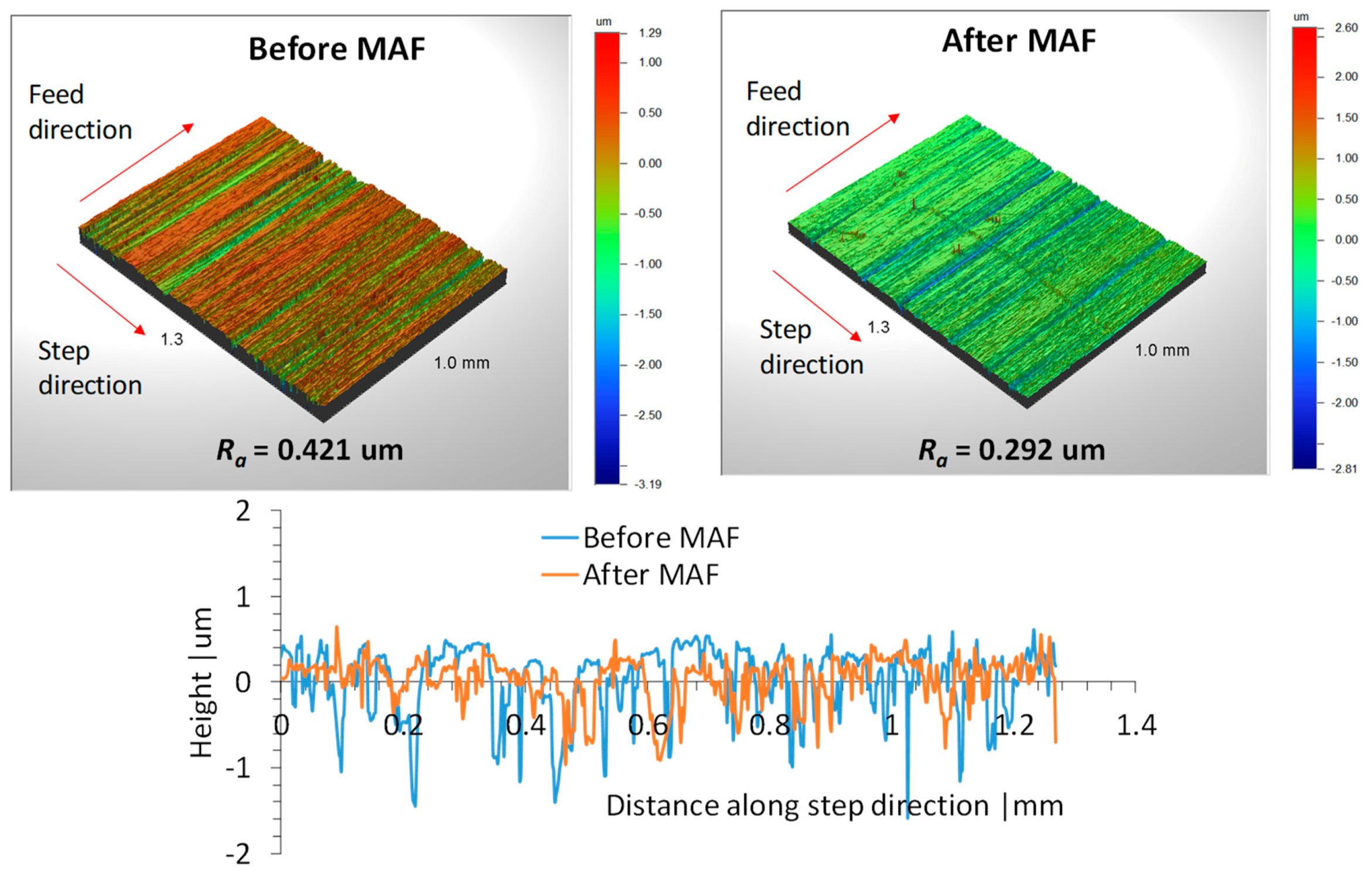
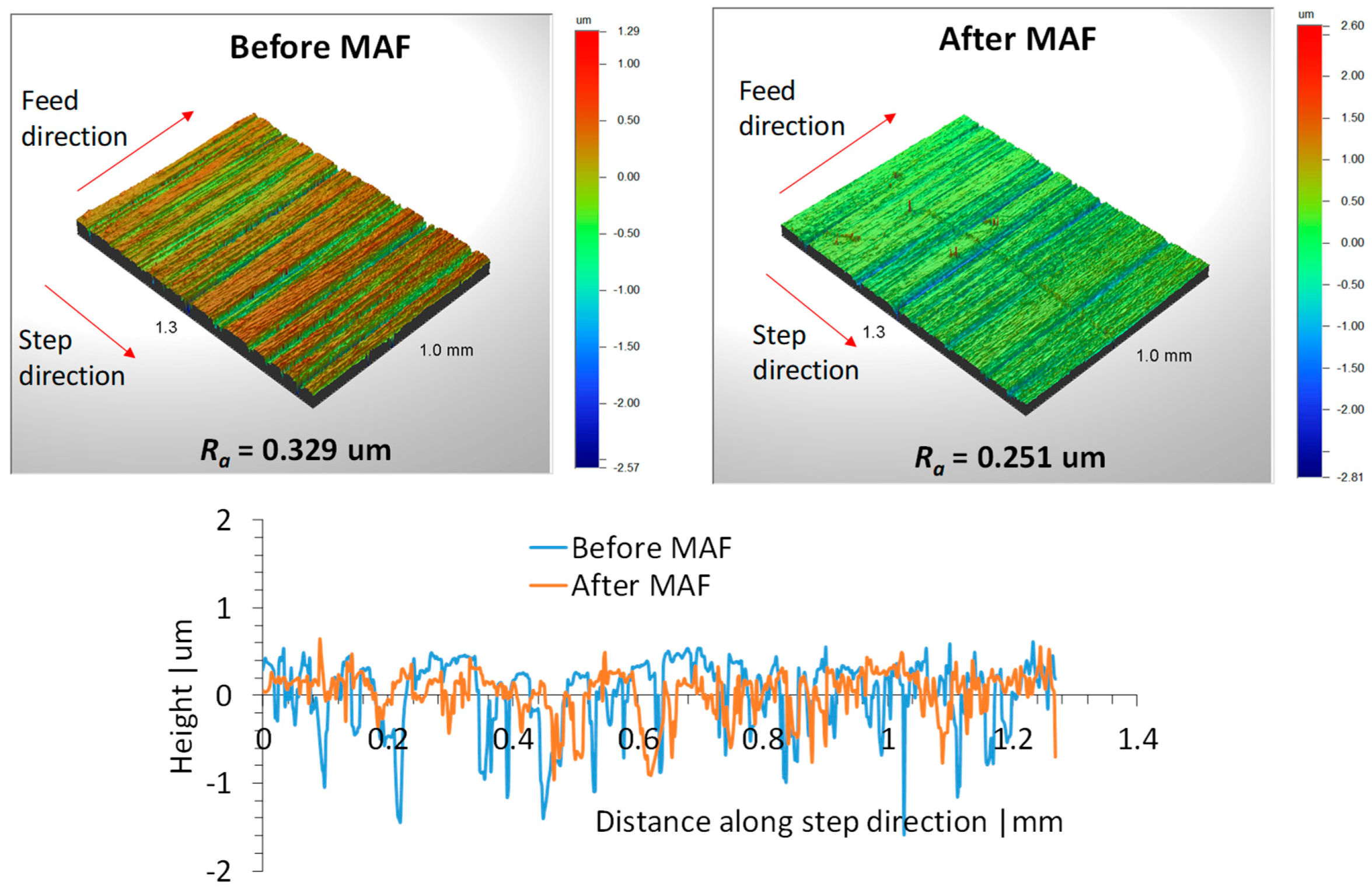
The interplay of different variables in MAF is very complex and, hence, the optimum condition is unique for a given type of abrasive material considered, i.e., the choice of the desired surface integrity dictates the appropriate control variables as demanded. It is, thus, evident that MAF has tremendous potential to minimize roughness on metallic surfaces, thereby enhancing the quality and life of the product.
Our results indicate that partially bonded particles, i.e., mixing particles with a small amount cutting oil, were found to be efficient in removing micro-particles. It was perceived that slightly bonded particles may create a uniform flexible magnetic abrasive brush with a favorable motion of particles within the brush, thereby resulting in a smoother surface without imparting any further skewedness into surface. It was reported by Guo et al. [
9] that, upon keeping other process variables constant in MAF, SiC and coarse abrasives show higher material removal rate (MRR) than Al
2O
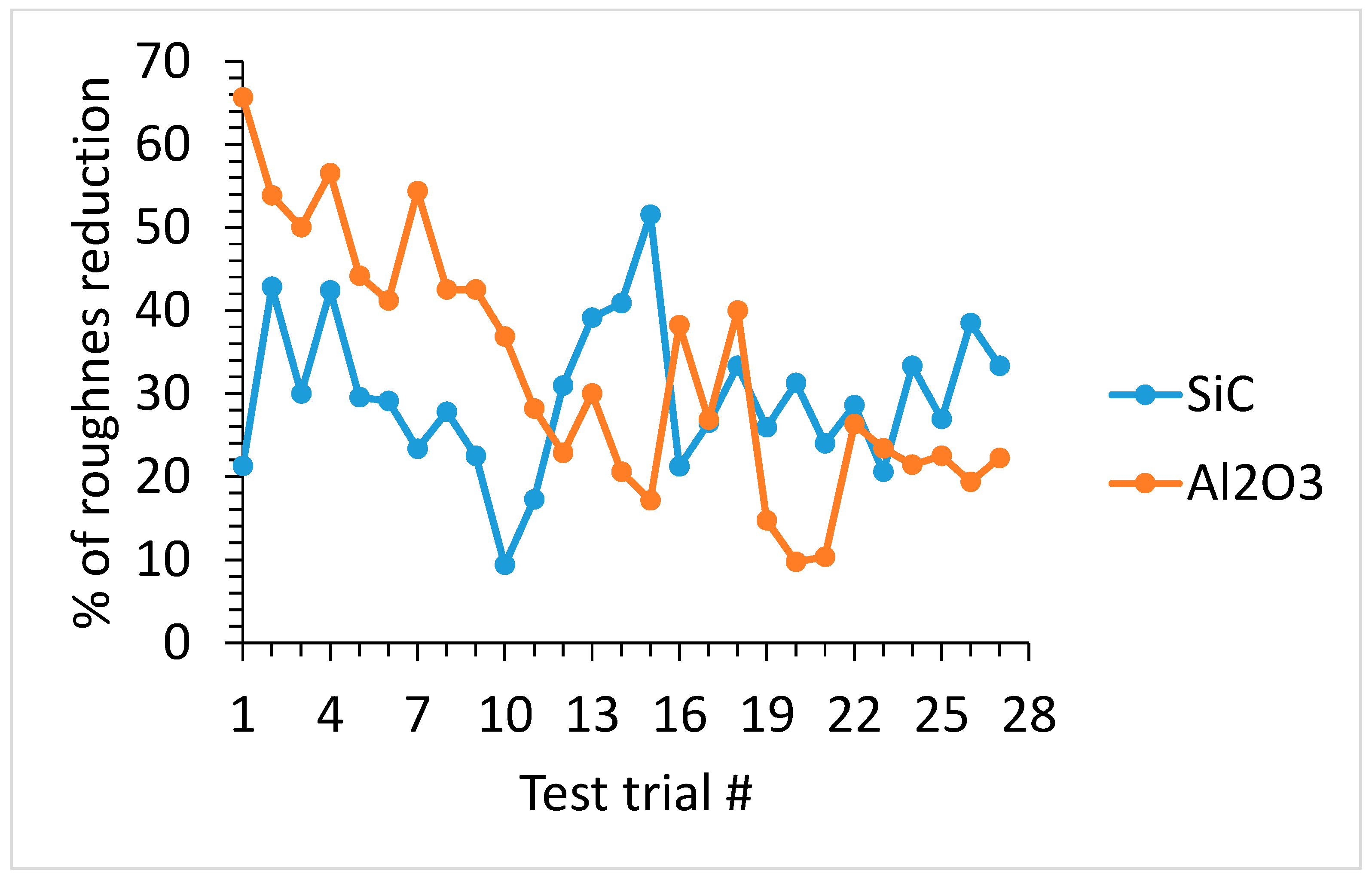
3 and fine abrasives, meaning that SiC with larger abrasives reduces surface roughness significantly. They also highlighted a slight discrepancy in the force data, indicating that finer abrasives cause higher force, which is not the case in the micro-cutting of material. Surprisingly, our results suggest an opposite perspective. In most cases, coarser Al
2O
3 was found to be more beneficial than finer SiC abrasives, although a moderate fluctuation of roughness reduction between them was observed across the test trials (see
Figure 13). This can be attributed to the long and sharp geometric edge of Al
2O
3 particles (see
Figure 2), which enabled removing more materials via significant grinding and polishing actions of abrasive particles as compared to round and spherically shaped SiC particles. Furthermore, due to successive grinding and polishing actions, long abrasive particles may break, which can result in sharper particles, thereby causing more material removal. A similar rationale was reported in Reference [
3] via a pertinent theoretical model elucidating the mechanism for material removal in MAF. Yan et al. [
22], however, reported that SiC removes slightly more material than Al
2O
3, but they did not explain the effect of particle size and shape other than their hardness difference. Nevertheless, it must be noted that, as MAF is an intricate process involving the dynamics of a range of parameters, comparing performance metrics against one or two process variable/s may not be a valid argument. Such a conclusion is often imperatively stressed elsewhere in literature [
23]. While surface roughness is considered a widely accepted performance indictor when the quality of surface is concerned, a more microscopic observation underpinning the material removal mechanism and surface damages, i.e., micro/nano cracks, fractures, and scratches, must be investigated to provide a holistic and informed quality evaluation of MAF [
9]. In other words, a future mathematical model may need to take those perspectives into account to solicit the quality prediction. Similar to conventional cutting, feed rate is a critical parameter affecting the material removal rate and roughness. In other words, a lower feed rate is often recommended while sacrificing productivity to some extent. Hence, an intermediate feed rate would be optimal. Our results indicate that, when MAFed with SiC, a high feed rate seems to improve the finish, while the opposite is true for Al
2O
3. This could be due to the multiple factors associated with the process, such as variation of the shape and size distribution of abrasive particles and the difference between actual and nominal (theoretical) feed rate. As can be seen in
Figure 2, irrespective of mesh size, Al
2O
3 abrasives show a very non-uniform shape (e.g., long strips), while SiC particles are of a more regular spherical shape. Furthermore, while the nominal (commanded) feed rate is 10 mm/min, a variation of actual feed rate with respect to finishing time is clearly observed (see
Figure 13), and the actual feed rate is always lower than the nominal. While this is a factor related to the machine’s limitation, such a discrepancy is likely to affect the overall material removal rate, which can result in a variation of roughness reduction between SiC and Al
2O
3.
Overall, it is imperative to say that the difference in important factors in the final roughness is intriguing and will require further investigations and experiments with other finishing (abrasive) materials and finished parts. This will determine if additional variables will need to be considered so as to develop a generalized model of the MAF, and a set of experiments will need to be conducted with each class of abrasive material, with specific models created as a result. For instance, other important parameters such as magnetic pressure (or force) and finishing time may change surface topography, as well as material removal mechanism, thus impacting polishing performance in MAF. Future works will aim to address the above to provide comprehensive insight into the process mechanics, thereby realizing the potential benefit and robust application of MAF. In particular, mechanisms of how different abrasive shapes or distributions dynamically interact with each other in cutting material via abrasive action need to be investigated. In addition, careful attention must be paid to experimental protocol, including preparing the initial surface and the abrasive mixture, in addition to the control of process parameters, to ensure consistency and reliability of response measurements.