Development of Steps in an Automated Process Chain for Piezoceramic-Metal Compound Production
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Adhesive Sika Fast 5215 NT
2.1.1. Curing Kinetics and Mechanical Properties
2.1.2. Identification of Rheological Properties
2.1.3. Dielectric Analysis (DEA)
2.2. Aluminum Sheets
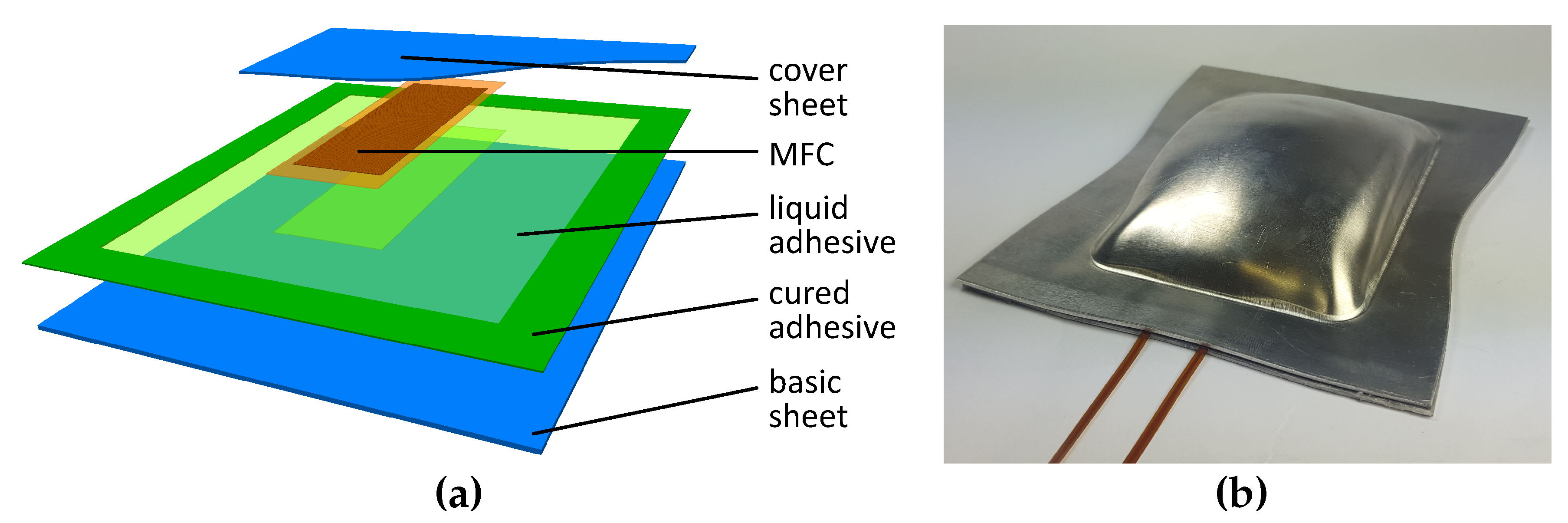
2.3. Macro Fiber Composites (MFC)
2.4. Piezoceramic-Metal Compounds
2.5. Production Process and Automated Fabrication Unit (AFU)
3. Results
3.1. Curing Model
3.2. Process Window
3.3. Investigation with Automated Process Chain
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DEA | Dielectric analysis |
| MFC | Macro fiber composite |
| AFU | Automated fabrication unit |
References
- Suleman, A.; Prasad, E.; Blackow, R.; Waechter, D. Smart Structures—An Overview. In Smart Structures: Applications and Related Technologies; Suleman, A., Ed.; Springer Verlag: Wien, Austria, 2001; pp. 3–16. [Google Scholar] [CrossRef]
- Bekas, D.G.; Sharif-Khodaei, Z.; Aliabadi, M.F. An Innovative Diagnostic Film for Structural Health Monitoring of Metallic and Composite Structures. Sensors 2018, 18, 2084. [Google Scholar] [CrossRef]
- Park, G.; Farrar, C.R.; di Scalea, F.L.; Coccia, S. Performance assessment and validation of piezoelectric active-sensors in structural health monitoring. Smart Mater. Struct. 2006, 15, 1673–1683. [Google Scholar] [CrossRef]
- Arrieta, A.F.; van Gemmeren, V.; Anderson, A.J.; Weaver, P.M. Dynamics and control of twisting bi-stable structures. Smart Mater. Struct. 2018, 27, 025006. [Google Scholar] [CrossRef] [Green Version]
- Asundi, A.; Choi, A.Y. Fiber metal laminates: An advanced material for future aircraft. J. Mater. Process. Technol. 1997, 63, 384–394. [Google Scholar] [CrossRef]
- Botelho, E.C.; Silva, R.A.; Pardini, L.C.; Rezende, M.C. A review on the development and properties of continuous fiber/epoxy/aluminum hybrid composites for aircraft structures. Mater. Res. 2006, 9, 247–256. [Google Scholar] [CrossRef] [Green Version]
- Burchitz, I.; Boesenkool, R.; van der Zwaag, S.; Tassoul, M. Highlights of designing with Hylite—A new material concept. Mater. Des. 2005, 26, 271–279. [Google Scholar] [CrossRef]
- Palkowski, H.; Lange, G. Austenitic Sandwich Materials in the Focus of Research. In Proceedings of the 2nd International Conference Deformation Processing and Structure of Materials, Belgrade, Serbia, 26–28 May 2005; pp. 19–27. [Google Scholar]
- Palkowski, H.; Giese, P.; Wesling, V.; Lange, G.; Spieler, S.; Göllner, J. Neuartige Sandwichverbunde—Herstellung, Umformverhalten, Fügen und Korrosionsverhalten. Materialwiss. Werkstofftechn. 2006, 37, 605–612. [Google Scholar] [CrossRef]
- Stegmaier, T.; Hager, T.; Yilmaz, D.; Vohrer, A.; Sürth, M.; Planck, H.; Wagner, S.; Becker, D.; Hahn, O.; Teutenberg, D. Stahlblech-Mehrschichtverbund mit textiler Einlage. Werkstattstech. Online 2008, 10, 866–870. [Google Scholar]
- Sexton, A.; Cantwell, W.; Kalyanasundaram, S. Stretch forming studies on a fibre metal laminate based on a self-reinforcing polypropylene composite. Compos. Struct. 2012, 94, 431–437. [Google Scholar] [CrossRef]
- Jackson, K.; Allwood, J.; Landert, M. Incremental forming of sandwich panels. J. Mater. Process. Technol. 2008, 204, 290–303. [Google Scholar] [CrossRef]
- Palkowski, H.; Lange, G. Creation of Tailored High-Strength, Hybrid Sandwich Structures. Adv. Mater. Res. 2007, 22, 27–36. [Google Scholar] [CrossRef]
- Sokolova, O.; Carradó, A.; Palkowski, H. Production of customized high-strength hybrid sandwich structures. Adv. Mater. Res. 2010, 137, 81–128. [Google Scholar] [CrossRef]
- Nestler, M.; Drossel, W.G.; Hensel, S.; Müller, R. Fabrication Method for Series Production of Sheet Metal Parts with Integrated Piezoelectric Transducers. Procedia Technol. 2014, 15, 494–502. [Google Scholar] [CrossRef] [Green Version]
- SikaFast®-5215 NT—Fast Curing, Two-Part Structural Adhesive; Version 1; Sika Schweiz AG: Zürich, Switzerland, 2013.
- Müller, M.; Müller, B.; Hensel, S.; Nestler, M.; Jahn, S.; Wittstock, V.; Schubert, A.; Drossel, W.G. Structural Integration of PZT Fibers in Deep Drawn Sheet Metal for Material-integrated Sensing and Actuation. Procedia Technol. 2014, 15, 658–667. [Google Scholar] [CrossRef]
- Thielicke, B.; Gesang, T.; Wierach, P. Reliability of piezoceramic patch sensors under cyclic mechanical loading. Smart Mater. Struct. 2003, 12, 993–996. [Google Scholar] [CrossRef]
- Drossel, W.G.; Müller, R.; Nestler, M.; Hensel, S. Integration in Sheet Metal Structures. In Material-Integrated Intelligent Systems—Technology and Applications; Wiley-Blackwell: Hoboken, NJ, USA, 2017; Chapter 8; pp. 201–216. [Google Scholar] [CrossRef]
- Kamal, M.R.; Sourour, S. Kinetics and thermal characterization of thermoset cure. Polym. Eng. Sci. 1973, 13, 59–64. [Google Scholar] [CrossRef]
- Sourour, S.; Kamal, M. Differential scanning calorimetry of epoxy cure: Isothermal cure kinetics. Thermochim. Acta 1976, 14, 41–59. [Google Scholar] [CrossRef]
- Lee, W.I.; Loos, A.C.; Springer, G.S. Heat of Reaction, Degree of Cure, and Viscosity of Hercules 3501-6 Resin. J. Compos. Mater. 1982, 16, 510–520. [Google Scholar] [CrossRef]
- Fereshteh-Saniee, N.; Reynolds, N.; Kelly, C.A.; Wilson, P.R.; Jenkins, M.J.; Kendall, K.N. Introducing Cryomilling for Reliable Determination of Resin Content and Degree of Cure in Structural Carbon Fibre Reinforced Thermoset Composites. Compos. Part A 2018. [Google Scholar] [CrossRef]
- Ferracane, J.; Condon, J. Post-cure heat treatments for composites: Properties and fractography. Dent. Mater. 1992, 8, 290–295. [Google Scholar] [CrossRef]
- Czasch, P.; Ilie, N. In vitro comparison of mechanical properties and degree of cure of bulk fill composites. Clin. Oral Investig. 2013, 17, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Lyon, R.E.; Chike, K.E.; Angel, S.M. In situ cure monitoring of epoxy resins using fiber-optic Raman spectroscopy. J. Appl. Polym. Sci. 1994, 53, 1805–1812. [Google Scholar] [CrossRef]
- Hardis, R.; Jessop, J.L.; Peters, F.E.; Kessler, M.R. Cure kinetics characterization and monitoring of an epoxy resin using DSC, Raman spectroscopy, and DEA. Compos. Part A 2013, 49, 100–108. [Google Scholar] [CrossRef]
- Bang, K.G.; Kwon, J.W.; Lee, D.G.; Lee, J.W. Measurement of the degree of cure of glass fiber–epoxy composites using dielectrometry. J. Mater. Process. Technol. 2001, 113, 209–214. [Google Scholar] [CrossRef]
- Sernek, M.; Kamke, F.A. Application of dielectric analysis for monitoring the cure process of phenol formaldehyde adhesive. Int. J. Adhes. Adhes. 2007, 27, 562–567. [Google Scholar] [CrossRef]
- Steinhaus, J.; Hausnerova, B.; Haenel, T.; Großgarten, M.; Möginger, B. Curing kinetics of visible light curing dental resin composites investigated by dielectric analysis (DEA). Dent. Mater. 2014, 30, 372–380. [Google Scholar] [CrossRef]
- White, S.R.; Mather, P.T.; Smith, M.J. Characterization of the cure-state of DGEBA-DDS epoxy using ultrasonic, dynamic mechanical, and thermal probes. Polym. Eng. Sci. 2002, 42, 51–67. [Google Scholar] [CrossRef]
- O’Brien, D.J.; Mather, P.T.; White, S.R. Viscoelastic Properties of an Epoxy Resin during Cure. J. Compos. Mater. 2001, 35, 883–904. [Google Scholar] [CrossRef] [Green Version]
- Hsich, H.S.Y. Kinetic model of cure reaction and filler effect. J. Appl. Polym. Sci. 1982, 27, 3265–3277. [Google Scholar] [CrossRef]
- Simon, S.L.; Mckenna, G.B.; Sindt, O. Modeling the evolution of the dynamic mechanical properties of a commercial epoxy during cure after gelation. J. Appl. Polym. Sci. 2000, 76, 495–508. [Google Scholar] [CrossRef]
- Kashani, P.; Minaie, B. An ex-situ state-based approach using rheological properties to measure and model cure in polymer composites. J. Reinf. Plast. Compos. 2011, 30, 123–133. [Google Scholar] [CrossRef]
- Holling, C.S. The Components of Predation as Revealed by a Study of Small-Mammal Predation of the European Pine Sawfly. Can. Entomol. 1959, 91, 293–320. [Google Scholar] [CrossRef]
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; van’t Riet, K. Modeling of the Bacterial Growth Curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [PubMed]
- Drossel, W.G.; Hensel, S.; Nestler, M.; Müller, R. Method for Large-Scale Production of Piezoceramic-Metal-Compounds. Adv. Eng. Mater. 2018. [Google Scholar] [CrossRef]
- Sodano, H.A.; Lloyd, J.; Inman, D.J. An experimental comparison between several active composite actuators for power generation. Smart Mater. Struct. 2006, 15, 1211. [Google Scholar] [CrossRef]

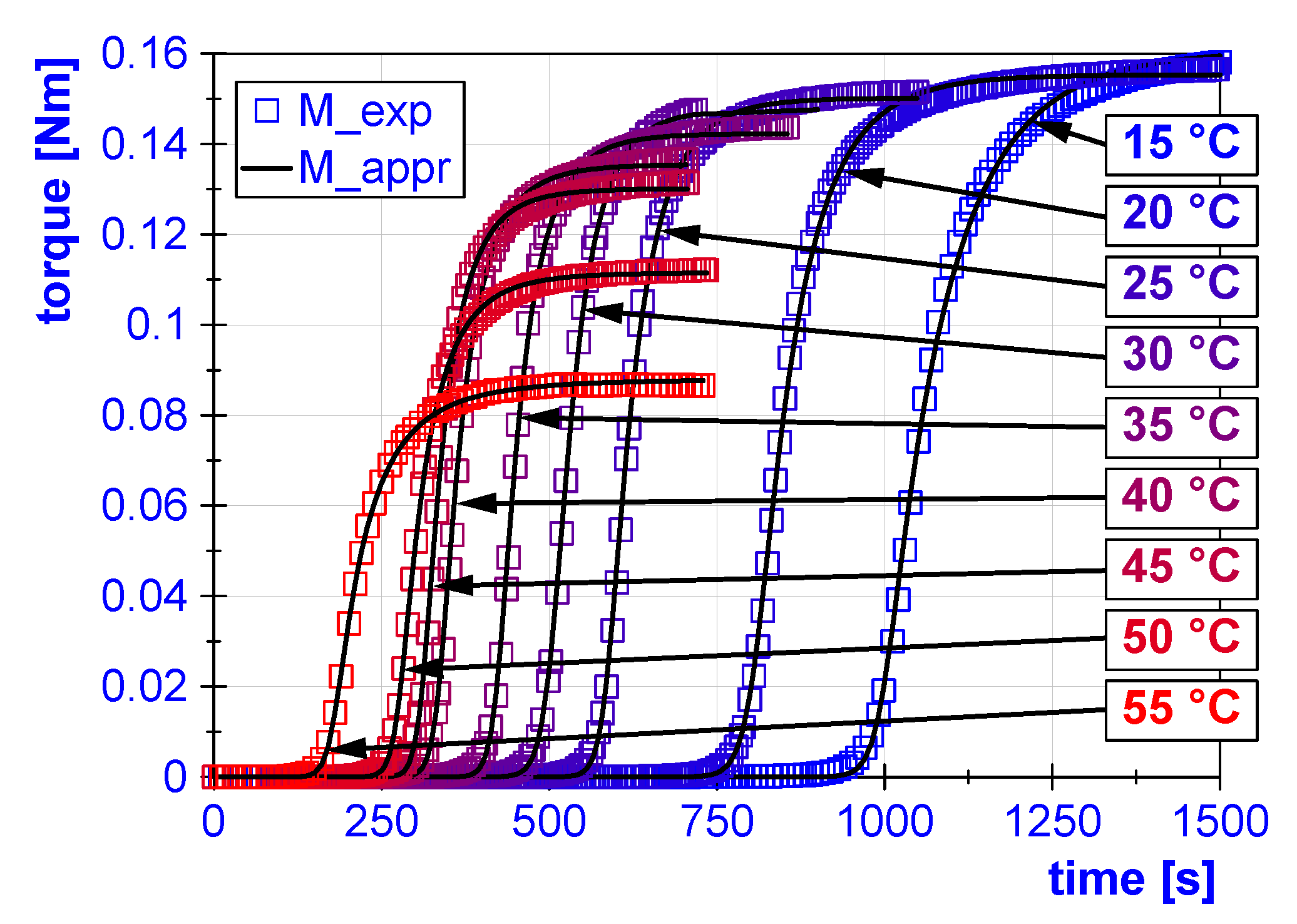
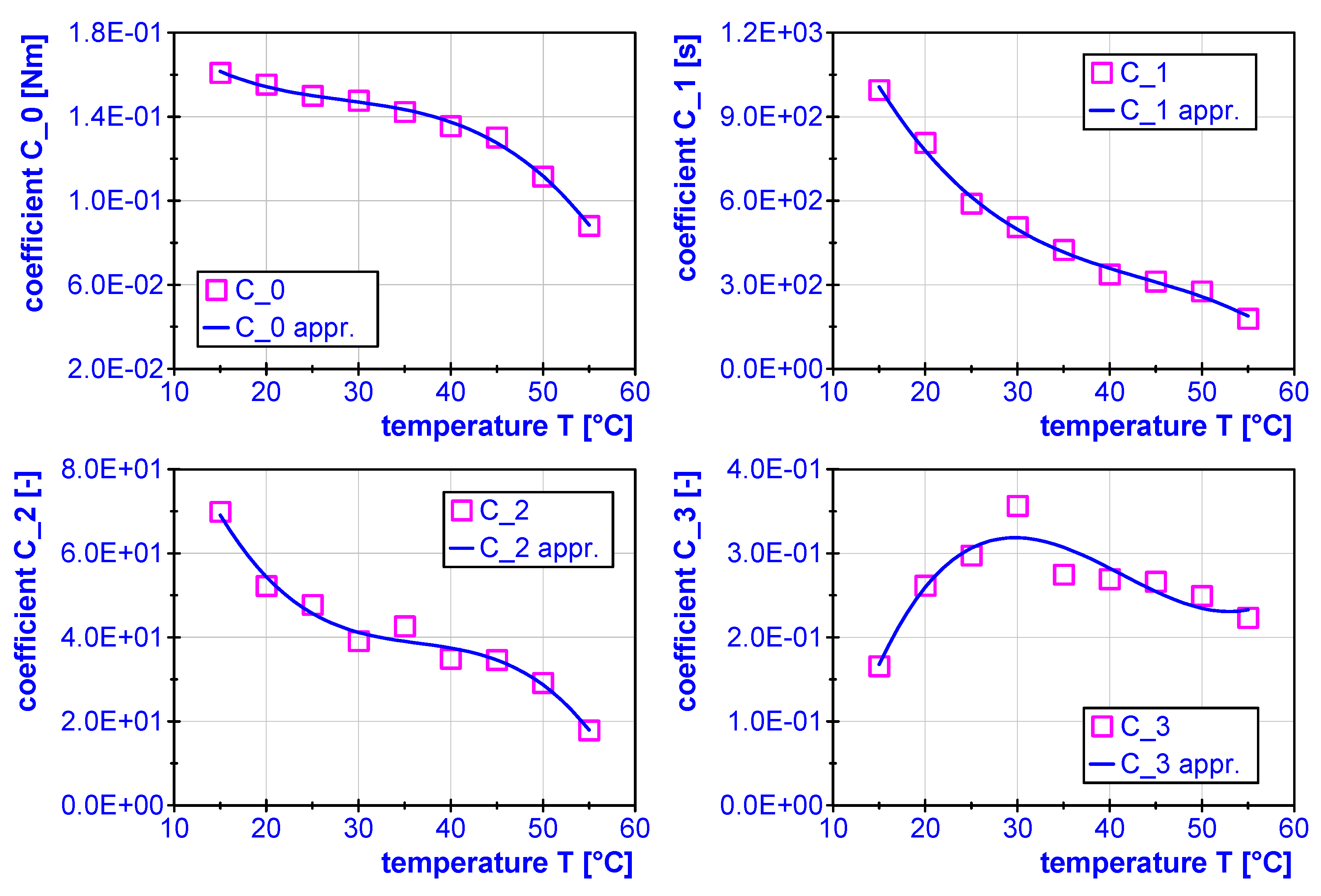
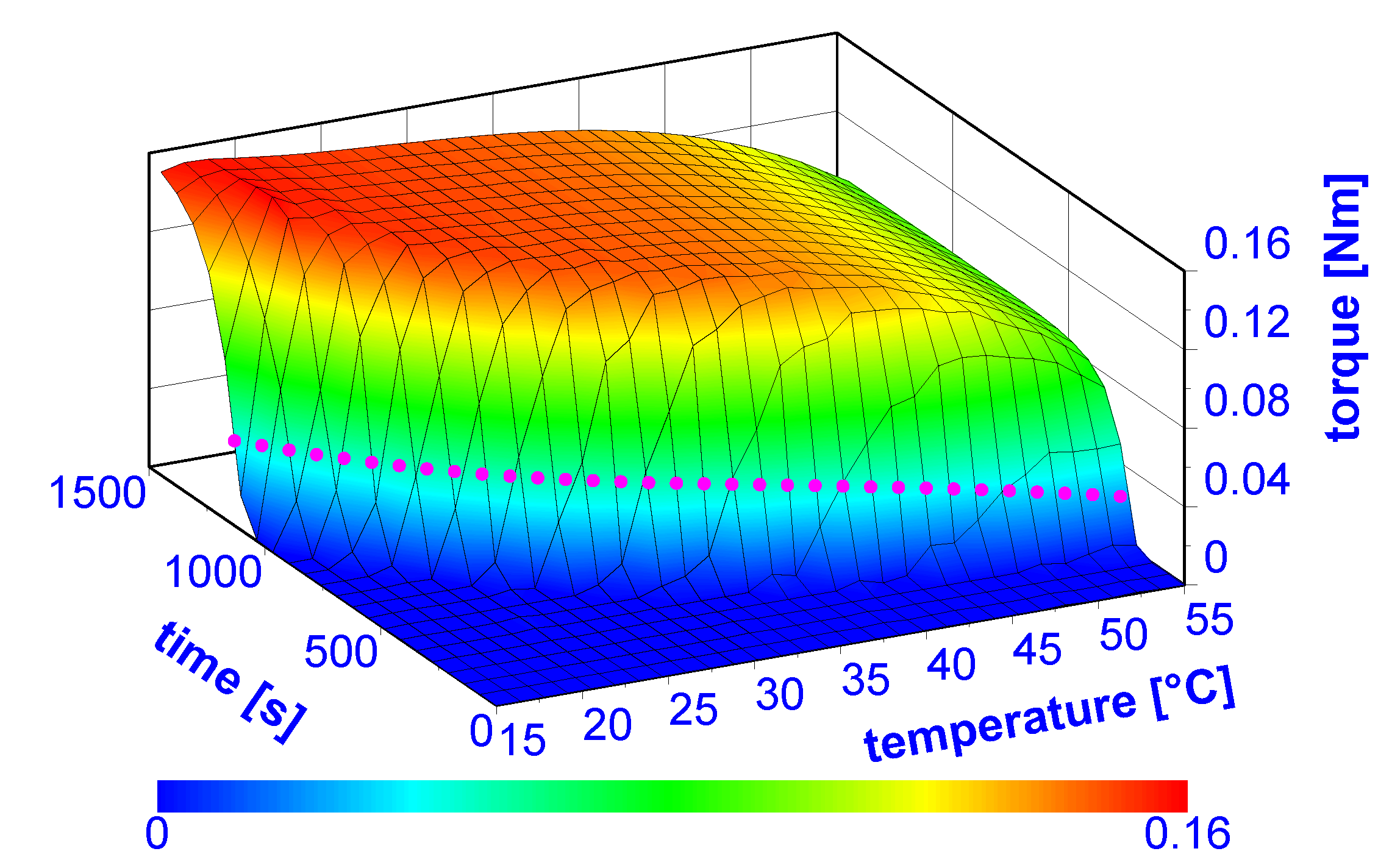
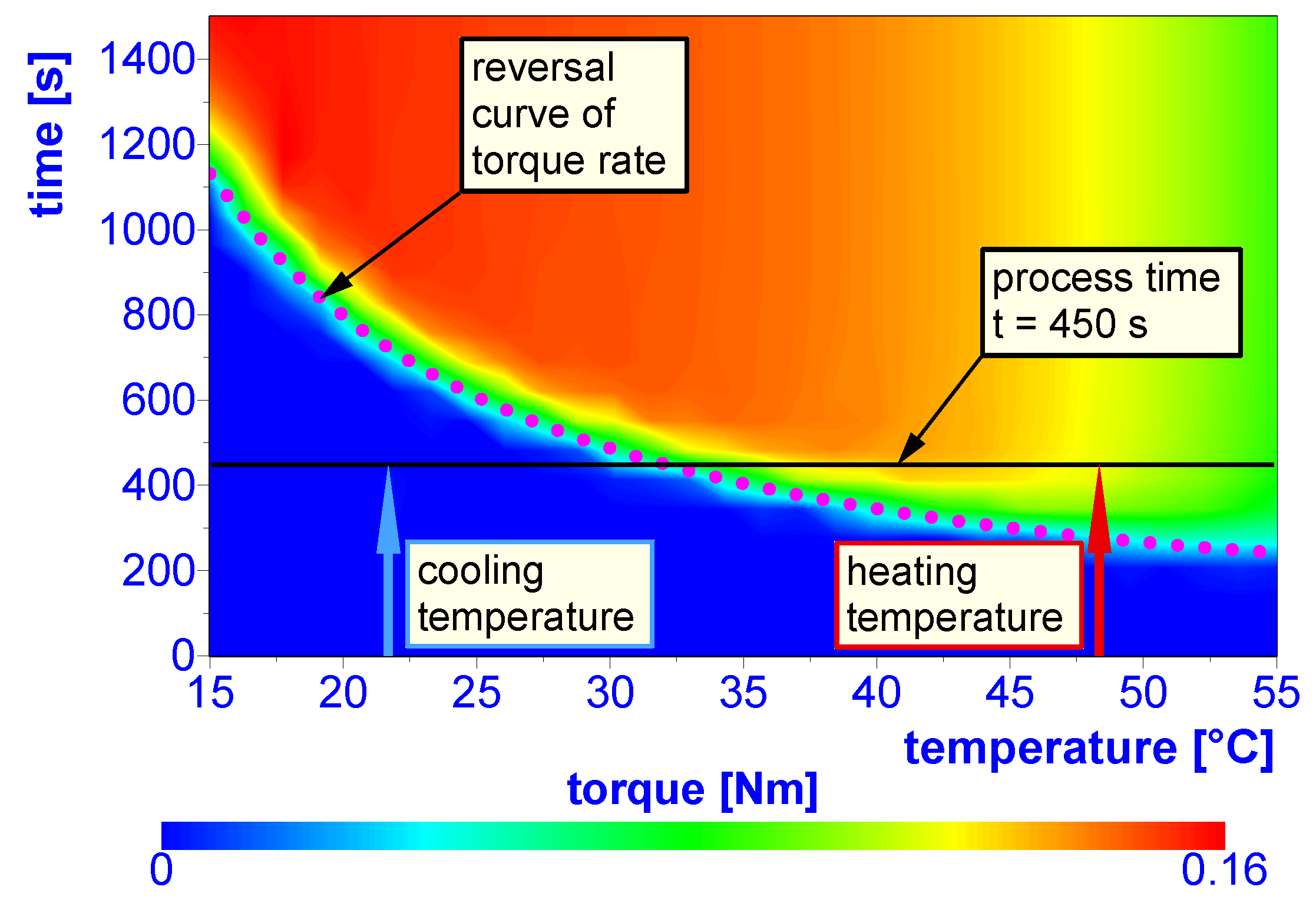
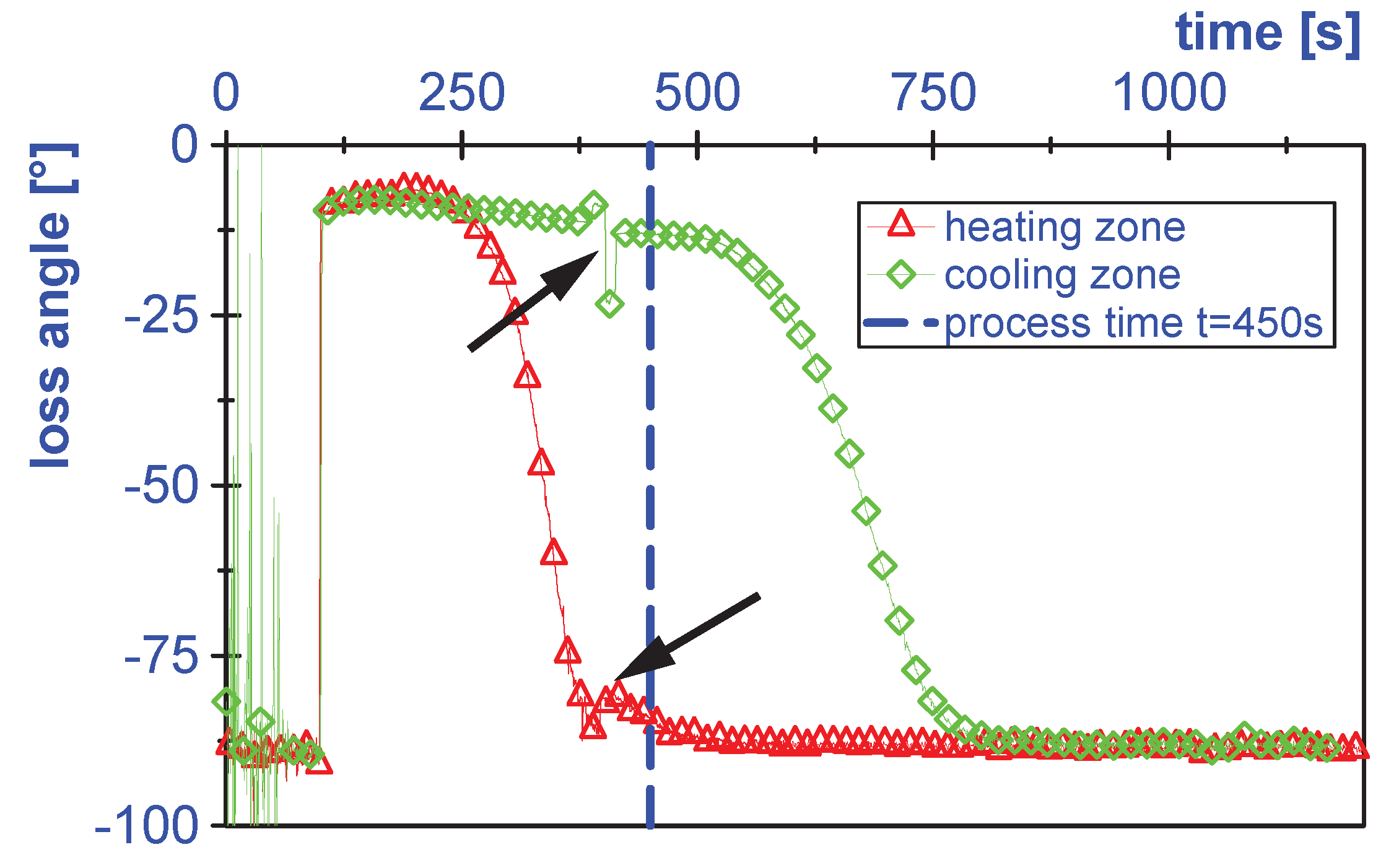

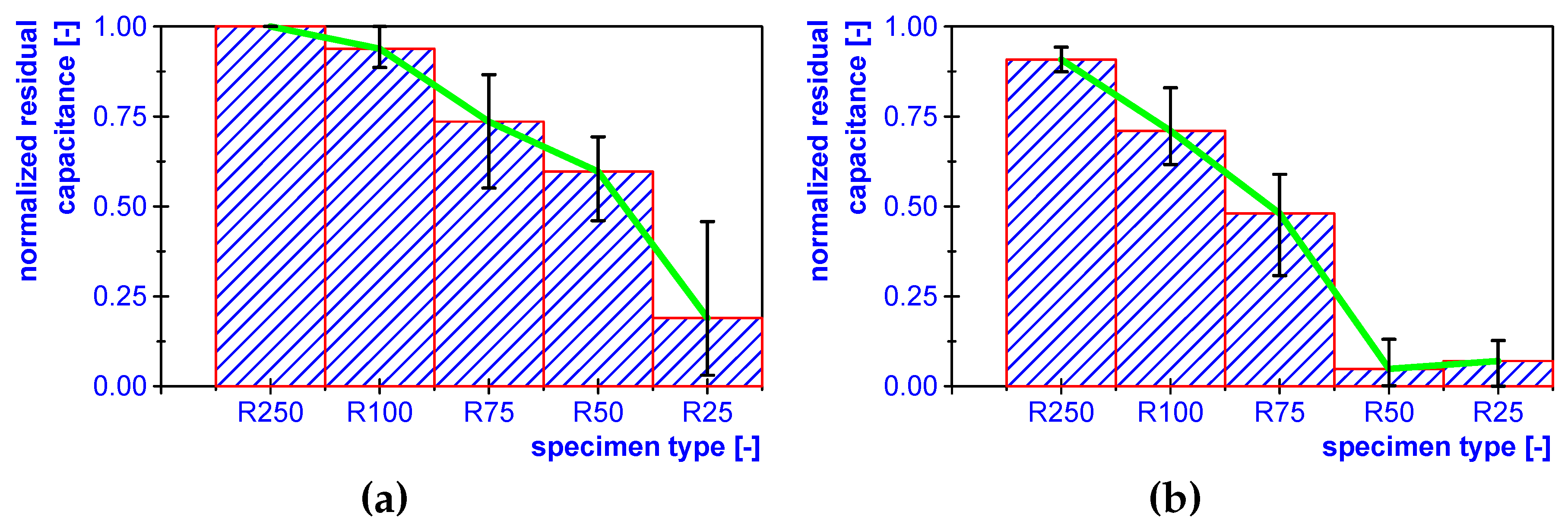
| T [C] | [N m] | [s] | [-] | [-] |
|---|---|---|---|---|
| 15 | 1.61 × 10−1 | 9.96 × 102 | 6.99 × 101 | 1.66 × 10−1 |
| 20 | 1.55 × 10−1 | 8.07 × 102 | 5.22 × 101 | 2.61 × 10−1 |
| 25 | 1.50 × 10−1 | 5.90 × 102 | 4.77 × 101 | 2.97 × 10−1 |
| 30 | 1.48 × 10−1 | 5.06 × 102 | 3.91 × 101 | 3.56 × 10−1 |
| 35 | 1.42 × 10−1 | 4.25 × 102 | 4.26 × 101 | 2.75 × 10−1 |
| 40 | 1.36 × 10−1 | 3.38 × 102 | 3.49 × 101 | 2.69 × 10−1 |
| 45 | 1.30 × 10−1 | 3.12 × 102 | 3.46 × 101 | 2.66 × 10−1 |
| 50 | 1.12 × 10−1 | 2.77 × 102 | 2.91 × 101 | 2.49 × 10−1 |
| 55 | 0.88 × 10−1 | 1.79 × 102 | 1.79 × 101 | 2.23 × 10−1 |
| i | ||||
|---|---|---|---|---|
| 0 | 1.999995 × 10−4 | −2.343313 × 10−6 | ||
| 1 | ||||
| 2 | ||||
| 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drossel, W.-G.; Nestler, M.; Hensel, S. Development of Steps in an Automated Process Chain for Piezoceramic-Metal Compound Production. J. Manuf. Mater. Process. 2019, 3, 3. https://doi.org/10.3390/jmmp3010003
Drossel W-G, Nestler M, Hensel S. Development of Steps in an Automated Process Chain for Piezoceramic-Metal Compound Production. Journal of Manufacturing and Materials Processing. 2019; 3(1):3. https://doi.org/10.3390/jmmp3010003
Chicago/Turabian StyleDrossel, Welf-Guntram, Matthias Nestler, and Sebastian Hensel. 2019. "Development of Steps in an Automated Process Chain for Piezoceramic-Metal Compound Production" Journal of Manufacturing and Materials Processing 3, no. 1: 3. https://doi.org/10.3390/jmmp3010003





