High Seam Surface Quality in Keyhole Laser Welding: Buttonhole Welding
Abstract
:1. Introduction
- full penetration through the sheet material
- the melt pool must be wider than the sheet thickness
- oversized melt pool widths lead to a buttonhole destabilization and the risk of pinholes
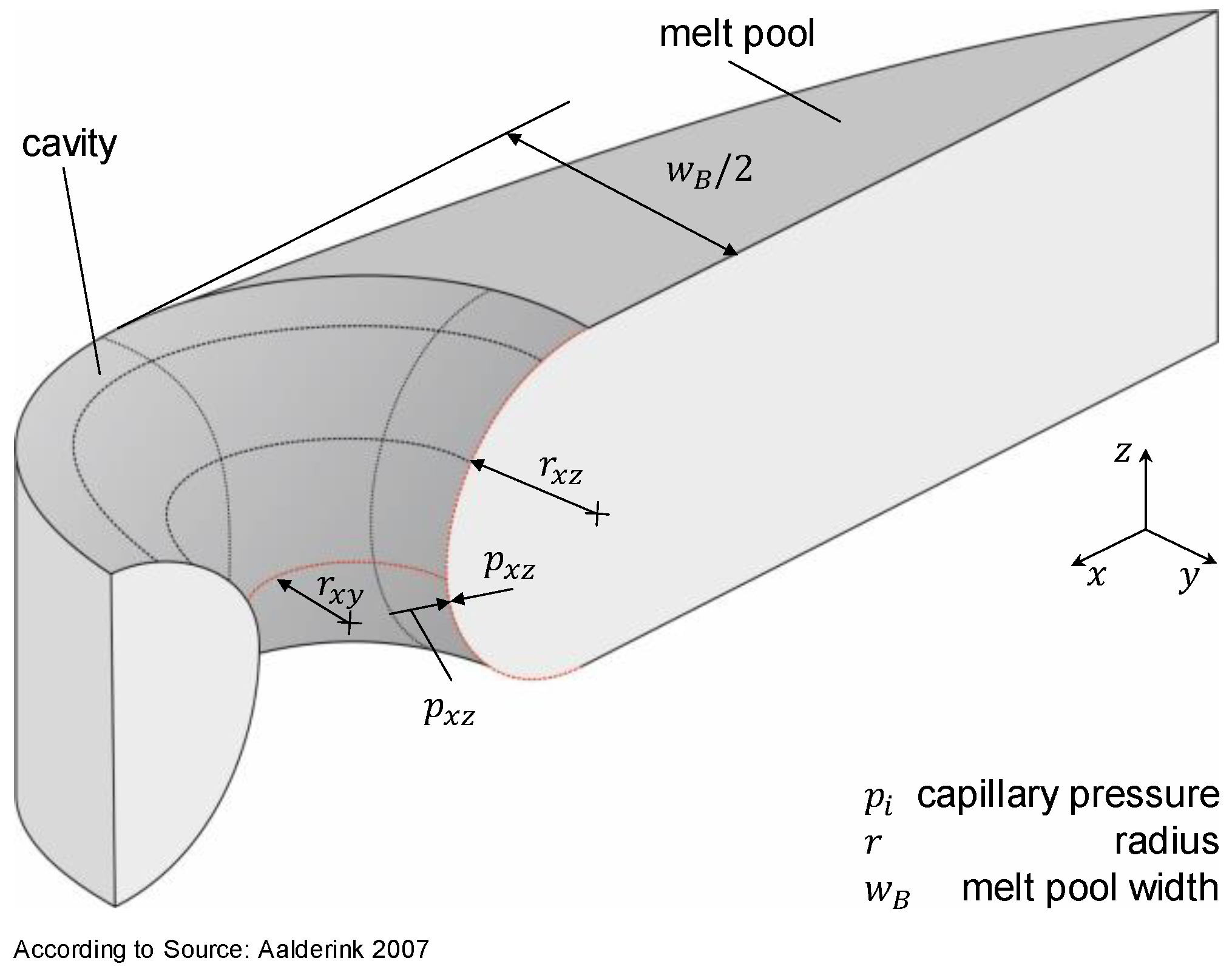
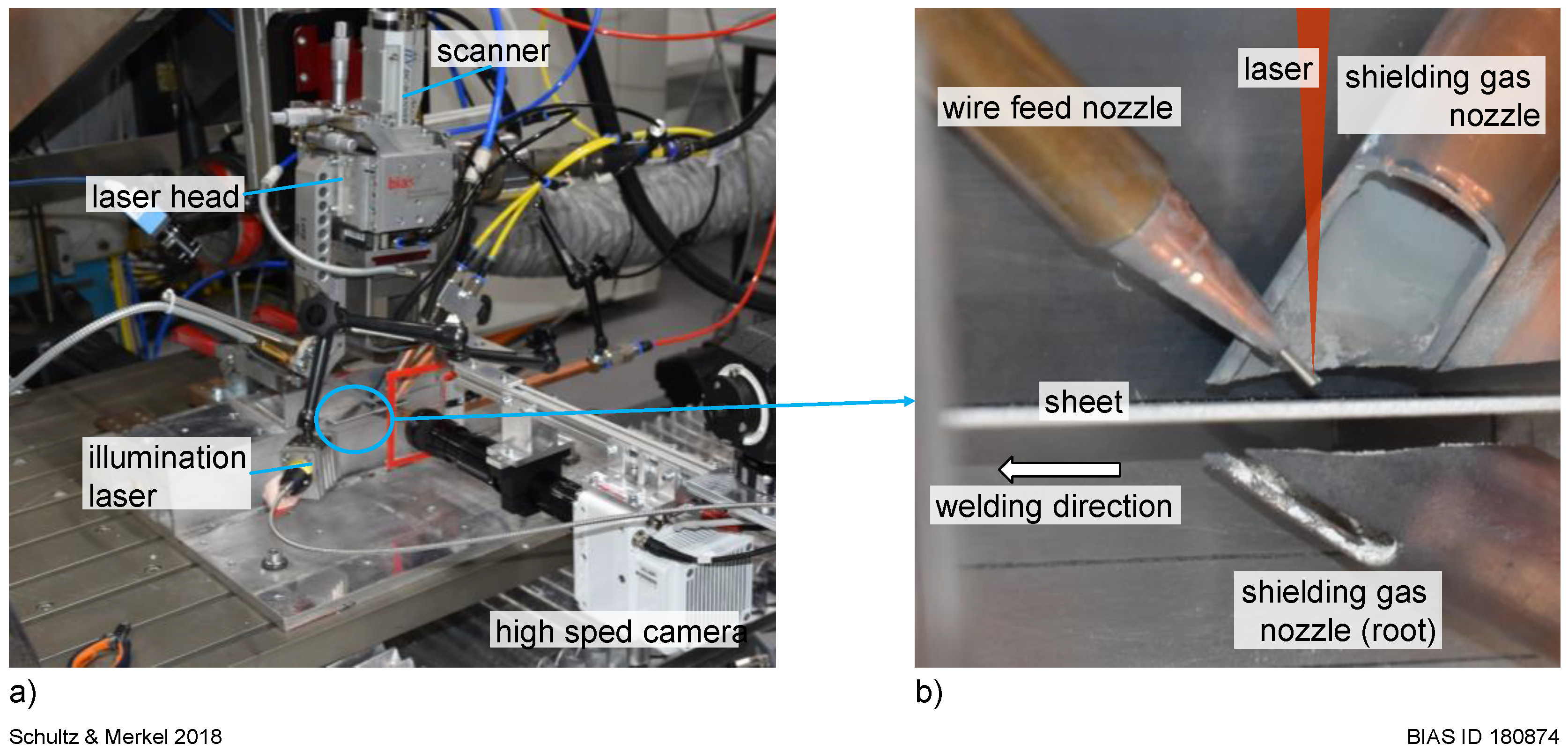
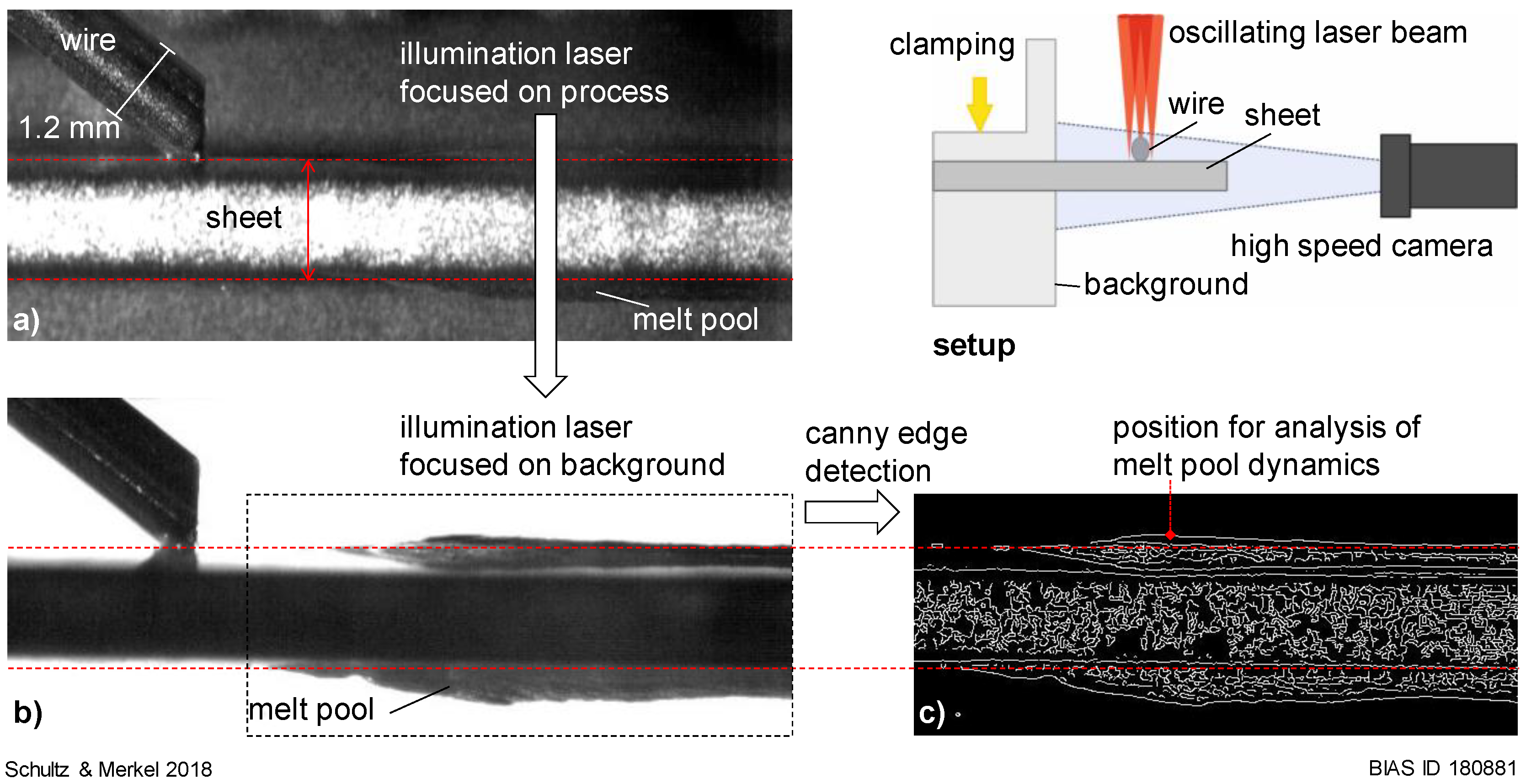
2. Materials and Methods
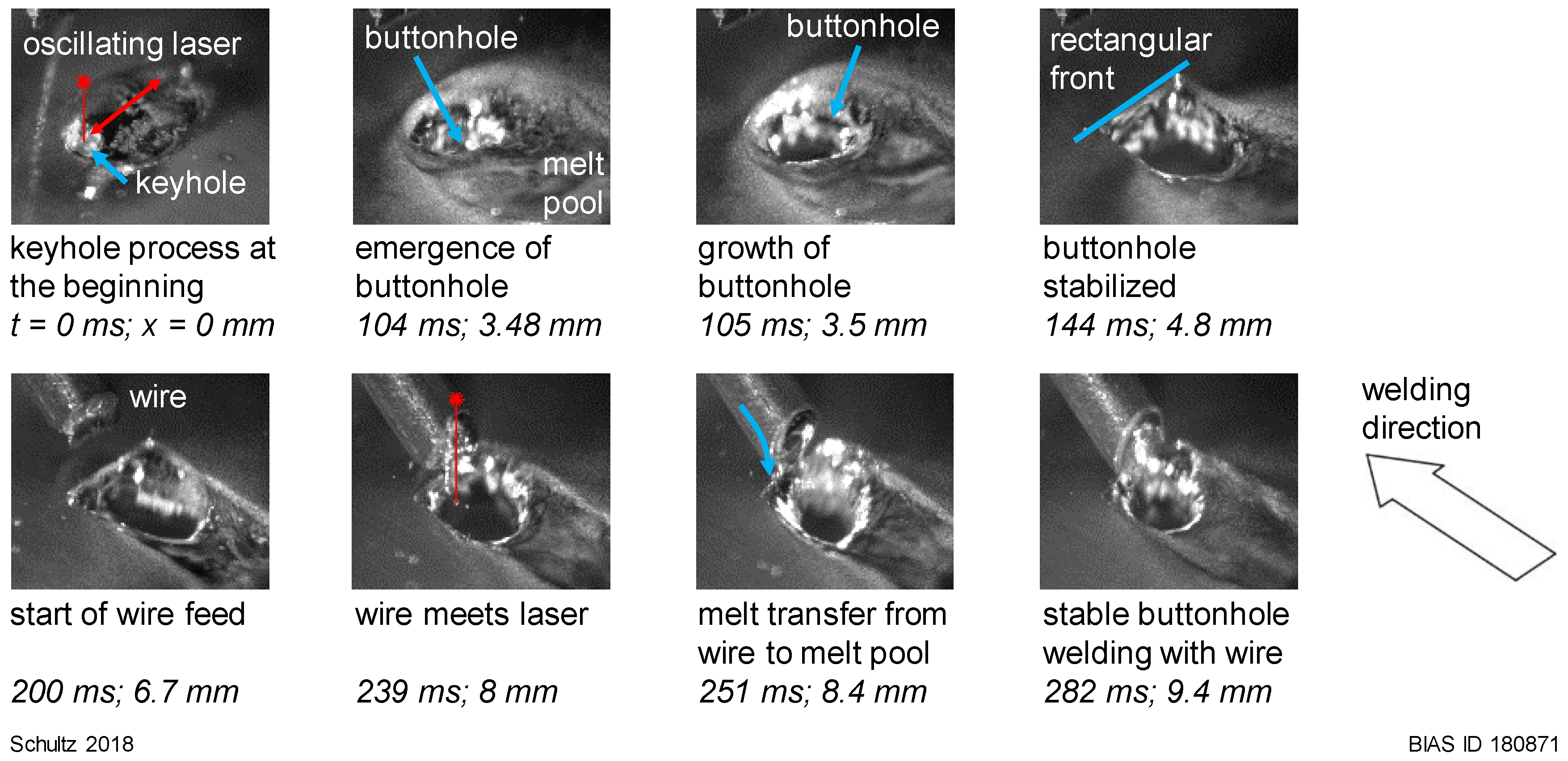
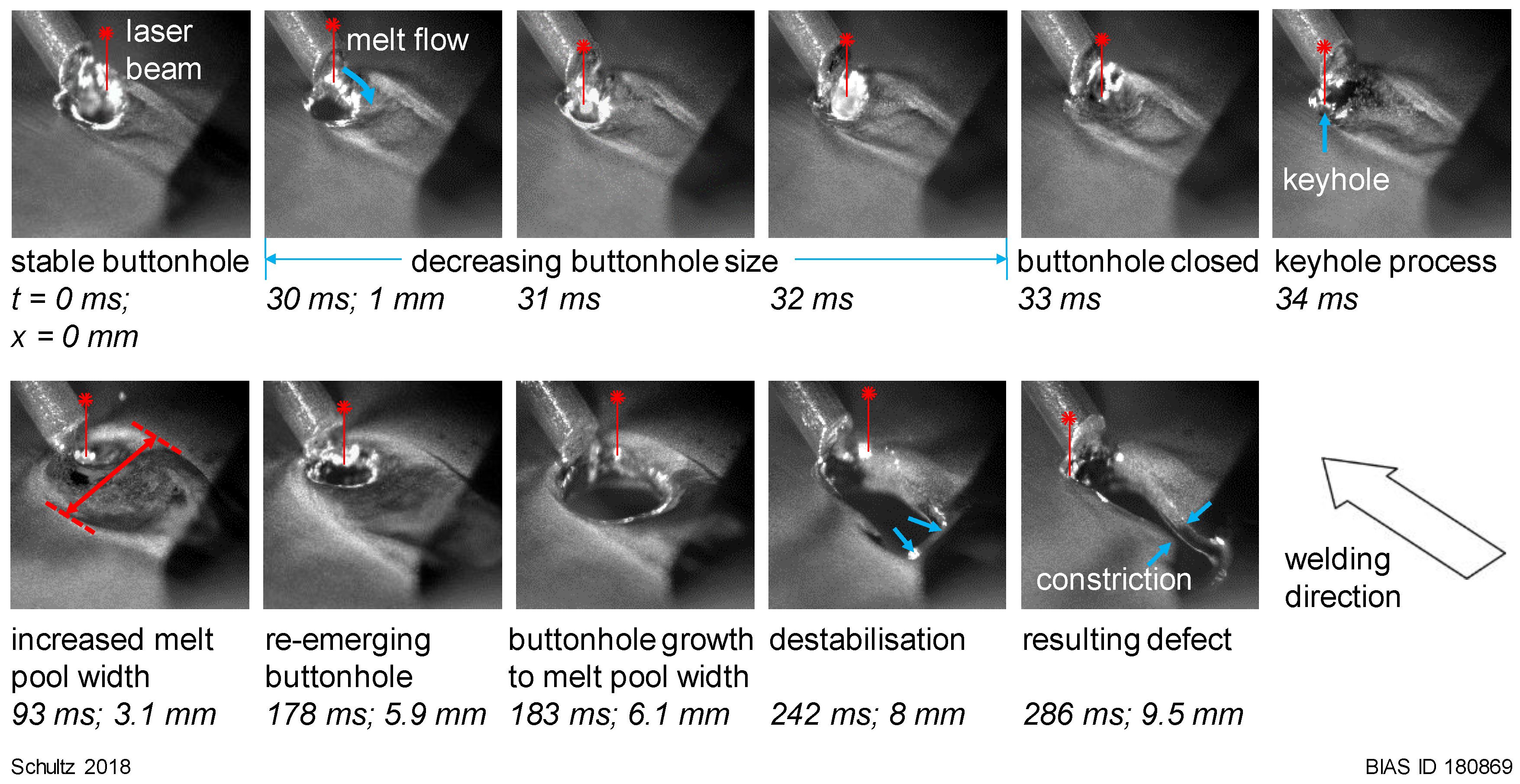
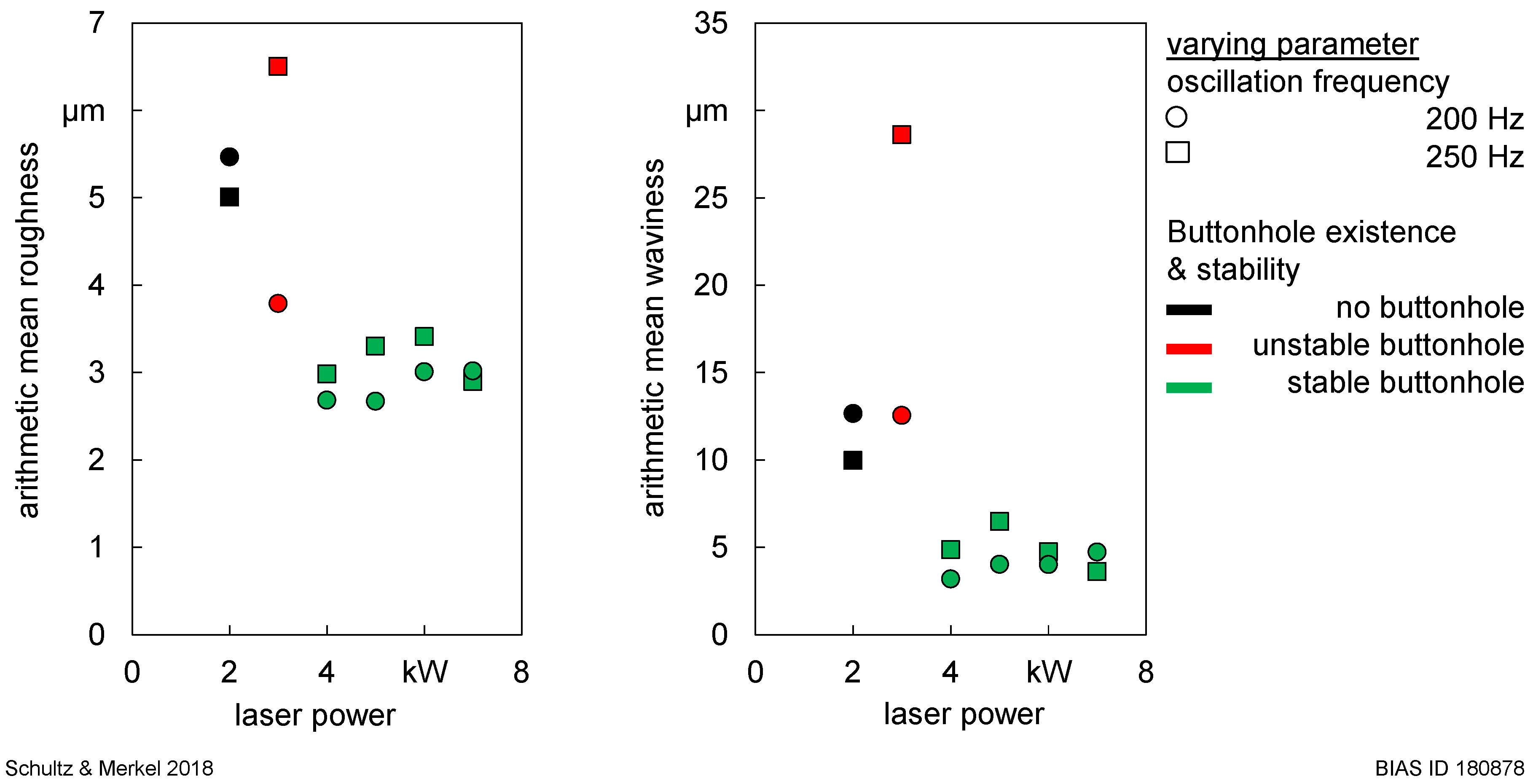
3. Results
4. Discussion
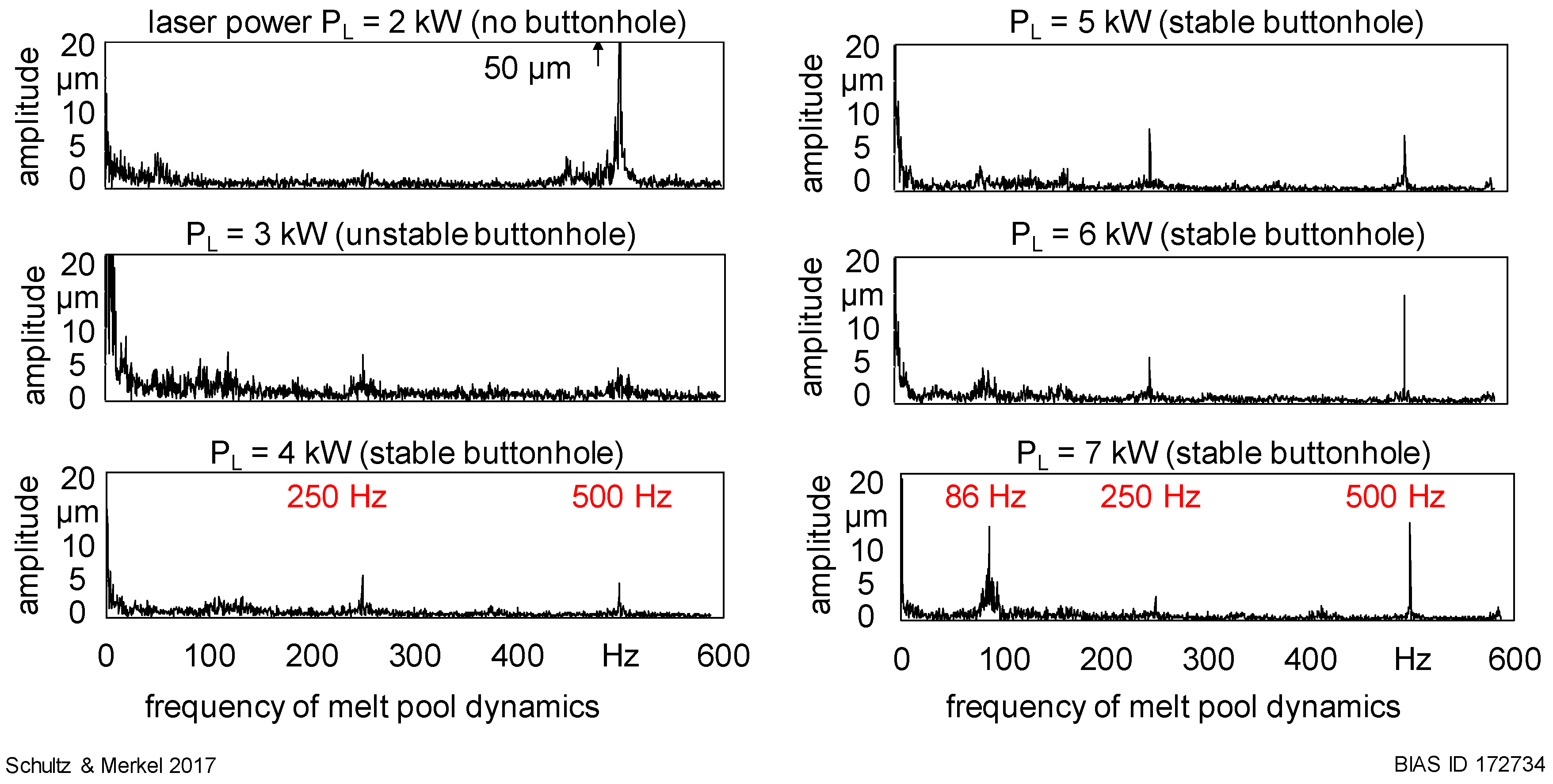
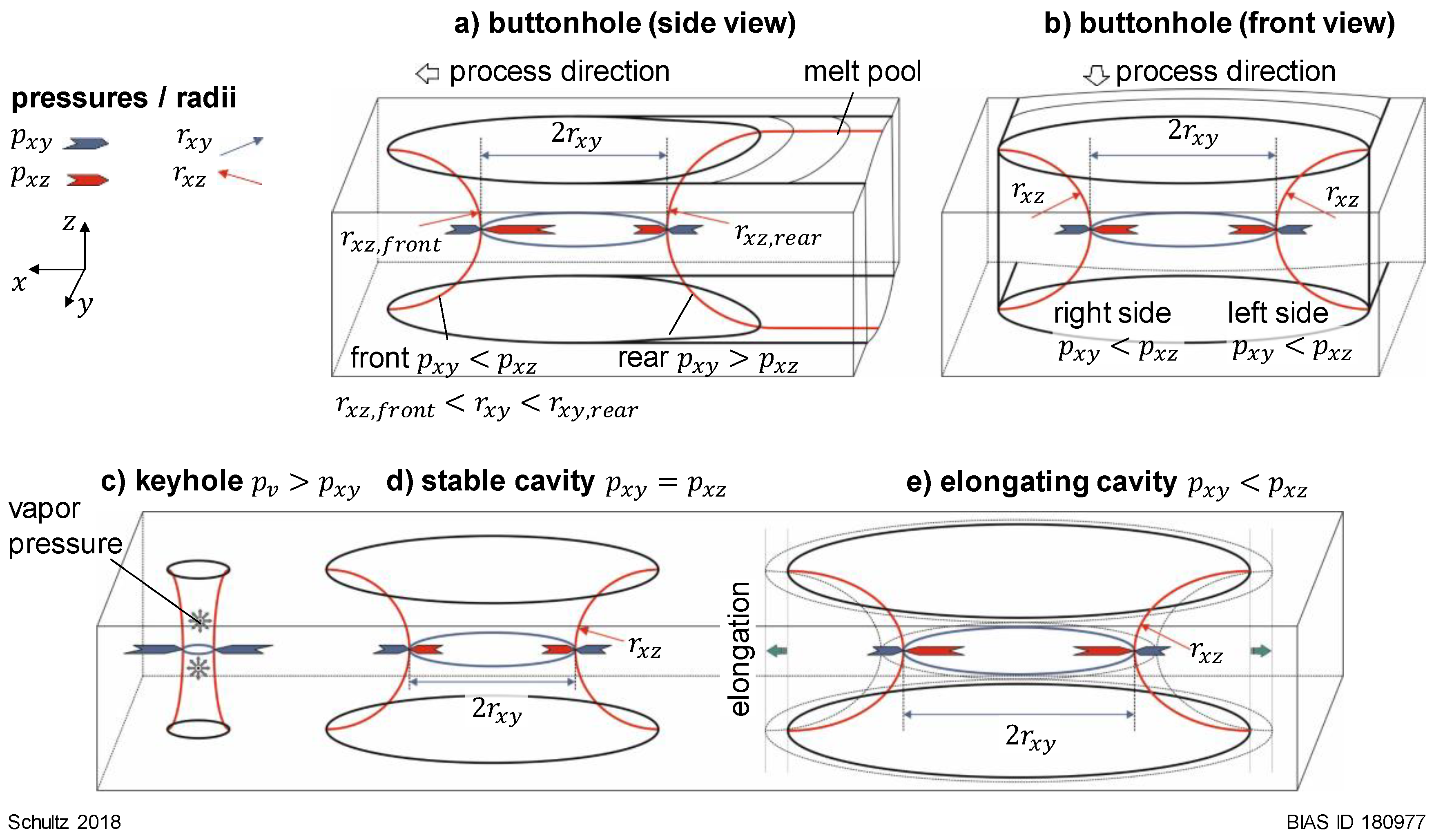
4.1. Buttonhole Movements with Process
4.2. Transition from Keyhole Welding with Oscillating Beam to Buttonhole Welding
4.3. Influence of Melt Pool Dynamics on the Surface Quality
5. Conclusions
- the movement of the buttonhole with the process is determined by the radii ratio
- a too large rear wall radius would result in the constriction of the buttonhole
- a too small rear wall radius would result in buttonhole elongation and remaining pinholes in the seam.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vollertsen, F.; Woizeschke, P.; Schultz, V.; Mittelstädt, C. Developments for laser joining with high-quality seam surfaces. Lightweight Des. Worldw. 2017, 5, 6–13. [Google Scholar] [CrossRef]
- Haenraets, U.; Ingwald, J.; Haselhoff, V. Gütezeichen und ihre Wirkungsbeziehungen—Ein Literaturüberblick. Int. J. Mark. 2012, 51, 147–163. (In German) [Google Scholar] [CrossRef]
- Braess, H.-H.; Seiffert, U. ATZ-MTZ-Fachbuch; Springer Vieweg Verlag: Wiesbaden, Germany, 2014; p. 548. (In German) [Google Scholar]
- Sander, J.; Reimann, W. Development of a benchmark criteria for the evaluation of optical surface appearance qualities of brazing and welding connections. In Proceedings of the 16th European Automotive Laser Applications (EALA), Bad Nauheim, Germany, 28–29 January 2015. [Google Scholar]
- Tang, Z.; Seefeld, T.; Vollertsen, F. Laser Brazing of Aluminum with a new filler wire AlZn13Si10Cu4. Phys. Procedia 2013, 41, 128–136. [Google Scholar] [CrossRef]
- Engelbrecht, L. Umstieg von YAG auf Diode: Mehr Prozessstabilität, weniger Kosten beim Laserlöten der Dachnullfuge mit angepassten Strahleigenschaften. In Proceedings of the 8th European Automotive Laser Applications (EALA), Bad Neuheim, Germany, 6–7 February 2009. (In German). [Google Scholar]
- Heitmanek, M.; Dobler, M.; Graudenz, M.; Perret, W.; Göbel, G.; Schmidt, M.; Beyer, E. Laser brazing with beam scanning: Experimental and simulative analysis. Phys. Procedia 2014, 56, 689–698. [Google Scholar] [CrossRef]
- Mittelstädt, C.; Seefeld, T.; Reitemeyer, D.; Vollertsen, F. Two-beam laser brazing thin sheet steel for automotive industry using Cu-base filler material. Phys. Procedia 2014, 56, 699–708. [Google Scholar] [CrossRef]
- Schwartz, M. Brazing, 2. Auflage; ASM International: Geauga County, OH, USA, 2003. [Google Scholar]
- Kawahito, Y.; Matsumoto, N.; Abe, Y.; Katayama, S. Relationship of laser absorption to keyhole thin um in high power fiber laser welding of stainless steel and thin um alloy. J. Mater. Process. Technol. 2011, 211, 1563–1568. [Google Scholar] [CrossRef]
- Volpp, J. Keyhole stability during laser welding—Part II. Prod. Eng. Res. Dev. 2017, 11, 9–18. [Google Scholar] [CrossRef]
- Farrel, W.J.; Ferrario, J.D. A computer-controlled, wide bandwidth deflection system for electron beam welding and heat treating. Weld. J. 1987, 10, 41–49. [Google Scholar]
- Albert, F.; Starcevic, D. Möglichkeiten zur Beeinflussung der Nahtrauheit beim Laserstrahlschweißen von Türen und Klappen aus Aluminium. In Proceedings of the 10th Laser-Anwenderforum (LAF’16), Bremen, Germany, 23–24 November 2016. (In German). [Google Scholar]
- Dittrich, D.; Schedewy, R.; Brenner, B.; Standfuß, J. Laser-multi-pass-narrow-gap-welding of hot crack sensitive thick Aluminium plates. Phys. Procedia 2013, 41, 225–233. [Google Scholar] [CrossRef]
- Mahrle, A.; Beyer, E. Control of the energy deposition during laser beam welding by oscillation techniques. In Lasers in Manufacturing; Vollertsen, F., Emmelmann, C., Schmidt, M., Otto, A., Eds.; AT-Fachverl: Stuttgart, Germany, 2007; pp. 97–103. [Google Scholar]
- Seefeld, T.; Schultz, V. New developments in filler wire assisted laser joining of Aluminium. In Proceedings of the LAMP2013—6th International Congress on Laser Advanced Materials Processing, Niigata, Japan, 23–26 July 2013. [Google Scholar]
- Schultz, V.; Seefeld, T.; Vollertsen, F. Gap Bridging Ability in Laser Beam Welding of Thin Aluminum Sheets. Phys. Procedia 2014, 56, 545–553. [Google Scholar] [CrossRef]
- Vollertsen, F. Loopless Production: Definition and Examples from Joining. In Proceedings of the 69th IIW Annual Assembly and International Conference, Melbourne Convention Exhibition Centre, Melbourne, Australia, 10–15 July 2016. [Google Scholar]
- Aalderink, B.J.; de Lange, D.F.; Aarts, R.G.K.M.; Meijer, J. Keyhole shapes during laser welding of thin metal sheets. J. Phys. D Appl. Phys. 2007, 40, 5388–5393. [Google Scholar] [CrossRef]
- Ericsson, I.; Powell, J.; Kaplan, A. Surface tension generated defects in full penetration laser keyhole welding. J. Laser Appl. 2014, 26, 012006. [Google Scholar] [CrossRef]
- Haglund, P.; Eriksson, I.; Powell, P.; Kaplan, A. Surface tension stabilized laser welding (donut laser welding)—A new laser welding Technique. J. Laser Appl. 2013, 25, 031501. [Google Scholar] [CrossRef]
- Cho, W.-I.; Schultz, V.; Vollertsen, F. Simulation of the buttonhole formation during laser welding with wire feeding and beam oscillation. In Proceedings of the Lasers in Manufacturing (LIM17), Munich, Germany, 26–29 June 2017. [Google Scholar]
- Schultz, V.; Cho, W.-I.; Woizeschke, P.; Vollertsen, F. Laser deep penetration weld seams with high surface quality. In Proceedings of the Lasers in Manufacturing (LIM17), Munich, Germany, 26–29 June 2017. [Google Scholar]
- Schultz, V.; Cho, W.; Woizeschke, P. Buttonhole welding—Laser deep penetration welds with smooth seam surface. In Proceedings of the IIW Intermediate Meeting 2018 Com. IV, Lendava, Slovenia, 12–14 March 2018. [Google Scholar]
- Cho, W.-I.; Schultz, V.; Woizeschke, P. Numerical study of the effect of the oscillation frequency in buttonhole welding. J. Mater. Process. Technol. 2018, 261, 202–212. [Google Scholar] [CrossRef]
- Cho, W.-I.; Woizeschke, P.; Schultz, P. Simulation of molten pool dynamics and stability analysis in laser buttonhole welding. Procedia CIRP 2018, 74, 687–690. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 6, 679–698. [Google Scholar]



| Parameter | Symbol | Unit | Value/Range |
|---|---|---|---|
| Laser power | 2 to 7 | ||
| Welding speed | 2 | ||
| Wire feed speed | 1.4 | ||
| Wire diameter | 1.2 | ||
| Oscillation width | 1.1 | ||
| Oscillation frequency | 200, 250 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schultz, V.; Woizeschke, P. High Seam Surface Quality in Keyhole Laser Welding: Buttonhole Welding. J. Manuf. Mater. Process. 2018, 2, 78. https://doi.org/10.3390/jmmp2040078
Schultz V, Woizeschke P. High Seam Surface Quality in Keyhole Laser Welding: Buttonhole Welding. Journal of Manufacturing and Materials Processing. 2018; 2(4):78. https://doi.org/10.3390/jmmp2040078
Chicago/Turabian StyleSchultz, Villads, and Peer Woizeschke. 2018. "High Seam Surface Quality in Keyhole Laser Welding: Buttonhole Welding" Journal of Manufacturing and Materials Processing 2, no. 4: 78. https://doi.org/10.3390/jmmp2040078
APA StyleSchultz, V., & Woizeschke, P. (2018). High Seam Surface Quality in Keyhole Laser Welding: Buttonhole Welding. Journal of Manufacturing and Materials Processing, 2(4), 78. https://doi.org/10.3390/jmmp2040078






