Experimental Investigation on the Geometrical Accuracy of the CNC Multi-Pass Sheet Metal Spinning Process
Abstract
1. Introduction
2. Materials and Experimental Methods
3. First Design of Experiments
3.1. Factors, Levels, and Responses
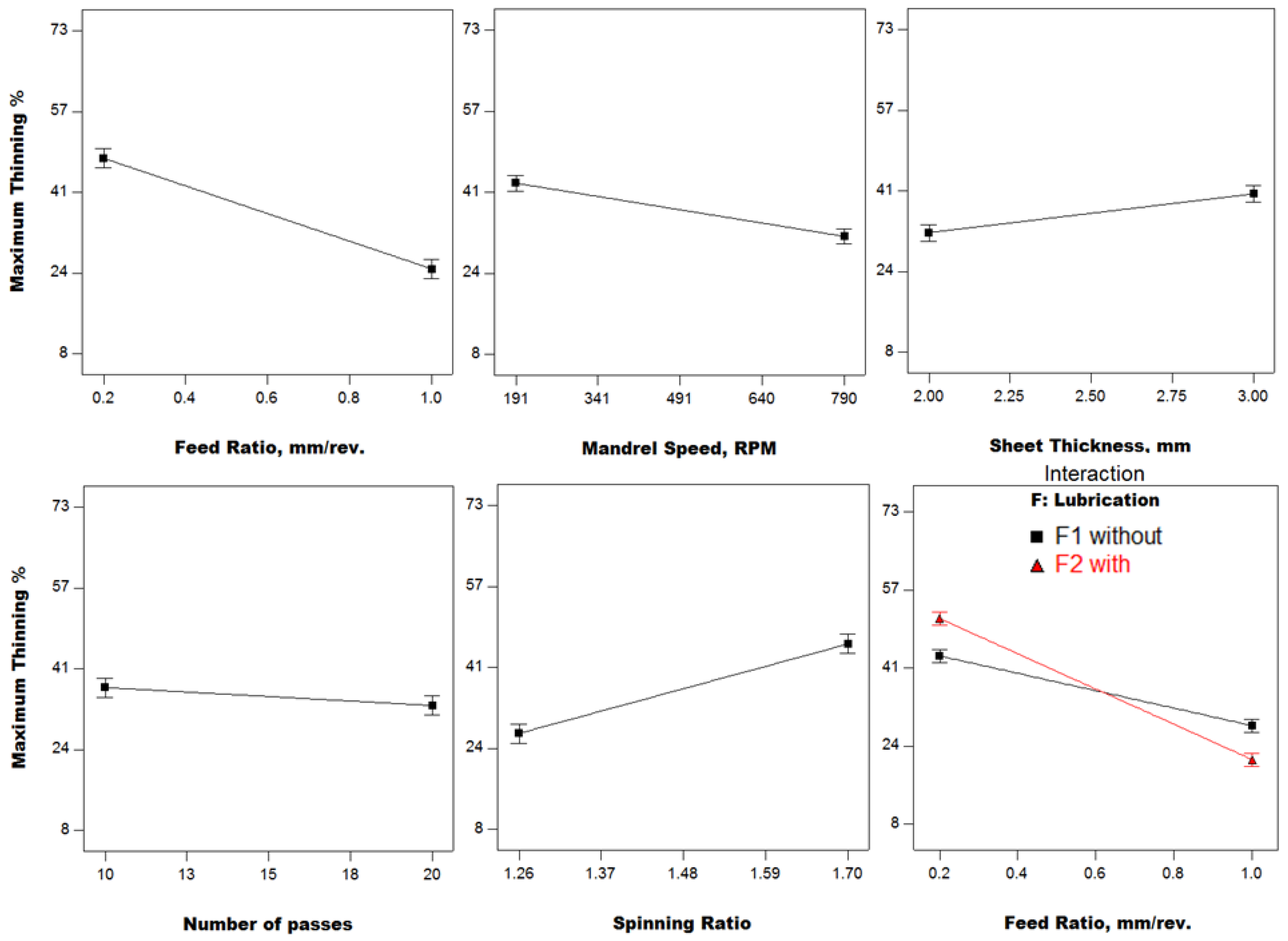
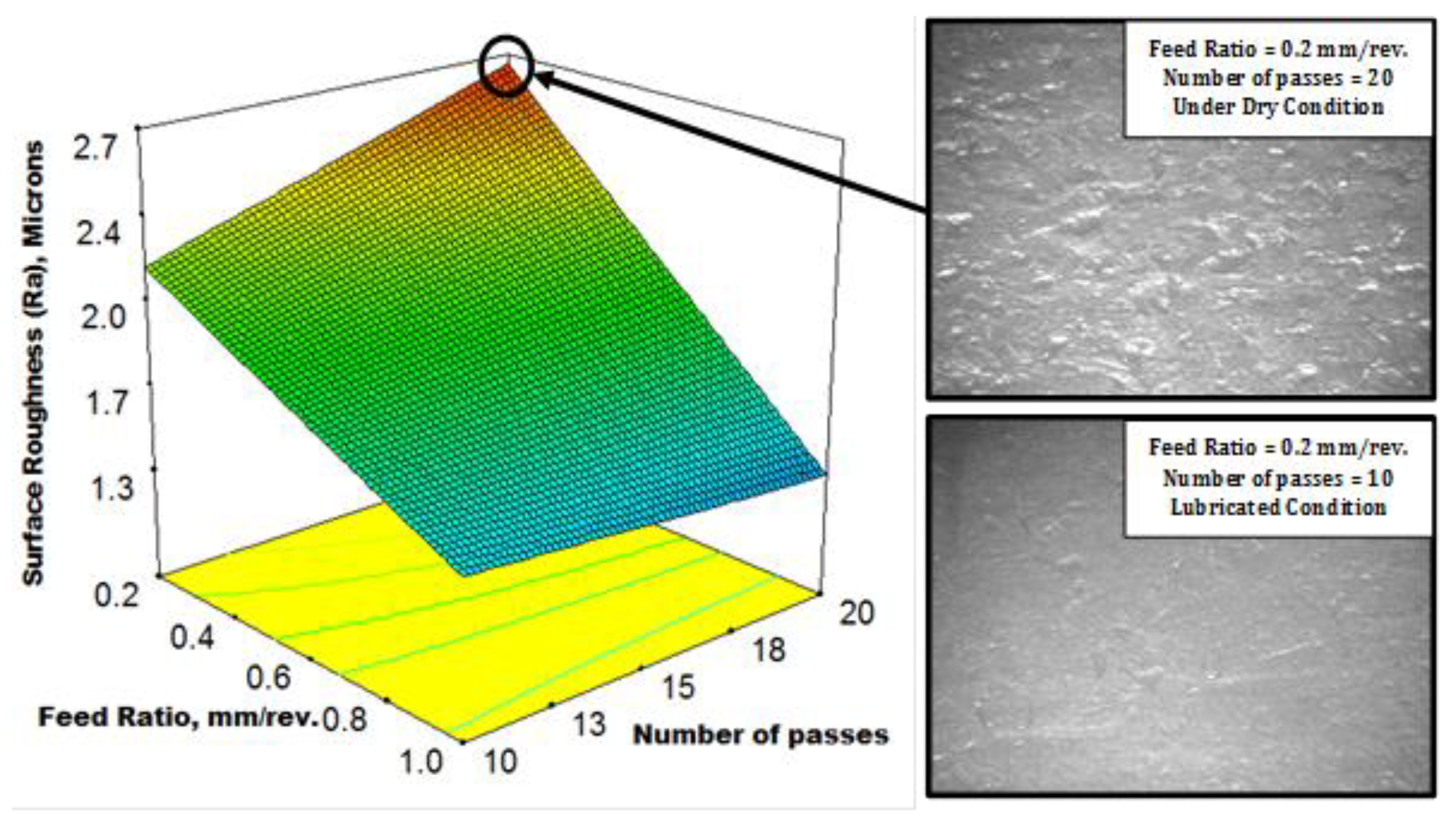
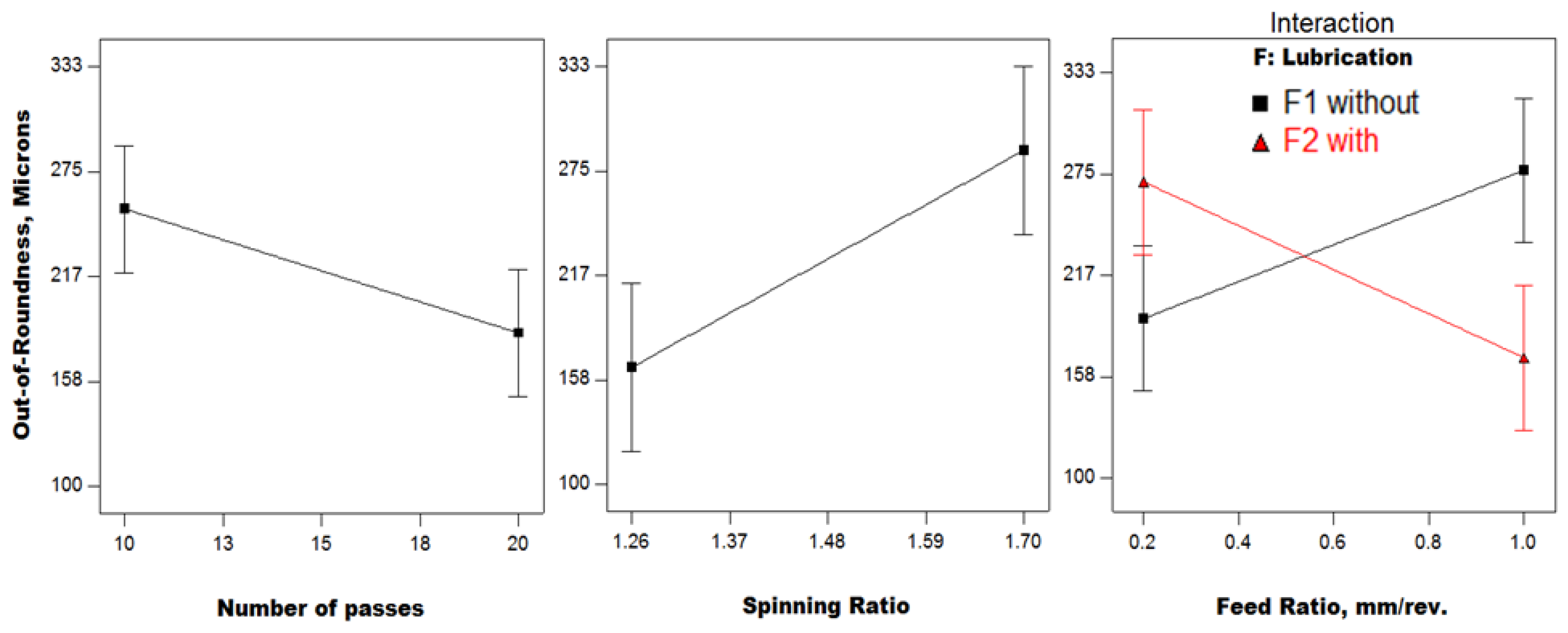
3.2. Results and Discussion
4. Second Design of Experiments
4.1. Factors, Levels, and Responses
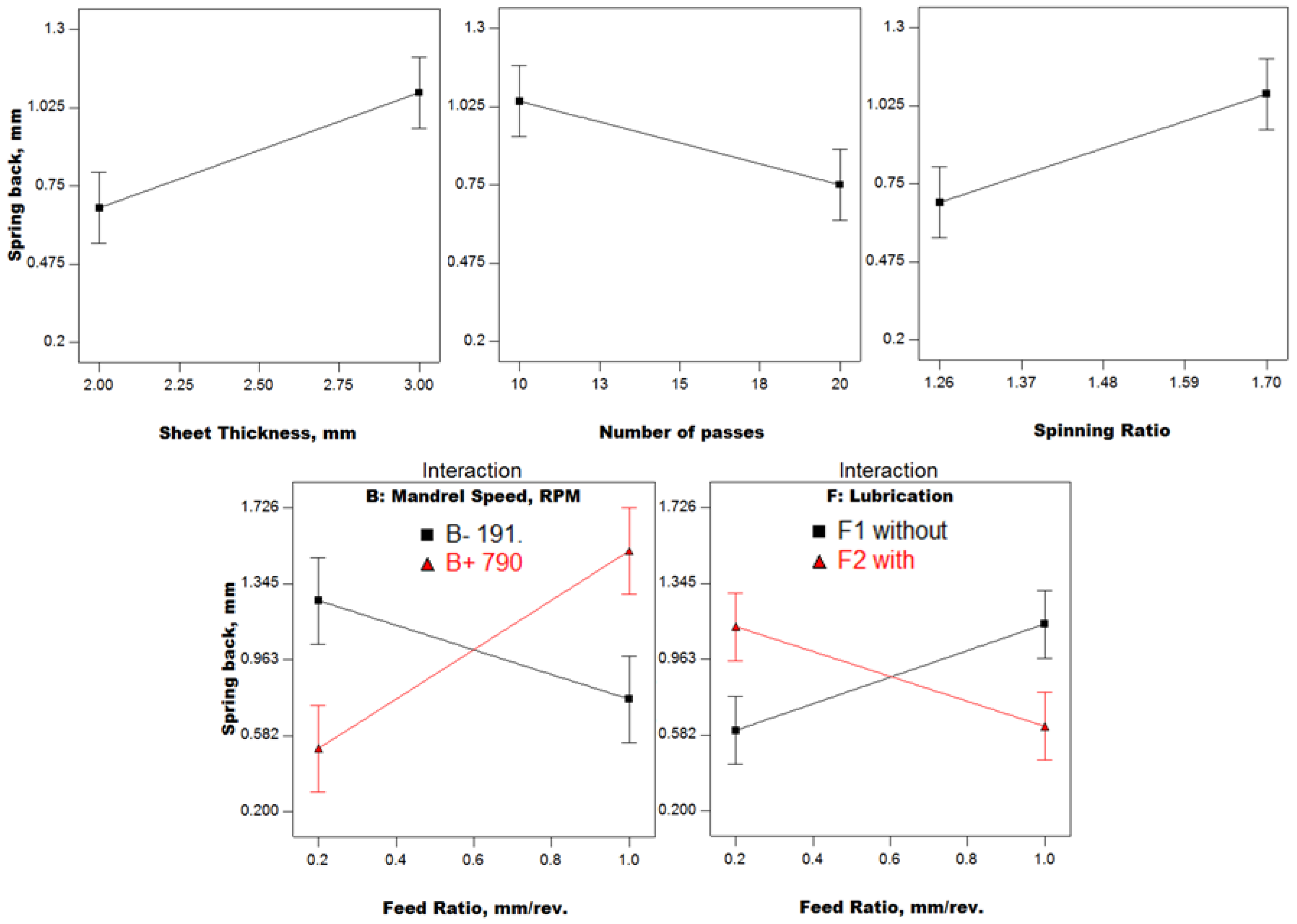
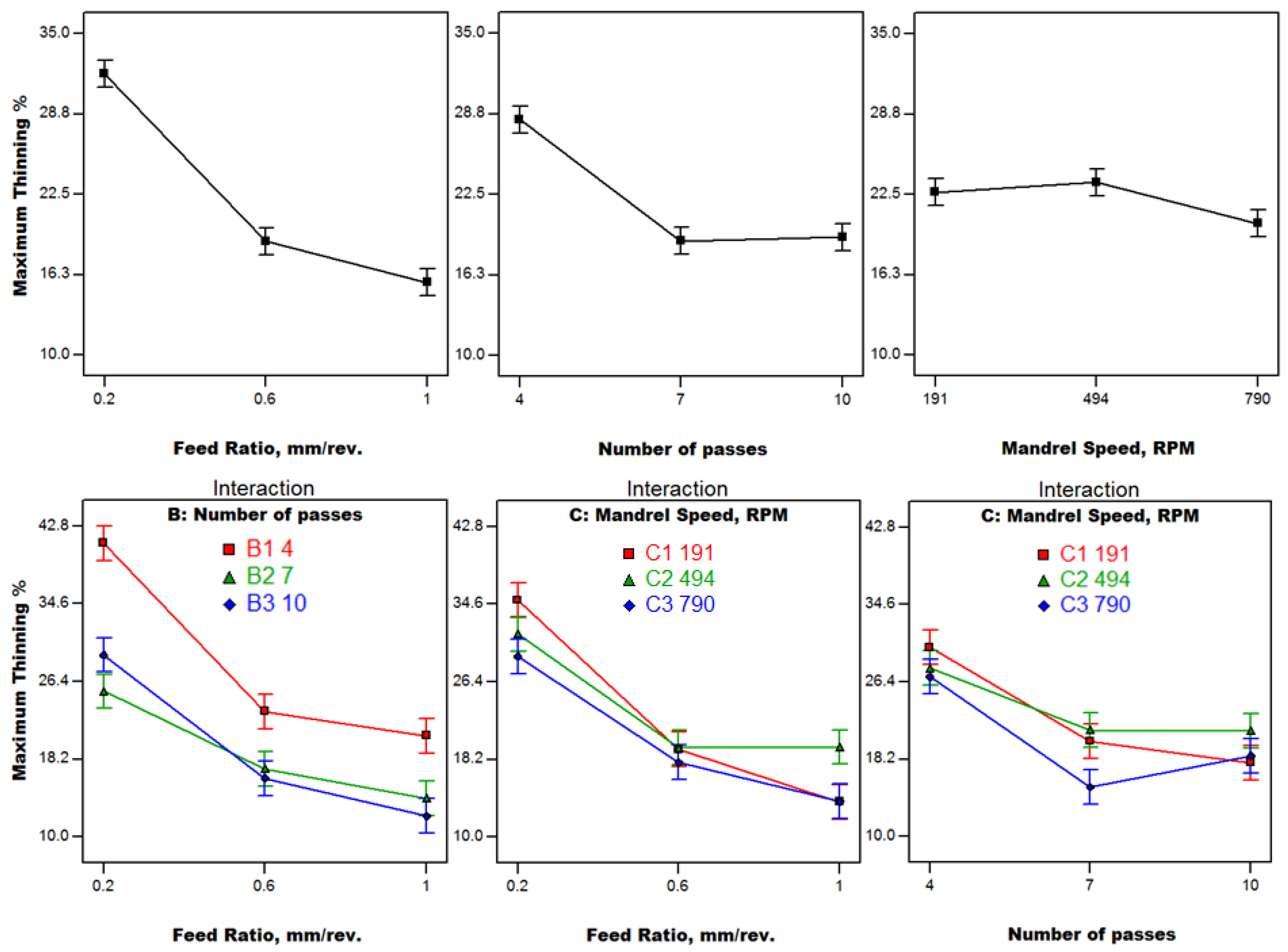
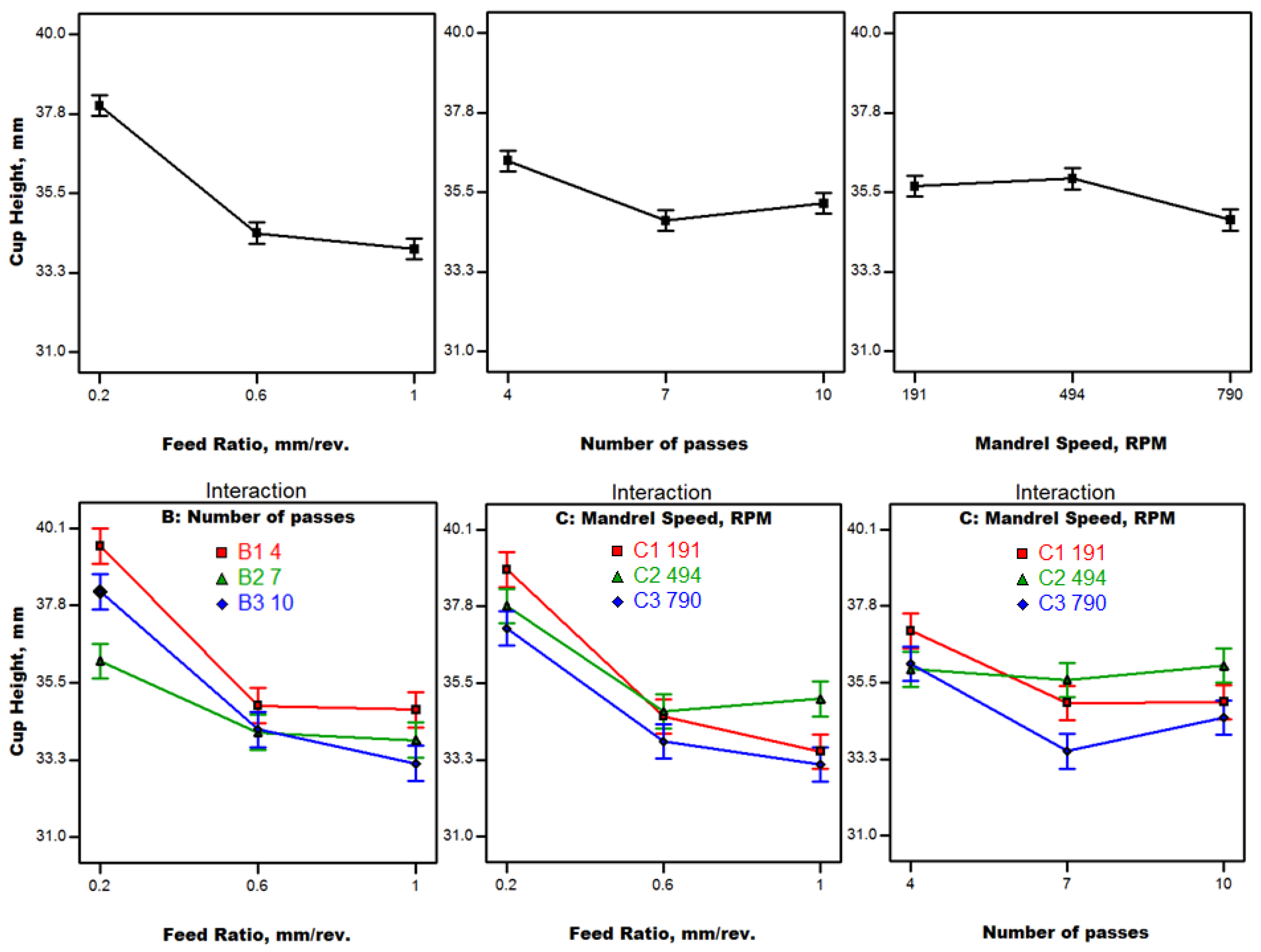
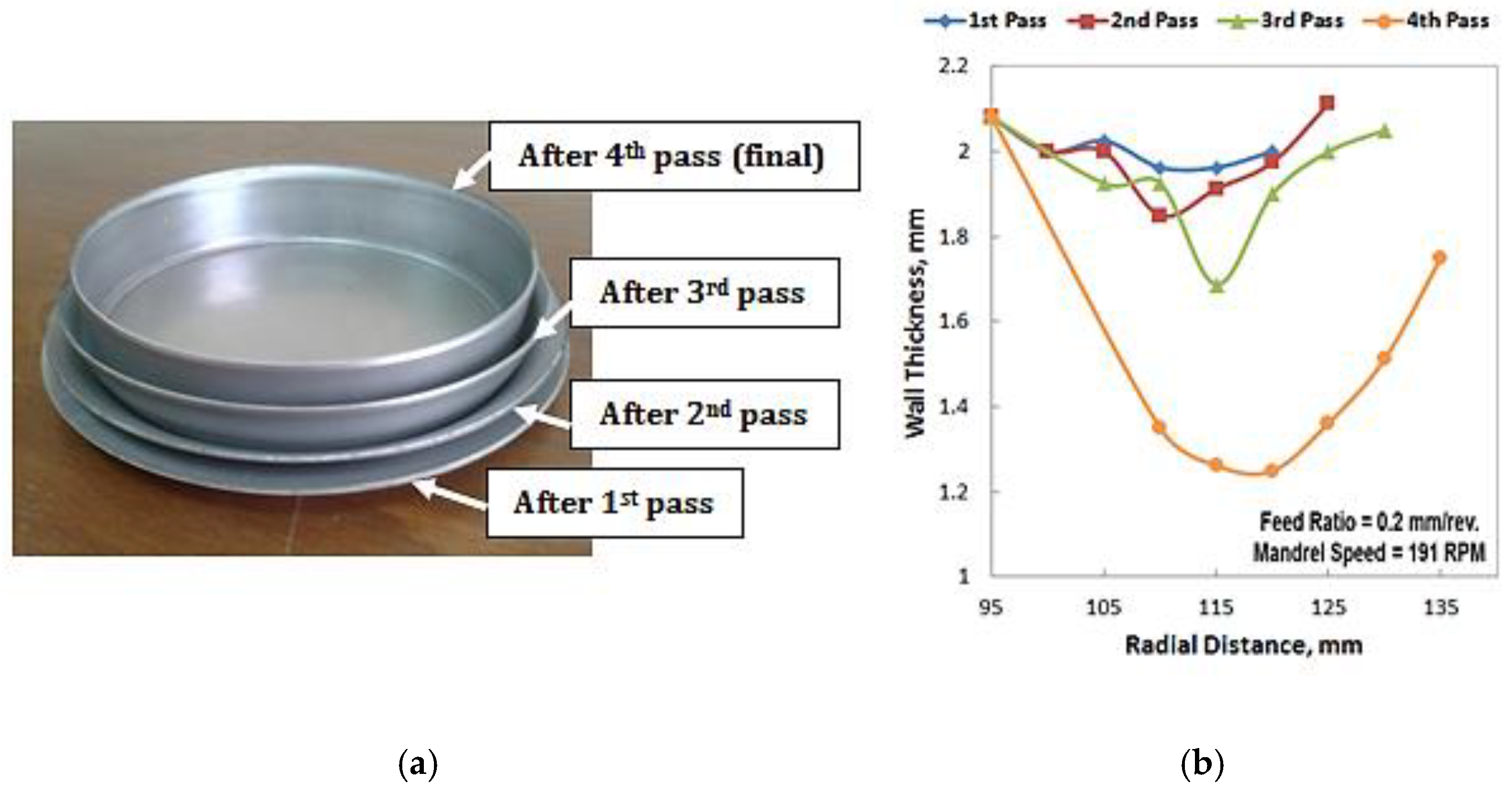
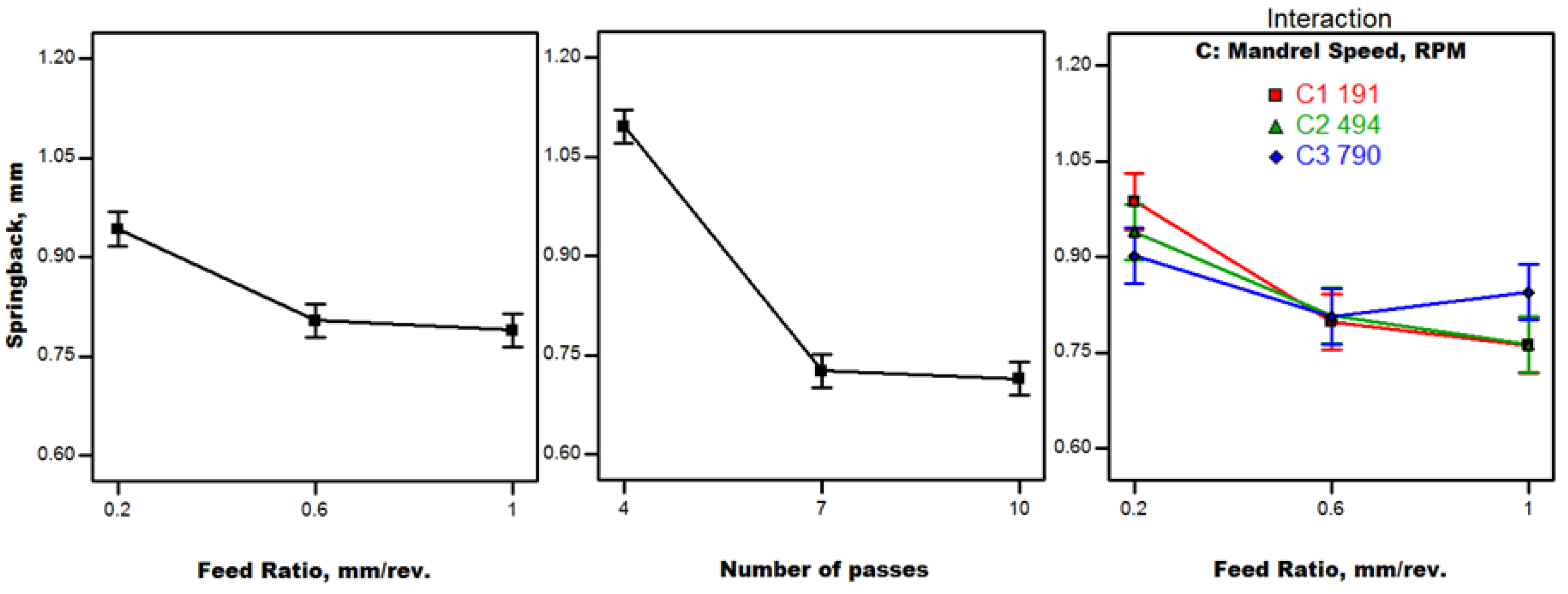
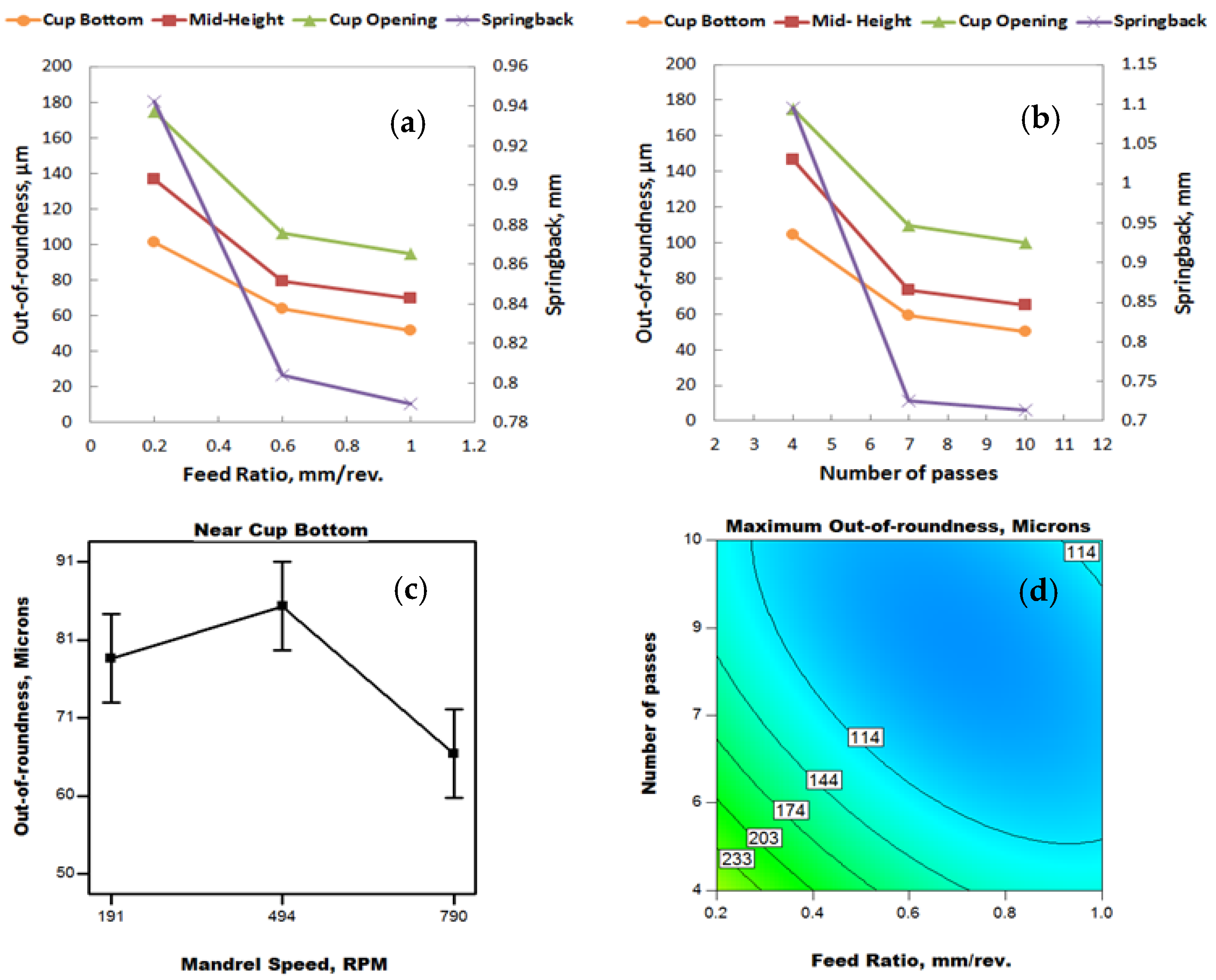
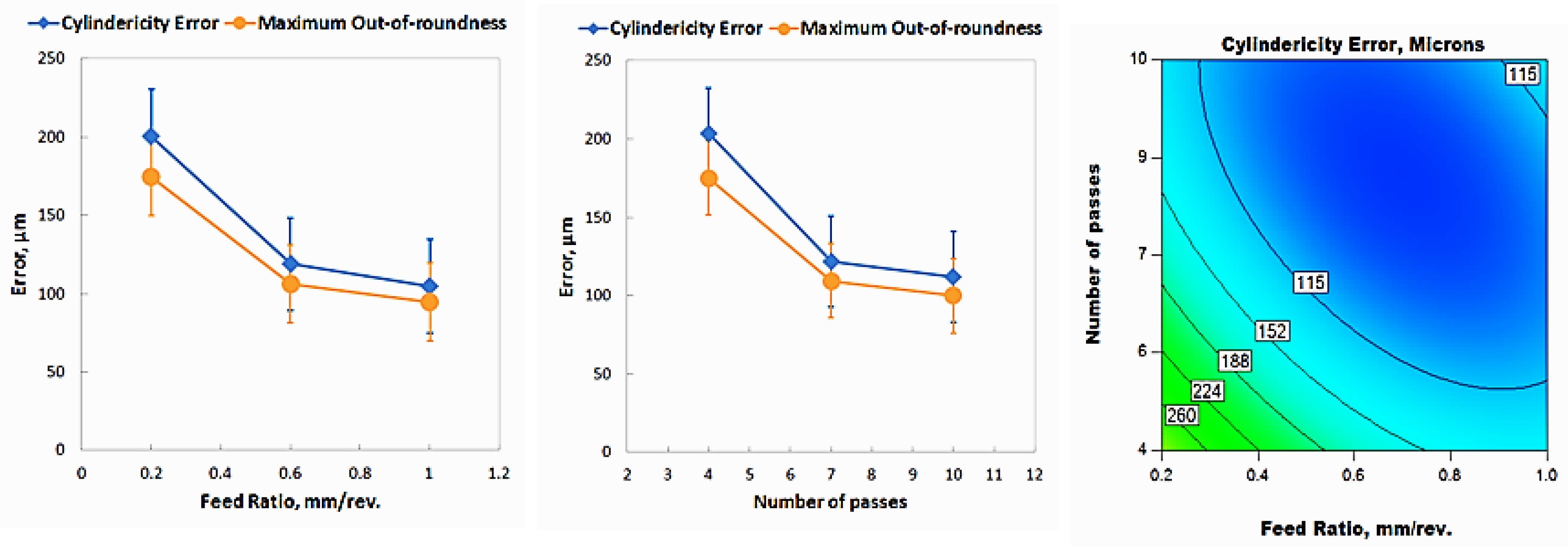
4.2. Results and Discussion
5. Conclusions
- With lubrication, it is possible to obtain minimum cup wall thinning, small springback, more uniform roundness, and cylindericity at a high feed ratio, which implies a high processing speed (productivity) associated with higher quality principally using a larger number of spinning passes. This finding breaks the rule that slow spinning is fundamental to acceptable quality, and assures the prospective features of cutting-edge spinning technology for both large and small size parts.
- Achieved levels of minimum wall thinning find applicability in high-pressure vessels.
- Larger product heights are essential for better material utilization in satellite nose cones and can be obtained at a low feed ratio and small number of passes.
- A compromise between wall thinning and product height is required to optimize both quality characteristics simultaneously.
- Obtained surface finish values are particularly advantageous to aerospace bearing cages, especially at small spinning ratios.
- There seems to be a direct relationship between springback and roundness of the spun cups due to the sheet metal anisotropy.
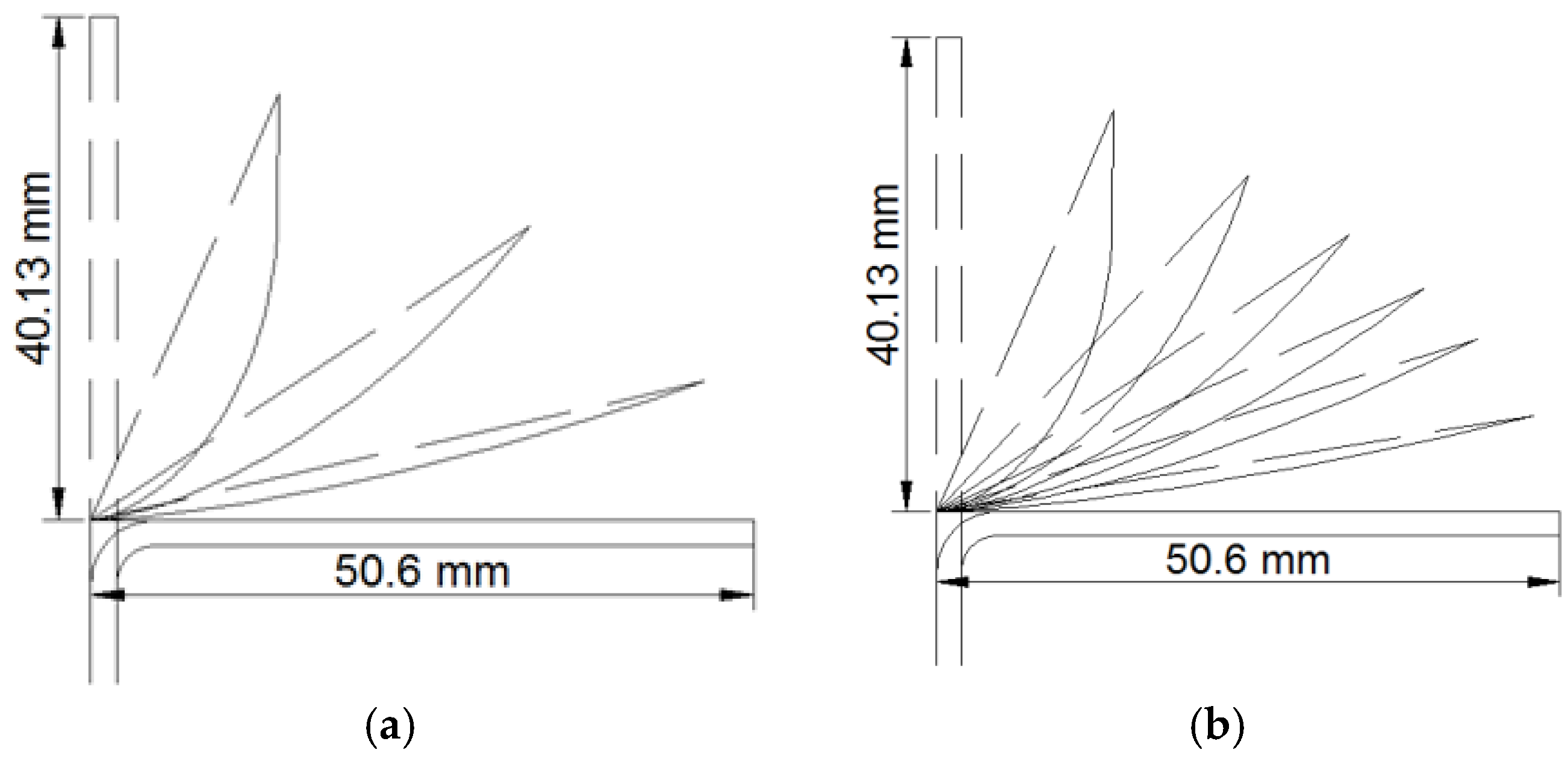
- It is recommended to examine the use of two roller tools on opposite sides for the straightness of the spun cup axis.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Run | Feed Ratio, mm/rev. | Mandrel Speed, RPM | Sheet Thickness, mm | No. of Passes | Spinning Ratio | Lubrication | Maximum Thinning% | Springback, mm | Surface Roughness, μm | Out-of-Roundness, μm |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 790 | 2 | 20 | 1.26 | without | 11.82 | 0.536 | 1.2 | 197 |
| 2 | 1 | 790 | 3 | 10 | 1.7 | without | 35.11 | 2.021 | 1.5 | 304 |
| 3 | 1 | 191 | 2 | 20 | 1.7 | with | 30.05 | 0.615 | 1.3 | 161 |
| 4 | 0.2 | 191 | 3 | 20 | 1.7 | without | 59.21 | 0.872 | 2.7 | 197 |
| 5 | 1 | 790 | 3 | 20 | 1.7 | with | 28.06 | 0.825 | 1.2 | 197 |
| 6 | 1 | 191 | 3 | 20 | 1.26 | without | 33.07 | 0.499 | 1.5 | 132 |
| 7 | 0.2 | 790 | 2 | 10 | 1.7 | with | 60.9 | 0.828 | 1.4 | 472 |
| 8 | 1 | 790 | 3 | 20 | 1.7 | with | 28.08 | 0.482 | 1.5 | 170 |
| 9 | 1 | 790 | 2 | 20 | 1.26 | without | 9.48 | 0.696 | 1.1 | 117 |
| 10 | 1 | 191 | 2 | 10 | 1.7 | without | 40.02 | 0.821 | 1.4 | 440 |
| 11 | 0.2 | 790 | 2 | 20 | 1.7 | without | 41.46 | 0.255 | 2.6 | 244 |
| 12 | 1 | 191 | 2 | 20 | 1.7 | with | 32.5 | 1.115 | 1.5 | 193 |
| 13 | 0.2 | 191 | 3 | 10 | 1.7 | with | 66.02 | 1.845 | 1.5 | 363 |
| 14 | 1 | 191 | 2 | 10 | 1.7 | without | 39.93 | 0.776 | 1.5 | 272 |
| 15 | 0.2 | 191 | 2 | 20 | 1.26 | with | 32.56 | 0.716 | 1.6 | 133 |
| 16 | 1 | 790 | 2 | 10 | 1.26 | with | 11.82 | 0.492 | 1.3 | 112 |
| 17 | 0.2 | 790 | 3 | 20 | 1.26 | with | 43.22 | 1.748 | 1.5 | 161 |
| 18 | 0.2 | 191 | 2 | 10 | 1.26 | without | 33.3 | 0.785 | 1.3 | 170 |
| 19 | 0.2 | 790 | 3 | 20 | 1.26 | with | 43.22 | 0.607 | 1.4 | 294 |
| 20 | 0.2 | 191 | 3 | 20 | 1.7 | without | 60.11 | 0.865 | 2.7 | 198 |
| 21 | 1 | 790 | 3 | 10 | 1.7 | without | 24.79 | 2.883 | 1.5 | 588 |
| 22 | 0.2 | 191 | 2 | 10 | 1.26 | without | 33.52 | 0.819 | 2 | 139 |
| 23 | 0.2 | 790 | 2 | 20 | 1.7 | without | 42.39 | 0.265 | 2.6 | 244 |
| 24 | 0.2 | 191 | 2 | 20 | 1.26 | with | 28.5 | 0.673 | 1.4 | 230 |
| 25 | 1 | 191 | 3 | 10 | 1.26 | with | 18.75 | 0.471 | 1.4 | 146 |
| 26 | 1 | 191 | 3 | 10 | 1.26 | with | 16.42 | 0.473 | 1.8 | 160 |
| 27 | 0.2 | 790 | 3 | 10 | 1.26 | without | 36.67 | 0.404 | 1.5 | 180 |
| 28 | 1 | 790 | 2 | 10 | 1.26 | with | 8.35 | 0.552 | 1.5 | 166 |
| 29 | 0.2 | 790 | 2 | 10 | 1.7 | with | 60.65 | 0.849 | 1.7 | 198 |
| 30 | 0.2 | 191 | 3 | 10 | 1.7 | with | 72.82 | 1.768 | 1.3 | 262 |
| 31 | 1 | 191 | 3 | 20 | 1.26 | without | 36.48 | 0.91 | 1.5 | 117 |
| 32 | 0.2 | 790 | 3 | 10 | 1.26 | without | 39.21 | 0.595 | 1.9 | 113 |
Appendix B
| Run | Feed Ratio, mm/rev | Number of Passes | Mandrel Speed, RPM | Maximum Thinning% | Cup Height, mm | Springback, mm | Surface Roughness (Ra), μm | Maximum Out-of-Roundness, μm | Cylindericity Error, μm |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.6 | 10 | 790 | 17.23 | 33.54 | 0.776 | 1.03 | 79 | 88 |
| 2 | 0.2 | 10 | 494 | 37.29 | 40.09 | 0.916 | 0.93 | 147 | 163 |
| 3 | 0.6 | 10 | 790 | 15.25 | 33.52 | 0.636 | 1.29 | 162 | 180 |
| 4 | 0.6 | 4 | 191 | 21.2 | 34.78 | 0.936 | 1.44 | 32 | 47 |
| 5 | 1 | 10 | 191 | 13.63 | 33.65 | 0.617 | 1.03 | 87 | 97 |
| 6 | 0.6 | 7 | 191 | 13.83 | 33.2 | 0.766 | 1.59 | 92 | 102 |
| 7 | 0.6 | 10 | 191 | 16.39 | 33.93 | 0.67 | 1.28 | 184 | 204 |
| 8 | 1 | 10 | 790 | 12.96 | 32.24 | 0.727 | 1.56 | 67 | 74 |
| 9 | 0.2 | 10 | 191 | 25.98 | 37.64 | 0.756 | 0.99 | 127 | 141 |
| 10 | 0.6 | 10 | 191 | 16.35 | 34.57 | 0.673 | 0.93 | 65 | 72 |
| 11 | 1 | 10 | 494 | 13.42 | 33.57 | 0.689 | 1.44 | 77 | 95 |
| 12 | 0.2 | 10 | 191 | 28.06 | 37.6 | 0.808 | 1.26 | 114 | 127 |
| 13 | 0.2 | 7 | 790 | 20.33 | 34.44 | 0.762 | 1.3 | 83 | 92 |
| 14 | 1 | 10 | 790 | 12.54 | 32.82 | 0.6 | 1.44 | 81 | 90 |
| 15 | 1 | 4 | 191 | 15.91 | 33.45 | 1.036 | 1.38 | 161 | 179 |
| 16 | 0.2 | 7 | 191 | 28.44 | 37.23 | 0.891 | 1 | 166 | 184 |
| 17 | 0.2 | 10 | 790 | 25.98 | 37.97 | 0.743 | 1.08 | 60 | 77 |
| 18 | 0.6 | 7 | 790 | 13.83 | 33.12 | 0.704 | 1.24 | 67 | 74 |
| 19 | 1 | 10 | 494 | 14.2 | 34.28 | 0.615 | 1.25 | 63 | 70 |
| 20 | 1 | 10 | 191 | 6.47 | 32.43 | 0.733 | 1.55 | 137 | 152 |
| 21 | 1 | 4 | 191 | 15.7 | 33.74 | 0.963 | 1.45 | 68 | 119 |
| 22 | 1 | 7 | 191 | 13.96 | 34.11 | 0.625 | 1.03 | 137 | 152 |
| 23 | 0.6 | 10 | 494 | 13.5 | 33.83 | 0.754 | 1.38 | 84 | 93 |
| 24 | 0.6 | 4 | 494 | 23.19 | 34.81 | 0.965 | 1.21 | 139 | 154 |
| 25 | 0.2 | 4 | 790 | 36.92 | 37.98 | 1.202 | 1.15 | 292 | 324 |
| 26 | 1 | 4 | 494 | 25.34 | 35.46 | 1.048 | 1.2 | 149 | 165 |
| 27 | 0.2 | 4 | 494 | 37.68 | 37.8 | 1.138 | 1.5 | 356 | 396 |
| 28 | 0.6 | 4 | 191 | 28.02 | 36.04 | 1.077 | 1.23 | 112 | 124 |
| 29 | 0.2 | 7 | 790 | 22.29 | 35.25 | 0.722 | 1.13 | 162 | 180 |
| 30 | 1 | 7 | 191 | 16.47 | 33.76 | 0.598 | 1.24 | 79 | 88 |
| 31 | 0.6 | 10 | 494 | 18.23 | 35.57 | 0.634 | 1.1 | 127 | 141 |
| 32 | 0.6 | 7 | 494 | 20.41 | 35.73 | 0.656 | 1.31 | 112 | 124 |
| 33 | 0.2 | 10 | 494 | 30.56 | 38.98 | 0.774 | 0.91 | 104 | 116 |
| 34 | 0.2 | 7 | 494 | 25.05 | 35.97 | 0.889 | 1.28 | 89 | 99 |
| 35 | 1 | 7 | 494 | 17.99 | 36 | 0.474 | 1.39 | 104 | 116 |
| 36 | 0.2 | 7 | 494 | 27.92 | 37.61 | 0.81 | 1.06 | 117 | 130 |
| 37 | 0.6 | 7 | 494 | 18.27 | 33.87 | 0.764 | 1.5 | 117 | 130 |
| 38 | 1 | 4 | 494 | 27.88 | 36.6 | 1.157 | 1.15 | 104 | 116 |
| 39 | 0.2 | 4 | 494 | 30.15 | 36.59 | 1.11 | 1.49 | 311 | 345 |
| 40 | 0.2 | 4 | 790 | 41.63 | 40.4 | 1.246 | 1.05 | 248 | 275 |
| 41 | 1 | 4 | 790 | 20.79 | 35.09 | 1.004 | 1.44 | 113 | 125 |
| 42 | 1 | 4 | 790 | 18.31 | 34.12 | 1.079 | 1.61 | 177 | 197 |
| 43 | 0.2 | 4 | 191 | 52.11 | 43.03 | 1.411 | 0.78 | 390 | 443 |
| 44 | 0.6 | 4 | 494 | 22.89 | 34.46 | 1.073 | 1.45 | 158 | 175 |
| 45 | 1 | 7 | 790 | 9.05 | 32.7 | 0.697 | 1.48 | 112 | 124 |
| 46 | 0.2 | 10 | 790 | 27.22 | 36.98 | 0.732 | 1.08 | 126 | 140 |
| 47 | 0.6 | 7 | 790 | 16.99 | 33.66 | 0.695 | 1.21 | 79 | 88 |
| 48 | 0.6 | 4 | 790 | 28.09 | 35.74 | 1.059 | 1.48 | 127 | 141 |
| 49 | 1 | 7 | 790 | 8.87 | 31.89 | 0.96 | 1.43 | 93 | 103 |
| 50 | 0.2 | 4 | 191 | 47.34 | 41.51 | 1.258 | 0.78 | 160 | 273 |
| 51 | 0.2 | 7 | 191 | 28.09 | 36.51 | 0.797 | 1.08 | 93 | 103 |
| 52 | 0.6 | 7 | 191 | 19.67 | 34.89 | 0.67 | 1.03 | 124 | 138 |
| 53 | 0.6 | 4 | 790 | 15.82 | 33.36 | 0.965 | 1.33 | 59 | 65 |
| 54 | 1 | 7 | 494 | 18.03 | 34.62 | 0.59 | 1.29 | 148 | 164 |
References
- Essa, K. Finite Element Prediction of Deformation Mechanics in Incremental Forming Processes. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2011. [Google Scholar]
- Wang, L. Analysis of Material Deformation and Wrinkling Failure in Conventional Metal Spinning Process. Ph.D. Thesis, Durham University, Durham, UK, 2012. [Google Scholar]
- Chen, M.-D.; Hsu, R.-Q.; Fuh, K.-H. Effects of over-roll thickness on cone surface roughness in shear spinning. J. Mater. Process. Technol. 2005, 159, 1–8. [Google Scholar] [CrossRef]
- Kong, Q.; Yu, Z.; Zhao, Y.; Wang, H.; Lin, Z. Theoretical prediction of flange wrinkling in first-pass conventional spinning of hemispherical part. J. Mater. Process. Technol. 2017, 246, 56–68. [Google Scholar] [CrossRef]
- Kong, Q.; Yu, Z.; Zhao, Y.; Wang, H.; Lin, Z. A study of severe flange wrinkling in first-pass conventional spinning of hemispherical part. Int. J. Adv. Manuf. Technol. 2017, 91, 1–16. [Google Scholar] [CrossRef]
- Polyblank, J.A.; Allwood, J.M. Parametric toolpath design in metal spinning. CIRP Ann. Manuf. Technol. 2015, 64, 301–304. [Google Scholar] [CrossRef]
- Rentsch, B.; Manopulo, N.; Hora, P. Numerical modelling, validation and analysis of multi-pass sheet metal spinning processes. Int. J. Mater. Form. 2017, 10, 641–651. [Google Scholar] [CrossRef]
- Wong, C.C.; Dean, T.A.; Lin, J. A review of spinning, shear forming and flow forming processes. Int. J. Mach. Tools Manuf. 2003, 43, 1419–1435. [Google Scholar] [CrossRef]
- Music, O.; Allwood, J.M.; Kawai, K. A review of the mechanics of metal spinning. J. Mater. Process. Technol. 2010, 210, 3–23. [Google Scholar] [CrossRef]
- Xiao, Y.; Han, Z.; Fan, Z.; Jia, Z. A study of asymmetric multi-pass spinning for angled-flange cylinder. J. Mater. Process. Technol. 2018, 256, 202–215. [Google Scholar] [CrossRef]
- Gan, T.; Yu, Z.; Zhao, Y.; Evsyukov, S.A.; Lai, X. Effects of backward path parameters on formability in conventional spinning of aluminum hemispherical parts. Trans. Nonferrous Met. Soc. China 2018, 28, 328–339. [Google Scholar] [CrossRef]
- Xia, Q.; Shima, S.; Kotera, H.; Yasuhuku, D. A study of the one-path deep drawing spinning of cups. J. Mater. Process. Technol. 2005, 159, 397–400. [Google Scholar] [CrossRef]
- Wang, L.; Long, H.; Ashley, D.; Roberts, M.; White, P. Effects of the roller feed ratio on wrinkling failure in conventional spinning of a cylindrical cup. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 1991–2006. [Google Scholar] [CrossRef]
- Ma, F.; Yang, H.; Zhan, M. Plastic deformation behaviors and their application in power spinning process of conical parts with transverse inner rib. J. Mater. Process. Technol. 2010, 210, 180–189. [Google Scholar] [CrossRef]
- Fazeli, A.R.; Ghoreishi, M. Statistical analysis of dimensional changes in thermomechanical tube-spinning process. Int. J. Adv. Manuf. Technol. 2011, 52, 597–607. [Google Scholar] [CrossRef]
- Wang, L.; Long, H. Roller path design by tool compensation in multi-pass conventional spinning. Mater. Des. 2013, 46, 645–653. [Google Scholar] [CrossRef]
- Essa, K.; Hartley, P. Optimization of conventional spinning process parameters by means of numerical simulation and statistical analysis. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 1691–1705. [Google Scholar] [CrossRef]
- Kang, D.-C.; Gao, X.-C.; Meng, X.-F.; Wang, Z.-H. Study on the deformation mode of conventional spinning of plates. J. Mater. Process. Technol. 1999, 91, 226–230. [Google Scholar] [CrossRef]
- Liu, J.H.; Yang, H.; Li, Y.Q. A study of the stress and strain distributions of first-pass conventional spinning under different roller-traces. J. Mater. Process. Technol. 2002, 129, 326–329. [Google Scholar] [CrossRef]
- Wang, L.; Long, H. Investigation of material deformation in multi-pass conventional metal spinning. Mater. Des. 2011, 32, 2891–2899. [Google Scholar] [CrossRef]
- Wang, L.; Long, H. A study of effects of roller path profiles on tool forces and part wall thickness variation in conventional metal spinning. J. Mater. Process. Technol. 2011, 211, 2140–2151. [Google Scholar] [CrossRef]
- Essa, K.; Hartley, P. Numerical simulation of single and dual pass conventional spinning processes. Int. J. Mater. Form. 2009, 2, 271–281. [Google Scholar] [CrossRef]
- Sugita, Y.; Arai, H. Formability in synchronous multipass spinning using simple pass set. J. Mater. Process. Technol. 2015, 217, 336–344. [Google Scholar] [CrossRef]
- Šugár, P.; Šugárová, J.; Petrovič, J. Analysis of the Effect of Process Parameters on Part Wall Thickness Variation in Conventional Metal Spinning of Cr-Mn Austenitic Stainless Steels. Stroj. Vestn. J. Mech. Eng. 2016, 62, 171–178. [Google Scholar] [CrossRef]
- EL-Khabeery, M.M.; Fattouh, M.; EL-Sheikh, M.N.; Hamed, O.A. On the Conventional Simple Spinning of Cylindrical Aluminium Cups. Int. J. Mach. Tools Manuf. 1991, 31, 203–219. [Google Scholar] [CrossRef]
- Kawai, K.; Yang, L.-N.; Kudo, H. A flexible shear spinning of axi-symmetrical shells with a general-purpose mandrel. J. Mater. Process. Technol. 2007, 192–193, 13–17. [Google Scholar] [CrossRef]
- Venkateshwarlu, G.; Kumar, K.R.; Reddy, T.A.J.; Gopi, G. Experimental Investigation on Spinning of Aluminum Alloy 19500 Cup. Int. J. Eng. Sci. Innov. Technol. 2013, 2, 357–363. [Google Scholar]
- Dong, H.; Mei, Z.; He, Y. Deformation Mechanism of TA15 Shells in Hot Shear Spinning under Various Load Conditions. Rare Met. Mater. Eng. 2013, 42, 243–248. [Google Scholar]
- Polyblank, J.A.; Allwood, J.M. Support roller control and springback compensation in flexible spinning. Procedia Eng. 2014, 81, 2499–2504. [Google Scholar] [CrossRef]
- Liu, C.-H. The simulation of the multi-pass and die-less spinning process. J. Mater. Process. Technol. 2007, 192–193, 518–524. [Google Scholar] [CrossRef]
- Marghmaleki, I.S.; Beni, Y.T.; Noghrehabadi, A.R.; Kazemi, A.S.; Abadyan, M. Finite Element Simulation of Thermomechanical Spinning Process. Procedia Eng. 2011, 10, 3769–3774. [Google Scholar] [CrossRef]
- Chen, M.-D.; Hsu, R.-Q.; Fuh, K.-H. Forecast of shear spinning force and surface roughness of spun cones by employing regression analysis. Int. J. Mach. Tools Manuf. 2001, 41, 1721–1734. [Google Scholar] [CrossRef]
- Fazeli, A.R.; Ghoreishi, M. Investigation of effective parameters on surface roughness in thermomechanical tube spinning process. Int. J. Mater. Form. 2009, 2, 261–270. [Google Scholar] [CrossRef]
- Chen, M.-D.; Hsu, R.-Q.; Fuh, K.-H. An analysis of force distribution in shear spinning of cone. Int. J. Mech. Sci. 2005, 47, 902–921. [Google Scholar] [CrossRef]
- Kleiner, M.; Ewers, R.; Kunert, J.; Henkenjohann, N.; Auer, C. Optimisation of the Shear Forming Process by Means of Multivariate Statistical Methods. 2005. Available online: http://www.statistik.tu-dortmund.de/fileadmin/user_upload/Lehrstuehle/MSind/SFB_475/2005/tr23-05.pdf (accessed on 17 August 2014).
- Jaromír, A. Spinning Force Characteristics in Forming Steel Blanks. Transf. Inovácií 2007, 10, 230–234. [Google Scholar]
- Udayani, K.; Veeranna, V.; Gajanana, S.; Reddy, K.H. Optimization of Process Parameters of Metal Spinning using Response Surface Methodology. Int. J. Emerg. Technol. Eng. Res. 2017, 5, 253–256. [Google Scholar]
- Kawai, K.; Yang, L.-N.; Kudo, H. A flexible shear spinning of truncated conical shells with a general-purpose mandrel. J. Mater. Process. Technol. 2001, 113, 28–33. [Google Scholar] [CrossRef]
- Razani, N.A.; Aghchai, A.J.; Dariani, B.M. Experimental study on flow forming process of AISI 321 steel tube using the Taguchi method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2011, 225, 2024–2031. [Google Scholar] [CrossRef]
- Imamura, Y.; Ikawa, K.; Sakane, Y.; Iwasaki, H.; Hirakawa, T. Investigation of forming accuracy in mandrel-free hot-spinning. Procedia Eng. 2017, 207, 1701–1706. [Google Scholar] [CrossRef]
- Valoppi, B.; Egea, A.J.S.; Zhang, Z.; Rojas, H.A.G.; Ghiotti, A.; Bruschi, S.; Cao, J. A hybrid mixed double-sided incremental forming method for forming Ti6Al4V alloy. CIRP Ann. Manuf. Technol. 2016, 65, 309–312. [Google Scholar] [CrossRef]
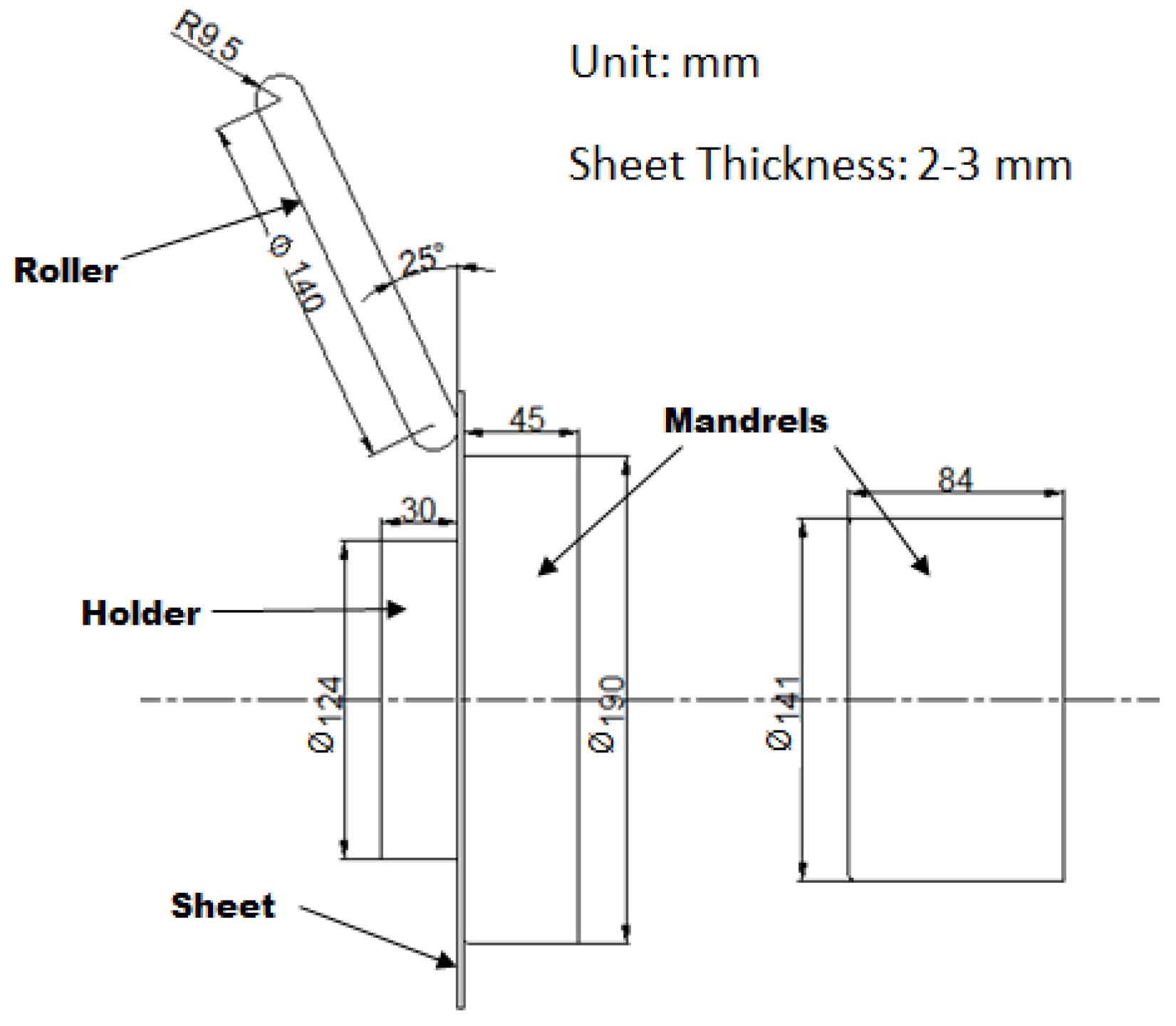
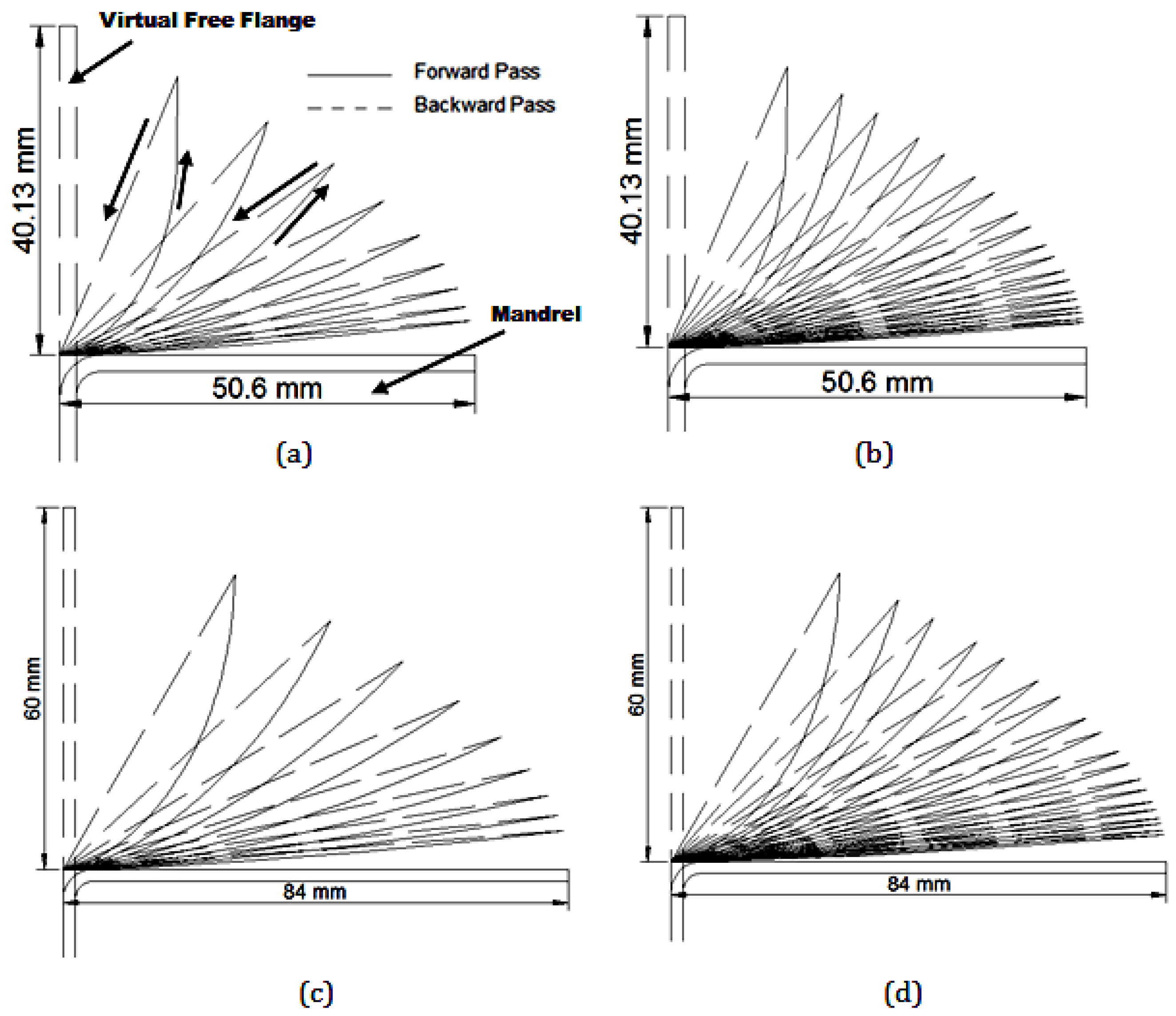



| Elements | Al | Si | Fe | Cu | Zn | Ni | Sn | Ti | p | Others |
|---|---|---|---|---|---|---|---|---|---|---|
| Weight (%) | 99.5 | 0.127 | 0.199 | 0.003 | 0.026 | 0.012 | 0.022 | 0.059 | <0.001 | 0.051 |
| Factors | Levels | |
|---|---|---|
| Feed Ratio (mm/rev.) | 0.2 | 1 |
| Mandrel Speed (RPM) | 191 | 790 |
| Sheet Thickness (mm) | 2 | 3 |
| Number of passes | 10 | 20 |
| Spinning Ratio | 1.26 | 1.7 |
| Lubrication | without | with |
| Factors | Maximum Thinning | Springback | Surface Roughness | Out-of-Roundness |
|---|---|---|---|---|
| Feed Ratio (A) | <0.0001 | x | <0.0001 | x |
| Mandrel Speed (B) | <0.0001 | x | x | x |
| Sheet Thickness (C) | <0.0001 | 0.0006 | x | x |
| Number of Passes (D) | 0.0194 | 0.0073 | 0.0074 | 0.0205 |
| Spinning Ratio (E) | <0.0001 | 0.001 | 0.0006 | 0.0002 |
| Lubrication (F) | x | x | <0.0001 | x |
| Interactions | ||||
| AxB | x | 0.002 | x | x |
| AxD | 0.0003 | x | <0.0001 | x |
| AxE | x | x | 0.0031 | x |
| AxF | <0.0001 | <0.0001 | <0.0001 | 0.0026 |
| BxF | <0.0001 | x | x | x |
| Factors | Levels | ||
|---|---|---|---|
| Feed Ratio (mm/rev.) | 0.2 | 0.6 | 1 |
| Number of Passes | 4 | 7 | 10 |
| Mandrel Speed (RPM) | 191 | 494 | 790 |
| Factors | Maximum Thinning | Cup Height | Springback | Surface Roughness | Out-of-Roundness | Cylindericity Error |
|---|---|---|---|---|---|---|
| Feed Ratio (A) | <0.0001 | <0.0001 | <0.0001 | 0.0004 | <0.0001 | <0.0001 |
| Number of passes (B) | <0.0001 | <0.0001 | <0.0001 | x | <0.0001 | <0.0001 |
| Mandrel Speed (C) | 0.0109 | 0.0009 | x | 0.0403 | x | x |
| Interactions | ||||||
| AxB | 0.0052 | 0.0017 | x | x | <0.0001 | <0.0001 |
| AxC | 0.0123 | 0.0175 | 0.0387 | x | x | x |
| BxC | 0.0425 | 0.0103 | x | x | x | x |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd-Alrazzaq, M.; Ahmed, M.; Younes, M. Experimental Investigation on the Geometrical Accuracy of the CNC Multi-Pass Sheet Metal Spinning Process. J. Manuf. Mater. Process. 2018, 2, 59. https://doi.org/10.3390/jmmp2030059
Abd-Alrazzaq M, Ahmed M, Younes M. Experimental Investigation on the Geometrical Accuracy of the CNC Multi-Pass Sheet Metal Spinning Process. Journal of Manufacturing and Materials Processing. 2018; 2(3):59. https://doi.org/10.3390/jmmp2030059
Chicago/Turabian StyleAbd-Alrazzaq, Mohamed, Mahmoud Ahmed, and Mohamed Younes. 2018. "Experimental Investigation on the Geometrical Accuracy of the CNC Multi-Pass Sheet Metal Spinning Process" Journal of Manufacturing and Materials Processing 2, no. 3: 59. https://doi.org/10.3390/jmmp2030059
APA StyleAbd-Alrazzaq, M., Ahmed, M., & Younes, M. (2018). Experimental Investigation on the Geometrical Accuracy of the CNC Multi-Pass Sheet Metal Spinning Process. Journal of Manufacturing and Materials Processing, 2(3), 59. https://doi.org/10.3390/jmmp2030059





