Abstract
In disaster relief operations, integrating disaster reconnaissance, material delivery, and effect evaluation into a temporal task chain can significantly reduce emergency response cycles and improve rescue efficiency. However, since multiple types of heterogeneous UAVs need to be coordinated during the rescue temporal task chains assignment process, this places higher demands on the real-time dynamic decision-making and system fault tolerance of its task assignment algorithm. This study addresses the sequential dependencies among disaster reconnaissance, material delivery, and effect evaluation stages. A task allocation model for heterogeneous UAV swarm targeting temporal task chains is formulated, with objectives to minimize task completion time and energy consumption. A dynamic coalition formation algorithm based on temporary leader election and multi-round negotiation mechanisms is proposed to enhance continuous decision-making capabilities in complex disaster environments. A simulation scenario involving twenty heterogeneous UAVs and seven temporal rescue task chains is constructed. The results show that the proposed algorithm reduces average task completion time by 15.2–23.7% and average fuel consumption by 18.3–26.4% compared with cooperative network protocols and distributed auctions, with up to a 43% reduction in fuel consumption fluctuations.
1. Introduction
At present, the field of rescue and relief is undergoing technological changes characterized by networking, intelligence, and system integration [1]. Natural disasters occur frequently and become more destructive on a global scale. The traditional rescue model has revealed limitations such as slow response and difficult coordination when dealing with complex disaster situations. Meanwhile, the development of new-generation information technologies has provided technical support for the innovation of rescue models: 5G networks enable high-speed and low-latency communication, edge computing ensures the processing capacity of on-site data, and artificial intelligence technology significantly improves decision-making efficiency. Against this backdrop, the “distributed collaborative rescue” model, which integrates characteristics of networking, intelligence, and system integration, has emerged and become an important development direction in the field of emergency rescue [2]. This rescue model presents two core features. The first is the system survivability advantage brought by capability distribution. By decomposing the rescue force into a large number of low-cost and replaceable heterogeneous platforms, the robustness of the rescue system is significantly improved. This decentralized deployment method allows the integrity of the system to be maintained when critical nodes are compromised, which greatly enhances the resilience of rescue operations. The second is the efficiency multiplication effect generated by dynamic collaboration. With the aid of an intelligent decision network, various rescue units can realize real-time situation awareness and autonomous task allocation. This adaptive coordination mechanism breaks through the response bottleneck of traditional centralized command and forms the effect of 1 + 1 > 2 through elastic task reorganization. The core of the rescue paradigm is to transform the quantity advantage into the quality advantage. The realization path is through the distributed intelligent decision-making architecture, which enables the swarm to have the ability of autonomous evolution and elastic expansion [3]. In the face of a dynamic disaster environment, it can quickly form a targeted task collaboration network and realize the coordination of complex rescue goals through the interaction and adaptive adjustment between agents, thus producing nonlinear and composite rescue effects. The current technical research focuses on the modeling and solving methods of the UAV swarm agent cooperation problem.
In terms of problem modeling, many different types of UAV task allocation problems have been extensively studied. Notable examples include the following: for the targeted priority-based multi-unmanned aircraft attack mission against moving targets, Sami Shahid et al. [4] proposed an autonomous and collaborative task allocation method based on the extended contract net protocol, which is used to handle the real-time position allocation and uniform resource allocation problems in multi-directional attacks. On the other hand, in view of the dynamic task planning problem caused by UAV operational disruptions in the operational environment, Shi Zhan et al. [5] established a multi-objective optimization model including equipment attrition factors. In this study, multi-dimensional parameters such as UAV cost, task timeliness, expected revenue, and cost loss were incorporated into the unified analysis framework. By quantitatively evaluating the impact of unit failure risk on task effectiveness, a dynamic task allocation mechanism with environmental adaptability is finally formed. With the increasing complexity of UAV application scenarios, researchers begin to introduce more constraints to simulate the actual task environment [6]. For example, the range constraint, the task time window constraint, the UAV communication distance constraint, and the payload constraint. For example, Li Xiangmin et al. [7] studied the task allocation problem of a multi-UAV agent coalition considering task time window requirements. Tang Jiayu et al. [8] studied the heterogeneous multi-agent distributed coalition task allocation problem considering task payload resource constraints, task coupling relationship constraints, and execution window constraints. Yan Ji et al. [9] studied the single-task multi-agent time-extended task allocation problem by considering the timing relationship between tasks, the synchronization requirement of starting time, and the waiting penalty of agents. However, the current UAV task allocation model has gradually taken into account the complex constraints such as range, communication, and resources. However, few scholars have carried out in-depth research on the complex task planning problem of multi-stage rescue cooperation and synchronous rescue of heterogeneous UAV swarms in complex interference relief environments.
In terms of solving methods, the solving methods of the heterogeneous UAV swarm task planning problem can be roughly divided into three categories: exact solving methods, heuristic solving methods, and multi-agent-based solving methods [10,11,12]. Exact solution methods, such as branch and bound methods and branch pricing methods, can obtain the optimal solution to the problem. In recent years, certain progress has been made in the research of task planning using exact solution methods. For example, Sundar et al. [13] proposed an exact solution algorithm based on branch-and-cut, which significantly improves the generation speed of optimal task allocation schemes in complex task environments by hierarchical decoupling of time and space constraints of information collection tasks. Andrea et al. [14] innovated to use the branch pricing algorithm to solve the UAV task planning problem with time-sensitive constraints, which significantly improved the solving efficiency of the algorithm while ensuring the timeliness of task execution. However, the solution time of the exact solution method increases exponentially with the problem size. For the task planning problem with a large-scale decision search space, the optimization efficiency of the exact solution algorithm is the main difficulty. To solve this problem, heuristics have been proposed in large numbers. Heuristic optimization methods can provide approximate optimal solutions to problems in finite time, and the degree of deviation between the generated solution and the optimal solution cannot be estimated theoretically. A large number of research applications have verified the good optimization effect of heuristic algorithms in optimization problems. For example, Edison et al. [15] designed an integrated solution method for simultaneous multi-UAV assignment and path planning based on the genetic algorithm of matrix coding for the problem of heterogeneous multi-UAV cooperative task allocation and path planning, and the algorithm can deal with related tasks with priorities. Wang et al. [16] designed a reverse double gene coding algorithm fused with target feature recognition for multimodal reconnaissance scenarios and achieved good results in large-scale reconnaissance task planning problems. However, with the increase in the complexity of the real environment, higher requirements are put forward for the robustness and resilience of the UAV swarm during task execution. Heuristic optimization methods usually have some limitations, the most significant of which is their centralized nature. Centralized methods rely on a single central control system to coordinate the task planning and execution of the UAV swarm, which makes the system vulnerable to a single point of failure. Especially in complex disaster relief environments, the central control system may be damaged or impaired, resulting in a significant decline in the task execution efficiency and overall system resilience. The distributed task planning method based on multi-agent systems has been adopted by a large number of scholars. For example, Choi et al. [17] successfully solved the collaborative decision-making problem under complex task constraints by improving the CBBA algorithm in the collaborative operation scene of a heterogeneous unmanned system swarm. Ponda et al. [18] used the validity time window of the task as part of the scoring scheme to solve the scenario with time constraints. In addition, Johnson et al. [19] proposed the CBBA algorithm based on the negotiation mechanism of asynchronous communication, which enables the system to have the distributed decision-making ability of autonomous coordination by removing the temporal coupling between agents in the negotiation phase. The distributed task planning method based on multi-agent significantly improves the anti-interference ability of UAV swarms in the process of executing tasks through decentralized decision-making mechanisms and collaboration. Therefore, the distributed task planning method based on multi-agent has significant advantages in the anti-jamming ability of UAV swarms, which can effectively deal with the complex and changeable disaster relief environment.
Based on the above analysis, there are two main problems in the current research. In terms of problem modeling, the existing research has not systematically solved the complex task planning problem of multi-stage rescue cooperation and synchronous rescue of heterogeneous UAV swarms in complex interference disaster relief environments. In terms of solution methods, the existing research still faces bottlenecks in improving the invulnerability of the system, and it is urgent to further improve the anti-jamming ability of the UAV swarm task allocation algorithm in complex disaster relief environments by improving the dynamic task coordination mechanism. Therefore, this paper considers the timing task chain problem and the task configuration problem of synchronous rescue UAV swarms for the first time. A mathematical model of the task allocation problem for the temporal task chain was constructed, and a task allocation algorithm for UAV swarms based on dynamic election and multi-round negotiation mechanisms was designed. The subsequent structure of this paper is as follows: Section 2 formulates the heterogeneous UAV swarm allocation problem for temporal task chains, including mathematical modeling of mission constraints. Section 3 details the proposed Dynamic Coalition Task Allocation (DCTA) algorithm, integrating election-based leadership selection and iterative negotiation processes. Section 4 validates the framework through high-fidelity simulations (twenty heterogeneous UAVs executing seven sequential rescue tasks) with comprehensive performance analysis. Section 5 concludes with findings and future directions.
2. Task Allocation Problem for Heterogeneous UAV Swarm with Temporal Task Chains
2.1. Problem Description
In the task allocation problem with temporal task chains, a set of m tasks needs to be assigned to a heterogeneous UAV swarm composed of n UAVs. Each task contains three stages of disaster reconnaissance, material delivery, and effect evaluation with strict timing constraints and needs to follow the serial execution order of reconnaissance → delivery → evaluation.
The UAV swarm comprises three specialized types of unmanned aerial vehicles: reconnaissance UAVs, delivery UAVs, and evaluation UAVs, each designed to perform their respective category of tasks exclusively. Owing to the constrained payload capacity of individual UAVs, the completion of a single reconnaissance, delivery, or evaluation subtask often necessitates the coordinated effort of multiple UAVs forming a temporary alliance. A critical requirement for successful task execution is the simultaneous arrival of all UAVs within such an alliance at the designated task location. Consequently, task allocation and path planning algorithms must account for UAV-specific kinematic constraints, including maximum velocity limitations and minimum turning radius requirements.
To further describe how UAVs form temporary alliances to accomplish disaster response tasks in a real-world scenario, the process is described in the following steps:
- When no collaborative task is triggered, the UAV swarm remains in a roaming state. UAVs perform random searches within the task space using swarm intelligence to maintain balanced payload coverage and avoid collisions while preserving communication links.
- When a UAV detects a disaster target via reconnaissance or communication, one UAV is randomly elected as the temporary leader for that task through dynamic leader election.
- UAVs share decision information with the Leader UAV. Through multiple rounds of negotiation, they reach a consensus on situational awareness and establish a recognized optimal collaborative rescue plan, forming a temporary alliance.
- The UAVs involved in the plan switch from the roaming state to trajectory flight and begin responding to the task.
- To maximize rescue effectiveness, each UAV plans its path according to its current position, speed, and turning radius, ensuring synchronized arrival at the task site.
- Upon arrival, UAVs complete the task and return to the roaming state (Step 1).
This study focuses on Steps 2 through 6, specifically how to dynamically form UAV alliances and assign tasks across the entire task chain.
2.2. Mathematical Modeling
To construct a mathematical model for the task allocation problem of a heterogeneous UAV swarm with temporal task chains, we first define the relevant parameters and then formulate a multi-objective optimization model with task completion time and energy consumption as the objectives. The model also includes multiple constraints to ensure feasibility.
2.2.1. Model Parameters
The model involves two categories of parameters: UAV-related parameters and task-related parameters. The definitions are shown in Table 1:

Table 1.
Model parameter table of task allocation problem for heterogeneous unmanned aerial vehicle swarm alliance oriented to temporal task chain.
2.2.2. Objective Function
The model considers two optimization objectives: the total task completion time and the total fuel consumption. The overall objective function is given by
where C is the fuel consumption coefficient per unit distance, represents the total fuel consumed by each UAV in the heterogeneous UAV swarm during its flight within the task time, represents the time spent by the heterogeneous UAV swarm to complete all tasks.
2.2.3. Constraints
In order to make the model conform to the actual disaster relief situation, considering the attributes of UAVs and tasks, this paper considers and sets three constraint conditions.
- UAV-type constraints
During the task execution process of a heterogeneous UAV swarm, reconnaissance tasks can only be assigned to reconnaissance UAVs for execution, delivery tasks can only be assigned to delivery UAVs for execution, and evaluation tasks can only be assigned to evaluation UAVs for execution. The specific UAV-type constraint formulas are shown in Equation (2).
In the formula, and represent reconnaissance, delivery, and evaluation tasks, respectively. and represent the maximum number for reconnaissance UAVs, delivery UAVs and evaluation UAVs.
- Resource constraints required for task completion
When heterogeneous UAV swarms are performing reconnaissance, delivery, and evaluation tasks, the total number of resources carried by the UAV alliance must be greater than or equal to the number of resources required to complete the task to be regarded as completed. The specific resource constraint formula required for task completion is shown in Equation (3).
- Task execution timing constraints
The three sub-tasks of reconnaissance, delivery, and evaluation for each task all need to be carried out in a strict temporal sequence of reconnaissance first, then delivery, and finally evaluation. Therefore, the temporal constraint formula for task execution is shown in Equation (4).
Moreover, we assume an idealized communication environment, i.e., the communication delay between UAVs is negligible. This assumption implies that the coordination and information exchange among UAVs are instantaneous and reliable, which allows us to focus on the task allocation and resource constraints without considering communication delays.
3. Dynamic Coalition-Based Task Allocation Algorithm for Heterogeneous UAV Swarm
In this section, the overall framework of the heterogeneous UAV swarm alliance task allocation algorithm is presented. Subsequently, detailed descriptions are provided for the three core algorithm modules: dynamic election, multi-round negotiation, and path planning.
3.1. Algorithm Framework
The overall framework is illustrated in Figure 1.
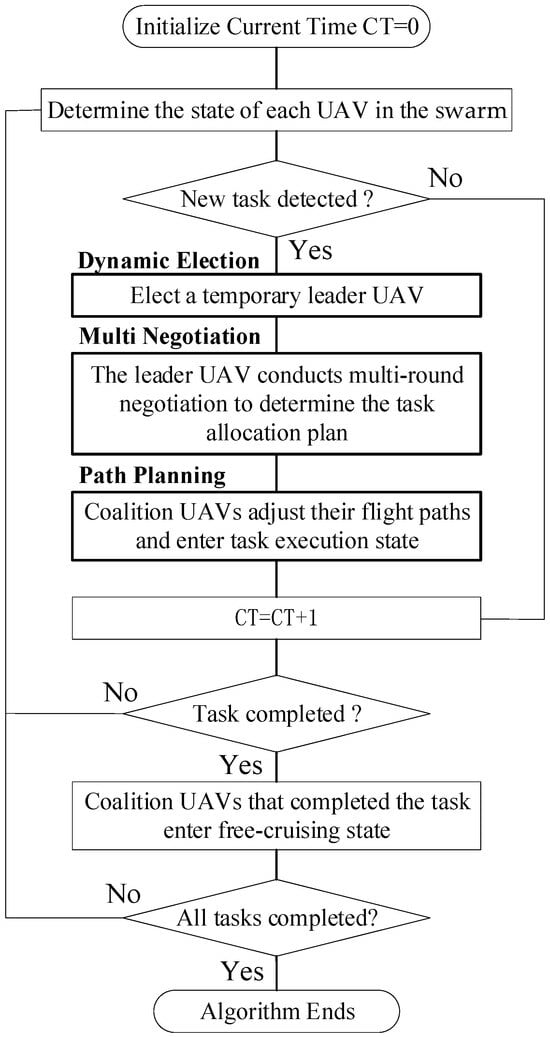
Figure 1.
Task allocation algorithm framework for heterogeneous UAV swarm alliance.
At the beginning stage of the algorithm, all UAVs are in a free cruising state. When a UAV detects a valid target or receives a collaborative task request, the dynamic alliance construction process is triggered, and the system immediately enters the election-negotiation cycle. After the negotiation is completed, the UAV alliance is determined, and the task is carried out. When the task is completed, each UAV in the UAV alliance re-enters the cruising state and waits for the next detection of an effective target or receipt of a collaborative task request. When all tasks are completed or the time limit is reached, the algorithm’s operation terminates. A detailed introduction of the three core algorithm modules: dynamic election, multi-round negotiation, and path planning is shown in Figure 1.
3.2. Dynamic Leader Election
To enhance the resilience of a UAV swarm in the face of uncertain environments and interference, this algorithm incorporates a dynamic leader election mechanism to assign a temporary leader (i.e., a task coordinator) for each task.
The dynamic election mechanism allows the UAV swarm to continuously assess the operational status, capabilities, and mission relevance of each UAV. By selecting the most suitable UAV to serve as the leader in real-time, the algorithm ensures robustness against single points of failure and improves fault tolerance and task continuity. This adaptability also enhances efficiency and task success rate in complex environments. The election process of the temporary Leader UAV is shown in Figure 2.
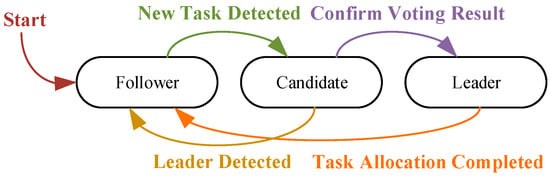
Figure 2.
The election process of the temporary Leader UAV.
As shown in Figure 2, the election process of the temporary Leader UAV can be roughly divided into the following seven steps:
- Task detection: All UAVs receive task information upon discovery.
- Broadcast candidacy: Each UAV broadcasts its candidacy, including its ID, capability, and current position.
- Evaluation: UAVs evaluate each candidate based on mission needs, capabilities, and distance.
- Voting: UAVs vote for their preferred candidate.
- Result aggregation: The candidate with the most votes is selected as the temporary leader.
- Confirmation: The elected leader is confirmed and begins coordinating the task.
- Release: Once the task is completed, the leader returns to fellow status; a new election will be triggered when the next task arises.
It is worth noting that in Step 3—Evaluation, each UAV evaluates every candidate UAV based on the received candidacy information (ID, position). The evaluation aims to select a leader optimally positioned for both task execution and intra-cluster coordination. The core evaluation metric is a Comprehensive Suitability Score (CSS) calculated using the following formula:
where and are predefined weighting coefficients (summing to 1) that balance the relative importance of task proximity (closeness to operational area) and group centrality (positional advantage for swarm coordination). denoted the Euclidean distance between candidate j’s coordinates and the task’s designated centroid. denoted the Euclidean distance between candidate j’s position and the real-time geometric centroid of the entire UAV swarm.
3.3. Multi-Round Negotiation
After confirming the Leader UAV responsible for task coordination, the multi-round negotiation process immediately began. During the multi-round negotiation process, the Leader UAV first confirms the task requirements and broadcasts them to all UAVs. Each UAV decides whether to participate and submit an application based on the task requirements and its own capabilities. Subsequently, the Leader UAV evaluates and selects the most suitable UAVs to join the task alliance based on factors such as the capabilities of the UAVs, task requirements, and distance. If the task requires more members, the Leader UAV will, through multiple rounds of negotiations, continuously adjust and select additional participants based on the selected members. Finally, the Leader UAV confirmed the alliance members of the task and issued instructions. All members began to carry out the task. The pseudo-code of the multi-round negotiation process is shown as Algorithm 1.
| Algorithm 1: Multi-round Negotiation Process Pseudo-code | |
| Input: Task information, capabilities, and status of all UAVs. | |
| Output: List of coalition UAVs for task execution. | |
| 1: | %Leader confirms and broadcasts task requirements leader_id = confirm_leader() task_info = get_task_info() broadcast_task_requirements(leader_id, task_info) |
| 2: | %UAVs submit applications applicants = [] for drone in drones: if evaluate_drone_for_task(drone, task_info) then applicants.append(drone.id) end if |
| 3: | %Leader UAV evaluates and selects members selected_members = [] for drone_id in applicants: if evaluate_membership(drone_id, task_info) then selected_members.append(drone_id) end if |
| 4: | %Multi-round negotiation while len(selected_members) < task_info.required_member_count: for drone_id in applicants: if drone_id not in selected_members: if evaluate_membership(drone_id, task_info) then selected_members.append(drone_id) if len(selected_members) >= task_info.required_member_count then break end if end if end for end while |
| 5: | %Confirm coalition members confirm_alliance_members(leader_id, selected_members) retuen selected_members |
3.4. Path Planning
After completing multiple rounds of negotiations and finally confirming the members of the UAV alliance to carry out the task, each UAV within the alliance will calculate its flight time based on its own geographical location, the position of the task, and the extraordinary speed of each UAV, independently adjust its course, and plan its trajectory to ensure reaching the designated task location in the shortest time. In addition, to ensure the effectiveness of the task execution, the UAV will coordinate and optimize the flight route to ensure that all members can arrive at the task site simultaneously and maximize the efficiency of the task execution. The pseudo-code for coordinating the flight trajectories of each UAV in the alliance is shown in Algorithm 2.
| Algorithm 2: UAV Path Planning Pseudo-code | |
| Input: Position, velocity, heading angle of each coalition UAV, and task location. | |
| Output: Flight trajectory for each coalition UAV. | |
| 1: | %Confirm minimum flight time for coalition UAVs Max Calculate time = dubins_distance(uav, uav.TargetLocation, Rmin) |
| 2: | %Calculate turning radius for each coalition UAV Initialize turn_radius = Rmin Calculate distance = dubins_distance(uav, target_location, turn_radius) while distance < distance_required: Increase turn_radius by 0.1 Recalculate distance = dubins_distance(uav, target_location, turn_radius) end while |
| 3: | %Return flight trajectories for coalition UAVs return uav_flight trajectory |
4. Simulation Experiment
To verify the effectiveness of the heterogeneous UAV swarm dynamic alliance task allocation algorithm proposed in this paper in solving the temporal task chains allocation problem, we set up simulation examples and conducted a comparative analysis with the existing algorithms. The simulations were executed on MATLAB 2022b, running on a computing system equipped with an AMD Ryzen 7 7840H processor at 3.80 GHz, 16 GB of RAM, and an NVIDIA GeForce RTX 4060 GPU.
4.1. Instance Settings
This section constructs a simulation experiment scenario for the collaborative task allocation of a heterogeneous UAV swarm. The simulation area is set as a rectangular task space of 5 km × 3 km. Within this area, there are seven temporal task chains. Twenty heterogeneous UAVs enter the task area from the left side of the map. The initial position distribution of the tasks and the UAVs is shown in Figure 3.
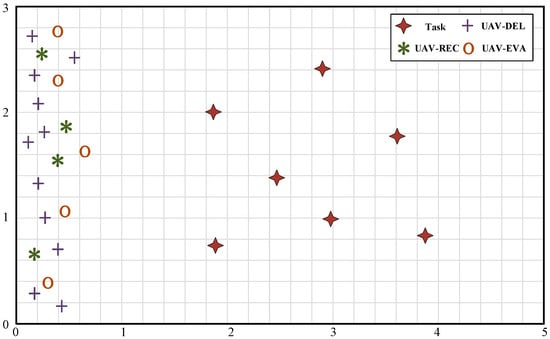
Figure 3.
Rescue tasks and the initial positions of heterogeneous UAVs.
Each rescue task consists of three sub-task stages with strict temporal constraints: Reconnaissance (REC), Delivery (DEL), and Evaluation (EVA), and each stage has differentiated resource requirements. The types of UAVs and the quantities of resources required at each stage of the rescue task are shown in Table 2.

Table 2.
Rescue task parameter table.
Furthermore, the experiment was equipped with 20 heterogeneous UAVs, which were classified into four reconnaissance UAVs (UAV-REC) according to their functions and were fitted with electro-optical/radar reconnaissance equipment. Eleven UAVs (UAV-DEL) carrying material payloads; and five evaluation UAVs (UAV-EVA) were equipped with rescue effect evaluation systems. The key performance parameters of various types of UAVs are shown in Table 3.

Table 3.
Table of key energy parameters of heterogeneous UAV.
4.2. Result Analysis
To demonstrate the performance of the algorithm proposed in this paper in the actual operation process, we present the task execution of the heterogeneous UAV swarm at each key decision-making moment during the operation of the algorithm, as shown in Figure 4.
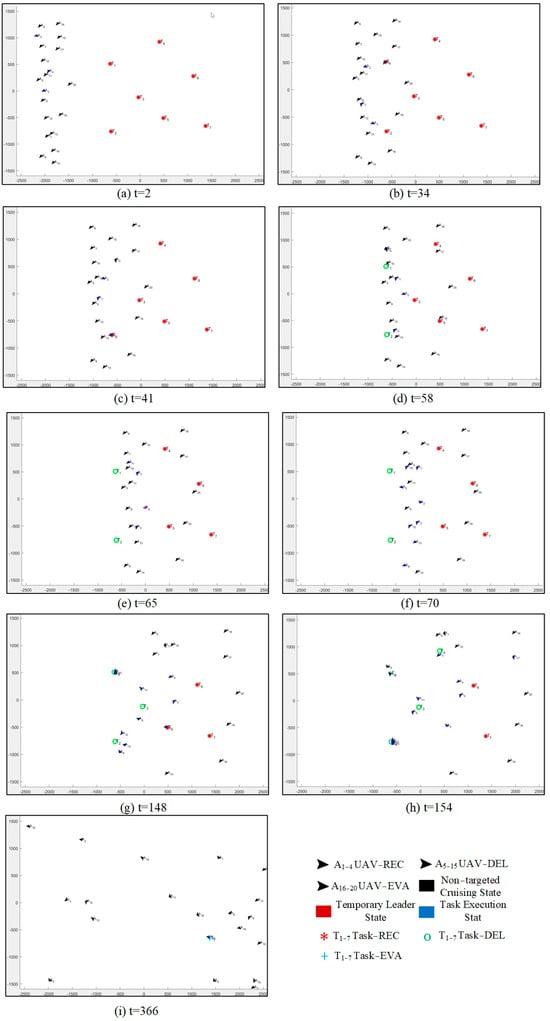
Figure 4.
The task execution situation of heterogeneous UAV swarm at each critical decision-making moment.
As shown in Figure 4a, at t = 2, unmanned aerial vehicles A2, A3, and A4, respectively, discovered the reconnaissance tasks that needed to be carried out. Since the number of resources required for the reconnaissance tasks was relatively small, after a simple negotiation, they, respectively, determined the reconnaissance tasks they needed to carry out. After 34 and 41 time steps, UAVs A4 and A3 completed the reconnaissance sub-task of tasks T1 and T2, respectively, as shown in Figure 4b,c. With the completion of the reconnaissance sub-task of tasks T1 and T2, the delivery sub-tasks of tasks T1 and T2 were released, as shown in Figure 4d. Immediately after, UAV A2 was selected to serve as the temporary lead UAV for the delivery sub-task of tasks T1 and T2 and began to assemble delivery UAVs to form a UAV alliance to complete the delivery sub-task of tasks T1 and T2, as shown in Figure 4e. As can be seen in Figure 4f, after multiple rounds of negotiations, UAVs A5 and A10 responded to the call of the temporary lead UAV A2 for the delivery sub-task of task T1, and delivery UAVs A12, A13, and A8 responded to the call of the temporary lead UAV A2 for the delivery sub-task of task T2, forming a UAV alliance. And start adjusting the flight path to ensure reaching the task location simultaneously and completing the delivery sub-task. Subsequently, the delivery sub-tasks of tasks T1 and T2 were completed by the formed delivery UAV alliances at time steps t = 148 and t = 154, respectively, as shown in Figure 4g,h. Ultimately, after 366 time steps, the UAV A20 reached the position of mission T7 and completed the evaluation sub-task of task T7. All tasks were accomplished, and the simulation ended.
Furthermore, in order to further analyze the specific allocation of heterogeneous UAV swarm in solving temporal task chains, Table 4 presents the UAVs that complete the sub-task of the three stages of reconnaissance—delivery—evaluation for each task.

Table 4.
Reconnaissance–delivery–assessment subtask distribution table.
It can be seen from Table 4 that the algorithm demonstrates significant load balancing and functional adaptation rationality in task allocation. For example, all UAVs in the reconnaissance unit pool (A1–A4) and the evaluation unit pool (A16–A20) are fully invoked without redundancy or waste. Among the eleven UAVs in the delivery unit pool (A5–A15), nine were invoked. The resource utilization rate reached 81.8%, and the idle rate was controlled within a reasonable range. Furthermore, by comparing the extreme differences in the number of tasks completed by each UAV, it can be found that the extreme difference in the number of tasks completed by a single UAV is ≤2, and the algorithm achieves a balanced distribution of UAV tasks.
4.3. Scalability Validation
To evaluate the algorithm’s performance under varying swarm sizes, we conducted large-scale simulations across five configurations: 20, 40, 60, 80, and 100 heterogeneous UAVs. For each size, 20 distinct disaster scenarios were randomly generated with proportional task quantities. Performance metrics were averaged across 20 runs per configuration.
Analysis of Table 5 reveals that when task quantities were proportionally scaled with the number of UAVs, the proposed algorithm demonstrated remarkable scalability and stability. Specifically, as the UAV swarm size expanded from 20 to 100, the task completion time exhibited only a modest increase from 396 s to 402 s, representing a minimal increment of merely 1.5%. Concurrently, the total system energy consumption rose from 20,889 units to 21,408 units, with the increase rigorously constrained below 2.5%. These results robustly validate the algorithm’s capability to efficiently address the challenges associated with scale expansion and maintain stable overall system performance within complex systems comprising heterogeneous UAV swarms ranging from 20 to 100 units.

Table 5.
Algorithm performance under different UAV sizes (average value and standard deviation).
4.4. Algorithm Comparison
In order to further prove the effectiveness of the heterogeneous UAV swarm dynamic alliance task allocation algorithm proposed in this paper in solving the temporal task chain allocation problem, we selected three algorithms from the existing literature for comparison. We compared the average task completion time and average fuel consumption of multiple algorithms under 20 simulation runs. The comparison results are shown in Figure 5. The benchmark algorithms were intentionally chosen to represent diverse methodological approaches: the cooperative network protocol exemplifies distributed consensus-driven strategies, while the distributed auction algorithm reflects market-based optimization frameworks. Although alternative algorithms (e.g., centralized optimization methods or rule-based heuristics) exist, the selected comparators provide rigorous baselines that dominate current literature in temporal constrained multi-UAV scenarios. Their widespread adoption and proven efficacy in chain-structured tasks ensure a fair and technologically relevant assessment of our method’s advancements.
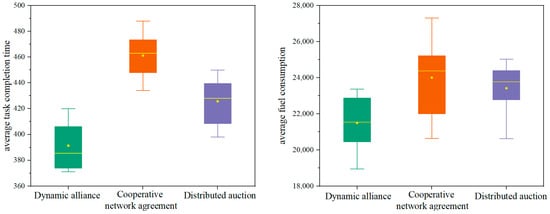
Figure 5.
Comparison of the average task completion time and average fuel consumption after running simulation examples with different algorithms.
It can be seen from Figure 5 that under the average data of 20 runs, the average fuel consumption and average completion time of the dynamic alliance are significantly lower than those of the cooperative network agreement and the distributed auction. Furthermore, by comparing and observing the ranges of fuel consumption and completion time of the three algorithms, it can be found that the fuel consumption data of the dynamic alliance fluctuates less (with a range of approximately 4000 units), while the fluctuations of the cooperative network protocol and the distributed auction are greater (with ranges of approximately 7000 and 5000 units, respectively), indicating that the energy consumption control of the dynamic alliance is more stable. Meanwhile, the completion time data distribution of the dynamic alliance is more concentrated (mostly between 370 and 420 units), while the completion time dispersion of the other two algorithms is higher. The possible reason lies in that the cooperative network protocol relies on global negotiation and is difficult to adapt to the dynamic task requirements, resulting in higher time costs and greater fuel consumption. Distributed auctions are prone to cause resource conflicts when making local decisions, requiring repeated coordination, which increases fuel consumption and uncertainty. The coalition game algorithm proposed in this paper effectively shortens the task completion time and fuel consumption by balancing global optimization and local efficiency, avoiding the delay of the centralized protocol and the conflict of the auction mechanism.
5. Conclusions
This paper proposes a task allocation algorithm based on the election of a temporary chief aircraft and the alliance negotiation mechanism for the collaborative requirements of a heterogeneous UAV swarm in complex disaster relief environments. By constructing a three-stage closed-loop task model of “reconnaissance—delivery—evaluation” and combining it with the theory of alliance formation game, the dynamic adaptation of heterogeneous resources and heterogeneous task requirements has been achieved. Research shows that the proposed algorithm can achieve the dynamic allocation of rescue tasks under temporal constraints. Compared with existing algorithms, the average task completion time and average fuel consumption of the algorithm proposed in this paper under multiple runs are both smaller than those of existing algorithms. Furthermore, the random temporary Leader selection mechanism can significantly enhance the resilience of the cluster system and improve the anti-interference ability of the UAV swarm.
It should be noted that this study has certain limitations: Simulations were conducted in simplified two-dimensional environments, omitting critical real-world factors including three-dimensional obstacles, wind disturbances, and aerodynamic interference. Environmental complexities such as altitude variations, turbulence-induced trajectory corrections, and physical barriers remain unaddressed, with communication delays during UAV coordination intentionally idealized to focus on core allocation mechanisms.
This research provides a new theoretical framework and technical approach for the collaboration of UAV swarms in complex disaster relief environments. The subsequent research will consider the task allocation problem of mobile targets, design a coalition reconstruction algorithm based on incomplete information games, and improve the robustness of the system under mobile task targets.
This research provides a new theoretical framework and technical approach for the collaboration of UAV swarms in complex disaster relief environments. The following research will cover three key aspects:
- (1)
- Dynamic target tracking algorithms for mobile rescue targets;
- (2)
- Coalition reconstruction mechanisms based on incomplete information game theory under uncertain environments;
- (3)
- Cross-domain adaptive optimization for rapidly evolving disaster scenarios;
- (4)
- These extensions will fundamentally enhance the system’s capability to address real-world rescue complexities.
Author Contributions
Conceptualization, H.L., Z.S. and S.Z.; methodology, H.L. and Z.S.; software, H.L.; validation, H.L., Z.S. and Q.Z.; formal analysis, H.L.; investigation, H.L.; resources, Z.S. and J.T.; data curation, H.L.; writing—original draft preparation, H.L.; writing—review and editing, H.L.; visualization, H.L.; supervision, Z.S., J.T. and H.L.; project administration, Z.S.; funding acquisition, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The project was supported by the Science and Technology Foundation of the State Key Laboratory (JZX7Y202301SY000601 and WDZC20245250402).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviation
| Abbreviation | Full Form |
| CSS | Comprehensive Suitability Score |
| REC | Reconnaissance |
| DEL | Delivery |
| EVA | Evaluation |
| UAV-REC | Reconnaissance UAVs |
| UAV-DEL | Delivery UAVs |
| UAV-EVA | Evaluation UAVs |
References
- Hu, X.R. Enhancing the Role of Artificial Intelligence Technology in Disaster Prevention, Mitigation and Relief. China Disaster Reduct. 2025, 9, 46–49. (In Chinese) [Google Scholar]
- Zhong, Y. Mission Planning and Dynamic Scheduling of Heterogeneous UAV Swarms in Disaster Relief Environments. Ph.D. Thesis, Donghua University, Shanghai, China, 2024. [Google Scholar] [CrossRef]
- Aramide, O.O. Edge AI and its Impact on Resilient AI Fabric Design: Distributed Intelligence and Data Locality. A J. Phy. Sci. Eng. Technol. 2025, 17, 12–24. [Google Scholar] [CrossRef]
- Shahid, S.; Zhen, Z.Y.; Umair, J. Cooperative Task Assignment of Heterogeneous Unmanned Aerial Vehicles for Simultaneous Multi-directional Attack on a Moving Target. Eng. Appl. Artifi. Intell. 2025, 13, 109595. [Google Scholar] [CrossRef]
- Shi, Z.; Chen, Q.W. Multi-UAV Cooperative Task Allocation Based on Improved Multi-Objective Quantum-Behaved Particle Swarm Optimization. J. Nanjing Univ. Sci. Technol. 2012, 36, 945–951. (In Chinese) [Google Scholar] [CrossRef]
- Gugan, G.; Anwar, H. Path Planning for Autonomous Drones: Challenges and Future Directions. Drones 2023, 7, 169. [Google Scholar] [CrossRef]
- Li, X.M.; Tang, J.Y.; Dai, J.J.; Bo, N. Dynamic Task Allocation for Heterogeneous Multi-Agent Coalitions. J. Northwest. Polytech. Univ. 2020, 38, 1094–1104. (In Chinese) [Google Scholar] [CrossRef]
- Tang, J.Y.; Li, X.M.; Dai, J.J.; Bo, N. Task Allocation for Heterogeneous Multi-Agent Coalitions Under Complex Constraints. Control Theory Appl. 2020, 37, 2413–2422. (In Chinese) [Google Scholar]
- Yan, J.; Li, X.M.; Liu, B. Multi-Agent Cooperative Task Allocation Considering Temporal Constraints. Control Decis. 2015, 30, 1999–2003. (In Chinese) [Google Scholar] [CrossRef]
- Cao, P.; Lei, L.; Cai, S.S.; Shen, G.; Liu, X.; Wang, X. Computational Intelligence Algorithms for UAV Swarm Networking and Collaboration: A comPrehensive Survey and Future Directions. IEEE Communic. Surv. Tuto. 2024, 26, 2684–2728. [Google Scholar] [CrossRef]
- Javed, S.; Hassan, A.; Ahmad, R.; Ahmed, W.; Ahmed, R.; Saadat, A. State-of-the-Art and Future Research Challenges in UAV Swarms. IEEE Internet Things J. 2024, 11, 19023–19045. [Google Scholar] [CrossRef]
- Ragab, A.R.; Ale Isaac, M.A.; Luna, M.A.; Peña, P.F. Unmanned aerial vehicle swarming. In Proceedings of the 2021 International Conference on Engineering and Emerging Technologies (ICEET), Istanbul, Turkey, 27–28 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Sundar, K.; Rathinam, S. Algorithms for Heterogeneous, Multiple Depot, Multiple Unmanned Vehicle Path Planning Problems. J. Intell. Robot. Syst. 2017, 88, 513–526. [Google Scholar] [CrossRef]
- Bettinelli, A.; Ceselli, A.; Righini, G. A Branch-and-Cut-and-Price Algorithm for the Multi-Depot Heterogeneous Vehicle Routing Problem with Time Windows. Transp. Res. Part C Emerg. Technol. 2011, 19, 723–740. [Google Scholar] [CrossRef]
- Edison, E.; Shima, T. Integrated Task Assignment and Path Optimization for Cooperating Uninhabited Aerial Vehicles Using Genetic Algorithms. Comput. Oper. Res. 2011, 38, 340–356. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, L.; Long, T.; Wen, Y. Multi-UAV Reconnaissance Task Allocation for Heterogeneous Targets Using an Opposition-Based Genetic Algorithm with Double-Chromosome Encoding. Chin. J. Aeronaut. 2018, 31, 339–350. [Google Scholar] [CrossRef]
- Choi, H.L.; Whitten, A.K.; How, J.P. Decentralized Task Allocation for Heterogeneous Teams with Cooperation Constraints. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3057–3062. [Google Scholar] [CrossRef]
- Ponda, S.; Redding, J.; Choi, H.L.; How, J.P.; Vavrina, M.; Vian, J. Decentralized Planning for Complex Missions with Dynamic Communication Constraints. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 3998–4003. [Google Scholar]
- Johnson, L.B.; Ponda, S.P.; Choi, H.L.; How, J.P. Asynchronous Decentralized Task Allocation for Dynamic Environments. In Proceedings of the Infotech@Aerospace 2011, St. Louis, MI, USA, 29–31 March 2011; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2011; p. 1441. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).