Data-Driven Optimal Bipartite Containment Tracking for Multi-UAV Systems with Compound Uncertainties

Abstract

With the increasing deployment of Unmanned Aerial Vehicle (UAV) swarms in uncertain and dynamically changing environments, optimal cooperative control has become essential for ensuring robust and efficient system coordination. To this end, this paper designs a data-driven optimal bipartite containment tracking control scheme for multi-UAV systems under compound uncertainties. A novel Dynamic Iteration Regulation Strategy (DIRS) is proposed, which enables real-time adjustment of the learning iteration step according to the task-specific demands. Compared with conventional fixed-step data-driven algorithms, the DIRS provides greater flexibility and computational efficiency, allowing for better trade-offs between the performance and cost. First, the optimal bipartite containment tracking control problem is formulated, and the associated coupled Hamilton–Jacobi–Bellman (HJB) equations are established. Then, a data-driven iterative policy learning algorithm equipped with the DIRS is developed to solve the optimal control law online. The stability and convergence of the proposed control scheme are rigorously analyzed. Furthermore, the control law is approximated via the neural network framework without requiring full knowledge of the model. Finally, numerical simulations are provided to demonstrate the effectiveness and robustness of the proposed DIRS-based optimal containment tracking scheme for multi-UAV systems, which can reduce the number of iterations by 88.27% compared to that for the conventional algorithm.

1. Introduction

In recent years, multi-UAV systems have emerged as a cornerstone in advancing low-altitude economies and intelligent autonomous systems owing to their advantages in task flexibility, environmental adaptability, and cooperative autonomy. Technically, system architectures have evolved from centralized schemes to distributed cooperative frameworks, thereby enhancing the robustness, scalability, and resilience in complex and dynamic environments. These advancements have facilitated the widespread deployment of multi-UAV systems across various domains. For example, in precision agriculture, UAV swarms are employed for real-time crop monitoring, field mapping, and pesticide application [1,2]. In urban logistics, UAV-based delivery networks enable efficient last-mile transportation and emergency responses [3,4]. In the energy sector, UAVs are increasingly used to inspect power lines, substations, and wind farms, providing high-frequency data acquisition with reduced operational risks [5,6]. These diverse applications highlight the critical role of multi-UAV systems in addressing real-world challenges across civil, industrial, and environmental domains.

Among various coordination strategies, containment tracking has emerged as a fundamental problem in the cooperative control of multi-UAV systems. The primary objective is to drive the follower UAVs to converge into the convex hull formed by multiple leader agents under a leader–follower architecture. Depending on the motion behavior of the leaders, containment control problems are generally classified into two categories: static and dynamic containment [7]. Static containment considers scenarios where the leaders remain stationary, and the followers are required to converge to a fixed convex region. This formulation simplifies the controller design by eliminating the need for velocity measurements and is well suited to applications such as satellite formation surveillance and area monitoring [8,9,10]. In contrast, dynamic containment addresses cases where the leaders follow time-varying trajectories. It necessitates the development of distributed velocity or acceleration observers to enable the followers to track a moving convex region, thereby enhancing the robustness under dynamic operating conditions. Dynamic containment has demonstrated substantial practical relevance in time-sensitive missions such as UAV-based logistics and aerial surveillance [11,12,13]. Nevertheless, practical deployments of multi-UAV systems often involve non-cooperative behaviors and resource contention, especially in congested airspace or adversarial environments [14,15]. Such scenarios naturally give rise to both cooperative and antagonistic interactions among agents, which conventional containment control frameworks fail to adequately address. To overcome these limitations, the concept of bipartite containment control has been introduced as a significant extension. This framework is designed to ensure group-level convergence even in the presence of both positive (cooperative) and negative (competitive) relationships among agents.

Within the framework of bipartite containment control, follower agents are guided to converge to the union of two convex hulls, each constructed by a distinct subgroup of cooperative or competitive leaders. These leader subgroups independently span their respective convex regions, while the system collectively ensures global convergence and stability [16]. Several recent studies have explored this problem from various perspectives. For instance, Wu et al. [17] investigated bipartite containment for heterogeneous marine aerial–surface systems and proposed an adaptive control scheme with prescribed performance guarantees. He et al. [18] tackled the containment tracking problem in nonlinear systems subject to false data injection (FDI) attacks using a model-free adaptive iterative learning control method. Furthermore, Fan et al. [19] formulated a problem under adversarial disturbances as a zero-sum game and employed game-theoretic strategies to achieve bipartite containment. Also contributing to the research on bipartite containment control are the works in [20,21], which have significantly advanced the field by enhancing robustness and addressing adversarial scenarios. However, most of the existing approaches primarily focus on feasibility and stability, while a critical gap persists in performance-oriented design. In particular, aspects such as minimizing the control effort, reducing the energy consumption, and improving transient behavior have received insufficient attention, despite their practical significance in real-world multi-UAV applications that operate under resource constraints and mission-critical timelines.

Moreover, most of the aforementioned studies do not explicitly account for the presence of uncertainties, which are ubiquitous in practical multi-UAV control scenarios. In real-world deployments, UAVs are often subjected to external disturbances such as gusty winds, atmospheric turbulence, and aerodynamic interactions with neighboring vehicles [22]. Simultaneously, internal uncertainties may stem from actuator degradation, sensor misalignment, mounting errors, and structural deformations [23]. These compound uncertainties introduce significant challenges into the design of control strategies that are both robust and performance-optimal. Consequently, there is a pressing need for control frameworks capable of achieving high-performance coordination while effectively accommodating such uncertainties.

In recent years, adaptive dynamic programming (ADP) has garnered considerable attention as an effective approach to solving the optimal control problem [24]. ADP facilitates online learning of the optimal control policies via iterative value function approximation and is particularly appealing due to its model-free nature, enabling adaptation to unknown or time-varying system dynamics [25]. Some representative studies [26,27] show that ADP exhibits adaptivity and practicality in both energy system optimization and UAV cooperative control. Meanwhile, to address the uncertainty in the control process, some works [28,29] propose robust ADP methods. Despite these advances, the majority of the existing ADP approaches rely on the generalized policy iteration (GPI) framework [30,31], which typically assumes a preassigned and fixed number of internal iterations. Such static iteration strategies may result in a suboptimal computational efficiency, particularly in scenarios with heterogeneous learning speeds or dynamic environmental conditions, thereby hindering real-time applicability in resource-constrained systems.

Therefore, to address the aforementioned challenges, this paper proposes a data-driven Dynamic Iterative Reward Shaping (DIRS) approach to achieve optimal bipartite containment control for multi-UAV systems subject to compound model uncertainties. The main contributions of this paper are summarized as follows:

(1) A data-driven control scheme is developed to address the problem of optimal bipartite containment tracking control for multi-UAV systems under compound uncertainties. The proposed scheme integrates task-specific cost function design with online policy learning, enabling performance-oriented and adaptive control. Compared with the existing approaches [32,33], this framework provides greater flexibility and applicability in real-world scenarios by allowing the control strategies to be tailored to mission-specific objectives and environmental conditions.

(2) By leveraging a critic–actor neural network architecture, the proposed scheme realizes a data-driven, online iterative control process that operates independently of explicit system model parameters. This model-free formulation enhances the robustness against compound uncertainties, including external disturbances and internal structural or parametric errors, thereby ensuring a reliable performance in uncertain and dynamically evolving multi-UAV environments.

(3) To enhance the computational efficiency of traditional ADP algorithms [34,35], this paper designs a novel DIRS method. By incorporating a dynamic regulation mechanism and an adaptive regulation threshold, the DIRS enables task-dependent adjustment of the learning iteration steps. This mechanism effectively eliminates redundant iterations, improves the computational efficiency, and facilitates a better trade-off between the control performance and resource cost, thereby making this approach more suitable for real-time deployment in complex multi-UAV systems.

The remainder of this paper is organized as follows. Section 2 presents the preliminary concepts in graph theory and formulates the optimal bipartite containment tracking problem for multi-UAV systems. Section 3 introduces a novel DIRS-based iterative strategy for solving the optimal control problem and analyzes its performance and further details the implementation of a critic–actor neural network for online approximation of the optimal control law. Section 4 provides numerical simulations to demonstrate the effectiveness of the proposed method. Finally, Section 5 concludes the whole paper.

2. Preliminaries and Problem Formulation

2.1. Preliminaries

Consider a multi-UAV system with N followers and M leaders, denoted as a structurally balanced graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$, which is used to model the interactions in the system, where $\mathcal{V}=\{v_1,\dots ,v_M,v_{M+1},\dots ,v_{M+N}\}$ is the set of nodes formed by all UAVs. ${\mathcal{V}}_L=\{v_1,\dots ,v_M\}$ and ${\mathcal{V}}_F=\{v_{M+1},\dots ,v_{M+N}\}$ are the subsets of nodes representing the leader UAVs and follower UAVs, respectively. In addition, $\mathcal{E}\subset \mathcal{V}\times \mathcal{V}$ is the set of edges, and $\mathcal{A}=\left[a_{ij}\right]$ is the adjacency matrix, which is used to represent the weight of each edge. If an edge from UAV $v_j$ to UAV $v_i$ exists, it is denoted as $\left(v_j,v_i\right)\in \mathcal{E}$, and the weight of the edge is $a_{ij}>0$ when these two UAVs are cooperative, and conversely, $a_{ij}<0$. If $a_{ij}=0$, that means that there is no interaction between UAVs $v_i$ and $v_j$. The set of neighbors of the UAV $v_i$ is defined as ${\mathcal{N}}_i=\{j\in \mathcal{V}\mid \left(v_j,v_i\right)\in \mathcal{E}\}$, which is the set of all UAVs that can directly communicate with UAV $v_i$.

Assumption 1.

The communication topology of the multi-UAV system is assumed to be a directed graph. In this topology, leader agents do not receive information from follower agents, reflecting a unidirectional leader–follower interaction structure. Furthermore, it is assumed that at least one directed path exists from each leader to every follower, thereby ensuring that the leader set maintains directed connectivity to the follower set.

2.2. Problem Formulation

In this subsection, we consider a multi-UAV system composed of M leaders and N followers operating under compound uncertainties. Dynamic models of both the leader and follower agents are constructed and simplified accordingly. Based on this, the problem of optimal bipartite containment tracking control is formally formulated.

2.2.1. Models of the UAVs

Consider a follower quadrotor UAV system in the Earth-fixed coordinate system ${\mathcal{O}}_e$, whose spatial information is determined by the position vector $x_i={[p_{i_x},p_{i_y},p_{i_z}]}^T$ and the attitude Euler angle vector ${\Omega }_i={[{\varphi }_i,{\theta }_i,{\psi }_i]}^T$, where $p_{i_x},p_{i_y},p_{i_z}$ are the three-axis co-ordinates of the ${\mathcal{O}}_e$ system. And ${\varphi }_i,{\theta }_i,{\psi }_i$ represent the roll, pitch, and yaw angles, respectively. Based on the rigid-body dynamics established in the literature [36], the model of the ith follower UAV can be expressed as follows:

$$\begin{array}{cc}\hfill x_i(t+1)& =x_i\left(t\right)+\mathcal{T}{v}_i\left(t\right)+o_1\left(t\right),\hfill \\ \hfill v_i(t+1)& =v_i\left(t\right)+\mathcal{T}\left(-g\overrightarrow{e_3}+{\displaystyle \frac{1}{m_i}}{T}_{bi}\left(t\right){\mathcal{R}}_{bi}^e\left(t\right)\overrightarrow{e_3}+o_2\left(t\right)\right),\hfill \end{array}$$

(1)

where the velocity vector ${\mathcal{v}}_i={[v_{i_x},v_{i_y},v_{i_z}]}^T$ to represent the velocity state of the ist UAV in the inertial system. Equally, the constant g denotes the gravity acceleration, whose direction is determined by the base vector $\overrightarrow{e_3}={[0,0,1]}^T$ (vertically downward positive). $m_i$ represents the total mass of the UAV body’s structure and payload. The nonlinear function terms $o_1\left(t\right)$ and $o_2\left(t\right)$ denote the external uncertainties for the follower UAV. The actuator characteristics are described by the total lift $T_{bi}$ in the body-fixed coordinate system ${\mathcal{O}}_b$, which is mapped to the Earth-fixed coordinate system ${\mathcal{O}}_e$ by the rotation matrix ${\mathcal{R}}_{bi}^e$.

$${\mathcal{R}}_{bi}^e\left(t\right)=\left[\begin{array}{ccc}\cos {\theta }_i\cos {\psi }_i& \cos {\psi }_i\sin {\varphi }_i\sin {\theta }_i-\cos {\varphi }_i\sin {\psi }_i& \sin {\varphi }_i\sin {\psi }_i+\cos {\varphi }_i\cos {\psi }_i\sin {\theta }_i\\ \cos {\theta }_i\sin {\psi }_i& \cos {\varphi }_i\cos {\psi }_i+\sin {\varphi }_i\sin {\theta }_i\sin {\psi }_i& \cos {\varphi }_i\cos {\theta }_i\sin {\psi }_i-\cos {\psi }_i\cos {\varphi }_i\\ -\sin {\theta }_i& \cos {\theta }_i\sin {\varphi }_i& \cos {\varphi }_i\cos {\theta }_i\end{array}\right].$$

(2)

To facilitate the analysis, we define $u_{i_x}\left(t\right)=T_{bi}\left(t\right)(\sin {\varphi }_i\sin {\psi }_i+\cos {\varphi }_i\cos {\psi }_i\sin {\theta }_i)/m_i$, $u_{i_y}\left(t\right)=T_{bi}\left(t\right)(\cos {\varphi }_i\cos {\theta }_i\sin {\psi }_i-\cos {\psi }_i\cos {\varphi }_i)/m_i$, and $u_{i_z}=T_{bi}\left(t\right)\left(\cos {\varphi }_i\cos {\theta }_i\right)/m_i-g$. Moreover, let $u_i={[u_{i_x},u_{i_y},u_{i_z}]}^T$ be the control inputs. A simplified form of the follower UAV dynamics with compound uncertainties can be obtained.

$$\begin{array}{cc}\hfill x_i(t+1)=& x_i\left(t\right)+\mathcal{T}{v}_i\left(t\right)+o_1\left(t\right),\hfill \\ \hfill v_i(t+1)=& v_i\left(t\right)+\mathcal{T}{u}_i\left(t\right)+o_2\left(t\right),i=1,2,\dots ,N.\hfill \end{array}$$

(3)

Similarly, the same simplification can be made for the dynamics of the leader UAVs, resulting in the following:

$$\begin{array}{cc}\hfill x_m(t+1)=& x_m\left(t\right)+\mathcal{T}{v}_m\left(t\right)+{\ell }_1\left(t\right),\hfill \\ \hfill v_m(t+1)=& v_m\left(t\right)+{\ell }_2\left(t\right),m=1,2,\dots ,M.\hfill \end{array}$$

(4)

According to (3) and (4), the dynamics of a multi-UAV system with compound uncertainties can be simplified into a second-order integrator. The subsequent controller design will be developed on this basis.

2.2.2. The Description of the Optimal Bipartite Containment Tracking Control Problem

Definition 1.

For a set of leader UAV positions $x_1,\dots ,x_M$, the corresponding convex hulls formed are defined as

$$co\{x_1,\dots ,x_M\}=\left\{\sum _{i=1}^M{\gamma }_i{x}_i|{\gamma }_i\in \mathbb{R},\gamma \ge 0,\sum _{i=1}^M{\gamma }_i=1\right\}.$$

(5)

Definition 2.

Bipartite containment control of a multi-UAV system (3), (4) can be achieved if driven by the control inputs, some of the followers converge to the convex hull $co\{x_j,j\in {\mathcal{V}}_L\}$ according to the topological relation, and the others converge to the bipartite convex hull $-co\{x_j,j\in {\mathcal{V}}_L\}$.

Remark 1.

In contrast to traditional containment control problems [9,12], the bipartite containment control framework divides the UAV agents into distinct groups that interact through both cooperative and antagonistic links within a signed communication network. Such interactions result in the follower UAVs asymptotically converging to two opposing convex hulls, each spanned by a subgroup of leader UAVs. Based on this structure, bipartite containment tracking control not only requires the follower UAVs to converge to the appropriate convex hull region in terms of the state but also mandates synchronization of the velocity with the corresponding convex hulls, thereby ensuring coordinated motion tracking in dynamic environments.

Therefore, to solve the bipartite containment tracking control problem in multi-UAV systems, the local neighbourhood bipartite containment tracking error is described as

$$\begin{array}{cc}\hfill e_i\left(t\right)=& \sum _{j\in {\mathcal{N}}_i}\left|a_{ij}\right|[(\mathrm{sign}\left(a_{ij}\right)x_j\left(t\right)-x_i\left(t\right))+(\mathrm{sign}\left(a_{ij}\right)v_j\left(t\right)-v_i\left(t\right))],i\in {\mathcal{V}}_F.\hfill \end{array}$$

(6)

To formulate the optimal containment control problem, the following performance index ${\mathcal{R}}_i$ is defined for each follower UAV i:

$$\begin{array}{c}\hfill {\mathcal{R}}_i(e_i\left(t\right),u_i\left(t\right))=\sum _{\tau =t}^{\infty }{\rho }^{\tau -t}{\mathcal{H}}_i(e_i\left(\tau \right),u_i\left(\tau \right)),\end{array}$$

(7)

where $\rho$ is a discount factor that ranges in (0, 1], which determines the relative importance of the future rewards to the current value estimates. Therefore, it is usually necessary in practice to balance the initial convergence speed with the final performance in order to select the optimal discount factor. And the utility function ${\mathcal{H}}_i$ can be denoted as

$$\begin{array}{cc}\hfill {\mathcal{H}}_i(e_i\left(t\right),u_i\left(t\right))=& e_i^T\left(t\right){\mathcal{P}}_i{e}_i\left(t\right)+u_i^T\left(t\right){\mathcal{Q}}_{ii}{u}_i\left(t\right).\hfill \end{array}$$

(8)

where ${\mathcal{P}}_i\ge 0$ corresponds to the weight matrix of the quadratic term of the tracking error, and the matrices ${\mathcal{Q}}_{ii}>0$ correspond to the weight matrix of the quadratic term of the control inputs. Therefore, different values for ${\mathcal{P}}_i$ and ${\mathcal{Q}}_{ii}$ can dynamically adjust the weights of the tracking error and control inputs in the utility function, which in turn determines the convergence speed.

Moreover, according to the admissible control set $\{u_1,u_2,\dots ,u_N\}$, the optimal performance metric function can be defined as

$$\begin{array}{cc}\hfill {\mathcal{R}}_i^{\ast }(e_i\left(t\right),u_i\left(t\right))=& \underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i(e_i\left(t\right),u_i\left(t\right))+\rho {\mathcal{R}}_i^{\ast }(e_i(t+1),u_i(t+1))\}.\hfill \end{array}$$

(9)

Meanwhile, the value function of the iteration process is

$$\begin{array}{c}\hfill V_i(e_i\left(t\right),u_i\left(t\right)=\sum _{\tau =t}^{\infty }{\phi }^{\tau -t}{\mathcal{H}}_i(e_i\left(\tau \right),u_i\left(\tau \right)).\end{array}$$

(10)

Furthermore, according to the Bellman optimality principle, $V_i$ should satisfy the following discrete-time HJB equation.

$$\begin{array}{cc}\hfill V_i^{\ast }(e_i\left(t\right),u_i\left(t\right)=& \underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i(e_i\left(t\right),u_i\left(t\right))+\rho {\mathcal{R}}_i^{\ast }(e_i(t+1),u_i(t+1))\}.\hfill \end{array}$$

(11)

The corresponding optimal bipartite containment tracking control law can be defined as

$$\begin{array}{cc}\hfill u_i^{\ast }\left(t\right)=& arg\underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i(e_i\left(t\right),u_i\left(t\right))+\rho {\mathcal{R}}_i^{\ast }(e_i\left(t\right),u_i\left(t\right))\}.\hfill \end{array}$$

(12)

Remark 2.

As mentioned in the literature [37], there is a correlation between the connectivity of the topology and the Laplace matrix eigenvalues. In general, if the connectivity is higher, the control is relatively better and converges relatively faster; however, greater connectivity means that each UAV also needs to obtain more information about its neighbors and therefore may consume more computational resources.

This section presents the formulation of the optimal bipartite containment tracking control problem for multi-UAV systems subject to compound uncertainties. It is important to note that the Bellman equation associated with the optimal value function (11) and the corresponding control law (12) are inherently nonlinear and lack closed-form analytical solutions. To address this challenge, online numerical methods with iterative approximation schemes are employed to solve the HJB equations and approximate both the optimal value function and the associated control inputs. Furthermore, in subsequent sections, an enhanced ADP framework is proposed by developing a novel DIRS, which significantly reduces the computational burden of the iterative process.

3. DIRS Algorithm Design, Analysis, and Online Implementation

In this section, a novel DIRS is proposed to adaptively adjust the sub-iteration step size. The proposed algorithm effectively eliminates redundant iterations and facilitates the solution of the optimal value function and the corresponding control inputs. A neural-network-based approximation scheme is then employed to enable an online implementation of the optimal bipartite containment tracking control. The overall DIRS-based control framework is illustrated in Figure 1.

3.1. The DIRS Algorithm Design

Let $u_i^b\left(t\right)$ and $V_i^b\left(e_i\left(t\right)\right)$ represent the control law and the value function, respectively. Furthermore, to simplify the iteration process, $V_i^{b,d}\left(e_i\left(t\right)\right)$ is defined as an adaptive sub-iteration value function with the sub-iteration indexes $b=0,1,2,\dots ,\phi ,\dots ,\Omega$. The symbol $\phi$ denotes the number of sub-iterations that are adaptively adjusted based on the convergence of the value function, while $\Omega$ represents the predetermined maximum number of sub-iterations. In order to facilitate the representation, all polynomials of a similar form have $V_i\left(e_i\left(t\right)\right)=V_i\left(t\right),{\mathcal{H}}_i(e_i\left(t\right),u_i\left(t\right))={\mathcal{H}}_i\left(t\right)$, for those mentioned later.

For the progress of the $\phi$th sub-iteration, the value function is

$$V_i^b\left(t\right)=V_i^{b,\phi }\left(t\right).$$

(13)

The DIRS algorithm’s iterative process is summarized below:

(1): Initializing the admissible control law $u_i^0\left(t\right)$, the initial value function $V_i^0\left(t\right)$ is determined as

$$\begin{array}{c}\hfill V_i^0\left(t\right)={\mathcal{H}}_i^0\left(t\right)+\rho V_i^0(t+1).\end{array}$$

(14)

For $b=1,2,\dots$, the iteration control law $u_i^b\left(t\right)$ is

$$\begin{array}{c}\hfill u_i^b\left(t\right)=arg\underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i^0\left(t\right)+\rho V_i^{b-1}(t+1)\}.\end{array}$$

(15)

(2): Let the control law $u_i^b\left(t\right)$ remain a constant value. For the bth step of the iteration, the value function $V_i^b\left(t\right)$ can be solved as follows.

For $b=1,2,\dots ,\Omega$,

$$\begin{array}{c}\hfill V_i^{b,d}\left(t\right)={\mathcal{H}}_i^b\left(t\right)+\rho V_i^{b,d-1}(t+1),\end{array}$$

(16)

where the initial value function of the sub-iterations is

$$\begin{array}{c}\hfill V_i^{b,0}\left(t\right)={\mathcal{H}}_i^b\left(t\right)+\rho V_i^{b-1}(t+1).\end{array}$$

(17)

If the difference in the value function in two iterations is required to satisfy the following equation,

$$\parallel V_i^{b,d}\left(t\right)-V_i^{b,d-1}\left(t\right)\parallel <\Theta ,$$

(18)

then the d sub-iteration terminates, while its iteration number is recorded as $\phi$. In particular, the threshold size is set to $\Theta$. In fact, a smaller $\Theta$ imposes stricter accuracy requirements, leading to more internal iterations to achieve a higher control accuracy. Conversely, a larger $\Theta$ relaxes the accuracy requirements, allowing the system to reach a steady state faster with fewer iterations.

In the $\phi$ step iteration,

$$V_i^b\left(t\right)=V_i^{b,\phi }\left(t\right).$$

(19)

Otherwise, the adaptive sub-iteration value function is

$$V_i^b\left(t\right)=V_i^{b,\Omega }\left(t\right).$$

(20)

This subsection presents a DIRS algorithm with an adaptive termination mechanism (18), which enables online solution of the HJB equation via alternating policy evaluations and policy improvements. Specifically, the algorithm reduces the number of iterations once sub-iteration convergence is detected, thereby accelerating computation and conserving resources. Moreover, by adjusting the termination threshold, the DIRS algorithm balances computational efficiency and solution accuracy, ensuring reliable approximation of the optimal value function with reduced computational costs.

Remark 3.

Compared with existing ADP algorithms [32,35] for which the number of internal iterations needs to be set in advance, the DIRS algorithm proposed in this paper can adaptively and dynamically adjust the iterative process when (18) is satisfied, avoiding unnecessary iterations after the internal iterations converge. Furthermore, the algorithm can satisfy the required control accuracy while performing the minimum number of iterations, thus saving computational resources and improving the efficiency of optimal bipartite containment control.

3.2. Stability, Convergence, and Optimality

In this subsection, the stability, convergence, and optimality properties of the proposed DIRS algorithm are analyzed, and the corresponding theoretical results are rigorously established. These results lay the theoretical foundation for solving the bipartite containment tracking control problem in multi-UAV systems.

Theorem 1.

The bipartite tracking control error $e_i\left(t\right)$ in the multi-UAV system can be asymptotically stabilized under the application of the optimal control input $u_i^{\ast }\left(t\right)$, which is obtained via the proposed DIRS algorithm. That is, the following condition holds:

$$\underset{t\to \infty }{\lim }{e}_i\left(t\right)\to 0.$$

(21)

Proof. 

According to the DIRS algorithm, the optimal value function $V_i^{\ast }$ satisfies the HJB equation as given in Equation (11) and consequently obtains

$${\mathcal{H}}_i^{\ast }\left(t\right)=V_i^{\ast }\left(t\right)-\rho V_i^{\ast }(t+1).$$

(22)

Multiply both sides of Equation (22) by ${\rho }^k$:

$$\begin{array}{c}\hfill {\rho }^k{\mathcal{H}}_i^{\ast }\left(t\right)={\rho }^k{V}_i^{\ast }\left(t\right)-{\rho }^{k+1}{V}_i^{\ast }(t+1).\end{array}$$

(23)

Define ${\rho }^k{V}_i^{\ast }\left(t\right)$ as the Lyapunov function for all agents. Consequently, the first-order difference form of the Lyapunov equation is derived as

$$\begin{array}{c}\hfill \Theta \left({\rho }^k{V}_i^{\ast }\left(t\right)\right)={\rho }^{k+1}{V}_i^{\ast }(t+1)-{\rho }^k{V}_i^{\ast }\left(t\right).\end{array}$$

(24)

By combining Equations (23) and (24), we obtain the following result.

$$\Theta \left({\rho }^k{V}_i^{\ast }\left(t\right)\right)=-{\rho }^k{\mathcal{H}}_i^{\ast }\left(t\right)\le 0.$$

(25)

From Equation (25), it is evident that the bipartite tracking control error $e_i\left(t\right)$ of multi-UAV systems is asymptotically stable, i.e., $e_i\left(t\right)\to 0$ when $t\to \infty$. This indicates that the system driven by the designed DIRS algorithm achieves bipartite tracking control and the agents track the leader’s trajectory.

The proof is completed. □

Theorem 2.

The value function, as determined by Equations (14) to (20) of the DIRS algorithm, forms a monotonically non-increasing sequence, satisfying the subsequent conditions:

$$V_i^{b,d+1}\left(t\right)\le V_i^{b,d}\left(t\right).$$

(26)

$$V_i^{b+1,d}\left(t\right)\le V_i^{b,d}\left(t\right).$$

(27)

Proof. 

The mathematical induction method will be employed to prove Equations (26) and (27).

As the DIRS algorithm incorporates an adaptive termination mechanism, the maximum number of sub-iterations for the value function becomes uncertain. The algorithm is designed to automatically terminate when the change in the sub-iteration value function is insignificant, recording the maximum number of sub-iterations as $\phi$, or $\Omega$ if it is not a termination. Therefore, in the subsequent proof, the maximum number of sub-iterations within a single iteration is denoted as ℑ, where $\Im \in \{\phi ,\Omega \}$.

Let $b=1$, and denote the value function as follows:

$$\begin{array}{cc}\hfill V_i^{1,0}\left(t\right)& ={\mathcal{H}}_i^1\left(t\right)+\rho V_i^0(t+1)\hfill \\ \hfill & =\underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i\left(t\right)+\rho V_i^0(t+1)\}\hfill \\ \hfill & \le {\mathcal{H}}_i^0\left(t\right)+\rho V_i^0(t+1)\hfill \\ \hfill & =V_i^0\left(t\right).\hfill \end{array}$$

(28)

Furthermore, when $d=0$, it follows that

$$\begin{array}{cc}\hfill V_i^{1,1}\left(t\right)& ={\mathcal{H}}_i^1\left(t\right)+\rho V_i^{1,0}(t+1)\hfill \\ \hfill & \le {\mathcal{H}}_i^1\left(t\right)+\rho V_i^0(t+1)\hfill \\ \hfill & =V_i^{1,0}\left(t\right).\hfill \end{array}$$

(29)

Let $d={\alpha }_1$, where ${\alpha }_1$ is a positive integer such that ${\alpha }_1\in (0,\Im -1]$. From this, it follows that

$$\begin{array}{cc}\hfill V_i^{1,{\alpha }_1+1}\left(t\right)& ={\mathcal{H}}_i^1\left(t\right)+\rho V_i^{1,{\alpha }_1}(t+1)\hfill \\ \hfill & \le {\mathcal{H}}_i^1\left(t\right)+\rho V_i^{1,{\alpha }_1-1}(t+1)\hfill \\ \hfill & =V_i^{1,{\alpha }_1}\left(t\right).\hfill \end{array}$$

(30)

Based on Equations (28) to (30), it is straightforward to demonstrate that inequality (26) from Theorem 2 is satisfied when $b=2$. Suppose further that inequality (26) from Theorem 2 holds for $b=\beta$. This leads to

$$\begin{array}{c}\hfill V_i^{\beta ,d+1}\left(t\right)\le V_i^{\beta ,d}\left(t\right).\end{array}$$

(31)

Consequently, it remains to establish that inequality (26) is also valid for $b=\beta +1$:

$$\begin{array}{cc}\hfill V_i^{\beta +1,0}\left(t\right)& ={\mathcal{H}}_i^{\beta +1}\left(t\right)+\rho V_i^{\beta }(t+1)\hfill \\ \hfill & =\underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i\left(t\right)+\rho V_i^{\beta }(t+1)\}\hfill \\ \hfill & \le {\mathcal{H}}_i^{\beta }\left(t\right)+\rho V_i^{\beta }(t+1)\hfill \\ \hfill & ={\mathcal{H}}_i^{\beta }\left(t\right)+\rho V_i^{\beta ,\Im }(t+1)\hfill \\ \hfill & \le {\mathcal{H}}_i^{\beta }\left(t\right)+\rho V_i^{\beta ,\Im -1}(t+1)\hfill \\ \hfill & =V_i^{\beta ,\Im }\left(t\right)\hfill \\ \hfill & =V_i^{\beta }\left(t\right).\hfill \end{array}$$

(32)

By using (29), for when $d=0$,

$$\begin{array}{cc}\hfill V_i^{\beta +1,1}\left(t\right)& ={\mathcal{H}}_i^{\beta +1}\left(t\right)+\rho V_i^{\beta +1,0}(t+1)\hfill \\ \hfill & \le {\mathcal{H}}_i^{\beta +1}\left(t\right)+\rho V_i^{\beta }(t+1)\hfill \\ \hfill & =V_i^{\beta +1,0}\left(t\right).\hfill \end{array}$$

(33)

Moreover, for $d=1$,

$$\begin{array}{cc}\hfill V_i^{\beta +1,2}\left(t\right)& ={\mathcal{H}}_i^{\beta +1}\left(t\right)+\rho V_i^{\beta +1,1}(t+1)\hfill \\ \hfill & \le {\mathcal{H}}_i^{\beta +1}\left(t\right)+\rho V_i^{\beta +1,0}(t+1)\hfill \\ \hfill & =V_i^{\beta +1,1}\left(t\right).\hfill \end{array}$$

(34)

Similarly, let $d={\alpha }_{\beta }$ and ${\alpha }_{\beta }$ be a positive integer satisfying ${\alpha }_{\beta }\in (0,\Im -1]$; then, it can be derived that

$$\begin{array}{cc}\hfill V_i^{\beta +1,{\alpha }_{\beta }+1}\left(t\right)=& {\mathcal{H}}_i^{\beta +1}\left(t\right)+\rho V_i^{\beta +1,{\alpha }_{\beta }}(t+1)\hfill \\ \hfill \le & {\mathcal{H}}_i^{\beta +1}\left(t\right)+\rho V_i^{\beta +1,{\alpha }_{\beta }-1}(t+1)\hfill \\ \hfill =& V_i^{\beta +1,{\alpha }_{\beta }}\left(t\right).\hfill \end{array}$$

(35)

From the derivation process outlined above, it can be summarized that when $\beta =1,2,\dots$

$$\begin{array}{cc}\hfill V_i^1\left(t\right)=& V_i^{1,\Im }\left(t\right)\le V_i^{1,0}\left(t\right)\le V_i^0\left(t\right),\hfill \\ \hfill V_i^2\left(t\right)=& V_i^{2,\Im }\left(t\right)\le V_i^{2,0}\left(t\right)\le V_i^1\left(t\right),\hfill \\ \hfill & ⋮\hfill \\ \hfill V_i^{\beta +1}\left(t\right)=& V_i^{\beta +1,\Im }\left(t\right)\le V_i^{\beta +1,0}\left(t\right)\le V_i^{\beta }\left(t\right).\hfill \end{array}$$

(36)

The proof is complete. □

An important lemma is introduced before determining the optimality of the DIRS algorithm.

Lemma 1

([38]). If the sequence ${\Pi }_{\mathit{ı}},\mathit{ı}=1,2,\dots$ is monotonically non-increasing, then it converges to the same limit as its subsequence.

Theorem 3.

The value function $V_i\left(t\right)$ and the control law $u_i\left(t\right)$, as determined by Equations (14) to (20) of the DIRS algorithm, converge to the optimal values $V_i^{\ast }\left(t\right)$ nd $u_i^{\ast }\left(t\right)$.

$$\underset{p\to \infty }{\lim }{V}_i^{b,d}\left(t\right)={\mathcal{R}}_i^{\ast }(e_i\left(t\right),u_i\left(t\right)).$$

(37)

$$\underset{b\to \infty }{\lim }{u}_i^b\left(t\right)=u_i^{\ast }\left(t\right).$$

(38)

Proof. 

Initially, construct the sequence associated with the value function according to the DIRS algorithm as follows:

$$\begin{array}{cc}\hfill \left\{V_i^{b,d}\left(t\right)\right\}=& \{V_i^0\left(t\right),\hfill \\ \hfill & V_i^{1,0}\left(t\right),V_i^{1,1}\left(t\right),\dots ,V_i^{1,\mu }\left(t\right),\hfill \\ \hfill & V_i^1\left(t\right),V_i^{2,0}\left(t\right),\dots ,V_i^{2,\mu }\left(t\right),\hfill \\ \hfill & V_i^2\left(t\right),\dots \}.\hfill \end{array}$$

(39)

Furthermore, define the sequence of the value function for the outer iterations as follows:

$$\begin{array}{c}\hfill \left\{V_i^b\left(t\right)\right\}=\{V_i^0\left(t\right),V_i^1\left(t\right),V_i^2\left(t\right),\dots \}.\end{array}$$

(40)

It is evident that the sequence (40) is a subsequence of the sequence (39). Moreover, given that sequence (39) is monotonically non-increasing, it follows from Lemma 1 that

$$\underset{p\to \infty }{\lim }{V}_i^{b,d}\left(e_i\left(t\right)\right)=\underset{p\to \infty }{\lim }{V}_i^b\left(e_i\left(t\right)\right).$$

(41)

Therefore, Theorem 3 to be proven is transformed into

$$\underset{p\to \infty }{\lim }{V}_i^b\left(e_i\left(t\right)\right)=V_i^{\ast }\left(e_i\left(t\right)\right).$$

(42)

Let the limit of $V_i^b\left(t\right)$ as p approaches infinity be denoted by $V_i^{\infty }\left(t\right)$. Given that sequence (40) is monotonically non-increasing, it follows that

$$\begin{array}{cc}\hfill V_i^{\infty }\left(e_i\left(t\right)\right)=& {\mathcal{H}}_i^{\infty }\left(t\right)+\rho V_i^{\infty }(t+1)\hfill \\ \hfill \le & {\mathcal{H}}_i^b\left(t\right)+\rho V_i^b(t+1)\hfill \\ \hfill =& \underset{u_i\left(t\right)}{\min }({\mathcal{H}}_i\left(t\right)+\rho V_i^b(t+1)).\hfill \end{array}$$

(43)

As $b\to \infty$, Equation (43) transforms into

$$\begin{array}{c}\hfill V_i^{\infty }\left(e_i\left(t\right)\right)\le \underset{u_i\left(t\right)}{\min }({\mathcal{H}}_i\left(t\right)+\rho V_i^{\infty }(t+1)).\end{array}$$

(44)

Further, suppose an arbitrarily small real number $\nu$ exists. Since the sequence $\left\{V_i^b\left(t\right)\right\}$ is monotonically non-increasing, there is a positive iteration index Y and

$$V_i^{{\rm Y}}(e_i\left(t\right))-\nu \le V_i^{\infty }\left(t\right)\le V_i^{{\rm Y}}\left(t\right).$$

(45)

According to Equation (46), it follows that

$$\begin{array}{cc}\hfill V_i^{\infty }\left(t\right)& \ge V_i^{{\rm Y}}\left(t\right)-\nu \hfill \\ \hfill & ={\mathcal{H}}_i^{{\rm Y}}\left(t\right)+\rho V_i^{{\rm Y}}(t+1)-\nu \hfill \\ \hfill & \ge {\mathcal{H}}_i^{{\rm Y}}\left(t\right)+\rho V_i^{\infty }(t+1)-\nu \hfill \\ \hfill & \ge \underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i\left(t\right)+\rho V_i^{\infty }(t+1)\}-\nu .\hfill \end{array}$$

(46)

Based on the prior definition, $\nu$ is an arbitrarily small real number, thus establishing that

$$V_i^{\infty }\left(e_i\left(t\right)\right)\ge \underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i\left(t\right)+\rho V_i^{\infty }(t+1)\}.$$

(47)

As Equations (44) and (47) are both satisfied, we derive the following conclusion:

$$V_i^{\infty }\left(e_i\left(t\right)\right)=\underset{u_i\left(t\right)}{\min }\{{\mathcal{H}}_i\left(t\right)+\rho V_i^{\infty }(t+1)\}.$$

(48)

It is clear that Equations (9) and (48) have the same right-hand side equation; hence, it can be concluded that

$$V_i^{\infty }\left(e_i\left(t\right)\right)={\mathcal{R}}_i^{\ast }(e_i\left(t\right),u_i\left(t\right)).$$

(49)

The proof for Equation (37) is thereby complete. With the value function converges to the optimal value, it is deduced from Equation (12) that the control law similarly converges to the optimal control law, i.e., ${\lim }_{b\to \infty }{u}_i^b\left(t\right)=u_i^{\ast }\left(t\right)$.

The proof is complete. □

In this subsection, a data-driven control scheme based on the proposed DIRS algorithm is developed to solve the optimal bipartite containment tracking control problem for multi-UAV systems. The DIRS algorithm incorporates a novel adaptive termination mechanism, which effectively reduces redundant iteration steps and improves the overall computational efficiency. Furthermore, the stability, convergence, and optimality of the proposed control framework are rigorously established using a Lyapunov-based analysis and mathematical induction.

3.3. The Neural Network Framework

The DIRS algorithm is implemented within a neural network framework using an actor–critic architecture to enable data-driven reinforcement learning. Specifically, the critic network is employed to approximate the value function $V_i$, while the actor network is used to generate the control input $u_i$. In this paper, two independent fully connected feedforward neural networks are used to approximate the optimal value function $V_i^{\ast }$ and the optimal control law $u_i^{\ast }$, respectively. These networks are updated using an error back-propagation algorithm.

3.3.1. The Critic Network

The critic network is employed to approximate the optimal value function $V_i^{\ast }$. The input to the critic network consists of the error state $e_i\left(t\right)$ and the control inputs $u_i\left(t\right)$ from the local agent, respectively. Accordingly, the output of the critic network is defined as follows:

$${\widehat{V}}_i\left(h_i\left(t\right)\right)=W_{ci}{\Phi }_i\left(h_i\left(t\right)\right),$$

(50)

where $h_i\left(t\right)={[e_i^T\left(t\right),u_i^T\left(t\right)]}^T$, ${\Phi }_i(·)$ is a function expression, and $W_{ci}$ is the network weight for the critic network.

Subsequently, the error function for the critic network is formulated as

$${\zeta }_{ci}\left(t\right)={\mathcal{H}}_i\left(t\right)+W_{ci}{\Phi }_i\left(h_i(t+1)\right)-W_{ci}{\Phi }_i\left(h_i\left(t\right)\right).$$

(51)

Therefore, the objective function within the critic network is defined as

$$E_{ci}\left(t\right)={\displaystyle \frac{1}{2}}{\zeta }_{ci}{\left(t\right)}^T{\zeta }_{ci}\left(t\right).$$

(52)

Furthermore, utilizing a gradient-descent-based approach, we derive the weight update rule for the critic network:

$$\begin{array}{cc}\hfill W_{ci}^{b+1}=& W_{ci}^b-\Delta W_{ci}^b=W_{ci}^b-{\kappa }_{ci}[{\mathcal{H}}_i\left(t\right)+{\widehat{V}}_i\left(h_i(t+1)\right)-{\widehat{V}}_i\left(h_i\left(t\right)\right)]\hfill \\ \hfill & \times {[{\Phi }_i\left(h_i(t+1)\right)-{\Phi }_i\left(h_i\left(t\right)\right)]}^T,\hfill \end{array}$$

(53)

where ${\kappa }_{ci}>0$ represents the learning rate of the critic network for the ith agent.

3.3.2. The Actor Network

The actor network is used to approximate the optimal control law $u_i^{\ast }$. The output vector of the actor network is given by

$${\widehat{u}}_i\left(t\right)=W_{ai}{\Xi }_i\left(e_i\left(t\right)\right),$$

(54)

where ${\Xi }_i(·)$ denotes the function expression, and $W_{ai}$ represents the network weight of the actor network.

When the value function $V_i$ of the ith agent converges to its optimal form, this implies that the corresponding control law is optimal. Based on this observation, the objective function for the actor neural network is designed as follows:

$$E_{ai}\left(t\right)={\displaystyle \frac{1}{2}}{\zeta }_{ai}{\left(t\right)}^T{\zeta }_{ai}\left(t\right),$$

(55)

where ${\zeta }_{ai}\left(t\right)={\widehat{V}}_i\left(t\right)$.

Similarly, the actor network updates its weights using a gradient-descent-based method, which can be expressed as follows:

$$\begin{array}{cc}\hfill W_{ai}^{b+1}=& W_{ai}^b-\Delta W_{ai}^b=W_{ai}^b-{\kappa }_{ai}{W}_{ci}^b{\Phi }_i\left(h_i\left(t\right)\right)W_{ci}^b{\Phi }_i^{\prime }{\mathcal{C}}_i{\Xi }_{ai}^T\left(e_i\left(t\right)\right),\hfill \end{array}$$

(56)

where ${\kappa }_{ai}>0$ is the learning rate of the actor network, ${\Phi }_i^{\prime }=\partial {\Phi }_i\left(g_i\right)/\partial h_i\left(t\right)$, and ${\mathcal{C}}_i=\partial h_i\left(t\right)/\partial {\widehat{u}}_i\left(t\right)$ is a constant matrix.

This subsection has established a reinforcement learning framework for the online approximation and implementation of the DIRS algorithm. The framework consists of two main components. First, the critic network evaluates the control law using real-time error data and estimates the approximate optimal value function, thereby enabling online learning of the system’s control behavior. Second, the actor network approximates the optimal control law using the learned value function, without relying on explicit system models, thus facilitating model-free optimal control. In the following section, this framework is applied to implementing the DIRS algorithm to achieve optimal bipartite containment tracking.

Remark 4.

It is worth noting that the designed DIRS-based controller is a data-driven model-free online control scheme. As mentioned in the literature [35,39], the neural network architectures introduced to solve the ADP-based control problem have only been used to fit the optimal value function and the optimal control inputs to solve nonlinear, non-analytic HJB equations. The data required for the neural network is generated entirely through the online interaction of the system, without the need for pre-collected or offline datasets. The whole training process is synchronized with the mission, and there is no independent offline phase.

4. Simulation Results

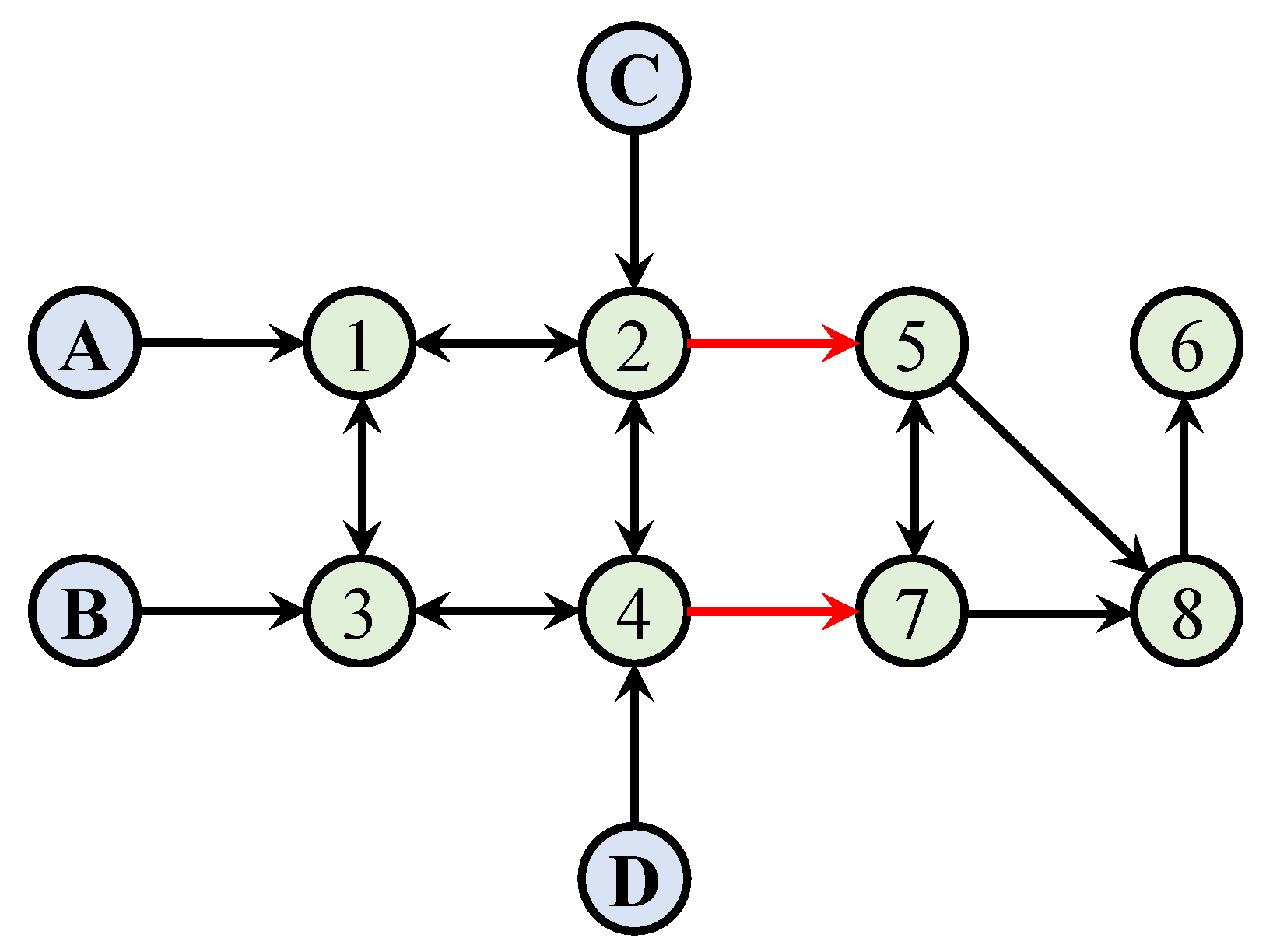
In this section, numerical simulations are conducted to validate the effectiveness of the proposed DIRS-based control framework and the neural network approximation scheme. The communication topology of the multi-UAV system considered, which incorporates both cooperative and competitive interactions, is depicted in Figure 2. In this topology, black arrows denote cooperative relationships, while red arrows represent competitive ones. The blue nodes correspond to the leader UAVs labeled A, B, C, and D, whereas the green nodes indicate the follower UAVs.

In the simulation, the value function parameters are initialized as ${\mathcal{P}}_i=1$ and ${\mathcal{Q}}_{ii}=1$. The dynamic behaviors of both the leader and follower UAVs are modeled according to (4) and (3), with a sampling time of $\mathcal{T}=0.01$. The uncertainties are defined as ${\ell }_1\left(t\right)=0.03\times {[\cos \left(0.3\mathcal{T}t\right),\sin \left(0.3\mathcal{T}t\right)]}^{\top }$ and ${\ell }_2\left(t\right)=0.0005\times {[\sin \left(0.15\mathcal{T}t\right),\cos \left(0.15\mathcal{T}t\right)]}^{\top }$, while the external disturbances are set as $o_1\left(t\right)=0.002\times {[\sin \left(\mathcal{T}t\right),\sin \left(\mathcal{T}t\right)]}^{\top }$ and $o_2\left(t\right)=0.002\times {[\cos \left(0.85\mathcal{T}t\right),\cos \left(1.25\mathcal{T}t\right)]}^{\top }$.

For spatial initialization, the leader UAVs are placed at fixed coordinates ${[14,14]}^{\top }$, ${[14,6]}^{\top }$, ${[6,14]}^{\top }$, and ${[6,6]}^{\top }$, whereas the initial positions of the follower UAVs are randomly generated. The hyperparameter variables used in the neural network architecture are summarized in

Table 1. The hyperparameter variables used in the neural network architecture.

	Critic Network	Actor Network
Learning rate $\kappa$	$0.01$	$0.01$
Discount factor $\rho$	$0.9$	$0.9$
Maximum sub-iteration limit $\Omega$	15	15
Dynamic iteration threshold $\Theta$	$1\times {10}^{-6}$	$1\times {10}^{-6}$
Activation function	${\Phi }_i\left(t\right)={[e_i^2\left(t\right),u_i^2\left(t\right)]}^T$	${\Xi }_i\left(t\right)=e_i\left(t\right)$
Weight initialization	0	Random numbers in (0, 1]

.

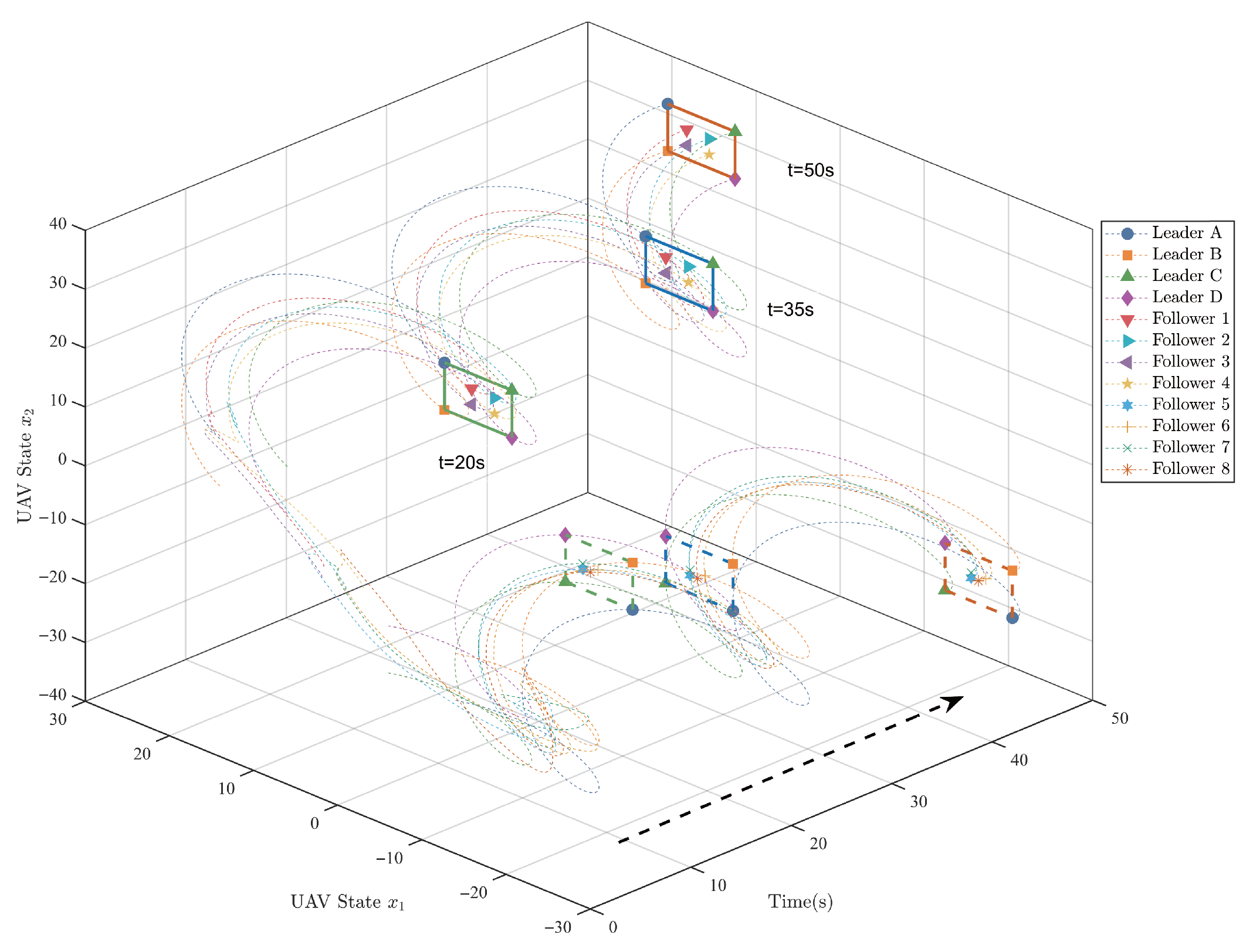
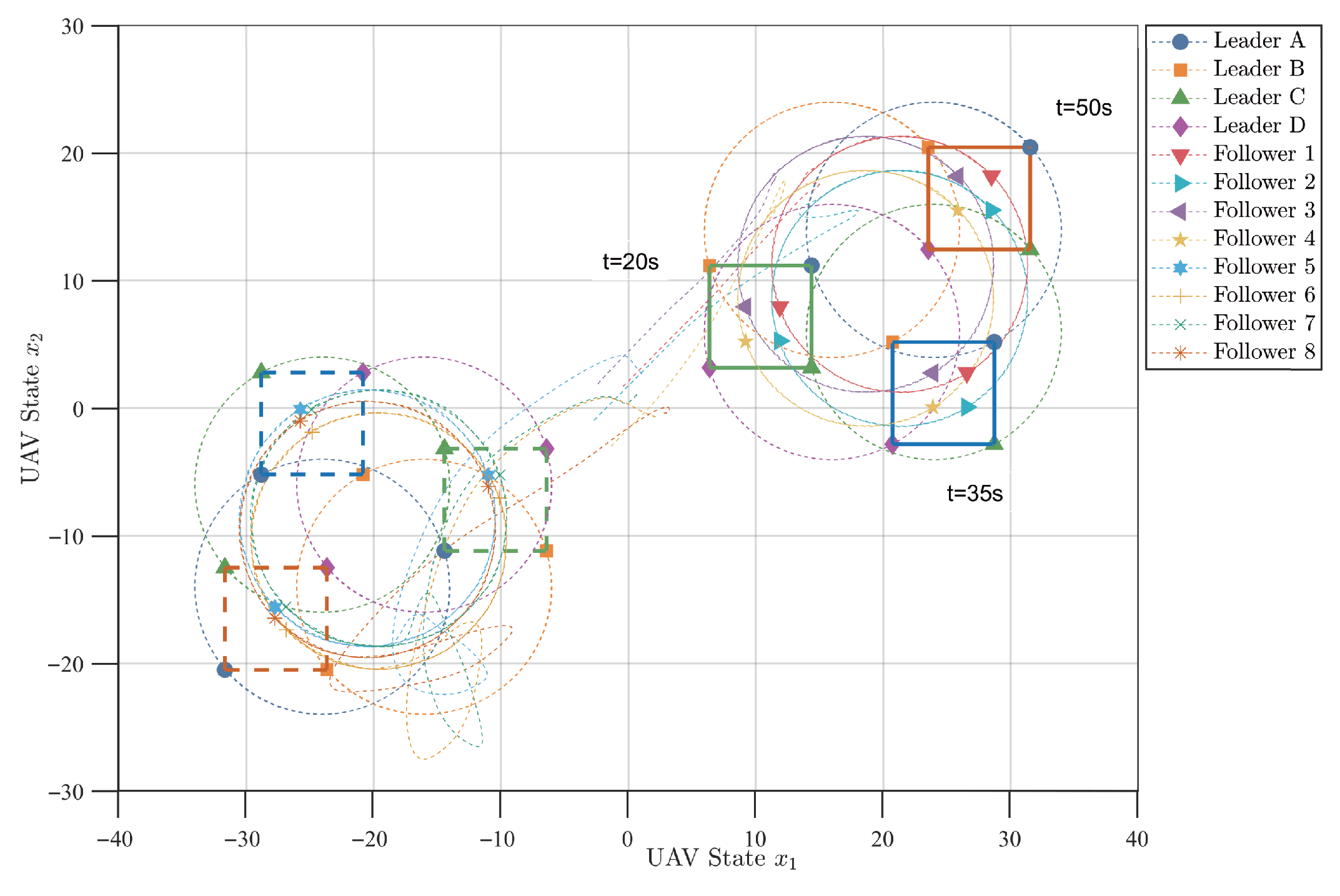
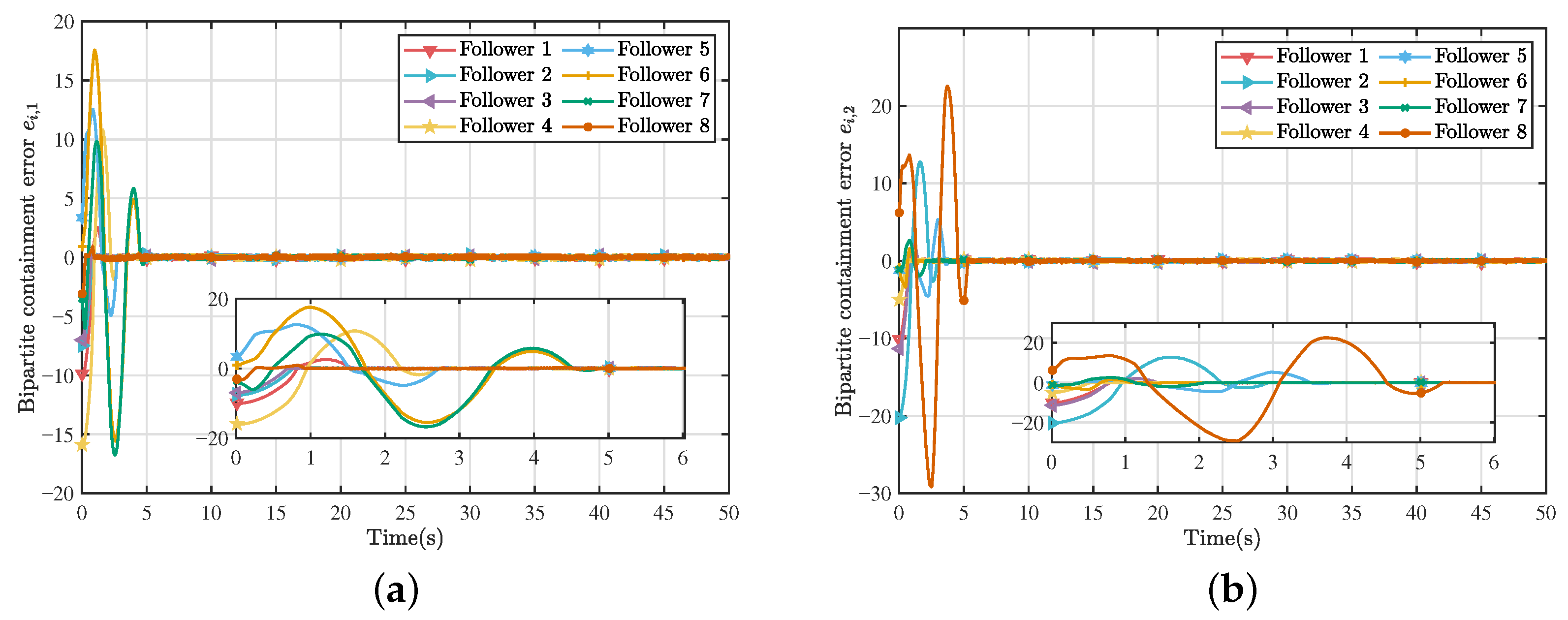
Figure 3 and Figure 4 depict the two-dimensional and three-dimensional trajectories of the optimal bipartite containment tracking for the multi-UAV system. Under the proposed optimal control strategy, all follower UAVs successfully converge to the bipartite convex hull spanned by the leader UAVs and achieve stable containment tracking. The corresponding bipartite containment tracking errors are illustrated in Figure 5, where the tracking errors of all follower UAVs asymptotically converge to zero, thereby validating the effectiveness of the proposed control law. 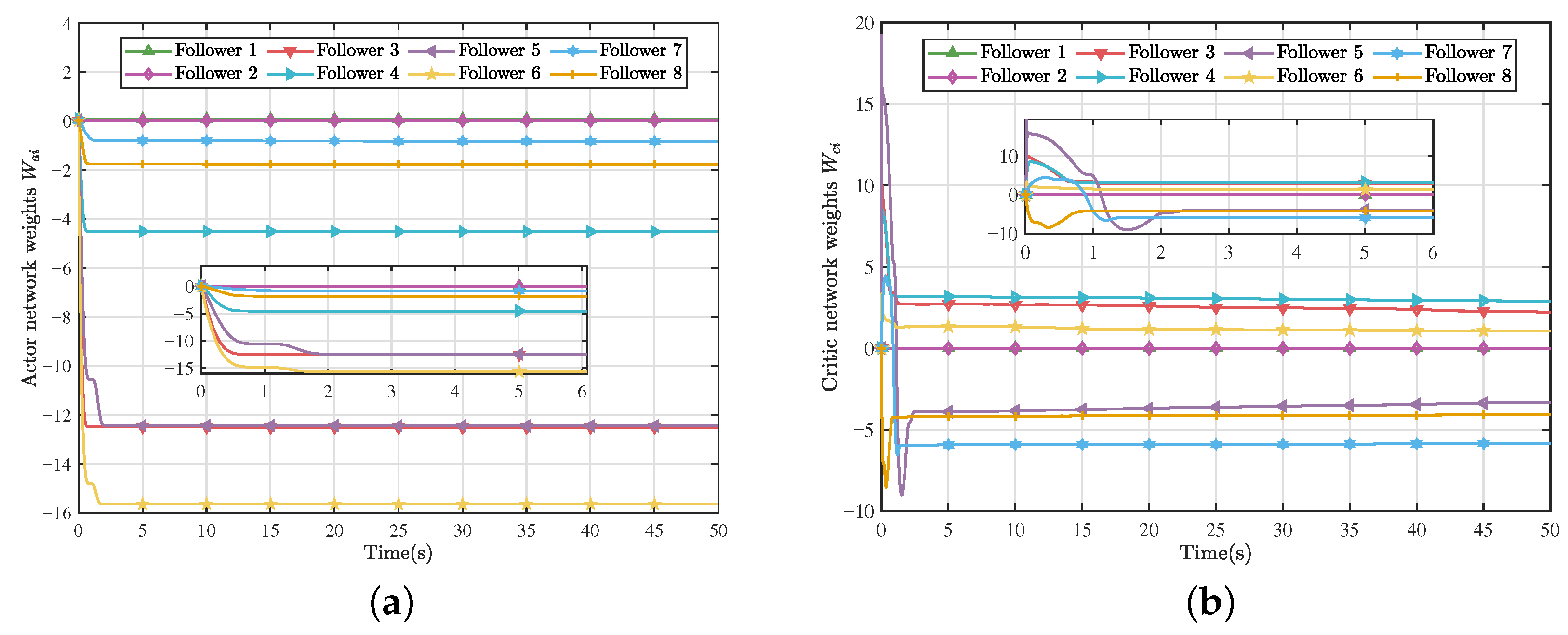Furthermore, Figure 6 presents the evolution of the weight vectors of the critic and actor networks, demonstrating the convergence behavior of the neural-network-based approximation process. Equally, according to the enlarged transient states in Figure 5 and Figure 6, it can be found that the system is in the regulation process in the first 6 s. The DIRS algorithm learns and continuously generates the optimal control inputs through the system data, and finally, the system achieves convergence after 6 s.

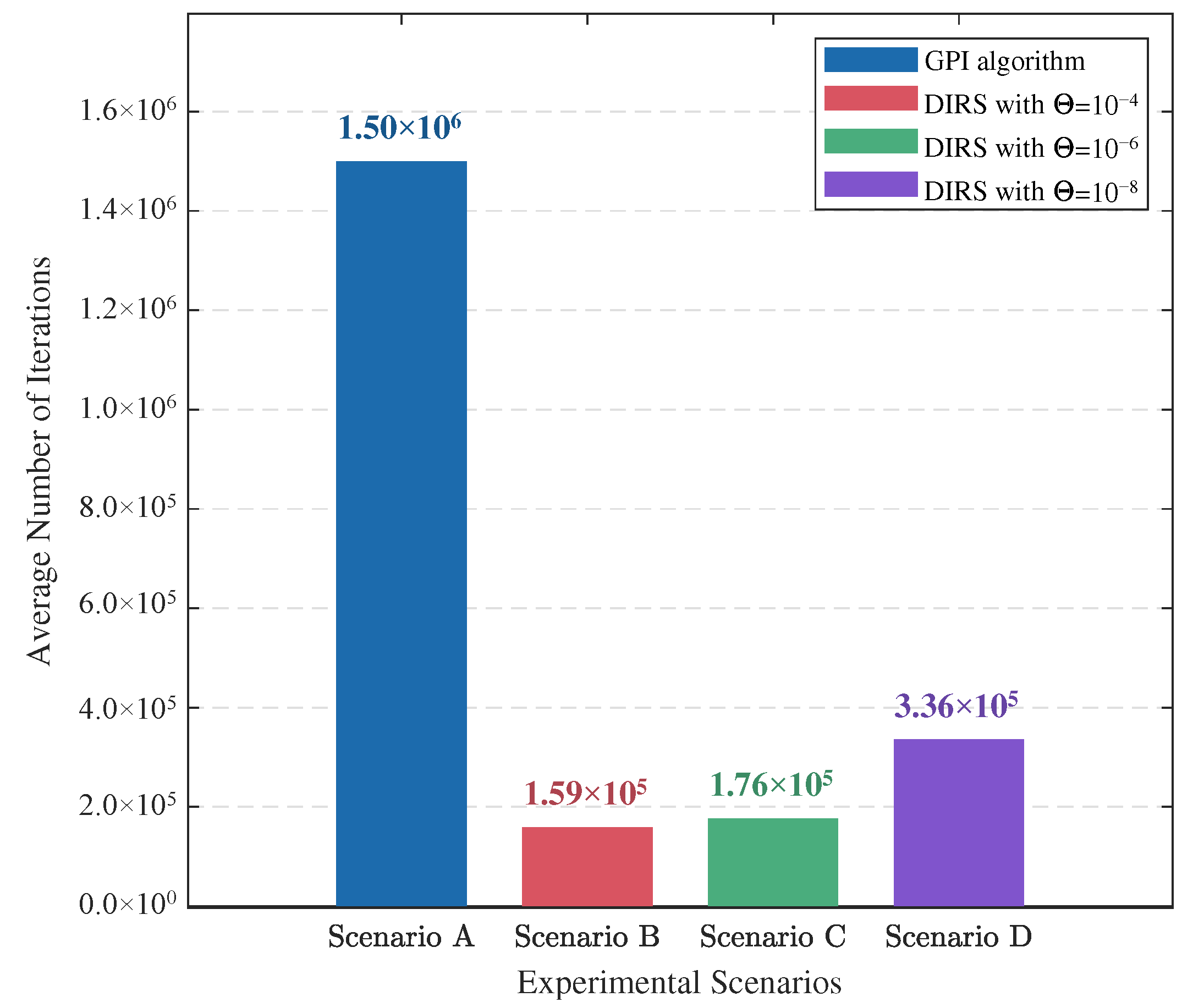
In order to further demonstrate the advantages of the designed DIRS in improving the efficiency of ADP computation, the same experimental conditions are used for comparison with the method in [34], and the average number of iterations for each UAV is calculated during the whole process of control. In addition, comparative experiments are conducted in order to assess the impact of the dynamic iteration threshold $\Theta$ on the iteration efficiency. Finally, the comparison results are shown in Figure 7. It can be seen that compared with the existing ADP algorithm, the introduction of the DIRS can effectively reduce the average number of iterations, and the DIRS with $\Theta ={10}^{-6}$ reduces the total number of iterations by 88.27% compared to that with the GPI. Meanwhile, the simulation results under different $\Theta$ values further illustrate that it is very important to choose a suitable iteration threshold to trade-off between control accuracy and computational efficiency in practical applications.

Remark 5.

In this paper, numerical simulations are conducted for the optimal bipartite containment tracking control problem for multi-UAV systems, mainly to verify the effectiveness of the designed DIRS algorithm-based controller. As mentioned in the literature [40,41,42], by extending the Newton’s second-law-compliant second-order integrator model and the disturbance model investigated in this paper, it could be deployed and developed in Gazebo, Webots, and IsaacSim. This has also inspired us to conduct more realistic flight experiments using Gazebo and other tools in the future.

5. Conclusions

In this paper, a data-driven optimal bipartite containment tracking control scheme is developed for multi-UAV systems subject to compound uncertainties. The dynamics of the multi-UAV system and the associated uncertainties are first modeled, followed by formulation of the optimal bipartite containment tracking problem and derivation of the corresponding coupled HJB equations. To alleviate the computational burden, a DIRS is introduced to adaptively adjust the number of iterations, thereby balancing the control accuracy and computational efficiency. Rigorous proofs are provided to establish the stability, convergence, and optimality of the proposed control framework. Furthermore, a neural-network-based online approximation method is employed to realize a model-free solution to the optimal control problem. Finally, the simulation results are also presented and compared with the existing ADP methods to verify the effectiveness of the proposed DIRS in saving computational resources.

The proposed DIRS framework is applicable to multi-UAV systems with compound uncertainties (e.g., external interference and internal modeling errors) and communication topologies that contain both cooperative and competitive interactions. Nonetheless, the framework suffers from a number of limitations, including the fact that the current design assumes a structural equilibrium map, which may be violated in the event of communication failures or switching topologies, and that practical constraints such as actuator saturation, failures, and communication delays have not yet been considered. Also, the current results build on numerical simulations to verify the effectiveness of the control algorithm. Therefore, future work will address these issues and extend the experimental results further to a UAV vehicle swarm for flight experiments to enhance its robustness and applicability.