1. Introduction
Target tracking in dynamic environments requires drones to efficiently locate and track moving targets while avoiding obstacles. Traditional methods, such as the APF [
1], are effective in path planning and obstacle avoidance [
2] but are prone to local optima, limiting their effectiveness in dynamic settings [
3]. MARL methods [
4], on the other hand, can optimize collaborative strategies but suffer from slow convergence and high computational consumption [
5], especially as the number of agents increases [
6].
In response to these challenges, this paper introduces a novel framework that integrates BCTD and MAPPO, which enhances both learning efficiency and stability by leveraging pre-training and fine-tuning strategies [
7]. Taking into account the above problems encountered in the multi-drone tracking task [
8], the proposed multistage collaborative tracking framework integrates expert guidance, imitation learning (IL) [
9] pre-training, and RL [
10] fine-tuning. First, the policy network is pre-trained via behavior cloning on expert data of the artificial potential field, enabling rapid acquisition of fundamental path planning and obstacle avoidance capabilities. Subsequently, the potential field weights are dynamically adjusted during reinforcement learning fine-tuning, using the MAPPO [
11] algorithm. A global reward signal, such as successful collaborative encirclement, is introduced to overcome local force balance and drive UAVs to bypass obstacles and continuously approach the target.
The MARL training process is often plagued by significant time and resource consumption. Traditional RL methods rely on agents exploring strategies solely through environmental interactions, necessitating numerous trial-and-error iterations to generate interaction data. This approach results in extended training periods and low sample efficiency. To address these challenges, this study employs BCTD to enhance the value network. This method enables drones to acquire skills in path planning and obstacle avoidance within dynamic environments, thereby streamlining subsequent agent fine-tuning processes.
A novel method was proposed in this study to enhance the operational efficiency of collaborative target tracking and encirclement tasks [
12]. The key contributions are as follows: 1. The integration of APF with IL. Drones are trained to acquire path planning and obstacle avoidance skills within the artificial potential field framework by initially imitating a pre-trained strategy based on APF principles, followed by fine-tuning through MARL to improve task performance. 2. A methodology employing BCTD is introduced to concurrently optimize the policy and value network. During the behavior cloning phase, the value network is refined using the temporal difference method to enable drones to learn path planning and obstacle avoidance in a dynamic environment, thereby facilitating subsequent agent fine-tuning. Generalized advantage estimation (GAE) is utilized to rectify the bias of the value function, prevent policy oscillation, reduce the duration of policy exploration, and enhance both evaluation accuracy and training efficiency.
3. Problem Formulation
3.1. Multi-Robot Pursuit Problem
In this work, we consider a cooperative target tracking problem involving multiple UAV agents operating in a 2D environment with obstacles. The set of pursuers is denoted by
, and the target as
E. Each agent
can observe the relative positions of nearby agents, obstacles, and the evader, but not the global state. Unlike traditional first-order models, all pursuers in this work are modeled as second-order point-mass systems, where the control input is acceleration, and the state includes both position and velocity. The continuous-time kinematic equations are
where
,
, and
represent the position, velocity, and acceleration of pursuer
i, respectively. In discrete time, the state transition is
In this paper, the movement of the tracking target selects the acceleration direction according to the APF rule, and thus also follows the second-order point-mass systems.
The pursuit task is deemed successful when all of the following conditions are met at a predefined terminal time :
Capture condition: Each pursuer is within a capture radius
from the target:
Collision avoidance: All inter-agent distances must exceed twice the safety radius
, and each agent must maintain a minimum distance from any obstacle:
where
is the Euclidean distance between pursuer
i and the evader;
is the distance between pursuers
i and
j;
is the distance between pursuer
i and the nearest obstacle.
Given that each agent relies exclusively on its local observation
to make decisions, the aim is to develop a set of decentralized policies
that together meet the specified constraints and complete the pursuit task in the most efficient manner. The primary objective is to maximize the expected cumulative discounted reward as follows:
where
is the discount factor, and
is the joint action vector. This issue showcases the amalgamation of dynamic constraints, partial observability, and decentralized coordination. The incorporation of acceleration-based control and second-order dynamics enhances the realism and intricacy of the scenario, thereby escalating the requirements for policy stability and generalization.
3.2. Decentralized Partially Observable Markov Decision Process (Dec-POMDP)
The multi-UAV pursuit problem can be formulated as a partially observable Markov Game (POMG) that is represented by the tuple , where denote the global state space, joint action space, local observation space, state transition probability, reward function, and discount factor, respectively. Each agent chooses an action based on its local observations, which are sampled from the global state, receives a reward, and collectively impacts the environment’s state. The objective for each agent is to learn the optimal policy that maximizes the cumulative rewards.
(1) State space
S: The state
represents the global configuration of the environment, which includes the position and velocity of all drones, the position and velocity of the target, and the positions of static obstacles. The total three-drone system state is
where
N,
K,
M represents the number of tracking drones, targets, and obstacles, respectively.
For each drone
, the state consists of its 2D position
, velocity
, agent radius
, maximum speed
.
Similarly, the state of target is
where
,
, and
are the location, velocity, and radius of the tracked entity, respectively. Additionally, the state of obstacle
k is
where
is the radius of the obstacle
k.
(2) Observation space
: Due to limited sensing and communication, each agent
i receives only partial observations
. The local observation of agent
i is as follows:
In the one-target scenario, the observation of targets is
, where the observation
includes the relative position
between the agent and the obstacle
j, relative velocity
, and its radius of size.
where
represents the relative position between the target and the agent. In the three-drone system, to consider cooperation between agents, all drones are included in the observation range.
where
, and uses zero padding when the agent is invisible. The observation of an obstacle contains the position relative to the agent and the obstacle radius, so the observation of each visible obstacle j is expressed as follows:
Similarly, compose all obstacle observations into .
Song et al. [
29] demonstrated that sparse feature selection enhances decision-making efficiency in high-dimensional settings. In line with this principle, the study’s observation space design focuses solely on essential interaction information (such as relative poses of agents/targets) to prevent irrelevant features from impacting policy learning.
(3) Action space
: The action of agent
i is denoted as
.
represents a set of feasible velocity vectors subject to fundamental kinematic equations and restrictions imposed by map boundaries, maximum velocity, and maximum acceleration limits.
The values represent acceleration in nine directions: static, upward, downward, left, right, upper right, lower right, lower left, and upper left. This design provides directional precision for path adjustments and obstacle avoidance. The discrete action space simplifies policy learning compared to continuous spaces.
(4) State transition model
P: The transition model
governs how the global state evolves based on the joint action
from all agents. Each UAV agent updates its velocity and position using Newtonian dynamics:
In the context of algorithm research, it is reasonable to assume a constant speed of action by the drone over the extremely short time interval .
(5) The reward function
guides agent
i by providing rewards for actions executed. It is a composite function combining dense and sparse components to promote effective and cooperative target tracking while discouraging unsafe or inefficient behaviors.
where
measures the change in distance between an agent and a target over time, promoting movement towards the target.
represents a penalty for collisions between agents or obstacles. This term encourages safe navigation and cooperative spacing:
is a step penalty that per timestep to penalize unnecessary wandering and incentivize task efficiency. It is typically linear with respect to the elapsed step ratio
. Additionally,
is a high-value sparse reward awarded only when all agents successfully surround the target within a predefined radius threshold. This strongly incentivizes cooperation and convergence as follows:
The reward structure combines short-term behavior shaping with long-term goal completion to encourage individual approach and effective coordination in completing a cooperative task, while minimizing collisions and delays. The weights of the reward components (such as , , , and ) were manually tuned using a grid search approach. We iterated over a set of values for each weight and selected the combination that yielded the most efficient training process and the best tracking performance. This manual tuning allowed us to strike a balance between encouraging rapid target approach, minimizing collisions, and penalizing unnecessary movements, ensuring robust collaboration among agents.
4. Approach
In response to the issue of the traditional methods of artificial potential field being susceptible to local optima in complex scenarios [
30], as well as the bottleneck of low training efficiency and slow convergence in MARL, this paper considers an innovative collaborative tracking framework. The key innovation lies in the architecture driven by expert experience in pre-training and fine-tuning architecture [
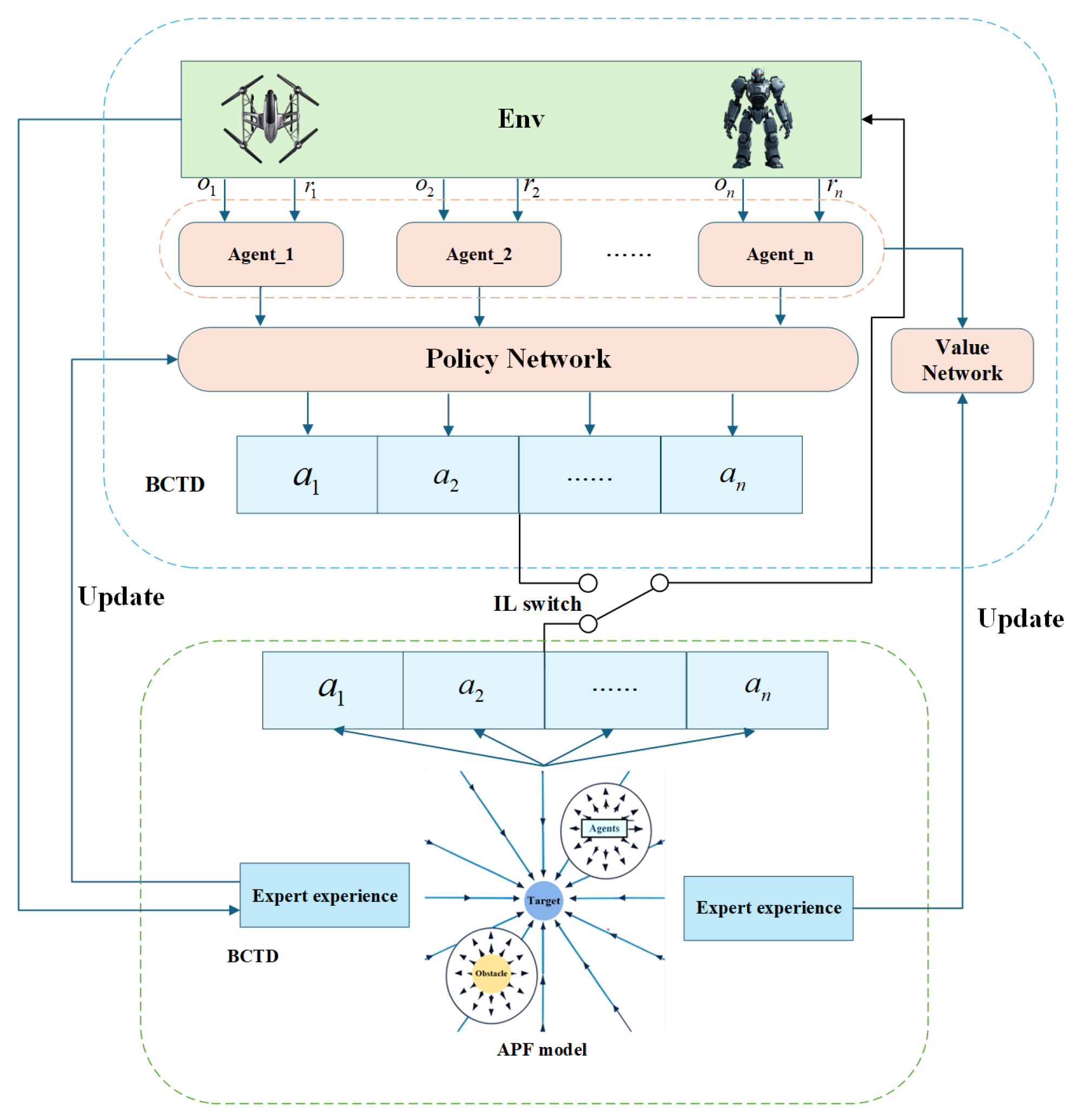
31], along with the combined optimization mechanism based on BCTD. Specifically, this framework effectively integrates expert trajectories produced through APF, BC in IL, value estimation mechanism optimized by TD, and reinforcement policy optimization capability of MAPPO. The goal is to attain effective initialization and consistent iteration of the agent’s strategy. The core process is structured as follows:
(1) Pre-training Guided by APF Expert Experience: Leverage expert trajectories from APF to pre-train the policy network, enabling rapid acquisition of fundamental tracking capabilities.
(2) BCTD Combined Optimization Mechanism: Employ BCTD to synchronize the optimization of both the policy and evaluation networks.
(3) MAPPO Dynamic Fine-tuning: Incorporate the MAPPO clipping mechanism along with a globally designed reward system to facilitate efficient multi-agent collaboration.
Figure 1 illustrates the algorithmic framework, which is systematically divided into three stages: “pre-training—combined optimization—dynamic adjustment,” ensuring a balance between path planning reliability and reinforcement learning efficiency.
In collaborative tracking and pursuit, the action space of the agent is usually represented as a set . The reinforcement learning policy is denoted as , where the input is the current state s and the output is a vector f with a dimension of , which is the size of the action space. Each element of the vector f corresponds to the probability value of an action, indicating the probability of choosing that action.
Initially, the APF method generates expert demonstration trajectories, forming a high-quality dataset that captures interactions among agents, targets, and obstacles. At this stage, the policy network undergoes pre-training via BC based on rule-driven trajectories. This process allows the agent to swiftly acquire fundamental path planning and obstacle avoidance skills, thereby minimizing exploration costs and easing learning challenges in the subsequent pure reinforcement learning phase. The policy network, structured as a multi-classifier, outputs the probability distribution of each discrete action. Expert actions serve as the supervision signal, and the network is trained using the cross-entropy loss function.
where
represents the expert actions in one-hot encoding, and
is the policy network.
Then, to address the limitations of BC in strategy generalization and stability, we present the BCTD mechanism. Using the attention mechanism for cross-modal alignment as proposed by Xu et al. [
32], the BCTD framework in this investigation accomplishes multiscale temporal feature integration by utilizing the GAE-weighted TD error, thus improving the robustness of value estimation. This approach simultaneously optimizes the policy and value networks during the imitation learning phase. Expert trajectories provide state–action–reward sequences, which are used to form pseudo-environment interaction paths. The GAE is employed for estimating and propagating value returns. The temporal difference error is defined by the following equation:
where
is the TD error at time step t, indicating the difference between the current valuation and the return after one step.The corresponding GAE estimate is as follows:
where
is the discount factor (set to 0.95 in our experiments). The GAE smooths the TD error across multiple timesteps to reduce variance. In our experiments, we used
, which allowed us to effectively balance bias and variance. For example, in one timestep, the TD error for an agent might be calculated as
, and the GAE estimate
would sum over multiple
values, weighted by
and
. Meanwhile, the value network aims to minimize the mean squared error. The primary advantage of BCTD is its ability to quantitatively evaluate and correct policy quality without adding to the environmental interaction burden. It mitigates training oscillations from early policy deviations, thereby enhancing convergence stability and the generalization capability of the policy during the imitation learning phase.
Finally, building on pre-training, we utilize MAPPO for policy fine-tuning via RL. Employing a centralized training and distributed execution (CTDE) framework, MAPPO shares global value network information while maintaining policy independence, enabling efficient collaboration. Agents receive real-time feedback from the environment, including rewards for target approach, penalties for collisions and step counts, and rewards for successful encirclement. MAPPO mitigates policy update fluctuations through a clipping mechanism and, combined with the value baseline from BCTD pre-training, significantly improves the collaborative capacity and learning efficiency of the multi-agent system in dynamic settings.
The evaluation metrics for the experiments in this chapter include the tracking success rate at convergence, the number of steps required to complete the task, the average reward tested after model convergence, and the number of training episodes required for the model to converge.
In the three-UAV target tracking scenario, analysis of the agent observation space reveals that computational complexity grows linearly with the number of nearby drones and obstacles when each UAV independently executes this cooperative tracking algorithm. The MAPPO+BCTD algorithm achieves convergence at approximately 65 k episodes, significantly lower than alternative approaches such as standard MAPPO, which requires 500 k episodes to converge. On an NVIDIA GeForce GTX 3090 GPU, each episode requires approximately 35 ms of processing time, resulting in a total training duration of roughly 6.3 h. These results highlight the computational efficiency of the proposed method, which benefits from the pre-training phase. Meanwhile, we conducted experiments with parameters detailed in
Table 1.
4.1. Three-UAV Target Tracking Test
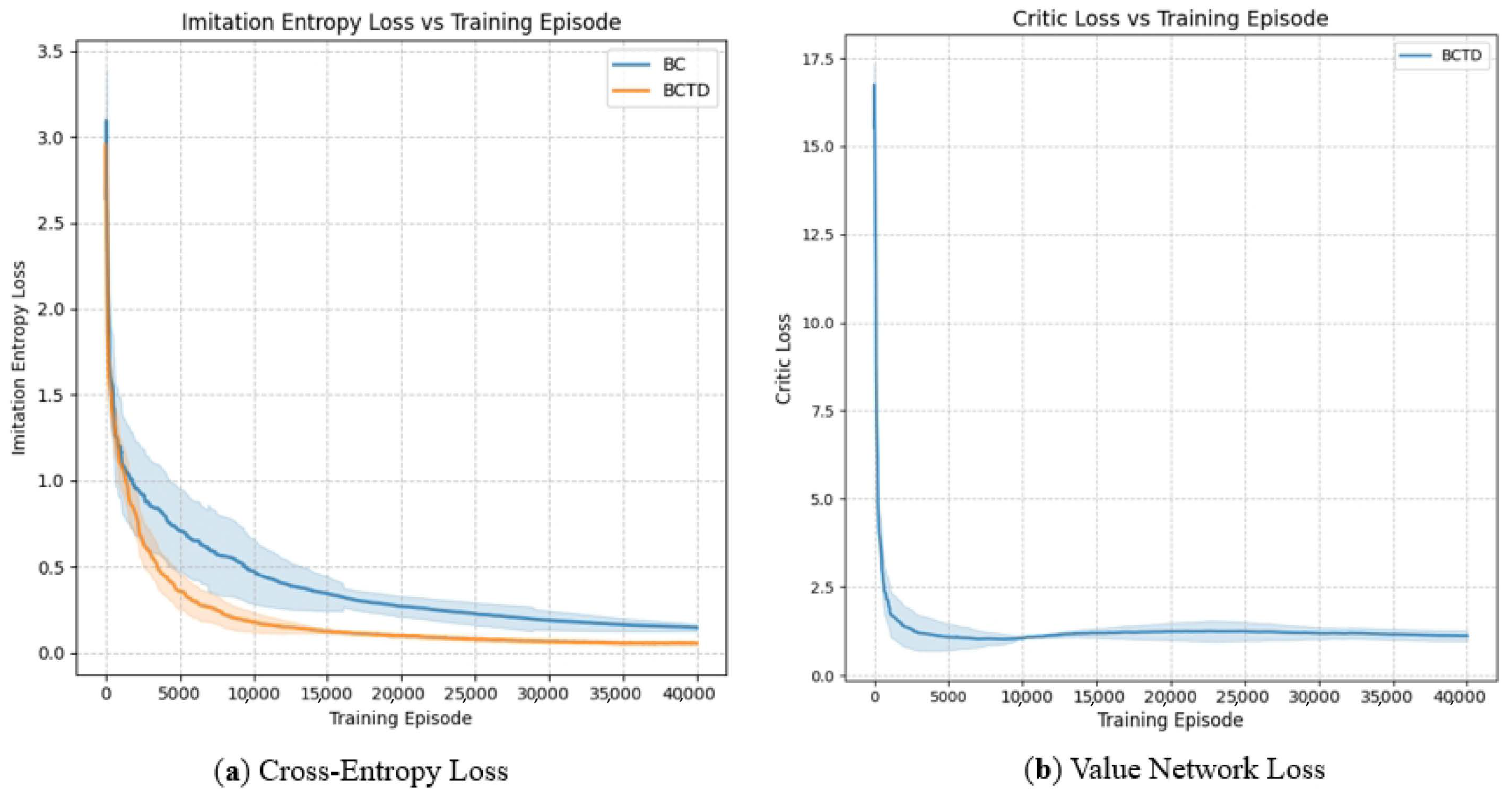
The BCTD method is used to introduce the tracking ability of the APF into the tracking agents, allowing the agents to learn this ability. By using cross-entropy loss as the optimization function, the agent’s policy model successfully learns the tracking ability of the APF model. Additionally, TD methods are used to achieve convergence of the value network.
The convergence curve of the policy network’s cross-entropy loss indicates that the cross-entropy loss may initially be large due to the complexity of the environment during the IL process. However, as the episodes progress, the cross-entropy loss gradually converges towards 0, showing that the policy network has effectively learned the tracking ability of the APF model. As shown in
Figure 2, the convergence of the value network through TD Mean Squared Error (MSE) Loss curve.
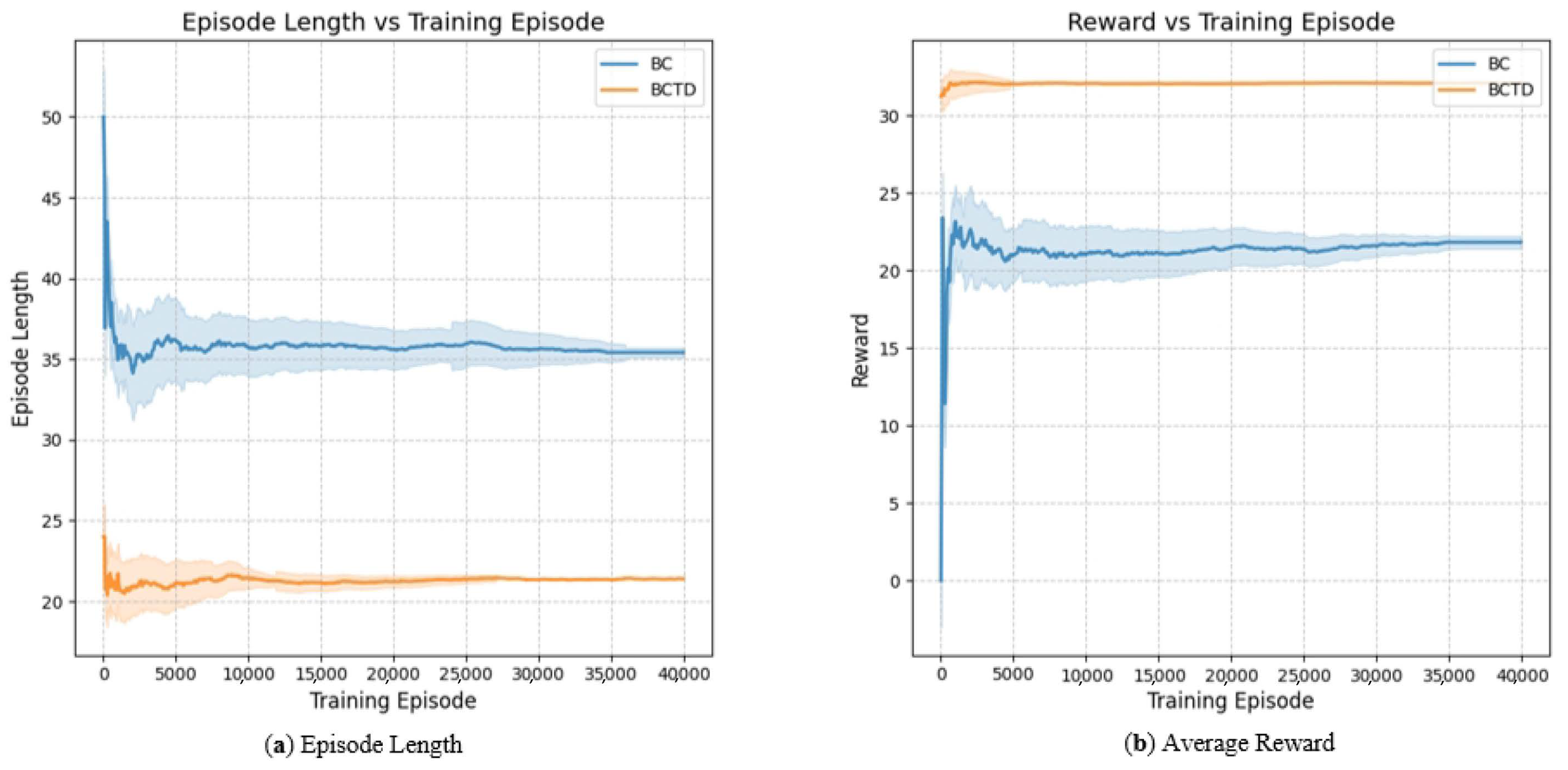
The role of APF is merely to generate expert behaviors through imitation learning to guide the path planning of the agent, without relying on the update of the value function. Therefore, there is no critic network and no critic loss. And the loss curve of the value network via TD shows rapid convergence in the early stages. Value loss based on TD decreases quickly. However, during the convergence process, due to the local optimal limitations of the APF mean that there are cases where agents cannot quickly catch up with the tracking target. This leads to some oscillation in the evaluation of the current value even after the tracking ability of the APF model has been learned. The average reward curve and the average number of steps to complete the task for the APF model were then tested, as shown in
Figure 3.
Through the reward and step completion curves, even with some local optima, the APF model still effectively completes the corresponding tracking tasks. Additionally, due to its rule-based nature, the tracking performance remains relatively stable.
In the experiments in this chapter, the number of drones is 3, and the number of tracking targets is 1. MAPPO + BCTD and other classic centralized training and distributed execution algorithms were selected for comparison experiments, including MAPPO based on policy, the MADDPG algorithm [
33], and the QMIX algorithm [
34] based on value. First, we analyze the application of the BCTD algorithm in the MAPPO algorithm, and then compare the performance of different algorithms based on the evaluation metrics in the collaborative tracking scenario.
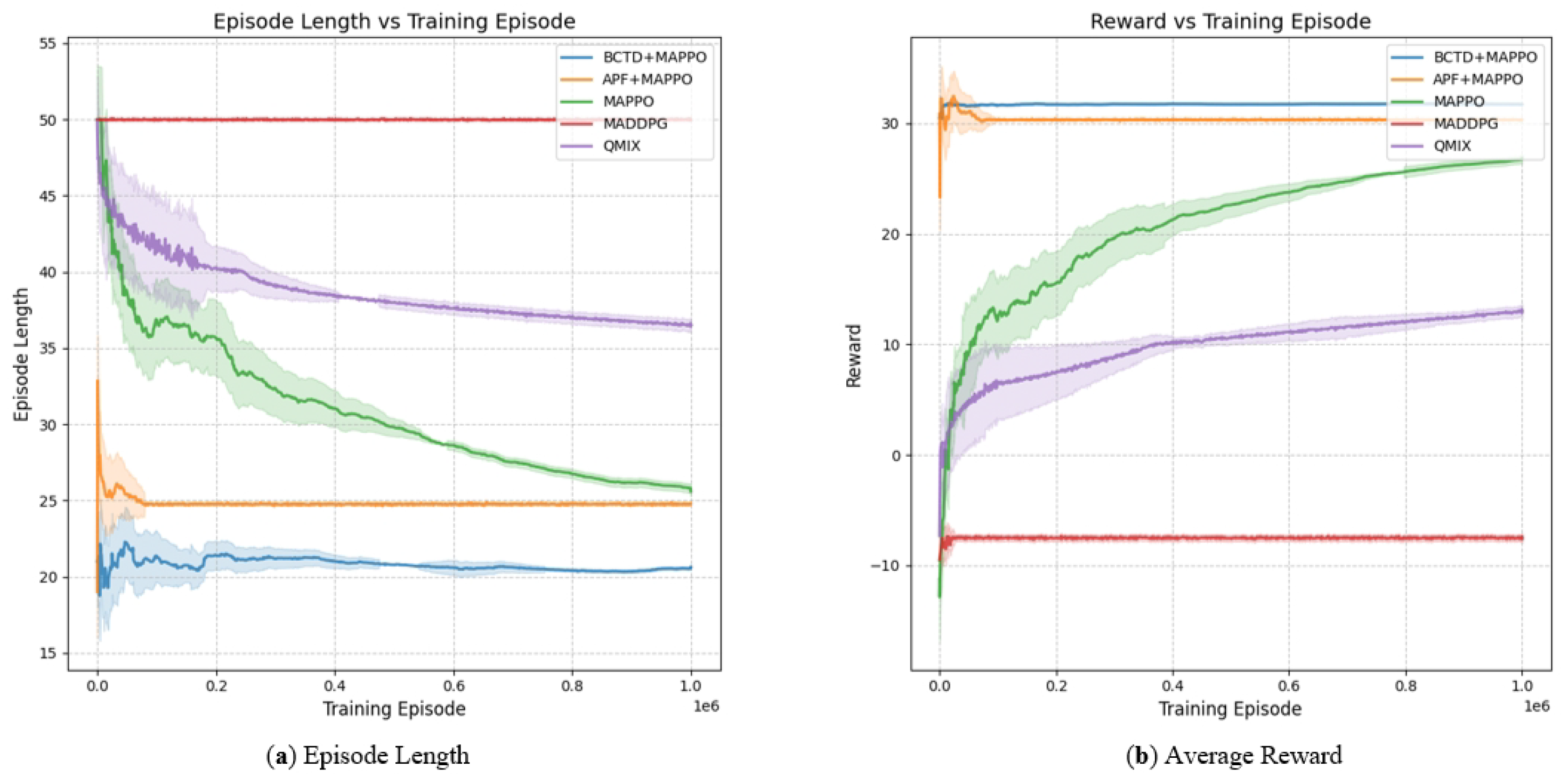
The average reward curve and the average number of steps for different algorithms during training were tested as shown in
Figure 4, which presents the average reward curve of the episode for different algorithms in the collaborative tracking scenario.
The curve with higher opacity and fluctuations represents the actual reward curve used, and the curve with lower opacity represents the curve after smoothing the raw rewards. The analysis of the episode reward convergence for different algorithms is as follows: In this experiment, MAPPO + BCTD demonstrated significant advantages. Compared with other algorithms, MAPPO + BCTD rapidly converged early in the training and stabilized at higher reward values, indicating that the pre-training via behavior cloning effectively accelerated the agents’ policy learning process. In contrast, MAPPO gradually improved rewards but had slower convergence and larger reward fluctuations during training, suggesting that without pre-training, the agent requires more time to adapt to the task. MADDPG showed unstable performance in the multi-agent environment with consistently low reward values, failing to effectively improve tracking ability. QMIX, though showing smoother reward changes, had lower final reward levels and could not overcome the influence of obstacles in the environment, leading to incomplete optimization of the policy. In complex tracking tasks, MAPPO + BCTD accelerated convergence and improved stability through pre-training in behavior cloning, making it the most effective algorithm.
As shown in
Figure 4, episode completion step curves for different algorithms in a collaborative tracking scenario, the curve with higher opacity and fluctuations represents the actual episode step curve, and the curve with lower opacity represents the episode step curve after the raw rewards have been smoothed.
In this experiment, MAPPO + BCTD performed the best overall, benefiting from the pre-training via behavior cloning, which effectively improved the agents’ learning efficiency and strategy collaboration capability. This led to a rapid decrease in the number of steps per episode, stabilizing around 20 steps, demonstrating excellent convergence speed and decision-making efficiency. MAPPO followed, with the number of steps stabilizing around 26, indicating its good multi-agent collaboration and environmental adaptation. In contrast, MADDPG performed poorly, with steps remaining around 50 and showing significant fluctuations, exposing its instability in learning for multi-agent cooperation tasks. QMIX, although better than MADDPG, still had a higher number of steps than MAPPO-like algorithms in complex environments, indicating limited policy flexibility and environmental adaptability. In summary, MAPPO + BCTD, with the advantage of pre-training, significantly improved policy convergence efficiency and collaboration capabilities, exhibiting optimal performance in multi-agent target tracking tasks.
The evaluation indicators of the collaborative tracking scenarios in the evaluation indicators of the MAPPO+BCTD, MAPPO, QMIX, MADDPG and APF algorithms were quantified, and the comparison of the tracking performance after convergence of different algorithms is shown in
Table 2:
As shown in the table, MAPPO + BCTD demonstrated significant advantages in multi-agent target tracking tasks, particularly in convergence speed, task completion efficiency, and strategy learning ability. With pre-training via behavior cloning, MAPPO + BCTD can converge quickly, completing training in only 65 k episodes, significantly reducing training time compared to other algorithms. At the same time, this algorithm stands out in terms of tracking success rate and average reward, with a tracking success rate of 100% and the highest average reward, indicating its stability and efficiency in task execution. Moreover, MAPPO + BCTD has the fewest average steps, further demonstrating that its optimized policy model can efficiently complete target tracking tasks. In terms of model convergence, MAPPO + BCTD, leveraging the advantages of IL, required the fewest episodes to converge among reinforcement learning algorithms.
4.2. Experimental Visualization Comparison
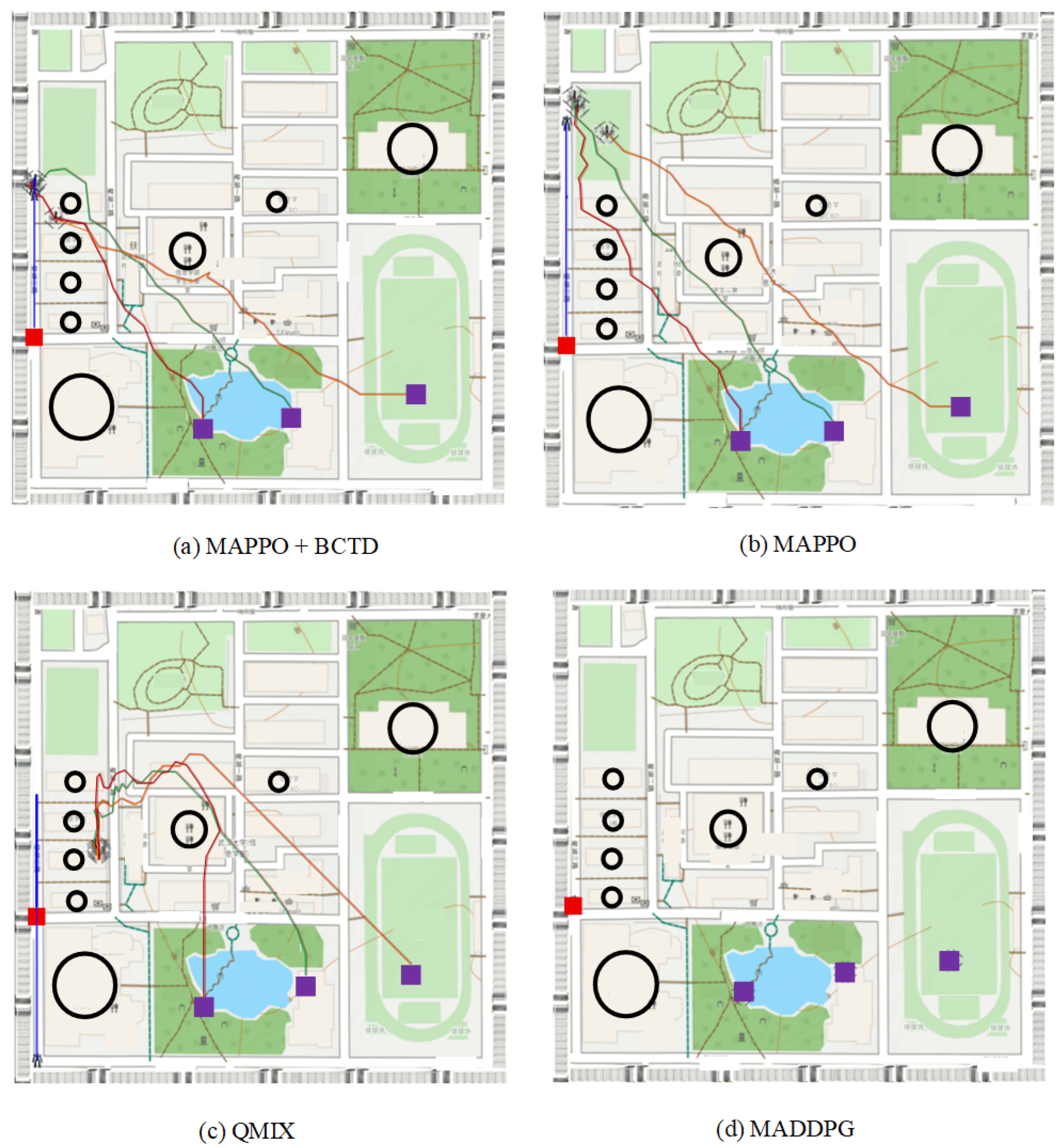
After all models completed convergence, the effects of different algorithms were tested in the tracking task environment. As shown below, the episode ends when the tracking task is completed within the maximum number of steps; otherwise, the episode ends when the maximum action steps are reached.
Figure 5 shows the visual demonstration of the experimental effects of different algorithms. The tracking drone’s trajectory is represented by a red line, and the tracking target robot’s trajectory is represented by a blue line. By comparing various algorithms, it is clear that MAPPO + BCTD demonstrates smoother drone paths and significantly fewer steps to complete the task. In contrast, the QMIX algorithm shows poor obstacle avoidance performance when faced with dense obstacles, causing the drone swarm to be unable to effectively avoid obstacles, which impacts tracking performance. The MADDPG algorithm, on the other hand, has a noticeable local optimum issue, where the drone swarm ultimately converges to a stationary state, failing to effectively track the target, performing much worse than other algorithms. These results indicate that MAPPO + BCTD can achieve more efficient and smoother tracking paths in complex environments, with stronger capabilities for handling dynamic obstacles.