Fusing Adaptive Game Theory and Deep Reinforcement Learning for Multi-UAV Swarm Navigation
Abstract
1. Introduction
- (1)
- An Efficient Mean-Field Game Acceleration Algorithm: By incorporating a dynamic density threshold and a Spiking Neural Network (SNN) similarity measure into a state aggregation strategy, we significantly reduce the computational complexity of large-scale swarm interactions from O() to O() while maintaining high clustering accuracy.
- (2)
- A Multi-Scale Attention-Based Policy Network: We design a hybrid spatial–temporal attention mechanism to enhance environmental perception. This model achieves an obstacle detection accuracy of 95.1% and reduces the response time to dynamic threats to under 0.3 s.
- (3)
- Formal Safety Guarantees: By embedding Control Barrier Functions (CBFs) into the policy network, we establish a safe reinforcement learning framework that confines trajectory deviations to within 2 m and provides formal safety guarantees throughout dynamic operations.
2. Traditional Theories of UAV Formation Cooperative Control
2.1. Rule-Based Bionic Control Method
2.2. Distributed Cooperative Control Method
2.3. DRL Control Method (Deep Reinforcement Learning)
3. A Fusion Framework of Adaptive Game Theory and Deep Reinforcement Learning
3.1. Improvement of Dynamic Game Theory
- (1)
- Incomplete Information Dynamic Game Modeling
- (2)
- Mean Field Game Acceleration Algorithm
- (3)
- Dynamic Weight Adjustment Mechanism
3.2. Enhanced Design of Deep Reinforcement Learning
- (1)
- Dual-Channel Experience Replay Mechanism
- (2)
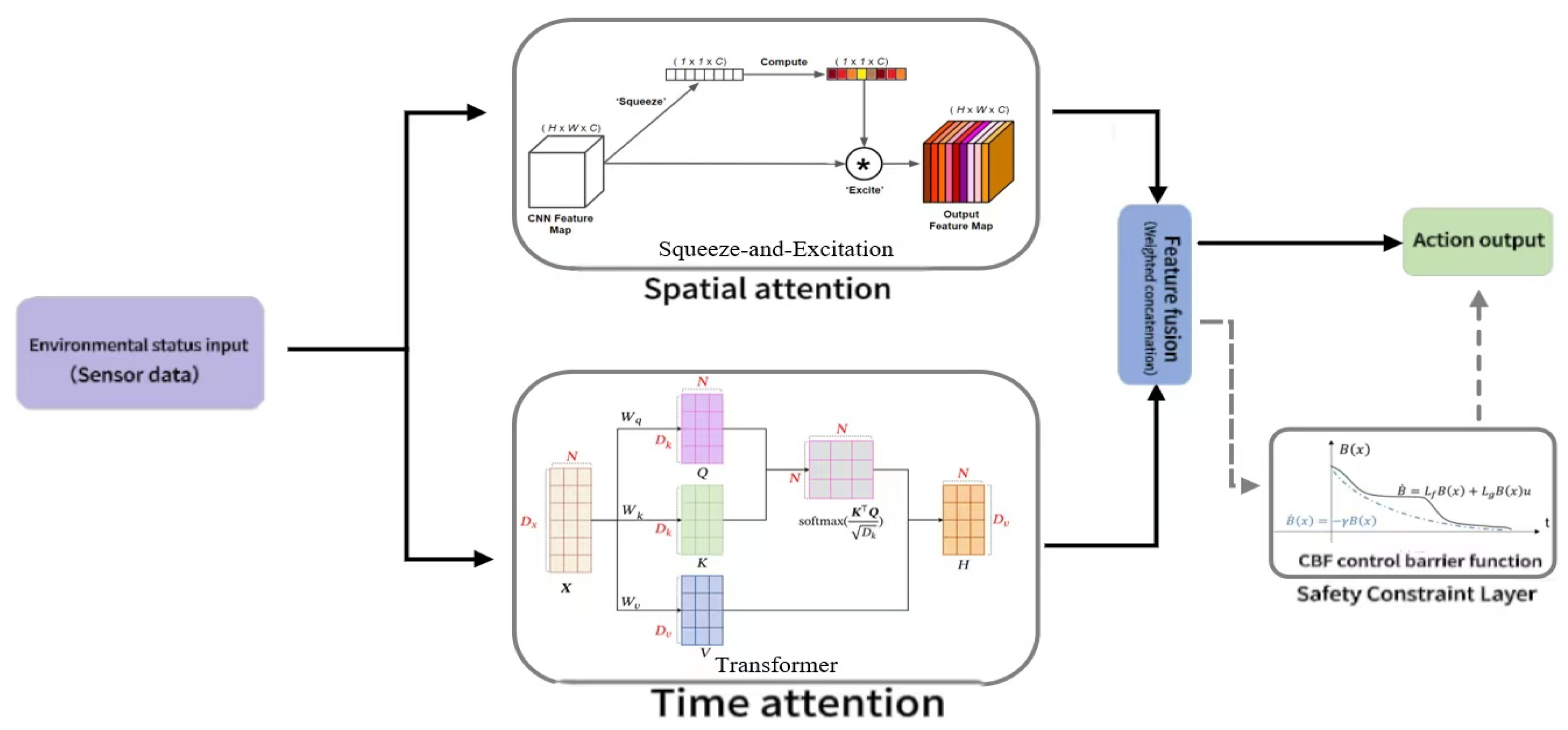
- Multi-Scale Attention Policy Network
- (3)
- Formal Safety Constraint Layer
4. Design of Dynamic Aggregation Cooperative Obstacle Avoidance Algorithm
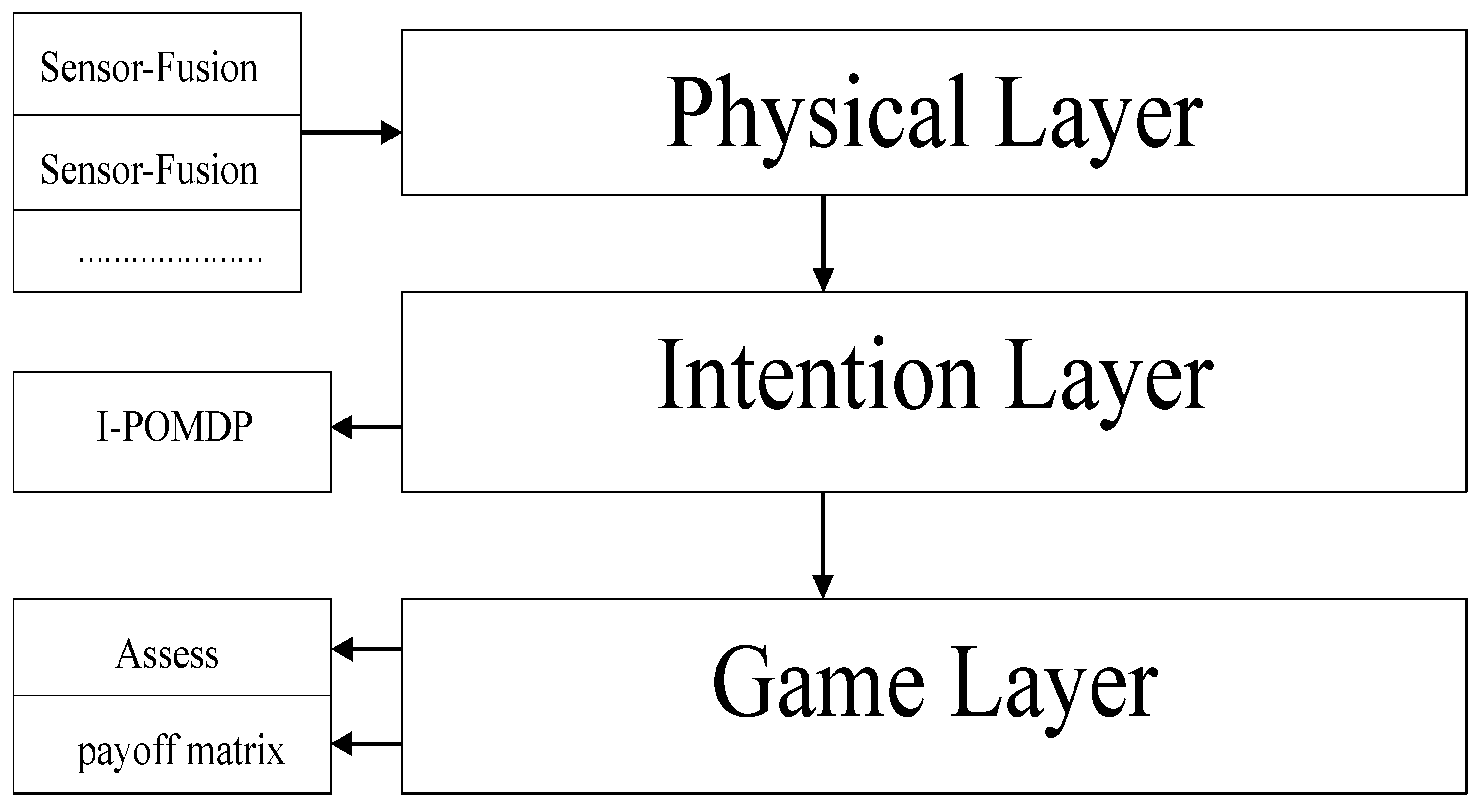
4.1. System Architecture and Mathematical Formulation
4.2. Multi-Modal Perception Fusion Model
- (1)
- Evidence Theory Fusion Mechanism
- (2)
- Spatiotemporal Feature Extraction Network
4.3. Game Theory-Based Threat Assessment Model
- (1)
- Modeling of Incomplete Information Dynamic Game
- (2)
- Mean Field Game Control Law
4.4. Adaptive Formation Control Algorithm
- (1)
- Improved Virtual Force Field Model
- (2)
- Dynamic Aggregation Reconstruction Strategy
4.5. Hybrid Decision Engine Design
- (1)
- AG-DRL Fusion Strategy
- (2)
- Formal Safety Constraint Layer
5. Simulation Verification
5.1. Construction of Simulation Environment
5.2. Design of Comparative Experiments
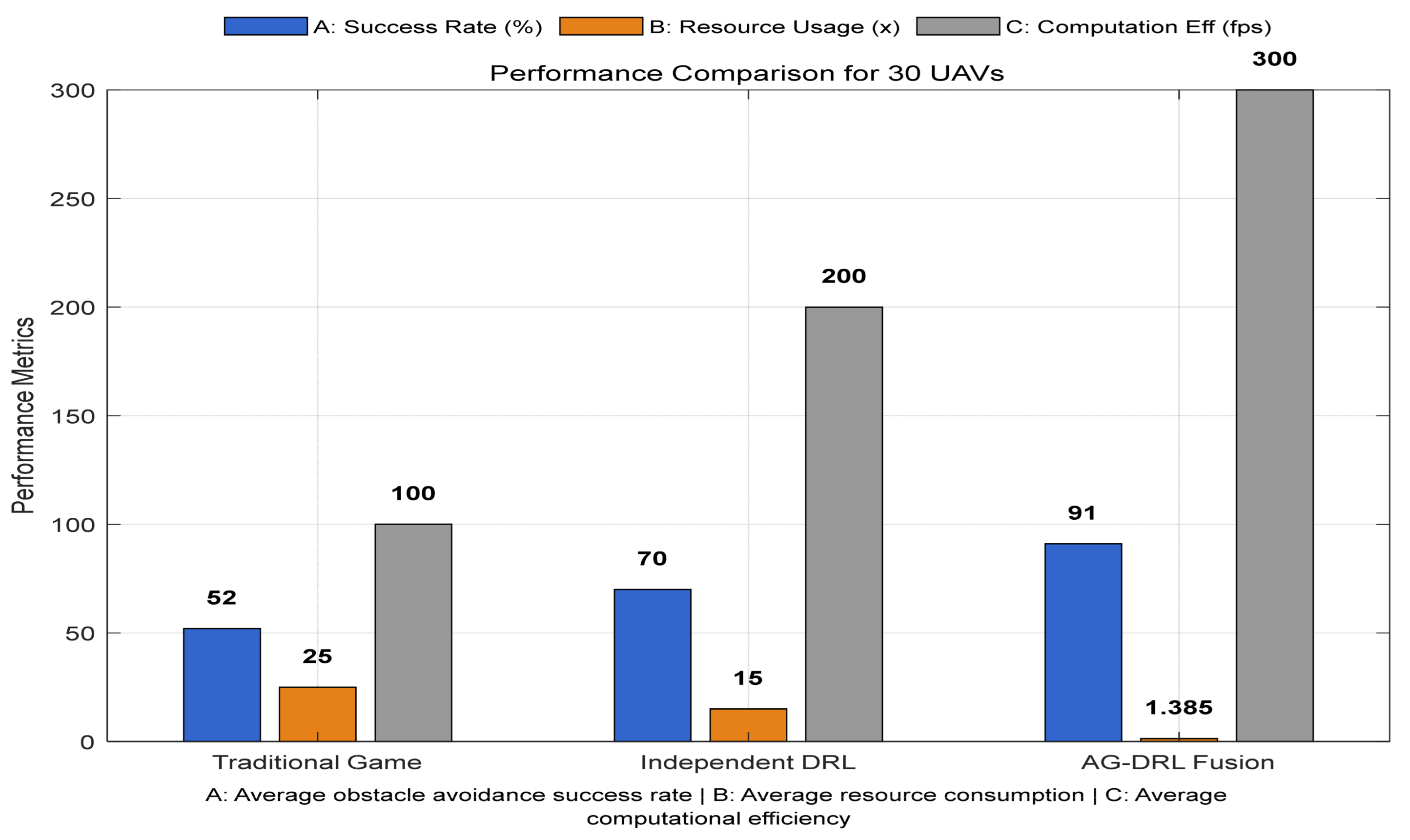
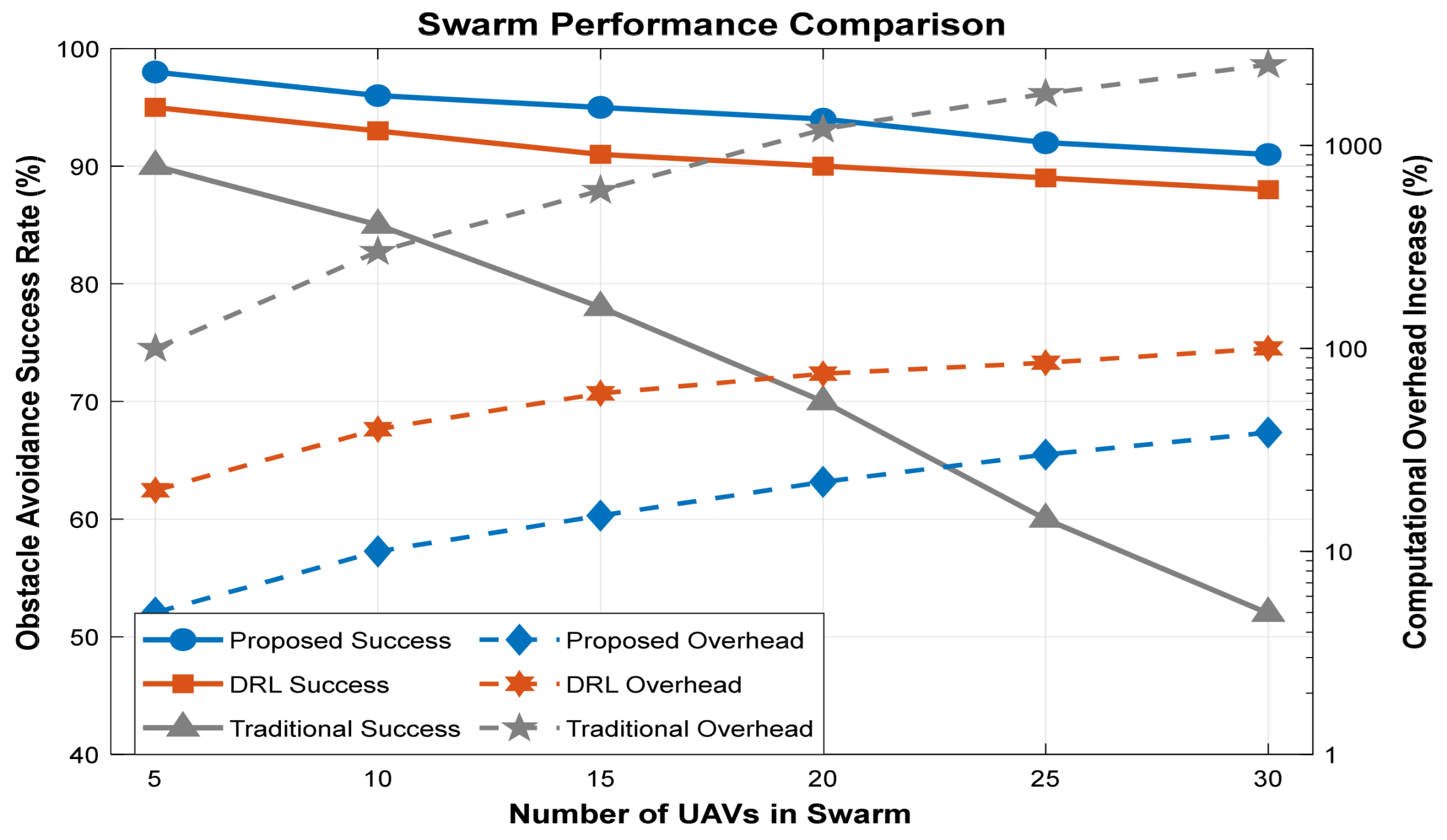
5.3. Empirical Results
- (1)
- Parallel Growth in System Overhead and Success Rate
- (2)
- Explanation of Resource Consumption
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Zhang, J.; Wang, Y. Game Theoretic Approach for MultiUAV Coordination under Communication Constraints. J. Guid. Control. Dyn. 2024, 47, 583–594. [Google Scholar]
- Dhuheir, M.; Baccour, E.; Erbad, A.; Al-Obaidi, S.S.; Hamdi, M. Deep Reinforcement Learning for Trajectory Path Planning and Distributed Inference in Resource-Constrained UAV Swarms. IEEE Internet Things J. 2023, 10, 8185–8201. [Google Scholar] [CrossRef]
- Hutter, F.; Kotthoff, L.; Vanschoren, J. Automated Machine Learning: Methods, Systems, Challenges; Springer: Berlin/Heidelberg, Germany, 2019; p. 219. [Google Scholar]
- Wen, L.; Zhen, Z.; Ding, J.; Tao, C.; Liu, S. Distributed self-organizing fencing strategy with UAV swarm under incomplete information. Adv. Eng. Inform. 2025, 68 Pt A, 103587. [Google Scholar] [CrossRef]
- Medani, K.; Gherbi, C.; Mabed, H.; Aliouat, Z. Energy-efficient Q-learning-based path planning for UAV-Aided data collection in agricultural WSNs. Internet Things 2025, 33, 101698. [Google Scholar] [CrossRef]
- Cao, Z.; Chen, G. Enhanced deep reinforcement learning for integrated navigation in multi-UAV systems. Chin. J. Aeronaut. 2025, 38, 103497. [Google Scholar] [CrossRef]
- Liu, X.; Yi, W.; Chen, P.; Tan, Y. Flight, path planning of UAV-driven refinement inspection for construction sites based on 3D reconstruction. Autom. Constr. 2025, 177, 106360. [Google Scholar] [CrossRef]
- Amodu, O.A.; Althumali, H.; Hanapi, Z.M.; Jarray, C.; Mahmood, R.A.R.; Adam, M.S.; Bukar, U.A.; Abdullah, N.F.; Luong, N.C. A Comprehensive Survey of Deep Reinforcement Learning in UAV-Assisted IoT Data Collection. Veh. Commun. 2025, 55, 100949. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, L.; Lin, Y.; Cai, A.; Fan, J.; Liu, C. Dynamic offloading strategy in SAGIN-based emergency VEC: A multi-UAV clustering and collaborative computing approach. Veh. Commun. 2025, 55, 100952. [Google Scholar] [CrossRef]
- Basavegowda, D.H.; Schleip, I.; Bellingrath-Kimura, S.D.; Weltzien, C. UAV-assisted deep learning to support results-based agri-environmental schemes: Facilitating Eco-Scheme 5 implementation in Germany. Biol. Conserv. 2025, 309, 111323. [Google Scholar] [CrossRef]
- Chen, H.; Liu, J.; Wang, Y.; Zhu, J.; Feng, D.; Xie, Y. Teaching in adverse scenes: A statistically feedback-driven threshold and mask adjustment teacher-student framework for object detection in UAV images under adverse scenes. ISPRS J. Photogramm. Remote Sens. 2025, 227, 332–348. [Google Scholar] [CrossRef]
- Lyu, C.; Lin, S.; Lynch, A.; Zou, Y.; Liarokapis, M. UAV-based deep learning applications for automated inspection of civil infrastructure. Autom. Constr. 2025, 177, 106285. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, X.; Miao, Z. Cooperative trajectory tracking control of USV-UAV with non-singular sliding mode surface and RBF neural network. Ocean Eng. 2025, 337, 121872. [Google Scholar] [CrossRef]
- Jia, R.; Li, H.; Sun, P.; Zheng, Z.; Li, M. UAV trajectory optimization for visual coverage in mobile networks using matrix-based differential evolution. Knowl.-Based Syst. 2025, 324, 113797. [Google Scholar] [CrossRef]
- Liu, H.; Long, X.; Li, Y.; Yan, J.; Li, M.; Chen, C.; Gu, F.; Pu, H.; Luo, J. Adaptive multi-UAV cooperative path planning based on novel rotation artificial potential fields. Knowl.-Based Syst. 2025, 317, 113429. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, N.; Yan, G.; Li, W. The development of distributed cooperative localization algorithms for Multi-UAV systems in the past decade. Measurement 2025, 256 Pt A, 118040. [Google Scholar] [CrossRef]
- Pan, Z.; Wang, K.; Liu, Y.; Guan, X.; Chen, C.; Liu, J.; Wang, Z.; Li, F.; Ma, G.; Yao, Y.; et al. Deep learning-enhanced safety system for real-time in-situ blade damage monitoring in UAV using triboelectric sensor. Nano Energy 2025, 140, 111063. [Google Scholar] [CrossRef]
- Ngo, Q.H.; Luu, T.H.; Nguyen, P.V.; El Makrini, I.; Vanderborght, B.; Cao, H.-L. InterDuPa-UAV: A UAV-based dataset for the classification of intercropped durian and papaya trees. Data Brief 2025, 61, 111843. [Google Scholar] [CrossRef]
- Liang, J.; He, Q. Joint optimization of VNF deployment and UAV trajectory planning in Multi-UAV-enabled mobile edge networks. Comput. Netw. 2025, 262, 111163. [Google Scholar] [CrossRef]
- Lu, Z.; Zhai, L.; Zhou, W.; Xue, K.; Gao, X. Beamforming design and trajectory optimization for integrated sensing and communication supported by multiple UAVs based on DRL. Veh. Commun. 2025, 54, 100932. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Hu, M.; Zhang, W. Resilient multi-UAV path planning for effective and reliable information collection. Phys. Commun. 2025, 71, 102685. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Yang, G.; Mo, Y.; Lv, C.; Zhang, Y.; Li, J.; Wei, S. A dual-layer task planning algorithm based on UAVs-human cooperation for search and rescue. Appl. Soft Comput. 2025, 181, 113488. [Google Scholar] [CrossRef]
- Zarychta, R.; Zarychta, A. Application of geostatistical approach in generating DEM for relief studies using UAV in forest areas. Geomorphology 2025, 487, 109916. [Google Scholar] [CrossRef]
- Ju, T.; Li, L.; Liu, S.; Zhang, Y. A multi-UAV assisted task offloading and path optimization for mobile edge computing via multi-agent deep reinforcement learning. J. Netw. Comput. Appl. 2024, 229, 103919. [Google Scholar] [CrossRef]
- Aloqaily, M.; Bouachir, O.; Al Ridhawi, I. UAV-supported communication: Current and prospective solutions. Veh. Commun. 2025, 54, 100923. [Google Scholar] [CrossRef]
- Grindley, B.; Phillips, K.; Parnell, K.J.; Cherrett, T.; Scanlan, J.; Plant, K.L. Avoiding automation surprise: Identifying requirements to support pilot intervention in automated Uncrewed Aerial Vehicle (UAV) flight. Appl. Ergon. 2025, 127, 104516. [Google Scholar] [CrossRef]
- Kutpanova, Z.; Kadhim, M.; Zheng, X.; Zhakiyev, N. Multi-UAV path planning for multiple emergency payloads delivery in natural disaster scenarios. J. Electron. Sci. Technol. 2025, 23, 100303. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhou, Y.; She, J.; Yu, A. Collaborative coverage path planning for UAV swarm for multi-region post-disaster assessment. Veh. Commun. 2025, 53, 100915. [Google Scholar] [CrossRef]
- Yue, S.; Zheng, D.; Wei, M.; Chu, Z.; Lin, D. Behavior-based cooperative control method for fixed-wing UAV swarm through a virtual tube considering safety constraints. Chin. J. Aeronaut. 2025, 38, 103445. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Gu, Y.; He, Q.; Zhou, P.; Zhang, A. UAV fault diagnosis based on collaborative sharing of generic and task-oriented features. Expert Syst. Appl. 2025, 296, 128940. [Google Scholar] [CrossRef]
- Darchini-Tabrizi, M.; Pakdaman-Donyavi, A.; Entezari-Maleki, R.; Sousa, L. Performance enhancement of UAV-enabled MEC systems through intelligent task offloading and resource allocation. Comput. Netw. 2025, 264, 111280. [Google Scholar] [CrossRef]
- Xiao, J.; Guo, H.; Zhou, J.; Zhao, T.; Yu, Q.; Chen, Y.; Wang, Z. Tiny object detection with context enhancement and feature purification. Expert Syst. Appl. 2023, 211, 118665. [Google Scholar] [CrossRef]
- Guo, Y.; Zhou, J.; Dong, Q.; Li, B.; Xiao, J.; Li, Z. Refined high definition map model for roadside rest area. Transp. Res. Part A Policy Pract. 2025, 195, 104463. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, G.; Guo, L.; Liao, H.; Wu, F. Fusing Adaptive Game Theory and Deep Reinforcement Learning for Multi-UAV Swarm Navigation. Drones 2025, 9, 652. https://doi.org/10.3390/drones9090652
Yao G, Guo L, Liao H, Wu F. Fusing Adaptive Game Theory and Deep Reinforcement Learning for Multi-UAV Swarm Navigation. Drones. 2025; 9(9):652. https://doi.org/10.3390/drones9090652
Chicago/Turabian StyleYao, Guangyi, Lejiang Guo, Haibin Liao, and Fan Wu. 2025. "Fusing Adaptive Game Theory and Deep Reinforcement Learning for Multi-UAV Swarm Navigation" Drones 9, no. 9: 652. https://doi.org/10.3390/drones9090652
APA StyleYao, G., Guo, L., Liao, H., & Wu, F. (2025). Fusing Adaptive Game Theory and Deep Reinforcement Learning for Multi-UAV Swarm Navigation. Drones, 9(9), 652. https://doi.org/10.3390/drones9090652







